How crystal structure and microstructure can influence the sodium-ion conductivity in halide perovskites

Abstract

The perovskite crystal structure with nominal composition ABX₃ offers a very flexible framework for sodium halide ionic conductors, an aspect not well defined in the current literature. This structure can accommodate a variety of sizes and oxidation states of cations, as well as different contents of cation vacancies. Different studies have shown that substitution of trivalent by tetravalent cations in the structure of some halides ‘double’ perovskites significantly improve their ionic conductivity, which can be explained by the creation of cation vacancies in the B-sites. The understanding of the structure opens the possibility to create cation vacancies, not only in the B-sites but also in the A-sites, by the replacement of the trivalent cations by pentavalent cations and to study their impact on the ionic transport of sodium halide materials. In this work, we show a study of the Na_3−2xIn(III)_1−xTa(V)_xCl₆ system with respect to their structure, microstructure, and ionic transport properties, demonstrating the coupling among these three aspects. This work aims to provide a detailed description of the current halide ionic conductors in the framework of the perovskite structure. By fully describing sodium ion conducting halides as perovskites, we hope to offer a reliable guidance to design improved solid-electrolyte materials.

---

Introduction

Solid-state batteries have emerged in the last few years as a potential candidate to complement conventional Li-ion battery technologies to meet the increasing demand for high energy density and safe storage system.^1,2 One of the bottlenecks in the field is the search for highly conductive, electrochemically stable ion conductors as separator materials or conductive electrolytes in the electrode composites.^3,4 Despite nearly matching the ionic conductivities of the liquid counterpart, the most promising solid electrolytes still lack chemical stability due to detrimental decomposition reactions at the interfaces.^5,6

Another challenge with the current Li-ion technology is the scarcity of Li metal, which urges to search for more convenient alternatives.⁷ Sodium containing solid electrolytes are emerging as promising substitutes to the lithium counterparts in the solid-state battery technology.⁸ Na₃PnX₄ (Pn = P, Sb, W; X = S, Se),^9–13 Na₁₁Sn₂PS₁₂,^14–18 NASICON-type Na_xM₂(PO₄)_3−x(SiO₄)_x^19–21 (M = Ti, Zr) compounds, are among the most encouraging families for this purpose. Nevertheless, besides the high conductivity, compatibility with the electrodes and a large voltage stability window are still required, hindering the implementation of Na⁺ containing chalcogenides in a near future.^22–26 Contrarily, NASICON oxides generally show a high ionic conductivity, good compatibility and high electrochemical stability. However, the costly production and tough processability are the major drawbacks for the current technologies, mainly, due to their large grain boundary resistances, unfavourable mechanical properties and harsher synthesis conditions.²⁷

Sodium containing halides could overcome those problematics since they could combine (1) high ionic conductivities up to ∼1–10 mS cm⁻¹ comparable to the chalcogenides and (2) an oxidative voltage for chlorides stability window up to 4 V if we look at Li-containing halides such as Li₃InCl₆, Li₃YCl₆ or Li₃ScCl₆. Those materials can be used as suitable catholytes in the current lithium-based solid-state batteries.^28,29

Although the sodium rare earth-containing ternary halides have long been known,^30–32 their ionic transport has not thoroughly been investigated so far. Recently, the Na-containing ternary halides Na₃MX₆ (M³⁺ = Sc³⁺, In³⁺, Y³⁺, Yb³⁺, Er³⁺; X⁻ = Cl⁻, Br⁻, I⁻) and derivatives have been theoretically predicted^33,34 and also, some of them, mainly chloride containing materials, have been experimentally reported as ionic conductors.^35–39 Among the different potential structures, Na₃MCl₆ (M³⁺ = In³⁺, Y³⁺ or Er³⁺) can crystallize in a perovskite-related structure. Typically, these materials are described in terms of their individual space group with the different Na⁺ crystallographic sites and a focus on the diffusion pathways, however, the aspect of being perovskite related is not sufficiently discussed in the literature.⁴⁰ Only some oxides crystallizing in the argyrodite structure and oxyhalides ionic conductors have been described, to the best of our knowledge, in terms of the anti-perovskite crystal structure.^41,42

The perovskite structure with nominal composition ABX₃ consists of corner sharing octahedra BX₆ connected along the three directions, which leave cubo-octahedral AX₁₂ sites occupied by the A-cations. Thus, a simplified model to describe the more complex Na₃MCl₆ can be regarded as a double perovskite (i.e. Na₂(NaM)Cl₆) with rock-salt ordering between the NaCl₆ and MCl₆ octahedra, which are corner sharing along the three directions and leave cubo-octahedral sites occupied by the remaining two Na⁺ cations (i.e.: NaCl₁₂). The ideal non-distorted crystal structure is depicted in Fig. 1.

Fig. 1 Ideal non-distorted Na₃MCl₆ perovskite crystal structure (hypothetical). (a) Full structure. (b) The building units of Na_BCl₆ and MCl₆ octahedra. (c) The building units of Na_ACl₁₂.

However, the ideal non-distorted perovskite structure cannot accommodate the Na⁺ and M³⁺ cations due to their different sizes and is more a hypothetical structure with the wrong assumption of being a rigid structure. Yet, due to the outstanding structural flexibility of the perovskite structure it can accommodate the different cations. Tilting of the chloride octahedral network is the distortion taking place for optimizing the matching between the Na–Cl and M–Cl bond distances, which reduces symmetry of the cell. In addition to its structural flexibility, the interplay between compositional diversity and rich defect-chemistry makes the perovskite structure a very interesting playground to tailor the structure to finely tune the transport properties of these solid electrolytes. Partial or total substitution of M³⁺ cations with different oxidation states and sizes allows to create Na⁺ cation vacancies that can be accommodated in the perovskite structure. Thus, partial substitution of trivalent by tetravalent cations can create cation vacancies by removing Na⁺ cations from only one type of sites, the B-sites, without any change in the symmetry of the unit cell. For instance, Zr⁴⁺ substitution in Na_3−xIn_1−xZr_xCl₆ shows large increases in the ionic conductivity, about two orders of magnitude higher with respect to the parent compound Na₃InCl₆.^36,38 Interestingly, different synthetic methods lead to a change in the trend of the ionic conductivity as function of Zr⁴⁺ content. Here, solid state synthesis results in a parabolic evolution of the ionic conductivity, with a maximum of 6.5 × 10⁻⁶ S cm⁻¹ for Na_2.4Zr_0.6In_0.4Cl₆ and characteristic of a Na⁺ vacancy-driven diffusion process.³⁶ However, mechanochemical synthesis leads to a continuously growing ionic conductivity as a function of Zr⁴⁺ content, which can be ascribed to a reduction in the crystallite size of the material.³⁸ These findings also highlight the importance of the microstructure in this class of materials.

Further substitution, replacing the trivalent cation metal by a pentavalent cation with the corresponding removal of Na⁺ cations from both, B- and also A-sites and its impact over the transport properties has recently been started to investigate. Recent studies show an enhanced ionic conductivity for NaTaCl₆ (ref. 40, 43 and 44) in comparison with the previous reported Na_3−xM_1−xZr_xCl₆ (M³⁺ = In³⁺, Y³⁺ or Er³⁺), but the structure–property relationship has not been well established yet.

Inspired by the high ionic conductivity of the halide solid electrolytes together with their perovskite structural origin, we present a study of the Na_3−2xIn(III)_1−xTa(V)_xCl₆ system, crystallizing in a perovskite-related structure. To analyse the relationship between the crystal structure, microstructure and ionic transport properties, all the materials were investigated by means of X-ray diffraction, pair distribution function analyses, solid-state nuclear magnetic resonance spectroscopy, quasi-elastic neutron scattering, and impedance spectroscopy. This work corroborates that the creation of cation vacancies on the different sites of the perovskite structure has a profound impact over the transport properties of the ionic conducting sodium halides, going hand in hand with slight structural distortions of the perovskite structure and a microstructure evolution of the materials. An elaborate study of this system with full structural description as shown here, we hope to serve as a direction to consider halide electrolytes as perovskite-type structures. By understanding the ion conducting metal halide classes as perovskite materials, we hope to spark further solid electrolyte research with the known toolbox from the field of perovskite materials.

Experimental section

Synthesis

All syntheses were performed under an inert Argon or vacuum atmosphere. For the mechanochemical synthesis, stoichiometric amounts of NaCl (Merck, 99.5%, pre-dried at 200 °C for 48 h under dynamic vacuum), InCl₃ (Merck, 99.99%), and TaCl₅ (Alfa Aesar, 99.99%) were put into 80 mL zirconia ball mill cups. The mass ratio between milling media (ZrO₂, 5 mm diameter) and precursors was 30 : 1. The planetary ball milling was carried out by the Fritsch Pulverisette 7 at 100 rpm and 300 rpm for 10 minutes to initially mix the precursors uniformly. Then ball-milling was performed for 99 cycles in reverse mode, with one cycle consisting of milling at 500 rpm for 15 minutes and rest for 5 minutes to allow for cooling. The ball-milled powders were pelletized using a custom-made manual screw press and transferred into a quartz ampoule, which was pre-dried at 800 °C under a dynamic vacuum for 2 h. For testing the effect of subsequent annealing onto the compounds prepared the two end members were transferred to ampoules. The ampoules were sealed under vacuum and then heated at 200 °C for 12 h and quenched in air. After annealing, the pellets were hand-ground into powders for further characterization (Fig. S1†).

X-ray diffraction

All samples were sealed in 0.5 mm-diameter glass capillaries for X-ray diffraction measurements because of their air sensitivity. X-ray diffraction measurements on both mechanochemically prepared and subsequently annealed samples were performed with a STOE STADI P diffractometer (Mo K_α1 radiation, λ = 0.7093 Å; curved Ge(111) monochromator, Mythen 2K detector) in Debye–Scherrer scan mode at room temperature. Data collection was carried out for every sample in 0.015° steps.

Symmetry analysis and Rietveld refinement

Symmetry analysis of the crystal structures was performed with the assistance of the ISODISTORT software package.^45,46 The Rietveld refinements against X-ray diffraction data were performed with the TOPAS Academic software package.^47,48 Rietveld refinements include (1) background of the Chebychev polynomial function, (2) scale factor, (3) peak shape parameters from the modified Thompson–Cox–Hastings pseudo-Voigt function, (4) lattice parameters, (5) site fractional coordinates and occupancy factors, and the (6) isotropic displacement parameters. At last, all parameters were allowed to refine simultaneously to ensure stability of the parameters of the best possible refinement. The quality of the refinements was estimated by the indicators R_wp and goodness-of-fit (GoF).⁴⁹

To get deeper insights about the crystallite size, peak shape was calculated from the integral breadth based LVol reported by Balzar et al.⁵⁰ and integrated in the TOPAS software. To perform that analysis, a diffraction pattern of LaB₆ was recorded under identical conditions of the materials in order to get the peak shape assuming only instrumental factors.

Pair distribution function analysis

X-ray diffraction data for conversion to pair distribution functions were measured with a STOE STADI P diffractometer (Ag K_α1 radiation, λ = 0.5594 Å; curved Ge(111) monochromator, Mythen 4K detector) in Debye–Scherrer scan mode at room temperature. Data collection was carried out for every sample in 0.015° steps. Then the collected X-ray diffraction data was converted to a pair distribution function by Fourier-transforming the obtained normalized structure function S(Q) using PDFgetX3.⁵¹Q-range cut-off of 13 Å⁻¹ was chosen because longer Q-range data was not able to be properly analysed due to the limited crystallinity of the ball milled samples. The fits were attempted using TOPAS Academic software package.⁴⁸ The instrumental resolution parameters qdamp (0.011) and qbroad (0.010) are determined on a NIST660c LaB₆ standard sample.⁵²

Nuclear magnetic resonance spectroscopy

Solid-state magic angle spinning (MAS) nuclear magnetic resonance spectra of ²³Na (ω_L = 132.36 MHz) were recorded at a Bruker DSX 500 spectrometer equipped with a 11.7 T wide-bore magnet, using a 4 mm Bruker MAS probe. A radiofrequency pulse of 4.0 μs at 120 W power was used as π/2-pulse for single-pulse MAS experiments at a rotation frequency of 12.5 kHz. Magic angle calibration was done using spinning sidebands of solid NaNO₃ and ²³Na chemical shift scale was referenced against freshly prepared 1 M NaCl solution at 0 ppm. The deconvolution of the ²³Na MAS spectra was performed with ssNake (v1.4)⁵³ Gaussian/Lorenzian peaks were used for the resonances from NaCl impurity and Na⁺ in B-site (Na_B), whereas, for Na⁺ in A-site (Na_A), the quadrupolar coupling model (with quadrupolar coupling constant C_Q and an asymmetry parameter η_Q) for spin-3/2 nuclei under finite MAS frequency was employed using the in-built ‘Quadrupole’ fitting model. Additionally, for Na₃InCl₆, ²³Na MAS experiments were conducted at four different rotation frequencies (ν_rot = 10, 15, 20 and 25 kHz) at the Bruker DSX 500 spectrometer using a 2.5 mm Bruker MAS probe (Fig. S2†).

Variable temperature static saturation recovery experiments for ²³Na were implemented on the Bruker Avance III 300 spectrometer connected to a wide-bore magnet of 7.05 T nominal magnetic field. Radio-frequency pulse lengths of 1.85–2.5 μs at 160 W was used as π/2-pulse for Na₃InCl₆ and NaTaCl₆, respectively. Recovery delay length was varied from t₁ = 10 μs to t₂₃ = 215.44 s with three steps increments per decade. All the free-induction decays were Fourier transformed to obtain frequency-domain signals which were integrated in TopSpin software and corresponding signal intensity curves were fitted with exponential type saturation function with a stretching exponent. ²³Na static saturation recovery data were recorded in the temperature range of 200 to 420 K with 20 K interval between successive measurements and 20 min of waiting period for temperature stabilization at each temperature. A combination of N₂ gas flow and electrical heating was used to regulate the temperature. In the sub-room temperature (T < 300 K) range, cooled N₂ gas flow from an Air Jet XR compressor from SP Scientific (FTS Systems) regulated the temperature whereas an uncooled stream of N₂ gas was utilized for temperature stabilization in T > 300 K range. Temperature calibration was done using temperature-dependent ¹H NMR signal-shifting of methanol (200–290 K) and ethylene glycol (320–420 K).⁵⁴ All samples were in powder form and packed under Ar atmosphere into cylindrical type 4 mm and 2.5 mm zirconia rotors with Teflon spacer to reduce air/moisture exposure during experiment.

Scanning electron microscopy-energy dispersive X-ray spectroscopy

Samples were prepared by sputter deposition with gold to enhance their electronic conductivity. The morphology and composition of the prepared samples were characterized with scanning electron microscopy (Merlin, Carl Zeiss Microscopy GmbH) and energy-dispersive spectroscopy (XMax, Oxford Instruments) respectively. The applied electron high tension (EHT) voltage was 20.0 kV.

Electrochemical impedance spectroscopy

About 150 mg of each sample was initially pelletized by a custom-made manual screw press and then isostatically pressed under 410 MPa for 40 min. Subsequently, the pellets were coated with thin gold electrodes of ∼80 nm thickness with sputter deposition and enclosed in pouch cells. The impedances were measured with a SP-300 impedance analyzer (Biologic) under an amplitude of 10 mV and frequencies from 7 MHz to 100 mHz in a temperature range of −40 °C to 60 °C. Some spectra at low temperatures are omitted from evaluation as the evaluated samples were too resistive in the monitored frequency range at those temperatures. The spectra were analyzed by RelaxIS 3 (rhd instruments). To get reliable fitting results, the ultrahigh or ultralow frequency range was discarded to reach < 2% relative residuals in the Kramers–Kronig test included in the software package over the evaluated frequency range.

Quasi-elastic neutron scattering (QENS)

Neutron scattering data were collected on the backscattering spectrometer IN16b at the Institute Laue-Langevin (ILL) in Grenoble, using an incident neutron wavelength of 6.271 Å and instrument resolution of ≈0.8 μeV (FWHM). This gives access to dynamics on a nanosecond timescale. The energy transfer window used for all QENS measurements was ± 30 μeV. Elastic (E = 0 μeV) and inelastic (E = 3 μeV) scattered intensities were measured, so called elastic and inelastic fixed window scans (EFWS, IFWS). Samples of (5–6 g) were filled under inert conditions into aluminium (1 mm-spaced double wall cylinder) and sealed mechanically with lead as a gasket. The sample holder was mounted in the spectrometer where a standard orange cryofurnace was used to measure at 150 K, 300 K, 350 K and 400 K for 4 h, respectively. Data reduction was carried out using the Mantid software package.

Bond valence sum analyses

The bond valence site energy (BVSE) landscapes of the materials were calculated by the softBV-GUI tool.^55,56 The analyses were performed for Na⁺ by utilizing the automatically calculated screening factor and a resolution of 0.1 Å.

Results & discussion

To investigate the effect of introduction of vacancies on the structure and transport in the perovskite related Na₃InCl₆, the series of Na_3−2xIn_1−xTa_xCl₆ is explored here. At first, the perovskite relation of the endmembers Na₃InCl₆ and NaTaCl₆ will be established, which will be followed by discussion on the changes in their solid solutions, Na_3−2xIn_1−xTa_xCl₆.

Crystal structure of Na₃InCl₆

To obtain a detailed crystal structure analysis of the known Na₃InCl₆ with the perovskite structure, a combination of X-ray diffraction and solid-state nuclear magnetic resonance is used. The monoclinic structure of Na₃InCl₆ at room temperature (Fig. 2 and S1†) can be confirmed by indexing the unit cell (a = 6.7401(2) Å, b = 7.1626(2) Å, c = 9.9394(3) Å, β = 90.539(2)°). The observed condition reflections: h0l:h + l = 2n;h00:h = 2n; 0k0: k = 2n; 00l:l = 2n are consistent with the space group P2₁/n. Full details of the structural refinement are shown in Table S1,† with selected bond lengths in Table S3† and the data shown in Fig. S3.† Pair distribution function analysis of Na₃InCl₆ confirms that the average structure model is also consistently describing the local short-range ordering (Fig. S5†). A ²³Na MAS nuclear magnetic resonance spectrum of Na₃InCl₆ (Fig. 2) shows two different signals for Na⁺ ions corresponding to the two different Na⁺ sites. Both the nuclear magnetic resonance and X-ray diffraction data also show the presence of a small amount (<3%wt) of NaCl in the sample. However, attempts to refine the structure with off-stoichiometry amounts of Na⁺ and Cl⁻ were unsuccessful.

Fig. 2 Structural characterization of Na₃InCl₆. (a) Structural analysis of Na₃M³⁺Cl₆; crystal structure constructed from the ideal cubic perovskite Na(Na_0.5M_0.5)Cl₃ by adding a rock-salt cation ordering between Na⁺ and In³⁺ in the B-sites, and a combination of an out-of-phase tilting along the a- and b-axis and an in-phase tilting along the c-axis. The Na_A-centred polyhedral are shown in the bottom of crystal structure schemes. Na_A is 12-fold coordinated by Cl⁻ in Pm3̄m and Fm3̄m phases while prismatically 6-fold coordinated by Cl⁻ in the P2₁/n phase. (b) X-ray diffraction pattern of Na₃InCl₆. (c) Room temperature ²³Na MAS NMR spectra collected from Na₃InCl₆ with three major components: Na⁺ in octahedral (Na_B) and prismatic (Na_A) coordination along with Na⁺ in the rock-salt NaCl structure. Note that the Na_A component is highly distorted giving rise to the quadrupolar line shape (C_Q = 1.05 MHz, η_Q = 0.98). The asterisk (*) denoted the contribution from the “zeroth order” spinning sideband from the underlying satellite transitions (±3/2 ↔ ±1/2) of the Na_A resonance, as confirmed using different rotation frequencies (Fig. S2†) The resonance indicated by solid triangle might be due to some amorphous impurity which could not be identified.

Na₃InCl₆ was synthesized here by ball milling without any further treatment crystallizing in a perovskite related structure with the monoclinic P2₁/n shows as has been shown before.^37,39 However, by annealing at 200 °C, Na₃InCl₆ changes this structure to crystallize in an ilmenite-related structure with P3̄1c space group,³⁶ See Fig. S1† for a comparison of the diffraction patterns of the polymorphs. Both polymorphs show a quite different structure without any group–subgroup relationship, the transformation from one to the other would require a lattice reconstruction. However, the small temperature difference in the synthesis of both polymorphs may indicate that the P2₁/n perovskite polymorph would be slightly less favourable than the P3̄1c ilmenite one from a thermodynamic point of view. The reason behind the instability associated with the perovskite polymorph may be attributed to the small size of Na⁺ cations to be accommodated within the A-sites, which leads to an extremely low Goldschmidt tolerance factor (t = 0.73).⁵⁷ This factor is used as an indicator for the stability and distortion of the perovskite crystal structures according to the cation and anion ionic radii. Thus, the particular conditions of ball milling synthesis leads to the formation of the perovskite-like structure. This synthetic approach may just stabilize a kinetically driven phase with a presumably lower energy activation barrier for its formation.⁵⁸ Indeed, the ilmenite-perovskite phase transition under subtle conditions in this material shows certain similarities with some oxides, such as NaSbO₃, which crystallizes in an ilmenite structure at ambient pressure but treatments under high temperature and pressure lead to the perovskite structure.⁵⁹

The perovskite-like crystal structure of Na₃InCl₆ can be constructed according to the scheme in Fig. 2. Starting from the ‘ideal’ cubic aristotype with lattice parameters a_p × a_p × a_p (a_p denotes the cell parameter of the cubic perovskite), space group Pm3̄m and formula ABX₃, Na₃InCl₆ can be rewritten as Na(Na_0.5In_0.5)Cl₃ with In³⁺ and Na⁺ cations in the B-sites, and the remaining Na⁺ cations in the A-sites. Due to the different size and oxidation state of In³⁺ and Na⁺ cations, they order in a rock-salt manner within the B-sites to minimize the electrostatic repulsion and the size mismatching. This leads to an expanded 2a_p × 2a_p × 2a_p unit cell and the space group Fm3̄m. The formula can be rewritten in terms of a A₂BB′X₆ ‘double’ perovskite as Na₂(NaIn)Cl₆ or Na₃InCl₆. The Na⁺ cations are too small to occupy the 12-fold coordinated A-sites and the size mismatch induces a cooperative tilting distortion to the network of apex-linked BCl₆ (B = In and Na) octahedra according to the a⁻a⁻c⁺ Glazer notation.⁶⁰ The Glazer notation is typically used to identify the cooperative octahedral tilting in the perovskite structure. In this notation, the sequence of symbols corresponds to the crystallographic axes and the type of tilting. For instance, in the case of a⁻a⁻c⁺ the first symbol a⁻ refers to an out-of-phase tilt along the x-axis and the last symbol c⁺ to an in-plane tilting along the z-axis. The distortion allows to accommodate the ‘small’ Na⁺ cations in the off-centred 6-coordination number prism-like sites within the A sites, which leads to the final 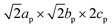unit cell with space group P2₁/n. A more detailed image from the final crystal structure is shown in Fig. 4. Thus, Na₃InCl₆ ‘double’ perovskite structure consists of octahedrally coordinated In³⁺ and one Na⁺ ordered within the B-sites in a rock-salt manner with the octahedra tilted according to the a^–a^–c⁺ tilting system. The tilt system shows that one can now observe an in-phase tilting of the octahedra along the a and b-axes and an out-of-phase tilting along the c-axis. The two remaining Na⁺ cations are occupying the off-centred 6-coordination number prism-like sites within the A sites. This site is highly distorted giving rise to the quadrupolar line shape with a C_Q = 1.05 MHz and a high asymmetry parameter η_Q (=0.98) in ²³Na MAS NMR, which is confirmed by the different Na–Cl bond distances within the prism extracted from the Rietveld refinement ranging from 3.205(7) Å to 2.797(7) Å (Table S3†). The trend in chemical shift for different ²³Na resonances do seem to reveal a gradual upfield shift (towards more negative ppm values) going from higher symmetry (e.g. Na-site in NaCl and octahedral Na_B sites of Na₃InCl₆) to lower symmetry (prismatic Na_A in Na₃InCl₆ followed by NaTaCl₆, Fig. 3c). A similar trend was also observed for Na₂ZrCl₆ and Na–Y–Zr–Cl systems where the ²³Na chemical shifts follow a gradual upfield shift from NaCl to octahedral to prismatic Na-sites^61,62 In addition, CASTEP calculations for Na_2.25Y_0.25Zr_0.75Cl₆ by Sebti et al. confirmed this experimentally observed trend, i.e., δ(²³Na) ≥ −5 ppm for octahedral Na-sites and a range of −5 to −17.5 ppm for prismatic Na-sites.⁶¹

Fig. 3 Structural characterization of NaTaCl₆. (a) Structural analysis of NaM⁵⁺Cl₆; crystal structure constructed from the ideal cubic perovskite Na_0.5[V_A]_0.5([V_B]_0.5M_0.5)Cl₃ by adding a rock-salt cation ordering between Ta and [V_B] in the B-sites, and a combination of an out-of-phase tilting along the a- and b-axis, and an in-phase and out-of-phase tilting along the c-axis. Light brown and blue are used to represent half-occupancy in A- and B- sites, respectively, of the ideal cubic perovskite structure. The Na_A-centred polyhedral are shown in the bottom of crystal structure schemes. Na_A is 12-fold coordinated by Cl⁻ in Pm3̄m and P4/mmm phases while prismatically 6-fold coordinated by Cl⁻ in the P2₁/c phase. (b) X-ray diffraction pattern of NaTaCl₆. Blue arrows indicate the reflections associated to the supercell with a doubling along the c-axis with respect to Na₃InCl₆. (c) Room temperature ²³Na MAS NMR spectra collected from NaTaCl₆ with Na in a prismatic coordination. ²³Na MAS NMR of Na₃InCl₆ has been included behind for comparison.

Crystal structure of NaTaCl₆

In contrast to Na₃InCl₆, with fully occupied Na⁺ positions, removing two Na⁺ cations from the structure gives rise to a different perovskite-related structure. NaTaCl₆ at room temperature can also be indexed using a monoclinic unit cell with a doubling along the c-axis with respect to Na₃InCl₆ (a = 6.4565(4) Å, b = 6.8810(5) Å, c = 18.994(1) Å, β = 90.829(5)°) considering the small reflections (indicated by arrows in Fig. 3) associated to a superstructure (Fig. 3). The observed condition reflections: h0l:l = 2n, 0k0:k = 2n, 00l:l = 2n correspond to the space group P2₁/c. Those results are consistent with the initially found NaTaCl₆.⁶³ However, a better description in terms of understanding the transport properties by relating them with the crystal structure is needed. The crystal structure of NaTaCl₆ can also be described in terms of perovskite structure. Full details of the structural refinement are shown in Table S2,† with selected bond lengths in Table S3† and a plot of the Rietveld Refinement shown in Fig. S4.† Pair distribution analysis of NaTaCl₆ confirms the average structure model consistently matches the local structure (Fig. S6†). In this case, ²³Na MAS NMR collected from NaTaCl₆ (Fig. 2) shows only one site for Na⁺ (Na_A), which confirms the Rietveld refinement results. A more symmetric signal is observed confirming a less distorted NaCl₆ prism.

Further annealing of NaTaCl₆ at 200 °C does not involve any significant change in the crystal structure (see Fig. S1†). The P3̄1c polymorph is not forming, and the perovskite-like crystal structure is preserved at that temperature. The interplay of three factors is considered to justify the stability of the perovskite-like structure in NaTaCl₆. (1) Na⁺ cations can be accommodated easier in the A-site due to the smaller size of Ta⁵⁺ (r(In³⁺)_VI: 0.80 pm, r(Ta⁵⁺)_VI: 0.64 pm). The reduction in the ionic radii increases the Goldschmidt tolerance factor up to t = 0.76 – assuming that vacancies have a Na⁺ cation radius – and reduce the average M–Cl distances (see Table S3†), which can provide slightly better stabilization of the perovskite crystal structure. (2) The removal of two Na⁺ cations will create cation vacancies in the crystal structure, which may favour the perovskite-like polymorph over the P3̄1c polymorph. (3) An enhanced stability of Na⁺ cation in the NaCl₆ A-sites in the NaTaCl₆ since the bond valence sum value (see Table S3†) of this site is much closer to unity with respect to Na₃InCl₆.

The crystal structure of NaTaCl₆ and its structural derivation from the ideal cubic perovskites is shown in detail first in Fig. 3. In comparison with Na₃InCl₆, NaTaCl₆ presents two missing Na⁺ cations, which correspond to the extraction of two different types of Na⁺ cations, all Na⁺ at the B-site (similar to the structure of Na₂ZrCl₆ in space group P2₁/n) and half of the Na⁺ at the A-sites. Like the Na₃InCl₆ structure, there is a rock-salt cation ordering but, the ordering is between the Ta⁵⁺ cations and the cation vacancies at B-sites [V_B], in this case. For easier structural reference we now name the vacancies [V_B], corresponding to a Kröger–Vink notation . Besides, a layered ordering between the Na⁺ and the Na⁺ vacancies within the A-sites, namely [V_A] (i.e.: ) takes place as it is shown in Fig. 4. This ordering, which is unstable by itself according to the Pauling bond valence sum, can be explained by the presence of the highly charged d⁰ Ta⁵⁺ cations,⁶⁴ which are able to displace out of the center of their octahedra by means of a second order Jahn–Teller (SOJT) distortion. It is worth mentioning that SOJT is playing a major role to this layered ordering since the NaSbCl₆ compound, where Sb⁵⁺ does not present SOJT, shows Na⁺ arranged in a columnar-like ordering.⁶³ These displacements are always towards the A-site cation layer that contains the vacancies. By moving toward the under bonded anions (those present in the layer containing the A-site vacancies) the bonding instability caused by the layered ordering is relieved. The resulting unit cell combining B- and A-site ordering shows the 2a_p × 2a_p × 2a_p dimensions and P4/mmm space group. NaTaCl₆ can be described as a AA′BB′X₆ (i.e.: Na[V_A]Ta[V_B]Cl₆) ‘double double’ perovskite with simultaneous 1 : 1 cation order at both A and B sites, in a layered and rock-salt manners, respectively, found in the literature in oxide compositions such as second-order Jahn Teller elements-containing NaLaScNbO₆, NaLaMgWO₆, NaLaInNbO₆, NaLaInTaO₆.^65–67 NaTaCl₆ represents the first example of a ‘double double perovskite halide’, and, to the best of our knowledge, the first compound crystallizing in this structural type because of the presence of cation vacancies in both sites.

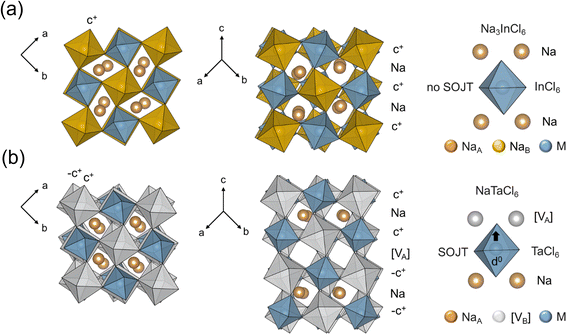Fig. 4 Crystal structure comparison of Na₃InCl₆ and NaTaCl₆. Most representative projections of the crystal structure of (a) Na₃InCl₆ and (b) NaTaCl₆.

This cation ordering is, in turn, accompanied by an in-phase tilting between the octahedral layers comprising the Na layers (as in the case of Na₃InCl₆) but, in NaTaCl₆, along with an out-of-phase octahedral layers comprising the cation vacancy layers [V_A] present in this material, which gives the following sequence of tilting – c⁺-Na – c⁺ – [V_A] – (–c⁺) – Na-(–c⁺) –, as shown in Fig. 4. The resulting unit cell combining B- and A-site ordering with this novel tilting system (a⁻a⁻c⁺/a⁻a⁻ (–c⁺)) doubles the cell along the c-axis and leads to a unit cell and P2₁/c space group. The crystal structure is depicted in Fig. 3 and 4. Thus, deviation from Na₃InCl₆ comes from the interplay between a different (a⁻a⁻c⁺/a⁻a⁻ (–c⁺)) tilting system for BCl₆ (B = Ta and Na) octahedra and the extraction of two Na⁺ cations, the one at the B-site (similar to the structure of Na₂ZrCl₆) and half of the Na⁺ within the A-sites extracted in a layered manner due to the presence of second order Jahn–Teller effect of Ta⁵⁺.

Crystal structure and microstructure evolution of Na_3−2xIn_1−xTa_xCl₆

X-ray diffraction data of the members of Na_3−2xIn_1−xTa_xCl₆ (x = 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875,1) series show that the solid solution is possible within the entire range (Fig. 5) despite the large size and charge mismatch between In³⁺ and Ta⁵⁺ cations. Electron dispersive X-ray Spectroscopy further confirms the homogeneity of Ta and In along the sample in the intermediate members (Fig. S7†). A gradual transition from the ‘double’ perovskite structure of Na₃InCl₆ to the ‘double double’ perovskite structure of NaTaCl₆ is observed. A detailed inspection of the data indicates that extra reflections associated to the NaTaCl₆ ‘double double’ perovskite crystal structure start appearing from x ≥ 0.75 while the rest of the compounds crystallize in the Na₃InCl₆ ‘double’ perovskite crystal structure.

Fig. 5 Crystal structure and microstructure evolution of Na_3−2xIn_1−xTa_xCl₆. (a) Collected X-ray diffraction data of Na_3−2xIn_1−xTa_xCl₆ samples. (b) Lattice parameters a, b and c evolution as a function of Ta content. (c) Unite cell volume and β angle evolution. Note that lattice parameters and volume have been normalized to the unit cell of the ideal cubic perovskite a_p × a_p × a_p (d) Na occupancies in A- and B-sites as a function of Ta content. (e) Pair distribution function data of Na_3−2xIn_1−xTa_xCl₆ (x = 0, 0.5, 1). (f) Crystallite size (left axis) and intensity ratio evolution (right axis) as function of Ta⁵⁺ content extracted from X-ray diffraction and pair distribution functions, respectively.

Rietveld refinements against the X-ray diffraction patterns are performed for all the solid solutions (see Fig. S8–14 and Tables S4–S10†). The refinements confirm the average crystal structure change from the ‘double’ to the ‘double double’ perovskite crystal structure at x = 0.75. Unit cell lattice parameters and volume variations as a function of Ta content do not follow a linear trend (Fig. 5b and c), as it may be expected from a system where there is not only a modification in the In/Ta ratio but the Na⁺ content is also changing. The extraction of Na⁺ cations as a function of Ta⁵⁺ content determined by Rietveld refinement as it is shown in Fig. 5 is taking place in a sequential manner. Three different stages are indicated with different colours in the Fig. 5d. (1) Na⁺ cations are mainly extracted from the B-sites in the 0 < x < 0.5 range, but – contrary to the Na_3−xIn_1−xZr_xCl₆ – a small fraction of Na⁺ cations are also extracted from the A-sites. (2) Na⁺ cations are mainly extracted in a disordered manner from the A-sites in the 0.5 < x < 0.75 range with the extraction of the residual Na⁺ cations from the B-sites. It is worth mentioning that in this intermediate range, the β angle increases in comparison to the rest of the series, suggesting a stronger distortion of the cell to accommodate the Na⁺ vacancies. (3) Eventually, the B-sites are emptied and Na⁺ cations are extracted only from the A-sites in the 0.75 < x < 1 range. A rearrangement of the Na_A sublattice occurs that is consistent with the symmetry change. The Na⁺ extraction occurs in an ordered fashion, from only one of the Na_A layers to get eventually to the layered structure of NaTaCl₆. In these two last regimes (2) and (3), we cannot rule out the coexistence of regions with ordered and disordered Na⁺ cations in the A-site but in (2) in average the Na⁺ cations seem disordered while in (iii) they seem to be ordered based on the X-ray diffraction data.

A closer inspection of the diffraction data shows differences in the broadening of the maxima depending on the Ta⁵⁺ content which can be associated with a different crystallinity degree of the materials. The analysis shows a valley-shape of the crystallite size as a function of the Ta⁵⁺ content with a minimum at x = 0.5–0.625. Note that both members show a comparable crystallite size. In order to analyse the coherence length of the materials, pair distribution function analyses are performed (see Fig. S15† and 5e). Pair distribution function analysis is a useful tool to investigate the crystal structures and coherence lengths of the mechanochemically prepared Na_3−2xIn_1−xTa_xCl₆ series, since it can be used to identify the average local structure of materials whose coherence extends even only over a few atom–atom distances.⁶⁸ Representative X-ray pair distribution functions of the mechanochemically prepared Na_3−2xIn_1−xTa_xCl₆ (x = 0, 0.5 and 1) are depicted in Fig. 5e. These pair distribution functions with similar features exhibit different damping profiles indicated by schematic envelope dashed lines. As previously reported, the damping features of the pair distribution function data can be associated to the crystal coherence length, often referred to as crystallite size.⁶⁹ It is worth mentioning that all the samples were measured in the same instrument under the same conditions, which lead to imply that the different dampening observed should be sample specific. Materials with high coherence will show long-range ordered domains while those with small coherence will present short-range ordered domains potentially embedded in an amorphous matrix or crystallite areas containing different Ta⁵⁺/In³⁺ ratios. Thus, the probability of finding atom pair correlations at a larger distance r in materials with high coherence is greater than in those with small coherence, which explains that the pair distribution function of samples with low coherence length dampens more remarkably at higher r. Contrary to the mechanochemically prepared Na_3−xIn_1−xZr_xCl₆ system,³⁸ where coherence length decreases continuously as a function of Zr content, in the case of the present system, the lowest coherence length is observed for the intermediate members. The great dampening and the limited pair distribution function data quality observed for the intermediate members do not allow us to give numerical values of the coherent length. Therefore, an estimation of the coherence length evolution has been performed by plotting the intensity ratio of the pair distribution data between the intensity extracted at 60 Å and at 10 Å as a function of the Ta content in Fig. 5f. Using this approach to qualitatively evaluate coherency confirms the results previously inferred by X-ray diffraction where the coherence length shows a valley-shape as a function of the Ta⁵⁺ content with a minimum at x = 0.5–0.625.

In summary, a correlation between the structural and microstructural evolution can be inferred. Thus, the lattice β angle and the coherence length shows a correlated opposite trend. The higher lattice β angle is observed for the intermediate members 0.5 < x < 0.75 where a significant amount of Na⁺ vacancies are arranged randomly within the A-sites. This scenario accompanied with an even distribution of Ta⁵⁺ and In³⁺ with a large mismatch between their radii would suggest a metastable and very distorted and strained frameworks that can be accommodated by increasing the β angle abnormally. These unstable frameworks are likely to be very difficult to grow within the matrix and showing a large strain, which could explain the low coherent length for the intermediate members. Differences in charge between the two metals could also play a role destabilizing the structures.

Transport properties

The Na⁺ ion transport in the whole range was evaluated by temperature-dependent electrochemical impedance spectroscopy. All impedance spectra of the samples at different temperatures can be fitted with an equivalent circuit model consisting of a parallel resistor-constant phase element (CPE) combination, in series with another CPE representing the blocking electrodes (see some representative examples in Fig. S16†). The resolved impedance spectra exhibit a CPE α of ∼0.95 and capacitances of ∼10⁻¹⁰–10⁻¹¹ F for all the materials. The contributions of grain bulk and grain boundary cannot be deconvoluted from the resolved impedance spectra and the fitted capacitances do not allow the exclusion of grain boundary contributions, thus the derived values represent the total ionic conductivity. The Na⁺ ionic conductivities of the samples exhibit linear Arrhenius behaviour in the measured temperature ranges (Fig. 6). The activation energies (E_a) were extracted from the linear Arrhenius fitting. NaTaCl₆ shows a room temperature (RT) ionic conductivity of 2.8 × 10⁻² mS cm⁻¹, in the range of previous reports⁴⁴ and about three orders of magnitude higher than Na₃InCl₆ with 1.7 × 10⁻⁵ mS cm⁻¹. Note that discrepancies in the actual value of the measured ionic conductivity from different laboratories can come from different preparation methods or measurement set-ups.⁷⁰

Fig. 6 Ionic transport of Na_3−2xIn_1−xTa_xCl₆. (a) Arrhenius plot of the ionic conductivity as a function of temperature for some members of Na_3−2xIn_1−xTa_xCl₆ (x = 0, 0.25, 0.5, 0.75 and1). Filled circles are indicating the values at room temperature. (b) Room temperature ionic conductivity evolution in Na_3−2xIn_1−xTa_xCl₆.

The room-temperature ionic conductivity of Na_3−2xIn_1−xTa_xCl₆ solid solution shows that the substitution of In by Ta has a profound impact on the ionic transport of the materials. It exhibits a sharp upward trend with the Ta content at first, reaching the peak of ∼0.1 mS cm⁻¹ at x = 0.5, and then a steady and moderate decrease with further increase of Ta content. Since Na⁺ vacancies are introduced in A- and B-sites in a random fashion, the room-temperature ionic conductivity is four orders of magnitude larger than that of the In end member but only around one order of magnitude than the Ta one. The trend observed here appears to be more like the one of the annealed Na_3−xIn_1−xZr_xCl₆ system than the one of the mechanochemically prepared Na_3−xIn_1−xZr_xCl₆ system.³⁸ Nevertheless, the trend observed for the Na_3−2xIn_1−xTa_xCl₆ system studied here may be dominated by the synergic effect of the Na⁺/vacancy ratio and microstructural disorder.³⁸ For the present system, Na_3−2xIn_1−xTa_xCl₆, those materials with a more random distribution of the Na⁺ vacancies result in higher (microstructural) disorder and optimum Na⁺/vacancy ratio, and thereby enhanced ionic conductivities. Thus, the evolution of the ionic conductivity in Na_3−2xIn_1−xTa_xCl₆ shows a correlation with the structural and microstructural evolution.

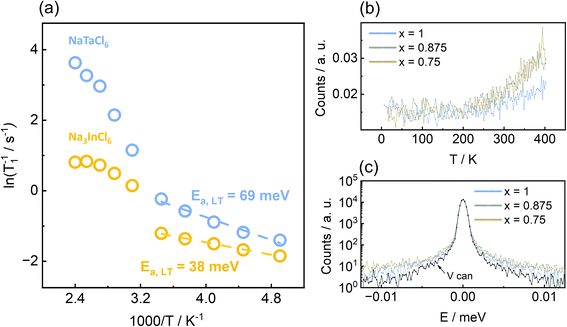
Na⁺ ion diffusion dynamics and pathways

Na⁺-dynamics were studied, in more detail, on the local scale (10⁻¹⁰ to 10⁻⁹ m) using ²³Na spin-lattice (T₁) relaxometry. The spin-lattice relaxometry can be utilized to probe MHz-range Na⁺-jump rates in solid Na⁺-conductors.^13,71 Here, the spin-lattice relaxation rate (T₁−¹) is measured for the end members as a function of temperature and plotted against inverse temperature to obtain activation energies of the thermally activated processes leading to relaxation. For fast ion conductors,^13,72 a rate peak (high- and low-temperature flank connected by a maximum)/overlapping peak can be observed, which is fitted using modified BPP (Bloembergen–Purcell–Pound) formula⁶⁸ describing three-dimensional ionic self-diffusion in solids. For relatively slower ion conductors, the maximum is either barely reached or only the low-temperature flank is observed.⁷³ Low-temperature flank with activation energies in meV range with less than 100 meV are manifestation of local jumps (e.g. within-sites forward–backward motions, jump between neighbouring sites) that do not necessarily lead to longer-range ionic transport as probed using impedance spectroscopy when evaluated toward dc-conductivities.^72,74 Generally, the activation energies obtained via spin-lattice relaxometry are lower in magnitude as it is related to ionic transport inside bulk of the material while impedance spectroscopy probe both bulk and grain boundary transport, leading to higher value of activation energies.⁷⁵ Here, the Arrhenius plots of relaxation rates (T₁−¹) in Fig. 7a indicate two types of Na⁺-jump processes for both ball milled Na₃InCl₆ and NaTaCl₆, depending on the temperature range. At lower temperatures (T < 300 K), the relaxation rates show a linear trend with activation energies in meV range. Such low activation energies at lower temperatures are indicative of microscopic back-and-forth motion of Na⁺-ions that can cause relaxation, but do not contribute to long range ionic diffusion.^72,74,76 Thus, we are observing the linear low temperature flank of a relaxation process whose rate-maximum lies far above our maximum attainable temperature during the experiment. These activation energies might be due to local jumps of Na⁺-ions between the Na_A and Na_B sites that do not significantly affect the long-range diffusion, but can be observed only at low temperatures. A similar trend in low-temperature activation energies (E_a,Na3InCl6 < E_a,NaTaCl6) observed in spin-lattice relaxometry and BVS approach (see Fig. 8) might be an indication of the correspondence of the jump processes probed. At higher temperatures (T > 300 K), the relaxation rates follow a characteristic BPP-behaviour which is generally observed in high ionic-conductivity Na⁺-solid electrolytes with long range ionic diffusion.^13,72 While the activation energies obtained from fitting with modified BPP-formula is a better descriptor for comparing the trends observed in impedance spectroscopy, insufficient data in the high-temperature range prevents us from unambiguous calculation of corresponding activation energies, hence prohibiting the comparison.

Fig. 7 Spin-lattice (T₁) relaxation behaviour and quasi-elastic neutron scattering of selected members in Na_3−2xIn_1−xTa_xCl₆. (a) Arrhenius plot of the ²³Na NMR T₁-relaxation rates for Na₃InCl₆ and NaTaCl₆ with activation energies from linear fit of corresponding low-temperature (T < 300 K) data. (b) IFWS intensity for Na_3−2xIn_1−xTa_xCl₆ (x = 0.75, 0.875 and 1) measured at 3 μeV and summed over all measured Q as a function of temperature. (c) Plots of the QENS spectra for Na_3−2xIn_1−xTa_xCl₆ (x = 0.75, 0.875 and 1) summed over all measured Q at 400 K. Vanadium sample is also included for a better comparison.

Fig. 8 Na⁺ diffusion pathways: The energy barrier and most plausible schematic diffusion paths of Na⁺ between Na_B depicted as a yellow octahedra and Na_A as brown 6-fold prism in (a) Na₃InCl₆ and (b) NaTaCl₆.

To further understand the local Na⁺-dynamics in this system, quasi-elastic neutron scattering (QENS) analysis was performed. Neutrons can exchange energy with the diffusing ions, which leads to a broadening of the elastic scattering signal. Fig. 7b shows the inelastic fixed window scans (IFWS) and the QENS spectra at 400 K for the members x = 0.75, 0.875 and 1 of Na_3−2xIn_1−xTa_xCl₆. Members with higher In contents were not measured due to the high inelastic absorption of this element. The IFWS for NaTaCl₆ shows an onset of the inelastic signal below 250 K, indicative of the starting point of the local Na⁺ diffusion in the material. Interestingly, this temperature is below the observed temperature at which the Na⁺ start diffusing in a long range-order in the nuclear magnetic resonance spectra. IFWS for the other two members shows a similar transition temperature with an increase in the signal with respect to NaTaCl₆. It is worth mentioning that the maximum is not reached at 400 K. However, the temperature experiment was limited to this value in order to avoid the mentioned phase transition from the perovskite to the ilmenite structure in this system. In turn, an increase in the broadening of the QENS spectra are observed as the Ta content decreases, which indicates a higher Na⁺ diffusion coefficient. This observation clearly matches with the tendency observed in the ionic transport properties of this system. The analyses of the spatial distribution to determine the actual values of the activation energies and diffusion coefficients was restricted by the limitations of the technique when the materials show diffusion coefficients below 10⁻¹⁰ m² s⁻¹; the analysis of the broadening as a function of wave vector Q could not be performed in order to apply the Chudley–Elliott model due to the limited broadening in the present system.⁷⁷ Combining NMR and QENS results, the local Na⁺ diffusion in this system starts being observable around 200 K and it expands into the long range below 300 K.

To identify the most likely diffusion pathways in these materials, a bond valence sum approach was used. Both end members were analysed. For Na₃InCl₆, the bond valence sum calculations, depicted in Fig. 8, show three main Na⁺ diffusion pathways: (1) a jump between the B-octahedral and the edge-sharing A-prismatic site (2) a jump between two B-octahedra involving the third interstitial site and, (3) an indirect jump between the corner-sharing B-octahedral and A-prismatic sites involving two interstitial sites. Another pathway (4) involving two A-sites with a higher energy barrier can also be considered. For NaTaCl₆, the bond valence calculations show similar diffusion pathways (Fig. 8b). In this case, pathway (2) is split into two similar different pathways (different pathways associated to the occupied and the vacant A-site layers), and pathway (IV) is divided into three (two interlayers jumps and one intralayer jump).

While the interstitial sites remain unoccupied in the resolution of the X-ray diffraction, the A- and B– Na⁺ site occupancies will be essential for the ionic transport in both materials as these perovskite materials show a vacancy-process for Na⁺ diffusion. In the case of Na₃InCl₆, A- and B-sites are fully occupied, which implies a very restricted Na⁺ diffusion since it requires the presence of some cation vacancies. Nevertheless, in the case of NaTaCl₆, only half of the A-sites are occupied in a layered way with many available empty sites for the diffusion process. In here, these Na⁺ cations may access an empty B-site or an empty A-site in the adjacent layer, which explain the larger ionic conductivity for NaTaCl₆ in comparison with Na₃InCl₆. In the case of the intermediate members, the Na⁺/vacancy ratio in both B- and A-sites is one of the factors behind the increase of the ionic conductivity since is the transport is a result of a vacancy driven process.

Although a vacancy driven process is the main mechanism to explain the Na⁺ diffusion in these materials, there are also additional differences in the electronic structure⁷⁸ that may be mediating a large difference in the ionic conductivity of these materials. For instance, changes in the electronegativity have been suggested to play a role in the overall transport.^40,78 In addition, the second-order Jahn–Teller effect associated to the highly charge Ta⁵⁺ d⁰ results in more distorted MCl₆ octahedra and at this stage it is unclear how a second-order Jahn–Teller may affect transport in superionic conductors as it has only shown to affect ion migration barriers as in the case of Li_xTiO₂.⁷⁹ The fact that the B-site is completely empty may be a result of Coulomb repulsion with the Ta⁵⁺, which may energetically prevent a strong Na⁺ mobility suggesting the need for solid solutions.

Microstructure seems to also correlate with the transport properties of these materials. If we only look at the end members, they show comparable coherence length and the difference on the ionic conductivity can be, therefore, ascribed to the many available empty sites for the diffusion process as we pointed out above. However, we can point out that the intermediate members with random distribution of the Na⁺ vacancies and a smaller coherence show an enhancement on the ionic transport properties. Therefore, the Na⁺/vacancy ratio, their arrangement, the electronic structure of the metals and the microstructure synergistically (see Fig. 9) affect the transport performance in the Na_3−2xIn_1−xTa_xCl₆ system.

Fig. 9 Crystal structure – microstructure – ionic transport coupling. Schematic of perovskite crystal structures illustrating the three different Na⁺ vacancy arrangements as function of the Na vacancy content. The different stages correlate with the coherence length and the ionic transport properties trends. Schematic of samples with large (yellow) and (small) coherence is also shown.

Conclusions

The perovskite structure is adopted by a significant number of sodium halide electrolytes, a fact often overlooked in the literature. Here, a study of the In(III) – Ta(V) Na_3−2xIn_1−xTa_xCl₆ system halides has been made to understand the impact of the perovskite structure on the ionic transport. The presence of cation vacancies, their arrangement, the size and the electronic nature of the metal cations determine the final crystal structure and the microstructure of these materials.

A change from a ‘double’ perovskite in the case of Na₃InCl₆ to a ‘double double’ perovskite in the case of NaTaCl₆ (Na[V_A]Ta[V_B]Cl₆ considering the Na⁺ cation vacancies) has been reported here. Na₃InCl₆, without any cation vacancy, crystallizes in a ‘simple double’ perovskite with a rock-salt cation ordering between In³⁺ and Na⁺ in the B-site due to their charge and size mismatch along with a combination of an out-of-phase and an in-phase BCl₆ octahedra tilting. NaTaCl₆, with cation vacancies in both A- and B-sites and Ta⁵⁺ showing second-order Jahn–Teller effect, represents the first example of a halide with a ‘double double’ perovskite structure. Besides, to the best of our knowledge, NaTaCl₆ is also the first example crystallizing in this structural type because of the presence of cation vacancies in both A- and B-sites. It shows a complex simultaneous 1 : 1 cation ordering at both A and B sites, in a layered and rock-salt manners, respectively along with a singular combination of out-of-phase and in-phase of octahedra tilting.

We have also shown that the solid solution between In³⁺ and Ta⁵⁺ can be prepared by mechanochemical synthesis. The change from the ‘double’ to the ‘double double’ perovskite is detected at x = 0.75 by means of X-ray diffraction. Different regimes associated to the Na⁺ cation vacancies content and their arrangement are detected in the solid solution, which, strikingly, correlates with the microstructure of the materials. It is observed that the presence of significant amount of Na⁺ cation vacancies randomly distributed in both A- and B-sites associated with a lower crystallite size in the materials.

The crystal structure and microstructure of these materials correlates with their ionic transport. NaTaCl₆ shows an enhancement of the ionic conductivity along with a lower activation energy in comparison with Na₃InCl₆ which can be explained in terms of easier accessible diffusion pathways in the vacancy-process for Na⁺ diffusion. A parabolic trend is observed in the solid solution reaching the peak of ∼0.1 mS cm⁻¹ at x = 0.5. This evolution, however, requires crystal structure and, also, microstructure considerations.

Describing sodium halide electrolytes as a perovskite-related structure provides better approaches in tuning the composition, structures, and microstructures considering the rich defect chemistry, the compositional versatility, and the structural flexibility inherent to the perovskite structure. In turn, these concepts could be also exported to other chemistries (i.e.: Li, K, Mg, Ca…) if the current synthetic processes allow those materials crystallizing in the versatile perovskite structure.

Data availability

The data supporting this article have been included as part of the ESI.† Data for this article, including XRD, PDF, NMR, Electrochemical impedance, SEM and EDX data as well as .cif files of the crystal structures are available at Münster University research data repository at https://doi.org/10.17879/35998140303.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work is funded by the NATTER project, funded by Bundesministerium für Bildung und Forschung (BMBF, project 03XP0525B). The authors acknowledge financial support from the Ministry of Culture and Science of the State North Rhine Westphalia in course of the International Graduate School of Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA). We further acknowledge funding from the Deutsche Forschungsgemeinschaft under project number 459785385. The authors also thank ILL for the allocation of beam time (doi:10.5291/ILL-DATA.7-03-229).⁸⁰ Data available at 10.17879/35998140303. The authors would also like to thank Eva Schlautmann for her assistance with SEM measurements.

References

1. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
2. J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
3. J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1–4.
4. J. Janek and W. G. Zeier, Nat. Energy, 2023, 8(3), 230–240.
5. W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schröder, R. Koerver, T. Leichtweiss, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835–17845.
6. R. Koerver, I. Aygün, T. Leichtweiß, C. Dietrich, W. Zhang, J. O. Binder, P. Hartmann, W. G. Zeier and J. Janek, Chem. Mater., 2017, 29, 5574–5582.
7. P. Barpanda, G. Oyama, S. I. Nishimura, S. C. Chung and A. Yamada, Nat. Commun., 2016, 1(4), 1–7.
8. B. L. Ellis and L. F. Nazar, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168–177.
9. T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett., 2020, 5, 146–151.
10. Z. Zhu, I. H. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27, 8318–8325.
11. T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 14464–14473.
12. T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869.
13. O. Maus, M. T. Agne, T. Fuchs, P. S. Till, B. Wankmiller, J. M. Gerdes, R. Sharma, M. Heere, N. Jalarvo, O. Yaffe, M. R. Hansen and W. G. Zeier, J. Am. Chem. Soc., 2023, 145, 7147–7158.
14. Z. Zhang, P. N. Roy, H. Li, M. Avdeev and L. F. Nazar, J. Am. Chem. Soc., 2019, 141, 19360–19372.
15. M. Duchardt, S. Neuberger, U. Ruschewitz, T. Krauskopf, W. G. Zeier, J. S. Auf Der Günne, S. Adams, B. Roling and S. Dehnen, Chem. Mater., 2018, 30, 4134–4139.
16. M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Angew. Chem. Int. Ed., 2018, 57, 1351–1355.
17. Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93.
18. M. A. Kraft, L. M. Gronych, T. Famprikis, S. Ohno and W. G. Zeier, Chem. Mater., 2020, 32, 6566–6576.
19. M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064.
20. C. Delmas, A. Nadiri and J. L. Soubeyroux, Solid State Ionics, 1988, 28–30, 419–423.
21. P. Fabry, J. P. Gros, J. F. Million-Brodaz and M. Kleitz, Sens. Actuators, 1988, 15, 33–49.
22. A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16.
23. Y. Kato, S. Shiotani, K. Morita, K. Suzuki, M. Hirayama and R. Kanno, J. Phys. Chem. Lett., 2018, 9, 607–613.
24. T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291.
25. Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031.
26. R. Prasada Rao, H. Chen and S. Adams, Chem. Mater., 2019, 31(21), 8649–8662.
27. N. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, J. Mater. Sci., 2011, 46, 2821–2837.
28. L. M. Riegger, R. Schlem, J. Sann, W. G. Zeier and J. Janek, Angew. Chem. Int. Ed., 2021, 60, 6718–6723.
29. C. Rosenbach, F. Walther, J. Ruhl, M. Hartmann, T. A. Hendriks, S. Ohno, J. Janek and W. G. Zeier, Adv. Energy Mater., 2023, 13(6), 22203673.
30. F. Stenxel, G. Meyer, F. Stenzel, C. Meyer, D. Syslcm Ag and N. Yci, Z. Anorg. Allg. Chem., 1993, 619, 652–660.
31. M. S. Wickleder and G. Meyer, Z. Anorg. Allg. Chem., 1995, 621, 457–463.
32. G. Meyer, S. Peter Ax, T. Schleid and M. Irmler, Z. fur Anorg. Allg. Chem., 1987, 554, 25–33.
33. J. Xu, Y. Wang, S. Wu, Q. Yang, X. Fu, R. Xiao and H. Li, ACS Appl. Mater. Interfaces, 2023, 15, 21086–21096.
34. D. Park, K. Kim, G. H. Chun, B. C. Wood, J. H. Shim and S. Yu, J. Mater. Chem. A, 2021, 9, 23037–23045.
35. R. Schlem, A. Banik, M. Eckardt, M. Zobel and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 10164–10173.
36. T. Zhao, A. N. Sobolev, R. Schlem, B. Helm, M. A. Kraft and W. G. Zeier, ACS Appl. Energy Mater., 2023, 6, 4334–4341.
37. T. Zhao, M. A. Kraft and W. G. Zeier, Inorg. Chem., 2023, 62(30), 11737–11745.
38. T. Zhao, A. N. Sobolev, X. M. de Irujo Labalde, M. A. Kraft and W. G. Zeier, J. Mater. Chem. A, 2024, 12, 7015–7024.
39. Y. Okada, T. Kimura, K. Motohashi, A. Sakuda and A. Hayashi, Electrochemistry, 2023, 91, 077009.
40. Z. Huang, S. Yoshida, H. Akamatsu, K. Hayashi and S. Ohno, ACS Mater. Lett., 2024, 1732–1738.
41. Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042–15047.
42. A. Morscher, M. S. Dyer, B. B. Duff, G. Han, J. Gamon, L. M. Daniels, Y. Dang, T. W. Surta, C. M. Robertson, F. Blanc, J. B. Claridge and M. J. Rosseinsky, Chem. Mater., 2021, 33, 2206–2217.
43. Y. Hu, J. Fu, X. Lin, J. Xu, J. Luo, F. Zhao, Y. Liu, W. Li, J. T. Kim, H. Su, X. Hao, H. Ren, M. Yang, Y. Huang and X. Sun, Matter, 2023, 7(3), 1018–1034.
44. K. Motohashi, H. Tsukasaki, A. Sakuda, S. Mori and A. Hayashi, ACS Mater. Lett., 2024, 6, 1178–1183.
45. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
46. ISOTROPY Software Suite, https://stokes.byu.edu/iso/isotropy.php, accessed 12 March 2024.
47. H. M. Rietveld, Phys. Scr., 2014, 89, 098002.
48. A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
49. R. A. Young, The Rietveld Method, Oxford Univ. Press, 1993.
50. D. Balzar, N. Audebrand, M. R. Daymond, A. Fitch, A. Hewat, J. I. Langford, A. Le Bail, D. Louër, O. Masson, C. N. Mccowan, N. C. Popa, P. W. Stephens and B. H. Toby, J. Appl. Cryst., 2004, 37, 911–924.
51. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566.
52. S. L. J. Thomae, N. Prinz, T. Hartmann, M. Teck, S. Correll and M. Zobel, Rev. Sci. Instrum., 2019, 90, 43905.
53. S. G. J. van Meerten, W. M. J. Franssen and A. P. M. Kentgens, J. Magn. Reson., 2019, 301, 56–66.
54. D. S. Raiford, C. L. Fisk and E. D. Becker, Anal. Chem., 1979, 51, 2050–2051.
55. H. Chen and S. Adams, IUCrJ, 2017, 4, 614–625.
56. H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18–33.
57. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
58. X. Zhi and A. R. West, Chem. Mater., 2023, 35(17), 6790–6798.
59. H. Mizoguchi, P. M. Woodward, S. H. Byeon and J. B. Pariset, J. Am. Chem. Soc., 2004, 126, 3175–3184.
60. A. M. Glazer and IUCr, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
61. E. Sebti, J. Qi, P. M. Richardson, P. Ridley, E. A. Wu, S. Banerjee, R. Giovine, A. Cronk, S. Y. Ham, Y. S. Meng, S. P. Ong and R. J. Clément, J. Mater. Chem. A, 2022, 10, 21565–21578.
62. P. Ridley, L. H. B. Nguyen, E. Sebti, B. Han, G. Duong, Y. T. Chen, B. Sayahpour, A. Cronk, G. Deysher, S. Y. Ham, J. A. S. Oh, E. A. Wu, D. H. S. Tan, J. M. Doux, R. Clément, J. Jang and Y. S. Meng, Matter, 2024, 7, 485–499.
63. H. Henke, Z. fur Krist. – New Cryst. Struct., 1992, 198, 1–16.
64. G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785.
65. M. C. Knapp and P. M. Woodward, J. Solid State Chem., 2006, 179, 1076–1085.
66. S. García-Martín, E. Urones-Garrote, M. C. Knapp, G. King and P. M. Woodward, J. Am. Chem. Soc., 2008, 130, 15028–15037.
67. G. King and S. Garcia-Martin, Inorg. Chem., 2019, 58, 14058–14067.
68. S. J. L. Billinge, Philos. Trans. R. Soc. A, 2019, 377, 20180413.
69. M. W. Terban and S. J. L. Billinge, Chem. Rev., 2022, 122, 1208–1272.
70. S. Ohno, T. Bernges, J. Buchheim, M. Duchardt, A. K. Hatz, M. A. Kraft, H. Kwak, A. L. Santhosha, Z. Liu, N. Minafra, F. Tsuji, A. Sakuda, R. Schlem, S. Xiong, Z. Zhang, P. Adelhelm, H. Chen, A. Hayashi, Y. S. Jung, B. V. Lotsch, B. Roling, N. M. Vargas-Barbosa and W. G. Zeier, ACS Energy Lett., 2020, 5, 910–915.
71. S. Lunghammer, D. Prutsch, S. Breuer, D. Rettenwander, I. Hanzu, Q. Ma, F. Tietz and H. M. R. Wilkening, Sci. Rep., 2018, 8(1), 1–8.
72. F. Stainer, B. Gadermaier, A. Kügerl, L. Ladenstein, K. Hogrefe, H. Martin and R. Wilkening, Solid State Ionics, 2023, 395, 116209.
73. K. Hogrefe, J. Königsreiter, A. Bernroitner, B. Gadermaier, S. E. Ashbrook and H. M. R. Wilkening, Chem. Mater., 2024, 36, 980–993.
74. B. Wankmiller and M. R. Hansen, J. Magn. Reson. Open, 2023, 14–15, 100098.
75. J. Hartel, A. Banik, J. M. Gerdes, B. Wankmiller, B. Helm, C. Li, M. A. Kraft, M. R. Hansen and W. G. Zeier, Chem. Mater., 2023, 35, 4798–4809.
76. Y. Chen, Z. Lun, X. Zhao, K. P. Koirala, L. Li, Y. Sun, C. A. O'Keefe, X. Yang, Z. Cai, C. Wang, H. Ji, C. P. Grey, B. Ouyang and G. Ceder, Nat. Mater., 2024, 2024, 1–8.
77. C. T. Chudley and R. J. Elliott, Proc. Phys. Soc., 1961, 77, 353.
78. S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Prog. Energy, 2020, 2, 022001.
79. A. A. Belak, Y. Wang and A. Van Der Ven, Chem. Mater., 2012, 24, 2894–2898.
80. W. Zeier, M. Appel, T. Bernges, A. Ghata, X. Martinez de Irujo-Labalde, O. Maus and T. Zhao, Understanding the ionic transport in the thermoelectric, mixed-conducting argyrodites Ag_8+xMSe₆ (M = Ge, Ga), Institut Laue-Langevin (ILL), 2023,  DOI:10.5291/ILL-DATA.7-03-229.

---

Footnote

† Electronic supplementary information (ESI) available: The supporting information includes comparison of X-ray diffraction data of the samples under different treatments, the Rietveld refinement, tables of crystallographic information from Rietveld refinement, and the pair distribution function data and refinements. See DOI: https://doi.org/10.1039/d4ta05371k

---