Insights into defect kinetics, mass transport, and electronic structure from spectrum effects in ion-irradiated Bi₂O₃

Abstract

The next generation of energy conversion and storage materials relies on the development of solid-state ion conductors. The crystal structure and defect concentration are key factors determining the rate of ion mobility through a material. Bi₂O₃ is polymorphic, with δ-Bi₂O₃ exhibiting the highest ionic conductivity. However, the monoclinic α-Bi₂O₃ is more easily synthesized and more stable at room temperature, making it more desirable for applications in diverse and extreme environments. Here, we present the first study on α-Bi₂O₃ ion irradiation tolerance using three noble gas species (He, Ne, and Ar) to assess the ion irradiation effects on ionic conductivity and mass transport. Ion irradiation of materials has been shown to disorder the materials, induce phase transformations and produce strain in materials, all of which can result in changes in ionic conductivity. An increased propensity for amorphization is observed with both fluence and ion species. He irradiation results in swelling, while Ne and Ar both induce amorphization. As a consequence of irradiation, mixed electronic and nuclear stopping is depth-dependent, with peak electronic stopping dominating near the surface and nuclear stopping becoming most significant at the peak damage level in the bulk. Mass transport is correlated with structural transformations, as indicated by bubble nucleation and coarsening. Changes in the electronic structure and band gap are observed, with the band gap widening from 2.6 eV to 3.5 eV upon full amorphization. Understanding the limitations of α-Bi₂O₃ in non-equilibrium environments and the impact of amorphization on mass transport enables the development of more robust materials for advanced energy applications.

---

1 Introduction

Oxide ceramics have been studied and proposed for a number of applications, including oxidative- and photo-catalysis, solid electrolyte batteries, and solid oxide fuel cells.^1–4 In some applications, such as in nuclear-fission fuels and waste storage materials, as well as more niche applications such as windows for fusion reactors, ceramics are subject to harsh radiation environments.^5–7 The evolution of radiation damage, in which atomic scale damage events generate macroscopic changes in properties, is ultimately dictated by the migration of point defects.^8,9 Given this dependency on mass transport, it is interesting to consider ceramics that have intrinsically high ionic conductivity.

Bismuth oxide, Bi₂O₃, exhibits a range of properties that make it well-suited for low-temperature solid-state ionic applications.¹ While δ-Bi₂O₃ is an exceptional fast-ion conductor, the monoclinic alpha phase (α-Bi₂O₃) is the most chemically stable phase at room temperature.¹⁰ Additionally, the α-Bi₂O₃ polymorph has a direct band gap ranging from 2.1 to 2.8 eV, which is tunable and advantageous for photocatalysis.^11,12 Mass transport is governed by material properties, including activation energy for ion migration, crystal structure, defect concentration, atomic size disparity, and electronic band structure.^13–17 The ability to modify one or more of these parameters allows for the development of novel ionic conductors for a variety of applications. For example, controlling mass transport in ceramics for use in radiation environments calls for materials capable of withstanding extreme conditions and phase transformations. Further, radiation can promote the transformation to metastable phases that then exhibit enhanced properties.^5,18 To advance the understanding of Bi₂O₃ behavior under irradiation and optimize its use in non-equilibrium environments, it is crucial to control the Bi₂O₃ microstructure and parameterize its response to ion irradiation, enabling its use in a variety of reaction environments.

Phase stability is crucial for understanding the response and tolerance of α-Bi₂O₃ to non-equilibrium environments, such as radiation exposure. The stability of each phase is governed by intricate phase transformation pathways, dependent on factors such as temperature, pressure, and stored energy, which might be introduced via irradiation.¹⁸ The α-phase of Bi₂O₃ is easily synthesizable under various conditions.¹² Furthermore, the structural configuration of α-Bi₂O₃ determines its optical, mass transport, and electronic properties.^{1,12,15,19,20} Additionally, δ-Bi₂O₃ can be fabricated via doping the alpha phase with various elements. Under irradiation, depending on the irradiation spectrum, defects are produced that can destabilize the material. In particular, ion beam implantation of noble gases leads to the nucleation and evolution of cavities and, at high enough doses, swelling and phase change.^21,22 The accumulation of vacancies and significant amorphization can enhance or diminish material properties.

In other ceramics, structural disorder has been linked to increased ionic conductivity. For example, cation disorder in the pyrochlore Gd₂Ti₂O₇ was found to substantially enhance ionic conductivity^23,24 and lattice distortions in bismuth ferrite solid electrolytes were used to control oxygen migration.²⁵ Within α-Bi₂O₃, ion irradiation induces phase changes, swelling, and amorphization. These alterations introduce heterogeneous structures that affect local transport properties, potentially impacting ionic conductivity through uneven ionic transport.^26,27 These structural changes modify the electronic structure of α-Bi₂O₃, altering its band gap and affecting electron mobility, which influences macroscopic performance. Radiation-induced microstructural changes, such as phase transitions and amorphization, exacerbate these issues by creating additional heterogeneities that influence bubble nucleation and coarsening, which are indicative of gas and ion mobility.²⁶ While disordered and amorphous systems have been studied for ionic transport due to their high vacancy concentrations, the impact of amorphization on mass transport has not been widely measured.^23,27,28 Understanding the relationship between the structure of α-Bi₂O₃ and its response to radiation exposure is essential for optimizing its potential in applications such as solid-state ionics with high mobility ions.

The objective of this study is to characterize the relationship between the ion irradiation spectrum and phase transformation conditions in α-Bi₂O₃, investigating the interplay between ion irradiation conditions, amorphization, and bubble size using three different ion species and various fluences that correspond to a range of displacements per atom (DPA) values between 0.125 and 11.5. Transmission electron microscopy (TEM) is employed for micron- and nano-scale structural characterization, while grazing-incidence X-ray diffraction (GIXRD) provides long-range structural information from the top 90 nm of the samples. Electron energy-loss spectroscopy (EELS) probes shift in the valence electron behavior and band gap as a result of radiation damage. Investigating the effects of ion irradiation, particularly from noble gas species such as He, Ne, and Ar, sheds light on material amorphization and bubble transport and structural properties. Bubble size and number density reflect the extent of mass transport involving both the irradiating gas and the constituent atoms of Bi₂O₃. Band gap measurements indicate changes in electron conduction and indirectly infer a shift in the balance between electron and ion mobility, which are often inversely related.²⁹ Noble gas species were selected due to their chemical inertness as compared to more chemically reactive ions, which thereby minimize dopant and stoichiometry effects. The ions used in this study produce a range of extremely dilute cascades with He to gradually more dense cascades produced with Ar. It also provides fundamental insight into how transport processes depend on the radiation-induced microstructure. Varying fluences of Ne are explored to define the relationship between the extent and depth of amorphization and ion fluence.

The results reveal that the radiation resistance and response of α-Bi₂O₃ are contingent upon the size of the irradiating ion, as well as the energy and fluence of irradiation. The degree of amorphization, in terms of the depth and extent of phase change, correlates with fluence and the electronic-to-nuclear stopping power ratio (ENSP). Bubble geometry is governed by the degree of amorphization, while bubble size is linked to both the microstructure and the ion species. Bubble nucleation and coarsening indicate that the amorphous phase enables faster diffusion rates. The ability of gas atoms to migrate to nucleation sites and undergo Ostwald ripening relates to a material's mass transport properties. Additionally, mixed electronic and nuclear stopping is depth-dependent, with electronic stopping dominating near the surface and nuclear stopping becoming more significant deeper into the bulk as the ENSP ratio shifts. Understanding the relationship between radiation conditions and the microstructure is crucial for parameterizing the response of Bi₂O₃ and maximizing its stability in non-equilibrium environments. This knowledge informs the radiation damage response, facilitates the material's use across diverse reaction environments, and broadens its applicability across various fields.

2 Experimental details

2.1 Bi₂O₃ irradiations

99.9% purity Bi₂O₃ sputtering targets were purchased from the Kurt J. Lesker Company. Pieces of the target, each approximately 3 mm thick, were sectioned from the target for ion irradiation. The samples were successively polished with finer grits of diamond polishing films, ending with a 1 μm grit. A final polish was performed using Syton 50HT, which is slightly basic and acts as a gentle chemical etchant to remove remaining damaged layers, resulting in a mirror finish.

Ion irradiations were performed using a 200 kV Danfysik Ion Implanter in the Ion Beam Materials Laboratory (IBML) at the Los Alamos National Laboratory. The samples were mounted on a Ni-block with double-sided carbon tape for good thermal contact. Active cooling was also used to ensure that the target temperature during the irradiation remained below 35 °C for room temperature irradiations. For irradiation performed at elevated temperatures, the target temperature was set to 150 or 300 °C. The target chamber vacuum was maintained near 1 × 10⁻⁷ torr during the irradiation. He, Ne, and Ar were used for the irradiations. Specific irradiation conditions, SRIM values, and structural observations for each sample are listed in Table 1, with the samples focused on in this investigation shown in bold text.

Table 1 Summary of ion-irradiation conditions, SRIM-calculated damage characteristics, and post-irradiation structure of Bi₂O₃. The samples in bold text are discussed in detail in this work and analyzed using TEM

Ion species	Energy	Fluence [ion per cm^2]	Temperature	DPA	Peak DPA depth	Structure
He	200 keV	1 × 10^17	22 °C	0.0025	600 nm	Minor swelling
He	200 keV	1 × 10^15	22 °C	0.025	600 nm	Minor swelling
He	200 keV	1 × 10^16	22 °C	0.25	600 nm	Minor swelling
He	200 keV	1 × 10 ^17	22 °C	2.5	600 nm	Minor swelling, small bubbles
Ne	200 keV	1 × 10^14	22 °C	0.05	156 nm	Minor swelling
Ne	200 keV	2.5 × 10 ^14	22 °C	0.125	156 nm	Polycrystalline (35 nm)
Ne	200 keV	5 × 10 ^15	22 °C	2.5	156 nm	Amorphous (215 nm), bubbles
Ne	200 keV	1 × 10 ^16	22 °C	5	156 nm	Amorphous (315 nm), bubbles
Ar	400 keV	1 × 10^14	22 °C	0.115	174 nm	Amorphous
Ar	400 keV	1 × 10^15	22 °C	1.15	174 nm	Amorphous
Ar	400 keV	1 × 10^15	150 °C	1.15	174 nm	Amorphous
Ar	400 keV	1 × 10^15	300 °C	1.15	174 nm	Amorphous
Ar	400 keV	1 × 10 ^16	22 °C	11.5	174 nm	Amorphous (440 nm), large bubbles
Ar	400 keV	1 × 10 ^16	300 °C	11.5	174 nm	Crystalline, small bubbles
Ar	400 keV	5 × 10^16	22 °C	55	174 nm	Amorphous

---

2.2 Simulation of radiation damage

Stopping Range of Ions in Matter (SRIM)³⁰ software was used to model radiation damage in Bi₂O₃ under various radiation conditions. The density of Bi₂O₃ was set to 9.4 g cm⁻² and a displacement threshold energy (E_d) of 40 eV for Bi and O was used.^15,31 The ion energy was set to 200 keV for He and Ne irradiations and to 400 keV for Ar irradiations to simulate experimental conditions. A detailed calculation with the full damage cascade was run for each set of conditions. SRIM outputs were used to determine the displacements per atom (DPAs) and implanted ion concentration for each set of experimental irradiation parameters. Table 2 summarizes electronic and nuclear energy as a function of depth in the samples and ENSP for simulated irradiation conditions.

Table 2 Electronic and nuclear dE/dx and ENSP ratio at the surface as a function of irradiation ion species and energy, as calculated using SRIM

Ion species	Energy	Electronic dE/dx [keV nm^−1]	Nuclear dE/dx [keV nm^−1]	ENSP
He	200 keV	0.355	0.003	139.592
Ne	200 keV	0.415	0.132	3.146
Ar	400 keV	0.734	0.400	1.846

---

2.3 Grazing-incidence X-ray diffraction

Grazing-incidence X-ray diffraction (GIXRD) analysis was used to determine the crystal structure of Bi₂O₃ after irradiation. GIXRD was performed using a Bruker AXS D8 Advance X-ray diffractometer equipped with a Gobel mirror and LYNXEYE XE-T energy detector. The measurements were conducted using Cu Kα radiation at 1.5406 Å in θ–2θ geometry, with the angle of incidence fixed at 1° relative to the specimen's surface. With a 1° angle of incidence, the X-ray penetration depth is approximately 90 nm (Fig. S1 of the ESI†). Scans were carried out for 2θ between 10 and 65° with a step size of 0.02° and a dwell time of 1 s per step. X-ray scattering provides the average positions of atoms in the bulk crystal, offering insights into the crystalline phases present and the relative degree of amorphization.

2.4 TEM imaging of cross-sections

Electron-transparent Bi₂O₃ cross-sections were prepared using a Helios NanoLab 600 dual-beam SEM-FIB. A protective layer of Pt was deposited on the sample surfaces. Thinning was performed iteratively on both sides of the lamellae with decreasing acceleration voltages and currents. Final thinning was performed at 2 keV with a current of 86 pA to minimize material redeposition and damage. For TEM imaging, the lamellae ranged in thickness from approximately 30 nm at the surface to 90 nm beyond the damage front, as measured by EELS.

Bright-field TEM images, Fig. 1 and 2, and EDS maps were acquired on an image-corrected FEI Titan operated at 300 keV with a OneView 4K CCD camera. The images are intentionally underfocused and a 100 μm objective aperture was used to increase contrast between features in the Bi₂O₃ lamella. The samples were observed to crystallize with prolonged exposure to the electron beam. With a dose rate of 1.6 × 10⁵ electrons per nm² s, care was taken to minimize exposure to any one region.

Fig. 1 Bright-field TEM images of Bi₂O₃ irradiated with different ion species at 22 °C, (a) He at 200 keV and a fluence of 1 × 10¹⁷ He ions per cm², (b) Ne at 200 keV and a fluence of 1 × 10¹⁶ Ne ions per cm², and (c) Ar at 400 keV and a fluence of 1 × 10¹⁶ Ar ions per cm². (a) Even at the highest fluence, α-Bi₂O₃ irradiated with He does not amorphize. Small bubbles form beneath the surface, extending to approximately 850 nm into the bulk crystal. (b) Ne irradiation results in the formation of a 315 nm thick amorphous layer beneath the surface. Visible large crystalline regions are present in the amorphous matrix, along with smaller crystallites, indicating partial amorphization. A large crystallite with bubbles along the crystalline–amorphous interface is magnified with enhanced contrast in the inset. (c) Irradiation with Ar, the largest species, leads to the formation of large bubbles within a 440 nm fully amorphous layer. DPA is given on the left vertical axis and implanted ion concentration on the right vertical axis. The SRIM damage profiles are scaled and replicated on the TEM images.

Fig. 2 Bright-field TEM images of Bi₂O₃ irradiated with Ne at 200 keV and three different fluences of (a) 2.5 × 10¹⁴ Ne ions per cm², (b) 5 × 10¹⁵ Ne ions per cm², and (c) 1 × 10¹⁶ Ne ions per cm². The samples are coated with a protective layer of Pt during FIB preparation. The depth of the amorphous front increases with increasing fluence. This is not captured by SRIM calculations since the depth at which peak DPA occurs is fluence independent. This phenomenon likely results from changes in the penetration depth following Bi₂O₃ amorphization and reduced atomic density or longer diffusion distances of defects generated during the collision cascade.^32,33 For the Ne irradiations performed at 200 keV with (b) 5 × 10¹⁵ Ne ions per cm² and (c) 1 × 10¹⁶ Ne ions per cm², large predominantly amorphous regions indicate the depth of damage-induced phase change. Below the amorphous layers are densely packed, overlapping dislocation loops likely formed by interstitial diffusing and accumulating past the end of the damage range.^32–34

Energy-dispersive X-ray spectroscopy (EDS) mapping was performed using an EDAX Octane Elite T – 70 mcm² detector with samples tilted to 15° to confirm the relative amounts of Bi and O in the lamella. Additionally, for samples irradiated with Ar, EDS was used to determine that radiation-induced cavities contained Ar. For samples in which radiation-induced bubbles were observed, custom scripts were used to determine cavity size and distribution characteristics from bright-field images. For this analysis, a Gaussian kernel was applied to the images to reduce intensity variations due to thickness, an intensity threshold mask was applied, and cavity features were identified. Cavity size and distribution as a function of depth into the Bi₂O₃ indicate differences in damage response between the three irradiation species (He, Ne, and Ar) and varying fluence and temperature.

2.5 Scanning nanodiffraction

To measure changes in the microstructure on the nm-length scale, 4D scanning transmission electron microscopy (4D-STEM) data sets, a form of scanning transmission electron microscopy (STEM),³⁵ were collected from the top 200 to 1000 nm of each sample, depending on the depth of the damage profile. The electron probe was rastered over the radiation-damaged surface and undamaged bulk crystal as well as along the interface between the regions, to understand the microstructural evolution as a result of irradiation with different noble gas species. 4D-STEM data were collected on the TEAM I at 300 keV operated in nanoprobe mode with custom apertures.³⁶ A 5 μm C2 aperture and a convergence angle of 0.6 mrad were used to produce a near-parallel beam condition and distinguishable Bragg diffraction spots. The tail of the central beam that is slightly visible in the diffraction images (Fig. 3) is due to an inability to position the C3 aperture such that it fully blocks the adjacent C2 aperture. Using a single electron-counting Dectris Arina detector, high dynamic range datasets were acquired with a 185 mm camera length, 2000 μs dwell time, and real-space step sizes of 4.12 nm. Analysis of 4D-STEM data sets was performed using the py4DSTEM Python package³⁵ and Python scripting. Scanning nanodiffraction patterns were aggregated along rows parallel to the irradiated Bi₂O₃ surface. Subsequently, mean and median patterns were generated for each row of aggregated patterns. The mean patterns for each row illustrate the average structure, including both crystalline and amorphous phases, along the direction of irradiation. The median patterns describe the prevailing microstructure at different depths, providing insight into phase distribution along the direction of irradiation.

Fig. 3 The microstructural evolution of irradiated Bi₂O₃ as a function of depth from the irradiated surface is measured using 4D-STEM and GIXRD. For irradiation conditions resulting in some degree of amorphization, a virtual dark-field image, mean and median diffraction patterns from select regions, and GIXRD with a 1° angle of incidence are shown. A reference α-Bi₂O₃ (ICDD PDF4+ Bi₂O₃-04-003-2034) spectrum in gray is overlaid on the acquired GIXRD data in blue. (a–c) For Ne irradiations with increasing fluence, the depth of the amorphous layer also increases. GIXRD shows a close match to the α-phase, with minor peak broadening, for the lowest Ne fluence. With increasing fluence and extent of amorphization, peaks in the GIXRD broaden, particularly between 2θ = 25 and 33°. The mean and median 4D-STEM patterns collected from the shaded regions in each virtual dark-field image show the average and most prevalent microstructures, respectively, as a function of depth below the irradiated surface. Diffuse halos in 4D-STEM are indicative of an amorphous material, while bright Bragg discs indicate crystallinity. (a) The lowest fluence Ne irradiation retains its original crystal structure, except for a 35 nm damaged layer just beneath the surface. For Ne fluences of (b) 5 × 10¹⁵ and (c) 1 × 10¹⁶ Ne ions per cm², the 4D-STEM data show that the damaged regions are predominantly amorphous (median patterns) and that the degree of remnant crystallinity increases with depth. (d) The Ar irradiation is highly amorphous, indicated by the bright halos in the diffraction patterns collected above the unconverted crystal. The GIXRD pattern has a broad peak centered at 28° and no sharp peaks, indicating that the material is amorphous.

2.6 Low-loss electron energy-loss spectroscopy

Electron energy-loss spectroscopy (EELS) was used to determine the low-loss energy-loss characteristics of pristine and irradiation-damaged Bi₂O₃. EELS measurements were carried out using the TEAM I microscope in scanning transmission electron microscopy (STEM) mode. The TEAM I is equipped with a GIF Continuum detector and energy filtering. Wien filter monochromation, a 5 mm beam slit, and an energy dispersion of 30 meV per channel produced an energy resolution of 0.18 eV, resulting in distinguishable features in the plasmon and valence energy regime extending to 77 eV. Analysis focused on spectral features emerging below 40 eV. The third condenser lens current was set to produce a convergence angle of 20.5 mrad and the resulting probe current was approximately 0.1 nA. EEL spectra were collected with a Gatan K3 single electron detector. EELS maps were collected from regions of the samples with thickness in units of the inelastic mean free path (t/λ) < 0.62 (t = 46 nm) to minimize plural scattering due to thickness effects. EELS maps were acquired with a 5–8 nm step size and 0.5% frame/pixel live time. The residual plural scattering signal was removed by deconvolving the spectra with the zero-loss peak (ZLP) and the ZLP was removed before performing Kramers–Krönig analysis to determine the energy-loss function (ELF) using Gatan's DigitalMicrograph package.³⁷ Spectral maps were collected from the three Bi₂O₃ samples shown in Fig. 1, each irradiated with a different ion species.

3 Results and discussion

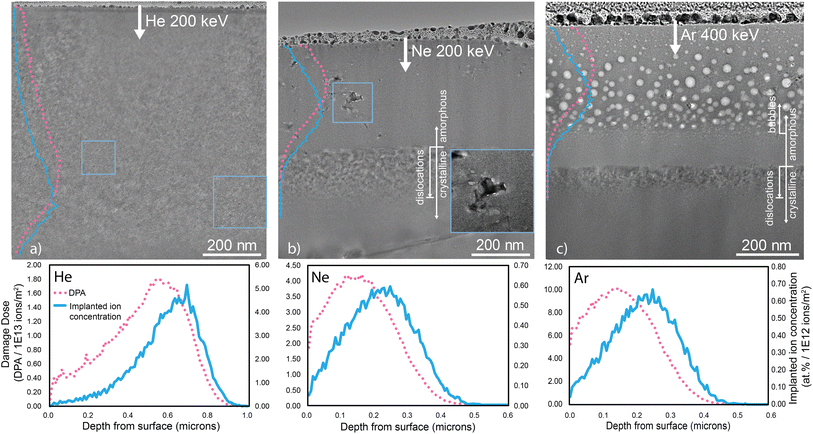
In Bi₂O₃, we observe increased amorphization with both fluence and ion species. To our knowledge, this is the first study on ion irradiation of Bi₂O₃. Ion stopping consists of mixed electronic and nuclear stopping that is depth-dependent, with electronic stopping dominating near the surface and nuclear stopping becoming more significant deeper into the bulk. Using multiple TEM techniques, structural transformations are correlated with changes in mass transport, indicated by bubble nucleation and coarsening, and changes in the electronic structure and band gap.

3.1 Structural characterization and phase transformation

He irradiation produces small bubbles throughout Bi₂O₃, resulting in minor swelling of the crystal structure without causing any phase transformation. Table 1 shows that even at the lowest fluence, Ar amorphizes Bi₂O₃, while at the highest fluence He does not. For Ne irradiation at 200 keV with 1 × 10¹⁶ Ne ions per cm², the damaged region has significantly amorphized. However, the amorphous region features small crystallites embedded within the matrix. Conversely, Ar irradiation leads to the formation of a nearly fully amorphous region, contrasting with the largely but not completely amorphous state induced by Ne irradiation. A comparison between Ne and Ar (1 × 10¹⁶ ions per cm²) irradiation reveals differences in the depth and extent of amorphization, with the amorphous band reaching approximately 315 nm and 440 nm depths, respectively (Fig. 1). Beneath each amorphous region, a crystalline region with densely entangled dislocation loops marks the termination of the amorphous front, emphasizing the species and fluence dependency of amorphization characteristics. The dislocation loop structures are similar for the Ne and Ar irradiations and likely result from high interstitial mobility past the end of the damage range.^31,32,34

3.2 Propensity for amorphization

The extent of Bi₂O₃ amorphization within the damaged regions is complexly governed by multiple irradiation parameters, including the fluence, the ion species, and the irradiating energy. Fig. 1 shows the impact of ion species on damage-induced amorphization. He irradiation mainly produces Frenkel pair defects in low-energy recoil events, while Ne and Ar predominantly produce Frenkel pair defects and defect clusters in energetic displacement cascades.^38,39 Radiation-induced damage is dependent on the collision cascade density of the irradiating ion species, with heavier ions having higher cascade energy densities. He, the smallest species, penetrates furthest into Bi₂O₃ without inducing a phase change in the crystal. The He irradiation was performed at a higher fluence, 1 × 10¹⁷ He ions per cm², than was used for the Ne and Ar irradiations because lower fluences produced no observable structural changes. The other fluences used for He irradiation at 200 keV are listed in Table 1. Even at 1 × 10¹⁷ He ions per cm², only minor swelling is observed. Minor swelling is supported by a slight downward shift (larger d-spacing indicative of increased volume) in the GIXRD pattern as compared to reference X-ray data for α-Bi₂O₃ (ICDD PDF4+ Bi₂O₃-04-003-2034), as shown in Fig. S3 of the ESI.† The resistance of Bi₂O₃ to phase change or amorphize under He irradiation can be explained by the relatively small energy transfer from the He ions to the Bi and O atoms (Table 3) and a dilute cascade density imparting damage over an approximately 1 μm depth.

Table 3 Calculated kinetic energy transferred between ion species and Bi₂O₃ constituent atoms. The efficiency factor, Λ, for constituent atoms is described, as the multiplier term for K_i. Bi has a mass of 208.98 amu and O has a mass of 16.00 amu. Bi₂O₃ was only experimentally irradiated with Ar at 400 keV, but 200 keV Ar irradiation (*) is included as a comparison for the He and Ne irradiations performed at 200 keV

Ion species	Mass	Energy	Efficiency factor, Bi	K f Bi [keV]	Efficiency factor, O	K f O [keV]
He	4.00 amu	200 keV	0.07	14.7	0.64	128.0
Ne	20.18 amu	200 keV	0.32	64.2	0.99	197.3
Ar	39.95 amu	400 keV	0.54	215.6	0.82	326.7
Ar	39.95 amu	200 keV*	0.54	107.8	0.82	163.4

---

The impact of ion species and kinetic energy is tabulated in Table 3, where it is shown that ion species with atomic masses more similar to those of Bi and O transfer the most energy and impart the most damage and that O is more readily displaced. The energy values in Table 3 represent the maximum energy imparted during collisions. The minimum energy required for displacement, E_d, is orders of magnitude lower and generally in the 30 to 60 eV range for binary ceramic systems.³¹

To understand to some extent the differences in damage produced by the different species, we consider the kinematics of energy transfer in the three different cases. For a two-body interaction, classical mechanical theory reveals that the fractional kinetic energy transfer for a head-on collision between two particles, known as the kinetic energy transfer efficiency factor (Λ), is the ratio of kinetic energy imparted to the resting target particle from the projectile (irradiating) particle to the initial kinetic energy of the projectile particle. The efficiency factor has no dependence on the magnitude of the irradiation energy. Also, the fractional energy transfer diminishes rapidly with increasing mass disparity between species Bi and O. Representative values for kinetic energy transfer are provided in Table 3, in which it is shown that He transfers a relatively small fraction of energy to Bi as compared to Ar, indicating that Ar will produce much more energetic collisions and thus much higher damage generation rates in the material. Further, the large mass disparity between Bi and O results in a discrepancy in the energy transferred to these two atoms during ion collisions. The discrepancy in energy transfer between Bi and O is greatest for He, the lightest ion, with Λ for He ion–O atom interaction being particularly low at 0.07. However, atomic displacement and the extent of amorphization are complexly governed by other factors, such as binding energy, which is best captured by the minimum required displacement energy E_d.

An interesting observation is that the amorphization begins from the surface of the sample and moves inward with increasing fluence, rather than first nucleating where the estimated DPA is highest, as happens with other oxides.^40,41 The mechanisms responsible for the downward propagation of the amorphous front from the surface are not clear. Amorphization in the Ne and Ar irradiations begins at the surface and propagates downward with increasing fluence, illustrating the complex interplay between surface sensitivity and damage accumulation. At lower fluences, the surface is more readily amorphized due to the higher relative impact of electronic stopping power and reduced defect recombination rates as some defects segregate to the nearly ideal surface sink. As fluence increases and more damage is introduced into the system, the amorphous region moves deeper into the material, eventually reaching the point where the maximum dpa is being introduced into the material. While we do not have a complete understanding of amorphization in Bi₂O₃, the Ne amorphizations with varying fluences indicate that amorphization extends deeper as now the amorphous–crystalline interface potentially acts as a defect sink (a hypothesis supported by the fact that in the Ne irradiated sample, there are bubbles at the crystalline–amorphous interfaces), further inhibiting the recombination of defects and exacerbating the amorphization process. Shen et al.⁴² proposed that this effect is due to a disparity in defect mobilities near the sample surface. For instance, fast-moving cation and anion interstitial point defects (Bi_i³⁺ and O_i²⁻, respectively) may migrate preferentially to the free surface and annihilate. The consequence of this would be that slower migrating vacancy defects are left behind in the near-surface sample region. These unpaired vacancies cannot annihilate harmlessly. In contrast, they destabilize the crystal structure and lead inevitably to amorphization. The segregation of these defects to the surface may also induce a space charge near the surface. We have shown previously that such space charges can dramatically impact the redistribution of defects in irradiated materials.⁴³ In this case, if one species segregates, it could prevent like-charged defects from also reaching the surface via electrostatic repulsion, hindering recombination. However, more work would be done to truly elucidate the origin of the enhanced surface amorphization.

The relationship between ion species, irradiation energy, and the atomic mass of constituent elements aids in understanding the amorphization observed in the Ne and Ar irradiated Bi₂O₃. For ion species capable of delivering sufficient energy for amorphization, the depth of the amorphization is dependent on the fluence, as evident in the series of Ne irradiations, as shown in Fig. 2. Higher fluences of 5 × 10¹⁵ Ne ions per cm² and 1 × 10¹⁶ Ne ions per cm² result in damage and amorphization deeper into the samples as well as increasing homogeneity in the amorphous structure as a result of reduction in crystallinity and destruction of crystallites that were observed in the amorphous zone at lower fluence. It is observed that the damage profile transmits downward with increasing fluence. This is notable, as amorphization and damage in irradiated metallic alloys and some ceramics tend to propagate from the maximum DPA depth, not from the surface into the bulk, with greater fluences. A similar downward propagation of the amorphous damage layer has been observed in some ceramics, including Al₂O₃,⁴⁴ γ-LiAlO₂,⁴⁵ TiO₂,⁴⁶ and MgGa₂O₄.⁴² The downward propagation of the amorphous front is not captured by SRIM, but is likely attributable to a supersaturation of defects resulting in amorphization. Similar to observations made by Shen et al.,⁴² the stratified amorphization likely results from disproportionate defect mobilities, with vacancies remaining in the structure and disrupting the crystal structure to the point of amorphization. Below the amorphized region, in the bulk, vacancy-interstitial recombination preserves the original crystal structure.⁴² The surface layer amorphizes due to combined electronic stopping and cascade effects, with electronic stopping dominating near the surface and cascade effects prevailing near the maximum DPA depth. DPA at a specific depth is proportional to ion fluence, resulting in thicker amorphous layers with increased fluences.^42,45

The dependence of phase transformation on ion fluence was determined from images collected from samples irradiated with Ne ions. TEM analysis of these samples demonstrates the critical fluence required for amorphization, with the amorphization depth increasing with fluence. The Bi₂O₃ irradiated with 2.5 × 10¹⁴ Ne ions per cm² exhibits a small, roughly 35 nm polycrystalline region beneath the surface, while the Bi₂O₃ irradiated with 5 × 10¹⁵ Ne ions per cm² displays a 215 nm amorphous layer with sparse crystallites (Fig. 2). Similar to other irradiated oxides,^42,44,45 this suggests that a critical fluence is necessary for amorphization and that electronic stopping dominates just below the surface while nuclear stopping dominates deeper into the bulk damaged material, highlighting the depth dependence of the ENSP ratio. ENSP influences radiation response and recovery, with greater ENSP values indicating ion–crystal structure interactions governed by inelastic scattering that results in heightened temperatures local to the site of ion collision.⁴⁷ Electronic and nuclear stopping energies as a function of incident ion energy (dE/dx) and ENSP ratios are provided in Table 2. The He irradiation conditions produce substantially higher ENSP values compared to the Ne and Ar irradiation conditions. Nuclear stopping is negligible for He irradiations, indicating that a lower ENSP ratio is required for amorphization and explaining the retained alpha structure of He-irradiated Bi₂O₃. Ar irradiation, despite having the highest electronic stopping power, leads to the most amorphization. While this is counter-intuitive as high electronic stopping could contribute to annealing,⁸ Ar also has the highest nuclear stopping power, suggesting that the ratio of electronic to nuclear stopping power is crucial, with nuclear stopping overwhelming electronic effects in this case.

To assess relative displacive radiation damage under different ion irradiation conditions, it is useful to calculate the total point defect production by an energetic ion, normalized by the longitudinal range of this ion. This normalization offers a crude means to account for differences in cascade volumes for various irradiation conditions. We will refer to this ratio, i.e., the ratio (total number of i–v pairs)/R, where R is the longitudinal (projected) ion range, as the linear displacement damage density (LDDD). For instance, comparing 200 keV He versus 400 keV Ar ion irradiation conditions, SRIM calculations reveal that LDDD^200keVHe = 0.1(i–v pairs)/(nm per ion), compared to LDDD^400keVAr = 9(i–v pairs)/(nm per ion). This nearly two order of magnitude difference translates to a similar difference in the displacement damage efficiency of 200 keV He versus 400 keV Ar, with Ar being the far more efficient damaging ion over the respective ion ranges of these two species. The SRIM-derived values used for these calculations are provided in the ESI,† but it is worth cautioning against using these calculations for more than qualitative comparisons, as the LDDD values above have the following problems: (1) they ignore the pear-shaped volume of the displacement cascade (with a wider girth near the end of range of the ion) and (2) they ignore the fact that the number density of i–v defects peaks near the end of range (so that the LDDD actually varies from a small value near the target surface to a value at the end of range that is a relatively large fraction of each calculated LDDD value provided above). In addition, for comparison, we note that LDDD^200keVNe = 0.3(i–v pairs)/(nm per ion) and LDDD^200keVAr = 10(i–v pairs)/(nm per ion). In summary, the heavier Ar ions yield the highest values of LDDD, while the lightest He ions produce far smaller displacement damage densities per ion (with the LDDD for Ne being intermediate between those of He and Ar). Also, the LDDD parameter seems to correlate with the degree of amorphization observed in Bi₂O₃, with Ar being highly efficient at inducing amorphization per unit fluence, while He does not result in amorphization, even at ion fluences 100 times that of Ar. Considering the representative LDDD and lambda values, the particular species used for irradiation contributes, along with the differences in the ENSP, to the amorphization due to the damage density and displacement of either Bi and O atoms.

While Ar was experimentally irradiated at 400 keV, the calculated kinetic energy transferred for 200 keV irradiation is also included in Table 3 for comparison with the He and Ne irradiations at 200 keV. Compared to Ne collisions at 200 keV, the relative energy transfer for Ar collisions at 200 keV is greater for Bi atoms than for O atoms, despite the overall transfer of energy remaining higher for O. At 400 keV, Ar irradiation with a fluence of 1 × 10¹⁶ Ar ions per cm² results in a large, roughly 440 nm layer of amorphous Bi₂O₃. Unlike the Ne irradiations, this amorphous region does not contain distinguishable crystallites of the pristine structure, aligning with a direct damage model, in which incident ions induce a crystalline-to-amorphous phase transformation.⁴⁸ Based on SRIM stopping calculations (Fig. 1(c)), 400 keV Ar irradiations impart significantly more damage in Bi₂O₃ than He and Ne at 200 keV, validating the observations of complete amorphization at the irradiated surface.

3.3 Bubble characteristics

Bubble formation is evident across all samples, but with diverse size and distribution characteristics. EDS, shown in Fig. S4 of the ESI,† confirm that the cavities are gas filled bubbles. Generally, bubble size correlates with the radiating species, with Ar generating the largest bubbles. Ion irradiation creates defects on all sublattices and of all species types, though, as discussed, with varying efficiency. This phenomenon has been demonstrated across various systems, including bulk metallic glasses⁴⁹ and ceramics.^50–52 In oxides, oxygen vacancy clusters often exhibit high mobility,⁵³ but the coarsening of gas bubbles indicates that the transport of multiple species, not just oxygen, is involved. Ultimately, bubbles coarsen through vacancy-mediated transport of gas species.⁵⁴ Critically, this involves transport of all matrix species; otherwise the bubbles would not form as three-dimensional cavities but rather as one- or two-dimensional linear or planar inclusions on one sublattice. In irradiated Bi₂O₃, the size and density of the gas bubbles vary with the atomic structure, indicating differing degrees of atomic mobility.

In the He-irradiated sample, small bubbles a few nanometers in size are dispersed throughout the crystalline structure within the top 850 nm of Bi₂O₃, with maximum density observed around 600 nm and maximum size occurring around 680 nm below the surface. This is observed in Fig. 1(a) and replicated as a larger image in Fig. S5 in the ESI.†

Two classes of bubbles are visible at the higher fluence Ne irradiations. For fluences of 5 × 10¹⁵ and 1 × 10¹⁶ Ne ions per cm², smaller bubbles form within the amorphous matrix, and larger non-circular bubbles appear at crystallite–matrix interfaces within the amorphous region, as seen in Fig. 1(b). The formation of anisotropic Ne bubbles is explained by a surface energy minimization argument. To minimize the total surface area of the bubbles, the bubbles extend in both directions along the interfaces.⁵⁵ Once the material amorphizes, vacancy transport seems to be much faster, with bubbles coarsening even at lower temperatures. They also nucleate at the interfaces between the amorphous matrix and the embedded crystallites, indicating their ability to transport over long distances. The larger bubbles, shown in the inset of Fig. 2(b), have high aspect ratios as they trace the interface.

Ar irradiation at room temperature yields the most significant variation in bubble sizes (Fig. 1(c)), with the largest bubbles positioned approximately 150 to 200 nm below the surface, closely matching the calculated peak DPA depth of 174 nm. The largest bubbles exhibit areas exceeding 700 nm², an order of magnitude larger than those observed in any other sample. This implies that mass transport is much higher in the amorphous phase, as bubbles can coarsen to quite large sizes. While additional factors, such as surface energy, likely contribute to bubble size, they do not explain the large difference in bubble sizes between the crystalline (He irradiated) and fully amorphous (Ar irradiated) cases. The He bubbles have an average projected area of 2.9 nm² with a standard deviation of 1.5 nm², while the Ar bubbles have an average projected area of 164.0 nm² with a standard deviation of 150.1 nm². The difference in the projected bubble area, which is roughly two orders of magnitude between these two cases, cannot be explained by structural relaxations alone; it must be primarily attributable to mass transport mediated bubble coarsening. That is, simply introducing the same number of gas atoms in a spherical inclusion in the two structures would not lead to such dramatic differences in size. The 4D-STEM diffraction patterns show negligible change in the (120) spacing and the packing density likely has not changed by more than 10%.⁵⁶ Further, while the bubble number density decreases significantly between the He and Ar irradiations, the bubbles are much larger, indicating that coalescence is mediated by transport mechanisms.

To emphasize the connection between amorphization and mass transport, Bi₂O₃ was irradiated with Ar with a temperature variation of 300 °C with the same fluence and energy (1 × 10¹⁶ Ar ions per cm² and 400 keV) as the room temperature (22 °C) irradiation. Bi₂O₃ does not amorphize at the higher temperature, as shown in Fig. S2 of the ESI.† Compared to the 22 °C Ar irradiation, a more dispersed layer of dislocation loops is seen 440 nm below the surface. Small bubbles are observed in the crystal above the dislocation loops. At an elevated temperature, despite presumably higher nucleation and growth kinetics, the Ar bubbles are smaller than they are at 22 °C. We attribute this to faster transport in the amorphous phase. While there is less coarsening at higher temperature, the lower temperature amorphous phase transformation promotes mass transport, much more effectively than the higher temperature does in the crystalline phase. The observed reduction in bubble coarsening in the Ar irradiation at 300 °C compared to amorphized samples signifies that mass transport is greater in the amorphous phase.²³ The lack of long range periodicity and increased free volume can act to promote ion migration. The ions may have an increased propensity for migration when they are unassociated with a defined crystal structure. For Ar, it means that the bubbles coarsen and for Ne, it means they segregate to traps, such as amorphous–crystalline interfaces.

3.4 Microstructural variations

Scanning nanodiffraction, shown in Fig. 3, was used to investigate crystal structure changes on the nanometer scale at varying depths beneath the irradiated surfaces. Fig. 3 includes virtual dark field images, where contrast is determined by diffraction scattering. Thus, crystalline regions appear darker, while voids and bubbles appear lighter. 4D-STEM data sets were acquired from cross-sections of the irradiated samples. From the data sets, diffraction patterns were aggregated along rows, indicated with shaded boxes in Fig. 3, at select depths beneath the surface. Mean and median patterns derived from the aggregated rows provide insights into the average and most prevalent microstructures, respectively, at various depths within the damaged Bi₂O₃. The presence of distinct Bragg spots is indicative of crystallinity, while a diffuse halo is evidence of an amorphous structure. 4D-STEM was used to index the crystallographic orientation of the structure beneath the amorphous zones, capture structural information from deeper into the sample than is possible with GIXRD, and measure the depth-dependence of crystallite prevalence in the amorphous zones.

As we have discussed, Bi₂O₃ irradiated with He retains full crystallinity throughout the damaged region. Bubbles are observed in the top 850 nm, within a single crystal structure and orientation that matched that of Bi₂O₃ below the penetration depth of the He ions. This is shown in Fig. S3 of the ESI,† accompanied by GIXRD, also indicating that the structure remains crystalline.

In contrast, samples irradiated with Ne displayed a fluence-dependent amorphization profile that changed across the depth of the damaged region. At the lowest fluence of 2.5 × 10¹⁴ Ne ions per cm², a 35 nm layer of polycrystalline and some amorphous character was observed beneath the surface. Higher fluences of 5 × 10¹⁵ Ne ions per cm² and 1 × 10¹⁶ Ne ions per cm² resulted in amorphization deeper beneath the surface. A comparison between the two high-fluence Ne irradiations revealed predominantly amorphous regions above the layer of dislocation loops, with the higher fluence resulting in a greater propensity for amorphization. This is best observed by comparing the mean and median of the summed patterns from approximately 150 nm below the sample surfaces, shaded in dark blue in Fig. 3(a and b). For both samples, at a depth of 150 nm, the median pattern indicates a predominantly amorphous structure. However, the mean patterns suggest a higher percentage of polycrystallinity in the lower fluence Ne irradiation. Additionally, from the mean patterns in Fig. 3(b and c), it is apparent that the prevalence of crystallites is depth dependent, as within the predominantly amorphized region, the amorphous halo signal dominates near the sample surface, while stronger crystalline scattering is observed deeper into the samples.

The presence of both a polycrystalline region near the surface for Ne irradiation with 2.5 × 10¹⁴ Ne ions per cm² and a dislocation region after the amorphous region suggests that interstitial mobility is relatively high. For Ar irradiation at 400 keV and 1 × 10¹⁶ Ar ions per cm², the impacted region displayed complete amorphization, evidenced by fully amorphous median and mean diffraction patterns. Unlike the Ne irradiation, which resulted in a depth-dependent propensity for amorphization, the extent of amorphization for Ar irradiation appears depth independent within the amorphized layer for Ar irradiation. The first amorphous halos in the Ne and Ar diffraction patterns have a d-spacing of 3.3 Å, matching the d-spacing of the α-Bi₂O₃ (120) peak at 27.36° from the GIXRD pattern in Fig. 3. While this nearest neighbor spacing remains similar, indicating that the short range order is also likely similar between the two structures, amorphization typically results in reduced atomic packing density, or increased volume, which we will analyze in more detail in future work. Except for the He-irradiated sample, structural changes on the nanometer-scale varied with depth, particularly near the interface between the ion damaged layer and the initial Bi₂O₃ structure.

3.5 Band gap widening and electronic structure

EELS measurements collected from the low-loss energy range show a change in the electronic structure of Bi₂O₃ as it is converted from the α-phase to an amorphous structure. Amorphization results in a wider band gap and more dispersed band structure. As seen in the ELFs shown in Fig. 4, the electronic band gap of the material increases with amorphization. The band gap is the energy onset corresponding to the first edge. The spectra are normalized by the maximum peak height in the 0 to 40 eV range to highlight relative differences in the intensities of spectral features. We measure a band gap of 2.64 eV for the original α-Bi₂O₃ structure (t/λ = 0.62), within the reported range of 2.1 to 2.8 eV for α-Bi₂O₃.^12,57 The band gap widens to 3.48 eV for the fully amorphized Ar irradiated Bi₂O₃ (t/λ = 0.50). Additionally, the slope of the spectra between the first edge onset (band gap) and the (a) edge peak increases with amorphization, indicating wider, more dispersed band tails. The ZLP energy resolution is 0.18 eV, introducing an equal amount of uncertainty to the measurements. The ZLP and the unprocessed EEL spectra are provided in Fig. S6 of the ESI.†

Fig. 4 Energy-loss functions (ELFs) from experimental EELS show differences in the dielectric properties and electron occupancy between pristine and irradiated α-Bi₂O₃. A band gap of 2.64 eV is measured for pristine Bi₂O₃ at the onset of the first edge. The band gap widens as the Bi₂O₃ is amorphized. Additionally, the primary plasmon edge shifts upward in energy for samples amorphized through irradiation. (a) The first edge results from direct, single-electron interband excitations above the Fermi level. (b) The second edge results from plasmon resonance. (c) The valence plasmon edge is positioned between 19.2 and 21.0 eV. There is an upward shift in the plasmon peak position for predominantly amorphous Bi₂O₃. Dashed gray lines denote the edge maxima. (d) A slight upward shift of the Bi O_4,5 edges is also observed for amorphized samples. (e) The feature around 30 eV is attributable to Bi. The band gaps are indicated by red lines at the onset of the (a) peaks. The inset shows the 0 to 10 eV region of the pristine and fully amorphized Bi₂O₃ spectra, highlighting the increase in the band gap and band tailing of the amorphous sample.

The labeled features in Fig. 4 are: (a) the lowest energy edge resulting from direct, single-electron interband excitations above the Fermi level. These electrons are directly emitted from the valence band.⁵⁸ The onset of the edge is the band gap energy. The band tail above the edge is typical of solid ionic conductors with high defect concentrations.⁵⁸ (b) The second edge results from plasmon excitations.⁵⁹ However, the Ne and Ar M_4,5 edges lie at 18 and 12 eV, respectively, and may contribute to their respective spectra.⁶⁰ (c) The most prominent peak, the valence plasmon edge, is positioned between 19.2 and 21.0 eV.^37,61 There is an upward shift in the plasmon peak position for predominantly amorphous Bi₂O₃. Dashed gray lines mark the edge maxima. (d) The small edges visible between 24 and 27 eV are the Bi O_4,5 edges excited from 5d electrons.⁵⁹ A slight upward shift in these features is also observed for amorphized samples. (e) The second largest edge is attributable to Bi and appears between 27 and 30 eV and is more pronounced for the amorphous sample regions.⁶⁰

Irradiation with He does not induce a phase transformation, but does result in minor swelling of the lattice and, presumably, introduces some degree of disorder. Consequently, the band gap increases to 2.94 eV. The band edges are most distinct in the EELS data for the unirradiated and He irradiated samples.

The Ne irradiated sample is amorphized with dispersed crystalline regions. The band gap associated with Ne irradiation is slightly more ambiguous as the edge onset has a gentler slope with small steps; however, the most obvious step in the slope is at 3.30 eV. The ambiguity is likely attributable, at least in part, to band smearing associated with structural disorder.⁶² Additionally, the mixed phase nature of the Ne irradiation likely superimposes multiple band structures, increasing the difficulty and uncertainty of extracting a single band gap value. For Ar irradiation resulting in nearly complete amorphization, the largest band gap observed is 3.48 eV. To our knowledge, this is the first band gap measurement on amorphous Bi₂O₃, so comparison against other reported values is not possible. However, amorphization resulting in wider band gaps has been observed in other amorphous oxides, such as TiO₂ (ref. 63 and 64) and ZnO.⁶⁵

The electronic density of states and localization are sensitive to the atomic structure. Lattice disorder causes electron localization, leading to overlapping bands and band tailing, resulting in modified band gaps.^62,66 The slope of the spectra between the band gap and the first edge, labeled (a), decreases as a function of amorphization. Pristine Bi₂O₃ has a more abrupt band edge compared to the amorphized Ar irradiated samples, which have a more gently sloped band edge. The gentler slope indicates greater band tailing and electron dispersion, which results in less efficient electron transport.^3,66 In addition to complete structural changes such as amorphization, irradiation can also introduce point defects into the original crystal structure. Compared to individual defects, the structural transformation of amorphization in ceramics has a greater impact on electron mobility and band structure.^67,68 Amorphization is an extreme form of disorder, resulting from defect accumulation and atomic displacements. While the generation of vacancies, antisites, and various defects due to irradiation is well documented, amorphization results in a highly disordered structure with disrupted electron mobility. In amorphous Bi₂O₃, the lack of crystalline periodicity impairs electron conduction. Additionally, variations within the amorphous structure may create localized trap states, similar to defects in a crystalline lattice, but with higher prevalence in the amorphous structure. While the band edge broadening and onset ambiguity for the Ne and Ar irradiations are attributed to the break down of the band structure with reduced structural ordering, the small spectral features observed prior to the band onset have two likely origins: remnant crystalline pockets on the order of a few nanometers within the amorphous matrix with band structures similar to that of the pristine structure or trap states due to localized electronic states in the disordered structure.^66,69

A wider band gap is desirable for Bi₂O₃-based solid electrolytes to reduce the electronic conductivity of the material.⁵⁸ Ionic mobility is mediated by intrinsic and extrinsic defects, and thus as non-equilibrium defect content increases with irradiation, ion mobility tends to increase as the ions can more easily maneuver between vacancy sites. However, these same defects can disrupt the electron structure, as evidenced in the band structural changes for He irradiated Bi₂O₃, which remained crystalline after irradiation (Fig. 4), impeding electron mobility by scattering or trapping them. Similarly, the structural disorder and reduced density inherent in amorphous materials can create pathways for ion conduction, but disrupt the periodicity required for electron conduction. This is also evident in Fig. 4 for the Ne and Ar irradiations. This is beneficial for mass transport as ion conductivity dominates over electron conductivity and the material is considered more insulating.^11,70 A widened band gap indicates decreased electron mobility and suggests improved ionic mobility. However, as noted in the Introduction, ionic conduction is complexly governed by multiple material parameters.²⁹

Irradiation results in a nonuniform damage region and variations in the electronic structure along the direction of irradiation. Microstructural alterations, shown with 4D-STEM in Fig. 3, induce variations in the electronic structure and ionic conductivity across the Ne irradiated Bi₂O₃. These changes are reflected as up-shifts in the energy-loss associated with electron transitions and plasmon edges. There are five main edge features in the spectra, labeled in Fig. 4. The amorphized samples exhibit an upward shift in energy for all edge features. The upward shift is most pronounced in the plasmon peak shift from 19.2 to 21.0 eV. Plasmons are collective oscillations of electrons and the plasmon edge energy is indicative of free volume per electron. The increase in plasmon energy associated with amorphization, as seen in Fig. 4, may result from the introduction of the irradiating species into the material or may be more directly related to the high degree of structural disorder in the amorphized (Ar) Bi₂O₃and Bi₂O₃amorphized with crystallites (Ne). Increased disorder can reduce electron screening, broaden and disperse band structures, and increase electron scattering, all of which can result in higher effective electron densities and localization.^66,71 Electron localization creates overlapping bands and band tailing, potentially interacting with plasmon dynamics.^62,66 Determining the precise cause of the energy shift is challenging because irradiation structurally introduces phase transformations that alter local bonding environments and compositionally alters the stoichiometry of the material through the introduction of an ion species.

3.6 Stoichiometric variations following irradiation

In addition to amorphization, Ne irradiation results in the formation of crystal structures that are off-stoichiometry from the original crystal. The result is a nonuniform damage region that, unlike the Ar irradiation, has an amorphous region punctuated by localized stoichiometric and crystal structure variations. Spectral mapping was conducted on and around a crystallite in the amorphous matrix of Bi₂O₃ irradiated at 200 keV with Ne and a fluence of 1 × 10¹⁶ Ne ions per cm², as shown in Fig. 5. EEL spectra were summed from a 100 nm² region containing the crystallite, the central portion of the crystallite (36 nm²) and from three 100 nm² regions of the amorphous structure adjacent to the crystallite. The three spectra from the amorphous phase are nearly identical and correspond to regions of approximately the same thickness, with t/λ = 0.35 to 0.37. Similar to the crystalline ELF for pristine and He irradiated Bi₂O₃, the low-loss EEL spectra from the crystallite region show a relative downward energy shift in edge features and the bulk plasmon peak. However, the spectrum from the center of the crystallite, the red line plotted in Fig. 5, exhibits a much lower energy plasmon edge, with a more substantial down shift in the maximum energy of the plasmon peak to 14.8 eV.

Fig. 5 EELS collected from Bi₂O₃ irradiated at 200 keV with Ne and a fluence of 1 × 10¹⁶ Ne ions per cm². (a and b) A spectral image, in which each probe position holds a corresponding energy-loss spectrum, was collected over a crystallite embedded in the amorphous matrix. (b) Five regions from the spectral image are selected, as indicated by five shaded boxes, and the spectral intensity is summed within each region. The central region contains a crystallite. The other three regions include portions of the surrounding amorphous matrix. (c) The spectra from the three amorphous regions are nearly identical to each other with features similar to those in the ELF of pristine Bi₂O₃ in Fig. 4. The spectra corresponding to the crystallite region exhibit a plasmon peak with an even more pronounced downward shift than the crystalline spectra in Fig. 4, but still follows the trend of lower energy plasmon peaks for the crystalline Bi₂O₃ structure. A spectrum (red) collected just from the central portion of the crystallite shows an even more pronounced downward shift and significantly less pronounced edge features around 29 eV.

The L_2,3 edges of Ne lie at 18 eV, so bubbles along the crystallite edge could contribute to the variations in plasmon energy, but do not fully explain the downward shift. On the high energy tail of the plasmon peak between 24 and 27 eV, there is an additional peak around 24 eV not visible in the amorphous spectra. Local atomic deficiencies and Ne bubbles could result in a heterogeneous damage region for 200 keV Ne irradiation.

The spectrum from undamaged Bi₂O₃ is shown in black for comparison. The dramatic reduction in the intensity of the edge feature near 29 eV signifies that its magnitude is dependent on Bi electron behavior and that Bi and O concentrations vary between the crystallite and amorphous matrix. This provides evidence that, in addition to amorphization, the Ne irradiation also results in stoichiometric variation concentrated in residual crystalline regions and at phase interfaces. Based on the differences between the crystallite and undamaged crystalline spectra, the crystallite shown in Fig. 5 does not have the same structure as the original crystal. The same is observed across other large crystallites in the amorphous matrix. The high degree of microstructural variation, as shown with 4D-STEM, points to significant variations in the electronic structure and ionic conductivity across the Ne irradiated Bi₂O₃.

4 Conclusions

In Bi₂O₃, we observe an increased propensity for amorphization with larger ion species and a greater depth of amorphization with higher fluence. This is the first study investigating the ion irradiation of α-Bi₂O₃. Combined electronic and nuclear stopping is depth-dependent, with electronic stopping dominating near the surface and nuclear stopping becoming more significant deeper into the bulk. This depth dependent stopping power leads to structural transformations correlated with changes in mass transport, as evidenced by bubble nucleation and coarsening. These structural changes also alter the electronic structure, including shifts in the band gap.

Specifically, the amorphization of Bi₂O₃ is associated with a wider band gap due to the disruption of the crystal lattice and subsequent electron localization, leading to less efficient electron transport. The amorphous phase exhibits higher mass transport properties, as indicated by bubble nucleation and coarsening, suggesting enhanced ionic mobility in the amorphized regions. This behavior is critical for applications in ionic conductors, where high ion mobility is essential. Understanding the relationship between the structure of α-Bi₂O₃ and its response to ion irradiation is crucial for optimizing its use in non-equilibrium environments and exploring pathways for producing δ-Bi₂O₃. We observe significantly different amorphization responses depending on the incident ion, with Ar inducing amorphization at extremely low fluences and He not amorphizing the material at all even at significantly higher fluences. We attribute this difference to both the much higher electronic stopping to nuclear stopping ratio (ENSP) for He and the much higher propensity for Ar to transfer energy to ions in Bi₂O₃ and to cause damage to the crystal structure, as represented by the LDDD metric. At this time, we cannot fully discern which factor is most important and this is left to future work. By irradiating with different species and observing differences in bubble evolution, we can reveal how defect kinetics vary with radiation-induced phase transformations. This study lays the groundwork for further exploration into the radiation resistance of Bi₂O₃ and similar solid-state ionic conductors, broadening their applicability across various advanced technological fields.

Data availability

The data supporting this article have been included as part of the ESI.† The data used to produce Fig. 4 is shown in Fig. S6 of the ESI.†

Author contributions

E. R. Kennedy: conceptualization, formal analysis, investigation, visualization, and writing – original draft. J. Valdez: conceptualization, formal analysis, investigation, and writing – original draft. Y. Wang: investigation and resources. S. Ribet: investigation and resources. K. Sickafus: conceptualization and investigation. C. Kreller: conceptualization and funding acquisition. B. P. Uberuaga: conceptualization, writing – original draft, supervision, and funding acquisition. B. Derby: conceptualization, writing – original draft, supervision, and funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. The Los Alamos National Laboratory, an affirmative action equal opportunity employer, is managed by Triad National Security, LLC for the U.S. Department of Energy's NNSA, under contract 89233218CNA000001. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. The authors thank Chengyu Song for maintenance of and assistance with the TEAM I TEM at the Molecular Foundry.

References

1. V. Fruth, G. Dobrescu, V. Bratan, C. Hornoiu, S. Preda, C. Andronescu and M. Popa, J. Eur. Ceram. Soc., 2007, 27, 4421–4424.
2. H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392.
3. D. Wohlmuth, V. Epp, P. Bottke, I. Hanzu, B. Bitschnau, I. Letofsky-Papst, M. Kriechbaum, H. Amenitsch, F. Hofer and M. Wilkening, J. Mater. Chem. A, 2014, 2, 20295–20306.
4. Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976.
5. Q. Wang, H. Fan, Y. Xiao and Y. Zhang, J. Rare Earths, 2022, 40, 1668–1681.
6. V. I. Hegde, M. Peterson, S. I. Allec, X. Lu, T. Mahadevan, T. Nguyen, J. Kalahe, J. Oshiro, R. J. Seffens, E. K. Nickerson, J. Du, B. J. Riley, J. D. Vienna and J. E. Saal, Digital Discovery, 2024, 3, 1450–1466.
7. G. Hopkins and R. Price, Nucl. Eng. Des./Fusion, 1985, 2, 111–143.
8. S. Zinkle, V. Skuratov and D. Hoelzer, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 191, 758–766.
9. J. Won, L. J. Vernon, A. Karakuscu, R. M. Dickerson, M. Cologna, R. Raj, Y. Wang, S. J. Yoo, S.-H. Lee, A. Misra and B. P. Uberuaga, J. Mater. Chem. A, 2013, 1, 9235–9245.
10. J. Wang, Z. Liu, B. Kong, X. An, M. Zhang and W. Wang, Phys. Chem. Chem. Phys., 2023, 25, 14417–14429.
11. X. Lei, W. Wu, B. Xu, C. Ouyang and K. Huang, Mater. Des., 2020, 185, 108264.
12. A. H. Zahid and Q. Han, Nanoscale, 2021, 13, 17687–17724.
13. Y.-C. Liang and Y.-H. Chou, RSC Adv., 2020, 10, 45042–45058.
14. A. Walsh, G. W. Watson, D. J. Payne, R. G. Edgell, J. H. Guo, P. A. Glans, T. Learmonth and K. E. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–13.
15. N. J. Madden, S. A. Briggs, D. Perales, T. J. Boyle, K. Hattar and J. A. Krogstad, Measuring Radiation Enhanced Diffusion Through in situ Ion Radiation Induced Sintering of Oxide Nanoparticles, Acta Mater., 2021 DOI:10.2139/ssrn.3951050.
16. H.-Y. Jiang, J. Liu, K. Cheng, W. Sun and J. Lin, J. Phys. Chem. C, 2013, 117, 20029–20036.
17. Y. Zhu, E. R. Kennedy, B. Yasar, H. Paik, Y. Zhang, Z. D. Hood, M. Scott and J. L. Rupp, Adv. Mater., 2024, 36, 2302438.
18. V. Kocevski, G. Pilania and B. P. Uberuaga, Mater. Des., 2023, 228, 111830.
19. C. N. R. Rao, G. V. S. Rao and S. Ramdas, J. Phys. Chem., 1969, 73, 672–675.
20. M. Vila, C. Díaz-Guerra and J. Piqueras, Appl. Phys. Lett., 2012, 101, 071905.
21. C. Lu, Z. Lu, X. Wang, R. Xie, Z. Li, M. Higgins, C. Liu, F. Gao and L. Wang, Sci. Rep., 2017, 7, 40343.
22. Y. Zhang, X. Wang, Y. N. Osetsky, Y. Tong, R. Harrison, S. E. Donnelly, D. Chen, Y. Wang, H. Bei, B. C. Sales, K. L. More, P. Xiu, L. Wang and W. J. Weber, Acta Mater., 2019, 181, 519–529.
23. C. R. Kreller, J. A. Valdez, T. G. Holesinger, J. Morgan, Y. Wang, M. Tang, F. H. Garzon, R. Mukundan, E. L. Brosha and B. P. Uberuaga, J. Mater. Chem. A, 2019, 7, 3917–3923.
24. B. P. Uberuaga and L. J. Vernon, Solid State Ionics, 2013, 253, 18–26.
25. J. S. Lim, H.-H. Nahm, M. Campanini, J. Lee, Y.-J. Kim, H.-S. Park, J. Suh, J. Jung, Y. Yang, T. Y. Koo, M. D. Rossell, Y.-H. Kim and C.-H. Yang, Nat. Commun., 2022, 13, 5130.
26. J. H. Lunsford, Effects of Irradiation on the Catalytic Activity of Metal Oxides, Rice University Library, 1961.
27. H. L. Tuller, Science and Technology of Fast Ion Conductors, Springer US, Boston, MA, 1989, pp. 51–87.
28. T. Holesinger, J. A. Valdez, M. T. Janish, Y. Wang and B. P. Uberuaga, Acta Mater., 2019, 164, 250–260.
29. Y. Orikasa, Y. Gogyo, H. Yamashige, M. Katayama, K. Chen, T. Mori, K. Yamamoto, T. Masese, Y. Inada, T. Ohta, Z. Siroma, S. Kato, H. Kinoshita, H. Arai, Z. Ogumi and Y. Uchimoto, Sci. Rep., 2016, 6, 26382.
30. J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823.
31. L. W. Hobbs, F. W. Clinard, S. J. Zinkle and R. C. Ewing, J. Nucl. Mater., 1994, 216, 291–321.
32. Y. Matsukawa and S. J. Zinkle, Science, 2007, 318, 959–962.
33. Q. Dong, Z. Yao, P. Saidi and M. R. Daymond, J. Nucl. Mater., 2018, 511, 43–55.
34. K. Vogel, P. Chekhonin, C. Kaden, M. Hernández-Mayoral, S. Akhmadaliev and F. Bergner, Nucl. Mater. Energy, 2021, 27, 101007.
35. B. H. Savitzky, S. E. Zeltmann, L. A. Hughes, H. G. Brown, S. Zhao, P. M. Pelz, T. C. Pekin, E. S. Barnard, J. Donohue, L. R. DaCosta, E. Kennedy, Y. Xie, M. T. Janish, M. M. Schneider, P. Herring, C. Gopal, A. Anapolsky, R. Dhall, K. C. Bustillo, P. Ercius, M. C. Scott, J. Ciston, A. M. Minor and C. Ophus, Microsc. Microanal., 2021, 1–32.
36. S. E. Zeltmann, A. Müller, K. C. Bustillo, B. Savitzky, L. Hughes, A. M. Minor and C. Ophus, Ultramicroscopy, 2020, 209, 112890.
37. J.-M. Costantini and J. Ribis, Materials, 2023, 16, 7610.
38. R. S. Averback, L. E. Rehn, W. Wagner and P. Ehrhart, J. Nucl. Mater., 1983, 118, 83–90.
39. N. M. Ghoniem and S. P. Chou, J. Nucl. Mater., 1988, 155–157, 1263–1267.
40. B. K. Derby, Y. Sharma, J. A. Valdez, M. Chancey, Y. Q. Wang, E. L. Brosha, D. J. Williams, M. M. Schneider, A. Chen, B. P. Uberuaga, C. R. Kreller and M. T. Janish, JOM, 2022, 74, 4015–4025.
41. M. T. Janish, M. M. Schneider, J. A. Valdez, K. J. McClellan, D. D. Byler, Y. Wang, D. Chen, T. G. Holesinger and B. P. Uberuaga, Acta Mater., 2020, 194, 403–411.
42. T. D. Shen, S. Feng, M. Tang, J. A. Valdez, Y. Wang and K. E. Sickafus, Appl. Phys. Lett., 2007, 90, 263115.
43. A. J. Samin, D. A. Andersson, E. F. Holby and B. P. Uberuaga, Electrochem. Commun., 2018, 96, 47–52.
44. N. Okubo, N. Ishikawa, M. Sataka and S. Jitsukawa, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 314, 208–210.
45. W. Jiang, L. Kovarik, M. G. Wirth, Z. Hu, L. Shao, A. M. Casella and D. J. Senor, J. Nucl. Mater., 2024, 591, 154925.
46. F. Li, P. Lu, M. Ishimaru and K. E. Sickafus, Philos. Mag. B, 2000, 80, 1947–1954.
47. R. Aughterson, G. Lumpkin, M. de los Reyes, B. Gault, P. Baldo, E. Ryan, K. Whittle, K. Smith and J. Cairney, J. Nucl. Mater., 2016, 471, 17–24.
48. K. E. Sickafus, Radiation Effects in Solids, Dordrecht, 2007, pp. 321–352.
49. J. Brechtl, S. Agarwal, X. Hu, D. Chen, M. Chancey, H. Bei, Y. Wang and S. Zinkle, J. Nucl. Mater., 2021, 543, 152617.
50. S. Zinkle, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 286, 4–19.
51. Y. Zhang, Z. Huang, J. Qi, Z. Tang, L. Wu, K. Zhang and T. Lu, J. Eur. Ceram. Soc., 2021, 41, 7868–7877.
52. E. Murray, Y. Zhou, P. Slater, R. Smith, P. Goddard and H. Steele, Phys. Chem. Chem. Phys., 2022, 24, 20709–20720.
53. D. A. Andersson, F. J. Espinosa-Faller, B. P. Uberuaga and S. D. Conradson, J. Chem. Phys., 2012, 136, 234702.
54. J. Yu, X. Zhao, W. Zhang, W. Yang and F. Chu, J. Nucl. Mater., 1997, 251, 150–156.
55. B. K. Derby, J. K. Baldwin, D. Chen, M. J. Demkowicz, Y. Q. Wang, A. Misra and N. Li, JOM, 2020, 72, 145–149.
56. X.-Y. Cui, S. P. Ringer, G. Wang and Z. H. Stachurski, J. Chem. Phys., 2019, 151, 194506.
57. N. S. Azhar, M. F. M. Taib, O. H. Hassan, M. Z. A. Yahya and A. M. M. Ali, Mater. Res. Express, 2017, 4, 034002.
58. P. Shuk, H.-D. Wiemhöfer and W. Göpel, Z. Anorg. Allg. Chem., 1997, 623, 892–896.
59. S. C. Liou, M.-W. Chu, R. Sankar, F.-T. Huang, G. J. Shu, F. C. Chou and C. H. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085126.
60. C. C. Ahn and O. L. Krivanek, EELS Atlas: A Reference Guide of Electron Energy Loss Spectra Covering All Stable Elements, Gatan, 1983.
61. R. F. Egerton, Rep. Prog. Phys., 2008, 72, 016502.
62. A. Iribarren, R. Castro-Rodríguez, V. Sosa and J. L. Peña, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4758–4762.
63. M. Hannula, H. Ali-Löytty, K. Lahtonen, E. Sarlin, J. Saari and M. Valden, Chem. Mater., 2018, 30, 1199–1208.
64. K. Kaur and C. V. Singh, Energy Procedia, 2012, 29, 291–299.
65. P. K. Bhujbal, H. M. Pathan and N. B. Chaure, ES Energy Environ., 2019, 4(June 2019), 15–18.
66. M. Lee, J. Lee, S. Kim, S. Callard, C. Seassal and H. Jeon, Sci. Adv., 2018, 4, e1602796.
67. A. Kozlovskiy, K. Dukenbayev, I. Kenzhina, D. Tosi and M. Zdorovets, Vacuum, 2018, 155, 412–422.
68. J. Robertson, J. Non-Cryst. Solids, 2008, 354, 2791–2795.
69. E. Feldbach, I. Kudryavtseva, K. Mizohata, G. Prieditis, J. Räisänen, E. Shablonin and A. Lushchik, Opt. Mater., 2019, 96, 109308.
70. T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. Garcia-Mendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468.
71. C. Kittel, Introduction to Solid State Physics, John Wiley Sons, Hoboken, NJ, 2005, pp. 161–181.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta05283h

---