Combinatorial screening of wide band-gap organic solar cell materials with open-circuit voltage between 1.1 and 1.4 V

Abstract

Wide band-gap organic solar cells are gaining interest due to their applications in emergent light-harvesting technologies such as underwater photovoltaics, multi-junction solar cells, or indoor photovoltaics. In this work, a combinatorial screening approach is used to explore binary combinations of three wide band-gap donors (PTQ10, PM6, and D18) and three wide band-gap acceptors (PMI-FF-PMI, O-IDFBR, and IO-4Cl) deposited from solution in two solvents (CB and CF). In total, 18 combinations are blade-coated with active layers exhibiting a thickness gradient generating solar cells with 12 different thicknesses. PTQ10:IO-4Cl and PTQ10:O-IDFBR are the most efficient blends with efficiencies of 7.31% and 6.87%, respectively. The voltage loss analysis shows that PTQ10-based devices exhibit the lowest non-radiative voltage losses, whereby the PTQ10:O-IDFBR combination has the lowest voltage loss of all studied blends, with a remarkably high open-circuit voltage (V_oc) of 1.35 V. Due to their high performance and V_oc, PTQ10:O-IDFBR devices were also studied for indoor light harvesting, achieving an efficiency of 22.6% and a V_oc of 1.21 V under 560 lux indoor illumination. To the best of our knowledge, this indoor V_oc value is the highest achieved in the field of indoor organic photovoltaics.

---

Introduction

The organic photovoltaics (OPV) field has recently surpassed 20% efficiency, mainly thanks to the development during the last years of non-fullerene acceptors (NFAs).^1–6 These molecules exhibit stronger absorption and broader energy level tunability compared to the fullerene acceptors used since the early days of OPV technology.⁷ The increased color tunability, as a result of the development of NFAs, together with the already well-known advantages of organic solar cells such as lightweight, flexibility, or up-scalability, have expanded the range of applications of organic photovoltaics.

Wide band-gap organic solar cells (here meaning cells with photo-active layer band-gaps of E_bg > 1.8 eV) are promising for harvesting light whose spectrum and conditions differ from the AM1.5G solar spectrum. This is the case, for example, for underwater light harvesting. Depending on the depth of water, sun light becomes increasingly filtered in color.^8,9 In general, this results in a blue-shift of the Shockley–Queisser optimum bad-gap as the device becomes deeper in the water, from the well-known 1.34 eV to values higher than 2 eV, depending on water depth and geographical area.^8,10 Yang et al. have already shown 23.11% efficiency with the wide band-gap blend PM6:IO-4Cl at a depth of 5 m.⁹ Furthermore, the study and development of wide band-gap solar cells is important for tandem multi-junction organic solar cells,^3,11–14 where the electrical series connection of sub-cells imposes the need for similar short-circuit currents in all sub-cells (current matching condition). The wide band-gap sub-cells need special attention due to the fewer investigations performed on wide band-gap cells as compared to the narrow E_bg sub-cells.^5,15 Other multi-junction geometries, such as lateral multi-junction cells (RAINBOW concept),¹⁶ or electrically separated tandem solar cells,¹⁷ would also directly benefit from an improvement in the efficiency of wide E_bg organic solar cells.

Another relevant application of wide E_bg organic solar cells is the harvesting of indoor light, in which the benchmark efficiency reached 36%.¹⁸ Other works also achieve high efficiencies with different materials and strategies, therefore showing the potential of OPV for indoor light harvesting.^19–25 For this application, solar cells with high E_bg are needed since the light source to be harvested is typically a light-emitting diode (LED), emitting between 400 and 700 nm with a variable spectrum depending on the LED bulb.^26,27 Therefore, devices with E_bg below 1.8 eV are expected to suffer from unnecessarily high thermalization losses.

As demonstrated in the literature, organic solar cells exhibit higher voltage losses compared to other photovoltaic technologies such as perovskites or silicon solar cells, resulting in a lower open-circuit voltage (V_oc).^12,15,28 The latter is understood as one of the main factors limiting the efficiency of organic solar cells. Precisely, non-radiative voltage losses (ΔV^nr_oc) due to the low emissivity nature of the charge-transfer state, are responsible for the high voltage loss compared with other technologies.^29,30 Nevertheless, literature also shows that as charge-transfer state energy increases, non-radiative voltage losses decrease.^31,32 Therefore, wide E_bg organic solar cells, prone to having higher charge-transfer state energies, also exhibit lower ΔV^nr_oc. Nonetheless, their efficiency is still far from the thermodynamic limit, and, in this case, the photo-generated current seems to be the bottleneck.^15,31 Due to the different methodologies used for characterizing voltage losses, the field lacks a systematic comparison of voltage losses to better understand the efficiency limitation of wide E_bg solar cells.^29,31,33,34

Additionally, the fast development of NFAs is generating a vast library of materials, thus opening enormous possibilities for active layer blends. Although efforts have been invested in developing a material selection and efficiency prediction algorithm, this is still an unsolved question for organic photovoltaics.^35–37 In this scenario, high-throughput and combinatorial screening approaches are needed for the faster discovery of efficient donor : acceptor blends with available materials. For this purpose, our group has developed a platform based on using thickness gradients, generally achieved by blade-coating with variable speed, for the rapid study of important parameters in organic solar cells such as active layer materials, composition, or thickness.^35,38–42

In this study, we used our high throughput screening methodology to explore the binary combinations of three wide E_bg donors (PTQ10, PM6, and D18) and three wide E_bg acceptors (PMI-FF-PMI, O-IDFBR, and IO-4Cl) shown in Fig. 1a, deposited from solutions using two different solvents (CB and CF). In total, 18 combinations of different active layers were blade-coated with a thickness gradient to generate solar cells with 12 different thicknesses. In this study, we fabricated and characterized 424 solar cells. We identified PTQ10:IO-4Cl and PTQ10:O-IDFBR as the best-performing blends. Additionally, a voltage loss analysis was performed for selected combinations to further understand the V_oc of the cells. PTQ10-based devices were found to show the lowest non-radiative voltage losses, with the PTQ10:O-IDFBR combination having the lowest losses of all the studied blends, leading to a V_oc of up to 1.35 V. Due to its high performance and V_oc, PTQ10:O-IDFBR devices were further studied under indoor light conditions, achieving a 22.6% and a V_oc of 1.21 V under 560 lux indoor illumination.

Fig. 1 Chemical structure and optical properties of active layer materials. (a) Chemical structure of donors (D18, PTQ10, and PM6) and acceptors (PMI-FF-PMI, O-IDFBR, and IO-4Cl) materials used in the active layer. (b) Refractive index (n) and extinction coefficient (k) measured by ellipsometry. (c) HOMO and LUMO levels of the materials as reported in ref. 12, 22, 42, 45 and 47 measured by cyclic voltammetry (CV) except for the acceptor PMI-FF-PMI that was measured by electrochemical voltage spectroscopy (EVS).

Experimental

Solar cell fabrication

All devices were manufactured with an inverted structure (glass/ITO/ZnO/AL/MoO₃/Ag) for illumination from the substrate (glass) side. The patterned ITO substrates (purchased from Ossila, 100 nm thick and 20 Ω per square sheet resistance) were cleaned by 10 minutes sonication sequentially in acetone, a 10% Hellmanex soap water solution, isopropanol, and finally a 10% NaOH water solution. Subsequently, the substrates were dried in compressed air. The ZnO electron-transport layer (ETL) was deposited by blade-coating from a nanoparticle dispersion in isopropanol purchased from Avantama (N-10). Afterwards, samples were placed inside a glove box with a controlled N₂ atmosphere, and the active layer was deposited by blade-coating with a velocity gradient resulting in an active layer thickness gradient from approximately 50 to 200 nm.⁴⁰ The combinatorial screening was performed in this active layer, with 18 processing conditions (three donors, three acceptors, and two solvents). More details about the active layer deposition are given in the next section. The MoO₃ hole-transport layer (HTL) and back reflective metal electrode (Ag), both purchased from Kurt J. Lesker, were thus evaporated through a shadow mask defining 24 cells, of 2 × 4 mm² area each. Finally, to reduce the degradation due to contact with moisture and oxygen, the solar cells were encapsulated with a UV-curable resin and a thin glass cover slide.

Active layer materials description

In this study, the active layer composition and fabrication are especially important because of the number of different conditions tested. This section describes the composition and fabrication procedures in detail.

Fig. 1a shows the chemical structure of the materials serving as electron-donors (D18,^43,44 PTQ10 (ref. 45 and 46) and PM6 (ref. 9 and 47)) and electron-acceptors (O-IDFBR,^40,48,49 PMI-FF-PMI,¹² and IO-4Cl^16,43) used as components in the different active layers. For the IUPAC names, the reader is referred to the ESI,† Section S1. D18 was purchased from Ossila, PMI-FF-PMI was prepared by J. Hofinger et al.¹² and the other active layer materials were purchased at 1-materials. All materials were used as received. The chosen materials are all wide band-gap materials, with gaps between 2.07 and 1.78 eV (≈600 and 700 nm, respectively), as demonstrated by the measured refractive index (n) and extinction coefficients (k) of thin films shown in Fig. 1b. D18 was chosen as a donor with relatively wide band-gap, which has shown a high efficiency of nearly 18% when blended with the benchmark non-fullerene acceptor Y6.^44,50 Hofinger et al. also demonstrated that D18:Y6 cells exhibit a low ΔV^total_oc of 0.51 V with especially low ΔV^nr_oc of 0.20 V. The donor polymer PTQ10 is a promising donor due to its low synthetic complexity and high efficiency, surpassing 16% when blended with Y6.^45,51 The other donor material is PM6, whose efficiency when blended with Y6 can surpass 17%.^47,52 It is the donor exhibiting the lowest band-gap, but it has already demonstrated very high efficiencies also for indoor applications (surpassing 26%) when blended with IO-4Cl.²³ This blend is also used in this work as a reference, therefore IO-4Cl is also included as NFA. PMI-FF-PMI is an NFA synthesized by J. Hofinger et al. which has shown V_oc over 1.4 V when blended with D18 and deposited by spin-coating, therefore being one of the highest V_oc reported in organic solar cells, with an efficiency of 5.34%.¹² The third NFA used here is O-IDFBR, first synthesized by Baran et al. in 2017 achieving an efficiency of 11% in a ternary blend with PCE10 and O-IDTBR.⁴⁸ To the best of our knowledge, there are very few studies addressing O-IDFBR,^38,40,49 but none exploring the combination of O-IDFBR with the donors selected here.

The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) levels shown in Fig. 1c are taken from cyclic voltammetry (CV) literature data,^23,45,48,50 except for the case of PMI-FF-PMI whose energetic levels, also from literature, were measured using electrochemical voltage spectroscopy (EVS).¹² According to the HOMO and LUMO levels, all donor–acceptor combinations form staggered (type-2) hetero-junctions (i.e. LUMO_donor > LUMO_acceptor > HOMO_donor > HOMO_acceptor) meaning that they could work as organic solar cells. Additionally, due to the similar band-gaps between all materials, the difference between HOMO_donor and HOMO_acceptor (ΔHOMO) as well as the difference between LUMO_donor and LUMO_acceptor (ΔLUMO) lay between 0.2 and 0.4 eV, being similar offsets compared to the standard value of 0.3 eV for efficient exciton dissociation.³¹ Nevertheless, many materials have already demonstrated high efficiencies (and therefore efficient enough exciton dissociation) with ΔHOMO or ΔLUMO lower than 0.3 eV.^4,47,53 It is worth mentioning that, since we have both donor and acceptor materials with similar E_bg, a low ΔHOMO implies a low ΔLUMO (and vice versa). This is not the case for most of the literature works that study small ΔHOMO or ΔLUMO which, to achieve a broad absorption spectrum, the materials composing the active layer need to absorb in different regions of the solar spectrum (i.e. significantly different E_bg). Thus, there are comparatively fewer reported works on both ΔHOMO and ΔLUMO being small.

As mentioned, the active layer deposition was done inside a glove box. Each donor : acceptor combination was prepared from chlorobenzene (CB) and chloroform (CF) solutions separately, therefore giving a total of 3 × 3 × 2 = 18 different solutions and active layers. The solutions were prepared in a 1 : 1.5 donor : acceptor ratio except for the case of PMI-FF-PMI solutions, where the donor : acceptor ratio was 1 : 1 according to ref. 12. Almost all active layer materials were dissolved attaining the same concentration of 20 mg mL⁻¹, irrespective of the solvent. D18-based solutions were diluted down to 10 mg mL⁻¹ due to its observed high viscosity at 20 mg mL⁻¹. The solutions were maintained in continuous stirring at 40 °C and 80 °C for CF and CB, respectively, for a minimum of 4 h to ensure proper dissolution of the solutes. The active layers were deposited via blade-coating with a velocity varying from 90 mm s⁻¹ to 10 mm s⁻¹ along the substrate, achieving a thickness gradient from 200 to 50 nm approximately.⁴⁰Fig. 2a depicts the thickness gradient of the blend PTQ10:O-IDFBR deposited from CF solution showing its efficiency dependence. The inset (photograph) shows the active layer thickness gradient increasing along the sample. The latter can also be observed in Fig. S1,† which shows a photograph of all 18 samples studied.

Fig. 2 Thickness dependent efficiency. (a) Power conversion efficiency (PCE) as a function of the cell pixel number (i.e. thickness) for a PTQ10:O-IDFBR cell deposited from chloroform solution. The inset shows the substrate with a thickness gradient achieved by varying blade-coater speed. (b) J–V curves of the best performing cells for each of the six materials tested (donors and acceptors).

Solar cell characterization

All samples were removed from the glovebox after encapsulation, and their current density–voltage (J–V) curves under the AM1.5G spectrum were measured using a custom-made multiplexer to electrically connect each cell in an automatized manner. A XES-100S1 solar simulator from SAN-EI Electric Co. was used (xenon arc-lamp) in combination with a filter to match the standard 1-Sun AM1.5G spectrum. The total power was calibrated using a silicon reference cell (Newport). In this way, for each materials combination we obtained J–V curves for 12 different thicknesses with two replicas of each thickness (left and right sides), which counts for a total of 24 cells per substrate. Fig. 2a shows an example of the power conversion efficiency (PCE) dependence on thickness from the described measurement on the sample of PTQ10:O-IDFBR deposited from the CF solution. Not all 24 devices were completely operative. In this case, there were discrepancies in the two replicas (right and left) of cells number 1, 3, 11, and 12. Nevertheless, it is easy to recognize thickness-dependent tendencies. In all cases, the best cell considered for each material and solvent combination was the one with the highest power-conversion efficiency (PCE) within the thickness range, with its replica having a similar efficiency value.

Electroluminescence and external quantum efficiency

To characterize the voltage losses, electroluminescence (EL) and external quantum efficiency (EQE_PV) were measured in the best-performing cell for the selected materials. In both measurements, encapsulated samples measured at room temperature and ambient conditions. EL measurements were carried out at a current density equal to the short-circuit photocurrent density (J_sc) previously measured. EQE_PV measurements were carried out with a spot size around 1.5 mm in diameter, being lower than the solar cell area.

Ellipsometry

In this study, we implemented variable-angle spectroscopic ellipsometry (VASE) to determine the refractive index (n) and extinction coefficient (k) of the materials from 1.2 to 5.4 eV. Thin films of donors and acceptors were deposited by blade-coating both from chlorobenzene and chloroform solutions, on glass substrates. The equipment used for the VASE measurements was a SOPRA GES5E with a rotating polarizer in reflection mode. The ellipsometry data was analyzed using WinElli 3.04, a commercial software supplied by SOPRA. A model based on Tauc–Lorentz (TL) oscillators was implemented, as it leads to accurate fits of the optical functions of our materials. The thicknesses deduced by these fits are in the range of ca. 17 to 147 nm, which is in good agreement with those obtained from surface profilometry, and the calculated absorption spectra using the optical constants match those measured by spectrophotometry.

Results and discussion

Optical properties of the materials

The results of the ellipsometry measurements are shown in Fig. 1b. From the extinction coefficient data (k), we have inferred the band-gap energy (E_bg) of each material as the inflection point of the extinction coefficient edge. When comparing the results with the E_bg computed from the difference between HOMO and LUMO in the literature (ESI Table S1†), one can see that the PTQ10 has an exceptionally high HOMO–LUMO difference compared to the band-gap value from the extinction coefficient. The latter suggests that the reported LUMO for PTQ10 is overestimated or that PTQ10 aggregation in the solid film compared to solution is significantly affecting its LUMO energy. The same comparison for the other materials yields percentage differences lower than 7.5%, indicating a much better agreement between the reported HOMO and LUMO energy levels and the measured refractive index (n) and extinction coefficient (k).

Efficiency and V_oc

The resulting figures-of-merit for each combination are summarized in Table 1. For completeness we show in Table S3 of the ESI† the values in parentheses of the different PV figures-of-merit also for each replica device (same fabrication parameters), corresponding to the counterparts tabulated in Table 1. Additionally, Fig. 2b shows the J–V curves from the best performing cells for each material, as an example of some of the best performing cells in this work. The best performing device for selected material combinations was further characterized in terms of its external quantum efficiency (EQE_PV), electroluminescence (EL) and photoluminescence (PL) to assess its V_oc losses.

Table 1 Figures-of-merit from J–V measurements. J–V curves results of the best performing devices for each combination tested. The * indicates the best performing device for each of the tested active layer materials, which J–V curves are shown in Fig. 2b

Donor	Acceptor	Solvent	V oc [V]	J sc [mA cm^−2]	FF [%]	PCE [%]
PTQ10	O-IDFBR	CF	1.33	8.05	50.85	5.44
PTQ10	O-IDFBR*	CB	1.35	9.06	56.05	6.87
PTQ10	PMI-FF-PMI	CF	1.38	3.63	39.52	1.98
PTQ10	PMI-FF-PMI	CB	1.36	1.70	37.80	0.87
PTQ10*	IO-4Cl*	CF	1.25	10.16	57.51	7.31
PTQ10	IO-4Cl	CB	1.22	8.09	56.37	5.55
D18	O-IDFBR	CF	1.29	5.16	47.08	3.15
D18	O-IDFBR	CB	1.33	3.92	50.49	2.62
D18	PMI-FF-PMI	CF	1.28	5.81	42.26	3.14
D18	PMI-FF-PMI*	CB	1.33	5.35	49.49	3.53
D18*	IO-4Cl	CF	1.24	8.32	57.13	5.91
D18	IO-4Cl	CB	1.21	8.13	51.85	5.10
PM6	O-IDFBR	CF	1.23	5.93	41.02	2.99
PM6	O-IDFBR	CB	1.24	4.91	48.95	2.98
PM6	PMI-FF-PMI	CF	1.26	2.20	43.07	1.19
PM6	PMI-FF-PMI	CB	1.26	2.48	52.49	1.64
PM6*	IO-4Cl	CF	1.18	9.29	57.03	6.23
PM6	IO-4Cl	CB	1.15	9.00	58.18	6.02

---

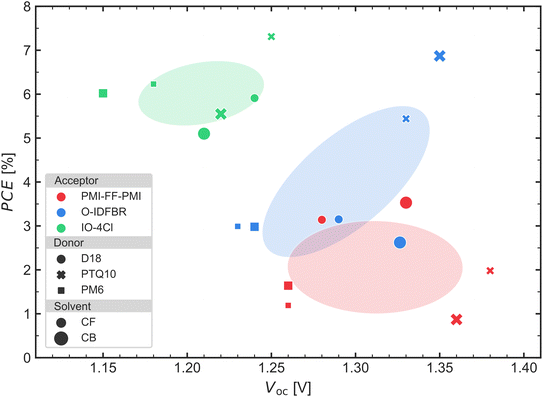
To compare the performance of the different active layer combinations, the device with the best PCE for each active layer combination (donor, acceptor, and solvent) is considered. The results are summarized in Fig. 3, where the PCE for each donor–acceptor combination deposited from the CB and CF solvents is plotted against their V_oc values. The different colors (red, blue, and green) indicate the acceptor used (PMI-FF-PMI, O-IDFBR, and IO-4Cl respectively). The coloured ellipses are the central regions where the points of each cell with the same acceptor are located within a one standard deviation confidence range. From these regions, it is clear that devices containing IO-4Cl achieve higher efficiencies but lower V_oc compared to O-IDFBR- and PMI-FF-PMI-based devices, because the confidence ellipse is located more in the upper left part. Nevertheless, the PTQ10:O-IDFBR cells (both deposited from CF and CB) are an exception and, apart from being the unique O-IDFBR devices with PCE comparable to IO-4Cl based cells, its V_oc is among the highest measured in this study.

Fig. 3 PCE results. Best power conversion efficiency (PCE) values as a function of the corresponding V_oc achieved for each donor–acceptor–solvent combination. The 18 points are taken from a total of 432 devices where the thickness is optimized for each combination due to the thickness gradient. The coloured ellipses represent confidence regions for the cells containing each acceptor with a 1σ confidence.

In Fig. 3, another important tendency is that devices containing PTQ10 as the donor (cross-shaped points) achieve the highest V_oc observed for each acceptor. In other words, the devices with the highest V_oc for all acceptors contained PTQ10 as the donor. This is the case for PTQ10:PMI-FF-PMI deposited from CF where the V_oc of 1.38 V is the highest achieved; for PTQ10:O-IDFBR blend deposited from CB with a V_oc of 1.35 V; as well as for the IO-4Cl:PTQ10 blend deposited from CF with a V_oc of 1.25 V. In contrast, the lowest V_oc for each acceptor occurs always for devices containing PM6 (square shape points), with V_oc of 1.15 V, 1.23 V and 1.26 V when blended with IO-4Cl, O-IDFBR and PMI-FF-PMI, respectively. Devices based on D18 as the donor show V_oc values in between those of PTQ10 and PM6-based solar cells. The V_oc is directly related to the energetic difference between the LUMO_acceptor and the HOMO_donor, therefore, when comparing blends with the same acceptor, the deeper the HOMO_donor, the higher the V_oc expected. This behavior agrees with the energy levels of the three donors shown in Fig. 1c, where the HOMO levels of PTQ10 and PM6 are the deepest and the shallowest, respectively. Notice that, in this simplified scenario, we are assuming that LUMO_acceptor and HOMO_donor do not depend on the materials blended, which may not be valid due to differences in morphology of donor and acceptor regions in the blend compared to pure material films. We are also assuming that V_oc losses are equal for all blends, which may not be the case. When plotting the LUMO_acceptor–HOMO_donor difference versus V_oc (Fig. S2 of ESI†), we observe a strong linear correlation between both parameters with a slope near 1 and a high Pearson's correlation parameter (r = 0.84) indicating that this simplified scenario is valid (at least) for our cells. Nevertheless, the difference in V_oc between CF and CB processing of the same blend material cannot be explained by this simple model.

For most of the donor : acceptor combinations, there is no literature to which to benchmark our results. Nonetheless, for the few cases where data is available, we obtained somewhat lower efficiencies (see Table S2†). For example, Y. Cui et al.⁵⁴ reached 9.80% efficiency for PM6:IO-4Cl cells deposited from CB, with a V_oc of 1.24 V; and Y. Yang et al.⁹ achieved 7.80% with a V_oc of 1.22 V for the same active layer material. Nevertheless, when comparing these results to ours (PCE of 6.20% and V_oc of 1.15 V for PM6:IO-4Cl deposited from CB), it is important to consider that we are using the inverted architecture and depositing the active layer from blade-coating. The latter is compatible with industrial roll-to-roll fabrication needed for organic solar cells up-scaling. On the other hand, the benchmark works use spin-coating instead of blade-coating, which is not a roll-to-roll-compatible coating technique, and are built with the standard architecture.

At this point, we want to comment on the IO-4Cl devices, which are the more efficient cells in all the studies. We tested two different batches of IO-4Cl material bought from the same provider. The results for the first tested batch of IO-4Cl are shown in Fig. S3.† In that case, the efficiency of the best devices does not exceed 5%. Furthermore, these results correspond to the best cells of a long optimization process where different processing conditions, such as donor : acceptor ratio, co-solvent addition, or different ETL materials, were optimized. In contrast, the second IO-4Cl batch tested improved all the previous cells on the first try with the conditions described in the experimental section (i.e. without further optimization), exceeding the 5% when blended with all 3 donors regardless of the CB or CF solvent. With this insight, we want to highlight the importance of repeatable material fabrication processes for improved batch-to-batch repeatability. Furthermore, this is highly relevant for the commercialization of organic solar cell technologies.

The other combination found in the literature is D18:PMI-FF-PMI. J. Hofinger et al.¹² achieved a PCE of 5.34% with a V_oc of 1.41 V. These values are considerably higher than our results (PCE = 3.53% and V_oc = 1.33 V). In this case, the reference work also used the standard architecture and deposited the active layer by spin-coating compared to our blade-coated inverted devices. A comparison of all the parameters is presented in Table S2 of ESI,† where it can be seen that all the J–V parameters are responsible for the efficiency difference between our devices and the literature. This might be due to the different materials used as well as the fabrication protocols (device geometry and processing methodology) followed in our laboratory.

Active layer morphology

The morphology of the active layer is a key parameter to achieve the best possible performance for a defined blend. Typically, crystalline domains are preferred since they favor higher exciton mean free paths as well as higher mobilities of free charges. This results in a better percolation of generated charges to the contacts. Nevertheless, when these crystalline domains are too large, exciton recombination happens before exciton dissociation, resulting in an efficiency drop. On the other hand, amorphous domains exhibit a more intermixed morphology favoring exciton dissociation. Anyway, non-geminate recombination and low percolation to the contacts (added to lower charge conductivity due to amorphous domains) can be a problem especially affecting the FF.

There are many parameters, related to the fabrication of the device, that can affect the active layer morphology: deposition technique, deposition temperature, or annealing conditions are just a few examples. Among them, the solvent is one of the most important because it directly affects the drying dynamics of the film while it is forming. For example, a solvent with a higher boiling point, such as chlorobenzene (CB), will give more time to donor and acceptor molecules to reorder before drying, typically resulting in more ordered films. In contrast, a solvent with a lower boiling point, such as chloroform (CF), will tend to evaporate faster, quenching the disordered liquid thin film and typically resulting in more amorphous domains. The different affinity of active layer components with the solvent is also an important factor during the formation of the thin film which directly relates to the final morphology.

Here, we measured Grazing Incidence X-ray Scattering (GIWAXS) of pure O-IDFBR and PTQ10 as well as the blend, all blade-coated from CF and CB on silicon substrates (Fig. S4 of ESI†). PTQ10 exhibits a stronger crystalline signal when deposited from CB, due to the higher boiling point of the solvent. For O-IDFBR, there is no significant difference between CF and CB GIWAX patterns. The blend films show that CB increases the crystallinity of the blend, while blended films prepared from CF are more amorphous. This agrees with the previously discussed role of solvent evaporation during the drying of the film. For PTQ10:O-IDFBR, the best performance is achieved with CB, which shows higher structural order than CF in its GIWAXS data. The latter is also in agreement with the previous assumption that the ideal morphology for any organic solar cell active layer is closer to the crystalline donor and acceptor domains rather than amorphous.

Similarly, GIWAXS measurements were performed for the blend PTQ10:IO-4Cl (Fig. S5†). The GIWAXS patterns found suggest packing motifs where NFA molecules pack into 1D-chain or multidimensional mesh-like structures.^55,56 Because 1D- or mesh-like packing motifs feature continuous aromatic structures that are separated by aliphatic domains, many large d-spacing symmetry planes exist, which are expected to give rise to multiple diffraction peaks in the low-q region, as found in our patterns.^55–57 Nevertheless, when IO-4Cl is blended with PTQ10, these reflections vanish and only the reflection from the lamellar-like packing of PTQ10 is observed. On the other hand, IO-4Cl deposited from CF shows a less defined (broader) GIWAXS signal, indicating less ordered crystalline domains. Nevertheless, the blend shows a GIWAXS signal preserving both donor and acceptor separately, indicating that both PTQ10 and IO-4Cl have a certain degree of crystallinity. Therefore, the assumption is also true since the blend with higher structural order (in this case deposited from CF) shows higher PCE. Additional evidence of microstructural differences among the studied blends is obtained from the d-spacing and coherence length values obtained from GIWAXS and listed in Table S4 in Section S6 of the ESI.† In conclusion, the performance differences between CF- and CB-processed blends arise from their different microstructures. Additionally, the results show that the optimization of the latter cannot be predicted from the solvent choice because there is no clear tendency of one solvent to achieve better performance devices than the other. This suggest that the boiling point is not the only parameter playing a role and other properties like solubility are also important.

J _sc analysis

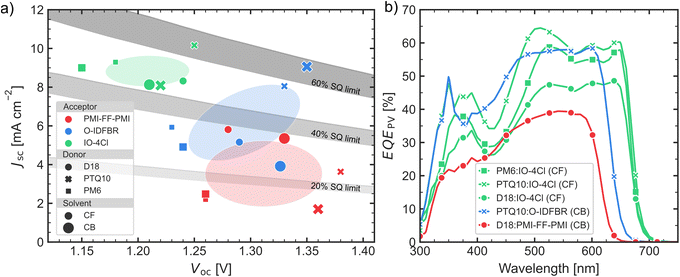
The PCE values are spread in a large range of almost one order of magnitude, from 0.82% for PTQ10:O-IDFBR in CB to 7.31% for PTQ10:IO-4Cl in CF. Nevertheless, not all figures-of-merit exhibit such large variations. For example, the fill factor (FF), shown in Fig. S6 of ESI,† varies between 40% and 60% without a clear correlation with V_oc. IO-4Cl-based devices show a FF which is independent of the V_oc while O-IDFBR and PMI-FF-PMI show a positive and a negative correlation, respectively.

The parameter which has the highest change and therefore affects more the PCE is the J_sc, which varies almost one order of magnitude, between 1.35 mA cm⁻² and 10.16 mA cm⁻² (Fig. 4a). As happens for the PCE, the cells based on IO-4Cl as acceptor have the highest J_sc compared to PMI-FF-PMI and O-IDFBR devices. In other words, for every donor (different data-point shape in Fig. 4a) the cell containing IO-4Cl has the highest J_sc. The later is in agreement with the extinction coefficients (Fig. 1b), which show that IO-4Cl is the acceptor with the highest k near its absorption edge and, at the same time, the acceptor with the lowest energy band-gap (E_bg), being about 0.4 eV lower than O-IDFBR and PMI-FF-PMI. The latter is also highlighted in Fig. 4b, where EQE_PV from IO-4Cl devices with the different donors (green lines) show a very similar optical band-gap, while the others containing O-IDFBR (blue) and PMI-FF-PMI (red) have a higher band-gap compared to the IO-4Cl devices containing the same donor.

Fig. 4 J _sc results. (a) J_sc as a function of the V_oc for the best performing cells of each donor–acceptor–solvent combination. The coloured ellipses represent confidence regions for the cells containing each acceptor with a 1σ confidence. Fractions (60, 40, and 20%) of the Shockley–Queisser limit J_sc are plotted considering a band-gap of V_oc + ΔV_loss being ΔV_loss 0.6 eV and 0.7 eV for high and low limits. (b) External quantum efficiency (EQE_PV) for some of the best performing cells.

This difference, although small, is in the spectral region where the flux of absorbed photons is the highest. Therefore, a small E_bg difference can make an important impact on the overall J_sc. This effect is clearly demonstrated by the Shockley–Queisser (SQ) limit, in which the EQE_SQ is considered to be zero for photons with energy lower than the E_bg and 100% for energies equal or higher than E_bg. However, the SQ limit assumes ideal, perfect absorption, exciton separation, and free-charge carrier transport to the contacts within the solar cells. The latter results in a J_sc decrease with increasing band-gap of the active layer. For comparison, Fig. 4a also shows different fractions (60, 40, and 20%) of the SQ limit (grey areas) considering a total voltage loss of ΔV^total_oc = 0.6 V (upper limit) and ΔV^total_oc = 0.7 V (lower limit), with E_bg = q(V_oc + ΔV^total_oc). The IO-4Cl devices lay between 60% and 40% of the SQ limit, while O-IDFBR and PMI-FF-PMI devices (except for the PTQ10:O-IDFBR) have a J_sc between 40 and 20% of the SQ limit, in some cases even lower. This indicates that the decrease in J_sc is not only related to a decrease in the band-gap, which would be related to absorption losses as described by the SQ limit, but also to a worse exciton separation and/or free-charge carrier extraction. Only PTQ10:O-IDFBR cells have a SQ limit J_sc percentage similar to PTQ10:IO-4Cl in CF, which indicates that the J_sc difference between those two cells is the expected from its E_bg difference. Nevertheless, the J_sc of the best devices being inside the 60% range, shows that there is still room for improvement.

V _oc loss analysis

In general, the total voltage loss (ΔV^total_oc) is defined as the energy difference between the energy band-gap of the solar cell (E_bg) and the measured open-circuit voltage (V_oc) under AM1.5G illumination, therefore given by ΔV^total_oc = E_bg/q − V_oc. E_bg is the optical band-gap of the cell, which has different definitions but is typically calculated as the inflection point of the EQE_PV edge. The V_oc is proportional to the natural logarithm of the ratio between the short-circuit current (J_sc) and the dark current (J₀). The latter²⁹ can be further divided in four quotients to give:Here J^SQ_sc and J^SQ₀ correspond to the short-circuit and saturation current densities in the Shockley–Queisser limit, respectively, and J^rad₀ corresponds to the saturation current density in the radiative limit. Eqn (1) can be rewritten as a sum of four terms:

V_oc = V^SQ_oc − ΔV^sc_oc − ΔV^r_oc − ΔV^nr_oc (2)

Each term has a different physical meaning. The first term corresponds to the V_oc at the Shockley–Queisser limit (V^SQ_oc). The difference between E_bg and V^SQ_oc is understood as a thermodynamical loss due to the difference in solid angles between the incoming light and the radiative light emitted by the cell, also known as étendue expansion.⁵⁸ The latter can be theoretically mitigated by equalizing both solid angle values, which can be done by sunlight concentration or by forcing the radiative emission to be at the same angle as the incoming light. We expect this difference to be constant in our cells since they have similar E_bg and we took all the measurements at the same temperature without light concentration.

The short-circuit loss term (ΔV^sc_oc) corresponds to the difference between the measured J_sc and the theoretical Sockley–Queisser value, J^SQ_sc. The main origin of this difference is the fact that the EQE_SQ is considered 100% for photons with energy higher than the band-gap, i.e. each photo-generated electron–hole pair is collected at the cell contacts. This is never the case in a real cell. Since J_sc is rarely lower than 10% of the J^SQ_sc, this loss is typically low. On the other hand, the radiative voltage loss (ΔV^r_oc) can be more important since it is related to the energy difference between the emission peak and the E_bg of the cell. Even a small energy difference can result in a value of hundreds of millivolts. This is due to the exponential energy dependence of the spectrum emitted by the solar cell. The last term is the non-radiative voltage loss (ΔV^nr_oc) which is the difference between the V_oc and the V_oc at the radiative limit, V^r_oc. ΔV^nr_oc considers all losses due to non-radiative recombination mechanisms such as trap-assisted (Shockley–Read–Hall) recombination.

For the V_oc losses analysis, V^SQ_oc, ΔV^sc_oc, and ΔV^r_oc were calculated using the current densities calculated as follows:

J^SQ_sc = q∫EQE_SQ(E)ϕ_AM1.5G(E)dE (3)

J^SQ₀ = q∫EQE_SQ(E)ϕ_BB(E)dE (4)

J^rad₀ = q∫EQE_PV(E)ϕ_BB(E)dE (5)

J_sc = q∫EQE_PV(E)ϕ_AM1.5G(E)dE (6)

Here ϕ_AM1.5G and ϕ_BB are the 1-sun and black-body spectra respectively. In the definition of ϕ_BB we are considering the geometry of our solar cells, i.e. the active layer only emits to its front side due to the Ag electrode acting as a back reflector.⁵⁹ EQE_SQ and EQE_PV corresponds to the Shockley–Queisser (a step-function that is 1 and 0 above and below E_bg, respectively) and photovoltaic external quantum efficiency respectively. We want to highlight that the Shockley–Queisser limit is well-known and studied, with V^SQ_oc being tabulated elsewhere.⁵⁹ Therefore, the calculation of V^SQ_oc is a good opportunity to double-check your calculation procedure. Notice that the integral for the determination of J^rad₀ (eqn (5)) is dominated by the lower energy tail of the EQE_PV spectrum due to the exponential nature of the black-body spectrum (ϕ_BB).^32,43,60 Therefore, to achieve a reliable J^rad₀ value, one needs a highly sensitive EQE_PV with several orders of magnitude. For this reason, the measured EQE_PV was extended (both in spectral and dynamic range) by means of electroluminescence (EL) results using the reciprocity relation by Rau (ref. 60) at an injected current density corresponding to the J_sc of the device. The results of these measurements, as well as a detailed explanation of the EQE_PV extension procedure, can be found in ESI Section S8 and Fig. S7.†

The non-radiative voltage loss term (ΔV^nr_oc) was calculated as the difference between the radiative open-circuit voltage, V^r_oc, and the measured V_oc. V^r_oc is the sum of the first 3 terms in eqn (2) which results in:

Fig. 5a shows the voltage loss analysis of the devices studied. The overall voltage loss is around 0.6 to 0.7 V. All exact values are listed in ESI, Tables S5 and S6.† Considering that voltage loss in literature lies between 0.5 and 0.8 V,³¹ our results are in the middle range, without being especially low or high. The difference between V^SQ_oc and E_bg/q is maintained constant around 0.3 V. This is the value one may expect from the Shockley–Queisser limit,¹⁰ especially considering that without light concentration the only parameter that can affect this difference is the E_bg, which is similar for all devices.

Fig. 5 V _ocloss analysis. (a) Open-circuit voltage losses due to a nonideal short-circuit current density (ΔV^sc_oc, green), due to radiative recombination (ΔV^r_oc, red), and due to non-radiative recombination (ΔV^nr_oc, yellow) for the different solar cells studied. The cells are ordered in ascending order (from top to bottom) in E_bg/q, which corresponds to the black line. (b) ΔV^nr_oc as a function of radiative V_oc (V^r_oc) compared with literature from ref. 31.

The largest voltage loss in all devices is ΔV^nr_oc (yellow boxes in Fig. 5a), which varies from 0.17 V, for PTQ10:O-IDFBR in CF, up to 0.38 V for D18:PMI-FF-PMI in CB. The ΔV^nr_oc is especially interesting since, a priori, is the parameter that can be more affected by the engineering of materials and processing conditions. This is the case, for example, of the PTQ10:O-IDFBR blend. When the blend is processed from CB, the cell has a higher V_oc showing lower ΔV^total_oc (the concrete values can be found at ESI Table S6†). Nevertheless, the blend processed from CF shows the lowest ΔV^nr_oc of 0.17 V at expenses of the highest ΔV^r_oc of 0.15 V, which are significantly different from the values measured with the same blend processed from CB (0.24 and 0.04 V, respectively). This is directly related to the measured EL spectrum (ESI Fig. S5,† central panel) where it can be seen that the highest EL peak of the PTQ10:O-IDFBR blend processed from CB is 1.95 eV while for the blend deposited from CF is approximately 1.55 eV. The latter results in a difference of two orders of magnitude in the EQE_PV tail, yielding a J^rad₀ ten times larger for the CF-processed device. Following eqn (7), the difference between both blends is approximately k_BT/q*ln(10) = 0.06 eV which is roughly the difference between the V^r_oc of the CF and the CB-processed solar cells (1.51 and 1.59 eV respectively). We attribute this considerable difference in EL spectrum to the different microstructure, as suggested by GIWAXS data. The increased intensity of the lower energy EL peak of the CF-processed cell indicates a higher recombination of injected electron–hole pairs though the charge-transfer state. On the other hand, the CB-processed cell shows a stronger emission of the singlet state of the donor and/or the acceptor materials (it is difficult to discern due to the overlap of both materials emission). The latter, together with GIWAXS data, suggests that the CF-processed blend has more donor–acceptor interfaces due to a more intermixed blend while the CB-processed blend has larger domains of pure donor and acceptor.

Fig. 5b shows the ΔV^nr_oc as a function of the V_oc. We observe that, even for a systematic study like the case of this work, there is a big dispersion of values. The latter is also seen in the literature points (Fig. 5b, brown points) indicating the difficulty to predict ΔV^nr_oc.³¹ Our work adds data points to the existing literature especially in the high V^r_oc region. The ΔV^nr_oc lay between 0.25 and 0.35 V, similar to the literature values trend.

LED indoor light performance

For indoor applications, wide band-gap active layer materials are especially interesting due to their E_bg matching indoor spectrum, which is especially true for the actual LEDs used in most modern indoor lighting. For real applications of OPV in indoor lighting, it is also worth mentioning the importance of having the highest possible V_oc. Although in wide gap blends an increase in V_oc results in a slightly lower J_sc, the overall performance improves. This is so because lower operating currents lead to lower series resistance, generally attributed to the contacts of the cells. For the same reason, a lower J_sc allows for the use of electrode materials with lower electrical conductivity, what is especially interesting for the up scalability of OPV. Additionally, due to the logarithmic dependence of V_oc on J_sc, a drop in J_sc of ca. 3 orders of magnitude due to the reduced input light of indoor illumination compared to AM1.5 G, represents the same V_oc drop in absolute value regardless of the V_oc of the cell at AM1.5G. Therefore, a solar cell with higher V_oc would benefit from a lower drop in efficiency, percentagewise.

Due to its high E_bg, V_oc, PCE, and low ΔV^nr_oc, the PTQ10:O-IDFBR cells deposited from CB are good candidates for indoor light harvesting. This sample was measured under LED indoor light conditions, using a Wavelabs SINUS-70 LED solar emulate a 560 Lux LED source, whose spectrum is shown in Fig. 6a together with the normalized EQE_PV of the measured device. The correlated color temperature (CCT) of the spectrum used is 12 200 K, meaning that it is seen as blue by the human eye. The reader is referred to Fig. S8† of the ESI for more details on the spectrum color. The associated J–V measurement is shown in Fig. 6a together with the parameters derived from the measurement. The cell exhibited a remarkable efficiency of 22.6% with a V_oc of 1.21 V. Fig. 6c show a comparison of the state-of-the-art indoor organic photovoltaic devices in the literature according to ref. 19 and 21 with LED-type light sources. To the best of our knowledge, the cell measured in this work made of PTQ10:O-IDFBR deposited from CB exhibits the highest V_oc achieved for indoor organic photovoltaics (V_oc = 1.21 V), and its indoor efficiency is among the best reported in literature (PCE = 22.6%).

Fig. 6 PTQ10:O-IDFBR indoor LED characterization. (a) Normalized LED spectrum used for the indoor light characterization of PTQ10:O-IDFBR deposited from chlorobenzene solution which normalized EQE_PV is also plotted. (b) J–V curve resulting from the indoor efficiency measurement with a PCE of 22.6% and a V_oc of 1.21 V. (c) Comparison with the state-of-the-art indoor organic solar cell efficiency extracted from reference reviews 19, 21. A table with all reference values is shown in ESI,† Table S7. The PTQ10:O-IDFBR cell fabricated and characterized in this work has a V_oc of 1.21 which is the highest reported for indoor cells, as far as we know.

Besides V_oc, the FF is another key aspect governing the indoor efficiency. We have performed a leakage current and shunt resistance analysis, using a custom built setup,⁶¹ and the results are summarized in Section S11 and Fig. S9 of the ESI.† It is observed that FF increases as the light is decreased until reaching a threshold illumination (or, equivalently, a threshold shunt resistance) below which, leakage dominates. Reassuringly, this threshold is significantly below the typical illumination intensities for indoors. For instance, the PTQ10:O-IDFBR cell, the FF increase by 22% for indoors conditions compared to 1 Sun. For completeness, we would like to note that the record cells under indoor conditions exhibited a thicker active layer compared to the highest efficiency obtained under at 1 sun.

Conclusions

We have studied 18 material systems combinations resulting from 3 donors (D18, PTQ10, and PM6), 3 acceptors (O-IDFBR, PMI-FF-PMI, IO-4Cl), and 2 solvents (chloroform and chlorobenzene). Owing to the variation in the blade-coating velocity used during active layer deposition, 12 different thicknesses (with duplicates for each layer) were tested for each combination, thus giving a total of 432 devices. From this combinatorial screening study, we found that IO-4Cl cells have the highest efficiency under AM1.5 G illumination, mainly because IO-4Cl is the material with the lowest E_bg, which is closer to the optimal Shockley–Queiser limit. PMI-FF-PMI-based devices showed the lowest efficiencies, mainly due to low J_sc, attributed not only to the lower absorption associated to the higher E_bg of the blends, but also to a worse exciton dissociation and/or charge carrier extraction. The O-IDFBR-based devices are in-between both cases, similar to PMI-FF-PMI for the case where D18 was used as the donor and similar to IO-4Cl when PTQ10 was used as the donor.

The V_oc losses analysis showed a ΔV^total_oc between 0.6 and 0.7 V, with cells containing PTQ10 always exhibiting the lowest ΔV^total_oc compared to their counterparts. The latter, together with PTQ10 being the donor with the deepest HOMO level, leads PTQ10-based devices to exhibit a higher V_oc. Based on these results, we suggest that PTQ10 is a suitable donor for wide band-gap organic solar cells.

Specially interesting was the PTQ10:O-IDFBR blend due to its low ΔV^nr_oc and relatively high efficiency (6.87%) and remarkably high V_oc (1.35 V). These cells were also tested under indoor light conditions showing an efficiency of 22.6% with a V_oc of 1.21 V. This blend efficiency under indoor lightning is among the best in the OPV field and the achieved V_oc is, as far as we know, the highest reported value of indoor OPV.

Author contributions

MCV: formal analysis, visualization, writing – original draft, investigation, methodology, conceptualization. DCP: investigation, writing – review and editing. AQ: investigation, writing – review and editing. MR: resources. GT: resources, investigation. MS: investigation. JM: investigation, writing – review and editing. ARG: funding acquisition, writing – review and editing. TK: validation, methodology, writing – review and editing. MCQ: supervision, project administration, resources, validation, writing – review and editing, conceptualization, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Spanish “Ministerio de Ciencia e Innovación (MICINN)” is gratefully acknowledged for its support through grant No. CEX2019-000917-S (FUNFUTURE) in the framework of the Spanish Severo Ochoa Centre of Excellence program and the AEI/FEDER(UE) grants PGC2018-095411-B-I00 (RAINBOW), TED2021-131911B-I00, and PID2021-128924OB-I00 (ISOSCELLES). The authors also thank the Catalan agency AGAUR for grant 2021-SGR-00444. M. C. V. acknowledges an FPI fellowship (PRE2019-089855) from MICINN co-financed by the European Social Fund. M. C. V. and A. Q. also thank the PhD program in Materials Science from Universitat Autònoma de Barcelona in which both were enrolled. M. C. V. acknowledges Dr Benjamin Klingebiel and Mr Markus Hülsbeck for their help during EL and PL measurements, Mr Wilfried Reetz for his help during EQE_PV measurements. Dr Markus Scharber is acknowledged for his insights in PMI-FF-PMI-based solar cells. Dr Alfonsina A. A. Torimtubun is acknowledged for her helpful discussions on device fabrication. M. R. and G. T. thank Birgit Ehmann, Colien Purkathofer, and Stefan Weber for synthesis of PMI-FF-PMI.

Notes and references

1. J. Wang, Z. Zheng, P. Bi, Z. Chen, Y. Wang, X. Liu, S. Zhang, X. Hao, M. Zhang, Y. Li and J. Hou, Natl. Sci. Rev., 2023, 10, nwad085.
2. Best Research-Cell Efficiency Chart|Photovoltaic Research|NREL, https://www.nrel.gov/pv/cell-efficiency.html, accessed 26 April 2024.
3. Z. Zheng, J. Wang, P. Bi, J. Ren, Y. Wang, Y. Yang, X. Liu, S. Zhang and J. Hou, Joule, 2022, 6, 171–184.
4. Y. Cui, Y. Xu, H. Yao, P. Bi, L. Hong, J. Zhang, Y. Zu, T. Zhang, J. Qin, J. Ren, Z. Chen, C. He, X. Hao, Z. Wei and J. Hou, Adv. Mater., 2021, 33, 2102420.
5. L. Zhan, S. Li, T.-K. Lau, Y. Cui, X. Lu, M. Shi, C.-Z. Li, H. Li, J. Hou and H. Chen, Energy Environ. Sci., 2020, 13, 635–645.
6. Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515.
7. C. B. Nielsen, S. Holliday, H. Y. Chen, S. J. Cryer and I. McCulloch, Acc. Chem. Res., 2015, 48, 2803–2812.
8. J. A. Röhr, J. Lipton, J. Kong, S. A. Maclean and A. D. Taylor, Joule, 2020, 4, 840–849.
9. Y. Yang, C. Xue, H. Yin, Z. Chen and X.-T. Hao, Cell Rep. Phys. Sci., 2022, 3, 100861.
10. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
11. D. Di Carlo Rasi and R. A. J. Janssen, Adv. Mater., 2019, 31, 1806499.
12. J. Hofinger, S. Weber, F. Mayr, A. Jodlbauer, M. Reinfelds, T. Rath, G. Trimmel and M. C. Scharber, J. Mater. Chem. A, 2022, 10, 2888–2906.
13. A. Hadipour, B. De Boer and P. W. M. Blom, Adv. Funct. Mater., 2008, 18, 169–181.
14. J. Wang, Z. Zheng, Y. Zu, Y. Wang, X. Liu, S. Zhang, M. Zhang and J. Hou, Adv. Mater., 2021, 33, 2102787.
15. O. Almora, C. I. Cabrera, S. Erten-Ela, K. Forberich, K. Fukuda, F. Guo, J. Hauch, A. W. Y. Ho-Baillie, T. J. Jacobsson, R. A. J. Janssen, T. Kirchartz, M. A. Loi, X. Mathew, D. B. Mitzi, M. K. Nazeeruddin, U. W. Paetzold, B. P. Rand, U. Rau, T. Someya, E. Unger, L. Vaillant-Roca and C. J. Brabec, Adv. Energy Mater., 2024, 14, 2303173.
16. M. Gibert-Roca, M. Casademont-Viñas, Q. Liu, K. Vandewal, A. R. Goñi and M. Campoy-Quiles, Adv. Mater., 2023, 2212226.
17. L. Liu, H. Xiao, K. Jin, Z. Xiao, X. Du, K. Yan, F. Hao, Q. Bao, C. Yi, F. Liu, W. Wang, C. Zuo and L. Ding, Nanomicro Lett., 2023, 15, 23.
18. T. H. Kim, N. W. Park, M. A. Saeed, S. Y. Jeong, H. Y. Woo, J. Park and J. W. Shim, Nano Energy, 2023, 112, 108429.
19. H. S. Ryu, S. Y. Park, T. H. Lee, J. Y. Kim and H. Y. Woo, Nanoscale, 2020, 12, 5792–5804.
20. M. A. Alkhalayfeh, A. Abdul Aziz, M. Z. Pakhuruddin, K. M. M. Katubi and N. Ahmadi, Phys. Status Solidi A, 2022, 219, 2100639.
21. Y. Cui, L. Hong and J. Hou, ACS Appl. Mater. Interfaces, 2020, 12, 38815–38828.
22. M. R. Busireddy, S. C. Huang, Y. J. Su, Z. Y. Lee, C. H. Wang, M. C. Scharber, J. T. Chen and C. S. Hsu, ACS Appl. Mater. Interfaces, 2023, 15, 24658–24669.
23. Y. Cui, Y. Wang, J. Bergqvist, H. Yao, Y. Xu, B. Gao, C. Yang, S. Zhang, O. Inganäs, F. Gao and J. Hou, Nat. Energy, 2019, 4, 768–775.
24. C. Lee, J. Lee, H. H. Lee, M. Nam and D. Ko, Adv. Energy Mater., 2022, 12, 2200275.
25. L.-K. Ma, Y. Chen, P. C. Y. Chow, G. Zhang, J. Huang, C. Ma, J. Zhang, H. Yin, A. M. Hong Cheung, K. S. Wong, S. K. So and H. Yan, Joule, 2020, 4, 1486–1500.
26. D. Lübke, P. Hartnagel, J. Angona and T. Kirchartz, Adv. Energy Mater., 2021, 11, 2101474.
27. V. Esen, Ş. Sağlam and B. Oral, Renewable Sustainable Energy Rev., 2017, 77, 1240–1250.
28. M. A. Green, Prog. Photovolt.: Res. Appl., 2012, 20, 472–476.
29. U. Rau, B. Blank, T. C. M. Müller and T. Kirchartz, Phys. Rev. Appl., 2017, 7, 044016.
30. J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. McGarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053.
31. X.-K. Chen, D. Qian, Y. Wang, T. Kirchartz, W. Tress, H. Yao, J. Yuan, M. Hülsbeck, M. Zhang, Y. Zou, Y. Sun, Y. Li, J. Hou, O. Inganäs, V. Coropceanu, J.-L. Bredas and F. Gao, Nat. Energy, 2021, 6, 799–806.
32. M. Azzouzi, J. Yan, T. Kirchartz, K. Liu, J. Wang, H. Wu and J. Nelson, Phys. Rev. X, 2018, 8, 031055.
33. K. Vandewal, J. Benduhn and V. C. Nikolis, Sustainable Energy Fuels, 2018, 2, 538–544.
34. Q. Liu and K. Vandewal, Adv. Mater., 2023, 35, 2302452.
35. X. Rodríguez-Martínez, E. Pascual-San-José and M. Campoy-Quiles, Energy Environ. Sci., 2021, 14, 3301–3322.
36. J. Yan, X. Rodríguez-Martínez, D. Pearce, H. Douglas, D. Bili, M. Azzouzi, F. Eisner, A. Virbule, E. Rezasoltani, V. Belova, B. Dörling, S. Few, A. A. Szumska, X. Hou, G. Zhang, H.-L. Yip, M. Campoy-Quiles and J. Nelson, Energy Environ. Sci., 2022, 15, 2958–2973.
37. S. Kim, J. A. Márquez, T. Unold and A. Walsh, Energy Environ. Sci., 2020, 13, 1481–1491.
38. A. Harillo-Baños, X. Rodríguez-Martínez and M. Campoy-Quiles, Adv. Energy Mater., 2020, 10, 1–12.
39. A. Harillo-Baños, Q. Fan, S. Riera-Galindo, E. Wang, O. Inganäs and M. Campoy-Quiles, ChemSusChem, 2022, 15, e202101888.
40. E. Pascual-San-José, X. Rodríguez-Martínez, R. Adel-Abdelaleim, M. Stella, E. Martínez-Ferrero and M. Campoy-Quiles, J. Mater. Chem. A, 2019, 7, 20369–20382.
41. X. Rodríguez-Martínez, S. Riera-Galindo, J. Cong, T. Österberg, M. Campoy-Quiles and O. Inganäs, J. Mater. Chem. A, 2022, 10768–10779.
42. V. Belova, A. Perevedentsev, J. Gorenflot, C. S. P. De Castro, M. Casademont-Viñas, S. H. K. Paleti, S. Karuthedath, D. Baran, F. Laquai and M. Campoy-Quiles, Sol. RRL, 2022, 6, 2100822.
43. J. Hofinger, C. Putz, F. Mayr, K. Gugujonovic, D. Wielend and M. C. Scharber, Mater. Adv., 2021, 2, 4291–4302.
44. Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275.
45. C. Sun, F. Pan, H. Bin, J. Zhang, L. Xue, B. Qiu, Z. Wei, Z. G. Zhang and Y. Li, Nat. Commun., 2018, 9, 1–10.
46. Z. Xu, F. Pan, C. Sun, S. Hong, S. Chen, C. Yang, Z. Zhang, Y. Liu, T. P. Russell, Y. Li and D. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 9537–9544.
47. Q. Liu, J. Fang, J. Wu, L. Zhu, X. Guo, F. Liu and M. Zhang, Chin. J. Chem., 2021, 39, 1941–1947.
48. D. Baran, R. S. Ashraf, D. A. Hanifi, M. Abdelsamie, N. Gasparini, J. A. Röhr, S. Holliday, A. Wadsworth, S. Lockett, M. Neophytou, C. J. M. Emmott, J. Nelson, C. J. Brabec, A. Amassian, A. Salleo, T. Kirchartz, J. R. Durrant and I. McCulloch, Nat. Mater., 2017, 16, 363–369.
49. J. Yan, E. Rezasoltani, M. Azzouzi, F. Eisner and J. Nelson, Nat. Commun., 2021, 12, 1–12.
50. S. Liu, Y. Zhou, Z. Liang, B. Zhao, W. Wang, Z. Xue, K. Ding, Z. Cong, H. Wu, G. Lu and C. Gao, ACS Appl. Energy Mater., 2023, 6, 5047–5057.
51. Y. Wu, Y. Zheng, H. Yang, C. Sun, Y. Dong, C. Cui, H. Yan and Y. Li, Sci. China Chem., 2019, 63, 265–271.
52. Q. Guo, Q. Guo, Y. Geng, A. Tang, M. Zhang, M. Du, X. Sun and E. Zhou, Mater Chem Front., 2021, 5, 3257–3280.
53. D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709.
54. Y. Cui, Y. Wang, J. Bergqvist, H. Yao, Y. Xu, B. Gao, C. Yang, S. Zhang, O. Inganäs, F. Gao and J. Hou, Nat. Energy, 2019, 4, 768–775.
55. H. Bristow, K. J. Thorley, A. J. P. White, A. Wadsworth, M. Babics, Z. Hamid, W. Zhang, A. F. Paterson, J. Kosco, J. Panidi, T. D. Anthopoulos and I. McCulloch, Adv. Electron. Mater., 2019, 5, 1900344.
56. S. Halaby, M. W. Martynowycz, Z. Zhu, S. Tretiak, A. Zhugayevych, T. Gonen and M. Seifrid, Chem. Mater., 2021, 33, 966–977.
57. S. Marina, A. D. Scaccabarozzi, E. Gutierrez-Fernandez, E. Solano, A. Khirbat, L. Ciammaruchi, A. Iturrospe, A. Balzer, L. Yu, E. Gabirondo, X. Monnier, H. Sardon, T. D. Anthopoulos, M. Caironi, M. Campoy-Quiles, C. Müller, D. Cangialosi, N. Stingelin and J. Martin, Adv. Funct. Mater., 2021, 31, 2103784.
58. T. Markvart, Appl. Phys. Lett., 2007, 91, 1–3.
59. S. Rühle, Sol. Energy, 2016, 130, 139–147.
60. U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085303.
61. M. Casademont-Viñas, M. Gibert-Roca, M. Campoy-Quiles and A. R. Goñi, Rev. Sci. Instrum., 2023, 94, 103907.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01944j

---