Overcoming the mobility penalty introduced by dipole disorder in small-molecule HTM films

Abstract

The importance of the hole-transport material (HTM) in perovskite solar cells (PSCs) is now very well-established, with state-of-the-art materials such as spiro-OMeTAD attracting significant attention in the last decade. The high cost of such materials still limits the commercialisation of these HTMs. To tackle this, the amide linker has recently been introduced into HTM systems viaEDOT-Amide-TPA, utilising condensation chemistry as a cheap and effective route to HTMs. EDOT-Amide-TPA is capable of a variety of intermolecular interactions such as dipole–dipole interactions and hydrogen bonding, both of which are beneficial for enhancing the film morphology and improving charge transport. However, the interplay between these different interactions is not trivial, and understanding how they affect each other is paramount to inform new HTM designs whilst minimising material waste. To date, studies investigating the combined effects of different intermolecular interactions within the HTL on the charge transport properties of these materials are lacking. Furthermore, dipole disorder within the film introduces a mobility ‘penalty’: mobility decreases with stronger overall dipole due to energetic disorder within the film, which hinders charge hopping. In this work, we investigate three amide-based HTM analogs with differing intermolecular interaction capabilities, and show that this penalty can be compensated by a preferentially increased dipole ordering, likely achieved through intermolecular hydrogen bonding. This effectively cancels out the dipole disorder while retaining the beneficial effects on the molecular packing. Our aim is that this work provides a good foundation for navigating the complex interplay between hydrogen bonding, dipole moments, conductivity, and film formation in small-molecule HTMs.

---

1 Introduction

Molecular hole transport materials (HTMs) are a key component of many different optoelectronic applications, ranging from light emitting diodes (LED) to solar cells.^1–3 This class of organic HTMs has garnered particular interest within the last decade, due to their practical benefits such as easy solution processing and purification, as well as tunable optical properties through structural modifications.⁴ They have been applied very successfully in perovskite solar cells (PSCs) to achieve record power conversion efficiencies (PCEs) currently certified at 25.7%.^5,6 As a result, PSCs have reached efficiencies now comparable to traditional silicon solar cells in a much shorter timeframe, making this an exciting avenue of research for next-generation solar cells.^7,8

The hole-transport layer (HTL) serves many important functions in a solar cell and is critical for efficient operation. These functions include: (i) efficient extraction of photogenerated holes from the perovskite layer to the back electrode through a well-matched HOMO level with the perovskite conduction band; (ii) providing an energy barrier for electrons through a sufficiently high LUMO level, thus preventing their injection into the HTL and reducing electron–hole recombination; and (iii) an organic HTL also serves as a hydrophobic barrier in regular n–i–p PSCs, protecting the perovskite layer against moisture-induced degradation.⁹ Therefore, there has been much focus into small molecule HTMs such as spiro-OMeTAD or polymeric alternatives such as poly[bis(4-phenyl)(2,4,6-trimethylphenyl)-amine] (PTAA). In particular, spiro-OMeTAD has reached record-holding PCE in solar cell architectures, and this has put it at the forefront of research in the field.^2,10 To achieve this, the action of chemical dopants is required to increase the hole conductivity of the HTM.¹¹ Commonly used p-dopants include ionic salts such as lithium or zinc bis(trifluoromethanesulfonyl)imide (LiTFSI, Zn(TFSI)₂), and the cobalt-based tris(2-(1H-pyrazol-1-yl)-4-tert-butylpyridine) cobalt(III) tri[bis(trifluoromethane)sulfonimide] (FK209). These dopants are used to partially oxidise the HTM, generating additional holes in the matrix thereby aiding conduction.

In most organic semiconductors, hole conduction occurs through a thermally assisted hopping mechanism between various HOMO energy levels within the layer.¹² The average hopping distance is therefore directly related to the conductivity, and is determined by myriad factors such as sterics and the geometry of the HTM packing. Many different intermolecular interactions such as hydrogen bonding, π–π stacking, and dipole–dipole interactions can also affect the packing and morphology of an amorphous HTL, especially when multiple competing interactions are present. Probing the effects of all possible interactions on the film morphology is challenging, as the average effect of all interactions makes it difficult to disentangle and isolate the individual effects. Through various measurements such as solid-state X-ray crystallography, solution NMR, and theoretical calculations on simulated HTM films, we can infer useful information into the interactions possibly occurring in small, ordered domains within the amorphous film. A good understanding of the combined intermolecular forces governing the packing distance in the hole transport layer is essential for tailoring the design of future HTMs. This will also help forthcoming research in the field to move away from trial-and-error approaches, greatly reducing waste and speeding up HTM design.

It has been previously shown by Pope, et al. that strong dipole moments through the HTM can significantly reduce conductivity due to increased energetic disorder.¹² This study showed, using Kinetic Monte Carlo (KMC) simulations, that a disordered energy landscape within the film gives rise to trap states and inefficient pathways for charge to percolate through the material. A very high degree of global dipole ordering is required to counteract this effect, which is unlikely to be achieved in a solution-processed film.¹² It is therefore essential to consider not just the effect of the dipoles in isolation, but the combined effects of all possible noncovalent interactions on the correlated disorder within a film.

A good-quality HTM film is essential to minimise series resistance in solar cells and reach optimum PCE.⁹ We have recently synthesised a family of HTMs with an amide-based backbone through the use of simple condensation chemistry, the first of which being EDOT-Amide-TPA (1). This molecule shows remarkable film-forming ability, yielding pinhole-free thin films and record PCEs comparable to those achieved by spiro-OMeTAD in PSC architectures.¹³ These benefits are in no small part due to the hydrogen bonding through the amide groups as well as the central dipole through the EDOT core, in contrast with spiro-OMeTAD which can form limited intermolecular interactions leading to significant pinhole formation within the film.

In this work, we aim to gain a fuller view on intermolecular interactions within HTM films, and compare three amides, these being EDOT-Amide-TPA (1), TPABT (3), and newly synthesised DEDOT-Amide-TPA (2). All studied compounds have dipoles through the core of the molecule, differing only in hydrogen bonding capability. We show through single-crystal X-ray data how modifying the hydrogen bonding properties of our molecules can promote the formation of intermolecularly hydrogen bonded molecular pairs with antiparallel-oriented dipoles in the crystal (compound 3). We also observe an order of magnitude increase in the film conductivity of compound 3 compared to compound 1 in which the amide bonds cannot form these molecular pairs. While observations of intermolecular interactions in crystalline states are not directly transferable to more disordered films, they provide valuable insight into the morphological behaviour of the films. We substantiate these points through theoretical calculations, showing how the formation of small amounts of these molecular pairs within an otherwise amorphous film could directly explain the observed increase in conductivity. We also provide NMR and FTIR evidence for the presence of hydrogen bonding in solution and solid state. Through our spectroscopic measurements, we observe very similar hydrogen bonding interactions between molecules in solution and in the solid. FTIR measurements also reveal that the solid state hydrogen bonding does not significantly differ between the crystal and the thin films. We can therefore reasonably conclude that hydrogen bond-assisted pairing is the most likely candidate for our observed conductivity improvement. This establishes useful guidelines for the design of future low-cost HTMs, particularly those featuring strong dipoles in their core. The energetic disorder arising from misaligned dipoles in the film can be effectively neutralised by the careful tailoring of hydrogen bonds to support the antiparallel arrangement of the dipoles, thus leading to improved conductivity.

2 Results and discussion

2.1 Synthesis and characterisation

To explore the effect of intermolecular interactions of molecular HTMs and their effect on the resulting charge transport properties, we must be able to control the molecular packing within the films. Here, hydrogen bonding is an easily modifiable property in our molecules, which has a strong effect on the resulting stacking.^13,14 In this work, we compare three molecules: EDOT-Amide-TPA which incorporates strong intramolecular hydrogen bonding, TPABT which possesses strong intermolecular bonding capability, and DEDOT-Amide-TPA where hydrogen bonding is not possible.

We prepared our three materials with through very simple condensation chemistry. Compound 2 is the N,N-dimethylated analog of compound 1, which allows a like-to-like comparison involving only a chemical change that thwarts the ability of compound 2 to form hydrogen bonds. Compound 3 is an analogue of 1 with a thiophene ring as the central core instead of EDOT. By employing readily available, carboxylic acid-functionalised cores, the triphenylamine donor units were attached to the acceptor cores following conversion of the acid groups to the acid chloride derivatives, as detailed in Scheme 1. The dimethylated analogue 2 was prepared from 1via a one-pot methyl substitution reaction at the amide nitrogens. These synthetic strategies allowed facile synthesis of 1 and 3, with 1 requiring very simple purification via recrystallisation from DMSO and washing with methanol. Compounds 2 and 3 were purified using column chromatography followed by recrystallisation from ethanol. As part of a comprehensive suite of characterisation, we studied our synthesised materials through ¹H and ¹³C NMR spectroscopy, as well as high-resolution mass spectrometry to ensure their identity and purity. The relevant spectra can be found in the ESI, Fig. S1–S4.†

Scheme 1 Condensation chemistry-based syntheses of the three HTMs used in this study. (i) K₂CO₃, copper powder, 18-crown-6, DMF, reflux (150 °C, 16 hours), yield 67%; (ii) 10% palladium on carbon, hydrazine hydrate, dry THF, reflux (66 °C, 16 hours); (iii) thionyl chloride, THF, reflux (66 °C, 2 hours); (iv) 4-amino-4′,4′′-dimethoxytriphenylamine, triethylamine, THF, room temperature, stir overnight, yield 70%; (v) sodium hydride, dry THF, iodomethane, 40 °C, overnight, yield 48%.

Condensation chemistry presents low-cost routes towards novel organic semiconducting molecules. The commercial applicability of any newly developed material hinges on its cost of production, which involves expenses from synthesis and purification. We performed a cost analysis of our three amide HTMs. HTM 1 proves to be the cheapest material to produce owing to its facile purification which does not require column chromatography.

This leads to a low material cost of $5.74 per g for HTM 1. HTMs 2 and 3, which require column chromatography using halogenated solvents for purification, have slightly increased production costs at $16.76 per g and $15.48 per g respectively. However, these are still far cheaper to produce than spiro-OMeTAD, which has been reported to cost around $91 per g as a result of numerous purification steps involving large quantities of halogenated solvents. The cost-effectiveness of condensation chemistry is thus demonstrated with our three amide HTMs.

2.1.1 Spectroscopy and electrochemistry. Knowledge about the electronic energy levels of prospective HTMs is crucial for their successful implementation into devices. For instance, to achieve maximum charge transfer efficiency in a perovskite solar cell, the HOMO energy level of the HTM must be aligned slightly shallower than the valence band of the perovskite, which is normally in the range of −5.4 to −5.7 eV.^15,16 Here, we study the optical properties of our molecules through light absorption measurements, as well as the electrochemical properties through cyclic voltammetry in order to estimate their electronic energy levels. The UV-visible absorption characteristics of our materials are depicted in Fig. 1b, and the main results are summarised in Table 1. Tauc plots (Fig. 1c) were used to find the absorption onset from the absorption spectra, from which the optical bandgaps (E_g) were estimated.

Fig. 1 (a) Cyclic voltammograms referenced to the Fc/Fc⁺ redox couple (CH₂Cl₂, 1 × 10⁻⁴ M), (b) solution UV-visible absorption (solid lines) and emission spectra (dashed lines) of the three amide-based HTMs, and (c) Tauc plots and corresponding optical bandgaps E_g.

Table 1 Optical properties measured from UV-visible absorption and fluorescence spectroscopy

HTM	λ max (nm)	λ em (nm)	Stokes shift (nm)	E g (eV)
1	387	572	185	2.78
2	352	492	140	3.77
3	340	480	140	3.27

---

All materials show very large Stokes shifts between their absorption and emission maxima (Fig. 1), showing that they undergo large geometrical deformations upon light excitation.^17,18 Interestingly, spiro-OMeTAD has a reported Stokes shift as low as 42 nm.¹⁶

The electrochemical behaviour of our materials is equally important in determining their charge transport properties within the context of a solar cell. Fig. 1a shows the cyclic voltammograms of our three amides, all of which show a reversible one-electron oxidation implying good electrochemical stability. The ionisation potentials (IPs) of our materials were then estimated from the electrochemical data, using square-wave voltammograms (SWVs, Fig. S7, ESI†) to better extract the oxidation peaks. The results from our electrochemistry experiments are given in Table 2.

Table 2 Estimated ionisation potentials (IPs) for our amide materials, from cyclic voltammetry measurements

	E 1/2 (V) vs. Fc^+/Fc	IP (eV)	IP + Eg (eV)
1	0.164	−4.97	−2.16
2	0.224	−5.04	−1.26
3	0.168	−4.96	−1.69

---

While IPs estimated from solution CV data should not be used as a direct measure of the HOMO energies in the solid state,¹⁹ they point towards the energy band alignment with many common perovskite compositions employed in solar cells, such as MAPbI₃ and various triple-cation (CsFAMA) perovskite compositions.^15,20 Our results above show that all three amide HTMs have ionisation potentials aligned slightly shallower than many common perovskite valence energy bands, facilitating easy hole injection into the HTL.

As the first reduction potentials were not experimentally accessible, a rough estimation of the LUMO was obtained by adding the optical bandgap to the ionisation potential (IP + E_g, Table 2). The very shallow values obtained indicate effective electron blocking capability, preventing their injection from the perovskite and thereby minimising charge recombination within the HTL.²¹

When investigating the suitability of new materials for use as HTMs, their thermochemical properties are important parameters to consider. Photovoltaic devices such as perovskite solar cells may reach temperatures up to 80 °C during their operation,¹³ thus the ideal HTM must remain in the amorphous state throughout the entire operational lifetime of the device for maximum stability.

Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) on our three amide materials reveals their high thermal stability, typical for aromatic amides (Fig. 2).¹³ The lowest thermal decomposition temperature (T_d) was recorded for HTM 3 at 310 °C, followed by compound 1 at 349 °C, and HTM 2 having the highest T_d at 370 °C. From the DSC results, there is a clearly observable trend in melting temperatures (T_m) arising from differing intermolecular hydrogen bonding capability. HTM 2 has the lowest T_m at 199 °C, followed by HTM 3 at 228 °C, then HTM 1 with the highest T_m of 294 °C. This correlates with a complete lack of hydrogen bonding in HTM 2, leading to weak intermolecular forces holding the solid together which can be easily broken with elevated temperature. Glass transitions (T_g) are also observed above 90 °C for all amides, indicating that they can exist in both amorphous and crystalline forms. For HTM 1, an additional cold crystallisation (T_c) is observed at 155 °C which is in good agreement with previous literature.¹³ As all thermal transitions exceed the operational temperatures of photovoltaic devices, these amides are expected to remain stable against thermally-induced morphological changes throughout the life cycle of the device.

Fig. 2 Stacked (a) TGA and (b) DSC curves for our three amide HTMs. Thermograms were recorded for pristine HTMs, at a rate of 5 °C min⁻¹ under nitrogen.

2.2 Spectroscopic insights into intermolecular interactions

In order to demonstrate that our HTMs indeed show distinct intermolecular interactions and the effects this has on the molecular packing, we performed a combined spectroscopic study employing NMR and FTIR. Here, a strong network of non-covalent interactions between HTM molecules is expected to promote compact and even film formation in the solid state, as has been observed in many studies in the literature.^22–24

We therefore probed the intermolecular interaction in solution via a series of ¹H-NMR experiments and in the solid-state using FTIR measurements.

We performed ¹H-NMR experiments on our three amide HTMs across a range of temperatures and concentrations in CDCl₃. CDCl₃ is an ideal solvent for this purpose, as its low polarity ensures that it forms no competing hydrogen bonds with our amides, and has thus been widely used in such studies.^24–26

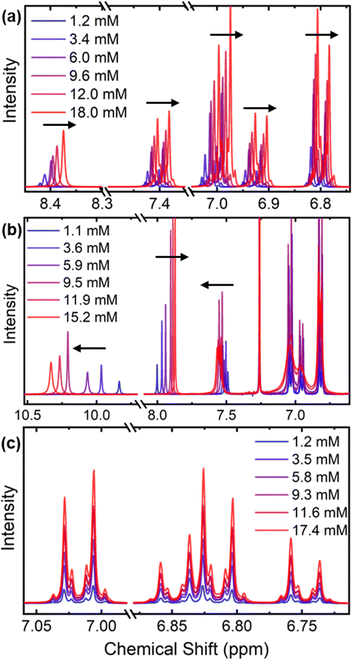
We observe an increasing upfield shift in the amide and aromatic proton resonances of compound 1 (8.4 ppm, 7.4–6.7 ppm respectively) as the solution concentration is increased (Fig. 3a). Such a shift pattern with increasing concentration is widely reported to be a result of increased π–π stacking, which exposes protons to secondary magnetic fields from ring currents that shield the signal.^27,28 Compound 1 is therefore able to undergo stacking interactions, suggesting that the core of the molecule is planar to allow for close proximity of neighbouring molecules. This geometry is likely to be induced by strong intramolecular hydrogen bonds between the amide linkers and the oxygen atoms on the EDOT moiety, which are concentration-independent and do not affect the chemical shifts across the series.^29,30 We can directly observe these intramolecular H-bonds by disrupting them through the addition of DMSO-d6 (Fig. 4a), or by increasing the temperature in a variable temperature NMR (VT-NMR) experiment (Fig. 4b). Increasing the temperature is widely known to break many non-covalent interactions, and similarly, DMSO is known to be a strong hydrogen bond acceptor and competes with hydrogen bonds in solution.^25,30,31 Increasing the fraction of DMSO-d6 in the CDCl₃ solution of HTM 1 leads to a progressive downfield shift of the amide proton resonances. This correlates with the disruption of the intramolecular hydrogen bonds in favour of stronger ones formed between DMSO and the amide protons. The VT-NMR experiment further supports this assignment, as increasing temperature is seen to disrupt both the intramolecular hydrogen bonding (leading to an upfield shift in the amide protons) and the π–π stacking (downfield shift in the aromatic protons).

Fig. 3 Partial ¹H-NMR spectra of (a) compound 1 and (b) compound 3 at different concentrations, showing shifts in their amide and aromatic proton resonances, and (c) compound 2, showing no shifts across the concentration range.

Fig. 4 Partial NMR spectra showing the aromatic and amide proton region in compound 1, (a) with increasing concentration of DMSO-d6, (b) with increasing temperature.

In compound 3, a more complex system of concentration-dependent interactions is observed, likely involving hydrogen bonding and aromatic stacking interactions simultaneously (Fig. 3b). The amide bonds in compound 3 are situated close enough that they can engage in one intramolecular hydrogen bond, leaving one hydrogen bond donor and one acceptor free for interactions with other molecules. We observe a downfield shift in the amide proton resonance (9.8 ppm) with increasing concentration as a result of increasing saturation of free hydrogen bonding sites. The thiophene proton signal at 8.0 ppm shifts upfield, indicating a π–π stacking interaction involving the core thiophene rings which may be brought together in solution by favourable intermolecular hydrogen bonding interactions at higher concentrations. All of these shifts could be directly replicated by increasing the temperature in VT-NMR, or increasing the fraction of DMSO-d6 in solution, which had the same effect as diluting the concentration of compound 3 (ESI, Fig. S2†). This further illustrates the complexity of the intermolecular interactions happening in solution, showing that the interactions occur in tandem, and are disrupted simultaneously. Nevertheless, we can still conclude that compound 3 has the capability to form strong intermolecular hydrogen bonds in solution.

Compound 2 was synthesised specifically to block hydrogen bonding by means of the methyl groups installed on the amide linkers. Fig. 3c shows that upon increasing concentration, we see no shifting in the aromatic region, indicating an absence of any concentration-dependent effects. Notably, this reveals that the steric bulk of the methyl groups combined with the lack of intramolecular hydrogen bonds (therefore a more twisted core) prevent π–π stacking through the core at higher concentrations, contrasting with our observations on compound 1.

Through these NMR studies, we have identified the nature of intermolecular interactions in solution, yet when employed in functional devices, these materials are generally used in the solid-state. It is therefore critical to ensure that these interactions are still present when deposited in thin film form. In order to verify the hydrogen bonding capabilities of the molecules, we conducted FTIR spectroscopy on neat powder samples of our three amide materials. Here, the ν_C=O and ν_N–H stretching modes are routinely used in many different fields to detect hydrogen bonding.

The FTIR spectra for compounds 1 and 3 are in good agreement with literature values.^13,14Fig. 5 shows the relevant regions in the FTIR spectra of the amides. We observe that all amides possessing N–H bonds (1 and 3) have N–H stretching bands at wavenumbers below 3400 cm⁻¹, characteristic of hydrogen bonded amides.^32,33 For compound 1, we observe sharp C=O and N–H stretches at 1662 cm⁻¹ and 3372 cm⁻¹ respectively. An N–H stretch at this position has previously been reported for an amide N–H intramolecularly hydrogen bonded to an EDOT oxygen atom,³⁴ further supporting a planar core for compound 1. Compound 3 presents two broadened N–H stretches at 3239 cm⁻¹ and 3180 cm⁻¹, and two broad C=O stretches at 1647 cm⁻¹ and 1628 cm⁻¹. N–H stretches below 3400 cm⁻¹ are characteristic of hydrogen bonding.^32,33 The presence of two resolved carbonyl and N–H stretching modes in compound 3 suggests that there are two different hydrogen bonding environments: a strong intramolecular hydrogen bond between amide the amide bonds, and a weaker intermolecular hydrogen bond between the free N–H and carbonyl groups of different molecules.³⁵ This complements the shift patterns observed in the solution NMR experiments on compound 3 (Fig. 3b), where increasing concentration favours more hydrogen bonding between different molecules. These intermolecular hydrogen bonds must therefore persist in the solid state, giving rise to two distinct signals in the FTIR spectrum. We can therefore conclude that our compounds 1 and 3 possess amide bonds capable of hydrogen bonding in both solution and solid state.

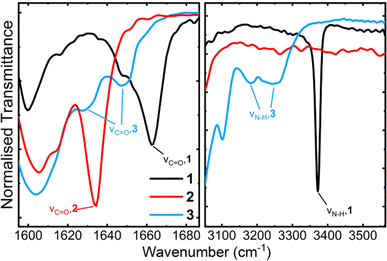Fig. 5 Partial FT-IR spectra obtained from powder samples of our three amides, showing the carbonyl stretch region (left) and the N–H stretching region (right).

2.3 Computational analysis of molecular dipoles

Besides the hydrogen bonding capabilities demonstrated above, all of our molecules also incorporate a dipole within the core which itself affects the film forming properties. Furthermore, dipole disorder in spin coated films has been shown to affect the energetic landscape of a film leading to negative effects on the resulting conductivity.¹² Computational methods are useful tools that allow modelling of the effect of the dipole and the ordering of many dipoles within a film on the resulting mobility.

2.3.1 Debye dipole moments and correlated energetic disorder. The conductivity of a HTM is strongly dependent on the overall dipole moment within the film, with a zero dipole moment expected to have the most ordered energy landscape and thus the most favourable conditions for efficient charge hopping. In amorphous materials, the interaction of randomly oriented, permanent dipole moments gives rise to correlated energetic disorder which scales with the size of the dipole moment. High dipole moments have been shown to quench charge mobility in both simulation and device-based experiments, as charges percolate through the system via energetically preferred routes.¹² Therefore, single molecule properties of our amides were investigated using density functional theory (PBE0/def2-sv(p)) in order to gain insight into their charge transport behaviour, and our results are summarised in Table 3. All three amides were found to have high dipole moments (p_DCM), with 2 having the lowest at 8 debye.

Table 3 DFT results performed at the DFT(PBE0)/def2-sv(p) level of theory as implemented within the Orca (v. 5.1) quantum chemistry package,³⁶ with predicted orbital energies and dipole moments for our three amide-based HTMs, compared to spiro-OMeTAD

HTM	p DCM (D)	HOMOvac^a (eV)	HOMODCM^b (eV)	HOMOcalc^c (eV)	LUMOvac^a (eV)	LUMODCM^b (eV)	GapDCM (eV)
a PBE0/def2-sv(p). b PBE0/def2-sv(p) with C-PCM(CH2Cl2) implemented. c based on HOMODFT,DCM with correction factor (−0.206 eV) applied.^37 ‘Gap’ in this case refers to the calculated HOMO–LUMO gap.
1	13.0	−4.87	−5.09	−5.29	−1.82	−2.01	3.08
2	8.0	−4.92	−5.23	−5.43	−1.30	−1.44	3.79
3	10.6	−4.87	−5.03	−5.23	−1.16	−1.34	3.69
Spiro-OMeTAD	3.3	−4.60	−4.91	−5.12	−0.75	−1.09	3.82

---

It has been speculated that high dipoles may drive self-assembly and reduce energetic disorder. However, previous work by Pope et al.¹² found that very high levels of order, unlikely to be achieved in solution-processed films, are required to counteract the deleterious effects of the dipole moment on hole mobility. The formation of highly ordered, low-dipole domains within an otherwise amorphous film could be possible through hydrogen bonding, and may assist in the formation of molecule pairs with antiferromagnetically oriented dipoles, resulting in a dramatic drop in the overall level of energetic disorder and improved charge transport behaviour.

2.3.2 Geometry and hydrogen bonding. The spatial orientation and geometry of our amide molecules is another key factor in determining their solid-state packing. Optimised geometries from DFT calculations (Fig. 6) provide some insight into possible intermolecular interactions within device films, with the availability of hydrogen bonding groups and relative planarity of these molecules likely affecting their preferred packing behaviour. In compound 3, the adjacent amide proton and oxygen are oriented towards each other across the ring with a calculated interatomic distance of 1.731 Å, consistent with strong intramolecular hydrogen bonding. Such a conformation would leave the remaining amide hydrogen atom and carbonyl oxygen atom free to participate in intermolecular hydrogen bonding while the V-shape exposes the core, facilitating interactions with multiple neighbouring molecules. Compound 1 was found to have a relatively flat structure, with its amide protons directed towards the dioxane oxygens, at a calculated distance of 2.014 Å. This conformation would facilitate close packing of molecules along one plane, in good agreement with our spectroscopic results. Our dimethylated amide 2 exhibits greatly reduced planarity, as expected due to the lack of intramolecular hydrogen bonding and steric hindrance from the bulky amide methyl groups. The preferred orientation of the molecule, when compared to the parent 1, suggests that this molecule might also exhibit a lower packing density within the film, which may result in larger hopping distances between HOMO levels in the film.

Fig. 6 (a) Theoretical (PBE0/def2-sv(p)) optimised structures in DCM, overlayed with visualisations of (b) HOMO and (c) LUMO of our three amide HTMs. For 3, we additionally show the destabilised HOMO−1 (−5.16 eV) and stabilised LUMO+1 (−1.18 eV) orbitals in cyan and magenta due to hydrogen bonding across the thiophene core.

2.4 Effect of intermolecular interactions on molecular packing

Spin coating of organic semiconducting materials often results in the creation of disordered films with highly amorphous character. For materials such as spiro-OMeTAD that can form no intermolecular interactions, spin coating notoriously produces highly porous films, requiring much more concentrated solutions to yield thicker films, ensuring good interfacial contact.^38,39 We sought to link the solid-state intermolecular interactions with the molecular packing properties of our materials. In this regard, single crystals are a very good tool to unambiguously show the conformation of molecules in the solid state, and act as the ideal scenario to show the effect of intermolecular interactions on the packing. Therefore, single-crystal X-ray diffraction (SCXRD) can provide conclusive evidence of the different packing properties of our three amides, brought about by their different hydrogen bonding and stacking properties. The resolved crystal structures also serve as a benchmark for DFT modelling and also FTIR measurements, where we can compare the hydrogen bonding environment in the crystal vs. films.

2.4.1 Single crystal X-ray diffraction (SCXRD). To determine how our materials align and interact in the solid state, as well as to investigate the influence of hydrogen bonding on molecular packing distance, we analysed the single crystal structures of our materials. While the molecular packing in an amorphous film is normally considerably more disordered than in a crystal structure, this analysis provides valuable information regarding the presence and significance of hydrogen bonding or dipole–dipole interactions within the film. To grow our single crystals, 2 mg of 2 and 3 were dissolved in 3 mL chlorobenzene in a capped vial, which was allowed to evaporate slowly through small holes in the lid. Crystals of 1 were significantly more challenging to grow, but suitable crystals were grown through a similar slow evaporation process from 3 mL of a 1 : 1 dichloromethane : ethanol mixture. The vastly different crystallisation properties of 1 compared to 2 and 3 are ascribed to this materials' low solubility in most solvents which often hindered slow nucleation of large crystals, in favour of more rapid precipitation.

The molecular structures from our X-ray data (Fig. 7) show that the conformations of 1 and 3 in the crystal structure are very similar to our DFT predicted structures (Fig. 6). We observe that 2 adopts an even more twisted structure in the solid state than theoretically predicted. Compound 2 is distinctly different from 1 and 3 as these have a planarised core by virtue of the intramolecular hydrogen bonding between the amide hydrogens and the dioxane oxygen lone pairs (1) or the amide carbonyl oxygen lone pairs (3). We expect this less twisted configuration to help compounds 1 and 3 pack closer together in thin films, bringing the HOMOs closer together, allowing more efficient charge hopping and thereby increasing conductivity. We have previously observed such inclination towards close packing in solution through our NMR studies (Fig. 3 and 4). We observe from our DFT results that the HOMOs are almost entirely located on the triphenylamine (TPA) side groups, with the LUMO being mostly located on the ethylenedioxythiophene (EDOT) or thiophene core. To quantify any improvement of packing and how this might affect charge transport, we compared the distance between the nitrogen atoms on the TPA side groups across different molecules in the crystal structures. This is worthy of investigation as charges hopping through an HTM film do so through the HOMOs mainly located on these TPA groups.

Fig. 7 Top and side-on views of our three amide HTMs from the resolved X-ray crystal structure data. We note a significantly more twisted structure for compound 2 compared to that observed from DFT.

In an amorphous film, such as one produced through spin coating, we anticipate more disordered packing compared to a crystal. However, the absence of long-range order does not necessarily negate the existence of small, ordered aggregates, which could significantly influence hole transport properties. In this context, X-ray crystal structures, while not representative of the amorphous film, provide us with some best-case scenarios for possible ordered domains and gives an idea of the expected configuration patterns. It is worth noting that compound 3 crystallised as a solvate, incorporating chlorobenzene molecules into the crystal structure, which is likely to have some effect on the packing density of the resulting crystal. We note that chlorobenzene is also the major component of the spin coating solution of all three materials, so any effects that the chlorobenzene molecules have on the crystallisation of compound 3 would also be expected in the amorphous film case.

From the resolved crystal structures, we clearly observe a reduction in the nearest measured TPA N–N distance from 5.166 Å in compound 2 to 5.040 Å in compound 3. Compound 1 has a shortest distance between that of 2 and 3 at 5.108 Å. Interestingly, in the crystal structure for compound 3 we see the formation of molecular pairs formed through intermolecular hydrogen bonds across the amide groups (Fig. 8, S6, ESI†). These can be thought of as isolated, tightly packed pairs where the dipoles are oriented antiparallel to each other thus leading to zero net dipole. Since the crystal of compound 3 formed as a solvate with chlorobenzene, these crystallisation conditions may have either promoted the formation of these molecular pairs, or alternatively the presence of these pairs may have allowed the crystal to trap solvent molecules. In any case the crystal structure indicates the propensity of the TPABT molecular structure to form these molecular pairs via H-bonding interactions through the amide bonds.

Fig. 8 Graphical representation of the crystal structure packing of compounds 1–3.

In 1, molecules form repeating units of closely packed antiparallel strands. This results in neighbouring molecules that are oriented both antiparallel to one another on the one hand, with dipole moments that cancel out, and neighbours that are oriented in the same direction on the other hand, where the dipole moment is enhanced. The calculated binding energies (ESI, Table S1†) of antiparallel pairs in 1 and 3 show that these are more stable than molecules oriented either orthogonally (3) or parallel (1) to one another. Therefore, while the dipole of monomers remains high, stable antiparallel pairs quench the dipoles on these sites so that the overall level of correlated energetic disorder in the film is reduced. In compound 2, parallel and antiparallel pairs have similar stabilities, so that the correlated energetic disorder remains high. Without any hydrogen bonding capability, compound 2 is likely to adopt a more disordered and less dense packing arrangement in the film which is expected to significantly hinder conductivity.¹²

2.4.2 FTIR analysis of crystals vs. thin films. In order to show the effect of the intermolecular interactions in disordered thin films, we performed FTIR measurements comparing the single crystals to spin coated films. Here, single crystals represent the most ordered system of a particular species when it is allowed to pack slowly into an extended network. Conversely, spin coating is a rapid and effective method for depositing thin films onto substrates. In order to discern whether rapid spin coating impedes the development of robust intermolecular hydrogen bonds within the film, we again employed FTIR spectroscopy to examine N–H and C=O stretches in the film vs. the crystal. Thin films were spin coated onto glass substrates from chlorobenzene solution (2) or mixtures of chloroform/chlorobenzene (1 and 3). The films were then removed with a razor and the resulting powder was collected for powder FTIR. Crystals were also grown for this measurement using the same methodologies as used for SCXRD, and were allowed to dry to remove residual mother solvent.

Fig. 9 illustrates that the bonding environment in both cases is remarkably similar, revealing a near-perfect overlap of peaks in both the C=O and N–H stretching regions for films vs. crystals. Notably, there is no significant broadening observed in the film IR spectrum, indicating that even in a thin film, the presence of non-hydrogen bonded amide linkers is minimal for compounds 1 and 3. The identical vibrational frequencies seen in all cases indicates that the hydrogen bonding systems in our thin films do not deviate significantly from the crystal, and any interactions observed in the crystal have sufficient time to form in the more rapid spin coating process. We can therefore reasonably claim that compounds 1 and 3 can form extensive hydrogen bonds when spin coated, with the crystal structure giving a good indication of preferred packing orientations between molecules.

Fig. 9 Comparative FTIR spectra of our three amides measured from either spin coated films (dotted lines) or from crystals (solid lines).

2.4.3 Kinetic Monte Carlo simulations of hole hopping. Having directly observed the effects of intermolecular hydrogen bonding from solution NMR data, as well as pairing interactions in the solid-state crystal data, we then sought to understand the effect of this molecular pairing on the hole mobility of high dipole, amorphous films of our materials. We performed simulations using an in-house kinetic Monte Carlo code,¹² where the HTM film was represented as a cubic lattice with 8 million hopping sites, with a lattice spacing of 10 Å. Site dipoles were initially set to 10 debye and oriented randomly as described in previous work.¹² In systems with a non-zero pair population, paired site dipoles were reset to 0 debye and aligned with the reference frame. Marcus hopping rates for a range of pair populations at different field strengths were found. All other parameters were kept constant including uncorrelated noise, hole density and reorganisation energy so that the effect of pair density on mobility could be definitively probed. Further simulation details are provided in the ESI.†

Fig. 10a shows the dependence of the hole mobility, μ_h, on the applied electric field, E_Field, for a range of systems with pair densities ranging from zero to 42%, fitted to a Poole–Frenkel-type equation . We see expected Poole–Frenkel behaviour, for electric fields between 4 × 10⁵ and 9.5 × 10⁵ V cm⁻¹, which was used to extrapolate to the zero-field mobility. Fig. 10b shows that the mobility increases logarithmically with the pair density from 7 ± 1 × 10⁻⁷ cm² V⁻¹ s⁻¹ to 2 ± 0.5 × 10⁻⁶ cm² V⁻¹ s⁻¹, with an increase from 0–42% in the pair population. We find that increasing the pair population to just 30% results in an almost three-fold increase in mobility, as shown in the normalised mobility plot in Fig. 10c. While a 30% pair population seems large for an amorphous material, it could be achieved if there is a large enough energetic driving force for stable molecular pairs to form, which we find to be the case for all three amides (Table S1, ESI†). While the material remains disordered and dipoles remain high, the molecular pairs with quenched dipoles serve to reduce the correlated noise width. We see that both the gradients in Fig. 10b for the zero field and high field case are similar, suggesting that the effect of the pair population on the mobility does not change with the applied electric field but instead results in a global increase in the mobility. While other parameters such as hopping distance and electronic coupling also influence the mobility, the effect of the dipole is included in the exponential term of the hopping rate equation and its influence is likely to be dominant.

Fig. 10 (a) Mobility against field at different pair densities, (b) mobility against pair density at a field strength of 5 × 10⁵ V cm⁻¹ and at zero field, (c) normalised mobility against pair density.

Therefore, the ability of 1 and 3 to form energetically favoured 0 debye hydrogen bonded pairs is consistent with these high dipole materials being able to have high mobilities. It is also worth noting that simulations were run for fully disordered systems and, therefore, introducing some degree of dipole ordering would further increase the mobility of these systems.¹²

2.5 Charge transport measurements

In order for these materials to function as effective HTMs, they need to have appreciable hole conductivity to quickly shuttle holes from the hole-injecting medium to the electrode. Conductivity in small-molecule HTMs is directly affected by the morphology of the film, with the molecular packing having a big effect on the percolation of charge through the material. Having demonstrated the robust intermolecular interaction capabilities of our molecules in both solution and solid state, we sought to investigate the effects these interactions have on their conductivities. We thus fabricated a series of thin films of our materials through solution spin coating to investigate their conductivities.

2.5.1 Action of chemical dopants. Like many organic semiconductors, our amide materials require the action of chemical doping to gain appreciable conductivity for solar cell applications. To maintain consistency in the oxidation of our HTMs, we opted to use only the redox dopant FK209, which undergoes a well-established redox reaction with our HTMs, introducing a hole into the HOMO levels with the concomitant reduction of its Co(III) centre to Co(II).⁴⁰ This has the added benefit of not requiring exposure to oxygen to achieve the requisite oxidation, as is the case with other conventional dopants such as LiTFSI. By employing FK209, we could ensure that oxidation is a direct result of the doping, eliminating the ambiguity that arises in Li-doped systems where a ‘curing’ process in a dry oxygen environment is needed for effective doping.⁴¹ As Fig. 11 shows, FK209 readily oxidises all of our HTMs, yielding well-defined growth of oxidised species peaks in their UV-visible absorption spectra.

Fig. 11 Doping trends in the film UV-visible absorption spectra of our amide-based HTMs (a–c) and spiro-OMeTAD (d), with increasing concentrations of FK209.

The presence of a small amount of oxidised HTM within the matrix is responsible for a great increase in conductivity. When working with doped HTM films, the standard practice in the field has normally involved monitoring the degree of oxidation using some measure of the equivalents of added dopant.^17,42,43 When comparing doping between different HTMs, this method completely negates the chemical reactivities of different HTMs to the dopant used, as well as the reactivity of a single HTM to different chemical additives, and instead effectively assumes a 1 : 1 reaction between HTM and dopant. This introduces errors when comparing different systems, so to standardise our experiments we introduce a new method to accurately quantify the degree of oxidation from the film UV spectra of doped solutions. We use the ratio of absorbances of oxidised peaks to unoxidised peaks in the film UV spectra as a measure of oxidation. This requires the molar extinction coefficients of both the neutral and the oxidised species to be known, so the extinction coefficients of all neutral species were estimated from UV-visible absorption spectra collected during their characterisation.

In order to determine the extinction coefficients of oxidised species, we used a titrimetric method published by Nguyen, et al.⁴⁴ to generate a precisely known amount of oxidised species using silver bis(trifluoromethanesulfonyl)imide (AgTFSI). This dopant has been previously used for its excellent chemical reactivity, as the reduction of Ag(I) to Ag_(s) and subsequent precipitation of metallic silver out of solution drives the reaction to completion.⁴⁵ Furthermore, it generates the same oxidised complex as FK209 would, i.e. HTM⁺TFSI⁻, thus producing the same spectral properties that can be used to calculate the molar extinction coefficient of the oxidised species. We show that AgTFSI can very easily oxidise solutions of all of our HTMs, as well as spiro-OMeTAD (Fig. S8, ESI†). Having estimated all of our relevant molar extinction coefficients (Table S3, ESI†), we were then able to use the calculated ratio of oxidised to unoxidised species to plot conductivities of our materials on the same axes, eliminating any errors arising from different reactivity.

2.5.2 Charge transport measurements. To assess and compare the conductivities of our materials, thin films were deposited onto patterned ITO substrates by solution spin coating. In addition to pristine films, films doped with increasing amounts of FK209 were also prepared for conductivity measurements (detailed in Table S4, ESI†). Our compiled conductivity results are shown in Fig. 12. We observe significant influence of the dipole ordering and HOMO packing distance and on the resulting conductivity, as compound 3 shows increased conductivity by an order of magnitude over compound 1 across most of the oxidation range. Our results agree well with the degree of dipole ordering seen through our crystal structures and predicted hole hopping behaviour from simulation experiments. Compound 3 showed the formation of stable, zero dipole pairs in the crystal structure, which are likely to also form during spin coating as demonstrated by FTIR (Fig. 9). Consequently, this amide gives the highest conductivity of our three amide materials at 50% oxidation. Compound 2 showed the lowest conductivity as there is no impetus for ordered dipoles due a lack of hydrogen bonding interactions, as well as a looser packing expected from its highly twisted structure. Our experimental results also show that the calculated single molecule dipole moments alone fail to predict the trend in conductivity, as the conductivity of compound 2 was orders of magnitude lower than that of compounds 1 and 3.

Fig. 12 Estimated conductivities of our HTMs with increasing extent of oxidation. Dashed lines added only to guide the eye.

Another important charge transport parameter to consider when developing new HTMs is the hole mobility. A high hole mobility is paramount to ensure the feasibility of organic semiconductors for energy applications. Here, in devices such as perovskite solar cells, a high mobility ensures efficient charge extraction from the active layer and efficient transport to the electrode, on which the PCE hinges.

For molecular materials, mobility is influenced by the packing of molecules within the film. Our computational results indicate that the presence of dipoles can negatively impact mobility if the relative orientation of the dipoles is disordered. However, we predict that the formation of zero-Debye molecular pairs will improve the hole mobility of the HTM by reducing the energetic disorder within the film.

In order to verify this effect, hole mobilities of our pristine amide HTMs were measured through space-charge limited current technique. Single-carrier devices were prepared using the following architecture: fluorine-doped tin oxide (FTO)/HTM/Ag. The current–voltage curves of the devices were then recorded, and the mobilities were calculated from the space-charge limited region at higher voltages. We find that the hole mobilities of the three amide HTMs follow a trend identical to that seen in the conductivity measurements. The JV-curves are shown in the ESI, Fig. S9.† HTM 3 is found to have the highest hole mobility at 3.2 × 10⁻⁶ cm² V⁻¹ s⁻¹, and HTM 2 has the lowest mobility at 1.6 × 10⁻⁶ cm² V⁻¹ s⁻¹. Compound 1 has an intermediate mobility of 2.4 × 10⁻⁶ cm² V⁻¹ s⁻¹. This trend correlates with the increase in dipole ordering in going from compounds 2 < 1 < 3. Spiro-OMeTAD has a measured hole mobility of 1.8 × 10⁻⁶ cm² V⁻¹ s⁻¹, comparable to the highly disordered compound 2. This further illustrates the importance of ordered dipoles within the film as a means towards efficient hole conduction.

2.6 Device characterisation

The amide HTMs were implemented into perovskite solar cells in order to test their photovoltaic performance as part of a full device. A triple-cation perovskite composition (CsFAMA) was used as the active layer, as such compositions have been reported to outperform single-cation alternatives such as MAPbI₃.⁴⁶

The device architecture employed was as follows: FTO/TiO₂/C₆₀-SAM/Al₂O₃ nanoparticles/CsFAMA/HTM/Au.^13,47 Hole transport layers were treated with FK209 and LiTFSI as oxidants, and tert-butylpyridine (tBP) was also included to aid the dissolution of the ionic additives and also to improve HTL film formation on top of the perovskite layer.⁴⁸ The experimental results for the champion devices are summarised in Fig. 13 and Table 4.

Fig. 13 JV-curves of our champion devices for each tested HTM, collected under AM 1.5 simulated sunlight.

Table 4 Solar cell performance parameters measured for our champion devices, containing spiro-OMeTAD or our amide materials as HTMs, extracted from the JV-curves in Fig. 13

HTL	J SC (mA cm^−2)	V OC (V)	FF	PCE (%)
Spiro	22.31	1.1	0.75	18.42
1	20.59	0.97	0.71	14.29
2	3.00	0.95	0.58	1.65
3	21.65	0.96	0.71	14.73

---

We find that HTMs 1 and 3, as well as the spiro-OMeTAD references significantly outperform HTM 2 with respect to all solar cell parameters. As a result of the reduced conductivity and mobility of HTM 2, devices which employ the dimethylated amide 2 as HTL suffer from high series resistance leading to insufficient short-circuit current. We can reasonably conclude that this drop arises from the reduced charge transport efficiency within the HTL, which allows more time for recombination processes to take place thus reducing the overall PCE.^49,50 The increase in dipole ordering through hydrogen bonding previously observed in HTM 3 results in an increase in J_SC compared to HTM 1, thus leading to HTM 3 achieving the highest PCE across the amide series.

3 Conclusions

The solid-state and solution hydrogen bonding behaviour, as well as charge transport properties of three amide-based HTMs have been investigated. Through a combination of single-crystal X-ray diffraction, NMR/FTIR spectroscopy, and DFT modelling, we show that we have increased the dipole ordering in the crystal structure of TPABT (3) compared to EDOT-Amide-TPA (1), with both materials having much more ordered dipoles than DEDOT-Amide-TPA (2). This increased ordering reflects the behaviour of ordered domains in an amorphous film. Previous research has shown the detrimental effect of dipole disorder on the hole conductivity of HTMs. Our results suggest that the observed improvement in charge transport is a result of increased dipole ordering within the film, likely achieved through hydrogen bond assisted pairing. Such pair formation would lead to increased dipole ordering and a reduced net dipole within the film, thus reducing the overall energetic noise and improving the film conductivity compared to a species that cannot form these aggregates. While EDOT-Amide-TPA (1) also shows pairing, the similar binding energies of parallel and antiparallel-oriented dipoles leads to no overall change in the net dipole ordering, as both orientations are equally likely to be present in the matrix.

Films of TPABT (3) show improved conductivity over EDOT-Amide-TPA (1), with an order of magnitude conductivity increase over DEDOT-Amide-TPA (2) which has no hydrogen bonding capacity. While many other parameters also influence the conductivity, the likelihood of compound 3 to form energetically favoured, zero Debye pairs through hydrogen bonding, in contrast with 1 and 2, may explain its order of magnitude higher measured conductivity. The increased ordering is further demonstrated to lead to increased PCE when TPABT (3) is employed in PSCs compared to EDOT-Amide-TPA. A complete lack of dipole ordering in DEDOT-Amide-TPA leads to severely impaired conductivity that severely hinders the PCE of the device. We thus believe that this work provides a solid basis for developing new HTMs, using tailored hydrogen bonds to ensure well-oriented dipoles within the film for maximum conductivities.

Data availability

Crystal structures for the amide compounds in this study have been deposited into the CCDC. CCDC Deposition numbers are: EDOT-Amide-TPA (Compound 1): Deposition number 2301541, Unit cell parameters: a 55.7783(6) b 55.7783(6) c 10.4905(2) I4₁/aDEDOT-Amide-TPA (Compound 2): Deposition number 2301539, Unit cell parameters: a 16.6681(5) b 18.0603(6) c 16.6318(5) P2₁/c TPABT (Compound 3): Deposition number 2301540, Unit cell parameters: a 12.1294(3) b 14.8596(3) c 27.9555(8) P2₁/c. Other data supporting this article have been included as part of the ESI.†

Author contributions

B. V.: synthesis, characterisation, conductivity, SCLC, thermochemistry, FTIR and NMR, experiment design, drafting; M. F.: simulations, molecular modelling, drafting; I. S.: conductivity measurements; C. W.: single-crystal X-ray analysis, review; M. C.: synthesis; M. G.: experiment design, PSC fabrication and measurement; F. A.: SCLC sample preparation; M. K. and P. L. L.: AFM depth profiling, supervision, review; T. P., T. J. P., P. D. and G. C.: supervision, experiment design, drafting and review.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

BV, PLL, MG, and FA gratefully acknowledge the University of Glasgow for financial support in this research through School of Chemistry scholarships. PD thanks the EPSRC for funding through grant EP/T010568/1. MHF was supported by the EPSRC Centre for Doctoral Training in Renewable Energy Northeast Universities (ReNU) EP/SO23836/1. TP and TJP acknowledge support from EPSRC through funding grant EP/T022442/1. GC and MC thank the EPSRC for funding (EP/E036244/1, EP/V027425/1), as well as the Leverhulme trust for the award of a Research Fellowship. This research made use of the Rocket High-Performance Computing service at Newcastle University.

Notes and references

1. S. Shahnawaz, S. Sudheendran Swayamprabha, M. R. Nagar, R. A. K. Yadav, S. Gull, D. K. Dubey and J. H. Jou, J. Mater. Chem. C, 2019, 7, 7144–7158.
2. S. Gangala and R. Misra, J. Mater. Chem. A, 2018, 6, 18750–18765.
3. S. Fantacci, F. De Angelis, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2011, 115, 23126–23133.
4. S. Li, Y. L. Cao, W. H. Li and Z. S. Bo, Rare Met., 2021, 40, 2712–2729.
5. J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385.
6. Best Solar Cell Efficiencies, https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies.20191115.pdf, accessed 13 April 2021.
7. M. Saliba, T. Matsui, J. Y. Seo, K. Domanski, J. P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997.
8. N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. Il Seok, Nature, 2015, 517, 476–480.
9. X. Yin, Z. Song, Z. Li and W. Tang, Energy Environ. Sci., 2020, 13, 4057–4086.
10. F. M. Rombach, S. A. Haque and T. J. Macdonald, Energy Environ. Sci., 2021, 14, 5161–5190.
11. T. H. Schloemer, J. A. Christians, J. M. Luther and A. Sellinger, Chem. Sci., 2019, 10, 1904–1935.
12. T. Pope, Y. Giret, M. Fsadni, P. Docampo, C. Groves and T. J. Penfold, Org. Electron., 2023, 115(1–6), 106760.
13. M. L. Petrus, K. Schutt, M. T. Sirtl, E. M. Hutter, A. C. Closs, J. M. Ball, J. C. Bijleveld, A. Petrozza, T. Bein, T. J. Dingemans, T. J. Savenije, H. Snaith and P. Docampo, Adv. Energy Mater., 2018, 8(32), 1801605.
14. E. A. A. Alkhudhayr, D. Sirbu, M. Fsadni, B. Vella, B. T. Muhammad, P. G. Waddell, M. R. Probert, T. J. Penfold, T. Hallam, E. A. Gibson and P. Docampo, ACS Appl. Energy Mater., 2023, 11573–11582.
15. S. Tsarev, I. K. Yakushchenko, S. Y. Luchkin, P. M. Kuznetsov, R. S. Timerbulatov, N. N. Dremova, L. A. Frolova, K. J. Stevenson and P. A. Troshin, Sustainable Energy Fuels, 2019, 3, 2627–2632.
16. S. Daskeviciute-Geguziene, Y. Zhang, K. Rakstys, C. Xiao, J. Xia, Z. Qiu, M. Daskeviciene, T. Paskevicius, V. Jankauskas, A. M. Asiri, V. Getautis and M. K. Nazeeruddin, Adv. Funct. Mater., 2023, 33(1–8), 2208317.
17. H. Li, K. Fu, A. Hagfeldt, M. Grätzel, S. G. Mhaisalkar and A. C. Grimsdale, Angew. Chem., Int. Ed., 2014, 53, 4085–4088.
18. Y. Liang, J. Chen, X. Zhang, M. Han, R. Ghadari, N. Wu, Y. Wang, Y. Zhou, X. Liu and S. Dai, J. Mater. Chem. A, 2022, 10, 10988–10994.
19. J. L. Bredas, Mater. Horiz., 2014, 1, 17–19.
20. B. Lyu, L. Yang, Y. Luo, X. Zhang and J. Zhang, J. Mater. Chem. C, 2022, 10, 10775–10798.
21. F. Lamberti, F. Schmitz, W. Chen, Z. He and T. Gatti, Sol. RRL, 2021, 5(10), 2100514.
22. K. H. Kim, H. Yu, H. Kang, D. J. Kang, C. H. Cho, H. H. Cho, J. H. Oh and B. J. Kim, J. Mater. Chem. A, 2013, 1, 14538–14547.
23. J. Wang, X. Wu, Y. Liu, T. Qin, K. Zhang, N. Li, J. Zhao, R. Ye, Z. Fan, Z. Chi and Z. Zhu, Adv. Energy Mater., 2021, 11(1–9), 2100967.
24. Z. Xiao, K. Sun, J. Subbiah, S. Ji, D. J. Jones and W. W. H. Wong, Sci. Rep., 2014, 4, 2–8.
25. A. M. Martin, R. S. Butler, I. Ghiviriga, R. E. Giessert, K. A. Abboud and R. K. Castellano, Chem. Commun., 2006, 4413–4415.
26. A. K. Patel, S. K. Mishra, K. Krishnamurthy and N. Suryaprakash, RSC Adv., 2019, 9, 32759–32770.
27. J. Wu, A. Fechtenkötter, J. Gauss, M. D. Watson, M. Kastler, C. Fechtenkötter, M. Wagner and K. Müllen, J. Am. Chem. Soc., 2004, 126, 11311–11321.
28. C. Shao, M. Grüne, M. Stolte and F. Würthner, Chem.–Eur. J., 2012, 18, 13665–13677.
29. J. Kroon, L. M. J. Kroon-Batenburg, B. R. Leeflang and J. F. G. Vliegenthart, J. Mol. Struct., 1994, 322, 27–31.
30. P. Froimowicz, K. Zhang and H. Ishida, Chem.–Eur. J., 2016, 22, 2691–2707.
31. S. K. Mishra and N. Suryaprakash, Molecules, 2017, 22(3), 423.
32. L. Han, K. Zhang, H. Ishida and P. Froimowicz, Macromol. Chem. Phys., 2017, 218, 1–10.
33. S. H. Gellman, G. P. Dado, G. B. Liang and B. R. Adams, J. Am. Chem. Soc., 1991, 113, 1164–1173.
34. A. G. Nurioglu, H. Akpinar, F. E. Kanik, D. Toffoli and L. Toppare, J. Electroanal. Chem., 2013, 693, 23–27.
35. J. Matern, Z. Fernández, N. Bäumer and G. Fernández, Angew. Chem., 2022, 61(1–9), e202203783.
36. F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78.
37. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
38. Z. Hawash, L. K. Ono, S. R. Raga, M. V. Lee and Y. Qi, Chem. Mater., 2015, 27, 562–569.
39. J. Luo, C. Jia, Z. Wan, F. Han, B. Zhao and R. Wang, J. Power Sources, 2017, 342, 886–895.
40. W. Zhang, F. Zhang, B. Xu, Y. Li, L. Wang, B. Zhang, Y. Guo, J. M. Gardner, L. Sun and L. Kloo, ACS Appl. Mater. Interfaces, 2020, 12, 33751–33758.
41. A. Abate, T. Leijtens, S. Pathak, J. Teuscher, R. Avolio, M. E. Errico, J. Kirkpatrik, J. M. Ball, P. Docampo, I. McPherson and H. J. Snaith, Phys. Chem. Chem. Phys., 2013, 15, 2572–2579.
42. T. Zhang, F. Wang, H.-B. Kim, I.-W. Choi, C. Wang, E. Cho, R. Konefal, Y. Puttisong, K. Terado, L. Kobera, M. Chen, M. Yang, S. Bai, B. Yang, J. Suo, S.-C. Yang, X. Liu, F. Fu, H. Yoshida, W. Chen, J. Brus, V. Coropceanu, A. Hagfelt, J.-L. Brédas, M. Fahlman, D. S. Kim, Z. Hu and F. Gao, Science, 2021, 377, 495–501.
43. A. Magomedov, E. Kasparavičius, K. Rakstys, S. Paek, N. Gasilova, K. Genevičius, G. Juška, T. Malinauskas, M. K. Nazeeruddin and V. Getautis, J. Mater. Chem. C, 2018, 6, 8874–8878.
44. W. H. Nguyen, C. D. Bailie, E. L. Unger and M. D. McGehee, J. Am. Chem. Soc., 2014, 136, 10996–11001.
45. B. Xu, J. Huang, H. Ågren, L. Kloo, A. Hagfeldt and L. Sun, ChemSusChem, 2014, 7, 3252–3256.
46. K. Pydzińska-Białek, V. Drushliak, E. Coy, K. Załęski, J. Flach, J. Idígoras, L. Contreras-Bernal, A. Hagfeldt, J. A. Anta and M. Ziółek, ACS Appl. Mater. Interfaces, 2020, 12, 30399–30410.
47. M. Schultes, N. Giesbrecht, J. Küffner, E. Ahlswede, P. Docampo, T. Bein and M. Powalla, ACS Appl. Mater. Interfaces, 2019, 11, 12948–12957.
48. S. Wang, Z. Huang, X. Wang, Y. Li, M. Günther, S. Valenzuela, P. Parikh, A. Cabreros, W. Xiong and Y. S. Meng, J. Am. Chem. Soc., 2018, 140, 16720–16730.
49. J. Lu, A. D. Scully, J. Sun, B. Tan, A. S. R. Chesman, S. Ruiz Raga, L. Jiang, X. Lin, N. Pai, W. Huang, Y. B. Cheng, U. Bach and A. N. Simonov, J. Phys. Chem. Lett., 2019, 10, 4675–4682.
50. T. S. Sherkar, C. Momblona, L. Gil-Escrig, J. Ávila, M. Sessolo, H. J. Bolink and L. J. A. Koster, ACS Energy Lett., 2017, 2, 1214–1222.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2301539, 2301540 and 2301541. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ta00956h

‡ These authors contributed their work equally.

---