Metalloid-doping in SMoSe Janus layers: first-principles study on efficient catalysts for the hydrogen evolution reaction

Abstract

B, Si, and Ge dopants are inserted into SMoSe Janus layers (JLs) at Mo, S, and Se as well as at interstitial sites. Spin-polarized density functional theory calculations are employed to investigate the modified structural and electronic properties of the layers, the energetics of dopant incorporation, and the effect of doping on the interaction of the two-dimensional material with hydrogen. The detailed structural analysis exposes the influence of dopant atomic sizes on lattice distortion. The formation energy E_f of dopant X (X = B, Si, and Ge) at substitutional and interstitial sites is studied for two different chemical environments: (i) bulk X – or X-rich conditions, and (ii) dimer X₂ – or X-poor conditions. It is found that under X-poor conditions, the stability of the dopants is always higher. Doping at the S site is energetically most favored, with E^B_f < E^Si_f < E^Ge_f. The electron redistribution in the JLs due to the presence of dopants is explored using Bader analysis. Atomic sites with a number of electrons different from that on atoms in pristine SMoSe JLs may be potential hydrogen traps and are therefore interesting for the hydrogen evolution reaction (HER). Consequently, the interaction of H atoms with these sites is studied and the H adsorption energy is calculated. While pristine SMoSe JLs repel H, several attractive sites are found in the vicinity of the dopant atoms. In order to quantify the feasibility of the doped SMoSe JLs for use as a catalyst for the HER, the free adsorption energy is determined. The data show that all dopants may improve SMoSe for HER applications. The most favorable sites are B at S and Se, Si at Mo and S, and Ge at Mo and S. In particular, adsorption and desorption of H on B-doped (at S and Se sites) and on Ge-doped (at an Mo site) JLs may be rapid. The present results demonstrate the potential of metalloid-doped SMoSe JLs as efficient HER catalysts.

---

1 Introduction

Transition metal dichalcogenide (TMD)-based two-dimensional (2D) materials have been strongly in focus recently due to their various structure-driven electronic and optical properties, suitable for a wide range of applications, such as in nanoelectronics,^1,2 spintronics,³ gas sensing,^4,5 photocatalysis,^1,6–9 electro-catalysis,^10–15 electrochemical energy storage,^16–19 and photonics.^20,21 The hexagonal phase is the most common stable phase of 2D materials. It has the form MA₂, where the transition metal (M) atomic plane is encompassed by two eclipsing chalcogen (A) atomic planes.²² Interestingly the out-of-plane mirror symmetry about the M atomic plane of the 2D materials significantly controls their electronic structure and hence the physico-chemical properties. By introducing asymmetric inversion about the M plane, it is possible to extend the variety of applications further to other domains.^23,24 A break in symmetry may be realized either by forming a 2D alloy via biased mixing of different chalcogen elements into the anionic sites, by ordered doping of different transition metals into the cationic sites, or by the formation of a new class of 2D materials with the formula A₁MA₂, where A₁ and A₂ are different chalcogen atoms. These materials of the form A₁MA₂ are called Janus layers (JLs) and potentially provide even more sophisticated properties, such as Rashba–Dresselhaus splitting,^25–28 magnetism,^29–31 and vertical piezoelectricity.^32–38 In particular, the relativistic phenomenon of spin–orbit coupling, which is due to the interaction of moving electrons in the nuclear electric field from the ions in the 2D planes, leads to the well-known Rashba–Dresselhaus splitting in asymmetric 2D materials.³⁹ Such splitting effects are being investigated for application in catalysis processes.^40,41 In addition, the potential difference between the chalcogen planes induces an internal field, which can be utilized for catalytic activities.⁴²

Recently, extensive theoretical and limited experimental studies have reported the photocatalytic activity of many JLs of various transition metal dichalcogenides.^1,32,43–51 Due to the challenges in synthetic processes, to date, only SMoSe,^{32,44,49,52,53} SWSe⁴⁹ and SPtSe⁵⁴ JLs have been experimentally realized, using chemical vapor deposition followed by sulfurization or pulsed laser deposition of Se. In particular, for the first time, the model representative of JLs, SMoSe, was experimentally realized from an MoS₂ precursor by Lu et al.⁵² and from MoSe₂ by Zhang et al.³² Since then, SMoSe has attracted more attention. The difference in S’s and Se’s electronegativities enables novel characteristics of this 2D material. Notably, the lifetime of excitons in the SMoSe JL is longer than that in MoS₂.^44,49 Hence, the electron and hole carriers are sufficiently spatially separated, which leading to formation of out-of-plane dipole. Moreover, adsorbed transition metal atoms on the JL can improve its intrinsic dipole moment;⁵⁵ thus, it is possible to tune the carrier recombination rate. In summary, control over the intrinsic dipole can be utilized to enhance the photocatalytic characteristics of SMoSe. On the other hand, the homogeneous charge distribution on S and Se atomic planes in SMoSe leads to a lack of activated sites, which are a crucial requirement for the adsorption process on any catalyst’s surface, such as hydrogen adsorption in the hydrogen evolution reaction (HER) to accomplish the water-splitting process.⁴⁴ A good photocatalyst should possess an appropriate band gap to absorb visible light, high carrier mobility, conduction and valence band edge alignments beyond the redox potential, and activated sites on the surface.^9,21

Several strategies, such as doping with impurities, applying an external strain or field, inducing defects, or exposing edges, can significantly enhance the catalytic activity of the MoS₂ layer.^5,8,21,48,56 Among these, doping with impurities is a widely used strategy in transition-metal chalcogenide-based catalysts. For instance, Zhao et al. demonstrated that the presence of a Ti impurity as an adatom in the Se atomic plane, along with an S vacancy, enhances the photocatalytic performance of SMoSe.⁹ Additionally, the doping mechanism generates local strain in the atomic planes of interest, which can activate surface sites for strong absorption of small molecules. Therefore, structural manipulation can lead to different charge distributions on atomic sites, ultimately activating the basal plane. Hence, doping cationic/anionic dopants at specific atomic sites can make JLs suitable for HER applications.

Considering the successful experimental fabrication^{32,44,49,52,53} and other prominent properties of SMoSe JLs, such as longer exciton lifetime,^44,49 in this study we focus on turning its application towards photocatalytic activity via doping with metalloid elements (B, Si, and Ge). The doping mechanism is chosen to redistribute the charges on the S and Se atomic planes, which is shown to result in the formation of new active sites for the HER. In this study, firstly the feasibility of doping of metalloid elements is analyzed in terms of formation energy to qualify the dopants for further investigation. The qualified doping cases are further subjected to charge-transfer analysis in order to identify the number of and the possible sites to adsorb H atoms. Then the HER activity is probed in terms of the change in Gibbs free energy. Overall, the combined discussion provides knowledge about the properties of doped SMoSe JLs and the potential candidates of doping elements that may turn the SMoSe JL into an efficient catalytic material for HER applications.

The study is organized as follows: the next section describes the computational settings. Then, the structural changes in the SMoSe JLs after doping are elucidated. Subsequently, the feasibility of the formation of doped JLs is explored. Furthermore, the electron redistribution in the environment of the dopant atoms is analyzed. The interaction of H atoms with atomic sites near the dopants is studied by calculating the adsorption enthalpy. Finally, the free adsorption energy is determined in order to quantify the feasibility of the doped SMoSe JLs for use as a catalyst for the HER.

2 Computational details

In this work, we carried out spin-polarized density functional theory (DFT) calculations using the VASP code⁵⁷ with projector augmented wave (PAW) pseudopotentials.⁵⁸ The generalized gradient approximation (GGA)⁵⁹ is applied to treat the exchange and correlation effects. An energy cutoff of 600 eV is used to generate plane waves. PAW potentials of atoms with valence configurations Mo(4p5s4d), S(3s3p), Se(4s4p), B(2s2p), Si(3s3p) and Ge(3d4s4p), and respective valencies 12, 6, 6, 3, 4, and 14 are used in the calculations. The atomic positions are optimized until the Hellmann–Feynman forces on each atom become less than 10⁻⁴ eV Å⁻¹ and the total energies are converged up to 10⁻⁶ eV. We considered a supercell consisting of 4 × 4 × 1 unit cells of SeMoS JL, i.e., the supercell contains 16 Mo, 16 S, and 16 Se atoms. Monkhorst–Pack⁶⁰ grids of 16 × 16 × 1 and 5 × 5 × 1 k-points are used for Brillouin-zone sampling of the unit cell and the 4 × 4 × 1 supercell, respectively. Within the supercell, in the direction perpendicular to the layer, a 15 Å vacuum is used to avoid inter-layer interactions. With these conditions, we introduce the selected metalloid element X at the (a) Mo site (X@Mo), (b) Se site (X@Se), (c) S site (X@S), and (d) interstitial site (X@Int); refer to Fig. 1. Here, we choose only non-hazardous elements from the metalloid group as dopants, so that they do not form alloys with elements of the SMoSe JL. The covalent radii of the dopant elements B (89 pm), Si (111 pm), and Ge (122 pm) change over a broader range in comparison to those of chalcogenides S (102 pm) and Se (116 pm) and the transition metal Mo (145 pm). Hence, electron redistribution is expected close to the dopant atoms due to the strong local strain field. The vibrational frequencies of attached H atoms are calculated using the finite-difference approach, as implemented in the VASP code.⁵⁷ The symmetrical displacement method is utilized to reduce the number of displacements. However, due to doping and H adsorption, the layer assumes P1 symmetry and hence a total of six displacements are created internally (three in the positive direction and three in the negative direction). For the vibrational calculations, the accuracies of the forces on each atom and the total energies are set to 5 × 10⁻⁷ eV Å⁻¹ and 10⁻⁷ eV, respectively.

Fig. 1 The schematic illustrates X-substitutional (X = B, Si, and Ge) as well as X-interstitial doping in SMoSe JLs before relaxation. Each doping illustration has both cross-sectional and perpendicular views, along with a polyhedron schematically showing the unrelaxed prismatic coordination that contains the dopant X. The relaxed structures are shown in SFig. 1–3 of the ESI.†

3 Results and discussion

3.1 Structural properties of X-doped (X = B, Si and Ge) SMoSe Janus layers

Firstly, we optimized the atomic structure of the SMoSe JL, as described in the Computational details section. The relaxed lattice parameters were found to be a = b = 3.249 Å, which is in agreement with the value (3.249 Å) reported in earlier theoretical studies.^32,61–63 The metalloid atoms B, Si, and Ge were placed at the sites shown in Fig. 1, and the respective relaxed structures are given in SFig. 1–3 of the ESI.† The detailed structural analysis shows that each dopant exhibits a unique behavior due to its atomic size when inserted at different sites. In SMoSe, a characteristic trigonal prismatic coordination is formed by three S atoms and three Se atoms with Mo at the center. Upon introducing the dopant X, a comparable coordination pattern emerges. When X is at Mo or interstitial sites, the dopant and neighboring chalcogens bond together, resulting in a prismatic coordination arrangement. In the case of X at S or Se sites, X contributes to this coordination with the nearby Mo atoms. In the analysis of the relaxed structures (see SFig. 1–3 of ESI†), this distinctive prismatic coordination is used to calculate the structural quantities, namely the average bond length (l_ave), polyhedral volume (V_poly), distortion index (d_idx), and the effective bond number (N_eff), to understand the impact of the dopant. The results are shown in Fig. 2. It is noteworthy that the distortion due to the dopant is a local effect and confined to the first or second neighbor distance from the dopant. The above-mentioned structural quantities are calculated using the VESTA package⁶⁴ and the respective definitions are given in the ESI, cf. Section 2.† The polyhedral volume (V_poly) in the pristine SMoSe JL is about 15 ų. Introducing dopants with different atomic sizes changes the value of V_poly. Notably, the presence of B dopants at all doping sites significantly alters the polyhedral volume. A similar effect is observed with Si and Ge doping at Mo, Se, and interstitial sites. However, in the case of Si and Ge at the S site, V_poly remains nearly the same as in the pristine JL, which indicates that the dopants occupy the lattice site without further distortions.

Fig. 2 The calculated structural quantities, polyhedral volume V_poly, effective bond number N_eff, average bond length l_ave, and the distortion index d_idx, of the trigonal prismatic coordination containing the dopant X, as shown schematically in Fig. 1. The data were obtained from the analysis of the relaxed structures. For X@Int, the bonds to neighboring S and Se are considered in the analysis.

The N_eff value shown in Fig. 2 elucidates the local changes induced by the dopant in the net number of bonds in the prismatic coordination. It is calculated by connecting the central atom to its nearby atoms, which are involved in the formation of coordination. In pristine SMoSe, N_eff is approximately six, as three S and three Se atoms surround Mo in a trigonal prismatic coordination. For B doping, both cases B@Mo and B@Int almost retain the same N_eff as in the pristine JL. B@Int leads to only small changes in N_eff, but B is pushed towards the S plane (see SFig. 1d†). For B@S and B@Se JLs, B is shifted towards the Mo sublattice (cf. SFig. 1b and 1c†), which causes a considerable reduction in N_eff. The introduction of Si and Ge dopants distorts the S and Se sublattices when doped at Mo and interstitial sites, leading to a reduced N_eff compared to that of the pristine JL (see SFig. 2a and d as well as 3a and d†). On the other hand, Si and Ge at S/Se sites persist in occupying the S/Se sites, leading to a similar N_eff as in the pristine JL.

The l_ave in pristine SMoSe is 2.477 Å, which comprises the average bond length of both Mo–S and Mo–Se bonding. Hence, shrinking/elongation of l_ave depicts the impact of the atomic sizes of the dopants and the interaction between the dopants and the layer atoms.

The distortion in the lattice can be further characterized using the distortion index d_idx, which is calculated based on the different bond lengths l in the prismatic coordination. Since l_Mo–S is 2.421 Å, and l_Mo–Se is 2.542 Å, the characteristic trigonal prismatic coordination of the pristine JL has a certain d_idx. The B@Mo dopant lowers this value, indicating that l_B–S and l_B–Se are similar. The B@Int dopant induces a similar d_idx as in the pristine JL, attributed to the fact that B@Int retains the pristine N_eff and B induces only slight distortion. For the B doping at the chalcogenide sites, the distortion is higher than that in the pristine JL, since B, as mentioned above, is shifted away from the doping site. Si and Ge doping at chalcogenide sites results in a similar d_idx to that of the pristine JL due to the N_eff value. On the other hand, these dopants on Mo and interstitial sites produce the largest observed distortion.

The quantities N_eff, d_idx, V_poly and l_ave provide valuable insights into the structural changes resulting from dopant incorporation within the JL, which can effectively alter the electron distribution in the doped layer and can enhance or originate the potential to trap H ions for HER applications.

3.2 Formation energy of dopant atoms at different sites

For all the atomic configurations with dopant atoms, the formation energy E_f is calculated using the equation^6,65

E_f = E_X+SMoSe − E_SMoSe + µ_y − µ_X (1)

where E_X+SMoSe and E_SMoSe are the total energies of the SMoSe JL with and without the X dopant, respectively. The terms µ_X and µ_y represent the chemical potentials of the dopant X and the atom removed from the JL. Thus, depending on the doping site, µ_y can be either µ_Mo, µ_S, or µ_Se or zero for the interstitial dopant configuration when no atoms are replaced by dopants. The chemical potentials of the S and Se atoms are obtained from the total energies of the S and Se dimers. The chemical potential of Mo is calculated from the total energies of bulk Mo as E^bulk_Mo/N_Mo, where E^bulk_Mo is the ground state energy of α-Mo bulk and N_Mo is the number of Mo atoms in the bulk reference system. Similarly, the chemical potentials µ_X of X (B, Si, and Ge) are calculated from the X₂ and the bulk structures of X, which respectively represent X-poor and X-rich conditions in the reaction chamber. Again, we fix the X-poor limit as E_X2/2 and the X-rich limit as E^bulk_X/N_X. In analogy, E^bulk_X and E_X2 are the ground state energies of X_bulk and X dimers, respectively, and N_X is the number of X atoms in the bulk crystal. From the values of E_f shown in Fig. 3, it is clear that the formation energy strongly depends on the reference systems being used to obtain the chemical potentials of the dopants, µ_X. Thus, it is essential to choose specific growth conditions and precursor elements in the formation process of X-doped SMoSe JLs. Here, we focus on the special chemical environments illustrated in Fig. 3. It must be emphasized that alternative routes for doped JL formation exist and will be investigated in future work.

Fig. 3 The formation energy of X (X = B (a), Si (b), and Ge (c)) doping at various relevant sites in the SMoSe JLs. The chemical potentials of Mo, S, and Se are calculated from the respective bulk and dimers, and those of X are derived from the X bulk (X-rich conditions) and X dimers (X-poor conditions). Comparing the doping sites, it is depicted that X@S is energetically most favorable. Overall E_f can be expressed as E^B_f < E^Si_f < E^Ge_f for the X@S doping. In contrast to B, the dopants Si and Ge do not favor interstitials.

Fig. 3a shows the energetics of B doping at different sites in the SMoSe JL. The chemical potential of B is derived from the B bulk (B-rich conditions) or the B₂ dimer (B-poor conditions). The B doping in the bulk region is energetically unfavorable, i.e., E_f > 0, since the combined process of decomposing the B bulk and incorporating decomposed B into the JL is energetically demanding. Utilizing B clusters, particularly B dimers, can reduce the energy demand for decomposition, and hence incorporating B can be carried out. Under the B-poor conditions, the doping can be carried out at all considered doping sites. The stability of different atomic configurations decreases in the order B@S > B@Se > B@Int > B@Mo. Thus, B substitution at the S site is more favorable than any other configuration under B-poor conditions.

The energetics for Si doping at different sites are compared in Fig. 3b. The energy of Si in the Si bulk determines the µ_Si of the Si-rich conditions, while the energy of the Si₂ dimer determines that of the Si-poor conditions. Unlike the B doping, interstitial Si is highly unfavorable compared to Si@S, Si@Se, and Si@Mo, due to the size effect. Since the atomic size of S is smaller than that of Se, Si substitutional atoms prefer S sites. Hence, the E_f is more negative for Si@S than for Si@Se. In addition, Si tends to occupy the Mo atomic sites. Interestingly, the E_f of Si@Mo is slightly higher than that of Si@S, differing only by 110–290 meV per atom across the µ_Si range. In contrast, the E_f of the Si@Mo configuration (Fig. 3b) is significantly (≈1–2 eV per atom) lower than that of Si@Se. Therefore, accounting for the E_f of the distinct doping sites, the stability decreases in the order of Si@S > Si@Mo > Si@Se > Si@Int.

Ge doping (Fig. 3c) leads to higher E_f values than in the Si case and to another sequence of stable X sites: the stability decreases in the order of Ge@S > Ge@Se > Ge@Mo > Ge@Int.

Considering the most feasible doping site, the S site, for all X dopants, E_f can be arranged in the order of E^B_f < E^Si_f < E^Ge_f. Interestingly Si can be doped at the Mo site with an excess of only ≈300 meV per atom. The X-poor limit supports doping X at all considered sites.

3.3 Electron redistribution due to the presence of dopants

After carefully analyzing the energetics of doping for the JLs, the interaction between the host atoms and the dopant X atoms is studied using Bader analysis (BA) to understand the electronic modifications of atoms within the JLs. In BA, the number q of electrons of an atom is determined using zero-flux surfaces, as implemented by Henkelman et al.^66,67 The gain or loss of electrons due to the fact that an atom i is part of the doped or undoped JL is calculated using the quantity Q_i, with

Q_i = Z_i − q_i (2)

where q_i is the number of electrons on atom i from BA and Z_i is the number of valence electrons, as defined in its pseudopotential. Thus, the negative and positive values of Q_i indicate the accumulation or depletion of electrons on that ith atom. In the present work, atoms related to prismatic coordination, as shown in Fig. 4, are the subject of BA. Additionally, a few example cases are studied using the differential charge difference approach⁶⁵ and the results are presented in the ESI† to show the similarity between BA and differential charge analysis.

Fig. 4 The atoms involved in electron redistribution are shown for the doping scenarios (a) X@Mo (b) X@S, (c) X@Se, and (d) X@Int as projections from the unrelaxed structures. The Q_i for Mo (given in Table 1) in X@Mo and X@Int is the average Q_i of Mo atoms shown in (a) and (d). The Q_i values of S and Se are also the average values of Q_i of the shown S and Se atoms. The used S and Se atoms are denoted. In the case of Si@Mo, in addition to the S1–S3 and Se1–Se3 atoms, which are the first nearest neighbors of X (here Si), the second nearest neighbors S4 and Se4 are shown in (e) where the projection is from the relaxed Si@Mo-doped SMoSe JL (in contrast to the lower figure in (a), which is the projection from the unrelaxed structure).

When we introduce a chemically different X atom at the substitutional or interstitial sites, the new atomistic arrangement causes local lattice displacements due to the size of the dopant and electronic modifications affecting the nearest neighbor atoms. Consequently, this causes a redistribution of electrons within the atoms of the JL. Gain or loss of electrons results in a negative or positive Q_i, respectively, indicating an anionic or cationic nature. Atoms that significantly gain electrons (in comparison to atoms in the pristine JL) are potential sites for the adsorption of hydrogen ions; see Section 3.4. For the atoms depicted in Fig. 4, the values of Q_i were calculated and the results are given in Table 1. The data for pristine SMoSe are also listed.

Table 1 The electron redistribution due to the presence of dopants is computed for Mo, S, Se, and X in both pristine and X-doped SMoSe JLs. The atoms involved in electron redistribution are shown in Fig. 4. The values of Q_i, see eqn (2), are the average values for Mo, S, and Se. The electron redistribution yields both cationic Si and Ge (i.e., dopants have positive Q_i) irrespective of doping sites. However, the B dopant attains the anionic state (i.e. dopants have negative Q_i) in B@S and B@Se JLs, and cationic states in B@Mo and B@Int JLs. In the case of Si@Mo, the S and Se atoms (the S1–S3 and Se1–Se3 atoms shown in Fig. 4) closest to Si show a strong gain of electrons (Q_i values are shown in boldface), but there is no significant change in charge on the second nearest neighbors (S4 and Se4 in Fig. 4; Q_i values are shown in normal face). Note that in this table, Q_i for the second nearest neighbors is given only for Si@Mo

Atom	Pristine	B@Mo	B@S	B@Se	B@Int
Mo	1.080	1.147	1.0312	1.069	1.019
S	−0.628	−0.568	−0.6507	−0.644	−0.590
Se	−0.452	−0.399	−0.3967	−0.466	−0.431
B		0.524	−0.349	−0.302	0.150

---

Atom	Si@Mo	Si@S	Si@Se	Si@Int
Mo	1.093	0.745	1.054	0.952
S	−1.244	−0.463	−0.643	−0.544
	−0.630
Se	−0.498	−0.323	−0.468	−0.442
	−0.456
Si	0.309	0.206	0.448	0.595

---

Atom	Ge@Mo	Ge@S	Ge@Se	Ge@Int
Mo	1.086	0.926	0.987	0.925
S	−0.661	−0.671	−0.657	−0.656
Se	−0.471	−0.473	−0.477	−0.471
Ge	0.975	0.091	0.047	0.569

---

When B is doped at the Mo site or in an interstitial position, it acquires the cationic state and at the S or Se site, B retains the anionic state, as of S or Se.

The Si dopants are cationic regardless of the doping site, mainly due to their reduced electronegativity. However, the extent of electron acquisition varies depending on the specific doping site. In the intriguing case of Si@Mo doping, the size of the Si atom emerges as a critical factor governing the charge states of the neighboring atoms. The size mismatch between Si and Mo induces local displacements, leading to significant alterations in Si–S and Si–Se bond lengths and causing an increase in the number of electrons surrounding the first nearest neighbor S and Se atoms, as shown by the values highlighted in boldface in Table 1. When Si occupies S sites, the electrons are redistributed from S or Se to Mo. A somewhat analogous trend, although less pronounced, is observed when Si occupies interstitial sites.

Though Si and Ge are isoelectronic, the electronegativity and atomic size of Ge are different from those of Si. These facts originate a slightly different local distortion around the Ge dopant than that observed from Si, and therefore different Q_i values.

In addition to exploring active sites, from Table 1 the concentration of active sites can be quantitatively assessed as follows. The lattice vectors of the considered 4 × 4 supercell are 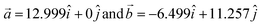, which raises a surface area of 146.37 Ų. In this area, the substitution of one X (B/Si/Ge) dopant reaches the doping concentration of 6.25% of the respective species and an overall concentration of 2.1 at%, which corresponds to a surface density of 6.83 × 10⁻³ Ų. This value is exclusively due to convergence reasons to prevent dopant–dopant interaction. While diluting the dopant concentration will not affect the results, increasing the concentration may lead to energetic deviations, although we still expect similar results for the 3 × 3 supercell (surface area of 82.33 Ų) with a surface density of 12.14 × 10⁻³ Ų.

3.4 H adsorption on pristine and X-doped SMoSe Janus layers

Three different H adsorption sites are investigated, namely, (a) H on S, (b) H on Se, and (c) H on X. The studied H sites on the relaxed JL with the dopant atom are shown schematically in Fig. 5. In the H on S and Se configurations, the H atom is placed on top of S and Se, respectively. In the H on X configuration, H is attached to the dopant X from either the S or Se atomic plane. All these sites are studied for H adsorption in X-doped and pristine JLs. Further, the HER process is quantified by calculating the change in Gibbs free energy ΔG.

Fig. 5 The figure depicts the relaxed JLs in the structural vicinity of the dopant atom, whereas the positions of H atoms are shown schematically. In X@Mo JLs, the following non-equivalent sites for H are studied: one where the S or Se atom is closest to X (denoted by 1 and 2), one near the other S or Se (next) neighbor of X (denoted by 3 and 4), and one near X (denoted by 5 and 6). The non-equivalent H sites considered for X@S, X@Se, and X@Int are also marked by numbers 1 for H on S, 2 for H on Se, and 3 for H on X. Note that the present numbering is also used in Table 2.

3.4.1 Enthalpy of H adsorption. A hydrogen evolution reaction (HER, 2H⁺ + 2e⁻ → H₂)⁶⁸ on a catalyst surface is a two-step electron-transfer reaction to produce H₂ at the end. In the first step, the proton (H⁺) gets adsorbed on the active site of the catalyst. Consequently, an electron is transferred to the H⁺ to form adsorbed H (*H) on the surface. In the Volmer–Tafel pathway, after two such *H formations on the surface, they react with each other to form a H₂ molecule. In the Volmer–Heyrovský pathway, the *H reacts with a solvated H⁺ + e⁻ couple to form H₂ on the surface of the catalyst.^69–71 In both pathways, the adsorption of H with optimal adsorption enthalpy for the reaction given in eqn (3) will determine the Gibbs free adsorption energy of the reaction. Thus, it is important to study the adsorption enthalpy before we proceed to the calculation of the change in Gibbs free energy, ΔG. The above-mentioned mechanism of electron transfer on a surface can be written as follows:

* + H⁺ + e⁻ → *H (3)

where * indicates the surface and *H is the adsorbed H on the surface. After two such adsorptions, both adsorbed H atoms may form the H₂ molecule:

*H + *H → H₂ (4)

In this study, the most feasible sites for the H atom on the X-doped JLs and their effect on the HER are investigated (Fig. 5). For comparison, H on pristine JLs is also considered. To quantify the strength of adsorption, the adsorption enthalpy E_ad of H is calculated using

E_ad = E_JL+*H − E_JL − µ_H (5)

where E_JL+*H and E_JL are the ground state enthalpy of the JL with and without an H atom, respectively. The chemical potential µ_H of H is calculated based on the equilibrium condition , where H is H⁺ + e⁻, since under the standard temperature and pressure conditions (p = 1 bar, T = 298 K) and assuming pH = 0, the change in Gibbs free energy of the 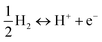reaction is zero.⁷² The calculated E_ad values for different H configurations are given in Table 2.

Table 2 Adsorption enthalpy E_ad of H on different sites in the X-doped JLs. The numbers in parentheses denote the adsorbed H atoms shown and numbered in Fig. 5. The positive and negative values represent repulsive and attractive interactions between H and the JLs, i.e., endothermic and exothermic reactions. All values are in the unit of eV

	Pristine	B@Mo	B@S	B@Se	B@Int
H on S	1.673	−2.563 (1)	0.322 (1)	0.211 (1)	0.552 (1)
H on Se	2.189	−2.817 (2)	1.096 (2)	0.908 (2)	1.153 (2)
H on B		−1.832 (5)	−0.373 (3)	−0.384 (3)	2.169 (3)
		−1.680 (6)

---

	Si@Mo	Si@S	Si@Se	Si@Int
H on S	−0.684 (1)	0.679 (1)	0.379 (1)	1.458 (1)
	0.451 (3)
H on Se	−0.480 (2)	1.204 (2)	1.291 (2)	2.273 (2)
	1.148 (4)
H on Si	1.232 (5)	−0.776 (3)	−0.826 (3)	2.205 (3)
	0.712 (6)

---

	Ge@Mo	Ge@S	Ge@Se	Ge@Int
H on S	−0.428 (1)	0.570 (1)	0.049 (1)	1.211 (1)
H on Se	−0.224 (2)	1.072 (2)	0.976 (2)	1.615 (2)
H on Ge	0.672 (5)	−0.594 (3)	−0.882 (3)	2.248 (3)
	0.884 (6)

---

In the pristine SMoSe JL, the adsorption energies for H on S and H on Se sites are positive, i.e., adsorption is not favored. This is primarily due to the chemical inertness of the basal planes. However, when examining Table 2, it becomes evident that the X-doped JLs display a more diverse behavior, showing both endothermic (i.e., E_ad > 0) and exothermic (i.e., E_ad < 0) interactions with H. The specific nature of the interaction depends on the local atomic configuration of the dopant. In the case of X@Int, for all H sites shown in Fig. 5, only positive values of E_ad are found.

In the X@S and X@Se doped JLs, the H on X configuration (site 3) exhibits an attractive interaction with E_ad < 0. On the other H sites (1 and 2), E_ad is positive. The difference between the values of E_ad on site 3 for the B, Si, and Ge dopants may be explained in terms of atomic size and the corresponding value of Q_i.

Intriguingly, the interaction of H with X@Mo-doped JLs reveals a fascinating diversity, which is heavily influenced by the specific X dopant introduced. In the case of B@Mo, a strong attraction is found for H on S and Se sites (1 and 2) which corresponds to the most negative E_ad found in this work. H on other tested sites (3 and 4) has a similar E_ad and hence E_ad values are given only for sites 1 and 2. For H on B (sites 5 and 6), an attractive interaction is obtained.

In the case of Si on the Mo site, H is attracted at sites 1 and 2 but repelled at sites 3 and 4. Remarkably, such distinguishable sites are available only through Si doping, whereas B and Ge doping does not lead to such differences, which may be explained by the atomic size and electronegativity. Furthermore, H is repelled at sites 5 and 6 for Si@Mo as well as in the Ge@Mo case. For Ge@Mo, H is attracted at sites 1 and 2, but the corresponding E_ad is less negative than in the case of Si@Mo. However, like in the B@Mo case, H on sites 3 and 4 exhibits a similar E_ad.

In conclusion, the above findings highlight the intricate interplay between the dopants and H in SMoSe JLs, emphasizing the potential for tailoring catalytic properties by strategically introducing dopants at different doping sites.

3.4.2 Gibbs free energy and exergonic behavior. We calculated the Gibbs free absorption energy ΔG using the formula^73–75

ΔG = E_ad − TΔS − ΔZPE (6)

where E_ad is the adsorption enthalpy (eqn (5)), which is equal to the enthalpy change (due to adsorption) in the ground state, ΔZPE is the change in zero-point energy of H during the adsorption, T is the temperature (273.15 K) and ΔS is the change in entropy. The term ΔZPE is computed as

ΔZPE = ZPE(H*) − ZPE(H) (7)

where ZPE(H*) and ZPE(H) are the zero-point energies of the adsorbed H and H₂ molecule, which are calculated using respective vibrational frequencies ω as , where ℏ is the Planck constant.⁷⁵ The vibrational entropy of the adsorbed H (i.e., the H* atoms) is small, and the entropy of adsorption of is , where is the entropy of H₂ in the gas phase under standard conditions.⁷⁴ In this work, ΔS is set to −0.205 eV, which is the value for standard pressure and temperature conditions, according to the NIST database.⁷⁶ The calculated values of each quantity in eqn (7) are given in Tables 1–4 in the ESI† for the pristine, B-, Si-, and Ge-doped SMoSe JLs, respectively.

The results are summarized in Fig. 6. A negative or positive ΔG indicates an attractive or repulsive interaction, respectively, between H and the JL. It should be noted that a too-negative ΔG value may hinder the potential application of the specific JL for the HER, as it requires high energy to separate H from the JL. Hence, to be a good candidate material for the HER, the ΔG of the adsorbed H on the material surface has to be only slightly negative.^73,74,77 The calculated ΔG’s of H on S and Se sites of the pristine JL show large positive values, as visible in Fig. 6a, which means that the pristine SMoSe JL is unfavorable for HER applications.

Fig. 6 The calculated Gibbs free energy of H adsorption (for standard temperature and pressure conditions) on (a) B-doped, (b) Si-doped, and (c) Ge-doped JLs. The reference levels of H⁺ + e⁻ and 1/2 H₂ are set to zero. From left to right, ΔG is given for the pristine, X@Mo-, X@S-, X@Se-, and X@Int-doped SMoSe JLs, respectively. The numbers near the markers represent the H sites shown in Fig. 5.

For B@Mo (Fig. 6a) and its structural vicinity (sites 1–6), there is a strong affinity of H towards the B, S, and Se sites. However, this interaction proves excessively potent, with ΔG values ranging from −1.3 eV to −2.4 eV, rendering B@Mo unsuitable for the HER (Fig. 6a) since H desorption is energy demanding in these cases. The case of B@Int does not significantly affect the HER properties of the doped layer, as for all H configurations ΔG is positive. On the other hand, B@S and B@Se lead to a reduction in ΔG compared to the pristine JL. However, for B@S and B@Se (sites 1 and 2), ΔG is still positive for H on S and Se, whereas H on B (site 3) shows a lower value at approximately −0.01 eV. Remarkably, this is even a lower negative value than the reported ΔG for the highly efficient Pt catalyst (−0.09 eV)^73,74 and makes B@S and B@Se doping an ideal doping choice for HER applications.

Si@Int (Fig. 6b), similar to the B dopant and pristine JL, provides only unfavorable sites due to the positive ΔG value for all H configurations. Focusing on Si@Mo, we encounter two distinct H sites on S (1 and 3) and two distinct H sites on Se (2 and 4), cf.Fig. 5. It is intriguing to note that for sites 1 and 2, the ΔG values range from −0.2 to −0.1 eV, and for H on sites 3 and 4 ΔG is positive. Notably, the ΔG values of H on sites 1 and 2 are comparable to those observed for graphitic carbon–nitrogen-doped graphene interfacing layers.⁷⁴ Finally, in Si@S and Si@Se, only site 3 is favorable, as the interaction with H becomes exergonic with a ΔG of −0.22 eV. In contrast, the remaining H configurations (sites 1 and 2) exhibit an endergonic nature. In comparison to B, Si doping at Mo, S, and Se provides potential sites for H adsorption and stays a potent candidate for doping for HER applications.

Despite being isoelectronic with Si, Ge exhibits subtle differences in its interaction with H due to its higher electronegativity and larger atomic size (Fig. 6c). Similar to Si and B, Ge@Int is also unsuitable for HER applications as ΔG > 0. In contrast to Si, for Ge@Mo, the ΔG values for H on sites 1 and 3 as well as those for H on sites 2 and 4 are similar. The ΔG values of H on S and H on Se, cf.Fig. 6c, are −0.05 eV and 0.05 eV, respectively (sites 1 and 2). Hence, the S plane of Ge@Mo JLs can effectively retain H in the HER, making Ge@Mo doping an optimal candidate for the HER. For Ge@S and Ge@Se, the interaction between H and Ge (site 3) is attractive, with a strength of −0.12 and −0.30 eV. The H–S and H–Se interactions (sites 1 and 2) are endergonic. Hence, Ge@S provides an optimal adsorption site on top of Ge in comparison to the stronger interaction site in Ge@Se. As a result, the Ge doping at Mo or S is recommended for HER applications.

The preceding findings underscore the significant advantages of X-doping of SMoSe JLs for use in the HER. Also, the findings provide insightful motivation for selecting appropriate doping cases for further applications that involve electron-transfer processes, such as H₂O reduction under different chemical conditions.

4 Conclusions

Spin-polarized first-principles calculations were carried out to explore whether B, Si, and Ge-doped SMoSe JLs can be used as potential catalysts in the hydrogen evolution reaction (HER). The dopant atoms X (X = B, Si and Ge) were inserted at Mo, S, Se, and interstitial sites. The analysis of the relaxed JLs demonstrates the effect of the atomic size of the dopants on the alteration of the layer structure in their structural vicinity. Furthermore, the formation energy E_f for substitutional and interstitial doping was studied for two different chemical environments: (i) bulk X – or X-rich conditions, and (ii) dimer X₂ – or X-poor conditions. The X-poor conditions yield lower E_f values in all cases investigated. Our results show that doping at the S site is energetically most favored. For X@S, the E_f can be arranged in the order E^B_f < E^Si_f < E^Ge_f. Interestingly, the value for Si@Mo differs from that for Si@S only by about 290 meV per atom, hinting at the possibility of Si@Mo doping. The differences in electronegativities and atomic sizes between the dopant and host atoms lead to electron redistribution, which was explored using Bader analysis. Atomic sites with a number of electrons different from that on atoms in the pristine SMoSe JL may be potential hydrogen traps and are therefore interesting for the HER. Hence, the interaction of H atoms with these sites was studied and the H adsorption energy E_ad was calculated. While the pristine SMoSe JL repels H, several attractive sites were found in the structural vicinity of the considered dopant atoms. Finally, the Gibbs free adsorption energy ΔG was determined in order to quantify the feasibility of the doped SMoSe JLs for use as a catalyst for the HER. Upon comparing the calculated ΔG values for various dopants and H configurations, it becomes evident that all dopants may play a vital role in improving SMoSe for HER applications. The ΔG values imply that B on S and Se sites, Si on Mo and S sites, and Ge on Mo and S sites are most favorable. Remarkably, the adsorption and desorption of H on the B-doped JLs (doped at S and Se sites) and H on Ge-doped JLs (at the Mo site) should show rapid kinetics. This finding signifies an encouraging step towards improving the performance of SMoSe JLs in HER applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MV and MZ acknowledge funding by the DFG within the project DFG 442646446, ZS 120/5-1. MV thanks both the Department of Information Services and Computing at Helmholtz-Zentrum Dresden-Rossendorf and the Center for Information Services and High-Performance Computing (ZIH), Technische Universität Dresden, for providing extensive computing facilities.

Notes and references

1. W. Chen, X. Hou, X. Shi and H. Pan, ACS Appl. Mater. Interfaces, 2018, 10, 35289–35295.
2. X. Yin, C. S. Tang, Y. Zheng, J. Gao, J. Wu, H. Zhang, M. Chhowalla, W. Chen and A. T. S. Wee, Chem. Soc. Rev., 2021, 50, 10087–10115.
3. T. Amrillah, A. Hermawan, Y. B. Cristian, A. Oktafiani, D. M. M. Dewi, I. Amalina, Darminto and J.-Y. Juang, Phys. Chem. Chem. Phys., 2023, 25, 18584–18608.
4. S. Y. Choi, Y. Kim, H.-S. Chung, A. R. Kim, J.-D. Kwon, J. Park, Y. L. Kim, S.-H. Kwon, M. G. Hahm and B. Cho, ACS Appl. Mater. Interfaces, 2017, 9, 3817–3823.
5. B. Kirubasankar, Y. S. Won, L. A. Adofo, S. H. Choi, S. M. Kim and K. K. Kim, Chem. Sci., 2022, 13, 7707–7738.
6. M. Vallinayagam, A. E. Sudheer, S. A. Aravindh, D. Murali, N. Raja, R. Katta, M. Posselt and M. Zschornak, J. Phys. Chem. C, 2023, 127, 17029–17038.
7. R. da Silva, R. Barbosa, R. R. Mançano, N. Durães, R. B. Pontes, R. H. Miwa, A. Fazzio and J. E. Padilha, ACS Appl. Nano Mater., 2019, 2, 890–897.
8. D. Er, H. Ye, N. C. Frey, H. Kumar, J. Lou and V. B. Shenoy, Nano Lett., 2018, 18, 3943–3949.
9. Y.-M. Zhao, P. Ren, X.-Y. Ma, J. P. Lewis, Q.-B. Yan and G. Su, J. Phys. Chem. C, 2021, 125, 11939–11949.
10. D. Yao, Y. Zhang, S. Zhang, J. Wan, H. Yu and H. Jin, J. Mater. Chem. A, 2023, 11, 16433–16457.
11. H. Li, C. Chen, D. Yan, Y. Wang, R. Chen, Y. Zou and S. Wang, J. Mater. Chem. A, 2019, 7, 23432–23450.
12. Z. Kang, M. A. Khan, Y. Gong, R. Javed, Y. Xu, D. Ye, H. Zhao and J. Zhang, J. Mater. Chem. A, 2021, 9, 6089–6108.
13. W. Kong, J. Deng and L. Li, J. Mater. Chem. A, 2022, 10, 14674–14691.
14. R. Woods-Robinson, K. A. Persson and A. Zakutayev, J. Mater. Chem. A, 2023, 11, 24948–24958.
15. S. Kansara, H. Kang, S. Ryu, H. H. Sun and J.-Y. Hwang, J. Mater. Chem. A, 2023, 11, 24482–24518.
16. F. Meutzner, M. Zschornak, A. A. Kabanov, T. Nestler, T. Leisegang, V. A. Blatov and D. C. Meyer, Chem.–Eur. J., 2019, 25, 8623–8629.
17. Z. Zhang, M. Yang, N. Zhao, L. Wang and Y. Li, Phys. Chem. Chem. Phys., 2019, 21, 23441–23446.
18. B. Chen, D. Chao, E. Liu, M. Jaroniec, N. Zhao and S.-Z. Qiao, Energy Environ. Sci., 2020, 13, 1096–1131.
19. W. Chen, Y. Qu, L. Yao, X. Hou, X. Shi and H. Pan, J. Mater. Chem. A, 2018, 6, 8021–8029.
20. B. Hou, Y. Zhang, H. Zhang, H. Shao, C. Ma, X. Zhang, Y. Chen, K. Xu, G. Ni and H. Zhu, J. Phys. Chem. Lett., 2020, 11, 3116–3128.
21. Z. Guan, S. Ni and S. Hu, J. Phys. Chem. C, 2018, 122, 6209–6216.
22. C. Ataca, H. Şahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999.
23. Z. Wang, J. Mater. Chem. C, 2018, 6, 13000–13005.
24. A. Ambrosi, Z. Sofer and M. Pumera, Chem. Commun., 2015, 51, 8450–8453.
25. J. Chen, K. Wu, W. Hu and J. Yang, J. Phys. Chem. Lett., 2021, 12, 12256–12268.
26. J. Chen, K. Wu, W. Hu and J. Yang, J. Phys. Chem. Lett., 2021, 12, 1932–1939.
27. Q.-F. Yao, J. Cai, W.-Y. Tong, S.-J. Gong, J.-Q. Wang, X. Wan, C.-G. Duan and J. H. Chu, Phys. Rev. B, 2017, 95, 165401.
28. S. D. Ganichev and L. E. Golub, Phys. Status Solidi B, 2014, 251, 1801–1823.
29. S.-S. Guan, S.-S. Ke, F.-F. Yu, H.-X. Deng, Y. Guo and H.-F. Lü, Appl. Surf. Sci., 2019, 496, 143692.
30. L. Yu, S. Sun and X. Ye, Phys. Chem. Chem. Phys., 2020, 22, 2498–2508.
31. K. Chen, W. Tang, M. Fu, X. Li, C. Ke, Y. Wu, Z. Wu and J. Kang, Nanoscale Res. Lett., 2021, 16, 1.
32. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198.
33. L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248.
34. K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876.
35. W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao, T. F. Heinz, J. Hone and Z. L. Wang, Nature, 2014, 514, 470–474.
36. M. Yagmurcukardes, Y. Qin, S. Ozen, M. Sayyad, F. M. Peeters, S. Tongay and H. Sahin, Appl. Phys. Rev., 2020, 7, 011311.
37. T. Hu, F. Jia, G. Zhao, J. Wu, A. Stroppa and W. Ren, Phys. Rev. B, 2018, 97, 235404.
38. M. Yagmurcukardes and F. M. Peeters, Phys. Rev. B, 2020, 101, 155205.
39. Y. C. Cheng, Z. Y. Zhu, M. Tahir and U. Schwingenschlögl, Europhys. Lett., 2013, 102, 57001.
40. K. Roy, D. Ghosh, S. Maitra and P. Kumar, J. Mater. Chem. A, 2023, 11, 21135–21145.
41. D. Ghosh, K. Roy, S. Maitra and P. Kumar, J. Phys. Chem. Lett., 2022, 13, 1234–1240.
42. N. Ghobadi, A. Rezavand, S. Soleimani-Amiri and S. Gholami Rudi, Appl. Surf. Sci., 2023, 639, 158278.
43. Z. Wang and G. Zhou, J. Phys. Chem. C, 2020, 124, 167–174.
44. L. Ju, M. Bie, J. Shang, X. Tang and L. Kou, J. Phys Mater., 2020, 3, 022004.
45. P. Wang, Y. Zong, H. Liu, H. Wen, H.-B. Wu and J.-B. Xia, J. Mater. Chem. C, 2021, 9, 4989–4999.
46. Y. Xu, Y. Yao, W. Yin, J. Cao, M. Chen and X. Wei, RSC Adv., 2020, 10, 10816–10825.
47. R. Li, Y. Cheng and W. Huang, Small, 2018, 14, 1802091.
48. L. Ju, M. Bie, X. Tang, J. Shang and L. Kou, ACS Appl. Mater. Interfaces, 2020, 12, 29335–29343.
49. T. Zheng, Y.-C. Lin, Y. Yu, P. Valencia-Acuna, A. A. Puretzky, R. Torsi, C. Liu, I. N. Ivanov, G. Duscher, D. B. Geohegan, Z. Ni, K. Xiao and H. Zhao, Nano Lett., 2021, 21, 931–937.
50. M. M. Petrić, M. Kremser, M. Barbone, Y. Qin, Y. Sayyad, Y. Shen, S. Tongay, J. J. Finley, A. R. Botello-Méndez and K. Müller, Phys. Rev. B, 2021, 103, 035414.
51. T. Zhang, J. Wang, P. Wu, A.-Y. Lu and J. Kong, Nat. Rev. Mater., 2023, 8, 799–821.
52. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749.
53. C. W. Jang, W. J. Lee, J. K. Kim, S. M. Park, S. Kim and S.-H. Choi, NPG Asia Mater., 2022, 14, 15.
54. R. Sant, M. Gay, A. Marty, S. Lisi, R. Harrabi, C. Vergnaud, M. T. Dau, X. Weng, J. Coraux, N. Gauthier, O. Renault, G. Renaud and M. Jamet, npj 2D Mater. Appl., 2020, 4, 41.
55. S. Tao, B. Xu, J. Shi, S. Zhong, X. Lei, G. Liu and M. Wu, J. Phys. Chem. C, 2019, 123, 9059–9065.
56. S. Pakhira and S. N. Upadhyay, Sustainable Energy Fuels, 2022, 6, 1733–1752.
57. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
58. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
60. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
61. Y. Ji, M. Yang, H. Lin, T. Hou, L. Wang, Y. Li and S.-T. Lee, J. Phys. Chem. C, 2018, 122, 3123–3129.
62. Y. Wang, R. Chen, X. Luo, Q. Liang, Y. Wang and Q. Xie, ACS Appl. Nano Mater., 2022, 5, 8371–8381.
63. C. Xia, W. Xiong, J. Du, T. Wang, Y. Peng and J. Li, Phys. Rev. B, 2018, 98, 165424.
64. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
65. N. N. T. Pham, K. H. Kim, B. Han and S. G. Lee, J. Phys. Chem. C, 2022, 126, 5863–5872.
66. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
67. G. Henkelman, A. Andri and J. Hannes, Comput. Mater. Sci., 2006, 36, 354–360.
68. A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098.
69. R. Kronberg, H. Lappalainen and K. Laasonen, Phys. Chem. Chem. Phys., 2020, 22, 10536–10549.
70. H. Prats and K. Chan, Phys. Chem. Chem. Phys., 2021, 23, 27150–27158.
71. T. Würger, C. Feiler, G. B. Vonbun-Feldbauer, M. L. Heludkevich and R. H. Meißner, Sci. Rep., 2020, 10, 15006.
72. A. Kumar, H.-P. Komsa, D. Praveen Pathak, B. Marriyappan Sivagnanam, A. S. K. Sinha and J. Karthikeyan, J. Phys. Chem. C, 2022, 126, 19627–19636.
73. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
74. Y. Zheng, Y. Jiao, Y. Zhu, L. H. Li, Y. Han, Y. Chen, A. Du, M. Jaroniec and S. Z. Qiao, Nat. Commun., 2014, 5, 3783.
75. Y. Liu, G. Yu, G.-D. Li, Y. Sun, T. Asefa, W. Chen and X. Zou, Angew. Chem., Int. Ed., 2015, 54, 10752–10757.
76. NIST-JANAF Thermochemical Tables-NIST Chemistry WebBook, SRD 69, https://webbook.nist.gov/cgi/cbook.cgi?ID=C1333740&Mask=1, accessed on 01.02.2023.
77. E. E. Siddharthan, S. Ghosh and R. Thapa, ACS Appl. Energy Mater., 2023, 6, 8941–8948.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta07243f

---