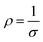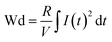Utilizing the synergistic effect between the Schottky barrier and field redistribution to achieve high-density, low-consumption, cellulose-based flexible dielectric films for next-generation green energy storage capacitors†
Received
1st October 2023
, Accepted 20th November 2023
First published on 20th November 2023
Abstract
After decades of development, the study of flexible dielectric materials has changed the focus from BOPP/PVDF/PI-based systems to those that can be biodegraded, not only because of several bottlenecks in the former systems but also because of the pollution they cause on the earth. Though various strategies were used, the improvement in the energy storage performance was slow. Recently, hydrogen bond replacement has been utilized for achieving a high energy density in sandwich-structured cellulose-based films; however, the efficiency was relatively low due to an uneven electric field distribution. In this work, a similar technology of the dissolution-regeneration route was used, and the multilayer-structured cellulose-based films were obtained by changing the sequence of fillers embedding in each sublayer. The differences in mechanical properties between films was revealed due to the different particle sizes and the presence of a slip layer effect. As a result of the synergistic effect between the field redistribution and the decreasing Fermi level, a breakdown strength as high as 6.24 MV cm−1 was achieved with a super high energy density of 31.07 J cm−3 and an efficiency of 80.03%, and the computer simulation fitted very well with the experimental data. The electric field distribution also help to reduce the energy consumption, for such a high energy density was triggered by a lower voltage. In addition, the film showed good fatigue endurance at both room temperature and 150 °C, which is caused by the intrinsic strong adiabaticity of cellulose. This work offers a unique approach to deeply understanding the electric breakdown mechanism in dielectric polymers and indicates the feasibility of cellulose in replacing petroleum-based polymers in the dielectric field.
1. Introduction
Flexible electronics have attracted much attention due to the advantages of their application in bionic devices, which are the most critical part of next-generation human-machine interactive systems compared to rigid materials. In such systems, power, and sensing units are the core components, and their fabrication is strongly dependent on dielectric energy storage and conversion polymers.1–14 After realizing the harmful effects of petroleum-based materials on the environment and human health, especially during their degradation process, in recent years, polymer-based dielectric materials have changed from biaxially oriented polypropylene (BOPP)-based, polyvinylidene fluoride (PVDF)-based, and polyimide (PI)-based systems to candidates exhibiting partial/complete biodegradability.15–18 Among them, cellulose is the most commonly used material, not only as it is the most abundant natural polymer on the earth but also for its intrinsic spontaneous polarization and good voltage endurance. The latter two properties can be further elaborated as follows: (1) the polarization of cellulose originates from three different hydroxyl groups, which form both the inter- and intramolecular hydrogen bonds in their polymeric chains as shown in Fig. 1(a). Such hydrogen bonds are highly ordered in local regions and thus form polarized dipoles.19–21 (2) The high insulating behavior comes from their strong adiabaticity, which blocks the conduction heat transfer under a high voltage.22 However, the polarization of a pristine cellulose film is relatively low, limiting the applications of cellulose-based dielectric materials; therefore, in most cases, ceramic powders with a higher polarization are embedded. For the application in a piezoelectric nanogenerator, for example, tetragonal phase BaTiO3 was added in regenerated cellulose films, and a maximum output voltage of 15.5 V with a power of 11.8 μW was obtained.23 In the energy storage field, cellulose/ceramic composites are more widely used. With morphological control, interface modification, and some other technologies, the energy storage density (ESD) of cellulose/ceramic composites has been increased from 5.7 J cm−3 to 23.5 J cm−3.24–32
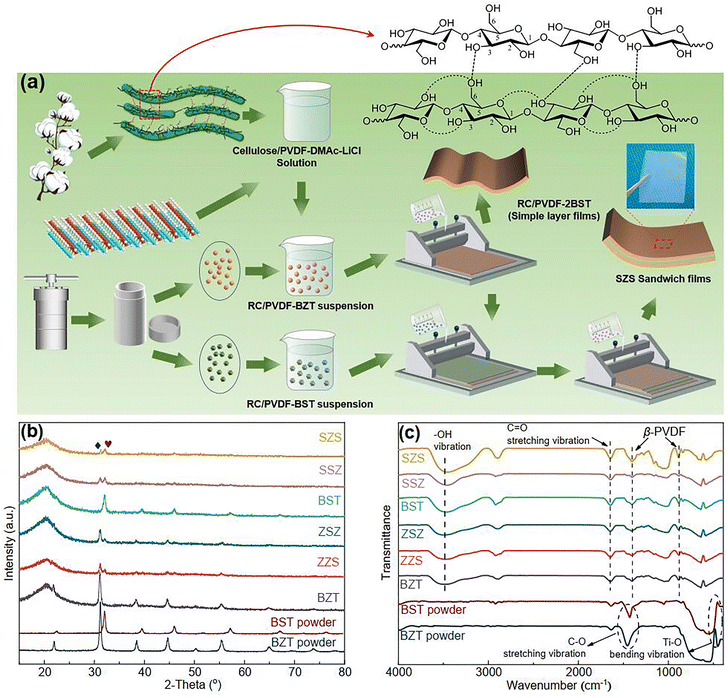 |
| | Fig. 1 (a) A schematic of the process route of multilayer-structured film constructed in this work; (b) the XRD pattern and (c) FT-IR spectra of all the films presented in our work. | |
Compared to traditional petroleum-based flexible films, the most significant advantages of cellulose/ceramic-based ones are much better mechanical properties such as higher tensile strength and elongation at break,13,33 which enable the latter to be used in more limited environments. However, it still suffers from two main drawbacks: high hydrophilic, which makes it impossible to be used in humid environments,34 and the difficulty of fabricating multilayer-structure, which is caused by the hydrogen bonds' strong self-assembly behavior and thus inhibits the formation of interfacial polarization. In our previous work, the first was solved by blending the cellulose with a small amount of PVDF by a dissolution-regeneration method. Compared with pristine PVDF, cellulose/PVDF-BaTiO3 (C8P2-BT) blend films' water contact angle was strongly increased, with an optimistic ESD of 10.81 J cm−3.35 A similar technology was also reported in other work,36 demonstrating that rendering a small amount of high electronegativity to the cellulose can significantly modify its physicochemical properties. The second drawback has remained for quite a long time as fabricating multilayer-structured cellulose-based films is difficult, which is caused by the strong self-assembly behavior of the hydrogen bond network. In our latest study, this problem was figured out. By the combination of hydrogen bond replacement strategy and the modified tape-casting technique, the sandwich-structured C8P2-BT film was successfully fabricated, with a super-high ESD of 27.2 J cm−3 achieved, which is the highest ESD of cellulose-based films as far as the author knows.21 However, its energy storage efficiency (η) is only about 50%, which is hard to be called an utterly environment-friendly energy storage capacitor. This is attributed to the unreasonable electric field distribution in the multilayers, for which many electrons were thus trapped in the C8P2 matrix, leading to low η. Besides, the electric field that is needed to trigger such a high ESD is up to 6 MV cm−1, which is a high value. If this parameter can be obtained at a lower field or a better value can be reached at the same voltage, achieving more environment-friendly capacitors can be considered a success.
Based on the discussion and clarification of the good mechanical properties and hydrophobicity, this work achieved the excellent energy storage performance of our multilayer-structured cellulose-based films containing two kinds of particles (BZT and BST), and the related mechanisms were systematically studied. The η was strongly increased with a decrement in the energy consumption. The reason for the change in Eb and polarization with the film structure was fully understood. The synergistic effect between the Fermi level movement and the electric field redistribution and the field distribution deviation were considered the main reasons, respectively. The computer simulation was employed using the finite element method on COMSOLMultiphysics6.0, and the result fits very well with the experimental data. In addition, the film with the structure of SZS has good reliability and shows excellent energy storage behavior in all kinds of harsh environments. These results again confirm that the cellulose has excellent potential to replace petroleum-based polymers such as PVDF in the field of flexible dielectrics.
2. Experimental section
The experiment process is illustrated in Fig. 1(a), and the related details are shown in the ESI.† From the photo, we can see that our films exhibit high transparency. Fig. 2(a) displays the sketches of all the composite films in this work, in which the green and orange ones represent the BZT layer and the BST layer, respectively, which are also referred to as Z and S in multilayers respectively. (In this manuscript, the ‘BZT powders’ and ‘BST powders’ refer to the corresponding ceramic powders, the ‘BZT single layer’ and ‘BST single layer’ refer to single-layer-structured cellulose/PVDF-BaZr0.2Ti0.8O3 film and cellulose/PVDF-Ba0.6Sr0.4TiO3 film, respectively, and the abbreviation with three capital letter like “SZS” means the multilayer-structured films, in which the Z and S represent the BZT layer and BST sub-layer, respectively. C8P2 means the cellulose/PVDF blend film matrix.)
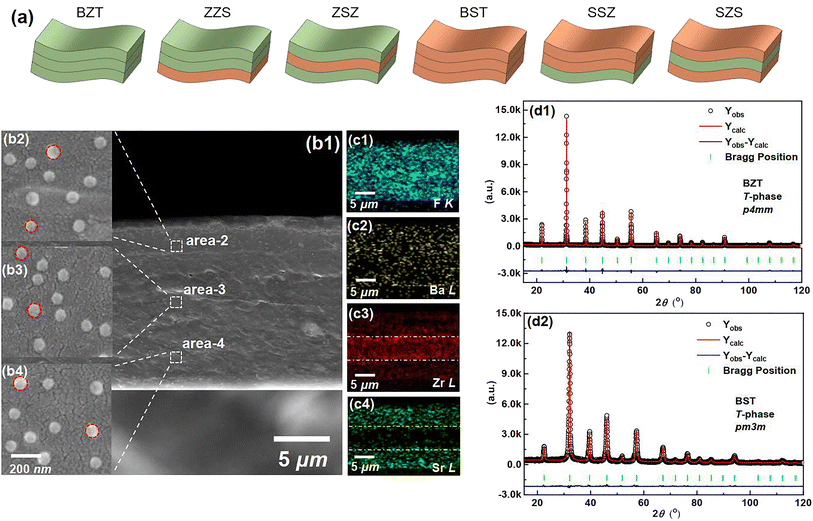 |
| | Fig. 2 (a) Sketches to show different structures of all the films in our work. (b1) A cross-sectional SEM image of the SZS. An enlarged-view of (b2) area-2 (b3) area-2 and (b4) area-4 in (b1). The EDS mapping for (c1) F–K, (c2) Ba–L, (c3) Zr–L, and (c4) Sr–L of Fig. 2(b1). The Rietveld XRD refinement of (d1) BZT. (d2) BST ceramic powders used in this work. | |
3. Results and discussions
3.1. Characterizations, results, and discussions of the phase and structure
Fig. 1(b) shows the XRD 2-theta (2θ) scans of all the films with different structures in this work, and the patterns for pure BZT and BST ceramic powders are also shown below. Both BZT and BST powders are single-phased perovskite structures without any impurity, and the lower 2θ angle position of all the peaks of BZT than those of BST demonstrates that the unit cell volume of BZT powders is bigger than that of BST. As expected, both BZT and BST powders' peaks are detected in ZZS, ZSZ, SSZ, and SZS. A broad peak, which is a result of the combination of the (110) plane of PVDF and cellulose, is detected around 21° in all the films.21 No peak position shifts in either the powders or the matrix is observed, indicating that the powders' lattice parameter and the matrix's hydroxyl groups remain unchanged before and after compositing. Fig. 1(c) shows the Fourier transform infrared (FT-IR) spectra of the films and two ceramic powders. To exclude the effect of absorbed water on the powders, both the films and powders were dried at 80 °C for 24 h before the measurement. As to the powders, the peaks around 460 cm−1 in two powders are due to Ti–O bending vibration in their lattices along the polar axis.37 The peak intensity of BZT is much higher than that of BST, indicating a higher polarization of BZT than that of BST. The peaks around 1420 cm−1 are related to the C–O stretching vibration, which comes from the absorbed CO2 on the particles' surface.38 As to the films, the 840 cm−1 and 1401 cm−1 peaks represent the characteristic of β-phase PVDF,39 and the peaks at 1650 cm−1 represent the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of the glucose units in cellulose chains.40 The broad peak around 3500 cm−1, which cannot be detected in ceramic powders, corresponds to the stretching vibration of hydroxyl in the C8P2 matrix, which also demonstrates the formation of hydrogen bond network among cellulose, PVDF, and ceramic particles during the dissolution-regeneration process as sketched in Fig. 1(a). Such a hydrogen network guarantees the successful preparation of a multilayered structure of our films, as we explained in previous work.21
O stretching vibration of the glucose units in cellulose chains.40 The broad peak around 3500 cm−1, which cannot be detected in ceramic powders, corresponds to the stretching vibration of hydroxyl in the C8P2 matrix, which also demonstrates the formation of hydrogen bond network among cellulose, PVDF, and ceramic particles during the dissolution-regeneration process as sketched in Fig. 1(a). Such a hydrogen network guarantees the successful preparation of a multilayered structure of our films, as we explained in previous work.21
Fig. 2(b1) displays the cross-sectional scanning electron microscopic (SEM) image of the SZS. Owing to the modified tape-casting technology, the film is very dense without any pores or obvious interfaces between adjacent sublayers. The enlarged views of area-2, -3, and -4 are inserted as Fig. 2(b2)–(b4), respectively. Seemingly, spherical-like particles are observed in both Fig. 2(b2) and (b4), and the hexagonal particles are observed in Fig. 2(b3), which corresponds to the BST and BZT particles, respectively. The energy-dispersive X-ray spectroscopy (EDS) mappings taken from Fig. 2(b1) of F, Ba, Zr, and Sr are displayed as Fig. 2(c1)–(c4). Fig. 2(c1) and (c2) indicate the monodisperse nature of the C8P2 matrix and ceramic particles, and Fig. 2(c3) and (c4) demonstrate the distribution area of BZT and BST, thus the sandwiched structure of SZS can be confirmed. The Rietveld method was used to refine their XRD data to explore the crystallographic structure of two powders deeply. As shown in Fig. 2(d1) and (d2), the BZT and BST powders exhibit tetragonal (T) and cubic (C) phases with space groups of P4mm and Pm3m, respectively. The refinement parameters are provided in Tab. S1,† according to which the refinement process's credibility can also be demonstrated. In addition, the larger c/a ratio of the BZT than that of the BST confirms the result in the FT-IR. The cross-sectional SEM images of the BST single layer and SSZ with their EDS mappings are displayed in Fig. S1,† and their structures can also be confirmed. Fig. 3(a1) is the transmission electron microscopic (TEM) image of a general area of the SZS, and the organic molecular chain with ceramic particles (bright white spots) is clearly detected. Comparing the corresponding EDS mappings of C, O, and F, as displayed in Fig. 3(a2)–(a4), the bright area for F is much shorter than the area for C and O, which indicates that the average length of cellulose fiber in our films might be greater than that of the PVDF chains. Besides, the PVDF and cellulose are adsorbed with each other tightly, which is probably a result of the effect of the hydrogen bond network. Higher-magnification images taken in specific areas containing BZT and BST particles are shown in Fig. 3(b1) and (c1), respectively. (The particle aggregation is seen because the samples for the TEM measurement were the sliced samples and overlapped with each other). Their EDS mappings of C and F, which is to reveal the PVDF and cellulose distribution near the ceramic particles, are illustrated in Fig. 3(b2), (b3), (c2) and (c3), respectively. Fig. 3(b4) and (c4) are their mappings of Zr and Sr in Fig. 3(b1) and (c1), respectively, which give us more evidence of the existence and distribution of BZT and BST particles. Comparing Fig. 3(b3) with Fig. 3(b4) and Fig. 3(c3) with Fig. 3(c4), we can see that the ceramic particles prefer to bond with PVDF rather than the cellulose because of the higher electronegativity of F− than O−.41 To confirm this assumption, we took the X-ray photoelectron spectroscopy (XPS) measurement of both the C8P2 matrix and SZS and the scanning data from 0 eV to 1300 eV are plotted in Fig. S1(c1).† Fig. S1(c2)† shows the C 1s spectra of two films that come from C atoms of both PVDF and cellulose. The peaks at ∼284.2 eV, ∼285.6 eV, and ∼287.8 eV correspond to C–C or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C in PVDF and cellulose, C–OH in the hydroxy group of cellulose, and C–O–C in the glucose unit of cellulose, respectively, and not much difference can be distinguished here. The most significant difference between these two films comes from the F 1s spectra, as shown in Fig. S1(c3).† Only one peak at ∼687.0 eV, which corresponds to F–C–F in PVDF can be detected in the C8P2 matrix, while an extra peak at ∼683.8 eV is observed in the SZS. Such a new peak has been confirmed to be related to induced F–C–H in the interface between the fillers and the PVDF.42,43Fig. 3(d1) and (e1) are the TEM images of single BZT and BST particles embedded in the SZS. Clearly, the former indeed has a hexagonal shape, while the latter has a spherical-like one, and BST exhibits a larger particle size. Fig. 3(d2) and (e2) are the enlarged view of the red dashed rectangle areas in Fig. 3(d1) and (e1), respectively, with the observation of clear lattice fringes. After calibrating, the crystal axis was confirmed, and the lattice parameters fit very well with the result of Rietveld refinement. Fig. 3(d3) and (e3) give the ball-stick models of the unit cell of BZT and BST particles drawn from the XRD refinement result using VESTA.44
C in PVDF and cellulose, C–OH in the hydroxy group of cellulose, and C–O–C in the glucose unit of cellulose, respectively, and not much difference can be distinguished here. The most significant difference between these two films comes from the F 1s spectra, as shown in Fig. S1(c3).† Only one peak at ∼687.0 eV, which corresponds to F–C–F in PVDF can be detected in the C8P2 matrix, while an extra peak at ∼683.8 eV is observed in the SZS. Such a new peak has been confirmed to be related to induced F–C–H in the interface between the fillers and the PVDF.42,43Fig. 3(d1) and (e1) are the TEM images of single BZT and BST particles embedded in the SZS. Clearly, the former indeed has a hexagonal shape, while the latter has a spherical-like one, and BST exhibits a larger particle size. Fig. 3(d2) and (e2) are the enlarged view of the red dashed rectangle areas in Fig. 3(d1) and (e1), respectively, with the observation of clear lattice fringes. After calibrating, the crystal axis was confirmed, and the lattice parameters fit very well with the result of Rietveld refinement. Fig. 3(d3) and (e3) give the ball-stick models of the unit cell of BZT and BST particles drawn from the XRD refinement result using VESTA.44
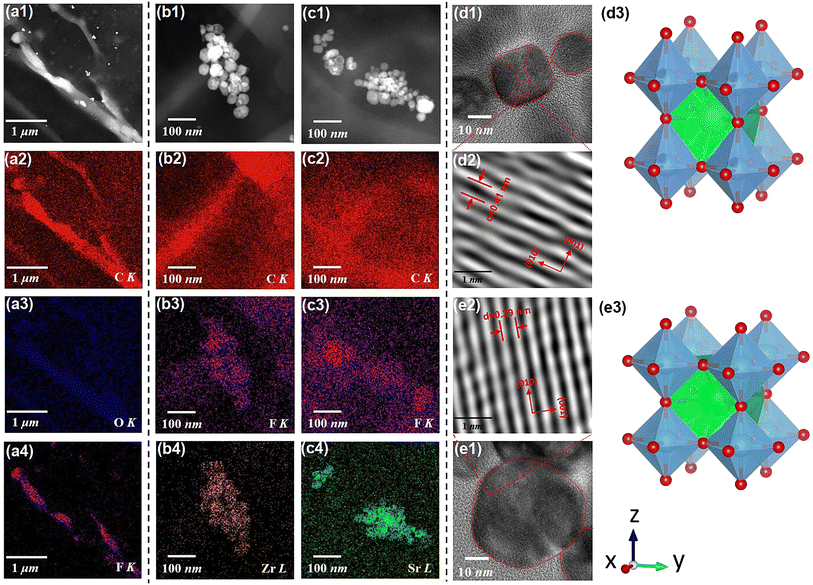 |
| | Fig. 3 (a1) The TEM image of a general area of the SZS film. The ESD mapping for (a2) C–K, (a3) O–K, and (a4) Fr–K of Fig. 3(a1). (b1) The TEM image of an area contains the BZT particles in the SZS film. The EDS mapping for (b2) C–K; (b3) F–K; and (b4) Zr–L of Fig. 3(b1). (c1) The TEM image of an area containing the BST particles in the SZS film; the EDS mapping for (c2) C–K, (c3) F–K, and (c4) Sr-L of Fig. 3(b1). The TEM image of (d1) single BZT; (e2) the single BST particle for confirming the morphology. The enlarged-view of (d2) the red dashed rectangle in (d1). (e2) The red dashed rectangle (e1) and the lattice fringes can be clearly seen. The ball-stick model of (d3) BZT and (e3) BST obtained the VESTA. | |
3.2. Brief results and discussions of mechanical and hydrophobic property
Compared to the PVDF-based flexible dielectric composites, one of the significant advantages of cellulose-based systems are their outstanding mechanical properties. Before introducing the energy storage performance of our films, the authors would like to show a brief characterization of this. Fig. 4(a) plots the stress–strain curves of all the films, and both the tensile strength and elongation at break are summarized in Fig. 4(b). For the two single-layered structures, the BST single layer exhibits a higher strain than the BZT single layer under the same stress and shows the highest elongation at break of 45% among all the films. In contrast, the latter shows a higher stress when experiencing the same strain, and its tensile strength is much better than the BST single layer. That is because, for 0–3 structured ceramic-polymer composites, (1) the tensile strength decreases with the increase in particle size of the fillers45 and (2) the interfacial adhesion, which is proportional to the tensile strength of composites, between the spherical-like fillers and the matrix is much lower than that between hexagonal fillers and the matrix.46 For the asymmetrical structure of ZZS and ZSS, the tensile strength and elongation at break have performance neutralization due to the difference in the Young modulus between different sublayers, as shown in the red and purple columns in Fig. 4(d). As to the sandwich-structured ones, the inner layer acts as a slip layer during the tensile process, and hence, the tensile strength and elongation at break can be further enhanced.47Fig. 4(c) compares the mechanical properties of ZSZ and SZS in our work with some typical cellulose- and PVDF-based 0–3 structured composites.17,26,27,35,48–62 According to the summary in the figure, the cellulose-based composites own better tensile strength but inferior elongation at break than the PVDF-based ones, which is because of the strong hydrogen bond in the cellulose molecular chain network.19,21,63 Here, the ZSZ shows a tensile strength of 139.05 MPa with elongation at break of 39.47%, and the SZS has a lower tensile strength of 133.96 MPa, but a higher elongation at break of 41.40%. The Young modulus of all the samples was calculated and is shown in Fig. 4(d). The two sandwich-structured films have a lower Young modulus than that of their asymmetrical counterparts, indicating their potential to be applied in complex spatial environments. Fig. 4(e) displays the films' water contact angle test. All the films show an angle of over 60°, quite larger than the pristine regenerated cellulose (normally ∼30°), manifesting a relatively good hydrophobicity. This is caused by adding a small amount of PVDF, as we introduced before.35 Besides, the BST sublayer shows an even better hydrophobicity than that of the BZT sublayer.
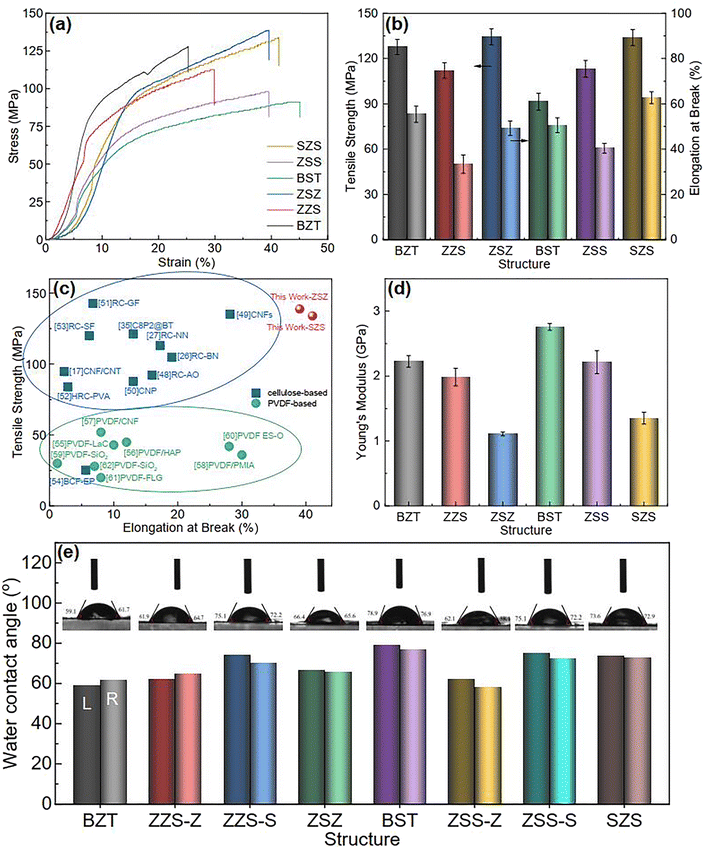 |
| | Fig. 4 (a) The stress–strain curves of all the films in this work; (b) the variation in tensile strength and elongation at break with structures of all the films in this work; (c) mechanical property comparison between our film and some typical cellulose-based and PVDF-based films; (d) the variation in the Young modulus with the structure of all the films in this work; (e) the water contact angle test of all the films in this work. | |
3.3. Results of the energy storage performance
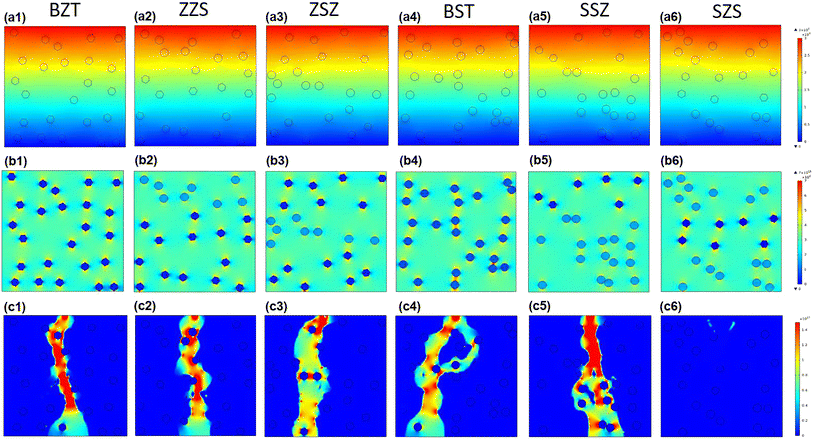
At the beginning of discussing the energy storage performance, each film's electric breakdown strength (Eb), generally calculated according to the Weibull distribution, must be confirmed. Details for such a calculation are provided in the ESI.†Fig. 5(a) shows the Weibull distribution results, and the Eb variation with the film structure is plotted in Fig. 5(b). From such a result, we can see that: (1) As to the single structures, the BST single layer possesses much better voltage endurance than that of the BZT. (2) The Eb value of the multilayer-structured ones is higher than that of single-layered ones. (3) The highest Eb, calculated to be 6.24 MV cm−1, is located in the SZS. In the actual experimental process, the increasing step of the electric field is 0.5 MV cm−1, and each film's ferroelectric hysteresis (P–E) loops under different electric fields are shown in Fig. S2.† A sketch is inserted in each figure to distinguish the electric field direction. (Here, the authors would like to emphasize that for asymmetrical structures such as ZZS and SSZ, the measuring direction has considerable effects on their electrical behavior, which deserves an independent study. To make the discussion logical, in this work, the negative side was connected to the BZT layer of BZT, ZZS, and ZSZ and to the BST layer of BST, SSZ, and SZS, which will be the only situation discussed in this work. The connection mode does not affect single-layered and symmetrical films.) After integration, both the ESD and η of each P–E loop in Fig. S2† were calculated, and are summarized in Fig. 5(c). With the increase in applied field, the ESD of all the films increases while η shows an opposite tendency. To make a more precise comparison, the P–E loops near the Eb of each film are summarized at the bottom of Fig. 5(d), and the variations in ESD and η with the film structure are plotted on the top. A super high ESD of 31.07 J cm−3 with an optimistic η of 80.03% was obtained under 6 MV cm−1 in the SZS. Compared to the C8P2-BT-based one, which was once reported to own the highest ESD of 27.2 J cm−3 among cellulose-based dielectric capacitors, the increment seems to be only 14.23%; however, the increment of η is as high as 56.3%.21 As a more environmentally friendly flexible dielectric capacitor than petroleum-based ones, the η of cellulose-based dielectric capacitor should be as crucial as the ESD. Moreover, humans always dream of storing the most energy with the lowest voltage. In this case, the authors put forward a new parameter, defined as the ratio of ESD/electric field (abbreviated to E/E ratio), to characterize the energy density that can be stored under per unit electric field. Fig. 5(e) compares the ESD and E/E ratio between the SZS and ZSZ in this work and some new cellulose-based dielectric capacitors that were newly reported.17,25–31,35,64–68 The two sandwich-structured films in our work perform very well: the SZS shows the highest value in the ESD with an E/E ratio of 5.17, while the ZSZ has an ESD of only 25.30 J cm−3, but its E/E ratio reaches as high as 5.57. Such a result indicates that our films have excellent energy storage performance and consume less energy. The comparison of energy storage performance between the SZS and some petroleum-based polymers that were reported in the last five years is also summarized in Fig. S3(b).†
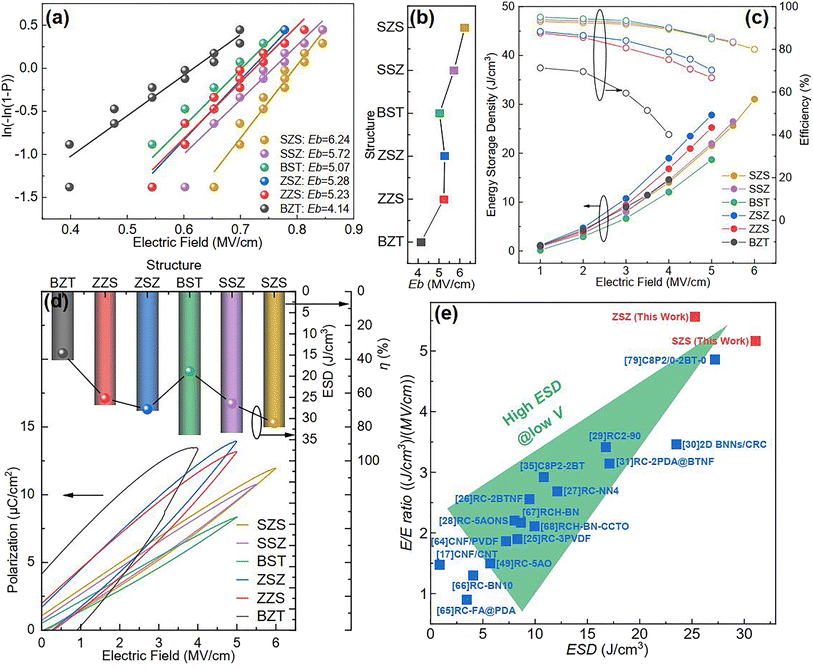 |
| | Fig. 5 (a) Weibull distribution result; (b) variation between Eb and the structure; (c) variation between the energy storage performance and electric field of all the films in our work; (d) the P–E loop near the Eb of all the film with the changing ESD and η with the film structure on the top; (e) the comparison of ESD and E/E ratio between our films and most of the cellulose-based dielectric capacitors that have been recently reported. | |
3.4. Discussions of the electric breakdown behavior
According to the Weibull distribution result, the Eb value of all the films is over 4.0 MV cm−1. The intrinsic good performance comes from the cellulose's good insulating properties and thermal stability, which is because the electric breakdown behavior is a combined effect of electric and thermal fields.69,70 The following discussion only focuses on Eb's differences between different films. Fig. 6(a1) plots the current density-electric field relationship (J–E curve) of all the films that converted from the measured current–voltage curve (I–V curve) according to the film's electrode size and film thickness. Fig. 6(a2) is the relationship between log J and E0.5 calculated from the Fig. 6(a1). Based on the definition of Schottky emission, which is expressed as follows:| | 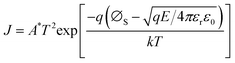 | (Eq. 1) |
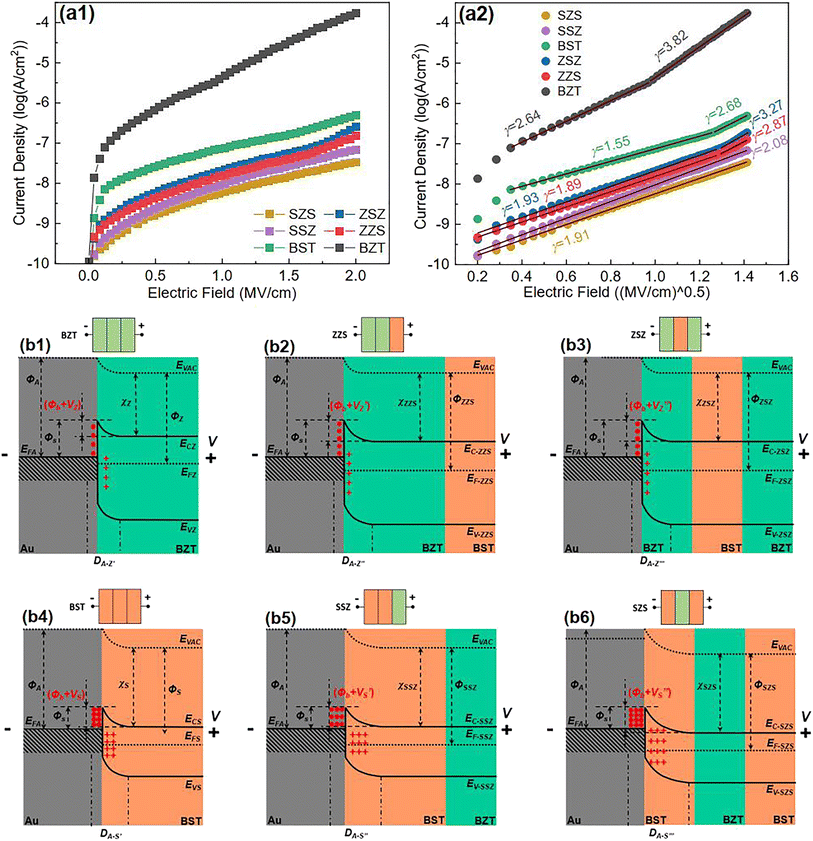 |
| | Fig. 6 (a1) J–E curves; (a2) the Schottky emission fitting result based on (a1) of all the films in our work; (b1–b6) the band diagram of all the films under a forward voltage (V). | |
Log J and E0.5 should have a linear relation if the conduction mechanism meets the Schottky emission mode. In Eq. (1), J, E, T, q, and ΦS are the current density, electric field, absolute temperature, electron charge, and the Schottky barrier height, respectively, A* and ε0 are the effective Richardson constant and the vacuum permittivity, which remains constant, and εr represents the optical dielectric constant, which is also the dynamic dielectric constant. After fitting, the conduction mode of all our films shows the Schottky emission but has different slopes. By comparing the relative dielectric constant determined from the line slope with the value measured at the optical frequency, the validity of this model can be verified, as reported in previous work.71–73 More precisely, this result can be classified into two different kinds: completely linear relationship with only one slope, as shown in SZS and SSZ, and segmented linear relationships with two different slopes, which signify the transformation of the Schottky barrier height with the increase in voltage, as shown in the remaining ones. The slope (γ) of each fitting line is also written in the figure. After contrastive analysis, (1) the J value of the BZT layer is much higher than that of the BST layer; (2) the J value of single-layered structures is higher than that of multilayered structures; and (3) the lowest J value is located in the SZS. Here, we can see that the J value of our films also varies strongly between different film structures and, more interestingly, is inversely proportional to the Eb value. To uncover the effects of the film structure on their Eb, the authors use the band theory for further analyses, and the band diagrams of all our films are displayed in Fig. 6(b1)–(b6). The physical meanings of all the symbols mentioned in these figures are explained in the ESI.†
To make things easier, in this work, the ceramic powders and the C8P2 matrix of each sublayer are considered as a whole, which differs from the previous assumption.21 Based on the electron affinity (generally defined as the lowest unoccupied molecular orbital or LUMO) of PVDF (3.5–3.9 eV) and cellulose (1.62 eV), the electron affinity of BaTiO3 (2.5 eV), BaZrO3 (lower than 2.5 eV), and SrTiO3 (3.9 eV), and the equivalent electron affinities of both BZT and BST single layers are lower than the work function of the Au electrode (ΦA) (5.1 eV).74–79 Therefore, the band diagrams of the interface between the Au electrode and the BZT single layer (cellulose/PVDF-BaZr0.2Ti0.8O3 film) and BST single layer (cellulose/PVDF-Ba0.6Sr0.4TiO3 film) under an applied voltage (V) are displayed in Fig. 6(b1) and (b4), respectively. Fig. S4† shows the band-bending process of these two physical conditions with the corresponding explanation provided. From such a discussion, we can conclude that the BST single layer owns a lower Fermi level but a broader depletion layer than the BZT single layer, which is thought to be the reason for the higher Eb of the former than the latter. Next, let us move to the multilayered structures. As to the ZZS, which can be regarded as the BZT single layer with the right third replaced by the same thickness of the BST layer, the Fermi levels of the two layers also needed to be aligned when connecting. Because the EFS moves down lower than the EFZ under forward voltage, as we concluded before, the newly formed Fermi level (EF-ZZS) should also be lower than the EFZ. The band bending in the ZZS under forward voltage thus becomes more significant than that in the BZT single layer, leading to a higher build-in potential (Φb + VZ′) and a broader depletion layer (DA-Z′′) with more electrons trapping in the interface, as shown in Fig. 6(b2). In brief, the BZT/BST interface helps to decrease the Fermi level in multilayered structures. Meanwhile, the Eb of the ZZS was thus increased. For the symmetrical counterpart, ZSZ, the situation is similar. Changing the structure has little effect on the band structure in this case, as shown in Fig. 6(b3), so these two structures have a similar Eb. With regard to the SSZ, the electric field redistribution of the structure under applied voltage, which follows Eq. (2), should be first considered.80 The UZ, EZ, εZ, and the US, ES, εS in Eq. (2) are the voltage, electric field, and dielectric constant of the BZT and BST single layer, respectively. Owing to the lower ε of the BST single layer than that of the BZT single layer, which can be confirmed in Fig. 8(e), the field applied on the BST sublayer in the SSZ is higher than that applied on the left two-thirds of the BST single layer, though they have the same thickness. Considering that the depletion layer is much narrower than one sublayer (∼5 μm), compared to the BST single layer, more electrons were trapped in the Au/BST interface of the SSZ, in which both a higher build-in potential (Φb + VS) and a broader depletion layer (DA-S′′) were formed, as displayed in Fig. 6(b5), resulting in a higher Eb ultimately. Besides such a field redistribution effect, for the SZS, as shown in Fig. 6(b6), the Fermi level of the SZS(EF-SZS) moves down further because of an extra BZT/BST interface. Both of these two factors have a positive synergistic effect on broadening the depletion layer of the SZS, leading to a quite high Eb value of 6.24 MV cm−1.
| | 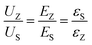 | (Eq. 2) |
To visually observe the electric breakdown process, computer simulation was applied by employing the finite element method, and the physical model is explained in the ESI.†Fig. 7(a1)–(a6) show the films' electric potential distribution. The hexagons and circles in each image represent the BZT and BST particles, respectively. The potential varies more significantly near the particles than at the matrix. Fig. 7(b1)–(b6) reflect the films' electric field distribution. Clearly, the field applied on the particles is much lower than that applied on the C8P2 matrix for all the films due to the permittivity difference, and for the multilayered ones, the BST particles suffer a higher field than the BZT particles, which is consistent with the above discussion. Because of this, not too much voltage was applied to the C8P2 matrix, contributing to the high η. Fig. 7(c1)–(c6) depicts the current density distribution of all the films under 6 MV cm−1 at over 0.01 ns after the voltage was applied. The electric breakdown occurred in all the structures except the SZS, and the result of Weibull distribution can be thus verified. Besides, in the BZT single layer, ZZS, and ZSZ, the current goes straight from the top to bottom without any obvious obstacle. In the BST and SSZ, however, the branches, which mostly happen near the BST particles, can be seen, demonstrating the better voltage endurance of the BST particles. Fig. S5† offers the current density spread at different times of all the films, in which the whole electric process can be restored.
 |
| | Fig. 7 (a1–a6) Electric potential distribution; (b1–b6) electric field distribution of all the films; (c1–c6) spread of the current density distribution of all the films under 6 MV cm−1 at over 0.01 ns after the voltage was applied. | |
 |
| | Fig. 8 (a) The P–E loop of all the films in the same electric field (3.0 MV cm−1); (b) polarization with the ESD and η of all the films at 3.0 MV cm−1, and the two dashed line and dotted dashed line represent the equivalent polarization of the multilayer-structured films in our work; a schematic of the film with the contribution of different kinds of polarization to the total polarization of (c1), (d1) ZZS; (c2) (d2) SSZ; (e) the frequency dependence of ε and tan δ of all the films. | |
At the end of this section, the author would like to give a short summary. (1) Due to the difference in the band structure, the depletion layer and barrier height in the Au/BZT and Au/BST interface are different, which is thought to be the critical factor for different Eb. (2) Higher Eb in the ZZS and ZSZ than in the BZT is mainly attributed to the moving down of the Fermi level, and the film structure does not affect it. (3) Higher Eb of the SSZ than that of the BST is due to the broadening of the depletion layer, which results from the field redistribution. For the SZS, both the field redistribution and the Fermi level's moving down synergistically led to the highest Eb among all the films. (4) The field redistribution also happens in the ZZS and the ZSZ, but because the BZT layer is much thicker than the BST in these two structures, the field decrement on the BZT layer would not have a significant effect on changing the band structure.
3.5. Discussions of the ferroelectric polarization with dielectric properties
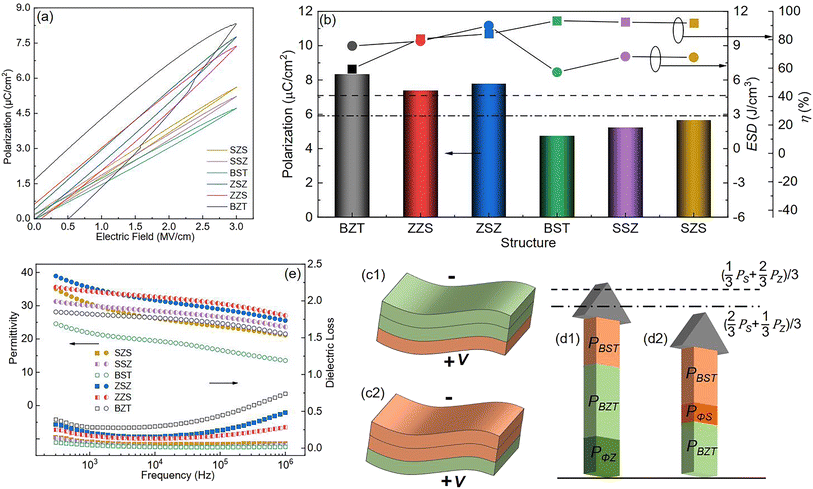
To reveal the effect of film structure on their ferroelectric polarization, the P–E loops measured under the same electric field (3 MV cm−1) of all the films are shown in Fig. 8(a). The films with thicker BZT sublayers have higher polarization but lower η than those with thicker BST sublayers. The ferroelectric polarization variation is summarized as a histogram in Fig. 8(b), and the variations in ESD and η are plotted on the top. For the multilayers in our work, their equivalent polarization should be obtained by the following formula if there is no external factor effect as follows:| | 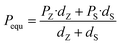 | (Eq. 3) |
where Pequ is the equivalent polarization of each multilayer, dZ, dS, and PZ, PS are the thickness of BZT, BST sublayer in the same multilayer and the polarization of BZT, BST single layer.81 Here, the polarizations of BZT and BST under 3 MV cm−1 are 8.32 μC cm−2 and 4.72 μC cm−2, respectively, so the Pequ of ZZS, ZSZ and SSZ, SZS should be 7.12 μC cm−2 and 5.92 μC cm−2, respectively, which are marked as the dashed line and the dash-dotted line in Fig. 8(b), whereas the actual polarization of both ZZS and ZSZ is larger than their Pequ, and the circumstance in SSZ and SZS is the opposite. To reveal this, we start the discussion from ZZS and SSZ, and the corresponding configurations under V are sketched in Fig. 8(c1) and (c2). As we mentioned above, in such configurations, depletion layers form in both the Au/BZT interface of ZZS and the Au/BST interface of SSZ, which inevitably increases the resistance of the BZT sublayer of the former and the BST sublayer of the latter. According to the relationship between ε and the conductivity (σ), as expressed below:| | σ = ωε0ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ | (Eq. 4) |
| | 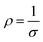 | (Eq. 5) |
where ρ is the resistivity,82,83ε is inversely proportional to ρ, meaning that compared with the BZT single layer, the BZT sublayer in ZZS has lower ε, and thus suffers a higher electric field, and then a larger polarization is triggered. The same circumstance occurs in the SSZ. The extra-triggered polarizations are defined as PΦZ and PΦS, and their contribution to the total polarization is illustrated in Fig. 8(d1) and (d2). Because the BZT layer has a larger intrinsic polarization than the BST layer, such a field distribution's deviation plays a positive effect in improving the total polarization on the ZZS but a negative effect in the SSZ. As a result, the actual total polarization of the former is larger than its Pequ, and the circumstance of the latter is the opposite. PΦZ and PΦS have the same effects on ZSZ and SZS, which is the result of a higher E/E ratio in the ZSZ than in the SZS, but the polarizations of the symmetrical ones are both higher than their asymmetrical counterparts. This can be explained as follows: there is interfacial polarization between different particles near the interface in different sublayers, and such kind of polarization is strongly proportional to the number of dipoles in unit volume, according to the deduction from Eq. S19–S25.† More interfaces between different particles exist in the symmetrical structures than in the asymmetrical ones, so the ZSZ and SZS have higher polarization than ZZS and SSZ.84,85 The frequency dependence of ε and dielectric loss (tan δ) of all the films are plotted in Fig. 8(e). Generally speaking, all the films show good ε frequency stability with low tan δ from 500 Hz to 106 Hz. An interesting phenomenon is noticed that even though the symmetrical structures, which are drawn by solid symbols, possess higher ε than their corresponding asymmetrical structures, which are symbolized by the half-solid ones at low-frequency range, their frequency stability is worse. That is because the ZSZ and SZS have more dipoles than ZZS and SSZ, and such dipoles' switching cannot keep up with the applied field, thus only contributing to ε in the low-frequency range.
3.6. Results and discussions of the energy storage reliability with the charge–discharge property at room temperature
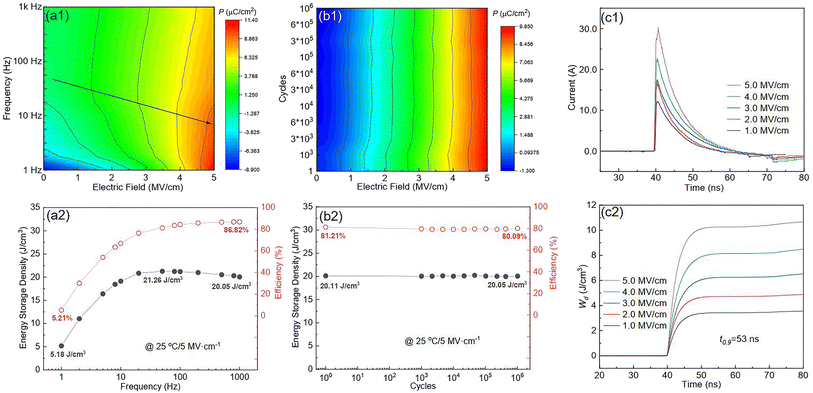
Fig. S6(a)† shows the P–E loops of the SZS measured from 1 Hz to 1000 Hz under 5 MV cm−1 at room temperature, and the polarization variation with both the electric field and frequency during the voltage ramping up is summarized in a mapping, as displayed in Fig. 9(a1). From this mapping, we can clearly see that the polarization increases faster with the increase in electric field in a lower frequency range than in a higher frequency range. Besides, we find that such curves are not monotonic when comparing the polarization at different frequencies by fixing the electric field. Due to the joint effect of electric field and frequency, the polarization peak position points from the top left to the bottom right, as marked with an arrow. The energy storage frequency stability was calculated according to the loops in Fig. S6(a)† and summarized in Fig. 9(a2). Both of these two parameters increase sharply from 1 Hz to 200 Hz; the ESD then decreases slightly in the higher frequency range while η keeps increasing. Such a phenomenon is ascribed to the relaxor-polarized dipoles in the films. Fig. S6(b)† shows the P–E loops of the SZS obtained during polarization fatigue from the 1st to 10e6th cycle. The mapping of polarization variation with both the electric field and cycling number during the voltage ramping up is displayed in Fig. 9(b1), and excellent fatigue endurance with almost no change in polarization is observed. The energy storage performance of SZS during such a process is summarized in Fig. 9(b2), and the decrement in ESD and η is only 0.3% and 1.4%, respectively. For assessing the figure-of-merits of our film in high-power application, the overdamped discharge current waveforms of SZS are plotted in Fig. 9(c1) by using the R–L–C circuit, as sketched in Fig. S7(a)† at different applied fields, and the undamped waveforms are shown in Fig. S7(b).† The current peak lies in about 40 ns without any noticeable change in the electric field. Based on this, the curves of discharge energy density (Wd) vs. time can thus be obtained and are plotted in Fig. 9(c2) using the following formula:| | 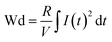 | (Eq. 6) |
where I, R, and V mean the discharge current, load resistance, and effective volume of SZS, respectively. The discharge time (t0.9), which indicates the time when 90% of stored energy has been released, is ∼53 ns, and it remains stable with the increase in field, indicating its possibility to replace the all-petroleum-based flexible dielectric capacitors.86 The Wd at 5 MV cm−1 was finally calculated to be ∼10.35 J cm−3. This value is smaller than that obtained in static P–E loop measurement due to the clamping effect on the polar regions of our film at high field frequency.87 Considering the high hydrophilicity of cellulose, which might decrease the energy storage performance of our capacitor when applied in humid environments, the environmental stability should also be characterized. Fig. S7(c)† plots the frequency dependence of the dielectric constant (ε–f) and dielectric loss (tan δ–f) of the SZS after being kept in a humid environment (RH = 70%) for different times. The ε and tan δ are both sensitive to the humid environment in lower frequency ranges, and both decrease with increasing time. Such a phenomenon is due to the presence of polar water molecules, the freeing of the polar groups, and the freeing of the ions in the fiber molecule as well as to the increase in the number of OH− and H+ ions, resulting from the ionization of water.88 Expectedly, this will also affect the SZS's energy storage performance. The P–E loops of the SZS being kept in a humid environment for different times are shown in Fig. S7(d)† with the corresponding calculated ESD and η displayed above in Fig. S7(e).† As shown, the ESD decreases from 31.07 J cm−3 to 26.15 J cm−3 with a small decrement of only 15.8%. For η, after 4 h, it decreases from 80.03% to 38.54%, with a decrement of as high as 51.8%.
 |
| | Fig. 9 (a1) Mapping for the polarization variation with both the electric field and frequency during the voltage ramping up at room temperature; (a2) variation in ESD and η with the frequency of the SZS at room temperature; (b1) mapping for the polarization variation with both the electric field and cycling number during the voltage ramping up of the SZS at room temperature; (b2) variation in ESD and η with f cycling numbers of the SZS at room temperature; (c1) overdamped discharge curves; (c2) Wd as a function of time of the SZS under different applied electric fields at room temperature. | |
3.7. Results and discussions of the energy storage thermal stability
Fig. S8(a)† plots the P–E loop of SZS measured from 25 °C to 150 °C at 5 MV cm−1, and the mapping of polarization variation with the electric field and temperature during the voltage ramping up is displayed in Fig. 10(a1). In lower fields (∼2 MV cm−1), the polarization varies significantly with the temperature, showing a decrement in temperature from 25 °C to 70 °C and then an increment with further temperature increases. As the field increases, such a variation weakens and transfers to an opposite tendency. This phenomenon can be explained as follows: In a low electric field, the polarization is dominant by the ferro-para phase transition, so the polarization–temperature relationship is similar to the ε–temperature(ε–T) curve, as shown in Fig. 10(c). The ε–T curves of all the other structures are displayed in Fig. S9.† With the increasing field, according to Eq. S25,† the polarization strongly depends on the dipole moment, so a relative polarization-thermal stability is observed. The effect of dipoles, in this case, is thought to be the space charges between ferroelectric and paraelectric phases in ceramic powders, as reported in our previous study.84 When the applied field is further increased, the polarization increases faster with the increase in temperature from 25 °C to 70 °C and decreases again from 70 °C to 150 °C. That is because the above-mentioned space charge-related dipoles are thermally activated and enhance the polarization during the former temperature range.89 The ceramic powders are in a paraelectric phase in the latter temperature range, so the polarization decreases. The discussion above illustrates the variation in ESD and η with temperature, as shown in Fig. 10(a2). To know more about the conducting behavior variation with the increase in temperature of the SZS, the J–E curves from room temperature (∼25 °C) to 150 °C were measured, and are displayed in Fig. S10.† From the fitting result, as shown in Fig. 10(d), the SZS show the Schottky emission mode during the whole temperature range, which means that increasing temperature from room temperature to 150 °C does not change its conducting mechanism. In the same electric field, the current only increases a little bit with the increase in temperature. All these conducting behaviors are mainly attributed to the good insulating property and thermal stability of cellulose, as we mentioned before. Fig. S8(b)† displays all the P–E loops obtained during polarization fatigue from the 1st to 10e6th cycle at 150 °C of the SZS, and the relative mapping and energy storage parameters are shown in Fig. 10(b1) and (b2), respectively. Surprisingly, the SZS also has good polarization fatigue without noticeable degradation under such harsh working conditions, revealing its high reliability in energy storage properties.
 |
| | Fig. 10 (a1) Mapping for the polarization variation with both the electric field and temperature during the voltage ramping up; (a2) variation in ESD and η with the temperature of the SZS from room temperature to 150 °C; (b1) mapping for the polarization variation with both the electric field cycling number during the voltage ramping up at 150 °C; (b2) variation in ESD and η with both the electric field and cycling number during the voltage ramping up of the SZS at 150 °C; (c) the temperature dependence of ε and tan δ of the SZS; (d) the fitting result of Fig. S10.† | |
4. Conclusions
By changing the fillers of BZT and BST in different sublayers, the cellulose-based flexible dielectric multilayers of different structures were fabricated via tape-casting technology. After a combination of characterizations on phase, functional group, and microstructure, the existence of a hydrogen bond network, which is thought to be the reason for its good mechanical properties among cellulose, PVDF, and ceramic particles, was confirmed. The result of J–E curves told us that the conduction mode of all films obeys the typical Schottky emission. When considering the C8P2 matrix and ceramic fillers in each sublayer as a whole, the band theory was successfully utilized to reveal the essential reason for the variation between the Eb and film structure. Due to the synergistic effect of field redistribution and the Fermi level's moving down, the highest Eb of 6.24 MV cm−1 was obtained in the SZS with the ESD and η of 31.07 J cm−3 and 80.03%, respectively, which are the best energy storage properties in cellulose-based dielectric capacitors to the authors' knowledge. Besides, the ZSZ exhibits a lower ESD of only 25.30 J cm−3 but the highest E/E ratio of 5.57 among all the films, which has also been dug out to be caused by the field distribution's deviation. Through a comprehensive characterization of energy storage reliability, the SZS exhibits very optimistic fatigue endurance at both room temperature and 150 °C with almost no decrement in ESD nor η. By illustrating a polarization mapping, at last, the polarization variation tendency was revealed to be caused by the co-effect of fillers' ferro-para phase transition and thermal-activated space charge polarization. In summary, our work offered an essential theoretical basis for preparing high-performance flexible dielectric energy storage capacitors with low energy consumption. More importantly, cellulose indeed can replace the PVDF-based polymers in the field of dielectric functional materials.
Author contributions
Zixiong Sun: conceptualization, methodology, writing-reviewing and editing, supervision, funding acquisition. Hansong Wei: data curation, formal analysis. Shibo Zhao: formal analysis. Qing Guo: data curation. Yuhan Bai: data curation. Siting Wang: formal analysis. Peiyao Sun: data curation, formal analysis. Kang Du: XRD refinement analysis. Ye Tian: writing-reviewing and editing. Xiaohua Zhang: writing-reviewing and editing. Hongmei Jing: writing-reviewing and editing. Sufeng Zhang: funding acquisition, supervision. Yongping Pu: funding acquisition, supervision.
Conflicts of interest
The authors declared that they have no conflicts of interest in this work.
Acknowledgements
Dr Z. Sun thanks S. Yin for the cover image design, and thanks N. Wei for the contribution to the revised manuscript. This work was financed by the National Natural Science Foundation of China (52002234, 22078187), the International Joint Research Center for Biomass Chemistry and Materials, Shaanxi international science and technology cooperation base (2018GHJD-19), Shaanxi key industry innovation chain projects (2020ZDLGY11-03), China-CEEC University Joint Education Project (2021099), the Open Foundation of Key Laboratory of Auxiliary Chemistry and Technology for Chemical Industry, Ministry of Education, Shaanxi University of Science and Technology (No. KFKT2021-09), and Shaanxi Collaborative Innovation Center of Industrial Auxiliary Chemistry and Technology, Shaanxi University of Science and Technology (No. KFKT2021-09).
References
- J. Ping, Q. Feng, Y. Zhang, X. Wang, L. Huang, S. Zhong and Z. Dang, Nano-Micro Lett., 2023, 15, 154 CrossRef CAS PubMed.
- P. Martins, A. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706 CrossRef CAS.
- M. Guo, J. Jiang, Z. Shen, Y. Lin, C. Nan and Y. Shen, Mater. Today, 2019, 29, 49–67 CrossRef CAS.
- Z. Sun, Z. Wang, Y. Tian, G. Wang, W. Wang, M. Yang, X. Wang, F. Zhang and Y. Pu, Adv. Electron. Mater., 2020, 6, 1900698 CrossRef CAS.
- Y. Qiao, X. Yin, T. Zhu, H. Li and C. Tang, Prog. Polym. Sci., 2018, 80, 153–162 CrossRef CAS.
- Y. Zhu, P. Jiang, Z. Zhang and X. Huang, Chin. Chem. Lett., 2017, 28, 2027–2035 CrossRef CAS.
- X. Hu, K. Yi, J. Liu and B. Chu, Energy Technol., 2018, 6, 849–864 CrossRef CAS.
- Z. Sun, Y. Bai, J. Liu, G. Jian, C. Guo, L. Zhang and Y. Pu, J. Alloys Compd., 2022, 909, 164735 CrossRef CAS.
- F. R. Fan, W. Tang and Z. L. Wang, Adv. Mater., 2016, 28, 4283–4305 CrossRef CAS PubMed.
- B. Stadlober, M. Zirkl and M. Irimia-Vladu, Chem. Soc. Rev., 2019, 48, 1787–1825 RSC.
- Y. Su, C. Chen, H. Pan, Y. Yang, G. Chen, X. Zhao, W. Li, Q. Gong, G. Xie and Y. Zhou, Adv. Funct. Mater., 2021, 31, 2010962 CrossRef CAS.
- D. Hu, M. Yao, Y. Fan, C. Ma, M. Fan and M. Liu, Nano Energy, 2019, 55, 288–304 CrossRef CAS.
- Y. Song, Z. Shi, G. Hu, C. Xiong, A. Isogai and Q. Yang, J. Mater. Chem. A, 2021, 9, 1910–1937 RSC.
- M. Zhang, H. Du, K. Liu, S. Nie, T. Xu, X. Zhang and C. Si, Adv. Compos. Hybrid Mater., 2021, 4, 865–884 CrossRef CAS.
- H. Shen, S. Peng, Q. Luo, J. Zhou, J. H. He, G. Zhou and X. Xu, Adv. Funct. Mater., 2023, 33, 2213820 CrossRef CAS.
- D. Zhao, Y. Zhu, W. Cheng, W. Chen, Y. Wu and H. Yu, Adv. Mater., 2021, 33, 2000619 CrossRef CAS PubMed.
- X. Zeng, L. Deng, Y. Yao, R. Sun, J. Xu and C. Wong, J. Mater. Chem. C, 2016, 4, 6037–6044 RSC.
- G. Du, J. Wang, Y. Liu, J. Yuan, T. Liu, C. Cai, B. Luo, S. Zhu, Z. Wei and S. Wang, Advanced Science, 2023, 10, 2206243 CrossRef CAS PubMed.
- B. Medronho, A. Romano, M. G. Miguel, L. Stigsson and B. Lindman, Cellulose, 2012, 19, 581–587 CrossRef CAS.
- F. Eiichi, J. Phys. Soc. Jpn., 1955, 10, 149–154 CrossRef.
- Z. Sun, J. Liu, H. Wei, Q. Guo, Y. Bai, S. Zhao, S. Wang, L. Li, Y. Zhang, Y. Tian, X. Zhang, H. Jing, Y. Pu and S. Zhang, J. Mater. Chem. A, 2023, 11, 20089–20101 RSC.
- M. Bisvvas and S. K. Das, Polymer, 1982, 23, 1713–1726 CrossRef.
- K. Shi, X. Huang, B. Sun, Z. Wu, J. He and P. Jiang, Nano Energy, 2019, 57, 450–458 CrossRef CAS.
- Y. Yin, J. He, C. Zhang, J. Chen, J. Wu, Z. Shi, C. Xiong and Q. Yang, Cellulose, 2021, 28, 1541–1553 CrossRef CAS.
- P. Wang, Y. Yin, L. Fang, J. He, Y. Wang, H. Cai, Q. Yang, Z. Shi and C. Xiong, Composites, Part A, 2023, 164, 107325 CrossRef CAS.
- C. Zhang, Y. Yin, Q. Yang, Z. Shi, G. Hu and C. Xiong, ACS Sustainable Chem. Eng., 2019, 7, 10641–10648 CrossRef CAS.
- J. He, Y. Yin, M. Xu, P. Wang, Z. Yang, Q. Yang, Z. Shi and C. Xiong, ACS Appl. Energy Mater., 2021, 4, 8150–8157 CrossRef CAS.
- X. Zheng, Y. Yin, P. Wang, C. Sun, Q. Yang, Z. Shi and C. Xiong, Int. J. Biol. Macromol., 2023, 125220 CrossRef CAS.
- Y. Yin, C. Zhang, W. Yu, G. Kang, Q. Yang, Z. Shi and C. Xiong, Energy Storage Mater., 2020, 26, 105–111 CrossRef.
- L. Wu, J. Zhao, Z. Li, Y. Zhai, Y. Zhang, Q. Zhen, Y. Cheng, X. Ding, P. Li and J. Liu, J. Mater. Chem. C, 2022, 10, 15416–15423 RSC.
- Y. Yin, C. Zhang, J. Chen, W. Yu, Z. Shi, C. Xiong and Q. Yang, Carbohydr. Polym., 2020, 249, 116883 CrossRef CAS PubMed.
- J. Lao, H. Xie, Z. Shi, G. Li, B. Li, G. Hu, Q. Yang and C. Xiong, ACS Sustainable Chem. Eng., 2018, 6, 7151–7158 CrossRef CAS.
- C. Zhang, R. Cha, P. Zhang, H. Luo and X. Jiang, Chem. Eng. J., 2022, 430, 132562 CrossRef CAS.
- C. Tang, R. Chen, J. Zhang, X. Peng, B. Chen and L. Zhang, Iet Nanodielectrics, 2022, 5, 63–84 CrossRef.
- S. Zhang, J. Liu, Q. Guo, N. Wei, Y. Ning, Y. Bai, Y. Tian, T. Wang, Z. Sun and Y. Pu, Composites, Part A, 2023, 165, 107329 CrossRef CAS.
- X. Zhang, J. Feng, X. Liu and J. Zhu, Carbohydr. Polym., 2012, 89, 67–71 CrossRef CAS PubMed.
- M. Singh, B. C. Yadav, A. Ranjan, M. Kaur and S. K. Gupta, Sens. Actuators, B, 2017, 241, 1170–1178 CrossRef CAS.
- T. T. M. Phan, N. C. Chu, V. B. Luu, H. Xuan, D. T. Pham, I. Martin and P. Carrière, J. Sci.: Adv. Mater. Devices, 2016, 1, 90–97 Search PubMed.
- T. He, X. Li, Q. Wang, Y. Zhou, X. Wang, Z. Wang, N. Tavajohi and Z. Cui, Appl. Water Sci., 2022, 12, 42 CrossRef CAS.
- W. Chen, H. He, H. Zhu, M. Cheng, Y. Li and S. Wang, Polymers, 2018, 10, 592 CrossRef PubMed.
- L. Ruan, X. Yao, Y. Chang, L. Zhou, G. Qin and X. Zhang, Polymers, 2018, 10, 228 CrossRef PubMed.
- P. Viswanath and M. Yoshimura, SN Appl. Sci., 2020, 1, 1519 CrossRef.
- A. M. Biyogo, L. Hespel, V. Humblot, L. Lebrun and F. Estour, Eur. Polym. J., 2020, 135, 109866 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- S. Y. Fu, X. Q. Feng, B. Lauke and Y. W. Mai, Composites, Part B, 2008, 39, 933–961 CrossRef.
- Y. C. Chen, H. C. Lin and Y. D. Lee, J. Polym. Res., 2003, 10, 247–258 CrossRef CAS.
- J. Hu, T. Zhang, L. Wang, Z. Shi and H. Xia, ACS Appl. Mater. Interfaces, 2023, 15, 12315–12326 CrossRef CAS.
- Y. Yin, J. He, C. Zhang, J. Chen, J. Wu, Z. Shi, C. Xiong and Q. Yang, Cellulose, 2021, 28, 1541–1553 CrossRef CAS.
- S. Chun, S. Lee, G. Doh, S. Lee and J. Kim, J. Ind. Eng. Chem., 2011, 17, 521–526 CrossRef CAS.
- Q. Wang, H. Du, F. Zhang, Y. Zhang, M. Wu, G. Yu, C. Liu, B. Li and H. Peng, J. Mater. Chem. A, 2018, 6, 13021–13030 RSC.
- X. Liu, J. Pang, X. Zhang, Y. Wu and R. Sun, Cellulose, 2013, 20, 1391–1399 CrossRef CAS.
- H. Lu, C. Wilkie, M. Ding and L. Song, Polym. Degrad. Stab., 2011, 96, 1219–1224 CrossRef CAS.
- J. Leitner, B. Hinterstoisser, M. Wastyn, J. Keckes and W. Gindl, Cellulose, 2007, 14, 419–425 CrossRef CAS.
- T. Lu, M. Jiang, Z. Jiang, D. Hui, Z. Wang and Z. Zhou, Composites, Part B, 2013, 51, 28–34 CrossRef CAS.
- A. Srivastava, K. Kumar Jana, P. Maiti, D. Kumar and O. Parkash, Mater. Res. Bull., 2014, 93, 83–89 CAS.
- J. Li, J. Sun, L. Ren, T. Lei, J. Li, J. Jin, S. Luo, S. Qin, C. Gao and T. Lei, Polym. Compos., 2023, 44, 7499–7509 CrossRef CAS.
- E. Barnes, J. Jefcoat, E. M. Alberts, M. McKechnie, H. R. Peel, J. P. Buchanan, C. A. W. Jr, K. L. Klaus, L. C. Mimun and C. M. Warner, Polymers, 2019, 11, 1091 CrossRef CAS.
- Y. Zhai, N. Wang, X. Mao, Y. Si, J. Yu, S. Al-Deyab, M. El-Newehy and B. Ding, J. Mater. Chem. A, 2014, 2, 14511–14518 RSC.
- W. Li, J. Tang and B. Li, J. Inorg. Organomet. Polym. Mater., 2013, 23, 831–838 CrossRef CAS.
- D. Durán-Rey, R. Brito-Pereira, C. Ribeiro, S. Ribeiro, J. A. Sánchez-Margallo, V. Crisóstomo, I. Irastorza, U. Silván, S. Lanceros-Méndez and F. M. Sánchez-Margallo, Front. bioeng. biotechnol., 2022, 10, 1044667 CrossRef PubMed.
- A. Islam, A. N. Khan, M. F. Shakir and K. Islam, Mater. Res. Express, 2019, 7, 015017 CrossRef.
- F. Kong, M. Chang and Z. Wang, Polymers, 2020, 12, 146 CrossRef CAS PubMed.
- E. Fukada, J. Phys. Soc. Jpn., 1955, 10, 149–154 CrossRef.
- S. Goodman, J. Che, W. Neri, J. Yuan and A. Dichiara, Energy Storage Mater., 2022, 48, 497–506 CrossRef.
- J. Bao, J. Lao, Y. Hu, Y. Song, M. Xu, F. Niu, Q. Yang, C. Xiong and Z. Shi, Cellulose, 2023, 30, 5259–5271 CrossRef CAS.
- J. Lao, H. Xie, Z. Shi, G. Li, B. Li, G. Hu, Q. Yang and C. Xiong, ACS Sustain. Chem. Eng., 2018, 6, 7051–7058 Search PubMed.
- H. Luo, D. Zhang, L. Wang, C. Chen, J. Zhou and K. Zhou, RSC Adv., 2015, 5, 52809–52816 RSC.
- S. Liu, S. Xue, S. Xiu, B. Shen and J. Zhai, Sci. Rep., 2016, 6, 26198 CrossRef CAS PubMed.
- P. Jusner, E. Schwaiger, A. Potthast and T. Rosenau, Carbohydr. Polym., 2021, 252, 117196 CrossRef CAS PubMed.
- J. Huang, Y. Zhou, L. Dong, Z. Zhou and R. Liu, Compos. Sci. Technol., 2017, 138, 40–48 CrossRef CAS.
- F. C. Chiu, Adv. Mater. Sci. Eng., 2014, 2014, 578168 Search PubMed.
- J. Dong, L. Li, P. Qiu, Y. Pan, Y. Niu, L. Sun, Z. Pan, Y. Liu, L. Tan, X. Xu, C. Xu, G. Luo, Q. Wang and H. Wang, Adv. Mater., 2023, 35, 2211487 CrossRef CAS.
- C. Yuan, Y. Zhou, Y. Zhu, J. Liang, S. Wang, S. Peng, Y. Li, S. Cheng, M. Yang, J. Hu, B. Zhang, R. Zeng, J. He and Q. Li, Nat. Commun., 2020, 11, 3919 CrossRef CAS PubMed.
- R. Chikkonda, A. Ravindran, S. Saikia, A. R. T. Sathyanathan, A. Chelvane, A. Subramanian, J. R. K. Chinnayya and R. B. Gangineni, J. Appl. Polym. Sci., 2021, 138, e50018 CrossRef.
- M. Kumar, D. G. Georgiadou, A. Seitkhan, K. Loganathan, E. Yengel, H. Faber, D. Naphade, A. Basu, T. D. Anthopoulos and K. Asadi, Adv. Electron. Mater., 2020, 6, 1901091 CrossRef CAS.
- R. Pontoh, V. E. Rarisavitri, C. C. Yang, M. F. Pura and D. S. B. Anugrah, Indones. J. Chem., 2022, 22, 253–262 CrossRef CAS.
- T. Schulmeyer, S. A. Paniagua, P. A. Veneman, S. C. Jones, P. J. Hotchkiss, A. Mudalige, J. E. Pemberton, S. R. Marder and N. R. Armstrong, J. Mater. Chem., 2007, 17, 4563–4570 RSC.
- M. Vagadia, A. Ravalia, P. S. Solanki, P. Pandey, K. Asokan and D. G. Kuberkar, AIP Adv., 2014, 4, 057131 CrossRef.
- J. Robertson, J. Vac. Sci. Technol. B, 2000, 18, 1785–1791 CrossRef CAS.
- S. Zhang, H. Wei, Q. Guo, J. Liu, N. Wei, Y. Bai, P. Sun, L. Li, Y. Zhang, Y. Tian, X. Zhang, Z. Sun and Y. Pu, Appl. Surf. Sci., 2023, 15, 158363 CrossRef.
- M. D. Nguyen, Y. A. Birkhölzer, E. P. Houwman, G. Koster and G. Rijnders, Adv. Energy Mater., 2022, 12, 2200517 CrossRef CAS.
- P. Shaikh, D. Shi, J. Retamal, A. Sheikh, Md. A. Haque, C. Kang, H. He, O. Bakr and T. Wu, J. Mater. Chem. C, 2016, 4, 8304–8312 RSC.
- A. B. Uluşan and A. Tataroğlu, Silicon, 2018, 10, 2071–2077 CrossRef.
- Z. Sun, Y. Bai, T. Ouyang, Q. Guo, Y. Ning, J. Liu, K. Du, H. Jing, Y. Tian and Y. Pu, Appl. Phys. Lett., 2023, 122, 263904 CrossRef CAS.
- Z. Sun, L. Wang, M. Liu, C. Ma, Z. Liang, Q. Fan, L. Lu, X. Lou, H. Wang and C. Jia, J. Mater. Chem. A, 2018, 6, 1858–1864 RSC.
- Y. Chen, Y. Yue, J. Liu, J. Shu, A. Liu, B. Chu, M. Xu, W. Xu, T. Chen, J. Zhang and Q. Shen, Phys. Chem. Chem. Phys., 2019, 21, 20661–20671 RSC.
- L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J. Li and S. Zhang, Prog. Mater. Sci., 2019, 102, 72–108 CrossRef CAS.
- S. Boutros and A. A. Hanna, J. Polym. Sci., Polym. Chem. Ed., 1978, 16, 89–94 CrossRef CAS.
- O. Fliunt, Appl. Nanosci., 2023, 13, 5303–5311 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *abcde,
Hansong
Wei
b,
Shibo
Zhao
a,
Qing
Guo
a,
Yuhan
Bai
a,
Siting
Wang
a,
Peiyao
Sun
f,
Kang
Du
g,
Yating
Ning
h,
Ye
Tian
*abcde,
Hansong
Wei
b,
Shibo
Zhao
a,
Qing
Guo
a,
Yuhan
Bai
a,
Siting
Wang
a,
Peiyao
Sun
f,
Kang
Du
g,
Yating
Ning
h,
Ye
Tian
 h,
Xiaohua
Zhang
h,
Hongmei
Jing
i,
Yongping
Pu
h and
Sufeng
Zhang
*b
h,
Xiaohua
Zhang
h,
Hongmei
Jing
i,
Yongping
Pu
h and
Sufeng
Zhang
*b


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of the glucose units in cellulose chains.40 The broad peak around 3500 cm−1, which cannot be detected in ceramic powders, corresponds to the stretching vibration of hydroxyl in the C8P2 matrix, which also demonstrates the formation of hydrogen bond network among cellulose, PVDF, and ceramic particles during the dissolution-regeneration process as sketched in Fig. 1(a). Such a hydrogen network guarantees the successful preparation of a multilayered structure of our films, as we explained in previous work.21
O stretching vibration of the glucose units in cellulose chains.40 The broad peak around 3500 cm−1, which cannot be detected in ceramic powders, corresponds to the stretching vibration of hydroxyl in the C8P2 matrix, which also demonstrates the formation of hydrogen bond network among cellulose, PVDF, and ceramic particles during the dissolution-regeneration process as sketched in Fig. 1(a). Such a hydrogen network guarantees the successful preparation of a multilayered structure of our films, as we explained in previous work.21
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C in PVDF and cellulose, C–OH in the hydroxy group of cellulose, and C–O–C in the glucose unit of cellulose, respectively, and not much difference can be distinguished here. The most significant difference between these two films comes from the F 1s spectra, as shown in Fig. S1(c3).† Only one peak at ∼687.0 eV, which corresponds to F–C–F in PVDF can be detected in the C8P2 matrix, while an extra peak at ∼683.8 eV is observed in the SZS. Such a new peak has been confirmed to be related to induced F–C–H in the interface between the fillers and the PVDF.42,43Fig. 3(d1) and (e1) are the TEM images of single BZT and BST particles embedded in the SZS. Clearly, the former indeed has a hexagonal shape, while the latter has a spherical-like one, and BST exhibits a larger particle size. Fig. 3(d2) and (e2) are the enlarged view of the red dashed rectangle areas in Fig. 3(d1) and (e1), respectively, with the observation of clear lattice fringes. After calibrating, the crystal axis was confirmed, and the lattice parameters fit very well with the result of Rietveld refinement. Fig. 3(d3) and (e3) give the ball-stick models of the unit cell of BZT and BST particles drawn from the XRD refinement result using VESTA.44
C in PVDF and cellulose, C–OH in the hydroxy group of cellulose, and C–O–C in the glucose unit of cellulose, respectively, and not much difference can be distinguished here. The most significant difference between these two films comes from the F 1s spectra, as shown in Fig. S1(c3).† Only one peak at ∼687.0 eV, which corresponds to F–C–F in PVDF can be detected in the C8P2 matrix, while an extra peak at ∼683.8 eV is observed in the SZS. Such a new peak has been confirmed to be related to induced F–C–H in the interface between the fillers and the PVDF.42,43Fig. 3(d1) and (e1) are the TEM images of single BZT and BST particles embedded in the SZS. Clearly, the former indeed has a hexagonal shape, while the latter has a spherical-like one, and BST exhibits a larger particle size. Fig. 3(d2) and (e2) are the enlarged view of the red dashed rectangle areas in Fig. 3(d1) and (e1), respectively, with the observation of clear lattice fringes. After calibrating, the crystal axis was confirmed, and the lattice parameters fit very well with the result of Rietveld refinement. Fig. 3(d3) and (e3) give the ball-stick models of the unit cell of BZT and BST particles drawn from the XRD refinement result using VESTA.44
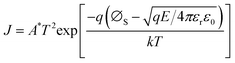

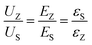
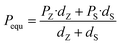
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ
δ