Application of large datasets to assess trends in the stability of perovskite photovoltaics through machine learning

Abstract

Current trends in manufacturing indicate that optimised decision making using new state-of-the-art machine learning (ML) technologies will be used. ML is a versatile technique that rapidly and accurately generates new insights from multifactorial data. The ML approach has been applied to a perovskite solar cell (PSC) database to elucidate trends in stability and forecast the stability of new configurations. A database consisting of 6038 entries of device characteristics, performance, and stability data was utilised, and a sequential minimal optimisation regression (SMOreg) model was employed to determine the most influential factors governing solar cell stability. When considering sub-sections of data, it was found that pin-device architectures provided the best model fittings with a training correlation efficiency of 0.963, compared to 0.699 for all device architectures. By establishing models for each PSC architecture, the analysis allows the identification of materials that can lead to improvements in stability. This paper also attempts to summarise some key challenges and trends in the current research methodologies.

---

Introduction

The necessity for the widespread adoption of solar energy has become increasingly pressing as the demand for renewable energy sources continues to rise. For deployment on a global scale, improvements in the properties and economic feasibility of the materials and fabrication methods employed in these devices are required. This will allow for an increase in the performance of solar cells and a reduction in production costs, providing a significant step forward in realising the full potential of solar energy.¹

PSCs are among the most intensely researched thin-film photovoltaic devices and have experienced rapid improvements in stability and efficiency.² Over the past decade, the efficiency of PSCs has increased from 3.8% to 25.8% for single-junction cells and from 33.2% for tandem cells, making them a promising option for large-scale deployment.³ Despite this rapid progress, the instability of perovskites under different environmental conditions remains a significant challenge for their commercialisation.⁴ As a result, extensive research has been conducted to identify patterns, critical factors, and trends in the properties and fabrication methods of PSCs to improve their stability and efficiency. The amount of data generated from this research has become vast, but much of it remains inaccessible owing to its complexity and nonuniform distribution.⁵

In light of these developments, machine learning (ML) has emerged as a popular computational method for analysing and interpreting large datasets in the field of PSCs. With quick processing, vast datasets, future predictions, and ease of incorporation, ML offers a valuable tool for uncovering patterns and relationships within complex data, leading to new insights and breakthroughs in the field.^6,7

Several studies have employed ML techniques such as decision trees (DT), random forests (RF), artificial neural networks (ANN), and gradient boosting regression (GBR) to predict material properties such as thermodynamic stability, band gap, and other PSC characteristics.⁸ For instance, Schmidt et al. used RF, ANN, and an extremely randomised tree (ERT) for thermodynamic stability prediction,⁹ and Allam et al. utilised an ANN to predict the bandgap of PSCs by analysing 220 cells with desirable radiation tolerance and octahedral factors.¹⁰ In addition, Jain et al. proposed an ML-based classification model utilising a support vector machine (SVM) approach to predict the formability of 454 ABX3 perovskite compositions. The model was trained on data from 189 inorganic ABX3 perovskite samples with a formation probability of 0.8 or higher for 45 compounds. The thermodynamic stability of the perovskites was compared in the materials project (MP), AFLOW, and OQMD, leading to the identification of 18 compounds for further investigation using DFT-based structural optimisation and electronic structure predictions. In terms of device performance, Odabaşi et al. employed descriptive statistics to examine the trends in perovskite solar cell performance using DT and RF algorithms. They identified the parameters that must be satisfied for highly efficient solar cells.¹¹ While continued advancements in ML algorithms, computer hardware, data management systems, and material science are expected to drive further growth in the study of PSCs, there are also challenges to the use of ML in this field. One of the main challenges is the limited availability of experimental and accurate datasets owing to the high cost and time required to collect such data. Additionally, models trained on small datasets may not be robust or generalisable, due to issues such as noise, outliers, and unbalanced data structures. To overcome these challenges, researchers will most likely need to refine their data collection strategies or select ML techniques that are ideally suited for small datasets, for example, through pre-processing to remove noise and outliers. ML also provides various data augmentation methods that can be used to construct more efficient, stable, and resilient PSCs.⁵

In this research, ML tools are implemented to assess the influence of materials and fabrication processes on the stability of PSCs, making use of the ‘perovskite database’ which contains stability data for 7026 devices extracted from literature data between 2012-2020, analysed and collated by Jacobsson et al.¹² This study represents one of the most rigorous literature reviews available, thereby demonstrating an invaluable resource for researchers to assess the state of PSCs as well as the ability to add to the resource through an interactive database. Our objective was to analyse the impact of various attributes on the stability of PSCs by applying data from relevant research outputs to multiple ML techniques. Through this process, we aim to enhance the understanding of PSCs as a source of energy harvesting and to identify trends in device stability based on various design architectures. Our results provide valuable insights into the stability of PSCs and hold promise for the development of new cell combinations with higher stability and efficiency. Furthermore, the ML approaches implemented in our study can be ranked to determine which is ideally suited to a given problem and dataset.

Methodology

This study emphasises maintaining data consistency, utilising the ‘OSEMN’ (Obtain, Scrub, Explore, Model, Interpret) method.^13,14 The initial stage of ‘obtain and scrub’ involves data collection and conversion into a format that is appropriate for utilisation by ML algorithms. To optimise the data analysis, we focused on specific areas of the dataset. This allowed us to extract the maximum information from relevant attributes without overwhelming the processing capacity. We further examined the attributes related to the construction and stability of PSCs and identified their impact on the final performance and stability. The original dataset consists of 45 attributes and 7025 instances. In this study, key attributes, such as cell architecture, substrate type, electrode type, transport layers, and perovskite compositions, were examined. Furthermore, measurement conditions, including bias conditions, test protocols, encapsulation, and light sources, are taken into consideration. An exhaustive list of the factors used for the processed database is provided in SI-1.† This is a provides readers with some insight into data labelling. The largest change we applied to the dataset was removal of data where there were less than 3 instances of a particular test, as it was discovered that this added significant noise to the analysis. We screened ten attributes with multiple categories in each section, as summarised in Table 1.

Table 1 List of attributes and their variable type

S/N	Attribute	Type
1	Substrate	Categorical
2	Electrode (first electrode)	Categorical
3	Active layer (perovskite)	Categorical
4	Active layer additive	Categorical
5	p-type transport layer	Categorical
6	n-type transport layer	Categorical
7	Electrode 2 (second electrode)	Categorical
8	Cell architecture	Categorical
9	Module	Categorical
10	Stability PCE T80	Numerical

---

In addition to the categorical attributes of the PSCs, the stability and performance parameters were retrieved (power conversion efficiency (PCE) and T₈₀ lifetime). The T₈₀ lifetime quantifies the time required for the devices to degrade to 80% of the initial efficiency and is used here as the primary indicator of stability for PSCs. In some instances, the T₉₅ value is preferred over T₈₀ as a metric for assessing thermal stability in devices with enhanced reliability, but the focus of this work is on device stability. Furthermore, T_S80 might be a more relevant metric for measuring the time taken for the efficiency of a solar cell to drop to 80% of the stabilised performance at the end of the burn-in region.¹⁵ However, there are not enough reports on T_S80 measurements available, thus making it difficult to obtain accurate and consistent stability measurements for PSCs. Despite this, T₈₀ remains the most suitable and comprehensive metric for examining the historical data pertaining to the stability of PSCs.

Following feature selection, the ‘scrub’ stage begins to clean and filter the data for consistency and accuracy in subsequent analyses. Careful examination of the data is necessary to verify that no unanticipated values exist which might have a substantial impact on the outcome. At this point, the researcher must use judgment in determine the amount of information contained in the data and how much detail is provided to the ML algorithm. This is important for reducing noise and ultimately for deriving a more meaningful model. For instance, if the same material is recorded with different names, these quantities are categorised as distinct features and must therefore be re-classified as one instance type. In addition, data have only been used for instances in which five or more occurrences have been reported.

Apart from the inconsistent format, missing or improper data can also be present. Several techniques, such as mean values,¹⁶ multivariate chained equations,¹⁷ and k-nearest neighbours,¹⁸ can be employed to handle missing data in ML. For this work, we focused on the attributes set out in Table 1. We eliminated rows with missing numerical entries and substituted blank spaces in categorical features with “unknown” to guarantee an equal distribution of instances for every attribute. The category with the highest number of unknowns was “p-type transport layer” which had 1.5% of data points listed as “unknown”. Categorical features were also encoded to integers, and all features were scaled between 0 and 1 to prevent the model from being biased toward attributes with higher values and to ensure uniformity. We used the Waikato Environment for Knowledge Analysis (WEKA 3.8) for ML modelling, utilising the built in ref. 19. The analysis uses sequential minimal optimisation regression (SMOreg), which is an extension of the SVM algorithm applied to regression tasks. SMOreg employs Lagrange multipliers and variational calculus to assign weights to features and find the hyperplane through a dataset that minimises the error function.²⁰ We selected this algorithm because of its ability to provide a model that can be evaluated based on attribute weights, allowing us to determine the importance of each attribute. The fabrication of PSCs involves the deposition of multiple thin layers of different materials, which can be stacked in various architectures, as depicted in Fig. 1.²¹Fig. 1(a) and (b) demonstrate an n–i–p architecture in which the top metal electrode is positioned on top of the hole transport layer (HTL), which is separated from the electron transport layer (ETL) by an active perovskite layer that enables efficient transport of charge carriers. In this arrangement, light enters via the ETL, and hence, is designated as the n–i–p structure. Planar structures with a reverse transport layer configuration are designated as p–i–n. In the n–i–p configuration, TiO₂ is the most widely employed material owing to its efficiency in transferring electrons and preventing electron–hole recombination; recently, SnO₂ has also been used because of its high mobility. Most HTL and ETL materials employed in n–i–p PSCs are unsuitable for p–i–n PSCs and vice versa. This is because these two types of PSCs have distinct charge transport and recombination properties.²² Thus, we employed the model by considering five different testing conditions for subgroups of the data: the entire dataset; data only consisting of a regular structure (n–i–p), where the solar cell is illuminated through the ETL side; regular mesoporous structure (n–i–p-(mp)); carbon-based mesoscopic structure, represented as (n–i–p-(mp-carbon)); and finally, the data represented with an inverted structure (p–i–n), where the solar cell is illuminated through the HTL side.

Fig. 1 Device structure of (a) mesoporous (n–i–p), (b) n–i–p planar and (c) p–i–n planar PSC.²¹

However, as shown in Fig. 2(b), n–i–p, p–i–n, and n–i–p-mp exhibit similar stability responses, whereas n–i–p-mp-carbon generally exhibits the greatest stability. It is worth noting that the sample size for n–i–p-mp-carbon is significantly smaller than that of the other cell architectures; therefore, more data would be useful to fully assess the stability of this architecture. Overall, these results suggest that the type of cell architecture has a significant impact on both the efficiency and stability of PSCs.

Fig. 2 Distribution of cell architecture plotted as a function of (a) J–V reverse scan and (b) T₈₀ lifetimes. Statistical test data for these graphs is shown in SI-2.† In the case of (a), all factors are statistically significant; in the case of (b), only the “nip-mp-carbon” is statistically significant at a risk level = 0.15.

The results in Fig. 3 demonstrate the impact of different substrates and electrode materials and their correlation with the performance and stability of PSCs. As shown, devices employing SLG substrates tend to give the highest PCEs when quantified by the median value and both the upper and lower quartile values. In contrast, devices employing a PET substrate demonstrate superior stability compared to SLG, as indicated by their high median and probability density. The reason for this is a secondary effect; the SLG substrate devices correspond to small “cells” and lower technology readiness level devices, rather than manufactured modules. Most PET-based samples are likely to be modules rather than small cells, which generally show better stability as they are encapsulated. Generally, modules are always encapsulated, but they also tend to possess lower efficiency than cells.²⁰

Fig. 3 Distribution of J–V reverse scan and T₈₀ lifetimes for (a and b) substrate, (c and d) electrode, and (e and f) electrode 2, respectively, in the dataset. The numbers represent the number of samples.

Tin-doped indium oxide (ITO) and fluorine-doped tin oxide (FTO) are the most used transparent conducting oxide electrodes for PSC fabrication. However, the use of graphene as an electrode material has shown improved stability compared to other electrode types and has the potential to generate PCE values comparable to those of ITO and FTO. Metallic back contacts, specifically copper, gold, aluminum, and silver, demonstrated a higher efficiency, with values ranging between 17–19%. This contrasts with non-metallic compounds, which predominantly exhibited efficiencies below 12%. However, when considering stability as a key parameter, materials such as nickel, indium tin oxide (ITO), and carbon-based electrodes stood out, showing enhanced stability despite a trade-off in efficiency. Copper has emerged as a material that offers an optimal balance between efficiency and stability.

Fig. 4 presents the distribution of the T₈₀ lifetimes for an array of significant testing variables within the dataset: potential bias conditions, stability protocols, edge sealant types, light sources, and encapsulation stacks. In terms of potential bias, as shown in Fig. 4(a), a standout observation was the superior median stability of testing under open-circuit conditions, as demonstrated in 4988 instances. The absence of current flow in the open-circuit system could be the driving force behind this superior stability, as it eliminates potential power-flow fluctuations that might disrupt the system's equilibrium.

Fig. 4 Distribution of T₈₀ lifetimes for different attributes in the dataset for (a) potential bias conditions, (b) testing protocol for stability tests, (c) edge sealant used, (d) light source used during testing, and (e) encapsulation stack.

Maximum Power Point Tracking (MPPT) follows closely, despite being an active power management system with only 368 instances. However, it is worth adding the caveat that any measurement setup holds devices at a constant potential close to the initial maximum power point and is not updated as a function of time. However, these differences in testing methodology are rarely differentiated in the reports. The data derived from these graphs are consistent with the literature, where specific tests have been conducted to determine the impact of bias conditions.^22,23

As depicted in Fig. 4(b), dark-storage methodologies, specifically ISOS-D, exhibited consistently superior stability across the entire evaluated dataset. Among these, ISOS-D-1 testing protocols gave the highest stability measurements, demonstrating not only robust median stability, but also unique upper quartile values. This is not surprising, as the ISOS-D-1 test is a benign and ‘storage’ test. Notably, the improved performance of ISOS-D-1I, an adapted version of the ISOS-D-1 protocol, allows the cell's intrinsic properties to be carefully controlled, typically in a nitrogen environment. This strategy improved all stability parameters, highlighting the advantages of precise control over cellular conditions. Enhanced cell stability was also obtained using the light-stimulated protocol, ISOS-L-3, and IEC 61646, two techniques characterised by higher average costs and a small number of data entries. However, the observed increased stability is derived from a more restricted dataset, which frequently consists of carefully engineered devices originating from industrial establishments or major research groups.

The effects of encapsulation and edge sealants are shown in Fig. 4(c) and (e). A variety of encapsulation strategies have different impacts. Aluminium oxide (Al₂O₃) encapsulation showed some of the best stability; this is ordinarily fabricated using atomic layer deposition (ALD). It has been widely reported as a successful method for protecting against oxygen and water ingress.²⁴ Nevertheless, conventional methods such as UV-curable epoxy and SLG have been demonstrated to be quite effective based on the dataset.

Fig. 4(d) illustrates the significant variability in stability due to different light sources, a factor often omitted in many publications. A significant portion of the tests were conducted under dark conditions. Dark testing offers a straightforward and energy-efficient approach, yielding higher median stabilities compared with various lit conditions. Numerous tests have utilised indoor lighting, which lacks the full solar spectrum, particularly UV rays. This results in improved stability but potentially less representative outcomes. Halogen and metal-halide light sources led to lower stability, whereas indoor lighting generally resulted in enhanced stability. This observation aligns with expectations, as indoor lighting, which often lacks UV emissions, does not contribute to the significant degradation typically seen in PSC absorber layers due to UV exposure.^24,25

The data in Fig. 3 and 4 reveal considerable variance in device PCE and stability when individual factors are considered, indicating that pre-processed data visualisation can only uncover general trends. This strengthens the view that machine learning is vital for obtaining more precise information about how materials, device structures, and testing conditions impact stability. This also merits the decision to separate data into subgroups based on the stability measurement protocol and device architecture.

ML of PSC device using SVR algorithms

The SMOreg algorithm, which is an extension of the SVR method, was initially applied to the complete dataset to understand and predict the stability variation in PSCs, based on the dataset. The kernel was chosen in the WEKA software to be a linear function such that the SVR weights could be associated with feature importance, and attribute significance could be determined. The weights of the different categories for each feature are reported in the derived model. From previous work,²⁰ it is evident that the model can be further applied in an innovative way to predict stability and understand how stability responds to each feature. Hence, SMOreg was applied again to the four data subsets sorted according to the cell architecture. This innovative split was necessary to confirm any bias in the complete dataset and to identify how each feature affected the stability of different cell architectures. The results of this experiment are summarised in Table 2.

Table 2 Performance of SMOreg machine learning algorithm in predicting stability

Measure	Complete data		n–i–p		p–i–n		n–i–p (mp)		n–i–p (mp-carbon)-
	Training	Testing	Training	Testing	Training	Testing	Training	Testing	Training	Testing
Correlation coefficient	0.699	0.683	0.692	0.957	0.963	0.933	0.602	0.597	0.625	0.689
Relative absolute error (%)	63.39	52.25	65.74	46.16	44.42	47.37	73.21	46.27	64.50	64.39
Root relative squared error (%)	73.96	70.50	64.00	34.91	32.82	36.33	68.73	72.41	76.79	72.96
Number of instances	3421	597	1255	220	1092	188	865	151	138	22

---

When the SMOreg algorithm is used on a dataset aimed at quantifying aspects, such as stability (expressed in terms of lifetime hours) or performance (expressed as a percentage), it utilises variational calculus and Lagrange multipliers to establish a hyperplane within the N-dimensional data space. This hyperplane is defined by a linear combination of attributes of the dataset, each modulated by specific weights. It is noteworthy, as previously indicated, that these weights can be interpreted as reflecting the ‘importance' of the corresponding attribute in modelling the target parameter. By analysing the output of the algorithm, a list of all attributes along with their respective weights emerges. Organising this list using these weights helps pinpoint both the most and least impactful features.

We have applied the SMOreg algorithm because the data contained within the dataset and used for training is highly non-linear in the context of the entire dataset. This allows us to achieve higher accuracy than can be achieved with a linear model. Other techniques such as neural networks, or k-nearest neighbors could be applied to build non-linear models.

The model was trained using a ‘Remove Percent’ filter to split the datasets into training and test sets and the split was randomly allocated and repeated five times to create the average in Table 2. The ratio of the training to test splits was 85 : 15. This split enabled evaluation of the performance of the trained model on the test set. The OSEMN process was conducted for the entire dataset and separately for each subcategory of the PSC architecture. This has led to the development of optimum models using ML. Data corresponding to low PCE values were removed such that noise within the dataset was minimised; therefore, the algorithm did not overfit and make predictions based on this noise. In addition, by removing low-performance devices, the algorithm focuses primarily on identifying the materials which lead to improved performance and stability. Based on the data presented in Table 2, it can be concluded that the p–i–n architecture achieved the highest level of performance for both the training and test datasets. Conversely, the n–i–p (mp) architecture exhibited the lowest correlation coefficient, followed closely by the n–i–p (mp-carbon) architecture. The n–i–p cell architecture, on the other hand, demonstrated the second-highest correlation coefficient.

We employed the SMOreg algorithm on an entire dataset covering various cell architectures to develop a predictive model. The model features were extracted and ranked, and those with the three highest weights and three lowest weights are summarised in Table 3. The ‘highest’ weights refer to materials or process steps that have a positive impact on stability, leading to better device stability, and the ‘lowest’ weights refer to the opposite and should be designed out of PSC manufacture. In the case of ‘module’; only the ‘true’ category is present in the model and ‘false’ is excluded. In this case, the SMOreg algorithm has selected the ‘true’ category because it aids the construction of the model. However, the ‘false’ category is excluded, which is likely to be the larger variation device stability from cells so this category is not selected for the model.

Table 3 SMOreg analysis results showing the top three ‘best and worst’ instances for stability for the entire dataset

Feature	Highest		Lowest
	Category	Weight	Category	Weight
1. Substrate	SLG	0.0165	PES	−0.0108
	PEN	0.0025	Ti	0
	PET	0.0013	PI	0
2. Electrode	Ag-grid	0.0165	Ti	−0.0044
	IZO	0.0100	AZO	−0.0034
	ITO	0.0044	PEDOT:PSS	−0.0011
3. A-ions	Ag (BEA)	0.403	MA	−0.075
	MA	0.019	MA, Cs	−0.052
4. B-ions	Pb	0.0297	Sn	−0.0077
	Pb, Zn	0.0124	Sn, Ge	−0.0052
5. C-ions	Br	0.401	I	−0.0524
	Br, I	0.390	I, Br	−0.031
6. Additives	SnF2	0.092	Pb(SCN)2	−0.032
	PCP	0.086	PS	−0.021
	Rb	0.032
7. HTL	PbTiO3	0.0306	P3HT; SWCNTs	−0.4939
	ZrO2-mp	0.2466	WO3; WO3-np PEI	−0.0843
	Graphene	0.1523		−0.074
8. ETL	Al2O3-mp	0.0683	PEI	−0.0646
	C60	0.0605	TiO2-c	−0.0621
	SnO2-c	0.0588	BCP	−0.0212
9. Electrode 2	CNT	0.0190	Cu	−0.0222
	Au	0.0150	Ag–Al	−0.0210
	Carbon	0.0091	ITO	−0.0146
10. Cell architecture	p–i–n	0.0294	n–i–p-mp	−0.0093
	n–i–p (mp)-carbon	0.0103	n–i–p	−0.0030
11. Module	True	0.0408

---

The weights obtained from the SMOreg analysis helped identify several essential attributes in the dataset. As summarised in Table 3, the different factors possessed relatively different weightings, indicating that some factors were more prominent than others. Several important features can be identified from the SMOreg weights. For the entire dataset, the attributes that most positively influenced the stability were the hole transport layer (HTL) materials (Al₂O₃-mp, ZrO₂-mp, and graphene) and absorber layer ions (Ag and Br were prominent). Significantly, the most dominant negative influences also corresponded to the HTL (P3HT; SWCNTs and WO₃; WO₃-np PEI). These showed strong negative weightings, although being a mixture of electron and hole transport layers in this case. Overall, the substrate type and electrode choice had much lower values of weightings, so it is clear that the absorber and transport layers have the greatest overall impact on device stability.

The algorithm also favoured the use of the module by weighting the category ‘true’ as the highest. However, it did not provide any results for the ‘false’ category. As straightforward as the results seem, it was noticed that the SMOreg weightings for the different categories differed across various architectures. The analysis of the different architectures reported high weightings for certain materials that were not included in the results of the complete dataset. This result is understandable because, as shown in the earlier analysis, cell architectures respond differently to stability.

After deriving the results summarised in Table 3, the SMOreg stability predictions for the four subsets of data were extracted. The results are summarised in Tables 4 and 5. It was necessary to further study how each category behaved in each cell architecture.

Table 4 SMOreg results showing the optimal materials in terms of cell architecture for stability

Feature	n–i–p		p–i–n		n–i–p-mp		n–i–p-mp -carbon
	Attribute	Weight	Attribute	Weight	Attribute	Weight	Attribute	Weight
Substrate	PEN	0.0063	PEN	0.0019	PEN	0.004	—	0
	SLG	0.0010	SLG	0.0010
Electrode	Graphene	0.0130	Ag-grid	0.0055	FTO	0.0205	ITO	0.021
			Ti	0.0017	ITO	0.0861	FTO	0.002
A-ions	Cs, MA	0.1735	(BEA) MA	0.0196	Ag	0.2007	Cs, Fa	0.3674
	Cs, FA, MA, (oFPEA)	0.1458	(ThMA) MA	0.0074	Cs, Fa	0.0623	Cs	0.0417
B-ions	Pb, Zn	0.0748	Pb	0.0015	Bi	0.033	Pb	0.1598
	Bi	0.0241	Fe	0.0008	Pb	0.0275	Pb, Sn	0.0004
X-ions	Br	0.0104	Br, I	0.0014	Br, I	0.0298	Br	0.1226
			Br	0.001	Br	0.0016	Br, Cl	0.1225
Additive compounds	NaF	0.012	Cl	0.018	BEA	0.0056
	TEOS	0.008	CEA	0.010	CEA	0.0090
	KI	0.008
HTL	pBBTa-BDT2	0.6535	NiO-c	0.24	ZnPC NiO	0.0262	WO3	0.152
	MoO3	0.0305	NiMgLiO	0.0111	2TPA-4-DP	0.019	ZTO	0.0085
	NiO(np)	0.0065	PTAA	0.0111	YT1	0.019
ETL	Graphene	0.5430	TiO2-np	0.3435	ZnO	0.0145	Al2O3-mp	0.0102
	C60	0.0876	TPD	0.256	Al2O3-mp	0.0112	ZrO2-mp	0.1451
	SnOx	0.0421	SnO2-c	0.0892	Graphene oxide	0.0266
Electrode 2	Carbon	0.0105	Au	0.0392	MWCNTs	0.0234	—	—
	Au	0.0015	Al	0.0302	Au	0.0082
Module	—	—	True	0.0053	True	0.012	True	0.0106

---

Table 5 SMOreg results showing the lowest performing materials in terms of cell architecture for stability

Feature	n–i–p		p–i–n		n–i–p (mp)		n–i–p (mp-carbon)
	Attribute	Weight	Attribute	Weight	Attribute	Weight	Attribute	Weight
Substrate	Ti	−0.0084	PET	−0.0018	SLG	−0.001	—	0
	PET	−0.0033	SLG	−0.0017
Electrode	AZO	−0.0071	Ag-grid	0.0085	ITO	−0.004	ITO	−0.024
	PEDOT:PSS	−0.0035	Ti	0.0028
Electrode	Ni	−0.0051	Ag-np	−0.0108	AgNW	−0.0082	—	—
	Ag-NW	−0.0032	PEDOT:PSS	−0.0035	Al	−0.075
A-ions	MA	−0.1306	(3AMP) FA, MA	−0.0076	GU, MA	−0.0425	Ma	0.2076
	Cs, FA, MA, BA	−0.0518	MA	−0.0054	(PEA) MA	−0.0413	Fa, Ma	0.0316
B-ions	Pb, Sn	−0.0509	Sn	−0.0012	Sn	−0.0206
	Ba, Pb	−0.153	Sn, Ge	−0.0012	Eu,Pb	−0.0111
X-ions	I, Br	−0.0435			I, Br	−0.0134	I, Br	0.207
	I	−0.1044			I	−0.0128	I	0.1361
Additives			I	−0.016	RbI	−0.047	Pb(SCN)2	−0.036
					Pb(SCN)2	−0.004
HTL	MoO3 p-DTS(FBTTh2)2	−0.0064	CuSCN	−0.0113	CuO	−0.0105
	Cu2O	−0.0122	PEI	−0.0105	Spiro-MeOTAD	−0.0019
		−0.0081	PEDOT:PSS	−0.0094
ETL	C60-SAM	−0.0198	Bphen	−0.0103	ZrO2-mp	−0.0134	Al2O3-mp	−0.0306
	PCBM-60	−0.0056	Ca	−0.0092	ZnO-np	−0.0108	SnO2-np	−0.0021
			LiF	−0.0054	SrTiO3	−0.0025
Electrode 2	ITO	−0.0102	Sb	−0.2904	Graphene	−0.0147	Graphite	−0.0114
	Al	−0.0033	Cu	−0.0035	Pt	−0.0102
Module	True	−0.0145	False	−0.0016	—	—	False	−0.0031

---

When considering the data subsets, it was noticed that the categories with the most significant positive influence were generally the A-ion, HTL, and ETL selections, similar to the results for the complete dataset. This pattern was also repeated in the negatively weighted categories, as most of the negatively influential materials also fell within the transport layers. This is also observed in the ranking of the attribute weights, which provides confidence in our approach of using the SMOreg algorithm to evaluate how the attributes affect stability. When considering the data, it was clear which factors had the greatest effect. Based upon this work, a sensible experimental strategy would be to use this analysis to identify high performing HTL, ETL and A-ions.

Implications for experiment and design

The focus of this work has been on obtaining greater insight and elucidating trends within the ‘perovskite database’. However, it is vital that the ML approaches employed are continued to be used to inform future experimental design. To achieve this, the analysis provided in the previous sections should be considered, along with an understanding of the boundaries and limitations of this study.

ML relies heavily on having a sufficient quantity and diversity of information to provide an accurate prediction of device stability and the ‘perovskite database’ does provide this. However, developing a model that can describe stability with all data present was not possible, and one must question why this is. Data demonstrating low efficiency and stability had to be removed to minimise the noise within the dataset. Ordinarily positive and negative results from stability tests should be considered equally important for ML, but our work found that the algorithm does overfit and make predictions based on the low performing ‘noise’. The consequence of this noise is that the model is disproportionately biased towards low-performing devices and is unable to identify the role of higher-performing devices, which do not play a significant role in overarching data distribution. This initially leads to low correlation coefficients since no clear data structure can be discerned. Secondly, this results in misleading findings when analysing the model weights, where an excess of attributes corresponding to low-performance results are highlighted. If the objective of the study were to identify the role of all attributes, whether they contribute to deteriorating or improving device performance, then low-performance devices could also be considered. However, since the aim of this study is to model high-performance devices and pinpoint materials that can enhance device functionality, low-performance devices are excluded. In addition, by removing low-performance devices, the algorithm focuses primarily on identifying the materials which lead to improved performance and stability. Furthermore, the number of materials in each layer that has been tested in the literature is relatively high, thus the possible stack combination is large. During the first stage of the analysis, it was discovered that some materials with three or fewer instances were highly weighted. This prompted a couple of follow-up analyses to confirm the instances of the categories with the highest and lowest weights. With this bias established in the results, some results with a very low number of instances were eliminated, and the results were further reinforced by investigating the data subsets. In our datasets we have removed materials that have been used three times or less. The results obtained from the subsets helped to confirm the accuracy of the weights of the categories on the complete dataset. Therefore, the original number of possible combinations in our ontology would be in the order of 10⁴⁸. However, only a fraction of those, 10²¹, are represented in our dataset. To our knowledge, this still represents the largest printed solar cell database analysed to date. Therefore, the modelling process incurs some uncertainty, it does not capture all possible non-linear interactions between layers, and also does not take synthesis into account. Finally, it is worth stressing that laboratory variability remained a major issue within the dataset. Fundamentally, the reasons we had to make this change was laboratory-to-laboratory variability. As an example, Fig. 5 shows an example of the variability in data from one of the most common stack sequences within the dataset (glass-FTO-TiO₂-c/TiO₂-mp-MAPbI-spiro-MeOTAD-Au); however, other factors, such as the deposition procedure, solvent, quenching media, and light source for the degradation study, have not been considered when deriving this configuration.

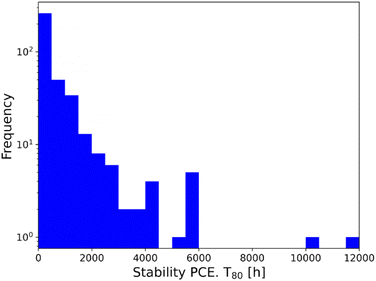Fig. 5 Histogram showing the variation in measured T₈₀ stability for devices made with the glass-FTO-TiO₂-c/TiO₂-mp-MAPbI-spiro-MeOTAD-Au configuration.

Nevertheless, our ML model was able to predict T₈₀ times with absolute errors of 44% (nip) and 73% (nip-mp). It is also interesting to see how well the best experimental data aligns with the model. Therefore, we considered the 20 most and 20 least stable devices within our dataset to evaluate the accuracy of our model in identifying the positive and negative attributes. Considering the most stable devices; we were able to see that 83% of the materials used correspond to materials with a positive rating from the SMOReg algorithm. In contrast, when considering the least stable devices, only 62% of the materials used corresponded to materials with a negative rating from the SMOreg algorithm. Therefore, it appears that the model is better at predicting highly stable devices than low-stability devices. This is likely to be the result of the removal of poorly performing device data, as mentioned earlier, since it introduced significant noise within our dataset. Overall, our results would encourage other groups to submit more data submissions in papers and more repeated data for new materials to avoid the creation of biases within the analysed machine learning model. Our second observation is the lack of encapsulated devices or modules. Our indication is that this produced the best performing device data and gave us the least noise when undertaking our analyses.

In the context of our study's findings, particularly the R² value of 0.683, it is beneficial to draw parallels with comparable research in our field. Other reports have indicated values of as low as 0.4 up to 0.9;^{5,11,15,21,26} but these studies have not used such large and complex datasets as that present in the perovskite database. This comparison is significant, as it demonstrates that our model's R² value, though seemingly moderate, is quite substantial when viewed against the backdrop of similar complex datasets.

Future work could also use databases to assess the optimum cost and sustainability of PSC modules by considering material/processing costs and environmental attributes, such as embodied carbon. From a computer software perspective, it would also be advisable to consider the development of a bespoke algorithm to handle the complexity of datasets, such as the perovskite database.

Conclusions

Supervised ML has been applied to investigate a comprehensive dataset from 2013 to 2020. This has allowed the influence of various materials on the stability of perovskite solar cells to be identified. We conducted this investigation in two parts. An innovative approach which entailed splitting the dataset by cell architecture was used, and the SMOreg ML algorithm was applied to identify how the materials under each feature influence stability. The results derived from the second analysis, suggest the ‘best’ performing two to three materials in each feature of the PSC, while the ‘bottom’ materials are also identified.

We also applied SMOreg to the data subsets, split according to the cell architecture. From the results, two to three materials with the best influence on stability were suggested. It is evident from the results that the p–i–n architecture is the most suitable for achieving higher stability, as the correlation obtained from both analyses for this architecture is above 0.9. The insight drawn from this research is that judicious attention should be given to optimising the materials used for the transport layers of PSC.

Our results serve as a promising foundation for carrying out further laboratory experiments to investigate the limitations of materials to improve PSC stability. Our methodology will influence further research towards applying a combination of ML methodologies and laboratory experiments to find a feasible solution for the poor stability of PSCs. The recommendations for further research are as follows.

Gathering a higher quantity of data to improve the results obtained by investigating datasets using ML.

The datasets could be further split according to modules, in addition to dividing them by cell architecture, to help achieve a more robust relationship within the data.

Data availability

Processed database information is available from the lead author upon request.

Author contributions

Bashayer Nafe N. Alsulami – conceptualization, methodology, software, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. Tudur Wyn David – conceptualization, methodology, software, formal analysis, investigation, data curation, writing – review & editing, visualization. Aniekan Akpan Essien – conceptualization, methodology, software, formal analysis, investigation, data curation, writing – review & editing, visualization. Samrana Kazim – investigation, data curation, writing, review & editing. Shahzada Ahmad – investigation, data curation, writing, review & editing. T. Jesper Jacobsson – conceptualization, investigation, data curation, writing – original draft, writing – review & editing. Andrew Feeney – investigation, data curation, writing, review & editing, project administration, funding acquisition. Jeff Kettle – conceptualization, methodology, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, project administration.

Conflicts of interest

There are no conflicts of interest to report.

Acknowledgements

This work was supported in part by the EPSRC Grant “Green Energy-Optimised Printed ICs (GEOPIC)” under Grant EP/W019248/1 and the grant “Technology critical metal recycling using ultrasonics and catalytic etchants” (EP/W018632/1). We would also like to thank Víctor Padrón for initial help on the project.

References

1. R. Wang, M. Mujahid, Y. Duan, Z. K. Wang, J. Xue and Y. Yang, A Review of Perovskites Solar Cell Stability, Adv. Funct. Mater., 2019, 29(47), 1808843.
2. P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Photovoltaic solar cell technologies: analysing the state of the art, Nat. Rev. Mater., 2019, 4(4), 269–285.
3. P. Roy, N. Kumar Sinha, S. Tiwari and A. Khare, A review on perovskite solar cells: Evolution of architecture, fabrication techniques, commercialization issues and status, Sol. Energy, 2020, 198, 665–688.
4. P. Tonui, S. O. Oseni, G. Sharma, Q. Yan and G. Tessema Mola, Perovskites photovoltaic solar cells: An overview of current status, Renewable Sustainable Energy Rev., 2018, 91, 1025–1044.
5. B. Yılmaz and R. Yıldırım, Critical review of machine learning applications in perovskite solar research, Nano Energy, 2021, 80, 105546.
6. R. Wang, M. Mujahid, Y. Duan, Z. K. Wang, J. Xue and Y. Yang, A Review of Perovskites Solar Cell Stability, Adv. Funct. Mater., 2019, 29(47), 1808843.
7. C. Chen, A. Maqsood and T. Jesper Jacobsson, The Role of Machine Learning in Perovskite Solar Cell Research, J. Alloys Compd., 2023, 170824.
8. O. Voznyy, L. Levina, J. Z. Fan, M. Askerka, A. Jain, M. J. Choi and E. H. Sargent, Machine learning accelerates discovery of optimal colloidal quantum dot synthesis, ACS Nano, 2019, 13(10), 11122–11128.
9. J. Schmidt, J. Shi, P. Borlido, L. Chen, S. Botti and M. A. L. Marques, Predicting the Thermodynamic Stability of Solids Combining Density Functional Theory and Machine Learning, Chem. Mater., 2017, 29(12), 5090–5103.
10. O. Allam, C. Holmes, Z. Greenberg, K. C. Kim and S. S. Jang, Density Functional Theory – Machine Learning Approach to Analyze the Bandgap of Elemental Halide Perovskites and Ruddlesden-Popper Phases, ChemPhysChem, 2018, 19(19), 2559–2565.
11. Ç. Odabaşı and R. Yıldırım, Performance analysis of perovskite solar cells in 2013–2018 using machine-learning tools, Nano Energy, 2019, 56, 770–791.
12. T. J. Jacobsson, et al., An open-access database and analysis tool for perovskite solar cells based on the FAIR data principles, Nat. Energy, 2021, 1–9.
13. K. Dineva and T. Atanasova, OSEMN process for working over data acquired by IoT devices mounted in beehives, Curr. Trends Nat. Sci., 2018, 7(13), 47–53.
14. J. D. Kelleher and B. Tierney, Data Science, MIT Press, 2018.
15. Z. Zhang, H. Wang, T. J. Jacobsson and J. Luo, Big data driven perovskite solar cell stability analysis, Nat. Commun., 2022, 13(1), 7639.
16. R. J. Little and D. B. Rubin, Statistical Analysis with Missing Data, John Wiley & Sons, 2019, vol. 793.
17. S. V. Buuren and K. Groothuis-Oudshoorn, mice: multivariate imputation by chained equations in R, J. Stat. Software, 2010, 1–68.
18. S. Zhang, Nearest neighbor selection for iteratively kNN imputation, J. Syst. Software, 2012, 85(11), 2541–2552.
19. S. R. Garner, Weka: The waikato environment for knowledge analysis, in Proceedings of the New Zealand Computer Science Research Students Conference, 1995, vol. 1995, pp. 57–64.
20. T. W. David, H. Anizelli, T. J. Jacobsson, C. Gray, W. Teahan and J. Kettle, Enhancing the stability of organic photovoltaics through machine learning, Nano Energy, 2020, 78, 105342.
21. T. W. David, H. Anizelli, P. Tyagi, C. Gray, W. Teahan and J. Kettle, Using large datasets of organic photovoltaic performance data to elucidate trends in reliability between 2009 and 2019, IEEE J. Photovoltaics, 2019, 9(6), 1768–1773.
22. M. V. Khenkin, K. M. Anoop, E. A. Katz and I. Visoly-Fisher, Bias-dependent degradation of various solar cells: lessons for stability of perovskite photovoltaics, Energy Environ. Sci., 2019, 12(2), 550–558.
23. P. Tyagi, T. W. David, V. D. Stoichkov and J. Kettle, Multivariate approach for studying the degradation of perovskite solar cells, Sol. Energy, 2019, 193, 12–19.
24. V. Zardetto, B. L. Williams, A. Perrotta, F. Di Giacomo, M. A. Verheijen, R. Andriessen, W. M. M. Kessels and M. Creatore, Atomic layer deposition for perovskite solar cells: research status, opportunities and challenges, Sustainable Energy Fuels, 2017, 1(1), 30–55.
25. A. A. Melvin, V. D. Stoichkov, J. Kettle, D. Mogilyansky, E. A. Katz and I. Visoly-Fisher, Lead iodide as a buffer layer in UV-induced degradation of CH₃NH₃PbI₃ films, Sol. Energy, 2018, 159, 794–799.
26. W. Sun, et al., Machine learning–assisted molecular design and efficiency prediction for high-performance organic photovoltaic materials, Sci. Adv., 2019, 5(11), eaay4275.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05966a

---