Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluation of in situ thermal stability assessment for flow batteries and deeper investigation of the ferrocene co-polymer†
Ivan A.
Volodin
 ab,
Katrin
Wulf
ab,
Felix
Tzschoeckell
ab,
Steffi
Stumpf
ac,
Stephanie
Hoeppener
ab,
Katrin
Wulf
ab,
Felix
Tzschoeckell
ab,
Steffi
Stumpf
ac,
Stephanie
Hoeppener
 ac,
Nicole
Fritz
ac,
Cristina F.
Morales-Reyes
ac,
Nicole
Fritz
ac,
Cristina F.
Morales-Reyes
 d,
Thomas
Wichard
d,
Thomas
Wichard
 d,
Nico
Ueberschaar
d,
Nico
Ueberschaar
 e,
Christian
Stolze
e,
Christian
Stolze
 ab,
Martin D.
Hager
ab,
Martin D.
Hager
 abc and
Ulrich S.
Schubert
abc and
Ulrich S.
Schubert
 *abcf
*abcf
aLaboratory of Organic and Macromolecular Chemistry (IOMC), Friedrich Schiller University Jena, Humboldtstraße 10, 07743 Jena, Germany. E-mail: ulrich.schubert@uni-jena.de
bCenter for Energy and Environmental Chemistry Jena (CEEC Jena), Friedrich Schiller University Jena, Philosophenweg 7a, 07743 Jena, Germany
cJena Center for Soft Matters (JCSM), Friedrich Schiller University Jena, Philosophenweg 7, 07743 Jena, Germany
dInstitute for Inorganic and Analytical Chemistry (IAAC), Friedrich Schiller University Jena, Lessingstraße 8, 07743 Jena, Germany
eMass Spectrometry Plattform, Friedrich Schiller University Jena, Humboldtstraße 8, 07743 Jena, Germany
fHelmholtz Institute for Polymers in Energy Applications Jena (HIPOLE Jena), Lessingstr. 12 – 14, 07743 Jena, Germany
First published on 23rd January 2024
Abstract
The stability of reported organic materials for redox flow batteries (RFB) continues to improve. Consequently, the relevance of analytical techniques to assess degradation rates also grows. To contribute to the development of in operando thermal stability assessment techniques, we evaluated the commonly-reported heating setups using the ferrocene-based FPMAm-co-METAC polymer (PFc) in a Zn-based hybrid RFB with a size-exclusion membrane. In the first stage, the conditions for RFB cycling were selected and evaluated. The amperometric SOC measurement technique revealed oxygen intolerance of the PFc. While no polymer cross-over was detected, cross-over of its hydrolysis products occurred and facilitated the capacity fade. Adjustment of membrane pore size and electrolyte composition helped to mitigate the hydrolyzed products' cross-over. In the second stage, different heating setups for the thermal stability evaluation of PFc were compared. Eventually, a thermostatic setup established the desired temperature most accurately and homogeneously, while the popular oil/sand bath setup exhibited a deviation of 22 °C down from the expected 60 °C. The PFc stability was further evaluated from ambient conditions (28 °C) to 60 °C. At temperatures above 50 °C a facilitated capacity fade was observed. The volumetrically unbalanced, compositionally symmetric flow cell cycling has unraveled that the degradation was caused by catholyte self-reduction and following half-cell imbalances. A mechanism involving the ferrocene complex decomposition is proposed as the origin of the catholyte self-reduction. Finally, the properties and thermal stability of the PFc material as well as the reliability of the studied heating setups are discussed.
1 Introduction
The redox flow battery (RFB) technology is highly interesting for the energy storage research.1–3 One of the actively studied parameters is the stability of – in particular – organic RFB electrolytes.4–6 Several inorganic systems already demonstrate long cycle and calendar life. These are represented by all-vanadium (VRFB), iron–chromium, and zinc–halogen (ZRFB) batteries.7 In the case of VRFBs and ZRFBs, the high stability with their other outstanding performance parameters led to commercialization. In contrast to that, organic RFBs (ORFBs) are still not yet massively commercialized, despite that they offer several advantages over the inorganic systems including tuned solubility and redox potential, faster redox kinetics on carbon-based electrode materials, exploitation of environmentally benign molecules, and in some cases using less corrosive, pH neutral electrolytes.8 Still, one of the drawbacks of organic materials is their lower stability compared to inorganic ones.4 To successfully implement organic materials-based RFBs, they should reach decently high stabilities, i.e., low or extremely low capacity fade rates (0.02–0.1 and ≤0.02% d−1, respectively).4 Some derivatives of viologen, anthraquinone, phenazine, phenothiazine, and ferrocene were already reported to exhibit the targeted degradation rates.4,9 However, the analytical techniques, which are so far used to assess the temporal capacity fade rate, are often lacking accuracy and reproducibility between the scientific groups.6,10,11 Reaching a sufficient level of confidence for RFB electrolyte stability assessment techniques for organic molecules represents an essential prerequisite to make the organic electroactive species more attractive for real application. In particular, developing in operando techniques is of outstanding interest, as that enables to test materials under the most realistic conditions. In addition, the relevance of developing stability assessment experiments at stressed conditions, such as elevated temperatures, becomes of high concern.Thermal stability assessment tests are frequently performed with electrolytes for the vanadium-based flow batteries (VRFBs).12 The conventional old-generation sulfuric acid vanadium battery anolyte is vulnerable to precipitation at temperatures below 10 °C. At the same time the catholyte starts to form deposits above 40 °C.13,14 Meanwhile, under real operation conditions the electrolyte temperature in the electrochemical flow reactor in an RFB may exceed 40 °C, in particular, if a battery is installed in regions with hot climate.15 Similarly, electrolyte temperatures in moderate climates may quickly decrease below 10 °C. Consequently, a thorough research on broadening the temperature stability range of the electrolyte for VRFB is ongoing.12 In particular, new-generation vanadium electrolytes can work at temperatures between approximately −5 and 50 °C.12,16 The same interest is expected to appear for the organic materials, when a question of commercialization seriously arises. The degradation mechanisms of organic materials-based electrolytes may be complex. The decomposition products may stay soluble in the electrolyte,17 they may exhaust into the gas phase,18 precipitate,19 exit a half-cell by crossing through the membrane.20 That renders capacity fade evaluations for organic materials more complex, and as a result, the analytical techniques should become more comprehensive. In addition, recent studies highlight the strong impact of temperature fluctuations on the measured capacity fade rates and, thus, emphasize the demand for methodologic developments in this area.10,11
With regard to the already published in operando thermal stability studies of organic materials for RFBs, there are only a few contributions reporting RFB anodic organic materials with moderate (0.1–1.0% d−1), low (0.02–0.1% d−1), and extremely low (≤0.02% d−1) capacity fade rate (classification by Kwabi et al.4) at 40 °C.21,22 In particular for cathodic organic materials, there have been only a few species with moderate to high capacity fade rate presented.18,23,24 Consequently, it is of great interest to assess the thermal stability of the currently developed stable RFB organic materials to indicate the promising species, and to better understand the mechanisms of the molecules' decomposition.
The recently reported ferrocene-based FPMAm-co-METAC polymer (PFc) was further investigated in a new system. Earlier in our group, the PFc was reported to demonstrate a moderately stable performance with a capacity fade rate of 0.2% d−1, while being tested at ambient temperature vs. the bis(3-trimethylammonium)propyl viologen (BTMAPV) in a RFB setup with an ion-exchange membrane. It is worth noting that after increasing the setup temperature by keeping both electrolyte tanks in a sand bath tempered to 60 °C, no further decay was registered during an additional 100 cycles of the RFB cycling.25 The counterintuitive increase in material stability remained without a detailed investigation, thus, in the study at hand we research the PFc in greater detail using zinc as an anode material. Compared to the BTMAPV anolyte, zinc has been researched in various RFB studies under high-temperature conditions.26–33 In particular, there are several thermal stability assessment studies in which the electrolyte in zinc flow batteries is heated to 60 °C.26,27,31 In these investigations, no degradation issues regarding the anode side are reported, and, consequently, it is safe to assume that for our material combination the capacity fade at temperatures as high as 60 °C is not limited by the degradation rate of the zinc-based anolyte but rather depends on the stability of the PFc system. Additionally, zinc is an abundant and relatively cheap electroactive material, its reduction potential is one of the lowest among anolyte species for water-based RFBs, it is sufficiently resistant to reacting with oxygen, and its reduced (solid) state cannot cross the membrane.34 Thus, testing PFc vs. zinc provides a possibility to elevate battery voltage, compared to the previous PFc study, to obtain a potentially air tolerant system (ferrocene and its derivatives are often also resistant to oxygen)35 and to switch from ion-exchange membranes to the cheaper size-exclusion type.
This contribution is structured as follows: first, optimizations of the setup and experimental parameters are investigated. This includes the estimation of the theoretical battery voltage and the optimization of the charge–discharge regime ensuring high material utilization, testing PFc oxygen sensitivity, and mitigating capacity fade by variation of size-exclusion membrane and electrolyte composition. As a second step, we compare the ability of different heating setups to establish a desired electrolyte temperature accurately and homogeneously. The best performing setup is further used for the stability evaluations at increased temperatures (i.e., 50 and 60 °C). Full-cell cycling results are complemented by unbalanced, compositionally symmetric flow cell cycling (UCSFCC) experiments on each of the stages in the investigation, which helps to unravel sophisticated mechanisms of capacity fade in the PFc-based RFB. Finally the PFc upper thermal stability threshold and the model to estimate the capacity fade rate in the range from ambient temperature to the threshold are presented. Additionally, the current state and ongoing developments regarding in situ thermal stability assessments are summarised.
2 Experimental
2.1 Materials
All materials were ordered from TCI, ThermoFisher, VWR, Alfa Aesar, Sigma Aldrich, and other suppliers and used as received. The synthesis of the ferrocene-based FPMAm-co-METAC polymer (PFc) was performed as detailed by Borchers et al.25 For the PFc dialysis, applied to remove low molar mass chains, the polymer was dissolved in water to prepare a concentrated solution, and placed inside of Spectra/Por 6 1 kDa dialysis membrane tubes. The tubes were closed and placed in a 5 L beaker, filled with distilled water. The water was exchanged each day. The dialysis was performed for at least three days with subsequent polymer separation by freeze-drying. The size-exclusion-chromatography (SEC) of the polymer before and after the dialysis is shown in Fig. S1 in the ESI.† The 1H nuclear magnetic resonance (1H NMR) of the dialysed PFc is presented in Fig. S2.†2.2 Potentiometric (redox) titration
The potentiometric titration using cerium(IV) solution was performed with a GMH 3530 digital pH-/mV-/thermometer (Greisinger electronic GmbH, Germany) equipped with a GR 105 redox electrode (Greisinger electronic GmbH, Germany, reference electrode: Ag wire in 3 M aq. potassium chloride solution). The titrant was a Ce(SO4)2 aqueous solution in 1 w/w%. H2SO4. The titrate was a 1 w/w% H2SO4 water-based solution of 180 mg of the PFc. Primarily to the titration, the titrant was calibrated for the Ce4+ concentration with the help of the (NH4)2Fe(SO4)2·6H2O standard and, consequently, the Ce4+ concentration was estimated to be 20.3 mM. The assessed steady-state potentials for each volume of the added titrant were plotted vs. the titrant volume and fitted by an S-shape function to assess the inflection point as suggested in work by Rohland et al.232.3 Atomic absorption spectroscopy
Iron determination by flame atomic absorption spectroscopy (F-AAS) was performed, using a ContrAA700 high-resolution continuum flame atomic absorption spectrometer (Analytik Jena GmbH, Germany). An air/acetylene flame was used to measure the atomic absorption of Fe at 248 nm. Operational parameters were set following the manufacturer's recommendations. Certified single-element standard solutions (Merck Certipur, NIST standard reference materials) were applied for calibration. HCl, 1% (v/v), was employed to dilute the samples and standards (TraceMetal Grade, Fisher Chemical, Germany). Iron concentrations were calibrated between 0.8 and 2.4 mg L−1.36 The parameters for the calibration procedure were determined according to the standards of DIN 32645.372.4 Full RFB testing
For the full RFB charge–discharge cycling, the applied flow cells were custom-made flow-through cells as reported in earlier studies.38 Graphite composite cathode and zinc anode current collectors, GFA-6 felts (SGL, Germany), and either Spectra/Por 6 1 kDa or OS-NF-8800 0.6 kDa size exclusion membrane with an active area of 5 cm2 were applied. Compared to Spectra/Por 6 membrane, being composed of regenerated cellulose, which is fairly stable and can be operated only in near-neutral aqueous conditions, the OS-NF-8800 is prepared from polypropylene reinforcement and polyether sulphone selective layers and, thus, has higher chemical stability and can perform on the whole pH range of 0 to 14. Therefore, the OS-NF-8800 represents a more selective and stable replacement for the purposes described in Subsection 3.1.3. The membranes were prewetted at least overnight in the corresponding electrolyte for all battery experiments. All battery experiments and the data acquisition were conducted in an argon-filled glovebox if no contrary information was stated. The oxygen content during the experiments was kept below 3 ppm. A 5-channel VSP potentiostat/galvanostat (Bio-Logic, France) was used for data acquisition. Two types of anolyte compositions were used for the measurement: (1) 0.1 M ZnCl2, 0.8 M NH4Cl (pH 4.5–5); (2) 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl (pH 4.5–5). The 0.1 M Zn2+ concentration was chosen for this experiment and for the following RFB tests because of possible interactions between zinc cations and the polymer. Zinc cations are known to interact with some quaternary ammonium groups and, thus, to form deposits in solution.7 In our system, if zinc salt concentration is increased above 0.1 M, the PFc becomes poorly soluble in the supporting electrolyte. Still, even the 0.1 M ZnCl2 concentration represents at least a 7.4 times capacity excess of the anolyte capacity compared to catholyte (if same volumes are used in the both half-cells) and, thus, even this concentration is sufficient for the fulfilling of the purposes of this scientific contribution: (1) more comprehensive investigation of PFc behavior in a RFB, (2) development of in situ thermal stability setups and (3) assessment of PFc thermal stability. The solutions have been prepared by dissolving the corresponding amount of salt in deionized water. The related two types of catholytes were obtained by dissolving an additional 0.27 mM PFc (with regard to electron equivalent concentration) in each of the two solution types. The PFc concentration was calculated assuming the mole electron equivalent mass as 1485 g per mole of electrons (see Subsection 3.1.1). In the full RFB tests from Section 3.1, equal anolyte and catholyte volumes were applied (either 10 vs. 10 mL or 9 vs. 9 mL). In the full RFB tests from Section 3.2, 15 mL of anolyte were tested vs. 10 mL of catholyte in order to keep sufficient electrolyte volume at the negative half-cell, despite the occurrence of slight migration of water to the positive half-cell due to osmosis. For the full battery tests, two different charge–discharge cycling regimes were applied: (1) galvanostatic charge–discharge at 80 mA (16 mA cm−2) current between 0.5 and 1.5 V cutoffs, followed by potentiostatic holding at the cutoffs until the current decreased to ≤2.5 mA (higher current regime); (2) galvanostatic charge–discharge at 10 mA (2 mA cm−2) current between 0.5 and 1.5 V cutoffs, followed by potentiostatic holding at the cutoffs until the current decreases to ≤2.5 mA (lower current regime). Before each experiment, at least half an hour-long open circuit voltage (OCV) period was performed to provide system equilibration at all interfaces. To compare the two membrane conductivities, potentiostatic electrochemical impedance spectroscopy was performed at 10 mV amplitude with respect to the equilibrium potential. Then, the charge–discharge cycling was performed.2.5 Unbalanced, compositionally symmetric flow cell cycling
For the unbalanced, compositionally symmetric flow cell cycling (UCSFCC), the same flow cell setup was used with graphite composite current collectors applied in both half-cells. The Spectra/Por 6 membrane was used for symmetric cycling in Subsections 3.1.3 and 3.1.5, whereas the OS-NF-8800 membrane was applied in the Subsection 3.2.3. During UCSFCC experiments, a two-fold excess of NCLS volume with regard to the CLS was used (i.e., 9 vs. 18 or 10 vs. 20 mL), if not stated otherwise. The applied symmetric 50% SOC electrolyte had the same composition as catholytes for the full RFB cycling. The 50% SOC was reached by charging the freshly prepared catholyte in a full RFB vs. zinc half-cell with potentiostatic holding at 1.5 V until the current decreased to ≤2.5 mA. Subsequently, the fully charged catholyte was removed from the RFB and mixed with the equal volume of the uncharged catholyte. For the UCSFCC, a potentiostatic charge–discharge cycling at 0.3 V overvoltage in either direction and with the 2.5 mA (0.5 mA cm−2) current cutoff was applied. Besides those experiments where the system required the time to heat up, no OCV periods preceded the potentiostatic cycling. The experimental procedure was adjusted to have a minimal time period between the 50% SOC catholyte preparation, RFB setup heating, and the start of the potentiostatic charge–discharge cycling to limit degradation prior to the beginning of the measurement.2.6 Cyclic voltammetry
Cyclic voltammetry was measured in a 5 mL electrochemical cell (ALS Japan), applying a three-electrode setup: Working electrode – 1.6 mm glassy-carbon disc electrode, Reference electrode – Ag/AgCl (3 M NaCl) standard reference electrode, Counter electrode – platinum wire. The working electrode was polished on a diamond polishing pad (ALS Japan) with a SiO2 < 0.05 μm polishing (Schmitz Metallographie) suspension primary to the measurement. The measurements have been performed with 100 mV s−1 sweep rate. The solutions for the cyclic voltammetry were prepared the same way as for the RFB charge–discharge cycling tests. After the CV measurement of the 1 mM PFc electrolyte, the reference electrode (RE) was removed to measure its steady-state potential vs. another pristine Ag/AgCl (3 M NaCl) used in our lab as a control standard, which never was in contact with solutions other than aqueous NaCl solutions. The steady-state potential was measured in the same electrochemical cell in a 1 M NaCl solution using a two-electrode setup and applying an OCV technique. A 40 mV drift of the applied RE was observed in the negative direction from the pristine RE. Therefore, to keep our results comparable, in all CV experiments presented in this contribution, the recorded potentials are shifted by 40 mV in the negative direction (e.g., if the recorded half-wave potential is 0.24 V vs. (our) Ag/AgCl RE, we state it as 0.20 V vs. (standard) Ag/AgCl RE).2.7 Validation of the amperometric SOC measurement method
For validation of the temperature-insensitive, calibration-free amperometric SOC measurement technique, a 0.1 M ZnCl2, 0.8 M NH4Cl, 27 mM PFc catholyte was charged vs. a zinc half-cell with potentiostatic holding at 1.55 V until the current decreased to ≤2.5 mA. The obtained maximum charged catholyte was mixed with the uncharged fresh catholyte to obtain solutions with 0%, 1%, 5%, 25%, 50%, 75%, 95%, and 99% SOCs. The measurement was performed in a 5 mL electrochemical cell, applying a three-electrode setup: Working electrode – 33 μm glassy-carbon disk microelectrode, Quasi-reference electrode – silver wire with AgCl coating, obtained by an anodization in 1 M NaCl solution, Counter electrode – 3 mm glassy-carbon disk electrode. Primary to each of the measurements the working electrode (WE) was polished on a diamond polishing pad with a SiO2 <0.05 μm polishing suspension and then on a wetted alumina polishing pad (no polishing suspension applied). After the measurement preparation, the electrochemical cell was kept steady until the WE open circuit voltage stabilized. The obtained equilibrium potential was later used to validate the SOC assessment via OCV measurements. Subsequently, a CV was performed from −0.1 to 0.5 V with a 100 mV s−1 sweep rate to ensure, that the overpotentials of −0.1 and 0.5 V, applied for each of the following chronoamperometry techniques correspond to the diffusion-limited area of the reaction (i.e., reduction peak/start of plateau occurred at a higher potential, then the cathodic chronoamperometric step at −0.1 V and oxidation peak/beginning of plateau happened at a lower potential, then the anodic chronoamperometric step at 0.5 V). Subsequently, the one-minute-long anodic chronoamperometric step at 0.5 V was performed and, as follows, the one-minute cathodic chronoamperometric step at −0.1 V was applied. Before and after each chronoamperometric step, the electrolyte was mixed and each potential holding technique was repeated three times. The limiting cathodic and anodic currents from 5%, 25%, 50%, 75%, 95% SOCs were plotted against each other to assess the DOxDRed−1, as described in our previous publications on this method.10,39 Here DOx and DRed correspond to diffusion coefficients of oxidized and reduced PFc species, respectively. Subsequently, the SOC of the solutions was calculated as:| SOC = (1 − (ia × ic−1) × (DOx × DRed−1))−1, | (1) |
2.8 Validation of the SOC measurement by OCV assessment
For the validation of the SOC measurement by OCV assessment method the equilibrium potentials, EEq, measured during the validation of the amperometric technique were applied. As the anodized silver wire was exploited as the quasi-RE during the EEq assessment, its potential could drift inside each of the measured solutions. Thus, the assessed EEq was shifted by ΔE = EPFc − E1/2, where EPFc is the PFc half-wave potential measured during the CV of 1 mM PFc electrolyte vs. a standard Ag/AgCl in 3 M NaCl reference electrode and E1/2 is a half-wave potential, measured during the validation of the amperometric technique vs. the anodized silver wire RE. Since the half-wave potential is independent on active material SOC, this approach helped to correct the drift of the RE potential in the measurement data. The shifted EEq were plotted vs. the SOCs of the prepared solutions and a fit, based on simple one electron transfer Nernst equation, was performed.40 Discussion of the accuracy and applicability of the technique was performed in Subsection 3.2.3.2.9 Oxygen sensitivity assessment
For the oxygen sensitivity assessment three samples of 0.1 M ZnCl2, 0.8 M NH4Cl, and 27 mM PFc were prepared and kept in closed RFB tanks. The tank sealing prevented water evaporation but did not sufficiently suppress oxygen diffusion through leads. The tanks were kept for one week at room temperature (appr. 21.5 °C), then the same time periods at 40, 60 °C, and r.t. once more. During storage at elevated temperatures, the tanks were placed in a thermostat. Once a day, the tanks were removed from the thermostat to measure the catholyte's SOC. For that purpose, each sample was left for 30 minutes to cool down (to ensure a constant temperature during each single SOC measurement for maximum accuracy) prior to the amperometric SOC measurement. For each sample, the following sequence was performed: (1) WE and CE polishing, (2) CV between −0.1 and 0.5 V potentials at 10 mV s−1 sweep rate, (3) WE polishing, (4) chronoamperometry at 0.5 V, (5) electrolyte mixing, and (6) chronoamperometry at −0.1 V. Three samples per SOC were measured.2.10 Cross-over assessment
The cross-over assessment by CV was carried out in the 5 mL electrochemical cell, using the three-electrode setup: WE – 1.6 mm glassy-carbon disc electrode, RE – Ag/AgCl in 3 M NaCl standard reference electrode, CE – platinum wire. The sweep was performed between −0.1 and 0.6 V with the 100 mV s−1 rate. Cross-over assessments via UV-vis were carried out in the wavelength range from 360 to 710 nm in a quartz cuvette (optical path length of 10 mm) using a Lambda 750 UV-vis spectrophotometer (PerkinElmer). Solely anolyte solutions of the corresponding composition were applied for absorbance baseline assessment and subsequent subtraction. For the calibration of the UV-vis analysis with the uncharged PFc solutions, the samples were prepared by dissolving 8.9 mM PFc in the corresponding anolyte and by consecutive dilutions using the anolyte as basis media. Primarily to calibration with the charged PFc solutions, a full RFB with 27 mM PFc catholyte was charged potentiostatically at 1.6 V with a 3 mA current cutoff. Subsequently, the obtained charged catholyte was consecutively diluted to obtain the required sample concentrations.2.11 EDX scanning
For the EDX measurements, a Sigma VP Field Emission Scanning Electron Microscope (Carl-Zeiss AG, Germany) in combination with an Oxford EDX system was used. The samples were fixed in a sample holder in a top-view position for elemental surface mapping and in an upright position to map the cross-sectional area. Mapping was performed with an acceleration voltage of 15 kV. Primarily for scanning, the post mortem RFB membranes were kept in deionized water at least overnight. Membrane cutting was carefully performed with a scalpel.2.12 ESI-MS measurements
For the ESI-MS analysis, all samples were analysed using a micrOTOF Q-II (Bruker Daltonics) mass spectrometer equipped with an automatic syringe pump from KD Scientific for sample injection. The ESI-Q-ToF mass spectrometer was operated at 4.5 kV, at a desolvation temperature of 180 °C, in the positive (or negative) ion mode. Nitrogen was used as the nebulizer and drying gas. All fractions were injected using a constant flow rate (3 μL min−1) of sample solution. The instrument was calibrated in the m/z range 50 to 3000 using sodium formate (HCOONa) solution, prepared in accordance with the Bruker instructions, as a calibration standard. All data were processed using Bruker Data Analysis software version 4.2.2.13 Thermal stability assessment
Thermal stability tests were performed in four different heating setups. For heating setups 1–3, a sand bath was used as a heating element. The temperature probe (T-probe) from the heating bath was used to measure the temperature. In setup 3, a second T-probe from a by-standing heating plate was used to obtain the temperature of the sand additionally to the temperature, assessed in the RFB anolyte with the help of the first T-probe. Furthermore, in setup 3, magnet stirrers were placed in the RFB tanks and mixing was switched on, and all the heating setup, besides the peristaltic pump head, was covered with a layer of a glass fiber thermal isolating fabric. Setup 4 was composed of a thermal-isolating box, a fan, a silicon heating pad 400 W, a heat dissipator and a temperature controller with a T-probe. The T-probe of the controller was placed near the flow cell. The whole RFB setup, besides the pump, was placed inside the thermally insulated box. The tubing around the pump head was covered with a layer of the glass fiber thermal isolating fabric. The additional T-probe from the heating plate (same as the probes applied during thermal assessments in setups 1–3) was placed in the anolyte during the full RFB cycling. During the symmetric cycling at the glovebox ambient temperature, the T-probe of the heating plate was placed in the NCLS overnight, and, as the assessed temperature stayed constant at 28 °C, the probe was removed from the electrolyte to avoid corrosion of the sensor. During the UCSFCC at 60 °C, to prevent corrosion, the same T-probe was wrapped with a PTFE temperature shrinking tube and a 3 mm diameter, 1 mm high PTFE cylinder as a cap for encapsulation. Subsequently, the probe was immersed in the NCLS tank daily to assess the actual electrolyte temperature. During the thermal assessment experiments in setup 4, the thermally insulated box atmosphere temperature varied between 62 and 65 °C, and the anolyte or NCLS temperature drifted between 60 and 61 °C, staying at 60 °C most of the time.2.14 Assessment of SOC in NCLS during the symmetric cycling
For NCLS SOC assessment during the UCSFCC at 60 °C, the OCV-based technique was applied. After the 50% SOC catholyte was prepared and before the charge–discharge cycling started, a 3 mL portion of the solution was taken to measure its SOC ex situ. The measurement was performed in a two-electrode setup, where the equilibrium potential of a 3 mm disk glassy carbon working electrode vs. an Ag/AgCl (3 M NaCl) standard reference electrode was measured. Subsequently, the analysed electrolyte portion was returned to the prepared batch, mixed, and the UCSFCC was performed as described before. Additionally, a one-hour waiting period before the battery cycling was introduced, in order to let the RFB setup heat up to the desired temperature. When the discharge capacity of the symmetric cell started to decrease gradually, the potentiostatic cycling was paused at the end of charging (i.e., PFc in CLS being oxidized to the maximum SOC allowed by the setup). Subsequently, a portion of the NCLS electrolyte was taken for the SOC assessment via OCV in the same way as at the start of the experiment. Then, the analyzed electrolyte portion was returned to the NCLS and the same procedure was repeated after the end of the battery discharge. A rebalancing procedure was applied in case of a significant SOC drift leading to a rollover, which would have turned the NCLS into the CLS. A portion of a compositionally identical catholyte from a previous experiment was charged vs. zinc and added to the NCLS to increase its capacity and average the SOC. After the rebalancing, the NCLS SOC was measured once more at the full battery charged and discharged states to validate the procedure. For the rebalancing, only catholyte samples that initially had 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl, 27 mM PFc composition, and that were kept frozen at −20 °C were applied. Before placing the catholytes into the glovebox, they were deoxygenated by bubbling argon for at least 40 minutes.2.15 GC-MS measurements
For the gas chromatography-mass spectrometry (GC-MS) analyses, 2 mL solutions and one empty “control” specimen were sampled through the septum from 4 mL HPLC vials. Samples were measured on a GC-MS system from Thermo Fisher Scientific GmbH (Bremen, Germany) consisting of a TRACE™ 1300 GC with an S/SL injector installed and a Polaris Q ion trap mass spectrometer. The scan range was set between 30 and 400 m/z. The transfer line temperature was set to 300 °C, the ion source temperature to 200 °C, and the damping gas flow was set to 0.3 mL min−1 helium. Three micro scans were recorded at a maximum ion time of 25 ms. After an initial 2 min at 40 °C, the GC oven temperature was raised to 100 °C with 10 °C min−1 and then to 200 °C with 50 °C min−1. The injector was operated in split mode at 270 °C with a flow rate of 10 mL min−1, the split ratio was 10 and the column flow was 1 mL min−1. As a column, a Zebron ZB-1MS 60 m from Phenomenex (Aschaffenburg, Germany) was used, with 0.25 mm inner diameter and 1 μm film thickness.2.16 Evaluation of PFc fade rates at different temperatures using first-order kinetic and Arrhenius models
The thermal stability assessment data was treated using the first-order reaction model:41| PFc → x × Deg | (2) |
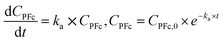 | (3) |
| ln(ka) = ln(A) − Ea × (RT)−1 | (4) |
3 Results and discussion
3.1 Primary investigation of PFc-Zn system
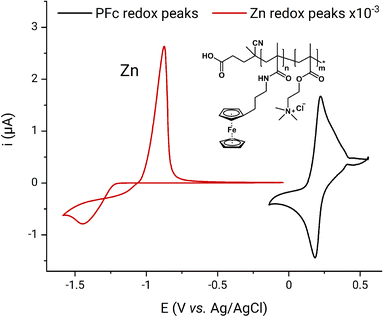
A schematic representation of the ferrocene-based FPMAm-co-METAC polymer applied in this study is depicted in Fig. 1. From the cyclic voltammetry of 1 mM PFc in 0.1 M ZnCl2, 0.8 M NH4Cl supporting electrolyte (Fig. 1), the polymer half-wave redox potential is determined to be 0.20 V vs. the Ag/AgCl reference electrode. The PFc concentration is calculated based on the polymer electron equivalent molar mass of 1485 g per mole of electrons. The evaluation of the molar equivalent concentration is described later in this Subchapter. The assessed PFc half-wave potential differs from the 0.52 V vs. Ag/AgCl reported for the same polymer by Borchers et al. previously.25 Such deviation may be caused by the different electrolyte composition applied in our current work. However, we suppose that the main source for the deviation is related to RE drift: In the publication by Borchers et al.25 the half-wave potential of the BTMAPV was assessed as −0.23 V vs. Ag/AgCl, though elsewhere in the literature, it is reported as −0.36 V vs. SHE (ca. −0.57 V vs. Ag/AgCl in 3 M NaCl).4 This indicates that in the previous work on the PFc, a RE with strong negative potential drift was applied and unfortunately not recognized. In our contribution, the potential of the applied Ag/AgCl was primarily corrected as described in the Experimental part, consequently, the 0.20 V vs. Ag/AgCl measured in this work are not affected by the RE drift. The 0.20 V potential also makes more sense, since it is in the range of the redox potentials reported for ferrocene and its derivatives elsewhere in the literature, i.e., 0.1 to 0.4 V vs. Ag/AgCl in 3 M NaCl electrode.4,42 The current shoulder after the oxidation and before the reduction peaks (Fig. 1) most probably originates from the polymer dispersity, from alternations in diffusion conditions caused by polymer adsorption–desorption, and changes in the solution viscosity at the electrode interface during the PFc redox process occurrence.
The zinc half-wave potential was estimated as −1.16 V vs. the Ag/AgCl electrode in the same setup. The observed redox potential is in excellent agreement with the −1.16 V vs. Ag/AgCl, previously reported for Zn-ammonia chloride electrolyte by Winsberg et al.43 The theoretical RFB voltage corresponds to 1.36 V, thus, being in line with the voltages of state-of-the-art aqueous organic RFB systems as MV/TEMPTMA, MV/FcNCl, 2,6-DBEAQ/K4Fe(CN)6, AQDS/HBr, and etc.4 In the following full RFB tests, a practical RFB charge–discharge voltage of 1.24 V was reached. The voltage was estimated as a cross-section of charge and discharge curves in Voltage–Capacity plots (Fig. S3†). Consequently, the 1.5 V battery voltage was chosen as a cutoff for the RFB charging. The cutoff provides 260 mV charging overvoltage, which is usually sufficient for complete material charging in a potentiostatic regime during UCSFCC.44 Higher voltage was not applied in order to avoid hydrogen evolution on the anode. The 0.5 V discharge cutoff was chosen because it provides sufficient overvoltage for the full RFB discharge and is not expected to cause the occurrence of any parasitic processes. The charging was performed in mixed galvanostatic–potentiostatic regime as described in the Experimental part. The galvanostatic part was introduced to keep the RFB current load low in order to avoid dendrite formation in the zinc half-cell. The potentiostatic part enabled a maximum of material utilization.
The mole fraction of ferrocene in the polymer was estimated by cerimetric redox titration and atomic absorption spectroscopy (AAS), yielding 14.1 ± 0.7% and 13.6 ± 1.8% respectively (ESI Fig. S4 and S5†). The mole fraction values are means from three measurements, with the error propagation calculated for each corresponding analysis. From the seven full RFB tests performed at room temperature in an argon-filled glovebox (exemplary voltage–current curves of the charge–discharge procedure are depicted in Fig. S6†), the average initial discharge capacity of a 396.6 mg PFc in 10 mL electrolyte corresponds to 7.6 ± 0.3 mA h (mean and standard deviation). Subsequently, based on battery testing the ferrocene mole fraction in the polymer can be calculated as 16.0 ± 0.5% which is in good agreement with the values determined by the potentiometric titration and AAS. Moreover, since the value estimated from the RFB cycling is slightly higher than the ex situ measured values, it was concluded that with the chosen battery cycling regime it is possible to access the full capacity of the material. Hence, we can exclude that any non-accessed capacity would influence the capacity fade rates obtained during studies at elevated temperatures, which could have been the case in our previous contribution.25 Based on the measured mole fractions from all the methods, an average value of 15 (n/n)% was assumed to be the real value throughout this study. Accordingly, the electron equivalent molar mass of the PFc is 1485 g per mole of electrons.
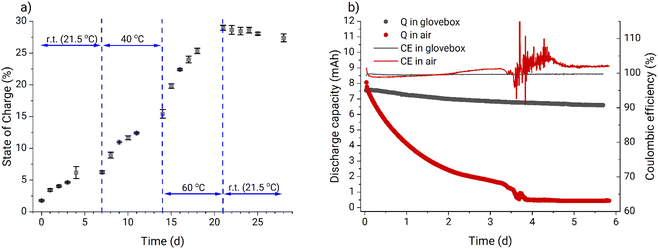
After the validation experiment, an uncharged PFc electrolyte sample was stored under ambient conditions and its SOC was measured once per day. From Fig. 2a it can be clearly seen that the SOC of the electrolyte increases over time, which indicates oxidation of the ferrocene polymer by oxygen from the air. At increased temperature, the oxidation rate also increases, further pointing to facilitation of the ongoing self-charge reaction. However, after the temperature was returned to the standard laboratory condition (21.5 °C), the SOC reached a saturation value of 28%. Therefore, the Zn-PFc RFB was expected to exhibit poorer stability under ambient conditions than in an inert atmosphere.
The results of a 5.7 days-long cycling of two Zn-PFc RFBs under both ambient conditions and in an argon-filled glovebox confirmed this expectation. Fig. 2b shows that the RFB in the glovebox exhibits significantly better performance compared to the RFB operated at ambient conditions both with regard to capacity fade rate and coulombic efficiency. Furthermore, we observed significant water transfer between the half-cells (Fig. S9†). At the end of the experiment, most of the water had migrated to the anolyte side transforming the catholyte into a gel with a volume of approximately 5 mL and increasing the anolyte volume to 15 mL. This effect was not detected during battery cycling in the glovebox (Fig. S10†). We attribute this difference to the fact that additional zinc dissolution compensating for the PFc self-discharge under ambient conditions caused a stronger osmotic pressure between the half-cells. Eventually, it was concluded that all the subsequent experiments should be performed in an argon-filled glovebox.
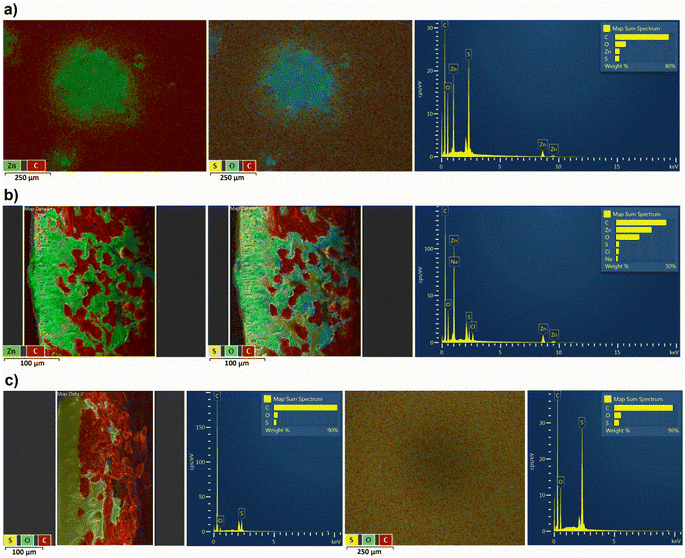
During the following full RFB tests using OS-NF-8800 membrane, zinc dendrite growth was evaluated (Fig. 3a and b). Decreasing the currents of the galvanostatic part of the RFB charge–discharge regime enabled mitigation of the dendrite growth (Fig. 3c). The more detailed discussion about the evaluation and mitigation of the zinc dendrite growth is presented in the ESI, page S5 and in Fig. S12–S28.† Eventually, the new, lower current cycling regime was adopted for all the following full RFB tests. The lower current regime represents galvanostatic charge–discharge at 2 mA cm−2 current in a 0.5 to 1.5 V voltage range with subsequent potentiostatic holding at the cutoff voltages till the absolute current value decreases to ≤0.5 mA cm−2 (exemplary charge–discharge cycles are depicted in Fig. S29†). In particular, to provide a better comparison of the experimental results the full RFB cycling applying the 1 kDa MWCO Spectra/Por 6 was also repeated using the new cycling regime.
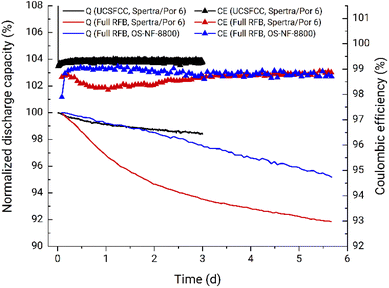
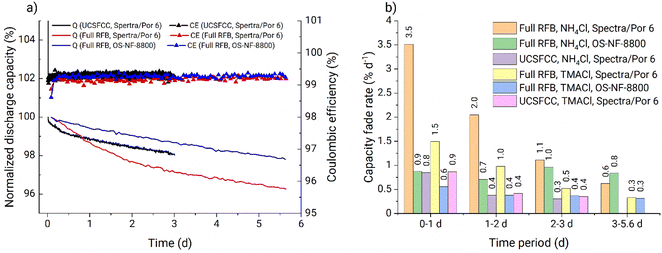
The battery performance from full RFBs and UCSFCC tests is presented in Fig. 4a. The RFB applying the OS-NF-8800 membrane exhibits linear capacity fade rate behavior, i.e., similar capacity fades of 0.7% d−1 and 0.9% d−1 are obtained for the experiment's first and fifth days, respectively. For comparison, the full RFB cycling with the 1 kDa MWCO (Spectra/Por 6) membrane (red line in Fig. 4a) exhibits similar capacity fade behavior to the previously observed in Fig. 2b in the glovebox, i.e., the non-linear capacity fade pattern where the capacity decay decreased from 3.7% d−1 during the first day to 0.6% d−1 during the fifth. Therefore, the application of the new membrane indeed caused other capacity fade patterns, confirming the statement that specifically cross-over processes are the reason for the difference in fade rates obtained from full RFB and UCSFCC tests.
Nevertheless, the UV-vis absorption analysis of the RFB anolyte did not reveal the presence of the PFc in negative half cells in each of the experiments (UV-vis calibration curves for charged and discharged PFc catholytes are presented in Fig. S30 and S31,† respectively, and the spectroscopy analysis of the post mortem anolytes of full RFBs using Spectra/Por 6 and OS-NF-8800 membranes are shown in Fig. S32 and S33,† respectively). In Fig. S32 and S33† for comparison with the post mortem anolytes' spectra, UV-vis spectra for freshly prepared 0.18 mM PFc catholytes are depicted. The 0.18 mM PFc concentration would correspond to a cross-over of 0.7% of PFc catholyte concentration to anolyte. The anolyte's absorption spectrum represents a nearly straight line compared to the 0.18 mM samples (Fig. S32 and S33†). Additionally, cyclic voltammetry was performed with the post mortem anolyte from the full RFB tests using OS-NF-8800 membrane and also did not reveal presence of the polymer (Fig. S34†).
The UV-vis and CV techniques may not detect PFc in the post mortem RFB anolyte if it is precipitated or fully degraded after crossing the membrane. To rule out this possibility a full RFB test with an intentionally PFc-contaminated anolyte was performed. The details of the experiment are described in ESI, page S6, Fig. S35 and S36.† Eventually the PFc stayed visible by both UV-vis and CV techniques even after the 5.7 days long full RFB test. Consequently, the techniques are sufficient to track the PFc cross-over and the PFc transfer to the anolyte indeed does not occur during the full RFB cycling. Nevertheless, in fact some cross-over process causes the observed difference in capacity fade rates in Fig. 4a. Therefore, a transfer of other species induces the observed differences in the capacity fade rates.
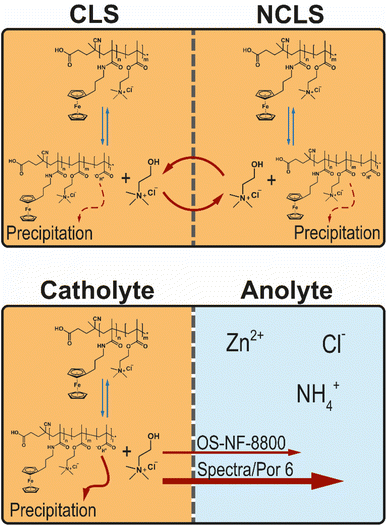 | ||
| Fig. 5 Schematic representation of the potential hydrolysis–condensation equilibrium of the methacrylic PFc block and its impact in a symmetric flow cell and in a full RFB. | ||
A portion of RFB anolyte from the full battery test with OS-NF-8800 membrane was subjected to an electrospray ionisation mass spectrometry (ESI-MS) analysis in order to search for the presence of the TMA-EtOH in the RFB anolyte (Fig. S37 and S38†). According to the spectra of positively charged particles (Fig. S38†), the solubilizing unit was present in the anolyte. Consequently, the suspected decomposition reaction occurs and, thus, may allow the TMA-EtOH cation to cross the OS-NF-8800 membrane, which could explain the differences between the capacity fade rates exhibited in Fig. 4a as rationalized in the beginning of this Subsection. The removal of the TMA-EtOH group from the polymer backbone is a reversible process. Consequently, the TMA-EtOH may reconnect to the backbone as long as both the polymer chain and the cleaved group stay in the solution. The scenarios for the TMA-EtOH cross-over and its influence on the PFc stability are depicted in the Fig. 5. In a symmetric RFB, the proposed equilibrium reaction is reached in both half-cells even if TMA-EtOH crosses the membrane. On the other hand, in full RFBs the TMA-EtOH is likely to diffuse from the catholyte to the anolyte through the size-exclusion membrane due to the large concentration gradient for this species. In other words, the decomposition product leaves the reaction side and, thus, shifts the reaction direction towards the decomposition. Both applied size-exclusion membranes are expected to be poorly selective for the TMA-EtOH since its molar mass is small compared with the membranes' MWCOs. However, the higher MWCO of the Spectra/Por 6 membrane is likely to conduct the TMA-EtOH better, which can explain the higher fade rates observed at the beginning of the experiment with this membrane (Fig. 4a). Over time, the fade rate decreases to lower values since the TMA-EtOH concentration accumulates in the anolyte, and the concentration gradient over the membrane decreases. TMA-EtOH is expected to be stable in the PFc/Zn RFB chemical environment. Both alcohol and tetraalkylammonium additives are used as additives to zinc-based batteries and provide significantly elongated cycling times due to staying inert and promoting homogeneous Zn electroplating.48,49 Therefore, the TMA-EtOH is not suspected to decompose in the presence of zinc and, thus, to be consumed at the zinc-half cell. Subsequently, the solubilizing unit accumulates in the anolyte until the TMA-EtOH cross-over between both half-cells occurs equally fast in both directions and, thus, reaches a dynamic equilibrium. This process takes longer in the RFB with the OS-NF-8800 membrane since its lower MWCO slows down the TMA-EtOH cross-over. Consequently, the capacity from the time dependency of RFBs with OS-NF-8800 generally appears to be more linear.
• Keeping the TMA-EtOH cation (contains OH– group) close to the hydrolyzed polymer group (contains HOOC– group) by including both ligands for coordination of each single zinc cation and, thus, facilitating backward reaction and shifting the hydrolysis equilibrium in the direction of the reagents.
• Involving TMA-EtOH in complex formation, increasing its hydrodynamic size in solution and, thus, preventing its cross-over.
Both possibilities could have a positive influence on the RFB stability. Nevertheless, the water and ammonia molecules can also be involved in the complex formation with zinc cations, thus replacing TMA-EtOH and polymer HOOC– groups in the zinc coordination sphere and decreasing the effect of the positive influences. Consequently, the NH4Cl-based supporting electrolyte was replaced by tetramethylammonium (TMA) chloride, which does not hydrolyse and does not exhibit Lewis base behavior. As a result, less ligands competed for zinc coordination in the catholyte, and the chances to either mitigate the hydrolysis or prevent the TMA-EtOH cross-over were increased. Furthermore, a TMA cation-based salt was applied for the supporting electrolyte replacement since it slows down zinc dendrite formation48 and is relatively small, which still keeps it possible to conduct current through the membranes. Thus, it became possible to both maintain normal flow cell performance and change zinc coordination in the electrolyte, obtaining other capacity fade rate results from RFB tests.
The PFc demonstrated similar behavior on a CV in 1 mM PFc, 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl, pH 4.5–5 electrolyte (Fig. S39†). Consequently, RFBs utilizing the OS-NF-8800 and the Spectra/Por 6 membranes were tested using the new supporting electrolyte (i.e., 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl, pH 4.5–5). The hydrochloric acid was used to keep the pH value of the anolyte in the same range as for the NH4-based solution in order to avoid zinc hydroxide formation and keep battery testing conditions more comparable. Fig. 6a displays the results for the full RFBs operated with 27 mM PFc in the catholyte. For both membranes, the capacity fade rates were smaller than the RFBs using NH4-based electrolyte at each corresponding time period. Fig. S40 and S41† show that no cross-over was detected by UV-vis and CV techniques for either of the full RFB tests. Furthermore, the fade rate in the full RFBs approached 0.3% d−1 at the last day of cycling, yielding a value that was previously observed during the symmetric cycling with the NH4-based electrolyte. To verify whether the decreased fade rate is caused by mitigation of the hydrolysis or of the TMA-EtOH cross-over, an additional UCSFFC experiment was performed. The newly adopted anolyte and catholyte were applied while keeping all the other experimental conditions equal to the first UCSFCC test (Fig. 6a). The capacity fade rate in this experiment resembles the results of the UCSFCC experiment with the NH4-based electrolyte; thus, it signifies that the hydrolysis is not mitigated in the TMACl-based electrolyte. Consequently, the higher stability observed in full RFB tests applying the TMACl-based electrolytes is reached via suppression of the TMA-EtOH cross-over.
Fig. 6b summarizes the capacity fade rates for the full and the symmetric RFBs presented in Section 3.1. Based on the discussion provided in Subsections 3.1.3 and 3.1.4, the final approved cycling conditions for the further thermal stability assessment are: (1) applying the OS-NF-8800 size-exclusion membrane, (2) battery cycling in the lower current regime, (3) applying 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl, pH 4.5–5 anolyte and 0.1 M ZnCl2, 0.8 M TMACl, 6 mM HCl, 27 mM PFc catholyte. For the finally adopted RFB charge–discharge cycling conditions, the corresponding practical battery voltage is 1.24 V (Fig. S42†), and coulombic and energy efficiencies are 99.3 and 90.0% respectively (Fig. S43†).
Further stability assessments were carried out under elevated temperatures to obtain a more detailed insight into both the reliability of the common heating setups and the thermal stability of PFc.
3.2 Thermal stability assessment
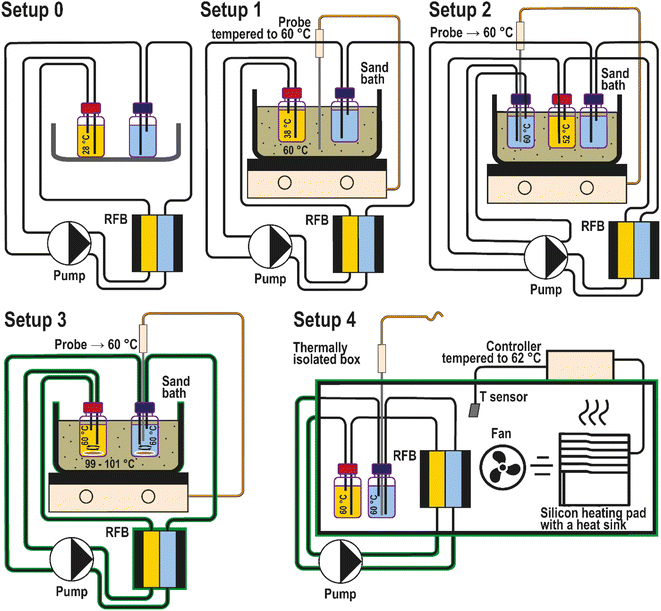
In the previous work by Borchers et al.,25 the PFc stability was assessed at room temperature and the desired 60 °C heating setup, which corresponds well to the high-temperature threshold we propose in this contribution. This experiment was performed in our group by positioning the RFB tanks in a sand bath tempered to 60 °C. As discussed and highlighted in our recent review article,6 the impact of sensor placement and heating setup type on the experimentally realized electrolyte temperature is poorly investigated. Specifically for the aforementioned setup, the heating occurs only at the interface between the electrolyte tanks and a sand/oil bath, neglecting the impact of heat exchange with the environment via tubings, the flow cell, and the pumps. To shed light on the accuracy of this and other possible heating setups, we have performed the thermal stability assessment in four different configurations (Fig. 7, setups 1 to 4). The applied configurations were chosen based on examples of heating setups previously reported in the literature. A detailed discussion about the related literature and reasons for our selection of the heating setups is provided in the ESI, page S9.†
The heating setups used for the comparison are depicted in Fig. 7. Each setup was adjusted to keep the catholyte temperature at 60 °C. At the end of each full RFB thermal stability tests, the catholyte temperature was measured by immersing the temperature probe into the catholyte. The probe was immersed only after the experiments to avoid corrosion and contamination of the catholyte half-cell. In the first setup, the temperature sensing probe of the sand bath was located in the sand of the bath and tempered to the desired 60 °C (Fig. 7). Astonishingly, the actual temperature reached in the catholyte corresponded to 38 °C. This difference between the desired and realized temperature presumably occurs because the RFB electrolyte is being heated only in the RFB tanks. At the same time, the rest of the fluid circuit is effectively cooled because of the heat exchange with the environment. Consequently, the capacity fade rates reported by Borchers et al. in the previous publication from our group correspond to an average bulk electrolyte temperature of 38 °C instead of 60 °C.
Positioning the blank temperature probe directly inside the catholyte causes corrosion of the (metal) probes. As a compromise, the temperature probe was placed into a separate tank in setup 2, which was filled with anolyte and not connected to the RFB. In this case, the anolyte solution was considered non-corrosive for the probe due to the anolyte's low standard redox potential. The liquid in the “control” tank is pumped out through a tube of the same length as in the RFB setup and then directly back into the tank. In this way, the T probe does not contact with the RFB at all, and heating conditions are better suited to heat up to the desired 60 °C. The measured catholyte temperature in this setup was 52 °C. The result highlights that the flow cell contributes significantly to the overall heat loss.
The T probe is positioned directly in the anolyte in the third setup. The tubes, the flow cell, and the sand bath were covered with a thermally insulating fiber material to avoid larger heat losses. Additionally, electrolyte mixing with a magnetic stirrer was performed to provide better temperature distribution in the tanks. Eventually, the desired 60 °C was reached for the catholyte. However, to establish these conditions, the sand in the bath was heated up to 100 °C.
Setup four corresponds to a thermostatic condition. It is hardly possible to place an actual thermostat inside a glovebox. Thus, a custom-made alternative was used in order to imitate a thermostat. In the setup the temperature probe from the heat bath is positioned inside the anolyte not for temperature control, but for its monitoring. The whole RFB setup (besides the pump) was placed inside the custom-made thermostat. Eventually, the measured temperature in the anolyte and the catholyte was 60 °C with this setup, while the surrounding gas temperature in the custom-made thermostat fluctuated between 62 and 65 °C.
Thus, the presented experiments reveal that the T probe's location in a setup strongly influences the accuracy of the established bulk electrolyte temperature. Only setups three and four enable the attainment of the 60 °C in the bulk catholyte.
Consequently, the uniformity of temperature distribution plays a vital role in the RFB thermal stability assessment, and it is the most homogeneous in thermostat-type heating setups. Thus, setup 4 is admitted to being the most suitable heating configuration for the thermal stability assessment. We emphasize the importance of this finding due to its significant influence on the reliability of the assessed data and compatibility of thermal stability assessment results across different studies.
Before applying the OCV technique for SOC assessment, its validation was performed. The catholyte OCV from SOC dependency is presented in Fig. S45.† According to the fit quality, the SOC measurement by OCV is of moderate accuracy; nevertheless, it is sufficient to detect significant SOC imbalances established during the UCSFCC experiment.
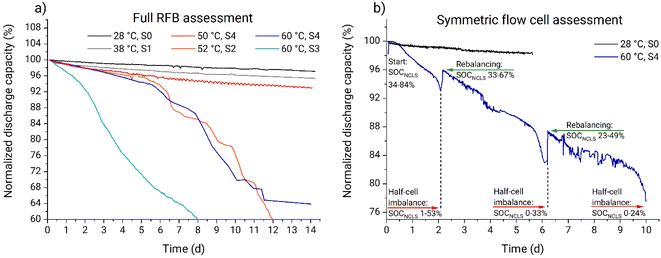
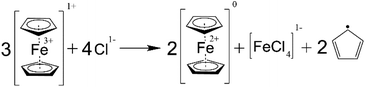
According to the measurement of the SOC in the NCLS which was performed on the days 0, 2, 6, and 10, the SOC range in the NCLS drifted to lower values during the symmetric cycling until the NCLS could not supply enough positive charges effectively becoming the capacity-limiting side (CLS) of the RFB (Fig. 8b). Consequently, this SOC imbalance manifested in an apparent, rapid capacity decrease of the symmetric RFB. Each time when the NCLS capacity was rebalanced by adding additional portions of fully charged catholyte, the accessible RFB capacity increased to the values that preceded the observed fade rate facilitations. This experiment confirmed that a self-discharge occurs at increased temperatures in the PFc solution. Subsequently, gas chromatographic-mass spectrometry (GC-MS) analysis was performed to analyse the gas above catholyte samples after keeping them at 60 °C overnight inside the glovebox. Both in the spectra of freshly prepared (not used in an RFB) and of cycled catholyte solutions, the pattern of cyclopentadiene rings was detected (Fig. S46–S48†). This indicates a decomposition of the ferrocene complex in the PFc polymer. While it is out of the scope of this study to unravel the exact mechanism, we are aware that a ferrocene decomposition, according to Scheme 1, was already reported for nonaqueous solutions.53,54 In acetone, nitromethane, and acetonitrile, a charged ferrocene complex decomposes in the presence of halogen anions (including chloride) forming two cyclopentadienyl anions which, subsequently, reduce the surrounding charged ferrocene molecules and form cyclopentadienyl radicals. While this reaction was not yet described for aqueous solutions, we believe the same or similar reaction causes the observed self-discharge and the detected cyclopentadiene in the gas phase above the electrolyte.
In addition, the PFc electrolyte self-reduction may occur via carboxylic acid groups' oxidation, performed by the charged ferrocene. The redox mediator activity of ferrocene during oxidation of carboxylic anions in acetonitrile solvent is comprehensively investigated by Hernández-Muñoz et al.55 The oxidation reaction mechanism for a diphenylacetate anion is depicted in ESI Scheme S1.† The particular anion was chosen since – as in our contribution – the α-carbon atom in the diphenylacetate structure (concerning the carboxylic group) has bulky substituents. According to the mechanism, two charged ferrocene molecules oxidize one carboxylic anion group, yielding two reduced ferrocenes, one carbon dioxide molecule, and one diphenyl methyl carbocation. Furthermore, it was proven that the occurring carbocations react with the solvent and ferrocene, causing subsequent fragmentation of the ferrocene. Such a mechanism can potentially explain both the observed PFc electrolyte self-reduction, and the presence of cyclopentadiene rings in the GC-MS spectra. Nevertheless, CO2 should then be one of the reaction products, though it was not detected during the GC-MS analysis. Consequently, we assume the occurrence of the carboxylic acid oxidation process is less likely, compared with the aforementioned direct decomposition of the charged ferrocene moieties. Hence, the same or similar reaction to the Scheme 1 is eventually assumed to cause the PFc electrolyte self-reduction.
One of the by-products of ferrocene decomposition is iron(III) chloride. The salt is also electrochemically active, thus, it is hard to conclude the rate of ferrocene decomposition from the flow cell capacity fade. Furthermore, other decomposition reactions may take place instead of the proposed mechanism. Regardless of the exact mechanism, the self-discharge intensively occurs for the PFc electrolyte at elevated temperatures, and one of the involved processes is the decomposition of the ferrocene complex. Consequently, we relate the facilitation of capacity fade observed for the full RFB cycling during longer-term thermal stability assessment to the self-discharge of the catholyte and to the subsequently caused half-cell imbalances.
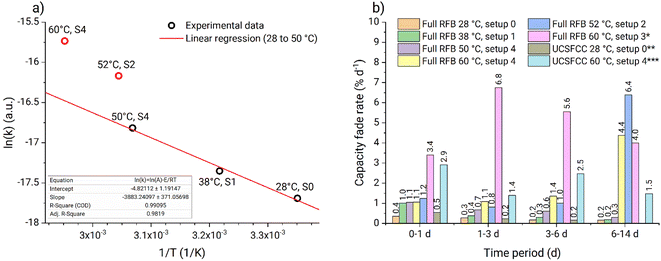
On the Arrhenius plot (Fig. 9a), the apparent fade rate constants obtained at temperatures from 28 to 50 °C form a straight line. Based on these three data points a linear regression was performed and the pre-exponential factor as well as the activation energy were estimated (Table 1). The apparent rate constant from experiment four (Table 1) is deviating because of the too high temperature gradient at the tank walls. Similarly, experiment six is deviating due to the gel phase formed on the tank walls (Fig. S44†). In contrast to that, no gelation was observed at any temperature using setup 4, where heating is performed homogeneously across the complete setup. Consequently, experiments four and five (Table 1) represent improper heating setups which had a significant influence on the obtained fade rates. Experiment two (Table 1) appeared to suit well into the linear regression. Most-likely, the temperature at the tank walls in setup 1 was not sufficiently high to cause the additional decomposition process. Thus, despite the low heating homogeneity provided by the setup, it did not influence the capacity fade rates. Consequently, experiment two can be used for the thermal stability evaluations. The ka from experiment five (Table 1) is measured in a suitable heating setup. However, faster fade rate is observed due to interference of the additional decomposition process at elevated temperatures. The facilitated capacity fade occurring in experiment five after 5.6 d also indicates the interference of the additional decomposition process.
| Nr | Setup | Bulk T, °C | k, s−1 | A, s−1 | E a, kJ mol−1 |
|---|---|---|---|---|---|
| 1 | 0 | 28 | 2.08 × 10−8 | 8.06 × 10−3 | 32.29 |
| 2 | 1 | 38 | 2.92 × 10−8 | ||
| 3 | 4 | 50 | 4.98 × 10−8 | ||
| 4 | 2 | 52 | 9.54 × 10−8 | ||
| 5 | 4 | 60 | 1.470 × 10−7 | ||
| 6 | 3 | 60 | — |
Therefore, we conclude that experiments performed in setups 0, 1, and 4 can be used for PFc thermal stability evaluation in our particular system. At temperatures from 28 to 50 °C the capacity fade rate exhibits linear behavior in Arrhenius coordinates. Thus, the stability of the catholyte in the full RFB can be estimated within 28 to 50 °C, using eqn (3) and (4) and the pre-exponential factor with the activation energy (Table 1). At 60 °C, the additional decomposition process starts to interfere; thus, 50 °C is considered the upper temperature stability threshold for the investigated PFc catholyte. Also, the model is considered to work accurately only for the range 28 to 50 °C.
The in operando thermal stability assessment results are summarized in Fig. 9b. Both at ambient temperature and 38 °C, the PFc electrolyte fade rate approaches 0.2% d−1 during the full RFB and symmetric cell tests, corresponding to moderate stability in accordance with the classification recently offered by Kwabi et al.4 At 50 °C, the fade rate stabilizes at 0.3% d−1. Above the 50 °C threshold, additional decomposition process starts to interfere, causing the parasitic self-discharge mechanism, increased half-cell charge imbalances, and facilitated capacity fade rate. Values obtained in setups 2 and 3 are considered invalid because of the too high inhomogeneity of the heating setups and electrolyte gelation at the tank walls. Prior to the rapid increase in RFB capacity fade at 60 °C in setup 4, the PFc catholyte exhibits a high capacity fade rate of 1.1% d−1. Overall, the observed fade rates for the PFc would translate to reaching the 80% SOH limit (commonly applied as the threshold for RFB lifetime) after roughly 110 days (<40 °C), 70 days (50 °C), and 20 days (60 °C, unlimited counter cell capacity is assumed, i.e., the facilitated capacity fade due to the half-cell imbalances is assumed not to interfere), respectively.
It is important to note that the capacity fade obtained during UCSFCC test at 60 °C in setup 4 is higher, than that obtained in full RFB test in the same conditions (Fig. 9b). Hereby we provide a hypothesis about possible origin of the observed deviation. The hypothesis represents a new perspective of the UCSFCC tests in general, thus, it should be comprehensively evaluated before accepting. The evaluation is out of the scope of the investigation; nevertheless, the hypothesis is briefly described to clarify the discrepancy of the full RFB and UCSFCC tests. The crucial processes that cause the discrepancy are the two-electrode configuration of the batteries and the half-cell charge imbalance. A RFB is a two-electrode cell, thus, the absolute potential adjusted by a potentiostat on the working electrode does not stay unchanged between charge–discharge cycles. It happens because the WE potential is controlled vs. the CE potential, that can drift along the charge–discharge cycling of the RFB. If an imbalance causes a negative drift of the CE absolute potential, then the WE absolute potential also undergoes the same negative drift. Subsequently, the charging cutoff overvoltage decreases with respect to the WE absolute redox potential, and smaller charging SOCs are reached. It causes a decrease of material utilization and an apparent facilitation of capacity fade rate. This process represents the first facilitation of the capacity fade, and it does not correspond to stability characteristics of a studied material, i.e., it causes capacity fade rate misinterpretation. Furthermore, if the imbalance continues to increase, the capacity of counter electrolyte (i.e., anolyte or NCLS in our contribution) becomes insufficient to provide charges to the working electrolyte (i.e., catholyte or CLS in our contribution). This causes the second facilitation of the capacity fade rate which also does not correspond to stability characteristics of a studied material and causes capacity fade rate misinterpretation.
This two-stage facilitation is well detectable in the UCSFCC test at 60 °C, in the Fig. 8b. During the first 0.5 d, the imbalance did not influence capacity fade. The periods 0.5 to 1.5 d, 2.5 to 5 d, and 6.5 to 9 d correspond to the first facilitation of the capacity fade. And the areas with fastest capacity fade occurring before rebalancing correspond to the second facilitation. At the same time, in the full RFB tests, the first facilitation is not detected. The reduced species in the anolyte are represented by zinc metal and are always not dissolved in the solution. Consequently, in full RFB tests, the imbalance does not cause increase of reduced species concentration in the anolyte with respect to the oxidized species, and thus, the negative drift of the counter-electrolyte potential is smaller. Thus, the drift of the working-electrolyte potential is also smaller and the effect of the first facilitation is weaker. Therefore, the first facilitation of the capacity fade occurs close to the second facilitation and cannot be distinguished from it.
In this contribution, in the symmetric battery, the NCLS has a two-fold excess capacity compared to the CLS. At the same time, in the full battery, the excess capacity corresponds to 11 times (i.e., 15 mL anolyte with 0.2 M electron equivalent concentration vs. the 10 mL catholyte with 0.027 M electron equivalent concentration in the thermal stability assessment tests). Consequently, the half-cell imbalances have significantly stronger influence on the obtained capacity fade during the symmetric cycling. In the full RFB at 60 °C using setup 6, the facilitated capacity fade occurred between days five and six (Fig. 8a); consequently, in the symmetric battery at same temperature, the imbalance is expected to influence the fade rate already starting from day one. This assumption confirms our previous statement that, in the UCSFCC test at 60 °C (Fig. 8b), the half-cell charge imbalance already started to facilitate the capacity fade rate after 0.5 d.
Generally, the UCSFCC tests are more preferable for the in operando stability assessment due to mitigation of cross-over effects.44 Nevertheless, specifically in this scientific contribution, the capacity fade rate from the UCSFCC is significantly more dependent on the half-cell charge imbalance than the full RFB cycling. Therefore, we suggest orienting on the results obtained in the full RFB tests since there the influence of the imbalance is smaller.
Given the lack of thermal stability experiments in organic RFB literature and the pitfalls of commonly applied heating setups unravelled in the study at hand, it is hard to set the result of our full RFB tests into a proper context. The only recent reports of dedicated thermal stability experiments we have found in the literature on organic cathodic substances are the following: TEMPO derivatives studied in aqueous-based electrolytes demonstrated capacity fade rates ranging from 0.4 (1.3 M TMA-TEMPO) to 3.4% d−1 (0.1 M TMA-TEMPO) at 40 °C oil bath temperature (cf.Fig. 7, setup 1). Considering the results presented in the present study, it must be expected that the actual temperature of the catholyte was lower than the stated value, since only the oil bath was tempered to 40 °C.18,23
Additionally, in the study by Quinn et al., the thermal stability of N-(2-(2-methoxyethoxy)-ethyl)phenothiazine (MEEPT) material was assessed in a non-aqueous electrolyte, applying a decently accurate heating setup (Table S1†) and performing in the 30 to 70 °C temperature range with 10 °C increments.24 Unfortunately, capacity fade values were not stated for the performed symmetric cycling and, thus, we have extracted the values from the figure five in the corresponding publication by converting the figure into data points using the WebPlotDigitizer program.56 The obtained charge capacity from time dependency is depicted in Fig. S54 in the ESI.† The values extracted by the program were used to calculate the capacity fade rate from the 10 cycles given at each temperature in the source publication. Accordingly, capacity fades of 4, 9, and 15% d−1 (for BF4 counterion) as well as 1, 8, and 18% d−1 (for TFSI counterion) were obtained for 40, 50, and 60 °C during the symmetric cycling of the MEEPT molecule, respectively (Fig. S54†). Due to the scarcity of the thermal stability evaluations of organic cathode materials, the obtained capacity fade rates of the newly emerged MEEPT study are valuable for providing an idea about the current state of the reported results. Nevertheless, we emphasize that the stated values represent a rough estimation, obtained by digitizing the graph from the work of Quinn et al.24 Hence, firstly, the capacity fades calculated from the original values may differ. Secondly, even if the digitalization of the figure was accurate, the statements on the fade rate behavior, which are based on such short battery tests, are of low reliability.
While the PFc investigated herein showed equal or superior thermal stability compared to currently existing literature reports on other organic redox-active molecules, it would probably not be suitable for practical applications in its current form without further optimisation of the ferrocene copolymer.
4 Conclusions
In this contribution, ferrocene-based FPMAm-co-METAC polymer (PFc) was applied as a catholyte in an aqueous, hybrid redox flow battery (RFB) vs. zinc. The polymer-based RFB exploits materials based on environmentally benign electroactive units and operates with a size-exclusion membrane (0.6 to 1 kDa) with no detectable PFc cross-over. It demonstrated a high voltage of 1.24 V, coulombic and energy efficiencies of 99.3% and 90.0%, respectively, and a capacity fade rate of 0.2% d−1 (after 14 days) at ambient temperatures (28 °C) in a glovebox. The PFc/Zn system was chosen to study the battery performance properties of the PFc thoroughly in order to extend our knowledge of this promising polymer. Furthermore, due to the reported high-temperature stability of the PFc it was considered an excellent candidate for conducting a comparative study of heating setups. Therefore, this study addresses the deficient understanding of thermal stability assessments in current organic RFB literature by unravelling the most common pitfalls.Furthermore, the PFc was utilized as a model system to validate the applicability of the steady-state amperometry for SOC measurement for polymer-based RFBs. The technique has provided deviations below 4% from the expected values in measurements over the complete SOC range at low PFc concentrations of 27 mM. The ex situ SOC analysis of the PFc at different temperatures has revealed an oxygen intolerance of the PFc, thus all subsequent tests were performed in an argon-filled glovebox.
Furthermore, the direct comparison of full cell tests and volumetrically unbalanced, compositionally symmetric PFc/PFc flow cell experiments at room temperature exhibited a more than four-fold higher capacity fade in the PFc/Zn RFB. After excluding PFc cross-over, subsequent ESI-MS analyses revealed detachment of the TMA-EtOH solubilizing unit from the polymer backbone. The reversible condensation-hydrolysis of the ester bond in the polymer solubilizing unit and the following cross-over of the TMA-EtOH unit to the anolyte were the main reasons for the significant deviation in the capacity fade rates. The unravelled decomposition mechanism is typical for polymer materials, since ester bonds are often applied to join polymer active groups to a backbone or to compose the latter.57,58 Nevertheless, it is worth noting that the capacity fade related to this decomposition in batteries can be influenced by regulating the hydrolysis product content in the electrolyte. Furthermore, this mechanism represents a good example of a case, when the cross-over of a side-reaction product that is not electroactive may facilitate the capacity fade rate of the RFB, whereas cross-over of the electroactive molecule does not occur to a measurable extent.
A sharp increase in capacity fade rate was observed during longer-term RFB cycling for temperatures equal to or above 52 °C. Subsequently, an additional UCSFCC experiment at 60 °C combined with ex situ SOC assessment via OCV measurement of the non-capacity-limiting side (NCLS) electrolyte revealed that a parasitic self-discharge reaction caused a SOC imbalance between the half-cells, which over time makes the NCLS the capacity-limiting side and pushes the observed capacity fade increase. GC-MS analysis of the gas phase above heat-treated catholyte samples (60 °C) has indicated the occurrence of 1,3-cyclopentadiene rings. While unravelling the exact mechanism was out of the scope of this study, these results indicate an intrinsic decomposition of the ferrocene complex with the following reduction of the PFc electrolyte. Therefore, the process causes RFB half-cell imbalances, and subsequent capacity fade.
Thermal stability of the PFc was assessed in operando in a combination of PFc/Zn full cells and volumetrically unbalanced, compositionally symmetric PFc/PFc flow cell experiments in the temperature range from 28 to 60 °C. The results suggest an intrinsic capacity fade rate of 0.2% d−1 (up to 38 °C, sand bath setup), 0.3% d−1 (at 50 °C, thermostat setup), and 1.1% d−1 (at 60 °C, thermostat setup) during the period before the battery failure (time before the sharp increase in capacity fade rate, which is discussed in the previous paragraph).
In conclusion, the additional insights obtained on the PFc redox-active polymer enhanced our understanding of this recently reported candidate for polymer-based flow batteries. Our results suggest that further research is required on more suitable and stable solubilizing groups for ferrocene-based copolymers. The exact mechanism of the ferrocene decomposition needs to be investigated to understand if and how it may be suppressed.
Finally, we would like to highlight the demand for the organic flow battery community to establish thermal stability assessment protocols. Based on the dedicated evaluation and comparison of thermal stability assessment setups and considering the current state of the literature, we would like to contribute the following suggestions to this process:
• The commonly applied heating setups, relying on oil/sand/water baths with temperature sensors placed not directly in the electrolyte, are suspected to control the temperature inaccurately;
• Exceptionally placement of the temperature sensing probe directly inside one of the RFB electrolytes provides significantly more accurate temperature establishment;
• Positioning of the probe outside from the RFB electrolyte and preliminary calibration for the proper correspondence of the probe readouts to the RFB reached electrolyte temperature as in the work of Quinn et al.24 may be a good alternative for an accurate heating setup;
• The oil/sand/water baths should be avoided since they provide strongly localized heating. Thus firstly, it is challenging to measure the average electrolyte temperature accurately, and secondly, such configuration can cause high-temperature gradients between the heat bath and bulk electrolyte, facilitating side reactions at the electrolyte–reservoir interface;
• Heat exchange with the environment via tubings and the flow cell is significant, and we strongly recommend utilizing commercial or custom-made thermostats similar to the one presented in this study to heat the complete flow battery setup (i.e., at least a large part of the tubing, the reservoirs, and the flow cell);
• We propose to measure thermal stability with an upper-temperature limit of up to 60 °C, because further temperature increase is hardly expected to happen in practically applied RFB systems;
• Additional studies devoted to RFB electrolyte temperature simulation in cold regions would help to better understand what lower limits should be applied in thermal stability assessment.
Proper, reproducible thermal stability assessment experiments will help to unravel decomposition mechanisms, discover new approaches to modify the existing redox-active molecules, and identify new capacity fade suppression/recovery approaches. This will eventually lead to the development of significantly more durable species for commercial applications.
Author contributions
Ivan A. Volodin: investigation (lead), conceptualization (lead), methodology (lead), resources (supporting), data curation (lead), writing – original draft (lead). Katrin Wulf: investigation (supporting). Felix Tzschoekell: resources (lead – synthesis of the PFc). Steffi Stumpf: investigation (supporting – EDX scanning). Stephanie Hoeppener: resources (supporting – EDX scanning). Nicole Fritz: investigation (supporting – ESI-MS analysis). Cristina F. Morales-Reyes: investigation (supporting – AAS analysis). Thomas Wichard: data curation (supporting – AAS analysis), resources (supporting – AAS analysis), writing – review and editing (supporting). Nico Ueberschaar: investigation (supporting – GC-MS), data curation (supporting – GC-MS and ESI-MS). Christian Stolze: conceptualization (supporting), methodology (supporting), supervision of I. A. V. (equal), writing – review and editing (lead). Martin D. Hager: supervision of I. A. V. (equal), funding acquisition (equal), writing – review and editing (supporting). Ulrich S. Schubert: supervision of I. A. V. (equal), funding acquisition (equal), writing – review and editing (supporting).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support by the Thuringian Ministry for Economic Affairs, Science and Digital Society (TMWWdG) (CEEC-01/2020) and the Thüringer Aufbaubank (TAB). The project on which these results are based was funded by the Free State of Thuringia under numbers 2016 IZN 0009, 2022 IZN 0011, 2022 IZN 0013 and co-financed by funds from the European Union within the European Regional Development Fund (ERFE) framework. Funding by the European Union (ERC, FutureBAT, 101054271) is greatly acknowledged. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. Furthermore, we acknowledge the German Research Foundation (DFG) for the grant for establishment of the SEM and EDX facilities in the Jena Center for Soft Matter (JCSM), and the Chilean National Agency for Research and Development (ANID) and German Academic Exchange Service (DAAD)/Scholarship Program bilateral agreement between Becas Chile–DAAD 2017 for financial support of Cristina F. Morales-Reyes.References
- A. B. Gallo, J. R. Simões-Moreira, H. K. M. Costa, M. M. Santos and E. Moutinho dos Santos, Renewable Sustainable Energy Rev., 2016, 65, 800–822 CrossRef CAS.
- A. G. Olabi, C. Onumaegbu, T. Wilberforce, M. Ramadan, M. A. Abdelkareem and A. H. Al – Alami, Energy, 2021, 214, 118987 CrossRef CAS.
- E. Sánchez-Díez, E. Ventosa, M. Guarnieri, A. Trovò, C. Flox, R. Marcilla, F. Soavi, P. Mazur, E. Aranzabe and R. Ferret, J. Power Sources, 2021, 481, 228804 CrossRef.
- D. G. Kwabi, Y. Ji and M. J. Aziz, Chem. Rev., 2020, 120, 6467–6489 CrossRef CAS PubMed.
- Y. Wen, Y. Xu, J. Cheng, G. Cao and Y. Yang, Electrochim. Acta, 2013, 96, 268–273 CrossRef CAS.
- O. Nolte, I. A. Volodin, C. Stolze, M. D. Hager and U. S. Schubert, Mater. Horiz., 2021, 8, 1866–1925 RSC.
- B. Hu, J. Luo, C. DeBruler, M. Hu, W. Wu and T. L. Liu, in Encyclopedia of Inorganic and Bioinorganic Chemistry, 2019, pp. 1–25, DOI:10.1002/9781119951438.eibc2679.
- X. Wei, W. Pan, W. Duan, A. Hollas, Z. Yang, B. Li, Z. Nie, J. Liu, D. Reed, W. Wang and V. Sprenkle, ACS Energy Lett., 2017, 2, 2187–2204 CrossRef CAS.
- E. F. Kerr, Z. Tang, T. Y. George, S. Jin, E. M. Fell, K. Amini, Y. Jing, M. Wu, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2022, 8, 600–607 CrossRef.
- I. A. Volodin, C. Stolze, O. Nolte, P. Rohland, M. D. Hager and U. S. Schubert, ACS Appl. Energy Mater., 2022, 6, 302–316 CrossRef.
- E. M. Fell and M. J. Aziz, J. Electrochem. Soc., 2023, 170, 100507 CrossRef.
- J. Ren, Y. Li, Z. Wang, J. Sun, Q. Yue, X. Fan and T. Zhao, Int. J. Heat Mass Transfer, 2023, 203, 123818 CrossRef CAS.
- L. Li, S. Kim, W. Wang, M. Vijayakumar, Z. Nie, B. Chen, J. Zhang, G. Xia, J. Hu, G. Graff, J. Liu and Z. Yang, Adv. Energy Mater., 2011, 1, 394–400 CrossRef CAS.
- M. Skyllas-Kazacos, L. Cao, M. Kazacos, N. Kausar and A. Mousa, ChemSusChem, 2016, 9, 1521–1543 CrossRef CAS PubMed.
- A. Tang and M. Skyllas-Kazacos, ChemPlusChem, 2015, 80, 368–375 CrossRef CAS.
- S. Xiao, L. Yu, L. Wu, L. Liu, X. Qiu and J. Xi, Electrochim. Acta, 2016, 187, 525–534 CrossRef CAS.
- Y. Jing, E. W. Zhao, M. A. Goulet, M. Bahari, E. M. Fell, S. Jin, A. Davoodi, E. Jonsson, M. Wu, C. P. Grey, R. G. Gordon and M. J. Aziz, Nat. Chem., 2022, 14, 1103–1109 CrossRef CAS PubMed.
- O. Nolte, P. Rohland, N. Ueberschaar, M. D. Hager and U. S. Schubert, J. Power Sources, 2022, 525, 230996 CrossRef CAS.
- A. Permatasari, W. Lee and Y. Kwon, Chem. Eng. J., 2020, 383, 123085 CrossRef CAS.
- L. J. Small, H. D. Pratt and T. M. Anderson, J. Electrochem. Soc., 2019, 166, A2536–A2542 CrossRef CAS.
- P. Rohland, K. Schreyer, M. D. Hager and U. S. Schubert, RSC Adv., 2021, 11, 38759–38764 RSC.
- J. C. Xu, S. Pang, X. Y. Wang, P. Wang and Y. L. Ji, Joule, 2021, 5, 2437–2449 CrossRef CAS.
- P. Rohland, O. Nolte, K. Schreyer, H. Gorls, M. D. Hager and U. S. Schubert, Adv. Mater., 2022, 3, 4278–4288 RSC.
- A. Quinn, K. Ripley, N. Matteucci, B. Neyhouse, C. Brown, W. Woltmann and F. Brushett, J. Electrochem. Soc., 2023, 170, 120520 CrossRef.
- P. S. Borchers, M. Strumpf, C. Friebe, I. Nischang, M. D. Hager, J. Elbert and U. S. Schubert, Adv. Energy Mater., 2020, 10, 2001825 CrossRef CAS.
- Y. Lee, D. Yun, J. Park, G. Hwang, D. Chung, M. Kim and J. Jeon, J. Power Sources, 2022, 547, 232007 CrossRef CAS.
- P. K. Leung, C. P. de Leon and F. C. Walsh, Electrochim. Acta, 2012, 80, 7–14 CrossRef CAS.
- G. Nikiforidis, L. Berlouis, D. Hall and D. Hodgson, J. Power Sources, 2013, 243, 691–698 CrossRef CAS.
- G. Nikiforidis, L. Berlouis, D. Hall and D. Hodgson, Electrochim. Acta, 2014, 115, 621–629 CrossRef CAS.
- H. Zhang, D. G. Lek, S. Huang, Y. M. Lee and Q. Wang, Adv. Mater., 2022, 34, 2202266 CrossRef CAS PubMed.
- X. J. Li, T. Y. Li, P. C. Xu, C. X. Xie, Y. H. Zhang and X. F. Li, Adv. Funct. Mater., 2021, 31, 2100133 CrossRef CAS.
- J. Hu, M. Yue, H. Zhang, Z. Yuan and X. Li, Angew Chem. Int. Ed. Engl., 2020, 59, 6715–6719 CrossRef CAS PubMed.
- B. Li, Z. M. Nie, M. Vijayakumar, G. S. Li, J. Liu, V. Sprenkle and W. Wang, Nat. Commun., 2015, 6, 6303 CrossRef CAS PubMed.
- Y.-P. Deng, R. Liang, G. Jiang, Y. Jiang, A. Yu and Z. Chen, ACS Energy Lett., 2020, 5, 1665–1675 CrossRef CAS.
- B. N. Jha, N. Singh, A. N. Sahay and A. Raghuvanshi, J. Electron. Mater., 2021, 50, 6073–6086 CrossRef CAS.
- S. Kügler, R. E. Cooper, C. E. Wegner, J. F. Mohr, T. Wichard and K. Küsel, Sci. Total Environ., 2019, 646, 972–988 CrossRef PubMed.
- M. Reichenbächer and J. W. Einax, in Challenges in Analytical Quality Assurance, Springer, Heidelberg, 2011, pp. 83–99 Search PubMed.
- T. Janoschka, N. Martin, U. Martin, C. Friebe, S. Morgenstern, H. Hiller, M. D. Hager and U. S. Schubert, Nature, 2015, 527, 78–81 CrossRef CAS PubMed.
- C. Stolze, J. P. Meurer, M. D. Hager and U. S. Schubert, Chem. Mater., 2019, 31, 5363–5369 CrossRef CAS.
- S. Ressel, F. Bill, L. Holtz, N. Janshen, A. Chica, T. Flower, C. Weidlich and T. Struckmann, J. Power Sources, 2018, 378, 776–783 CrossRef CAS.
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, Great Britain, 9th edn, 2010 Search PubMed.
- Y. Ding, C. Zhang, L. Zhang, Y. Zhou and G. Yu, Chem. Soc. Rev., 2018, 47, 69–103 RSC.
- J. Winsberg, C. Stolze, A. Schwenke, S. Muench, M. D. Hager and U. S. Schubert, ACS Energy Lett., 2017, 2, 411–416 CrossRef CAS.
- M.-A. Goulet and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A1466–A1477 CrossRef CAS.
- C. Stolze, P. Rohland, K. Zub, O. Nolte, M. D. Hager and U. S. Schubert, Energy Convers. Manage., 2022, 14, 100188 CrossRef CAS.
- V. S. Meka, M. K. G. Sing, M. R. Pichika, S. R. Nali, V. R. M. Kolapalli and P. Kesharwani, Drug Discovery Today, 2017, 22, 1697–1706 CrossRef CAS PubMed.
- C. E. Sing and S. L. Perry, Soft Matter, 2020, 16, 2885–2914 RSC.
- D. P. Trudgeon, K. Qiu, X. Li, T. Mallick, O. O. Taiwo, B. Chakrabarti, V. Yufit, N. P. Brandon, D. Crevillen-Garcia and A. Shah, J. Power Sources, 2019, 412, 44–54 CrossRef CAS.
- X. S. Lin, Z. R. Wang, L. H. Ge, J. W. Xu, W. Q. Ma, M. M. Ren, W. L. Liu, J. S. Yao and C. B. Zhang, ChemElectroChem, 2022, 9, e202101724 CrossRef CAS.
- S. Di Bella, Dalton Trans., 2021, 50, 6050–6063 RSC.
- A. Krezel and W. Maret, Arch. Biochem. Biophys., 2016, 611, 3–19 CrossRef CAS PubMed.
- S.-S. Chen, J. Fan, T.-a. Okamura, M.-S. Chen, Z. Su, W.-Y. Sun and N. Ueyama, Cryst. Growth Des., 2009, 10, 812–822 CrossRef.
- R. Prins, A. R. Korswagen and A. G. T. G. Kortbeek, J. Organomet. Chem., 1972, 39, 335–344 CrossRef CAS.
- L. Briot, M. Petit, Q. Cacciuttolo and M.-C. Pera, J. Power Sources, 2022, 536, 231427 CrossRef CAS.
- L. S. Hernández-Muñoz, A. Galano, P. D. Astudillo-Sánchez, M. M. Abu-Omar and F. J. González, Electrochim. Acta, 2014, 136, 542–549 CrossRef.
- WebPlotDigitizer Programm, https://automeris.io/WebPlotDigitizer/, accessed November 2023 Search PubMed.
- S. Huang, X. Kong, Y. Xiong, X. Zhang, H. Chen, W. Jiang, Y. Niu, W. Xu and C. Ren, Eur. Polym. J., 2020, 141, 110094 CrossRef CAS.
- A. Saal, T. Hagemann and U. S. Schubert, Adv. Energy Mater., 2020, 11, 2001984 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Evaluation and mitigation of the zinc dendrite growth; a brief review of temperatures applied during in operando thermal stability assessment in redox flow batteries (RFBs); reasoning of the choice of the heating setups for the investigation; heating setups applied for in situ thermal stability assessment in RFBs; chemical characterization of the PFc; full RFB practical voltage; potentiometric titration; atomic absorption spectroscopy; exemplary curves from the RFB tests in higher current cycling regime; validation of the calibration-free amperometric SOC measurement technique; photographs on the post mortem RFB electrolytes; capacity fade during the UCSFCC test in, utilizing NH4Cl-based electrolyte; comparison of RFB performances, utilizing OS-NF-8800 membrane and cycling in different regimes; dendrite formation evaluation and studies; exemplary curves from the RFB tests in lower current cycling regime; UV-vis calibration for PFc containing solutions; cross-over evaluation in the NH4Cl-based electrolytes; qualitative analysis of PFc capacity fade in RFB anolyte via CV; electrospray ionisation mass spectrometry; cyclic voltammetry of the PFc in the newly applied tetramethylammonium-based electrolyte; cross-over evaluation in TMACl-based electrolytes; estimation of RFB technical parameters under the finalized testing conditions; photographs depicting precipitate formation on RFB tank walls in setup 3; validation of the SOC assessment by the OCV measurement technique; GS-MS results; evaluation of the apparent rate constants for PFc catholyte fade in full RFBs using different heating setups; capacity fade rates estimated from the digitized results from the study by Quinn et al.; mechanism of the diphenylacetate oxidation redox mediated by ferrocene. See DOI: https://doi.org/10.1039/d3ta05809c |
| This journal is © The Royal Society of Chemistry 2024 |