Machine learning facilitated by microscopic features for discovery of novel magnetic double perovskites

Abstract

Double perovskites are a growing class of compounds with prospects for realization of novel magnetic behaviors. The rich chemistry of double perovskites calls for high-throughput computational screening that can be followed by or combined with machine-learning techniques. Yet, most approaches neglect the bulk of microscopic information implicitly provided by first-principles calculations, severely reducing the predictive power. In this work, we remedy this drawback by including onsite energies and transfer integrals between the d states of magnetic atoms. These quantities were computed by Wannierization of the relevant energy bands. By combining them with the experimental information on the magnetism of studied materials and applying machine learning, we constructed a model capable of predicting the magnetic properties of the remaining materials whose magnetism has not been addressed experimentally. Our approach combines classification learning to distinguish between double perovskites with dominant ferromagnetic or antiferromagnetic interactions and regression employed to estimate magnetic transition temperatures. In this way, we identified one antiferromagnet and three ferromagnets with a high transition temperature. Another 28 antiferromagnetic candidates were identified as magnetically frustrated compounds. Among them, cubic Ba₂LaReO₆ shows the highest frustration parameter, which is further validated by a direct first-principles calculation. Our methodology holds promise for eliminating the need for resource-demanding calculations.

---

1. Introduction

Discovering new materials with desired functionalities and understanding physical mechanisms behind these functionalities are central goals of materials science and engineering. For systematic studies, particularly advantageous are material classes in which the small number of structure types is contrasted by possibly rich chemistry. One such class is double perovskites with the general chemical formula A₂BB′O₆, where A cations occupy voids of the three-dimensional framework formed by corner-sharing BO₆ and B′O₆ octahedra. The interplay between electronic correlations and the spin–orbit coupling (SOC) in the d-shells of B and/or B′ can facilitate applications of double perovskites in data storage, energy conversion, contactless sensing, spin-polarized electrical conductivity, superconductivity, and catalysis.^1–3

The magnetic properties of double perovskites are very diverse. Following the discovery of large magnetoresistance in Sr₂FeMoO₆,⁴ several promising candidates with high magnetic transition temperature (T_c) were suggested for spintronic applications, such as Sr₂FeReO₆ (T_c = 401 K), Sr₂CrWO₆ (T_c = 450 K), Sr₂CrReO₆ (T_c = 625 K) and Sr₂CrOsO₆ (T_c = 725 K).⁵ On the other hand, long-range magnetic ordering in double perovskites can be suppressed by magnetic frustration, giving rise to the valence bond glass state in Ba₂YMoO₆.⁶

This remarkable disparity is driven not only by chemistry, but also by structural degrees of freedom. Alternating BO₆ and B′O₆ octahedra form a three-dimensional framework; A cations occupy the voids of this framework. In a regular octahedral environment, the d orbitals of B and B′ split into threefold degenerate t_2g (d_xy, d_yz, d_xz) and twofold degenerate states. While the strict degeneracy is often lifted by distortions of octahedra, the crystal field splitting remains significant and largely shapes the electronic properties of double perovskites. In addition to distortions, different sizes of A and B/B′ ions may give rise to octahedral tilts and rotations. As a result, various structural types can be formed, such as cubic Fm3̄m, tetragonal I4/m, monoclinic P2₁/n, I2/m, rhombohedral R3̄ and R3. Both distortions and tilts play a major role in the physical properties, as they are strongly intertwined with the charge, orbital, and spin degrees of freedom.⁷

The magnetic exchange in double perovskites strongly depends on the atomic arrangement and the valence of B and B′ cations. Exchange interactions are contributed by different virtual electron transfer processes that can couple the t_2g or e_g states of B with the t_2g or e_g states of B′, giving rise to multiple – and often competing – processes. Two such processes are illustrated in Fig. 1, where the t_2g states of B′ are coupled to the t_2g states of the B cation on the right, and the e_g states of B′ are coupled to the e_g states of the B cation on the left. In this case, B and B′ ions in double perovskites interact strongly with each other, and the magnetism is driven predominantly by the B–B′ interaction. Electron transfer processes within each sublattice, B or B′, are also possible. If B′ has an empty d shell, the interaction within the B sublattice determines the magnetic order, despite the large separation between the nearest neighbors.

Fig. 1 The workflow of the machine-learning part of this work. The training data set comprises 113 experimentally studied double perovskites; the resulting model is used to predict the magnetic properties of the remaining 68 materials. In the first step, a classification model is constructed to distinguish between antiferromagnetic and ferromagnetic compounds. Here, only atomic features are used. In the second step, the regression model is constructed based on the transfer integrals. This latter model predicts the ordering temperature.

Transfer integrals are quantum-mechanical amplitudes describing the virtual electron transfer between a certain pair of orbitals. In the literature,⁸ the respective terms are called “onsite” if the pertinent orbitals belong to the same atom, and “transfer integrals” or “transfers” otherwise. Unfortunately, the knowledge of all transfer integrals between the magnetically active orbitals is not sufficient to evaluate the respective magnetic exchange: strong electronic correlations in the d shell lead to a many-body quantum problem whose generic solution is unknown. For specific electronic configurations, such as heavy d⁵ metals in an edge-sharing octahedral environment,⁹ perturbative treatments or solving the problem on a small cluster can deliver parameterized solutions, provided that interaction parameters and the strength of SOC are known. In all other situations, insights are limited to empirical assessments, such as the Goodenough-Kanamori rules, that are at best qualitative. Therefore, predicting the magnetic ground state is difficult even on a case-by-case basis, let alone in high-throughput calculations.

An alternative, more direct way of obtaining exchange integrals is performing density functional theory (DFT) calculations of different spin configurations. If only collinear arrangements are considered, the DFT total energies can be mapped onto a Heisenberg Hamiltonian and its classical ground state can be addressed by energy minimization. The treatment of noncollinear configurations is even more complicated: the inclusion of a full spin-density matrix and the necessary symmetry reduction leads to a considerably longer computational time.¹⁰ Therefore, screening the total energy of various configurations is almost impossible in a high-throughput fashion, especially for systems with metastable solutions that are sensitive to initially set magnetic moments and U values.¹¹

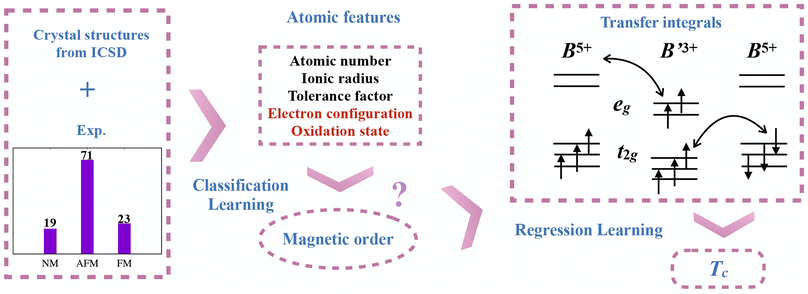
Because no method can be universally applied to derive magnetic interactions, magnetic double perovskites have not been studied much by high-throughput calculations. Machine learning^12–14 assisted high-throughput computations show excellent potential for exploring the physical properties particularly when the understanding of underlying mechanisms is elusive. Even though the majority of them don't have a large amount of training data, with experimental inputs or more in-depth features, a machine learning model is capable of accurate predictions for a small dataset.^11,14–17 For example, a regression model with 157 experimental known data points proposed 26 new high Curie temperature two-dimensional ferromagnetic materials with a testing root-mean-square error (RMSE) of 174 K.¹¹ Here, we're inclined to explore representative magnetic features which can further improve the predictive power and make up for the limited experimental sample size.

Presently, there are more than 400 ordered double perovskites known experimentally (including doped, high-pressure and high-temperature synthesized phases),¹⁸ and this number is sufficient for several machine-learning techniques. But at present, machine learning studies are either based on simple inputs (e.g. radius, valence difference, atomic mass, tolerance factor and so on)¹³ or total energies obtained for collinear configurations,¹⁰ limiting their predictive power. For more accurate assessments, it is crucial to resort to physically relevant inputs and accurate targets which determine the predictive precision of the machine learning.

In this work, we demonstrate that using the microscopic information contained in the transfer integrals in combination with the experimental information can drastically enhance the accuracy, leading to accurate predictions of the magnetically ordered state and the critical temperature. As shown in Fig. 1, by using 113 experimentally known double perovskites as the training dataset, we were able to predict the magnetic properties of 68 further double perovskites. This is done in two steps. First, a classification machine-learning model with atomic features was used to distinguish between antiferromagnets and ferromagnets. In the second step, we constructed a regression model which comprises the onsite energies and the transfer integrals between the first few neighbors; leading transfer integrals in the three channels – t_2g–e_g, t_2g–t_2g, and e_g–e_g – are included separately. Note that these microscopic terms underlie different exchange mechanisms, including direct exchange, superexchange and double exchange. All these terms were calculated by Wannierization of the nonmagnetic band structures of the respective materials. In this way, we obtained a model which predicts the ordering temperature with a RMSE of 18 and 61 K, for antiferromagnets and ferromagnets, respectively. One antiferromagnet and three ferromagnets with a high ordering temperature were identified. We also found 28 antiferromagnets combining a low transition temperature (≤50 K) with sizable transfer integrals (≥100 meV); these materials are likely magnetically frustrated and therefore may harbor exotic magnetic ground states. Since frustration is often assessed as the ratio of the Weiss temperature and the magnetic ordering temperature, we constructed an additional regression model to predict the Weiss temperature (RMSE = 76 K) and identify systems with a large frustration parameter. We obtained the largest ratio of 12 for cubic Ba₂LaReO₆; the sizable frustration was subsequently confirmed by a direct DFT + U + SOC calculation. This demonstrates that transfer integrals can be efficiently used in machine-learning models that aim at describing magnetic properties.

2. Methods

2.1 Wannier function calculations

Experimentally reported crystal structures of double perovskites are drawn from the inorganic crystal structure database (ICSD),¹⁹ including structures synthesized at high pressure or high temperature. We restrict ourselves to the fully ordered and slightly doped (with <0.1 fractional occupancy of a certain element within an individual Wyckoff position) structures; doping is neglected in the calculations of the latter structures. For all materials, internal atomic coordinates were optimized with respect to the GGA energy by keeping all symmetry operations of the respective space group; the resulting residual forces do not exceed 0.005 eV Å⁻¹. Density functional theory band-structure calculations and Wannier projections are performed using an all-electron full potential local-orbital scheme implemented in the FPLO code;²⁰ the initial projections are done for the d-dominated bands of B and B′ cations in the relevant energy range around the Fermi level. The Brillouin zones were sampled using meshes of 500, 1715 and 1470 k-points per reciprocal atom for cubic Fm3̄m, tetragonal I4/m and monoclinic P2₁/n space groups, respectively. The Wannier basis, i.e. the presence of t_2g and/or e_g as well as B and/or B′, and the energy window depend on the material. For instance, in Ba₂CoMoO₆ we consider the energy range between −2 and 2 eV which contains besides the t_2g and e_g orbitals of Co also the t_2g orbitals of Mo. The 4f electrons of Pr, Nd, Sm, Eu, Gd, Tb, Dy, Er, Tm, and Yb are treated by the open-core approach by putting electrons of each spin channel into the core.

2.2 Machine learning models

Machine learning contains two parts. As mentioned before, the Goldschmidt tolerance factoris a simple, yet powerful descriptor for addressing the structural stability.¹² Therefore, we use this tolerance factor together with other atomic features like atomic numbers, ionic radius, electron count of the partly occupied s, d and f shells and oxidation states of B and B′ cations as inputs for three classifier ML models: neutral network (MLP),²¹ gradient boosting (XGBoost)²² and adaptive boosting (AdaBoost)²³ implemented in the scikit-learn²⁴ package. Leave-one-out validation was used to evaluate the performance of the classification model. This validation leaves one sample to test and the remaining samples to train the model. The accuracy is defined by the number of true cases divided by the total number of datasets.

Then with the computed matrices of the largest t_2g–e_g, t_2g–t_2g, e_g–e_g transfer integral of the short-range connections plus the onsite energies, the AdaBoost regression model was used to fit the magnetic transition temperature (T_c) and Curie–Weiss temperature (Θ). The dataset is randomly split into 80/20 training/testing datasets for validation.

2.3 DFT + U + SOC calculations of Ba₂LaRe/RuO₆

First-principles DFT calculations of Ba₂LaReO₆ and Ba₂LaRuO₆ are performed with the projector-augmented-wave basis set implemented in the Vienna ab initio simulation package.²⁵ The exchange-correlation energy is evaluated within the generalized gradient approximation (GGA) using Perdew, Burke, and Ernzerhof parametrization²⁶ and a roughly constant density of k-points (30 ų) of a Monkhorst-Pack²⁷ mesh is used to sample the Brillouin zones. Electron correlation effects were treated within DFT + U + SOC with the Coulomb repulsion U = 2 eV (6 eV) and the Hund exchange J = 0.4 eV (0.5 eV) for Re (Ru). For Ba₂LaReO₆ (Ba₂LaRuO₆), the total energies of one FM and one (six) AFM spin configurations are mapped onto a Heisenberg model; magnetic exchanges were obtained by a least-squares solution to the system of linear equations. Detailed expressions are provided in the ESI.†

3. Results

3.1 Magnetic order: classification machine learning

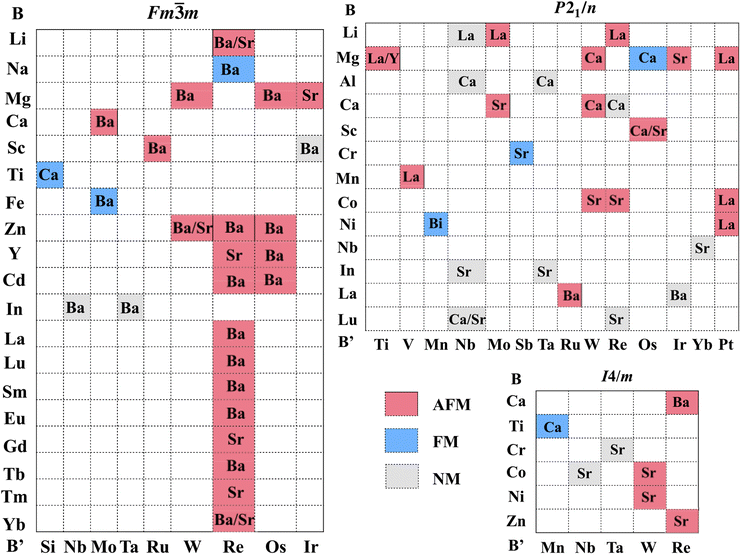
The classical review by Vasala and Karppinen summarizes the experimental information on more than 400 ordered double perovskites.¹⁸ In this work, we first focus on three most populated space groups: cubic Fm3̄m, tetragonal I4/m, and monoclinic P2₁/n (Fig. 2). These three space groups comprise 181 magnetic and non-magnetic stoichiometric double perovskites with structures available in the Inorganic Crystal Structure Database (ICSD). This set includes, in addition to structures stable under ambient conditions, also high-pressure and high-temperature phases that can be stabilized after quenching.²⁸ For 113 double perovskites the magnetism has been addressed experimentally. We use these experimental observations to train the machine-learning models, which are later applied to the remaining 68 materials. To make the problem tractable, we consider a simplified classification scheme which approximates canted (e.g., Sr₂CoOsO₆ (ref. 29)) and quasi-two-dimensional (e.g., Sr₂YRuO₆ (ref. 30)) antiferromagnets as antiferromagnetic (AFM). Similarly, we do not distinguish between ferro- and ferrimagnetic (FM) order. Paramagnetic and spin-glass double perovskites are classified as nonmagnetic (NM). This three-valued classification splits the data set into 19 NM, 23 FM and 71 AFM compounds.

Fig. 2 Crystal structures of A₂BB′O₆ double perovskites crystallizing in various space groups: (a) Fm3̄m, (b) I4/m, and (c) P2₁/n.

Our first task is to assess the ground states of 68 double perovskites whose magnetism remains unknown. Following earlier studies that addressed thermodynamic stability,³¹ we consider geometric atomic features (such as tolerance factor, ionic radius, and atomic number). These are supplemented by electronic atomic features such as the number of electrons in the outermost shell and the oxidation states of B and B′ atoms. To surmount the relatively small size of the data set, leave-one-out validation was used to evaluate the performance. We applied three extensively used multi-class classifiers: MLP, XGBoost and AdaBoost that yielded an accuracy of 63%, 73%, and 78%, respectively. Unfortunately, using microscopic parameters such as transfer integrals (which we do use for predictions of the ordering temperatures, see the next section) as features does not improve the performance of the classification models. We attribute this to the excessive dimensions of such features and the small size of the dataset. The AdaBoost model with the highest accuracy was further used to predict the magnetic order of the 68 remaining double perovskites. In this way, we identified 45 AFM, 7 FM, and 16 NM compounds depicted in Fig. 3 with red, blue, and gray squares.

Fig. 3 Classification ML-model-predicted 16 nonmagnetic (gray cells), 7 ferromagnetic (blue cells) and 45 AFM (red cells) double perovskites with the cubic Fm3̄m (left), monoclinic P2₁/n (top right), and tetragonal I4/m (bottom right) space groups. Rows and columns denote B and B′ cations, respectively. Atomic symbols in the cell denote A cations; double entries with atomic symbols separated by a slash pertain to both compounds.

3.2 Magnetic ordering temperature: regression machine learning

After applying the classification model to distinguish between potential ferro- and antiferromagnets, we turn to the magnetic ordering temperature T_c. In this case, atomic features are not sufficient. Magnetic ordering is driven by different, sometimes competing magnetic exchanges, that are in turn implicitly (and nontrivially) governed by transfer integrals. While the number of such parameters in each material amounts to several hundreds, the magnetism is mostly determined by the largest transfer integrals between the first, second or third neighbors. Depending on the number of electrons in the d shells and the orbital sector (t_2g–t_2g, t_2g–e_g, or e_g–e_g), such terms contribute to the antiferro- or ferromagnetic exchange; the overall sign and strength depend on the balance between these contributions.

To illustrate how such balance is realized in practice, we consider three Co²⁺-containing double perovskites: the cubic Ba₂CoReO₆, the tetragonal Sr₂CoReO₆, and the monoclinic La₂CoIrO₆. Since Re⁶⁺ (Ir⁴⁺) has one (five) electron in the 5d shell, exchanges between B and B′ as well as within each sublattice has to be considered. Possible relevant exchanges in these three structure types are schematically illustrated in the left panel of Fig. 4, where the purple, green and orange solid lines represent B–B, B′–B′, and B–B′ exchanges, respectively. Respective directions in the crystal lattice are denoted by superscripts, i.e. is exchange between B and B along the a axis, is the direction along the body diagonal between B′ and B′, etc. In the right panel of Fig. 4, we show the strongest transfer integrals for a given interatomic separation in each orbital sector; the color map spans the range between −300 (blue) and 300 (red) meV. For the cubic Ba₂CoReO₆, three first Co–Re nearest-neighbor bonds are identical, with three large t_2g–t_2g transfer integrals (three blue squares in the third row) around −225 meV. Besides, two e_g–e_g Co–Co transfer integrals and two t_2g–t_2g terms of Re–Re 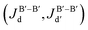are around −100 meV.

Fig. 4 Transfer path and corresponding largest t_2g–t_2g, t_2g–e_g, and e_g–e_g transfer integrals of Ba₂CoReO₆ (Fm3̄m), Sr₂CoReO₆ (I4/m), and La₂CoIrO₆ (P2₁/n), respectively. The purple, green and orange solid lines represent the first nearest neighbors of B–B, B′–B′ and B–B′, respectively. The color from purple to red indicates the value of transfer integrals ranging between −300 and 300 meV.

For Sr₂CoReO₆ crystallizing in the I4/m space group, leading transfer integrals are three t_2g–t_2g (one blue and two red squares in the third row) of −167 and 193 meV and two t_2g–e_g (two red squares in the third row) around 203 meV of the three shortest Co–Re bonds, and

For the monoclinic La₂CoIrO₆, the largest components (100 to 200 meV) also pertain to the short-range B–B′ connections. At the same time, both t_2g–e_g and t_2g–t_2g channels are active, as evidenced by five blue and one red squares in the third row of Fig. 4 (right). In addition, there are four e_g (t_2g) transfer integrals operating within the Co (Ir) sublattice. The structure of these matrices determines the sign and the strength of the respective magnetic exchanges.

The leading transfer integrals are complemented by the onsite energies of B and B′ d-orbitals. The resulting model is trained on a dataset of experimental transition temperatures (T_c), which is separated into 21 ferro- and 66 antiferromagnets. To assess the predictive power, we randomly divided each set following the 80/20 rule for the training/testing. As shown in Fig. 5, the training data set of antiferromagnets yields very high accuracy, which allows us to achieve the root mean square error (RMSE) of 18 K for the testing data set. In contrast, RMSE is sizable (around 61 K) for ferromagnets, which can be traced back to the small size of the dataset and the broad distribution of ordering temperatures.

Fig. 5 Magnetic transition temperature T_c predicted by the regression models in comparison with the experimental value. Antiferromagnetic (a) and ferromagnetic (b) materials are treated separately. The training and testing data sets are green and blue dots, respectively.

These two pre-trained models are further used to predict the transition temperatures of prospective 45 antiferromagnets and 7 ferromagnets. Among them, we find antiferromagnetic Ba₂TbReO₆ and three ferromagnets with high predicted critical temperatures: −51 K for Ba₂TbReO₆ (Fm3̄m), 172 K for Bi₂NiMnO₆ (P2₁/n), 209 K for Ba₂FeMoO₆ (Fm3̄m) and 99 K for Ca₂TiMnO₆ (I4/m). While the predicted ordering temperature (209 K) of Ba₂FeMoO₆ is sensibly lower than in the recent experiment (345 K³²), our model correctly identifies this material as a high-temperature magnet. Considering this deviation, to test whether the regression models are at risk of overfitting, different validations using resampling are conducted. As shown in Fig. S1,† the robust behavior of the model for antiferromagnets against overfitting gives us hope that the deviations in the model for ferromagnets can be overcome if more samples are added to the training dataset.

3.3 Identification and validation of prospective frustrated magnets

Except for the handful of prospective high-temperature antiferromagnets, all remaining antiferromagnets are predicted to have low T_c below 50 K. Among these 44 compounds, 28 feature sizable transfer integrals (≥100 meV) that can underlie strong antiferromagnetic exchange. To test this assumption, we turn to another characteristic temperature – the Weiss temperature Θ. This quantity represents a sum of all magnetic exchanges (multiplied with respective multiplicities) and can be estimated by fits to the magnetic susceptibility at high temperatures. Since strong antiferromagnetic exchanges give rise to sizable Θ, the magnetic frustration is often characterized by the ratio f = |Θ|/T_c, where T_c is the magnetic ordering temperature. Values of f exceeding ∼5 indicate sizable magnetic frustration, which gives rise to an exotic spin-liquid regime between Θ and T_c.³⁰

To identify relevant candidates, we collect experimentally reported the Curie–Weiss temperatures (Θ) of 63 known antiferromagnetic double perovskites, and then used the transfer integrals to train the regression ML model (leaving as before 20% for testing). In this way, we obtain a RMSE of 76 K for the testing data set (Fig. 6). Next, we calculate Θ for each of the 45 prospective antiferromagnets. As shown in Fig. 7, most monoclinic double perovskites like Ba₂LaRuO₆ (T_c = −30 K and Θ = −127 K) lie near the f = 5 isoline. At the same time, many cubic double perovskites lie in a more frustrated regime. In particular, three Re-based compounds are predicted to have f > 10: Ba₂LuReO₆₆ (T_c = −43 K and Θ = −485 K), Ba₂EuReO₆ (T_c = −50 K and Θ = −572 K) and Ba₂LaReO₆ (T_c = −42 K and Θ = −521 K). We note that the predicted temperatures for Ba₂LuReO₆ are consistent with recent experimental work³³ reporting T_c = −31 K and Θ = −678 K.

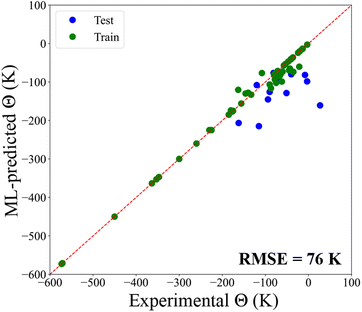Fig. 6 Regression ML model predicted as well as experimentally reported Weiss temperature Θ of AFM candidates. The training and testing dataset are green and blue dots, respectively.

Fig. 7 Magnetic transition temperature T_c and the Weiss temperature Θ for 45 prospective antiferromagnets as predicted by the regression model. Light yellow shading marks the strongly frustrated regime (f > 5). The red rhombus, green square and purple pentagon represent materials crystallizing in the cubic Fm3̄m, tetragonal I4/m and monoclinic P2₁/n space groups, respectively.

For an independent assessment of the accuracy, we consider the cubic Ba₂LaReO₆ and perform DFT + U + SOC calculations for the commonly observed AFM configuration in experiment³⁴ as well as the ferromagnetic configuration. The energy of the antiferromagnetic configuration is lower by −151.7 meV/f.u., indicating that 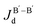and are exchanges that are sizable (110 K assuming S = 1) and antiferromagnetic, which is in line with large (−154 meV, see Fig. 8) transfer integrals in the t_2g channel. We note that in the absence of magnetic moments on B atoms, B′ moments (localized on Re) form a face-centered cubic lattice, which is geometrically frustrated.³⁴

Fig. 8 Transfer paths and transfer integrals of Ba₂LaReO₆ and Ba₂LaRuO₆. To be consistent with the visual representation of Fig. 4, we show B–B and B–B′ parts despite the absence of a partly filled electronic shell in La³⁺. Parameters whose absolute value is around 100 meV or larger are labeled; other terms are denoted by color.

For comparison, we perform a similar DFT + U + SOC calculation for the monoclinic Ba₂LaRuO₆. Since the low symmetry generates several independent terms, more supercells with different magnetic configurations (ferromagnetic and six antiferromagnetic) are needed. Total energies for all magnetic configurations are listed in the ESI.† By mapping these energies onto a Heisenberg model, we estimate the short-range exchange integrals J_a, J_b, J_d and J_d′. For simplicity, the difference between J_d and J_d′ is neglected; this is justified by the similarity of crystalline environments pertaining to both exchange pathways.³⁵ The resulting J_a, J_b, and J_d = J_d′ are 20, 11 and 11 K, respectively, with an accuracy of 0.5 K. These antiferromagnetic exchanges mainly stem from electron transfer in the t_2g channel; due to the smaller spatial extent of 4d orbitals compared to 5d, these transfer integrals are much weaker than in Ba₂LaReO₆.

4. Conclusions

We develop a machine learning model to discover new magnetic double perovskites. Our two-step procedure includes classification learning based on atomic inputs and regression learning based on microscopic inputs – transfer integrals and onsite energies. The goal of the first step is to distinguish between prospective antiferromagnets and ferromagnets; this model is reasonably reliable, particularly for antiferromagnets (78%). The second model aims at predicting the magnetic transition temperature. Here, we achieve a root mean square error (RMSE) of 18 and 61 K for antiferro- and ferromagnets, respectively.

We identify Ba₂TbReO₆ as an antiferromagnet with a high magnetic ordering transition temperature of about 50 K, and three prospective ferromagnets – Bi₂NiMnO₆, Ba₂FeMoO₆, and Ca₂TiMnO₆ – with the ordering temperatures of 172, 209, and 99 K, respectively. We additionally identified 28 prospective frustrated antiferromagnets that combine sizable transfer integrals (100 meV and larger) with a low ordering temperature (below 50 K). Detailed total-energy calculations of magnetic supercells support this conjecture for Ba₂LaReO₆.

In addition to providing new candidate double perovskites with high magnetic transition temperature or sizable magnetic frustration, our work opens new insights for machine learning assisted high-throughput calculations. Estimation of transfer integrals is becoming a routine task that can be done in a high-throughput fashion. These microscopic parameters underlie the electronic and magnetic properties, but quantitative information on the magnetic properties can be obtained using analytical or perturbative expressions that are available for several specific cases only.^9,36,37 Machine learning methods can be an appealing alternative to such analytical approaches, because of its potential to capture the elusive, yet inherent link between the transfer integrals and physical observables.

Author contributions

S. G. and O. J. devised the research. S. G. conducted the research and drafted the manuscript. S. G., R. M., J. v. d. B. and O. J. analyzed the results and edited the manuscript. J. v. d. B. and O. J. supervised the research.

Conflicts of interest

All authors declare no competing interests.

Acknowledgements

S. G., R. M. and O. J. acknowledge financial support from the IFW Excellence Program. R. M., J. v. d. B. and O. J. were supported by the Collaborative Research Center SFB 1143 (Project No. 247310070). J. v. d. B. thanks the Deutsche Forschungsgemeinschaft (DFG) for support through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter ct.qmat (EXC 2147, Project No. 39085490). S. G. thanks fruitful discussions with Prof G. Jeffrey Snyder (Northwestern University), Denys Kononenko (IFW Dresden) and Dmitry Chernyavsky (IFW Dresden) as well as technical assistance of Ulrike Nitzsche (IFW Dresden). S. G. acknowledges computing resources provided by HPC-TU Dresden.

References

1. C. Jia, S. Onoda, N. Nagaosa and J. H. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144424.
2. A. Rüegg and G. A. Fiete, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 201103.
3. A. Erickson, S. Misra, G. J. Miller, R. Gupta, Z. Schlesinger, W. Harrison, J. Kim and I. Fisher, Phys. Rev. Lett., 2007, 99, 016404.
4. K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680.
5. A. E. Taylor, R. Morrow, M. D. Lumsden, S. Calder, M. H. Upton, A. I. Kolesnikov, M. B. Stone, R. S. Fishman, A. Paramekanti, P. M. Woodward and A. D. Christianson, Phys. Rev. B, 2018, 98, 214422.
6. M. A. de Vries, A. Mclaughlin and J.-W. Bos, Phys. Rev. Lett., 2010, 104, 177202.
7. R. Morrow, J. W. Freeland and P. M. Woodward, Inorg. Chem., 2014, 53, 7983–7992.
8. K. Koepernik, O. Janson, Y. Sun and J. van den Brink, Phys. Rev. B, 2023, 107, 235135.
9. S. M. Winter, Y. Li, H. O. Jeschke and R. Valentí, Phys. Rev. B, 2016, 93, 214431.
10. M. K. Horton, J. H. Montoya, M. Liu and K. A. Persson, NPJ Comput. Mater., 2019, 5, 64.
11. A. Kabiraj, M. Kumar and S. Mahapatra, NPJ Comput. Mater., 2020, 6, 35.
12. A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Chem. Mater., 2021, 33, 845–858.
13. A. Halder, A. Ghosh and T. S. Dasgupta, Phys. Rev. Mater., 2019, 3, 084418.
14. P. V. Balachandran, B. Kowalski, A. Sehirlioglu and T. Lookman, Nat. Commun., 2018, 9, 1668.
15. Z.-X. Shen, C. Su and L. He, NPJ Comput. Mater., 2022, 8, 132.
16. W. Liu, Y. Lu, D. Wei, X. Huo, X. Huang, Y. Li, J. Meng, S. Zhao, B. Qiao and Z. Liang, et al. , J. Mater. Chem. A, 2022, 10, 17782–17789.
17. Y. Hu, X. Hu, L. Zhang, T. Zheng, J. You, B. Jia, Y. Ma, X. Du, L. Zhang and J. Wang, et al. , Adv. Energy Mater., 2022, 12, 2201463.
18. S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1–36.
19. A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2002, 58, 364–369.
20. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
21. X. Glorot and Y. Bengio, J. Mach. Learn. Res., 2010, 9, 249–256.
22. J. H. Friedman, Ann. Stat., 2001, 1189–1232.
23. T. Hastie, S. Rosset, J. Zhu and H. Zou, Statist. Interface, 2009, 2, 349–360.
24. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
25. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
28. P. Kayser, S. Injac, B. Ranjbar, B. J. Kennedy, M. Avdeev and K. Yamaura, Inorg. Chem., 2017, 56, 9009–9018.
29. B. Yan, A. K. Paul, S. Kanungo, M. Reehuis, A. Hoser, D. M. Többens, W. Schnelle, R. C. Williams, T. Lancaster and F. Xiao, et al. , Phys. Rev. Lett., 2014, 112, 147202.
30. E. Granado, J. W. Lynn, R. F. Jardim and M. S. Torikachvili, Phys. Rev. Lett., 2013, 110, 017202.
31. A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Chem. Mater., 2021, 33, 845–858.
32. S. B. Kim, E. J. Hahn and C. S. Kim, J. Korean Phys. Soc., 2019, 75, 466–470.
33. J. Xiong, J. Yan, A. A. Aczel and P. M. Woodward, J. Solid State Chem., 2018, 258, 762–767.
34. C. Wang, Y. Xu, W. Hao, R. Wang, X. Zhang, K. Sun and X. Hao, Phys. Rev. B, 2019, 99, 035126.
35. H. Wang, S. Zhu, X. Ou and H. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054406.
36. V. Mazurenko, S. Skornyakov, A. Kozhevnikov, F. Mila and V. Anisimov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224408.
37. S. M. Winter, J. Phys. Mater., 2022, 5, 045003.

---

Footnote

† Electronic supplementary information (ESI) available: Full lists of experimental and machine learning predicted magnetic transition temperature, Weiss temperature and frustration parameters; detailed formulae of DFT + U + SOC calculations. See DOI: https://doi.org/10.1039/d3ta05679a

---