Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reversible interfacial Li-oxide formation on germanium and silicon anodes revealed by time-resolved microgravimetry†
Ke
Wang
 a,
Yug
Joshi
a,
Yug
Joshi
 *abc,
Tobias
Kohler
a,
Monica
Mead
*abc,
Tobias
Kohler
a,
Monica
Mead
 a and
Guido
Schmitz
*a
a and
Guido
Schmitz
*a
aUniversity of Stuttgart, Institute for Materials Science, Chair of Materials Physics, Heisenbergstr. 3, 70569 Stuttgart, Germany. E-mail: Yug.Joshi@mp.imw.uni-stuttgart.de; Guido.Schmitz@mp.imw.uni-stuttgart.de
bKarlsruhe Institute of Technology, Institute for Applied Materials – Energy Storage Systems, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
cMax-Planck Institut für Eisenforschung GmbH, Max-Planck-Straße 1, 40237 Düsseldorf, Germany
First published on 18th January 2024
Abstract
Germanium has received recent attention as a promising candidate for the next generation of Li-ion anodes due to its high capacity, higher conductivity, and faster lithium-ion diffusivity relative to silicon. However, the uncertainty in the Li-storage mechanism and the formation of a solid electrolyte interface (SEI) has hampered its further development. Herein, operando microgravimetry on the Ge electrode has been conducted to determine the SEI mass (irreversibly deposited) and to distinguish it from the reversibly cycled species, and their individual contributions to the total capacity. From the obtained time-resolved mass spectra, determined by correlating gravimetry and charge flux, Li2O along with Li is identified as a reversibly cycled species, contributing significantly to the electrochemical capacity. The amount of this cycled Li2O depends on (i) the cycling rate and (ii) the thickness of the anode. Interestingly, the amount of Li2O decreases if pronounced anode cracking appears. A direct comparison between Si and Ge indicates that the amount of the reversible Li2O is predominantly controlled by the diffusivity of lithium into the electrodes. The study provides a general mechanism for balancing the interfacial and bulk storage of Li in the form of an oxide or by alloying, respectively.
1 Introduction
Commercial lithium-ion batteries (LIB) are efficient devices of energy storage that are being used for various applications.1–3 However, with the demand for higher gravimetric capacity of LIBs, the commercialized graphite anode would have to be replaced due to its relatively low theoretical capacity (372 mA h g−1).4 Other group IV elements, such as silicon, germanium, and tin have attracted considerable attention in recent years, because of their high theoretical capacity (4200 mA h g−1 for Si, 1640 mA h g−1 for Ge, and 990 mA h g−1 for Sn) and low working voltages. However, huge volume expansion caused by the formation of the Li4.4X (X = Si, Ge, and Sn) intermetallic phase, leads to the fracture of the electrode and the continuous formation of SEI during cycling. This decreases the mechanical/chemical stability of the electrode and results in a continuous capacity fade.5 In comparison to silicon, which is the most probable candidate to replace graphite (by incorporating various modifications such as surface treatments6 and interfacial engineering7), Ge has faster lithiation diffusivity and higher electronic conductivity, around 400 times and 5000 times those of Si, respectively.8 Thus, it is suggested to understand the cycling process of Ge anodes to further optimize its electrochemical performance.Generally, the reactions in a lithium-ion battery can be classified into reversible and irreversible ones. For the irreversible reactions: if the electrochemical potential for lithium insertion in the anode is lower than the reduction potential of the electrolyte, the electrolyte is reduced to form an SEI layer during cycling down to the insertion potential of the anode. This is a self-limiting process as the formed SEI layer (electronically insulating) will drop the potential at the contact surface to the electrolyte and will prevent further degradation of the electrolyte.9–11 Moreover, there might be other kinds of irreversible reactions derived from the instability of the electrodes, as known for example, the oxidization of Sn,12,13 the oxygen removal from the electrode,14 and the Co dissolution from LiCoO2 (ref. 15) or Mn from LiMn2O4. For the reversible reactions: Naturally, the most important reversible process is the insertion and extraction of lithium. However, there might be also other reversible reactions occurring at the interface of the electrode, like the Li2O formed at the surface of Si16,17 and/or the reversible reduction of Li2CO3 in the presence of Co nano-particles.18 Besides, it is worth noting that the conversion of some metal oxides (e.g. SnO2 (ref. 19)) into metal elements is also reversible during charge and discharge.
In this work, microgravimetry with a Quartz Crystal Microbalance (QCM) is applied to probe the reversible and irreversible reactions in Ge and Si anodes. The QCM is an emerging tool for probing the long-term evolution of SEI. It is a non-destructive-electrode characterization20 technique that can precisely detect the loading/unloading of mass on the electrode in operando conditions. The instrument reads out the change of the oscillating frequency of the quartz crystal which is inherently related to the thickness or the mass of the electrode according to the well-known Sauerbrey equation.21 The sensitive detection of the frequency change upon de-/lithiation allows a precise measurement within the range of nanograms per square centimeter.22 Combining the mass change detected by QCM and the charge transfer, evaluated by the current response during an electrochemical reaction, the mass per charge accumulated/depleted within a small time interval can be obtained.23 This can be used to investigate the mass and composition of the SEI and that of the reversibly inserted/extracted species.
Herein, QCM and cyclic voltammetry (CV) were combined to investigate the irreversible SEI formation (mass) and the reversibly cycled species with thin film germanium (d ≤ 100 nm) electrodes under operando conditions (see Fig. 1a for a scheme of the experimental setup). The binder-free and dense thin-film electrodes were deposited by ion-beam sputtering on copper-coated single crystalline AT-cut quartz crystals. The sputter deposition allows the preparation of a reliably controlled sample thickness with negligible surface roughness. The “pure” Ge electrode excludes potential side reactions derived from the decomposition of the binder or conductive additives like carbon-black/graphite. Also, the compact film morphology prevents any direct contact of the electrolyte with the current collector. So, it enables a quantitative and reliable investigation of the intrinsic behavior of Ge with regard to the SEI formation and lithium de-/alloying.
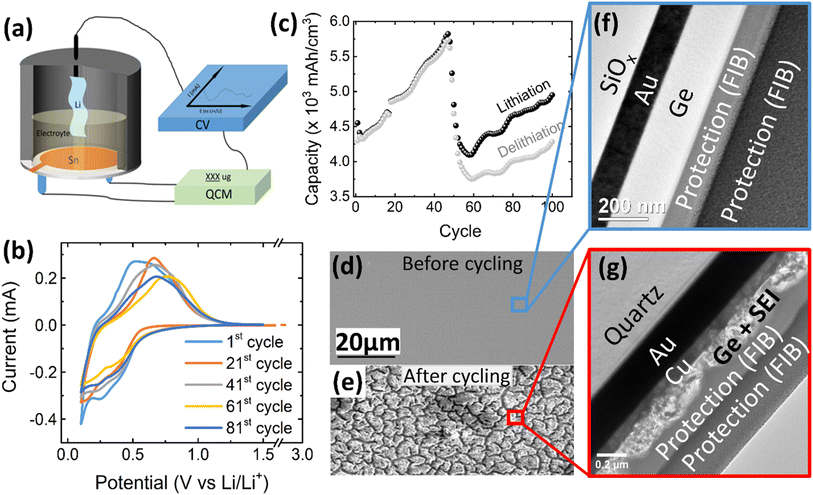 | ||
| Fig. 1 (a) Schematic of the electrochemical cell for operando QCM-CV measurement, (b) exemplary CV curves and (c) electrochemical capacity of a 100 nm Ge film at a scan rate of 0.5 mV s−1 in the potential window of 0.1–1.5 V. The SEM images of the 100 nm Ge electrode before and after cycling are presented in (d) and (e), respectively. TEM cross section image of: (f) as-deposited Ge thin film and (g) after 100 cycles. Two layers of protecting Pt were deposited during FIB preparation by two different methods, electron and ion cracking of metal–organic precursors. (See also additional images in Fig. S1 in the ESI.†) | ||
From the current investigations, it is reported herein that Ge anodes show, in addition to Li ions, a reversible processing of another molecule which, based on its mass, is most probably identified as Li2O. The reversible formation and dissolution of Li2O contributes to the extra capacity of Ge. A similar effect is observed at Si electrodes.16 In direct comparison to Si, the amount of formed Li2O appears to depend predominately on the different diffusivity of lithium inside the electrodes, while different onset potentials of Lithium insertion have a lesser influence. This observation brings in a new variable to control the amount of reversible Li2O, which will potentially help in a better microstructural design of electrode materials. The discovered mechanism of Li2O formation, driven by the kinetic over-potential, can be presumably directly translated to bulk powdered electrodes as the size of the powdered particles is usually more than 100 nm, hence the kinetic over-potential will be even larger in comparison to the presented study.
2 Experiment
2.1 Thin film deposition
Germanium (Ge) and copper (Cu) thin films were deposited via a custom-made ion-beam sputtering system equipped with a 3 cm beam diameter Kaufmann type ion-source (Veeco Inc.). The base pressure prior to deposition was 1 × 10−7 mbar. During the sputtering, 30 sccm argon (99.999%) was used as process gas resulting in a working pressure of 2 × 10−4 mbar. The applied beam voltage and current were adjusted to 600 V and 20 mA, respectively. This resulted in a moderately fast growth rate (8.4 nm min−1 for Cu and 10.2 nm min−1 for Ge). For operando QCM and CV measurement, a gold-coated 5 MHz quartz sensor (delivered from Renlux Crystal) was used as the substrate. 100 nm of copper, serving as the current collector, was directly deposited upon this QCM sensor. Next, a Ge thin-film of two different thicknesses (20 nm or 100 nm) was deposited. During sputter deposition, the thickness of the coating was recorded and controlled by another quartz crystal microbalance located close to the substrates. The final thickness and the microstructure of the deposited layers were further determined by Transmission Electron Microscopy (TEM). For comparison, a few Si films were produced with the same methods.2.2 In-operando mass change during charging and discharging
Operando measurement of mass change during cycling was carried out by a quartz crystal microbalance (Maxtex RQCM). Simultaneously, CV measurements were performed using a BioLogic VSP-300 potentiostat at a scan rate of 0.5 mV s−1 (unless otherwise mentioned) in different potential windows to charge and discharge the electrode. A custom-made cell was used,12 the schematic of the measurement setup is shown in Fig. 1a. The QCM sensor, coated with Cu (as a current collector) and Ge, served as a working electrode, and lithium foils worked as counter and reference electrodes. Hence, all the potentials are stated with respect to lithium. A mixture of 50 wt% ethylene carbonate (EC, alpha Aesar, 99%), 50 wt% dimethyl carbonates (DMC, sigma Aldrich, 99%), containing 1 mol L−1 lithium perchlorate (LiClO4, sigma Aldrich, 99.99%) was used as electrolyte. To prevent contamination by air and humidity, both the assembly and the operando QCM-CV measurements were executed inside a glovebox (O2 and H2O content < 0.5 ppm). To stabilize the signal, an open circuit relaxation was carried out for 24 h before cycling.2.3 Characterization
Before any structural or chemical characterization, the electrodes were cleaned with DMC three times to remove the residual electrolyte. XPS was performed to characterize chemical modifications. For this, a spectrometer from Thermo Fischer Scientific Inc. was used, equipped with an Al Kα X-ray source emitting radiation with an energy of 1486.4 eV. The surface morphology of the electrodes was characterized by Scanning Electron Microscopy (SEM) operated at 5 kV and 1.6 nA. The microstructure of the electrode was characterized by Transmission Electron Microscopy (TEM) with a Philips CM200-FEG instrument operated at 200 kV. Required electron transparent TEM lamella were prepared by the standard FIB lift-out technique using a Thermo Fischer SCIOS Dual-beam microscope.242.4 Data analysis
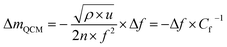 | (1) |
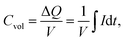 | (2) |
The volume of the electrode (V) was determined as the area of the thin-film electrode immersed in the electrolyte times its thickness, while ΔQ denotes the total charge transferred in a half-cycle.
The mass change during a half cycle can be estimated from the number of transferred electrons (ΔmCV) as in eqn (3), under the assumption that only single-charged Li ions are processed:
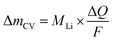 | (3) |
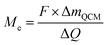 | (4) |
Assuming both Li and Li2O are simultaneously processed, only an average MPE can be determined when using eqn (4). This may be expressed by the weighted contributions of Li oxide and Li ions:
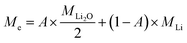 | (5) |
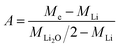 | (6) |
Knowing A, the absolute mass of transferred Li2O is given by
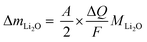 | (7) |
3 Results and discussion
3.1 100 nm Ge film cycled between 1.5–0.1 V vs. Li/Li+ at 0.5m V s−1
Fig. 1b shows the CV of 100 nm Ge cycled at a scan rate of 0.5 mV s−1 in a potential window of 0.1–1.5 V, where the 1st, 21st, 41st, 61st, and 81st cycles are selected to represent the different stages of the battery “life”. At the initial stage (1st cycle), the lithiation appears below 0.58 V, while the delithiation peak is centered at 0.66 V. This matches well with previous works.26 Interestingly, with progress in cycling, the peak of delithiation shifts “chaotically”, within a voltage range of about 0.25 V. This is likely due to random cracking and fracture of the formed SEI which abruptly changes the conductive pathways and hence the overpotentials driving the reaction. Initiation of cracks exposes fresh Ge surfaces to the electrolyte and introduces deep short-circuit transport paths into the film that are filled with liquid electrolyte. Thus, momentarily the ohmic losses and the necessary overpotential become reduced. During further cycling, fresh SEI closes these fast transport paths again raising the overpotential to the previous level until further cracks arise. This interpretation is strongly supported by the behavior of thinner films (presented later). Very thin films prevent the crack formation and consequently show a constant position of the delithiation peak during all cycles.As shown in Fig. 1c, the capacity steadily increases with increasing cycle number until a cliff-drop at around 50th cycle. In view of the big volume expansion caused by a huge theoretical volumetric capacity (8630 mA h cm−3), the Ge anode is probably majorly fractured at around the 50th cycle. This conclusion is also supported by a severely reduced efficiency after the 55th cycle (see ESI, Fig. S1(c)†). By cracking, the fresh electrode surface is being exposed to the electrolyte, which leads to further decomposition of the electrolyte and SEI formation. To visualize the rupture of the Ge thin-film anode, SEM micrographs of the electrode before cycling (Fig. 1d) and after 100 cycles were captured and shown in Fig. 1e. The SEM surface image shows that the as-deposited Ge thin-film (Fig. 1d) has a smooth surface without any features, which is further proved by the TEM cross-sectional micrograph shown in Fig. 1f. The as-deposited layer appears to be amorphous without any crystallographic features like grains or grain boundaries. In contrast to previous work on Sn films,12,13 the amorphous growth is probably linked to the higher recrystallization temperature of Ge. However, after 100 cycles, many cracks have appeared at the surface of Ge (Fig. 1e) leading to island-like structures (of 3–6 μm size) which are evenly distributed throughout the electrode. Moreover, the microstructure of the unbroken parts (marked by the red cycle area) was investigated in TEM cross-sections. As shown in Fig. 1g, the thin-film electrode appears completely fragmented to particles that are heterogeneously embedded in the SEI. Considering that the total thickness of Ge and SEI combined is 157 ± 12 nm, while the thickness of the Ge has been 100 nm before cycling, the effective thickness of SEI amounts to 57 ± 12 nm.
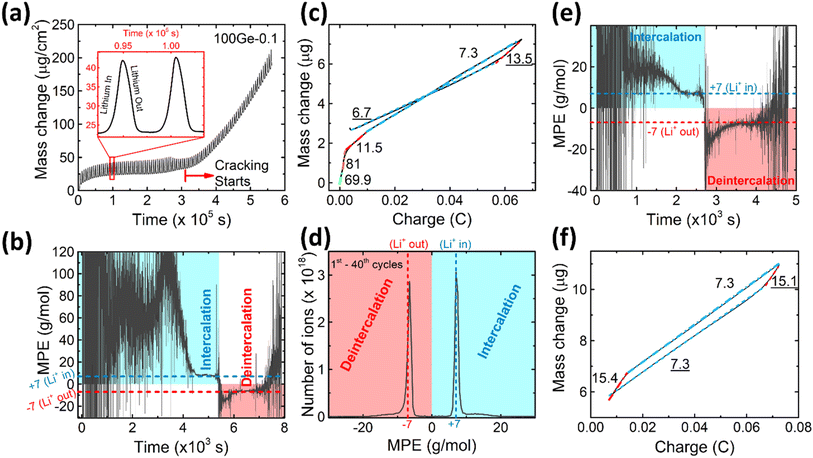
To further characterize the SEI formation and cycling behavior, the mass change has been measured during electrochemical operation by QCM as shown in Fig. 2a. A point to note, the graph is labelled as 100Ge-0.1, signifying 100 nm thick Ge film cycled down to 0.1 V vs. Li/Li+; a similar notation is followed throughout the remainder manuscript. The trend line averaging the mass oscillations indicates the irreversible mass deposition, which must be attributed to the SEI formation, while the amplitude of the characteristic periodic oscillations, shown in the inset of Fig. 2a, represents the reversible mass change of lithiation and delithiation. Quantitatively, the big irreversible mass change (2.69 μg, or specifically 8.11 μg cm−2) of the first cycle is attributed to the initial SEI formation derived from the reduction of the electrolyte.
As shown in Fig. 2a, after the initial SEI formation, the trend line of the mass remains almost constant until a rapid increase sets in at around the 45th cycle (after the red dashed line in Fig. 2a). As reported in previous work,16 such a sharp increase is most likely attributed to the onset of pronounced electrode cracking which leads to the accelerated decomposition of the electrolyte and formation of new SEI. This interpretation is corroborated by the simultaneous (after about the 45th cycle) reduction of capacity and efficiency presented before and the SEM and TEM images after 100 cycles (see Fig. 1e and g).
To investigate the species involved in the SEI formation during the first cycle, the MPE determined for many short time intervals is plotted versus time in Fig. 2b and, alternatively its integral versus processed charge in Fig. 2c. The signal of the individual MPE values becomes very noisy at the beginning and the ending of the cycle so that only lithiation and delithiation are clearly identified by the mass of ±7 g mol−1. However, in the time-integrated data of Fig. 2c the noise is largely suppressed, so that the slope of the graph can identify several dominating masses. At the initial stage of the first cycle (1.4–0.8 V), the MPE value of 81 g mol−1 (yellow line in Fig. 2c) is well understood by the decomposition products of solvents. E.g. from the reduction of EC (C4H4O6Li2) we can expect an MPE = 80.9 g mol−1, see eqn (8.1), and from the reduction of DMC (C2H3O3Li) with an MPE of 81.9 g mol−1, see eqn (8.2).27 The MPE value of 69.9 g mol−1 (green line) is probably attributed to a superposition of heavier and lighter decomposition products of DMC (eqn (8.2) and (8.3)28) which are adsorbed simultaneously.
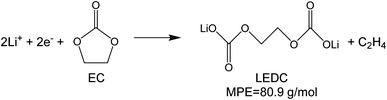 | (8.1) |
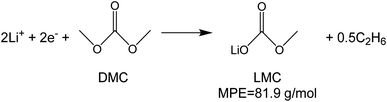 | (8.2) |
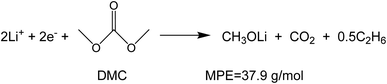 | (8.3) |
Later during this cycle, in the potential range of 0.48–0.41 V, the rather low average MPE value of 11.5 g mol−1 (red solid line) indicates the formation of lighter inorganic species, such as Li2O (14.9 g mol−1), LiOH (23.9 g mol−1) or Li2CO3 (36.9 g mol−1) superposed with the simultaneous insertion of Li (MPE = 6.9 g mol−1), since lithiation into Ge sets in at already 0.5 V. Finally, the MPE value decreases close to 7 g mol−1 (blue dashed-dotted line) which demonstrates almost exclusive lithiation.
After the onset of major mechanical failure, the cycling behavior of the electrode appears too complex for a detailed QCM analysis. Thus, in the following, we restrict to the stable stage before the 45th cycle. Fig. 2d shows the MPE mass spectrum collected from 1st to 40th cycle. There are two peaks located at 7 g mol−1 and −6.5 g mol−1, clearly representing the lithiation and delithiation, respectively. Strikingly, both peaks reveal an additional tail ranging from about 10 g mol−1 to 20 g mol−1 (positive and negative values represent mass loading and unloading, respectively). These tails indicate that some species heavier than Li are reversibly processed. As suggested in previous similar work on Si,16 such tails are probably related to a predominant species with an MPE of 15 g mol−1. In order to prove this suggestion for Ge and locate the relevant voltage range of formation, the MPE-based curves of the exemplary 10th cycle are shown in Fig. 2e and f. Indeed, the integrated MPE (Fig. 2f), which suppresses noise, clearly identifies beside the expected mass of Li (≈7 g mol−1), the additional mass changes of +15.4 g mol−1 (lithiation half cycle) and −15.1 g mol−1 (delithiation half cycle) at the beginning of the half cycles. Further similar data obtained for different cycle numbers are shown in the ESI Fig. S2.†
Table 1 presents various known candidates of molecules that could be potentially formed, the designated value close to 15 g mol−1 per charge only matches to Li2O (14.9 g mol−1). Similar to the observation with Si,16 we see that the additional mass of Li2O is adsorbed before major lithiation (at 1.15–0.56 V) and, remarkably, also desorbed before major delithiation, in the potential range of 0.28–0.42 V.
| Molecule | Molar mass [g mol−1] | MPE | Density [g cm−3] | Ref. |
|---|---|---|---|---|
| Li2O | 29.9 | 14.45 | 2.01 | 29 |
| C2H3O | 43 | 21.5 | 30 | |
| LiCl | 42.4 | 42.4 | 2.07 | 29 |
| Li2C2 | 37.9 | 18.95 | 1.3 | 29 |
| CH3OLi | 37.9 | 37.9 | 28 | |
| LiC2H3O2 | 65.9 | 32.95 | 31 | |
| Li2CO3 | 73.9 | 36.95 | 2.11 | 32 |
| LiOCO2CH3 (LMC) | 81.9 | 81.9 | 27 | |
| Li(CH2)2OCO2Li | 101.9 | 50.95 | 17 | |
| (CH2OCO2Li)2 (LEDC) | 161.8 | 80.9 | 27 | |
| ((CH2)2CO2OLi)2 | 189.9 | 94.95 | 17 |
Clearly, it has to be noted that the identification of Li2O is here achieved only by using the exclusion principle among various options. Furthermore, the QCM only identifies the additionally loaded mass. Thus strictly, we cannot exclude that instead of Li2O, a more complex oxide in combination with Ge is formed, of which however the mass of Ge or possible other species that might be already deposited on the electrode cannot be detected. However further confirmation for Li2O as the relevant species is obtained by XPS. Ex situ XPS measurements of 100 nm Ge were obtained after cycling to different end voltages. Quantitative results are shown in the ESI, Fig. S3.† Two samples are compared: sample 1 experienced one complete cycle and subsequent lithiation to 0.45 V vs. Li/Li+, while sample 2 just experienced one complete cycle. Thus, the extra signal of sample 1 must stem from the additional adsorbed reversible species. As shown in Fig. S3(b),† the Li2O signals at 55.1 eV (Li 1s), even more the clear shoulder at 528.3 eV (O 1s) (Fig. S3(c)†) prove that the additional reversible species is indeed Li2O. Furthermore, correlating the signals of Ge2+ and Ge4+ shown in Fig. S3(d) and (d′)† with that of O 1s shows that this Li2O must be located close to the Ge thin film as it is significantly affecting the oxidation state of Ge.
3.2 Influence of the voltage range of cycling
Due to the rather limited mechanical stability of the electrode reported above (only up to 45 cycles could be reliably processed), attempts were made to stabilize the electrode. Limiting the amount of inserted lithium is an effective way to reduce the volume expansion of the electrode. Consequently, we reduced the working potential window to 0.3–1.5 V. As shown in Fig. 3a, in direct comparison to the previous experiment, the amplitude of the periodic QCM oscillations decreases and the irreversible mass change becomes more stable (only a tiny increase in the last five cycles) pointing out significantly less cracking when using the smaller voltage window. As shown in Fig. 3b, the SEM micrograph reveals only local ruptures instead of the completely damaged surface observed previously. Furthermore, the microstructure of the electrode (marked by red cycle area) was investigated by analyzing the cross-section of the electrode by TEM (see ESI, Fig. S4†). After 100 cycles, the Ge thin-film is well intact. SEI formation happened only at the surface and did not destroy the morphology of the electrode. Still, the thickness of the formed SEI appears inhomogeneous. The thickness of the continuous SEI amounts to 15.2 ± 2.4 nm.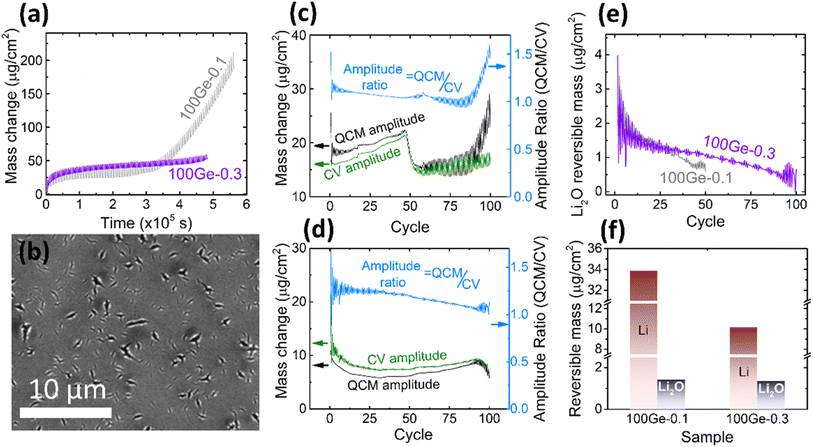 | ||
| Fig. 3 (a) The QCM mass change of 100Ge-0.1 (grey) and 100Ge-0.3 (purple); (b) the SEM of the surface of 100Ge-0.3 after 100 cycles (see also Fig. S4(a) in ESI† for the raw image); the amplitude of the reversible QCM mass change (black), the CV mass change (green) and the ratio between both (light blue, note different y-axes) in the case of (c) 100Ge-0.1 and (d) 100Ge-0.3, (e) the mass of reversibly processed Li2O on 100Ge-0.1 (grey) and 100Ge-0.3 (purple) versus the cycle number, (f) the amount of reversibly processed Li and Li0.5O at the 10th cycle of 100Ge-0.1 and 100Ge-0.3. | ||
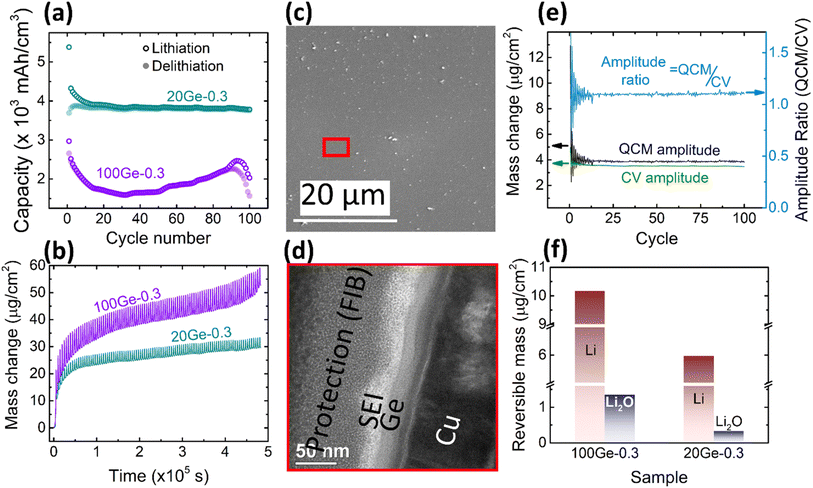
In order to further explore the cycling behavior of the Ge anodes and to quantify the relative contributions of processed species, the amplitudes of the periodic oscillations in the QCM mass may be compared to those expected from the electrical signals, see Fig. 3c and d. The processed masses in each half cycle were strictly calculated from the QCM data as the absolute difference between the ending mass of a half cycle and its starting mass (black curve), while the CV mass oscillations (green curve) were calculated from the processed charge in each half cycle under the assumption that only Li-ions are reversibly processed (eqn (3)). For exclusive lithium insertion, both masses should be identical, meaning the ratio between both curves should be one. In contrast, the experimental data (see light blue line) reveal that the QCM mass oscillations are significantly larger than the CV mass oscillations, especially at the early stages of cycling. Thus, together with Li, a significant proportion of Li2O is reversibly processed and this proportion slowly varies with the cycle number. This could be due to a variation in the amount of adsorbed Li2O or in the amount of inserted Li (or both). Based on Fig. 3c and d and eqn (6) and (7), the total amounts of reversible Li2O were calculated as shown in Fig. 3e.
For both sampling windows, the amount of reversible Li2O decreases during longer cycling. Remarkably, in the case of the larger voltage window (1.5–0.1 V) with significantly stronger cracking, this decrease is much more pronounced. This will be further discussed in the subsequent sections. The amounts of reversible processed Li and Li2O are shown in Fig. 3f for both tested voltage windows (for the 10th cycle). As discussed above (Fig. 2c and d), Li2O is predominantly formed in the voltage range from 1.15 to 0.56 V. This lies fully within both processed potential windows. Consequently, the amount of reversible Li2O is almost not affected by shifting the lower boundary of potential window. But it makes a significant difference to the amount of alloying with Li, since this appears only below 0.5 V.
3.3 Influence of electrode thickness
In order to clarify major factors that control the amount of the reversibly processed Li2O, the thickness of the film was reduced to 20 nm. Reducing in this way the diffusion length of alloyed Li, the kinetic overpotential is also expected to be reduced. Also, the risk of a mechanical failure should be significantly less. As shown in Fig. 4a, in contrast to 100Ge-0.3 and 100Ge-0.1, the sample 20Ge-0.3 exhibits a highly stable capacity of 3750 mA h cm−3 (except for a slight capacity fade in the initial cycles), and the coulombic efficiency after 100 cycles stays way above 90%. This clearly demonstrates that indeed Ge can be used as a reliable anode material, although it would be stable only in a nano-structured morphology. In addition to the data shown in Fig. 4, the ESI (see Fig. S5†) also presents the cyclic voltammetry of different cycles. Except the first cycle that show significant effect of initial SEI formation, the remaining current voltage curves of the CV cycles are highly stable showing no variation among different cycles. This corroborates our earlier statement that without cracking stable CV cycles are achieved with well-fixed peak positions. As shown in Fig. 4b, the QCM mass of 20Ge-0.3 still shows an irreversible increase, however, predominantly at the very beginning, attributed to SEI mass (see black curve). In subsequent cycles, however, the QCM mass data of 20Ge-0.3 shows a way more constant baseline when compared to the thicker Ge film. The total irreversible mass uptake after 100 cycles amounts to 29.57 μg cm−2. Fig. 4c shows the SEM micrograph of the surface after 100 cycles and Fig. 4d a TEM cross section micrograph. Both micrographs prove that no cracking appears in case of the 20 nm Ge film. The average SEI thickness on 20Ge-0.3 amounts after 100 cycles to 21.5 ± 7.55 nm. As shown in Fig. 4e, also the stable amplitudes of the periodic oscillations of QCM and CV mass demonstrate that all reactions after the initial SEI formation are practically reversible. When comparing QCM and CV mass amplitude quantitatively, the relative contribution of reversible Li2O amounts to only ca. 4%, way less than in the two examples of thicker films before. Remarkably, no variation is seen over 100 cycles, which leads us to the conclusion that the decrease of the Li2O contribution with progress in cycling that we previously demonstrated for the thicker Ge films must be probably attributed to irregular cracking.The dependency of the amount of reversible Li2O on the thickness of the studied Ge films is presented in Fig. 4f. Clearly, the amount of Li2O increases with increase of the layer thickness. The same is observed for Li alloying. However, it must be pointed out that the amount of Li alloying is naturally expected to be proportional to the bulk volume and thus to the film thickness. But Li2O formation as a surface reaction is at first hand expected to be independent of the thickness. Thus, the nevertheless observed thickness dependence needs a valid explanation (see later mechanism of reversible Li2O formation).
3.4 Dependence on the scanning rate
Finally, we need to check the effect of the scanning rate on the contribution of the reversibly processed Li2O. As shown in Fig. 5a, a 20 nm Ge was cycled at different scan rates in the fixed potential window of 0.3–1.5 V. The Ge anode exhibits similar redox behavior at all scan rates. But, according to the Butler–Volmer equation, the overpotential to drive the ions into the electrode increases with the current density. Thus, with the increasing rate, the de-lithiation peak shifts towards higher voltages. Correspondingly, the electrochemical capacity reduces (quantitative data on capacity and peak shift are presented in Fig. S6 of the ESI†). However, more important in this context is the quantitative contribution of the Li2O. The ratio of Li2O/Li is presented as a function of scan rate in Fig. 5c, whereas Fig. 5d shows the respective absolute amounts at the different scan rates. Obviously, the amount of alloyed Li significantly decreases when increasing the scan rate, while, remarkably, the amount of reversible LiO0.5 remains almost constant (only a very slight decrease). As shown in Fig. S6(b),† the faster the scan rate, the lower is the potential at which adsorption of Li2O switches to the insertion of Li, which is due to the fact that the over potential increases with the current density or scan rate.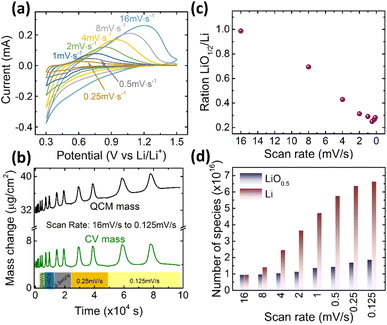 | ||
| Fig. 5 (a) The CV curves, (b) the mass change during CV cycling, (c) the ratio of LiO0.5/Li, and (d) the absolute amounts of Li and LiO0.5 of 20Ge-0.3 cycled at different scan rates. | ||
3.5 Silicon versus germanium
After the detailed investigation of the reversible Li2O formation on Ge anodes, it is naturally suggested to compare the behavior of Ge to that of chemically similar Si electrodes. Si electrodes have been fabricated and cycled under the same conditions as the previously presented Ge films. As an example, the QCM and CV mass changes of 20Si-0.1 are presented in Fig. 6a and evaluated for the amount of reversible Li2O as shown in Fig. 6b and S7.† Additional data of cyclic voltammetry (capacity and efficiency) are presented in the ESI (see Fig. S8†). As clearly demonstrated by Fig. 6b, Si shows a significantly larger (almost double) amount of reversible Li2O than germanium.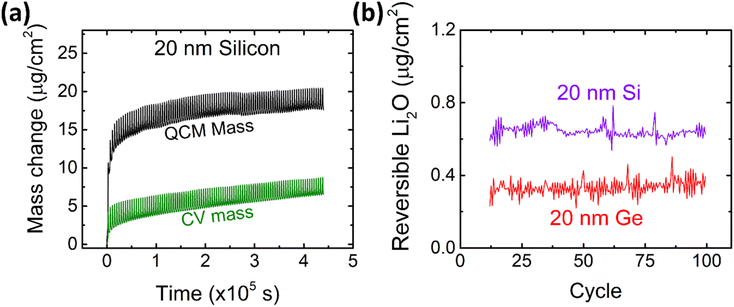 | ||
| Fig. 6 (a) Mass change as derived from CV and QCM of 20 nm Si at a scan rate of 0.5 mV s−1 in the potential window of 0.1–1.2 V. Further data on Si are presented elsewhere.16 (b) The amount of reversible Li2O on 20 nm Si and 20 nm Ge in comparison. | ||
3.6 Mechanism of reversible Li2O formation
The presented various experimental observations of the mass-change during CV experiments demonstrate clearly that the storage of Li by alloying of Ge and Si anodes is accompanied by a reversible ad- and desorption of molecular species with a characteristic mass per charge close to 15 u e−1. In view of known small inorganic molecules (see Table 1) and confirmation by XPS, the relevant reversible species is probably best understood as Li2O. Since combination with existing components of the electrode would not be visible as an additional mass in the QCM data, more complex combinations of Li2O with Si or Ge are also a possible interpretation.The quantitative contribution of this additional reversible species depends on various significant factors. Our experiments have shown that the absolute amount:
(i) Increases strongly with the thickness of the Ge or Si anodes,
(ii) Increases only weakly with the decreasing scanning rate,
(iii) Decreases when pronounced cracking of the electrode during cycling, and finally
(iv) It is significantly larger in the case of Si than in case of Ge electrodes at comparable scanning rate and electrode thickness.
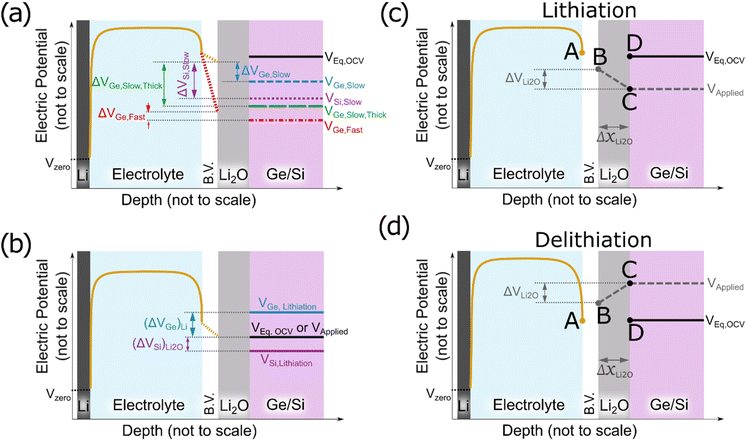
To understand these experimentally observed dependencies at least in a qualitative manner, we may start from our earlier suggestion and interpret the formation of Li2O as a reaction at the surface of the electrode derived from the reduction of the electrolyte (see also ref. 16). Since we observed in the XPS data the indication that the reversible product lies in contact to the Ge, we consequently assume the Li2O as an additional thin oxide layer between the SEI and the electrodes. Electrons are needed to reduce the electrolyte and to form further oxide, the final thickness of the oxide layer is expected to be controlled by the maximum available driving force that pushes electrons through the already formed oxide from the electrode to the electrolyte side, meaning the voltage drop across the already formed Li2O layer. Fig. 7a presents a principal sketch of this arrangement, where the growing Li2O layer is shown in grey. As indicated in the sketch, the voltage drop is essentially determined by a balance between the Butler–Volmer over-potential (at the interface to the liquid electrolyte, increasing upon increasing scan rate) that depresses the voltage at the left boundary and the diffusional or kinetic over-potential appearing at the electrode (increasing upon rate and upon thickness, but decreasing with increasing diffusivity) that suppresses the voltage at the right side of the oxide layer. Since the voltage drop between the two sides of the oxide provides the driving force, an increase of the B.V. overpotential decreases the driving force to oxide formation, but an increase of the diffusion overpotential increases the driving force.
Various voltage levels are indicated in the Fig. 7a. Obviously, a larger electrode thickness at constant charging rate requires the diffusional over-potential to increase proportional to the thickness, but keeps the Butler–Volmer overpotential almost constant (comparing ΔVGe, Slow, Thick (green) and ΔVGe, Slow (blue)). In consequence, the voltage drop (ΔVGe, Slow, Thick (green)) across the oxide increases substantially for a thicker electrode. Thus, the thickness (or the amount) of the formed oxide becomes large. By contrast, increasing the charging rate at constant electrode thickness needs faster transport at the Butler–Volmer interface as well as faster diffusion in the electrode. Thus, both overpotentials increase simultaneously, but they have opposite effects on the oxide growth. In consequence, the dependence of the oxide thickness on the charging rate is comparably weak (compare ΔVGe, Fast (red) and ΔVGe, Slow (blue)).
Cracks inherently reduce the length of the migration pathways for lithium by short-circuit transport (as the electrolyte can easily penetrate into the cracks) which has the same effect as reducing the thickness of the electrode. So, the more cracks, the less is the formation of reversible oxide due to a reduction of the diffusional over-potential (compare blue short-dashed line and green long-dashed line in Fig. 7a). This expectation matches strikingly well with the observed stronger decrease of Li2O formation during cycling in case of 100Ge-0.1 (strong cracking) compared to 100Ge-0.3 (weak cracking).
The stated difference in the amount of produced Li2O in the cases of Si or Ge must be attributed to the different thermodynamic and/or kinetic properties of the anode materials. The potentially interesting properties of Si and Ge are summarized in Table 2. For the case of Si, we had already considered the poor electronic conductivity in our prior study.16 Still, silicon has a much lower ionic than electronic conductivity (see Table 2). In view of this, we can safely say that it is the slow ionic migration which controls the necessary transport over-potential. This has also been shown similarly for other comparable electrode materials.33,34 With regard to the data in Table 2, the same argument holds even more so for Ge, as both its ionic and electronic conductivities are orders of magnitude larger than in Si, but the electronic even more so than the ionic.
| Anode | Voltage vs. Li/Li+ to form X1Li1 (V) | Li diffusion coefficient at RT (cm2 s−1) | Ionic conductivity (from diffusion coefficient) (S cm−1) | Intrinsic electronic resistivity (ohm cm) |
|---|---|---|---|---|
| Ge | 0.55 | 6.14 × 10−12 | 1.84 × 10−6 | 47 |
| Si | 0.4 | 3 × 10−14 | 1.01 × 10−8 | 2.3 × 105 |
Since Li diffusivity in Si is slower than in Ge, the diffusional over-potential at the same lithiation rate must obviously be higher and, therefore, the voltage drop across the Li2O layer is significantly higher in the case of Si than in the case of Ge. These voltage drops have been highlighted in Fig. 7a by purple-dotted and blue short-dashed lines for Si and Ge, respectively, indicating the necessary voltage to achieve the same state of charge (neglecting thermodynamic dissimilarities). So, for the same thickness, voltage range, and scanning rate, Si is naturally expected to show a larger amount of Li2O formation, which matches very well to the experimental findings reported here. The principal concentration profiles leading to the potentials shown in Fig. 7a are presented in Fig. S9 of the ESI.†
The different thermodynamic stability of the intermetallic phases, meaning the different onset voltages of lithiation (for the first intermetallic phase Li1X1, where X is Si or Ge), which are 0.55 V and 0.40 V vs. Li/Li+ for Ge and Si, respectively,35 may lead to an additional contribution. As illustrated in Fig. 7b, only if the applied voltage (black solid line) falls below the equilibrium lithiation potential, the alloying into the electrode can start. This happens in Ge sooner than in silicon. In other words, in the case of silicon, due to the lower onset potential for lithiation, the voltage range for exclusive Li2O formation is wider than for Ge. Thus, thermodynamically as well, Si may be expected to produce more reversible Li2O than Ge. However, when estimating the diffusion over-potentials from the ionic conductivities stated in Table 2, it is concluded that the kinetic effect owing to the difference in diffusivities has a much larger effect.
That far, we have discussed the formation of the Li2O layer upon the electrode's surface before lithiation but also its dissolution in the subsequent half cycle needs consideration. According to the operando QCM data, this also happens interestingly before delithiation (see Fig. 2f, dashed red line). Since we justified before that the Li2O formation is controlled by the potential difference between the electrode's surface and the B.V. interface, the same argument must hold during delithiation as well. Fig. 7c shows the postulated mechanism for the formation of the Li2O during lithiation (as discussed above). At the beginning of the cycle all potential points A to D are at the same level (the open circuit voltage). First, the applied voltage is lowered (point C) to drive ions into the electrode. As a consequence of the developing flux, point B is lowered by the B.V. drop. As soon as a negative voltage gradient is present across the oxide, electrons will flow towards the electrolyte side, where they induce fresh oxide (e.g. according to eqn (9) or (10a), see below). During lithiation, the growing Li2O layer (ΔxLi2O in Fig. 7c) reduces the gradient and hence further growth is decelerated with time. During delithiation, however, the voltage gradient is established in the opposite direction, driving electrons into the electrode and thus dissolving the oxide at the surface (e.g., as per eqn (9) or (10b)). Remarkably, in this case, shrinkage of the oxide increases the gradient and thus even accelerates the further dissolution, which explains why dissolution of the oxide is fast and can be almost completed before major delithiation sets in.
From the presented experiments, the exact chemical reactions leading to the formation of Li2O remain unclear. Presently, we may speculate the following possible options:
(i) Li2O formation/dissolution assisted by the decomposition of anions of the lithium salt
| ClO4− + 2Li+ + 2e− ⇌ ClO3− + Li2O | (9) |
(ii) Or decomposition of the solvent:
| 2EC + 2Li+ + 2e− → Li2O + 2C2H4 + 2CO2 + ½O2 (Li2O formation) | (10a) |
| Li2O → 2Li+ + 2e− + ½O2 (Li2O decomposition) | (10b) |
The existence of the second reaction of Li oxide formation, according to eqn (10a), has been at least reported by Liu et al.27 However, since the gases formed therein will likely escape from the electrolyte, the reversibility of the reaction (10a) is questionable. In this regard, only the first reaction (eqn (9)) seems to be a likely explanation, even though one could argue that the amount of ClO3− ions is significantly less compared to ClO4− which hinders the reversion of eqn (9) in view of mass-action law. Alternatively, we could imagine the dissolution viaeqn (10b), but thereby releasing oxygen. Although the reversibility of the additional mass of 15 a.m.u per electron has been directly proven in our experiments, a dissolution of the oxide exclusively according to eqn (10b) is problematic from a thermodynamics point of view. It would require a very high electrode potential of 2.91 V,39 way higher than observed in our experiments.
To further clarify the reaction, an in situ gas analysis would be highly recommended. In the identification of the reaction products also advanced TEM, possibly with cryo-preparation of samples and electrochemical titration experiments (to maintain equilibrium conditions), would be suggested to complement these methods. Noteworthy, this reversible Li2O formation and dissolution could be a mechanism for additionally stabilizing nano-structured Ge electrodes. However, its exact impact on the mechanical and chemical stability should be determined by depositing an artificial Li2O layer on different thickness of the electrode. These more advanced experiments are currently beyond the scope of this study but left for our future work.
4 Conclusion
In this paper, quartz crystal microbalance and cyclic voltammetry were combined to quantitatively investigate the SEI formation and cycling behavior of Ge battery anodes and compared with the behavior of Si.(I) A 100 nm thick Ge anode layer undergoes severe cracking upon lithiation down to 0.1 V vs. Li/Li+. However, cracking is reduced by limiting the minimum voltage to 0.3 V. A 20 nm thick layer experiences no cracking at all when cycled till 100 cycles.
(II) The SEI mass increases drastically upon cracking due to exposure of fresh surface to the electrolyte. In this case, the electrode is converted into a heterogeneous compound of Ge particles and SEI.
(III) Evidenced by QCM mass spectrometry, a further redox species of about 15 a.m.u per electron, probably Li2O, has been identified as a reversible species aside Lithium which is formed/removed during lithiation/delithiation of Ge anodes. The conclusion for Li2O is further supported by XPS data. Its quantitative amount is affected by (a) the thickness of the electrode and (b) the scan rate of cycling and (c) the cracking stability of the electrode. When varying these factors, the observed trends are in a convincing qualitative agreement with a proposed model based on the balance between Butler–Volmer and diffusional overpotentials, which controls the electric driving force to form the oxide layer.
(IV) A direct comparison of the amount of Li2O formed at the surface of Si and Ge shows that formation of Li2O and the insertion of Li are competitive reactions. The slower lithiation of Si, caused by lower diffusivity in comparison to Ge, provokes a larger amount of Li2O. In addition, the amount of the reversible Li2O weekly depends on the different onset potentials of lithiation in both electrode materials.
The study has clearly demonstrated the storage of the overall charge either in the form of alloyed/intercalated species or as a reversibly formed surface oxide layer. Their relative contributions can be conveniently controlled by the microstructure and the kinetics of lithium in the electrode.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
KW would like to acknowledge China Scholarship Council (CSC, China) for financial support of his PhD study. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 492318587 (SCHM 1182/25-1). YJ would like to thank BMBF for the funding of the project AQua IQ-El.References
- F. Wu, J. Maier and Y. Yu, Chem. Soc. Rev., 2020, 49, 1569–1614 RSC.
- X. Fan and C. Wang, Chem. Soc. Rev., 2021, 50, 10486–10566 RSC.
- Y. Chen, Y. Kang, Y. Zhao, L. Wang, J. Liu, Y. Li, Z. Liang, X. He, X. Li, N. Tavajohi and B. Li, J. Energy Chem., 2021, 59, 83–99 CrossRef CAS.
- S. L. Candelaria, Y. Shao, W. Zhou, X. Li, J. Xiao, J. G. Zhang, Y. Wang, J. Liu, J. Li and G. Cao, Nano Energy, 2012, 1, 195–220 CrossRef CAS.
- W. Li, X. Sun and Y. Yu, Small Methods, 2017, 1, 1600037 CrossRef.
- H. T. Gobena, Y. L. Samson, Y. K. Alexey, J. P. Maehlen, F. Ghamouss and D. Lemordant, Battery Energy, 2023, 2, 20220062 CrossRef CAS.
- Y. Lv, Z. Han, R. Jia, L. Shi, S. Yuan and C. Yingying Lv, Battery Energy, 2022, 1, 20220009 CrossRef CAS.
- L. Y. Lim, N. Liu, Y. Cui and M. F. Toney, Chem. Mater., 2014, 26, 3739–3746 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- E. Peled and S. Menkin, J. Electrochem. Soc., 2017, 164, A1703–A1719 CrossRef CAS.
- P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309 RSC.
- K. Wang, Y. Joshi, H. Chen and G. Schmitz, J. Power Sources, 2022, 535, 231439 CrossRef CAS.
- K. Wang, Y. Joshi, H. Chen and G. Schmitz, J. Power Sources, 2023, 569, 232919 CrossRef CAS.
- H. A. Müller, Y. Joshi, E. Hadjixenophontos, C. Peter, G. Csiszár, G. Richter and G. Schmitz, RSC Adv., 2020, 10, 3636–3645 RSC.
- J. Zhang, P. F. Wang, P. Bai, H. Wan, S. Liu, S. Hou, X. Pu, J. Xia, W. Zhang, Z. Wang, B. Nan, X. Zhang, J. Xu and C. Wang, Adv. Mater., 2021, 34, 2108353 CrossRef PubMed.
- T. Kohler, E. Hadjixenophontos, Y. Joshi, K. Wang and G. Schmitz, Nano Energy, 2021, 84, 105886 CrossRef CAS.
- A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15 CrossRef.
- N. Tian, C. Hua, Z. Wang and L. Chen, J. Mater. Chem. A, 2015, 3, 14173–14177 RSC.
- R. Hu, D. Chen, G. Waller, Y. Ouyang, Y. Chen, B. Zhao, B. Rainwater, C. Yang, M. Zhu and M. Liu, Energy Environ. Sci., 2016, 9, 595–603 RSC.
- N. Shpigel, M. D. Levi, S. Sigalov, L. Daikhin and D. Aurbach, Acc. Chem. Res., 2018, 51, 69–79 CrossRef CAS PubMed.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- Z. Yang, M. C. Dixon, R. A. Erck and L. Trahey, ACS Appl. Mater. Interfaces, 2015, 7, 26585–26594 CrossRef CAS PubMed.
- J. Terwort, F. Berkemeier and G. Schmitz, J. Power Sources, 2016, 336, 172–178 CrossRef CAS.
- L. A. Giannuzzi, B. W. Kempshall, S. M. Schwarz, J. K. Lomness, B. I. Prenitzer and F. A. Stevie, in Introduction to Focused Ion Beams, 2005, pp. 201–228 Search PubMed.
- D. Aurbach and A. Zaban, J. Electroanal. Chem., 1995, 393, 43–53 CrossRef.
- T. Yoon, G. Song, A. M. Harzandi, M. Ha, S. Choi, S. Shadman, J. Ryu, T. Bok, S. Park and K. S. Kim, J. Mater. Chem. A, 2018, 6, 15961–15967 RSC.
- T. Liu, L. Lin, X. Bi, L. Tian, K. Yang, J. Liu, M. Li, Z. Chen, J. Lu, K. Amine, K. Xu and F. Pan, Nat. Nanotechnol., 2019, 14, 50–56 CrossRef CAS PubMed.
- G. V. Zhuang, H. Yang, P. N. Ross, K. Xu and T. R. Jow, Electrochem. Solid-State Lett., 2006, 9, A64 CrossRef CAS.
- E. Peled, D. Bar Tow, A. Merson, A. Gladkich, L. Burstein and D. Golodnitsky, J. Power Sources, 2001, 97–98, 52–57 CrossRef CAS.
- P. Ganesh, P. R. C. Kent and D. E. Jiang, J. Phys. Chem. C, 2012, 116, 24476–24481 CrossRef CAS.
- M. Martins, D. Haering, J. G. Connell, H. Wan, K. L. Svane, B. Genorio, P. Farinazzo Bergamo Dias Martins, P. P. Lopes, B. Gould, F. Maglia, R. Jung, V. Stamenkovic, I. E. Castelli, N. M. Markovic, J. Rossmeisl and D. Strmcnik, ACS Catal., 2023, 13, 9289–9301 CrossRef CAS.
- D. Aurbach, B. Markovsky, I. Weissman, E. Levi and Y. Ein-Eli, Electrochim. Acta, 1999, 45, 67–86 CrossRef CAS.
- N. J. J. De Klerk and M. Wagemaker, ACS Appl. Energy Mater., 2018, 1, 5609–5618 CAS.
- L. H. J. Raijmakers, D. L. Danilov, R. A. Eichel and P. H. L. Notten, Electrochim. Acta, 2020, 330, 135147 CrossRef CAS.
- A. J. Morris, C. P. Grey and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054111 CrossRef CAS.
- J. Graetz, C. C. Ahn, R. Yazami and B. Fultz, J. Electrochem. Soc., 2004, 151, A698 CrossRef CAS.
- D. A. Porter, K. E. Easterling and M. Y. Sherif, Phase Transformations in Metals and Alloys, CRC Press, 3rd edn, 2009 Search PubMed.
- F. Ozanam and M. Rosso, Mater. Sci. Eng. B, 2016, 213, 2–11 CrossRef CAS.
- K. C. Lau, L. A. Curtiss and J. Greeley, J. Phys. Chem. C, 2011, 115, 23625–23633 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05641d |
| This journal is © The Royal Society of Chemistry 2024 |