Effects of droplet deposition on aerosol capture efficiency of bipolarly charged fibers

Abstract

Aerosol filters composed of electrostatically charged bipolar fibers are referred to as electret filters. A novel computational model is developed in this work to study the impact of droplet deposition on aerosol capture efficiency of electret fibers. The electret fibers were assumed to have a dipole orientation that was either parallel or perpendicular to the airflow direction. The simulations were conducted using the ANSYS CFD code after it was enhanced with a series of in-house subroutines. Our simulations revealed that droplet deposition on electret fibers decreases their ability to capture airborne particles. More specifically, the simulations were devised to isolate droplet's physical and electrical properties (e.g., surface tension, electrical conductivity…) and quantify their impact on fiber capture efficiency. It was found, in particular, that droplet's electrical conductivity and permittivity have the most adverse impact on the performance of an electret fiber. This is perhaps because higher droplet conductivity results in severe fiber charge neutralization, and higher droplet permittivity leads to a stronger fiber charge shielding. In contrast, fiber wettability was found to have a negligible impact on fiber efficiency. The work presented in this paper offers valuable insights into the complex nature of electret filters used in different industrial and environmental applications.

---

1 Introduction

Electret filters are widely used in respiratory masks and HVAC filters for their high particle capture efficiency.^1,2 Electrostatic attraction is the primary mechanism of particle capture in an electret aerosol filter. The airborne particles naturally carry some positive and negative electrostatic charges according to the Boltzmann equilibrium charge distribution (they carry equal numbers of positively charged and negatively charged particles). Electrostatic attraction enables a higher aerosol collection efficiency without increasing the filter's pressure drop.

A charged fiber attracts neutral particles via polarization force (induced dipole) and attracts charged particles via a combination of polarization and Coulomb forces.^3–7 Particle capture in an electret filter is due to a combination of mechanical (inertial impaction, interception, and diffusion) and electrostatic (coulombic and polarization) capture mechanisms.^8–15 The capture efficiency of a mechanical filter generally increases with solid particle accumulation on the fiber. This, however, is not necessarily the case with electret filters.^16–19 Various factors (e.g., fiber charge neutralization and charge shielding) can impact the collection efficiency of an electret filter. For this reason, it is hard to draw a universal conclusion about the performance of electret filters when loaded with particles. For instance, Brown et al.²⁰ reported that the decrease in filtration efficiency of their dust-loaded electret filters was due to the dendritic particle-deposits that formed on the surface of the fibers (i.e., the charge shielding effect). In contrast to solid particles, liquid droplets behave very differently when they are captured by a fiber as they can deform and spread on and between the fibers.^21–23 There are only a few studies focused on performance degradation of electret filters exposed to organic solvents (e.g., dioctyl phthalate (DOP), poly-α-olefins (PAO), or isopropyl alcohol (IPA)).^24–28 Because of its complex nature, the physics behind charge decay in droplet-loaded electret filters has remained unclear. This complexity arises from the intricate interplay between various factors, including the electrical and interfacial properties of the droplets as well as the wetting properties of the fibers.

To the best of our knowledge, no study has yet proposed a theoretical framework to analyze the effects of droplet deposition on the performance of electret filters. In this concern, we have developed a 3-D model to simulate the interactions between liquid aerosols (DOP and water) and charged fibers, and to also quantify the aerosol capture efficiency of a droplet-loaded electret fiber. Our results predict a significant reduction in the collection efficiency of an electret fiber due to droplet deposition and shed some light on underlying physics of fiber charge degradation.

The remainder of this paper is organized as follows. In Section 2, we describe the problem and present the governing equations that need to be solved for the electrohydrodynamic field around an electret fiber. In Section 3, we describe the governing equations for the aerodynamic field around the fiber as well as the balance of force that acts on aerosol particles. Our results and discussion are presented in Section 4 followed by our conclusions in Section 5.

2 Governing equations for electrohydrodynamic flow

The computational domain considered for this work has a length, width, and height of 60 μm, 32 μm, and 5 μm, respectively. It consists of a square cell zone, in which an electret fiber is placed (the cell size was determined based on the desired solid volume fraction). For simplicity, we have assumed the bipolar fibers to have equal amounts of dissimilar charges on their opposite sides. The magnitude of surface charge density of fibers considered in this work is based on the experimental work of Chang et al.²⁹ Two additional zones, upstream and downstream of the fiber, were considered and meshed using polyhedron elements. The mesh was refined near the fiber surface where strong gradients were expected (see Fig. 1). Our simulations of droplet deposition on electret fibers took advantage of the volume of fluid (VOF) method in the presence of an electrostatic field. More specifically, a body force term (electrical stress) was added to the Navier–Stokes equations to account for the impact of the electrostatic field on droplet motion. The electric field was obtained from solving the electrostatic potential equation (assuming neutral droplets). Dioctyl phthalate (DOP) or water droplets with a diameter of d, a density of ρ_i, viscosity of μ_i, relative permittivity of ε_i, and an electrical conductivity of σ_i were initially placed near the fiber and allowed to evolve (and move solely under the influence of the electrostatic field) with time. The properties of the fluids used in the simulations are listed in Table 1.

Fig. 1 Computational domain and its boundary conditions. The yellow-filled cells represent the droplets at time zero.

Table 1 Properties of the material

Material	d (μm)	ρ (kg m^−3)	μ (Pa s)	σ (S m^−1)	ε r	γ (N m^−1)	θ (°)
Air	—	1.205	1.79 × 10^−5	1.0 × 10^−20	1.0	—	30,65,108
DOP	1.0	988	5.77 × 10^−3	2.67 × 10^−12	5.1	0.015
Water	1.0	988	1.0 × 10^−3	5.5 × 10^−6	80.18	0.072
Fiber	8.0	1000	—	—	1.5	—

---

The mesh size was selected such that each droplet was represented by at least 68 cells. To achieve this, a mesh size of approximately 200 nm (or smaller) was used to simulate a droplet with a diameter of 1 μm. The air velocity at the inlet was set to zero to prevent droplet movement induced by drag force. The outlet was designated as the pressure outlet, and the side walls were treated as symmetric boundary conditions. The top and bottom walls were assigned a periodic boundary condition. Furthermore, a no-slip boundary condition with a specified contact angle was imposed on the fiber wall. Additionally, we also assumed that the free charges developed at the droplet–air interface do not alter the fiber's surface charge density due to contact with the fiber. This assumption was made to simplify the complicated nature of the problem at hand. VOF method relies on solving the mass and momentum conservation equations for each phase. The mass conservation across the entire domain can be expressed as follows:

∇·(ρU) = 0 (1)

where ρ and U are the density and velocity of the fluid, respectively. The two-phase fluid flow field under investigation here was also affected by the electrostatic field. Additional terms were added to the Navier–Stokes equations to incorporate the influence of surface tension at the droplet–air interface F_st and the electric stress F_es, i.e.,

The volume fraction of each phase was determined by solving the subsequent equation.

where the subscript q refers to either the droplet (o) or air (a) phase. In the VOF method, the properties such as density, viscosity, and permittivity in each computational cell are dependent on the cell's volume fraction. Therefore, such physical properties are interpolated using the Weighted Arithmetic Mean (WAM), defined as:

ρ = α_oρ_o + (1 − α_o)ρ_a (4)

μ = α_oμ_o + (1 − α_o)μ_a (5)

ε = α_oε_o + (1 − α_o)ε_a (6)

σ = α_oσ_o + (1 − α_o)σ_a (7)

The volumetric surface tension force F_st was defined using the Continuum Surface Force (CSF) model.³⁰ The model treats surface tension as a continuous, 3-D force along the interface, rather than a boundary condition applied directly at the interface. The expression for the volumetric surface tension force is given by:

Here, γ is the surface tension coefficient, and κ is the curvature of the droplet–air interface. The VOF method obtains the curvature of the droplet–air interface κ using the unit normal vector n̂i.e.,

The VOF formulation defines the surface normal vector at the droplet–air interface 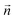as the gradient of the phase volume fraction, i.e.,

The surface tension force is applied using a piecewise linear interface calculation (PLIC) scheme, which accurately computes curvatures to reconstruct the droplet–air interface.

The electrostatic body force F_es can be derived by taking the divergence of the Maxwell stress tensor τ_m, and is given as,

F_es = ∇·τ_m (11)

where ρ_e is the volumetric charge density and E is the electric field strength. The first term on the right-hand side of eqn (12) represents the electrophoretic (Coulomb) force arising from the interaction between the electric charges and the external electric field (aligned with the electric field direction). The second term accounts for the dielectrophoretic (polarization) force which is due to the permittivity gradient at the fluid–fluid interface (acting in a direction normal to the interface). The last term arises from the changes in the material density, and is typically known as the electrostriction force.³¹ In this study, the effect of electrostriction forces was considered negligible due to the assumption that the fluids are incompressible.

In an electrohydrodynamic flow, the dynamic currents are small because the time scales at which the magnetic induction effect becomes important are significantly smaller than the flow time scales.^32,33 Therefore, we ignored the electromagnetic coupling and assumed that the electric field E was curl free, i.e., ∇ × E = 0 and E = −∇ϕ. Since F_es depends on E and ρ_e (see eqn (12)), we solved the Poisson (eqn (13)) and charge conservation equations (eqn (14))³⁴ by assuming zero electrostatic potential and zero charge flux at the inlet and outlet boundaries. A constant potential flux and a fixed charge density were assigned to the fiber surface.

∇·(εE) = ∇·(ε(−∇ϕ)) = ρ_e (13)

In eqn (14), the second term represents the ohmic charge conduction, the third term accounts for the convection of charges, and the fourth term accounts for ion diffusion in the fluid. The diffusivity of the ion is denoted by D. In this study, droplets (water or DOP) had extremely low ion concentrations, and the air contained no ions.

3 Governing equations for aerosol flow modeling

To simulate the capture of aerosol particles by a droplet-loaded bipolar fiber using ANSYS, we started by storing the electrostatic field intensity and its gradients in different user defined memory (UDM), as described in Section 1 of the ESI.† The flow field around the fiber is characterized by the Reynolds number, which represents the ratio of inertial to viscous forces. The Reynolds number, defined using the fiber diameter, was found to be Re = 0.0539, which is much less than one, indicating that the flow around the fiber is dominated by viscous force (i.e., the Stokes flow regime). Therefore, we obtain the aerodynamic field in the computational domain by solving eqn (15), derived from eqn (2).

∇·p = μ∇²U (15)

Aerosol capture efficiency calculations started by releasing a certain number of particles in the computational domain and then tracking their trajectories via integrating Newton's second law applied to each particle. This resulted in the position and velocity of each particle as a function of time.^35,36 For a spherical particle in the Stokes regime, the equation of motion was expressed as follows:

where, m_p, u_i^p, U_i, d_p, ρ_p, and C^c are the particle mass, particle velocity, fluid velocity, particle diameter, particle density, and Cunningham correction factor, respectively. The first term on the right-hand side of eqn (16) is the drag force per unit mass of the particle, while the second and the third terms, respectively, represent the polarization force f_Di and the Coulomb force f_ci, i.e.,where ε_p is the dielectric constant of the particle and q(n) = ne is the total number of elementary charges e carried by the particle. Eqn (17) and (18) were added to the standard discrete phase model (DPM) module in ANSYS via a UDF. Numerical simulations for the capture of aerosol particles by a droplet-loaded bipolar fiber were conducted by solving eqn (15) and (16) with boundary conditions given in Table 2.

Table 2 Hydrodynamic and electrostatic boundary conditions used in the simulations

Boundary	Aerodynamic	Particle trajectory
Inlet	Velocity inlet: ux = u∞; uy = 0	Escape
Outlet	Pressure outlet	Escape
Sides		—
Fiber surface	No slip	Trap
Top and bottom sides	Periodic	—

---

We defined single fiber efficiency (SFE) as the ratio of the number of particles captured by a fiber (or by loaded droplets) n_cap to the number of particles injected from the inlet boundary n_inj, i.e.,

In predicting SFE, a given number of particles were injected at the inlet boundary using a UDF. Particles that encountered the fiber or deposited droplets were removed from the simulations. For these calculations, an interception UDF was used to monitor the distance between the surface of the particle and the surface of the fiber (or the surface of the deposited droplets). Aerosol particles in the size range of 50 to 1000 nm were considered for the simulations and it was assumed that they each carried a single positive or negative charge (i.e., q_p = ±1e). The properties of the electret filter and solid aerosol particles employed in the simulations are listed in Table 3.

Table 3 Properties of the filters and particles considered in the simulations

Parameters	Values
Filter thickness, H	0.70 mm
Face velocity, U0	0.1 m s^−1
Fiber charge density, σf	25 or 50 μC m^−2
Solid volume fraction, α	5.0%
Particle diameter, dp	50–1000 nm
Dielectric constant of particle, εp	4.6
Particle density, ρp	1980 kg m^−3
Particle charge	±1e

---

Due to its complex nature, not many empirical correlations have been developed to predict the performance of electret fibers. In addition, the presence of liquid droplets on the surface of the electret fibers further complicates the problem. Electret fibers capture aerosol particles mostly via the Coulomb and polarization forces. We considered both the electrostatic capture and interception mechanisms for the collection of aerosol particles in this study. Note that the inertial impaction mechanism plays a negligible role in the capture of small particles, especially in comparison to electrostatic and interception mechanisms. This can easily be examined by calculating the Stokes number (St), which measures the ratio of a particle's inertia to the viscous forces exerted on it by the fluid. For the particles considered in our study, the Stokes number varies in the range of 0.00097 < St < 0.0885, which is much less than unity, i.e., the particles follow the air streamlines perfectly.⁸ We have extensively investigated the role of Brownian diffusion in aerosol capture in our previous work (see ref. 9, 19, 37 and 38 and references therein). For this reason, we intentionally excluded the effects of Brownian diffusion in the current study to better isolate the role of electrohydrodynamic and electrostatic forces in aerosol filtration. It is well known that the Brownian force increases the collection efficiency of fibers for particles smaller than 200 nm. Including the Brownian diffusion does not add much to the physics of the problem at hand, but it makes it harder to explain the effects of droplet deposition on the electrostatic capture efficiency of the fiber. The empirical SFE correlation along with related equations and discussion are provided in Section 2 of the ESI.† Moreover, the percentage reduction in the SFE of clean and droplet-loaded fibers was determined using the average SFE values for both the droplet-loaded and clean fibers as per eqn (20).

Here, η_SFE,Clean and η_SFE,Droplet represent the SFE of clean and droplet-loaded electret media, respectively.

A validation study for our numerical simulations of electrohydrodynamic aerosol flow is given in Section 3 of the ESI.†

4 Results and discussion

4.1 Fiber properties

This section presents simulation results for the interactions between an electret fiber and DOP droplets. This will be in terms of volumetric charge development in the droplets and the decrease of the fiber's electrostatic field due to droplet deposition.

Neutral DOP droplets become polarized when they are in the proximity of charged bipolar fibers. The polarized droplet is then attracted to the fiber due to the electrostatic field and the permittivity gradient at the air–liquid interface. The polarization force is always attractive due to the negative gradient of the permittivity towards the fiber (see eqn (12)). The nature of the Coulomb force depends on the polarity of the charges on the droplet and the fiber. Initially, the electrohydrodynamic forces were weaker than the surface tension force, so the droplet remained spherical and stationary (Fig. 2a). Over time, the total electrostatic force became stronger than the surface tension force causing the droplet to become elongated and accelerate towards the fiber (Fig. 2b). Once the droplet deposited on the fiber, the tangential and radial components of the electrostatic forces (i.e., Coulomb and polarization forces) worked to spread the droplet on the fiber surface. The capillary force helped the droplet spread on the fiber, when the contact angle was less than 90 degrees (Fig. 2c), and resisted against it when the contact angle was greater than 90 degrees. The droplets stopped spreading when their kinetic energy, generated by the electrohydrodynamic forces acting on them, was exhausted by the frictional viscous forces between the droplets and the fiber surface (Fig. 2d). A similar phenomenon has been observed in studies focused on the electrowetting effect on dielectrics.^39,40

Fig. 2 Simulation of DOP droplets' travel towards the charged fiber due to electrostatic attraction and their spread on the surface of the fiber are shown in (a) through (d) as a function of time. The surface charge density of the fiber and its contact angle with DOP were assumed to be σ_f = 25 μC m⁻² and 30°, respectively.

Fig. 3 shows examples of particle trajectory calculations around clean and droplet-loaded electret fibers. Two dipole orientations (parallel or perpendicular to the airflow direction) were considered. Aerosol particles considered in this figure had a diameter of 100 nm and carried a charge of −1e or +1e. Here, we considered a fiber diameter of d = 8 μm, a fiber surface charge density of σ_f = 25 μC m⁻², and a contact angle of θ = 30°. It can be seen in this figure that particles were attracted to the side of the bipolar fiber that had a charge polarity opposite to that of the particles. Moreover, it can be noted that collection efficiency against 100 nm particles was lower when the fiber dipole was parallel to the airflow direction and was higher when it was perpendicular (fibers with a parallel dipole repelled the positive particles with a strong Coulomb force, as shown in Fig. 3b and d). It can also be noted that collection efficiency decreased when the fiber was loaded with DOP droplets. A similar result was observed in the experiments of ref. 8, 28, and 41, where the deposition of DOP aerosols reduced the particle collection efficiency of an electret filter. This is because the charges that develop at the air–droplet interface generate an electrostatic field that opposes the field created by the charges of the fibers. This reduced the net intensity of the electrostatic field around the fiber, a phenomenon known as fiber charge neutralization. Moreover, the particle trajectories in Fig. 3c, g and h suggested that the repulsive Coulomb force exerted on the airborne particles by the droplet was weaker than the attractive Coulomb force exerted on them by the fiber.

Fig. 3 The impact of dipole orientation on the trajectory of particles with a diameter of 100 nm carrying charges of −1e and +1e are shown for clean (a, b, e and f) and DOP-loaded (c, d, g and h) charged fibers. Figures a–d and e–h show fibers with a parallel dipole and with a perpendicular dipole, respectively. A contact angle of 30° and a surface tension of 0.015 N m⁻¹ were considered for the DOP droplets. For illustration purposes, only a few number of trajectories are shown.

The electrostatic field around clean and droplet-loaded fibers is shown in Fig. 4a–d using the field vector plots overlaid on the contour plots of the electric field magnitude. Here, we considered a fiber surface charge density of σ_f = 25 μC m⁻² and a contact angle of θ = 30°. The electrostatic field emerges from the positive charge (indicated by arrows pointing outward away from the fiber) and converges on the negative charge of the fiber (indicated by arrows pointing towards the fiber). The red and blue colors represent the maximum and minimum magnitudes of the electrostatic field, respectively. The highest magnitude of the electrostatic field appears to be on the fiber surface where the gradient of the electrostatic potential changes sign (E = −∇ϕ), indicating a change in charge polarity. More interestingly, this figure shows that the magnitude of the electrostatic field decreases on the surface of the fiber where a DOP droplet is deposited (see the blue-colored droplets on the surface of the fibers in Fig. 4c and d). This effect is due perhaps to the differences between the permittivity of DOP and air. In addition, for the case of the parallel dipole (Fig. 4a and c), the maximum reduction in electrostatic field intensity was observed on the side of the fiber facing the air flow, while for the perpendicular dipole orientation (Fig. 4b and d), it was on the side of the fiber perpendicular to the air flow. More quantitative comparisons between the performance of fibers with perpendicular and parallel dipole orientations are given in Fig. 4e for clean and droplet-loaded fibers. This figure shows the percentage reduction in the SFE due to droplet deposition on an electret fiber versus particle size when the dipole orientation is parallel to the air flow (black symbols) and when it is perpendicular (red symbols). The inset in Fig. 4e shows the SFE of the clean fibers, and it indicates that SFE is higher for fibers with a perpendicular dipole when the aerosol particles are smaller than about 300 nm, but the role of dipole orientation becomes insignificant when particles are larger. The results presented in the inset of Fig. 4e are in qualitative agreement with the observations of Wang et al.² who reported that the dipole orientation of an electret fiber plays an insignificant role in the capture of large particles. Fig. 4e shows that the largest decrease in SFE occurred for larger particles and when the fiber dipole was oriented perpendicular to the air flow. This can be explained by considering that the gradient of the electrostatic field decreased more significantly with droplet loading on the fiber in the perpendicular dipole configuration. Note that for the larger aerosol particles, collection efficiency depends on the magnitude of the electrostatic field gradient and on the mass of the particle (see eqn (17)). For the smaller particles (less than 300 nm) on the other hand, the reduction in the magnitude of the electrostatic field was countered by an increase in the charge-to-mass ratio of the particles (the collection efficiency of the smaller particles depends on the magnitude of the electrostatic field and the charge-to-mass ratio of the particles, see eqn (18)).^3,14,15,19

Fig. 4 The electrostatic field around bipolar fibers with parallel and perpendicular dipoles are shown in (a) and (b) for clean fibers and in (c) and (d) for DOP-loaded fibers. SFE reduction due to the DOP loading is shown in (e) with the SFE of the clean fiber shown as the inset. A contact angle of 30° and a surface tension of 0.015 N m⁻¹ were considered for the DOP droplets.

Fig. 5a and b show contour plots of volumetric charge density of the DOP droplets deposited on fibers with two different surface charge densities of σ_f = 25 μC m⁻² and σ_f = 50 μC m⁻², respectively, in the parallel dipole orientation. Here the droplet-to-air conductivity and permittivity ratios , were considered to be 2.67 × 10⁸ and 5.1, respectively. As expected, increasing the surface charge density of the fiber resulted in an increase in the volumetric charge induced on the droplets. This is because the conduction of ohmic charges increased with increasing intensity of the electrostatic field (eqn (14)), and that enhanced the migration of charges from within the droplet to its surface. Also note that droplets deposited on the fiber's positive side acquired a negative volumetric charge (shown in blue), while those on the fiber's negative side acquired a positive charge (shown in red).

Fig. 5 Volumetric charge density contour plots for DOP droplets deposited on bipolarly charged fibers having surface charge density of σ_f = 25 μC m⁻² and σ_f = 50 μC m⁻² are shown in (a) and (b), respectively. SFE reduction due to the DOP loading is shown in (c) with the SFE of the clean fiber shown as the inset. A contact angle of 30° and a surface tension of 0.015 N m⁻¹ were considered for the DOP droplets.

Our predictions of the positive and negative charge development on the droplet–air interface are in qualitative agreement with the observations of Das et al.³³ and those of Reddy and Esmaeeli.⁴² The charge developed at the air–droplet interface generated an electrostatic field in the opposite direction to that produced by the fiber. Therefore, the induced charges reduce the net intensity of the electrostatic field around the fiber.

Fig. 5c shows the reduction percentage of SFE (due to droplet deposition) versus particle size. In this figure, two different surface charge densities are considered for the case of the parallel dipole configuration. The inset figure shows the SFE of the clean fibers, and it illustrates that increasing the fiber surface charge density increases the magnitude of the electrostatic field (and its gradient) leading to an increase in SFE. A similar phenomenon was reported by Podgorski and Balazy⁴³ in their numerical simulation. Notably, the results in Fig. 5c show a more severe decline in the capture of smaller particles (smaller than 300 nm) when the fiber was charged more strongly (blue symbols). This indicates that the droplet loading impacts the Coulomb force more severely than the polarization force, for fibers with a higher surface charge density. The average SFE reduction over the entire range of particle diameters was found to be 46% for the fiber with a surface charge density of σ_f = 25 μC m⁻² and 34% for the fiber with a surface charge density of σ_f = 50 μC m⁻².

4.2 Electrical properties of droplets

This section presents simulation results on how the electrical properties of DOP influence the electrostatic field around an electret fiber, and how that affects the electrostatic forces experienced by an aerosol particle traveling near the fiber.

Fig. 6a and b show the contour plots of electrostatic field magnitude around a fiber loaded with droplets having relative permittivity values of 5.1 and 80.18, respectively. The other properties considered in producing these figures were those of DOP droplets. The fiber was assumed to have a parallel dipole, a surface charge density of σ_f = 25 μC m⁻², and a contact angle of θ = 30°. In these plots, the red and blue colors represent the maximum and minimum values of the electrostatic field magnitude, respectively. It is evident from the figures that increasing the relative permittivity of the droplets resulted in a decrease in the magnitude of the electrostatic field (see the droplet colors in Fig. 6a and b). This decrease is because droplets with higher relative permittivity values can become more polarized and consequently, weaken the electric field around the fiber. Motevaselian and Aluru⁴⁴ also reported similar findings in their study, where they investigated the variation of perpendicular dielectric permittivity as a function of the electric field. They found that liquids with higher permittivity more effectively oppose the external electric field (thereby reducing the net electrostatic field within the computational domain). This effect is often referred to as electrostatic shielding. Fig. 6c shows the negative effect of loading a fiber with droplets of different relative permittivity values. This adverse effect was measured relative to the data from the clean fiber simulations shown as the inset in Fig. 5c. It can be seen in Fig. 6c that droplets with a higher relative permittivity value degraded the performance of the fiber more severely (i.e., more electrostatic shielding is expected from droplets with a higher permittivity). Moreover, the highest performance reduction seemed to occur against particles of about 500 nm in diameter. This is perhaps because both the polarization and Coulomb forces were at their minimum level for this particle size. The average SFE reduction over the entire range of particle diameters was found to be 46% for droplets with a relative permittivity of 5.1, and 57% for droplets with a relative permittivity of 80.18.

Fig. 6 Contour plots of electrostatic field magnitude around a DOP-loaded charged fiber are shown in (a) and (b) for relative permittivity values of ε_D = 5.1 and ε_D = 80.18, respectively. SFE reduction due to the DOP loading is shown in (c) which is relative to the data of clean fibers shown as the inset in Fig. 5c for σ_f = 25 μC m⁻². In this figure, the fiber has a parallel dipole.

The effect of droplet electrical conductivity is studied in Fig. 7. Here, the fiber is loaded with droplets of different electrical conductivity values. Fig. 7a and b show contour plots of polarization force exerted on an aerosol particle with a diameter of 1000 nm and a charge of −1e. Here the fiber was loaded with droplets having conductivity values of 2.67 × 10⁻¹² and 5.5 × 10⁻⁶ S m⁻¹, respectively. As can be seen, polarization force decreased with increasing droplet conductivity (see the color of the deposited droplets). This effect is due perhaps to a more efficient transfer of electrical charges inside the droplet with a higher conductivity value which reduces the gradient of the electrostatic field near the fiber (polarization force is proportional to the gradient of the electrostatic field). The polarization force vector field is overlaid on the contour plots in Fig. 7a and b, and it clearly confirms that polarization force is an attractive force by its nature, and it is independent of the charge polarity of particles or that of the fiber (the force vectors are always towards the fiber).^2,14,19

Fig. 7 Contour plots of the polarization and Coulomb forces exerted on aerosol particles with a diameter of d_p = 1 μm and a charge of q_p = −1e by a DOP-loaded bipolar fiber with a parallel dipole orientation. Electrical conductivity of DOP was assumed to be 2.67 × 10⁻¹² S m⁻¹ in (a) and (c) but 5.5 × 10⁻⁶ S m⁻¹ in (b) and (d). SFE reduction due to the DOP loading is shown in (e) which is relative to the data of clean fiber shown as the inset in Fig. 5c for σ_f = 25 μC m⁻².

Fig. 7c and d show similar results but for the Coulomb force experienced by the same aerosol particles. As can be seen, the Coulomb force decreases with increasing droplet conductivity (see the color of the deposited droplets). This occurs because increasing electrical conductivity enhances the ohmic conduction (eqn (14)), which leads to more charge transfer to the droplet surface, and in turn, enhances the charge neutralization effect. Also, note how the Coulomb forces converge towards the positive side of the fiber (i.e., attracting the negatively charged aerosols) but diverge from the negative side of the fiber (repelling the negatively charged aerosols). Fig. 7e quantifies the negative effect of droplet deposition on the performance of the aforementioned fiber. This adverse effect was measured relative to the data from the clean fiber simulations shown as the inset in Fig. 5c. It can be seen in Fig. 7e that deposition of high-conductivity droplets severely weakens the performance of the fiber. The performance reduction seems to be due to the weakened electrostatic forces (polarization and Coulomb) caused by electrostatic shielding and charge neutralization. It is worth noting that electrical conductivity has the most significant impact on the performance of a droplet-loaded electret fiber. This is confirmed by calculating the average SFE reduction over the entire range of particles, which was found to be about 46% for droplets with an electrical conductivity of 2.67 × 10⁻¹² S m⁻¹ and 60% for droplets with an electrical conductivity of 5.5 × 10⁻⁶ S m⁻¹.

4.3 Wetting properties

The wetting behavior of a fiber is generally characterized by the contact angle between the parent material of the fiber and the droplet of interest. Fig. 8a and b show the trajectory of particles with diameters of d_p = 0.2 μm and d_p = 1.0 μm, respectively, around a droplet-loaded electret fiber. Two different contact angles of 65° and 108° are considered for the deposited droplets. The aerosol particles in Fig. 8a carried a charge of q_p = −1e while those in Fig. 8b carried a charge of q_p = 1e. The fiber dipole was parallel to the airflow direction, the fiber surface charge density was σ_f = 25 μC m⁻², and the properties of the liquid were those of water.

Fig. 8 Aerosol particle trajectories are shown for particles with a diameter of d_p = 0.2 μm and a charge of q_p = −1e in (a) and for d_p = 1 μm and q_p = 1e in (b). The fiber in these figures is loaded with water droplets having contact angles of 65° and 108° with the fiber. SFE reduction due to the water droplet loading is shown in (c) which is relative to the data of the clean fiber shown as the inset in Fig. 5c for σ_f = 25 μC m⁻².

Fig. 8 shows that the negatively charged small particles were attracted towards the positive side of the fiber but they were repelled by the negative (back) side of the fiber. Fig. 8b shows the trajectory of positively charged large particles. Despite their charge polarity, these particles were also attracted towards the positive side of the fiber (as well as to some areas of the negative side). This behavior is due to the fact that large particles are predominantly affected by the polarization force (which is an attractive force regardless of the charge polarity of the particles) while the smaller particles are governed by the Coulomb force (an attractive or repulsive depending on the charge polarity of the particles relative to that of the fiber surface).^14,19 More interestingly, the deposited droplets repelled the incoming particles, as seen in Fig. 8a for Young–Laplace contact angles (YLCAs) of 65° and 108°. This is because the negative side of the fiber creates positive volumetric charges on the deposited droplets. Similarly, the positive side of the fiber creates negative volumetric charges on the droplets. It is also interesting to note that in the case of the more wettable fiber, i.e., θ = 65°, the droplets spread more on the fiber surface and so they receive more induced charges compared to the case of the less wettable fiber.

Consequently, smaller airborne particles (d_p = 0.2 μm and q_p = −1e) experience more repulsion at θ = 65° compared to θ = 108° as shown in Fig. 8a. However, larger particles (d_p = 1.0 μm and q_p = +1e) do not experience a repulsion force because the polarization force is much stronger than the Coulomb force, as illustrated in Fig. 8b. The effect of droplet deposition on the capture efficiency of the fiber is shown in Fig. 8c for both YLCAs considered. This adverse effect was measured relative to the data from the clean fiber simulations shown as the inset in Fig. 5c. As can be seen, fiber's YLCA in the range of 65 to 108 degrees seems to play a minor role in particle capture. Moreover, since common water (water with dissolved impurity) has a significantly higher conductivity than other common liquids and since water has the highest dielectric constant than other common liquids, deposition of water droplets on an electret fiber can affect its electrostatic field. Our analysis, illustrated in Fig. 8e and 6c, indicates that water droplet deposition has a more adverse effect on fiber performance compared to DOP droplets. This is because the movement of the volumetric charges from inside the droplet to the air–liquid interface is greatly enhanced when a droplet with high electrical conductivity is placed in an external electric field. Once such a droplet deposits on the fiber, the free charges at the air–liquid interface spread across the fiber surface, and since these charges are opposite in polarity to those of the fiber, the net electric field around the fiber decreases. As a result, the conductive droplet serves as a pathway for charge dissipation, thereby reducing the fiber's electrostatic collection efficiency. Additional information about the impact of humidity on the performance of electret filters can be found in ref. 8 and 36.

5 Conclusions

A computational model is developed in this work to study the effect of liquid droplet deposition on the aerosol capture efficiency of electrostatically charged fibers, for the first time. The aerosol particles were assumed to hold an equal number of positive and negative charges and to have a diameter in the range of 50 to 1000 nm. The droplets (either DOP or water) were assumed to be one micron in diameter and electrically neutral. The simulations were used to quantify the impact of droplet deposition on fiber's aerosol capture efficiency. Special attention was paid to the role of droplets’ wetting and electrical properties. Our simulations revealed that the deposition of such droplets on an electret fiber tends to decrease its particle capture efficiency. It was also concluded that droplet's electrical conductivity (due to severe charge neutralization) and droplet's permittivity (via charge shielding) have the most negative effect on fiber's efficiency. This is in contrast to the droplet's wetting properties that seemed to have a minimal effect on fiber performance. In addition to offering insights into the electrohydrodynamic behavior of a droplet-loaded electret fiber, this paper presents a simulation framework for the design and optimization of future electret media for different industrial and environmental applications.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported through Advanced Functional Fabrics of America (AFFOA), by NIST US Department of Commerce, award number 70NANB22H009.

References

1. L. Javidpour, A. Božic, A. Naji and R. Podgornik, Soft Matter, 2021, 17, 4296–4303.
2. Y. Wang, Z. Lin and W. Zhang, Aerosol Sci. Technol., 2020, 54, 1479–1491.
3. R. Lathrache, H. Fissan and S. Neumann, J. Aerosol Sci., 1986, 17, 446–449.
4. C. Kanaoka, H. Emi, Y. Otani and T. Iiyama, Aerosol Sci. Technol., 1987, 7, 1–13.
5. C. Kanaoka, S. Hiragi and W. Tanthapanichakoon, Powder Technol., 2001, 118, 97–106.
6. Y.-W. Oh, K.-J. Jeon, A.-I. Jung and Y.-W. Jung, Aerosol Sci. Technol., 2002, 36, 573–582.
7. M.-W. Kim, S. An, H. Seok, S. S. Yoon and A. L. Yarin, ACS Appl. Mater. Interfaces, 2019, 11, 26323–26332.
8. R. C. Brown, Air Filtration: An Integrated Approach to the Theory and Applications of Fibrous Filters, 1st edn, Pergamon Press, 1993, p. 258.
9. S. Hosseini and H. V. Tafreshi, Powder Technol., 2010, 201, 153–160.
10. S. Hosseini and H. V. Tafreshi, Comput. Fluids, 2012, 66, 157–166.
11. R. Labbé and C. Duprat, Soft Matter, 2019, 15, 6946–6951.
12. H. Gao, G. Liu, J. Guan, X. Wang, J. Yu and B. Ding, Chem. Eng. J., 2023, 458, 141412.
13. M. Jamali, S. Atri, S. Gautam, A. Saleh, H. Tafreshi and B. Pourdeyhimi, Aerosol Sci. Technol., 2023, 57, 700–711.
14. A. Kumar, S. Gautam, S. Atri, H. Tafreshi and B. Pourdeyhimi, Langmuir, 2023, 39, 17653–17663.
15. S. Gautam, A. Kumar, H. Tafreshi and B. Pourdeyhimi, Chem. Eng. Sci., 2024, 286, 119680.
16. M. Kerner, K. Schmidt, S. Schumacher, C. Asbach and S. Antonyuk, Sep. Purif. Technol., 2020, 251, 117299.
17. S.-J. Wu, R.-R. Cai and L.-Z. Zhang, Build. Sci., 2022, 207, 108554.
18. S. Gautam, A. Saleh, H. Tafreshi, J. Radney and B. Pourdeyhimi, J. Aerosol Sci., 2023, 173, 106212.
19. A. Kumar, S. Gautam, S. Atri, H. Tafreshi and B. Pourdeyhimi, J. Aerosol Sci., 2024, 106426.
20. R. Brown, D. Wake, R. Gray, D. Blackford and G. Bostock, Ann. Occup. Hyg., 1988, 32, 271–294.
21. Z. Rozynek, J. Banaszak, A. Mikkelsen, K. Khobaib and A. Magdziarz, Soft Matter, 2021, 17, 4413–4425.
22. N. Bhatta, H. V. Tafreshi and B. Pourdeyhimi, Int. J. Multiphase Flow, 2024, 170, 104641.
23. N. Bhatta, S. Gautam, N. M. Farhan, H. V. Tafreshi and B. Pourdeyhimi, Ind. Eng. Chem. Res., 2024, 63, 18147–18159.
24. L. L. Janssen, J. O. Bidwell, H. E. Mullins and T. J. Nelson, J. Int. Soc. Respir. Prot., 2003, 20, 71–80.
25. W. Jasper, J. Hinestroza, A. Mohan, J. Kim, B. Shiels, M. Gunay, D. Thompson and R. Barker, J. Aerosol Sci., 2006, 37, 903–911.
26. H.-J. Choi, E.-S. Park, J.-U. Kim, S. H. Kim and M.-H. Lee, Aerosol Sci. Technol., 2015, 49, 977–983.
27. P. Sachinidou, C. Heuschling, J. Schaniel and J. Wang, Polymer, 2018, 145, 447–453.
28. Y. Kitagawa, Electret and electret filter, US Pat., 10940415, 2021.
29. D.-Q. Chang, S.-C. Chen and D. Y. Pui, et al. , Aerosol Air Qual. Res., 2016, 16, 3349–3357.
30. J. U. Brackbill, D. B. Kothe and C. Zemach, J. Comput. Phys., 1992, 100, 335–354.
31. J. Hua, L. K. Lim and C.-H. Wang, Phys. Fluids, 2008, 20, 113302.
32. D. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64.
33. S. K. Das, A. Dalal and G. Tomar, J. Fluid Mech., 2021, 915, A88.
34. R. D. Selvakumar and H. Lee, Int. J. Heat Mass Transfer, 2022, 191, 122837.
35. S. Atri, A. Kumar, S. Gautam, H. Tafreshi and B. Pourdeyhimi, Powder Technol., 2024, 431, 119094.
36. W. C. Hinds and Y. Zhu, Aerosol technology: properties, behavior, and measurement of airborne particles, John Wiley & Sons, 2022.
37. N. Bhatta, S. Gautam, A. Kumar, H. V. Tafreshi and B. Pourdeyhimi, J. Aerosol Sci., 2024, 106486.
38. S. Hosseini and H. V. Tafreshi, Sep. Purif. Technol., 2010, 74, 160–169.
39. M. W. Lee, S. S. Latthe, A. L. Yarin and S. S. Yoon, Langmuir, 2013, 29, 7758–7767.
40. J. Plog, J.-M. Lowe, Y. Jiang, Y. Pan and A. Yarin, Langmuir, 2019, 35, 11023–11036.
41. Y. Yu, D. Pan, K. Kang, S.-P. Bai, H. Han, H. Song and J. Kang, Separations, 2022, 9, 320.
42. M. N. Reddy and A. Esmaeeli, Int. J. Multiphase Flow, 2009, 35, 1051–1065.
43. A. Podgórski and A. Balazy, Aerosol Sci. Technol., 2008, 42, 123–133.
44. M. H. Motevaselian and N. R. Aluru, ACS Nano, 2020, 14, 12761–12770.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01105h

---