 Open Access Article
Open Access ArticleMorphology and line tension of twist disclinations in a nematic liquid crystal†
Yihao
Chen
 *a,
Mina
Mandić
*a,
Mina
Mandić
 b,
Charlotte G.
Slaughter
b,
Charlotte G.
Slaughter
 a,
Michio
Tanaka
a,
Michio
Tanaka
 a,
James M.
Kikkawa
a,
James M.
Kikkawa
 a,
Peter J.
Collings
a,
Peter J.
Collings
 ab and
A. G.
Yodh
ab and
A. G.
Yodh
 a
a
aDepartment of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: ychen258@sas.upenn.edu
bDepartment of Physics and Astronomy, Swarthmore College, Swarthmore, PA 19081, USA
First published on 30th October 2024
Abstract
We deploy optical microscopy with and without an applied magnetic field to characterize the three-dimensional morphology and measure the line tension of twist disclinations in twisted nematic liquid crystal (LC) sample cells. Twist disclinations are generated by quenching the LC, 5CB (4-cyano-4′-pentylbiphenyl), into the nematic phase; 5CB is confined between substrates with in-plane anchoring directions perpendicular to one another. The disclinations form loops separating domains of opposite twist handedness. Many segments of these loops are pinned to the substrates, and the ends of some pinned segments connect to free disclination segments that penetrate into the bulk nematic. We use confocal microscopy to measure the profiles of these free disclinations and test theoretical predictions about their shape, yielding a lower bound of ∼32 nm for the disclination core radius. We then use an applied magnetic field to deform the free disclinations into circular arcs whose curvature increases with magnetic field strength and depends on the field-induced energy difference between opposite twist domains. The line tension of the disclinations is derived from an energy-balance equation that relates disclination curvature to magnetic field. The measured line tension increases logarithmically with sample cell thickness; it ranges from 75 to 200 pN in samples with thickness spanning from 6 to 27 μm. In total, the investigation introduces new non-invasive methodologies for studies of defects in LCs, and it provides new information about the line tension and character of isolated twist disclinations, thereby testing theory and laying experimental foundation for the study of ensembles of disclinations.
1 Introduction
Disclinations are defects in matter. They have been observed in many materials,1 including liquid crystals (LCs),2 colloids in 2-dimensions (2D),3,4 type-2 superconductors,5 topological crystalline insulators,6 photonic cavities,7 and acoustic metamaterials.8 In LCs, disclinations are line-shaped defects that exhibit a discontinuity of the director field across the line and add significant free energy to the system. LC disclinations are important structural features that can influence material properties and response to external fields.9,10 Their formation is driven by topological constraints, and they typically arise at interfaces that separate LC domains with different director field configurations.11 Exciting recent work with these line defects has focused on the design of ensembles of disclinations in nematic LCs (NLCs) via photo-alignment and custom surface anchoring;12–18 this research aims to create disclination-dominated fluids with unique responses.19–21Here we study fundamental properties of single disclinations in LCs. Many of these properties are not known or well understood and could be useful for control of disclination-dominated fluids. For example, a simple mechanical property such as disclination line tension, which influences the curvature and localization of disclinations in three dimensions (3D), has received only limited attention. Additionally, basic questions about the disclination core size and director configuration have not been definitively answered. Notable theoretical work on these questions includes predictions of the line tension of an infinitely long disclination in a twisted planar liquid crystal cell via analytic solution,12,22 and predictions of the director field and the forces on disclinations via generalized vector representation approaches.23 Experimentally, the line tensions of qualitatively different disclinations have been estimated using an elastic string model and observations of the thermal fluctuations of disclinations trapped between two untreated substrates,24 and by optical tweezer-driven movement of trapped particles near disclinations.25 Recently, transmission electron microscopy was employed to estimate disclination core sizes from the spatial extent of photo-cross-linked assemblies of macromolecules.26
In this contribution, we address basic questions about disclinations by combining experimental observations and simple theory. Specifically, we utilize confocal microscopy to study the morphology of 1/2-strength twist disclinations in 3D. For twist disclinations, the rotation of the director when following a loop around the disclination is about an axis perpendicular to the disclination; this contrasts with a wedge disclination, for which the rotation of the director when following a loop around the disclination is about an axis parallel to the disclination. These disclinations arise at the boundaries between LC domains twisting with opposite handedness in 90° twisted planar NLC cells. Our observations of disclination morphology directly test theoretical predictions of their shape and facilitate estimation of a lower bound of the disclination core size. We then use magnetic fields to deform these domains and measure the disclination line tension. In contrast to previous experiments, the magnetic field permits both manipulation and characterization of disclinations in a non-invasive manner. Broadly, with the director field controlled by substrate coatings, this measurement approach enables quantitative understanding of the influence of elastic and external fields on disclination response and can, in principle, be generalized to study the properties of other defects in LCs.
Briefly, the walls of our twisted LC cells are planar substrates with unidirectional in-plane anchoring; the anchoring directions of the upper and lower substrates are perpendicular. Therefore, the liquid crystal director field (local molecular orientation) twists, either clockwise (CW) or counter-clockwise (CCW), as a function of depth below the upper substrate. For achiral LCs such as 5CB, the director configurations with different handedness have the same free energy. Thus, after quenching the LC from the isotropic to nematic phase, regions of both CW and CCW director configurations nucleate into domains, and twist disclinations form closed loops at their interfaces. This phenomenon bears some similarity to the formation of domain walls in magnetic materials.27,28 The contour shape of both free disclinations and surface disclinations can be seen in Fig. 1. More details are provided in Section 4.1.
In our confocal microscopy experiments, fluorescent dye is introduced into the sample. The dye molecules tend to concentrate in the disclinations, thereby facilitating 3D confocal imaging of the twist disclination profiles.29 Free disclinations that penetrate into the bulk LC appear straight when viewed in image planes parallel to the cell walls; disclination bending is readily apparent when viewed in image planes that are perpendicular to the cell walls. The 3D shape of the disclination profile is thus determined, and when measured with respect to the end-to-end distance and cell wall separation, the disclination contour offers a quantitative test of specific features of analytic line tension models12 and a means to estimate disclination core size.
To measure line tension, we employ magnetic fields to deform the twist disclinations. Magnetic fields have been used in two prior studies of disclination dynamics in NLCs,22,30 and recently to study the director defect reconfiguration in NLC drops.31,32 In the present experiments, a uniform field is applied in a direction parallel to the cell walls. The field breaks the free energy degeneracy of the CW and CCW twisted NLC domains. As a result, their domain sizes change and the twist disclination is correspondingly deformed. The free disclinations bend and form circular arcs, and the arc curvature increases with increasing magnetic field strength. We introduce a simple model that captures the relationship between disclination curvature and magnetic field strength. The model accounts explicitly for the free energy balance between LC elastic and magnetic energy. We then use the data and model to extract the disclination line tension in sample cells with varying thickness. The line tensions we obtain are significantly larger than theoretical predictions but are roughly consistent with previous experiments that studied qualitatively different disclinations and employed qualitatively different line tension measurement schemes.
2 Theory
2.1 Profile of a disclination with its two ends pinned to a surface
The line tension of an infinitely long twist disclination, aligned parallel to the cell walls of a twisted cell, is predicted to be (ref. 12): | (1) |
Based on eqn (1), it is possible to derive an expression for the shape of disclinations with two ends originating from (i.e., pinned to) the substrate. In this case, we expect it is favorable for the disclination to bend towards the middle of the cell. Bending increases the total length of the disclination, but this energy cost is compensated by a decrease in line energy when the disclination moves closer to the middle of the sample. The total line energy is computed from an integral of the line tension along the disclination profile. Employing variational calculus (using an approach similar to that in ref. 33), we obtain an equation for the optimal disclination profile z(ξ):
 | (2) |
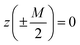 . M is the distance between the two pinned ends of the disclination on the substrate, measured along the ξ-axis.
. M is the distance between the two pinned ends of the disclination on the substrate, measured along the ξ-axis.
The predicted form of the line tension, eqn (1), can be rearranged into the following form:
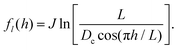 | (3) |
 cancels out in eqn (2) and in the solutions of eqn (2). Dc = πδc
cancels out in eqn (2) and in the solutions of eqn (2). Dc = πδc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−fc/J) is a quantity associated with the disclination core; it affects the shape of the disclination profile. Fig. 2 shows the shape of disclinations with two ends pinned on the same substrate; these shapes are numerically obtained from eqn (2) with various values of Dc and M. Fig. S1 of the ESI,† shows predicted profiles for disclinations with ends pinned on opposite substrates; additionally, a derivation of eqn (2), and details of the numerical methods we employed to solve eqn (2), are given in the first subsection of the ESI.† For Fig. 2 and throughout the rest of this investigation, the following elastic constants of 5CB are used: K11 = 5.9 pN, K22 = 4.5 pN, K33 = 9.9 pN, and K = (K11 + K33)/2 = 7.9 pN.34
exp(−fc/J) is a quantity associated with the disclination core; it affects the shape of the disclination profile. Fig. 2 shows the shape of disclinations with two ends pinned on the same substrate; these shapes are numerically obtained from eqn (2) with various values of Dc and M. Fig. S1 of the ESI,† shows predicted profiles for disclinations with ends pinned on opposite substrates; additionally, a derivation of eqn (2), and details of the numerical methods we employed to solve eqn (2), are given in the first subsection of the ESI.† For Fig. 2 and throughout the rest of this investigation, the following elastic constants of 5CB are used: K11 = 5.9 pN, K22 = 4.5 pN, K33 = 9.9 pN, and K = (K11 + K33)/2 = 7.9 pN.34
 | ||
| Fig. 2 Disclination profiles predicted by eqn (2) with sample thickness L = 9 μm and with various values of Dc and various distances (M) between the two pinned ends (see legends). ξ is the transverse (horizontal) axis that connects the two pinned ends. | ||
2.2 Magnetic field induced bending of the disclinations
The free energy of a disclination and nearby CW and CCW domains can be written as| F = fCCWtACCWL + fCWtACWL + fCCWHACCWL + fCWHACWL + fll + FS, | (4) |
Additionally, ft is the average free elastic energy density due to director twisting
 | (5) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) denotes the director field and the brackets represent an average over volume. fH is the average free energy density of the liquid crystal due to the magnetic field35
denotes the director field and the brackets represent an average over volume. fH is the average free energy density of the liquid crystal due to the magnetic field35 | (6) |
In practice, the strength of the magnetic field is kept small so that the twist of the director field versus depth within the cell is minimally affected, i.e., the director field far from the disclination has a uniform twist from one surface to the other. More discussion about the effect of a magnetic field on the director field is provided in Section 5.
In our computations, we also account for potential deviations (misalignment) from perfect anchoring directions of the two substrates, i.e., deviations from 90° which could arise in the rubbing and assembly process. We assume the anchoring direction difference to be 90° + θ, with θ ∼ 0. Thus, the director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) varies from 0 to 90° + θ in the CW regions and from 0 to −90° + θ in the CCW regions.
varies from 0 to 90° + θ in the CW regions and from 0 to −90° + θ in the CCW regions.
Minimizing the free energy in eqn (4) with respect to a perturbation in the disclination length, l, yields
 | (7) |
3 Methods
We used 4-cyano-4′-pentylbiphenyl (5CB) for the experiments. For the fluorescence microscope observations, we added 0.01 wt% of the dye pyrromethene 597 (PMN) to our 5CB LC sample. To ensure good mixing, these sample mixtures are heated to 60 °C with vortexing at that temperature for ∼30 minutes.The sample cell consisted of a microscope slide and a coverslip. For epifluorescence and confocal microscopy experiments, the slide and coverslip were cleaned by an air plasma; for the magnetic field experiments, the slide and coverslip were cleaned by soaking overnight in a solution of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 (v/v) Millipore water and ethanol with 1 g mL−1 NaOH. After cleaning, the surfaces were spin-coated (2000 rpm for 40 s) with a 2 wt% polyvinyl alcohol (PVA) (31
40 (v/v) Millipore water and ethanol with 1 g mL−1 NaOH. After cleaning, the surfaces were spin-coated (2000 rpm for 40 s) with a 2 wt% polyvinyl alcohol (PVA) (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MW) solution in Millipore water; they were dried overnight, and they were then rubbed by hand with a soft cloth to introduce specific planar boundary conditions for the LC director. The rubbing directions of the two substrates were oriented at 90°. The slides/coverslips were separated by either a Mylar film or glass micro-rod spacers mixed with epoxy glue. Sample cells of thickness 5 < L < 10 μm were used for the epifluorescence and confocal observations. Sample cells with four thicknesses (L = 5.9, 7.2, 15.9, and 27.3 μm) were used for experiments with a magnetic field. 5CB and the 5CB/PMN mixture were introduced into the sample cell at 60 °C via capillary action and were left for ∼10 minutes to equilibrate. Then the cell was transferred to a large metal plate at room temperature for quenching. The rest of the experiments were carried out at room temperature.
000 MW) solution in Millipore water; they were dried overnight, and they were then rubbed by hand with a soft cloth to introduce specific planar boundary conditions for the LC director. The rubbing directions of the two substrates were oriented at 90°. The slides/coverslips were separated by either a Mylar film or glass micro-rod spacers mixed with epoxy glue. Sample cells of thickness 5 < L < 10 μm were used for the epifluorescence and confocal observations. Sample cells with four thicknesses (L = 5.9, 7.2, 15.9, and 27.3 μm) were used for experiments with a magnetic field. 5CB and the 5CB/PMN mixture were introduced into the sample cell at 60 °C via capillary action and were left for ∼10 minutes to equilibrate. Then the cell was transferred to a large metal plate at room temperature for quenching. The rest of the experiments were carried out at room temperature.
Sample cells prepared for epifluorescence or confocal microscopy were first examined with either a Leitz Laborlux 12 Pol microscope, equipped with a Zeis AxioCam ICc 1 camera using crossed polarizers and either a 10× or 25× objective, or a Nikon Eclipse Ci-L fluorescence microscope with a FLIR Flea 3 FL3-U3-13E4M camera and both 10× and 40× objectives.
A Zeiss LSM 980 microscope was used for the epifluorescence and confocal microscopy experiments. Excitation wavelengths of 475 nm (LED) and 488 nm (laser) were employed for the epifluorescence and confocal observations, respectively. Dye emission was monitored through spectral filters of varying bandwidths centered at 530 nm. Optical Z-scans using a 63× oil objective were made with a voxel size roughly 0.3 μm on a side. With unpolarized epifluorescence excitation, the twist disclinations appeared bright because the dye concentration in the disclinations is larger than outside the disclinations. The situation for confocal microscopy is different. Since the transition dipole moment of the dye aligns with the liquid crystal director, illumination with polarized light generates bright or dark disclinations depending on the orientation of the sample in the microscope.38 Sometimes all disclinations appear dark or light regardless of their depth in the cell. However, sometimes if disclinations on the first surface and the free disclinations are bright, then the disclinations pinned to the second substrate are dark, and vice versa. The 3D profile of the disclination was reconstructed from the Z-stack images using ImageJ.39 For quantitative measurements of position, Lorentzian or Gaussian functions were fit to the image intensity near the disclination to extract its location in the x–y plane and along the z-axis (perpendicular to the substrate). Examples of these procedures are shown in the ESI.†
For the experiments with a magnetic field, the samples were first examined by a microscope (Leica DM RD) equipped with crossed polarizers and a white light source; images were taken using a digital camera (UNIQ685CL). The thickness of the sample cell was measured in a microscope (Leica DMi8) equipped with a piezo stage. Images in the magnetic field were obtained using a custom-made microscope consisting of a 10× objective lens and a digital camera (Kiralux 8.9 MP Monochrome CMOS Camera, Thorlabs).
To measure the line tension of the disclinations, an Alpha Magnetics electromagnet was employed to generate a uniform magnetic field B parallel to the substrate surfaces.31 Specifically, the sample cell was placed in the magnetic field such that B is parallel to the substrate surfaces and aligned at 45° with respect to the anchoring direction of both surfaces. The sample was imaged between crossed polarizers; the polarization direction of the first (input) polarizer in the light path was set to align perpendicular to B. The magnetic field was increased from 0 up to 0.4 T in increments of 0.01 T for all but the thinnest samples; for the thinnest samples increments of 0.02 T were used. The magnetic field was held constant for 2 minutes after each increment, providing sufficient time for the sample to reach a steady state. One image was taken at the end of each 2-minute period.
To further elucidate and compare the director field configurations in the vicinity of the disclination under different conditions, we employed a Q-tensor-based Landau-de-Gennes numerical model to simulate the director field of a nematic liquid crystal confined in a twist cell. Using a finite difference scheme, the free energy of the system was minimized with a nonlinear conjugate gradient algorithm from the ALGLIB library for C++.40,41 More details of the simulation method are presented in the ESI,† including Fig. S5 showing the initial conditions used for the simulations.
4 Results
4.1 Disclination morphology via confocal microscopy
Fig. 1(a) shows a 3D (angled view) and 2D (top view) schematic of a typical experiment, and Fig. 1(b) shows a top view experimental image of the NLC 5CB in a twisted cell (L = 15.9 μm) between crossed polarizers. In the schematics, the red line represents a free disclination that penetrates into the bulk LC, and the green line represents a pinned disclination on the substrate surface. Notice that the two ends of the free disclination terminate at points on the ends of surface disclinations. The transverse distance between the pinned end points is M, and the ξ-axis is oriented in the direction of the straight-line segment that connects the two pinned ends on the substrate. In the schematic, the CW and CCW domains separated by the disclination loop are also indicated.In Fig. 1(b), the black lines are the disclinations. In this view, it is straightforward to appreciate that the disclinations form loops enclosing and separating regions of either CW or CCW twist. The loop morphology is imposed by the constraints that only two twist directions exist (CW, CCW), and that regions on opposite sides of a disclination twist in different directions. Three-way dislocation junctions are not permitted (nor observed). Disclinations form in spatial regions wherein different twist domains come into contact. In practice, most disclination segments we observe are pinned to the surface. We believe that the surface pinning of disclination segments arises because the rubbing technique we use for the PVA layer introduces imperfections. Machine rubbing or optical patterning of the alignment layer reduces the pinning effect.12,18,42 Additionally, we observe fewer free disclination loops because they shrink under tension. Notice in (Fig. 1(b)), the surface disclination segments (indicated by green arrows) are thick and have irregular shapes, while the free disclination segments (indicated by red arrows) are thin and straight. Similar morphologies have been observed in prior work.22,43 Note, the actual diameter of the disclination is much, much smaller than the spatial width of the dark lines in the image.
The analytic theory12 does not address interactions that might cause a disclination to be pinned to the surface, but it predicts that the surface disclination (h = L/2) will have a logarithmically diverging line tension. In practice this divergence is averted because the disclination has a finite size core, i.e., the surface disclination is displaced from the surface by a distance of order the core radius (h = L/2 − δc). We believe the surface disclinations primarily result from strong interactions that arise between surface imperfections and the LC material in the vicinity of the surface disclination. However, our understanding of these energetics is not quantitative, and for this reason, we focus our study on only free disclinations. More information about surface disclinations is given later in the manuscript and the ESI,† including their behavior in a magnetic field and a few measurements comparing surface and free disclinations.
A bright-field image and another polarized optical microscopy (POM) image are included in the ESI.† The bright-field image (Fig. S7, ESI†) shows a case with surface disclinations on both surfaces and short free disclinations that go from one surface to the other. The POM image (Fig. S8, ESI†) shows disclinations on both surfaces and free disclinations.
Epifluorescence reveals the disclination best because the enhanced emission with unpolarized excitation light occurs only where the concentration of the dye is greater than in the rest of the sample. The images, a video, and measurements of the disclination width in the x–y plane (the plane parallel to the substrates) using epifluorescence microscopy are included in the ESI† (see Fig. S9, ESI†). The width (i.e., apparent width in the image rather than true width) of a front surface disclination is ∼0.7 μm; this is the smallest width measured by any of our techniques. The width of a free disclination appears slightly larger (∼1 μm), due to the loss of resolution when focusing deeper into the sample. Since both of these measurements are resolution limited, it is impossible to discern any differences that might exist between the surface and free disclinations.
A confocal image of disclinations (Fig. S10, ESI†) and measurement of their width in the x−y plane (Fig. S11, ESI†) are shown in the ESI.† Due to the polarization effects described earlier, the contrast in the confocal images depends on both the increased dye concentration within the disclination and the orientation of the director in the vicinity of the disclination. Notice, in these images, the width of a free disclination is ∼0.8 μm, while the width of a surface disclination is significantly larger (∼2.2 μm). Note, the analytic theory12 does not predict a larger region of director perturbation for a surface disclination as opposed to a free disclination; thus, the interactions that pin the disclination to the surface must strongly influence the director configuration near the surface disclination.
The 3D morphology of the disclinations is clearly observed with confocal microscopy. From confocal microscopy, we directly observe that the wide disclination segments are pinned and are located on either the first or second substrate surface. We also observe that the thin free disclination segments penetrate into the bulk NLC, and that their two ends connect to surface disclination segments on either the same substrate or on opposite substrates. Moreover, from confocal microscopy, we directly observe that the central portions of long free disclinations are located in the middle of the NLC sample. Fig. 3(a) shows the profiles of seven free disclinations in the z–ξ plane; each free disclination is characterized by a different distance (M) between its pinned ends on the same substrate. These disclinations appear dark when viewed in both the x–y and z–ξ planes, but in the z–ξ plane the disclination separates a lighter region toward the first substrate from a moderately dark region toward the second substrate. All of these disclinations bend into the sample cell. Notice, when the distance, M, between the two free disclination endpoints increases, the free disclination extends more deeply into the middle of the sample cell.
 | ||
| Fig. 3 (a) Vertical cross section in the z–ξ plane of free disclinations with two ends pinned to the same substrate. The disclination is the dark line that separates a lighter region from a moderately dark region. The distance between the two ends (M) are 42.1, 37.9, 23.9, 19.2, 17.1, 14.5, and 12.6 μm from top to bottom. The cell thickness is 8.3 μm. (b) Vertical cross section in the z–ξ plane of a free disclination with ends pinned to different substrates. The disclination appears bright compared to the region surrounding it. The red bar is 5 μm and the grey bar is 63 μm. (c)–(e) Experimental profiles of three of the disclinations (M = 12.6, 19.2, and 42.1 μm). The solid line is the best fit using eqn (2). (f) Experimental maximum depth (H) of the free disclination as a function of the distance between the two pinned ends. Red points correspond to the profiles in (c)–(e). The solid line is the best fit using eqn (2). Inset: The fraction of a free disclination within a range of 5% L of the middle of the sample cell using eqn (2) with Dc = 102 nm as a function of the distance between the two pinned ends (M). Results from various cell thicknesses (L) are shown: 5 μm (red dots), 15 μm (blue squares), 50 μm (black diamonds), and 100 μm (cyan triangles). | ||
Fig. 3(b) shows a profile of a free disclination with two ends on different substrates; notice that the central part of this disclination resides in the mid-plane of the sample cell. Fig. 3(c)–(e) show the profiles of three free disclinations extracted from their images; the profiles are derived as described in the Methods section (for more details, see the explanation and Fig. S12 of the ESI†), and the best fit to their profile (using eqn (2)) is also shown. Our theoretical model captures the shapes of these free disclinations very well, and it yields Dc = (102 ± 10) nm averaged over the three profiles. Note, information about the prefactor (J) cannot be obtained by fitting the disclination profile, since J cancels out in eqn (2) and in its solutions.
Nevertheless, from these data we can further connect experiment to theories22,23via their prediction that the free energy is minimum when the disclination resides at the middle of the cell. Fig. 3(f) shows the maximum depth, H, of penetration for each disclination as a function of the distance between its two pinned ends on the same substrate; the best fit to these data using eqn (2) is also shown. The model (eqn (2)) captures the trend, and a best-fitting routine yields Dc = (113 ± 33) nm, which is consistent (within error estimates) with the result obtained by direct fitting to the vertical profiles. The good agreement between the experimental profile shape of the disclinations and the prediction of eqn (2) provides support for the predicted dependence of line tension on depth in the sample of eqn (1). The value of Dc obtained from fittings of the three full profiles of the disclinations has a smaller uncertainty than that obtained from fittings of H/L and M/L. This is because more data points are utilized in the former fittings. Therefore, we believe that our best estimate for Dc from the data is Dc = (102 ± 10) nm.
The inset in Fig. 3(f) shows the fraction of the length of free disclination located within 5% L of the middle of the sample cell (i.e., the fraction with h < 5% L) using eqn (2) with Dc = 102 nm. The fraction of the length is plotted as a function of the distance between its two ends (M). As expected, if all other factors are held constant, a larger fraction of the disclination resides near the middle of the cell as M increases.
The definition of Dc gives a relationship involving the core radius δc and the core free energy fc, namely: fc/J = ln(πδc/Dc). Since fc and J are positive, this means that δc > Dc/π, which equals about (32 ± 3) nm. Thus, this analysis of disclination contour shape provides an estimate of the lower bound on the core radius.
It is illuminating at this juncture to compare simulations to the analytical solutions. Our simulations of an infinitely long twist disclination in a twisted nematic cell (with K11 ≠ K33) demonstrate that the disclination is straight (parallel to the y-axis), lies halfway between the two surfaces, and runs along the boundary line between the two twist domains. The director field ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) lies in the x–y plane and makes an angle ϕ with one of the rubbing directions. Fig. 4(a) and (b) show the director field and contour levels of ϕ, respectively, in a plane perpendicular to the disclination. Notice that the nematic director just above and below the disclination exhibits a 90° jump, and also that the director field smoothly rotates through 180° (about the z-axis) as it traverses a loop in the x–z plane around the disclination. This rotation of the director field is about an axis perpendicular to the disclination, which is oriented along the y-axis, as opposed to rotation about an axis parallel to the disclination that occurs for more common wedge disclinations.
lies in the x–y plane and makes an angle ϕ with one of the rubbing directions. Fig. 4(a) and (b) show the director field and contour levels of ϕ, respectively, in a plane perpendicular to the disclination. Notice that the nematic director just above and below the disclination exhibits a 90° jump, and also that the director field smoothly rotates through 180° (about the z-axis) as it traverses a loop in the x–z plane around the disclination. This rotation of the director field is about an axis perpendicular to the disclination, which is oriented along the y-axis, as opposed to rotation about an axis parallel to the disclination that occurs for more common wedge disclinations.
 | ||
| Fig. 4 (a) and (c) The component of the director around a free twist disclination in the x–z plane from simulation as described in the text and from the analytical solution of eqn (8) with h = 0, respectively. (b) and (d) Contour levels of the director twist angle relative to the rubbing direction on the bottom substrate from simulation and the analytical solution of eqn (8) with h = 0, respectively. | ||
We compared our numerical simulations to the analytical solution of the director field in the vicinity of an infinitely long twist disclination along the y-axis from ref. 12, i.e.,
 | (8) |
Although the simulation result is similar to the analytical solution in many respects, upon careful examination, a difference in the size of the distorted region around the disclination is apparent. The distorted region of the simulation result is roughly 50% smaller than the distorted region of the analytical solution. We believe that this effect is real, i.e., it should be present in the experiments. While neither result includes an isotropic core, the simulation allows the order parameter to decrease in the vicinity of the disclination to minimize the total free energy (elastic and phase), while the analytical theory assumes the order parameter is constant throughout the sample.
Fig. S6 of the ESI,† also shows simulation results for disclinations oriented at various angles with respect to the rubbing directions. As mentioned previously, with the assumption that K11 = K33, the director configuration in the plane perpendicular to the disclination is independent of its orientation except for a rotation of the entire director configuration around the axis defined by the disclination. Even though K11 ≠ K33 in the simulation, and even though the simulation models the disclination quite differently from the analytical solution, the very close overlap of the simulation contour levels for the different disclination orientation confirms that this property of the director configuration remains valid.
4.2 Magnetic field induced bending of the disclination and line tension measurements
Magnetic fields offer an opportunity to characterize the line tension of free disclinations in a noninvasive way. Fig. 5(a)–(c) show that a free disclination bends in response to an applied magnetic field and that the associated curvature of the bend increases as the strength of the magnetic field increases. At these (relatively small) field strengths, the bending shape is very well captured by a circular arc of radius R. As the strength of the magnetic field is further increased, the disclinations become heavily bent, make contact with one another, and then merge. At these fields, the surface disclinations do not respond due to both the large line tension and the strong interactions between the surface and the liquid crystal. In the largest fields, even the surface disclinations become unpinned and free to move; eventually all disclinations shrink and disappear and only a single large CW region remains at >0.8 T.As discussed in Section 2, the bending behavior of free disclinations is due to a free energy balance between the bulk free energy of the liquid crystal, including both elastic and magnetic contributions, and the free energy of the disclination. Conceptually, the magnetic field is oriented partially parallel with the CW regions and partially perpendicular with the CCW regions; in this case, the CW regions have a lower free energy in the magnetic field due to magnetic anisotropy in the susceptibility of 5CB.31,35 As a result, it is energetically favorable for CW regions to expand and CCW regions to shrink. The disclinations at these interfaces are driven to deform by the energy difference between these two domains.
Fig. 6(a) shows the curvature 1/R of the free disclination in Fig. 5 as a function of magnetic field strength (B). A best fit to these data using eqn (7) is also shown, where fl and θ are the two fitting parameters. Generally, for our analysis, we focus only on long free disclinations (i.e., M/L > 20). As shown in the inset of Fig. 3(f), when M/L > 20 most of the disclination resides in the middle of the sample cell; therefore, the line tension can reasonably be approximated as constant. The model (eqn (7), M/L > 20) captures the disclination's field-dependent behavior for all sample cell thickness and even for situations where there is a (small) misalignment in the anchoring directions (see Fig. S3 of the ESI†). Fig. 6(b) shows the line tension of these disclinations as a function of the sample cell thickness. The tension indeed increases with increasing thickness of the sample cell. Specifically, the relation between line tension and cell thickness is captured by the predicted logarithmic form of eqn (3) in the middle plane (h = 0), i.e.,
fl = J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(L/Dc). ln(L/Dc). | (9) |
 | ||
| Fig. 6 (a) Curvature of the disclination as a function of the magnetic field strength. Sample cell thickness is 15.9 μm. The solid line is the best fit using eqn (7). (b) Line tension as a function of cell thickness. The solid line is the best fit according to eqn (9). For comparison, the dashed line is the best fit using eqn (9) with Dc fixed at 102 nm. | ||
Lastly, we note that the deviation of the difference in the anchoring directions from 90° was very small (|θ| < 2°) for all the samples studied (see Fig. S4 of the ESI†).
5 Discussion
Our confocal microscopy measurements have characterized the profiles of the disclination contours of finite-length free twist disclinations with ends pinned to the substrate surface. The profiles are consistent with the predictions of an analytical theory,12 and by combining theory and experiment we were able to compute a lower bound of ∼32 nm for the disclination core radius. For comparison, the core radius of a half-integer wedge disclination was predicted to be ∼10 nm based on Landau–de Gennes theory,44 and the core radius of −1/2-strength disclinations in 5CB was estimated as ∼15 nm via scanning electron microscopy, i.e., from the width of the crosslinked polymer assembly at the disclination core.26In parallel, using magnetic fields, we performed microscopy measurements to determine the line tension of finite-length free twist disclinations in a twisted nematic liquid crystal cell. This work determined the variation of bending curvature with respect to field strength, and it verified the logarithmic dependence of line tension on sample thickness predicted by theories.12,22
Of course, assumptions associated with the confocal and magnetic field experiments, as well as with the analytic theory have limitations that may diminish their agreement. We identified six potential issues. (1) The theoretical models assume infinite anchoring strength for the rubbed PVA surfaces, which is clearly not the case experimentally. Anchoring strength measurements tend to vary widely. For example, the azimuthal anchoring strength at room temperature for 5CB on rubbed polyimide surfaces has been measured to be 44 and 160 μJ m−2.45,46 The polar anchoring strength at room temperature of 5CB on polyvinyl formal is about 400 μJ m−2,47 and it is known that the azimuthal anchoring strength is one to two orders of magnitude less.48 A reasonable estimate for the anchoring strength (W) at room temperature of 5CB on a rubbed PVA surface is 20 μJ m−2, which implies an extrapolation length LW = K22/W of ∼0.2 μm. We do not expect such a short extrapolation length in the experiment to cause a large deviation from the infinite anchoring case, since the free energy changes only by ∼5% for a 10 μm sample cell. (2) When the disclination deforms in a magnetic field, both bending and elongation require energy; however, standard definitions of line tension are usually dependent only on elongation. Our model (eqn (4)) does not distinguish between these effects and considers their sum as the line tension. Thus, the bending free energy of disclinations per unit length in the model should lead to an overestimation of the line tension (according to the standard definition); this overestimation can be approximated by  ,49 which is very small (∼0.002 pN). (3) In practice, the entire disclination is never fully in the middle plane of the sample cell, and the part of the disclination farther away from the middle-plane is predicted to have a higher tension (see eqn (1)). Using the profile of the disclination obtained from our model (eqn (2)), we computed the contour average of the line tension (i.e., the line integral of the tension along the disclination divided by the contour length). We found the average line tension to be larger than the tension at the middle-plane by only ∼2% (i.e., M/L > 20). (4) Theoretical predictions of line tension (eqn (1)) assume K11 = K33. Although the splay and bend elastic constants are not exactly the same for 5CB, we found that the first order correction to the elastic free energy of the director field around the disclination when K11 ≠ K33 is zero (see supplementary information of ref. 12). (5) The magnetic free energy term (eqn (6)) in our model only considers the contribution of the director field far from the disclination. However, from symmetry, we believe the contribution of the director field around the disclination (eqn (1)) to the magnetic free energy is zero. (6) The magnetic coherence length
,49 which is very small (∼0.002 pN). (3) In practice, the entire disclination is never fully in the middle plane of the sample cell, and the part of the disclination farther away from the middle-plane is predicted to have a higher tension (see eqn (1)). Using the profile of the disclination obtained from our model (eqn (2)), we computed the contour average of the line tension (i.e., the line integral of the tension along the disclination divided by the contour length). We found the average line tension to be larger than the tension at the middle-plane by only ∼2% (i.e., M/L > 20). (4) Theoretical predictions of line tension (eqn (1)) assume K11 = K33. Although the splay and bend elastic constants are not exactly the same for 5CB, we found that the first order correction to the elastic free energy of the director field around the disclination when K11 ≠ K33 is zero (see supplementary information of ref. 12). (5) The magnetic free energy term (eqn (6)) in our model only considers the contribution of the director field far from the disclination. However, from symmetry, we believe the contribution of the director field around the disclination (eqn (1)) to the magnetic free energy is zero. (6) The magnetic coherence length  50 is larger than 10 μm in our experiment, which suggests that the magnetic field could have a moderate effect on the director field. Minimization of the sum of elastic and magnetic free energies (eqn (5) and (6), respectively) in the region far from the disclination shows that the deviation of the director field from a uniform twist is small for the magnetic fields used in our experiments; for example, energy differences of less than ∼5% could arise.
50 is larger than 10 μm in our experiment, which suggests that the magnetic field could have a moderate effect on the director field. Minimization of the sum of elastic and magnetic free energies (eqn (5) and (6), respectively) in the region far from the disclination shows that the deviation of the director field from a uniform twist is small for the magnetic fields used in our experiments; for example, energy differences of less than ∼5% could arise.
Individually, none of the limitations noted above appear to be substantial. However, perhaps surprisingly, our experiments and analysis were not in agreement in all respects. The magnetic field experiments exhibit a discrepancy in the prefactor of the logarithmic term in eqn (1) between theory and experiment. Specifically, the measured J = (78 ± 11) pN is substantially greater than the theoretical prefactor  . In addition, the fit value for Dc obtained from the magnetic field study was very large (2000 ± 500) nm, i.e., quite a bit larger than the values we obtained from the confocal microscopy experiments (Dc = (102 ± 10) nm).
. In addition, the fit value for Dc obtained from the magnetic field study was very large (2000 ± 500) nm, i.e., quite a bit larger than the values we obtained from the confocal microscopy experiments (Dc = (102 ± 10) nm).
We can reduce some of this discrepancy by noting that both J and Dc were treated as free parameters when eqn (9) was used to fit the dependence of line tension on sample thickness. By contrast, Dc was the only free parameter used when eqn (2) was fit to the profiles of free disclinations studied by confocal microscopy. If instead, the data in Fig. 6(b) are fit to eqn (9) but with the value of Dc set to 102 nm, then J is the only free parameter. The result of such a fitting gives the dashed curve in Fig. 6(b) and a fit value for J of (30 ± 2) pN. Given the spread of the data, in our view, this 1-parameter fit still captures the general trend of the data, and the fit value of J is significantly closer to the theoretical value (4.7 pN) than the results from the 2-parameter fit, albeit it is still different by a factor of six. In other words, our measured values of the line tension are significantly greater than what theory predicts using reasonable values for Dc.
Our result for the line tension is of the same order of magnitude as previous experimental results for different types of 1/2-strength disclinations. The tension of 1/2-strength disclinations of 5CB in untreated sample cells was measured using the temporal autocorrelation function of their thermal fluctuations in the viscous liquid; the resultant estimated line tension was found to be ∼100 pN.24 The line tension of 1/2-strength disclinations in the nematic liquid crystal, ZLI2806, was measured by deforming the disclination using a colloid trapped with an optical tweezer and was found to be ∼72 pN.25 Finally, the line tension of disclinations of 1/2-strength in 4′-octyl-4-biphenylcarbonitrile (8CB) was measured via the curvature of the disclination induced by translation and rotation of the substrates and was found to be ∼100 pN (using K = 9.9 pN and K22 = 4.8 pN for 8CB51).17 Interestingly, as in the case of our analysis, this investigation reported that the experimental result was larger than a numerical/theoretical prediction of the line tension by a factor greater than four. Further work is needed to clarify the origin of this discrepancy.
6 Conclusions
We characterized the 3D morphology and line tension of twist disclinations in twisted nematic liquid crystal cells with confocal microscopy and magnetic field measurements. The morphology of disclinations is affected by both topological constraints and surface effects. The disclinations form loops separating regions of different twist handedness and have segments pinned to or free from the substrate. The shapes of the free disclinations, both perpendicular to the substrates without an external field and parallel to the substrates in a magnetic field, are captured by theoretical models based on line tension. Comparison of the former profiles to theory enabled us to compute a lower bound for the disclination core size. From the magnetic-field induced bending of the disclination contours, we obtain the disclination line tension. The dependence of the line tension on cell thickness and on position in the cell were consistent with theory.Overall, we have introduced and demonstrated two methodologies, based on confocal microscopy and traditional microscopy in a magnetic field, that offer excellent non-invasive means to probe defect shapes in LCs and mechanical properties of liquid crystals containing disclinations (and perhaps other defects), e.g., compared to invasive methods such as optical tweezers,25 or substrate rotation.17,20,21 The work exhibits the mechanical stability of disclinations against bending and elongation, and in addition, reveals a quantitative discrepancy between the experimentally determined line tension and current theoretical models. Future investigations should explore reasons for the line tension discrepancies and continue efforts to quantitatively determine disclination core size. Finally, our findings about disclinations lay foundation for studying interactions between LC disclinations and added materials, such as freely moving or trapped particles, and opens opportunities for disclinations-based micro-rheology.
Author contributions
Y. C. performed the magnetic field experiments, developed the theory for analysis of all the imaging experiments, quantitatively compared theory and the experiments, and wrote the first draft of the manuscript. M. M. carried out the POM, fluorescence, and confocal microscopy observations, extracted data from the images, and analyzed the results. C. G. S. carried out all of the simulations, assisted with their analysis, and assisted with the magnetic field experiments. M. T. developed the initial code to track the bending of the disclinations in a field and provided assistance with data analysis. J. M. K. developed and supplied the electromagnet instrumentation and trained others on its use. P. J. C. and A. G. Y. conceptualized and supervised the project. All authors reviewed and edited the manuscript.Data availability
Additional data supporting this article have been included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NSF through Grant No. DMR-2003659 and by the NSF Penn Materials Research Science and Engineering Center through Grant No. DMR-2309043, including its Optical Microscopy Shared Experimental Facility (SEF) and Property Measurement SEF. We also acknowledge the support of Swarthmore College for the use of the confocal microscope. We thank Hannah Gruner, Cheng Long, Alvin Modin, Jonathan Selinger, and Hiroshi Yokoyama for helpful discussions.References
- A. E. Romanov and A. L. Kolesnikova, Prog. Mater. Sci., 2009, 54, 740–769 CrossRef CAS.
- M. Kleman and J. Friedel, Rev. Mod. Phys., 2008, 80, 61–115 CrossRef CAS.
- S.-C. Kim, L. Yu, A. Pertsinidis and X. S. Ling, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13220–13226 CrossRef CAS PubMed.
- P. Yunker, Z. Zhang and A. G. Yodh, Phys. Rev. Lett., 2010, 104, 015701 CrossRef PubMed.
- I. Guillamón, H. Suderow, A. Fernández-Pacheco, J. Sesé, R. Córdoba, J. De Teresa, M. Ibarra and S. Vieira, Nat. Phys., 2009, 5, 651–655 Search PubMed.
- Y. Liu, S. Leung, F.-F. Li, Z.-K. Lin, X. Tao, Y. Poo and J.-H. Jiang, Nature, 2021, 589, 381–385 CrossRef CAS PubMed.
- M.-S. Hwang, H.-R. Kim, J. Kim, B.-J. Yang, Y. Kivshar and H.-G. Park, Nat. Photonics, 2024, 18, 286–293 CrossRef CAS.
- Y. Chen, Y. Yin, Z.-K. Lin, Z.-H. Zheng, Y. Liu, J. Li, J.-H. Jiang and H. Chen, Phys. Rev. Lett., 2022, 129, 154301 CrossRef CAS PubMed.
- A. Saupe, Mol. Cryst. Liq. Cryst., 1973, 21, 211–238 CrossRef CAS.
- E. Terentjev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 1330 CrossRef CAS PubMed.
- G. P. Alexander, B. G.-g Chen, E. A. Matsumoto and R. D. Kamien, Rev. Mod. Phys., 2012, 84, 497 CrossRef CAS.
- M. Wang, Y. Li and H. Yokoyama, Nat. Commun., 2017, 8, 388 CrossRef PubMed.
- K. Sunami, K. Imamura, T. Ouchi, H. Yoshida and M. Ozaki, Phys. Rev. E, 2018, 97, 020701 CrossRef CAS PubMed.
- T. Ouchi, K. Imamura, K. Sunami, H. Yoshida and M. Ozaki, et al. , Phys. Rev. Lett., 2019, 123, 097801 CrossRef CAS PubMed.
- B. Berteloot, I. Nys, G. Poy, J. Beeckman and K. Neyts, Soft Matter, 2020, 16, 4999–5008 RSC.
- Y. Guo, M. Jiang, S. Afghah, C. Peng, R. L. Selinger, O. D. Lavrentovich and Q.-H. Wei, Adv. Opt. Mater., 2021, 9, 2100181 CrossRef CAS.
- A. Modin, B. Ash, K. Ishimoto, R. L. Leheny, F. Serra and H. Aharoni, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2300833120 CrossRef CAS PubMed.
- X. Wang, J. Jiang, J. Chen, Z. Asilehan, W. Tang, C. Peng and R. Zhang, Nat. Commun., 2024, 15, 1655 CrossRef CAS PubMed.
- H. Yoshida, K. Asakura, J.-I. Fukuda and M. Ozaki, Nat. Commun., 2015, 6, 7180 CrossRef CAS PubMed.
- C. Long, M. J. Deutsch, J. Angelo, C. Culbreath, H. Yokoyama, J. V. Selinger and R. L. Selinger, Phys. Rev. X, 2024, 14, 011044 CAS.
- S. Yi, H. Chen, X. Wang, M. Jiang, B. Li, Q. Huo Wei and R. Zhang, Line defects in nematic liquid crystals as charged superelastic rods with negative twist-stretch coupling, arXiv, preprint, 2023 DOI:10.48550/arXiv.2312.14735.
- J. Geurst, A. Spruijt and C. Gerritsma, J. Phys., 1975, 36, 653–664 CrossRef CAS.
- C. Long, X. Tang, R. L. Selinger and J. V. Selinger, Soft Matter, 2021, 17, 2265–2278 RSC.
- A. Mertelj and M. Čopič, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021711 CrossRef CAS PubMed.
- I. I. Smalyukh, B. I. Senyuk, S. V. Shiyanovskii, O. D. Lavrentovich, A. N. Kuzmin, A. V. Kachynski and P. N. Prasad, Mol. Cryst. Liq. Cryst., 2006, 450, 79–279 CAS.
- J. Noh, W. Cao, H. Sun, Y. Yang, N. C. Gianneschi and N. L. Abbott, Chem. Mater., 2020, 32, 6753–6764 CrossRef CAS.
- A. Mertelj, D. Lisjak, M. Drofenik and M. Čopič, Nature, 2013, 504, 237–241 CrossRef CAS PubMed.
- G. Venkat, D. Allwood and T. Hayward, J. Phys. D: Appl. Phys., 2023, 57, 063001 CrossRef.
- T. Ohzono, K. Katoh and J.-I. Fukuda, Sci. Rep., 2016, 6, 36477 CrossRef CAS PubMed.
- C. Gerritsma, J. Geurst and A. Spruijt, Phys. Lett. A, 1973, 43, 356–358 CrossRef CAS.
- S. Ettinger, C. G. Slaughter, S. H. Parra, J. M. Kikkawa, P. J. Collings and A. Yodh, Phys. Rev. E, 2023, 108, 024704 CrossRef CAS PubMed.
- P. Salamon, Z. Karaszi, V. Kenderesi, Á. Buka and A. Jákli, Phys. Rev. Res., 2020, 2, 023261 CrossRef CAS.
- J. S. Angelo, PhD thesis, Kent State University, 2018.
- E. Nowinowski-Kruszelnicki, J. Kedzierski, Z. Raszewski, L. Jaroszewicz, M. A. Kojdecki, W. Piecek, P. Perkowski, M. Olifierczuk, E. Miszczyk and K. Ogrodnik, et al. , Opto-Electron. Rev., 2012, 20, 255–259 CAS.
- P.-G. De Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, 1993 Search PubMed.
- A. Buka and W. De Jeu, J. Phys., 1982, 43, 361–367 CrossRef CAS.
- B. J. Frisken, PhD thesis, University of British Columbia, 1989.
- T. Ohzono, K. Katoh, C. Wang, A. Fukazawa, S. Yamaguchi and J.-I. Fukuda, Sci. Rep., 2017, 7, 16814 CrossRef PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- D. M. Sussman and D. A. Beller, Front. Phys., 2019, 7, 204 CrossRef.
- ALGLIB – Numerical Analysis Library, https://www.alglib.net.
- X. Wang, D. Miller, E. Bukusoglu, J. de Pablo and N. Abbott, Nat. Mater., 2016, 15, 107–112 Search PubMed.
- A. Spruijt, Solid State Commun., 1973, 13, 1919–1922 CrossRef CAS.
- N. Schopohl and T. Sluckin, Phys. Rev. Lett., 1987, 59, 2582 CrossRef PubMed.
- F. Yang, H. Cheng, H. Gao and J. Sambles, J. Opt. Soc. Am. B, 2001, 18, 994–1002 CrossRef CAS.
- T. Yu, Y. Lo and R. Huang, Opt. Express, 2010, 18, 21169–21182 CrossRef CAS PubMed.
- J. T. Gleeson, PhD thesis, University of British Coloumbia, 1988.
- L. Blinov and V. Chigrinov, Electrooptic Effects in Liquid Crystal Materials, Springer-Verlag, 1993, p. 117 Search PubMed.
- A. Shams, X. Yao, J. O. Park, M. Srinivasarao and A. D. Rey, Soft Matter, 2015, 11, 5455–5464 RSC.
- N. Mottram and S. Hogan, Continuum Mech. Thermodyn., 2002, 14, 281–295 CrossRef CAS.
- H. Hakemi, E. Jagodzinski and D. DuPre, J. Chem. Phys., 1983, 78, 1513–1518 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01076k |
| This journal is © The Royal Society of Chemistry 2024 |


