Nanoconfinement effects on the dynamics of an ionic liquid-based electrolyte probed by multinuclear NMR

Abstract

The measurement of ion diffusivity inside nanoporous materials by Pulsed-Field Gradient (PFG) NMR is not an easy task due to enhanced NMR relaxation. Here, we employed multinuclear (¹H, ³¹P, and ⁷Li) NMR spectrometry and diffusometry to probe ion dynamics of a fluorine-free battery electrolyte comprising the [P_4,4,4,4][MEEA] ionic liquid (IL) and LiMEEA salt in a 7 : 3 molar ratio, confined in three different nanoporous SiO₂ glasses with pore diameters of 3.7, 7 and 98 nm. Confinement of the electrolyte leads to NMR resonance line broadening and variation in the ³¹P and ⁷Li NMR chemical shifts. The complicated diffusion decays are explained taking into consideration the complex porous structure of the porous glasses, the presence of pore “necks” and the “partially isolated volumes” containing the liquid, which is in a “slow exchange” regime with the rest of the liquid. The mean apparent diffusivity is controlled by the exchange of ions between the “narrow” and the “large” pores and the boundary separating these pores to measure diffusion coefficients by PFG NMR is in the range of pore sizes of Vycor and Varapor. The temperature-dependent ion diffusivities in the “large” pores deviate from the Arrhenius law and the exchange of diffusing units between the “narrow” and the “large” pores leads to abnormal temperature-dependent diffusion coefficients. Like the bulk, diffusivity of the small Li⁺ is slower than that of the larger organic ions in the confinement, demonstrating the solvation of Li⁺ inside the pores.

---

Introduction

Ionic liquids (ILs) are organic salts containing cations and anions that are liquids at temperatures below 100 °C, while some remain as liquids at ambient temperature commonly known as room temperature ionic liquids (RTILs). Depending on the cation–anion combination, ILs offer attractive physicochemical properties such as thermal and chemical stabilities, non-flammability, low volatility, and high ionic conductivity. These properties make ILs desirable for many applications, including greener solvents for different applications, gas separation, conductive lubricants, electrolytes, etc.^1–4 However, most of the studied ILs are heavily based on fluorinated anions that pose safety and environmental problems. In this context, fluorine-free ILs are emerging as potential replacements for the fluorinated ILs in different applications.^3–6

The use of ILs as electrolytes in electrochemical applications is receiving attention due to their unique properties and, therefore, understanding the dynamics of such electrolytes in bulk and in confinement is of fundamental and practical importance. Confined ILs have been investigated using a broad range of experimental and computational techniques such as X-ray and neutron scattering, nuclear magnetic resonance (NMR) spectroscopy, and molecular dynamics simulation.^6–13 The proximity of the confined medium to the surface may alter the structure and ordering of the ions in a different way. It has been shown that the most typical structure formed near the surface is layered, with alternating layers of cations and anions with preferential orientation of ions;^3,14 the charge of the layer contacting the surface is determined by the surface properties. The layering can extend over a few nanometers of the surface.^15–17 The physical properties of confined ILs are generally compared with those of molecular liquids: in particular, the melting temperature of the nanoporous-confined ILs decreases according to the Gibbs–Thomson equation.¹⁸

The structure and dynamics of the confined ILs can be described as the sum of several factors: the surface contribution arising from the ions in contact with the surface and the bulk-like contribution arising from the ions located in the pore center.^19,20 Significant layering (alternating regions of anions and cations) over a few nanometers from the pore wall has been observed,^19,20 which is mostly driven by electrostatic interactions.²⁰ The mobilities of confined ILs either increase^10,21–23 or decrease^13,14,24,25 and the trend as well as the extent both depend on the molecular structure of ILs and properties of the surface. The increase in ion diffusivities as a function of decreasing pore size would allow the development of new batteries operating at lower temperatures.⁸ Conductivity is the integrated dynamic property of ions: it might be comparable to the bulk ionic conductivity²⁰ or even higher.²⁶ In a series of studies, the ion diffusivity and the phase structure of ionic liquid-based compositions with different cations and nitrate anions have been studied in micrometre-spaced enclosures formed by glass and quartz glass plates.^{11,12,27–2915}N NMR spectroscopy revealed preferential orientation of the principal axis of the nitrate anion relative to the surface that is typical for liquid crystals.³⁰

A wider practical perspective on confined IL-based electrolytes in the form of ionogels is opened for supercapacitors, fuel cells and biosensors.¹⁸ Typically, ionogels are solid or quasi-solid electrolytes based on the trapping of ILs in a silica matrix.^31,32 Nanoporous silica is the preferred confining matrix because of its easy synthesis, well-characterized properties of its internal surface, its known pore diameter distribution and other characteristics of the pores. The system formed by an IL confined in a controlled porous glass is a type of ionogel.^19,24,33 Controlled porous glass (CPG) is derived from a glass that is heat treated to form two interconnecting phases: a silica-rich phase and an alkali-rich borate phase.^34,35 The heat-treated glass is then leached selectively to remove the alkali-rich phase. Diffusion of several ILs confined in porous glasses has been studied earlier.^8,10,13,36 For example, Frielinghaus et al.⁸ have studied the structure and diffusion behavior of aqueous solutions of 1-ethyl-3-methylimidazolium acetate in nanoporous glasses by X-ray diffraction and high-resolution neutron spectroscopy. They found that the confinement leads to distortion of domains formed in the bulk, which gives more room for diffusion. In the narrow pores of Vycor porous glasses the strong distortion gives even more room for diffusion such that the hydrogen bonds between acetate and water seem to be even stronger.

Filippov et al.¹⁰ have studied the diffusion of a phosphonium bis(salicylato)borate IL in Vycor at 296 K by ¹H pulsed field gradient NMR (PFG NMR). They observed multi-component diffusion decays for cations and anions and the mean values of diffusion coefficients were higher than bulk diffusion coefficients. Also, it was mentioned that some components of diffusion decays demonstrated values of apparent diffusion coefficients much lower than mean diffusion coefficient values. Therefore, at a temperature of 330 K changes in the diffusivity of the ions were observed. One of the possible reasons for these changes is their redistribution among the pores. The size of the bounded regions is of the order of 1 μm, as estimated from the dependence of the ion diffusivity on the diffusion time. Diffusion of the ethyl ammonium nitrate (EAN) IL has been studied by ¹H NMR in the temperature range of 295–325 K within pores of two types of porous glasses: Vycor (∼7 nm) and Varapor pores (∼9.8 nm).¹³ It was shown that the diffusivity of EAN confined in Varapor is controlled by the tortuosity of the porous system and must consider the interaction with the surface of the discrete pore walls. In the case of Vycor, the long-term diffusivity is a factor of 1.5 lower than that expected in the absence of interaction with the pore walls. Two possible mechanisms that may explain this discrepancy were proposed: (1) the EAN–surface interaction and (2) the retardation of EAN diffusion in comparison to n-decane in narrow pores. Wei et al.³⁶ have studied [BMIM][BF₄], [BMIM][PF₆] and [HMIM][NTf₂] ILs confined in Vycor and Varapor nanoporous glasses by ¹H, ¹¹B and ³¹P PFG NMR. The in-pore diffusion coefficients of IL ions are lower than the corresponding bulk IL diffusion coefficients at the same temperature. Especially, the diffusion coefficients of the ILs confined in the 7 nm Vycor or Varapor pores decrease by one order of magnitude approximately in comparison with the bulk ones. This effect can be related to the strong attraction of ions to the pore surface. The decrease in the magnitude is higher for Vycor than that for Varapor because of the difference in the pore size distribution. It is noteworthy that the strong attraction of ions to the pore surface is also the possible reason for the faster dynamics of the calculated bulk diffusion coefficients compared to the confined ones. The decreasing trend of the NMR-measured diffusion coefficient agrees well with the results of MD simulations.³⁶

Despite the growing interest in the development of functional electrolytes of energy storage devices including batteries and supercapacitors, fundamental understanding of the transport behaviour of electrolytes within restricted geometries is not adequate. The phenomena occurring with ions of electrolytes are due to the presence of a restrictive barrier, absorption–desorption processes, exchange between pores of different sizes leading to modification of their translational mobility, and interactions between ions changing their association.^21,25,29 In this context, nuclear magnetic resonance (NMR) is a unique, noninvasive method to study the diffusivity of molecules and different ions in multi-component and multi-phase, opaque and porous media.^{10,13,21,25,36–40} The PFG NMR method covers a wide range of diffusion times: from milliseconds to seconds. This allows us to use this method for observing molecular displacements in sub-micrometer and micrometer ranges. The presence of NMR-active nuclei in ILs permits the widespread application of multinuclear NMR experiments^21,38,40 for these systems. Chemical shifts and multinuclear coupling constants are used routinely for elucidation of the structure of ILs and the products formed by their covalent interactions with other materials. Furthermore, the availability of a multitude of NMR relaxation and NMR diffusometry techniques has facilitated the study of IL dynamic processes. In this work, we analyzed NMR spectra and diffusivities of ions of a lithium battery electrolyte comprising a fluorine-free IL (Fig. 1) and lithium salt in nanopores of SiO₂ with three different pore diameters to investigate the structure and dynamics of ions within the confinement.

Fig. 1 Chemical structures of the cations and anions of the electrolyte investigated in this study.

Experimental

Materials and methods

The synthesis and physicochemical properties of the [P_4,4,4,4][MEEA] IL and the lithium salt Li[MEEA] are reported in our recent publication.³⁹ [P_4,4,4,4] is the tetrabutylphosphonium cation and [MEEA] is the 2-[2-(2-methoxyethoxy)ethoxy] acetate anion. The Li⁺ conducting electrolyte is created by doping the [P_4,4,4,4][MEEA] IL with 30 mol% LiMEEA to get a concentrated solution. The bulk and the confined electrolytes were kept in a vacuum oven at 80 °C for about six days until the water content was less than 100 ppm as determined by the Karl Fischer titration using a 917 coulometer (Metrohm), placed inside a glovebox with water and oxygen contents less than 1 ppm.

The structure and dynamics of the electrolyte are studied in bulk as well as under confinement in nano-porous controlled porous glasses (CPG): AGC-40, Vycor (Vycor® 7930) and Varapor produced by Advanced Glass and Ceramics, https://www.porousglass.com. The pore structure of CPG is complicated and presents different levels of organization on different scales. The typical structure of a liquid confined in CPG is three-dimensional and sponge-like and can be supplemented with rigid barriers spaced on the nanoscale. This can be realized from the SEM^41,42 and TEM⁴³ images as well as the reconstructed images.^44,45 The pore space can be described by using two variables, the pore diameter d and the chord length l.⁴⁶ These parameters vary with the method of determination. The pore diameter is an opening or a gap for filtering and is the closest distance between the opposite pore walls. The pore radius distribution for Vycor 7930 has been determined initially by Levitz et al. using the nitrogen desorption isotherm and has an average value of about 3.5–3.7 nm (mean pore diameter ∼7 nm).⁴³ This value was comparable to that determined and used in other studies,^42,47–49 while from SAS X-ray data it was obtained as 4 nm.⁴⁶ The chord length is a geometrical parameter that describes the length between the intersections of lines with the interface.⁵⁰ The chord length distribution in Vycor was estimated from digitalized images to be about 10 nm (ref. 43) and 15 nm.⁴⁶ Pore radii and chord length distributions obtained by Levitz et al. are reproduced in Fig. S1 in the ESI.† The parameters of pore diameters (pore diameter distributions) of AGC-40 and Varapor are 3.7 nm (5.0 ± 1.7 nm) and 9.8 nm (13.5 ± 4.4 nm), respectively.⁵¹ The values of pore diameters as well as some other parameters of the used CPG obtained from Advanced Glass and Ceramics are shown in Table S1 of the ESI.†

Each of the used samples of porous glasses has a cylinder form with a length of 15 mm and a diameter of 4 mm. The porous glass cylinders were thoroughly cleaned with a boiling 50% hydrogen peroxide aqueous solution at 393 K for 48 h. Afterwards, the glasses were washed with distilled water and dried under vacuum. These glasses were activated at 723 K for 2 h and then cooled and placed in the electrolyte under vacuum at 298 K and finally stored within the electrolyte for two days at an ambient temperature. After that, the sample was removed from the electrolyte, wiped with paper, placed in a 5-mm standard NMR sample tube, heated at 330 K for 3 hours and subjected to several cycles of heating and cooling (363–295 K) to homogenize the distribution of the electrolyte inside the pores.

NMR techniques

A Bruker Ascend Aeon WB 400 (Bruker BioSpin AG) nuclear magnetic resonance (NMR) spectrometer was used for recording NMR spectra. The working frequencies were 400.21 MHz for ¹H, 162.01 MHz for ³¹P and 155.56 MHz for ⁷Li. For diffusion measurements a Diff50 pulsed-field-gradient (PFG) probe with exchangeable ¹H, ⁷Li and ³¹P inserts was used. The diffusional decays (DDs) were recorded using the stimulated echo (StE) pulse sequence. For a single-component diffusion, the form of the DD can be described as:^37,52

Here, A is the integral intensity of the NMR signal, τ and τ₁ are the time intervals in the pulse sequence; γ is the gyromagnetic ratio of magnetic nuclei; g and δ are the amplitude and the duration of the gradient pulse; t_d = (Δ − δ/3) is the diffusion time; Δ = (τ + τ₁); and D is the diffusion coefficient. δ was in the range of 0.5–3 ms, t was in the range 2–5 ms, and g was in the range 0.06–29.73 T m⁻¹. Diffusion time t_d was varied from 20 to 300 ms. The recycle delay during accumulation of signal transients was 3.5 s. DDs were obtained by the increase of g in all the experiments. Non-linear least square regression was used to fit the experimental data with eqn (1) to extract mean D values.

For multicomponent DDs mean apparent diffusion coefficients were obtained from the initial slope of the experimental DDs in accordance with the equation:^37,5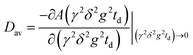2

To demonstrate the absence of internal field gradient effects a 13-interval stimulated echo sequence with bipolar gradient pulses,⁵³ modified by including a longitudinal Eddy-current-delay,⁵⁴ was used.

Results and discussion

The NMR spectra of the bulk and the confined electrolytes are shown in Fig. 2. The ¹H NMR resonance lines in the range from 1 to 3 ppm are attributed to the [P_4,4,4,4] cation, and the ¹H resonance lines around 4 ppm are due to the [MEEA] anion (Fig. 2a). In contrast, all the ¹H NMR resonance lines became broader and the resolution of the spectra became much poorer for the electrolytes confined in the porous glasses, which is in accordance with the previous studies.^55,56 This might be caused by the restricted rotational mobility of ions as well as translational diffusion in the presence of background gradient or between different magnetically non-equivalent sites.⁵⁶ The broadening of NMR spectral lines is related to reduction of the effective transverse NMR T₂ relaxation time.⁵⁷ Interaction of ions with rigid barriers leads to spatial restrictions of ion mobility and to ineffectual averaging of the contribution to relaxation from the dipole–dipole interactions. Since in this work all the porous systems are based on silicon oxide and the behavior of the same electrolyte is investigated, the pore size may have the greatest influence on the behavior of the electrolyte. As obvious from the ¹H NMR spectra, the broadening of the spectral lines is maximum for AGC-40 and Vycor systems with the smallest average diameter (3.7 nm and 7 nm) and the lines get narrower as the average pore size increases in the case of Varapor (9.8 nm).

Fig. 2 (a) ¹H NMR, (b) ³¹P NMR, and (c) ⁷Li NMR spectra of the bulk and the confined electrolytes at 295 K.

The ³¹P NMR spectra characterize the phosphonium cation, while the ⁷Li NMR spectra correspond to lithium ions in the electrolyte (Fig. 2b and c). The single ³¹P (34.5 ppm) and ⁷Li NMR (−1 ppm) resonance lines corresponding to the chemical structure of the electrolyte have symmetric forms. As expected, like the ¹H NMR spectra, the ³¹P and ⁷Li NMR resonance lines also get broader and the trend of increasing spectral line broadening with the decreasing average pore diameter is maintained.

Another feature of the ³¹P and ⁷Li NMR spectra of the electrolyte in pores is the shift of the resonance lines, which increases with decreasing average pore diameter (Fig. 3). The ³¹P chemical shift values of the [P_4,4,4,4] cation in different pores increase in a similar way with increasing temperature (Fig. 3a). In contrast, the ⁷Li chemical shift remained unchanged as a function of temperature for the bulk electrolyte and the one confined in Varapor. However, for the electrolyte in AGC-40 and Vycor, the chemical shift values moved sharply downfield, especially in the temperature range from 290 to 310 K (Fig. 4a).

Fig. 3 (a) ³¹P NMR chemical shift and (b) ³¹P resonance line broadening for the bulk and confined electrolytes.

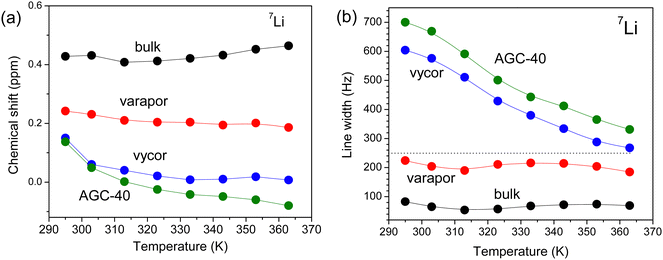Fig. 4 (a) ⁷Li NMR chemical shift and (b) ⁷Li resonance line broadening for the bulk and confined electrolytes.

Generally, NMR chemical shift of a nucleus alongside the chemical structure is determined by the surrounding environment.⁵⁷ Therefore, the variation of NMR chemical shifts of different nuclei for ILs and electrolytes in the confinement is expected. For example, Brinkkötter et al.⁵⁸ observed an upfield shift of the ¹⁹F spectral line with increasing salt concentration for electrolytes based on the [Pyr_12O1] cation and the [FTFSI] asymmetric anion, which was attributed to the increasing fraction of the side groups coordinating to Li⁺. The lower chemical shifts are associated with the stronger coordination and the change in ⁷Li chemical shift corresponds to the deshielding of Li⁺. In another study, a downfield shift in ¹H NMR was observed for a protic diethylmethylammonium methanesulfonate IL confined in pores of nano-porous silica micro-particles.⁵⁹ Similarly, a downfield shift in ¹⁹F NMR of [BMIm][TFSI] was observed in the pores of active carbon.⁵⁵ The observed resonance shift in the pores of carbon materials is due to the aromatic ring currents in the pore walls, which shields the external magnetic field, thereby lowering the resonance frequency of the in-pore spins.

For the [BMIm][BF₄] IL confined in a polymer gel electrolyte matrix,⁶⁰ the decrease in molecular mobility was accompanied by the ⁷Li and ¹⁹F NMR resonance line broadening and the ⁷Li signal was shifted downfield, while the ¹⁹F signal was shifted upfield. In our case, the increase in temperature leads to a downfield shift of the ³¹P resonance lines (Fig. 3a), which is expected due to the faster ion mobility (this is also clear from the line narrowing, Fig. 3b). This is a result of the decreasing interactions between the organic cation and the Li⁺ with increasing temperature in the bulk as well as confined electrolytes. In addition, the decrease in the pore size leads to an upfield shift of the ³¹P resonance lines, again suggesting a weaker coordination of the organic cation by Li as the pore size decreases (Fig. 3a). This occurs evidently for the same reason as the temperature variation. The ⁷Li NMR chemical shifts remained almost unchanged with increasing temperature (Fig. 4a), but the lines systematically shift upfield as the pore size decreases. According to the previous studies conducted by Brinkkötter, et al.,⁵⁸ this corresponds to the deshielding of Li⁺, which is related to the increase in the fraction of the organic ions contributing to the coordination. Additionally, this can also be attributed to the changing ion associated structures in the system.

Unlike chemical shift, the ³¹P and ⁷Li resonance line broadenings have some peculiarities (Fig. 3b and 4b): the forms of dependencies for bulk electrolyte and electrolyte in Varapor are similar and remain almost unchanged with increasing temperature. On the other hand, forms of the dependencies for electrolytes confined in AGC-40 and Vycor are also similar and line broadening decreases with increasing temperature. In the temperature range from 290 to 310 K, the line broadening is higher by a factor of six and three for ⁷Li and ³¹P, respectively, as compared to the line broadening of the bulk electrolyte. In the temperature range from 320 to 360 K, the difference in the line broadening decreased significantly for both ⁷Li and ³¹P.

To get insights into the effect of confinement on the ion dynamics of the electrolytes, systematic multinuclear (¹H, ³¹P and ⁷Li) PFG NMR studies are performed over a wide temperature range. The sharp resonance lines of the ¹H NMR spectra for the bulk electrolyte allowed us to analyze diffusivities of the [P_4,4,4,4] cation and [MEEA] anion separately. It appeared that ¹H NMR diffusional decays (DDs) of the [P_4,4,4,4] cation and [MEEA] anion can be described by a single-component decay (eqn (1)) and the diffusion coefficients of the cation and the anion are very similar in the studied temperature range (Fig. 5). The DDs of the [P_4,4,4,4] cation were also measured by ³¹P NMR PFG and they showed a single-component form. The diffusion coefficients of the [P_4,4,4,4] cation obtained by ¹H and ³¹P PFG NMR are comparable. As expected, the diffusion coefficients of the cation and anion in the bulk electrolyte monotonously increase with increasing temperature and follow the VFT behavior:⁶¹

where D₀, T₀ and E_D are the adjustable parameters.

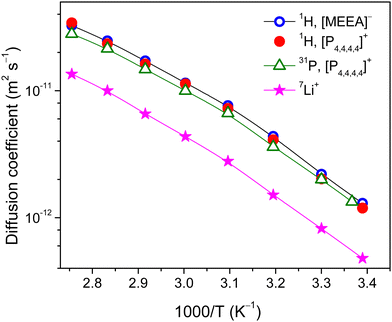Fig. 5 Diffusion coefficients of the [P_4,4,4,4] cation, Li⁺ and [MEEA] anion in the bulk electrolyte as measured by ¹H, ³¹P and ⁷L PFG NMR.

The ⁷Li DDs are in one decimal order and demonstrated single-component forms (Fig. S2, ESI†). Despite the smallest size, Li⁺ diffusivities are less by a factor of 1.7–3.7 as compared to the organic [P_4,4,4,4] cation and [MEEA] anion and agree well with the previous reports.^3,6 This is primarily due to the bulky lithium aggregates and/or formation of solvation shells near Li⁺ ions. It is worth noting that no signs of restricted molecular and ion mobility are observed due to the spatial limitations or exchange processes in the time range from 20 to 1000 ms as detected by PFG NMR.

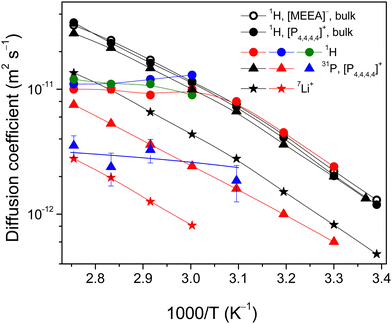
For the confined electrolytes in porous glasses, the ¹H NMR spectral resolution became poorer and the separation contribution of the anion and cation to DDs became problematic. In this context, the most reliable information about the [P_4,4,4,4] cation diffusivity can be obtained by ³¹P PFG NMR. The ³¹P PFG NMR signal of the confined electrolytes was decreased in comparison with the bulk electrolyte because of enhanced T₂ NMR relaxation. This did not allow us to perform the experiment for electrolyte confined in AGC-40 pores. However, DDs were obtained at temperatures of 303 K and higher (323 K) for electrolytes confined in Varapor and Vycor, respectively (Fig. 7). Even though dynamic ranges of DDs are less than one decimal order (Fig. 6), they allow the estimation of the mean values of apparent diffusion coefficients using eqn (2). For the electrolyte in Varapor (Fig. 6b), an increase in the temperature leads to an increase in the slope of the ³¹P DDs. At higher temperatures (353 and 363 K), the form of the decay evidently deviates from the single-component one. This is typical for the short- and intermediate-diffusion time regimes in the pores.³⁷

Fig. 6 ³¹P NMR diffusion decays for the electrolyte confined in: (a) Vycor porous glass, diffusion time 10 ms and (b) Varapor porous glass, diffusion time is 20 ms. DDs in (a) are shifted along the Y-axis for clarity.

The values of D_av for the [P_4,4,4,4] cation of the electrolyte confined in Varapor and Vycor were estimated from the ³¹P PFG NMR DDs (Fig. 6) and are presented in Fig. 7 (red triangles). The ability to measure diffusion using PFG NMR is determined by the T₂ value of the nuclei of interest. In the case of AGC-40, and in Vycor at low temperatures, spectral lines are broad (Fig. 3b) and the corresponding T₂ values are too short. It is seen that the possibility to measure diffusion by PFG NMR agrees with the NMR spectra line broadening less than ∼160 Hz for ³¹P.

Fig. 7 Comparison of the diffusion coefficients of the [P_4,4,4,4] cation, Li⁺ and [MEEA] anion in the bulk and confined electrolytes. The black color represents diffusion of ions in the bulk electrolyte, red in pores of Varapor, blue in pores of Vycor and green in AGC-40.

The ⁷Li NMR spin echo signal for the electrolyte confined in Varapor was obtained only at temperatures higher than 333 K. ⁷Li DDs for the Varapor samples were obtained in less than one decimal order (Fig. S3 in the ESI†) and no diffusion time dependence of the ⁷Li DDs was observed in the range of 20 to 100 ms. The diffusivity of Li⁺ in the electrolyte confined in Varapor was measured by ⁷Li PFG NMR (Fig. 7, red stars). The temperature-dependent diffusion coefficients of Li⁺ in the Varapor confined electrolyte demonstrate a convex form and are a factor of ∼5 less than the Li⁺ diffusivity in the bulk electrolyte. The measurement of Li⁺ diffusivity in the pores of Vycor and AGC-40 did not succeed due to enhanced ⁷Li NMR relaxation.

Overall, confinement of the electrolyte in pores of Varapor leads to a decrease in the diffusivity of the [P_4,4,4,4] cation by a factor of ∼3.6 in comparison to the bulk electrolyte. Both cation (³¹P data, red triangles) and lithium (red stars) diffusivities increase with temperature similarly to bulk electrolytes. However, in the case of electrolyte confined in Vycor, the apparent diffusion coefficients of the [P_4,4,4,4] cation are in the range of ∼2–3 × 10⁻¹² m² s⁻¹ in a temperature range of 323–363 K and remain unchanged with increasing temperature (blue triangles), which are a factor of 3–10 less than that in the bulk electrolyte.

Because of poor resolution of ¹H NMR spectra of the confined electrolytes (Fig. 2A), we analyzed diffusion decays of integral intensities of the whole ¹H NMR signals. Generally, ¹H diffusion decays for ions in pores demonstrated no-single component form (Fig. 8), which can be characterized as a distribution (spectrum) of apparent diffusion coefficients. It is clearly seen that at 333 K slopes of the initial parts of decays are comparable, while they diverge from the exponential form as far as the amplitude of PFG, g, increases. The difference increases with decreasing pore size – from bulk to Varapor, further to Vycor and finally to AGC-40. The effects of diffusion time on the forms of DDs were analyzed for the electrolyte confined in AGC-40, Vycor (t_d was varied from 20 to 100 ms) and Varapor samples (20–300 ms) and no clear dependencies were observed (Fig. S4–S6 in the ESI†).

Fig. 8 ¹H NMR diffusion decays for the [MEEA] anion (open circles) and [P_4,4,4,4] cation (solid circles) and for both (half-solid circles) in the pores of the porous glasses. The diffusion time is 20 ms and the temperature is 333 K. In the case of Varapor, Vycor and AGC-40, the ¹H signals belong to both the [P_4,4,4,4] cation and [MEEA] anion.

Because of enhanced T₂ NMR relaxation in narrow pores, the amplitude of the stimulated echo in the ¹H PFG NMR experiment is low and depends on temperature differently for different porous glasses. The signal-to-noise (S/N) ratios measured at 343 K are: 47.5 (varapor), 2.65 (vycor) and 0.16 (AGC-40). This shows correlation with the pore size distributions in these porous glasses. Therefore, DDs in the ¹H PFG NMR experiment were obtained in limited temperature ranges, which were different for different systems: 303–363 K for Varapor, 333–363 K for Vycor and 333–363 K for AGC-40.

The typical variations of the ¹H DDs as a function of temperature for the organic anion and cation of [P_4,4,4,4][MEEA] as an example for Varapor (the most extended temperature range) are shown in Fig. 9. Similar results for Vycor and AGC-40 systems are shown in Fig. S8 and S9 (ESI†), respectively.

Fig. 9 ¹H NMR diffusion decays as a function of temperature for the electrolyte confined in the pores of Varapor. The diffusion time is 20 ms.

Overall, the forms of DDs are not single component for all the systems. Therefore, no complete averaging of diffusivities over the porous system occurs in the diffusion time range of the experiment in the whole studied temperature range. Dependencies of mean values of apparent diffusion coefficients on temperature are shown in Fig. 7 as solid-colored circles. In the case of Varapor (red circles), proton diffusion coefficients at 303–323 K are comparable with those of the cation and anion in bulk, while in the higher temperature range from 323 to 363 K, the proton diffusivity does not change and remains close to 1 × 10⁻¹¹ m² s⁻¹. For the electrolyte in Vycor and AGC-40 pores (blue and green circles, respectively), the diffusion coefficients are also close to 1 × 10⁻¹¹ m² s⁻¹ at 333–363 K.

To analyze the transport properties of GPG, its porous space was described as curved cylindrically shaped voids.⁴⁷ An adsorption–desorption and Monte Carlo study showed that Vycor has a highly disordered silica matrix with a network of pores containing alternating enlargements (“voids”) and constrictions (“necks”) that determine the diffusion properties of Vycor.⁴⁷ The fraction of the “necks” estimated from the distribution function is nearly 0.4.⁴⁷ Therefore, diffusion of these ions through such “necks” can be effectively hindered.¹⁰ The “necks” can affect the diffusion of low-molecular hydrocarbons. In the case of n-decane confined in pores of Vycor, the ¹H NMR diffusion decay showed single-component form in three decimal orders of the signal decay.²⁷ However, for 4.5 decimal orders of the signal decay the form of the decay is clearly complicated and is like a sum of the two components (Fig. S7, ESI†). In this work, DDs obtained for the IL electrolyte presented in Fig. 8 are similar to those observed for the confined n-decane. All the controlled porous glasses prepared with the same technology evidently have similar structures. Therefore, it is reasonable to suggest that the fraction of “necks” increases as the mean pore diameter decreases. As the fraction controlled by the “necks” is independent of diffusion time, it follows that the corresponding areas of space inside pores form “partially isolated volumes” containing the liquid, which is in a so-called “slow exchange” regime with the rest of the liquid.¹⁰ The size of “partially isolated volumes”, as estimated from the dependence of ion diffusivity on the diffusion time, is on the order of 1 μm.¹⁰

The fraction of the porous space controlled by the “necks” (“partially isolated volumes”) increases from ∼0.2 in Varapor to ∼0.6 in AGC-40 (Fig. 8). Because of the lower apparent diffusivity corresponding to this fraction, there is no effect on the mean apparent diffusion coefficient. Therefore, to further explain diffusivities inside pores as a function of temperature and pore-size, a different and at the same time rather broad distribution of pore diameters of the used porous glasses should be taken into consideration. At least two effects may influence the mean apparent diffusivity of a liquid in the nano-pores: (1) the pore-size dependence of the NMR relaxation time and (2) the exchange of moving particles between the pores with different diameters. In the first case, the contributions of the electrolyte confined in pores with different diameters in the stimulated echo NMR signal (DDs) are different: the “large” pores give higher contribution, while signals from the “narrow” pores are reduced and/or even vanished. Here the term “large” refers to the pores that contribute to the signal of the stimulated echo NMR. The exchange of particles between pores, which is accelerated as a function of temperature, leads to an averaging of both the NMR relaxation times and the diffusion coefficients. The effect of exchange between the pores of different sizes on the line broadening was described by Forse et al.⁵⁶ As the ions diffuse from “large” pores to “narrow” pores, their NMR signal decreases, and, therefore, their contribution to the DDs decreases. As a result, the apparent diffusivity may decrease as the intensity of the exchange between pores intensifies.

Now these ideas can be applied to analyze the experimental dependencies on proton diffusivities (Varapor, Vycor and AGC-40 samples) and phosphorus diffusivity (Vycor sample). In the case of Varapor, because the diffusivity of the [P_4,4,4,4] cation according to ³¹P PFG NMR data is a factor of 3.6 less than the ones measured by ¹H PFG NMR, the measured averaged ¹H diffusion coefficient D_av according to the averaging rule for diffusivities:

D_av = P₁·D₁ + P₂·D₂ (4)

corresponds to a higher degree to diffusivities of the [MEEA] anion. Here D_i and P_i are diffusivities and fractions of the diffusing components, respectively. In the temperature range from 303 to 333 K, ¹H diffusivity of the anion corresponds to the “large” pores and there is no effect of exchange between the “large” and the “narrow” pores, while protons in the “narrow” pores are not detected due to NMR relaxation. As the temperature exceeds 333 K, thermal intensification of mobility begins, which leads to the appearance of a signal from the “narrow” pores and manifestation of molecular exchange between the “large” pores and a part of “narrow” pores with higher diameters from the pore diameter distribution. This leads to a decrease of the average apparent diffusion coefficients. As the temperature increases, higher fractions of the ions from the “narrow” pores became involved in the exchange. Together with the thermal activation of diffusivity, this leads to the almost constant apparent diffusivity of the [MEEA] anion in the temperature range from 333 to 363 K. At the highest temperature of 363 K, the cation diffusivity measured by ¹H PFG NMR reaches the diffusivity measured by ³¹P PFG NMR.

The same effect is observed for ¹H PFG NMR in Vycor and AGC-40 systems (blue and green circles in Fig. 7); the only difference is the absence of the “large” pores in these porous glasses. Therefore, there is no ¹H NMR stimulated echo signal at temperatures below 333 K. However, as temperature exceeds 333 K, the stimulated echo signal begins to appear and the effect of exchange manifests and develops as the temperature increases. From the ¹H PFG NMR data, it is evident that the boundary between the “large” and “narrow” pores is in the pore size range between those of Vycor and Varapor. A similar effect of exchange is observed in ³¹P PFG NMR for the [P_4,4,4,4] cation in pores of Vycor (blue triangles in Fig. 7). From the trend of the measured apparent diffusion coefficient of the [P_4,4,4,4] cation at higher temperatures, it is seen that diffusivity of the cation in pores of Vycor is lower than that in Varapor.

It is also quite possible that the electrolyte present on the outer surface of the CPG cylinder is involved in the exchange with “narrow” pores, alongside with the “large” pores. Although the outer electrolyte from the sample was carefully removed by wiping, the increasing temperature can cause thermal expansion of both the porous matrix and the electrolyte. The thermal expansion coefficient of liquids is much higher than those of the Vycor type porous glasses (∼7.5 × 10⁻⁷/°C). Therefore, some amount of the liquid could be expelled from the sample upon heating. However, there is a possibility that the expelled out-pore electrolyte has NMR relaxation like the bulk electrolyte. The ¹H NMR resonance lines from the out-pore electrolyte might be a factor of two broader than that from the in-pore due to diffusion in the background gradient.⁵⁹ Additionally, for our consolidated porous samples the border between the out-pore and the in-pore is located on the surfaces of the sample cylinders. Keeping in mind the diffusion coefficient ∼10⁻¹¹ m² s⁻¹ and the diffusion time 20 ms, the region of the pore exchange is ∼0.6 μm. This is a negligible part of the porous cylinder diameter. Therefore, even if some of the electrolyte is expelled from glass samples, which has bulk-like NMR relaxation properties, it does not essentially contribute to the observed temperature dependencies of the apparent diffusion coefficients.

These PFG NMR data suggest that confinement of an electrolyte in silica pores decreases the diffusivity of the [P_4,4,4,4] cation to a much higher degree in comparison with the [MEEA] anion. This might be due to the reason that the silica and silicate glass surfaces acquire a negative surface charge density because of deprotonation.⁶² Therefore, interaction of the [P_4,4,4,4] cation with the negative surface might be the possible mechanism of its greater decrease in translational diffusion as compared with the [MEEA] anion. Concerning the diffusivity of the small Li⁺, it diffuses much more slowly than the larger organic ions when solvation of the Li⁺ occurs.⁶³ Furthermore, as the concentration of the lithium salt increases, the diffusivities of all the ions decrease due to increased electrostatic interactions, demonstrating solvation of Li⁺ in the system. Similarly, in the confinements (Fig. 7), diffusivity of the small Li⁺ decreases and remains slower than the diffusivities of the larger organic ions of the system, confirming the solvation of Li⁺ inside the pores.

In contrast to the previous studies of ionic liquids confined in nanopores,^10,11,21 no enhancement of ion diffusivities is observed for the studied electrolyte. However, this agrees well with previously observed decrease of ion diffusivity in various nanopores^13,36 and this might be related to the specificity of the used ILs and IL-based compositions. The interactions of the electrolyte components with the pore surface and change in the nanostructure of electrolyte in the nanoconfinement may contribute to the enhancement of the NMR relaxation. However, in the time scale of the PFG NMR experiment and for the observed effect of molecular exchange between the pores these small-scale processes are dynamically averaged.

Conclusions

The confinement of a fluorine-free ionic liquid-based electrolyte in nanopores of controlled porous glasses caused several NMR spectroscopy effects. The broadening of ¹H, ³¹P and ⁷Li NMR resonance lines increased with decreasing pore size and the confinement led to a variation in the ³¹P and ⁷Li NMR chemical shifts. While ions of the bulk electrolyte exhibited a single-component diffusional behavior, a distribution of apparent diffusion coefficients was observed for the organic ions inside the nanopores. The complicated diffusion decays are due to the complex porous structure of the porous glasses, the presence of pore “necks” and “partially isolated volumes” containing the liquid, which is in a “slow exchange” regime with the rest of the liquid. The mean apparent diffusivity is controlled by the exchange of ions between the “narrow” and the “large” pores in the pore size distribution. The frequent exchange of ions between the “narrower” and the “larger” pores resulted in an abnormal variation of diffusion coefficients with increasing temperature. Like bulk electrolytes, the Li⁺ ions are solvated inside porous glasses and their diffusivity remained slower as compared to the organic ions. This study provides a foundation to study ion dynamics of electrolytes under confinement and design new fluorine-free electrolytes with desired transport properties for various energy storage devices.

Author contributions

A. F.: conceptualization, methodology, writing – original draft; M. R.: NMR experiment, data curation; V. P. A.: diffusion data analysis; and F. U. S.: validation, writing – reviewing and editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationship that could have appeared to influence the work reported in this paper.

Acknowledgements

The financial support from the Swedish Research Council for Sustainable Development (Grant number: 2020-00969) is gratefully acknowledged.

References

1. M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239.
2. S. P. M. Ventura, F. A. Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. P. Coutinho, Chem. Rev., 2017, 117, 6984–7052.
3. S. Bhowmick, G. Tatrari, A. Filippov, P. Johansson and F. U. Shah, Phys. Chem. Chem. Phys., 2023, 25, 19815–19823.
4. A. B. Reddy, F. U. Shah, J. Leckner, M. W. Rutland and S. Glavatskih, Colloids Surf., A, 2024, 683, 132875.
5. F. U. Shah, S. Glavatskih, D. R. MacFarlane, A. Somers, M. Forsyth and O. N. Antzutkin, Phys. Chem. Chem. Phys., 2011, 13, 12865–12873.
6. M. Ahmed, S. Rao, A. Filippov, P. Johansson and F. U. Shah, Phys. Chem. Chem. Phys., 2023, 25, 3502–3512.
7. J. Lin, D. Noferini, E. Veroutis, C. Korte and O. Holderer, J. Mol. Liq., 2021, 343, 117712.
8. H. Frielinghaus, M. Fomina, D. Hayward, P. S. Dubey, S. Jaksch, P. Falus, P. Fouquet, L. Fruhner and O. Holderer, Front. Phys., 2022, 10, 872616.
9. S. M. Chathoth, E. Mamontov, P. F. Fulvio, X. Wang, G. A. Baker, S. Dai and D. J. Wesolowski, Europhys. Lett., 2013, 102, 16004.
10. A. Filippov, N. Azancheev, F. U. Shah, S. Glavatskih and O. N. Antzutkin, Microporous Mesoporous Mater., 2016, 230, 128–134.
11. A. Filippov, O. I. Gnezdilov, N. Hjalmarsson, O. N. Antzutkin, S. Glavatskih, I. Furó and M. W. Rutland, Phys. Chem. Chem. Phys., 2017, 19, 25853–25858.
12. A. Filippov and O. N. Antzutkin, Phys. Chem. Chem. Phys., 2018, 20, 6316–6320.
13. A. Filippov, O. N. Antzutkin, V. P. Arkhipov and O. I. Gnezdilov, J. Mol. Liq., 2022, 356, 118998.
14. E. H. Lahrar, I. Deroche, C. M. Ghimbeu, P. Simon and C. Merlet, ACS Appl. Nano Mater., 2021, 4, 4007–4015.
15. M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224.
16. E. Sloutskin, R. M. Lynden-Bell and S. Balasubramanian, J. Chem. Phys., 2006, 125, 174715.
17. R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168.
18. M. P. Singh, R. K. Singh and S. Chandra, Prog. Mater. Sci., 2014, 64, 73–120.
19. J. M. Otero-Mato, H. Montes-Campos, O. Cabeza, L. J. Gallego and L. M. Varela, J. Mol. Liq., 2020, 320, 114446.
20. G. Ori, F. Villemot, L. Viau, A. Vioux and B. Coasne, Mol. Phys., 2014, 112, 1350–1361.
21. C. Iacob, J. R. Sangoro, W. K. Kipnusu, R. Valiullin, J. Kärger and F. Kremer, Soft Matter, 2012, 8, 289.
22. C. Pinilla, M. G. Del Popolo, R. M. Lynden-Bell and J. Kohanoff, J. Phys. Chem. B, 2005, 109, 17922–17927.
23. Q. Berrod, F. Ferdeghini, P. Judenstein, N. Genevaz, R. Ramos, A. Fournier, J. Dijon, J. Olliver, S. Rols, D. Yu, R. A. Moled and J.-M. Zanotti, Nanoscale, 2016, 8, 7845–7848.
24. S. Zhang, J. Zhang, Y. Zhang and Y. Deng, Chem. Rev., 2017, 117, 6755–6833.
25. C. Iacob, J. R. Sangoro, P. Papadopoulus, T. Schubert, S. Naumov, R. Valiullin, J. Kärger and F. Kremer, Phys. Chem. Chem. Phys., 2010, 12, 13798–13803.
26. C. Tasserit, A. Koutsioubas, D. Lairez, G. Zalczer and M. C. Clochard, Phys. Rev. Lett., 2010, 105, 260602.
27. O. I. Gnezdilov, O. N. Antzutkin, R. Gimatdinov and A. Filippov, Magn. Reson. Imaging., 2020, 74, 84–89.
28. A. Filippov, R. Gimatdinov, O. N. Antzutkin, N. A. Kuzina and O. I. Gnezdilov, J. Mol. Liq., 2021, 323, 115008.
29. A. Filippov, A. S. Alexandrov, R. Gimatdinov and F. U. Shah, J. Mol. Liq., 2021, 340, 116841.
30. A. Filippov and O. N. Antzutkin, Phys. Chem. Chem. Phys., 2023, 25, 14538–14545.
31. M. Brachet, T. Brousse and J. Le Bideau, ECS Electrochem. Lett., 2014, 3, A112–A115.
32. L. Negre, B. Daffos, V. Turq, P. L. Taberna and P. Simon, Electrochim. Acta, 2016, 206, 490–495.
33. J. Le Bideau, L. Viau and A. Vioux, Chem. Soc. Rev., 2011, 40, 907–925.
34. “What is Vycor glass?,” Applied Optics, 1979, 18, 3208–3248, https://opg.optica.org/ao/abstract.cfm?URI=ao-18-19-3208.
35. D. Enke, F. Janowski and W. Schweiger, Microporous Mesoporous Mater., 2003, 60, 19–30.
36. Y. Wei, Z. Dai, Y. Dong, A. Filippov, X. Ji, A. Laaksonen, F. U. Shah, R. An and H. Fuchs, Phys. Chem. Chem. Phys., 2022, 24, 12808–12815.
37. P. T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy, Clarendon, Oxford, 1991.
38. V. Overbeck, A. Appelhagen, R. Rößler, T. Niemann and R. Ludwig, J. Mol. Liq., 2021, 322, 114983.
39. P. Linse and O. Söderman, J. Magn. Reson., Ser. A, 1995, 116, 77–86.
40. K. Damodaran, Progr. Nucl. Magn. Reason. Spectrosc., 2022, 129, 1–27.
41. M. Hubert and A. J. Faber, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2014, 55, 136–158.
42. H. Bian, L. Ai, K. Hellgardt, G. C. Maitland and J. Y. Y. Heng, Crystals, 2021, 11, 201.
43. P. Levitz, G. Ehret, S. K. Sinha and J. M. Drake, J. Chem. Phys., 1991, 95, 6151–6161.
44. D. P. Bentzy, E. J. Garboczi and D. A. Quenard, Modell. Simul. Mater. Sci. Eng., 1998, 6, 211–236.
45. M. H. Kim and C. J. Glinka, Microporous Mesoporous Mater., 2006, 91, 305–311.
46. W. Gille, D. Enke and F. Janowski, J. Porous Mater., 2002, 9, 221–230.
47. R. Cimino, K. A. Cychosz, M. Tommers and A. V. Neimark, Colloids Surf., A, 2013, 437, 76–89.
48. P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102.
49. A. Ch Mitropoulos, J. Colloid Interface Sci., 2009, 336, 679–690.
50. S. Torquato and B. Lu, Phys. Rev. E, 1992, 47, 2950–2953.
51. D. Noferini, O. Holderer and H. Frielinghaus, Phys. Chem. Chem. Phys., 2020, 22, 9046–9052.
52. J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526.
53. R. M. Cotts, M. J. R. Hoch, T. Sun and J. T. Markert, J. Magn. Reson., 1989, 83, 252–266.
54. S. J. Gibbs and C. S. Johnson Jr., J. Magn. Reson., 1991, 93, 395–402.
55. J. Cui, X. Lin, W. Zhao, P. T. Cummings, M. Pruski and T. Kobayashi, J. Phys. Chem. B, 2022, 126, 4889–4898.
56. A. C. Forse, J. M. Griffin, C. Merlet, P. M. Bayley, H. Wang, P. Simon and C. P. Grey, J. Am. Chem. Soc., 2015, 137, 7231–7242.
57. M. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, 2nd ed., Wiley, Chichester, 2008.
58. M. Brinkkötter, A. Mariani, S. Jeong, S. Passerini and M. Schönhoff, Adv. Energy Sustainability Res., 2020, 1, 2000078.
59. M. N. Garaga, M. Persson, N. Yaghini and A. Martinelli, Soft Matter, 2016, 12, 2583–2592.
60. V. I. Volkov, O. V. Yarmolenko, A. V. Chernyak, N. A. Slesarenko, I. A. Avilova, G. R. Baymuratova and A. V. Yudina, Membranes, 2022, 12, 416.
61. A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603–4610.
62. S. Kralj, A. Zidansek, G. Lahajnar, S. Zumer and R. Blinc, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3021–3031.
63. F. U. Shah, O. I. Gnezdilov, I. A. Khan, A. Filippov, N. A. Slad and P. Johansson, J. Phys. Chem. B, 2020, 124, 9690–9700.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01058b

---