 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bubble dynamics manipulation in polymeric foaming†
Lorenzo
Miele
ab,
Antonio
Abate
a,
Kentaro
Taki
*c and
Ernesto
Di Maio
 *ab
*ab
aDipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, University of Naples Federico II, Naples, Italy. E-mail: edimaio@unina.it
bFoamlab, University of Naples Federico II, Naples, Italy
cFaculty of Frontier Engineering, Institute of Science and Engineering, Kanazawa University, Kanazawa, Japan. E-mail: taki@se.kanazawa-u.ac.jp
First published on 22nd October 2024
Abstract
The release of pressure from a high-pressure-stable polymer/gas solution is a common method for creating gas bubbles and forming foam with a typical polyhedral cell structure. We propose a new approach to control the foaming process by pausing the bubble growth at intermediate pressure before reaching ambient pressure. This allows us to control the growth of the bubbles and investigate various physical phenomena involved in polymer foaming, such as Ostwald ripening, bubble interactions, coalescence, and different bubble growth regimes. We conducted these studies in a model system PP/N2 by subjecting the solution to non trivial pressure histories. Our method will have an impact on the study of fundamental phenomena involved in foaming and their application in creating new materials.
1 Introduction
Bubbles are ubiquitous in everyday life and industry, for example when embedded in liquid1 or solid matrices2 to form foams. The bubble formation and evolution process, with the stages of bubble nucleation, growth, and stabilization, is central to optimizing processes and performance. Specifically, bubble growth is a complex phenomenon in which mass, momentum, and energy are transported in a two-phase, two-component system comprising many bubbles within a viscoelastic fluid.3,4 In modeling approaches, simplified approximations are necessary to reduce the complexity of the problem and address the lack of experimental data for specific polymer/blowing agent systems.5From an experimental point of view, monitoring bubble formation and evolution is required to validate the models. Specifically, concerning polymer foaming, numerous custom apparata for the visualization of bubbles have been developed.6–9 These systems were designed to enable the study of different foaming stages, including bubble nucleation in both homogeneous and heterogeneous cases,10–12 bubble growth,13,14 and eventually, setting or coalescence.11 Furthermore, they have been used to validate various processes, such as the core back operation of injection moulding.15 While the proposed techniques offer significant consistency and flexibility, there are some drawbacks. With regard to the study of bubble growth, the time interval during which bubble analysis can be performed is limited due to the interaction and overlapping of bubbles in the image. In 2003, Acierno and Grizzuti16 introduced the so called “inverse quenching” technique to study rheological properties of a semi-crystalline polymer at a given degree of crystallization. The technique exploits the effect of temperature on the dynamics of crystallization to regulate degree of crystallinity of the polymer. By lowering the temperature, on a molten polymer, they initiate the crystallization, and by subsequently raising the temperature, they preserve the crystalline phase in a quenched state and gain the opportunity of long-term study. The present work somehow resembles and was inspired by the “inverse quenching” technique using pressure rather than temperature, to quench bubbles, rather than crystals. In particular, the presented technique will exploit the effect of pressure over the bubble dynamics, leveraging the compressibility of the gas within the bubbles and the ability to inflate or deflate the same. This allows us to control and decouple bubble nucleation, growth, and collapse, hence controlling the bubble dynamics. We will show how this simple idea discloses a wealth of important outcomes, together with the abundance of collectable data.
2 Materials and methods
2.1 Materials
Isotactic homopolypropylene granules (PP, F-300SP, Prime Polymer Japan, melting temperature of 165 °C) were compression molded at 230 °C and 10.0 MPa for 10 min, then slowly cooled to ambient temperature to achieve slab thickness of 0.5 mm. Eventually, 5 mm diameter disks were formed by punching. Nitrogen with purity >99.999% was used as a physical blowing agent.2.2 Visual observation apparatus
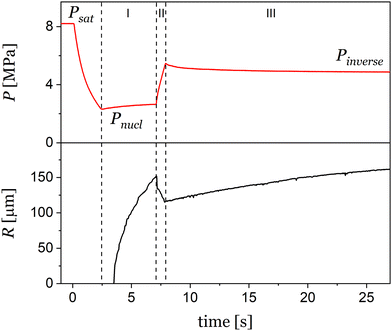
The bubbles dynamics manipulation experiments were performed using a custom-made visual observation apparatus. The apparatus consists of a high-pressure autoclave with sapphire windows and automatic valves to finely control the pressure of the gas, as described elsewhere.17 The PP disk was sandwiched between the sapphire windows, and a 0.5 mm thick C-shaped spacer fixes the distance between the windows. A camera (EMVC-CB130C3, MISUMI, Japan) with a long-distance microscope (VH-Z50L, KEYENCE, Japan) was used to capture the bubble evolution. The autoclave pressure (P) is controlled by two solenoid valves (SSPD-8, Keihin, Japan) connected to a programmable logic controller (PLC, KV-Nano, Keyence, Japan) that operated the valves at a response time of 10 ms. In addition, needle valves were used to adjust the gas flows. In a typical test, after the sample is loaded, the autoclave is purged with nitrogen and heated to the set temperature (T = 180 °C), which is kept constant for the duration of the experiment. When the test temperature is reached, P is brought to and held constant for 60 min at saturation pressure, Psat (in the range 6.5–8.5 MPa), to form a polymer/gas solution in equilibrium with the external gas phase. Starting from equilibrium conditions, a general pressure treatment is shown in Fig. 1. Here, after saturation, the pressure treatment starts with a pressure quench to nucleate bubbles, from Psat to the nucleation pressure, Pnucl (details are reported in Section 3.1). After a certain time, tnucl, the pressure is slightly increased to Pinverse, in order to control the bubble growth stage, in fact, decoupling the growth from the nucleation stage. The pressure is maintained constant for a sufficient period of time, designated as tgrowth, during which various bubble dynamics can be observed and modeled (details are reported in Section 3.2.1). Eventually, to tailor the bubble morphology, in some experiments pressure is periodically changed in a range from Pdown to Pup, ncycle times, with a period ti (details are reported in Section 3.3).2.3 Image analysis
Using ImageJ (FIJI) software,18 the images were binarized, then the “fill holes” and “watershed” functions were used to erase the light reflection inside the bubbles and to separate the overlapped bubbles, respectively. The bubble properties were then quantified using the “analyze particle” tool (considering bubbles as particles). The resulting details of the bubbles are: the area (A), the major radius (Rmax) and the minor radius (Rmin) – the primary and secondary semi-axis of the best-fitting ellipse, their average (the bubble radius, R), the coordinates of the center of mass of each bubble (XMi,YMi), the distance between two bubbles (d), and the roundness (RND), defined as: | (1) |
As we are interested in studying each and every bubble separately, all the data collected in the previous operation were analyzed with a custom-made MATLAB script to track the bubbles, thus measuring the time evolution of the details listed above.
3 Results and discussion
3.1 Bubble number density
We use the pressure quench technique to induce bubble nucleation. From Psat, P is rapidly reduced to the nucleation pressure, Pnucl. As extensively reported in the literature, the driving force for bubble nucleation is the associated gain in the volumetric Gibbs energy,5 ΔG. According to the classical nucleation theory,19 in the simple case of homogeneous nucleation, | (2) |
 | (3) |
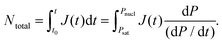 | (4) |
N total can be measured (at least, estimated), for example, by looking at the cross section of a foam, and eqn (4) can be experimentally validated. For example, several authors have reported an exponential increase of Ntotal with an increase of Psat, when quenching to ambient pressure and the other processing variables are kept constant.8,13,20 In the present work, to vary Ntotal, we modulate Pnucl at constant Psat, instead of changing Psat. Specifically, for the sake of clarity, Pnucl varies from ambient pressure to any higher pressure. Fig. 2 reports the effect of the pressure reduction (Psat − Pnucl) on Ntotal at fixed Psat = 8.0 MPa, T = 180 °C and pressure drop rate of 500 MPa s−1. As expected in view of eqn (2)–(4), the adjustment of Pnucl in the present work proves to be an effective tool to control bubble nucleation and allows us to design the pressure treatment required to achieve the desired bubble morphology, as described in the following sections.
 | ||
| Fig. 2 Bubble number density vs. pressure reduction at a fixed Psat = 8.1 MPa. Scale bar is 1000 μm. | ||
3.2 Bubble growth manipulation
Following nucleation, the evolution of bubbles is driven by the pressure difference between the bubble pressure (Pbub) and P, as well as interfacial and viscoelastic forces. The multitude of nucleated bubbles, with a variety of sizes, relative distances, shape, and gas concentration profiles, creates a rich landscape of behaviors and phenomena that can be simultaneously observed and studied. For example, Fig. 3 provides a (partial) glimpse of the observable phenomena. In particular, we observed various growth regimes of isolated bubbles (a), Ostwald ripening (b), bubble coalescence (c), and bubble interaction causing shape changes (d). As reported in previous works which made use of visual observation apparata,9,11,14 the extent of bubble growth eventually (quite rapidly) leads to interactions and overlap among bubbles, in fact terminating the visual observation experiment. To avoid such a scenario and maintain a long-lasting bubble playground, it is sufficient to reduce bubble growth. As described in detail in the next section, increasing the pressure may serve this purpose.In Fig. 5 we can compare the effect of the inverse pressure quench treatment (Psat = 8.0 MPa, Pnucl = 2.8 MPa and Pinverse = 4.2 MPa – red curve and red-framed image in Fig. 5) with two pressure quench treatments (without the inverse pressure quench): one quenching from Psat = 8.0 MPa to Pnucl ≈ 0 MPa (black curve and black-framed image in Fig. 5) and one quenching from Psat = 8.0 MPa to Pnucl = 4.2 MPa (blue curve and blue-framed image in Fig. 5). For each pressure treatment, the bubble images at t = 20 s are reported. It is quite evident that the large pressure drop from 8.0 to 2.8 MPa (black) is responsible for the nucleation of a large number of bubbles and their rapid overlap due to growth, impeding long-term growth study. Reduction of pressure quench from 8.0 to 4.2 MPa (blue) induces the nucleation of a small number of bubbles, too small to get a wide perspective of the different growing behavior and coupled phenomena. Instead, the pressure quench treatment allows the formation of a large number of bubbles (comparable to the case of the 8.0 to 2.8 MPa drop – black) but the subsequent pressure increase impedes the bubbles overlapping and allows long-term growth monitoring. The value of inverse pressure quench treatment emerges with the use of two additional examples (Fig. 6). In a first example, to study a system with virtually all isolated bubbles, we can induce the nucleation of a small number density of bubbles (see Section 3.1) and then use the inverse pressure quenching treatment to keep them small so that the average inter-bubble distance is larger than the bubble radius (Fig. 6a). Fig. 6b reports the temporal evolution of R for 3000 s. To the best of our knowledge, this is the first reported experiment in which bubble growth in polymeric foaming is observed for so long, allowing for a thorough study of the growth phenomena.
In a second example, to study a system with interacting bubbles, we can induce the nucleation of a larger number density of bubbles, and then use the inverse pressure quenching treatment to prevent bubbles overlapping in the image. In this case, a long-lasting bubble observation (Fig. 6c), allows the study of the mechanical interaction (leading to impingement, shape variation, Ostwald ripening or coalescence, as will be detailed in the following (Fig. 6d)).
While in the first example (Fig. 6a and b), the undisturbed growth of bubbles with a relatively narrow size distribution can be monitored for hours, in the second example (Fig. 6c and d), the wealth of different observable phenomena is evident: coalescence (underlined by the presence of peaks in the curves, as in Fig. 3c), Ostwald ripening (underlined by the presence of monotonically decreasing curves – as in Fig. 3b), as well as growth and shape change, all concurrently occur.
In fact, the inverse pressure quench technique proves to be an effective tool for decoupling nucleation from growth, for regulating the average value of R, and for preventing bubbles from overlapping. This allows us to study growth and to interrogate and validate the growth, impingement, ripening, and coalescence models. Finally, we foresee the use of such an experimental platform for the characterization of the properties of the polymer/gas system relevant to foaming and to derive constitutive models.
Several models have been proposed in the literature to describe the dynamics of bubble growth in the case of isolated as well as of multiple bubbles.6,13,22–25 In order to support our experimental evidence and help the discussion, it is worth describing a simplified model that fits our case. The experimentally observed characteristic growth time is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102 s), while the relaxation time of the polymer is
(102 s), while the relaxation time of the polymer is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (100 s) (see ESI†). We may hence neglect the elastic contribution of the polymer response to deformation. The characteristic strain rate can be experimentally evaluated as Ṙ/R =
(100 s) (see ESI†). We may hence neglect the elastic contribution of the polymer response to deformation. The characteristic strain rate can be experimentally evaluated as Ṙ/R = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−2 s−1) and, based on the flow curve reported in the ESI,† we can assume Newtonian behavior, with viscosity η = 104 Pa s. Finally, inertial forces Fi = 4πρR2Ṙ2 are negligible with respect to the others. From the momentum balance, in a spherical coordinate system with the origin in the center of the bubble, the one-dimensional ordinary differential equation describing the evolution of R reads:
(10−2 s−1) and, based on the flow curve reported in the ESI,† we can assume Newtonian behavior, with viscosity η = 104 Pa s. Finally, inertial forces Fi = 4πρR2Ṙ2 are negligible with respect to the others. From the momentum balance, in a spherical coordinate system with the origin in the center of the bubble, the one-dimensional ordinary differential equation describing the evolution of R reads:
 | (5) |
 | (6) |
 | (7) |
This model assumes the initial bubble radius (R0) as the hypothetical radius of a stable nucleus.13,25,26 The experimental validation of this assumption is not trivial, as is the measurement of the radius of a gas nucleus. After applying the inverse pressure quench treatment, we are able to stabilize the growing bubble radius over time by keeping the system at constant pressure Pinverse (Fig. 6a and b). Starting from this point, we can manipulate the bubble dynamics by modulating P. In this way, we can study the growth dynamics decoupled from the nucleation.
An example is shown in Fig. 7, in which the effect of the modulation of P on the bubble dynamics is reported. The graph reports the value of R over time for a bubble R0 ≈ 160 μm, previously stabilized using the inverse pressure quench technique (see Section 3.2.1). By decreasing the pressure from Pinverse to Pdown, R increases accordingly. After P reaches the set value, the bubble growth proceeds. Furthermore, increasing the pressure from Pdown to Pup, R decreases, following similar, although mirrored dynamics.
The observation of bubble growth dynamics over a long period unveils a rather unexpected behavior. After the pressure variation, R evolves towards a stable value in a non-monotonic way, going through a maximum or minimum value depending on the pressure change sign (negative or positive, respectively). More studies are required to investigate this phenomenon, not excluding the effects of multiple-bubble interaction. Finally, the possibility of manipulating the growth rate and thus the deformation rate of the polymer/gas solution surrounding the bubbles is considered with the aim of exploiting the treatment for measuring the physical properties of the polymer/gas solution involved in the growth dynamics, listed in eqn (5)–(7), as proposed in the work of Garbin and colleagues.3,27 For example, Fig. 8 shows the effect of the pressure variation rate on the bubble growth dynamics, for treatments where the pressure is reduced at various rates, from 0.002 MPa s−1 to 5.0 MPa s−1. Here, R is normalized with the plateau value of R long after the pressure variation (Rst). Specific studies devoted to the implementation of the proposed treatment for the characterization of the polymer/gas solution are required, which is outside the experimental and theoretic scope of the present work.
On the other hand, the effect of Ostwald ripening can be analyzed by observing the evolution of each single bubble within the system, as shown in Fig. 6d. The curves with a negative slope are related to dissolving bubbles, which eventually disappear. A quantitative analysis of the dissolution of smaller bubbles can be performed based on the data reported in Fig. 9, which shows the evolution of R over time for the small, dissolving bubbles. Epstein and Plesset37 derived an analytical expression for the diffusion-controlled dissolution of a single isolated air bubble in water, considering the effect of interfacial tension on the internal pressure of the bubble. The model has been later validated both on water-based systems38,39 and on molten polymer-based systems40 and describes the evolution of R as follows:
| R(t)3 − R03 + A(R(t)2 − R02) = Bt, | (8) |
 | (9) |
 | (10) |
 | ||
| Fig. 9 Bubble dynamics of dissolving bubbles. Experimental data and results of fitting with the Epstein and Plesset model.37,38 The experimental data are referred to the dissolution curves of Fig. 6. | ||
In eqn (9) and (10), ρg is the density of the gas, Mw is the molar mass of the polymeric matrix, and kH is Henry's constant. A and B can be evaluated by fitting the experimental data and the averaged results of the fitting procedure are reported in Table 1 along with values predicted using literature data for the parameter in eqn (9) and (10) (ρg = 101 kg m−3, Mw = 102 kg mol−1, T = 180 °C, γ = 10−2 N m−1, D = 10−9 m2 s−1, kH = 10−4 mol N−1 m−1).41–43 While A shows a good agreement with the predicted value, we note a large discrepancy for B, probably indicating a delay in the observed dissolution dynamics with respect to predictions. To further analyse the problem, we examine the dissolution time, td, which can be derived by the Epstein–Plesset model38 as follows:
 | (11) |
Using data from the literature, td ≈ 101 s, which is much smaller than the experimental value (![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (103 s)). This delay in the dissolution time has been reported in the literature, in particular with reference to multiple bubble systems, and is attributed to the so-called diffusive shielding, by which a bubble dissolves slower than an equivalent isolated one, due to the increase in local gas concentration caused by dissolution of neighboring bubbles.44,45 The interplay between Ostwald ripening and diffusive shielding can lead to delayed dissolution or even stabilize a bubble to an equilibrium radius, as reported by Weijs et al.46 The use of a more complex model with respect to the isolated bubble model is in order and is left for future work. Here, we demonstrate the use of the proposed treatment as a novel experimental platform to study the dynamics of bubble dissolution and, more generally, the physics of bubble interaction.
(103 s)). This delay in the dissolution time has been reported in the literature, in particular with reference to multiple bubble systems, and is attributed to the so-called diffusive shielding, by which a bubble dissolves slower than an equivalent isolated one, due to the increase in local gas concentration caused by dissolution of neighboring bubbles.44,45 The interplay between Ostwald ripening and diffusive shielding can lead to delayed dissolution or even stabilize a bubble to an equilibrium radius, as reported by Weijs et al.46 The use of a more complex model with respect to the isolated bubble model is in order and is left for future work. Here, we demonstrate the use of the proposed treatment as a novel experimental platform to study the dynamics of bubble dissolution and, more generally, the physics of bubble interaction.
In the simple case of two impinging bubbles of almost the same size in which the viscoelastic effects are negligible, the thin film is flat (Fig. 10a). The polymer/gas solution is squeezed out of the thin film, pushed by capillary pressure, and undergoes a biaxial elongation.49 When the strain rates are higher and the viscoelastic effects are relevant, the thin film assumes a parabolic shape, extending into one of the bubbles, before rupture occurs (Fig. 10b). In this study, even higher deformation rates are observed and novel coalescence patterns are observed, in which the thin film is highly elongated inside one of the who bubbles (Fig. 10c). Additional research is required to elucidate the physics that govern these new patterns.
 | ||
| Fig. 10 Observed coalescence patterns. The shape of the thin film between the bubbles can be: (a) flat; (b) parabolic; (c) elongated inside one of the two bubbles. Scale bar is 500 μm. | ||
Once the two bubbles establish contact, the film rupture occurs and a ring-shaped neck is formed.50 First, this expands rapidly, due to the relaxation of the elastic energy built up during bubble expansion.51 Then, the high curvature of the neck leads to the generation of a considerable capillary pressure, which, at this point, drives the neck expansion against inertial and viscous forces. The resulting expansion progresses with the following scaling law:52–54
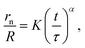 | (12) |
 .
.
Fig. 11 reports characteristic images of the coalescence of two bubbles of almost the same size in the case of the PP/N2 system, at a temperature of 180 °C and a pressure of 4.0 MPa. Fig. 11 also reports, for several couples of coalescing bubbles, the normalized neck radius rn/R, against the dimensionless time t/τ, where τ = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102 s) is the visco-capillary time (with Oh =
(102 s) is the visco-capillary time (with Oh = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (105)). Data for each coalescence event follow the power law with an exponent α ≈ 1, for the t/τ < 0.2, decreasing to 1/4 for longer times, which is similar to what was reported in the literature. In particular, the evolution of the neck in water-based systems has been observed to follow a power law with an exponent α ≈ 1/2 for t/τ < 0.2, after which the exponent decreases.52,54 In viscous liquid systems, the evolution of the neck is significantly slower but follows the same dynamics, with α ≈ 1/2.53
(105)). Data for each coalescence event follow the power law with an exponent α ≈ 1, for the t/τ < 0.2, decreasing to 1/4 for longer times, which is similar to what was reported in the literature. In particular, the evolution of the neck in water-based systems has been observed to follow a power law with an exponent α ≈ 1/2 for t/τ < 0.2, after which the exponent decreases.52,54 In viscous liquid systems, the evolution of the neck is significantly slower but follows the same dynamics, with α ≈ 1/2.53
 | ||
| Fig. 11 Coalescence of two bubbles of almost the same size in a PP/N2 system, at P = 4.0 MPa. Evolution of the normalized neck radius (rn/R) against the dimensionless time (t/τ). | ||
The analysis of the coalescence patterns, together with the evolution of the neck, represents a powerful experimental platform to characterize the system, as it involves both interfacial tension and viscoelastic properties of the polymer/gas solution. In this framework, control over the occurrence and velocity of coalescence, triggered by the growth stage, is crucial.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102 s) (see Section 3.2.4), when major shape change occurs. When the curvature approaches 1/R the driving force for the shape variation is no longer related to the capillary effect, slowing the kinetics.53 A detailed description of the corresponding dynamics and the relative descriptive model is left for future work.
(102 s) (see Section 3.2.4), when major shape change occurs. When the curvature approaches 1/R the driving force for the shape variation is no longer related to the capillary effect, slowing the kinetics.53 A detailed description of the corresponding dynamics and the relative descriptive model is left for future work.
3.3 Periodic treatment
Controlling the dynamics of bubble growth by applying a given pressure treatment can be used to tailor the morphology of a multi-bubble system. We demonstrated in the previous sections that we can control the amount of nucleated bubbles and their final radius by modulating the pressure. We will now show how to modulate the bubble relative position towards a total control of the foam features. Here, we exploit polymer viscoelasticity and apply periodic pressure treatments to determine non-reversible movements (in terms of d) among the bubbles. Two impinging bubbles are subjected to forces which are normal to the plane that separates them (or parallel to d). In particular, when they grow, they are pushed more far apart (d increases), and when they shrink, they are brought closer. Any imbalance may induce a permanent change in d, in principle at constant R. To do so, we imposed a negative pressure change ≈1 MPa within a characteristic time![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102 s ≫ τ) and a positive pressure change with an identical absolute value but within a characteristic time
(102 s ≫ τ) and a positive pressure change with an identical absolute value but within a characteristic time ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (100 s ≈ τ). The presence of the elastic contribution of the polymer response in only one of the two stages gives the desired imbalance. As expected in a viscous polymer/gas system under typical processing conditions, the change in d is small. However, repeating the sequence may induce an arbitrarily large movement. Fig. 12a shows the temporal evolution of P, R and d in a treatment with 30 cycles, inducing a bubble movement depicted in Fig. 12b, with the largest net increase in the distance between bubbles ≈70 μm.
(100 s ≈ τ). The presence of the elastic contribution of the polymer response in only one of the two stages gives the desired imbalance. As expected in a viscous polymer/gas system under typical processing conditions, the change in d is small. However, repeating the sequence may induce an arbitrarily large movement. Fig. 12a shows the temporal evolution of P, R and d in a treatment with 30 cycles, inducing a bubble movement depicted in Fig. 12b, with the largest net increase in the distance between bubbles ≈70 μm.
4 Conclusions
We introduced the inverse pressure quench treatment on nucleated polymer/gas systems to manipulate bubble growth dynamics. This allows for broadening the observation window and thoroughly investigating the numerous phenomena and material properties related to bubble growth. By focusing on the model system PP/N2, we reported using of the treatment to decouple bubble nucleation and growth, towards the design of foams with a defined number density and size of bubbles. Furthermore, the treatment proved suitable for studying bubble impingement, Ostwald ripening, and bubble coalescence. We foresee using of the same to measure the physical properties of polymer/gas systems, as we showed for the variables utilised in the Epstein and Plesset model for the diffusion-controlled dissolution of isolated bubbles. Finally, by using a periodic pressure treatment, we show that it is possible to move the bubbles and design their relative position, towards total control of all the foam features, opening novel opportunities for the design of foam processing technologies. This approach could be further explored for industrial applications, such as large-scale production of porous membranes for separation processes, scaffolds for tissue engineering, as well as thermal insulators and electrodes. Finally, to build on the findings of this study, future research could explore the exciting overshoot (undershoot) observed after a pressure step decrease (increase) (see Fig. 7).Author contributions
LM: writing – review & editing, writing – original draft, validation, methodology, investigation, formal analysis, data curation, conceptualization. AA: review & editing, writing, supervision. KT: writing – review & editing, writing – original draft, supervision, formal analysis, resources. EDM: writing – review & editing, writing – original draft, supervision, investigation, formal analysis, conceptualization. All authors commit to equity and inclusion for all races, genders, age, religion, identity, and experience.Data availability
The data that support the findings of this study are available online on figshare (https://doi.org/10.6084/m9.figshare.26535577.v2).Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this document.References
- S. Deotale, S. Dutta, J. Moses, V. Balasubramaniam and C. Anandharamakrishnan, Food Eng. Rev., 2020, 12, 229–250 CrossRef.
- G. Wu, P. Xie, H. Yang, K. Dang, Y. Xu, M. Sain, L.-S. Turng and W. Yang, J. Mater. Sci., 2021, 56, 11579–11604 CrossRef CAS.
- B. Dollet, P. Marmottant and V. Garbin, Annu. Rev. Fluid Mech., 2019, 51, 331–355 CrossRef.
- A. Arefmanesh and S. Advani, Rheol. Acta, 1991, 30, 274–283 CrossRef CAS.
- E. Di Maio, S. Iannace and G. Mensitieri, Foaming with Supercritical Fluids, Elsevier, 2021 Search PubMed.
- C. D. Han and H. J. Yoo, Polym. Eng. Sci., 1981, 21, 518–533 CrossRef.
- M. Shimoda, I. Tsujimura, M. Tanigaki and M. Ohshima, J. Cell. Plast., 2001, 37, 517–536 CrossRef CAS.
- J. Yang, T. Jiang, B. Liu, C. Zhang, X. Zeng, L. He and W. Gong, Mater. Des., 2021, 203, 109577 CrossRef CAS.
- K. Taki, T. Nakayama, T. Yatsuzuka and M. Ohshima, J. Cell. Plast., 2003, 39, 155–169 CrossRef CAS.
- Q. Guo, J. Wang, C. B. Park and M. Ohshima, Ind. Eng. Chem. Res., 2006, 45, 6153–6161 CrossRef CAS.
- K. Taki, K. Tabata, S.-I. Kihara and M. Ohshima, Polym. Eng. Sci., 2006, 46, 680–690 CrossRef CAS.
- S. N. Leung, A. Wong, L. C. Wang and C. B. Park, J. Supercrit. Fluids, 2012, 63, 187–198 CrossRef CAS.
- K. Taki, Chem. Eng. Sci., 2008, 63, 3643–3653 CrossRef CAS.
- S. N. Leung, C. B. Park, D. Xu, H. Li and R. G. Fenton, Ind. Eng. Chem. Res., 2006, 45, 7823–7831 CrossRef CAS.
- K. Taki, M. Menale, G. Pisante and E. Di Maio, J. Appl. Polym. Sci., 2022, 139, e53121 CrossRef CAS.
- S. Acierno and N. Grizzuti, J. Rheol., 2003, 47, 563–576 CrossRef CAS.
- T. Ishikawa, K. Taki and M. Ohshima, Polym. Eng. Sci., 2012, 52, 875–883 CrossRef CAS.
- R. WS, 2011, https://imagej.nih.gov/ij/.
- V. Talanquer and D. W. Oxtoby, J. Chem. Phys., 1995, 102, 2156–2164 CrossRef CAS.
- S. K. Goel and E. J. Beckman, Polym. Eng. Sci., 1994, 34, 1137–1147 CrossRef CAS.
- I. Tsivintzelis, A. G. Angelopoulou and C. Panayiotou, Polymer, 2007, 48, 5928–5939 CrossRef CAS.
- D. E. Rosner and M. Epstein, Chem. Eng. Sci., 1972, 27, 69–88 CrossRef CAS.
- N. Ramesh, D. H. Rasmussen and G. A. Campbell, Polym. Eng. Sci., 1991, 31, 1657–1664 CrossRef CAS.
- D. C. Venerus, N. Yala and B. Bernstein, J. Non-Newtonian Fluid Mech., 1998, 75, 55–75 CrossRef CAS.
- M. Shafi and R. Flumerfelt, Chem. Eng. Sci., 1997, 52, 627–633 CrossRef CAS.
- J. J. Feng and C. A. Bertelo, J. Rheol., 2004, 48, 439–462 CrossRef CAS.
- B. Saint-Michel and V. Garbin, Curr. Opin. Colloid Interface Sci., 2020, 50, 101392 CrossRef CAS.
- P. Taylor, Adv. Colloid Interface Sci., 1998, 75, 107–163 CrossRef CAS.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- C. Wagner, Z. Elektrochem. Ber. Bunsenges. Phys. Chem., 1961, 65, 581–591 CrossRef CAS.
- P. W. Voorhees, J. Stat. Phys., 1985, 38, 231–252 CrossRef.
- B. L. Cushing, V. L. Kolesnichenko and C. J. O’connor, Chem. Rev., 2004, 104, 3893–3946 CrossRef CAS PubMed.
- R. Lemlich, Ind. Eng. Chem. Fundam., 1978, 17, 89–93 CrossRef CAS.
- R. I. Saye and J. A. Sethian, Science, 2013, 340, 720–724 CrossRef CAS PubMed.
- R. D. MacPherson and D. J. Srolovitz, Nature, 2007, 446, 1053–1055 CrossRef CAS PubMed.
- J. A. Glazier and D. Weaire, J. Phys.: Condens. Matter, 1992, 4, 1867 CrossRef.
- P. S. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505–1509 CrossRef CAS.
- P. B. Duncan and D. Needham, Langmuir, 2004, 20, 2567–2578 CrossRef CAS PubMed.
- V. Poulichet and V. Garbin, Langmuir, 2015, 31, 12035–12042 CrossRef CAS PubMed.
- M. Kontopoulou and J. Vlachopoulos, Polym. Eng. Sci., 1999, 39, 1189–1198 CrossRef CAS.
- Y. Sun, Y. Ueda, H. Suganaga, M. Haruki, S.-I. Kihara and S. Takishima, J. Supercrit. Fluids, 2015, 103, 38–47 CrossRef CAS.
- P. L. Durrill and R. G. Griskey, AIChE J., 1966, 12, 1147–1151 CrossRef CAS.
- G. Li, F. Gunkel, J. Wang, C. Park and V. Altstädt, J. Appl. Polym. Sci., 2007, 103, 2945–2953 CrossRef CAS.
- G. Laghezza, E. Dietrich, J. M. Yeomans, R. Ledesma-Aguilar, E. S. Kooij, H. J. Zandvliet and D. Lohse, Soft Matter, 2016, 12, 5787–5796 RSC.
- S. Michelin, E. Guérin and E. Lauga, Phys. Rev. Fluids, 2018, 3, 043601 CrossRef.
- J. H. Weijs, J. R. Seddon and D. Lohse, ChemPhysChem, 2012, 13, 2197–2204 CrossRef CAS PubMed.
- C. Hill and J. Eastoe, Adv. Colloid Interface Sci., 2017, 247, 496–513 CrossRef CAS PubMed.
- Y. Ge, J. Lu and T. Liu, AIChE J., 2020, 66, e16862 CrossRef CAS.
- M. Borrell and L. G. Leal, J. Colloid Interface Sci., 2008, 319, 263–269 CrossRef CAS PubMed.
- D. Langevin, Curr. Opin. Colloid Interface Sci., 2019, 44, 23–31 CrossRef CAS.
- D. Tammaro, R. Pasquino, M. M. Villone, G. DAvino, V. Ferraro, E. Di Maio, A. Langella, N. Grizzuti and P. L. Maffettone, Langmuir, 2018, 34, 5646–5654 CrossRef CAS PubMed.
- C. R. Anthony, P. M. Kamat, S. S. Thete, J. P. Munro, J. R. Lister, M. T. Harris and O. A. Basaran, Phys. Rev. Fluids, 2017, 2, 083601 CrossRef.
- A. T. Oratis, V. Bertin and J. H. Snoeijer, Phys. Rev. Fluids, 2023, 8, 083603 CrossRef.
- Á. M. Soto, T. Maddalena, A. Fraters, D. Van Der Meer and D. Lohse, J. Fluid Mech., 2018, 846, 143–165 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01040j |
| This journal is © The Royal Society of Chemistry 2024 |







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm3 s−1 (ref.
000 μm3 s−1 (ref. 