Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CO2-induced drastic decharging of dielectric surfaces in aqueous suspensions†
Peter
Vogel
 *a,
David
Beyer
*a,
David
Beyer
 b,
Christian
Holm
b,
Christian
Holm
 b and
Thomas
Palberg
b and
Thomas
Palberg
 a
a
aInstitute of Physics, Johannes Gutenberg University, 55128 Mainz, Germany. E-mail: petvogel@uni-mainz.de
bInstitut für Computerphysik (ICP), Universität Stuttgart, 70569 Stuttgart, Germany
First published on 15th November 2024
Abstract
We study the influence of airborne CO2 on the charge state of carboxylate stabilized polymer latex particles suspended in aqueous electrolytes. We combine conductometric experiments interpreted in terms of Hessinger's conductivity model with Poisson–Boltzmann cell (PBC) model calculations with charge regulation boundary conditions. Without CO2, a minority of the weakly acidic surface groups are dissociated and only a fraction of the total number of counter-ions actually contribute to conductivity. The remaining counter-ions exchange freely with added other ions like Na+, K+ or Cs+. From the PBC-calculations we infer a corresponding pKa of 4.26 as well as a renormalized charge in reasonably good agreement with the number of freely mobile counter-ions. Equilibration of salt- and CO2-free suspensions against ambient air leads to a drastic de-charging, which exceeds by far the expected effects of to dissolved CO2 and its dissociation products. Further, no counter-ion-exchange is observed. To reproduce the experimental findings, we have to assume an effective pKa of 6.48. This direct influence of CO2 on the state of surface group dissociation explains our recent finding of a CO2-induced decrease of the ζ-potential and supports the suggestion of an additional charge regulation caused by molecular CO2. Given the importance of charged surfaces in contact with aqueous electrolytes, we anticipate that our observations bear substantial theoretical challenges and important implications for applications ranging from desalination to bio-membranes.
1. Introduction
Dielectric surfaces in contact with aqueous electrolytes may charge up by dissociation of ionogenic surface groups or by adsorption of ions, and develop an electric double layer (EDL) by counterion accumulation.1 Due to pH-driven charge regulation,2 this process depends on the surface chemistry and the pH of the adjacent electrolyte solution.3–5 Further, the type of added electrolytes and its concentration influence the charge state.6–9 In addition, it varies with the degree of double layer overlap between suspended dielectric particles.10–13 Constituting a many-body soft matter system, the charging process and the structure of the EDL are of fundamental interest but at the same time are quite complex.1,2 Approaches on different levels of sophistication have been developed for theoretical calculations of the charge state of dielectric surfaces14–22 as well as for the determination of electro-kinetic properties and their interpretation.23–32 Moreover, charging bears important implications for the functioning of dielectric surfaces in many contexts ranging from biology over climate physics to waste water treatment.33–37A particularly interesting class of potentially charge-regulating additives are dissolved molecular gases like O2, N2 and CO2. These are inevitably present in any system allowed to have contact with ambient air38,39 including standard doubly distilled water or dialyzed systems, but can be efficiently removed by degassing. Molecular gases may adsorb reversibly on dielectric surfaces,40,41 alter the surface structure,42 and influence the colloid stability.43,44 Unlike its inert counterparts, CO2 partially dissociates to form carbonic acid,38,39,45 which in turn provides additional screening electrolyte and shifts the pH.46 Increasing the electrolyte content affects double layer extension leading to a drop in the Debye screening length. At the same time, a decrease in bulk pH affects the charge state by a shift in the surface group dissociation equilibrium47–49 thus resulting in altered suspension properties.50,51 It therefore is paramount to work at well-defined CO2-concentrations,52e.g., by initial selective CO2-removal via exhaustive ion exchange in air-tight vessels or closed conditioning circuits and subsequent addition via contact with ambient air.23,53,54
Recently, we performed electrophoretic experiments at constant background concentrations of the inert gases but various concentrations of molecular CO2.55 There, we found the effects of molecular CO2 on the charge state of dielectric surfaces to go way beyond the expected effects of screening and pH-variation.10,47,48,56 In particular, upon equilibration in contact with ambient air, the magnitudes of the electrokinetic ζ-potential dropped significantly. The process could be driven even further towards full decharging by equilibrating the suspension against pure CO2-atmospheres.57 Accompanying MD simulations revealed the formation of a thin, diffuse layer of molecular CO2 very close to the surface for both hydrophobic and hydrophilic dielectric materials. From that, we proposed dielectric charge regulation as the underlying mechanism:55 the presence of CO2 lowers the local dielectric constant and thus enhances the electrostatic interaction at and/or between dissociated surface groups. The corresponding Coulomb-energy causes an increase of the dissociation energy and/or introduces an energetic penalty for closely spaced surface groups. In effect this leads to a decrease of the ζ-potential. However, no direct information on the degree of dissociation, the bare charge, the effective charge or the surface chemistry is obtained from electrophoretic experiments.
The present study therefore complements our previous investigations by a comprehensive conductometric charge characterization as well as by Poisson–Boltzmann cell (PBC) model calculations with charge regulation boundary conditions. As a model system, we use negatively charged polystyrene particles of low size dispersity carrying ionizable carboxylate groups from synthesis. Specifically, we perform conductivity experiments in dependence on different variables, like number density, n, or type and concentration c of added 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte (NaCl, HCl, NaOH). Our results are interpreted within Hessinger's model of independent ion migration.58 The model gives access to three complementary charge numbers: the number of ionogenic surface groups N, the bare charge, Z, and the number of freely mobile counter-ions, i.e., the effective conductivity charge Zσ. It successfully described the density and temperature dependent conductivity of deionized and decarbonized suspensions,59 it applies to single component suspensions as well as mixtures thereof.54 While a rigorous theoretical description of the relation between different effective charges is still under discussion60–62 experimentally determined effective conductivity charges generally agree rather well with effective electrokinetic charges and with renormalized charges, at least as long highly charged particles in 1
1 electrolyte (NaCl, HCl, NaOH). Our results are interpreted within Hessinger's model of independent ion migration.58 The model gives access to three complementary charge numbers: the number of ionogenic surface groups N, the bare charge, Z, and the number of freely mobile counter-ions, i.e., the effective conductivity charge Zσ. It successfully described the density and temperature dependent conductivity of deionized and decarbonized suspensions,59 it applies to single component suspensions as well as mixtures thereof.54 While a rigorous theoretical description of the relation between different effective charges is still under discussion60–62 experimentally determined effective conductivity charges generally agree rather well with effective electrokinetic charges and with renormalized charges, at least as long highly charged particles in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes are considered.8,25
1 electrolytes are considered.8,25
We compare experiments in the absence and presence of CO2 to isolate and discuss the effects of carbonization. We show that the presence of CO2 has significant quantitative and even qualitative effects on the resulting density- and concentration-dependent conductivities which go way beyond the effects expected for dissolved CO2 and its dissociation products. Next to an overall CO2-induced decharging, manifest via decreased bare and effective charges, we observe the absence of ion-exchange between the immobile and mobile EDL populations. This unexpected finding is shown by the PBC-calculations to relate to a significant increase of the effective surface group pKa. Our results therefore confirm and extend the results of our previous electrophoretic experiments in several ways. We anticipate that our findings will stir further theoretical interest in the structure and properties of the EDL at charged dielectric surfaces under ambient conditions and may contribute to a fundamentally improved understanding of the resulting performance of dielectric surfaces.
In what follows, we first shortly introduce the experimental system and our conditioning procedure techniques before describing the actual conductivity measurements and recalling Hessinger's conductivity model. The results section shows the obtained conductivities and interprets these in terms of characteristic charge numbers. We rationalize our findings using complementary Poisson–Boltzmann cell model calculations. We then discuss our findings in relation to the recently proposed decharging of dielectric surfaces by adsorbed molecular CO2. We conclude with a short outlook on further experiments and some practical consequences of our results.
2. Materials and sample preparation
We used spherical copolymer particles synthesized by radical emulsion-polymerization from 60% w/w butylacrylamide, 38% w/w styrene, 2% w/w acrylic acid, and 0.5% w/w sodium-peroxodisulfate, kindly provided by BASF, Ludwigshafen (Lab code PNBAPS359, manufacturer batch number 2168/7390). Their diameter of 2a = 359 nm was determined by the manufacturer using analytical ultracentrifugation. Stock suspensions of particle number densities n ≈ 1 × 1018 m−3 were prepared by dilution with deionized (DI) water. Subsequently, mixed-bed ion exchange resin (IEX) (Amberjet, Carl Roth GmbH + Co. KG, Karlsruhe, Germany) was added and the suspensions were left to stand under occasional stirring for some weeks. They were then coarsely filtered using Sartorius 5 μm syringe-driven membrane filters to remove dust, ion-exchange debris, and coagulate regularly occurring upon first contact with IEX. All further sample preparation/conditioning steps including the conductivity measurements were performed in a peristaltically driven circuit described in detail elsewhere.54Briefly, appropriately diluted stock suspensions were loaded into the circuit under filtering with Sartorius 1.2 μm and 0.8 μm filters. Then, the suspension is pumped through the air-tight tubings connecting (i) the IEX filled ion exchange chamber, (ii) a reservoir under inert gas atmosphere (Ar) to add suspension, water, or electrolyte solutions, (iii) the conductivity measurement cell and (iv) a rectangular quartz-cell (5 mm × 10 mm) for turbidity measurements52 for in situ control of the number density, n = 3Φ/(4πa3), respectively the particle volume fraction, Φ.
3. Conductivity experiments
Bulk conductivities, σ, were measured at a frequency of ω = 400 Hz (electrodes LTA01 and LR325/01 with bridge LF538 or electrode LR325/001 with bridge LF340, WTW, Germany). This frequency is low enough to stay in the DC-limit, but large enough to avoid electrode polarization effects.For measurements starting from the thoroughly deionized and decarbonized reference state, the sample is cycled until after about an hour a stable minimum conductivity is reached. Control experiments with pure water yield a background conductivity of σB = (55–60) nS cm−1 due to auto-dissociation of water. For experiments in presence of CO2, thoroughly deionized and decarbonized suspensions are brought into contact with ambient air by opening the reservoir while cycling under bypass of the IEX column. After about half an hour, the CO2 dissolving and dissociation reactions have equilibrated increasing σB by the amount of carbonic acid present in solution. In the electrolyte concentration dependent measurements, starting from either state, the IEX column was bypassed and electrolyte solution (Titrisol 0.1 mol L−1 NaCl, HCl or NaOH, Merck, Germany) was added in small quantities under conductometric control.
Measured conductivities are interpreted using Hessinger's conductivity model and reported in terms of charge numbers. This model approximates the radial dependence of micro-ionic diffusivities12 by considering a bimodal distribution of either zero or bulk mobility for the counter-ions. The composition of both fractions is assumed to be identical. Assuming Drude-type conductivity, the model sums over the conductivity contributions of all ionic species i:
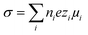 | (1) |
Here, e is the elementary charge, ni is the number density, μi the mobility, and zi the valency of any species, respectively. Note that the sum includes the contributions of particles, counter-ions, ions from water auto-protolysis, added (and reacted) electrolyte ions as well as the dissociation products of CO2. The respective micro-ionic mobilities μi are taken from literature,63 while the particle mobilities μP are determined in independent experiments.52 To be specific, we consider a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte at T = 298.15 K, where the valence is zi = 1, and the number density of each micro-ionic species is ni = ci1000NA, with ci being the electrolyte molar concentration. At ambient conditions, the saturation concentration of ambient CO2 dissolved in water amounts to cCO2 = 1.18 × 10−5 mol L−1 (nCO2 = 7.1 × 1021 m−3). Due to partial dissociation of its reaction product carbonic acid, cHCO3− = cH+ = 3.16 μmol L−1, and we have pH = 5.5.46 Further, at 298.15 K, the bulk mobilities of particles, H+, OH−, CO3H−, Na+, and Cl− are μP ≈ (2–5) × 10−8 m2 s−1 V−1,52μH+ = 36.23 × 10−8 m2 s−1 V−1, μOH− = 20.52 × 10−8 m2 s−1 V−1, μHCO3− = 4.61 × 10−8 m2 s−1 V−1, μNa+ = 5.19 × 10−8 m2 s−1 V−1, and μCl− = 7.91 × 10−8 m2 s−1 V−1, respectively.63
1 electrolyte at T = 298.15 K, where the valence is zi = 1, and the number density of each micro-ionic species is ni = ci1000NA, with ci being the electrolyte molar concentration. At ambient conditions, the saturation concentration of ambient CO2 dissolved in water amounts to cCO2 = 1.18 × 10−5 mol L−1 (nCO2 = 7.1 × 1021 m−3). Due to partial dissociation of its reaction product carbonic acid, cHCO3− = cH+ = 3.16 μmol L−1, and we have pH = 5.5.46 Further, at 298.15 K, the bulk mobilities of particles, H+, OH−, CO3H−, Na+, and Cl− are μP ≈ (2–5) × 10−8 m2 s−1 V−1,52μH+ = 36.23 × 10−8 m2 s−1 V−1, μOH− = 20.52 × 10−8 m2 s−1 V−1, μHCO3− = 4.61 × 10−8 m2 s−1 V−1, μNa+ = 5.19 × 10−8 m2 s−1 V−1, and μCl− = 7.91 × 10−8 m2 s−1 V−1, respectively.63
This yields a general expression to describe the conductivity of suspensions containing negatively charged particles with their counter-ions and additional non-reacting 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte:
1 electrolyte:
| σ = ne(μP + 〈μ+〉) + M(〈μ+〉 + 〈μ−〉) + σB | (2) |
Here, we used the arithmetic means of all cationic (+), respectively anionic (−) micro-ionic mobilities:
 | (3a) |
 | (3b) |
4. Experimental results
4.1 Particle number density dependent conductivities in the deionized state
Fig. 1 compares the particle number density dependence of the background-corrected conductivity of deionized suspensions in the decarbonized state and the CO2-equilibrated state. In both cases, we obtain a strictly linear dependence of the background corrected conductivity on the particle number density (dashed lines). However, in the presence of ambient CO2, we observed a significantly lower slope. For evaluation, we rewrite eqn (2) to read:| σ = σ0 + σB = neZσ(μP + μH+) + σB. | (4) |
 | ||
| Fig. 1 Density-dependent conductivity of deionized colloidal suspensions. Background-corrected conductivities as a function of number density n for the two representative states as indicated in the key. The upper scale shows the volume fraction, Φ = (4/3)πa3n with 2a = 359 nm being the particle diameter. The dashed lines are least squares fits of eqn (4) returning values of Zσ = (2.35 ± 0.04) × 103 and Zσ = (1.30 ± 0.07) × 103 for the CO2-free and the CO2-saturated cases, respectively. | ||
Least squares fits of eqn (4) to the data in Fig. 1 (dashed lines) yield Zσ = (2.35 ± 0.04) × 103 for the decarbonized and Zσ = (1.30 ± 0.07) × 103 for the CO2-saturated state. Where not indicated otherwise, quoted errors denote the standard error at a confidence level of 0.95. The corresponding diffuse layer charge-densities are: |σel| = (9.3 ± 0.1) × 10−2 μC cm−2 and |σel| = (5.1 ± 0.1) × 10−2 μC cm−2, respectively, where |σel| = Zσe/4πa2.37 We thus see a 45% reduction of the conductivity charge in the presence of CO2.
4.2 Conductivity titration with NaOH
Upon adding a reactive species like NaOH to thoroughly deionized and decarbonized suspensions, we observe the well-known non-monotonic conductivity dependence in Fig. 2a.3,5 Each background-corrected data set shows an initial, roughly linear descent. Past the minimum we observe a moderate, again roughly linear ascent, which steepens past the equivalence point. For increasing n, the minima shift upward and further to the right. In Fig. 2b, we replot the data versus M+. Now the minima are at the same salt concentration. From fits of linear functions to the middle and final parts we infer the total number of surface groups to be N = (134 ± 2) × 103. During the initial, n-dependent decrease of conductivity, only dissociated ions are exchanged. Eqn (2) reads: | (5) |
 | ||
| Fig. 2 CO2-free conductometric titration with NaOH. (a) Background-corrected conductivities in dependence on the concentration of added NaOH. Data are taken for different number densities as indicated in the key. (b) The same, now plotted in dependence on the number of cations added per particle. Dashed and dotted black lines denote fits of linear functions to the middle and final part of the curves, respectively. From their crossing point, we infer a total number of ionizable surface groups of NCO2H = (134 ± 2) × 103. The red solid lines are least squares fits of eqn (5) to the data. From these, we obtain an average value for the bare charge of Z = (10.4 ± 0.5) × 103. | ||
Here the mobility difference Δμ = μNa+ − μH+ has been introduced. The initial slope is dσ/dM+ = neΔμZσ/Z. With Zσ taken from the density dependent experiment at no added salt, fits of eqn (5) to the initial descent yield the charge ratio Zσ/Z, respectively the bare charge Z. From the fits shown in Fig. 2b as red solid lines, we obtain an average charge ratio of Zσ/Z = 0.23 (Fig. S1 in the ESI†) and an average value for the bare charge of Z = (10.4 ± 0.5) × 103.
4.3 Addition of non-reacting electrolyte
For the addition of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes to our suspensions of negatively charged colloidal spheres, we started from either a thoroughly deionized, salt and CO2-free, or from a thoroughly deionized state subsequently equilibrated against ambient air. Fig. 3 compares the background-corrected conductivities for different n upon addition of a simple strong acid (HCl) and a simple electrolyte (NaCl). For HCl, we observe a linear increase irrespective of the state of carbonization (Fig. 3a and b). For NaCl, the situation is qualitatively different in the absence and presence of CO2. In the decarbonized state (Fig. 3c), the curves initially show a steep increase. They then bend over and continue in a linear fashion at lesser slope. With increasing n, the cross-over region between the two characteristic slopes shifts towards higher c. In the presence of CO2, the dependence is again linear (Fig. 3d).
1 electrolytes to our suspensions of negatively charged colloidal spheres, we started from either a thoroughly deionized, salt and CO2-free, or from a thoroughly deionized state subsequently equilibrated against ambient air. Fig. 3 compares the background-corrected conductivities for different n upon addition of a simple strong acid (HCl) and a simple electrolyte (NaCl). For HCl, we observe a linear increase irrespective of the state of carbonization (Fig. 3a and b). For NaCl, the situation is qualitatively different in the absence and presence of CO2. In the decarbonized state (Fig. 3c), the curves initially show a steep increase. They then bend over and continue in a linear fashion at lesser slope. With increasing n, the cross-over region between the two characteristic slopes shifts towards higher c. In the presence of CO2, the dependence is again linear (Fig. 3d).
For each situation, the data collapse on single master curves, when scaled by the particle number density and plotted versus number of added cations per particle, M (Fig. S2 and S3 in the ESI†). To isolate the conductivity contribution of added electrolyte per particle, (σ − σ0 − σB)/n, data are additionally corrected for the particle contribution to conductivity, σ0 (Fig. S4 and S5 in the ESI†). In Fig. 4, we show the collapsed data for the addition of NaCl to CO2-free and to CO2-equilibrated suspensions. Fig. 4a and c focus on the initial stages of the titrations and emphasize the different shapes of the master curves. Without CO2, the addition of small amounts of NaCl yields a bent curve initially following the limiting conductivity contribution of HCl. At larger M, the curve straightens and runs parallel to the limiting conductivity contribution of NaCl. In the presence of CO2, we obtain a linear increase with a slope corresponding to the limiting conductivity contribution of NaCl. Fig. 4b and d highlight the collapse of data taken at different n over several orders of magnitude in salt concentration. In the absence of CO2 we see a well-defined transition between the two linear regimes with its turning point occurring around M ≈ 1 × 104.
 | ||
| Fig. 4 Conductivity contribution of added electrolytes per particle under ideal (no CO2) and environmental conditions (with CO2). The data are plotted in dependence on the number of Na+ added per particle, M. The red solid lines are least squares fits of eqn (6) to obtain the corresponding particle bare charge, Z, as indicated in the keys. For comparison, we also show the limiting conductivity contributions HCl (das-dotted) and NaCl (short dashed). (a) No CO2. The fit of eqn (6) returns Z = (9.92 ± 0.05) × 103, with the error denoting the standard error at a confidence level of 0.95. (b) Double logarithmic rendering of the same data. A transition between two linear regimes is observed at M ≈ 1 × 104. (c) and (d) With CO2. The fit of eqn (6) now returns Z = (1.34 ± 0.06) × 103. | ||
To describe the data quantitatively, we rewrite eqn (2) to read:
| (σ − σ0 − σB)/n = e(Zσ(〈μ+〉 − μH+) + M(〈μ+〉 + μCl−)) | (6) |
Note that with Zσ known from the previous experiment, the only free parameter in eqn (6) is the charge ratio Zσ/Z, respectively the bare charge Z entering via 〈μ+〉 (see also Fig. S8 of the ESI†). Fits of eqn (6) to the data use the conductivity charges Zσ = (2.35 ± 0.04) × 103 and Zσ = (1.30 ± 0.07) × 103 as input for the CO2-free and the CO2-saturated state, respectively. They return Z = (9.92 ± 0.05) × 103 and Z = (1.34 ± 0.06) × 103. In the absence of CO2, the derived bare charge is in good agreement with the result from the titrations with NaOH. However, the presence of CO2 reduces the bare charge to about 14% of its value under CO2-free conditions.
Within Hessinger's model, our results signify the exchange of low-mobility Na+ added to the mobile part of the EDL for highly mobile H+ stemming from the stagnant part of the EDL.58 Initially, practically all Na+ are exchanged for protons and the bulk conductivity increases strongly with a slope similar to the limiting conductivity contribution of HCl. The increase slows as the compositions in the mobile and stagnant parts of the EDL approach each other. After completion of the exchange, the slope is determined solely by the addition of NaCl to water. The situation is strikingly different in the CO2-saturated case. Here, any curve bending effect is practically absent. This signifies the absence of any ion exchange between the mobile and the immobile fractions of the micro-ionic population. This can be rationalized considering the here observed coincidence of Zσ and Z. The total number of freely mobile counter-ions coincides with the total number of counterions: practically all counter-ions are freely mobile at this low bare charge. The same behavior is seen for the addition of KCl and CsCl. This shows that the presence of exchange in the CO2-free state and its absence in the CO2-saturated state are well reproducible and independent of the type of cation used (Fig. S7 of the ESI†).
The absence of exchange seen in Fig. 4c and d is different to its non-observability upon the addition of HCl (cf. Fig. S4a, b and S6 of the ESI†). There, we have an identity of counter-ions and added cations. No change in average cation mobility occurs and thus no change of slope.
5. Charge renormalization of charge-regulating colloids – Poisson–Boltzmann theory
To rationalize our experimental observations, we utilize Poisson–Boltzmann theory. We employ the cell-model approximation66 to reduce the complicated many-body system of a colloidal solution to a computationally tractable problem. Thus, we consider a single spherical colloid of radius a, centered in a spherical cell of radius R = aΦ−1/3 that is overall electroneutral. For computational convenience, we couple the cell at its outside to a reservoir at a given pH-value. Note that the reservoir is a purely theoretical construct which has no analogue in the experimental setup. Due to the spherical symmetry, the problem reduces to a one-dimensional problem in the radial coordinate r ∈ [a, R]. In order to obtain the (reduced) electrostatic potential Ψ and the distribution of ions, we solve the Poisson–Boltzmann equation | (7) |
 is the inverse Debye length of the reservoir with λB = e2/(4πε0εrkBT) denoting the Bjerrum length. In the salt-free (apart from the autoionization) case considered here, n0 and thus κ0 is fully determined by the pH-value of the reservoir:
is the inverse Debye length of the reservoir with λB = e2/(4πε0εrkBT) denoting the Bjerrum length. In the salt-free (apart from the autoionization) case considered here, n0 and thus κ0 is fully determined by the pH-value of the reservoir:n0 = max(10−pHres,10−(14−pHres)) mol L−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NA. NA. | (8) |
The PB equation given in eqn (7) is a second-order ODE that has to be supplemented with two boundary conditions. At the cell boundary, the electric field has to vanish due to the overall electroneutrality, resulting in the Neumann boundary condition
| Ψ′(R) = 0. | (9) |
At the surface of the colloidal particle, the condition
 | (10) |
| Z = −Nα(pHsurface,pKa) = −Nα(pHres + log10(e)Ψ(a)pKa). | (11) |
Here, N is the total number of ionizable surface groups and α is the average degree of their ionization and e is Euler's number. The specific functional form of α depends on the employed model of charge regulation. In our calculations, we employ the Henderson–Hasselbalch equation
 | (12) |
We use the boundary value problem solver implemented in the open-source library SciPy.68 To solve the PB equation with the specified boundary conditions for a given value of pHres numerically, we use an iterative procedure, where the charge Z of the colloid is adjusted until self-consistency is achieved. Because the colloidal particle cannot leave the cell, there emerges a Donnan potential Ψ(R) between the reservoir and the cell, leading to a concentration difference of protons. In order to obtain the bare charge of the colloid for a desired bulk pH-value (which we identify with the local pH-value at the cell boundary, pHbulk = pHres + Ψ(R)log10(e)) we solve the PB equation for a range of reservoir pH-values, calculate the bulk pH for each of them and linearly interpolate the result to the desired bulk pH-value. Similarly, we obtain the renormalized/effective charge of the colloid, which we calculate from our numerical solution using the analytical prescription of Trizac et al.17 Note that there exist several distinct charge renormalization schemes, which result in slightly differently effective charges.61 However, given the inherent uncertainty of the experimental system, we argue that the choice of the method is only of secondary importance and we opt for the most popular one. To ensure numerical stability of the solver, we start at a very low pH-value, where the colloid is barely charged, and increase the pH-value only in small steps. In each step, the numerical solution of the previous pH-value is used as initial guess, which leads to rapid convergence and avoids numerical instabilities. Fig. 5 displays the results obtained for the present particles of a = 179.5 nm, N = 134 × 103 and Φ = 4 × 10−3.
In Fig. 5a we show the calculated bare charge as a function of the surface-group pKa-value for the two experimentally realized situations. The corresponding average bare charges from the experiments are indicated as dashed lines of the same color. In the CO2-free state, we consider pHbulk = 7.0. Within the considered charge regulation model, we can identify a value of pKa ≈ 4.26 leading to the dissociation of Z ≈ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 surface groups. In the CO2-equilibrated state we consider pHbulk = 5.5 and cB = 3.16 μmol L−1 and the experimentally determined bare charge is Z ≈ 1340. We observe a drastic change in the surface-group pKa needed to realize this bare charge. In fact, the pKa shifts to an effective value of pKa ≈ 6.48.
000 surface groups. In the CO2-equilibrated state we consider pHbulk = 5.5 and cB = 3.16 μmol L−1 and the experimentally determined bare charge is Z ≈ 1340. We observe a drastic change in the surface-group pKa needed to realize this bare charge. In fact, the pKa shifts to an effective value of pKa ≈ 6.48.
The decrease of bare charge is mirrored by the accompanying decrease of the renormalized charge. Fig. 5b shows the theoretically calculated renormalized charge as a function of the bare charge for both considered bulk pH-values. Initially following the relation ZPBC = Z, it bends over and approaches a limiting value. Note that with CO2, there are overall more ions in the cell, and, consistent with the results of Alexander et al.,15 the renormalized charge shows a larger saturation value. At pHbulk = 7.0, where the experimentally determined average bare charge was Z = (10.4 ± 0.5) × 103, the theory predicts a renormalized charge of ZPBC = 2100. For pHbulk = 5.5, where the experimentally determined bare charge was Z = 1340, the theory predicts a renormalized charge of ZPBC = 1170.
6. Discussion
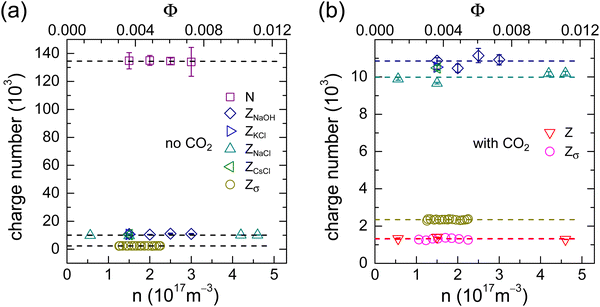
We summarize our findings in Fig. 6. Fig. 6a shows the results for the CO2-free cases. The average values of N = (134 ± 2) × 103, Z = (10.4 ± 0.5) × 103 and Zσ = (2.35 ± 0.04) × 103 reflect the well-known sequence of charge number magnitudes: N ≫ Z > Zσ. Only a very small part of the weakly acidic surface groups is dissociated and only a fraction of the total number of counter-ions is actually mobile. From the PBC-calculations with pH-driven charge regulation (Fig. 5a) we infer a corresponding pKa of 4.26. This is slightly lower than previously reported values for carboxylate stabilized particles.3 However, it appears well-compatible with a dominance of carboxylate surface groups and a small admixture of a few sulfate groups stemming from the initiator. The calculations further predict a renormalized charge of ZPBC = 2.1 × 103. This figure is in reasonable agreement with the experimentally obtained value. The small deviation is attributed to the simplifications made in the present theoretical approach, e.g., the neglect of microscopic surface geometry and of ion correlations. Overall, the comparison demonstrates the excellent performance of Hessinger's conductivity model.In Fig. 6b, we replot the Z- and Zσ-data from the CO2-free experiments on an enlarged scale and compare them to the results obtained in the presence of CO2 (reddish symbols). For the latter, we found an average bare charge of Z = (1.34 ± 0.06) × 103 and an average conductivity charge of Zσ = (1.30 ± 0.06) × 103. If CO2 had no influence on the pKa, we would expect a bare charge of Z ≈ 6 × 103. However, the much smaller experimental bare charge is observed in the charge regulating PBC-calculations for an effective surface pKa of pKa ≈ 6.48. The PBC-prediction for the renormalized charge at pH = 5.5 then is ZPBC = 1200 in reasonable agreement with the experimentally obtained value (the small deviation is, again, attributed to the neglect of ion correlations). At such low bare charge numbers, there is no substantial charge renormalization. If we follow previous work and identify ZPBC with Zσ, this finding explains the absence of ion exchange in the presence of CO2. There are, simply speaking, hardly any immobile ions to be exchanged. The final charge number magnitude sequence reads:  .
.
The drastic reduction of the effective conductivity charge and the renormalized charge in the presence of CO2 is in line with the previous electrophoretic results,55,57 where we had reported a decrease of the ζ-potential from ζ = (61 ± 4) mV to ζ = (35 ± 2) mV after equilibration to ambient air and even further to ζ = (3 ± 2) mV after equilibration to a CO2 atmosphere. These experiments could, however, not directly demonstrate an underlying decrease of the bare surface charge. The present combination of conductivity experiments under various conditions with charge-regulating PBC-calculations unequivocally revealed that CO2 directly exerts a strong decharging effect on the bare surface charge. The reduction in ζ-potential and conductivity charge, respectively renormalized charge simply follows suit, and the absence of ion exchange effects upon the addition of pH neutral 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes to CO2-equilibrated systems is readily explained by the negligible amount of charge renormalization under these conditions.
1 electrolytes to CO2-equilibrated systems is readily explained by the negligible amount of charge renormalization under these conditions.
Granting that the observed effect can be expressed as a significant shift of the surface pKa, the observed shift is much larger than the known difference for COOH-groups in the bulk and at surfaces, which typically amounts to ≈0.5 pKa units. Further the observed shift by more than two units exceeds by far the expectable uncertainties in the theoretical calculations introduced by employing the PBC model. We therefore believe that this unforeseen observation poses a considerable challenge to explain, how dissolved molecular CO2 could possibly influence the dissociation equilibrium. In our previous work, we had tentatively considered several alternatives regarding the underlying mechanisms. All of them were motivated by the results of our molecular dynamics simulations, where we observed the formation of a diffusely adsorbed monolayer of CO2 very close to the surface.55 In principle, such a layer could lead to surface modifications shifting the shear plane further outward and thus decrease the ζ-potential without influencing the particle charge.42,69 Since we here directly observed a decrease in the bare charge, we can now rule out this possibility. Alternatively, the layer could decrease the dielectric permittivity close to the surface and thus strengthen any electrostatic interactions. Enhanced attractive interactions could increase the dissociation energy. Stronger repulsion between neighboring surface charges could introduce a Coulomb penalty for dissociation. Both would counteract dissociation and the corresponding shift in effective surface pKa would directly lower the bare charge. Which of these effects dominates the observed dielectric charge regulation cannot be decided within the present approach. A detailed treatment remains a theoretical challenge but should be accessible within recent analytic approaches accounting for spatially variable dielectric permittivities, hydrodynamics and finite ion size effects.32,70 It should also be in reach of computer simulations.71 Overall, we anticipate, that the present observations should motivate enhanced theoretical interest in an improved modelling of double layer properties.
On the experimental side, the CO2 layer could be characterized further by X-ray and/or element selective neutron reflectometry.40 Its consequences for colloid–colloid interactions could be determined with high distance resolution by colloidal probe experiments.2,10,11 But also the conductivity experiments could be extended to include a back-titration by HCl starting from the NaCl-saturated state. Up to now, we had studied polymer lattices stabilized by weak acids, hydrophilic silica surfaces, and super-hydrophobically coated surfaces, but also further surfaces should be addressed to firmly establish the CO2 adsorption as general phenomenon.
A final remark addresses the implications of our findings for future experiments at low salt conditions. First, the significant influence of CO2 on the charge state of dielectric surfaces in contact with aqueous electrolytes will require utmost care in characterizing and controlling its concentration in any precision measurement of suspension properties and surface characteristics. The techniques employed in the present paper may serve as a starting point. Second, the novel decharging effects exerted by molecular CO2 will certainly affect many surface and suspension properties. Occasional consequences of CO2-contaminations have been reported.51 Möller et al. used treatment of surfaces with CO2-equilibrated DI water and subsequent partial CO2-removal to improve control for writing and drawing in water via modified diffusiophoretic transport of the ink particles.72 Systematic experiments comparing the structure and phase behavior in dependence on electrolyte concentration and number density with and without CO2 are now under way and will be reported elsewhere. Overall, we believe that the controlled application of molecular CO2 will open novel ways of manipulating the performance of functional colloidal systems and solid–water interfaces.
7. Conclusions
We demonstrated the direct influence of molecularly dissolved CO2 on the state of surface group dissociation. We observe a drastic reduction of the number of dissociated surface groups and a halving of effective charges. Such a reduction is significantly stronger than the expected effects induced by the CO2-reaction products in salt-free water, i.e., an altered local pH and an increased salinity caused by the formation of carbonic acid which partially dissociates. The present study therefore confirmed and substantially extended previous investigations and further supported our suggestion of an additional charge regulation by CO2. Given the relatively small concentration of CO2 in ambient air of 421 ppm, the extent of decharging dielectric surfaces by a charge neutral molecule is equally impressive and surprising. In fact, while there existed some literature on the effects of degassing in general, the specific effects of CO2 had been largely ignored. However, in view of the ubiquitous nature of water-solid interfaces and their importance in geology, meteorology, biology as well as in technical applications, we feel that much further research is needed to explain our unexpected findings.Author contributions
P. V. performed the experiments and the evaluations. D. B. performed the PBC-calculations. C. H. supervised the theoretical and T. P. the experimental part. P. V. and T. P. wrote the original manuscript. All authors contributed equally in discussing the data and finalizing the manuscript.Data availability
Raw data are obtainable from the authors upon reasonable request. The source code used for the PB cell-model calculations is freely available on GitHub (https://github.com/davidbbeyer/pb_solver).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank J. Yamanaka, L. Belloni and Y. Levin for fruitful discussions. Financial Support by the German Research Foundation (DFG) is gratefully acknowledged. D. B. and C. H. received funding within the Research Unit FOR2811 “Adaptive Polymer Gels with Model Network Structure” under grant 423791428 along with grant 397384169 (TP7). C. H. is partially funded by the Deutsche Forschungsgemeinschaft (DFG) in project ID 358283783 – CRC 1333/2. P. V. and T. P. were financially supported by the DFG through grant no. Pa459-18.2, Pa459-19.1 and Pa459-23-1.References
- J. Lyklema, Fundamentals of Interface and Colloid Science: Solid-Liquid Interfaces, Academic Press, London, 1995, vol. II Search PubMed.
- S. H. Behrens and M. Borkovec, Electrostatic Interaction of Colloidal Surfaces with Variable Charge, J. Phys. Chem. B, 1999, 103, 2918–2928 CrossRef CAS.
- J. P. H. Zwetsloot and J. C. Leyte, Conductometric Titration of Latex with Acidic Surface Groups, J. Colloid Interface Sci., 1994, 163, 362–371 CrossRef CAS.
- T. Gisler, S. F. Schulz, M. Borkovec, H. Sticher, P. Schurtenberger, B. D’Aguanno and R. Klein, Understanding colloidal charge renormalization from surface chemistry: Experiment and theory, J. Chem. Phys., 1994, 101, 9924–9936 CrossRef CAS.
- J. Yamanaka, Y. Hayashi, N. Ise and T. Yamaguchi, Control of the surface charge density of colloidal silica by sodium hydroxide in salt-freeand low-salt dispersions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3028–3036 CrossRef CAS.
- C. F. Zukoski and D. A. Saville, The interpretation of electrokinetic measurements using a dynamic model of the stern layer: I. The dynamic model, J. Colloid Interface Sci., 1986, 114, 32–44 CrossRef CAS.
- C. F. Zukoski and D. A. Saville, The interpretation of electrokinetic measurements using a dynamic model of the stern layer: II. Comparisons between theory and experiment, J. Colloid Interface Sci., 1986, 114, 45–53 CrossRef CAS.
- H. Reiber, T. Köller, T. Palberg, F. Carrique, E. Ruiz Reina and R. Piazza, Salt concentration and particle density dependence of electrophoretic mobilities of spherical colloids in aqueous suspension, J. Colloid Interface Sci., 2007, 309, 315–322 CrossRef CAS PubMed.
- I. Semenov, S. Raafatnia, M. Sega, V. Lobaskin, C. Holm and F. Kremer, Electrophoretic mobility and charge inversion of a colloidal particle studied by single-colloid electrophoresis and molecular dynamics simulations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 22302 CrossRef PubMed.
- G. Trefalt, T. Palberg and M. Borkovec, Forces between colloidal particles in aqueous solutions containing monovalent and multivalent ions, Curr. Opin. Colloid Interface Sci., 2017, 27, 9–17 CrossRef CAS.
- G. Trefalt, S. H. Behrens and M. Borkovec, Charge Regulation in the Electrical Double Layer: Ion Adsorption and Surface Interactions, Langmuir, 2016, 32, 380–400 CrossRef CAS PubMed.
- V. Lobaskin, B. Dünweg and C. Holm, Electrophoretic mobility of a charged colloidal particle: a computer simulation study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 16, S4063–S4073 CAS.
- V. Lobaskin, B. Dünweg, M. Medebach, T. Palberg and C. Holm, Electrophoresis of colloidal dispersions in the low-salt regime, Phys. Rev. Lett., 2007, 98, 176105 CrossRef PubMed.
- E. J. W. Verwey, Theory of the stability of lyophobic colloids, J. Phys. Colloid Chem., 1947, 51, 631–636 CrossRef CAS PubMed.
- S. Alexander, P. M. Chaikin, P. Grant, G. J. Morales, P. Pincus and D. Hone, Charge renormalization, osmotic pressure, and bulk modulus of colloidal crystals: Theory, J. Chem. Phys., 1984, 80, 5776–5781 CrossRef CAS.
- L. Belloni, Colloidal interactions, J. Phys.: Condens. Matter, 2000, 12, R549–R587 CrossRef CAS.
- E. Trizac, L. Bocquet, M. Aubouy and H. H. von Grünberg, Alexander's Prescription for Colloidal Charge Renormalization, Langmuir, 2003, 19, 4027–4033 CrossRef CAS.
- Y. Levin, Electrostatic correlations: from plasma to biology, Rep. Prog. Phys., 2002, 65, 1577 CrossRef CAS.
- M. Heinen, E. Allahyarov and H. Löwen, Highly asymmetric electrolytes in the primitive model: hypernetted chain solution in arbitrary spatial dimensions, J. Comput. Chem., 2014, 35, 275–289 CrossRef CAS PubMed.
- R. Podgornik, General theory of charge regulation and surface differential capacitance, J. Chem. Phys., 2018, 149 Search PubMed.
- N. Adžić and R. Podgornik, Field-theoretic description of charge regulation interaction, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 5 CrossRef PubMed.
- T. Colla, A. Bakhshandeh and Y. Levin, Charge regulation of nanoparticles in the presence of multivalent electrolytes, J. Chem. Phys., 2024, 161 Search PubMed.
- N. Garbow, M. Evers, T. Palberg and T. Okubo, On the electrophoretic mobility of isolated colloidal spheres, J. Phys.: Condens. Matter, 2004, 16, 3835–3842 CrossRef CAS.
- R. Galneder, V. Kahl, A. Arbuzova, M. Rebecchi, J. O. Rädler and S. McLaughlin, Microelectrophoresis of a Bilayer-Coated Silica Bead in an Optical Trap: Application to Enzymology, Biophys. J., 2001, 80, 2298–2309 CrossRef CAS PubMed.
- L. Shapran, M. Medebach, P. Wette, T. Palberg, H. J. Schöpe, J. Horbach, T. Kreer and A. Chatterji, Qualitative characterisation of effective interactions of charged spheres on different levels of organisation using Alexander's renormalised charge as reference, Colloids Surf., A, 2005, 270–271, 220–225 CrossRef CAS.
- G. S. Roberts, T. A. Wood, W. J. Frith and P. Bartlett, Direct measurement of the effective charge in nonpolar suspensions by optical tracking of single particles, J. Chem. Phys., 2007, 126, 194503 CrossRef PubMed.
- F. Strubbe, F. Beunis, M. Marescaux and K. Neyts, Charging mechanism in colloidal particles leading to a linear relation between charge and size, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 31405 CrossRef PubMed.
- A. V. Delgado, F. González-Caballero, R. J. Hunter, L. K. Koopal and J. Lyklema, Measurement and interpretation of electrokinetic phenomena, J. Colloid Interface Sci., 2007, 309, 194–224 CrossRef CAS PubMed.
- F. Carrique, E. Ruiz-Reina, R. Roa, F. J. Arroyo and Á. V. Delgado, General electrokinetic model for concentrated suspensions in aqueous electrolyte solutions: Electrophoretic mobility and electrical conductivity in static electric fields, J. Colloid Interface Sci., 2015, 455, 46–54 CrossRef CAS PubMed.
- Á. V. Delgado, F. Carrique, R. Roa and E. Ruiz-Reina, Recent developments in electrokinetics of salt-free concentrated suspensions, Curr. Opin. Colloid Interface Sci., 2016, 24, 32–43 CrossRef.
- D. Botin, J. Wenzl, R. Niu and T. Palberg, Colloidal electro-phoresis in the presence of symmetric and asymmetric electro-osmotic flow, Soft Matter, 2018, 14, 8191–8204 RSC.
- F. Carrique, E. Ruiz-Reina, F. J. Arroyo, J. J. López-García and A. V. Delgado, Effects of finite counterion size and nonhomogeneous permittivity and viscosity of the solution on the electrokinetics of a concentrated salt-free colloid, Phys. Rev. E, 2024, 110 Search PubMed.
- J. Gapinski, A. Wilk, A. Patkowski, W. Häussler, A. J. Banchio, R. Pecora and G. Nägele, Diffusion and microstructural properties of solutions of charged nanosized proteins: experiment versus theory, J. Chem. Phys., 2005, 123, 54708 CrossRef CAS PubMed.
- A. Gulotta, M. Polimeni, S. Lenton, C. G. Starr, A. Stradner, E. Zaccarelli and P. Schurtenberger, Combining Scattering Experiments and Colloid Theory to Characterize Charge Effects in Concentrated Antibody Solutions, Mol. Pharmaceutics, 2024, 21, 2250–2271 CrossRef CAS PubMed.
- N. Maeda, Brief Overview of Ice Nucleation, Molecules, 2021, 26, 392 CrossRef CAS PubMed.
- M. Lukas, R. Schwidetzky, A. T. Kunert, U. Pöschl, J. Fröhlich-Nowoisky, M. Bonn and K. Meister, Electrostatic Interactions Control the Functionality of Bacterial Ice Nucleators, J. Am. Chem. Soc., 2020, 142, 6842–6846 CrossRef CAS PubMed.
- A. V. Delgado, M. L. Jiménez, G. R. Iglesias and S. Ahualli, Electrical double layers as ion reservoirs: applications to the deionization of solutions, Curr. Opin. Colloid Interface Sci., 2019, 44, 72–84 CrossRef CAS.
- F. J. Millero, R. Feistel, D. G. Wright and T. J. McDougall, The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale, Deep Sea Res., Part I, 2008, 55, 50–72 CrossRef.
- K. Gilbert, P. C. Bennett, W. Wolfe, T. Zhang and K. D. Romanak, CO2 solubility in aqueous solutions containing Na+, Ca2+, Cl−, SO42− and HCO3−: The effects of electrostricted water and ion hydration thermodynamics, Appl. Geochem., 2016, 67, 59–67 CrossRef CAS.
- D. A. Doshi, E. B. Watkins, J. N. Israelachvili and J. Majewski, Reduced water density at hydrophobic surfaces: Effect of dissolved gases, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9458–9462 CrossRef CAS PubMed.
- S. M. Dammer and D. Lohse, Gas Enrichment at Liquid-Wall Interfaces, Phys. Rev. Lett., 2006, 96, 206101 CrossRef PubMed.
- B. İlhan, C. Annink, D. V. Nguyen, F. Mugele, I. Siretanu and M. H. G. Duits, A method for reversible control over nano-roughness of colloidal particles, Colloids Surf., A, 2019, 560, 50–58 CrossRef.
- R. M. Pashley, Effect of Degassing on the Formation and Stability of Surfactant-Free Emulsions and Fine Teflon Dispersions, J. Phys. Chem. B, 2003, 107, 1714–1720 CrossRef CAS.
- N. Maeda, K. J. Rosenberg, J. N. Israelachvili and R. M. Pashley, Further Studies on the Effect of Degassing on the Dispersion and Stability of Surfactant-Free Emulsions, Langmuir, 2004, 20, 3129–3137 CrossRef CAS PubMed.
- F. J. Millero, Thermodynamics of the carbon dioxide system in the oceans, Geochim. Cosmochim. Acta, 1995, 59, 661–677 CrossRef CAS.
- Aqion freeware program, Aqion 8.4.1 (release 9.23), available at: https://www.aqion.de/, accessed 18 August 2022.
- F. Carrique, E. Ruiz-Reina, F. J. Arroyo and A. V. Delgado, Dynamic electrophoretic mobility of spherical colloidal particles in realistic aqueous salt-free concentrated suspensions, J. Phys. Chem. B, 2010, 114, 6134–6143 CrossRef CAS PubMed.
- M. Heinen, T. Palberg and H. Löwen, Coupling between bulk- and surface chemistry in suspensions of charged colloids, J. Chem. Phys., 2014, 140, 124904 CrossRef CAS PubMed.
- A. Bakhshandeh, D. Frydel and Y. Levin, Theory of Charge Regulation of Colloidal Particles in Electrolyte Solutions, Langmuir, 2022, 38, 13963–13971 CrossRef CAS PubMed.
- N. Lorenz, I. Gupta and T. Palberg, Microstructural diversity, nucleation paths, and phase behavior in binary mixtures of charged colloidal spheres, J. Chem. Phys., 2023, 158, 114902 CrossRef CAS PubMed.
- N. Lorenz, C. Wittenberg and T. Palberg, Porous crystals in charged sphere suspensions by aggregate-driven phase separation, Soft Matter, 2023, 19, 5076–5091 RSC.
- D. Botin, F. Carrique, E. Ruiz-Reina and T. Palberg, Non-monotonic concentration dependence of the electro-phoretic mobility of charged spheres in realistic salt free suspensions, J. Chem. Phys., 2020, 152, 244902 CrossRef CAS PubMed.
- T. Okubo and H. Fujita, Phase diagram of alloy crystal in the exhaustively deionized suspensions of binary mixtures of colloidal spheres, Colloid Polym. Sci., 1996, 274, 368–374 CrossRef CAS.
- P. Wette, H. J. Schöpe, R. Biehl and T. Palberg, Conductivity of deionized two-component colloidal suspensions, J. Chem. Phys., 2001, 114, 7556 CrossRef CAS.
- P. Vogel, N. Möller, M. N. Qaisrani, P. Bista, S. A. L. Weber, H.-J. Butt, B. Liebchen, M. Sulpizi and T. Palberg, Charging of Dielectric Surfaces in Contact with Aqueous Electrolytes – the Influence of CO2, J. Am. Chem. Soc., 2022, 144, 21080–21087 CrossRef CAS PubMed.
- F. Carrique and E. Ruiz-Reina, Effects of water dissociation and CO2 contamination on the electrophoretic mobility of a spherical particle in aqueous salt-free concentrated suspensions, J. Phys. Chem. B, 2009, 113, 8613–8625 CrossRef CAS PubMed.
- P. Vogel and T. Palberg, Electrokinetic effects of ambient and excess carbonization of dielectric surfaces in aqueous environments, J. Colloid Interface Sci., 2024, 656, 280–288 CrossRef CAS PubMed.
- D. Hessinger, M. Evers and T. Palberg, Independent ion migration in suspensions of strongly interacting charged colloidal spheres, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5493–5506 CrossRef CAS PubMed.
- M. Medebach, R. C. Jordán, H. Reiber, H.-J. Schöpe, R. Biehl, M. Evers, D. Hessinger, J. Olah, T. Palberg, E. Schönberger and P. Wette, Drude-type conductivity of charged sphere colloidal crystals: Density and temperature dependence, J. Chem. Phys., 2005, 123, 104903 CrossRef PubMed.
- A. Diehl and Y. Levin, Smoluchowski equation and the colloidal charge reversal, J. Chem. Phys., 2006, 125, 54902 CrossRef PubMed.
- M. E. Brito, G. Nägele and A. R. Denton, Effective interactions, structure, and pressure in charge-stabilized colloidal suspensions: Critical assessment of charge renormalization methods, J. Chem. Phys., 2023, 159 Search PubMed.
- T. Colla, I. M. Telles, M. Arfan, A. P. Dos Santos and Y. Levin, Spiers Memorial Lecture: Towards understanding of iontronic systems: electroosmotic flow of monovalent and divalent electrolyte through charged cylindrical nanopores, Faraday Discuss., 2023, 246, 11–46 RSC.
- CRC handbook of chemistry and physics, A ready-reference book of chemical and physical data, ed. D. R. Lide, CRC Press, Boca Raton, 76th edn, 1996 Search PubMed.
- R. Niu, P. Kreissl, A. T. Brown, G. Rempfer, D. Botin, C. Holm, T. Palberg and J. de Graaf, Microfluidic pumping by micromolar salt concentrations, Soft Matter, 2017, 13, 1505–1518 RSC.
- Electrostatic Effects in Soft Matter and Biophysics. Proceedings of the NATO Advanced Research Workshop on Electrostatic Effects in Soft Matter and Biophysics Les Houches, France 1–13 October 2000, ed. C. Holm, P. Kékicheff and R. Podgornik, Springer Netherlands; Imprint: Springer, Dordrecht, 1st edn, 2001, vol. 46 Search PubMed.
- M. Deserno and C. Holm, in Electrostatic Effects in Soft Matter and Biophysics. Proceedings of the NATO Advanced Research Workshop on Electrostatic Effects in Soft Matter and Biophysics Les Houches, France 1–13 October 2000, ed. C. Holm, P. Kékicheff and R. Podgornik, Springer Netherlands; Imprint: Springer, Dordrecht, 1st edn, 2001, pp. 27–52 Search PubMed.
- B. W. Ninham and V. A. Parsegian, Electrostatic potential between surfaces bearing ionizable groups in ionic equilibrium with physiologic saline solution, J. Theor. Biol., 1971, 31, 405–428 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- J. E. Seebergh and J. C. Berg, Evidence of a hairy layer at the surface of polystyrene latex particles, Colloids Surf., A, 1995, 100, 139–153 CrossRef CAS.
- J. J. López-García, J. Horno and C. Grosse, Ionic size, permittivity, and viscosity-related effects on the electrophoretic mobility: A modified electrokinetic model, Phys. Rev. Fluids, 2019, 4, 103702 CrossRef.
- N. Aho, P. Buslaev, A. Jansen, P. Bauer, G. Groenhof and B. Hess, Scalable Constant pH Molecular Dynamics in GROMACS, J. Chem. Theory Comput., 2022, 18, 6148–6160 CrossRef CAS PubMed.
- N. Möller, L. Hecht, R. Niu, B. Liebchen and T. Palberg, Writing Into Water, Small, 2023, 19, e2303741 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00957f |
| This journal is © The Royal Society of Chemistry 2024 |