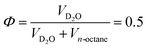Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Confined bicontinuous microemulsions: nanoscale dynamics of the surfactant film†‡
Margarethe
Dahl
 *a,
Olaf
Holderer
*a,
Olaf
Holderer
 b,
René
Haverkamp
b,
René
Haverkamp
 c,
Ingo
Hoffmann
c,
Ingo
Hoffmann
 d,
Kathleen
Wood
d,
Kathleen
Wood
 e,
Jessica
Hübner
a,
Thomas
Hellweg
e,
Jessica
Hübner
a,
Thomas
Hellweg
 c and
Stefan
Wellert
c and
Stefan
Wellert
 a
a
aDepartment of Chemistry, Technische Universität Berlin, Straße des 17. Juni 124, 10623 Berlin, Germany. E-mail: a.dahl@tu-berlin.de
bJülich Centre for Neutron Science (JCNS) at Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany
cDepartment of Chemistry, Physical and Biophysical Chemistry Group, University of Bielefeld, Universitätsstraße 25, 33615 Bielefeld, Germany
dInstitut Laue-Langevin, 71 avenue des Martyrs, F-38042 Grenoble, France
eAustralian Nuclear and Technology Organisation, New Illawarra Rd, Lucas Heights, NSW 2234, Australia
First published on 16th October 2024
Abstract
A confined bicontinuous C10E4–D2O–n-octane microemulsion is studied using neutron spin echo spectroscopy (NSE). Controlled pore glasses serve as confining matrices with pore diameters ranging from 24 to 112 nm. Firstly, the microemulsion in bulk is investigated by NSE and dynamic light scattering, which allows the determination of the unperturbed collective dynamics as well as the observation of the undulation of the surfactant film. In confinement, it is observed that the collective modes are drastically slowed down in all investigated pore sizes. The undulations of the surfactant film in the largest pores are found to be comparable to those of the bulk and decrease with decreasing pore diameter. Fitting procedures of the intermediate scattering function revealed that the long wavelength undulations are cut off from the spectrum of fluctuation modes due to the interactions with the pore walls.
1 Introduction
The influence of hard confinement on simple fluids, binary fluid mixtures and colloidal liquids has attracted considerable attention during the last two decades.1–5 It was found theoretically and experimentally, that significant changes in the fluid properties occur when the confinement becomes comparable to a characteristic length of the confined liquid.6 In simple fluids, it is primarily the molecular size and the extent of the wetting layers away from the confining surface that determine the structural properties of the fluid.1,7 For example, the NMR field-gradient technique was used to explore the dynamics of cyclohexane inside controlled pore glasses (CPG) and a decrease of the self-diffusion coefficients was observed and attributed to the existence of free liquid and adsorbed liquid. In that case, the observed decrease of the diffusivity was mainly due to the geometric restriction rather than to the interaction with the surface.8 The fundamental work shows that even simple liquids in pores exhibit strong changes in phase behavior. Mixtures, and especially binary mixtures that have been studied extensively, show changes in their critical behavior inside porous materials compared to free mixtures.9,10 In both, experiments and theoretical work, a particularly complex phase behavior was found. Here, the geometric properties of the pore network, the details of the penetration of the fluids, the pore matrix as well as the potentially competitive wetting behavior of the liquid components and the resulting preferential adsorption play a major role.11,12 For the binary model system isobutyric acid and D2O the concentration fluctuations during the phase transition from the one-phase to the two-phase region was monitored in confinement with neutron spin echo spectroscopy (NSE) showing that the method is able to reveal interesting information also for 3D confined systems. It was found that the fluid behaves in a bulk-like manner until the correlation length of the fluctuations exceeds the pore size. The microphase separation extends over a wider temperature range than in bulk.13,14In more complex structured fluids, additional length scales become important. In systems such as bicontinuous microemulsions, correlation functions exhibit exponentially damped oscillatory behavior and an isotropic periodic internal structure occurs, in which randomly oriented oil and water domains, separated by a surfactant interface, form a sponge-like structure.
In addition to the fundamental structural and physical properties of such complex fluids, the physical properties in restricted geometries also play a significant technical role and, as a result, attract scientific interest. For example, this includes the flow properties of such fluids when forced through porous or membrane-like structures or technically relevant microchannels such as in microfluidic applications15 or the formation of microemulsions when penetrating porous rocks, which plays a major role in enhanced oil recovery when surfactant solutions are used to extract the reservoir fluid.16 A series of experimental and numerical works explored the properties of these situations. For example, in rheological and small angle neutron scattering experiments (SANS) it was found that at sufficient high shear flow a transition from a sponge-like or bicontinuous to a lamellar structure is induced, which is accompanied by a change in the dynamic viscosity of the complex fluid.15,17,18 Moreover, the influence of confinement by planar surfaces on the equilibrium structure and the related physical properties was explored with scattering experiments. The near-surface structure of sponge phases and bicontinuous microemulsions on planar surfaces was investigated by scattering methods (neutron reflectometry, grazing incidence scattering).19,20 Additionally, the combination of grazing incidence geometry with neutron spin echo spectroscopy was established and used to study the dynamics of CiEj and sugar surfactant based bicontinuous microemulsions near solid surfaces as a function of the neutron penetration depth.21,22 Surface force measurements were performed to study surface induced phase transitions of bicontinuous microemulsions of different compositions. Due to the flexibility of the interfaces, bicontinuous microemulsions exhibit repulsive force barriers which is attributed to the overlap of the lamellar structures induced between the confining mica surfaces. Depending on the composition of the microemulsion and hence, its position inside the phase diagram, additional attractive forces due to water capillary condensation were observed.23 It was found that the presence of the confining solid surface modifies the free energy of the surfactant interface due to the interaction of the microemulsion with the solid surface. In the case of a C10E4–D2O–n-decane bicontinuous microemulsion adhered to a hydrophilic planar surface an increase of the relaxation times of the height fluctuations of the surfactant interface was found.21 In the case of a sugar surfactant-based microemulsion from the system C8/10G1.3–pentanol–D2O–cyclohexane, a slight increase of the relaxation times was observed but without a notable difference between hydrophilic and hydrophobic planar surfaces.22
These previous studies of the dynamics in confined bicontinuous microemulsions have mainly focused on the one-sided confinement by a planar surface. Their results raise the question of how a three-dimensional confinement, as represented by a mesoporous structure, will influence the structure and phase behavior of the microemulsions and how this manifests in the observable dynamics.
In the present work, we use NSE to investigate the thermally activated internal dynamics of a bicontinuous C10E4–D2O–n-octane microemulsion with a temperature-dependent phase behavior after imbibition into hydrophilic and hydrophobic geometric confinements without external flows when the system has reached its equilibrium state inside the confinement. The observed dynamics is compared with the dynamics of a free bicontinuous microemulsion of the same composition, which was measured with dynamic light scattering and NSE. The numerous previous studies with this microemulsion system make it a very well characterized reference system.15,24–26 As confining matrices we use CPG particles with pore sizes of 24, 46 and 112 nm which are pressed into pills (see Fig. 1). NSE enables a direct measurement of the bending elasticity constant κ of the surfactant film in the microemulsion as a characteristic feature of the interface.27 This avoids possible ambiguities in the determination of κ due to the complex superposition of the individual contributions in the SANS data.
2 Experimental part
2.1 Materials
Water was purified using a Milli-Q system (Millipore) reaching a final resistance of 18 MΩ. Tetraethylene glycol monodecyl ether (C10E4) (>95%) was purchased from Bachem. n-Octane, dichlorodimethylsilane (DCDMS), and anhydrous toluene (99.8%) were purchased from Sigma-Aldrich. Sulfuric acid (95%) and aqueous H2O2 solution (30%, stabilized) were purchased from VWR Chemicals. Deuterated water (D2O, 99.9%) was purchased from Deutero. Chemicals were used as received.2.2 Surface modification of porous glasses
The surface polarity of the native CPG is hydrophilic due to the terminal hydroxy groups of the silica skeleton. The surface polarity was altered following a modified procedure of Bosley and Clayton.28 Therefore, as described above, the CPG was freeze-dried to remove any residual moisture. Then 1.5 g CPG-powder was filled into PTFE tubes with a total volume of 25 mL. 60 mL anhydrous toluene was transferred into a glass reactor, purged with nitrogen for 30 min, and stirred at 300 rpm. Afterwards, 14.8 mL DCDMS was added to the toluene and stirred for 5 min at 500 rpm. Then 25 mL of this solution was added to each PTFE tube and placed on an orbital shaker for 1 h at room temperature. The CPG powder was separated from the solution by centrifugation and washed twice with toluene, acetone, and Milli-Q water. After freeze-drying, the surface modification was verified by elemental analysis where it was monitored as an increase in the carbon content. The hydrophobically modified CPG is labeled as CPG-CH3. For statements that hold for both CPG-CH3 and CPG-OH, the abbreviation CPG is used.2.3 Methods
and a surfactant amount of 12.84 wt% obtained from
To ensure that the samples are bicontinuous and single-phase the microemulsion samples were stored in a thermostated cabinet at T = 22.5 °C prior to all measurements.
| CPG | d N2,Hg (nm) | V P (mL g−1) | ε | A s (m2 g−1) | d P (nm) |
|---|---|---|---|---|---|
| CPG17 | 24.4 | 0.87 | 0.66 | 124.6 | 20.4 ± 0.3 |
| CPG50 | 46.0 | 1.16 | 0.72 | 68.1 | 42.9 ± 3.0 |
| CPG100 | 112 | 1.57 | 0.78 | 35.9 | 122.5 ± 7.0 |
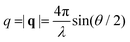 , where θ is the scattering angle and λ is the neutron wavelength. The CPG powder was pressed into cylindrical tablets to minimize the voids between the CPG particles. 0.1 g CPG was pressed into a PTFE ring with a diameter of 10 mm and a height of 0.1 mm.
, where θ is the scattering angle and λ is the neutron wavelength. The CPG powder was pressed into cylindrical tablets to minimize the voids between the CPG particles. 0.1 g CPG was pressed into a PTFE ring with a diameter of 10 mm and a height of 0.1 mm.
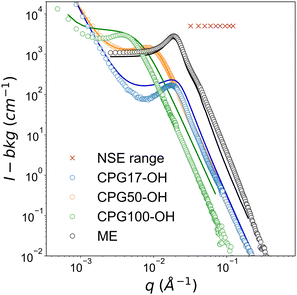 | ||
| Fig. 2 SANS signal of the hydrophilic D2O-filled CPG and the bicontinuous microemulsion in bulk (ME). The solid line represents the fit to the eqn (2). The red crosses represent the investigated q-range by NSE. | ||
3 Results and discussion
3.1 Structural properties of the confining matrices and the confined microemulsion
The CPGs are formed by a silica skeleton which establish interconnected pores with a sponge-like structure, similar to the bicontinuous structure from the microemulsion.33–35 Therefore, all SANS curves exhibit the characteristic broad correlation peak and are described by the Teubner–Strey (TS) model.36 A detailed description of the structure of the confining matrices and the confined microemulsion can be found in our previous work.37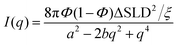 | (1) |
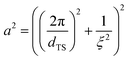 and
and  .
.
The SANS curves of the D2O-filled CPGs are shown in Fig. 2. Additionally, the surface of the powder particles contributes with a power-law decay at low q. Combined the SANS signal can be described by:
| I(q) = Aqn + (1 − A)I(q)TS. | (2) |
 | (3) |
| Label | d TS (nm) | ξ TS (nm) |
|---|---|---|
| CPG17 | 31.1 ± 0.5 | 12.8 ± 1.8 |
| CPG50 | 59.7 ± 4.2 | 16.3 ± 1.5 |
| CPG100 | 158.0 ± 9.1 | 20.3 ± 1.0 |
| ME | 32.7 ± 3.3 | 22.2 ± 1.5 |
Using the parameters from Table 2 the bending elasticity of the bicontinuous microemulsion is κSANS = 0.577kBT, which is in good agreement with the literature.15
A comparison of the results from SANS measurements shown in Tables 1 and 2 shows that the structural sizes of the microemulsion fit several times into the largest pores and are comparable to the diameter of the smallest pores. Accordingly, the strongest effect on the dynamics can be expected for the smallest pores.
3.2 Confinement effect on bicontinuous microemulsion dynamics
The thermally excited dynamics in a bicontinuous microemulsion extend over several q regions and time scales, which can be observed using dynamic light scattering and NSE. In the q range q ≥ 1/dTS, height fluctuations of the amphiphilic interface predominate, while in the range q ≤ 1/dTS, continuous topological changes of the structure (rearrangement, new formation and degradation of channels and connections between membranes) occur. These can be observed very well with NSE. At q ≪ 1/dTS, long-range collective fluctuations occur in the oil and water domains, which is optimal for observation with DLS.313.2.1.1 Dynamic light scattering measurements. With its q-range from 7 × 10−4 Å−1 to 2 × 10−3 Å−1, DLS observes concentration fluctuations inside the bicontinuous microemulsion structure at lengths of several 10 nm. That extends over several oil and water domains. Hence, the measured intensity autocorrelation functions were fitted with a simple exponential to extract the decay rate ΓDLS
g2(τ) − 1 = β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2ΓDLSτ) exp(−2ΓDLSτ) | (4) |
| ΓDLS = Dc,DLSq2. | (5) |
From fitting eqn (4) to the measured intensity-autocorrelation functions g2(τ) − 1 the relaxation rates ΓDLS were extracted and plotted as a function of q2, which can be seen in the ESI,‡ Fig. S3. The inset exemplarily depicts the correlation function measured at a scattering angle of 90°. The monomodal behavior of the correlation function is clearly visible. A linear fit to ΓDLS(q2) confirms the validity of eqn (5) from which the diffusion coefficient Dc,DLS = 1.98 × 10−11 m2 s−1 was determined. This corresponds well to Dc values of previously measured bicontinuous microemulsions.31
Although derived as the relation between the diffusion coefficient of spherical particles in a dilute suspension, the Stokes–Einstein equation can be applied to estimate a characteristic length  of the concentration fluctuations. With
of the concentration fluctuations. With
 | (6) |
 was estimated. The use of the average of the solvent viscosity η = ηwϕw + ηoϕo is based on the assumption that on the observed length scale mainly membrane fluctuations and solvent flow of the bulk solvent domains contribute to the friction dissipating the thermal activation while the sample averaged viscosity is up to 5 times larger than the pure solvent viscosities.31,40
was estimated. The use of the average of the solvent viscosity η = ηwϕw + ηoϕo is based on the assumption that on the observed length scale mainly membrane fluctuations and solvent flow of the bulk solvent domains contribute to the friction dissipating the thermal activation while the sample averaged viscosity is up to 5 times larger than the pure solvent viscosities.31,40
3.2.1.2 Neutron spin echo spectroscopy measurements. Neutron spin echo (NSE) spectroscopy studies on bicontinuous microemulsion capture the height fluctuations of the amphiphilic interface due to undulations. Additionally, hydrodynamic modes with characteristics of diffusive motion contribute to the measured normalized intermediate scattering functions S(q,τ)/S(q,0), within the length and time scale of the technique. In Fig. 3 a set of normalized intermediate scattering functions is shown for the q-range from 0.03 Å−1 to 0.122 Å−1. It can be seen that with increasing q-values the curves decrease with an increasing relaxation rate. In accordance with previously published results on the dynamics in bicontinuous microemulsions we analyze the data within the Zilman–Granek approach for thermally excited membrane undulations.41 Thus, the NSE signal can be described by the following equation which combines the stretched exponential relaxation for the membrane undulations with a single exponential relaxation for the concentration fluctuations:
 | (7) |
 | (8) |
 | ||
| Fig. 3 Normalized intermediate scattering functions of (a) the bicontinuous microemulsion in bulk and the confined microemulsion in the hydrophilic CPG100-OH (b), CPG50-OH (c) and CPG17-OH (d) for several q values. The solid lines are fits to the eqn (7). The dotted lines are the fit to the eqn (9). Bottom: Normalized residuals of the fit. | ||
The solid lines in Fig. 3 are fits of eqn (7) to the data. The fitted values for A, Γz and Γc are listed in the ESI,‡ Tables S1–S7. According to the predictions of eqn (5) and (8) in Fig. 4 the resulting relaxation rates are plotted, as Γc ∝ q2 in graph (a) and as Γz ∝ q3 in graph (b) and the amplitude A is shown as a function of q in plot (c).
 | ||
| Fig. 4 Results of fitting the NSE data of Fig. 3(a) with eqn (7): (a) relaxation rate Γc of the collective motions inside the bicontinuous microemulsions (b) relaxation rate Γz of the membrane undulations and (c) amplitude A as a measure of the weight of the contribution of both dynamics. | ||
The slope in graph (a) of Fig. 4 yields the collective diffusion coefficient Dc = 1.83 × 10−11 m2 s−1 which corresponds well with Dc,DLS obtained in the DLS measurements. This is a strong indication that the underlying diffusive contribution stems from the breathing modes measured with DLS. Note, that at q ≥ 0.1 Å−1 the results deviate significantly from the initial progress. That indicates the onset of an increasing contribution of the membrane undulations.
A linear fit to the data in Fig. 4(b) yields a slope of D* = 167 Å3 ns−1. This is in agreement with values of D* of other microemulsions.
A direct way to analyze the intermediate scattering functions that avoids simplifications and assumptions leading to eqn (7) and (8) uses a previously developed numerical computation routine for S(q,τ).31,42
 | (9) |
The dotted lines in Fig. 3 are fits of the dynamic structure factor using eqn (9). In Fig. 5 the fitted dynamic structure factor for the microemulsion in bulk and confined in hydrophilic CPG is shown exemplary for q = 0.095 Å−1. The fit for the other tested q-values can be found in the ESI,‡ Fig. S4. To reduce the ambiguity in the fitting, the superimposed relaxation of the collective diffusion of the oil and water domains was fixed based on Dc,DLS from the results of the DLS measurements as discussed above. As in eqn (8), the viscosity of the solvent surrounding the amphiphilic membrane is a crucial parameter in the determination of the bending elasticity constant. On the very local scale, we assume that the activation energy of the membrane fluctuations is dissipated by friction from the molecules of the pure bulk phase liquids. The resulting bending elasticity constant κ yields 2.9kBT with ξ = 22.2 nm and Dc,DLS as obtained with DLS and is somewhat larger than calculated from the SANS results.
 | ||
| Fig. 5 Normalized intermediate scattering function of the bicontinuous microemulsion in bulk (ME) and confined in CPG100-OH, CPG50-OH, CPG17-OH at q = 0.095 Å−1 with the fit to the eqn (9). | ||
| Label | D c (×10−11 m2 s−1) | D* (Å3 ns−1) |
|---|---|---|
| ME | 1.82 ± 0.13 | 167 ± 14 |
| CPG17-OH-ME | ≈0 | 62 ± 21 |
| CPG17-CH3-ME | ≈0 | 82 ± 14 |
| CPG50-OH-ME | 0.22 ± 0.03 | 135 ± 31 |
| CPG50-CH3-ME | 0.32 ± 0.05 | 138 ± 30 |
| CPG100-OH-ME | 0.31 ± 0.03 | 139 ± 32 |
| CPG100-CH3-ME | 0.49 ± 0.06 | 133 ± 26 |
 | ||
| Fig. 6 Relaxation rate Γc obtained from fitting eqn (7) in dependence on q2 of the microemulsion confined in hydrophilic (a) and hydrophobic CPG (b). | ||
The collective diffusion coefficient is reduced from Dc = 1.83 × 10−11 m2 s−1 to Dc ≈ 0 in CPG17. The decrease of Dc correlates with the decrease of the pore diameter. In the smallest pores with dP = 20.4 nm the collective motions are barely detectable in the time range accessible by NSE and the collective diffusion coefficient Dc ≈ 0. (The fits of eqn (7) to the data of CPG17 was refined with Γc = 0, but there were only minimal differences as shown in Tables S8 and S9 of the ESI.‡) Although collective diffusion is significantly slower in both glasses, there is a notable distinction between hydrophilic and hydrophobic pores except for CPG17. The diffusion coefficient Dc extracted from the data measured in the hydrophilic pores is lower than that within hydrophobic pores. This implies that the motions of the oil and water domains depend on the interaction with the pore wall. The interaction with the hydrophilic pore wall seems to lower the relaxation rate of the collective motions, probably due to a stronger adhesion to the hydrophilic pore wall. Such differences in the diffusion of simple fluids and binary liquid mixtures inside porous media have previously been reported in literature44 and were observed by NMR measurements,45 incoherent quasielastic neutron scattering46 and forced Rayleigh scattering.47
The observed decrease in Dc may have several reasons. Eqn (6) shows that the decrease occurs due to an increase of the size of the regions involved in the concentration fluctuations or an increase in the friction responsible for dissipating the thermal excitation. This means, for the investigated system, that two effects are possible. Either an increase of the fluctuating domains due to an increase of the oil and water domain sizes of the bicontinuous microemulsion or an increase in the effective viscosity. The latter could be caused by a hindered fluctuation due to interactions and adhesion to the randomly oriented rough surfaces of the pore walls. In literature, the upper limit of the pore wall roughness was estimated to be 2 nm.35
The fits of eqn (7) yield relaxation rates of the surfactant film Γz, which are in the same order of magnitude as in the bulk. However, the obtained values appear to deviate from the expected linear behavior of Γz ∝ q3 at large q, as shown in Fig. 7. The residuals of the fit are slightly larger for the normalized intermediate scattering functions measured at high q, which limits the accuracy of these data points. Values of D* = 140 Å3 ns−1 for the CPG50 and CPG100 with pore diameters of 42.9 nm and 122.9 nm, respectively, were determined. These values are still comparable to the bulk value of 167 Å3 ns−1, indicating that the height fluctuations of the surfactant film are only slightly restricted by large pores. In the case of CPG17 with the smallest pores, it is difficult to determine the apparent diffusion coefficient D*, since Γz ≈ 0.5 ns−1 over the investigated q-range. Thus fitting the slope without an intercept, according to eqn (8) leads to large uncertainties. Nonetheless, the overall decrease of Γz in CPG17 indicates that the undulations of the surfactant film are slowed down compared to the unconfined microemulsion or confined in CPG50 and CPG100. Moreover, as can be seen in the ESI,‡ Fig. S7 the amplitude A(q) of the undulation decreases with decreasing pore size and as the relaxation of the concentration fluctuations slows down.
 | ||
| Fig. 7 Relaxation rate Γz obtained from fitting eqn (7) in dependence on q3 of the microemulsion confined in hydrophilic (a) and hydrophobic CPG (b). | ||
The undulations of the surfactant film are not influenced by the chemical composition of the pore wall, as there are no differences between the D* in hydrophilic and hydrophobic pores measured in the current work.
According to eqn (8) the expected slope in D* ∝ q3 depends on the bending elasticity constant κ, the local viscosity η and, embedded in the pre-factor γκ, on the correlation length ξ. Since the bending elasticity constant is mainly determined by the surfactant composing the interface48 and its intermolecular interactions we propose that the main effect of the confinement is on the fluctuation modes. The porous structure of a CPG provides a certain distribution of interconnected pores with a rough surface. A decrease of D* is in agreement with a decrease of ξ. In eqn (9) this is related to an increase of kmin due to the decrease of the correlation length ξ of the bicontinuous structure resulting in an exclusion of fluctuations with longer wavelengths from the fluctuation mode spectrum. Experimentally, in the NSE measurement this effect manifests itself in a decrease of Γz. To test this hypothesis, the fit of the structure factor given by eqn (9) and described above for the bulk microemulsion was performed with a fixed value of κ = 1kBT and the fixed averaged value of the local viscosity. The resulting fits with ξ and amplitude (A = 1 ± 0.02) are shown as dotted lines in Fig. 3 and 5. The fits to the data yield decreasing values of ξ, in particular 11.6 nm for CPG100-OH, 9.5 nm for CPG50-OH and 6.4 nm for CPG17-OH. Inside CPG100-OH the correlation length is only slightly smaller compared to the bulk value of 12.2 nm. In case of CPG17-OH with the smallest pore size, ξ reduces to half the value in bulk. As mentioned above, the size of one oil or water domain (dTS/2) of the bulk structure mathematically fits up to 10 times the mean pore diameter in CPG100-OH. Therefore, we expect the least disturbance of the thermodynamic equilibrium structure and observe a slight slowdown of the dynamics and the corresponding reduction of ξ. In the case of CPG17-OH, the domain size of the microemulsion and the pore size of the CPG coincide, which leads to the strongest effect on the dynamics and, accordingly, the equilibrium fluctuations with large wavelengths are cut off from the fluctuation mode spectrum. The χ2 value of the simultaneous fit with 9 increases from 5 for the pure microemulsion to 10 for the strongest confinement, indicating (as also visible in the fit) that the model does not fully describe the NSE data. The restrictions of the model do not permit a better data description for the confined case and show the limitations of the fits. A more detailed discussion is given with the model from eqn (7), allowing an easier qualitative assessment of collective modes vs. height fluctuations and elastic contributions.
In addition to a decrease of ξ and the associated limitation of the mode spectrum of the thermal fluctuations, it cannot be ruled out that an increase in the local viscosity is also caused by interactions with the walls or distortions of the local flow fields due to the solid, rough and strongly curved pore walls. In addition, increased interaction between the amphiphilic membranes can also contribute to the damping of the height fluctuations. These findings are in agreement with previous NSE measurements under grazing incidence with bicontinuous microemulsions of the C10E4–H2O–n-decane system at planar substrates. In this case an acceleration of the membrane dynamics was observed due to the unhindered propagation of long-wavelength fluctuations.21,43 One can consider the confinement on an extended planar surface with very low roughness below 1 nm and the confinement in a porous structure with highly curved, rough surfaces and pore sizes similar to the domain size in a confined bicontinuous microemulsion as the two extreme situations of confinement of a soft complex fluid by hard impenetrable surfaces.
In a previous publication37 we have put forward the hypothesis that surfactant adsorption to the pore walls leads to a shift of the surfactant concentration γ in the microemulsion towards lower values and hence to a transition into the three-phase region. A possibly associated change in the dynamics of the microemulsion seems to be overcompensated by the observed slowing down of the dynamics due to the influence of the confinement, which seems to figuratively freeze the structure as known for a glass transition of a liquid to a solid-like state. This damping and decreasing of the fluctuations is only observable in a NSE measurement since SANS measures the time-averaged structure of the microemulsion.
4 Conclusions
The objective of this investigation was to gain insight into the structural properties and the dynamics of a bicontinuous microemulsion in mesoporous confinement and to compare it with its behavior in bulk. The bulk behavior was examined through the use of SANS, DLS and NSE measurements. The combination of the latter two methods enabled the collective dynamics of the oil and water domains and the undulations of the surfactant film to be identified separately. The first mentioned follows the typical q2-dependence, which is a hallmark of this type of process. The later exhibited a q3 dependency, in accordance to the theory of Zilman and Granek. In order to study the influence of confinement, the bicontinuous microemulsion was imbibed into CPGs with three distinct pore diameters and studied using NSE spectroscopy. The pore diameters were chosen in such a way that the sizes of the oil and water domains in the microemulsion were significantly smaller than the pore size in one case and larger in another case. The collective dynamics of the oil and water domains are found to be impeded in all investigated pore sizes, with a more pronounced decrease in samples with pore diameter smaller than the characteristic lengths of the microemulsion in bulk. The undulations of the surfactant film in the macroporous sample remain within the same range as those observed in bulk, though the spectrum of undulation modes seems to be cut off as the pore diameter decreases. Since both pore diameter and specific surface area vary among the samples, the reduction in dynamics can be linked to either parameter. The fit results suggest that increased interaction with the pore walls cuts off long-wavelength fluctuations from the undulation mode spectrum. Interestingly, the influence of the chemical composition of the solid pore walls played a minor role, as the undulations of the surfactant film remained consistent for both hydrophilic and hydrophobic pore walls. However, collective dynamics of the oil and water domains are slightly further reduced in hydrophilic pores, indicating that the interaction with the solid interface has an influence on these motions. Time-dependent Gaussian field models can be used to analyze NSE data of microemulsions.49 This approach will be explored in future work to describe the dynamics of bicontinuous microemulsions in confinement.Data availability
Data for this article are available https://doi.org/10.14279/depositonce-20993. The raw NSE data from the experiments at IN15 can be accessed via the DOI: https://doi.org/10.5291/ILL-DATA.9-10-1764.Conflicts of interest
There are no conflicts to declareAcknowledgements
The authors thank the Deutsche Forschungsgemeinschaft (DFG) for financial support (project number 455432427). We thank the Institut Laue-Langevin (ILL, Grenoble, France) and the Australian Nuclear and Technology Organisation (ANSTO, Sydney, Australia) for the allocation of beamtime through proposal numbers 9-10-1764 and 16582, respectively.Notes and references
- J. Baumert, B. Asmussen, C. Gutt and R. Kahn, J. Chem. Phys., 2002, 116, 10869–10876 CrossRef CAS
.
- T. Hellweg, S. Schemmel, G. Rother, A. Brûlet, H. Eckerlebe and G. H. Findenegg, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12(Suppl. 1), S1–S4 CAS
.
- A. Kusmin, S. Gruener, A. Henschel, N. de Souza, J. Allgaier, D. Richter and P. Huber, Macromolecules, 2010, 43, 8162–8169 CrossRef CAS
.
- S. Mitra, V. Sharma and R. Mukhopadhyay, Rep. Prog. Phys., 2021, 84, 066501 CrossRef CAS PubMed
.
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed
.
- K. Nygård, Phys. Chem. Chem. Phys., 2017, 19, 23632–23641 RSC
.
- T. Hofmann, D. Wallacher, M. Mayorova, R. Zorn, B. Frick and P. Huber, J. Chem. Phys., 2012, 136, 124505 CrossRef PubMed
.
- R. Kimmich, S. Stapf, A. I. Maklakov, V. D. Skirda and E. V. Khozina, Magn. Reson. Imaging, 1996, 14, 793–797 CrossRef CAS PubMed
.
- L. Tremblay, S. M. Socol and S. Lacelle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 656–659 CrossRef CAS PubMed
.
- K. Binder, J. Horbach, R. Vink and A. de Virgiliis, Soft Matter, 2008, 4, 1555–1568 RSC
.
- F. Brochard and P. G. de Gennes, J. Phys., Lett., 1983, 44, 785–791 CrossRef CAS
.
- F. Formisano and J. Teixeira, J. Phys.: Condens. Matter, 2000, 12, A351–A356 CrossRef CAS
.
- S. Schemmel, D. Akcakayiran, G. Rother, A. Brulet, B. Farago, T. Hellweg and G. Findenegg, Mater. Res. Soc. Symp. Proc., 2004, 2004, 7.2.1–7.2.6 Search PubMed
.
- S. Schemmel, G. Rother, H. Eckerlebe and G. H. Findenegg, J. Chem. Phys., 2005, 122, 244718 CrossRef PubMed
.
- J. Fischer, L. Porcar, J. T. Cabral and T. Sottmann, J. Colloid Interface Sci., 2023, 635, 588–597 CrossRef CAS PubMed
.
- A. Mahboob, S. Kalam, M. S. Kamal, S. S. Hussain and T. Solling, J. Pet. Sci. Eng., 2022, 208, 109312 CrossRef CAS
.
- M. E. Cates and S. T. Milner, Phys. Rev. Lett., 1989, 62, 1856–1859 CrossRef CAS PubMed
.
- O. Diat, D. Roux and F. Nallet, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 3296–3299 CrossRef CAS PubMed
.
- J. Bowers, M. C. Vergara-Gutierrez and J. R. P. Webster, Langmuir, 2004, 20, 309–312 CrossRef CAS PubMed
.
- W. A. Hamilton, L. Porcar, P. D. Butler and G. G. Warr, J. Chem. Phys., 2002, 116, 8533–8546 CrossRef CAS
.
- H. Frielinghaus, M. Kerscher, O. Holderer, M. Monkenbusch and D. Richter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041408 CrossRef CAS PubMed
.
- S. Wellert, R. Stehle, S. Micciulla, M. Dahl, R. Steitz, T. Hellweg and O. Holderer, Front. Soft Matter, 2022, 2, 887610–887611 CrossRef
.
- P. Petrov, U. Olsson and H. Wennerström, Langmuir, 1997, 13, 3331–3337 CrossRef CAS
.
- M. Kahlweit and R. Strey, Angew. Chem., Int. Ed. Engl., 1985, 24, 654–668 CrossRef
.
- T. Sottmann, R. Strey and S.-H. Chen, J. Chem. Phys., 1997, 106, 6483–6491 CrossRef CAS
.
- S. Burauer, T. Sachert, T. Sottmann and R. Strey, Phys. Chem. Chem. Phys., 1999, 1, 4299–4306 RSC
.
- O. Holderer, H. Frielinghaus, M. Monkenbusch, M. Klostermann, T. Sottmann and D. Richter, Soft Matter, 2013, 9, 2308 RSC
.
- J. A. Bosley and J. C. Clayton, Biotechnol. Bioeng., 1994, 43, 934–938 CrossRef CAS PubMed
.
- M. Kahlweit, R. Strey and G. Busse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 4197–4209 CrossRef CAS PubMed
.
- K. Wood, J. P. Mata, C. J. Garvey, C.-M. Wu, W. A. Hamilton, P. Abbeywick, D. Bartlett, F. Bartsch, P. Baxter, N. Booth, W. Brown, J. Christoforidis, D. Clowes, T. d'Adam, F. Darmann, M. Deura, S. Harrison, N. Hauser, G. Horton, D. Federici, F. Franceschini, P. Hanson, E. Imamovic, P. Imperia, M. Jones, S. Kennedy, S. Kim, T. Lam, W. T. Lee, M. Lesha, D. Mannicke, T. Noakes, S. R. Olsen, J. C. Osborn, D. Penny, M. Perry, S. A. Pullen, R. A. Robinson, J. C. Schulz, N. Xiong and E. P. Gilbert, J. Appl. Crystallogr., 2018, 51, 294–314 CrossRef CAS
.
- M. Mihailescu, M. Monkenbusch, H. Endo, J. Allgaier, G. Gompper, J. Stellbrink, D. Richter, B. Jakobs, T. Sottmann and B. Farago, J. Chem. Phys., 2001, 115, 9563–9577 CrossRef CAS
.
- Albert Prause, SimplightQt, https://git.tu-berlin.de/MolMat/SimplightQt.
- P. Wiltzius, F. S. Bates, S. B. Dierker and G. D. Wignall, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 2991–2994 CrossRef CAS PubMed
.
- N. F. Berk, C. J. Glinka, W. Haller and L. C. Sandert, MRS Proc., 1989, 166, 409–414 CrossRef
.
- P. Levitz, G. Ehret, S. K. Sinha and J. M. Drake, J. Chem. Phys., 1991, 95, 6151–6161 CrossRef CAS
.
- M. Teubner and R. Strey, J. Chem. Phys., 1987, 87, 3195–3200 CrossRef CAS
.
- M. Dahl, C. J. Gommes, R. Haverkamp, K. Wood, S. Prévost, P. Schröer, T. Omasta, T. J. Stank, T. Hellweg and S. Wellert, RSC Adv., 2024, 14, 28272–28284 RSC
.
- G. Gompper, H. Endo, M. Mihailescu, J. Allgaier, M. Monkenbusch, D. Richter, B. Jakobs, T. Sottmann and R. Strey, Europhys. Lett., 2001, 56, 683–689 CrossRef CAS
.
- S. Komura, T. Takeda, Y. Kawabata, S. K. Ghosh, H. Seto and M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041402 CrossRef CAS PubMed
.
- B. K. Paul and S. P. Moulik, Proc. Indian Natl. Sci., 2000, 499–519 CAS
.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS PubMed
.
- M. Monkenbusch, O. Holderer, H. Frielinghaus, D. Byelov, J. Allgaier and D. Richter, J. Phys.: Condens. Matter, 2005, 17, S2903–S2909 CrossRef CAS
.
- F. Lipfert, O. Holderer, H. Frielinghaus, M.-S. Appavou, C. Do, M. Ohl and D. Richter, Nanoscale, 2015, 7, 2578–2586 RSC
.
- G. Buntkowsky, H. Breitzke, A. Adamczyk, F. Roelofs, T. Emmler, E. Gedat, B. Gruünberg, Y. Xu, H.-H. Limbach, I. Shenderovich, A. Vyalikhzb and G. Findenegg, Phys. Chem. Chem. Phys., 2007, 9, 4843–4853 RSC
.
- M. Vogel, Eur. Phys. J.: Spec. Top., 2010, 189, 47–64 CAS
.
- A. Jani, M. Busch, J. B. Mietner, J. Ollivier, M. Appel, B. Frick, J.-M. Zanotti, A. Ghoufi, P. Huber, M. Fröba and D. Morineau, J. Chem. Phys., 2021, 154, 094505 CrossRef CAS PubMed
.
- J. M. Drake and J. Klafter, Phys. Today, 1990, 43, 46–55 CrossRef CAS
.
- S. Safran, Surf. Sci., 2002, 500, 127–146 CrossRef CAS
.
- C. J. Gommes, R. Zorn, S. Jaksch, H. Frielinghaus and O. Holderer, J. Chem. Phys., 2021, 155, 1–16 CrossRef PubMed
.
Footnotes |
| † All data is accessible at https://doi.org/10.14279/depositonce-20993. |
| ‡ Electronic supplementary information (ESI) available: Fitted parameters and additional figures. See DOI: https://doi.org/10.1039/d4sm00925h |
| This journal is © The Royal Society of Chemistry 2024 |