The fluctuation–dissipation relation holds for a macroscopic tracer in an active bath

Abstract

The fluctuation–dissipation relation (FDR) links thermal fluctuations and dissipation at thermal equilibrium through temperature. Extending it beyond equilibrium conditions in pursuit of broadening thermodynamics is often feasible, albeit with system-dependent specific conditions. We demonstrate experimentally that a generalized FDR holds for a harmonically trapped tracer colliding with self-propelled walkers. The generalized FDR remains valid across a large spectrum of active fluctuation frequencies, extending from underdamped to critically damped dynamics, which we attribute to a single primary channel for energy input and dissipation in our system.

---

The fluctuation–dissipation relation (FDR) is a fundamental result in nonequilibrium statistical mechanics. Its significance lies in providing a means to compute how a system statistically responds to small external perturbations, in terms of the correlations in the unperturbed dynamics. A classic example of the FDR is the Einstein relation,¹D = μk_BT, linking the diffusivity (fluctuations) D with the mobility (response) μ for a Brownian particle in equilibrium with a bath at temperature T (k_B denotes the Boltzmann constant). This relation, known as a static FDR, is established under constant force conditions. On the other hand, the dynamic FDR broadens this concept by encompassing time or frequency-dependent forces via linear response theory.^2,3

Specifically, for a system slightly perturbed from its stable equilibrium condition, the mean response of an observable x, denoted as R_x(t > 0), to an abrupt arrest of a force F₀ at time t = 0, is connected to the autocorrelation function C_x(t) in the unperturbed condition. The dynamic FDR then states,^4,5

A static FDR is recovered at t = 0. Namely, C_x(t) → 〈Δx²〉₀ and R_x(t) → δ〈x(0)〉 and we obtain a relation in terms of energies, F₀〈Δx²〉₀/δ〈x(0)〉 = k_BT. The dynamic FDR (eqn (1) and its equivalent forms) has been utilized as a model-free method to assess equilibrium in various experimental systems.^6–8 If the relationship in eqn (1) is violated, it indicates that the system is operating outside of thermal equilibrium.

Extensions of the FDR to perturbations of nonequilibrium steady states were derived previously, both for weak perturbations (e.g.,^9–14) and for strong perturbations leading to a nonlinear form of FDR.^5,15,16 However, most of these relations usually require a variable transformation or are derived for special non-equilibrium models (such as spiking neurons as in ref. 13). Alternatively, in nonequilibrium scenarios, a key theoretical use of the FDR is the introduction of an effective temperature T_eff,^17–31 satisfying a generalized FDR by substituting T = T_eff in eqn (1). When T_eff remains constant, irrespective of time and perturbation magnitude, the analogy to an equilibrium description becomes rather transparent: the response to an external perturbation is directly proportional to the unperturbed correlations, with F₀/k_BT_eff serving as the constant of proportionality.

An archetypal model for studying the validity range of the FDR out of equilibrium, and the emergence of an effective temperature, is a tracer particle trapped in a harmonic potential and subject to both thermal and active collisions,^32–38e.g., an optically trapped colloidal particle in a suspension of self-propelled organisms.^39–44 Within this model, which is typically overdamped, there are two timescales of interest: the typical relaxation time τ_r to the steady state, and the characteristic time of the active stochastic forces τ_c. In previous demonstrations involving such a system, it was established that the generalized FDR holds for large times only under the condition that τ_c is smaller than the longest relaxation time in the steady state.²² Specifically, the FDR holds when the external driving dominantly determines both fluctuations and dissipation.

On a different scale, far from thermal equilibrium, numerical investigations of a tracer particle within an athermal uniformly driven granular gas^45–47 validate a generalized FDR solely for nearly elastic collisions.^48,49 In this scenario, the effective temperature was determined through the tracer's mean kinetic energy, T_eff ∼ 〈v²〉.¹⁸ We note that the effective temperature defined through the FDR was shown to be equivalent to other independent definitions of effective temperatures in driven granular media.^50,51

These findings suggest that the generalized FDR remains applicable when the same physical process governs the dissipation of external perturbations while simultaneously driving the tracer's fluctuations around its steady state. To test this hypothesis for a completely athermal system, we study a harmonically trapped macroscopic tracer particle in an active bath of self-propelled walkers. In our previous work,¹⁶ we demonstrated that the tracer particle's dynamics are consistent with Markovian dynamics, as evidenced by the fulfillment of a non-linear FDR. Notably, this non-linear FDR applies only to a unique conjugated variable and does not yield a straightforward definition of an effective temperature. Here, we find that a generalized FDR holds in a wide range of experimental conditions with a naturally defined effective temperature that coincides with the unperturbed mean potential energy of the tracer, . Here, 〈Δx²〉₀ = 〈(x − 〈x〉)²〉 is the variance of the tracer's position in the unperturbed steady state.

Our experiments are conducted as depicted in Fig. 1A: a Styrofoam ball is placed in a parabolic plastic arena and is driven into a nonequilibrium steady state by random collisions with an assembly of vibration-driven bristle robots (bbots, Hexbugs™ nano,^16,52–55). The motion of the ball is recorded by a top-view camera (Brio 4K, Logitech) at 30 fps. An image analysis algorithm is used to extract the ball's trajectory projection on the XY plane from top-view images. We assume independent motion along all three axes and focus on analyzing the tracer's movement along the X-axis, where the perturbation occurs. The collisions are non-elastic, i.e., the tracer's restitution coefficient depends on impact velocities (r ≈ 0.8 for low velocities, see ESI†). We note that in contrast to shaken granular matter, the embedding media is active on the single particle level and exhibits emergent collective motion typical for active matter systems.^52,55 The characteristics of the bbot bath are added in the ESI.† Namely, a single bbot generally performs circular motion in a parabolic arena when it has sufficient inertia.⁵³ Placing additional bbots and a tracer ball in the harmonic well randomizes the bbot motion due to collisions, resulting in an active gas-like state (see ESI,† Movie S1). Notably, the speed distribution of the bbots remains independent of N_b, while their spatial distribution increasingly deviates from the initial circular motion as N_b increases. As a result, the tracer is randomly kicked by the bbots and exhibits Brownian-like motion (Fig. 1B).

Fig. 1 Experimental setup. (A) A Styrofoam ball (diameter ∼ 4 cm) is trapped in a gravitational harmonic potential, a plastic bowl (diameter 38 cm, depth 5 cm), and subjected to collisions with N_b = 15 self-propelled bbots (inset: standard bbot, 4 × 1 cm). The ball is repeatedly perturbed with a uniform air stream created by an external fan along the x-axis (white arrow) to test a fluctuation-response relation. To enforce an abrupt onset and release of the perturbation, a mechanical shutter is used (denoted by ‘S’). (B) Part (30 s) of a typical trajectory of the Styrofoam ball in the bbot arena. (C) Normalized measured position autocorrelation as a function of time (circles), and fit to eqn (2), with τ_r = 0.336 ≈ τ_Ω = 0.340 s (solid line). The inset shows the autocorrelation of an equivalent experiment with N_b = 4 (τ_r = 0.54 s, τ_Ω = 0.23 s). The results present an average over M = 375 sequences. (D) The cross-section probability density distributions across the x axis (blue), and the y axis (green), for N_b = 15.

To measure the system's mean response, we introduce a mechanical perturbation by activating an external fan (Yate Loon electronics 12 V 0.30 A cooling fan) to create an airflow. After the tracer settles into a perturbed steady state, we abruptly deactivate the disturbance, with a physical shutter, allowing the ball to return to its original steady state. We use the number of bbots N_b as a control parameter, keeping the trapping stiffness constant, i.e., the arena shape and tracer size are held constant. Naturally, the mean free time between collisions τ_c decreases with N_b, and the collision frequency increases‡ (see below).

Since thermal forces are negligible, the ensemble of bbots N_b acts as a dry active bath, meaning that the tracer is subjected to a single active noise source (bbot impacts). Therefore, the noise characteristic time τ_c and the stationary relaxation time τ_r are intrinsic system timescales. Particularly, we expect that sufficiently frequent collisions will dominate the tracer's dissipation rate of small external perturbations. In this scenario, the main channel for dissipation is the same process that induces active fluctuations, and we expect a generalized FDR to hold as was suggested by Kubo for equilibrium conditions.²

Stationary dynamics and statistics

We start our experiments by characterizing the nonequilibrium steady state, which we will later perturb. To this end, we focus on a system with a relatively large number of bbots, N_b = 15, in which the tracer particle is subjected to frequent collisions with τ_c = 0.28 s, extracted by image analysis identification of collisions. We record 375 experiments of duration 30 s from which the tracer particle trajectory is extracted. From the extracted trajectories, we calculate the tracer's (ensemble) average normalized position autocorrelation,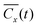 (Fig. 1C). It turns out that this correlation is well fit by the generic autocorrelation function of a damped noisy harmonic oscillator,^32,49where 〈Δx²〉₀ = C_x(0) is the variance and ω² = τ_Ω⁻² − τ_r⁻². This fit provides effective values of the system's time scale, the damping rate, 2τ_r⁻¹, and the (effective) natural frequency of the harmonic trap§, τ_Ω⁻¹, for which we obtain τ_r = 0.336 ≈ τ_Ω = 0.340 s. These values suggest that the tracer dynamics exhibit critically damped behavior. We note that underdamped relaxation (τ_r > τ_Ω) is observed for much lower N_b = 4 (inset of Fig. 1C).

Next, we consider the position probability distribution P(x,y), of the tracer particle (Fig. 1D). We find that P(x,y) fits well to a Boltzmann-like Gaussian distribution in both x and y projections, with a small expected deviation near the arena boundaries (|x| > 10 cm). We estimate the gravitational potential acting on the tracer particle by , with k = mga = 28.2 ± 3 g s⁻², m = 1 ± 0.1 g – the tracer mass, g – the gravitational acceleration (not to be confused with the unit of mass, g, used before), and a – the curvature of the arena. Plotting the estimated U_x(x) and fitting it to our Boltzmann-like position distribution (see ESI†), we obtain an effective temperature of T_eff ≈ 3.1 × 10¹⁸ K, 16 orders of magnitude higher than room temperature. Interestingly, the tracers potential energy set by the effective temperature is comparable to the mean kinetic energy of the bristle bots, E_b ≈ 7 μJ: we observe that k_BT_eff ≈ 7E_b.

Fluctuation–dissipation relation

With a full characterization of the nonequilibrium steady state dynamics and statistics of the system, we continue by measuring the system's response to a small mechanical perturbation (10 V fan operating voltage, force F₀ ≈ 62 μN). We use the following protocol to measure the ensemble average response of the system (see also ref. 16 for a similar procedure): during an experiment, every two minutes, the fan is turned on for a minute and abruptly turned off at t₀ = 60 s for the following minute (see Fig. 2A). Fig. 2B shows the time-dependent mean value 〈x(t)〉 for M = 375 perturbation sequences, constituting both the mean motion of the tracer at the perturbed and unperturbed steady states (parts II and IV) and the transition between them (parts I and III).

Fig. 2 An experimental FDR test. (A) Typical perturbation sequence x(t): the fan is turned on for a minute and then abruptly turned off for the following minute. (B) The time-dependent mean value 〈x(t)〉 is obtained within a time-window of 2 minutes. The displacement Δx is the mean distance between states II and IV. (C) The individual time-dependent quantities of transient response 〈x(t₁)〉 − 〈x〉₀ (bottom), and unperturbed autocorrelation function C_x(t₁) (top), are displayed. The dashed lines are standard errors. (D) The generalized FDR of eqn (1) with an effective temperature T = T_eff ∼ 〈Δx²〉₀. The results present an average over M = 375 sequences with N_b = 15 and fan operating voltage 10 V. The vertical dashed line is T_c = 1 s and the horizontal dot-dashed lines are the standard deviations of part IV.

The response of the system to the perturbation arrest, at t₁ = t − t₀, given by R_x(t₁) = δ〈x(t₁)〉 = 〈x(t₁)〉 − 〈x〉₀, and the unperturbed autocorrelation function, C_x(t₁) = 〈x(t₁)x(0)〉₀, are therefore measured from parts III, and IV respectively (Fig. 2C). According to the generalized FDR, eqn (1) should hold exactly for our measured response and autocorrelation if we define T = T_eff and F₀ = kΔx, where Δx ≡ 〈x〉_F0 − 〈x〉₀. This is verified in Fig. 2D with good accuracy, where we have used the value of T_eff obtained from the stationary position distribution. We note that at t₁ > T_c = 1 s the stationary noise becomes significant and the agreement or disagreement of C_x and R_x is hard to assess. Therefore, we cannot rule out an FDR violation beyond T_c. Since T_eff fulfills the generalized FDR for any t₁ < T_c, it also fulfills it at t₁ = 0. Therefore, k_BT_eff = k〈Δx²〉₀, which is trivial for a system exhibiting Boltzmann-like statistics. However, this relation should generally hold for any P(x,y) (with different N_b).

Our experimental findings establish a consistent effective temperature, T_eff, derived from the generalized FDR. This T_eff is consistent with the temperature determined by the average potential energy and remains independent of the force (see ESI†). With this defined T_eff, we can further explore the conditions under which the generalized FDR remains applicable.

Range of validity of the FDR.

First, we obtain the nonequilibrium steady state dynamics and statistics of the system (Fig. 1) with different numbers of bbots N_b, the results are displayed in Fig. 3. We find that P(x, N_b) transitions into a non-Gaussian distribution as N_b decreases (Fig. 3A). This is expected as the typical time between collisions τ_c increases beyond the typical relaxation of the tracer to the bottom of the well.⁴² By using a consistent definition of effective temperature for all configurations, k_BT_eff = k〈Δx²〉₀, we observe a monotonic increase in T_eff with N_b (Fig. 3B, upper panel). We quantify the departure from Boltzmann statistics by calculating the non-Gaussian parameter (excess kurtosis) of the position distribution, (Fig. 3B, lower panel).

Fig. 3 Stationary dynamics and statistics. We consider configurations of N_b = {2, 3, 4, 6, 10, 12, 15, 17} bbot baths. (A) Position probability density (symbols) and the normal (Gaussian) distribution for N_b = 15 (dashed line). (B) Effective temperature T_effvs. N_b (upper panel), and corresponding non-Gaussian parameter (lower panel). Error bars are standard deviations. (C) The (ensemble) averaged normalized position autocorrelation for different N_b. (D) Different characteristic timescales as a function of N_b: mean free time between collisions τ_c (line), steady-state dynamical timescales (obtained by a fit to eqn 2) τ_r (squares) and τ_Ω (crosses), the tracer's damping timescale in the absence of bbots τ⁰_r = 0.9 s and (horizontal lines). The results were obtained for an ensemble average of M = 375 sequences, with the same tracer m≈1 g, and gravitational stiffness k ≈ 28.2 g s⁻².

In Fig. 3C and D we plot the normalized autocorrelation and its characteristic times, τ_r and τ_Ω, from a fit to eqn (2). A transition from under- to critically damped dynamics as N_b increases is manifested in the reduction of the oscillations in and in the relaxation time to the steady state τ_r. The diminished influence of the tracer's inertia for larger N_b is clearly due to an increase of dissipation caused by more frequent collisions of tracer particle and bbots. The evaluated mean free time between collisions τ_c results in values similar to τ_r, except for the limiting case of N_b = 2. In the latter, the bbots rarely collide and mainly drive the ball around the trap. The dissipative timescale associated with the arena was probed by applying the FDR step-perturbation protocol with the bbots removed (see ESI†). The passive damping time τ⁰_r = 0.9 s was obtained by fitting the non-fluctuating response to eqn (2), with s directly calculated (Fig. 3D, horizontal lines). Note that τ_Ω shows a non-trivial dependence on N_b, due to the physical presence of the bbots in the harmonic trap.

Fig. 4A shows a parametric plot of the generalized FDRs for different N_b. The normalized mean response δ〈x〉/Δx is plotted versus the autocorrelation C_x, within the response time regime t₁ < T_c. Rescaling the autocorrelation by T_eff, we obtain a master curve (Fig. 4A, inset) in which all the systems obeying the FDR collapse to a single line. A clear deviation is seen for N_b = 2 and 3, which violates the FDR. In our experiments, it is clear that the main source of the tracer's fluctuations is the collisions with the bbots. To determine the dominant dissipation source we compare the (normalized) mean response δ〈x〉 of the two extreme cases, N_b = 17 and N_b = 3, to the deterministic response of the tracer in the absence of bbots δx₀ (Fig. 4B, upper and lower panel, respectively). For N_b = 17 collisions are sufficiently frequent (τ_c < τ⁰_r) such that the mean response deviates significantly from δx₀. In this regime, the dissipation is predominantly governed by the collisions between the tracer and the bbots. In contrast, for N_b = 3 collisions are rare (τ_c ≈ τ⁰_r), and the mean response of the tracer closely resembles δx₀. While collisions play a role in the dissipation, the primary source of dissipation in this case is the friction between the tracer and the bowl. Consequently, this scenario leads to a violation of the FDR.

Fig. 4 Validity range of the FDR. The results are for experimental configurations with different N_b, as in Fig. 3. (A) The generalized FDRs are displayed in a parametric plot with the normalized response δ〈x〉/Δx versus the autocorrelation C_x, for times t₁ < T_c. Error bars are standard errors. The straight linear lines correspond to a perfect FDR with slope = (k_BT_eff)⁻¹. The inset shows a unitary parametric plot, where a deviation (FDR violation) is observed for lowest bbot numbers N_b = 3 and 2 (triangles). (B) Normalized plot of generalized FDRs for N_b = 17 (upper panel) and N_b = 3 (lower panel). Here, δx(t₁)/Δx is plotted against 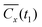, and is compared to the normalized non-fluctuating response under the same perturbation (10 V fan voltage), in the absence of bbots. See ESI† for all dynamic FDR results.

Discussion

In summary, we have experimentally confirmed the validity of a generalized FDR, far from equilibrium. We find that for N_b > 3 the FDR holds with an effective temperature that is given by the tracer's mean potential energy, T_eff ∼ 〈Δx²〉₀, even when the steady state dynamics are underdamped and the probability distribution is non-Gaussian. We note that at N_b > 17, bbots frequently tumble and form long-lived static clusters at the center trap region. This is reflected in a small flat region in the center of the tracer's position distribution for N_b = 17 (see ESI†). The presence of the bbot cluster changes the trap's properties and the tracer's dynamics, hindering accurate FDR tests for N_b > 17.

Moreover, our light tracer can move out of the plane, evading entrapment within large clusters of bbots. Therefore, in contrast to previous reports in which caging and memory effects have been shown to result in FDR violations at high bath densities,^5,56 we did not observe such a violation in our experiments. However, we expect to see FDR violations once collisions are not sufficiently frequent to act as the main source for dissipation to external perturbations. This is the case for the lowest numbers of bbots N_b = 2 and 3, where the generalized FDR fails.

Our findings for a single tracer system suggest that the FDR should hold for many tracer systems if tracer–tracer interactions are non-dissipative. However, previous evidence of FDR violations in dense active assemblies⁵⁷ and reported non-trivial effects of bath density on tracer-bath interactions⁵⁸ point to a more complex situation.

The confirmation of a generalized FDR, across an extensive range of effective temperatures, raises the following three broader issues. Is there an overarching equipartition relation that connects these effective temperatures to T_eff defined via momentum variables rather than positional ones? Preliminary results indicate that a linear relation between T_eff and the tracer's mean kinetic energy, , holds up to N_b = 10 in our experiments (see ESI†), in accord with a previous study.⁵⁰ Secondly, do these temperatures hold significance within the thermodynamic framework governing these systems? For instance, could they dictate energy flow in scenarios where two such systems are in contact? Lastly, one feature of our experimental system that was observed in a previous study is that its dynamics are consistent with Markovian dynamics.¹⁶ While Markovianity is not essential for the FDR to prevail in thermal equilibrium, an intriguing avenue of exploration involves assessing its validity in weakly perturbed systems immersed in an active, non-Markovian environment, where dissipation and fluctuation derive from the same underlying physical process.

Data availability

The data that support the findings of this study are available from the corresponding author, Y. R., upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. B. and Y. R. acknowledge support from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant agreement No. 101002392).

References

1. A. Einstein, Ann. Phys., 1905, 17, 208.
2. R. Kubo, Rep. Prog. Phys., 1966, 29, 255.
3. R. Kubo, Science, 1986, 233, 330–334.
4. U. M. B. Marconi, A. Puglisi, L. Rondoni and A. Vulpiani, Phys. Rep., 2008, 461, 111–195.
5. M. Baldovin, L. Caprini, A. Puglisi, A. Sarracino and A. Vulpiani, The many faces of fluctuation-dissipation relations out of equilibrium, Springer, 2022, pp. 29–57.
6. P. Martin, A. Hudspeth and F. Jülicher, Proc. Natl. Acad. Sci., 2001, 98, 14380–14385.
7. D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Science, 2007, 315, 370–373.
8. H. Turlier, D. A. Fedosov, B. Audoly, T. Auth, N. S. Gov, C. Sykes, J.-F. Joanny, G. Gompper and T. Betz, Nat. Phys., 2016, 12, 513–519.
9. L. Berthier and J.-L. Barrat, Phys. Rev. Lett., 2002, 89, 095702.
10. J. Prost, J.-F. Joanny and J. M. Parrondo, Phys. Rev. Lett., 2009, 103, 090601.
11. J. Mehl, V. Blickle, U. Seifert and C. Bechinger, Phys. Rev. E, 2010, 82, 032401.
12. L. Willareth, I. M. Sokolov, Y. Roichman and B. Lindner, Europhys. Lett., 2017, 118, 20001.
13. B. Lindner, Phys. Rev. Lett., 2022, 129, 198101.
14. A. Pérez-Cervera, B. Gutkin, P. J. Thomas and B. Lindner, PNAS, 2023, 120, e2303222120.
15. E. Lippiello, F. Corberi, A. Sarracino and M. Zannetti, Phys. Rev. E, 2008, 78, 041120.
16. K. Engbring, D. Boriskovsky, Y. Roichman and B. Lindner, Phys. Rev. X, 2023, 13, 021034.
17. R. Ojha, P.-A. Lemieux, P. Dixon, A. Liu and D. Durian, Nature, 2004, 427, 521–523.
18. D. Villamaina, A. Puglisi and A. Vulpiani, J. Stat. Mech.: Theory Exp., 2008, 2008, L10001.
19. A. R. Abate and D. J. Durian, Phys. Rev. Lett., 2008, 101, 245701.
20. C. Maggi, M. Paoluzzi, N. Pellicciotta, A. Lepore, L. Angelani and R. Di Leonardo, Phys. Rev. Lett., 2014, 113, 238303.
21. G. Szamel, Phys. Rev. E, 2014, 90, 012111.
22. E. Dieterich, J. Camunas-Soler, M. Ribezzi-Crivellari, U. Seifert and F. Ritort, Nat. Phys., 2015, 11, 971–977.
23. F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Phys. Rev. X, 2015, 5, 011004.
24. S. Steffenoni, K. Kroy and G. Falasco, Phys. Rev. E, 2016, 94, 062139.
25. C. Maggi, M. Paoluzzi, L. Angelani and R. Di Leonardo, Sci. Rep., 2017, 7, 17588.
26. M. Han, J. Yan, S. Granick and E. Luijten, PNAS, 2017, 114, 7513–7518.
27. I. Petrelli, L. F. Cugliandolo, G. Gonnella and A. Suma, Phys. Rev. E, 2020, 102, 012609.
28. E. Flenner and G. Szamel, Phys. Rev. E, 2020, 102, 022607.
29. A. Solon and J. M. Horowitz, J. Phys. A, 2022, 55, 184002.
30. J. F. Boudet, J. Jagielka, T. Guerin, T. Barois, F. Pistolesi and H. Kellay, Phys. Rev. Res., 2022, 4, L042006.
31. L. F. Cugliandolo, J. Phys. A, 2011, 44, 483001.
32. G. E. Uhlenbeck and L. S. Ornstein, Phys. Rev., 1930, 36, 823.
33. C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
34. É. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. Van Wijland, Phys. Rev. Lett., 2016, 117, 038103.
35. V. Démery and É. Fodor, J. Stat. Mech., 2019, 2019, 033202.
36. S. Ye, P. Liu, F. Ye, K. Chen and M. Yang, Soft Matter, 2020, 16, 4655–4660.
37. J. Shea, G. Jung and F. Schmid, Soft Matter, 2022, 18, 6965–6973.
38. A. Jayaram and T. Speck, Europhys. Lett., 2023, 143, 17005.
39. X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017.
40. L. Angelani, R. Di Leonardo and G. Ruocco, Phys. Rev. Lett., 2009, 102, 048104.
41. J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304.
42. J. T. Park, G. Paneru, C. Kwon, S. Granick and H. K. Pak, Soft Matter, 2020, 16, 8122–8127.
43. R. Goerlich, L. B. Pires, G. Manfredi, P.-A. Hervieux and C. Genet, Phys. Rev. E, 2022, 106, 054617.
44. S. Paul, A. Jayaram, N. Narinder, T. Speck and C. Bechinger, Phys. Rev. Lett., 2022, 129, 058001.
45. A. Puglisi, V. Loreto, U. M. B. Marconi and A. Vulpiani, Phys. Rev. E, 1999, 59, 5582.
46. T. Pöschel and S. Luding, Granular Gases, Springer Science & Business Media, 2001, vol. 564.
47. J. Van Zon and F. MacKintosh, Phys. Rev. Lett., 2004, 93, 038001.
48. A. Puglisi, A. Baldassarri and V. Loreto, Phys. Rev. E, 2002, 66, 061305.
49. Y. Shokef and D. Levine, Phys. Rev. Lett., 2004, 93, 240601.
50. J.-Y. Chastaing, J.-C. Géminard and A. Naert, J. Stat. Mech.: Theory Exp., 2017, 2017, 073212.
51. Z. Zeng, S. Zhang, X. Zheng, C. Xia, W. Kob, Y. Yuan and Y. Wang, Phys. Rev. Lett., 2022, 129, 228004.
52. L. Giomi, N. Hawley-Weld and L. Mahadevan, Proc. R. Soc. London, Ser. A, 2013, 469, 20120637.
53. O. Dauchot and V. Démery, Phys. Rev. Lett., 2019, 122, 068002.
54. A. Altshuler, O. L. Bonomo, N. Gorohovsky, S. Marchini, E. Rosen, O. Tal-Friedman, S. Reuveni and Y. Roichman, Phys. Rev. Res., 2024, 6, 023255.
55. O. Chor, A. Sohachi, R. Goerlich, E. Rosen, S. Rahav and Y. Roichman, Phys. Rev. Res., 2023, 5, 043193.
56. A. Gnoli, A. Puglisi, A. Sarracino and A. Vulpiani, PLoS One, 2014, 9, e93720.
57. D. Levis and L. Berthier, Europhys. Lett., 2015, 111, 60006.
58. L. Caprini, A. Ldov, R. K. Gupta, H. Ellenberg, R. Wittmann, H. Löwen and C. Scholz, Commun. Phys., 2024, 7, 52.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00808a

‡ The mean free time between collisions τ_c was estimated by tracking both the bbots and the tracer, averaging over the times in which there's no physical contact between the bbots and the tracer.

§ Note that since the bbots are confined within the same gravitational well as the tracer, the harmonic trap's natural frequency τ_Ω⁻¹ depends on N_b and does not coincide with the measured stiffness, i.e., .

---