Active nematics in corrugated channels
Jaideep P.
Vaidya
a,
Tyler N.
Shendruk
 b and
Sumesh P.
Thampi
b and
Sumesh P.
Thampi
 *a
*a
aDepartment of Chemical Engineering, Indian Institute of Technology Madras, Chennai 600036, India. E-mail: sumesh@iitm.ac.in
bSchool of Physics and Astronomy, The University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK
First published on 24th September 2024
Abstract
Active nematic fluids exhibit complex dynamics in both bulk and in simple confining geometries. However, complex confining geometries could have substantial impact on active spontaneous flows. Using multiparticle collision dynamics simulations adapted for active nematic particles, we study the dynamic behaviour of an active nematic fluid confined in a corrugated channel. The transition from a quiescent state to a spontaneous flow state occurs from a weak swirling flow to a strong coherent flow due to the presence of curved-wall induced active flows. We show that the active nematic fluid flows in corrugated channels can be understood in two different ways: (i) as the result of an early or delayed flow transition when compared with that in a flat-walled channel of appropriate width and (ii) boundary-induced active flows in the corrugations providing an effective slip velocity to the coherent flows in the bulk. Thus, our work illustrates the crucial role of corrugations of the confining boundary in dictating the flow transition and flow states of active fluids.
1 Introduction
Active and living systems are out of equilibrium due to continuous influx of energy at microscopic scales. Common examples of these systems are suspensions of cytoskeletal filaments powered by molecular motors,1–4 bacterial suspensions,5,6 cellular layers7–9 and Janus catalysts.10–12 Continuous energy injection not only leads to the motion of individual active particles but also results in a rather exciting phenomenon of collective motion. Collective dynamics in dense suspensions of active particles usually consist of jets and circulations – a state commonly called active turbulence.13–15 Several experimental realizations of active turbulence have been demonstrated in the literature.2,5,16–19Active nematics are model fluids that capture the dynamics of some of the above mentioned systems.13,20–22 By incorporating the active stress generated by microscopic active entities, active nematics build upon the theory of passive nematic liquid crystals.23–25 Hence, mechanisms such as generation and dynamics of topological defects that sustain active turbulence, are inherent features of active nematic fluids.13,26–29 Active stress generates hydrodynamic instabilities overcoming the elastic, viscous and frictional forces in the active fluid. In a confined active nematic fluid, the competition between activity and the opposing forces gives rise to a spontaneous flow transition at a critical activity.3,21,30–32
Confinements play a major role in dictating the dynamic state of active systems, much different from those of driven systems. For example, when active nematics are confined in microchannels of square cross section, they exhibit a multitude of states, such as a state of no fluid flow, streaming states like unidirectional, oscillatory or double helix flows and swirling states including vortex lattices or turbulent flows. All these depend on varying a single parameter, namely the ratio of the channel width to the active length scale.21,33,34 Despite the crucial importance of boundaries in dictating the dynamics of active fluids, most investigations so far have considered only channels with flat walls,3,31,32,35–38 cylindrical channels,39 or annular rings.33,40–42 The effect of non-uniformity of the channel walls on the dynamics of active fluids has not been addressed in the literature yet.
However, some of the previous investigations have hinted at the effect of non-uniform boundary walls on the dynamics of active nematic fluids. In the experiments of Wu et al.,33 asymmetric corrugations of the channel walls were used to direct streaming flows generated by mixtures of microtubule bundles and kinesin molecular motors. When the active suspension was confined in a toroid of square cross section it produced a streaming flow in the channel, with equal probability of streaming in clockwise and counter clockwise directions. On the other hand, when the channel walls of the toroid were modified by providing saw-tooth like notches, it was possible to control the directionality of the streaming flows. Such a control on the directionality of active fluid flows is essential for any future engineering applications. While the exact mechanism that leads to directionality is not clear, it was shown that the directionality of the flow in the toroid was accompanied by swirls in the undulated sections of the channel wall. Being at low Reynolds number, the presence of swirling flows in the undulations of the channel is also intriguing. Asymmetric structures driving directionality have also been demonstrated in other active systems.43 Another feature the curved boundaries provide is their capability to drive active fluid flows. The boundary curvature driven flows arise since active entities preferentially orient at the solid wall, as demonstrated using theoretical,44,45 computational46 and experimental47 tools. However, the role of these boundary-induced active flows in dictating the flow transition, the directionality of flow or the flow state itself has not yet been analyzed.
In this work, we computationally investigate the flow generated by active nematic fluids when confined in corrugated channels. Since the spontaneous flow transition in an active nematic fluid is well studied theoretically,30 experimentally3,32 and numerically,13,21 we primarily focus on the effect of corrugations on the flow transition from a no-flow state to a flow state of an active nematic fluid. The resulting flow state immediately after the transition is, typically, a streaming flow state and analysis of this flow further allows us to isolate the role of corrugations and boundary-induced active flows. The investigation is performed using a numerical framework based on multiparticle collision dynamics.48
In Section 2, we discuss the system and the multiparticle collision dynamics algorithm for active nematic fluids. We first demonstrate the validity of the algorithm illustrating the spontaneous flow transition in flat-walled channels (Section 3). This is followed by an analysis of flow states generated in corrugated channels and contrasted with those in a flat-walled channel. Further, the role of geometry in establishing the flow transition and streaming-flow state is characterised and generalised. Finally, we provide a slip-based mechanism to understand the spontaneous flow transition in a corrugated channel and conclude the work (Section 4).
2 Methodology
2.1 Active nematic multiparticle collision dynamics (AN-MPCD)
The active nematic fluid confined in a corrugated channel is simulated using the active-nematic multiparticle collision dynamics (AN-MPCD) algorithm. The AN-MPCD algorithm is a particle based, mesoscopic algorithm proven to be useful to simulate various soft matter systems. By assigning a nematic stress to the particles, the AN-MPCD algorithm simulates the dynamics of active nematic fluids.48–51 The AN-MPCD algorithm discretizes the continuum into N point-like particles, each with mass m, position ri, velocity vi and orientation ui. The algorithm comprises two steps: streaming and collision. During streaming, each particle moves ballistically for a time δt to a new position| ri(t + δt) = ri(t) + vi(t)δt. | (1) |
| vi(t + δt) = v(t) + Ξi | (2) |
The collision operator injects energy into the system, corresponding to an extensile or contractile force dipole density. This is achieved by incorporating the local active stress proportional to the nematic tensor order parameter Q, such that the force dipole coaligns with the local director field n of the cell. Thus, the collision operator is a linear combination of passive and active contributions:
 | (3) |
The collision operator also updates particle orientation ui, thus computing the dynamics of the nematic tensor order parameter, defined as Q = 〈2uiui − ![[1 with combining circumflex]](https://www.rsc.org/images/entities/b_char_0031_0302.gif) 〉. Here
〉. Here ![[1 with combining circumflex]](https://www.rsc.org/images/entities/b_char_0031_0302.gif) denotes the identity matrix. The tensor order parameter Q quantifies the extent and direction of orientational order through its largest eigenvalue S and the corresponding eigenvector n in the cell. The orientations are updated based on the local equilibrium distribution of the orientation field
denotes the identity matrix. The tensor order parameter Q quantifies the extent and direction of orientational order through its largest eigenvalue S and the corresponding eigenvector n in the cell. The orientations are updated based on the local equilibrium distribution of the orientation field
| ui(t + δt) = n(t) + ηi | (4) |
2.2 Simulation details
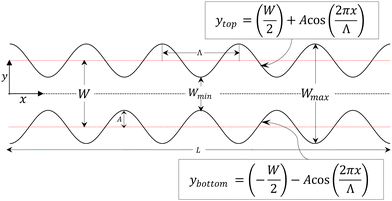
We consider flow aligning nematics with extensile activity (α > 0) confined in a corrugated channel.53 A schematic of the corrugated channel used for the simulations is shown in Fig. 1. Cartesian coordinates are adopted − x along the length of the channel and y in the perpendicular direction, i.e., across the channel, and the channel centerline is at y = 0. The profile of the corrugated walls in the channel is represented by cosine functions and the equations describing the top and bottom wall are ytop(x) = (W/2) + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πx/Λ) and ybottom(x) = (−W/2) − A
cos(2πx/Λ) and ybottom(x) = (−W/2) − A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πx/Λ), respectively. Here, W is the mean width of the channel and A and Λ are the amplitude and wavelength of the corrugations respectively. Since the width varies along the channel, the minimum width, Wmin, is defined as the distance between the trough of the top wall, W/2 − A, and the crest of the bottom wall, −W/2 + A, i.e., Wmin = W − 2A. Similarly the maximum width in the corrugated channel is Wmax = W + 2A.
cos(2πx/Λ), respectively. Here, W is the mean width of the channel and A and Λ are the amplitude and wavelength of the corrugations respectively. Since the width varies along the channel, the minimum width, Wmin, is defined as the distance between the trough of the top wall, W/2 − A, and the crest of the bottom wall, −W/2 + A, i.e., Wmin = W − 2A. Similarly the maximum width in the corrugated channel is Wmax = W + 2A.
As discussed in Section 2.1, the total activity of the fluid in the channel is proportional to the number of active particles in the system. Therefore, for a fair comparison, (i) it is necessary for the volume of the fluid in the corrugated and flat channel to be identical and (ii) the fluid is of the same density and viscosity in both the cases. In this work, two-dimensional simulations are considered; therefore, the area of the corrugated channel occupied by the active fluid (volume per unit length) is given by
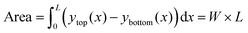 | (5) |
The results are reported in MPCD units of cell size l = 1, particle mass m = 1 and thermal energy kBT = 1, which leads to units of time 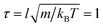 . The AN-MPCD particles are initialised with random velocities and oriented along the y axis. In the simulations, the mean-field interaction constant U = 10 is set to achieve the nematic phase.48 The tumbling parameter λ = 2 is chosen for the active nematic fluid to be in the shear-aligning regime.48 The heuristic coupling coefficient χ is fixed at 0.5 and the viscous rotation coefficient is fixed at γR = 0.01. The time step is set to δt = 0.1 and simulations are run for a total of 6 × 105 time steps which includes a warm-up phase of 3 × 105 time steps. The channels investigated are of the following dimensions: (i) a flat-walled channel (A = 0) with length L = 100 and width W = 20 and (ii) a corrugated channel with wavelength Λ = 20, amplitude A = 3 and the same length and width as in (i) unless specified otherwise. Periodic boundary conditions are imposed along the x direction for the flow velocity and orientation tensor (see Appendix B.3.1). The walls of the channel are impermeable with no-slip boundary conditions using phantom particles (see Appendix B.3.2). A strong homeotropic boundary condition is enforced for the director field ensuring that the director field is oriented perpendicular to the channel walls (see Appendix B.2).
. The AN-MPCD particles are initialised with random velocities and oriented along the y axis. In the simulations, the mean-field interaction constant U = 10 is set to achieve the nematic phase.48 The tumbling parameter λ = 2 is chosen for the active nematic fluid to be in the shear-aligning regime.48 The heuristic coupling coefficient χ is fixed at 0.5 and the viscous rotation coefficient is fixed at γR = 0.01. The time step is set to δt = 0.1 and simulations are run for a total of 6 × 105 time steps which includes a warm-up phase of 3 × 105 time steps. The channels investigated are of the following dimensions: (i) a flat-walled channel (A = 0) with length L = 100 and width W = 20 and (ii) a corrugated channel with wavelength Λ = 20, amplitude A = 3 and the same length and width as in (i) unless specified otherwise. Periodic boundary conditions are imposed along the x direction for the flow velocity and orientation tensor (see Appendix B.3.1). The walls of the channel are impermeable with no-slip boundary conditions using phantom particles (see Appendix B.3.2). A strong homeotropic boundary condition is enforced for the director field ensuring that the director field is oriented perpendicular to the channel walls (see Appendix B.2).
2.3 Corrugated channel boundaries
The boundary conditions that simulate the active nematic fluid in a corrugated channel as shown in Fig. 1 comprise two parts: (i) the wall surface and (ii) the boundary rules for the transformation of the velocity during the collision event. The channel walls are sinusoid functions as described in Appendix B. The rules for velocity transformation during the collision event with a wall are bounce-back. The transformation of the orientation of the particle involves multiple operations to obtain the desired anchoring on the curved wall. The details of implementation of these boundary conditions are provided in Appendix B.3, and is closely adapted from Wamsler et al.533 Results and discussion
We now present the results of two dimensional simulations of an active nematic fluid confined in flat and corrugated channels. We first investigate the active nematic fluid flow in a flat-walled channel by systematically varying the activity α and channel width W. The results confirm that AN-MPCD simulations are in agreement with previous studies30,34,55 (Sections 3.1 and 3.2). Subsequently, by replacing the flat walls with corrugated walls, we identify the differences in the fluid flow behaviour and the underlying physical mechanisms involved (Sections 3.3 and 3.4). The amplitude, A, and the wavelength, Λ, of the corrugations are altered to understand the effect of geometrical parameters. Lastly, the influence of circulations trapped in the corrugations is discussed along with the results of a linear stability analysis where the effect of the swirls trapped in the corrugations of the channel is interpreted as an effective slip velocity (Section 3.5).3.1 Spontaneous flow transition in a flat-walled channel
Theoretical30,34,55 and experimental32 investigations have shown that a confined active nematic fluid undergoes a spontaneous flow transition at a threshold critical activity,30 herein denoted as αc. This flow transition can be characterised by a non-flowing state when α < αc and a spontaneous flow state when α > αc. To test this, using the AN-MPCD algorithm, we simulate an active nematic fluid confined in a flat-walled channel with systematic increments in the value of activity. Both unidirectional and bidirectional flows have been discussed in the literature following a spontaneous flow transition;13,30,32,34,55–57 however, in this manuscript, we focus on unidirectional flows and the scaling30,55 relationships that connect the strength of the flow, activity and confinement length scale. The flow in the channel is characterized by the root-mean-squared velocity, , where v is the fluid velocity in the cell. The calculation of Vrms is a multi-step process; first the squared fluid velocity v2 is computed within each cell and spatially averaged to obtain 〈v2〉(t). Subsequently, a steady-state is identified and the time average of
, where v is the fluid velocity in the cell. The calculation of Vrms is a multi-step process; first the squared fluid velocity v2 is computed within each cell and spatially averaged to obtain 〈v2〉(t). Subsequently, a steady-state is identified and the time average of  is computed. It is evident that a no-flow state (negligible Vrms) is observed for α < αc and a flow state is observed for α > αc (Fig. 2(a)). Above αc, Vrms continues to increase as a function of activity. The sudden change in Vrms is indicative of phase transition-like behavior. We determine the critical activity by curve fitting the Vrms data of both no-flow and flow states to the mathematical form
is computed. It is evident that a no-flow state (negligible Vrms) is observed for α < αc and a flow state is observed for α > αc (Fig. 2(a)). Above αc, Vrms continues to increase as a function of activity. The sudden change in Vrms is indicative of phase transition-like behavior. We determine the critical activity by curve fitting the Vrms data of both no-flow and flow states to the mathematical form  (dashed curves in Fig. 2(a)). The critical activity αc of the system is identified from the intersection point (diamond in Fig. 2(a)) of the fitted curves.
(dashed curves in Fig. 2(a)). The critical activity αc of the system is identified from the intersection point (diamond in Fig. 2(a)) of the fitted curves.
The critical activity for spontaneous flow transition of confined active nematics can be calculated from a linear stability analysis of the governing continuum equations55 to be of the form
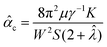 | (6) |
![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) is the flow aligning parameter. We use
is the flow aligning parameter. We use ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c and
c and ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) for critical activity and flow aligning parameter in continuum theory to differentiate the parameters from their AN-MPCD counterparts. From eqn (6), it is apparent that apart from the fluid properties, critical activity is also a function of the channel width, W. This indicates that the presence of a critical width Wc, is also a function of activity.
for critical activity and flow aligning parameter in continuum theory to differentiate the parameters from their AN-MPCD counterparts. From eqn (6), it is apparent that apart from the fluid properties, critical activity is also a function of the channel width, W. This indicates that the presence of a critical width Wc, is also a function of activity.
To quantify spontaneous flow transition using Wc, we systematically increase the width of the channel for various activities (Fig. 2(b)), where Vrms is plotted as a function of channel width W. The active nematic fluid undergoes the transition from no-flow to spontaneous flow as the channel width is increased beyond Wc for a specified activity. The critical width is computed using a similar methodology to determining critical activity by curve fitting the data using  and extracting Wc. The critical width Wc decreases as activity increases (Fig. 2(c)). This analysis confirms that for a flat-walled channel, the critical width scales as
and extracting Wc. The critical width Wc decreases as activity increases (Fig. 2(c)). This analysis confirms that for a flat-walled channel, the critical width scales as  , consistent with eqn (6) and previous investigations.30
, consistent with eqn (6) and previous investigations.30
Further, it can be seen that the dependence of Vrms on W is similar for different activities (Fig. 2(b)). Therefore, we collapse the data by plotting Vrms/α1/2 as a function of (W − Wc)/Wc (Fig. 2(d)). This collapse is explained through a scaling analysis from the linear stability results. At steady state, the active stress (∼αSθ) and the viscous stress (∼μv/W) balance
 | (7) |
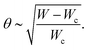 | (8) |
Thus, the angle scales with the reduced width, which acts as a non-dimensional function of the channel width akin to a second order phase transition. Since W ≈ Wc near the transition, combining eqn (6)–(8) gives the velocity of the active nematic fluid
 | (9) |
3.2 Coherent flows in a flat-walled channel
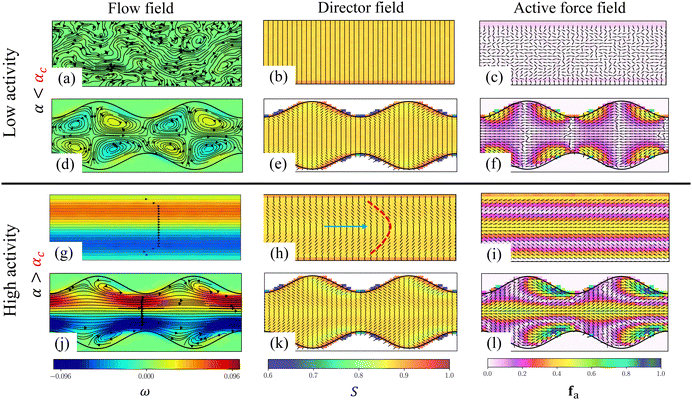
When confined, an active nematic fluid undergoes a spontaneous flow transition, and a coherent flow is usually observed immediately above the transition point.31,36,58,59 Coherent flow is characterized by velocity fields that are dominant along the length of the channel vx ≈ |v|. We now discuss the underlying physical mechanism associated with flow transition to a coherent flow in a flat-walled channel (Fig. 3). The flow field is plotted by superimposing streamlines on fluid vorticity, ω = (∇ × v)z, where the colors represent the clockwise (blue) and anticlockwise (red) rotation of the fluid elements. The local director field n is shown by a black dashed line color shaded by the scalar order parameter, S. Active force, fa, produced by the nematic fluid is calculated as fa ∝ ∇·Q and is shown with black arrows depicting the direction and color shading depicting the magnitude of the force produced.For a lower activity (α < αc), in a flat-walled channel a no-flow state is observed in the flow domain (Fig. 3(a)), with the director field aligned in the nematic phase (Fig. 3(b)). The active forcing produced by the fluid is insignificant (Fig. 3(c)). However, at a higher activity (α > αc), a bend-like deformation of the director field is observed as shown in Fig. 3(h), in which the thick dashed line is a visual representation of the bend deformation and the arrow represents the direction of fluid flow. The active force produced by the fluid corresponding to the bend deformation is maximum at the center of the channel and is oriented along the x axis (Fig. 3(i)). Thus, the active force drives the flow along the length of the channel producing coherent flows (Fig. 3(g)).
3.3 Coherent flows in a corrugated channel
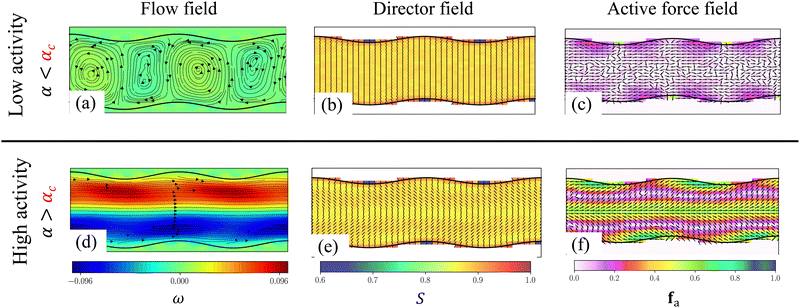
In the case of a corrugated channel, when the activity α is lower than a critical value αc, swirling flows constituted by closed streamlines are observed. This is illustrated in Fig. 3(d) for an amplitude of A = 3 and wavelength Λ = 20, demonstrating a significant difference from the no-flow state observed in a flat-walled channel when α < αc.The origin of swirling flows can be explained by observing the director field (Fig. 3(e)). Due to the strong homeotropic anchoring boundary condition, the director field aligns perpendicular to the wall. However, due to the reflection symmetry about the channel centerline, the director field within the bulk of the channel remains oriented perpendicular to the centerline. Therefore, the nematic elasticity induces a bend-like deformation close to the channel wall which is visually depicted by thick dashed lines in Fig. 4(a). As a consequence of this bend, the fluid experiences an active force near the walls (Fig. 3(f)), where the magnitude of force is maximum at the bends. This active force drives the flow towards the centre of the corrugation, as indicated by the arrows in Fig. 4(a). Since the corrugation is symmetric with respect to the y-axis, two bends are observed near the wall, facing each other. As a consequence, the flow converges at the center of the corrugations and is subsequently driven towards the bulk of the channel. This dynamics leads to the formation of counter-rotating swirls. Due to the symmetry of the channel, a pair of bends are observed at both the top and bottom walls, resulting in four swirls within the fluid (Fig. 3(d)). The swirling flows prior to spontaneous flow transitions have been analyzed by Zumdieck et al.44 Calculations in the limit A/Λ ≪ 1 and W ≪ Wc ≪ Λ showed that the velocity of the swirls depends on the geometry of the channel as 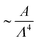 .
.
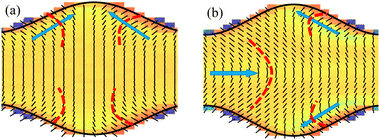 | ||
| Fig. 4 An enlarged view of the director field in the corrugated channel: (a) below critical value α < αc from Fig. 3(e) and (b) above the critical value α > αc from Fig. 3(k). The red dashed lines represent the bend like deformation and the blue arrows point in the direction of the active forcing and the subsequent fluid flow. | ||
At higher activities (α > αc) in the corrugated channels, coherent fluid flow is obtained alongside the swirls near the walls (Fig. 3(j)). From Fig. 3(k) we observe that a bend like deformation can be noticed in the bulk of the channel (Fig. 4(b)), which results in coherent flow in the channel. This is in contrast to lower activities (Fig. 4(a)). The combination of strong anchoring boundary condition and nematic elasticity induces a bend-like deformation in the director field close to the channel wall with opposite polarity to the bend in the bulk (Fig. 4(b)). The bend in the director field close to the wall generates an active force, driving the fluid towards the centre of undulation and then towards the bulk of the fluid resulting in swirling flows. From Fig. 3(l), it is evident that the active force corresponding to the bend in the director field close to the wall is pronounced compared to the bulk of the channel. It is these regions of high bend and strong active forcing that drive and sustain the swirling flow alongside the bulk coherent flow. The swirls generated remain trapped inside the corrugations and coexist along with coherent fluid flow along the center of the channel (Fig. 3(j)). It is interesting to note that in a flat-walled channel, for α > αc, the fluid at the centerline of the channel experiences a large active force (Fig. 3(i)). In this case, although the active force near the walls is of comparable strength but opposite polarity, it is the active force along the centerline of the channel that dictates the direction of the coherent flow. Similarly, in the corrugated channel the active force is large around the centerline and drives the coherent flow along the length of the channel (Fig. 3(l)). However, the active force experienced by the fluid close to the walls has a higher intensity but with an opposite polarity.
The existence of coherent flows with swirls aligns with the experimental observations reported by Wu et al.33 When the active nematic fluid (suspension of microtubule and motor protein mixture) is confined in a ratchet like geometry, coherent flows were produced but were accompanied by swirls trapped in the corrugations. This observation also emphasizes that the channel geometry can influence the flow dynamics and behavior of an active nematic fluid confined within it.
3.4 Effect of changing the amplitude and wavelength of the corrugations
In a flat-walled channel, the active nematic fluid undergoes a flow transition from a state of no-flow to a state of coherent flow. In contrast, corrugated channels exhibit counter rotating swirls prior to the flow transition. Therefore, we now investigate the effects of change in the corrugation geometry on the spontaneous flow transition of an active nematic fluid to a coherent flow state. This is achieved by varying the amplitude, A, and wavelength, Λ, of the corrugations of the channel.The results of change in amplitude are shown in Fig. 5(a), where root-mean-squared velocity, Vrms, of the fluid is plotted as a function of activity α for various amplitudes. The active nematic fluid undergoes a flow transition at all amplitudes. However, above the critical activity, the velocity of the fluid decreases with the increase in amplitude. Further, it is also observed that larger amplitudes shift the critical activity at higher values. Note that all simulations have been carried out at a fixed mean width W, and therefore, an increase in the amplitude A reduces the minimum width, Wmin, of the channel. Therefore, the active fluid encounters a stronger geometric constriction with the increase in the amplitude of the corrugation, and thus causing the shift of the flow transition to higher activities.
To determine the critical activity of the active nematic fluid in the corrugated channel, the corrugated channel is split into two domains: region I represents the center of the channel, |y| < (Wmin/2), and region II represents the fluid trapped in the corrugations, (Wmin/2) < |y| < (W/2 + A) (see the schematic in Fig. 7(a)). The root-mean-squared velocity of the fluid calculated in the central region I, VIrms, and in region II within the corrugations, VIIrms, is shown as a function of activity in Fig. 5(b) and (c) respectively. As in a flat channel, VIrms remains small below the critical activity but increases rapidly as 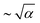 beyond the flow transition. The critical activity αc corresponding to the corrugated wall is determined from Fig. 5(b). On the other hand, the fluid velocity in the corrugations, VIIrms, continues to gradually increase with increasing activity without a discernible indication of the spontaneous flow transition (Fig. 5(c)). The velocity of the fluid trapped in the corrugations VIIrms increases with the increase in the amplitude of the corrugations. A larger amplitude results in a stronger bend in the director field that generates a stronger flow in the corrugations. The critical activity required for flow transition determined from Fig. 5(a) is shown in Fig. 5(e) as a function of amplitude A of the corrugations. The increase in critical activity with amplitude appears to show a quadratic dependence.
beyond the flow transition. The critical activity αc corresponding to the corrugated wall is determined from Fig. 5(b). On the other hand, the fluid velocity in the corrugations, VIIrms, continues to gradually increase with increasing activity without a discernible indication of the spontaneous flow transition (Fig. 5(c)). The velocity of the fluid trapped in the corrugations VIIrms increases with the increase in the amplitude of the corrugations. A larger amplitude results in a stronger bend in the director field that generates a stronger flow in the corrugations. The critical activity required for flow transition determined from Fig. 5(a) is shown in Fig. 5(e) as a function of amplitude A of the corrugations. The increase in critical activity with amplitude appears to show a quadratic dependence.
To study the effect of the wavelength of the corrugations Λ on the active nematic fluid flow, we vary Λ for a fixed amplitude and mean width of the channel. A comparison of the root-mean-squared velocity Vrms of the fluid as a function of activity α for various wavelengths (Fig. 5(d)) with Vrms as a function of amplitude (Fig. 5(a)) demonstrates that the influence of wavelength in the investigated range is weaker. Changing the wavelength of the corrugations affects the velocity of the coherent flow of the active nematic fluid, with larger wavelengths resulting in larger velocity. Further, increasing the wavelength of the channel reduces αc, the critical activity required for the spontaneous flow transition (Fig. 5(f)). The critical activity decreases with wavelength, showing a strong power law decay.
A corrugated channel can be perceived as a geometry in between two flat-walled channels of different width, as schematically illustrated in Fig. 6. The two limiting cases Λ → 0 and Λ → ∞ both approach the geometry of flat-walled channels with W ≈ Wmin and W ≈ Wmax respectively (see Fig. 6). In the simulations analyzed above Λ/W ≈ 1 as indicated by the illustration in panel (c) in Fig. 6. Reducing Λ/W leads to a denser packing of corrugations (panel (b)). The limiting case Λ/W → 0 (panel (a)) corresponds to a flat-walled channel of width Wmin. On the other hand, an increase in Λ/W leads to a channel geometry shown in panel (d) with limiting case Λ/W → ∞ (panel (e)), that again corresponds to a flat-walled channel but now of width Wmax. Therefore, to first order, any corrugated channel can be thought of as a construction intermediate between the limits of two flat-walled channels of width Wmin and Wmax. As a consequence, the critical activity required for spontaneous flow transition of an active nematic confined in a corrugated channel falls between the critical activity of two flat-walled channels of width Wmin and Wmax. This was also evident in Fig. 5(b) where the root-mean-squared velocity data were plotted against activity for various wavelengths.
Since critical activity is inversely proportional to the square of channel width, critical activity required for spontaneous flow transition in a flat-walled channel of width Wmin is larger than that in a channel of width Wmax. Therefore, the critical activity required for the spontaneous flow transition in intermediate configurations will be smaller than that of a flat-walled channel of width Wmin but greater than that of a flat-walled channel of width Wmax.
Yet another way to perceive the coherent flows in corrugated channels when wavelength is increased from that corresponding to Wmin to Wmax is the reduction in the number of geometrical constrictions or correspondingly the increase in the volume occupied by the fluid between the crests, where swirls are present. Hence the reduction in critical activity with the increase in wavelength can also be thought of as providing an effective slip to the fluid in the bulk.
3.5 Effect of swirls on the coherent flow of active nematics in corrugated channels
We have seen that coherent flows in the center of a corrugated channel are accompanied by swirls trapped in the corrugations (Fig. 3(j)). The presence of swirls in region II (Fig. 7(a)) uniquely differentiates the coherent flows in corrugated channels compared to flat-walled channels. To elucidate the role of swirls in supporting coherent flows, we interpret the swirls as a mechanism to provide a slip velocity to coherent flows in the center of the channel (region I; Fig. 7(a)).We model the effect of swirling fluid in the corrugations (region II) on the flow in the central region (in region I) as providing a slip at the interface of two regions, y = ±Wmin/2. This model is schematically illustrated in Fig. 7(a). The extent of slip is characterised by a slip velocity vs and the corresponding slip length β. The slip length corresponds to a fictitious distance at which the fluid velocity in region II decays to zero if the velocity gradient very close to the boundary in region I is linearly extrapolated as
 | (10) |
The above equation assumes that viscous stress dominates the interface between region I and region II and hence utilises the Newtonian constitutive relation in evaluating the slip length β. Due to the variation in the geometry along the channel length, slip length is not a constant. The function β(x) accounts for the effect of the fluid that is present in the corrugations on the coherent flow in the center of the channel.
An example of the slip length β(x) extracted from eqn (10) for a coherent flow state in a corrugated channel is shown in Fig. 7(b). The horizontal dashed blue line demarcates region I from region II. The dashed red lines connecting the symbols indicate the slip length β(x) from the boundary y = ±Wmin. As expected the slip length goes to zero at the constriction, where the interface separating region I and II coincides with the rigid boundary. The slip length is a periodic function but not mirror symmetric with respect to its zero value due to the asymmetry of the swirls in region II (Fig. 3(j)). The slip length is positive on the left hand side and negative on the right hand side of the corrugation when the coherent flow is from left to right, as shown in Fig. 7(b). The positive slip length indicates a support in maintaining the coherent flow. The negative slip length indicates the resistance offered by the swirls towards the coherent flow on the right hand side of the corrugation, which occurs due to the presence of the counter clockwise rotating swirls in this case. However, as evident from Fig. 7(b), the extent of positive slip on the left side is more than that on the right side, indicating that the fluid in region I experiences a net positive slip due to the presence of fluid in region II. Thus, the overall effect of active nematic fluid entrapped in the corrugations is to endow a positive slip to the coherent flow in the center of the channel.
Since the amount of fluid contained in the corrugations varies with the amplitude and wavelength which changes the behaviour of swirls in corrugations, the slip length β(x)/A is plotted for various amplitudes and wavelengths of the corrugations in Fig. 7(c) and (d). In Fig. 7c and d(i), the abscissa is normalised with Λ for comparison between various cases. It is clear that the slip length increases with amplitude.
The variation with wavelength is more intricate (Fig. 7d(i)). To better understand how the effective slip length calculated from eqn (10) varies with wavelength, we average the slip length over an integer number of wave,  . The average slip length is plotted separately as a function of amplitude and wavelength in Fig. 7c and d(ii). Increasing the amplitude increases the average slip length monotonically. However, increasing the wavelength seems to show two distinct behaviours: when the wavelength is small (Λ/W < 1), slip length increases with the increase in wavelength, but it becomes independent of wavelength for large wavelength (Λ/W > 1).
. The average slip length is plotted separately as a function of amplitude and wavelength in Fig. 7c and d(ii). Increasing the amplitude increases the average slip length monotonically. However, increasing the wavelength seems to show two distinct behaviours: when the wavelength is small (Λ/W < 1), slip length increases with the increase in wavelength, but it becomes independent of wavelength for large wavelength (Λ/W > 1).
To understand the implications of these variations we analyze the flow transition in corrugated channels through an analytical approach. Since the fluid in the center of the channel (region I) exhibits a flow transition similar to that in a flat-walled channel, the role of the slip in the spontaneous flow transition may be analyzed using a linear stability analysis (see Appendix C for detailed calculations). We consider an active nematic fluid contained in a flat-walled channel of width W. The channel walls are characterised by a slip length β, resulting in a slip velocity at the channel boundary. A quasi 1D channel geometry is assumed, i.e., flow occurs only along the channel length but neither the flow nor director field exhibits any variations along the channel length. As described above we assume that viscous stresses dominate the boundary and hence eqn (10) based on the Newtonian constitutive relation is used as a boundary condition on the channel walls. Following ref. 30 and 55, the linearised governing equations for the director field θ(y) and the stream-wise velocity field vx(y) are
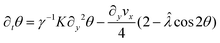 | (11) |
ρ∂tvx = ∂y(μ∂yvx + ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) S S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ). 2θ). | (12) |
Subjected to the slip boundary conditions  and strong homeotropic anchoring
and strong homeotropic anchoring 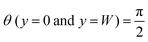 , we seek stationary solutions of eqn (11) and (12). The condition for the existence of flow for a nonzero activity is found to be
, we seek stationary solutions of eqn (11) and (12). The condition for the existence of flow for a nonzero activity is found to be
1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TW + βT TW + βT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TW = 0, TW = 0, | (13) |
 (see Appendix C) is an inverse length scale. Together, TW represents a dimensionless activity number that represents the competition between confinement and active nematicity. The solution of eqn (13) prescribes the critical activity
(see Appendix C) is an inverse length scale. Together, TW represents a dimensionless activity number that represents the competition between confinement and active nematicity. The solution of eqn (13) prescribes the critical activity ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,s required for spontaneous flow transition in a flat-walled channel endowed with slip boundary conditions. An explicit expression for critical activity cannot be written down due to the non-linearity of eqn (13), and must be found numerically. However, for small slip lengths (β/W → 0), eqn (13) can be further simplified to obtain an explicit expression for critical activity
c,s required for spontaneous flow transition in a flat-walled channel endowed with slip boundary conditions. An explicit expression for critical activity cannot be written down due to the non-linearity of eqn (13), and must be found numerically. However, for small slip lengths (β/W → 0), eqn (13) can be further simplified to obtain an explicit expression for critical activity | (14) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,0 is the critical activity required for spontaneous flow transition in a flat-walled channel with no-slip boundary conditions (eqn (6)). Clearly, eqn (14) recovers the correct limit of
c,0 is the critical activity required for spontaneous flow transition in a flat-walled channel with no-slip boundary conditions (eqn (6)). Clearly, eqn (14) recovers the correct limit of ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,s →
c,s → ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,0 when the slip length β = 0. Further, the critical activity is reduced in a channel with slip boundary conditions compared to that with no-slip boundary conditions, and the reduction is proportional to square of the slip length at leading order.
c,0 when the slip length β = 0. Further, the critical activity is reduced in a channel with slip boundary conditions compared to that with no-slip boundary conditions, and the reduction is proportional to square of the slip length at leading order.
We now compare the results of the linear stability analysis with that from AN-MPCD simulations in Fig. 8. Firstly, the root-mean-square velocity Vrms is plotted against activity for a corrugated channel of Wmin = 16 and A = 2 in comparison with a flat-walled channel of width W = 16 (Fig. 8(a)) and in Fig. 8(b)Vrms is plotted against activity for a corrugated channel of Wmin = 12 and A = 4 in comparison with that in a flat-walled channel of width W = 12. In each figure the fluid in the corrugated channel undergoes spontaneous flow transition at a lower activity compared to that of a flat-walled channel. This reduction is indicated in the figure using yellow arrows. The reduction in the value of critical activity for the corrugated channel can be attributed to the slip velocity provided by the fluid trapped in the corrugations, consistent with the predictions of the linear stability analysis. The fluid in the center of the channel (region I) is separated from the no-slip walls because of the presence of region II. On the other hand, in a flat-walled channel, the fluid is always in contact with the channel wall and the no-slip boundary condition on the channel walls mandates a higher activity for a spontaneous flow transition.
 | ||
| Fig. 8 Reduction in the critical activity for spontaneous flow transition in a corrugated channel of minimum width Wmin compared to a flat walled channel of width W = Wmin. Vrms is plotted as a function of α for (a) a corrugated channel of Wmin = 16 and A = 2 in comparison with a flat-walled channel of W = 16 and (b) a corrugated channel of Wmin = 12 and A = 4 in comparison with a flat-walled channel of W = 12. (c) Results from the linear stability analysis – the critical activity in a flat-walled channel with slip boundary conditions, αc,s, normalised with that in a channel with no-slip boundary conditions, αc,0, is plotted against the slip length as a continuous line (full solution given by eqn (13)). The approximate solution given by eqn (14) is shown as the dashed line. Critical activity for the corrugated channel, αc, is normalised with that of a flat-walled channel αc,0, obtained from AN-MPCD simulations, and is plotted against the normalised average slip length, 〈β〉/Wmin which are shown by the markers in the figure. | ||
We now compare the prediction of the linear stability analysis, eqn (13), quantitatively with the results from AN-MPCD simulations. The critical activity ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,s in a flat-walled channel endowed with a slip velocity is plotted as a function of slip length β (Fig. 8(c)). In this plot, the critical activity is normalised by
c,s in a flat-walled channel endowed with a slip velocity is plotted as a function of slip length β (Fig. 8(c)). In this plot, the critical activity is normalised by ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) c,0, the critical activity in a rigid channel that imposes no-slip boundary conditions (eqn (6)). The slip length is normalised with the channel width W. As expected, both the full solution (eqn (13)) and the approximate solution (eqn (14)) of the critical activity decrease with increasing slip length. The AN-MPCD data confirm that the critical activity decreases with slip length. The significant match between the results from the linear stability analysis and the AN-MPCD simulations suggests that the effect of active swirling flows that are generated in the corrugations due to the distortions in the director field is equivalent to an effective slip for the active coherent flow that develops in the center of the corrugated channel.
c,0, the critical activity in a rigid channel that imposes no-slip boundary conditions (eqn (6)). The slip length is normalised with the channel width W. As expected, both the full solution (eqn (13)) and the approximate solution (eqn (14)) of the critical activity decrease with increasing slip length. The AN-MPCD data confirm that the critical activity decreases with slip length. The significant match between the results from the linear stability analysis and the AN-MPCD simulations suggests that the effect of active swirling flows that are generated in the corrugations due to the distortions in the director field is equivalent to an effective slip for the active coherent flow that develops in the center of the corrugated channel.
4 Conclusions
In this work, we have performed numerical simulations using the active nematic multi-particle collision dynamics (AN-MPCD) algorithm to study the spontaneous flow transition and the resulting flow state of an active nematic confined in a corrugated channel. Active nematics confined between two parallel plates is a well studied system.34,44,60 At low activities, the active nematic fluid is stationary with nematic elasticity dominating the system. At sufficiently high activity, the nematic fluid undergoes a spontaneous flow transition. The resulting velocity of the fluid is proportional to the square root of activity, while the critical activity is inversely proportional to square of the channel width. In this work, we first demonstrated these scalings for an AN-MPCD fluid.We extended channel-confined active fluids to study the behaviour of active nematics confined in corrugated channels. In this study, the wavy walls on the top and bottom of the corrugated channel are out-of-phase, but qualitatively similar conclusions are reached in a snaking channel in which the bottom and top walls are in-phase (Appendix D). We find that the distinguishing feature of the spontaneous flow transition in corrugated channels is the transition from a weak flow state to a strong flow state. This is in contrast to a flat-walled channel where the transition is from a no-flow state to a flowing state. The weak flows before the transition originate from distortions in the director field arising from the preferred anchoring of the active nematic to the curved boundaries. The critical activity required for flow depends upon the channel geometry. Increasing the amplitude of the corrugations while keeping the mean width of the channel fixed increases the constrictions in the channel and thus increases the critical activity required for flow transition. On the other hand, changing the wavelength of the corrugations can be understood by regarding the corrugated channel as intermediate between two flat-walled channels of different widths, Wmin and Wmax. The critical activity for the corrugated channel is smaller than that for a flat-walled channel of width Wmin and higher than that for a flat-walled channel of width Wmax. The current study limited itself to the transition to unidirectional flow. However, it is well-known that bidirectional flow32,56,57 and higher modes frequently occur13,34,55 in flat channels. Future work should consider how undulations, slip length or roughness affect the stability of bidirectional flow states.
At activities above the flow transition, the boundary-induced swirling flows are confined to the corrugations. These swirls can be contrasted with Newtonian flows in corrugated micro-channels: (i) Newtonian fluids at low Reynolds number do not generate swirls in symmetric corrugated channels due to reversibility61 and (ii) swirls generated by a Newtonian fluid at high Reynolds number are driven by the flow in the center of the channel.62,63 In contrast the swirls observed in the active nematics in corrugations are generated by the active stress arising from the distortions in the director field. Our analysis shows that the effect of these swirls can be modelled as an effective slip to the coherent fluid flow that occurs in the bulk. Using this principle, we performed a linear stability analysis to determine the effect of the slip mechanism on the spontaneous flow transition, and matched the results from the simulations of corrugated channels with predictions from the stability analysis. Our study reveals the physical mechanisms at play when active nematics are confined in corrugated channels and further highlights the significant role of the boundaries in determining the dynamics of confined active systems.
Finally, our studies also suggest the possible mechanism by which asymmetric notches/teeth on the channel wall can direct coherent flows of channel confined active nematics, as seen in experiments.33 Active swirls generated inside the notches due to deformations in the director field provide a slip to the coherent flow, and thus, the chirality of the stronger and bigger swirl of the asymmetric notches dictates the direction of the flow in the center of the channel. Future studies should focus on validating this hypothesis and investigating the role of asymmetry of the channel corrugations in dictating the direction of coherent flows.
Data availability
The MPCD code used in the simulations reported in the article is available at https://github.com/Shendruk-Lab/MPCD.Conflicts of interest
There are no conflicts to declare.Appendices
A Nematic multi-particle collision operator
The nematic collision operator ΞNi is a version of the Anderson-thermostatted collision operator52,64 | (15) |
 for point particles relative to the cell's center of mass rcm, where
for point particles relative to the cell's center of mass rcm, where 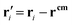 . The third term in eqn (15) removes spurious angular momentum introduced by collision operation
. The third term in eqn (15) removes spurious angular momentum introduced by collision operation 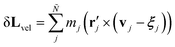 or by the rotation of the nematogens δ
or by the rotation of the nematogens δ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ori. Including δ
ori. Including δ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ori in ΞNi ensures conservation of angular momentum and accounts for the nematic back flow. The rotation of the nematogens arises from the stochastic orientational collision operation (eqn (4)) and from the response of nematogens to velocity gradients, which is accounted for through Jeffery's equation
ori in ΞNi ensures conservation of angular momentum and accounts for the nematic back flow. The rotation of the nematogens arises from the stochastic orientational collision operation (eqn (4)) and from the response of nematogens to velocity gradients, which is accounted for through Jeffery's equationδuJi = δtχ[ui·Ω + λ(ui·E − uiuiui![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E)] E)] | (16) |
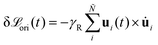 , where γR is the viscous rotation coefficient.
, where γR is the viscous rotation coefficient.
B Corrugated boundary implementation
In AN-MPCD, boundary conditions comprise two pieces: boundary surfaces, which are sinusoids, and the boundary rules which are applied to fluid particles when they violate the boundary surfaces. To implement wavy walls we follow Wamsler et al.53B.1 Boundary surfaces
The boundaries are represented by surfaces![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(r) = 0 expressed in the form
b(r) = 0 expressed in the form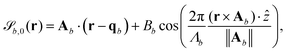 | (17) |
When the ith MPCD particle resides on the bth surface, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(ri) = 0. At all other points,
b(ri) = 0. At all other points, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(ri) ≠ 0. Whenever the MPCD particle is inside the control volume,
b(ri) ≠ 0. Whenever the MPCD particle is inside the control volume, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(ri) > 0, but whenever the MPCD particle has impinged on the wall,
b(ri) > 0, but whenever the MPCD particle has impinged on the wall, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(ri) < 0. If an MPCD particle impinges on a wall, its ballistic trajectory is ray-traced back to the surface and a collision event is initiated. The collision is represented by a set of boundary rules.
b(ri) < 0. If an MPCD particle impinges on a wall, its ballistic trajectory is ray-traced back to the surface and a collision event is initiated. The collision is represented by a set of boundary rules.
B.2 Boundary rules
The surface boundary defined by eqn (17) exists at![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(r) = 0. Therefore for a particle with position ri, if
b(r) = 0. Therefore for a particle with position ri, if ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b(r) ≥ 0, then it is defined as to be inside the channel. Whenever an MPCD particle is outside a boundary, a set of rules defines how the position ri(t), velocity vi(t) and orientation ui(t) are transformed.
b(r) ≥ 0, then it is defined as to be inside the channel. Whenever an MPCD particle is outside a boundary, a set of rules defines how the position ri(t), velocity vi(t) and orientation ui(t) are transformed.
The boundary rules are applied in directions that depend on the local surface normal
 | (18) |
Upon crossing the boundary b, particle i's position is updated to ri → ri + ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) bnb, where
bnb, where ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) b represents a shift in particle's position in the normal direction. Periodic boundary conditions (Section B.3.1) set
b represents a shift in particle's position in the normal direction. Periodic boundary conditions (Section B.3.1) set ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) b equal to the system size, whereas impermeable walls set
b equal to the system size, whereas impermeable walls set ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) b = 0.
b = 0.
The particle velocity upon colliding with the boundary b is updated using parameters ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n (normal) and
b,n (normal) and ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t (tangential) and is transformed as vi →
b,t (tangential) and is transformed as vi → ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n(nb ⊗ nb)·vi +
b,n(nb ⊗ nb)·vi + ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t(1 − nb ⊗ nb)·vi. Here, (nb ⊗ nb) and (1 − nb ⊗ nb) are normal and tangential projection operators. Periodic boundary conditions do not change a particle's velocity and so
b,t(1 − nb ⊗ nb)·vi. Here, (nb ⊗ nb) and (1 − nb ⊗ nb) are normal and tangential projection operators. Periodic boundary conditions do not change a particle's velocity and so ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n =
b,n = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t = +1. On the other hand, impermeable no-slip boundaries require bounce-back rules with
b,t = +1. On the other hand, impermeable no-slip boundaries require bounce-back rules with ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n =
b,n = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t = −1.
b,t = −1.
The orientation of the particle also has multiplicative operators and is transformed to ui → μb,n(nb ⊗ nb)b·ui + μb,t(1 − nb ⊗ nb)·ui, which is rescaled back to the unit vector. Here, μb,n and μb,t are normal and tangential orientation parameters used to update particle orientation upon crossing the boundary. Free anchoring is implemented through μb,n = μb,t = 1 such that the orientation is unchanged. Setting μb,t = 0 imposes homeotropic anchoring, while μb,n = 0 results in planar anchoring. In this study, we consider only homeotropic channel walls (μb,t = 0).
B.3 Boundary conditions
The system is enclosed by four boundaries. Two of these are the left periodic boundary condition (PBC) b = 0 and the right PBC b = 1. The other two are the impermeable no-slip walls at the bottom b = 2 and top b = 3.![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n =
b,n = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t = μb,n = μb,t = 1 and
b,t = μb,n = μb,t = 1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) b,n = L, where L ∈ {100, 200} is the channel length. For the PBC on the left of the system, A0 =
b,n = L, where L ∈ {100, 200} is the channel length. For the PBC on the left of the system, A0 = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , q0 = 0 and B0 = 0. For the PBC on the right, A1 = −
, q0 = 0 and B0 = 0. For the PBC on the right, A1 = −![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , q1 = L
, q1 = L![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and B1 = 0.
and B1 = 0.
On these solid walls, the no-slip boundary condition is applied by enforcing the bounce-back rule ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,n =
b,n = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) b,t = −1 for b ∈ {2, 3}. The particle is rewound to the location where it crossed the boundary so that it streams with update velocity for rest of the time step. Solid walls do not impose a translational shift,
b,t = −1 for b ∈ {2, 3}. The particle is rewound to the location where it crossed the boundary so that it streams with update velocity for rest of the time step. Solid walls do not impose a translational shift, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) b,n = 0. The intersection of boundaries with MPCD cells results in lower particle density as part of the cell is inaccessible to MPCD particles, which in turn lowers the local viscosity64 and causes an effective slip. Therefore, to enforce a perfect no-slip boundary condition on solid walls, ‘phantom’ particles are added to ensure correct average density in the cell.65,66
b,n = 0. The intersection of boundaries with MPCD cells results in lower particle density as part of the cell is inaccessible to MPCD particles, which in turn lowers the local viscosity64 and causes an effective slip. Therefore, to enforce a perfect no-slip boundary condition on solid walls, ‘phantom’ particles are added to ensure correct average density in the cell.65,66
Here, the walls are chosen to be homeotropic, so μb,t = 0 for b ∈ {2, 3} However, for the no-slip boundary condition, the boundary rules are insufficient for imposing strong anchoring because the particles that cross the boundary are immediately mixed with particles that have not.67 To ensure strong anchoring, the particles in the cells intersecting the boundary ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) b are all aligned along nb. Since the intersecting cells are subjected to anchoring conditions, this results in the generation of strong anchoring.67
b are all aligned along nb. Since the intersecting cells are subjected to anchoring conditions, this results in the generation of strong anchoring.67
C Linear stability analysis in a flat walled channel with slip boundary conditions
Neglecting the variation in the channel geometry and slip length along x, we calculate the critical activity for onset of spontaneous flow transition in a flat walled channel endowed with slip boundary conditions.In addition to the equation for conservation of mass, the generalised Navier-Stokes equation for the active nematic fluid is given as
| ρ(∂t + v·∇v) = ∇·σ | (19) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) Q. In the definition of the total stress tensor (σ), μ corresponds to the fluid viscosity, E is the strain-rate tensor
Q. In the definition of the total stress tensor (σ), μ corresponds to the fluid viscosity, E is the strain-rate tensor  , P is the pressure and σ(e) is the elastic stress tensor. The elastic stress tensor is given as σ(e)ij = −
, P is the pressure and σ(e) is the elastic stress tensor. The elastic stress tensor is given as σ(e)ij = −![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) SHij + QikHkj − HikQkj, where Hij is the molecular tensor and
SHij + QikHkj − HikQkj, where Hij is the molecular tensor and ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) is the flow aligning parameter. The molecular tensor is given as Hij = −δF/δQij.
is the flow aligning parameter. The molecular tensor is given as Hij = −δF/δQij.
In a corrugated channel, coherent flow in region I is predominantly unidirectional and thus assuming a translationally invariant flow in the x direction, the flow field is described by the velocity field vx = vx(y) and vy = 0. The strain-rate tensor E has only one no-zero component Exy = ∂yvx, and thus eqn (19) is reduced to the following form:
| ρ∂tvx = ∂yσxy. | (20) |
On solving for the total stress tensor σxy and neglecting non-linear terms and elasticity, the aforementioned equation can be written as
ρ∂tvx = ∂y(μ∂yvx + ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) S S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ). 2θ). | (21) |
The hydrodynamic equation for the nematic tensor order parameter Q can be written in the form
[∂t + v·∇]Q = ![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) SE + Q·Ω − Ω·Q + γ−1H SE + Q·Ω − Ω·Q + γ−1H | (22) |
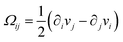 . Following ref. 55 and decoupling the equation for the orientation angle θ of the nematogens from that of the scalar order parameter S, we obtain
. Following ref. 55 and decoupling the equation for the orientation angle θ of the nematogens from that of the scalar order parameter S, we obtain | (23) |
Assuming that the viscous stress dominates at the boundary, and hence using the Newtonian constitutive relation, the boundary conditions can be written as
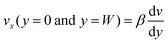 | (24) |
 | (25) |
For the linear stability analysis, we consider φ(y,t) = φ0 + εφ1(y,t), where φ = {θ,vx}, φ0 = {π/2,0} and ε ≪ 1. Substituting θ and vx in eqn (21) and (23) and considering the system at steady state yields the linearised system of equations:
μ∂y2v1 − 2![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) S∂yθ1 = 0 S∂yθ1 = 0 | (26) |
 | (27) |
Solving the coupled homogeneous differential equations we obtain
 | (28) |
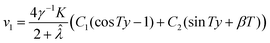 | (29) |
 | (30) |
Applying the boundary conditions we obtain the condition for the critical activity for spontaneous flow transition:
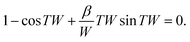 | (31) |
This equation is further simplified by considering ε = β/W as a small parameter, and the critical activity is obtained as
 | (32) |
D In-phase corrugated channel
Here we present some results of active nematic confined in a corrugated channel, with the top and bottom walls in-phase, unlike the out-of-phase channel walls described in the main manuscript. The boundary conditions are as mentioned in Section 2.2: homeotropic anchoring for the director field and no-slip for the velocity field on the walls. The channel walls have an amplitude A = 1, wavelength = 20 and a mean width of W = 20.When the activity α is less than critical activity αc, the channel with in-phase walls shows a lattice of swirling flow structures centred on the centreline (Fig. 9(a)). Since the curvature of the top and bottom channel walls is the same, the anchoring boundary conditions (namely the geometry) will result in variations in the director field primarily along the channel length. The variations are in an anti-symmetric fashion such that the corresponding flow generated will be in opposite directions. Hence, vortices span the width of the channel (Fig. 9(a) in contrast to Fig. 3(d)). It is interesting to note that the structure of the flow is similar to the well-known dancing flow state in confined active nematics, but now with a major difference: here, the lattice structure of the flow vortices arises purely from the geometry without the presence of topological defects31,35,36,58 (Fig. 9(b)).
Upon spontaneous flow transition, symmetry along the channel length is broken, and a coherent flow is observed. The sinusoidal variations in the active force field will follow the geometry of the channel with in-phase walls as shown in Fig. 9(f), which is unlike the reflection symmetry in the active force field observed in the case of channels with out-of-phase walls (Fig. 3(l)). A comparison of root mean square velocity of the active nematic fluid as a function of activity is shown in Fig. 10(a) for both in-phase and out-of-phase channels. In accordance with the discussion above, the strength of the flow before the flow transition is different in the two channels, but the strength of the flow is comparable in the two channels after the flow transition. Fig. 10(b) shows a comparison of the slip length as a function of channel length in both types of channels. It may be seen that the magnitude and variation of slip length β in both out-of-phase and in-phase channels are similar. It is clear from the above discussions that the qualitative features and the mechanisms at play in channels with walls of broken symmetry remain the same.
 | ||
| Fig. 10 (a) Comparison of spontaneous flow transition observed in channels with in-phase and out-of-phase walls by plotting root mean square velocity as a function of activity. (b) Variation in slip length β(x) for the in-phase and out-of-phase corrugated channels at α = 0.024. The parameters used in the simulations are same as those mentioned in the caption of Fig. 9. | ||
Acknowledgements
SPT acknowledges the support by the Department of Science and Technology, India, via the research grant CRG/2023/000169. This research has received funding (T. N. S.) from the European Research Council under the European Unions Horizon 2020 research and innovation programme (Grant Agreement No. 851196).Notes and references
- B. Martnez-Prat, J. Ignés-Mullol, J. Casademunt and F. Sagués, Nat. Phys., 2019, 15, 362–366 Search PubMed.
- T. Sanchez, D. T. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef PubMed.
- P. Chandrakar, M. Varghese, S. A. Aghvami, A. Baskaran, Z. Dogic and G. Duclos, Phys. Rev. Lett., 2020, 125, 257801 CrossRef PubMed.
- P. Chandrakar, M. Varghese, S. Aghvami, A. Baskaran, Z. Dogic and G. Duclos, Phys. Rev. Lett., 2020, 125, 257801 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef PubMed.
- S. Liu, S. Shankar, M. C. Marchetti and Y. Wu, Nature, 2021, 590, 80–84 CrossRef PubMed.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi, Y. Toyama, P. Marcq, C. T. Lim, J. M. Yeomans and B. Ladoux, Nature, 2017, 544, 212–216 CrossRef.
- J.-M. Armengol-Collado, L. N. Carenza, J. Eckert, D. Krommydas and L. Giomi, Nat. Phys., 2023, 19, 1773–1779 Search PubMed.
- O. Hallatschek, S. S. Datta, K. Drescher, J. Dunkel, J. Elgeti, B. Waclaw and N. S. Wingreen, Nat. Rev. Phys., 2023, 5, 407–419 Search PubMed.
- Z. Lin, C. Gao, M. Chen, X. Lin and Q. He, Curr. Opin. Colloid Interface Sci., 2018, 35, 51–58 CrossRef.
- M. N. Popescu, Langmuir, 2020, 36, 6861–6870 CrossRef.
- J. Wang, M.-J. Huang, R. D. Baker-Sediako, R. Kapral and I. S. Aranson, Commun. Phys., 2022, 5, 176 CrossRef.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 CrossRef.
- R. K. Gupta, R. Kant, H. Soni, A. Sood and S. Ramaswamy, Phys. Rev. E, 2022, 105, 064602 CrossRef PubMed.
- P. Arora, A. Sood and R. Ganapathy, Phys. Rev. Lett., 2022, 128, 178002 CrossRef.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 CrossRef.
- I. S. Aranson, Rep. Prog. Phys., 2022, 85, 076601 CrossRef.
- L. Balasubramaniam, R.-M. Mège and B. Ladoux, Curr. Opin. Genet. Dev., 2022, 73, 101897 CrossRef PubMed.
- S. P. Thampi, Curr. Opin. Colloid Interface Sci., 2022, 61, 101613 CrossRef.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef.
- D. L. Koch and G. Subramanian, Annu. Rev. Fluid Mech., 2011, 43, 637–659 CrossRef.
- S. P. Thampi, R. Golestanian and J. M. Yeomans, Europhys. Lett., 2014, 105, 18001 CrossRef.
- S. P. Thampi and J. M. Yeomans, Eur. Phys. J.: Spec. Top., 2016, 225, 651–662 Search PubMed.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. Cristina Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
- L. C. Head, C. Doré, R. R. Keogh, L. Bonn, G. Negro, D. Marenduzzo, A. Doostmohammadi, K. Thijssen, T. López-León and T. N. Shendruk, Nat. Phys., 2024, 20, 492–500 Search PubMed.
- R. Voituriez, J. F. Joanny and J. Prost, Europhys. Lett., 2005, 70, 404 CrossRef.
- A. Samui, J. M. Yeomans and S. P. Thampi, Soft Matter, 2021, 17, 10640–10648 RSC.
- G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J.-F. Joanny, J. Prost and P. Silberzan, Nat. Phys., 2018, 14, 728–732 Search PubMed.
- K.-T. Wu, J. B. Hishamunda, D. T. N. Chen, S. J. DeCamp, Y.-W. Chang, A. Fernández-Nieves, S. Fraden and Z. Dogic, Science, 2017, 355, eaal1979 CrossRef.
- D. Marenduzzo, E. Orlandini, M. E. Cates and J. M. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031921 CrossRef CAS.
- T. N. Shendruk, A. Doostmohammadi, K. Thijssen and J. M. Yeomans, Soft Matter, 2017, 13, 3853–3862 RSC.
- S. Chandragiri, A. Doostmohammadi, J. M. Yeomans and S. P. Thampi, Phys. Rev. Lett., 2020, 125, 148002 CrossRef CAS.
- H. Wioland, E. Lushi and R. E. Goldstein, New J. Phys., 2016, 18, 075002 CrossRef.
- M. Varghese, A. Baskaran, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2020, 125, 268003 CrossRef CAS PubMed.
- M. Ravnik and J. M. Yeomans, Phys. Rev. Lett., 2013, 110, 026001 CrossRef PubMed.
- C. Joshi, Z. Zarei, M. M. Norton, S. Fraden, A. Baskaran and M. F. Hagan, Soft Matter, 2023, 19, 5630–5640 RSC.
- S. Chen, P. Gao and T. Gao, J. Fluid Mech., 2018, 835, 393–405 CrossRef CAS.
- C. Joshi, Z. Zarei, M. M. Norton, S. Fraden, A. Baskaran and M. F. Hagan, Soft Matter, 2023, 19, 5630–5640 RSC.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- A. Zumdieck, R. Voituriez, J. Prost and J. F. Joanny, Faraday Discuss., 2008, 139, 369–375 RSC.
- A. J. Houston and G. P. Alexander, New J. Phys., 2023, 25, 123006 CrossRef.
- S. P. Thampi, A. Doostmohammadi, T. N. Shendruk, R. Golestanian and J. M. Yeomans, Sci. Adv., 2016, 2, e1501854 CrossRef PubMed.
- S. Ray, J. Zhang and Z. Dogic, Phys. Rev. Lett., 2023, 130, 238301 CrossRef PubMed.
- T. Kozhukhov and T. N. Shendruk, Sci. Adv., 2022, 8, eabo5788 CrossRef PubMed.
- H. Híjar and A. Majumdar, Soft Matter, 2024, 20, 3755–3770 RSC.
- R. R. Keogh, T. Kozhukhov, K. Thijssen and T. N. Shendruk, Phys. Rev. Lett., 2024, 132, 188301 CrossRef PubMed.
- T. Kozhukhov, B. Loewe and T. N. Shendruk, arXiv, 2024, preprint, arXiv:2401.17777 DOI:10.48550/arXiv.2401.17777.
- T. N. Shendruk and J. M. Yeomans, Soft Matter, 2015, 11, 5101–5110 RSC.
- K. Wamsler, L. C. Head and T. N. Shendruk, Soft Matter, 2024, 20, 3954–3970 RSC.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, in Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids, ed. C. Holm and K. Kremer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, pp. 1–87 Search PubMed.
- L. Giomi, L. Mahadevan, B. Chakraborty and M. F. Hagan, Nonlinearity, 2012, 25, 2245 CrossRef.
- Z.-Y. Li, D.-Q. Zhang and B. Li, Phys. Rev. Res., 2021, 3, 023253 CrossRef CAS.
- V. J. Pratley, E. Caf, M. Ravnik and G. P. Alexander, Commun. Phys., 2024, 7, 127 CrossRef.
- S. Chandragiri, A. Doostmohammadi, J. M. Yeomans and S. P. Thampi, Soft Matter, 2019, 15, 1597–1604 RSC.
- R. R. Keogh, S. Chandragiri, B. Loewe, T. Ala-Nissila, S. P. Thampi and T. N. Shendruk, Phys. Rev. E, 2022, 106, L012602 CrossRef CAS.
- K. Thijssen, D. A. Khaladj, S. A. Aghvami, M. A. Gharbi, S. Fraden, J. M. Yeomans, L. S. Hirst and T. N. Shendruk, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2106038118 CrossRef CAS.
- L. G. Leal, Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, Cambridge University Press, 2007 Search PubMed.
- T. Nishimura, Y. Ohori and Y. Kawamura, J. Chem. Eng. Jpn., 1984, 17, 466–471 CrossRef CAS.
- F. Oviedo-Tolentino, R. Romero-Méndez, A. Hernández-Guerrero and B. Girón-Palomares, Int. J. Heat Fluid Flow, 2008, 29, 1233–1239 CrossRef.
- H. Noguchi, N. Kikuchi and G. Gompper, Europhys. Lett., 2007, 78, 10005 CrossRef.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, Europhys. Lett., 2001, 56, 319 CrossRef CAS.
- D. S. Bolintineanu, J. B. Lechman, S. J. Plimpton and G. S. Grest, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 066703 CrossRef.
- L. C. Head, Y. A. G. Fosado, D. Marenduzzo and T. N. Shendruk, Soft Matter, 2024 10.1039/D4SM00436A.
| This journal is © The Royal Society of Chemistry 2024 |