 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shape and size tunability of sheets of interlocked ring copolymers†
Juan
Luengo-Márquez
 *ab,
Salvatore
Assenza
*ab,
Salvatore
Assenza
 bcd and
Cristian
Micheletti
bcd and
Cristian
Micheletti
 *e
*e
aDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: juan.luengo@uam.es
bInstituto Nicolás Cabrera, Universidad Autónoma de Madrid, 28049 Madrid, Spain
cDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain
dCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
eInternational School for Advanced Studies (SISSA), I-34136 Trieste, Italy. E-mail: cristian.micheletti@sissa.it
First published on 30th July 2024
Abstract
Mechanically bonded membranes of interlocked ring polymers are a significant generalization of conventional elastic sheets, where connectivity is provided by covalent bonding, and represent a promising class of topological meta-materials. In this context, two open questions regard the large-scale reverberations of the heterogeneous composition of the rings and the inequivalent modes of interlocking neighboring rings. We address these questions with Langevin dynamics simulations of chainmails with honeycomb-lattice connectivity, where the rings are block copolymers with two segments of different rigidity. We considered various combinations of the relative lengths of the two segments and the patterns of the over- and under-passes linking neighboring rings. We find that varying ring composition and linking patterns have independent and complementary effects. While the former sets the overall size of the chainmail, the latter defines the shape, enabling the selection of starkly different conformation types. Notably, one of the considered linking patterns favors saddle-shaped membranes, providing a first example of spontaneous negative Gaussian curvature in mechanically bonded sheets. The results help establish the extent to which mechanically bonded membranes can differ from conventional elastic ones, particularly for the achievable shape and size tunability.
1. Introduction
The large-scale conformations of polymerized or crystalline membranes, elastic sheets formed by particles tethered or bonded in a two-dimensional network, can be highly susceptible to local structural details.1–7 For instance, introducing isolated defects can cause otherwise flat membranes to buckle out-of-plane and acquire positive or negative Gaussian curvatures over large scales.4–10 More strikingly, introducing even a short-ranged self-avoidance in tethered membranes can prevent their transition from flat to crumpled as temperature increases.2,11–14 These consequential demonstrations of the coupling of small and large-scale structural properties have no analog in linear polymers and originate from the unique balance between entropic and enthalpic (elastic) contributions to the free-energy of quasi-two-dimensional systems embedded in three-dimensions. Devising ways to offset this balance has been a major objective both theoretically and for applicative purposes, especially the design of tunable materials.15–17In addition to the above endeavors, entirely new perspectives for designing membranes and tuning their elastic properties are being opened by recent advancements in supramolecular chemistry, which have made it possible to obtain extended low-dimensional materials by harnessing mechanical or topological bonds in place of conventional covalent ones.18–23 Examples include the synthesis or assembly of responsive molecular constructs,24,25 networks of interlocked molecules,26–29 and long linear catenanes.20,30 In consideration of their one-dimensional character, the latter systems have represented the simplest setting for understanding the effects of mechanical bonding on conformational,31–34 dynamical35–38 and mechanical20,39 properties, also by contrast with conventional bonding. It is thus natural to ask what novel large-scale behavior can emerge in two-dimensional elastic sheets that, instead of being made by bonded particles, consist of a chainmail of linked molecular rings.
Polymerized and mechanically bonded membranes are similar in some respects and radically different in others, making their comparison ideal to further our understanding of elastic sheets and topological materials. A fundamental common element is that the underlying topology is permanently fixed for both types of membranes, insofar as conventional and mechanical bonds are “unbreakable”. In addition, the distance of mechanically bonded rings can fluctuate within specific limits, similar to the distance of neighboring nodes in tethered sheets. However, while traditional tethered membranes are structures where the connecting elements – ranging from simple chemical bonds to linear polymer chains – converge and bind at the nodes, in chainmails the closed polymer chains serve at one time as tethers as well as nodes, their bonding arising from topological constraints.
These differences are expected to be consequential for at least two reasons. First, large-scale properties of membranes can be sensitive to small-scale features, as noted before. Second, topological constraints can endow mechanically bonded structures with emerging physical properties. A case in point are circular catenanes of rigid rings, which behave similarly to elastic ribbons, even though the rings interact only sterically and not via bending or torsional potentials.40 In addition, the fact that the elementary concatenated units are extended structures, e.g. ring polymers, generally suffices to introduce new physical regimes not accessible to the covalently bonded counterparts, from dynamical relaxation35–37 to the response to mechanical stretching20,39,41 or spatial confinement,42 to the available modes of entanglement.43
Further reasons for considering sheets of linked ring polymers come from biological systems, as best illustrated by the mitochondrial DNA of trypanosomes44,45 that consists of thousands of interlocked DNA rings. Intriguingly, the rings show a significant presence of sequence stretches known as A-tracts,46 which are characterized by a stiff mechanical response,47 thus providing an example of rings with heterogeneous elasticity in vivo. Single-molecule experiments have recently clarified that these long-known DNA chainmails have the shape of relatively smooth curved membranes.48–50 The membrane is bound by a rigid perimeter, possibly itself formed by redundantly linked DNA rings,51 but is otherwise flexible and hence endowed with significant conformational plasticity that confers unusual mechanical and dynamical properties to the system. For instance, the DNA chainmail can transition reversibly from expanded to collapsed states as the concentration of crowders in solution is varied,52 but it deforms continuously and without the equivalent of a coil–stretch transition in elongational flows.49 Various theoretical and computational models have been introduced to understand the observed properties of kinetoplast DNA,22,48,50,53–56 including how they depend on the network of the linked rings.56 Notably, the lateral and transverse size of rigid-ring chainmails were found to scale with the system area similarly to flat covalent membranes, and yet, the chainmails invariably featured a spontaneous curvature and precisely a positive Gaussian curvature, absent from conventional membranes.56 The positive Gaussian curvature was consistently observed across kinetoplast models differing by system sizes and types of linking networks. Such systematicity suggests that the positive Gaussian curvature emerges from the bonding topology, which introduces anisotropies in the steric interactions of the rigid rings,56 although other features such as connectivity defects and edge “purse-string” effects might be also important.
Two general aspects have remained virtually unexplored for mechanically bonded membranes: (i) the effect of sequence-dependent heterogeneity of the constitutive rings, particularly the sequence-dependent bending rigidity,57–59 and (ii) the effects of the inequivalent modes of linking the same set of neighboring rings. Various considerations suggest that both aspects could be consequential for the properties of chainmails. On the one hand, sequence heterogeneity has been previously studied in systems where topological constraints were intra-molecular, namely block-copolymer knotted rings where the different flexibility of the segments was varied explicitly, via the local bending rigidity,60 or implicitly, via charged/neutral character of the monomers and the ionic strength.61,62 In both cases, the sequence-modulated elasticity could either pin or delocalize the essential crossings of the knot, allowing, in turn, to tune the global metric properties. Thus, it is relevant to ask whether similar pinning of the essential crossings can be achieved for the inter-molecular topological constraints of chainmail and what the implications are for the conformational properties. On the other hand, the inequivalent modes in which a ring can be linked to its neighbors, that is, the inequivalent networked patterns of over- and under-passes, arguably provide the most straightforward way of exploring the cooperative effects of mechanical bonding and establishing whether and to what extent mechanically-bonded membranes are affected by features beyond those encoded in the pairwise linking graph of the chainmail.
Here, we study both aspects with Langevin dynamics simulations on block-copolymer chainmails with honeycomb lattice topology and different patterns of linking modes for the constitutive rings, which comprise a rigid and flexible segment. We considered five different compositions of the rings, from fully flexible to rigid, and two different linking patterns. For each of the ten combinations of ring composition and linking pattern, we sampled the equilibrium ensemble of the mechanically bonded membranes and analyzed various local and global observables to characterize how the interplay of local flexibility and linking modes defines the chainmail properties.
The main findings of our study are three. First, we observe that different modes of linking rings to their neighbors can dramatically alter the conformational ensemble of chainmails with the same honeycomb connectivity. Second, we show that a specific pattern of linking modes systematically favors saddle shapes, thus providing the first example of negative Gaussian curvature in mechanically-bonded membranes. Finally, we find that varying the composition of the block-copolymer rings can alter membrane size and bias the nature of the contacting (interlocked) segments but has no significant effects on membrane shape.
2. Methods
2.1. Model: chainmail types
We studied systems of rings of beads interlocked in a chainmail with the connectivity of a honeycomb lattice consisting of two interleaved triangular sublattices. We considered the honeycomb lattice for two main reasons. First, despite being a simple two-dimensional lattice, it has not been considered before in models of topological membranes. Second, it was an early proposed model for kinetoplasts,45 mainly inspired by the correspondence of the (monodispersed) honeycomb connectivity and the average one of kinetoplast DNA rings.50 Although this correspondence is too crude for accurately modeling kinetoplasts, it still makes the honeycomb lattice relevant for topologically bonded membranes.The mechanical bonding between neighboring rings is provided by the Hopf-type linking, the simplest instance of topological interlocking (Fig. 1a). There exist several different modes for interlocking the rings of one triangular sublattice with those of the other, corresponding to different successions of over- and under-passes.40 To explore the impact of different modes on the conformational properties of the membranes, we consider here two types of chainmails, P1 and P2 in Fig. 1b. In the case of P1, all rings are connected with the same mode (Fig. S1 top in the ESI†). The linking pattern P2 was instead chosen to include multiple linking modes into the same membrane, thus enabling the exploration of the effect of mode heterogeneity (Fig. S1 bottom in the ESI†).
The initial conformations of P1 and P2 were obtained starting from the same overlapping coplanar honeycomb arrangement of rings of m = 40 beads of size σ. The rings were perfectly circular with radius r ≃ 6.4σ, and the spacing of neighboring rings was set to approximately 1.5r. We retained rings at a distance smaller than about 52.44σ from a designated central site, obtaining quasi-hexagonal, hence roughly circular, cutouts of 68 rings.
The first chainmail type, P1, was obtained by tilting the rings in the two triangular sublattices by opposite off-plane rotations. For the system at hand, setting the rotation angle to +π/8 for the rings in sublattice A (purple) and −π/8 for sublattice B (black) yielded the sought linking pattern.
The alternative type, P2, was obtained with a different strategy. Rings in sublattice B (black) were kept in their coplanar configurations. Rings in sublattice A were divided into two sets, corresponding to the green and purple alternating columns in the rightmost panel of Fig. 1b. Next, green and purple rings were deformed with suitable out-of-plane undulations to realize the over- and under-passes sketched in Fig. 1c. In the resulting staggered pattern, the over- and under-passes of the sublattice “A” rings with their nearest neighbors are reversed in alternating rows.
We note that, although the local configurations of Fig. 1c can be interconverted by flipping the outer rings, such interconversion does not extend to the considered P1 and P2 patches. This is because each ring in the patches, including peripheral ones, take part to closed concatenated paths, which are topologically constrained,40 so that P1 and P2 are topologically inequivalent.
2.2. Model: ring polymers
The excluded-volume interaction of any pairs of monomers in the same or different rings is treated with a standard Weeks–Chandler–Andersen (WCA) potential, corresponding to a truncated and shifted Lennard-Jones potential, | (1) |
The backbone connectivity of the rings was provided by adding a bond potential between consecutive monomers in the form of a standard finitely extensible nonlinear elastic (FENE) term63
 | (2) |
We considered diblock copolymer rings with one rigid segment of nr = {0, 13, 20, 27, 40} monomers and one flexible segment composed of the remaining m − nr monomers. In the present context, a monomer is considered “rigid” or “flexible” depending on the local bending stiffness, see further below. The considered ring length, m = 40, is consistent with previous studies of interlocked ring polymers (catenanes), where it was shown to be adequate for the emergence of mechanical-bonding effects.31,34–36,42,43 The limiting cases nr = 0 and nr = 40 correspond to fully flexible and fully-rigid rings. The bending potential is
 | (3) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) i is the unit vector from monomer i − 1 to monomer i, assuming periodic bead indexing along the ring contour. The bending stiffness was set to κbend(i) = 10ε and κbend(i) = 0 for rigid and flexible monomers, respectively. We note that the nominal persistence length associated to the bending stiffness is about ¼ of the contour of the rings, and thus large enough to ensure the smoothness of the rigid blocks.
i is the unit vector from monomer i − 1 to monomer i, assuming periodic bead indexing along the ring contour. The bending stiffness was set to κbend(i) = 10ε and κbend(i) = 0 for rigid and flexible monomers, respectively. We note that the nominal persistence length associated to the bending stiffness is about ¼ of the contour of the rings, and thus large enough to ensure the smoothness of the rigid blocks.
The five above-mentioned block copolymer compositions that we considered corresponded to 0, 33%, 50%, 67%, and 100% of particles in a ring belonging to the rigid segment and were adopted uniformly for all rings in the chainmail.
2.3. Langevin molecular dynamics simulations
The canonical equilibrium properties of the chainmails were studied with Langevin molecular dynamics simulations, which were integrated with the LAMMPS software package.64 We set the temperature of the system as kBT = ε applying the Schneider–Stoll formulation as implemented in LAMMPS.65 We used a periodic cubic simulation box large enough to accommodate the entire initial (planar) chainmail. The dynamics was integrated with a damping factor of 2τ and a time step of 0.005τ, where is the characteristic simulation time and m is the monomer mass, set equal to unity. For each combination of linking pattern and block-copolymer ring composition, we collected two independent trajectories of duration 2.5 × 105τ and 3.5 × 105τ, respectively, discarding an initial interval of 5 × 104τ corresponding to the system relaxation time, see Fig. S2 in the ESI.† Configurations were sampled at intervals of 50τ. The adequate coverage of the sampling was verified a posteriori from the consistency of the expectation values of various observables computed separately for the two trajectories.
is the characteristic simulation time and m is the monomer mass, set equal to unity. For each combination of linking pattern and block-copolymer ring composition, we collected two independent trajectories of duration 2.5 × 105τ and 3.5 × 105τ, respectively, discarding an initial interval of 5 × 104τ corresponding to the system relaxation time, see Fig. S2 in the ESI.† Configurations were sampled at intervals of 50τ. The adequate coverage of the sampling was verified a posteriori from the consistency of the expectation values of various observables computed separately for the two trajectories.
2.4. Observables
To characterize the conformational ensemble of the chainmails we used a combination of local and global observables.First, for each sampled chainmail configuration, we computed the gyration tensor, R, whose general entry is:
 | (4) |
The ranked eigenvalues of the gyration tensor, λ12 ≥ λ22 ≥ λ32, were used to characterize the shape anisotropy of the chainmail and compute its squared gyration radius, Rg2 = λ12 + λ22 + λ32. The canonical expectation values of the same quantities were obtained by averaging over the sampled conformations at given chainmail type and ring composition.
We analyzed the spontaneous curvature of the chainmail by computing the local Gaussian curvatures in the neighborhood of each ring using the method of ref. 66. The algorithm applies to three-dimensional embeddings of triangular meshes and thus it is well suited to the honeycomb connectivity of our chainmails. Specifically, a natural triangulation of the neighborhood of ring i is obtained by connecting its center of mass with those of its nearest neighbor rings of the same (A or B) sublattice. This procedure yields six or fewer triangular facets depending on whether the ring i is inside or at the boundary of the chainmail. Based on the Gauss–Bonnet theorem, the local Gaussian curvature is then computed as:
 | (5) |
 | ||
Fig. 2 Computation of the local Gaussian curvature. The angle of the triangular facet k (red area) at the central vertex i is θk(i). The contribution of facet k to A(i) in eqn (5) is  if the red triangle is acute or right. Instead, if the red triangle is obtuse, the contribution of facet k to A(i) is Ak/2 if θk is obtuse, or Ak/4 if αk or βk are obtuse, where Ak is the area of facet k. if the red triangle is acute or right. Instead, if the red triangle is obtuse, the contribution of facet k to A(i) is Ak/2 if θk is obtuse, or Ak/4 if αk or βk are obtuse, where Ak is the area of facet k. | ||
Following ref. 56, we computed the global Gaussian curvature of the entire chainmail as
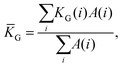 | (6) |
 denotes the sum over all rings in the chainmail.
denotes the sum over all rings in the chainmail.
3. Results and discussion
We used Langevin molecular dynamics simulations to explore the conformational properties of honeycomb chainmails of diblock copolymer rings, each made of one rigid and one flexible segment. Our specific aim was to understand whether the large-scale properties of chainmails with the same honeycomb connectivity could significantly depend on the composition of the rings and the inequivalent modes that the rings can be linked with their neighbors. To this end, we considered various relative sizes of the rigid and flexible segments and two different patterns of chainmail linking, as summarised in Fig. 1.For the block copolymer composition, we considered five different rigid-segment coverages, corresponding to 0, 33, 50, 67, and 100% of ring monomers belonging to the rigid segment.
For the linking patterns, we exploited the bipartite nature of the honeycomb lattice, made of two interleaved triangular sublattices, to design two different chainmail types, as sketched in Fig. 1b. The first type, P1, is homogeneous in that rings in the two triangular sublattices present the same linking mode, i.e., a succession of over and underpasses, with their mechanically-bonded neighbors, modulo finite size effects. The second type, P2, is instead heterogeneous, with the rings of one triangular sublattice switching between the two linking modes of Fig. 1c in alternating columns.
We considered all combinations of the selected ring compositions and linking patterns, ten in total, and used Langevin dynamics simulations to sample the equilibrated conformational ensembles. Typical configurations for P1 and P2 chainmails for rings with equally long rigid and flexible blocks (50% rigid-segment coverage) are shown in Fig. 3. For clarity, the front and side views of the chainmail are complemented with a wireframe representation, where the nodes correspond to the centers of mass of the rings, and the connecting edges represent the mechanical bonding of the corresponding rings.
Although they share the same ring composition and honeycomb lattice organization, the two representative chainmails present noticeable structural differences, which we next examined with a systematic quantitative analysis.
3.1. Metric properties
Fig. 4 presents a comparative overview of the average metric properties of chainmails with different compositions of the ring diblock copolymers and linking patterns. | ||
Fig. 4 Metric properties of the system. (a) Gyration radius of the chainmails  at different compositions. (b) Square root of the eigenvalues of the gyration tensor normalized by the Rg at the corresponding composition at different compositions. (b) Square root of the eigenvalues of the gyration tensor normalized by the Rg at the corresponding composition 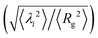 . Normalization with Rg evidences the scaling effect of the rigidity. (c) . Normalization with Rg evidences the scaling effect of the rigidity. (c) 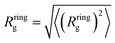 of single rings inside chainmails with P1 (purple dots) and P2 (green diamonds). The orange crosses corresponds to the observed values for an isolated ring. (d) Mechanical bond length, b, versus ring gyration radius, Rringg, for P1 and P2 patterns. Error bars represent statistical uncertainty, calculated as half the difference between the average values of observables from the two collected trajectories, except for the Rg of isolated rings, whose errors are computed with block analysis and bootstrapping, see S2 in the ESI.† of single rings inside chainmails with P1 (purple dots) and P2 (green diamonds). The orange crosses corresponds to the observed values for an isolated ring. (d) Mechanical bond length, b, versus ring gyration radius, Rringg, for P1 and P2 patterns. Error bars represent statistical uncertainty, calculated as half the difference between the average values of observables from the two collected trajectories, except for the Rg of isolated rings, whose errors are computed with block analysis and bootstrapping, see S2 in the ESI.† | ||
The root mean square gyration radii  of the chainmails are shown in panel a, where they are profiled for increasing rigid-segment coverage. The plot establishes that P2 chainmails are systematically larger than P1 ones. The size difference is maximum when the interlocked rings are fully flexible and progressively diminishes for increasing length of the rigid segment, becoming negligible in the limit case of fully rigid rings. These differences are a first indication of how the conformational space of mechanically bonded membranes with the same honeycomb connectivity and the same ring composition can be varied by solely intervening on the different modes for interlocking the same set of neighboring rings.
of the chainmails are shown in panel a, where they are profiled for increasing rigid-segment coverage. The plot establishes that P2 chainmails are systematically larger than P1 ones. The size difference is maximum when the interlocked rings are fully flexible and progressively diminishes for increasing length of the rigid segment, becoming negligible in the limit case of fully rigid rings. These differences are a first indication of how the conformational space of mechanically bonded membranes with the same honeycomb connectivity and the same ring composition can be varied by solely intervening on the different modes for interlocking the same set of neighboring rings.
Further and more consequential differences emerge when comparing shape data, illustrated in Fig. 4b in terms of the ensemble-averaged eigenvalues of the gyration tensor. To discount effects related to the noted different overall sizes of P1 and P2, the three averaged eigenvalues were normalized by the mean squared gyration radius. The first noteworthy feature is that the curves of the normalized eigenvalues are approximately horizontal, i.e. independent of the rigid-segment coverage. Next, the flat profiles of the two largest eigenvalues of P1 and P2 are well-superposed and compatible within statistical errors. Significant deviations are instead observed for the smallest eigenvalue, which is systematically smaller for P2, indicating that it adopts flatter shapes than P1. Similarly to the Rg results, the difference is largest for fully flexible rings and negligible for rigid ones. We conclude that P2 is systematically flatter than P1.
The fact that the P1–P2 differences of both size and shape are largest for fully flexible rings is a noteworthy result in itself (see Fig. S5, ESI†). In fact, one could have anticipated that the flexible rings, with their convoluted conformations, could screen better than rigid ones the anisotropic steric interactions resulting from the over- and under-passes of neighboring rings and hence be less conducive to emergent large-scale conformational properties. The largest difference observed for fully-flexible rings can be attributed to their smaller size compared to rigid rings, which allows them to interlock more tightly, thereby amplifying the effects of topological constraints. The conclusion is supported by similar results observed in linear catenanes.34
A pertinent question related to the observations above is how exactly the conformations of the rings depend on being part of P1 or P2 membranes. Analogously to the case of linear catenanes, this question is best addressed by comparing the size of the mechanically-bonded rings with isolated ones and by exploring the connection between the size of linked rings and their distance31–34,36 To this end, we considered the average mechanical bond length, defined as the average distance between the centers of mass of pairs of linked rings. For such an average, we considered all pairs except those with one or both rings at the boundary.
The data are presented in Fig. 4c and d and provide several indications. First, at all considered rigid-segment coverages, the size of chainmailed rings, Rringg, and the mechanical bond length, b, are practically indistinguishable between P1 and P2. Second, chaimailed rings are significantly larger than isolated ones. This is consistent with previous results for one-dimensional (linear) catenanes, where the steric interactions of mechanically-bonded neighbors make concatenated rings larger than isolated ones.34 Finally, the two sizes b and Rringg are proportional to each other.
The results reinforce the conclusion that the observed size difference of P1 and P2 chainmails directly arises from the different linking patterns, given that the size of the constitutive rings and mechanical bond length is the same for P1 and P2 at fixed ring composition. This fact implies that the two chainmail types cannot be distinguished by measuring simple metric properties locally, meaning at the scale of one or two rings.
The results of Fig. 4 establish that the overall size and shape of the chainmails are emergent properties depending on their linking pattern and ring composition, as exemplified by the conformations in Fig. 3. Specifically, (i) the rigid/flexible block-copolymer composition impacts primarily the overall size of the chainmails and only secondarily its shape, while (ii) varying the pattern of neighboring rings’ linking modes at fixed chainmail connectivity has a limited but still discernible effect on size and very pronounced impact on the shape, which can be selectively varied from approximately flat to highly non-planar.
3.2. Co-localization of rigid vs. flexible regions of linked rings
A relevant question for our system of linked block-copolymer rings is whether the flexible and rigid segments tend to segregate or mix in the chainmail due to their steric interaction at the mechanically bonded regions. This question arises naturally considering conventional systems of block copolymers, where effective repulsive interactions between segments of different types cause the latter to segregate, forming ordered structures such as cylindrical, lamellar, or spherical domains.67–69To address this point, for each sampled conformation, we first identified the contacting pairs of monomers in neighboring rings, that is, the pairs of monomers belonging to linked rings that are at a distance smaller than the interaction range of the WCA potential,  . Next, each pair was assigned to one of three mutually exclusive classes, depending on whether the contacting monomers both belonged to rigid segments (rr), flexible segments (ff), or were in segments of different stiffness (fr). By cumulating this information over the sampled conformations, we obtained the probabilities of the contacting pairs to be in the three classes, Prr, Pff and Pfr = 1 − Prr − Pff.
. Next, each pair was assigned to one of three mutually exclusive classes, depending on whether the contacting monomers both belonged to rigid segments (rr), flexible segments (ff), or were in segments of different stiffness (fr). By cumulating this information over the sampled conformations, we obtained the probabilities of the contacting pairs to be in the three classes, Prr, Pff and Pfr = 1 − Prr − Pff.
The profiles of the three probabilities are given in Fig. 5a–c as a function of the rigid-segment coverage for both chainmail types. The data show that the two limiting cases of membranes made of fully rigid (Prr = 1) and fully flexible (Pff = 1) rings are bridged by probability curves that are noticeably asymmetric with respect to the 50–50 composition. The data reveal that rr contacts are over-represented compared to the baselines obtained by mean-field-like (MF) combinatorial considerations based on the fraction of monomers in rigid segments, x, which yield PMFff = (1 − x)2, PMFfr = 2x(1 − x), and PMFrr = x2, see dashed curves in Fig. 5.
 | ||
| Fig. 5 Ring composition and contacting regions of linked rings. Probability of establishing a contact between two monomers belonging to flexible blocks (a), one belonging to a flexible and one belonging to a rigid block (b), and between two particles of rigid blocks (c). Results for P1 and P2 chainmails are shown with purple dots and green diamonds, respectively. Continuous lines correspond to the parameterized curve (Pff, panel a) and predictions (Pfr and Prr, panels b and c) of the model (eqn (7) with ΔF ≃ 0.496kBT) while dashed lines show the predicted curves when there is no entropic gain/cost for the different combinations of contacts (ΔF = 0). The error bars, calculated as half the difference between the average values of observables from the two collected trajectories (see S2 in the ESI†), are smaller than the symbols. | ||
This bias is evident when considering the 50–50 composition where the probability of rr contacts (Prr(50%) ≃ 0.39) is not equal to the value obtained in the flexible case (Pff(50%) ≃ 0.14) as in the mean-field estimate for the balanced case, but is approximately threefold larger. Furthermore, when as much as one-third of the rings’ contour is flexible, the probability of ff contacts is only marginally higher than in the fully rigid ring case.
The robustness of the observed segregation tendency of rr contacts was tested by adopting a different criterion for selecting contacting monomer pairs. Specifically, for any two mechanically bonded rings, we exclusively selected the two monomers (again, one per ring) at the shortest distance. If the latter was smaller than the contact cutoff distance,  , then the pair was assigned to the ff, rr or rf class as before. Otherwise, it was labeled as not in contact. This alternative counting of contact interactions is an apt complement of the one discussed before because a single pair of monomers is considered for any two linked rings. The data, shown in Fig. S8 of the ESI,† present a bias for rr contacts analogous to that of Fig. 5. An interesting insight emerging from the alternative analysis is that, although the rings in P1 and P2 have about the same average size and mechanical bonding distance, the fraction of selected pairs not in contact is larger for P1 chainmails.
, then the pair was assigned to the ff, rr or rf class as before. Otherwise, it was labeled as not in contact. This alternative counting of contact interactions is an apt complement of the one discussed before because a single pair of monomers is considered for any two linked rings. The data, shown in Fig. S8 of the ESI,† present a bias for rr contacts analogous to that of Fig. 5. An interesting insight emerging from the alternative analysis is that, although the rings in P1 and P2 have about the same average size and mechanical bonding distance, the fraction of selected pairs not in contact is larger for P1 chainmails.
Based on these converging results and considering that non-bonded monomers exclusively interact via a steric repulsion, we conclude that contacts between flexible regions of mechanically bonded rings are entropically disfavoured. This is arguably due to linked rings having more wiggle room or conformational freedom when they come into contact with their smooth, rigid regions rather than the crumpled, flexible ones.
To estimate the entropic cost of bringing flexible regions in contact, we fitted the probability data with a minimalistic model that improves on the mean-field-like combinatorial argument by introducing an excess free energy, ΔF, for each contacting monomer belonging to a flexible segment rather than a rigid one,
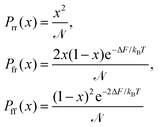 | (7) |
 is the normalization factor.
is the normalization factor.
Although the model of eqn (7) is crude, it can reproduce and predict the observed data remarkably well. To show this, we fixed the single free parameter by solely fitting the Pff data (solid line in Fig. 5a), obtaining ΔF ≃ 0.496kBT. Next, we used the fixed ΔF parameter to obtain predictions for Pfr and Prr. The resulting curves agree well with the observed contact probabilities, see solid curves in panels b and c, respectively.
The inferred ΔF value is comparable to the thermal energy, which is not surprising considering the entropic origin of the observed bias for rr contacts. At the same time, because the contour length of the regions establishing the interlockings does not scale linearly with the ring's contour length,39,70 we expect that the magnitude of the rr entropic segregation could significantly vary with the length of the rings, which could thus be a relevant design parameter for tuning chainmail properties.
3.3. Gaussian curvature
Taking into account the qualitatively different shapes of the representative P1 and P2 conformers in Fig. 3, we systematically analyzed the Gaussian curvature, KG, of P1 and P2 chainmails both locally and globally. A further motivation for this analysis is to compare our honeycomb chainmails with previous results based on different architectures.56 For such systems, it was consistently observed that the membranes invariably acquired a cup-like shape, i.e. a spontaneous positive Gaussian curvature, independently of the lattice shape or the thickness of the rigid constitutive rings.56
Fig. 6 presents the average global Gaussian curvature, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G, for various ring compositions of the two types of membranes. The plot reveals that both P1 and P2 have a negative spontaneous curvature. At any given composition, the two membrane types are clearly distinguished by the magnitude of
G, for various ring compositions of the two types of membranes. The plot reveals that both P1 and P2 have a negative spontaneous curvature. At any given composition, the two membrane types are clearly distinguished by the magnitude of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G, whose modulus is at least fivefold larger for P1 than for P2. Because negative Gaussian curvatures are associated with saddle-like shapes, one has that saddles such as the one of Fig. 3 are indeed typical for P1, and that P2 conformers, while appearing overall flat, are slightly concave–convex, too. In addition,
G, whose modulus is at least fivefold larger for P1 than for P2. Because negative Gaussian curvatures are associated with saddle-like shapes, one has that saddles such as the one of Fig. 3 are indeed typical for P1, and that P2 conformers, while appearing overall flat, are slightly concave–convex, too. In addition, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G becomes significantly more negative as the length of the flexible segment increases. A two-fold increase of |
G becomes significantly more negative as the length of the flexible segment increases. A two-fold increase of |![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G| for P1 is observed going from fully rigid to fully flexible rings, a point further discussed later.
G| for P1 is observed going from fully rigid to fully flexible rings, a point further discussed later.
 | ||
Fig. 6 Average Gaussian curvature of the membranes for both linking patterns. P2 membranes have a |![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G| an order of magnitude smaller than P1 membranes. In both cases | G| an order of magnitude smaller than P1 membranes. In both cases |![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G| decreases with the overall ring rigidity. Error bars represent statistical uncertainty, calculated as half the difference between the average values of observables from the two collected trajectories, see S2 in the ESI.† G| decreases with the overall ring rigidity. Error bars represent statistical uncertainty, calculated as half the difference between the average values of observables from the two collected trajectories, see S2 in the ESI.† | ||
The observed negative curvature is remarkable considering that, to our knowledge, only positive Gaussian curvatures have been reported before for chainmails, constructed starting from square and triangular architectures.56 Here, the systematic emergence of negative ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) G – irrespective of the linking pattern (P1/P2) and ring composition – gives a strong indication that the honeycomb lattice connectivity is conducive to saddle-like shapes. This predisposition can be very strongly modulated by the modes that neighboring rings are linked with one another and, to a comparable but lesser extent, by the ring composition.
G – irrespective of the linking pattern (P1/P2) and ring composition – gives a strong indication that the honeycomb lattice connectivity is conducive to saddle-like shapes. This predisposition can be very strongly modulated by the modes that neighboring rings are linked with one another and, to a comparable but lesser extent, by the ring composition.
For a more detailed insight into the emergence and persistence of saddle-shaped conformations, we analyzed KG at the local level. To do so, we considered the longest trajectory and, for each sampled conformation, we first computed the instantaneous value of KG in the neighborhood of each ring. Then we calculated the time-averaged value of the local curvatures, and reported them as heatmaps on a regular (flattened) representation of the underlying honeycomb lattice.
The resulting heatmaps for the case of fully flexible rings, where |KG| is largest, are shown in the leftmost column of Fig. 7. The time-averaged heatmap of P1 is biased towards negative KG values, characteristic of saddle-like states. On the contrary, the time-averaged heatmap of the P2 membrane of fully flexible rings displays no significant negative curvature pattern but smaller domains with both signs of KG.
We repeated the curvature analysis for the average chainmail structure to better interpret the time-averaged heatmaps. This structure was obtained with a structural alignment of all configurations (snapshots) sampled in the trajectory. To this end, we employed the Kabsch optimal roto-translation71 to align the centers of mass of each conformer with those of a reference one. The reference configuration was selected as the conformer with the smallest average root-mean-square deviation from all other snapshots in the trajectory. The resulting P1 and P2 average structures are shown in the right panel of Fig. 7, where the beads correspond to the centers of mass of the rings and are colored according to their local KG values, using the same color scheme of the accompanying heatmaps.
On the one hand, the average structures provide an intuitively interpretable counterpart of the KG heatmaps, evidencing the negative KG regions of the P1 saddle and the localized KG domains of the slight P2 undulations. On the other hand, the fact that the heatmaps of the time-averaged curvatures closely resemble those of the KG computed for the average structure implies that the observed curvature patterns are very persistent in time and correlated over timescales exceeding the duration of the simulations. We recall that the latter is several-fold larger than the autocorrelation time of the gyration radius (Fig. S2 in the ESI†), which is thus amply surpassed by the long lifetimes of the observed curvature patterns. The latter eventually ought to switch between the different states compatible with the chainmail symmetry; consistent with this, symmetry-related patterns are observed in different trajectories (Fig. S11 in the ESI†).
3.4. Ring composition: effect on KG magnitude and istotropic rescaling
The spontaneous curvature results discussed in Fig. 7 for membranes with fully flexible rings are consistently observed across the considered ring compositions, albeit to a diminishing degree as the rigid-segment coverage grows larger. This conclusion emerges from the series of heatmaps in Fig. 8. The images also illustrate the point noted above that the conformational ensemble of the chainmails comprises states related by the discrete symmetries of the chainmails, which depend on the symmetry of the connectivity network, the pattern of linking modes, and the shape of the finite chainmails. Indeed, the principal axes of the various P1 heatmaps can be aligned along one of three possible symmetry axes.The combined effect of ring composition and ring linking modes on the Gaussian curvature is recapitulated in Fig. 9, which presents the cumulative distribution function (CDF) of the local curvatures of P1 and P2 chainmails sampled across an entire trajectory. The P1 and P2 CDFs of panel (a) correspond to the case of fully flexible rings. The P1 curve is shifted to the left, i.e., skewed towards more negative values, consistently with the larger value of the average curvature reported above. Instead, the effect of ring composition is shown in the top panels of Fig. 9b and c. For both P1 and P2, the sigmoidal CDF curves cross approximately at the same point, although with different slopes, indicative of sharper KG distributions for higher rigid-segment coverage. The median KG values, corresponding to CDF equal to 0.5, are shifted towards more negative values as the rigid-segment coverage diminishes, again consistent with the previous conclusions based on Fig. 6.
To more directly ascertain the size rescaling effect, we investigated whether the probability distributions of the local Gaussian curvature at different rigid-segment coverage are consistent with a simple isotropic size rescaling of the membranes. To this end, we consider the affine transformation of a membrane corresponding to multiplying the Cartesian coordinates of all the nodes by the same scale factor, q. Based on the Gaussian curvature definition, the local Gaussian curvatures of corresponding points on the original and isotropically rescaled membrane satisfy ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) G/KG = q−2, where the ∼ superscript refers to the transformed membrane.
G/KG = q−2, where the ∼ superscript refers to the transformed membrane.
Accordingly, we took for reference the KG cumulative distribution of the fully flexible rings case and asked whether the CDFs for any other rigid-segment coverage could be collapsed on it by rescaling the argument, i.e., the x axis of the plots in Fig. 9b and c, by a suitable multiplicative factor, q−2, corresponding to rescaling by q the coordinates of the conformational ensemble of the membranes.
Using a best-fit procedure to superpose the CDFs yields the curves in the bottom panels b and c for types P1 and P2, respectively. The collapse of the curves for all ring compositions is noticeably good, particularly for the P1 chainmail type.
It is interesting to consider the real-space scaling factors, q, inferred from the best fit. The data, given in Fig. 9d, indicate that q has a general increasing trend with the length of the rigid block. Pleasingly, the reported values of q are comparable with the ratios of other characteristic lengthscales, such as the chainmail gyration radius and mechanical bond length. For instance, the CDF[KG] curves for fully rigid and fully-flexible rings are optimally superposed for q equal to 1.26 (P1) and 1.14 (P2), which are not dissimilar from the corresponding ratios of Rg, 1.39 (P1) and 1.29 (P2), and of b, 1.44 (both P1 and P2) in Fig. 4.
Overall, the above results support the notion that the composition of the rings primarily defines the overall size of the chainmails, not their shape, which can dramatically vary with the pattern of ring linking modes. Our preliminary calculations indicate that this property is preserved as system size increases. This emerges from additional simulations for P1 chainmails where we increased the number of constitutive rings from 68 to 100. The results, which are presented in Fig. S12 in the ESI,† suggest that the shape equivalence under isotropic rescaling can hold not only across different ring rigidities, but across chainmail sizes, too. This preliminary result thus reinforces the notion that the membrane properties studied here ought to be robustly preserved as system size increases, consistent with results for other models of mechanically bonded membranes. Additionally, It would be interesting to explore the effect of varying the length of the constitutive rings to ascertain if it could have global implications beyond the expected impact on chainmail size.
4. Conclusions
We considered two-dimensional chainmails of interlocked ring polymers and used Langevin dynamics simulations to study the effects of ring composition and chainmail topology on the equilibrium conformations. We considered two chainmail types, P1 and P2, with the same honeycomb architecture but different local patterns of over- and under-crossings of the linked rings; the latter were modeled as diblock copolymers made of rigid and flexible segments at five different relative compositions.By examining various local and global metric observables, we found that ring composition and linking patterns affect chainmails in different and complementary ways. Specifically, while the former primarily sets the overall size of the chainmail, the latter defines the shape.
The P1 chainmail, where all rings have the same linking pattern, innately adopts saddle-like shapes characterized by negative Gaussian curvatures both locally and globally. Instead, the P2 chainmail, where the above pattern is interrupted by regularly spaced rows of differently linked rings, is flat. The imprinting of the linking topology is so strong that the above shapes emerge systematically throughout the considered range of block copolymer compositions, from fully rigid to fully flexible. Remarkably, the repercussions of the lattice topology on the conformations of the membranes are more prominent when the rings are more flexible, as seen both in the global metric properties and in the curvature patterns.
In line with this result, we found that the conformational ensembles of chainmails with the same linking pattern but different ring compositions can be superposed with an affine transformation corresponding to a uniform rescaling. The composition-dependent scaling factor is defined by the characteristic gyration radius of the individual rings or, equivalently, by the mechanical bond length.
While it is intuitively plausible that varying ring composition can modulate the chainmail's overall size via the linked rings' size and distances, the shape equivalence under isotropic rescaling is a noteworthy and non-intuitive result. For instance, because flexible rings have a smaller metric footprint and are more convoluted than rigid ones, one could have surmised that the interface regions of linked flexible rings would be intricate, preventing the details of the linking pattern from reverberating globally. It is thus surprising that such topological screening is not observed and that average structures of chainmails with fully rigid and fully flexible rings can be superposed by isotropic rescaling. At the same time, ring composition does have implications for the microscopic organization of the chainmails and precisely for type of blocks preferentially co-opted at the interlocked regions. In fact, we observed that rigid blocks are systematically over-represented over flexible ones.
The above results have several implications worthy of future investigations. Primarily, they establish that at least one linking pattern can yield conformations with negative Gaussian curvature. This class of shapes, which has not been reported before for chainmails, is relevant in supramolecular synthetic chemistry.72,73 Our results show that by extending considerations to metamaterials based on mechanical bonding, the saddle shape can be achieved with an entirely new design principle, namely by controlling the local linking patterns. The observed robustness of the shape-conditioning effect of the linking pattern suggests that chainmail architectures other than the honeycomb one could yield saddle-shaped membranes, too. In this regard, we note the parallel work by Klotz et al.,74 which we became aware of after completing this study's manuscript, that reported negative Gaussian curvature for chainmails with different network connectivity than we considered. The convergence of our study and the one of ref. 74 supports the broader relevance of negative Gaussian curvature in chainmails and motivates the systematic search for the network topologies where it can spontaneously emerge. Next, the shape equivalence – up to an overall scale factor – of chainmails of different ring compositions indicates that the latter could be a relevant tunable parameter for designing chainmails according to given size specifications. It would also be appealing to co-opt and generalize analysis methods developed for networks of linked polymers75–77 to formulate free-energy-based arguments to predict the Gaussian curvature of chainmails as well as their elastic properties for different ring composition and linking patterns.
In addition to the above considerations, there are several additional elements related to the interplay of ring composition and linking topology that would be worthy of future investigation, including aspects pertinent to biological systems such as kinetoplasts. For instance, while here we focused on rings with different flexibility and no intrinsic bending, one could extend considerations to circular polymers with intrinsic curvature, which can be relevant for DNA rings. Furthermore, it would be interesting to relax the constraint of homogeneity and isotropy of the linking network; membranes composed of rings with polydispersed lengths and with linking defects would arguably be closer to prospective experimental realizations of mechanically-bonded membranes. Such applicative avenues might involve using molecular weaving techniques78 and molecular constructs with rigidities tunable via external conditions, such as the pH or the ionic strength of the solution.
In conclusion, we have introduced a set of topological and composition features that lead to a rich phenomenology of membrane conformations at different scales, where simple rationalizing rules emerge despite the complexity of the system. Given the wide possibilities in which the basic ingredients can be combined, we expect many novel scenarios to be uncovered upon systematically exploring the physics of this setup, advancing the rational design of mechanically bonded meta-materials.
Data availability
Data for this article are available at https://github.com/JnLuengo/2D_Chainmail.git.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are grateful to Alexander Klotz for helpful feedback on the manuscript and for sharing in return his manuscript titled “Chirality Effects in Molecular Chainmail” co-authored with Michael Dimitriyev and Caleb Anderson that has been jointly uploaded on arXiv along with the original draft of this study.74 J. L. M. would like to acknowledge the Erasmus+ Programme for Traineeships for financial support. The project that gave rise to these results received the support of a fellowship from the “la Caixa” Foundation (ID 100010434) and from the European Unions Horizon research and innovation programme under Marie Skłodowska-Curie grant agreement no. 847648. The fellowship code is LCF/BQ/PI20/11760019. S. A. acknowledges support from a Ramón y Cajal Fellowship (ref. RYC2022-037744-I), funded by MICIU/AEI/10.13039/501100011033 and FSE+. C. M. acknowledges support by the European Union – NextGenerationEU, in the framework of the PRIN Project “The Physics of Chromosome Folding” (code: 2022R8YXMR, CUP: G53D23000820006) and by PNRR Mission 4, Component 2, Investment 1.4_CN_00000013_CN-HPC: National Centre for HPC, Big Data and Quantum Computing – spoke 7 (CUP: G93C22000600001). The views and opinions expressed are solely those of the authors and do not necessarily reflect those of the European Union, nor can the European Union be held responsible for them.References
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1986, 57, 791 CrossRef CAS PubMed.
- Y. Kantor and K. Kremer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 2490 CrossRef CAS PubMed.
- S. J. Barsky and M. Plischke, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 3911 CrossRef CAS PubMed.
- M. J. Bowick and A. Travesset, Phys. Rep., 2001, 344, 255–308 CrossRef CAS.
- T. A. Witten, Rev. Mod. Phys., 2007, 79, 643 CrossRef.
- J. Sakamoto, J. van Heijst, O. Lukin and A. D. Schlüter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069 CrossRef CAS PubMed.
- M. Gandikota and A. Cacciuto, Soft Matter, 2023, 19, 5328–5335 RSC.
- H. S. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005 CrossRef PubMed.
- G. Gompper and D. Kroll, Phys. Rev. Lett., 1997, 78, 2859 CrossRef CAS.
- T. Zhang, X. Li and H. Gao, J. Mech. Phys. Solids, 2014, 67, 2–13 CrossRef CAS.
- M. Plischke and D. Boal, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4943 CrossRef PubMed.
- F. F. Abraham, W. Rudge and M. Plischke, Phys. Rev. Lett., 1989, 62, 1757 CrossRef CAS PubMed.
- M. Murat and G. S. Grest, Macromolecules, 1996, 29, 1278–1285 CrossRef CAS.
- M. Spector, E. Naranjo, S. Chiruvolu and J. Zasadzinski, Phys. Rev. Lett., 1994, 73, 2867 CrossRef CAS PubMed.
- Y. Zhang, Z. Yan, K. Nan, D. Xiao, Y. Liu, H. Luan, H. Fu, X. Wang, Q. Yang and J. Wang, et al. , Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11757–11764 CrossRef CAS PubMed.
- D. Yllanes, S. S. Bhabesh, D. R. Nelson and M. J. Bowick, Nat. Commun., 2017, 8, 1–8 CrossRef CAS PubMed.
- M. Fokker, S. Janbaz and A. Zadpoor, RSC Adv., 2019, 9, 5174–5188 RSC.
- Z. Niu and H. W. Gibson, Chem. Rev., 2009, 109, 6024–6046 CrossRef CAS PubMed.
- G. Gil-Ramírez, D. A. Leigh and A. J. Stephens, Angew. Chem., Int. Ed., 2015, 54, 6110–6150 CrossRef PubMed.
- Q. Wu, P. M. Rauscher, X. Lang, R. J. Wojtecki, J. J. de Pablo, M. J. A. Hore and S. J. Rowan, Science, 2017, 358, 1434–1439 CrossRef CAS PubMed.
- L. F. Hart, J. E. Hertzog, P. M. Rauscher, B. W. Rawe, M. M. Tranquilli and S. J. Rowan, Nat. Rev. Mater., 2021, 6, 508–530 CrossRef CAS.
- E. Orlandini and C. Micheletti, J. Phys.: Condens. Matter, 2021, 34, 013002 CrossRef PubMed.
- R. Bai, Z. Zhang, W. Di, X. Yang, J. Zhao, H. Ouyang, G. Liu, X. Zhang, L. Cheng and Y. Cao, et al. , J. Am. Chem. Soc., 2023, 145, 9011–9020 CrossRef CAS PubMed.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- C. P. Collier, G. Mattersteig, E. W. Wong, Y. Luo, K. Beverly, J. Sampaio, F. M. Raymo, J. F. Stoddart and J. R. Heath, Science, 2000, 289, 1172–1175 CrossRef CAS PubMed.
- J. B. Lee, S. Peng, D. Yang, Y. H. Roh, H. Funabashi, N. Park, E. J. Rice, L. Chen, R. Long and M. Wu, et al. , Nat. Nanotechnol., 2012, 7, 816–820 CrossRef CAS PubMed.
- B. A. Krajina, A. Zhu, S. C. Heilshorn and A. J. Spakowitz, Phys. Rev. Lett., 2018, 121, 148001 CrossRef CAS PubMed.
- D. P. August, R. A. Dryfe, S. J. Haigh, P. R. Kent, D. A. Leigh, J.-F. Lemonnier, Z. Li, C. A. Muryn, L. I. Palmer and Y. Song, et al. , Nature, 2020, 588, 429–435 CrossRef CAS PubMed.
- Y. Sakai, G. D. Wilkens, K. Wolski, S. Zapotoczny and J. G. Heddle, ACS Nanosci. Au, 2022, 2, 57–63 CrossRef CAS PubMed.
- S. Datta, Y. Kato, S. Higashiharaguchi, K. Aratsu, A. Isobe, T. Saito, D. D. Prabhu, Y. Kitamoto, M. J. Hollamby, A. J. Smith, R. Dalgliesh, N. Mahmoudi, L. Pesce, C. Perego, G. M. Pavan and S. Yagai, Nature, 2020, 583, 400–405 CrossRef CAS PubMed.
- Z. Ahmadian Dehaghani, I. Chubak, C. N. Likos and M. R. Ejtehadi, Soft Matter, 2020, 16, 3029–3038 RSC.
- H. Lei, J. Zhang, L. Wang and G. Zhang, Polymer, 2021, 212, 123160 CrossRef CAS.
- J. Li, F. Gu, N. Yao, H. Wang and Q. Liao, ACS Macro Lett., 2021, 10, 1094–1098 CrossRef PubMed.
- P. Chiarantoni and C. Micheletti, Macromolecules, 2022, 55, 4523–4532 CrossRef CAS.
- P. M. Rauscher, S. J. Rowan and J. J. de Pablo, ACS Macro Lett., 2018, 7, 938–943 CrossRef CAS PubMed.
- P. M. Rauscher, K. S. Schweizer, S. J. Rowan and J. J. de Pablo, Macromolecules, 2020, 53, 3390–3408 CrossRef CAS.
- P. M. Rauscher, K. S. Schweizer, S. J. Rowan and J. J. de Pablo, J. Chem. Phys., 2020, 152, 214901 CrossRef CAS PubMed.
- R. A. Farimani, Z. Ahmadian Dehaghani, C. N. Likos and M. R. Ejtehadi, Phys. Rev. Lett., 2024, 132, 148101 CrossRef CAS PubMed.
- M. Caraglio, C. Micheletti and E. Orlandini, Polymers, 2017, 9, 327 CrossRef PubMed.
- L. Tubiana, F. Ferrari and E. Orlandini, Phys. Rev. Lett., 2022, 129, 227801 CrossRef CAS PubMed.
- M. Caraglio, E. Orlandini and S. G. Whittington, Macromolecules, 2017, 50, 9437–9444 CrossRef CAS.
- P. Chiarantoni and C. Micheletti, Macromolecules, 2023, 56, 2736–2746 CrossRef CAS.
- Z. A. Dehaghani, P. Chiarantoni and C. Micheletti, ACS Macro Lett., 2023, 12, 1231–1236 CrossRef CAS PubMed.
- A. H. Fairlamb, P. O. Weislogel, J. Hoeijmakers and P. Borst, J. Cell Biol., 1978, 76, 293–309 CrossRef CAS PubMed.
- J. Chen, C. A. Rauch, J. H. White, P. T. Englund and N. R. Cozzarelli, Cell, 1995, 80, 61–69 CrossRef CAS PubMed.
- S. Johnson, Y.-J. Chen and R. Phillips, PLoS One, 2013, 8, e75799 CrossRef CAS PubMed.
- S. Assenza and R. Pérez, J. Chem. Theory Comput., 2022, 18, 3239–3256 CrossRef CAS PubMed.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 121–127 CrossRef CAS PubMed.
- B. W. Soh and P. S. Doyle, ACS Macro Lett., 2020, 9, 944–949 CrossRef CAS PubMed.
- P. He, A. J. Katan, L. Tubiana, C. Dekker and D. Michieletto, Phys. Rev. X, 2023, 13, 021010 CAS.
- J. Ragotskie, N. Morrison, C. Stackhouse, R. C. Blair and A. R. Klotz, J. Polym. Sci., 2024, 62, 1287–1295 CrossRef CAS.
- I. Yadav, D. Al Sulaiman, B. W. Soh and P. S. Doyle, ACS Macro Lett., 2021, 10, 1429–1435 CrossRef CAS PubMed.
- J. Arsuaga, Y. Diao, M. Klingbeil and V. Rodriguez, Comput. Math. Biophys., 2014, 2, 98–106 Search PubMed.
- Y. Diao, V. Rodriguez, M. Klingbeil and J. Arsuaga, PLoS One, 2015, 10, e0130998 CrossRef PubMed.
- L. Ibrahim, P. Liu, M. Klingbeil, Y. Diao and J. Arsuaga, J. Phys. A: Math. Theor., 2018, 52, 034001 CrossRef.
- J. M. Polson, E. J. Garcia and A. R. Klotz, Soft Matter, 2021, 17, 10505–10515 RSC.
- S. Geggier and A. Vologodskii, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15421–15426 CrossRef CAS PubMed.
- A. Marin-Gonzalez, J. Vilhena, R. Perez and F. Moreno-Herrero, Q. Rev. Biophys., 2021, 54, e8 CrossRef CAS PubMed.
- C. Roldán-Piñero, J. Luengo-Márquez, S. Assenza and R. Pérez, J. Chem. Theory Comput., 2024, 20, 2261–2272 CrossRef PubMed.
- E. Orlandini, M. Baiesi and F. Zonta, Macromolecules, 2016, 49, 4656–4662 CrossRef CAS.
- A. Tagliabue, L. Izzo and M. Mella, J. Phys. Chem. B, 2020, 124, 2930–2937 CrossRef CAS PubMed.
- A. Tagliabue, C. Micheletti and M. Mella, ACS Macro Lett., 2021, 10, 1365–1370 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302 CrossRef CAS.
- M. Meyer, M. Desbrun, P. Schröder and A. H. Barr, Visualization and mathematics III, 2003, pp. 35–57 Search PubMed.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 7641–7644 CrossRef CAS.
- C. M. Bates and F. S. Bates, Macromolecules, 2017, 50, 3–22 CrossRef CAS.
- H. Feng, X. Lu, W. Wang, N.-G. Kang and J. W. Mays, Polymers, 2017, 9, 494 CrossRef PubMed.
- M. Caraglio, C. Micheletti and E. Orlandini, Sci. Rep., 2017, 7, 1156 CrossRef PubMed.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 827–828 CrossRef.
- J. F. Woods, L. Gallego, P. Pfister, M. Maaloum, A. Vargas Jentzsch and M. Rickhaus, Nat. Commun., 2022, 13, 3681 CrossRef CAS PubMed.
- J. F. Woods, L. Gallego, A. Maisch, D. Renggli, C. Cuocci, O. Blacque, G. Steinfeld, A. Kaech, B. Spingler and A. Vargas Jentzsch, et al. , Nat. Commun., 2023, 14, 4725 CrossRef CAS PubMed.
- A. R. Klotz, C. J. Anderson and M. S. Dimitriyev, arXiv, 2024, preprint, arXiv:2406.13590.
- A. M. Grillet, N. B. Wyatt and L. M. Gloe, Rheology, 2012, 3, 59–80 Search PubMed.
- V. Sorichetti, A. Ninarello, J. M. Ruiz-Franco, V. Hugouvieux, W. Kob, E. Zaccarelli and L. Rovigatti, Macromolecules, 2021, 54, 3769–3779 CrossRef CAS PubMed.
- T. Katashima, Polym. J., 2021, 53, 1073–1082 CrossRef CAS.
- Z.-H. Zhang, B. J. Andreassen, D. P. August, D. A. Leigh and L. Zhang, Nat. Mater., 2022, 21, 275–283 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details about the model, the system setup, and the conformational properties of chainmails for various combination of ring composition and pattern of linking modes. See DOI: https://doi.org/10.1039/d4sm00694a |
| This journal is © The Royal Society of Chemistry 2024 |





