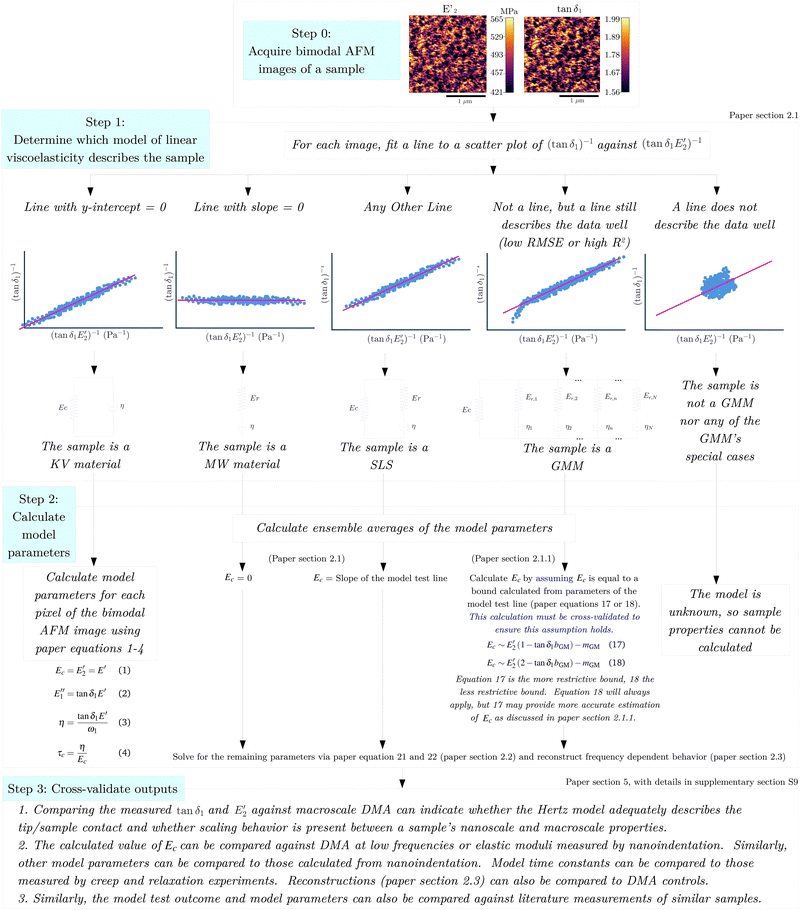
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing nanoscale viscoelasticity characterization in bimodal atomic force microscopy†
Casey Erin
Adam
a,
Alba Rosa
Piacenti
a,
Sarah L.
Waters
b and
Sonia
Contera
 *a
*a
aDepartment of Physics, University of Oxford, Oxford, OX1 3PU, UK. E-mail: sonia.antoranzcontera@physics.ox.ac.uk
bDepartment of Applied Mathematics, Mathematical Institute, University of Oxford, OX2 6GG, UK
First published on 2nd September 2024
Abstract
Polymeric, soft, and biological materials exhibit viscoelasticity, which is a time dependent mechanical response to deformation. Material viscoelasticity emerges from the movement of a material's constituent molecules at the nano- and microscale in response to applied deformation. Therefore, viscoelastic properties depend on the speed at which a material is deformed. Recent technological advances, especially in atomic force microscopy (AFM), have provided tools to measure and map material viscoelasticity with nanoscale resolution. However, to obtain additional information about the viscoelastic behavior of a material from such measurements, theoretical grounding during data analysis is required. For example, commercially available bimodal AFM imaging maps two different viscoelastic properties of a sample, the storage modulus, E′, and loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, with each property being measured by a different resonance frequency of the AFM cantilever. While such techniques provide high resolution maps of E′ and tan
δ, with each property being measured by a different resonance frequency of the AFM cantilever. While such techniques provide high resolution maps of E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, the different measurement frequencies make it difficult to calculate key viscoelastic properties of the sample such as: the model of viscoelasticity that describes the sample, the loss modulus, E′′, at either frequency, elasticity E, viscosity η, and characteristic response times τ. To overcome this difficulty, we present a new data analysis procedure derived from linear viscoelasticity theory. This procedure is applied and validated by performing amplitude modulation–frequency modulation (AM–FM) AFM, a commercially available bimodal imaging technique, on a styrene–butadiene rubber (SBR) with known mechanical behavior. The new analysis procedure correctly identified the type of viscoelasticity exhibited by the SBR and accurately calculated SBR E, η, and τ, providing a useful means of enhancing the amount of information gained about a sample's nanoscale viscoelastic properties from bimodal AFM measurements. Additionally, being derived from fundamental models of linear viscoelasticity, the procedure can be employed for any technique where different viscoelastic properties are measured at different and discrete frequencies with applied deformations in the linear viscoelastic regime of a sample.
δ, the different measurement frequencies make it difficult to calculate key viscoelastic properties of the sample such as: the model of viscoelasticity that describes the sample, the loss modulus, E′′, at either frequency, elasticity E, viscosity η, and characteristic response times τ. To overcome this difficulty, we present a new data analysis procedure derived from linear viscoelasticity theory. This procedure is applied and validated by performing amplitude modulation–frequency modulation (AM–FM) AFM, a commercially available bimodal imaging technique, on a styrene–butadiene rubber (SBR) with known mechanical behavior. The new analysis procedure correctly identified the type of viscoelasticity exhibited by the SBR and accurately calculated SBR E, η, and τ, providing a useful means of enhancing the amount of information gained about a sample's nanoscale viscoelastic properties from bimodal AFM measurements. Additionally, being derived from fundamental models of linear viscoelasticity, the procedure can be employed for any technique where different viscoelastic properties are measured at different and discrete frequencies with applied deformations in the linear viscoelastic regime of a sample.
1 Introduction
The mechanical properties of soft and polymeric materials underpin material function and application.1,2 Most soft materials, from biological structures to rubbers, are considered to be viscoelastic, meaning they respond to externally applied deformations with time delays, τ, that emerge from a combination of both elastic (with elasticity E, Pa) and viscous (with dynamic viscosity η, Pa s) behavior.1,2 Material properties E, η, and τ arise from nanoscale interactions between polymers and other molecules within the material when a stimulus is applied.1,2 Each constituent molecule of the material, and each conformation of the constituent molecules, potentially contributes a unique E, η, and τ to the material's viscoelastic response across temporal and spatial scales.1–6 Quantifying E, η, and τ of a material, especially at the nanoscale, provides insight into how polymers interact within a material, and how the material functions.1–5Often, viscoelasticity is measured by dynamic experiments, which quantify the complex modulus E* of a material.1,2E* contains a storage component E′, called the storage modulus, and a dissipative/loss component E′′, called the loss modulus.1,2E′ (Pa) measures the contribution of the sample's response that is in-phase with the applied stimulus, and represents energy stored by the sample per unit volume.1,4,5,7E′′ (Pa) measures the out-of-phase component of the sample's response, and quantifies the energy per unit volume dissipated by the sample during mechanical stimulus.1,4,5,7 The ratio between both quantities, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = E′′/E′, is a measure of mechanical damping by the material.7 Both E′ and E′′ are functions of material E and η, and τ, as well as the frequency at which the material is deformed.1,2 The exact relation between E′, E′′, tan
δ = E′′/E′, is a measure of mechanical damping by the material.7 Both E′ and E′′ are functions of material E and η, and τ, as well as the frequency at which the material is deformed.1,2 The exact relation between E′, E′′, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and E, η, τ depends on a model of viscoelasticity specific to the material.1,2
δ, and E, η, τ depends on a model of viscoelasticity specific to the material.1,2
One of the most widely used models of viscoelasticity is the General Maxwell Model (GMM).1,5,6,8 The GMM assumes that a material exhibits linear viscoelasticity, where all E and η are constants independent of the applied stimulus.1,5,8 As shown in Fig. S1 (ESI†), the GMM is often represented as a spring with elastic constant Ec connected in parallel with N arms that each consist of a spring with elastic constant En and damper with dynamic viscosity ηn connected in series.1,5,8 Here, subscript n represents the nth arm of the material. Each arm has a unique relaxation timescale τn = ηn/En and creep timescale τc = ηn/Ec.1,5,8 Subscript c denotes that a spring contributes to the creep timescale. The simplest GMM contains N = 1 arms, thereby three material constants: Ec, Er, and η, two timescales: τc = η/Ec and τr = η/Er, and is called the standard linear solid (SLS).1,5,8 Since N = 1 for the SLS, the subscript r denotes that the spring in arm 1 is the only spring that contributes to the relaxation timescale of the SLS. The GMM is several SLSs connected in parallel.1,8 Special cases of the SLS are the Maxwell (MW) and Kelvin–Voigt (KV) models.1,8 For the MW model, Ec → 0 and the material has two constants: Er, and η.4 MW materials have only one relaxation timescale, τr = η/Er.1,5,8 For the KV model, Er → ∞ and the material has two constants: Ec, and η.1,5,8 KV materials have only one creep timescale, τc = η/Ec.1,5,8 Experimentally, it is often not possible to measure all N arms of a GMM's response because N can be large, unless the material obeys the SLS, MW, or KV models.9–13
Often, the model to describe a sample's viscoelastic response, as well as the relevant material constants, are calculated from experimental measurements, and not measured directly.1,2 For example, dynamic experiments, where an oscillatory stimulus is applied to a sample, are used to quantify E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, of a sample.1,2 The model, and the relevant model parameters (E, η, τ) to describe the material's response are then determined from these dynamic quantities.1,2 Several experimental techniques exist to perform dynamic measurements. One widely used technique for macroscale measurements is dynamic mechanical analysis (mDMA), which applies an oscillating axial or torsional stimulus to a sample.2,14 For measurements at the nanoscale, atomic force microscopy (AFM) is a particularly useful tool because AFM can probe a sample with nanometer resolution, can be performed in liquid, does not require sample processing, and has higher resolution and more localized control than other techniques such as optical and magnetic tweezers.15,16 Additionally, cutting edge developments in AFM allow more sophisticated dynamic measurements to be performed. For example, novel AFM developments use photothermal excitation of a cantilever to perform nanoscale dynamic mechanical analysis (nDMA) to measure E′, E′′, and tan
δ, of a sample.1,2 The model, and the relevant model parameters (E, η, τ) to describe the material's response are then determined from these dynamic quantities.1,2 Several experimental techniques exist to perform dynamic measurements. One widely used technique for macroscale measurements is dynamic mechanical analysis (mDMA), which applies an oscillating axial or torsional stimulus to a sample.2,14 For measurements at the nanoscale, atomic force microscopy (AFM) is a particularly useful tool because AFM can probe a sample with nanometer resolution, can be performed in liquid, does not require sample processing, and has higher resolution and more localized control than other techniques such as optical and magnetic tweezers.15,16 Additionally, cutting edge developments in AFM allow more sophisticated dynamic measurements to be performed. For example, novel AFM developments use photothermal excitation of a cantilever to perform nanoscale dynamic mechanical analysis (nDMA) to measure E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ over a continuous range of frequencies that covers several orders of magnitude.14,17 Additionally, bimodal imaging techniques such as amplitude modulation–frequency modulation AFM (AM–FM AFM) exploit cantilever resonances to obtain high resolution quantitative maps (images) of a sample's nanoscale mechanical properties.15,18–28 Bimodal imaging is particularly convenient because sample indentations are small, typically only a few nanometers,19 allowing measurement of thinner samples, and increasing measurement spatial resolution.19 Additionally due to the small indentations,19 it is reasonable to assume that samples are measured in their linear viscoelastic regime.5
δ over a continuous range of frequencies that covers several orders of magnitude.14,17 Additionally, bimodal imaging techniques such as amplitude modulation–frequency modulation AFM (AM–FM AFM) exploit cantilever resonances to obtain high resolution quantitative maps (images) of a sample's nanoscale mechanical properties.15,18–28 Bimodal imaging is particularly convenient because sample indentations are small, typically only a few nanometers,19 allowing measurement of thinner samples, and increasing measurement spatial resolution.19 Additionally due to the small indentations,19 it is reasonable to assume that samples are measured in their linear viscoelastic regime.5
In bimodal AFM, the surface of a sample is intermittently tapped via a tip connected to a cantilever that is oscillated at two of the cantilever's eigenmodes.18,19,25 At the lower frequency eigenmode, with frequency f1 and angular frequency ω1 = 2πf1, the cantilever has stiffness k1, and the resonance peak at f1 has quality factor Q1.18,19,25 The cantilever's vibration at the first mode has amplitude Ar,1 far from the sample, amplitude A1 on the sample, and phase ϕ1.18,19,25 Similarly, the oscillation at the higher frequency eigenmode has frequency f2, angular frequency ω2 = 2πf2, stiffness k2, quality factor Q2, amplitude Ar,2 far from the sample, amplitude A2 on the sample, and phase ϕ2.18,19,25 These properties of the cantilever (k, Q, f) and bimodal oscillation (Ar, A, ϕ) can be used to calculate viscoelastic properties of a sample as detailed in Section S4 (ESI†).18,26–28 Briefly, each eigenmode is subjected to various types of feedback, depending on the bimodal imaging technique.18 The lower eigenmode is typically subjected to amplitude modulation, which allows calculation of a sample's tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 (subscript 1 indicates that tan
δ1 (subscript 1 indicates that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is measured at f1) from power dissipated and stored by the cantilever (see note S4.1, ESI†).26,27 The higher eigenmode, with frequency f2 and angular frequency ω2 = 2πf2, is subjected to various types of modulation, and allows calculation of a sample's
δ is measured at f1) from power dissipated and stored by the cantilever (see note S4.1, ESI†).26,27 The higher eigenmode, with frequency f2 and angular frequency ω2 = 2πf2, is subjected to various types of modulation, and allows calculation of a sample's 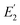 (subscript 2 indicates that E′ is measured at f2) from the frequency shift of the second eigenmode caused by tip/sample interaction forces (details in Section S4.1, ESI†).18,28 The most common form of bimodal AFM applies amplitude modulation to the first mode, frequency modulation to the second, and is referred to as amplitude modulation–frequency modulation AFM (AM–FM AFM).18
(subscript 2 indicates that E′ is measured at f2) from the frequency shift of the second eigenmode caused by tip/sample interaction forces (details in Section S4.1, ESI†).18,28 The most common form of bimodal AFM applies amplitude modulation to the first mode, frequency modulation to the second, and is referred to as amplitude modulation–frequency modulation AFM (AM–FM AFM).18
In order to calculate  in bimodal AFM, knowledge of the tip/sample interaction geometry is required.18,28 In most cases, the Hertz contact model is applied.18,28 The Hertz model assumes that both the indenter and sample are spherical, homogeneous, elastic materials, and that no adhesion is present between the indenter and sample.5 Therefore, the calculated
in bimodal AFM, knowledge of the tip/sample interaction geometry is required.18,28 In most cases, the Hertz contact model is applied.18,28 The Hertz model assumes that both the indenter and sample are spherical, homogeneous, elastic materials, and that no adhesion is present between the indenter and sample.5 Therefore, the calculated  can be incorrect for samples with an adhesive contact.5 More details on the calculation of tan
can be incorrect for samples with an adhesive contact.5 More details on the calculation of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  are provided in Section S4.1 (ESI†). Additionally, the fact that
are provided in Section S4.1 (ESI†). Additionally, the fact that  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 are characterized only at two discrete and different frequencies in bimodal imaging means that the full sample response remains unknown without additional data processing. Since bimodal AFM was developed to accurately quantify tan
δ1 are characterized only at two discrete and different frequencies in bimodal imaging means that the full sample response remains unknown without additional data processing. Since bimodal AFM was developed to accurately quantify tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and 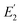 from the cantilever's motion,18,26–28 less emphasis has been placed on extracting additional information about the sample's viscoelastic response. This article describes how additional information about the viscoelastic behavior of a sample can be obtained from tan
from the cantilever's motion,18,26–28 less emphasis has been placed on extracting additional information about the sample's viscoelastic response. This article describes how additional information about the viscoelastic behavior of a sample can be obtained from tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  .
.
Bimodal AFM does not directly quantify a sample's loss modulus E′′, nor material constants such as τ, Ec, Er, and η. Quantification of E′′ and material constants from bimodal AFM's tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  is not straightforward because tan
is not straightforward because tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and E′′ depend on the frequency of the applied stimulus (per the formulas in Table S1, ESI†). Therefore, tan
δ and E′′ depend on the frequency of the applied stimulus (per the formulas in Table S1, ESI†). Therefore, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  cannot be directly combined to calculate a sample's E′′ and material constants. To circumvent this issue, it is typically assumed that the sample is a KV material, for which E′ is independent of frequency.24 Under this assumption, E′′ and material constants Ec, η, and τc can be calculated from the measured tan
cannot be directly combined to calculate a sample's E′′ and material constants. To circumvent this issue, it is typically assumed that the sample is a KV material, for which E′ is independent of frequency.24 Under this assumption, E′′ and material constants Ec, η, and τc can be calculated from the measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and 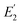 as follows.24 In the following equations, numbers in subscripts indicate the eigenmode to which the quantity corresponds.24
as follows.24 In the following equations, numbers in subscripts indicate the eigenmode to which the quantity corresponds.24
 | (1) |
 | (2) |
 | (3) |
 | (4) |
 and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. Second, for samples that exhibit relaxation such as MW materials, SLSs, or GMMs, assuming that the sample is a KV material prevents quantification of the sample's relaxation time(s). Therefore, a new method of analyzing bimodal AFM data is needed.
δ1. Second, for samples that exhibit relaxation such as MW materials, SLSs, or GMMs, assuming that the sample is a KV material prevents quantification of the sample's relaxation time(s). Therefore, a new method of analyzing bimodal AFM data is needed.
This article describes the development and validation of a bimodal AFM data analysis procedure to extract additional information about sample viscoelasticity. This additional information includes the linear viscoelastic model that describes a sample and estimates of model parameters, which represent ensemble averages for the sample. The new analysis procedure first uses measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  to determine the best model of linear viscoelasticity to describe a sample. Only models of linear viscoelasticity are considered in this analysis, due to the fact that bimodal AFM indentations are small,19 and therefore likely in the linear viscoelastic regime of a sample. Once the model is determined from the model test, the sample's viscoelastic material constants are calculated from model test parameters. Finally, applying the selected model and calculated material constants allows reconstruction of the sample's E′(f), E′′(f), and tan
to determine the best model of linear viscoelasticity to describe a sample. Only models of linear viscoelasticity are considered in this analysis, due to the fact that bimodal AFM indentations are small,19 and therefore likely in the linear viscoelastic regime of a sample. Once the model is determined from the model test, the sample's viscoelastic material constants are calculated from model test parameters. Finally, applying the selected model and calculated material constants allows reconstruction of the sample's E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f). In this article, the analysis procedure is derived first, then validated on AM–FM AFM measurements of a styrene–butadiene rubber (SBR) with known viscoelastic properties.
δ(f). In this article, the analysis procedure is derived first, then validated on AM–FM AFM measurements of a styrene–butadiene rubber (SBR) with known viscoelastic properties.
This article also addresses another potential issue in bimodal AFM experiments in the calculation of  . As detailed in Section S4.1 (ESI†), calculation of
. As detailed in Section S4.1 (ESI†), calculation of  in bimodal AFM requires knowledge of tip geometry, in particular the tip radius, R.18 Typically, R is determined via calibration on a sample of known
in bimodal AFM requires knowledge of tip geometry, in particular the tip radius, R.18 Typically, R is determined via calibration on a sample of known  .19 For this calibration, the user manually enters R in the software so the measured
.19 For this calibration, the user manually enters R in the software so the measured  matches the expected
matches the expected 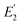 of the calibration sample.19 Calibration of R can also indicate whether the Hertz contact model on which bimodal AFM's calculation of
of the calibration sample.19 Calibration of R can also indicate whether the Hertz contact model on which bimodal AFM's calculation of  is based,18,28 is a good model for the tip/sample interaction.19 When it is not possible to obtain the expected
is based,18,28 is a good model for the tip/sample interaction.19 When it is not possible to obtain the expected  by calibrating R, it is a sign that the contact may be adhesive, and therefore that the Hertz model inadequately describes the contact geometry.19
by calibrating R, it is a sign that the contact may be adhesive, and therefore that the Hertz model inadequately describes the contact geometry.19
In spite of the benefits of calibrating R, it is sometimes difficult to determine the best calibration sample for materials with multiple components. Additionally, calibration can damage or blunt the tip, changing R, before bimodal AFM is performed on the actual sample. Therefore, it would be convenient to skip calibration of R while still being able to correctly quantify material  . The feasibility of doing so is assessed in this article.
. The feasibility of doing so is assessed in this article.
2 Development of a novel analysis procedure for bimodal AFM data
It is not trivial to calculate the material constants of a sample (such as τ, Ec, Er, and η) from bimodal AFM observables ( and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1) because both E′ and tan
δ1) because both E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ are frequency dependent. To overcome this difficulty, a new bimodal AFM analysis procedure is derived in this section. The procedure uses the measured tan
δ are frequency dependent. To overcome this difficulty, a new bimodal AFM analysis procedure is derived in this section. The procedure uses the measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and 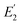 to determine which model of viscoelasticity a sample obeys (Section 2.1), calculate the relevant material constants of the sample (Section 2.2), and use these material constants to reconstruct E′(f), E′′(f), and tan
to determine which model of viscoelasticity a sample obeys (Section 2.1), calculate the relevant material constants of the sample (Section 2.2), and use these material constants to reconstruct E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) of the sample over a large frequency range (Section 2.3).
δ(f) of the sample over a large frequency range (Section 2.3).
2.1 Determining the viscoelastic model that describes a sample
The first step in the new bimodal AFM data analysis procedure is to determine which model of viscoelasticity applies. It is reasonable to assume that samples exhibit linear viscoelasticity during a bimodal AFM experiment because sample deformations during bimodal imaging are small, typically only a few nanometers,19 and are therefore likely in the sample's linear viscoelastic regime.5 Therefore, only standard models of linear viscoelasticity: the MW, KV, SLS, and GMM are considered here.A test to determine whether a sample is a MW, KV, or SLS material can be derived from the following expressions for E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of the SLS.1,5,8
δ of the SLS.1,5,8
 | (5) |
 | (6) |
 | (7) |
| E′ = Ec + τrωE′′ | (8) |
Eqn (7) can be rewritten in terms of τc = η/Ec and τr = η/Er as follows.
 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ measured at two different frequencies, such as the first and second eigenmode of the cantilever, can therefore be calculated as follows.
δ measured at two different frequencies, such as the first and second eigenmode of the cantilever, can therefore be calculated as follows. | (10) |
Next, eqn (8) can be re-written in terms of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ by dividing both sides of the equation by E′ and rearranging terms.
δ by dividing both sides of the equation by E′ and rearranging terms.
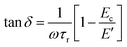 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ2, then substituted into eqn (10).
δ2, then substituted into eqn (10). | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1−1 against
δ1−1 against  should be linear, with a slope m = Ec and a y-intercept b dictated by material τr and τc, if the material is a SLS.
should be linear, with a slope m = Ec and a y-intercept b dictated by material τr and τc, if the material is a SLS.
For a MW material, Ec ≈ 0 and τc → ∞. Substituting these conditions into eqn (12) gives m = 0. Additionally, since τc ≫ τr and τc ≫ ω1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2−2, the intercept, b, can be approximated as follows.
2−2, the intercept, b, can be approximated as follows.
| b = ω1τr | (13) |
 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1−1 against
δ1−1 against  (eqn (12)) will be a horizontal straight line for a MW material.
(eqn (12)) will be a horizontal straight line for a MW material.
For a KV material, Er ≈ ∞ and τr ≈ 0. Substituting these conditions into eqn (12), m is the same as that for the SLS, but b = 0. Eqn (12) simplifies to the following.
 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1−1 against
δ1−1 against  will be a straight line through the origin for a KV material.
will be a straight line through the origin for a KV material.
In summary, if a plot of bimodal AFM observables tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1−1vs.
δ1−1vs. is linear, the sample can be modeled as a SLS, MW, or KV material. It remains unclear whether the plot will also be linear for a GMM, which will be assessed in the following section. Goodness of fit metrics, such as the R2 value, for linear fits to bimodal AFM data can determine if one of these three models describes the sample. The slope and y-intercept of the fit can then be used to distinguish between each model.
is linear, the sample can be modeled as a SLS, MW, or KV material. It remains unclear whether the plot will also be linear for a GMM, which will be assessed in the following section. Goodness of fit metrics, such as the R2 value, for linear fits to bimodal AFM data can determine if one of these three models describes the sample. The slope and y-intercept of the fit can then be used to distinguish between each model.
For most GMM materials, the total number of arms in the GMM, N, is large. However, the distribution of the N different τn typically only has a few peaks, with values at different orders of magnitude (i.e. τn = ns, μs, ms, s, min, etc…).9–13 Depending on the excitation stimulus, some peaks (subgroups) in the distribution of τn will contribute more to the sample's response than others. Arms that contribute most to the material's response to a dynamic stimulus of frequency f have τn on the order of 1/f,29 because arms with larger τn respond too slowly to contribute much to the material's response, and arms with faster τn only contribute briefly to the material's initial response to the stimulus, leaving arms with τn ≈ 1/f to dominate the majority of the response. For example, a material's response to a dynamic stimulus with a frequency in the kHz range, like that applied by bimodal AFM, is more likely to be dominated by GMM arms with τn on the order of μs–ms.29
Assuming that bimodal AFM only excites one subgroup of GMM arms that have similar τn, the subgroup could be approximated as a single SLS, likely with a large standard deviation in Ec, Er, and η due to the variety of arms contributing to this approximation. In other words, the model test line in eqn (12) could still be fitted to bimodal data from a GMM. However, because the governing equations of the GMM and SLS are different, the slope and y-intercept of the GMM model test line (eqn (12)) are not the same as that for the SLS, as follows.
While the line in eqn (12) could still be fit to bimodal measurements of a GMM, it is not possible to directly relate Ec or other material parameters to the slope, mGM, and y-intercept, bGM, of this line because there are too few AFM observables and too many unknowns, even if only a subgroup of GMM arms is excited. The unknowns include:  , tan
, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ2,
δ2,  ,
,  , Ec, the number of arms N (for the material as a whole or for the subgroup of arms), and the N different En and ηn. However, it is possible to use mGM and bGM to obtain bounds for the GMM's Ec, as detailed in Section S6 (ESI†). Briefly, algebraic manipulations (see Section S6, ESI†) of the expressions for E′ and tan
, Ec, the number of arms N (for the material as a whole or for the subgroup of arms), and the N different En and ηn. However, it is possible to use mGM and bGM to obtain bounds for the GMM's Ec, as detailed in Section S6 (ESI†). Briefly, algebraic manipulations (see Section S6, ESI†) of the expressions for E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of a GMM (Section S1 and Table S1, ESI†) result in the following expression.
δ of a GMM (Section S1 and Table S1, ESI†) result in the following expression.
 | (16) |
 . For a GMM (see formulas in Table S1, ESI†), 0 < Ec/E′ ≤ 1. These limits can be substituted into eqn (16) to obtain a more
. For a GMM (see formulas in Table S1, ESI†), 0 < Ec/E′ ≤ 1. These limits can be substituted into eqn (16) to obtain a more  or less
or less  restrictive bound on Ec. Assuming that Ec is close to the bound on Ec allows the value of Ec to be approximated from these bounds. The more restrictive bound results in eqn (17).
restrictive bound on Ec. Assuming that Ec is close to the bound on Ec allows the value of Ec to be approximated from these bounds. The more restrictive bound results in eqn (17). | (17) |
 | (18) |
To estimate Ec of a GMM for this article, it is assumed that the value of Ec is approximately equal to this upper bound. Therefore, this method has the potential to overestimate the value of a GMM's Ec in samples where this assumption does not hold. Before applying this method, the reliability of calculating Ecvia this assumption, and compared to treating the sample solely as a SLS must be assessed (see Table 1).
| Parameter | Cantilever | GMM | SLS |
|---|---|---|---|
| E c (Pa) | AC240TSA | 2.65 × 106 ± 2.27 × 106 | 1.97 × 108 ± 1.26 × 108 |
| AC160TSA | 4.42 × 107 ± 1.07 × 108 | 5.23 × 109 ± 1.00 × 109 | |
| E r (Pa) | AC240TSA | 4.23 × 108 ± 2.86 × 108 | 3.32 × 108 ± 2.61 × 108 |
| AC160TSA | 8.22 × 109 ± 1.50 × 109 | 3.81 × 109 ± 1.70 × 109 | |
| η (Pa s) | AC240TSA | 533.91 ± 257.52 | 406.57 ± 304.47 |
| AC160TSA | 2.82 × 103 ± 534.20 | 1.61 × 103 ± 636.79 | |
| τ r (s) | AC240TSA | 1.73 × 10−6 ± 0.97 × 10−6 | 1.34 × 10−6 ± 0.18 × 10−6 |
| AC160TSA | 4.48 × 10−5 ± 8.08 × 10−5 | 2.34 × 10−5 ± 4.80 × 10−5 | |
| τ c (s) | AC240TSA | 3.45 × 10−4 ± 5.37 × 10−4 | 2.10 × 10−4 ± 1.85 × 10−4 |
| AC160TSA | 3.44 × 10−7 ± 0.40 × 10−7 | 4.29 × 10−7 ± 0.32 × 10−7 |
2.2 Solving for material constants from bimodal AFM data
Note that, if the sample is a KV material, all material constants (τc, η, Ec) can be calculated for each point in the bimodal AFM map viaeqn (1)–(4). Therefore, the calculations in this section are to determine ensemble average material properties (τc, τr, η, Ec, Er) of MW, SLS, and GMM materials.For materials obeying the GMM, there are too few knowns to calculate all material constants. Since only Ec (viaeqn (12) for SLS or MW materials or viaeqn (17) or (18) for GMM materials), tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 (via bimodal AFM measurements), and
δ1 (via bimodal AFM measurements), and  (via bimodal AFM measurements) are known, it is not possible to calculate the number of arms N in the material, nor all N values of En, ηn, and τn. Therefore, to estimate properties of a sample obeying the GMM, it is necessary to again assume that the subgroup of GMM arms contributing most to the sample's response can be approximated as a single SLS, likely with a large standard deviation in the values of Er and η. Therefore, the following manipulations apply for all but KV materials.
(via bimodal AFM measurements) are known, it is not possible to calculate the number of arms N in the material, nor all N values of En, ηn, and τn. Therefore, to estimate properties of a sample obeying the GMM, it is necessary to again assume that the subgroup of GMM arms contributing most to the sample's response can be approximated as a single SLS, likely with a large standard deviation in the values of Er and η. Therefore, the following manipulations apply for all but KV materials.
As derived in the previous sections, Ec = 0 for MW materials. The slope and y-intercept of the model test line (eqn (12)) can be used to calculate Ec for the SLS and the upper bound of Ec (eqn (17) or (18)) for a GMM. The remaining material constants (Er, η, τr = η/Er, and τc = η/Ec) can be determined from  , tan
, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1, and Ecvia the expressions for E′ and tan
δ1, and Ecvia the expressions for E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of the SLS (eqn (5) and (7), respectively) as follows.
δ of the SLS (eqn (5) and (7), respectively) as follows.
Eqn (7) in terms of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1, ω1, Ec, τr, and Er is as follows.
δ1, ω1, Ec, τr, and Er is as follows.
 | (19) |
 , ω2, Ec, τr, and Er is as follows.
, ω2, Ec, τr, and Er is as follows.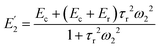 | (20) |
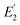 , and ω2) by rearranging eqn (20). Substituting the result (eqn (22)) into eqn (19) eliminates Er and provides an expression for τr (eqn (21)). For ease of writing, E′ of a GMM and SLS (formulas in Table S1, ESI†) is written as E′ = Ec + χ, where χ represents the contribution to E′ from the N GMM arms (or single SLS arm) at a particular ω. The value of χ2 is the difference between
, and ω2) by rearranging eqn (20). Substituting the result (eqn (22)) into eqn (19) eliminates Er and provides an expression for τr (eqn (21)). For ease of writing, E′ of a GMM and SLS (formulas in Table S1, ESI†) is written as E′ = Ec + χ, where χ represents the contribution to E′ from the N GMM arms (or single SLS arm) at a particular ω. The value of χ2 is the difference between  and Ec.
and Ec. | (21) |
 | (22) |
Since eqn (21) is a cubic polynomial, there are three possible values for τr. The root corresponding to the sample's τr can be determined by excluding negative and/or complex roots. If there is more than one real positive root, the root corresponding to the sample's τr can be selected by calculating tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  from the material constants via the relevant equation (formulas in Table S1 (ESI†), use SLS formulas if the material is a GMM or SLS, or MW formulas if the material obeys the MW model) and choosing the value of τr which gives the closest calculated tan
from the material constants via the relevant equation (formulas in Table S1 (ESI†), use SLS formulas if the material is a GMM or SLS, or MW formulas if the material obeys the MW model) and choosing the value of τr which gives the closest calculated tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  to the measured tan
to the measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and 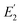 . If there are no real or positive roots, which can occur for numerical solvers if polynomials are flat in the root vicinity, alternate means of calculating sample parameters are described in Section S7 (ESI†).
. If there are no real or positive roots, which can occur for numerical solvers if polynomials are flat in the root vicinity, alternate means of calculating sample parameters are described in Section S7 (ESI†).
2.3 Reconstructing frequency-dependent behavior
Once a sample's material constants are known, it is possible to calculate E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of the material for a dynamic stimulus at any frequency by substituting the material constants into the relevant equation (Table S1, ESI†). Since GMM samples must be approximated as a SLS in order to calculate sample material constants, SLS equations should be used in the reconstruction for both SLS and GMM materials.
δ of the material for a dynamic stimulus at any frequency by substituting the material constants into the relevant equation (Table S1, ESI†). Since GMM samples must be approximated as a SLS in order to calculate sample material constants, SLS equations should be used in the reconstruction for both SLS and GMM materials.
3 Analysis of error caused by performing bimodal AFM without tip radius calibration
For a spherical tip of radius R, is proportional to
is proportional to 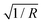 (details in Section S4.1 and eqn (S14), ESI†).18,28 Typically, R is estimated by measuring a calibration sample of known
(details in Section S4.1 and eqn (S14), ESI†).18,28 Typically, R is estimated by measuring a calibration sample of known 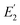 , and manually altering R in the software until the measured
, and manually altering R in the software until the measured  agrees with the known calibration
agrees with the known calibration 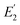 .19 The calibration sample should have similar
.19 The calibration sample should have similar  to the actual sample.19 However, selecting a calibration sample can be difficult for materials made of multiple components.
to the actual sample.19 However, selecting a calibration sample can be difficult for materials made of multiple components.
Without calibration, a less exact R can be obtained from the manufacturer's specifications for the tip, which include the mean tip radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and range of possible radii. By definition of the standard deviation, the full range of R is larger than the standard deviation, SR. However, equating SR with the full range of possible radii provides a worst case estimate of the error caused by lack of R calibration.
and range of possible radii. By definition of the standard deviation, the full range of R is larger than the standard deviation, SR. However, equating SR with the full range of possible radii provides a worst case estimate of the error caused by lack of R calibration.
The additional error in 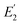 caused by taking R and SR from the manufacturer specifications can be estimated from
caused by taking R and SR from the manufacturer specifications can be estimated from ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) , SR, the mean value of the measured
, SR, the mean value of the measured 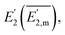 and the standard deviation of the measured
and the standard deviation of the measured 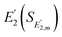 via error propagation. The result is eqn (23), as derived in Section S5 (ESI†).
via error propagation. The result is eqn (23), as derived in Section S5 (ESI†).
 | (23) |
 due to uncertain R, written here as fER, is calculated as follows.
due to uncertain R, written here as fER, is calculated as follows.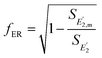 | (24) |
Note that it is possible that R changes during an experiment due to tip blunting.30 However, blunting can be discounted for two reasons. First, significantly blunt tips often prevent a repulsive tip/sample interaction.30 As described in Section S4 (ESI†), calculation of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 (eqn (S13), ESI†) requires a repulsive interaction, and the tan
δ1 (eqn (S13), ESI†) requires a repulsive interaction, and the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 map will be lost if this interaction is not repulsive.26,27,30 Therefore, as long as a repulsive tip/sample interaction is maintained, it can be assumed that blunting is not significant enough to change
δ1 map will be lost if this interaction is not repulsive.26,27,30 Therefore, as long as a repulsive tip/sample interaction is maintained, it can be assumed that blunting is not significant enough to change ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and SR. Additionally, tips can become blunted during a measurement regardless of whether R is calibrated, so neglecting blunting in measurements with uncalibrated R does not introduce any additional error compared to calibrated R.
and SR. Additionally, tips can become blunted during a measurement regardless of whether R is calibrated, so neglecting blunting in measurements with uncalibrated R does not introduce any additional error compared to calibrated R.
4 Validation of the novel analysis procedure
4.1 Materials and methods
A styrene–butadiene rubber (SBR) was used as a test sample for the new bimodal AFM analysis procedure due to the fact that SBRs are widely used, and therefore their properties are well known.31 This particular SBR has already been characterized,14,17 as published in Macromolecules.17 Data from this characterization are reused here with permission from Macromolecules (see data permission at the end of the article for more details) to validate the new analysis procedure. The SBR is a GMM,32 and possesses an adhesive tip/sample contact.14,17 These characteristics are ideal in testing how the new analysis procedure performs, because they are most likely to challenge bimodal AFM measurements. Specifically, the fact that the SBR obeys the GMM32 will test whether a GMM can indeed be approximated as a SLS (as assumed in Section 2.1.1). Additionally, since calculation of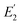 uses the Hertz contact model and thereby assumes a non-adhesive contact,18,28 the fact that the SBR has an adhesive tip/sample contact means that the measured
uses the Hertz contact model and thereby assumes a non-adhesive contact,18,28 the fact that the SBR has an adhesive tip/sample contact means that the measured  is inaccurate.6,17 If the new analysis procedure successfully works for the SBR in spite of these difficulties, the method is robust.
is inaccurate.6,17 If the new analysis procedure successfully works for the SBR in spite of these difficulties, the method is robust.
As detailed in the Macromolecules publication,17 AFM experiments were performed on dry SBR samples with an Oxford Instruments Asylum Research Cypher ES AFM, using Oxford Instruments Asylum Research software version 16.9.220 in Igor Pro software version 6.38B01. AFM experiments were performed using AC240TSA cantilevers (kc,1 ∼ 2.5 N m−1, kc,2 ∼ 50 N m−1, fc,1 ∼ 60 kHz in air, and fc,2 ∼ 390 kHz in air, R ∼ 7 ± 3 nm) and AC160TSA cantilevers (kc,1 ∼ 13 N m−1, kc,2 ∼ 364 N m−1, fc,1 ∼ 290 kHz in air, and fc,2 ∼ 1.5 MHz in air, R ∼ 7 ± 3 nm), driven via photothermal actuation with full excitation laser (Oxford Instruments Asylum Research blueDriveTM, 405 nm wavelength) power, and calibrated via Asylum Research's GetRealTM calibration method30,33,34 in order to avoid blunting the tip.
Amplitude modulation–frequency modulation AFM (AM–FM AFM) was performed on the SBR. AM–FM AFM is a bimodal imaging technique that drives the AFM cantilever at two eigenmodes, measuring sample tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1via the lower frequency eigenmode undergoing amplitude modulation (AM)26,27 and sample
δ1via the lower frequency eigenmode undergoing amplitude modulation (AM)26,27 and sample  via the higher frequency eigenmode undergoing frequency modulation (FM).18,19,25,28 The second mode is also subject to a dissipation feedback loop to prevent the second mode's oscillation from dropping beneath the detection limit.19,25,28 Further details on AM–FM AFM can be found in note S4 (ESI†), and the formulas to calculate tan
via the higher frequency eigenmode undergoing frequency modulation (FM).18,19,25,28 The second mode is also subject to a dissipation feedback loop to prevent the second mode's oscillation from dropping beneath the detection limit.19,25,28 Further details on AM–FM AFM can be found in note S4 (ESI†), and the formulas to calculate tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  in Section S4.1 (ESI†).
in Section S4.1 (ESI†).
Two AM–FM AFM experiments were performed. First, a single spot on the SBR was scanned multiple times with a variety of drive amplitudes and setpoints, to test if AM–FM AFM could provide stable quantification of  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 without calibrating R. Second, multiple spots on the SBR were scanned to quantify the SBR's
δ1 without calibrating R. Second, multiple spots on the SBR were scanned to quantify the SBR's  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. After the final spot on the SBR surface, nanoscale dynamic mechanical analysis (nDMA) was performed at select points in the final AM–FM AFM image. The second AM–FM AFM scan (over different spots on the sample), nDMA, and macroscale DMA (mDMA) of the SBR have already been published,6,14,17 and are used here with permission to serve as controls for the output of the novel analysis procedure. Macroscale DMA details are provided in Section S2 (ESI†). Nanoscale DMA details can be found in Section S3 (ESI†).
δ1. After the final spot on the SBR surface, nanoscale dynamic mechanical analysis (nDMA) was performed at select points in the final AM–FM AFM image. The second AM–FM AFM scan (over different spots on the sample), nDMA, and macroscale DMA (mDMA) of the SBR have already been published,6,14,17 and are used here with permission to serve as controls for the output of the novel analysis procedure. Macroscale DMA details are provided in Section S2 (ESI†). Nanoscale DMA details can be found in Section S3 (ESI†).
For data processing, AM–FM AFM height images of SBR topography were flattened using Asylum Research software version 16.10.208 in Igor Pro software version 6.38B01, in order to remove any variations in sample topography that were not due to SBR features. This flattening was done by hand, in order to avoid introducing flattening artifacts. The processed files were then analyzed by a custom script in MATLAB R2019b 9.7.0.1261785 that calculated tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  of the sample (eqn (S13) and (S14), Section S4.1, ESI†), then applied the new bimodal AFM analysis procedure (Section 2). Results from the analysis procedure developed in this paper were compared to both nDMA and mDMA measurements.14,17 The new bimodal AFM analysis procedure was considered valid if the calculated SBR parameters reproduced values similar to nDMA and mDMA measurements of the SBR.
of the sample (eqn (S13) and (S14), Section S4.1, ESI†), then applied the new bimodal AFM analysis procedure (Section 2). Results from the analysis procedure developed in this paper were compared to both nDMA and mDMA measurements.14,17 The new bimodal AFM analysis procedure was considered valid if the calculated SBR parameters reproduced values similar to nDMA and mDMA measurements of the SBR.
4.2 SBR results
 and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. Such variation likely arose from variation in the features, curvature, or topography, of the sample surface at any given area, since the shallow indentations in AM–FM AFM render AM–FM AFM measurements susceptible to sample topography.19,27 Histograms of all pixel values in a single image of tan
δ1. Such variation likely arose from variation in the features, curvature, or topography, of the sample surface at any given area, since the shallow indentations in AM–FM AFM render AM–FM AFM measurements susceptible to sample topography.19,27 Histograms of all pixel values in a single image of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 or
δ1 or  exhibited unimodal or bimodal distributions. As shown in Fig. 1(A), the presence of bimodal distributions in the data influenced calculation of the mean and standard deviation of AM–FM AFM measurements, and thereby resulted in values that did not accurately represent the data. To overcome this issue, the mean and standard deviation of AM–FM AFM measurements of the SBR were calculated by fitting Gaussians to the data distributions, as described in Section S8 (ESI†), rather than via the standard formulas. Fig. 1(A) shows that calculating the mean from Gaussians results in statistics that represent the most prominent peak of the distribution. Fig. 1(B) shows that this Gaussian fit method of calculating sample statistics matches the values from the standard formulas if the data distribution is unimodal. For individual image statistics, the distribution used for the fit comprised of pixel values from a single AM–FM AFM image. For overall statistics, the distribution comprised of pixel values from all AM–FM AFM images of the SBR. Note that this method of calculating the mean and standard deviation was only necessary for
exhibited unimodal or bimodal distributions. As shown in Fig. 1(A), the presence of bimodal distributions in the data influenced calculation of the mean and standard deviation of AM–FM AFM measurements, and thereby resulted in values that did not accurately represent the data. To overcome this issue, the mean and standard deviation of AM–FM AFM measurements of the SBR were calculated by fitting Gaussians to the data distributions, as described in Section S8 (ESI†), rather than via the standard formulas. Fig. 1(A) shows that calculating the mean from Gaussians results in statistics that represent the most prominent peak of the distribution. Fig. 1(B) shows that this Gaussian fit method of calculating sample statistics matches the values from the standard formulas if the data distribution is unimodal. For individual image statistics, the distribution used for the fit comprised of pixel values from a single AM–FM AFM image. For overall statistics, the distribution comprised of pixel values from all AM–FM AFM images of the SBR. Note that this method of calculating the mean and standard deviation was only necessary for  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1, and was not employed for other SBR parameters.
δ1, and was not employed for other SBR parameters.
 | ||
Fig. 1 Representative distributions of SBR AM–FM AFM measurements. All distributions were obtained from the values of individual pixels from a single AM–FM AFM image of the styrene–butadiene rubber sample (SBR). Two different AM–FM AFM images, collected on different areas of the SBR surface, are shown. Storage modulus,  , and loss tangent, tan , and loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1, distributions from the first image are shown in (A) and (B), respectively, and from the second image are shown in (C) and (D), respectively. A Gaussian fit (see Section S8, ESI†) to the distribution is shown as a magenta line if a two term Gaussian was used or as a dark blue line if a single term Gaussian was used. The mean (points) and standard deviation (error bars) calculated via the standard formulas and via the Gaussian fit constants are shown as an orange × or a purple asterisks, respectively. These measurements were obtained with an AC240TSA cantilever, but are also representative of those obtained with an AC160TSA. δ1, distributions from the first image are shown in (A) and (B), respectively, and from the second image are shown in (C) and (D), respectively. A Gaussian fit (see Section S8, ESI†) to the distribution is shown as a magenta line if a two term Gaussian was used or as a dark blue line if a single term Gaussian was used. The mean (points) and standard deviation (error bars) calculated via the standard formulas and via the Gaussian fit constants are shown as an orange × or a purple asterisks, respectively. These measurements were obtained with an AC240TSA cantilever, but are also representative of those obtained with an AC160TSA. | ||
 and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. To this end, the effect of user controlled parameters during an AM–FM AFM experiment was studied by scanning a single spot on the SBR multiple times, with a variety of drive amplitudes and setpoints, in order to ensure that, regardless of how the user handled the AFM, the measured
δ1. To this end, the effect of user controlled parameters during an AM–FM AFM experiment was studied by scanning a single spot on the SBR multiple times, with a variety of drive amplitudes and setpoints, in order to ensure that, regardless of how the user handled the AFM, the measured  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 were consistent.
δ1 were consistent.
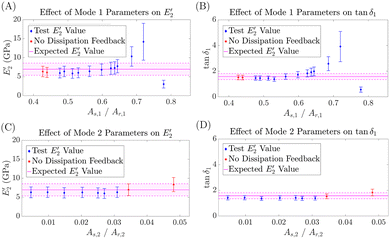
As detailed in Section S4 (ESI†), during an AM–FM AFM experiment, the user controls the amplitude feedback loops for both modes (AM for the first mode, and dissipation feedback for the second mode) by changing the setpoint, As, and drive amplitude of each mode.19,25,30 Note that the user does not directly control FM of the second mode because the cantilever's resonance frequency is what regulates the FM feedback loop.19,25,30 The drive amplitude determines the free amplitude, used as a reference amplitude, Ar, of the cantilever's oscillation.30 Combinations of user-controlled parameters (As and Ar) can be summarized by a single metric for each eigenmode, the ratio of As,1/Ar,1 and As,2/Ar,2. The lower the ratio, the harder the user is tapping on the sample.30
To examine the feasibility of performing bimodal AFM without first calibrating R, AM–FM AFM was performed on the SBR with a variety of As/Ar combinations for each mode. This test was performed to ensure that: (i) AM–FM AFM could still correctly quantify a sample's  even without first calibrating R, (ii) that uncertain R did not result in too large an error in
even without first calibrating R, (ii) that uncertain R did not result in too large an error in  (see Section 3), and (iii) test how tan
(see Section 3), and (iii) test how tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  depended on user-determined parameters. The test in (iii) is necessary to ensure that the values of tan
depended on user-determined parameters. The test in (iii) is necessary to ensure that the values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  are stable regardless of how the user handles the AFM during an experiment. If tan
are stable regardless of how the user handles the AFM during an experiment. If tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  vary with As/Ar, it would be difficult to determine the actual value of the sample without calibrating R.
vary with As/Ar, it would be difficult to determine the actual value of the sample without calibrating R.
Fig. 2 shows the effect of As/Ar on the mean  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. Results were similar for both cantilevers. The dissipation feedback parameters (As,2/Ar,2) did not affect tan
δ1. Results were similar for both cantilevers. The dissipation feedback parameters (As,2/Ar,2) did not affect tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  . This result is expected, because the dissipation feedback of mode 2 prevents the mode's amplitude from falling below the detection floor, and is not used in AM–FM AFM calculations (Section S4).19,25,28
. This result is expected, because the dissipation feedback of mode 2 prevents the mode's amplitude from falling below the detection floor, and is not used in AM–FM AFM calculations (Section S4).19,25,28
AM feedback parameters affected  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. In general, if As,1/Ar,1 was too high, the value of tan
δ1. In general, if As,1/Ar,1 was too high, the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  varied more in response to changes in As,1/Ar,1. If As,1/Ar,1 was too low, the topography image became distorted or the dissipation feedback could no longer operate. In the later case, the dissipation feedback was likely lost because the tip was tapping the sample too hard, interfering with the AFM's ability to drive the second mode. Regardless, loss of the dissipation image or distortion in the sample's features during the scan are signs that the user's As,1/Ar,1 is too high or too low to accurately quantify the sample. Still, AM–FM AFM quantification of tan
varied more in response to changes in As,1/Ar,1. If As,1/Ar,1 was too low, the topography image became distorted or the dissipation feedback could no longer operate. In the later case, the dissipation feedback was likely lost because the tip was tapping the sample too hard, interfering with the AFM's ability to drive the second mode. Regardless, loss of the dissipation image or distortion in the sample's features during the scan are signs that the user's As,1/Ar,1 is too high or too low to accurately quantify the sample. Still, AM–FM AFM quantification of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  was stable for several values of As,1/Ar,1. These results suggest that reliable and consistent quantification of tan
was stable for several values of As,1/Ar,1. These results suggest that reliable and consistent quantification of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  can be obtained as long as the user decreases As,1/Ar,1 just enough to ensure a repulsive tip/sample interaction (where phase one obeys ϕ1 < 90°, to employ eqn (S13), ESI†) and a stable value of
can be obtained as long as the user decreases As,1/Ar,1 just enough to ensure a repulsive tip/sample interaction (where phase one obeys ϕ1 < 90°, to employ eqn (S13), ESI†) and a stable value of  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. Representative AM–FM AFM images of the SBR obtained using this procedure are shown in Fig. 3.
δ1. Representative AM–FM AFM images of the SBR obtained using this procedure are shown in Fig. 3.
After performing AM–FM AFM at multiple spots on the SBR surface, resulting in 25 AM–FM AFM images from AC240TSA scans and 13 images from AC160TSA scans, the mean  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 were calculated by fitting a Gaussian to the resulting distributions for each quantity as described in Section 4.2.1. The mean ± standard deviation of the SBR's tan
δ1 were calculated by fitting a Gaussian to the resulting distributions for each quantity as described in Section 4.2.1. The mean ± standard deviation of the SBR's tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 was 1.9 ± 0.5 for the AC240TSA and 1.6 ± 0.4 for the AC160TSA. The mean ± standard deviation of the SBR's
δ1 was 1.9 ± 0.5 for the AC240TSA and 1.6 ± 0.4 for the AC160TSA. The mean ± standard deviation of the SBR's  was 570 MPa ± 89 MPa for the AC240TSA and 7.0 GPa ± 0.6 GPa for the AC160TSA. Applying eqn (24), the uncertainty in R contributed to 79% of
was 570 MPa ± 89 MPa for the AC240TSA and 7.0 GPa ± 0.6 GPa for the AC160TSA. Applying eqn (24), the uncertainty in R contributed to 79% of  from AC240TSA measurements and 65% of
from AC240TSA measurements and 65% of  from AC160TSA measurements. These results suggest that, if R is not calibrated, the uncertainty in R is not negligible, and should be propagated through the measured
from AC160TSA measurements. These results suggest that, if R is not calibrated, the uncertainty in R is not negligible, and should be propagated through the measured  . However,
. However,  can still be reliably measured, even without calibrating R. Note that one downside to lack of R calibration is that there is no longer an indication of tip/sample pairings where the Hertz contact model does not apply (e.g. adhesive contacts)19 without the use of additional experiments like indentations, nDMA, or mDMA.
can still be reliably measured, even without calibrating R. Note that one downside to lack of R calibration is that there is no longer an indication of tip/sample pairings where the Hertz contact model does not apply (e.g. adhesive contacts)19 without the use of additional experiments like indentations, nDMA, or mDMA.
In order to ensure that AM–FM AFM measurements correctly quantified  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1, both quantities were compared with the nDMA and mDMA controls, and these results have already been published.6,14,17 In summary, the measured tan
δ1, both quantities were compared with the nDMA and mDMA controls, and these results have already been published.6,14,17 In summary, the measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 agreed well with the mDMA control.6,14,17 However, AM–FM AFM's
δ1 agreed well with the mDMA control.6,14,17 However, AM–FM AFM's  was 10–100× larger than E′ measured by mDMA.6,14,17
was 10–100× larger than E′ measured by mDMA.6,14,17
Comparison of mDMA and AM–FM AFM data with nDMA measurements shows that the discrepancy between  and the mDMA control is not due to uncertain R or the use of an incorrect As,1/Ar,1.6,14,17 Instead, the observed overestimation of
and the mDMA control is not due to uncertain R or the use of an incorrect As,1/Ar,1.6,14,17 Instead, the observed overestimation of  by AM–FM AFM is due to the fact that AM–FM AFM employs the Hertz contact model to calculate
by AM–FM AFM is due to the fact that AM–FM AFM employs the Hertz contact model to calculate  ,18,28 since E′ of nDMA calculated with the Hertz contact model shows similar disagreement with mDMA.6,14,17E′ of nDMA calculated by modeling the contact geometry as a hyperboloid indenter with adhesion14,17 agrees well with mDMA, suggesting that this model is the best contact model for the tip/SBR interaction.6,14,17 In other words, adhesion is present between the tip and SBR. The Hertz contact model upon which AM–FM AFM relies assumes that no adhesion is present between the tip and sample,5 and therefore inadequately describes the tip/SBR interaction.6,14,17 While reliance on the Hertz model results in an incorrect estimation of
,18,28 since E′ of nDMA calculated with the Hertz contact model shows similar disagreement with mDMA.6,14,17E′ of nDMA calculated by modeling the contact geometry as a hyperboloid indenter with adhesion14,17 agrees well with mDMA, suggesting that this model is the best contact model for the tip/SBR interaction.6,14,17 In other words, adhesion is present between the tip and SBR. The Hertz contact model upon which AM–FM AFM relies assumes that no adhesion is present between the tip and sample,5 and therefore inadequately describes the tip/SBR interaction.6,14,17 While reliance on the Hertz model results in an incorrect estimation of  for AM–FM AFM, the value of tan
for AM–FM AFM, the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 is correct because tan
δ1 is correct because tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is independent of contact geometry.6,14,17,35
δ is independent of contact geometry.6,14,17,35
In summary, quantification of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  in AM–FM AFM is still possible, even without using a sample of known modulus to calibrate R. Regardless of R calibration, incorrect quantification of
in AM–FM AFM is still possible, even without using a sample of known modulus to calibrate R. Regardless of R calibration, incorrect quantification of  will occur if the Hertz contact model is not suitable to describe the tip/sample interaction.
will occur if the Hertz contact model is not suitable to describe the tip/sample interaction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1−1vs.
δ1−1vs. (Section 2.1, eqn (12)) for AM–FM AFM data at a single spot on the SBR, that is, for a single AM–FM AFM image. Each image was fit with the model test line (eqn (12)). Fit metrics for each image can be found in Table S2 (ESI†). The mean ± standard deviation R2 value of the fits was 0.99 ± 0.02 for data measured with an AC240TSA, and 0.95 ± 0.04 for data measured with an AC160TSA. For both cantilevers, the slope and y-intercept of the fit were greater than zero (see Table S2, ESI†).
(Section 2.1, eqn (12)) for AM–FM AFM data at a single spot on the SBR, that is, for a single AM–FM AFM image. Each image was fit with the model test line (eqn (12)). Fit metrics for each image can be found in Table S2 (ESI†). The mean ± standard deviation R2 value of the fits was 0.99 ± 0.02 for data measured with an AC240TSA, and 0.95 ± 0.04 for data measured with an AC160TSA. For both cantilevers, the slope and y-intercept of the fit were greater than zero (see Table S2, ESI†).
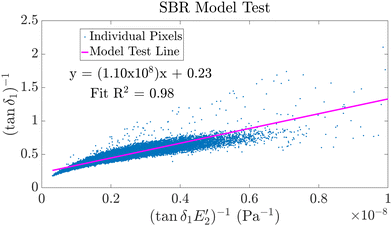 | ||
| Fig. 4 Representative model test for a single AM–FM AFM image of the SBR. All pixels from a single AM–FM AFM image of the SBR are shown (points) along with the linear fit to the data (magenta line, eqn (12)), used to determine the best description of the SBR's viscoelastic response. The fit equation and R2 value are also shown. The data in this figure are taken from a single AM–FM AFM image, but are representative of the fits to other images (fit details in Table S2, ESI†). | ||
It is already known that the SBR is a GMM.32 The good linear fit of the model test (eqn (12)) derived from SLS equations (Section 2.1) to SBR AM–FM AFM data suggests that a subgroup of GMM arms within the SBR, all with similar τn, contributed most to  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1. Specifically, the AM–FM AFM excitation frequencies in these experiments are more likely to excite GMM arms with τn on the order of 0.1–10 μs. The good fit of the SBR data to the model test line supports the notion that this subgroup of arms can be approximated as a single SLS, likely with a large standard deviation in its parameter values (Ec, Er, and η), as discussed in Section 2.1.1.
δ1. Specifically, the AM–FM AFM excitation frequencies in these experiments are more likely to excite GMM arms with τn on the order of 0.1–10 μs. The good fit of the SBR data to the model test line supports the notion that this subgroup of arms can be approximated as a single SLS, likely with a large standard deviation in its parameter values (Ec, Er, and η), as discussed in Section 2.1.1.
While the model test plot in Fig. 4 can be fit with a line, the points seem to have a hyperbolic or logarithmic shape, rather than a linear shape. This observation suggests that the model test has a curve if the sample obeys the GMM, and a line if the sample obeys the SLS. It is reasonable to hypothesize that the curve in the model test line for a GMM may be due to superposition of all SLSs in the material that responded to the stimulus. Future investigation of this observation may improve the calculation of GMM material constants from AM–FM AFM data. Regardless, the large R2 values of the linear fits suggest that, even though the model test appears to have a hyperbolic shape, a line still approximates the trend in the data well. Again, this observation supports the notion that bimodal AFM excites a subset of GMM arms, all with similar τn, and that can be approximated as a single SLS.
 | ||
Fig. 5 Frequency dependent behavior of the SBR (AC240TSA). Storage moduli (E′), loss moduli (E′′), and loss tangents (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) over a range of frequencies are shown in (A)–(C), respectively. Mean AM–FM AFM reconstructions are compared to control macroscale dynamic mechanical analysis (mDMA, squares) and nanoscale DMA (nDMA, lines) measurements. All data besides the reconstructions have been published previously,17 and are used here with permission. AM–FM AFM reconstructions from each of the 25 individual AM–FM AFM images are also shown in gray. Red arrows indicate regions where the reconstruction deviates from the controls by failing to account for all arms in the GMM. E′ and E′′ of nDMA measurements were calculated using the Hertz contact model. AM–FM AFM and nDMA were performed using an AC240TSA cantilever. Error bars and shading represent the standard deviation. δ) over a range of frequencies are shown in (A)–(C), respectively. Mean AM–FM AFM reconstructions are compared to control macroscale dynamic mechanical analysis (mDMA, squares) and nanoscale DMA (nDMA, lines) measurements. All data besides the reconstructions have been published previously,17 and are used here with permission. AM–FM AFM reconstructions from each of the 25 individual AM–FM AFM images are also shown in gray. Red arrows indicate regions where the reconstruction deviates from the controls by failing to account for all arms in the GMM. E′ and E′′ of nDMA measurements were calculated using the Hertz contact model. AM–FM AFM and nDMA were performed using an AC240TSA cantilever. Error bars and shading represent the standard deviation. | ||
The values of SBR E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ over a range of frequencies (E′(f), E′′(f), and tan
δ over a range of frequencies (E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f)) were calculated by substituting the GMM material constants in Table 1, into eqn (5)–(7), respectively. This reconstruction of the SBR's frequency-dependent behavior is shown in Fig. 5 for AC240TSA cantilevers, and Fig. S2 (ESI†) for AC160TSA cantilevers. Reconstructions using SLS material constants are not shown, since GMM parameters (Table 1 and Section 2.1.1) are more accurate.
δ(f)) were calculated by substituting the GMM material constants in Table 1, into eqn (5)–(7), respectively. This reconstruction of the SBR's frequency-dependent behavior is shown in Fig. 5 for AC240TSA cantilevers, and Fig. S2 (ESI†) for AC160TSA cantilevers. Reconstructions using SLS material constants are not shown, since GMM parameters (Table 1 and Section 2.1.1) are more accurate.
The accuracy of reconstructed E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) can be assessed via comparison to nDMA and mDMA control data (the control data has been previously published,17 and is reused here with permission). Even though a hyperboloid indenter with adhesion is a better model of the tip/SBR interaction,14,17 AM–FM AFM only uses the Hertz contact model to calculate
δ(f) can be assessed via comparison to nDMA and mDMA control data (the control data has been previously published,17 and is reused here with permission). Even though a hyperboloid indenter with adhesion is a better model of the tip/SBR interaction,14,17 AM–FM AFM only uses the Hertz contact model to calculate  .18,28 Therefore, AM–FM AFM reconstructions should be compared to nDMA data calculated with the Hertz contact model, not the adhesive hyperboloid model. In other words, AM–FM AFM reconstructions of E′(f) and E′′(f) should match nDMA curves (Hertz model) at low frequencies, but should be 10–100× larger (Section 4.2.2) than mDMA values. The reconstructed tan
.18,28 Therefore, AM–FM AFM reconstructions should be compared to nDMA data calculated with the Hertz contact model, not the adhesive hyperboloid model. In other words, AM–FM AFM reconstructions of E′(f) and E′′(f) should match nDMA curves (Hertz model) at low frequencies, but should be 10–100× larger (Section 4.2.2) than mDMA values. The reconstructed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) should match both nDMA and mDMA data because tan
δ(f) should match both nDMA and mDMA data because tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is independent of contact geometry.14,17,35 At low frequencies, where E′ ∼ Ec (see Section S1, Table S1, ESI†), the reconstruction aligns with the nDMA, suggesting that assuming Ec is close to the upper bound of Ec was correct for this sample. However, as previously described (Section 4.2.2), the estimated Ec, reconstruction E′, and nDMA results are higher than mDMA values because the nanoscale measurements employ the Hertz contact model.
δ is independent of contact geometry.14,17,35 At low frequencies, where E′ ∼ Ec (see Section S1, Table S1, ESI†), the reconstruction aligns with the nDMA, suggesting that assuming Ec is close to the upper bound of Ec was correct for this sample. However, as previously described (Section 4.2.2), the estimated Ec, reconstruction E′, and nDMA results are higher than mDMA values because the nanoscale measurements employ the Hertz contact model.
Red arrows in Fig. 5(A) indicate frequencies where the reconstruction of E′(f) deviates from the controls. There are two main regions where the reconstruction does not accurately predict E′. First (i) is the transition between the low frequency and high frequency plateaus of E′ (the glass transition of the SBR36), which occurs between 102–108 Hz in the mDMA. Second (ii) is the glassy plateau8,36 of E′ (at f > 109 Hz in the mDMA).
(i) For the glass transition,8,36 mDMA shows that SBR E′ transitions gradually (between 102–108 Hz) from the low frequency to the high frequency plateau. The transition in the reconstruction is sharper (ranges only between 104–106 Hz) and underestimates E′ between 102–104 Hz. These observations suggest that the glass transition of the SBR results from a sum of the various contributions of multiple different τn of different orders of magnitude (i.e. ns, μs, ms, etc…). This sum results in a broad glass transition, as expected for a GMM.8 Since the AM–FM AFM reconstruction only uses a single τn, the transition is much sharper than the reality. Therefore, these results suggest that GMM arms in the subgroup that contribute to the SBR's response to AM–FM AFM stimulus are only part of the subgroup of arms that contributes to the SBR's glass transition.
(ii) For the glassy plateau8,36 of the SBR (at f > 109 Hz), the reconstruction underestimates E′(f). Again, this observation suggests that GMM arms that contribute most to this plateau are not part of the subgroup that dictates the SBR's response to AM–FM AFM stimulus. This observation is not surprising, since the microsecond τn that dictate the SBR's response to AM–FM AFM stimulus would respond too slowly to affect the SBR's response to higher frequency stimuli (f > 107 Hz).
As shown in Fig. 5(B), the reconstructed E′′(f) aligns well with nDMA results between 103–106 Hz. As expected, the value of E′′ calculated by nDMA and the reconstruction is higher than that of mDMA due to the use of the Hertz contact model (as already discussed Section 4.2.2). For frequencies outside of this 103–106 Hz range, E′′ is underestimated by the reconstruction (indicated by red arrows in Fig. 5(B)). This observation is a byproduct of using the SLS to approximate the GMM for the reconstruction. For the SLS, N = 1, and E′′ increases to a peak at frequencies near the glass transition of the sample, then decreases again (eqn (6)). For a GMM, E′′ can have a broader peak due to contributions from the additional τn.8 Therefore, it is not surprising that E′′(f) is not adequately reconstructed for frequencies too slow or too fast for the subgroup of GMM arms that respond to AM–FM AFM stimulus.
In general, the reconstructed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) agrees with the nDMA and mDMA controls where E′(f) and E′′(f) also agree with the controls, and deviates from nDMA and mDMA results when the reconstructed E′ and E′′ do so as well (Fig. 5(C)). Specifically, reconstructed tan
δ(f) agrees with the nDMA and mDMA controls where E′(f) and E′′(f) also agree with the controls, and deviates from nDMA and mDMA results when the reconstructed E′ and E′′ do so as well (Fig. 5(C)). Specifically, reconstructed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ matches the controls well between 102–103 Hz, and again between 104–106 Hz. The lack of agreement between the reconstructed tan
δ matches the controls well between 102–103 Hz, and again between 104–106 Hz. The lack of agreement between the reconstructed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and controls at 103–104 Hz is due to the reconstruction's inability to capture the glass transition between the low and high frequency plateaus in E′. The discrepancies between reconstruction tan
δ and controls at 103–104 Hz is due to the reconstruction's inability to capture the glass transition between the low and high frequency plateaus in E′. The discrepancies between reconstruction tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) and the controls at frequencies larger than 106 Hz, or smaller than 102 Hz are due to the reconstruction's inability to accurately model E′′(f).
δ(f) and the controls at frequencies larger than 106 Hz, or smaller than 102 Hz are due to the reconstruction's inability to accurately model E′′(f).
Reconstructions performed with an AC160TSA (Fig. S2, ESI†) showed similar results. However, estimation of the transition in E′ was more accurate, and therefore the reconstructed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was more accurate (although not an exact match to the controls) between 105 and 106 Hz. Additionally, reconstructed Ec was higher than that of the AC240TSA. This observation suggests that the accuracy of the reconstruction may vary, depending on where f1 and f2 occur relative to the glass transition of a sample. Based on mDMA, the SBR's glass transition was between 104 and 106 Hz. For the AC240TSA, f1 and f2 were roughly in the middle of this transition. For the AC160TSA, f1 and f2 occurred toward the higher frequency end of the transition. These results suggest that the reconstruction may be better at predicting lower frequency behaviors of a sample when f1 and f2 are lower than or inside the glass transition. If f1 and f2 are higher than the glass transition, the reconstruction may be better at predicting glass transition and high frequency behavior. These differences likely stem from assuming that Ec is approximately its upper bound (eqn (17) or (18)). Since f1 and f2 are higher for the AC160TSA, and measure values closer to the SBR's glassy plateau, the upper bound of Ec is calculated to be higher. In the future, it would be interesting to further test this hypothesis with additional cantilevers that have f1 and f2 at different frequencies relative to the glass transition of the sample.
δ was more accurate (although not an exact match to the controls) between 105 and 106 Hz. Additionally, reconstructed Ec was higher than that of the AC240TSA. This observation suggests that the accuracy of the reconstruction may vary, depending on where f1 and f2 occur relative to the glass transition of a sample. Based on mDMA, the SBR's glass transition was between 104 and 106 Hz. For the AC240TSA, f1 and f2 were roughly in the middle of this transition. For the AC160TSA, f1 and f2 occurred toward the higher frequency end of the transition. These results suggest that the reconstruction may be better at predicting lower frequency behaviors of a sample when f1 and f2 are lower than or inside the glass transition. If f1 and f2 are higher than the glass transition, the reconstruction may be better at predicting glass transition and high frequency behavior. These differences likely stem from assuming that Ec is approximately its upper bound (eqn (17) or (18)). Since f1 and f2 are higher for the AC160TSA, and measure values closer to the SBR's glassy plateau, the upper bound of Ec is calculated to be higher. In the future, it would be interesting to further test this hypothesis with additional cantilevers that have f1 and f2 at different frequencies relative to the glass transition of the sample.
Together, these results suggest that bimodal AFM data can be used to perform limited reconstructions of a GMM sample's frequency dependent E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f). For the most-accurate measurement of a sample's frequency dependent behavior, it is best to combine bimodal AFM data with other techniques like nDMA, rather than rely only on the reconstruction of E′(f) and E′′(f) from bimodal AFM data. However, bimodal AFM reconstructions can capture important quantities of a sample's frequency dependent behavior, especially for frequencies near f1 and f2. At the bare minimum, the reconstruction allows for fairly-accurate estimation of E′ at f1, E′′ of at least one of the two measurement frequencies, and can be used to predict Ec of a sample. The method described here can still be used to approximate Ec of a GMM, as long as it is acknowledged that the value of Ec of a GMM is the upper bound, and not necessarily the exact value of Ec. To improve reconstruction accuracy, bimodal AFM measurements of the same sample with different cantilevers could be combined, for example by comparing
δ(f). For the most-accurate measurement of a sample's frequency dependent behavior, it is best to combine bimodal AFM data with other techniques like nDMA, rather than rely only on the reconstruction of E′(f) and E′′(f) from bimodal AFM data. However, bimodal AFM reconstructions can capture important quantities of a sample's frequency dependent behavior, especially for frequencies near f1 and f2. At the bare minimum, the reconstruction allows for fairly-accurate estimation of E′ at f1, E′′ of at least one of the two measurement frequencies, and can be used to predict Ec of a sample. The method described here can still be used to approximate Ec of a GMM, as long as it is acknowledged that the value of Ec of a GMM is the upper bound, and not necessarily the exact value of Ec. To improve reconstruction accuracy, bimodal AFM measurements of the same sample with different cantilevers could be combined, for example by comparing  and tan
and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 between cantilevers. However, such reconstruction is beyond the scope of this work. The analysis procedure presented here can be employed even if only one cantilever is used to measure the sample. Additionally, for bimodal AFM measurements of samples that obey the GMM, it would be interesting to derive a method of estimating N from bimodal AFM data, possibly by comparing observations made with several cantilevers with different f1 and f2.
δ1 between cantilevers. However, such reconstruction is beyond the scope of this work. The analysis procedure presented here can be employed even if only one cantilever is used to measure the sample. Additionally, for bimodal AFM measurements of samples that obey the GMM, it would be interesting to derive a method of estimating N from bimodal AFM data, possibly by comparing observations made with several cantilevers with different f1 and f2.
5 Discussion
The SBR selected to validate procedure outputs was well characterized,17 but also likely to confound bimodal AFM measurements via the non-Hertzian tip/sample contact,17 and test the limits of the analysis procedure by adhering to the GMM32 (Section 4.1). In spite of these complications, the procedure still yielded useful information about the sample's viscoelastic behavior. Additionally, the steps used in this article to assess procedure outputs are among several that can be employed to cross-validate procedure outputs for any sample. The following discussion describes potential means of improving bimodal measurements of samples like the SBR and how to cross-validate analysis procedure outputs for any sample measured by bimodal AFM.The main confounding property of the SBR sample in this article was the adhesive, non-Hertzian tip/sample contact, meaning that bimodal AFM's use of the Hertz contact model to calculate  ,14,17 and therefore analysis procedure calculations of sample elastic constants and E′′, yielded artificially high values compared to the mDMA control. To improve measurement accuracy, it is either necessary to apply additional contact models to bimodal AFM or place the sample in conditions that render the tip/sample contact Hertzian. The first, and most versatile, means of addressing the tip/sample contact would be to derive expressions to calculate
,14,17 and therefore analysis procedure calculations of sample elastic constants and E′′, yielded artificially high values compared to the mDMA control. To improve measurement accuracy, it is either necessary to apply additional contact models to bimodal AFM or place the sample in conditions that render the tip/sample contact Hertzian. The first, and most versatile, means of addressing the tip/sample contact would be to derive expressions to calculate  in bimodal AFM measurements using other contact models besides the Hertz model. Currently,
in bimodal AFM measurements using other contact models besides the Hertz model. Currently,  can also be calculated using the Lennard-Jones force (LJF) and Derjaguin–Muller–Toporov (DMT) contact models.28 However, bimodal AFM theory could be expanded to include other contact models like the Johnson–Kendall–Roberts (JKR) model or the adhesive hyperboloid.
can also be calculated using the Lennard-Jones force (LJF) and Derjaguin–Muller–Toporov (DMT) contact models.28 However, bimodal AFM theory could be expanded to include other contact models like the Johnson–Kendall–Roberts (JKR) model or the adhesive hyperboloid.
A second means to potentially eliminate non-Hertzian contacts on samples in air is to perform measurements in liquid instead. Liquid environments can reduce adhesive forces37,38 and therefore increase the likelihood that the Hertz model applies. While liquid environments can reduce adhesive forces,37,38 the mechanical properties of a sample often differ between air and liquid environments.1 Therefore, control measurements such as mDMA or nDMA should be performed in similar conditions to bimodal measurements. It is also important to note that measuring a sample in liquid does not guarantee a Hertzian, or even a nonadhesive contact. For example, many biological samples still exhibit adhesion, even in liquid environments.16
Regardless of whether a non-Hertzian tip/sample contact can be addressed, the measurements in this paper demonstrate that the new analysis procedure can still be applied even if the Hertz model does not accurately describe the tip/sample interaction. At minimum, the procedure can help the user determine how best to model the sample's viscoelastic behavior. To assess the reliability of procedure outputs for a given sample, procedure outputs should be compared against other measurements, as in this article. Such cross-validation can be accomplished in several ways, depending on the control data available for comparison. Measurements that can be used to cross-validate analysis procedure outputs include: mDMA, nDMA, nanoindentation, relaxation experiments, creep experiments, and literature measurements of similar samples. The pros and cons of each cross-validation measurement, and how cross-validation can be performed with each measurement, are elaborated in Section S9 (ESI†).
At minimum, it is important to cross-validate Ec of a GMM material. As described in Section 2.2, Ec is calculated first, then used to solve for the remaining material constants (eqn (21) and (22), Section 2.2). Additionally, if the sample is a GMM, it is necessary to assume that Ec is close to the bound on Ec (Section 2.1.1 and Section S6, ESI†). If this assumption does not apply, the estimation of Ec, and therefore all other parameters, will not be accurate. Therefore, it is essential to cross-validate Ec (see Section S9, ESI†) for any GMM sample. If procedure Ec does not match that of the cross-validation experiment, GMM parameter estimation should not be employed because the assumption necessary for the procedure to estimate Ec does not hold.
5.1 Likelihood of encountering a special case of the GMM
Note that it is difficult to find samples guaranteed to behave as one of the GMM's special cases, since the behavior of a sample is affected by experimental conditions. For example, collagen has been modeled with either the GMM or SLS, depending on experimental conditions.9,39–44 While there is no guarantee that a sample will behave as a MW, KV, or SLS material, knowledge of each model's characteristics can help identify candidate samples more likely to obey the GMM's special cases.In general, MW materials tend to be more fluid.36 Therefore, samples with little crosslinking, weak iterations between constituent polymers, or made of mobile constituents would be more likely to obey the MW model. KV materials are more difficult to identify than MW materials. However, since τr = 0 for a KV material, samples that do not exhibit relaxation are more likely to behave as a KV material. Relaxation experiments16 could help identify candidate samples that do not relax. Finally, the SLS will apply in conditions that restrict the number of arms in a GMM that respond to bimodal stimulus. Such conditions might include thin and uniform samples, since there are fewer unique constituents in uniform samples, and fewer dimensions for polymers in the material to interact in thin samples, thereby reducing the number of arms in the GMM.
6 Conclusions
In summary, bimodal AFM techniques such as AM–FM AFM can be performed on samples to quantify tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  of the sample, even without first calibrating the AFM tip radius on a sample of known modulus. If tip radius is not calibrated, the additional uncertainty in
of the sample, even without first calibrating the AFM tip radius on a sample of known modulus. If tip radius is not calibrated, the additional uncertainty in  should be taken into account by propagating the uncertainty in R through measurements of
should be taken into account by propagating the uncertainty in R through measurements of 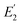 (eqn (23)). Additionally, without tip radius calibration, there may be no indicator if the Hertz contact model does not apply unless bimodal AFM is performed together with other types of experiments such as nDMA, nanoscale indentations, or mDMA. Regardless of tip calibration or lack thereof, the measured
(eqn (23)). Additionally, without tip radius calibration, there may be no indicator if the Hertz contact model does not apply unless bimodal AFM is performed together with other types of experiments such as nDMA, nanoscale indentations, or mDMA. Regardless of tip calibration or lack thereof, the measured  can be incorrect if the Hertz contact model, on which bimodal AFM calculation of
can be incorrect if the Hertz contact model, on which bimodal AFM calculation of  relies,18,28 is not a good model for the tip/sample interaction. In the future, it would be prudent to expand (as already done for the DMT model and the Lennard-Jones potential via fractional calculus28) the calculation of
relies,18,28 is not a good model for the tip/sample interaction. In the future, it would be prudent to expand (as already done for the DMT model and the Lennard-Jones potential via fractional calculus28) the calculation of  in bimodal AFM to include other contact models like the Johnson–Kendall–Roberts model5 and the adhesive hyperboloid.14,17,45
in bimodal AFM to include other contact models like the Johnson–Kendall–Roberts model5 and the adhesive hyperboloid.14,17,45
The new analysis procedure developed in this article (Section 2) can be used on bimodal AFM data to extract additional information about a sample's viscoelastic response. A flow chart of the procedure is shown in Fig. 6. First, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ1 and
δ1 and  can be used to test whether the sample obeys any of the standard models of linear viscoelasticity (MW, KV, SLS, and GMM), and distinguish between each model (Section 2.1, eqn (12)). Ability of the model test to distinguish different sample components that potentially obey different models of viscoelasticity was not assessed in this article. However, if material components do not all fall in the same group of points for the model test, it may be possible to use the model test to identify viscoelasticity of multiple components within a sample.
can be used to test whether the sample obeys any of the standard models of linear viscoelasticity (MW, KV, SLS, and GMM), and distinguish between each model (Section 2.1, eqn (12)). Ability of the model test to distinguish different sample components that potentially obey different models of viscoelasticity was not assessed in this article. However, if material components do not all fall in the same group of points for the model test, it may be possible to use the model test to identify viscoelasticity of multiple components within a sample.
Once the best model for a sample's viscoelastic response is known, model parameters can then be calculated (Section 2.2), and the frequency dependent behavior of a sample's E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f) can be reconstructed (Section 2.3). Accuracy of the reconstruction is limited if the sample is a GMM, and depends on where the measurement frequencies fall in the sample's rheological behavior (for example, relative to the glass transition), but can at minimum, provide the value of
δ(f) can be reconstructed (Section 2.3). Accuracy of the reconstruction is limited if the sample is a GMM, and depends on where the measurement frequencies fall in the sample's rheological behavior (for example, relative to the glass transition), but can at minimum, provide the value of  , a bound for Ec, and E′′ of at least one of the two measurement frequencies. For the most accurate measurement of E′(f), E′′(f), and tan
, a bound for Ec, and E′′ of at least one of the two measurement frequencies. For the most accurate measurement of E′(f), E′′(f), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(f), it is best to combine bimodal AFM with other techniques like nDMA, rather than rely solely on the reconstruction. Regardless, future bimodal AFM experiments can use the analysis procedure developed in this article to gain additional insight into a sample's viscoelastic behavior, especially which model of linear viscoelasticity best applies to the sample, and thereby gain additional insight into a sample's function or application.
δ(f), it is best to combine bimodal AFM with other techniques like nDMA, rather than rely solely on the reconstruction. Regardless, future bimodal AFM experiments can use the analysis procedure developed in this article to gain additional insight into a sample's viscoelastic behavior, especially which model of linear viscoelasticity best applies to the sample, and thereby gain additional insight into a sample's function or application.
Author contributions
C. E. A. conceptualized and designed the new bimodal AFM analysis procedure. C. E. A. performed AM–FM AFM measurements and reconstructions of the SBR, and carried out data visualization. C. E. A. and A. R. P. discussed validation of the new analysis procedure and SBR data interpretation. A. R. P., C. E. A., and S. C. are authors on the previously-published SBR data. C. E. A and S. C. wrote the article with feedback from all other authors. S. W. and S. C. supervised the work.Data availability
Several of the SBR measurements, specifically the mean and standard deviation of SBR AM–FM AFM measurements (displayed as lines in Fig. 2 and filled points in Fig. 5 and Fig. S2, ESI†), nDMA measurements (displayed in Fig. 5 and Fig. S2, ESI†), and mDMA measurements (displayed in Fig. 5 and Fig. S2, ESI†) in this paper have previously been published in Macromolecules,17 and are used here with permission. The Macromolecules publication can be found at https://pubs.acs.org/doi/10.1021/acs.macromol.3c02052 or https://doi.org/10.1021/acs.macromol.3c02052.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge Dr. Jacob Seifert Kineast and Dr Joe A. Adam for the helpful discussions, Dr. Steven Tucker for his feedback, and Dr. Núria Gavara for her feedback and insights into the new analysis procedure. Additionally, Alba R. Piacenti (second author of this article) was funded by a UK Engineering and Physical Sciences Research Council (EPSRC) graduate scholarship, the Sidney Perry Foundation, the Blanceflor Boncompagni Ludovisi née Built Foundation, the Sapienza University of Rome's Borsa di Perfezionamento all’Estero, and the Angelo Della Riccia Foundation.Notes and references
- M. Doi, Soft matter physics, Oxford University Press, 1st edn, 2013 Search PubMed.
- R. S. Lakes, Rev. Sci. Instrum., 2004, 75, 797–810 CrossRef CAS.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- J. Seifert, In vivo dynamic AFM mapping of viscoelastic properties of the primary plant cell wall, 2018 Search PubMed.
- V. L. Popov, M. Heß and E. Willert, Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems, Springer Berlin Heidelberg, 2019 Search PubMed.
- C. Adam, Physical Regulation of Cell Behaviors: Multifrequency AFM Measurement of Mechanoelectric, Mechanochemical, and Hydration Shell Effects on ECM and Cell Substrate Viscoelasticity, 2021 Search PubMed.
- L. E. Nielsen, Mechanical properties of polymers and composites, M. Dekker, New York, 1974 Search PubMed.
- J. D. Ferry, Viscoelastic properties of polymers, Wiley, 3rd edn, 1980 Search PubMed.
- B. Xu, H. Li and Y. Zhang, Biomatter, 2013, 3, e24651 CrossRef PubMed.
- R. Y. Dhume and V. H. Barocas, Acta Biomater., 2019, 87, 245–255 CrossRef PubMed.
- J. Honerkamp and J. Weese, Macromolecules, 1989, 22, 4372–4377 CrossRef CAS.
- N. Orbey and J. M. Dealy, J. Rheol., 1991, 35, 1035–1049 CrossRef CAS.
- S. L. Hansen, P. M. Ray, A. O. Karlsson, B. Jørgensen, B. Borkhardt, B. L. Petersen and P. Ulvskov, Plant Physiol., 2011, 155, 246–258 CrossRef CAS PubMed.
- A. R. Piacenti, Atomic Force Microscope-Based Methods for the Nano-Mechanical Characterisation of Hydrogels and other Viscoelastic Polymeric Materials for Biomedical Applications, 2021 Search PubMed.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81 RSC.
- A. R. Piacenti, C. Adam, N. Hawkins, R. Wagner, J. Seifert, Y. Taniguchi, R. Proksch and S. Contera, Macromolecules, 2024, 57, 1118–1127 CrossRef CAS PubMed.
- A. Labuda, M. Kocuń, W. Meinhold, D. Walters and R. Proksch, Beilstein J. Nanotechnol., 2016, 7, 970–982 CrossRef CAS PubMed.
- M. Kocun, A. Labuda, W. Meinhold, I. Revenko and R. Proksch, ACS Nano, 2017, 11, 10097–10105 CrossRef CAS PubMed.
- S. D. Solares and G. Chawla, Meas. Sci. Technol., 2010, 21, 125502 CrossRef.
- G. Haugstad, Atomic force microscopy: understanding basic modes and advanced applications, John Wiley & Sons, 2012 Search PubMed.
- R. García, Surf. Sci. Rep., 2002, 47, 197–301 CrossRef.
- R. Castro García, Amplitude modulation atomic force microscopy, 2011 Search PubMed.
- Z. Al-Rekabi and S. Contera, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2658–2663 CrossRef CAS PubMed.
- S. Benaglia, V. G. Gisbert, A. P. Perrino, C. A. Amo and R. Garcia, Nat. Protoc., 2018, 13, 2890–2907 CrossRef CAS PubMed.
- R. Proksch and D. G. Yablon, Appl. Phys. Lett., 2012, 100, 073106 CrossRef.
- R. Proksch, M. Kocun, D. Hurley, M. Viani, A. Labuda, W. Meinhold and J. Bemis, J. Appl. Phys., 2016, 119, 134901 CrossRef.
- E. T. Herruzo and R. Garcia, Beilstein J. Nanotechnol., 2012, 3, 198–206 CrossRef PubMed.
- J. Seifert, C. Kirchhelle, I. Moore and S. Contera, Acta Biomater., 2021, 121, 371–382 CrossRef CAS PubMed.
- Applications Guide Version 16 Revision, Oxford Instruments Asylum Research Manual, 2018 Search PubMed.
- M. H. Harandi, F. Alimoradi, G. Rowshan, M. Faghihi, M. Keivani and M. Abadyan, Results Phys., 2017, 7, 338–344 CrossRef.
- R. Esmaeeli and S. Farhad, Mech. Mater., 2020, 146, 103369 CrossRef.
- M. J. Higgins, R. Proksch, J. E. Sader, M. Polcik, S. Mc Endoo, J. P. Cleveland and S. P. Jarvis, Rev. Sci. Instrum., 2006, 77, 013701 CrossRef.
- Get Real – Automated Probe Calibration, Oxford Instruments Asylum Research Forums, https://support.asylumresearch.com/articles/video-tutorials-aa/19721-getreal-automated-probe-calibration, 2014.
- K. Menard, Dynamic Mechanical Analysis: A Practical Introduction, CRC Press, 2nd edn, 2008 Search PubMed.
- D. Roylance, Engineering Viscoelasticity, Massachusetts Institute of Technology, https://web.mit.edu/course/3/3.11/www/modules/visco.pdf, 2001 Search PubMed.
- A. L. Weisenhorn, P. K. Hansma, T. Albrecht and C. F. Quate, Appl. Phys. Lett., 1989, 54, 2651–2653 CrossRef.
- Encyclopedia of Nanotechnology, ed. B. Bhushan, Springer, 2012 Search PubMed.
- E. J. Amis, C. J. Carriere, J. D. Ferry and A. Veis, Int. J. Biol. Macromol., 1985, 7, 130–134 CrossRef CAS.
- S. Meghezi, F. Couet, P. Chevallier and D. Mantovani, Int. J. Biomater., 2012, 1–9 Search PubMed.
- S. Nam, K. H. Hu, M. J. Butte and O. Chaudhuri, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5492–5497 CrossRef CAS PubMed.
- N. Sasaki, in Viscoelasticity – From Theory to Biological Applications, ed. J. De Vicente, InTech, 2012 Search PubMed.
- Z. Shen, H. Kahn, R. Ballarini and S. Eppell, Biophys. J., 2011, 100, 3008–3015 CrossRef CAS PubMed.
- R. Sopakayang, R. De Vita, A. Kwansa and J. W. Freeman, J. Theor. Biol., 2012, 293, 197–205 CrossRef CAS PubMed.
- Y. Sun, B. Akhremitchev and G. C. Walker, Langmuir, 2004, 20, 5837–5845 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00671b |
| This journal is © The Royal Society of Chemistry 2024 |