Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revealing microscale bulk structures in polymer–carbon nanocomposites using spin-echo SANS
L. V.
Tiihonen
a,
M. P.
Weir
b,
A. J.
Parnell
 c,
S. C.
Boothroyd
d,
D. W.
Johnson
e,
R. M.
Dalgliesh
f,
M.
Bleuel
g,
C. P.
Duif
c,
S. C.
Boothroyd
d,
D. W.
Johnson
e,
R. M.
Dalgliesh
f,
M.
Bleuel
g,
C. P.
Duif
 a,
W. G.
Bouwman
a,
R. L.
Thompson
a,
W. G.
Bouwman
a,
R. L.
Thompson
 d,
K. S.
Coleman
d,
N.
Clarke
d,
K. S.
Coleman
d,
N.
Clarke
 c,
W. A.
Hamilton
h,
A. L.
Washington
c,
W. A.
Hamilton
h,
A. L.
Washington
 f and
S. R.
Parnell
f and
S. R.
Parnell
 *af
*af
aFaculty of Applied Sciences, Delft University of Technology, Mekelweg 15, 2629 JB Delft, The Netherlands. E-mail: s.r.parnell@tudelft.nl
bSchool of Physics and Astronomy, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
cDepartment of Physics and Astronomy, The University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
dDepartment of Chemistry, University of Durham, Durham, DH1 3LE, UK
eCentre for Process Innovation, TS21 3FE, Durham, UK
fISIS, Rutherford Appleton Laboratory, Chilton, Oxfordshire, OX11 0QX, UK. E-mail: Steven.Parnell@stfc.ac.uk
gNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA
h(Retired) Neutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, 37831, USA
First published on 1st October 2024
Abstract
We have used spin-echo small-angle neutron scattering (SESANS) to probe the hierarchy of structures present in polymer–carbon nanocomposites, with length scales spanning over three orders of magnitude, from 10 nm to 16 μm. The data processing and reduction show a unified approach across two SESANS instruments (TU Delft and Larmor at the ISIS neutron source) and yield consistent data that are able to be modelled using well-established hierarchical models in freely available software such as SasView. Using this approach, we are able to extend the measured length scales by over an order of magnitude compared to traditional scattering methods. This yields information about the structure in the bulk that is inaccessible with conventional scattering techniques (SANS/SAXS) and points to a way for interrogating and investigating polymer nanocomposites routinely across multiple length scales.
I Introduction
Polymer–carbon nanocomposites1–3 exhibit useful structural, thermal and electrical properties which depend on the volume fraction, geometry and level of aggregation of the carbon nanofiller within the polymer matrix. Typically, these nanocomposites have structures present over multiple length scales, starting with relevant polymer chain dimensions (on the order of 1–10 nanometres).4 The filler material itself may be hierarchical in nature, which is the case for example with carbon black. High aspect ratio fillers made from (nominally) two-dimensional (2D) materials, such as graphene,5 functionalised graphenes,6 or graphene nanoplatelets,7 themselves comprise a wide range of length scales where their thickness, which can be comparable to polymer chain length scales, is usually orders of magnitude smaller than their lateral size. Furthermore, 2D materials may additionally undergo differing degrees of folding and crumpling.8 Together with agglomeration (also applicable in the case of carbon black), this leads to the possibility of structural hierarchies ranging from tens of nanometers to tens of microns. This depends on several factors, including polymer–nanoparticle interactions, polymer processing methods9 (melt/extruder processed and solvent processed) and thermal history (heating above the glass transition temperature and crystallization of the polymer matrix).10 Polymer nanocomposite structures can exhibit power law scaling in both the mass- and surface fractal regimes, due to the roughness of the resulting nano- and microstructures.11The matrix polymers used in this article, polystyrene (PS) and poly(methyl methacrylate) (PMMA), are electrical and thermal insulators. They are chiefly chosen as model polymers for scattering studies (for example, due to the good availability of well-controlled molecular weight synthesis and/or deuteration). Additionally, polystyrene is also a suitable polymer of choice for melt processing. The carbon nanofiller tends to be responsible for the desirable functionality of the composite, usually in terms of improved strength and enhanced thermal and electrical conductivity. Furthermore, the network formed by the nanofiller after processing is of great importance when understanding and tuning the final composite properties. For example, whether or not percolation is achieved within the network is of critical importance to the sample's electrical conductivity.12
The non-destructive characterisation of structures in nanocomposites relies primarily on small-angle scattering. This is an effective and powerful approach allowing statistical averaging over a large sample volume. Scattering reveals dominant length scales such as the average sizes of particles or agglomerated structures, the regularity (or irregularity) of their arrangements, and the roughness of phase interfaces or complex spatial structures. While conventional real-space microscopy techniques cover a larger range of length scales than conventional small-angle scattering, they are often not capable of providing the same level of statistical sampling that is possible with a (neutron or X-ray) scattering approach. This is due to the serial nature of image acquisition, which can skew the data to an unrepresentative portion of the sample such as surface features which may not represent the bulk majority phase. High sample opaqueness can severely limit transmission microscopy methods, while cross-sections are also prone to sampling problems, as sectioning is destructive and sectioning artefacts can give rise to distortion.
Small-angle scattering techniques and associated analysis tools have yielded great insight into materials which exhibit structures over multiple length scales. A good example of this is the Unified Fit model of Beaucage,13,14 which offers a robust method to construct hierarchical scattering models where explicit analytical scattering functions for a given system are either difficult or impossible to compute.
Small-angle scattering measurements are subject to instrumental limitations in the smallest measurable momentum transfer (q) value corresponding to the largest measurable length scale. For dedicated ultra-small angle scattering instruments, the maximum accessible length scale is in the region of several microns. Correspondingly, each instrument will have the smallest measurable length scale relating to the highest possible q value, thus defining a measurement range. Theoretically, it is possible to ‘stitch’ data from different instruments into a single master dataset with an enhanced q range. This relies on precise calibration and data reduction, and the comparison of data from the same sample across different instruments can be helpful in this regard.
The interpretation and analysis of inverse-space scattering techniques usually take place by calculating the appropriate transform of a real-space model that is iteratively evolved until a good fit is reached. In rarer cases, the data may be transformed directly into real space. A prime example of this is the correlation function or the CORFUNC approach for a two-phase system pioneered by Ströbl.15,16 Inverse-space scattering data are a valid source of structural information in its own right, but the scientific literature still appears to favour real-space images for their impact and aesthetic appeal, although reciprocal space scattering data are often more information rich and statistically more rigorous.
A limitation for measurements of nanocomposites using standard small-angle scattering techniques is that the samples tend to exhibit structural length scales beyond the lowest observable q. These can take the form of density inhomogeneities of dispersed nanofillers or large-scale aggregate networks of up to several microns. This has been observed for instance in polymer nanocomposites with carbon black,17,18 spherical silica,19,20 nanoclay21 and silver nanoparticles.12 To address this limitation, suitable ultra-small-angle scattering techniques can be used.
Spin echo small angle neutron scattering (SESANS) is a powerful statistical averaging technique that covers length scales from 10 nm up to 10–20 μm (depending upon the instrument), which enables a full statistical average of the sample structure over macroscopic illuminated volumes (≈cm3). It is therefore well suited to the study of polymer nanocomposites, which normally contain nanoparticles, mass fractals and agglomerates with length scales in the nanometre range up to microns. SESANS also yields information on the spatial arrangement and length scales within a sample in real space, thus providing an interesting counterpoint to real space imaging and reciprocal-space scattering.
There are now a number of SESANS instruments at neutron sources around the world22–25 along with developments of related techniques.26–32 Rather than measuring the structure factor of a sample directly, the method relies on measuring the change in beam polarisation caused by the sample. Depolarisation is measured for different real-space correlation lengths, the experimental spin-echo length, and the obtained data can be directly related to a Hankel transform of the sample structure factor. In the past, we have applied SESANS to polymer nanocomposites, where we looked at the behaviour of extruded polystyrene with fullerene C60 nanoparticles.33,34 In this previous work, SESANS was able to measure the larger extended network; furthermore, it was used to quantify the resulting structural changes depending on where the composite was sampled, i.e., at which extruder position, and also how the feeding composition affected the structure. In another work,11 we used SAXS and SANS to look at graphene oxide (GO) in polymer composites. The resultant small-angle scattering (SAS) spanned over two decades in reciprocal space and we were able to observe well-exfoliated sheets of GO in both PS and PMMA. However, larger length scale structures were only observed via AFM images, where these were on the micron length scale.
In this article, we demonstrate the effectiveness of SESANS for studying polymer–carbon nanocomposites with hierarchical length scales, revealing larger structural length scales that have been previously accessible via conventional scattering measurements. The nanocomposites studied consist of polymers loaded with graphene oxide (GO), graphene nanoplatelets (GNP), and carbon black (CB), with a broad range of length scales and structural complexity. There has been growing interest in graphene oxide35 and graphene nanoplatelet36 nanocomposites as they allow improved mechanical,37–39 thermal40–42 and electrical properties,43–45 filtration properties in membrane materials,46,47 and emulsion stabilisation in composite polymer systems.48,49 Graphene oxide and graphene nanoplatelet composites have structural elements with lateral sizes on the order of 5 microns, whose aggregates are understood to percolate throughout the sample forming macroscopic networks.50 The treatment of graphene to form graphene oxide, which is relatively rich in functional groups, disrupts the planar network of (sp2) bonded carbon and thus make it more prone to wrinkling when compared with graphene nanoplatelets. These two materials can therefore be compared as platelet-like additives with very different propensities to wrinkle, buckle, or fold. Carbon black, in addition to its traditional role as a reinforcing additive to rubber, has shown promise as a dual nanofiller for improved mechanical properties,51–53 and improved thermal54–56 and electrical properties57–59 in nanocomposite materials. Carbon black is understood to show length scales from the structural units of its constituent nanoparticles60 (70 Å) and carbon black aggregates (500 Å) to larger agglomerate structures which may form a percolated network,61,62 thus providing a structural counter-example to the platelet-like GO and GNP. SESANS measurements are combined with traditional small- and ultra-small-angle scattering techniques (SAXS and USANS respectively) and optical microscopy for validation and demonstrating the simultaneous resolving power of large and small structures.
II Scattering models
Despite SESANS, USANS, and SAXS all having different functional forms, the necessary transformations can now be implemented in modern scattering analysis software. This allows standard forms of the scattering intensity (I(q)) to be used across all the methods.For the SESANS data, this work makes use of the highly general Guinier–Porod model63 which allows good empirical estimation of single length scales with the surface or mass fractal substructure. The model can be used as an empirical approximation for various scattering systems, ranging from densely packed or swollen polymers to platelet systems or dense particles with smooth surfaces. Details on the form of the Guinier–Porod model are provided in Appendix, Section VI E.
For USANS and SAXS data, a simple power law is applied in the absence of a distinguishable length scale. When multiple length scales can be distinguished, the unified fit model13,14 provides an appropriate empirical approximation.
In all cases, the scattering data were analysed using the open source software SasView. The SasView package comprises a library of small angle scattering models and uses a least squares fitting algorithm to fit the scattering data. SasView has recently been updated to include the necessary Hankel transforms to relate the scattering models to data measured using SESANS.64 The theoretical derivation of this is detailed in ref. 65. These transforms allow a chosen scattering intensity function I(q) to be transformed into a sample correlation function as would be measured in a SESANS experiment, allowing direct fitting of SESANS data. This means that common small angle scattering models can easily be applied across the various scattering techniques and compared for consistency.
III Materials and methods
A Sample preparation
The nanocomposite samples were prepared by solvent processing using N-methyl-2-pyrrolidone (NMP). Polystyrene was dissolved in NMP to a final concentration of a 10 wt% polymer. The appropriate quantity of GNPs or carbon black was added to the polymer solution and the sample was transferred to a mixing roller for 18 h. Samples were then sonicated with a solid probe sonicator (300 W, 20 minutes, 5 second pulses, Cole Parmer 750), to disperse the filler in the polymer solution. Sonication was performed on no more than 50 mL of the dispersion at a time. The composite solution was then immediately precipitated by adding dropwise into methanol (10 volume excess to NMP). The resulting precipitate was stirred in methanol (30 minutes), isolated by filtration, and stirred in fresh methanol (18 h) and then finally isolated by filtration. The resulting powder was then dried in vacuo (50 °C, 18 h). Polystyrene was supplied from Sigma Aldrich (SKU 441147, measured Mw = 273![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, Mn = 113
000 g mol−1, Mn = 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1). GNPs were supplied by XG Sciences (xGNP® Graphene nanoplatelets grade M). Carbon black was supplied by Sigma Aldrich (SKU 699624) and graphitized with a particle size of <500 nm. NMP was supplied by Fisher Scientific (127630025 Acros Organics 99% extra pure). All materials were used as supplied. Samples were heat pressed at a temperature of 160 °C with a load of 6 tonnes for 30 minutes into 25 mm diameter discs of approximately 0.5 mm thickness.
000 g mol−1). GNPs were supplied by XG Sciences (xGNP® Graphene nanoplatelets grade M). Carbon black was supplied by Sigma Aldrich (SKU 699624) and graphitized with a particle size of <500 nm. NMP was supplied by Fisher Scientific (127630025 Acros Organics 99% extra pure). All materials were used as supplied. Samples were heat pressed at a temperature of 160 °C with a load of 6 tonnes for 30 minutes into 25 mm diameter discs of approximately 0.5 mm thickness.
B Spin-echo small angle neutron scattering – (SESANS)
SESANS measurements were performed at two separate institutes. One dataset was measured at the Reactor Institute Delft (TU Delft) using the dedicated SESANS instrument.22 This uses a monochromatic neutron beam of a wavelength of 2.06 Å accessing length scales in the size range of 0.1–16 μm. The maximum spin echo length was enabled by a shallow angle (15°) of magnetic foils in the SESANS instrument despite the low wavelength. The second instrument used was the instrument Larmor in SESANS mode at the ISIS Neutron and Muon Source (Rutherford Appleton Laboratory, UK). Larmor was used for measurements that cover the shorter length scale region of 0.1–2 μm. This instrument uses a pulsed beam of neutrons with a wavelength band of 3–8 Å. This instrument is capable of covering a length scale range than spans 10 nm–30 μm in SESANS mode and 5 Å–3 μm in SANS/SEMSANS mode; however, the maximum spin echo length was limited by the thickness of the sample, whereby at higher wavelengths the sample fully depolarised the incident neutrons. Since in Larmor the higher wavelengths correspond to higher probed spin echo lengths, this total depolarisation resulted in high noise effectively limiting the maximum length scale (see Appendix VI D for Larmor error bars).In both cases, the instrument was calibrated in spin-echo length using patterned silicon gratings which have a period of 1 μm. For the Delft instrument, the beam polarisation was observed with the sample in and out of the beam over 11 echo points. This was to determine P/P0 per each probed spin-echo length as determined by the magnetic fields. Meanwhile, for Larmor, the instrument is in echo and the ratio P/P0 is determined for the sample in and out. For the Larmor instrument, the data were corrected to account for the portion of the beam that is scattered and not captured, using an established procedure to account for the fraction of scattered neutrons which are not incident upon the neutron detector.30
C Ultra-small angle neutron scattering – (USANS)
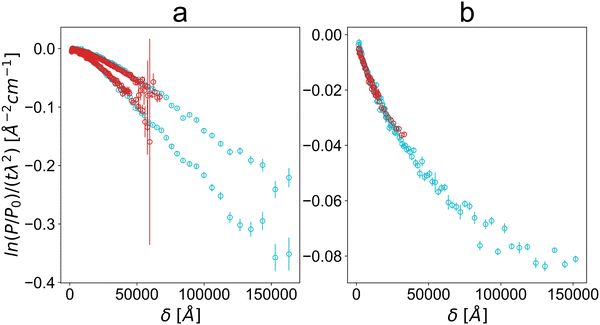
USANS measurements were carried out using a BT5 perfect crystal diffractometer at NCNR (NIST, USA). A q-range of 3 × 10−5 Å−1 to 1 × 10−3 Å−1 was achieved using a neutron wavelength of 2.4 Å at a resolution of 6% Δλ/λ. Briefly, the neutron beam was monochromated using a pyrolytic graphite premonochromator, followed by a triple-bounce Si(220) monochromator before encountering the sample. The resulting scattering pattern was collected using a triple-bounce Si(220) analyser moving in synchronisation with the detector to map the neutron intensity as a function of angle (subsequently converted into q-space). The sample scattering intensity was adjusted for empty cell scattering and sample transmission. The USANS data were reduced and de-smeared using the standard procedures within the NCNR USANS macros.66 These data are displayed in Fig. 1 in the Results section.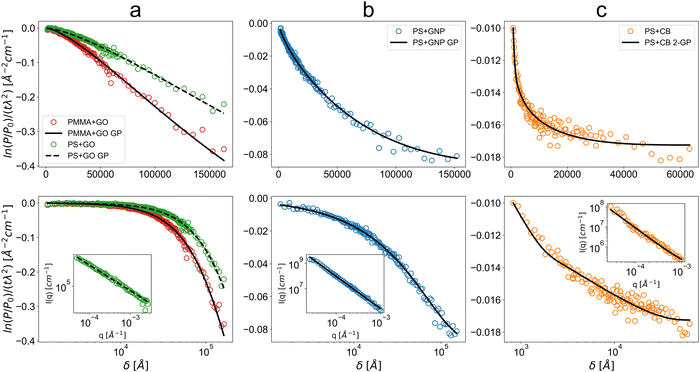 | ||
Fig. 1 Measured SESANS depolarisation over real-space spin-echo length δ, normalised by neutron wavelength and sample thickness Solid lines are the respective numerically Hankel-transformed Guinier–Porod (GP) fits. USANS data are displayed in the insets in the bottom row of plots. The top row shows the data on a linear scale over spin-echo length, while the bottom row shows the data on a logarithmic scale over spin-echo length. This is to distinguish low-δ features. These are for (a) graphene oxide in PS (PS+GO) and PMMA (PMMA+GO), (b) graphene nanoplatelets in PS (PS+GNP) and (c) carbon black in PS (PS+CB) where the fit is a two-term Guinier–Porod (2-GP) fit with the lower term fixed based on parameters from SAXS. The directly probed length scales reach from 800 Å or 0.08 μm up to 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å or 16 μm. The USANS data over the reciprocal q-space and their simple power law fits demonstrate that the scattering over the range probed in USANS does not reveal obvious flattening in the low-q, meaning that SESANS is needed to probe the higher length scale beyond this range. The PS+GO USANS data have been reproduced from ref. 11 with permission. Respective error bars are on the order of deviations from the displayed fit curves. Matching between the SESANS data for the Delft and ISIS Larmor instruments is illustrated in Appendix VI D. 000 Å or 16 μm. The USANS data over the reciprocal q-space and their simple power law fits demonstrate that the scattering over the range probed in USANS does not reveal obvious flattening in the low-q, meaning that SESANS is needed to probe the higher length scale beyond this range. The PS+GO USANS data have been reproduced from ref. 11 with permission. Respective error bars are on the order of deviations from the displayed fit curves. Matching between the SESANS data for the Delft and ISIS Larmor instruments is illustrated in Appendix VI D. | ||
D Small-angle X-ray scattering – (SAXS)
SAXS patterns were recorded using a laboratory SAXS instrument (Xeuss 2.0, Xenocs, France) equipped with a liquid gallium MetalJet X-ray source (Excillum, Sweden). A monochromatic X-ray radiation (wavelength λ = 1.34 Å) and a 2D Dectris Pilatus 1M pixel detector were used for these experiments. A SAXS camera was placed at a distance of 6.4 m from the sample position and thus covered a q range of 0.0015–0.1 Å−1, where q = (4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ is the modulus of the scattering vector and θ is half of the scattering angle. X-ray scattering data were integrated and normalised using the software package Foxtrot (Soleil, France). Irena SAS macros67,68 for Igor Pro were utilised for background subtraction.
θ)/λ is the modulus of the scattering vector and θ is half of the scattering angle. X-ray scattering data were integrated and normalised using the software package Foxtrot (Soleil, France). Irena SAS macros67,68 for Igor Pro were utilised for background subtraction.
E Optical microscopy
Thin samples for imaging with optical microscopy were prepared by additional heat pressing of the previously prepared samples of the composites on a stainless steel die between sheets of aluminium foil at 160 °C with a load of 6 tonnes until a thickness of approximately 100 microns was obtained. Images were acquired with an Olympus BX51 optical microscope in bright field transmission mode. The sample was illuminated from beneath using a standard white light source and images acquired using a Basler Ace acA4024-29uc USB 3.0 colour camera using objective lenses providing 5× and 20× magnification.IV Results
Measurements using SESANS, USANS, and SAXS as detailed in Section III were taken on a series of carbon–polymer nanocomposites with dimensionally distinctive fillers. We present the data for each nanocomposite sample and discuss how the different scattering methods are compared. The first results discussed are two graphene oxide polymer nanocomposite samples as these have been previously studied in detail,11 followed by the graphene nanoplatelet sample as a novel system and finally the carbon black sample to understand the utility of SESANS for strongly hierarchical systems. Optical microscopy images are provided and the validation they provide is discussed. Tables of SasView fitting outputs are provided in Appendix VI A to VI C.A Graphene oxide
The graphene oxide samples measured by SESANS are well described by Guinier–Porod fits in Fig. 1a. These yields estimated radii of gyration of 31 μm and 19 μm, respectively, for PS and PMMA and Porod exponents of 3.57 and 3.58. The length scales obtained are substantially greater than previously observed for dispersed sheets seen with atomic force microscopy by Weir et al.,11 suggesting dominant maximum feature sizes of >50 μm. Furthermore, the Porod exponents obtained are substantially in the surface fractal regime of 3 < m < 4 rather than in the mass fractal regime of m < 3 expected for highly wrinkled exfoliated sheets observed in USANS measurements (approximately m = 2.7 for the USANS data reproduced in the PS+GO inset of Fig. 1). This suggests the presence of compact packed phases of graphene oxide with rough surfaces when observed using SESANS, which may then dominate the SESANS signal over the lower length scales of individual sheets. A relatively high volume fraction of 4.3% indicates that this should be the length scale of a connected network of compact phases of poorly dispersed graphene oxide through the sample. Poor dispersion was also indicated by atomic force microscopy (AFM) performed previously in ref. 11. The microscopy image in Fig. 2b supports the presence of these large >50 μm features with a high degree of connection, with the comparison with Fig. 2a further demonstrating the poor dispersion at a high volume fraction. The difference seen between PS and PMMA is then interpreted as PMMA resulting in a more compact structure of smaller graphene oxide phases with a similar surface roughness. An illustration of the proposed structure is provided in Fig. 4a.The validity of the fitting outputs depends on modeling assumptions of the Guinier–Porod model, since the data for graphene oxide over linear spin-echo length δ in Fig. 1a do not show saturation, i.e. flattening which would allow the maximum present length scale to be estimated directly from the plot. In this case, the outputs are only physically valid if there is only one greater (average) length scale of irregular structures in the low-q, with a single power law exponent describing their internal or surface roughness, rather than a hybrid structure consisting of multiple phases with different length scales and exponents. The microscopy supports the validity of these assumptions; however, this must be treated with caution due to inherent poor sampling of the bulk structure by microscopy.
Alternative explanations for the lack of saturation at large length scales are the presence of significant voids within the polymer matrix or refractive effects which may be seen in the ultra-small-angle regime. Voids on the order of 10–50 μm with irregular interfaces could result in a Porod exponent in the surface fractal regime. In this case, graphene oxide would be well-dispersed rather than forming compact phases, with a little contribution to scattering in the SESANS range. However, this appears unlikely as the void-polymer scattering contrast is around 15 times lower than carbon–polymer scattering contrast. The volume fraction of voids would have to be substantially greater than that of the graphene oxide nanofiller. Furthermore, the nanocomposites with graphene nanoplatelets and carbon black were prepared with an identical method and they do not display the presence of a comparably large structure.
Refractive effects could however result from the graphene oxide itself. Applying a heuristic calculation based on the neutron wavelength used and scattering contrast presented by Berk and Hardman-Rhyne,69 we can estimate the presence of refractive effects. Taking the smallest and greatest wavelengths used, this results in λminρ ≈ 1.1 and λmaxρ ≈ 6.1. For voluminous particles of a radius R of 10 μm, such as spheres, values in the proximity of and above λρ = 5 would indicate a substantial refractive contribution to scattering. However, graphene oxide particles are thin sheets on the nanoscale rather than globular or voluminous particles relative to their lateral extent of several microns. This means the heuristic values computed in the case of graphene oxide should greatly overestimate the effect, so significant refractive effects from the graphene oxide are unlikely.
B Graphene nanoplatelets
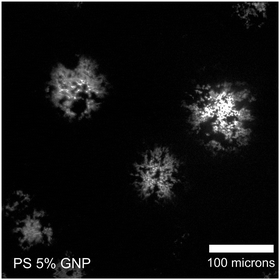
For the graphene nanoplatelet nanocomposite, a Guinier–Porod model gives a good fit for both SESANS and USANS (see Fig. 1b). The data further suggest saturation (flattening in the data) beginning within the measured range, observed in the plot over a linear spin-echo length δ. This results in a radius of gyration of 7.8 μm for SESANS and a redundant length scale for USANS due to the data containing no distinguishable length scale relative to the noise present. The Porod exponents found were 2.72 and 2.64 for SESANS and USANS, respectively. The length scale obtained from SESANS matches the extent of 5–25 μm expected for the GNPs, while the Porod exponent of 2.7 deviates from m = 2 expected for thin platelets in a dilute configuration.70 This deviation suggests an additional structure factor applying on length scales smaller than 7.8 μm. GNPs have a planar structure rather than thin exfoliated and wrinkled sheets, which rules out wrinkling as the source of mass fractal scattering. Since GNPs are in general not monodisperse, the higher Porod exponent could result from the aggregation of increasingly small GNPs into dense clusters on the order of 10–20 μm. This interpretation is supported by the microscopy shown in Fig. 3, where inhomogeneities are seen on length scales that support the output from SESANS fitting; however, caution must be taken due to the poor sampling provided by microscopy. The propensity of GNPs to aggregate at concentrations as low as 0.1 wt% due to intermolecular forces has also been suggested by Wei et al.71 The high volume fraction of ∼5% and the very small thickness of GNPs suggest that these structures should be connected throughout the sample, as illustrated in Fig. 4b. Void scattering or refraction effects can be ruled out on the same basis as was done for graphene oxide.C Carbon black
The carbon black nanocomposite is well described by a Guinier–Porod model in SESANS, a power law in USANS, and a multi-level unified fit in SAXS. SESANS indicates the presence of a maximal radius of gyration on the order of 1.8 μm. A clear saturation level is evident in the plot over a linear spin-echo length δ in Fig. 1c. The fit indicates a Porod exponent of 1.9, consistent with the presence of agglomerates with chain-like extensions built up of the carbon black. This demonstrates the ability of SESANS to resolve diffusion- or reaction-limited aggregate structures. The description of the agglomerate level by a Guinier–Porod model and the high carbon black concentration suggests that these large-scale structures connect into a network across the sample. Microscopy for PS+CB was found to provide no transmission under the measurement conditions specified. This suggests a much greater degree of homogeneity on large length scales as compared to both the GO and GNP samples, and supports the validity of a substantially lower fitted radius of gyration. USANS provides no stable length scale parameter, suggesting that the length scale is beyond the q-range of the USANS instrument or the low-q region suffers from direct beam effects due to insufficient scattering. This again demonstrates the value of SESANS for characterisation. The USANS data have the form of a power law, described simply by a Porod exponent of 1.6, which is a significant deviation from the exponent observed in SESANS. Since the USANS should give a direct measurement of the sample structure factor, this indicates that SESANS fitting gives an overestimated value and the exact output parameters must be interpreted with caution. A Porod exponent of 1.6 indicates chain-like extensions that are much less folded than the nearly Gaussian chains indicated by 1.9, but notably both measurements still indicate a chain-like aggregate morphology. The consistency of the obtained information was evaluated by fitting a multi-level unified fit to SAXS data (see Appendix VI C), yielding a carbon black nanoparticle length scale of 6.3 nm, an aggregate length scale of 83 nm with a Porod exponent 3.4, consistent with dense clusters of particles with a structural roughness, and an estimated largest length scale of 1 μm. This was obtained by fixing the Porod exponent of the highest level at 1.61 indicated by USANS, and notably the largest length scale indicated by SAXS is within the same order as the fitted length scale from SESANS. The SESANS fit made use of the aggregate length scale and the Porod exponent determined from SAXS, further showing the consistency between the different techniques. The structural interpretation obtained from the fitting is in agreement with the findings in ref. 61.The length scales of the nanoparticles and their aggregated clusters determined from the SESANS and SAXS correspond well with known values from past studies of carbon black polystyrene nanocomposites.60 This demonstrates the consistency of a SESANS–USANS–SAXS characterisation despite some limitations of SESANS for low Porod exponents or highly complex samples. The full proposed hierarchical structure is illustrated in Fig. 5. One limitation with SESANS is due to the Hankel transform which often reduces the features in the measured correlation function, resulting in ambiguous fits when not applying the resulting length scales and scaling exponents from SAXS and USANS as fixed inputs. Another limitation is the possibility of acceptance effects (due to a significant fraction of scattered neutrons lost beyond the angular acceptance of the detector) when measuring samples with small length scales or low Porod exponents, as the SESANS detector may not capture the q-range necessary to accurately measure the sample correlation function. However, even when such limitations are present, good comparative measurements are possible to study structural variations in nanocomposites, since information is still obtained about the order of length scales and the regime of mass fractal scattering. This also shows how a combination of different scattering techniques can be used to expand the range of length scales (10 nm–20 μm) that can be probed.
V Conclusions
SESANS revealed structures in polymer–carbon nanocomposites that were previously inaccessible through small-angle and ultra-small-angle scattering methods. The range of length scales that can be studied for these materials has been extended by an order of magnitude or more, up to a maximum of at least 20 μm. The graphene oxide and graphene nanoplatelet samples were characterised by SESANS measurements using an empirical Guinier–Porod fit, which allowed us to determine characteristics of the nano to micro scale structures. Carbon black showed a discrepancy between the outputs from SESANS and well-accepted USANS, which is explained through detector acceptance limitations in SESANS relative to the slow decay of the Porod scattering for a sparse mass fractal structure. In this case, SESANS still yields a strong indication of the existence of a sparse mass fractal structure and can allow accurate comparative measurements between samples. The results obtained with SESANS were supported by optical transmission microscopy. SESANS also showed consistency with the information obtained from SAXS measurements of carbon black, demonstrating the presence of intermediate length scale information in SESANS. At greater Porod exponents and length scales for GO and GNP samples, the outputs can be considered physically accurate but care must be taken to interpret the possible sources of scattering in strongly scattering thick samples in the ultra-small-angle regime, such as refraction or void scattering. These results demonstrate the value of SESANS for extending the characterisation of nanocomposites both as a standalone method and in combination with other scattering methods, offering the valuable characterisation of the bulk microstructure for further understanding and tuning of material properties.Conflicts of interest
There are no conflicts to declare.VI Appendix
In the Appendix section, we summarise the various fit results and the Guinier–Porod fitting model together with estimated correlation lengths for each sample and illustrate the data matching between Delft and ISIS (Larmor) SESANS instruments.A Graphene oxide
Fits were performed using the Guinier–Porod model on the SESANS data of the two GO samples (Table 1).| Guinier–Porod | PS+GO | PMMA+GO |
|---|---|---|
| Reduced χ2 | 1.68 | 2.07 |
| Scale [Å−2 cm−1] | 2.62 ± 0.38 × 1011 | 9.24 ± 0.90 × 1010 |
| R g [Å] | 3.15 ± 0.14 × 105 | 1.94 ± 0.61 × 105 |
| m | 3.57 ± 0.01 | 3.58 ± 0.01 |
B Graphene nanoplatelets
Table 2.| Guinier–Porod | SESANS | USANS |
|---|---|---|
| a Diverging or unstable parameters. b The high χ2 is due to low error estimates on the USANS data. The residuals were well-distributed around the fit. | ||
| Reduced χ2 | 2.27 | 22.0b |
| Scale [Å−2 cm−1; cm−1] | 1.29 ± 0.08 × 109 | 3.84 ± 0.05 × 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| R g [Å] | 7.81 ± 0.20 × 104 | 4.79 ± 0.03 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| m | 2.72 ± 0.01 | 2.64 ± 0.01 |
C Carbon black
Fig. 6 and Tables 3, 4. | ||
| Fig. 6 Data and fit plots of SAXS for carbon black in PS (PS+CB) with a 3-level unified fit (PS+CB 3-UF). Respective error bars are smaller or equal to the size of the data markers. | ||
| Guinier–Porod | SESANSb | USANS |
|---|---|---|
| a Diverging or unstable parameters. b The SESANS fit was obtained through the summation of two Guinier–Porod terms where the lower term had fixed Rg = 826 Å and m = 3.43 taken from the aggregate level of the SAXS fit below. The displayed parameters are the resulting fitted parameters for the Guinier–Porod term of the upper aggregate level. c The high χ2 is due to low error estimates on the USANS data. The residuals were well-distributed around the fit. | ||
| Reduced χ2 | 1.35 | 58.2c |
| Scale [Å−2 cm−1; cm−1] | 2.77 ± 0.85 × 106 | 1.46 ± 1.00 × 108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| R g [Å] | 1.82 ± 0.32 × 104 | 5.3 ± 2.3 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| m | 1.97 ± 0.04 | 1.61 ± 0.01 |
| Unified fit 3-level | Agglomerate | Aggregate | Nanoparticle |
|---|---|---|---|
| a Parameters that were fixed for fitting. b The high χ2 is partially due to low error estimates on the SAXS data and partially due to unaccounted structural information. The residuals are evenly distributed around the fit with some oscillation. | |||
| Reduced χ2 | 14.596b | 14.596b | 14.596b |
| R g [Å] | 1.07 ± 0.01 × 104 | 826 ± 4 | 63.3 ± 0.3 |
| P | 1.61a | 3.43 ± 0.01 | 4a |
| B [cm−1] | 2.23 ± 0.02 | 2.09 ± 0.06 × 10−4 | 1.91 ± 0.02 × 10−4 |
| G [cm−1] | 0a | 2.23 ± 0.02 × 105 | 299 ± 4 |
D Data matching for Larmor and Delft SESANS instruments
Fig. 7.E SESANS fitting for the Guinier–Porod model
The Guinier–Porod model formulated by Hammouda63 can be used to empirically fit a variety of data from both dilute and concentrated two-phase systems described by an average length scale and a structural or an interface roughness. The Guinier–Porod model is a combination of two basic scattering functions, a Guinier law and a Porod law, with a continuity condition establishing their boundary. When Rg is the greatest length scale present as observed in a SESANS experiment, the model for the scattered intensity I(q) is defined in terms of the scale factor A, radius of gyration Rg and Porod exponent m as: | (1) |
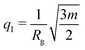 | (2) |
 | (3) |
In an ideal SESANS experiment, the projected correlation function G(δ) defining the beam depolarisation is given by the Hankel transform of the differential scattering cross-section Î(q) = dσ/dΩ(q) as:
 | (4) |
The measured log-polarisation in SESANS for a two-phase system and the volume fraction are given as:65
 | (5) |
 | (6) |
This allows the estimation of the correlation length ξ using estimated saturation levels from the data plots (Table 5):
These match reasonably well the order of magnitudes of the length scales obtained through the Guinier–Porod fits.
Acknowledgements
We gratefully acknowledge the Science and Technology Facilities Council (STFC) for access to the neutron beamtime at ISIS at the Larmor instrument and access to sample preparation facilities. Data obtained at ISIS are available through 10.5286/ISIS.E.RB1810597. Access to the USANS instrument was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under agreement no. DMR-2010792. This work benefited from SasView software, originally developed by the DANSE project under NSF award DMR-0520547. We gratefully acknowledge EPSRC for support by the grant number EP/K016784/1 (“Grapol”). Certain commercial equipment, instruments, materials, suppliers, or software are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology (NIST) nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.References
- H. Kim, A. A. Abdala and C. W. Macosko, Graphene/polymer nanocomposites, Macromolecules, 2010, 43(16), 6515–6530, DOI:10.1021/ma100572e.
- A. K. Anam Afzal and M. Siddiq, Perspectives of polystyrene composite with fullerene, carbon black, graphene, and carbon nanotube: A review, Polym.-Plast. Technol. Eng., 2016, 55(18), 1988–2011, DOI:10.1080/03602559.2016.1185632.
- A. Kausar, Poly(methyl methacrylate) nanocomposite reinforced with graphene, graphene oxide, and graphite: a review, Polym.-Plast. Technol. Eng., 2019, 58(8), 821–842, DOI:10.1080/25740881.2018.1563112.
- M. P. Weir, D. W. Johnson, S. C. Boothroyd, R. C. Savage, R. L. Thompson, S. M. King, S. E. Rogers, K. S. Coleman and N. Clarke, Distortion of chain conformation and reduced entanglement in polymer-graphene oxide nanocomposites, ACS Macro Lett., 2016, 5(4), 430–434 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6(3), 183–191, DOI:10.1038/nmat1849.
- T. Kuila, S. Bose, A. K. Mishra, P. Khanra, N. H. Kim and J. H. Lee, Chemical functionalization of graphene and its applications, Prog. Mater. Sci., 2012, 57(7), 1061–1105, DOI:10.1016/j.pmatsci.2012.03.002 , https://www.sciencedirect.com/science/article/pii/S0079642512000254.
- P. Cataldi, A. Athanassiou and I. S. Bayer, Graphene nanoplatelets-based advanced materials and recent progress in sustainable applications, Appl. Sci., 2018, 8(9), 1438, DOI:10.3390/app8091438 , https://www.mdpi.com/2076-3417/8/9/1438.
- S. Deng and V. Berry, Wrinkled, rippled and crumpled graphene: an overview of formation mechanism, electronic properties, and applications, Mater. Today, 2016, 19(4), 197–212, DOI:10.1016/j.mattod.2015.10.002 , https://www.sciencedirect.com/science/article/pii/S1369702115003119.
- D. N. Trivedi and N. V. Rachchh, Graphene and its application in thermoplastic polymers as nano-filler- a review, Polymer, 2022, 240, 124486, DOI:10.1016/j.polymer.2021.124486 , https://www.sciencedirect.com/science/article/pii/S0032386121011095.
- M. Vinyas, S. J. Athul, D. Harursampath, M. Loja and T. Nguyen Thoi, A comprehensive review on analysis of nanocomposites: from manufacturing to properties characterization, Mater. Res. Express, 2019, 6(9), 092002 CrossRef CAS.
- M. P. Weir, D. W. Johnson, S. C. Boothroyd, R. C. Savage, R. L. Thompson, S. R. Parnell, A. J. Parnell, S. M. King, S. E. Rogers, K. S. Coleman and N. Clarke, Extrinsic wrinkling and single exfoliated sheets of graphene oxide in polymer composites, Chem. Mater., 2016, 28(6), 1698–1704 CrossRef CAS.
- Q. Fang and K. Lafdi, Effect of nanofiller morphology on the electrical conductivity of polymer nanocomposites, Nano Express, 2021, 2(1), 010019, DOI:10.1088/2632-959X/abe13f.
- G. Beaucage, Approximations Leading to a Unified Exponential/Power-Law Approach to Small-Angle Scattering, J. Appl. Crystallogr., 1995, 28(6), 717–728 CrossRef CAS.
- G. Beaucage, Small-Angle Scattering from Polymeric Mass Fractals of Arbitrary Mass-Fractal Dimension, J. Appl. Crystallogr., 1996, 29(2), 134–146 CrossRef CAS.
- G. R. Strobl and M. Schneider, Direct evaluation of the electron density correlation function of partially crystalline polymers, J. Polym. Sci., Polym. Phys. Ed., 1980, 18(6), 1343–1359, DOI:10.1002/pol.1980.180180614.
- A. J. Parnell, A. L. Washington, O. O. Mykhaylyk, C. J. Hill, A. Bianco, S. L. Burg, A. J. C. Dennison, M. Snape, A. J. Cadby, A. Smith, S. Prevost, D. M. Whittaker, R. A. L. Jones, J. P. A. Fairclough and A. R. Parker, Spatially modulated structural colour in bird feathers, Sci. Rep., 2015, 5(1), 18317, DOI:10.1038/srep18317.
- A. McGlasson, K. Rishi, G. Beaucage, M. Chauby, V. Kuppa, J. Ilavsky and M. Rackaitis, Quantification of dispersion for weakly and strongly correlated nanofillers in polymer nanocomposites, Macromolecules, 2020, 53(6), 2235–2248 CrossRef CAS.
- K. Rishi, G. Beaucage, V. Kuppa, A. Mulderig, V. Narayanan, A. McGlasson, M. Rackaitis and J. Ilavsky, Impact of an emergent hierarchical filler network on nanocomposite dynamics, Macromolecules, 2018, 51(20), 7893–7904 CrossRef CAS.
- S. Sen, Y. Xie, S. K. Kumar, H. Yang, A. Bansal, D. L. Ho, L. Hall, J. B. Hooper and K. S. Schweizer, Chain conformations and bound-layer correlations in polymer nanocomposites, Phys. Rev. Lett., 2007, 98, 128302, DOI:10.1103/PhysRevLett.98.128302.
- A. Banc, A.-C. Genix, C. Dupas, M. Sztucki, R. Schweins, M.-S. Appavou and J. Oberdisse, Origin of small-angle scattering from contrast-matched nanoparticles: A study of chain and filler structure in polymer nanocomposites, Macromolecules, 2015, 48(18), 6596–6605, DOI:10.1021/acs.macromol.5b01424.
- J. Bandyopadhyay and S. Sinha Ray, The quantitative analysis of nano-clay dispersion in polymer nanocomposites by small angle x-ray scattering combined with electron microscopy, Polymer, 2010, 51(6), 1437–1449, DOI:10.1016/j.polymer.2010.01.029 , https://www.sciencedirect.com/science/article/pii/S0032386110000583.
- M. T. Rekveldt, J. Plomp, W. G. Bouwman, W. H. Kraan, S. Grigoriev and M. Blaauw, Spin-echo small angle neutron scattering in delft, Rev. Sci. Instrum., 2005, 76(3), 033901 CrossRef.
- S. R. Parnell, A. L. Washington, K. Li, H. Yan, P. Stonaha, F. Li, T. Wang, A. Walsh, W. C. Chen, A. J. Parnell, J. P. A. Fairclough, D. V. Baxter, W. M. Snow and R. Pynn, Spin echo small angle neutron scattering using a continuously pumped 3he neutron polarisation analyser, Rev. Sci. Instrum., 2015, 86(2), 023902 CrossRef CAS PubMed.
- J. Plomp, V. O. de Haan, R. M. Dalgliesh, S. Langridge and A. A. van Well, Neutron spin-echo labelling at offspec, an isis second target station project, Thin Solid Films, 2007, 515(14), 5732–5735 CrossRef CAS.
- F. Funama, C. M. Wolf, K. Weigandt, J. Shen, S. R. Parnell and F. Li, Spin echo small-angle neutron scattering using superconducting magnetic Wollaston prisms, Rev. Sci. Instrum., 2024, 95(7), 073709, DOI:10.1063/5.0217884 , https://arXiv:https://pubs.aip.org/aip/rsi/article-pdf/doi/10.1063/5.0217884/20052580/073709_1_5.0217884.pdf.
- M. Strobl, J. Valsecchi, R. Harti, P. Trtik, A. Kaestner, C. Gruenzweig, E. Polatidis and J. Capek, Achromatic non-interferometric single grating neutron dark-field imaging, Sci. Rep., 2019, 9(1), 19649 CrossRef CAS PubMed.
- W. G. Bouwman, C. P. Duif and R. Gähler, Spatial modulation of a neutron beam by larmor precession, Phys. B, 2009, 404(17), 2585–2589 CrossRef CAS.
- W. G. Bouwman, C. P. Duif, J. Plomp, A. Wiedenmann and R. Gähler, Combined sans-sesans, from 1 nm to 0.1 mm in one instrument, Phys. B, 2011, 406(12), 2357–2360 CrossRef CAS.
- A. Kusmin, W. G. Bouwman, A. A. van Well and C. Pappas, Feasibility and applications of the spin-echo modulation option for a small angle neutron scattering instrument at the european spallation source, Nucl. Instrum. Methods Phys. Res., Sect. A, 2017, 856, 119–132 CrossRef CAS.
- F. Li, S. R. Parnell, R. Dalgliesh, A. Washington, J. Plomp and R. Pynn, Data correction of intensity modulated small angle scattering, Sci. Rep., 2019, 9(1), 8563 CrossRef PubMed.
- F. Li, N.-J. Steinke, R. M. Dalgliesh, A. L. Washington, J. Shen, R. Pynn and S. R. Parnell, Probing magnetic correlations with spin-echo modulated small angle neutron scattering (semsans), Nucl. Instrum. Methods Phys. Res., Sect. A, 2021, 1014, 165705 CrossRef CAS.
- J. Schmitt, J. J. Zeeuw, J. Plomp, W. G. Bouwman, A. L. Washington, R. M. Dalgliesh, C. P. Duif, M. A. Thijs, F. Li and R. Pynn, et al., Mesoporous silica formation mechanisms probed using combined spin-echo modulated small-angle neutron scattering (semsans) and small-angle neutron scattering (sans), ACS Appl. Mater. Interfaces, 2020, 12(25), 28461–28473 CrossRef CAS PubMed.
- H. Gaspar, P. Teixeira, R. Santos, L. Fernandes, L. Hilliou, M. P. Weir, A. J. Parnell, K. J. Abrams, C. J. Hill, W. G. Bouwman, S. R. Parnell, S. M. King, N. Clarke, J. Covas and G. Bernardo, A journey along the extruder with polystyrene:c60 nanocomposites: Convergence of feeding formulations into a similar nanomorphology, Macromolecules, 2017, 50(8), 3301–3312 CrossRef CAS.
- H. Gaspar, R. Santos, P. Teixeira, L. Hilliou, M. P. Weir, C. P. Duif, W. G. Bouwman, S. R. Parnell, S. M. King, J. Covas and G. Bernardo, Evolution of dispersion in the melt compounding of a model polymer nanocomposite system: A multi-scale study, Polym. Test., 2019, 76, 109–118 CrossRef CAS.
- B. M. Rahim Shah, A. Kausar and S. Shah, Progression from graphene and graphene oxide to high performance polymer-based nanocomposite: A review, Polym.-Plast. Technol. Eng., 2015, 54(2), 173–183, DOI:10.1080/03602559.2014.955202.
- A. Kausar, Advances in polystyrene/graphene nanoplatelet nanocomposites, J. Plast. Film Sheeting, 2022, 38(1), 130–146, DOI:10.1177/87560879211029690.
- S. A. A. D. Zaid, G. Mohammadsalih, N. Mullin and I. U. Rehman, Nanomechanical behavior of polystyrene/graphene oxide nanocomposites, Fullerenes, Nanotubes Carbon Nanostruct., 2024, 32(1), 106–118, DOI:10.1080/1536383X.2023.2263597.
- R. J. Young, I. A. Kinloch, L. Gong and K. S. Novoselov, The mechanics of graphene nanocomposites: A review, Compos. Sci. Technol., 2012, 72(12), 1459–1476, DOI:10.1016/j.compscitech.2012.05.005 , https://www.sciencedirect.com/science/article/pii/S0266353812001789.
- R. J. Young, M. Liu, I. A. Kinloch, S. Li, X. Zhao, C. Valles and D. G. Papageorgiou, The mechanics of reinforcement of polymers by graphene nanoplatelets, Compos. Sci. Technol., 2018, 154, 110–116, DOI:10.1016/j.compscitech.2017.11.007 , https://www.sciencedirect.com/science/article/pii/S026635381732482X.
- Z. G. Mohammadsalih, B. J. Inkson and B. Chen, The effect of dispersion condition on the structure and properties of polystyrene/graphene oxide nanocomposites, Polym. Compos., 2021, 42(1), 320–328, DOI:10.1002/pc.25827 , https://4spepublications.onlinelibrary.wiley.com/doi/pdf/10.1002/pc.25827.
- X. Huang, C. Zhi, Y. Lin, H. Bao, G. Wu, P. Jiang and Y.-W. Mai, Thermal conductivity of graphene-based polymer nanocomposites, Mater. Sci. Eng., R, 2020, 142, 100577, DOI:10.1016/j.mser.2020.100577 , https://www.sciencedirect.com/science/article/pii/S0927796X20300358.
- Z. A. Ayesha Kausar and B. Muhammad, Overview of nonflammability characteristics of graphene and graphene oxide-based polymeric composite and essential flame retardancy techniques, Polym.-Plast. Technol. Eng., 2017, 56(5), 488–505, DOI:10.1080/03602559.2016.1233274.
- N. Yousefi, M. M. Gudarzi, Q. Zheng, S. H. Aboutalebi, F. Sharif and J.-K. Kim, Self-alignment and high electrical conductivity of ultralarge graphene oxide–polyurethane nanocomposites, J. Mater. Chem., 2012, 22, 12709–12717, 10.1039/C2JM30590A.
- S. N. Tripathi, P. Saini, D. Gupta and V. Choudhary, Electrical and mechanical properties of pmma/reduced graphene oxide nanocomposites prepared via in situ polymerization, J. Mater. Sci., 2013, 48(18), 6223–6232, DOI:10.1007/s10853-013-7420-8.
- M. H. Al-Saleh and S. Abdul Jawad, Graphene nanoplatelet-polystyrene nanocomposite: Dielectric and charge storage behaviors, J. Electron. Mater., 2016, 45(7), 3532–3539, DOI:10.1007/s11664-016-4505-6.
- A. Kausar and P. Bocchetta, Polymer/graphene nanocomposite membranes: Status and emerging prospects, J. Compos. Sci., 2022, 6(3), 76, DOI:10.3390/jcs6030076 , https://www.mdpi.com/2504-477X/6/3/76.
- J. Yin, G. Zhu and B. Deng, Graphene oxide (go) enhanced polyamide (pa) thin-film nanocomposite (tfn) membrane for water purification, Desalination, 2016, 379, 93–101, DOI:10.1016/j.desal.2015.11.001 , https://www.sciencedirect.com/science/article/pii/S001191641530103X.
- Y. Liu, Y. Zhang, L. Duan, W. Zhang, M. Su, Z. Sun and P. He, Polystyrene/graphene oxide nanocomposites synthesized via pickering polymerization, Prog. Org. Coat., 2016, 99, 23–31, DOI:10.1016/j.porgcoat.2016.04.034 , https://www.sciencedirect.com/science/article/pii/S030094401630008X.
- K. Suresh I., K. Chidambaram, V. Vinod, N. Rajender, R. M. Venkateswara and E. Miroslav, Synthesis, characterization and optical properties of graphene oxide–polystyrene nanocomposites, Polym. Adv. Technol., 2015, 26(3), 214–222, DOI:10.1002/pat.3435 , https://onlinelibrary.wiley.com/doi/abs/10.1002/pat.3435.
- R. Verdejo, M. M. Bernal, L. J. Romasanta and M. A. Lopez-Manchado, Graphene filled polymer nanocomposites, J. Mater. Chem., 2011, 21, 3301–3310, 10.1039/C0JM02708A.
- K. W. P. S. F. F. Shahamatifard, D. Rodrigue and F. Mighri, Natural rubber nanocomposites: effect of carbon black/multi-walled carbon nanotubes hybrid fillers on the mechanical properties and thermal conductivity, Polym.-Plast. Technol. Eng., 2021, 60(15), 1686–1696, DOI:10.1080/25740881.2021.1930044.
- M. Bhattacharya and A. K. Bhowmick, Synergy in carbon black-filled natural rubber nanocomposites. part i: Mechanical, dynamic mechanical properties, and morphology, J. Mater. Sci., 2010, 45(22), 6126–6138, DOI:10.1007/s10853-010-4699-6.
- M. Maiti, S. Sadhu and A. K. Bhowmick, Effect of carbon black on properties of rubber nanocomposites, J. Appl. Polym. Sci., 2005, 96(2), 443–451, DOI:10.1002/app.21463 , https://onlinelibrary.wiley.com/doi/abs/10.1002/app.21463.
- X. Wen, Y. Wang, J. Gong, J. Liu, N. Tian, Y. Wang, Z. Jiang, J. Qiu and T. Tang, Thermal and flammability properties of polypropylene/carbon black nanocomposites, Polym. Degrad. Stab., 2012, 97(5), 793–801, DOI:10.1016/j.polymdegradstab.2012.01.031 , https://www.sciencedirect.com/science/article/pii/S014139101200050X.
- Y.-H. Zhao, Y.-F. Zhang, Z.-K. Wu and S.-L. Bai, Synergic enhancement of thermal properties of polymer composites by graphene foam and carbon black, Composites, Part B, 2016, 84, 52–58, DOI:10.1016/j.compositesb.2015.08.074 , https://www.sciencedirect.com/science/article/pii/S1359836815005144.
- J. Hong, D. W. Park and S. E. Shim, Electrical, thermal, and rheological properties of carbon black and carbon nanotube dual filler-incorporated poly(dimethylsiloxane) nanocomposites, Macromol. Res., 2012, 20(5), 465–472, DOI:10.1007/s13233-012-0066-6.
- H. Shivashankar, K. A. Mathias, P. R. Sondar, M. H. Shrishail and S. M. Kulkarni, Study on low-frequency dielectric behavior of the carbon black/polymer nanocomposite, J. Mater. Sci.: Mater. Electron., 2021, 32(24), 28674–28686, DOI:10.1007/s10854-021-07242-1.
- K. Wu, T. Ting, G. Wang, W. Ho and C. Shih, Effect of carbon black content on electrical and microwave absorbing properties of polyaniline/carbon black nanocomposites, Polym. Degrad. Stab., 2008, 93(2), 483–488, DOI:10.1016/j.polymdegradstab.2007.11.009 , https://www.sciencedirect.com/science/article/pii/S0141391007003540.
- S. Zhou, A. N. Hrymak and M. R. Kamal, Effect of hybrid carbon fillers on the electrical and morphological properties of polystyrene nanocomposites in microinjection molding, Nanomaterials, 2018, 8(10), 779, DOI:10.3390/nano8100779 , https://www.mdpi.com/2079-4991/8/10/779.
- D. J. Growney, O. O. Mykhaylyk, L. Middlemiss, L. A. Fielding, M. J. Derry, N. Aragrag, G. D. Lamb and S. P. Armes, Is carbon black a suitable model colloidal substrate for diesel soot?, Langmuir, 2015, 31(38), 10358–10369 CrossRef CAS PubMed.
- T. Koga, T. Hashimoto, M. Takenaka, K. Aizawa, N. Amino, M. Nakamura, D. Yamaguchi and S. Koizumi, New insight into hierarchical structures of carbon black dispersed in polymer matrices: a combined small-angle scattering study, Macromolecules, 2008, 41(2), 453–464, DOI:10.1021/ma071867l.
- H.-J. Choi, M. S. Kim, D. Ahn, S. Y. Yeo and S. Lee, Electrical percolation threshold of carbon black in a polymer matrix and its application to antistatic fibre, Sci. Rep., 2019, 9(1), 6338, DOI:10.1038/s41598-019-42495-1.
- B. Hammouda, A new guinier-porod model, J. Appl. Crystallogr., 2010, 43(4), 716–719 CrossRef CAS.
- J. H. Bakker, A. L. Washington, S. R. Parnell, A. A. van Well, C. Pappas and W. G. Bouwman, Analysis of sesans data by numerical hankel transform implementation in sasview, J. Neutron Res., 2020, 22(1), 57–70 Search PubMed.
- R. Andersson, L. F. Van Heijkamp, I. M. De Schepper and W. G. Bouwman, Analysis of spin-echo small-angle neutron scattering measurements, J. Appl. Crystallogr., 2008, 41(5), 868–885 CrossRef CAS.
- S. R. Kline, Reduction and analysis of SANS and USANS data using IGOR Pro, J. Appl. Crystallogr., 2006, 39(6), 895–900 CrossRef CAS.
- J. Ilavsky and P. R. Jemian, Irena: tool suite for modeling and analysis of small-angle scattering, J. Appl. Crystallogr., 2009, 42(2), 347–353 CrossRef CAS.
- [cited 10th June 2020] [link]. URL https://usaxs.xray.aps.anl.gov/staff/ilavsky/irena.html.
- N. Berk and K. Hardman-Rhyne, Characterization of alumina powder using multiple small-angle neutron scattering. i. theory, J. Appl. Crystallogr., 1985, 18(6), 467–472 CrossRef CAS.
- E. M. Milner, N. T. Skipper, C. A. Howard, M. S. P. Shaffer, D. J. Buckley, K. A. Rahnejat, P. L. Cullen, R. K. Heenan, P. Lindner and R. Schweins, Structure and morphology of charged graphene platelets in solution by small-angle neutron scattering, J. Am. Chem. Soc., 2012, 134(20), 8302–8305, DOI:10.1021/ja211869u , pMID: 22574888.
- J. Wei, R. Atif, T. Vo and F. Inam, Graphene nanoplatelets in epoxy system: Dispersion, reaggregation, and mechanical properties of nanocomposites, J. Nanomater., 2015, 2015, 561742, DOI:10.1155/2015/561742.
| This journal is © The Royal Society of Chemistry 2024 |