Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding slow compression of frictional granular particles by network analysis†
Kianoosh
Taghizadeh
 *ab,
Stefan
Luding
*ab,
Stefan
Luding
 a,
Rituparna
Basak
c and
Lou
Kondic
a,
Rituparna
Basak
c and
Lou
Kondic
 c
c
aMSM, TFE-ET, MESA+, University of Twente, PO Box 217, 7500AE Enschede, The Netherlands. E-mail: k.taghizadehbajgirani@utwente.nl
bInstitute of Applied Mechanics (CE), SC SimTech, University of Stuttgart, Germany
cDepartment of Mathematical Sciences, New Jersey Institute of Technology, University Heights, Newark, NJ 07102, USA. E-mail: kondic@njit.edu
First published on 2nd August 2024
Abstract
We consider frictional granular packings exposed to quasi-static compression rates, with a focus on systems above the jamming transition. For frictionless packings, earlier work (S. Luding et al., Soft Matter, 2022, 18(9), 1868–1884) has uncovered that the system evolution/response involves smooth evolution phases, interrupted by fast transitions (events). The general finding is that the force networks’ static quantities correlate closely with the pressure, while their evolution resembles the kinetic energy for both frictionless and frictional packings. The former represents reversible (elastic) particle deformations with affine and non-affine components, whereas the latter also involves much stronger, irreversible (plastic) rearrangements of the packings. Events are associated with jumps in the overall kinetic energy as well as dramatic changes in the force networks describing the particle micro-structure. The frictional nature of particle interactions affects both their frequency and the relevant time scale magnitude. For intermediate friction, events are often followed by an unexpected slow-down during which the kinetic energy drops below its average value. We find that these slow-downs are associated with a significant decrease in the non-affine dynamics of the particles, and are strongly influenced by friction. Friction modifies the structure of the networks, both through the typical number of contacts of a particle, and by influencing topological features of the resulting networks. Furthermore, friction modifies the dynamics of the networks, with larger values of friction leading to smaller changes of the more stable networks.
1 Introduction
Particulate materials exist in large quantities in nature and many industrial processes deal with materials that are particulate in structure.1 Granular materials are relevant for a wide range of materials such as pharmaceutical powders, agricultural products, sands and gravels, or chemical pellets. Despite their prevalence in applications, there is still a large discrepancy between results predicted by analytical or numerical solutions and the behavior observed in experiments.2,3One major challenge is that granular assemblies, e.g., soil, can both flow like a fluid or be static like a solid, i.e., when granular materials experience enough stress, they can start to behave in a fluid-like manner. Unlike fluid–solid coupling, where two different materials in different states come together, in particulate systems their fluid–solid-state behavior already occurs for a single material. The coexistence of multiple states and their transitions are among the ultimate research challenges in mechanics and physics. Unlike solid–fluid coupled problems, the discrete nature of particulate materials leads to rich unpredictable behavior, i.e., a given particulate material can behave in both a fluid-like or a solid-like manner.4–6 Depending on the situation (e.g., process conditions, energy input), the material will achieve one state or the other. One high-profile disastrous example (of many varied cases) is a landslide, which is caused by a transition in state from solid (desired) to fluid (undesired) – and back to solid at the terminal run-out;7–9 or in process engineering, transport problems (silo clogging or collapse10–12) occur due to the coexistence of, and transitions between states.
Alongside the repulsive, dissipative (and frictional) nature of their interactions,13 crucial properties influencing particle behavior involve inter-particle friction and cohesion, mixtures of different species,14–16 particle shape, size distribution, and anisotropy. Friction serves as one important controlling force that influences the transition from the static phase, where particles are relatively stationary, to the dynamic phase, where particles start moving and interacting more vigorously. Friction between particles creates resistance against movement and acts as a threshold that must be overcome for particles to transition from a state of rest to motion. The phase transition from fluid to solid17–20 (stagnation/jamming) can be caused directly by friction and other aforementioned properties, which tend to slow down motion. In contrast, the transition from solid to fluid (start of flow/unjamming) is due to failure and instability21 when (for example) friction is not strong enough to avoid flow and various other mechanisms kick in.
When the considered systems are exposed to a confining pressure, their response involves enduring contacts among particles, which results in the spontaneous formation of mesoscale force networks,22–27 which are known to be related to the system macroscopic response.28,29 Forces tend to be transmitted along so-called ‘force chains’,26 which continuously form and break, resulting in substantial variations in force magnitudes.30 These exhibit a spatiotemporal nature, related to significant stress fluctuations.31 In such a confined regime, the system evolution involves evolving networks32–35 that could be system-spanning or fragile.36 Even for perhaps the simplest case of frictionless systems exposed to quasi-static compression, the system evolution is far from simple.37–42 Such systems were considered in our earlier work,29 which uncovered that smooth compression was interrupted by fast transitions (events) with rapid rearrangements of the particles and therefore of contact and force networks. Despite attempts to discover the nature of granular fluctuations at the mesoscale,29,43,44 the effect of friction in controlling transitions for dense granular assemblies remains an open question.
Discrete element method (DEM)45 is a powerful tool offering deeper insights into the micro-mechanics of granular packings that are difficult to obtain experimentally. DEM allows for inspecting and understanding the influence of microscopic contact properties of its constituents on the bulk behavior. To bridge between the particle scale, considered by DEM-based simulations, and the system scale, one needs to use other methods that consider meso-scale organization of the particle interactions. Network-based approaches, such as the ones discussed in ref. 46–48, among others, provide new insights into the mechanisms that govern the statics and dynamics of granular materials. Such approaches provide quantitative descriptions of how the structure of a dense granular material evolves as a system deforms under external loads (such as those induced by compression, shear, tapping, or impact), and can help to describe complex aspects of granular flows.
Our research focuses on the influence of friction on the system response to quasi-static compression49 building on studies of frictionless systems.29,43,44 Some of the questions that we ask are whether the fast events found for frictionless systems are still present and, if so, how the presence of friction influences them. Another related question is whether the presence of even very weak friction modifies the system evolution in general, and the properties of the events in particular. We will answer these (and other) questions by consideration of both classical measures, such as kinetic energy of the evolving packings, and by carrying out the computational topology-based persistence analysis48 that allows us to quantify statics and dynamics of the force networks. Such ability turns out to be particularly useful for developing a better understanding of the influence of friction on the force networks.
The paper is organized as follows. Discrete element method and computational topology based method used for quantifying force networks are introduced in Section 2. Section 3 contains the results obtained during sample compression. Further, a regime is selected from the preparation path for further detailed analysis. Then, in Section 4 we discuss the results obtained by applying persistent analysis to the considered system, as well as by developing the relation of the quantities derived based on persistence analysis to classical measures, such as pressure, kinetic energy, and coordination number. Section 5 is devoted to understanding the effect of inter-particle friction on the time-averaged quantities. Finally, conclusions are given in Section 6.
2 Methods
2.1 Discrete element method
The discrete particle modeling approach towards a microscopic understanding of macroscopic particulate material behavior is the so-called discrete element method (DEM),50–53 a numerical scheme originally formulated and developed by Cundall et al.45DEM is a straightforward algorithm to solve the translational and rotational equations of motion for a system of many interacting particles:
 | (1) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i, velocity
i, velocity  , acceleration
, acceleration  , and angular velocity
, and angular velocity ![[small omega, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13e.gif) i.
i.
There are three kinds of forces: (i) the volume forces (i.e. due to gravity acceleration, ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) ) are neglected in this study; (ii) the “background” damping forces with dissipation coefficients γb and γbr mimic energy loss due to viscous, velocity dependent drag on each particle, as by a background medium; and (iii) the contact forces with other particles:
) are neglected in this study; (ii) the “background” damping forces with dissipation coefficients γb and γbr mimic energy loss due to viscous, velocity dependent drag on each particle, as by a background medium; and (iii) the contact forces with other particles: 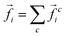 , as well as the torques:
, as well as the torques: 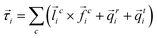 , where
, where ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) ci is the branch vector. The additional torques due to rolling and torsion,
ci is the branch vector. The additional torques due to rolling and torsion, ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ri,
ri, ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ti, are neglected.
ti, are neglected.
At the basis of our simple DEM, the contact force laws relate the interaction forces to the overlap/deformation of two particles, decomposed into normal and tangential components as: ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) ci =
ci = ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) n +
n + ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) t. With given normal and tangential forces acting on all contacts, c, one can numerically integrate the equations of motion with time-step Δt, to obtain the positions of the particles as a function of time.
t. With given normal and tangential forces acting on all contacts, c, one can numerically integrate the equations of motion with time-step Δt, to obtain the positions of the particles as a function of time.
δn = (ri + rj) − (![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i − i − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) j)· j)·![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) > 0, > 0, | (2) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) = (
= (![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i −
i − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) j)/|
j)/|![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i −
i − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) j| is the unit vector pointing from particle j to particle i.
j| is the unit vector pointing from particle j to particle i.
The most simple contact model in DEM is a linear spring-dashpot visco-elastic force magnitude:50,52,54–56
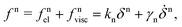 | (3) |
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) n = fn
n = fn![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) , where kn is the elastic spring stiffness and γn is the viscous dashpot damping constant, causing dissipation proportional to the relative velocity,57
, where kn is the elastic spring stiffness and γn is the viscous dashpot damping constant, causing dissipation proportional to the relative velocity,57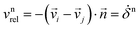 .
.
In this formulation of DEM, each contact force is considered independently.58–60 This is an appropriate approximation for relatively small deformations, considering only binary pair contact interactions.
When two contacting surfaces are subjected to an increasing tangential displacement, δt, then relative slip is initiated at the perimeter and progresses inward over an annular area of the contact surface.
An approach based on the constant normal force solution of Mindlin was proposed already by Tsuji et al.65 Analogously to the normal force, the tangential force involves a linear (tangential) spring with stiffness kt and a viscous damping with γt, similar to the model used in ref. 58, 64 and 66. The linear visco-elastic tangential test force magnitude:
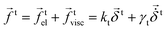 | (4) |
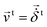 .
.
The elastic tangential displacement, 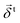 , is obtained by integrating the relative tangential velocity vector during elastic deformations, see ref. 64, 67 and 68. The test tangential force in eqn (4) is subjected to Coulomb's particle contact friction criterion. In simple words, dynamic friction happens when the tangential component of force, ft ≥ μdfn, while elastic, static friction is active otherwise, ft ≤ μsfn, where we use μ = μd = μs – details are given in ref. 64.
, is obtained by integrating the relative tangential velocity vector during elastic deformations, see ref. 64, 67 and 68. The test tangential force in eqn (4) is subjected to Coulomb's particle contact friction criterion. In simple words, dynamic friction happens when the tangential component of force, ft ≥ μdfn, while elastic, static friction is active otherwise, ft ≤ μsfn, where we use μ = μd = μs – details are given in ref. 64.
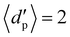 , and maximum to minimum size distribution width, w = dmaxp/dminp = 3, from a homogeneous size distribution, are placed in a 3D periodic box. The primed parameters given in the following, e.g., density
, and maximum to minimum size distribution width, w = dmaxp/dminp = 3, from a homogeneous size distribution, are placed in a 3D periodic box. The primed parameters given in the following, e.g., density 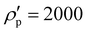 or
or 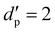 , are dimensional (ESI† units implied like mm, kg m−3 and μs) and used in the simulations shown in this paper. For non-dimensionalisation, as presented in the rest of the paper, units are chosen based on particle properties. Here, the unit of length is chosen as the mean particle diameter,
, are dimensional (ESI† units implied like mm, kg m−3 and μs) and used in the simulations shown in this paper. For non-dimensionalisation, as presented in the rest of the paper, units are chosen based on particle properties. Here, the unit of length is chosen as the mean particle diameter, 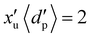 , so that
, so that 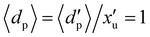 is the dimensionless diameter. The second unit is the material density,
is the dimensionless diameter. The second unit is the material density, 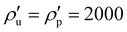 , so that one has a dimensionless density, ρ = 1, and thus the unit of mass,
, so that one has a dimensionless density, ρ = 1, and thus the unit of mass, 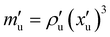 , i.e., the particle mass, mp = (π/6). For the third unit, one has several choices, where we adopt here the units of elastic stress,
, i.e., the particle mass, mp = (π/6). For the third unit, one has several choices, where we adopt here the units of elastic stress, 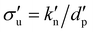 , with the linear normal contact stiffness,
, with the linear normal contact stiffness, 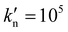 , which yields the dimensionless stress
, which yields the dimensionless stress 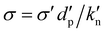 , and results in the unit of time
, and results in the unit of time 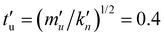 . In the chosen units, the dimensionless linear stiffness is
. In the chosen units, the dimensionless linear stiffness is 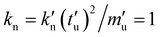 , and the linear contact viscosity,
, and the linear contact viscosity, 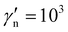 , becomes
, becomes 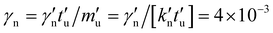 , with background viscosity,
, with background viscosity, 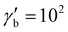 , resulting in
, resulting in 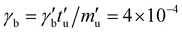 . For the tangential forces, the parameters are: various values of μ ∈ [0
. For the tangential forces, the parameters are: various values of μ ∈ [0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1], kt = kt/kn = 0.2, and γt/γn = 0.2 (γt = 8 × 10−4), and γbr/γb = 0.2 (γbr = 8 × 10−5); in this study, rolling and torsion resistances are not considered.
1], kt = kt/kn = 0.2, and γt/γn = 0.2 (γt = 8 × 10−4), and γbr/γb = 0.2 (γbr = 8 × 10−5); in this study, rolling and torsion resistances are not considered.
The consequent physically relevant properties are the restitution coefficient r = exp(−ηntc) ≈ 0.855, with damping factor ηn = γn/(2m12), reduced mass, m12 = 0.063, and contact duration, 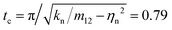 , (or
, (or 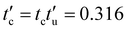 ), all considered for a contact between the largest and the smallest particle, with a larger viscous damping time-scale, tv = 2m12/γn ≈ 5, and even a larger background damping time-scale tb = 2m12/γb ≈ 50. Note that this choice of units corresponds to setting
), all considered for a contact between the largest and the smallest particle, with a larger viscous damping time-scale, tv = 2m12/γn ≈ 5, and even a larger background damping time-scale tb = 2m12/γb ≈ 50. Note that this choice of units corresponds to setting 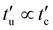 , leading to collapsing different stiffness simulations in the elastic regime.19,69
, leading to collapsing different stiffness simulations in the elastic regime.19,69
To prepare samples, first, particles are randomly placed in a 3D simulation box, with a system size equal in all directions (L = Lx = Ly = Lz), with a periodic boundary condition at a low volume fraction (ϕ ≈ 0.5). Second, the simulation box is compressed homogeneously,43 from all directions, up to volume fraction ϕ = 0.82. Recognizing that conventional DEM may not accurately capture granular packings at high-volume fractions,58,70–72 we focus in this work on volume fractions just slightly above jamming. In particular, for topological analysis, we have chosen a pressure corresponding to approximately 2% deformation.29,43 In this study, the focus is on isotropic compression, where the same compression rate is applied in all directions, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v =
v = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) xx =
xx = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) yy =
yy = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz. Simulations are carried out using widely different isotropic strain rates,
zz. Simulations are carried out using widely different isotropic strain rates, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v ∈ [10−5:10−9] A typical (isotropic) inertial number for one of the moderately slow rates (
v ∈ [10−5:10−9] A typical (isotropic) inertial number for one of the moderately slow rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v ≈ 10−7) is of the order of 10−5, for small p ≈ 10−4, which confirms that the simulations are in the quasi-static, rate-independent regime.
v ≈ 10−7) is of the order of 10−5, for small p ≈ 10−4, which confirms that the simulations are in the quasi-static, rate-independent regime.
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v(L/2))2, with total mass M, system size L, and isotropic-strain rate
v(L/2))2, with total mass M, system size L, and isotropic-strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v.
v.
The kinetic energy due to affine displacements is a system size-dependent (extensive) energy, scaling with system size, Ea/M ∝ L2, for details see ref. 43. Therefore, it is disregarded in the present paper. Instead, we focus only on the part of the kinetic energy caused by (i) velocity fluctuations and (ii) non-affine displacements. This part of the kinetic energy, which we denote by Ek in what follows, is proportional to the usual granular temperature, TG, as Ek = (3/2)TG/M, but notably contains two vastly different contributions (i) and (ii), see ref. 43.
2.2 Persistent diagrams and derived measures
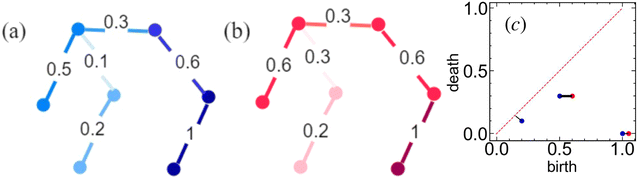
Persistent diagrams, PDs, are obtained by application of the tools of persistent homology to an object, which in our case is a force network describing interactions between granular particles.73–76 In simple terms, persistent homology could be thought of as a mapping from the (weighted) network describing particle interactions to one or more persistent diagrams. The number of PDs is equal to the number of physical dimensions, with PD β0 corresponding to open components (that do not form loops), PD β1 to loops, and PD β2 to holes in three dimensional space, not commonly present in force networks for granular systems, and thus not considered further.In our previous work,29 we constructed PDs for frictionless granular systems, including a toy example describing how to construct PDs. A simple two dimensional network can contain both components (vague analogy to so-called ‘force chains’) and loops (analogy to cycles). Here we provide another toy example that focuses on an even simpler configuration (networks without loops), and use this network to describe some additional concepts needed for the present study.
Fig. 1(a) and (b) shows two networks. In this representation, nodes (circles) can be interpreted as particle centers, while edges represent the branch vectors of interacting particles (in the context of this toy example, we do not discuss normal and tangential forces separately). For simplicity, we choose two networks with the same connectivity, but different forces (in the context of granular physics, we are considering a single contact network supporting two force networks).
The PDs shown in Fig. 1(c) represent the generators associated with the networks in (a) and (b) by point clouds; in our toy example, the number of points in each cloud is very small; for the real networks considered later in the paper, the number of points could reach hundreds or thousands. These points are obtained by thresholding from above (going from large to small forces) and by observing at which force magnitude a given component appears (is born) and at which force it merges with another component (it dies). By convention, the component that is born first dies last, and in particular the component that corresponds to the largest threshold level (1 in our example) never dies (for the two considered PDs, the two generators with coordinates (1,0)). Simple diagrams as shown in (a and b) lead to simple PDs; for the present networks, PDs have only three (a) and two (b) generators. For example, the blue generator with coordinates (0.5, 0.3) corresponds to the component marked by 0.5 in (a); this component connects to the (older) component (1) at the level 0.3.
One approach towards quantifying a PD is to describe its structure in terms of its global features, such as the number of generators, NG, and their typical distance from the diagonal (generators very close to the diagonal ‘live’ for very short force range and therefore do not contribute significantly to the force network structure). The measures used later in the paper are based on the life-span, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = B–D (where B and D are birth and death coordinates, respectively) of each generator, and then total persistence, TP, defined by
= B–D (where B and D are birth and death coordinates, respectively) of each generator, and then total persistence, TP, defined by 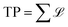 , where the sum goes over all generators. More elaborate measures could be defined of course, but for our purposes the specified ones are sufficient. For our toy examples in Fig. 1, we have for (a) NG = 3, TP = 1.3, and for (b) NG = 2, TP = 1.3.
, where the sum goes over all generators. More elaborate measures could be defined of course, but for our purposes the specified ones are sufficient. For our toy examples in Fig. 1, we have for (a) NG = 3, TP = 1.3, and for (b) NG = 2, TP = 1.3.
The most important features of the PDs (discussed in more detail in29) are as follows: stability (small changes in networks lead to small changes in the corresponding PDs), capture of the most important topological properties of the original networks, and data reduction (point clouds, PDs, could be presented in much more concise manner than the original networks). Note that data reduction leads to some information loss, however, for all practical purposes, the main features of the underlying networks are accurately presented by the PDs.48 Another important property of PDs is that they live in a metric space, and therefore can be compared, see48 for further discussion. This fact is crucial since it allows for the comparison of the PDs and, therefore, by extension, for the comparison of the underlying networks.
The comparison of two PDs can be carried out by defining the concept of distance (difference) between the diagrams. Loosely speaking (see48 for precise definition), the distance between two diagrams measures the minimum of the sum of all the Euclidian distances by which the generators of one PD need to be translated to make them match the generators of the other PD. We note that finding matching pairs is the most computationally intensive task involved in computing the distances. The exact value of a distance depends on the norm used. In this paper, we consider two norms and associated distances: Wasserstein q distance, where q stands for the norm being used (we use q = 2, leading to the L2 norm), and also the bottleneck distance, which records only the maximum distance between the generators in any of the matching pairs (therefore corresponding to the L∞ norm). Computing the distances is computationally expensive if PDs contain many generators since one needs to identify all the matching pairs. If the number of generators is not the same between two PDs being compared, the extra generator(s) are matched to the diagonal. The toy example in Fig. 1(a) contains such a generator at (0.2, 0.1). For Fig. 1, the Wasserstein 2 distance, 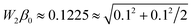 , and the bottleneck distance, Bβ0 = 0.1 (shown by the thick line in (c)).
, and the bottleneck distance, Bβ0 = 0.1 (shown by the thick line in (c)).
The comparison of the numerical values of W2β0 and Bβ0 carries some relevant information, as it quantifies the importance of the largest difference between two probability distributions (and, by extension, two networks); for our toy example, Bβ0/W2β0 ≈ 0.1/0.1225 ≈ 1, and therefore the distance between two networks is dominated by the single largest distance between any two matching points. In our toy example, for simplicity, we focus only on β0 PDs (there are no loops in the networks shown in Fig. 1(a) and (b)). The distance between the loop structures is formulated in a similar manner, which we do not discuss here for brevity. Interested readers may find more information in29 and much more in-depth discussion in.48 The calculations of both PDs and distances in the present paper are carried out using GUDHI library.77
3 General results: full compression branch
In this section, we discuss the response of prepared samples under varying friction coefficients, μ, using classical measures as well as the results of persistence analysis. In the following Section 4, we will focus on a small window of the data and discuss insight from the force network PDs and their relation to the classical measures. Finally, in Section 5 we consider window averaged results showing how inter-particle contact friction influences the force networks.3.1 Classical measures from DEM
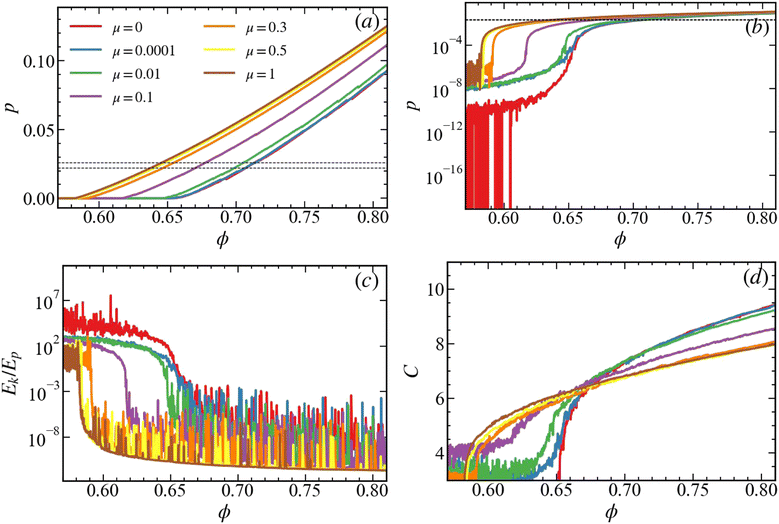
Fig. 2(a) shows the dimensionless pressure, p, for isotropic compression from low ϕ below jamming (where the phase transition from liquid- to solid-like behavior occurs18,36,44,54,78–80), ϕ0 = 0.50, up to ϕmax = 0.82 (isotropic loading path), for samples with different contact frictions, μ, starting all from the same initial configuration at ϕ0, obtained using μ = 0.29As expected, we see an increase in pressure as the samples are compacted above jamming, while for a given volume fraction, the pressure increases as μ increases. Fig. 2(b) shows the same data in logscale, highlighting the dynamics and fluctuations below jamming as well as a sharp increase of pressure at different ϕJ(μ). The dotted lines indicate the range of pressure on which we zoom-in later in Section 4.
Fig. 2(c) shows the ratio of kinetic to potential energy (Ek/Ep) for the loading path. Potential energy contains both normal and tangential contributions (Ep = Enp + Etp) since friction is active. The rotational energy ratio (Er/Ep) shows the same pattern as the kinetic energy with relatively one/two magnitude smaller values (data not shown, it does not add new information). For larger μ, at a given volume fraction above jamming, the energy ratio is smaller due to the lower jamming density and for two other reasons that will be explored further below: larger μ leads to (1) relatively more dissipation, and (2) higher tangential components of inter-particle forces, which stabilize the packings, decrease the mobility of the particles and correspondingly the kinetic energy. Below jamming, however, the systems, compressed under constant strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v = 10−7 are in the collisional regime, featuring large fluctuations: pressure increases with μ, but the energy ratio systematically decreases.
v = 10−7 are in the collisional regime, featuring large fluctuations: pressure increases with μ, but the energy ratio systematically decreases.
The coordination number shown in Fig. 2(d) is defined as the average number of contacts per particle (C = 2M/N, where M is the total number of contacts involving two particles and N is the total number of particles). It shows strong fluctuations before jamming with no evident trend since collisions dominate these systems below jamming. On the other hand, above jamming all curves obey a similar power law as reported in ref. 36, 80 and 81, where it has been shown that the jamming transition occurs at the isostatic point, where the static pressure is no longer zero,18,36,82 or where other features change.83,84 The macroscopic quantity plots (Fig. 2(a)–(d)) consistently show that as the contact friction increases, the jamming packing fraction, ϕJ(μ), decreases,85 see Table 1. Finally, we note that the level of fluctuations below jamming non-systematically changes with increasing friction from large (μ = 0) via moderate back to large (μ ≥ 0.3); the explanation of this effect goes beyond the scope of the present study.
| μ | ϕ J | ϕ(pz) | E k(pz)/Ep(pz) | C(pz) |
|---|---|---|---|---|
| 0 | 0.652 | 0.707 | 77 × 10−10 | 7.72 |
| 10−4 | 0.650 | 0.706 | 20 × 10−10 | 7.71 |
| 10−3 | 0.647 | 0.705 | 10 × 10−10 | 7.69 |
| 0.01 | 0.643 | 0.698 | 3.4 × 10−10 | 7.46 |
| 0.1 | 0.614 | 0.672 | 1.6 × 10−10 | 6.78 |
| 0.3 | 0.591 | 0.646 | 1.1 × 10−10 | 6.14 |
| 0.5 | 0.584 | 0.640 | 0.6 × 10−10 | 5.91 |
| 1 | 0.582 | 0.638 | 0.3 × 10−10 | 5.90 |
We note that in the previous work29 instead of C we used reduced coordination number, C* = C/(1 − ϕr), where ϕr is the fraction of rattlers, defined here as the particles with less than 4 contacts. C* is a measure commonly used for frictionless systems, and theoretically at the jamming point is exactly 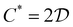 where
where 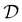 is a system dimension.86–88 When friction and, consequently, tangential contact forces are involved, smaller coordination numbers are expected. For frictional particles considered here, we will see that C is a more appropriate quantity to use, as it helps in explaining the scaling of the results when friction is modified.
is a system dimension.86–88 When friction and, consequently, tangential contact forces are involved, smaller coordination numbers are expected. For frictional particles considered here, we will see that C is a more appropriate quantity to use, as it helps in explaining the scaling of the results when friction is modified.
3.2 Persistence measures from force networks
We provide a brief description of the influence of friction between particles on the overall behavior of packings from a persistence analysis point of view. Fig. 3 shows the results for TP0 of normal, fn, and tangential, ft, forces of the same samples as discussed in Fig. 2. The first observation is that TP0 behaves similarly to the pressure, as reported previously for frictionless packings29: these measures systematically increase with μ, as in Fig. 2(b), including the jamming transition as a sharp increase (in log-scale). Regarding the numerical values, we note that while a comparison between the measures for components does not contain easy to interpret information, the numerical values for TP0 can be compared between different values of μ, or between normal and tangential forces for components. While the TP0 measure based on normal forces converges for different μ for large ϕ, the tangential forces based TP0 measures behave qualitatively differently: due to the Coulomb coefficient of contact friction, the tangential forces are proportional to μ, which is reflected in the magnitude of the corresponding TP0 measures. A similar conclusion was drawn for the results of TP1 of normal, fn, and tangential, ft, forces of the same samples, see Appendix A for further details. | ||
| Fig. 3 (a) TP0n and (b) TP0t plotted against volume fraction, ϕ, for samples prepared with different friction coefficients, μ. | ||
4 Results on a fast time scale (events)
4.1 Events: simulations setup
Consistently with the literature,83,89Fig. 2 shows that the jamming volume fraction is strongly influenced by friction between the grains. Thus, samples at the same volume fraction, ϕ, do neither feature similar microscopic (e.g. coordination number) nor macroscopic (e.g. pressure) properties, since they differ significantly in their distance to jamming.90,91 Therefore, it is not appropriate to compare packings of different materials with different values of μ at the same ϕ. Instead, we use a given value, pz, of pressure as a useful variable for the comparison of structures/packings. The crucial aspect is that at the same pressure, the distance to the jamming point remains consistently similar ϕ(pz) − ϕJ ≈ const. for all friction coefficients.80,92After sample preparation (loading), a configuration at a small pressure pz = 0.022, corresponding to a small deformation, is chosen to zoom-in – the same pz for all samples. In earlier studies on frictionless systems,29,43,44,80 we checked and confirmed that the choice of pz does not change the qualitative conclusions. In particular, we studied packings at pz values of 0.002, 0.01, 0.022, and 0.06, covering a range from very loose to highly dense packings. Since the qualitative observations and conclusions remain consistent across all cases tested for different μ, we present the representative results for pz = 0.022. Table 1 summarises the DEM results of packings at jamming and at pz. These configurations are then further compressed, from pz to pz + 0.004 (dotted lines in Fig. 2(a) and (b)), with a smaller isotropic strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v = 10−8, and a higher output frequency.
v = 10−8, and a higher output frequency.
We note in passing a few technical issues related to computational implementation. Given that our algorithm is second order correct for the elastic, conservative forces, but only first order accurate for dissipation and rotation, loss of precision may occur. Another possible issue related to restarts mentioned above is that our code is not storing binary (full precision) but only 15/16 digits. To address these concerns, we have verified for a number of representative cases that loss of precision appears very rarely, and only around events with considerable jumps in energy by more than eight to ten orders of magnitude. Therefore, we are confident that numerical precision does not change any of our conclusions concerning the statistics/occurrence of events.
4.2 Events: relaxation mechanism
Fig. 4 depicts the kinetic to potential energy ratio (Ek/Ep) in the chosen pressure window, for systems with different values of μ. The evolution is not smooth:93,94 it proceeds along the base-line, interrupted by discrete ‘events’, characterized by large changes in the energy ratio, associated with mostly small drops in pressure, as discussed earlier in the context of frictionless simulations.29 A characteristic feature is that as μ increases, both the base-line value and the number of events decrease, in particular, there is only one event for μ = 1 in this pressure window (further inspection finds a very limited number of events on the whole loading branch). While the small friction data are very noisy around their base-lines, they are almost perfectly flat for large μ. The decrease in the number of events as μ increases could be explained, at least in principle, by the increased importance of the tangential forces that reduce the number of degrees of freedom of particles. Although the coordination number of samples with higher friction is lower, higher resistance to motion due to tangential forces makes particle rearrangements more difficult.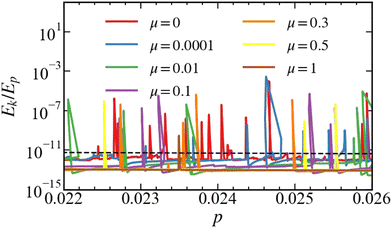 | ||
| Fig. 4 Kinetic to potential energy ratio, Ek/Ep, plotted against pressure, p, for samples prepared with different values of friction, μ, for the pressure range from pz = 0.022 up to 0.026. The dashed line represents the affine kinetic energy (defined in Section 2.1.4 and ref. 43) ratio, Ea/Ep. Note that for considered system size, the base-lines for the non-affine fluctuation kinetic energy ratio, are small, from Ek/Ea ≃ 0.034 for μ = 0 down to Ek/Ea ≃ 0.029 for μ = 1. | ||
For 0 < μ ≲ 0.3, the presence of friction affects the properties of the events qualitatively. We observe two relaxation periods after each event: first, a rapid decay of the energy ratio Ek/Ep down to below its plateau value, and second, a slower increase back to the base-line. Surprisingly, for μ ≳ 0.3, the events do not show such undershoots. Further analysis of data (details not shown for brevity) suggests that they take place on a short time scale, similarly to the events seen for μ = 0. The details of the relaxation periods are further discussed in what follows.
To support the hypothesis that events correspond to re-structuring of the packing, Fig. 5 shows gained and lost contacts, obtained by comparing consecutive snapshots, so to provide an insight into the microstructure evolution during loading. In Fig. 5(a), red/blue curves show gained/lost contacts; while the contacts are slowly formed during smooth parts of loading, the events result in sudden and significant losses of many contacts. Fig. 5(b) provides a visual comparison of the microstructure before and after an event, represented by points A and B in Fig. 5(a). In this comparison, particles gaining new contacts are shown in red, while particles losing contacts are shown in blue. This analysis confirms the occurrence of large, irreversible events, such that the system transitions from one equilibrium state (A) to another (B) to establish a new equilibrium. These findings are consistent with previous studies.85,95–98
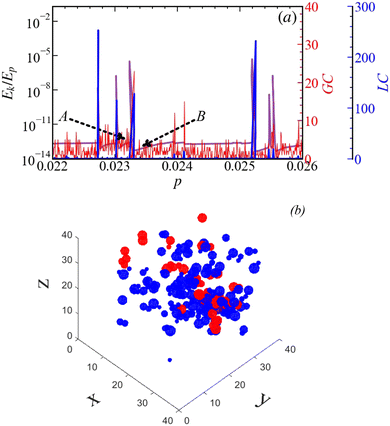 | ||
| Fig. 5 (a) Gained contacts (GC, red data) and lost contacts (LC, blue data) of the sample with friction μ = 0.1, on top of the energy ratio (purple data), plotted against pressure, for the same window as in Fig. 4. (b) Red and blue particles depict the creation of new contacts and the loss of contacts when two frames are considered: before (A) and after (B) one large event (frames A, B marked in (a)); around 25 contacts are gained, and around 150 are lost. | ||
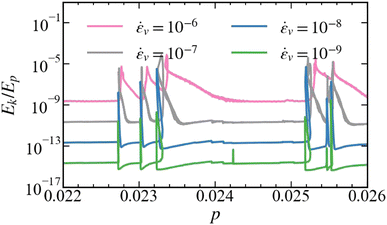
Returning now to the relaxation following the events, Fig. 6 shows Ek/Ep for given μ = 0.1 and for four strain rates. The events are followed by a dissipation of the kinetic energy which appears exponential in time, as Ek/Ep ∝ exp(−t/tr), with dissipative relaxation time tr. Careful analysis of the data shows that tr is essentially strain rate independent (recall that the rate of change of pressure is proportional to the strain rate). Along the base-lines, the kinetic energy ratio relates the non-affine continuously created kinetic energy to the stored elastic, potential energy, as Ek/Ep ∝ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v2. The slower the compression, the smaller the base-line value of the energy ratio. During events, the energy ratio increases by orders of magnitude, with peak size dependent on the specific event, but not directly on the strain rate, contrary to the base-line value.
v2. The slower the compression, the smaller the base-line value of the energy ratio. During events, the energy ratio increases by orders of magnitude, with peak size dependent on the specific event, but not directly on the strain rate, contrary to the base-line value.
4.3 Events: undershoot relaxation
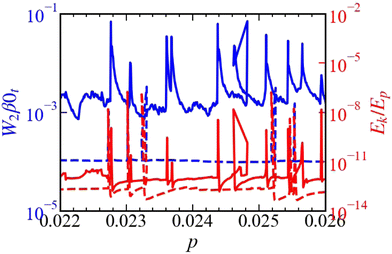
As shown in Fig. 5, some particles lose their contacts following a rearrangement (event). The use of a visco-elastic contact model means that the particles involved in these rearrangements are primarily responsible for dissipating kinetic energy. This leads to undershoots below the base-line of the energy ratio after such events, as illustrated in Fig. 6. These undershoots occur only when the system compresses slowly enough, allowing particles sufficient time to relax to their most stable configuration before further compression occurs beyond this minimum. However, confirming whether this dissipation is localized solely to those particles or if other factors contribute to the dissipation of the assemblies requires further investigation. This aspect falls outside the scope of the current research.We note that the undershoots relax differently from the exponential decay: their decay is governed by strain (pressure), not by strain rate (time). To gain better insight into this difference, we proceed by considering the properties of the particle contacts after the events, focusing in particular on the influence of the friction coefficient.
The new, surprising insight from the data is that during each event, the fraction of sliding contacts Pslide, as shown in Fig. 7, drops considerably, followed by a qualitatively different relaxation to its level before the event for different values of μ. This level is strongly μ-dependent, with Pslide ≃ 1 for small μ down to Pslide ≈ 0.01 for μ = 1. Regarding the relaxation, our basic interpretation is the following: during events, the dynamic, non-affine motion is dissipated on the time-scale tr. During this time, many contacts break, and some new contacts form. Most of the contacts that break are sliding, and the newly formed contacts are mostly stable, non-sliding. While compression continues, some of these stable contacts are shifted towards their fully activated, sliding limit by tangential deformation. Fig. 7 shows that this mechanism is strain driven, in contrast to the exponential decay, which is time-driven. The stronger the friction, the more stable are the packings and the longer it can take until the static contacts reach their sliding limit.
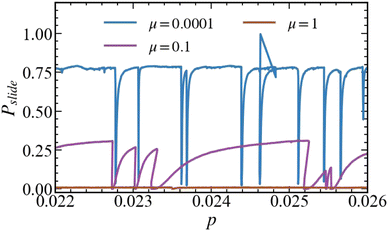 | ||
Fig. 7 Probability of sliding contacts, Pslide, for samples with friction coefficient μ = 0.0001, 0.1, and 1, plotted against pressure, for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v = 10−8. v = 10−8. | ||
More quantitatively, after an event, the fraction of sliding contacts Pslide increases with strain to recover the level preceding the event. Therefore, the dimensionless dissipative relaxation time, the ratio, τr = tr![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) v, of strain rate and relaxation rate, determines whether the system undershoots or not. Only if τr is sufficiently small, can one observe the undershoots. This explains why they show up only for strong enough dissipation and for slow enough strain rate. While for μ = 0, with Pslide = 1, no undershoots are observed, for very weak friction, Pslide ≲ 1, some undershoots appear, for intermediate friction, the undershoots are most pronounced, and for large friction, μ = 1, the networks are stable to the degree that no undershoots are observed, for the cases tested.
v, of strain rate and relaxation rate, determines whether the system undershoots or not. Only if τr is sufficiently small, can one observe the undershoots. This explains why they show up only for strong enough dissipation and for slow enough strain rate. While for μ = 0, with Pslide = 1, no undershoots are observed, for very weak friction, Pslide ≲ 1, some undershoots appear, for intermediate friction, the undershoots are most pronounced, and for large friction, μ = 1, the networks are stable to the degree that no undershoots are observed, for the cases tested.
4.4 Events: persistence dynamic measures
We continue with the discussion of the distances between the frames, using the concepts discussed in Section 2 (essentially, force networks corresponding to successive frames are compared; W2 is one of the measures quantifying this difference). Fig. 8 shows the W2 distance between the force networks, quantified by W2β0n, as discussed in Section 2 for different values of friction coefficient, μ. In this and the following figures, the forces are normalized to remove their relative magnitude. The normal forces are normalized by the average force, defined by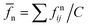 , producing normalized force
, producing normalized force 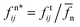 , where the sum goes over all contacts. The tangential forces, ftij, are normalized by μ
, where the sum goes over all contacts. The tangential forces, ftij, are normalized by μ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) n, so that
n, so that 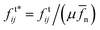 . We observe that, due to force scaling, the results for the normal forces, Fig. 8(a) and (b) essentially collapse, with smaller values of μ producing slightly larger W2 magnitudes. This trend is consistent with the Ek/Ep results shown in Fig. 4.
. We observe that, due to force scaling, the results for the normal forces, Fig. 8(a) and (b) essentially collapse, with smaller values of μ producing slightly larger W2 magnitudes. This trend is consistent with the Ek/Ep results shown in Fig. 4.
 | ||
| Fig. 8 W 2 distance for different values of friction coefficient, μ, for normal (a), (b) and tangential (c), (d) forces, and for both components (a), (c) and loops (b), (d). | ||
The results for tangential forces, Fig. 8(c) and (d), however, show a strong influence of friction. Here, for small values of μ, W2 is significantly larger, showing that (scaled) tangential forces vary considerably between consecutive frames; in other words, the tangential forces explore a large space of different force networks. For large values of μ, however, W2 is much smaller than the values found for the normal force. The interpretation, which will be confirmed in what follows, is that the tangential forces are smaller in magnitude compared to the normal ones, leading in turn to smaller values of W2 as well. This finding applies to both components, shown in Fig. 8(c), and loops, shown in Fig. 8(d). We note that we have also considered other distance measures, such as bottleneck distance, discussed in Section 2 that capture only the largest change in the networks (plots not shown for brevity). Bottleneck distance shows similar features as W2, but is 2–3 orders of magnitude smaller, suggesting that the largest network change, captured by the bottleneck measure, is just a small part of the overall network change. The fact that this result also applies to the distances computed during events is consistent with the earlier discussed finding that events involve changes in a large number of particle contacts.
While the direct comparison of Fig. 8 with the results for the energy ratio shown in Fig. 4 already indicates the relation between the two considered quantities, we emphasize this connection by plotting W2β0t and the energy ratio, Ek/Ep, together in Fig. 9 for two representative friction values. This figure shows clearly the close correlation between the non-affine motion and the dynamics of force networks. The events involving large non-affine energy ratio are clearly very well captured by W2β0t, while the additional evolution of W2β0t visible in particular for μ = 0.0001 illustrates some degree of network evolution between the events. Furthermore, we note that for μ = 0.0001, W2β0t distance is orders of magnitude larger compared to the values found for μ = 0.1, illustrating significant dynamics of force networks for small friction values.
Fig. 9 also illustrates some differences between the considered W2 and Ek/Ep measures: the relaxation after the events visible when considering Ek/Ep is barely captured by W2β0t or order W2 measures shown in Fig. 8. We explain this result by recalling that the W2 measure includes all the changes in the interaction network, while Ek/Ep focuses on the non-affine contributions only. Similar results are found when considering W2 measure for loops (not shown for brevity). The distances keep track of force network changes, both due to broken/new contacts and due to changes in forces. Therefore affine compression will influence the distance measure, while this contribution is taken out of (non-affine) kinetic energy.
5 Influence of friction on statics and dynamics of force networks
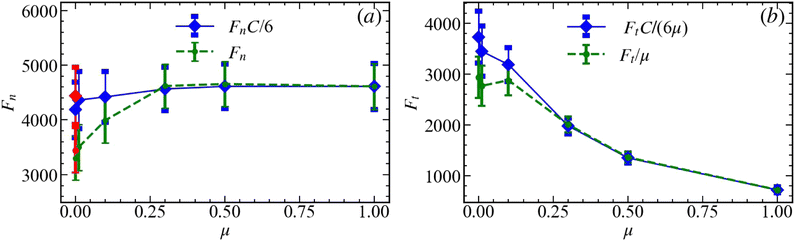
In this section we consider averaged results from the selected pressure window to be able to focus on the overall trends with varying friction coefficient, μ. We first discuss the forces (normal and tangential), and then focus on the dynamic measures. The results for static measures, such as the total persistence, the number of generators, and the life-spans, and their dependence on μ can be found in Appendices B and C. The main focus is on quantifying in a simple manner how the friction coefficient, μ, influences the statics and dynamics of the force networks.Fig. 10 shows the pressure window averaged (a) normal, Fn, and (b) tangential, Ft, forces as a function of μ. For illustration, we use (in this and the following figures) two types of scaling, multiplying with the average number of contacts per particle, C/C1, or not (with C1 = 6, the specific value to be discussed below). The former is the average per reference particle (referred to as force/particle in what follows), while the latter is the average per reference contact (force/contact). The number of contacts per particle, C, for different values of μ is given in Table 1 (for simplicity of notation, we use C instead of Cz = C(pz) since there is no possibility of confusion). For completeness, we also include the results for μ = 0 (in red), from ref. 29. Fig. 10(a) shows that the normal force increases with μ (green symbols in Fig. 10(a)), up to μ ≲ 0.3, and is constant for larger values of μ. Since C decreases in the same μ range, the scaled normal force (force/particle) remains essentially constant (blue symbols). We note that for μ ≳ 0.3, the average number of contacts per particle is C ≈ 6; this particular numerical value is serendipitous since the average number of contacts is of this value only at the pressure window that we consider here, see Fig. 2. In that follows, we mostly focus on the results that use force/particle for brevity.
Fig. 10(b) shows the average tangential force, Ft (normalized by μ to bring the highly different Ft into the same data range). For larger values of μ, the average Ft decreases following approximately 1/μ scaling with increasing μ, as does the tangential force scaled with C/C1. Only for the smallest coefficients of friction, we observe a different behavior, with Ft (either scaled or not) decreasing slower than 1/μ with increasing μ. Recall that if all contacts were sliding, so that Ft ≲ μFn, normalized Ft would be constant; therefore, a slower decrease of Ft for small values of μ suggests a significant contribution of sliding contacts. For larger values of μ, fewer contacts are sliding, and Ft < μFn. Regarding the behavior of Ft as μ → 0, we note that the red data in Fig. 10(a) and (b) confirm that the case μ = 0 is the accurate limit of μ → 0.
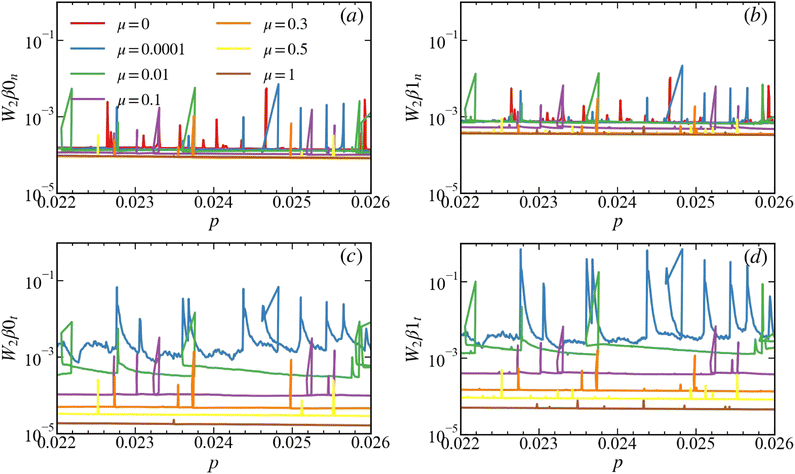
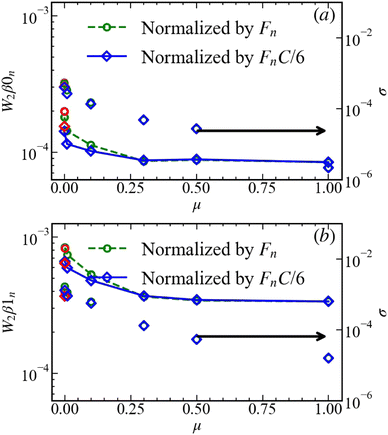
As mentioned at the beginning of this section, the results describing the static measures emerging from persistence analysis can be found in Appendices B and C. Here we discuss briefly the dynamical properties, and therefore consider in Fig. 11 and 12 the Wasserstein distance averaged over all snapshots in the considered pressure window. The picture that is emerging from these figures is that the evolution of force networks for small values of μ is significantly stronger than for larger values of μ, in particular for the tangential forces. Therefore, friction plays a stabilizing role, reducing the changes in the force networks from one snapshot to the next, i.e., during one isotropic strain increment.
 | ||
| Fig. 11 Average of normalized (a) W2β0n and (b) W2β1n (shown by symbols and lines). W2 are calculated between two consecutive frames as represented by persistence diagrams. The results are normalized in two ways: normalization by the average Fn, shown in Fig. 10 (green dots), or normalization by FnC/C1 (blue diamonds). Red symbols show frictionless results; σ is the standard deviation shown by symbols without lines (right-pointing arrow serves to remind which symbols represent σ). Note that the results for the two considered scaling mostly overlap each other. | ||
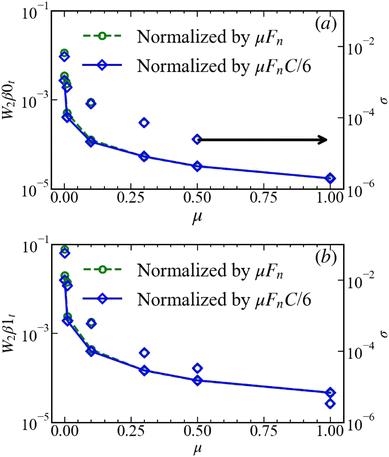 | ||
| Fig. 12 Average of normalized (a) W2β0t and (b) W2β1t. W2 is normalized as in Fig. 11 and σ shows the standard deviation. | ||
6 Conclusion and outlook
In this study, we investigate the behavior of frictional granular packings subject to slow quasi-static (isotropic) compression rates, focusing specifically on the regime above the jamming transition. The system response involves smooth evolution phases that are interrupted by fast, violent transitions or rearrangements, also referred to as events. The smooth evolution phases correspond to reversible (elastic) deformations, which can be split into comparable (same order of magnitude), but qualitatively different affine and non-affine components; in contrast, the events involve irreversible (plastic) rearrangements of the packings, stronger by orders of magnitude.These events can be detected as jumps in the overall kinetic energy of the system, as well as dramatic changes in (de-)stabilization within a packing, triggering avalanche-like transitions. Friction significantly influences the frequency of transitions, with the number of events decreasing notably as friction increases. This phenomenon can be attributed to the tangential components of forces; particularly, large friction restricts degrees of freedom, leading to a decrease in the probability of sliding contacts.
In contrast to frictionless systems, we observe that in a specific range of friction coefficients and for sufficiently slow compression, the events are followed by an undershoot, a dynamic slow-down, during which the kinetic energy of the system drops below the average value (baseline) that it had in the preceding smooth phase. Before undershoots the kinetic energy decays exponentially due to dissipation. The exponential decay and the recovery of the undershoots turn out to be the outcome of different relaxation mechanisms, a point clearly manifested by their different behavior as the control parameters are changed. The exponential decay occurs on the mechanical dissipation time scale, which is strain rate independent above jamming. However, the recovery of the undershoots evolves on another time scale which is determined by the pressure (or equivalently, the strain), i.e., also not directly strain rate dependent. Considering sliding contacts helps to understand both the relevant relaxation time scale and the role of friction.
Despite DEM providing rich information on the evolution of the granular structures, it cannot provide detailed information about the force network topology of the events without strong particle dynamics (kinetic to potential energy ratio). The topology-based analysis of the force networks, carried out by considering persistence diagrams that quantify the main features of the force networks, reveals that the networks evolve considerably during the events. Their static behavior correlates closely with the pressure, while their evolution resembles the kinetic energy of the packings – similarly to the frictionless case.29 Persistence analysis further shows that the force networks' structure is strongly friction-dependent. The analysis of the dynamics of force networks shows a much faster evolution of the networks of small friction packings, particularly tangential ones. Further, averaging the calculated quantities within the considered pressure window shows a pronounced increase in normal forces with rising coefficient of friction μ, reaching a plateau above μ ≈ 0.3 where the results are essentially μ-independent, while tangential forces exhibit a decreasing trend, closely approximating 1/μ scaling for higher μ.
Future work should focus on conducting a more quantitative analysis of strongly compressed granular packings using improved DEM models, and also on very slow shear deformations – in the same spirit as present – where the particle deformability and intermittent dynamics are fully taken into account. Furthermore, there are many interesting open questions regarding the interplay between dynamic and quasi-static mechanisms, deformation rates, not only for compression loading–unloading cycles, but also for shear-cycles of granular materials.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There is no conflict of interest.Appendices
Appendix A: persistence measures from force networks
Fig. 13 shows the results for TP1 of normal, fn, and tangential, ft, forces of the same samples as discussed in Fig. 2. The observation is that TP1 behaves similarly to TP0 as shown in Fig. 3, thus the pressure, as reported in Section 3.2 and previously for frictionless packings:29 they systematically increase with μ. Comparing the TP1 measure based on normal forces for different μ shows that they converge for large ϕ. On the contrary, the tangential forces based on TP1 measures behave qualitatively differently. This is due to the Coulomb coefficient of contact friction, which gives different tangential forces for different μ. This result is reflected in the magnitude of the corresponding TP1 measures.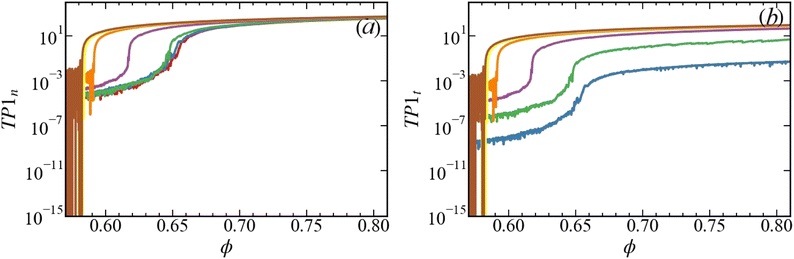 | ||
| Fig. 13 (a) TP1n and (b) TP1t plotted against volume fraction, ϕ, for samples prepared with different friction coefficients, μ. | ||
Appendix B: pressure-window averaged total persistence
In this Appendix, we discuss pressure-window averaged total persistence, see Section 5. Fig. 14 and 15 show TP for normal and tangential forces, respectively. For the normal forces, Fig. 14, for both components and loops we observe that for μ ≲ 0.3, TP, when normalized by Fn (green dots and dashed lines), decreases as μ increases, while remaining essentially constant for μ ≳ 0.3. This finding suggests that the structure of the force network depends on friction, with increasingly complex networks (to be discussed further below) for smaller values of μ. When scaled with the additional factor of C/C1, however, TP becomes essentially constant (within the error bars).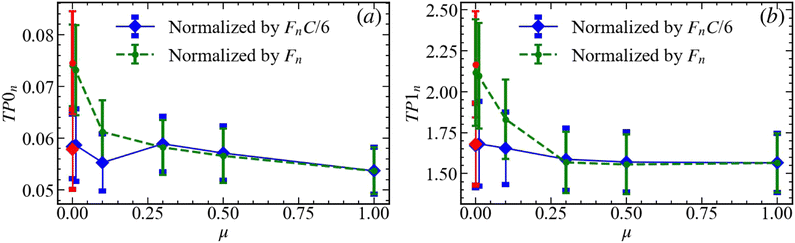 | ||
| Fig. 14 Average of total persistence (a) TP0n and (b) TP1n. For each μ, we first calculate TP per particle, i.e., TP is divided by the number of particles, N, and averaged over the considered pressure window. The results are normalized in two ways: normalization by the average Fn, shown in Fig. 10 (green dots), or normalization by FnC/C1 (blue diamonds). Red symbols show frictionless results. The error bars represent the standard deviations of the data within the pressure window. | ||
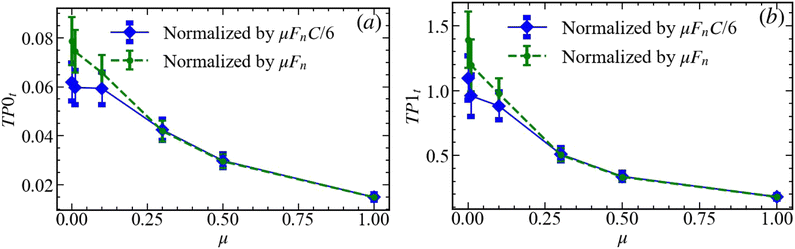 | ||
| Fig. 15 Average of total persistence (a) TP0t, and (b) TP1t. The averaging is carried out as described in the caption of Fig. 14. | ||
Fig. 15 shows a different trend for the tangential force TP for components and loops: they are continuously decreasing as μ increases, showing the strong importance of μ in determining the tangential force network properties. This finding illustrates significantly more structured tangential force networks for smaller values of μ. To understand these results more precisely, we need to consider the quantities defining TP; therefore we next analyze the pressure-window averaged number of generators, NG, and lifespans, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , discussed in Section 2.
, discussed in Section 2.
Appendix C: pressure-window averaged number of generators and lifespans
In this Appendix we continue discussing pressure-window averaged persistence measures, in particular the number of generators and lifespan of the generators, see Section 2 for definitions, Appendix B for the discussion of total peristence, and Section 5 for the discussion of pressure-window averages.As a reminder, thinking of force networks as a landscape, NG counts the number of hills and valleys, while ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) measures how tall are the hills relative to the valleys around them. Fig. 16 shows the number of generators, NG. For normal force network components (a), NG is essentially constant. For loops (b), we observe a decrease of NG for increasing μ ≲ 0.3 (consistently with a decrease in the number of contacts). Fig. 16(c) and (d) shows NG for the tangential force networks. Here we observe an increasing trend with μ for the components, while the generators for the loops behave just as for the normal forces.
measures how tall are the hills relative to the valleys around them. Fig. 16 shows the number of generators, NG. For normal force network components (a), NG is essentially constant. For loops (b), we observe a decrease of NG for increasing μ ≲ 0.3 (consistently with a decrease in the number of contacts). Fig. 16(c) and (d) shows NG for the tangential force networks. Here we observe an increasing trend with μ for the components, while the generators for the loops behave just as for the normal forces.
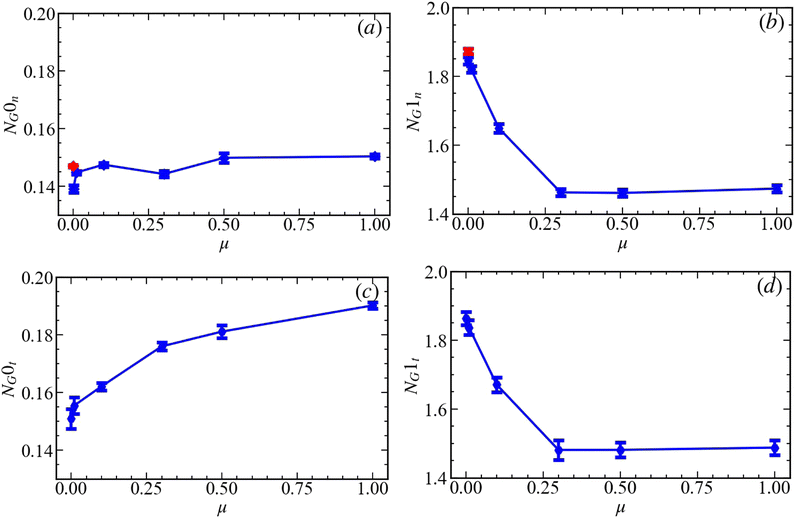 | ||
| Fig. 16 Average of (a) NG0n, (b) NG1n, (c) NG0t, and (d) NG1t. At each snapshot, the number of generators is divided by the particle number, N, and then averaged over all snapshots. | ||
Fig. 17 and 18 provide the last piece of information needed to understand the influence of friction on static properties of the force networks (focusing for brevity only on the results obtained when the forces/particle are considered). Fig. 18(a) shows that for the normal force components, lifespans are essentially μ-independent; recalling that the number of generators is also μ-independent, we conclude that with the considered scaling, properties of the components of the normal force networks are essentially μ-independent. Regarding the loops, shown in Fig. 18(b), lifespans grow for μ ≲ 0.3. This growth, combined with the fact that NG decreases for the same friction range, gives almost constant TP1n. Therefore, as μ increases, the number of loops decreases, but they also become ‘deeper’, meaning that they form for larger force values (further away from the diagonal in corresponding PDs). While TP remains almost the same, the topological properties of the loops/cycles formed by the normal force networks are, therefore, strongly friction-dependent. Regarding the tangential forces, the components ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) decrease as μ increases faster than NG increases, leading to an overall decrease in TP. For the loops,
decrease as μ increases faster than NG increases, leading to an overall decrease in TP. For the loops, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) similarly decreases and, combined with the decreased NG for μ ≲ 0.3, leads to an overall decrease of TP1t.
similarly decreases and, combined with the decreased NG for μ ≲ 0.3, leads to an overall decrease of TP1t.
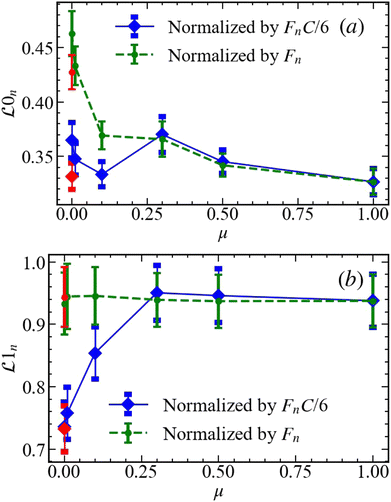 | ||
Fig. 17 Average of lifespans of (a) ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) 0n and (b) 0n and (b) ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) 1n. First, we calculate the average lifespan within the pressure window and then normalize as specified in the caption of Fig. 14. 1n. First, we calculate the average lifespan within the pressure window and then normalize as specified in the caption of Fig. 14. | ||
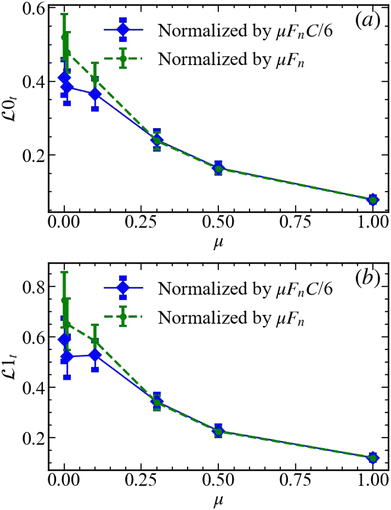 | ||
Fig. 18 Average of (a) ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) 0t and (b) 0t and (b) ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) 1t. The normalization is done as described in the caption of Fig. 17. 1t. The normalization is done as described in the caption of Fig. 17. | ||
Acknowledgements
RK and LK acknowledge support from the US Army Research Office grant no. W911NF1810184; LK also acknowledges support from U. Twente Da Vinci visiting program. SL and KT acknowledge funding from the German Science Foundation (DFG) through the project STE-969/16-1 within the SPP 1897 “Calm, Smooth and Smart”.References
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Granular solids, liquids, and gases, Rev. Mod. Phys., 1996, 68(4), 1259 CrossRef
.
- M. Lätzel, S. Luding, H. J. Herrmann, D. W. Howell and R. P. Behringer, Comparing simulation and experiment of a 2d granular couette shear device, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 325–333 CrossRef PubMed
.
- Y. Li, Y. Xu and C. Thornton, A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles, Powder Technol., 2005, 160(3), 219–228 CrossRef CAS
.
- A. J. Liu and S. R. Nagel, Jamming is not just cool any more, Nature, 1998, 396(6706), 21–22 CrossRef CAS
.
- S. Wilken, R. E. Guerra, D. Levine and P. M. Chaikin, Random close packing as a dynamical phase transition, Phys. Rev. Lett., 2021, 127(3), 038002 CrossRef CAS PubMed
.
- M. van Hecke, Jamming of soft particles: geometry, mechanics, scaling and isostaticity, J. Phys.: Condens. Matter, 2009, 22(3), 033101 CrossRef PubMed
.
- P. Coussot, N. Roussel, S. Jarny and H. Chanson, Continuous or catastrophic solid-liquid transition in jammed systems, Phys. Fluids, 2005, 17(1), 011704 CrossRef
.
- R. Kostynick, H. Matinpour, S. Pradeep, S. Haber, A. Sauret and E. Meiburg,
et al., Rheology of debris flow materials is controlled by the distance from jamming, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(44), e2209109119 CrossRef CAS PubMed
.
- N. Prime, F. Dufour and F. Darve, Unified model for geomaterial solid/fluid states and the transition in between, J. Eng. Mech., 2014, 140(6), 04014031 CrossRef
.
- J. Tang and R. P. Behringer, How granular materials jam in a hopper. Chaos: An Interdisciplinary, J. Nonlinear Sci., 2011, 21(4), 041107 CAS
.
- S. Dunatunga and K. Kamrin, Modelling silo clogging with non-local granular rheology, J. Fluid Mech., 2022, 940, A14 CrossRef CAS
.
- I. Zuriguel, L. A. Pugnaloni, A. Garcimartn and D. Maza, Jamming during the discharge of grains from a silo described as a percolating transition, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68(3), 030301 CrossRef PubMed
.
-
T. Pöschel and S. Luding, Granular gases, Springer Science & Business Media, 2001, vol. 564 Search PubMed
.
- K. Taghizadeh, M. Ruf, S. Luding and H. Steeb, X-ray 3D imaging-based micro understanding of granular mixtures: Stiffness enhancement by adding small fractions of soft particles, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(26), e2219999120 CrossRef CAS PubMed
.
- K. Taghizadeh, H. Steeb, S. Luding and V. Magnanimo, Elastic waves in particulate glass-rubber mixtures, Proc. R. Soc. A, 2021, 477(2249), 20200834 CrossRef PubMed
.
- K. Taghizadeh, H. Steeb, V. Magnanimo and S. Luding, Elastic waves in particulate glass-rubber mixture: experimental and numerical investigations/studies, EPJ Web Conf., 2017, 140, 12019 CrossRef
.
- D. Vescovi, D. Berzi and C. di Prisco, Fluid-solid transition in unsteady, homogeneous, granular shear flows, Granular Matter, 2018, 20, 1–10 CrossRef CAS
.
- S. Luding, So much for the jamming point, Nat. Phys., 2016, 12(6), 531–532 Search PubMed
.
- D. Vescovi and S. Luding, Merging fluid and solid granular behavior, Soft Matter, 2016, 12(41), 8616–8628 RSC
.
- M. Yang, M. Taiebat and F. Radjai, Liquefaction of granular materials in constant-volume cyclic shearing: Transition between solid-like and fluid-like states, Comput. Geotech., 2022, 148, 104800 CrossRef
.
- H. Laubie, F. Radjai, R. Pellenq and F. J. Ulm, Stress transmission and failure in disordered porous media, Phys. Rev. Lett., 2017, 119(7), 075501 CrossRef PubMed
.
- M. Ruf, K. Taghizadeh and H. Steeb, Multi-scale characterization of granular media by in situ laboratory X-ray computed tomography, Gamm, 2022, 45(3–4), e202200011 CrossRef
.
- K. Taghizadeh, R. K. Shrivastava and S. Luding, Stochastic model for energy propagation in disordered granular chains, Materials, 2021, 14(7), 1815 CrossRef CAS PubMed
.
- K. Taghizadeh, H. Steeb and S. Luding, Energy propagation in 1D granular soft-stiff chain, EPJ Web Conf., 2021, 249, 02002 CrossRef
.
- C. Giusti, L. Papadopoulos, E. T. Owens, K. E. Daniels and D. S. Bassett, Topological and geometric measurements of force-chain structure, Phys. Rev. E, 2016, 94(3), 032909 CrossRef PubMed
.
- D. S. Bassett, E. T. Owens, M. A. Porter, M. L. Manning and K. E. Daniels, Extraction of force-chain network architecture in granular materials using community detection, Soft Matter, 2015, 11(14), 2731–2744 RSC
.
- L. Kondic, A. Goullet, C. S. O'Hern, M. Kramar, K. Mischaikow and R. P. Behringer, Topology of force networks in compressed granular media, Europhys. Lett., 2012, 97(5), 54001 CrossRef
.
- D. S. Bassett, E. T. Owens, K. E. Daniels and M. A. Porter, Influence of network topology on sound propagation in granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(4), 041306 CrossRef PubMed
.
- S. Luding, K. Taghizadeh, C. Cheng and L. Kondic, Understanding slow compression and decompression of frictionless soft granular matter by network analysis, Soft Matter, 2022, 18(9), 1868–1884 RSC
.
- R. P. Behringer, K. E. Daniels, T. S. Majmudar and M. Sperl, Fluctuations, correlations and transitions in granular materials: statistical mechanics for a non-conventional system, Philos. Trans. R. Soc., A, 2008, 366(1865), 493–504 CrossRef CAS PubMed
.
- B. Miller, C. O'Hern and R. P. Behringer, Stress fluctuations for continuously sheared granular materials, Phys. Rev. Lett., 1996, 77(15), 3110 CrossRef CAS PubMed
.
-
F. Radjai, D. E. Wolf, S. Roux, M. Jean and J. J. Moreau, Force Networks in Granular Packings, in Friction, Arching and Contact Dynamics, ed. D. E. Wolf and P. Grassberger, World Scientific, Singapore, 1997 Search PubMed
.
- R. Arévalo, L. A. Pugnaloni, I. Zuriguel and D. Maza, Contact network topology in tapped granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(2), 022203 CrossRef PubMed
.
- L. Kondic, M. Kramár, L. A. Pugnaloni, C. M. Carlevaro and K. Mischaikow, Structure of force networks in tapped particulate systems of disks and pentagons. II. Persistence analysis, Phys. Rev. E, 2016, 93(6), 062903 CrossRef CAS PubMed
.
- S. Shah, C. Cheng, P. Jalali and L. Kondic, Failure of confined granular media due to pullout of an intruder: from force networks to a system wide response, Soft Matter, 2020, 16(33), 7685–7695 RSC
.
- N. Kumar and S. Luding, Memory of jamming-multiscale models for soft and granular matter, Granular Matter, 2016, 18(3), 1–21 CrossRef
.
- A. L. Thomas, Z. Tang, K. E. Daniels and N. M. Vriend, Force fluctuations at the transition from quasi-static to inertial granular flow, Soft Matter, 2019, 15(42), 8532–8542 RSC
.
- T. T. T. Nguyen, T. Doanh, A. Le Bot and D. Dalmas, High-temporal-resolution quasideterministic dynamics of granular stick-slip, Sci. Rep., 2021, 11(1), 2902 CrossRef CAS PubMed
.
- T. Doanh, N. Abdelmoula, L. Gribaa, T. T. T. Nguyên, S. Hans and C. Boutin,
et al., Dynamic instabilities under isotropic drained compression of idealized granular materials, Acta Geotech., 2017, 12, 657–676 CrossRef
.
- M. Yang, M. Taiebat, P. Mutabaruka and F. Radja, Evolution of granular materials under isochoric cyclic simple shearing, Phys. Rev. E, 2021, 103(3), 032904 CrossRef CAS PubMed
.
- M. Yang, M. Taiebat, P. Mutabaruka and F. Radja, Evolution of granular media under constant-volume multidirectional cyclic shearing, Acta Geotech., 2022, 17(3), 779–802 CrossRef
.
- T. T. Vo, P. Mutabaruka, S. Nezamabadi, J. Y. Delenne and F. Radjai, Evolution of wet agglomerates inside inertial shear flow of dry granular materials, Phys. Rev. E, 2020, 101(3), 032906 CrossRef CAS PubMed
.
- S. Luding, Elastic-plastic intermittent re-arrangements of frictionless, soft granular matter under very slow isotropic deformations, Front. Phys., 2023, 11, 1211394 CrossRef
.
- S. Luding, How does static granular matter re-arrange for different isotropic strain rate? In: Powders and Grains 2021, EPJ Web Conf., 2021, 249, 10001 CrossRef
.
- P. A. Cundall and O. D. L. Strack, A discrete numerical model for granular assemblies, Géotechnique, 1979, 29(1), 47–65 CrossRef
.
- L. Papadopoulos, M. A. Porter, K. E. Daniels and D. S. Bassett, Network analysis of particles and grains, J. Complex Netw., 2018, 6(4), 485–565 CrossRef
.
- D. M. Walker and A. Tordesillas, Topological evolution in dense granular materials: a complex networks perspective, Int. J. Solids Struct., 2010, 47(5), 624–639 CrossRef
.
- M. Kramár, A. Goullet, L. Kondic and K. Mischaikow, Quantifying force networks in particulate systems, Phys. D, 2014, 283, 3–55 CrossRef
.
- K. Taghizadeh, N. Kumar, V. Magnanimo and S. Luding, Understanding the effects of inter-particle contact friction on the elastic moduli of granular materials, IOP Conf. Ser. Earth Environ. Sci., 2015, 26, 012008 CrossRef
.
- S. Luding, Introduction to discete element methods: Basics of contact force models and how to perform the micro-marco transition to continuum theory, Eur. J. Environ. Civ. Eng., 2008, 12(7–8), 785–826 CrossRef
.
-
D. C. Rapaport, The art of molecular dynamics simulation, Cambridge university press, 2004 Search PubMed
.
- K. Taghizadeh, S. Luding and V. Magnanimo. DEM applied to soil mechanics. ALERT Doctoral School 2017 Discrete Element Modeling. 2017:129.
-
F. Radjai and F. Dubois, Discrete-element modeling of granular materials, Wiley-Iste, 2011 Search PubMed
.
- H. P. Zhang and H. A. Makse, Jamming transition in emulsions and granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 11301 CrossRef CAS PubMed
.
-
K. L. Johnson and K. L. Johnson, Contact mechanics, Cambridge university press, 1987 Search PubMed
.
- C. Thornton, S. J. Cummins and P. W. Cleary, An investigation of the comparative behaviour of alternative contact force models during elastic collisions, Powder Technol., 2011, 210(3), 189–197, DOI:10.1016/j.powtec.2011.01.013
.
- K. Saitoh, K. Taghizadeh and S. Luding, Sound characteristics of disordered granular disks: effects of contact damping, Front. Phys., 2023, 11, 402 Search PubMed
.
- K. Giannis, C. Schilde, J. H. Finke, A. Kwade, M. A. Celigueta and K. Taghizadeh,
et al., Stress based multi-contact model for discrete-element simulations, Granular Matter, 2021, 23(2), 1–14 CrossRef
.
- F. Radjai and V. Richefeu, Contact dynamics as a nonsmooth discrete element method, Mech. Mater., 2009, 41(6), 715–728 CrossRef
.
- F. Radjai, Contact dynamics method, Eur. J. Environ. Civ. Eng., 2008, 12(7–8), 871–900 CrossRef
.
- H. Kruggel-Emden, S. Rickelt, S. Wirtz and V. Scherer, A study on the validity of the multi-sphere Discrete Element Method, Powder Technol., 2008, 188(2), 153–165 CrossRef CAS
.
- A. Alenzi, M. Marinack, C. F. Higgs and J. J. McCarthy, DEM validation using an annular
shear cell, Powder Technol., 2013, 248, 131–142 CrossRef CAS
.
- R. D. Mindlin and H. Deresiewicz, Elastic spheres in contact under varying oblique forces, J. Appl. Mech., 1953, 20, 327–340 CrossRef
.
- S. Luding, Cohesive, frictional powders: contact models for tension, Granular Matter, 2008, 10(4), 235–246, DOI:10.1007/s10035-008-0099-x
.
- Y. Tsuji, T. Tanaka and T. Ishida, Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe, Powder Technol., 1992, 71, 239–250 CrossRef CAS
.
-
K. Taghizadeh, Elasticity and Wave Propagation in Granular Materials, University of Twente, Netherlands, 2019 Search PubMed
.
- J. Schäfer, S. Dippel and D. E. Wolf, Force schemes in simulations of granular materials, J. Phys. I, 1996, 6(1), 5–20 CrossRef
.
- L. E. Silbert, D. Ertacs, G. S. Grest, T. C. Halsey and D. Levine, Geometry of frictionless and frictional sphere packings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(3), 31304 CrossRef PubMed
.
- A. Singh, V. Magnanimo, K. Saitoh and S. Luding, Effect of cohesion on shear banding in quasistatic granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(2), 022202, DOI:10.1103/PhysRevE.90.022202
.
- S. Nezamabadi, F. Radjai, J. Averseng and J. Y. Delenne, Implicit frictional-contact model for soft particle systems, J. Mech. Phys. Solids, 2015, 83, 72–87 CrossRef
.
- S. Nezamabadi, F. Radjai, J. Averseng and J. Y. Delenne Modeling soft granular media. In: Modeling Granular Media Across Scales-MGMAS2014; 2014.
- N. Brodu, J. A. Dijksman and R. P. Behringer, Multiple-contact discrete-element model for simulating dense granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(3), 032201 CrossRef PubMed
.
- J. Mei, G. Ma, J. Liu, F. Nicot and W. Zhou, Modeling shear-induced solid-liquid transition of granular materials using persistent homology, J. Mech. Phys. Solids, 2023, 176, 105307 CrossRef
.
- J. Liu, X. Wu, J. Jiang, Z. Ding, C. Lü and X. Shi, A network-based investigation on the strong contact system of granular materials under isotropic and deviatoric stress states, Comput. Geotech., 2023, 153, 105077 CrossRef
.
- F. Patino-Ramirez, C. OÔÇÖSullivan and D. Dini, Percolating contacts network and force chains during interface shear in granular media, Granular Matter, 2023, 25(2), 31 CrossRef
.
- S. Ardanza-Trevijano, I. Zuriguel, R. Arévalo and D. Maza, Topological analysis of tapped granular media using persistent homology, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(5), 052212 CrossRef CAS PubMed
.
- GUDHI library – Topological data analysis and geometric inference in higher dimension, https://gudhi.inria.fr/.
- D. Wang, J. Ren, J. A. Dijksman, H. Zheng and R. P. Behringer, Microscopic origins of shear jamming for 2d frictional grains, Phys. Rev. Lett., 2018, 120(20), 208004 CrossRef CAS PubMed
.
- D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Jamming by shear, Nature, 2011, 480(7377), 355–358, DOI:10.1038/nature10667
.
- S. Luding, Y. Jiang and M. Liu, Un-jamming due to energetic instability: statics to dynamics, Granular Matter, 2021, 23, 80 CrossRef
.
- F. Göncü, O. Durán and S. Luding, Constitutive relations for the isotropic deformation of frictionless packings of polydisperse spheres, C. R. – Mec., 2010, 338(10–11), 570–586 CrossRef
.
- M. M. Bandi, M. K. Rivera, F. Krzakala and R. E. Ecke, Fragility and hysteretic creep in frictional granular jamming, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(4), 42205 CrossRef CAS PubMed
.
- F. Göncü, O. Durán and S. Luding, Jamming in frictionless packings of spheres: determination of the critical volume fraction, AIP Conf. Proc., 2009, 1145, 531–534 CrossRef
.
-
P. Wang, Computational Studies of the Protocol-dependent Mechanical Properties of Granular Materials, Yale University, 2021 Search PubMed
.
- F. Xiong, P. Wang, A. H. Clark, T. Bertrand, N. T. Ouellette and M. D. Shattuck,
et al., Comparison of shear and compression jammed packings of frictional disks, Granular Matter, 2019, 21(4), 109 CrossRef
.
- S. Alexander, Amorphous solids: their structure, lattice dynamics and elasticity, Phy. Rep., 1998, 296(2–4), 65–236 CrossRef CAS
.
- A. V. Tkachenko and T. A. Witten, Stress propagation through frictionless granular material, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60(1), 687 CrossRef CAS PubMed
.
- K. Wang, C. Song, P. Wang and H. A. Makse, Edwards thermodynamics of the jamming transition for frictionless packings: Ergodicity test and role of angoricity and compactivity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(1), 011305 CrossRef PubMed
.
- S. Inagaki, M. Otsuki and S. Sasa, Protocol dependence of mechanical properties in granular systems, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34(11), 124 CrossRef CAS PubMed
.
- B. A. Klumov, Y. Jin and H. A. Makse, Structural properties of dense hard sphere packings, J. Phys. Chem. B, 2014, 118(36), 10761–10766 CrossRef CAS PubMed
.
- M. Hanifpour, N. Francois, V. Robins, A. Kingston, S. M. Vaez Allaei and M. Saadatfar, Structural and mechanical features of the order-disorder transition in experimental hard-sphere packings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(6), 062202 CrossRef CAS PubMed
.
- L. E. Silbert, Jamming of frictional spheres and random loose packing, Soft Matter, 2010, 6(13), 2918–2924 RSC
.
- M. R. Kuhn and A. Daouadij, Stress fluctuations during monotonic loading of dense three-dimensional granular materials, Granular Matter, 2019, 21, 10, DOI:10.1007/s10035-018-0861-7
.
- A. Clerc, A. Wautier, S. Bonelli and F. Nicot, Meso-scale signatures of inertial transitions in granular materials, Granular Matter, 2021, 23(2), 28 CrossRef
.
- A. A. Long, D. V. Denisov, P. Schall, T. C. Hufnagel, X. Gu and W. J. Wright,
et al., From critical behavior to catastrophic runaways: comparing sheared granular materials with bulk metallic glasses, Granular Matter, 2019, 21(4), 99, DOI:10.1007/s10035-019-0946-y
.
- L. Sibille, F. Nicot, F. V. Donzé and F. Darve, Analysis of failure occurrence from direct simulations, Eur. J. Environ. Civ. Eng., 2009, 13(2), 187–201 CrossRef
.
- J. D. Goddard, Nonlinear elasticity and pressure-dependent wave speeds in granular media, Proc. – R. Soc. Edinburgh, Sect. A: Math., 1990, 430(1878), 105–131 Search PubMed
.
- J. P. Bardet, Observations on the effects of particle rotations on the failure of idealized granular materials, Mech. Mater., 1994, 18, 159–182 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00560k |
| This journal is © The Royal Society of Chemistry 2024 |