Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Many-body dissipative particle dynamics simulations of micellization of sodium alkyl sulfates†
Rachel L.
Hendrikse
 *a,
Carlos
Amador
b and
Mark R.
Wilson
*a,
Carlos
Amador
b and
Mark R.
Wilson
 a
a
aDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: rachel.hendrikse@durham.ac.uk
bProcter and Gamble, Newcastle Innovation Centre, Whitley Road, Newcastle upon Tyne, NE12 9BZ, UK
First published on 22nd July 2024
Abstract
We present a study of micelle formation in alkyl sulfate surfactants using the simulation method of many-body dissipative particle dynamics (MDPD). We parametrise our model by tuning the intermolecular interactions in order to reproduce experimental values for the chemical potential and density at room temperature. Using this approach, we find that our model shows good agreement with experimental values for the critical micelle concentration (CMC). Furthermore, we show that our model can accurately predict CMC trends, which result from varying properties such as surfactant tail length and the salt concentration. We apply our model to investigate the effect of aggregation number on various micellar properties, such as the shape of individual micelles and the fraction of bound counterions. We show that micelles become aspherical at large aggregation numbers, in line with experimental predictions, and that longer tail surfactants are generally more spherical at all aggregation numbers compared to those which are shorter. We find excellent agreement between our simulations and experimental values for the degree of counterion binding, a factor that is crucial to accurately studying micellar shape, but one that is typically overlooked in the existing literature.
1 Introduction
Surfactants are key components in a huge variety of everyday products, including detergents and personal care items. Surfactants are surface-active amphiphilic molecules that are capable of forming micelles in solution when the concentration is above a critical micelle concentration (CMC). At higher concentrations, lyotropic liquid crystal phases can be produced,1–3 however, most commercial products are at concentrations in the micellar range: the phase region of interest in this article.One of the most widely studied surfactants is the anionic surfactant sodium dodecyl sulfate (SDS), which is present in a large range of products such as shampoos and cleansers. Due to its widespread use in commercial products, there has been a great deal of experimental research dedicated to studying the size and shape of SDS micelles,4–15 as well as determining the CMC value.16–19 Therefore, the creation of an accurate model for studying and understanding SDS aggregation behaviour is of great interest, particularly to aid the design of commercial products. We developed our model with the primary objective of studying SDS. However, this model can be easily extended to other surfactants. Consequently, we also investigate the variation in the length of the surfactant tail, allowing us to also study sodium octyl sulfate and sodium hexadecyl sulfate; together with the effects of additional salt.
Simulating surfactant solutions is challenging, primarily because of the time scales involved in micelle formation. While molecular dynamics (MD) simulations for SDS micelles can be found in existing literature,20–25 these studies are typically limited to simulating single preassembled micelles. These limitations motivated the development of coarse-grained simulation methods, such as dissipative particle dynamics (DPD).26 DPD is computationally faster than traditional MD techniques, which opens up the possibility of simulating larger length and time scales. This speed-up is partly because molecules are simulated using ‘beads’, which represent groups of atoms as opposed to simulating individual atoms, but is also due to the form of forces which represent the intermolecular interactions between beads. The forces between beads are designed in DPD to enhance diffusion, leading to shorter equilibration periods. DPD has been shown across the literature to be a highly useful tool for modelling surfactant systems, in particular for predicting critical micelle concentrations27–29 and for studying micellar shape and size.28,30,31 DPD has also been shown to be useful for studying systems at higher concentrations, including surfactants which form liquid crystal structures.31–34
One of the drawbacks of the DPD method is that there is not yet a force field which can be readily applied to any molecule of choice. There are several existing parametrisation attempts in the literature,26,35–47 including for SDS,28,29,32 but these approaches are typically limited to small subsets of molecules. These parametrisation attempts have also had varying success in being able to make qualitative predictions, which agree with experimental data since, for example, the aggregation number is typically underestimated in existing models.28,29
Since its inception, traditional DPD methods have been extended and modified to make them more versatile and applicable to a greater range of systems. This includes the adaptation of many-body dissipative particle dynamics (MDPD),48 which we will use in this work. MDPD is a variation of standard DPD, in which the conservative interaction force between beads is altered from being purely repulsive to one with long-range attractive and short-range repulsive components. This makes the potential more comparable to a molecular dynamics pair potential, such as the Lennard-Jones potential. Adapting the potential in this way has benefits, including the ability to simulate coexisting liquid and vapour phases. It also allows for the possibility of reproducing realistic chemical potentials since it allows negative potential energies to be calculated. In Section 2 of this article we highlight why this makes MDPD an attractive choice for studying micelles.
This article is structured as follows. We first present a brief overview of the many-body dissipative particle dynamics method, before presenting our approach to parametrising surfactant simulations. We then calculate the CMC of SDS molecules and show how this can be influenced by varying the surfactant tail length and the addition of salt. Finally, we calculate the aggregation number and present a short study of how the aggregation number influences micelle shape.
2 Many-body dissipative particle dynamics
2.1 Background and overview
In standard DPD, nonbonded beads are acted upon by three forces, which are typically referred to as the conservative, random, and dissipative forces. For the conservative force, the interaction between beads i and j is given by | (1) |
The remaining two non-bonding forces are the dissipative (or drag) force FDij and a random pairwise force FRij, which act as the simulation thermostat. The dissipative force is calculated using
FDij = −γωD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (2) |
FRij = σωR(rij)ζij![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ijΔt−1/2, ijΔt−1/2, | (3) |
| ωD = [ωR]2 | (4) |
| σ2 = 2γkBT, | (5) |
Individual DPD beads can be chemically bonded to create coarse-grained molecules. The bonding force is calculated via the potential UBij, which is represented as a harmonic spring using
 | (6) |
 | (7) |
In this paper, we choose to use an adaptation of DPD called many-body dissipative particle dynamics (MDPD). In MDPD, the form of the forces used is identical to the standard case for all except for the conservative force. The conservative force is altered to include both attractive and repulsive components, taking the form
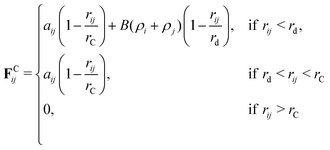 | (8) |
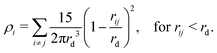 | (9) |
2.2 Electrostatics
Charged systems are also subject to an additional electrostatic force FEij acting on the beads. In molecular dynamics simulations, it is typical to treat charged atoms as point charges. However, in standard DPD simulations, it is usually the case that researchers28,29,31,54 choose to use a smeared charge approach instead, where the charge is spread over a finite volume. Because of the soft-repulsive nature of the DPD conservative force, treating DPD beads as having a point charge can result in artificial ion-pair formation where oppositely charged ionic beads may collapse on top of each other, forming infinitely strong ion pairs. When treated as point charges, research55 has shown that the percentage of artificial pairs formed decreases as the magnitude of the conservative force repulsion between beads increases (corresponding to an increasing value of |aij|). Therefore, at sufficiently high values of aij, it is suggested that one can still use point charges as opposed to requiring smeared approaches.Due to the different form of the conservative force (eqn (8)) it is unknown whether smeared charges are required in MDPD simulations. We have not found any previous work investigating artificial ion pair formation in the existing MDPD literature. Therefore, before studying micelle solutions, we first present a short investigation into the behaviour of charges in MDPD in Section 4 of this article. It will be shown that we can safely treat our beads as point charges for studying surfactant aggregation. Therefore, the electrostatic force in the study of micellar solutions will be calculated using the standard Coulombic potential
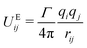 | (10) |
2.3 Interaction parameters aij
Self-interaction parameters aii are often calculated for DPD simulations by aiming to reproduce experimental densities28,56 or compressibilities.29,38,55,57 In this work, we choose to define our self-interaction parameters by matching to experimental values for the density as well as chemical potentials of pure water and octane.Various approaches have been proposed to calculate cross-interaction parameters aij, including matching to experimentally derived quantities such as partition coefficients44 or solubility parameters.58,59 Other approaches include matching to quantities obtained from molecular dynamics simulations, such as the radial distribution.60 In this work, we will base our parameterisation on reproducing experimental activity coefficients at infinite dilution γ∞ (IDACs), an approach which has also been used by various previous authors.29,38,57,61
The chemical potential can be split into two components62 for computational purposes:
| μ = μexcess + μideal | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρΛ3 where Λ is the thermal de Broglie wavelength and ρ is the number density. We calculate the excess potential energy μexcessvia the Widom insertion method, using the equation
ρΛ3 where Λ is the thermal de Broglie wavelength and ρ is the number density. We calculate the excess potential energy μexcessvia the Widom insertion method, using the equation | (12) |
The total chemical potential of substance A in solution can be represented in terms of its activity coefficient γA63 as
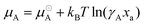 | (13) |
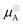 is the chemical potential of pure component A, μA is the chemical potential of A in the solution (where the units of chemical potential μ are energy per molecule), and xA is the mole fraction of A in the solution. Supposing that the solution consists of A at infinite dilution in a solvent of type B, then combining eqn (11) and (13) leads to the following expression
is the chemical potential of pure component A, μA is the chemical potential of A in the solution (where the units of chemical potential μ are energy per molecule), and xA is the mole fraction of A in the solution. Supposing that the solution consists of A at infinite dilution in a solvent of type B, then combining eqn (11) and (13) leads to the following expression | (14) |
Since in previous works (using traditional DPD), the self-interactions are usually matched to density or compressibility, the individual chemical potentials μ are usually incorrect and do not match experimental values. Instead, the focus is on matching to the IDAC alone. However, in any case, due to the form of the conservative force (eqn (1)), in DPD it would be impossible to correctly reproduce the chemical potentials of pure components anyway. To correctly reproduce the chemical potentials of pure components, this will usually require negative μexcess values (due to the negative chemical potential of most liquids). It is clear from eqn (12) that, in order to generate μexcess < 0, in general, the insertion due to a single bead should result in a negative change in the potential energy (ΔU < 0). In liquids such as water, this is due to the attractive forces between water molecules.
However, since the conservative force in standard DPD is purely repulsive, this makes it impossible to generate these negative excess chemical potential values. This is one of the reasons we chose to use MDPD for our simulations. The presence of the attractive term in MDPD means that negative values of μexcess can be generated, therefore making it possible to reproduce the correct pure chemical potential values. In this work, we match not only the experimental values for ln(γ∞), but also the pure chemical potentials of the solute and solvent, and also the experimental densities.
3 Parameterisation approach
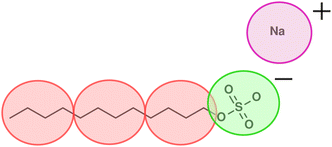
In this work, we focus on a DPD model for anionic surfactant sodium dodecyl sulfate (SDS). As discussed in Section 2, we base the parameterisation of the tail and water beads on experimental densities, chemical potentials, and IDACs. An illustration of the coarse graining used for SDS is shown in Fig. 1, such that a single DPD tail bead represents four carbon atoms, and the head group is represented by a single negatively charged bead. The counterion is represented by its own positively charged bead, in which the sodium atom is hydrated with water. The stages for parameterisation are as follows:1. Set tail bead self-interactions aTT based on the experimental chemical potential of octane, which we determine by performing Widom insertion calculations.
2. Define rC (length scale for conversation into real units) based on matching the experimental density of octane (703 kg m−3) to the density of the DPD fluid at the value of aTT determined in the previous step.
3. Define the coarse graining of water and aWW based on matching to the density (using the value of rC from the previous step) and chemical potential of water. Note that the two unknowns (aWW and the level of water coarse graining N, i.e. water molecules per coarse-grained bead), can in theory be solved exactly using the two equations (density and chemical potential).
For the charged beads (the SO4− head group and sodium, Na+, counterion), we choose to set the aij interactions to be the same as those with water. This decision is based on the assumption that charged beads will mostly be surrounded by water molecules in solution; therefore, at short range, the beads will interact similarly to water beads. All simulations described are performed using the DL_MESO software package64 and we perform all simulations using a time step of Δt = 0.01.
3.1 Tail self-interactions (aTT)
The tail self-interactions (aTT) are based on reproducing the chemical potential of octane. This calculation is performed by simulating a cubic box with periodic boundary conditions, which is entirely filled with octane beads. Therefore, before performing the Widom insertions to calculate the chemical potential, one must first know the choice of aTT relates to the resulting bead density of the system. Knowing the bead density of octane as a function of aTT will allow us to correctly set the box sizes for the Widom insertion calculation.To find a general relationship between aTT and the bead density ρ, we perform a parameter sweep in the range −26 ≤ aTT ≤ −18, with an interval of ΔaTT = 1. We simulate two bonded beads to represent octane with an equilibrium bond length of l0 = 0.6 (note that we make our initial choice of bond length based on results from our previous work,61 more details of which can be found in the ESI†). These simulations are conducted in the const-NVT ensemble, in a box with periodic boundaries with dimensions 10rC × 10rC × 100rC. The beads are initialised with a random initial configuration using n = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads (5000 molecules). For this number of beads, following equilibration the simulations produce coexisting regions of liquid and vapour, an example of which is shown in Fig. 2. Therefore, from this, the bead density of the liquid phase can be determined.
000 simulation beads (5000 molecules). For this number of beads, following equilibration the simulations produce coexisting regions of liquid and vapour, an example of which is shown in Fig. 2. Therefore, from this, the bead density of the liquid phase can be determined.
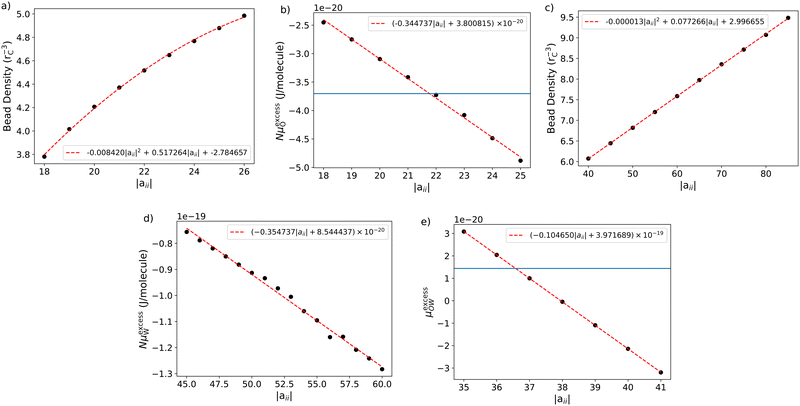
Fig. 3a shows the relationship between aTT and the bead density, ρT. We fit a general expression in the form of a second-order quadratic, such that the density can be calculated using the expression:
| ρTrC3 = −(8.42 × 10−3)|aTT|2 + (5.17 × 10−1)|aTT| − 2.78. | (15) |
Following this, we perform a separate set of simulations to calculate the chemical potential. Once again, we perform a parameter sweep in the range 18 ≤ aTT ≤ 26, with an interval of ΔaTT = 1. These simulations are conducted in a cubic box of length L, with periodic boundaries and beads initialised with a random initial configuration. The simulation is also conducted in the const-NVT ensemble.
For each simulation, we use n = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads (25
000 simulation beads (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules), and the dimensions L of the box are calculated individually for each value of aTT. The value of L is chosen to generate the correct density as determined by eqn (15). This approach produces a domain completely filled with liquid so that Widom insertions can be performed without concern about potential insertions into a vapour phase. Note that for inserting the octane molecules during the Widom insertion, we choose to use a bond length of l0 = 0.6 for all insertions.
000 molecules), and the dimensions L of the box are calculated individually for each value of aTT. The value of L is chosen to generate the correct density as determined by eqn (15). This approach produces a domain completely filled with liquid so that Widom insertions can be performed without concern about potential insertions into a vapour phase. Note that for inserting the octane molecules during the Widom insertion, we choose to use a bond length of l0 = 0.6 for all insertions.
For each simulation box (corresponding to different aTT) we calculate the excess chemical potential μexcess by Widom insertion using eqn (12). We convert the energy calculated in DPD units to real units using kBT = 4.11 × 10−21 J at room temperature.
The relationship between the calculated excess potential energy and aTT is shown in Fig. 3b, and we can fit the general relationship for calculating the chemical potential in units of J,
| μexcessO = (−3.45 × 10−21)|aTT| + 3.80 × 10−20. | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 (or −3.703 × 10−20 J per molecule); therefore, we determine that the value of aTT which produces the correct excess chemical potential is aTT = −21.775.
65 (or −3.703 × 10−20 J per molecule); therefore, we determine that the value of aTT which produces the correct excess chemical potential is aTT = −21.775.
At the value aTT = −21.775, eqn (15) can be used to determine a bead density of ρ = 4.486. Matching to the experimental density of octane (703 kg m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66) at room temperature allows us to determine that rC = 8.45 Å. Note that this produces a bond length in real units of about 5.07 Å. If we assume that the C–C–C angles are tetrahedral (approximately 109.5°) and that the experimental C–C bond is 1.543 Å,67 the separation between four carbon atoms (or two adjacent beads) is calculated at around 5.04 Å, meaning that the equilibrium bond length of 0.6rC is an appropriate choice.
66) at room temperature allows us to determine that rC = 8.45 Å. Note that this produces a bond length in real units of about 5.07 Å. If we assume that the C–C–C angles are tetrahedral (approximately 109.5°) and that the experimental C–C bond is 1.543 Å,67 the separation between four carbon atoms (or two adjacent beads) is calculated at around 5.04 Å, meaning that the equilibrium bond length of 0.6rC is an appropriate choice.
3.2 Water self-interaction aWW
In this section, we perform a similar series of calculations for water beads (as for octane). In order to find a relationship between the density and value of aWW, we perform a parameter sweep in a similar way to that performed in Section 3.1 for octane, however, the simulation for water contains no bonded beads. The relationship between aWW and ρW is shown in Fig. 3c. We fit a general expression in the form of a second-order quadratic, such that the density can be calculated using the expression:| ρWrC3 = −(1.29 × 10−5)|aWW|2 + (7.73 × 10−2)|aWW| + 3.00 | (17) |
Similarly, to calculate the chemical potential, we now perform a parameter sweep over different aWW values. Once again we perform const-NVT simulations in a cubic simulation box where the entire domain is filled with water beads, this time setting the box size to reproduce the density in eqn (17).
The experimental value for the excess chemical potential of water is taken as −6.33 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 (or −4.4 × 10−20 J per molecule). It should be noted that because one bead represents more than one molecule, this must be taken into account in the calculation. Therefore, the calculated chemical potential depends on the coarse graining level, N, chosen for the water molecules. This means that we can, in theory, find the values of N and aWW that reproduce the experimental value for the density of water at room temperature, as well as the chemical potential, where N could (in principle) take a non-integer value.
65 (or −4.4 × 10−20 J per molecule). It should be noted that because one bead represents more than one molecule, this must be taken into account in the calculation. Therefore, the calculated chemical potential depends on the coarse graining level, N, chosen for the water molecules. This means that we can, in theory, find the values of N and aWW that reproduce the experimental value for the density of water at room temperature, as well as the chemical potential, where N could (in principle) take a non-integer value.
The relationship between the excess chemical potential of water and aWW is shown in Fig. 3d. The relationship can be fit using a first-order equation (in units of J)
| NμexcessW = (−3.55 × 10−21)|aWW| + 8.54 × 10−20 | (18) |
3.3 Cross interaction (aTW)
The cross-interaction, aTW, is calculated by reproducing the experimental IDAC of octane in water, which has an experimental value of ln(γ∞) = 16.0268 at room temperature. Using eqn (14), we find the target value μ*,excess = 3.5 (units of kBT). A sweep over aTW parameter, calculating μ*,excess in each case, gives the results shown in Fig. 3e. By fitting a first-order equation of the form (in units of J)| NμexcessW = (−1.05 × 10−20)|aWW| + 3.97 × 10−19, | (19) |
| Tail (T) | Head (H) | Ion (I) | Water (W) | |
|---|---|---|---|---|
| Tail (T) | 21.775 | — | — | — |
| Head (H) | 36.576 | 57.793 | — | — |
| Ion (I) | 36.576 | 57.793 | 57.793 | — |
| Water (W) | 36.576 | 57.793 | 57.793 | 57.793 |
4 Electrostatics study
Studies have shown that in traditional DPD, when the short-range repulsion between oppositely charged beads is high enough (aij ≳ 100 in eqn (1)), point charges can comfortably be used with no ion-pair formation.55 In MDPD the short-range force is a combination of a repulsive contribution and an attractive contribution, and therefore, the magnitude of the repulsion at short range differs from that of standard DPD. In the limit of when rij → 0, the magnitude of force approaches |FCij| → [aij + B(ρi + ρj)]. Therefore, we investigate the effect that varying aij has on the average value of 〈aij + B(ρi + ρj)〉 for each pair of interacting beads. Increasing |aij| has the effect of increasing local densities, making it possible that the net force is sufficiently repulsive to prevent ion collapse.We perform these calculations using data from the water bead parameter sweep, described previously in Section 3.2. We create an additional Python script to determine the magnitude of the average 〈aij + B(ρi + ρj)〉. For a given trajectory output at time t, we compose a list of local densities for every bead in the system using eqn (9), and find the average local density per bead 〈ρi〉 = ρL. We then calculate
| 〈Fij〉i,j = 〈aij + B(ρi + ρj)〉i,j | (20) |
| 〈Fij〉i,j = A + B〈(ρi + ρj)〉i,j = A + 2BρL | (21) |
 | ||
| Fig. 4 Magnitude of the conservative force in MDPD in the limit of rij → 0. Force is presented in DPD units. | ||
To verify that our choice of parameters and point charges does not lead to artificial ion pair formation, we performed test simulations on simple salt solutions. We perform our simulations in a box with periodic boundary conditions and dimensions 7rC × 7rC × 50rC. The domain is populated with 500 positively charged beads, 500 negatively charged beads, and 2000 neutral beads representing water. We initialise with random placement throughout the entire simulation box, and after a short time, the beads form coexisting vapour and liquid phases. Following this equilibration period, we start data collection.
Fig. 5 shows the radial distribution function between the oppositely charged beads, where we confirm that there is no artificial pair formation, even at this relatively high salt concentration. If there was any ion collapse in the system, we would expect to see this reflected at short distances in the value of g(r).
5 Critical micelle concentration (CMC)
In this section, we calculate the CMC for sodium alkyl surfactants of varying tail length (Section 5.1) and for SDS solutions with added salt (Section 5.2). Although the CMC is fairly well defined experimentally, there is no universally agreed best approach to calculating the CMC from simulations. This means that a variety of approaches have been used by various authors, and in this section, we begin by comparing a selection of the most common methods.One common approach is to simulate at concentrations well above the CMC and calculate the CMC from the number of free surfactants.28,29,38,69 Another proposed method is to simulate at lower concentrations and define CMC as the concentration at which half of the surfactant material is free (as both monomers and submicellar aggregates) and half exists as micelles.28,70,71 Of course, different authors may define the size at which an aggregate can be considered a micelle differently, complicating direct comparisons between parameterisation schemes. Other proposed approaches include defining the CMC as the concentration at which a significant change in viscosity occurs,72 or when there is a significant change in the relationship between aggregation and concentration, i.e., where one performs a linear fit of the submicellar concentration in regions both above and below an estimated CMC, where the crossing is defined as the CMC.27,73
One further complication that arises for ionic surfactants is that there is a strong dependence of the number of free monomers on the concentration of micelles. In other words, the number of free monomers cannot be considered independent of the overall concentration.28,29,69 Therefore, to calculate the CMC concentration CCMC from the free monomer concentration CF, one should make use of the following relation74
 | (22) |
Throughout the literature, different approaches have been taken to choose a suitable value of α. One approach is to select a value of α derived from experiment,29 while others determine the value directly from the simulations using the radial distribution function and an appropriate choice of cutoff distance.69 However, it has been reported that the calculated CMC can be relatively insensitive to the precise value used.28,69 It will be shown in Section 6 that we also find this to be the case. In this work, we choose to determine the CMC using three of the different approaches discussed. These include:
• Method A – defined as the concentration at which half of the surfactant molecules are in micelles (CF = CT/2);
• Method B – via calculating the free concentration and using eqn (22);
• Method C – by performing linear fits to the relationship between aggregation and concentration and identifying a cross-over point.
5.1 Pure aqueous surfactant systems
To test our model, we simulate SDS surfactants and also investigate the impact of varying the length of the hydrocarbon chain. This allows us to check the robustness of our parameterisation scheme. We calculate the CMC for molecules containing 8, 12, and 16 carbon atoms (which we henceforth refer to as S8S, S12S and S16S). In practice, this involves varying the number of tail beads from 2–4 in our coarse-grained representation. The molecules are initially placed at random in a cubic box with periodic boundary conditions, subject to constant pressure.We set the box pressure to be equivalent to that of pure water, which we calculate to be P = −0.37 (in DPD units). It should be noted that when the liquid phase is in coexistence with a very low-density vapour (as in our simulations), the pressure which generates liquid phase density ρL can be estimated50 as P(ρL) = 0. Therefore we expect setting P = 0 would generate very similar results. However, to ensure we generate the exact same density described in Section 3, we run a bulk NVT simulation of our water beads a cubic simulation box at this density, to determine a precise value for P. We discuss setting the pressure of the system in more detail in the ESI.†
For each of the three different molecules, we choose a different box size owing to the differences expected in their CMC where we want to ensure there will be sufficient free monomers in the simulation boxes, choosing a total of n = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (S8S), n = 300
000 (S8S), n = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (S12S) and n = 340
000 (S12S) and n = 340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (S16S) beads in each case. Note that although it would be desirable to have a larger simulation box in the S16S case, we choose a moderate-size simulation for computational reasons. We allow each simulation to equilibrate until the number of free monomers is approximately constant, which takes considerably more computational effort for the larger molecules as a result of their larger simulation sizes.
000 (S16S) beads in each case. Note that although it would be desirable to have a larger simulation box in the S16S case, we choose a moderate-size simulation for computational reasons. We allow each simulation to equilibrate until the number of free monomers is approximately constant, which takes considerably more computational effort for the larger molecules as a result of their larger simulation sizes.
In order to determine the number of free monomers, one must define a cutoff to distinguish between micelles and free molecules (i.e., how large does an aggregate have to be to be considered a micelle). We determine this cutoff by plotting a histogram of aggregate sizes, from which we determine it is sensible to define micelles as aggregates containing 8 or more surfactant molecules.
Fig. 6 shows the results of this study, and presents plots of the surfactant molecules which can be considered to reside in micelles as a function of concentration. From this, we can determine the CMC using method A (CF = CT/2) and method C (using the cross-over point), which are both highlighted in Fig. 6. From the free concentration, we also determine a CMC value using method A (eqn (22)), where we use an experimentally74 obtained estimate for the number of bound ions, α = 0.7.
Table 2 presents a summary of the different CMC values calculated using different approaches, as well as a comparison with experimental data. Generally, we find that our simulations slightly underpredict the CMC; however, given the magnitude of variation between different length molecules (i.e. over an order of magnitude difference in the experimental CMC values between molecules which differ by only a single DPD bead), we consider this underprediction to be relatively small. Fig. 7 compares the change in the log(CMC/mM) as a function of chain length with the experimental data, which calculates the CMC using conductivity measurements. We see that the experimental trend of Aniansson et al.,16 showing a linear decrease in log(CMC/mM) with chain length, is accurately reproduced by the simulations.
 | ||
| Fig. 7 CMC of alkyl sulfate surfactants as a function of tail length, where simulated results are compared with experimental data obtained from Aniansson et al.,16 who calculate the CMC using conductivity measurements. | ||
5.2 Addition of salt
We also investigate the impact of salt, by calculating the CMC of SDS in the presence of sodium chloride at various NaCl concentrations. Experimentally, the CMC is expected to decrease with increasing concentrations of salt.18,19We perform these calculations in a similar manner to those described in the previous section, keeping the number of water beads the same as that described previously for S12S. We modelled the additional salt using two oppositely charged beads (each possessing a charge q = |e|), which represent a single NaCl molecule. The short-range interactions with other beads in the system are the same as those for water, based on the reasoning outlined in Section 4. We simulate two different salt concentrations using 220 and 1500 Na+ and Cl− ions, which correspond to salt concentrations 15 and 100 mM respectively.
Fig. 8 shows the percentage of surfactant molecules in micelles for the different salt concentrations, and we see that micelles form more readily at higher salt concentrations as expected. We also observe that there is a relatively short concentration range where the solution transforms from consisting entirely of free monomers to complete aggregation. As the region is much narrower than in the salt-free simulations, this makes determining the CMC using method A more difficult. From Fig. 8, we estimate the CMC value as the point where there is an abrupt change in the number of surfactants in micelles (similar to using method C). These calculated CMC values are shown in Table 3 alongside experimentally determined values. We also show an approximate lower bound based on the highest concentration at which no aggregation is observed.
| Salt concentration | Simulated CMC | Experimental CMC |
|---|---|---|
| 15 | 2.5 (2.1) | 4.2 |
| 100 | 1.3 (1.0) | 1.7 |
Since it was shown in the previous section that the values of the CMC are slightly underpredicted using our model (even in the absence of salt), it is unsurprising that the values in Table 3 are lower relative to experiment. However, the general trend for the simulated results is in excellent agreement with the experimental data. From the data presented by Dutkiewicz and Jakubowska,18 we know that the CMC CCMC and salt concentration CS should obey the relationship CCMC = a(CS)k where a and k are fitted constants. From our simulated data, we calculate a gradient value of, k = −0.35, which is reasonably good agreement with the experimental value of k = −0.48.
Suppose we now once again consider eqn (22). If we use the definition that the CMC is the concentration at which micelles first start appearing, then we can say CF = CT = CCMC. If we also suppose that the surfactant concentration at the CMC is small (VCCMC ≪ 1) then eqn (22) simplifies to
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CCMC = (1 + α)log(C0CMC) − α CCMC = (1 + α)log(C0CMC) − α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(CCMC + CS). log(CCMC + CS). | (23) |
| log(CCMC(CCMC + CS)α) = (1 + α)log(C0CMC) | (24) |
| CCMC = [(C0CMC)(1+α)](CS)−α. | (25) |
6 Aggregation number and micelle shape
In this section, we use our model to determine the equilibrium aggregation number for surfactants S8S, S12S and S16S. For each surfactant, we do this for a range of concentrations: 2.5, 5, 7.5, 10 wt%. The simulations are set up in the same way as described in Section 5, however, here we use much smaller boxes than those that were required for calculating the CMC. We take an approach that has previously been used by other authors,28 in which we keep the number of surfactant molecules NS in the box constant and alter the number of water beads NW to vary the concentration of the box. We use NS = 500 surfactant molecules, meaning that the smallest simulation box used is for the S8S surfactant at a concentration of 10% (NW = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168), and our largest box is for the S16S surfactant at a concentration of 2.5% (NW = 136
168), and our largest box is for the S16S surfactant at a concentration of 2.5% (NW = 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010). Each simulation is equilibrated for long simulations until the aggregation number is determined to no longer change.
010). Each simulation is equilibrated for long simulations until the aggregation number is determined to no longer change.
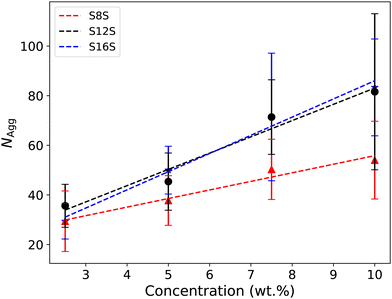
Fig. 9 shows the final aggregation number calculated for each simulation case. We see that the aggregation size generally increases with both tail length and concentration. There is a reasonably broad distribution of micelle sizes in each simulation case, represented by the relatively large error bars shown in Fig. 9. For example, for C16 at a concentration of 10%, we find that 6 micelles form of various sizes in the range 50–113. Experimentally,77 S8S is reported to have an aggregation number at around NAgg ≈ 40 at 6.4 wt%, which is in good agreement with our simulated results. However, S12S is reported as having NAgg ≈ 80 at 2.9 wt%, indicating that our simulated value of around NAgg ≈ 36 is a significant underestimate.
Other authors have commonly reported that the aggregation number for micelles formed by ionic surfactants in DPD simulations are underpredicted.28,29 One suggestion is that this underprediction is due to problems with equilibration. This stems from the fact that micelles with a net charge would have a significant amount of repulsion between them. Therefore, on the time scale of the simulation, they may not meet sufficiently to come together and aggregate to form larger micelles.
In order to test the impact of the charges on equilibration, we performed simulations in which the charges were initially turned off. We expect that this will allow the surfactant molecules to aggregate significantly more easily, due to the reduced repulsion between head groups. In all cases, we simulate using a total of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads, and we vary the number of surfactant molecules NS in the box.
000 beads, and we vary the number of surfactant molecules NS in the box.
In the NS range studied (20 < NS < 220) we observe that the surfactants quickly aggregate into a single, large micelle, often significantly above the experimental aggregation number. An example is shown in Fig. 10a. Note that the formation of large micelles is to be expected because one would expect head group repulsion to be a limiting factor on micelle size. However, this approach allows us to treat this single large micelle as an ‘initial state’ for studying anionic micelles. It has been shown20 that when simulations are initialised with micelles larger than their experimental values, they can break down into micelles, which are closer in size to those expected experimentally.
When the charges are turned on, the micelle transforms its shape and the counterions move to surround the micelle. However, the micelle does not necessarily break down into smaller aggregates, as one might expect. The S12S and S16S molecules always remain as a single micelle, during the run time, albeit with a significant shape change at high aggregation numbers (see Fig. 10b). This behaviour allows us to study micelles as a function of their aggregation number, and, in particular, study shape changes. However, for S8S surfactants, which have weaker attraction between (shorter) chains, the micelles exhibit different behaviour and break down once the electrostatic interactions are turned on when the initial micelle is above a particular size (NS ⪆ 80). This suggests that for S8S, large metastable micelles are significantly less stable than for the two longer surfactant molecules. This may also be reflective of the fact that experiments have shown that the width of the distribution of stable micelles increases with chain length.16
To quantify the non-spherical nature of the large micelles, we calculate the moment of inertia Im (where m = x,y,z). From this, we define the eccentricity:
 | (26) |
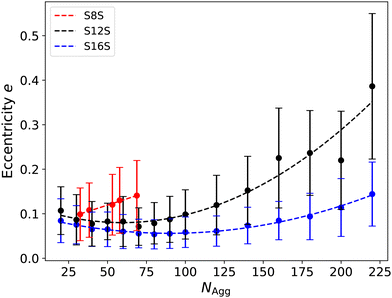
A plot of eccentricity as a function of aggregation number is shown in Fig. 11. For S8S surfactants, we are limited to studying a reduced range of surfactant sizes due to the breakdown of micelles when initialised at larger aggregation numbers. The bars plotted illustrate the standard deviation of the eccentricity over the measurement period, highlighting the significant fluctuations in shape we observe, particularly as the micelle sizes increase. We observe that the eccentricity increases with decreasing tail length, with S16S micelles being the most spherical at all micelle sizes. For the S12S and S16S surfactants, there appears to be a minima illustrating an optimal value of the aggregation number for which the micelles are most spherical, which is located around 60 for S12S and 90 for S16S. It is of interest that these values are very close to the experimental values for the average aggregation numbers at the CMC (where NAgg = 64 and NAgg = 100 for S12S and S16S respectively16), and small angle scattering studies5,78 and packing parameter calculations79,80 indicate that SDS micelles at this concentration should be relatively spherical. Following this plateau, the eccentricity increases with larger aggregation size as the micelles begin to alter their shape. This increase is significantly more rapid for S12S compared to S16S, with the S12S micelles showing a more rapid transition to rod-like shapes. Spin probe experiments have indicated that SDS micelles start to become rod-like at aggregation numbers around 130,81 which is in agreement with what we observe in our simulations.
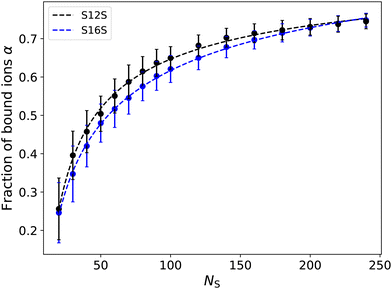
In Section 5 we chose to define the degree of counterion binding as α = 0.7. Using our simulations of single micelles, we are now able to calculate the degree of binding as a function of micelle size, to investigate whether this was a suitable choice. We calculate α by determining the number of sodium ions within a specified cutoff range RIons of the micelle head groups. This cutoff range is refined using the first peak of the radial distribution function between the head groups and the counterions. Fig. 12 shows examples of the radial distribution function for different molecules of various sizes. While the magnitude of the g(r) peaks varies significantly, we note that the local minima between the two first peaks (at a distance of 0.9rC) does not significantly vary in position. Therefore, we choose a cutoff distance of RIons = 0.9 in all calculations for determining α.
 | ||
| Fig. 12 Radial distribution function between the head groups and counterions for molecules of different size and type. | ||
In order to determine the number of ions which are bound to the micelle, our aim is to calculate the average number of ions which are within cutoff radius RIons of the head groups in the micelle (i.e. the surface of the micelle). Here we can use the simplification that all surfactants are contained within the micelle (that is, there are no free surfactants). This can be done in one of two ways. The first is to make use of the radial distribution g(r) directly and calculate the number of particles within distance RIons
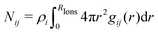 | (27) |
| α = P(n ≥ 1) = 1 − e−Nij(RIons). | (28) |
Fig. 13 shows how the number of ions bound to a micelle depends on the aggregation size. Here we focus on the S12S and S16S micelles due to the wide range of micelle sizes we have available for study. While we do not observe a significant dependence on tail length, we see a strong dependence on micelle size. With increasing size, the micelle increases its net charge, likely increasing the percentage of bound ions to aid its electrostatic screening. At larger micelle sizes (NS ⪆ 100) the number of bound ions is in agreement with experimental values, and therefore in line with what was used in Section 5 to calculate the CMC in this work.
However, since the value of α appears to be affected by varying the concentration/size of the system (particularly at lower sizes), we investigate the impact this has on our previous calculation of the CMC since our micelles are typically smaller in these simulations. However, similarly to others,28,69 we observe that varying α ≈ 0.4–0.8 does not have a significant impact on the calculated CMC. For example, using a value of α = 0.4 yields an estimate for the CMC of 2.70 mM (compared to a CMC value of 2.65 when using α = 0.7). Thereby making our previous choice of α = 0.7 a reasonable one.
We also note that it is possible to predict the degree of counter-ion binding using eqn (23), and measurements of the CMC in the presence of salt. We take the experimental value for the CMC of saltless SDS as 8.2 mM16,17 (Table 2) and the CMC in the presence of 15 mM and 100 mM of salt as 4.2 mM and 1.7 mM,18 respectively (Table 3). Using eqn (23) yields estimates for the counter-ion binding of α = 0.79 and α = 0.62, where the average of these two values α = 0.71 almost perfectly matches our choice of α = 0.7.
7 Discussion
We discuss here some of the key results and considerations for our model, including the choice to use point charges as opposed to smeared charges; issues related to equilibration and aggregation number prediction; the impact of the tail–water interaction on our parameterisation scheme and the quantities we calculate; and finally, how our results compare with those from other experiments and simulations.7.1 Use of point charges
As a result of our choice to use MDPD compared to standard DPD, we are able to use point charges as opposed to smeared charges. The smeared charge approach, which is typically used in traditional DPD methods, is usually applied to deal with the fact that the soft repulsion experienced by DPD beads is not strong enough to prevent ion-pair formation. However, in this work, we show that there is no evidence of ion collapse occurring in our MDPD simulations.The ability to use point charges was hypothesised as a result of our analysis of the strength of the repulsion at short ranges and was confirmed by checking the radial distribution functions from salt solutions at high concentrations. We check that our charged ions in micelle simulations behave correctly by calculating the number of bound ions as a function of aggregation number. This allows us to confirm that the degree of dissociation of the counterions is in excellent agreement with experimental values, which is crucial for studying the shape and size of simulated micelles.
The use of point charges is simpler than smeared charges, and eliminates the issue that there are often several unknowns when charges are smeared over the bead volume. For example, various forms of the smear function have been proposed82–85 and various degrees of smearing have been used by different authors.29,83 The function and degree of smearing are typically chosen for computational efficiency reasons as opposed to scientific reasoning, with little attention paid to the impact this has on the simulated results. However, we note that the use of smeared charges is perfectly possible within MDPD, is fully implemented within codes such as DL_MESO, and potentially could remove the danger of stability issues in some cases (noting the Fisher–Ruelle stability criterion86).
7.2 Equilibration of aggregation number
We observe that our calculated aggregation number equilibrates very slowly, such that it can be difficult to ascertain when equilibration has completed. We also observe that our aggregation numbers are somewhat lower than might be expected for the S12S2 and S16S surfactants. Once formed, charged micelles do not meet on the time scales we look at. The net repulsion between charged micelles is so great, that the micelles never get close enough to aggregate into larger micelles. This creates a difficulty in generating larger aggregation numbers.In experimental reality, micelles are in dynamic equilibrium constantly disintegrating and reforming, and it is generally considered that micellar solutions exhibit two relaxation processes16,87,88 characterised by relaxation times τ1 and τ2. The first timescale τ1 relates to the exchange of surfactant monomers between micelles (order of microseconds), while τ2 relates to micellization-dissolution equilibrium (order of milliseconds). Experiments16 on sodium alkyl sulfate solutions have shown that, in general, τ1 and τ2 decrease with surfactant concentration and also increase with increasing alkyl chain length. This may partially explain our difficulty in equilibrating micelles at lower concentrations and longer tail lengths. To overcome these time-scale limitations, a potentially interesting approach for future researchers might be the use of a biased Monte Carlo simulation technique, in which one computes micelle free energies as functions of aggregation number in order to determine the equilibrium aggregation numbers.89
7.3 Choice of tail–water interaction
In Section 3.3 it was shown that the tail–water interaction is defined based on a Widom insertion approach, with octane being the reference molecule. The choice to use octane was based on the fact that, in our coarse-grained representation, it can be represented by two single-bonded beads. While matching a longer hydrocarbon might be more desirable for calculating the CMC for larger molecules, such as dodecane or even hexadecane, it is worth noting that the Widom insertion calculation is much more complex for longer molecules. Firstly, it would involve more than two beads, and therefore conformation needs to be taken into account when performing insertions. Secondly, a larger molecule would result in finding an accurate value for μexcess very difficult. For a larger molecule, the available space in the simulation box in which the molecule can be inserted is very limited. This means that most insertion attempts result in very high insertion energies ΔU, resulting in exp(−ΔU/kBT) becoming negligibly small most of the time. This means that determining μexcess is statistically difficult and inefficient. For these reasons, we chose to focus on insertions of octane.However, we observe that the precise value of the CMC calculated is very sensitive to the value of aTW. This has been commented on in conventional DPD by previous authors.29 To illustrate this point, we calculate a value for the CMC of S12S if we increase the value of the tail–water interaction by a small amount, choosing ΔaTW = 0.5 (such that the new value aTW = 37.076, an increase of about 1.4%). In this case, we calculate a CMC value (using method A) as CCMC = 9.1 mM (see ESI† for details), compared to the value of 5.04 mM calculated using our original parameters. Therefore, we caution that it is possible that small inaccuracies in the calculated value of aTW can lead to large changes in the CMC, and that our exact values of CMC could be improved by matching tail–water interactions to different choices of molecules. However, we also note both the aggregation number and micellar shape are relatively insensitive to the exact choice of aTW, at least to a significantly lesser extent than the CMC.
7.4 Comparison with earlier studies
In this article, we report values for the CMC and aggregation number for sodium octyl sulfate, sodium dodecyl sulfate and sodium hexadecyl sulfate. We also report on the change in the CMC for additional salt for SDS solutions. Finally, we also report the fraction of bound ions α as a function of aggregation number, as well as their eccentricity as a means to quantify micellar shape.We showed that both without (Table 2) and with (Table 3) salt, our CMC values are underpredicted in comparison with the experimental data, however, the trends of CMC with tail length match experimental data reasonably well. It is an issue that other authors have also found when using standard DPD approaches,28,38 and it is difficult to attribute an exact reason for this. However, we will note that accurate prediction of the CMC is expected to be difficult from theoretical reasons alone. The Gibbs free energy change for micelle formation from 1 mol surfactant is related to the CMC by
ΔG0 = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CMC, CMC, | (29) |
We discussed in the previous section the sensitivity that the CMC has to the tail–water interaction, however, the CMC mismatch is most likely to result from how we treat charges in the system since these have the greatest impact on altering the CMC behaviour. We made no attempt to parameterise the charged beads in our model, and it is highly likely that the treatment of charges will need to be tuned to accurately reproduce the correct ΔG0. Up until now, direct parameterisation of charged beads has been largely neglected, with most authors taking the simple approach to assign beads as having the same aij interactions as water. However, an interesting study by Lavagnini et al.90 indicated that for salt solutions, even for nonionic surfactants, the calculated CMC values depend largely on the ion-tail repulsion parameter, meaning that this is likely to be a source of error in our approach.
Turning our attention now to the shape of micelles, it was noted in Section 6 that spin probe experiments indicate that SDS micelles start to become rod-like at aggregation numbers which are comparable to those we see in our simulations. There is also a wealth of literature using small-angle neutron scattering (SANS)4–10 and small-angle X-ray scattering13–15 (SAXS) to investigate the shape and size of SDS micelles. Typically it is concluded that micelles at equilibrium are nearly spherical, but slightly prolate, which is in agreement with what we see in our study. Fig. 11 shows that we never determine an eccentricity of 0 (which would correspond to a spherical micelle), instead usually taking larger values of 0.1 < e. Interestingly, a molecular dynamics study by Palazzesi et al.24 reported an eccentricity value of around e = 0.15 for SDS micelles at aggregation numbers of N = 60, which is in reasonably good agreement with that we have reported at in this article. Other DPD studies31 have also found similar degrees of eccentricity for micelles of around this size.
Finally, we discuss the binding of ions to micelles. It was noted in Section 6 that our calculated fraction of bound ions α is generally in line with experimental measurements74 at comparable micelle sizes. It is difficult to compare with experimental data for smaller micelles, as data only exists for micelles at their equilibrium, larger sizes. However, it was shown that the counter ion binding varies very little over SDS micelles in the range 60 ≤ N ≤ 110, which is broadly what we see in Fig. 13.
The degree of counterion binding is a quantity that can also be determined by molecular dynamics simulations of single micelles. It has been shown that α can depend on the choice of force field21 (where Tang et al.21 define bound ions to be sodium atoms which exist within 0.6 nm of the oxygen atoms in the head group). Authors report that for an SDS micelle with aggregation number N = 60, α ranges from 45–70% for the six force fields tested, which is generally in line with experimental values. Using a cutoff of 0.9rC (0.76 nm), we determined in our simulations that micelles of the same size have α = 0.55, while if we use a cutoff 0.71rC (which translates in real units to a more comparable value to Tang et al.21) we find α = 0.48. This puts our MDPD simulated value in reasonable agreement with those from MD simulations. However, it is still worth noting that this still is not exactly comparable, since the distance used in our calculation is the centre of the bead rather than the oxygen atoms, and if calculated equivalently our values are likely to have even closer matching.
8 Conclusion
In this article, we present a comprehensive parameterisation scheme for MDPD simulations. We conclude that our MDPD model provides good estimates for the CMC as a function of tail length and salt concentration. Our model also allows us to easily study micelles, including their size, shape, and charge, making it a useful tool for studying charged surfactants. We believe that, using the methodology presented here, the model could easily be extended to other ionic and nonionic surfactants, to oils, to mixed surfactant systems and to higher concentration phases.Author contributions
RH: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. CA: project administration, writing – review and editing. MW: funding acquisition, project administration, supervision, writing – review and editing.Data availability
The data that support the findings of this study are available from the corresponding author, RH, upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the support of Durham University for the use of its HPC facility, Hamilton. RH would like to acknowledge support through an EPSRC/P&G funded Prosperity Partnership grant EP/V056891/1.Notes and references
- P. Kékicheff, C. Grabielle-Madelmont and M. Ollivon, J. Colloid Interface Sci., 1989, 131, 112–132 CrossRef.
- A. S. Poulos, C. S. Jones and J. T. Cabral, Soft Matter, 2017, 13, 5332–5340 RSC.
- A. Capaccio, S. Caserta, S. Guido, G. Rusciano and A. Sasso, J. Colloid Interface Sci., 2020, 561, 136–146 CrossRef CAS.
- S. S. Berr and R. R. M. Jones, Langmuir, 1988, 4, 1247–1251 CrossRef CAS.
- B. Cabane, R. Duplessix and T. Zemb, J. Phys., 1985, 46, 2161–2178 CrossRef CAS.
- M. Bergstrom and J. S. Pedersen, Phys. Chem. Chem. Phys., 1999, 1, 4437–4446 RSC.
- L. J. Magid, Z. Li and P. D. Butler, Langmuir, 2000, 16, 10028–10036 CrossRef CAS.
- M. Kakitani, T. Imae and M. Furusaka, J. Phys. Chem., 1995, 99, 16018–16023 CrossRef CAS.
- M. Ludwig, R. Geisler, S. Prévost and R. von Klitzing, Molecules, 2021, 26, 4136 CrossRef CAS PubMed.
- B. Hammouda, J. Res. Natl. Inst. Stand. Technol., 2013, 118, 151–167 CrossRef CAS.
- S. Khodaparast, W. N. Sharratt, G. Tyagi, R. M. Dalgliesh, E. S. Robles and J. T. Cabral, J. Colloid Interface Sci., 2021, 582, 1116–1127 CrossRef CAS.
- V. Y. Bezzobotnov, S. Borbely, L. Cser, B. Farago, I. A. Gladkih, Y. M. Ostanevich and S. Vass, J. Phys. Chem., 1988, 92, 5738–5743 CrossRef CAS.
- S. L. Gawali, M. Zhang, S. Kumar, D. Ray, M. Basu, V. K. Aswal, D. Danino and P. A. Hassan, Langmuir, 2019, 35, 9867–9877 CrossRef CAS.
- J. Lipfert, L. Columbus, V. B. Chu, S. A. Lesley and S. Doniach, J. Phys. Chem. B, 2007, 111, 12427–12438 CrossRef CAS.
- Y. Mirgorod, A. Chekadanov and T. Dolenko, Chem. J. Mold., 2019, 14, 107–119 CAS.
- E. A. G. Aniansson, S. N. Wall, M. Almgren, H. Hoffmann, I. Kielmann, W. Ulbricht, R. Zana, J. Lang and C. Tondre, J. Phys. Chem., 1976, 80, 905–922 CrossRef CAS.
- F. H. Quina, P. M. Nassar, J. B. Bonilha and B. L. Bales, J. Phys. Chem., 1995, 99, 17028–17031 CrossRef CAS.
- E. Dutkiewicz and A. Jakubowska, Colloid Polym. Sci., 2002, 280, 1009–1014 CrossRef CAS.
- H. Khan, J. M. Seddon, R. V. Law, N. J. Brooks, E. Robles, J. T. Cabral and O. Ces, J. Colloid Interface Sci., 2019, 538, 75–82 CrossRef CAS PubMed.
- S. D. Peroukidis, D. G. Mintis, I. Stott and V. G. Mavrantzas, JPhys Mater., 2021, 4, 044001 CrossRef CAS.
- X. Tang, P. H. Koenig and R. G. Larson, J. Phys. Chem. B, 2014, 118, 3864–3880 CrossRef CAS PubMed.
- S. Jalili and M. Akhavan, Colloids Surf., A, 2009, 352, 99–102 CrossRef CAS.
- N. Yoshii and S. Okazaki, Condens. Matter Phys., 2007, 10, 573 CrossRef.
- F. Palazzesi, M. Calvaresi and F. Zerbetto, Soft Matter, 2011, 7, 9148 RSC.
- B. J. Chun, J. I. Choi and S. S. Jang, Colloids Surf., A, 2015, 474, 36–43 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- D. Nivón-Ramírez, L. I. Reyes-García, R. Oviedo-Roa, R. Gómez-Balderas, C. Zuriaga-Monroy and J.-M. MartínezMagadán, Colloids Surf., A, 2022, 645, 128867 CrossRef.
- R. L. Anderson, D. J. Bray, A. Del Regno, M. A. Seaton, A. S. Ferrante and P. B. Warren, J. Chem. Theory Comput., 2018, 14, 2633–2643 CrossRef CAS PubMed.
- R. Mao, M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2015, 119, 11673–11683 CrossRef CAS PubMed.
- M. Panoukidou, C. R. Wand, A. Del Regno, R. L. Anderson and P. Carbone, J. Colloid Interface Sci., 2019, 557, 34–44 CrossRef CAS.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed.
- S. J. Gray, M. Walker, R. Hendrikse and M. R. Wilson, Soft Matter, 2023, 19, 3092–3103 RSC.
- T. L. Rodgers, O. Mihailova and F. R. Siperstein, J. Phys. Chem. B, 2011, 115, 10218–10227 CrossRef CAS PubMed.
- S. Jury, P. Bladon, M. Cates, S. Krishna, M. Hagen, N. Ruddock and P. Warren, Phys. Chem. Chem. Phys., 1999, 1, 2051–2056 RSC.
- R. D. Groot, Langmuir, 2000, 16, 7493–7502 CrossRef CAS.
- G. Kacar, E. A. J. F. Peters and G. de With, EPL, 2013, 102, 40009 CrossRef.
- M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Chem. Theory Comput., 2015, 11, 4395–4403 CrossRef CAS.
- M.-T. Lee, R. Mao, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2016, 120, 4980–4991 CrossRef CAS.
- A. Maiti and S. McGrother, J. Chem. Phys., 2004, 120, 1594–1601 CrossRef CAS PubMed.
- L. Rekvig, M. Kranenburg, J. Vreede, B. Hafskjold and B. Smit, Langmuir, 2003, 19, 8195–8205 CrossRef CAS.
- K. P. Travis, M. Bankhead, K. Good and S. L. Owens, J. Chem. Phys., 2007, 127, 014109 CrossRef PubMed.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS.
- A. Vishnyakov, R. Mao, M.-T. Lee and A. V. Neimark, J. Chem. Phys., 2018, 148, 024108 CrossRef PubMed.
- R. L. Anderson, D. Bray, A. S. Ferrante, M. G. Noro, I. P. Stott and P. Warren, J. Chem. Phys., 2017, 147, 094503 CrossRef.
- A. Truszkowski, M. Epple, A. Fiethen, A. Zielesny and H. Kuhn, J. Colloid Interface Sci., 2013, 410, 140–145 CrossRef CAS PubMed.
- M. Walker, A. J. Masters and M. R. Wilson, Phys. Chem. Chem. Phys., 2014, 16, 23074–23081 RSC.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8588–8594 RSC.
- I. Pagonabarraga and D. Frenkel, J. Chem. Phys., 2001, 115, 5015–5026 CrossRef CAS.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- P. B. Warren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 066702 CrossRef CAS.
- P. B. Warren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 045303 CrossRef.
- Y.-C. Li, H. Liu, X.-R. Huang and C.-C. Sun, Mol. Simul., 2011, 37, 875–883 CrossRef CAS.
- A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2012, 8, 787–791 CrossRef CAS.
- R. Hendrikse, A. Bayly and P. Jimack, J. Chem. Phys., 2023, 158, 214906 CrossRef CAS PubMed.
- K. A. Terrón-Mejía, R. López-Rendón and A. G. Goicochea, J. Phys.: Condens. Matter, 2016, 28, 425101 CrossRef PubMed.
- D. J. Bray, R. L. Anderson, P. B. Warren and K. Lewtas, J. Phys. Chem. B, 2022, 126, 5351–5361 CrossRef CAS.
- H. Alasiri and W. G. Chapman, J. Mol. Liq., 2017, 246, 131–139 CrossRef CAS.
- A. Khedr and A. Striolo, J. Chem. Theory Comput., 2018, 14, 6460–6471 CrossRef CAS.
- K. Shi, C. Lian, Z. Bai, S. Zhao and H. Liu, Chem. Eng. Sci., 2015, 122, 185–196 CrossRef CAS.
- P. M. Pieczywek, W. Płazinski and A. Zdunek, Sci. Rep., 2020, 10, 14691 CrossRef CAS.
- R. L. Hendrikse, C. Amador and M. R. Wilson, Soft Matter, 2023, 19, 3590–3604 RSC.
- A. Ben-Naim, J. Phys. Chem., 1978, 82, 792–803 CrossRef CAS.
- I. Levine, Physical Chemistry, McGraw-Hill Education, 2009, pp. 295–302 Search PubMed.
- M. A. Seaton, The DL_MESO Mesoscale Simulation Package, STFC Computational Science and Engineering Department, 2012, https://www.ccp5.ac.uk/DL_MESO.
- J. Chang, J. Chem. Phys., 2009, 131, 074103 CrossRef.
- W. Hayduk and C.-F. Wong, Can. J. Chem. Eng., 1990, 68, 653–660 CrossRef CAS.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19 RSC.
- K. Kojima, S. Zhang and T. Hiaki, Fluid Phase Equilib., 1997, 131, 145–179 CrossRef CAS.
- S. A. Sanders, M. Sammalkorpi and A. Z. Panagiotopoulos, J. Phys. Chem. B, 2012, 116, 2430–2437 CrossRef CAS.
- S. A. Sanders and A. Z. Panagiotopoulos, J. Chem. Phys., 2010, 132, 114902 CrossRef.
- M. S. Hossain, S. Berg, C. A. S. Bergström and P. Larsson, AAPS PharmSciTech, 2019, 20, 61 CrossRef CAS.
- Y. Ruiz-Morales and A. Romero-Martínez, J. Phys. Chem. B, 2018, 122, 3931–3943 CrossRef CAS.
- M. A. Johnston, W. C. Swope, K. E. Jordan, P. B. Warren, M. G. Noro, D. J. Bray and R. L. Anderson, J. Phys. Chem. B, 2016, 120, 6337–6351 CrossRef CAS.
- B. L. Bales, J. Phys. Chem. B, 2001, 105, 6798–6804 CrossRef CAS.
- H. Lange and M. J. Schwuger, Colloid Polym. Sci., 1968, 223, 145–149 CrossRef CAS.
- H. Kumar and G. Kaur, J. Dispersion Sci. Technol., 2021, 42, 970–983 CrossRef CAS.
- R. Ranganathan, L. Tran and B. L. Bales, J. Phys. Chem. B, 2000, 104, 2260–2264 CrossRef CAS.
- A. T. Gubaidullin, I. A. Litvinov, A. I. Samigullina, O. S. Zueva, V. S. Rukhlov, B. Z. Idiyatullin and Y. F. Zuev, Russ. Chem. Bull., 2016, 65, 158–166 CrossRef CAS.
- T. S. Banipal, H. Kaur and P. K. Banipal, J. Mol. Liq., 2016, 218, 112–119 CrossRef CAS.
- Z. Ettarhouni, F. Elarbei, A. Jangher and L. Abusen, Am. J. Eng. Res., 2020, 9, 118–126 Search PubMed.
- B. L. Bales, L. Messina, A. Vidal, M. Peric and O. R. Nascimento, J. Phys. Chem. B, 1998, 102, 10347–10358 CrossRef CAS.
- P. B. Warren and A. Vlasov, J. Chem. Phys., 2014, 140, 084904 CrossRef PubMed.
- R. D. Groot, J. Chem. Phys., 2003, 118, 11265–11277 CrossRef CAS.
- M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107 CrossRef.
- P. B. Warren, A. Vlasov, L. Anton and A. J. Masters, J. Chem. Phys., 2013, 138, 204907 CrossRef PubMed.
- M. E. Fisher and D. Ruelle, J. Math. Phys., 1966, 7, 260–270 CrossRef CAS.
- J. Lang, C. Tondre, R. Zana, R. Bauer, H. Hoffmann and W. Ulbricht, J. Phys. Chem., 1975, 79, 276–283 CrossRef CAS.
- A. Patist, J. R. Kanicky, P. K. Shukla and D. O. Shah, J. Colloid Interface Sci., 2002, 245, 1–15 CrossRef CAS PubMed.
- J. A. Mysona, A. V. McCormick and D. C. Morse, Phys. Rev. E, 2019, 100, 012602 CrossRef.
- E. Lavagnini, J. L. Cook, P. B. Warren and C. A. Hunter, J. Phys. Chem. B, 2022, 126, 2308–2315 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00533c |
| This journal is © The Royal Society of Chemistry 2024 |