Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Entangled nematic disclinations using multi-particle collision dynamics
Louise C.
Head
 *ab,
Yair A. G.
Fosado
*ab,
Yair A. G.
Fosado
 a,
Davide
Marenduzzo
a,
Davide
Marenduzzo
 a and
Tyler N.
Shendruk
a and
Tyler N.
Shendruk
 *a
*a
aSchool of Physics and Astronomy, The University of Edinburgh, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK. E-mail: t.shendruk@ed.ac.uk
bDepartment of Physics and Astronomy, Johns Hopkins University, Baltimore, MD, USA. E-mail: l.c.head@jhu.edu
First published on 22nd August 2024
Abstract
Colloids dispersed in nematic liquid crystals form topological composites in which colloid-associated defects mediate interactions while adhering to fundamental topological constraints. Better realising the promise of such materials requires numerical methods that model nematic inclusions in dynamic and complex scenarios. We employ a mesoscale approach for simulating colloids as mobile surfaces embedded in a fluctuating nematohydrodynamic medium to study the kinetics of colloidal entanglement. In addition to reproducing far-field interactions, topological properties of disclination loops are resolved to reveal their metastable states and topological transitions during relaxation towards ground state. The intrinsic hydrodynamic fluctuations distinguish formerly unexplored far-from-equilibrium disclination states, including configurations with localised positive winding profiles. The adaptability and precision of this numerical approach offers promising avenues for studying the dynamics of colloids and topological defects in designed and out-of-equilibrium situations.
1 Introduction
Dispersions of colloidal particles in liquid crystals1 are of interest to physicists because they provide a pathway to realise soft materials with interesting target properties, such as photonic crystals,2 cloaks and metamaterials,3 or self-quenched glasses.4 This versatility is due to the fact that topology and elastic distortions in the liquid crystalline host lead to long-range interactions which can be tuned by varying particle size, shape and liquid crystalline properties, even in a simple nematic. When combined with a suitable kinetic protocol, these interactions can be harnessed to self-assemble different types of materials.5To understand the physical mechanisms underlying the self-assembly of different structures, a useful and popular starting point is that of two colloidal particles in a nematic, with normal anchoring at the colloidal surface. On the one hand, analysing this geometry leads to an estimate of the effective pair potential between particles, which includes elasticity and defect-mediated interactions, and which is important for self-assembly in many-particle systems.6–8 On the other hand, the problem of a colloidal dimer in a liquid crystal is interesting from a fundamental point of view, due to the central role played by topology.9 Indeed, the liquid crystalline pattern needs to be topologically trivial overall,6,7 but this can be realised in a number of possible ways. For instance, each colloid can be surrounded by a topologically charged Saturn ring,10,11 as the total topological charge in the system only needs to equal 0 modulo 2 in three dimensions.6,12 However, another topologically allowed configuration is one where a single writhed disclination loop wraps around both colloids. Configurations such as these are referred to as entangled disclinations, and the writhe in the loop cancels the topological charge which would otherwise be present.7 The relation between writhe and topological charge can be understood by introducing the self-linking number,6,13 which describes the topology of a disclination loop, in the case where the local director field profile (in the plane perpendicular to the loop tangent) is topologically equivalent to that of a planar defect with winding number −1/2, or a triradius. In such cases, the loop possesses the same topology as a ribbon.7 In this way, colloids dispersed in liquid crystals can act as probes for fundamental questions of topology.
Colloidal dispersions in nematics have mainly been studied with continuum models, either via free energy minimisation techniques,4,7 or by means of hybrid lattice Boltzmann simulations.14 In this work, we employ a different methodology to study a single colloid or a pair of colloids in a nematic host, based on multi-particle collision dynamics (MPCD). Though it was traditionally applied to moderate-Péclet number situations within isotropic fluids, the MPCD algorithm has recently been extended to simulate fluctuating, linear nematohydrodynamics15,16 or to be hybridised with continuum descriptions of the nematic.17–20 Importantly, this nematic algorithm (N-MPCD) captures the competing influences of thermal fluctuations, elastic interactions, and hydrodynamics, and hence can be used to study the topological evolution of defect structures over time. The natural inclusion of noise makes it possible to consider the case of small particles, where the free energy profile of the system is rid of large barriers, which otherwise dominate the colloidal kinetics.3 The fact that N-MPCD provides a particle-based description of the nematic fluid also simplifies the treatment of boundary conditions, and hence makes it easier to extend this algorithm to complex surface geometries, such as rodlike particles21 or wavy channels.22 Additionally, MPCD can be readily extended to study active nematics23,24 and systems with many colloids, thereby providing a powerful package to study the hydrodynamics of topological composite materials.25
Here, the N-MPCD algorithm is validated by computing the elastic force between a colloid and a wall, or between two colloids. These follow scaling laws in agreement with previous theoretical predictions and numerical estimates. The topological patterns are studied, both over time and in steady state with a single colloidal particle or a colloidal dimer. The steady-state patterns broadly confirm the set of structures predicted in the literature by elastic energy minimisation.26 Thus, a pair of Boojums for colloids with tangential anchoring are found. With normal anchoring, a Saturn ring and a dipolar halo are found. A colloidal dimer with normal anchoring results in either two topologically charged loops or an uncharged but writhed loop with non-trivial self-linking numbers. However, thermal fluctuations and boundary influences can lead to tilted and non-ideal versions of these entangled structures. Although disclination loops are always associated with local director field patterns with −1/2 profiles in steady state, a wider variety of states are observed en route to equilibrium. These are found to differ substantially in their geometric features. Examples of transient patterns include longer loops with twist and even +1/2 local director profiles, as well as skewed rings.
2 Methods
Multi-particle collision dynamics is a coarse-grained mesoscopic particle-based hydrodynamic solver that is versatile for simulating a wide variety of Newtonian,27 complex28 and active fluids.23,24 It has found particular utility simulating suspensions of polymers,29 colloids30,31 and bacteria,32,33 because its intrinsic thermal noise makes it ideal for moderate Péclet numbers. Since N-MPCD can support elastic and hydrodynamic interactions, combined with thermal diffusivity, this offers a promising avenue for studying topological microfluidics,34,35 design principles for self assembly kinetics, defect interactions with active fields,23,24 and microfluidic transport through harnessing energy landscapes.22,362.1 Bulk nematohydrodynamic evolution
Nematic multi-particle collision dynamics discretises continuous hydrodynamic fields for mass, momentum and orientational order into N point particles, indexed by i, with mass mi, position xi, velocity vi and orientation ui in d dimensions. N-MPCD is a two-step algorithm, in which particles evolve through (i) streaming and (ii) collision steps, dictating how the particles move and interact with their local environment.27The streaming step controls the spatial evolution of each particle position, defined as ballistic streaming over the time interval δt
| xi(t + δt) = xi(t) + vi(t)δt. | (1) |
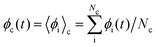 . The evolution equations for vi and ui have contributions from cell-based momentum-conserving collision operators. First considering the translational momentum collision
. The evolution equations for vi and ui have contributions from cell-based momentum-conserving collision operators. First considering the translational momentum collision| vi(t + δt) = vc(t) + Ξveli,c(t). | (2) |
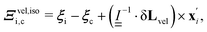 | (3) |
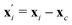 with a moment of inertia tensor
with a moment of inertia tensor 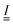 and angular momentum Lvel about xc. Since the collision operator is applied to lattice-based cells, a random grid shift is included to preserve Galilean invariance.39,40
and angular momentum Lvel about xc. Since the collision operator is applied to lattice-based cells, a random grid shift is included to preserve Galilean invariance.39,40
A cell-based collision operation is also applied to orientations
| ui(t + δt) = nc(t) + Ξorii,c(t). | (4) |
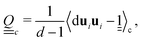 allows the local scalar order parameter Sc and director nc to be found as the largest eigenvalue and corresponding eigenvector. Treating the cell's orientational order parameters as a mean field, the orientation collision Ξorii,c stochastically draws orientations from a local Maier–Saupe distribution fori = f0
allows the local scalar order parameter Sc and director nc to be found as the largest eigenvalue and corresponding eigenvector. Treating the cell's orientational order parameters as a mean field, the orientation collision Ξorii,c stochastically draws orientations from a local Maier–Saupe distribution fori = f0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(USc(ui·nc)2/kBT), centered about nc with a normalisation constant f0 and a mean field interaction constant U. The interaction constant is linearly proportional to the one-constant approximation of Frank elasticity K.15 For large U, the particle orientations are deep in the nematic phase, aligning close to the free energy minimum, with small thermal fluctuations.
exp(USc(ui·nc)2/kBT), centered about nc with a normalisation constant f0 and a mean field interaction constant U. The interaction constant is linearly proportional to the one-constant approximation of Frank elasticity K.15 For large U, the particle orientations are deep in the nematic phase, aligning close to the free energy minimum, with small thermal fluctuations.
Nematohydrodynamics requires coupling terms in eqn (2) and (4) to account for velocity gradients rotating orientations and orientational motion generating nematic backflows. This can be cast in terms of an overdamped bulk-fluid torque equation for each particle i
| Γcoli + ΓHIi + Γdissi = 0. | (5) |
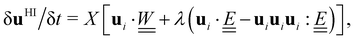 where X is a shear coupling coefficient that influences the relaxation time of alignment relative to δt, λ is the flow tumbling parameter, and
where X is a shear coupling coefficient that influences the relaxation time of alignment relative to δt, λ is the flow tumbling parameter, and 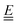 and
and 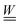 are the symmetric and skew-symmetric components of the velocity gradient tensor. The remaining contribution is the dissipative torque Γdiss, which is converted into backflow in the velocity evolution equation through an angular momentum correction
are the symmetric and skew-symmetric components of the velocity gradient tensor. The remaining contribution is the dissipative torque Γdiss, which is converted into backflow in the velocity evolution equation through an angular momentum correction 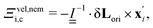 where
where 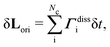 which goes into eqn (2). By including Ξvel,nemi,c in the translational collision operation (eqn (2)), the effect of reorientation-induced flow (backflow) is accounted for. Backflow is small when γRX ≪ 1.16
which goes into eqn (2). By including Ξvel,nemi,c in the translational collision operation (eqn (2)), the effect of reorientation-induced flow (backflow) is accounted for. Backflow is small when γRX ≪ 1.16
This orientation collision operator approach has been demonstrated to simulate linearised Qian–Sheng nematohydrodynamics,41,42 with a one elastic constant approximation15 and isotropic viscosity with backflow effects.16 For this study of entangled nematic disclinations, this approach is preferred over hybrid MPCD/continuum approaches17–20 because of the advantages of particle-based methods over mesh-based approaches to mobile boundaries and its track-record simulating molecular-dynamics-based colloidal liquid crystals.21,30,43–45
2.2 Boundary conditions
The bulk fluid domain is maintained by (i) defining surface equations representing boundaries, and (ii) setting rules on N-MPCD particles that violate the surface equation. Each boundary, with index b, has a surface equation with an implicit form Sb(x) = 0, where x satisfy the set of points on the surface. Particles violate a surface equation if| Sb(xi) ≤ 0, | (6) |
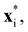 at time t* < δt (found where particle path and Sb(xi) = 0 intersect). Boundary rules are then applied, and the particle resumes streaming for remaining time δt − t*.
at time t* < δt (found where particle path and Sb(xi) = 0 intersect). Boundary rules are then applied, and the particle resumes streaming for remaining time δt − t*.
Boundary rules operate on the particle's generalised coordinates, xi, vi and ui. For periodic boundary conditions, xi → xi + Dνbνb where Dνb is a scalar shift in the surface normal direction νb of boundary b. Operators on the velocity are required for solid impermeable walls, vi → Mνbproj(vi;νb) + Mtbproj(vi;tb), where Mνb and Mtb are scalar multipliers on the projection of vi in the surface normal νb and tangent tb directions. The surface normal projections have the form proj(f;ν) = (ν·f)ν and surface tangent projections, proj(f;t) = f − (ν·f)ν. No-slip boundary conditions require bounce-back multipliers Mνb = Mtb = −1. Additionally ghost particles are required to ensure that vc extrapolates to zero in cells that are intersected by boundaries.29,46 Anchoring conditions operate on the particle's orientation through 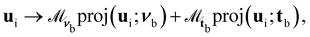 with the constraint that ui maintains unit magnitude (ui·ui = 1). Homeotropic (normal) anchoring is achieved with
with the constraint that ui maintains unit magnitude (ui·ui = 1). Homeotropic (normal) anchoring is achieved with 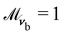 and
and 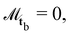 and planar (tangential) anchoring with
and planar (tangential) anchoring with 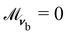 and
and 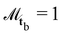 .
.
Despite 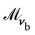 and
and 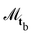 setting the orientation of any particles that violate eqn (6), the anchoring is not infinitely strong. This is because, of the Nc particles in any cell that intersects Sb only some fraction
setting the orientation of any particles that violate eqn (6), the anchoring is not infinitely strong. This is because, of the Nc particles in any cell that intersects Sb only some fraction 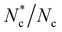 would have collided with the surface. Although those
would have collided with the surface. Although those 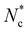 particles have their orientation set, the collision operation (eqn (4)) stochastically exchanges orientations between all Nc particles, effectively weakening the anchoring condition. To strengthen the anchoring, the orientational boundary condition is applied to all Nc particles within cells that are intersected by the surface Sb (Section 5.1).
particles have their orientation set, the collision operation (eqn (4)) stochastically exchanges orientations between all Nc particles, effectively weakening the anchoring condition. To strengthen the anchoring, the orientational boundary condition is applied to all Nc particles within cells that are intersected by the surface Sb (Section 5.1).
2.3 Mobile colloids
One way to incorporate colloids is to include them as embedded molecular dynamics particles, with radial interaction potentials.21,30 In contrast, the present work treats each colloid as a mobile surface that interacts with the hydrodynamic fields via conserving the linear and angular impulse generated by each of the incremental particle transformations. The surface equation| Sb(x) = [x − qb(t)]2 − R2 = 0, | (7) |
Analogous to the particle streaming eqn (1), the colloid coordinate translates assuming ballistic streaming qb(t + δt) = qb(t) + vb(t)δt, where vb(t) is the colloid's centre of mass velocity, which is sufficient under the viscously overdamped assumption. Since spheres have inherent rotational symmetry, eqn (7) is invariant under colloid rotation with angular velocity wb, defined relative to qb. Each colloidal vb(t) and wb(t) are determined by the incremental sum over all 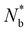 particles that violate eqn (6) in the current timestep
particles that violate eqn (6) in the current timestep
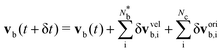 | (8) |
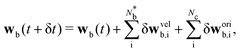 | (9) |
| δvvelb,i = proj(Jb;νb)/mb | (10) |
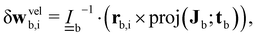 | (11) |
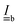 is the moment of inertia and rb,i is the vector from the centre of the colloid to the collision point on the boundary. The contributions from orientation rules are calculated from conserving a torque balance due to anchoring
is the moment of inertia and rb,i is the vector from the centre of the colloid to the collision point on the boundary. The contributions from orientation rules are calculated from conserving a torque balance due to anchoring| Γanchi + Γanchb,i = 0, | (12) |
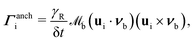 | (13) |
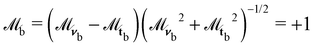 for homeotropic, and
for homeotropic, and 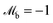 for planar anchoring (Section 5.2). The denominator ensures that the final particle orientation has unit magnitude. By defining the angle cos
for planar anchoring (Section 5.2). The denominator ensures that the final particle orientation has unit magnitude. By defining the angle cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi = ui·νb, the torque magnitude can be written in terms of a single variable
αi = ui·νb, the torque magnitude can be written in terms of a single variable 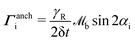 . The odd nature of Γanchi with respect to αi, means that the torque balance can be satisfied by introducing a virtual particle, oriented initially at −αi to νb (with orientation unit vector ub,i). Over the time δt, the virtual particle reorients to align with νb through application of the torque −Γanchi. The initial orientation of the virtual particle ub,i is related to the N-MPCD particle ui by a mirror reflection about νb.
. The odd nature of Γanchi with respect to αi, means that the torque balance can be satisfied by introducing a virtual particle, oriented initially at −αi to νb (with orientation unit vector ub,i). Over the time δt, the virtual particle reorients to align with νb through application of the torque −Γanchi. The initial orientation of the virtual particle ub,i is related to the N-MPCD particle ui by a mirror reflection about νb.
Torque is converted to a force acting on the boundary via
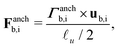 | (14) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) u is required to represent the lengthscale of the MPCD nematogens and control the rotational susceptibility. The head–tail symmetry of the particle orientation ub,i provides ambiguity on the sign of Fanchb,i, which is chosen to be oriented towards the boundary as Fanchb,i·νb < 0. For spherical colloids, the force at the boundary can be converted into linear and angular velocity contributions, through projecting Fanchb,i in the surface normal and tangential directions
u is required to represent the lengthscale of the MPCD nematogens and control the rotational susceptibility. The head–tail symmetry of the particle orientation ub,i provides ambiguity on the sign of Fanchb,i, which is chosen to be oriented towards the boundary as Fanchb,i·νb < 0. For spherical colloids, the force at the boundary can be converted into linear and angular velocity contributions, through projecting Fanchb,i in the surface normal and tangential directions| δvorib,i = proj(Fanchb,i;νb)δt/mb | (15) |
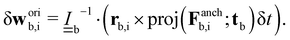 | (16) |
2.4 Units and parameters
Values are given in MPCD units of cell size a = 1, particle mass m = 1 and thermal energy kBT = 1. This results in units of time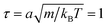 . Simulation time iterates with time-step size δt = 0.1. Simulations are performed in two (d = 2) and three (d = 3) dimensions with system sizes [Lx, Ly] and [Lx, Ly, Lz] respectively, aligned with a Cartesian basis ex, ey, ez. The average particle density per cell is 〈Nc〉 = 20. The nematic mean field potential is set to U = 20, corresponding to deep in the nematic phase,15 which is an idealisation that ensures variations in the scalar order parameter are localised to defect cores and the strength of elastic interactions is large. Other nematohydrodynamic parameters include the rotational friction γR = 0.01, shear susceptibility X = 0.5 and tumbling parameter set to be in the shear aligning regime with λ = 2. Unless otherwise stated, colloids with radii R = 6 are used in three-dimensions, and R = 10 in two-dimensions. The effective particle rod-length
. Simulation time iterates with time-step size δt = 0.1. Simulations are performed in two (d = 2) and three (d = 3) dimensions with system sizes [Lx, Ly] and [Lx, Ly, Lz] respectively, aligned with a Cartesian basis ex, ey, ez. The average particle density per cell is 〈Nc〉 = 20. The nematic mean field potential is set to U = 20, corresponding to deep in the nematic phase,15 which is an idealisation that ensures variations in the scalar order parameter are localised to defect cores and the strength of elastic interactions is large. Other nematohydrodynamic parameters include the rotational friction γR = 0.01, shear susceptibility X = 0.5 and tumbling parameter set to be in the shear aligning regime with λ = 2. Unless otherwise stated, colloids with radii R = 6 are used in three-dimensions, and R = 10 in two-dimensions. The effective particle rod-length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) u = 0.006, tunes the strength of the interaction between nematic bulk elasticity and colloid mobility. In all simulations, MPCD particles start with randomly generated positions and velocities. While the bulk fluid properties remain constant between simulations, the boundary conditions and initial conditions vary between studies. Additional system specific parameters are given in the Appendix.
u = 0.006, tunes the strength of the interaction between nematic bulk elasticity and colloid mobility. In all simulations, MPCD particles start with randomly generated positions and velocities. While the bulk fluid properties remain constant between simulations, the boundary conditions and initial conditions vary between studies. Additional system specific parameters are given in the Appendix.
Simulation parameters can be given in dimensionless numbers or mapped experimental units by fixing three base units. First, we choose thermal energy at room temperature kBT = 4.1 × 10−21 J. Units of length a ∼ 1 μm are found by relating the 5CB Frank elasticity K ∼ 10−11 N47 to the N-MPCD elasticity of K = 2200kBT/a.15 Finally, time units τ ∼ 10 ns are found by comparing the kinematic viscosity ν = 4 × 10−5 m2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 to the numerical value of ν ≈ 10kBTτ/a3 at a density of ρ = 20m/a3.22 These scales suggest that the 3D colloidal particles considered here are microscopic (R ≈ 6 μm), while the extrapolation length is nanoscopic ξK ≈ 150 nm, which is consistent with expectations.48 The longest simulations explored in this study run for TS = 0.3 ms.
47 to the numerical value of ν ≈ 10kBTτ/a3 at a density of ρ = 20m/a3.22 These scales suggest that the 3D colloidal particles considered here are microscopic (R ≈ 6 μm), while the extrapolation length is nanoscopic ξK ≈ 150 nm, which is consistent with expectations.48 The longest simulations explored in this study run for TS = 0.3 ms.
3 Results
3.1 Defects around a single colloid
To examine the defect structures around isolated nematic colloids, a single sphere is initialised within a nematic field that is initialised with randomised orientations (a thermal quench) in an Lx = Ly = Lz = 40 domain with periodic boundary conditions on all walls. The simulations are run for a duration of TS = 1400, with data recorded for t ≥ 400. After long times (t ∼ 600), the nematic field approaches its equilibrium state, which includes static defects that accompany the colloidal particle (Fig. 1a–c). For the case of planar anchoring (Fig. 1a), the inability for a tangential vector field to continuously coat a sphere necessitates two surface defects at the colloidal antipodes, known as Boojums.49,50 Their two opposite surface defects give the colloid/Boojums complex a quadrupolar structure. For spherical surfaces, these can either be hyperbolic point defects split in half by the mirror plane of the colloid, or separated into handle-shaped semi-loops that connect two +1/2 closely separated surface defects,50 with the latter case being observed for simulations from a quench (Fig. 1a). The handle-shaped structures are consistent with Landau–de Gennes simulations on a fine mesh with strong anchoring.50,51Colloids with homeotropic anchoring supply the bulk fluid with a hedgehog charge (point charge) of p = 1 (Fig. 1b and c). This nucleates one of two configurations, each of which has an odd point charge to conserve topological charge. The first configuration is a Saturn ring–a closed −1/2 disclination loop surrounding the equatorial axis10,11 (Fig. 1b). The Saturn ring results in a quadrupolar far-field character. The second configuration is a hyperbolic hedgehog, forming a topological dipole with the colloid,52 which in N-MPCD manifests as a dipolar halo (Fig. 1c). Of the 20 independent simulations initialised with random director field, 17 ended with a Saturn ring, and 3 with a dipolar halo. The configuration is primarily controlled by the dimensionless number R/ξK, which is the ratio of colloid radius to Kleman–de Gennes extrapolation length ξK.53,54 However, initial configuration can also effect the likelihood of the system becoming stuck in a metastable state: when the director field is uniformly initalised, we find 100% of simulations result in Saturn rings. In experiments, topological dipoles are the stable state when the ratio of colloid radius to Kleman–de Gennes extrapolation length R/ξK is large (see Section 5.1), while Saturn rings are preferred in confinement and for smaller colloids with weaker anchoring (larger extrapolation length).1,48 Generally, simulations predominantly reproduce Saturn rings55,56 and this is shown to be true in N-MPCD as well. For the three dimensional colloids considered here, R/ξK ≈ 40 (Section 5.1).
As a fluctuating nematohydrodynamic solver, N-MPCD can also simulate the coarsening dynamics of the disclination loops (Fig. 1d). Soon after the quench, the nematic field far from the colloid has ordered, but a single, large loop remains, relaxing into a Saturn ring configuration. The loop is free to sample disclination profiles outside of purely trefoil-like −1/2. This is demonstrated by colouring the disclinations with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = Ω·T where Ω is the rotation vector57 and T is the tangent vector of the line. Where cos
β = Ω·T where Ω is the rotation vector57 and T is the tangent vector of the line. Where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 1, Ω is parallel to T and the disclination line has a local +1/2 wedge profile. On the other hand, where cos
β = 1, Ω is parallel to T and the disclination line has a local +1/2 wedge profile. On the other hand, where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = −1, Ω is antiparallel to T and the disclination locally has a −1/2 wedge profile. The director can also rotate out of this plane passing through cos
β = −1, Ω is antiparallel to T and the disclination locally has a −1/2 wedge profile. The director can also rotate out of this plane passing through cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 0, which represent twist-type profiles. Visualising disclinations in this way has been particularly insightful for interpreting disclination behaviours during phase transitions58 and in three-dimensional active nematics.59–61 The loop in Fig. 1d is charged, requiring Ω to make a full revolution. However, the rotation is not homogeneous and Ω remains largely uniform for large segments of the disclination that are distant from the colloid. Conversely, the segments of the disclination closest to the colloidal surface support nearly the entire variation of Ω. At later times (t ∼ 600), the loop reduces in size and the anchoring constraint on the colloid enforces Ω to rotate into the expected anti-parallel configuration Ω·T = −1, forming the Saturn ring.
β = 0, which represent twist-type profiles. Visualising disclinations in this way has been particularly insightful for interpreting disclination behaviours during phase transitions58 and in three-dimensional active nematics.59–61 The loop in Fig. 1d is charged, requiring Ω to make a full revolution. However, the rotation is not homogeneous and Ω remains largely uniform for large segments of the disclination that are distant from the colloid. Conversely, the segments of the disclination closest to the colloidal surface support nearly the entire variation of Ω. At later times (t ∼ 600), the loop reduces in size and the anchoring constraint on the colloid enforces Ω to rotate into the expected anti-parallel configuration Ω·T = −1, forming the Saturn ring.
3.2 Elastic interactions
Colloid-defect complexes with homeotropic anchoring can have a quadrupolar (Saturn ring; Fig. 1b) or dipolar (dipolar halo; Fig. 1c) nature.62 These configurations correspond directly to the form of far-field elastic interactions between pairs of nematic colloids. N-MPCD reproduces elastic forces that are long ranged, with power laws dictated by the dominant multipole moment (Section 3.2.1), as well as anisotropic, with attraction and repulsion zones with angular variation between interacting colloids (Section 3.2.2).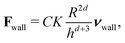 | (17) |
Elastic forces are largest at smaller colloid separations from the wall, with magnitudes Fwall ≈ 10 for heq/R ≈ 1.5 in 2D (Fig. 2a) and Fwall ≈ 50 for heq/R ≈ 1.6 in 3D (Fig. 2b). At increasing separations, these forces rapidly decay. Comparing with predictions (eqn (17); black slope), N-MPCD elastic forces decay with the expected power laws. In two-dimensions, Fwall ∼ h−5 holds well for all sampled colloid radii. In three-dimensions, the repulsion matches Fwall ∼ h−6 for R = 6, but experiences a smaller power law for R = 4. The elastic force also scales with R2d for sufficiently large colloid radii (R > 6 in 2D and R > 4 in 3D), as shown by the collapsed curves (inset of Fig. 2). These force scalings identify a lower bound R ≳ 6 for accurately resolving the elastic stresses on the colloidal surface. Since Fwall ∝ R2d/hd+3 is satisfied, N-MPCD is utilised to calculate the strength of the elastic interaction. Fits to the data (black curves in the inset of Fig. 2) obtain C = 0.138 ± 0.001 (2D) and C = 0.64 ± 0.02 (3D). In three-dimensions, quadrupolar interactions with a homeotropic wall predict C = 15πβ2/2, where β quantifies the strength of the elastic quadrupole moment associated with the colloid-defect complex.63 N-MPCD finds β = 0.37 ± 0.06, which is in good agreement with experimentally reported values of β in the range β = 0.2 ± 0.167 to β = 0.52 ± 0.12.68 These force measurements demonstrate that N-MPCD accurately simulates long-range quadrupolar deformation in the bulk nematic order and that the colloids dynamically respond to elastic stresses on their surface.
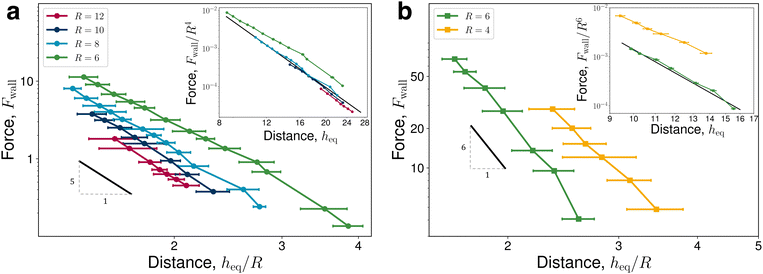 | ||
| Fig. 2 Elastic interaction forces between quadrupolar colloids of radius R and a homeotropic anchored wall. (a) Two-dimensional elastic repulsion force Fwall measured at equilibrium colloid–wall separation distances heq. Distances are scaled by the colloid radius R. (b) Same as (a) but for three-dimensions. The black lines, shown for comparison with the expected scaling (eqn (17)), represent decaying power laws of −5 (2D) and −6 (3D). Errorbars represent the standard error between independent runs. | ||
The N-MPCD mobile colloid does indeed exhibit regions of both repulsion and attraction. The repulsive regions are clearest for pole-to-pole orientations and exist in the far-field limit of small-angle defect-to-defect orientations (Fig. 3). Configurations with intermediate relative angles exhibit attractive interactions. Far-field interactions between two quadrupolar colloids separated by a distance h with a relative angle θ are predicted to have the form
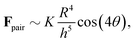 | (18) |
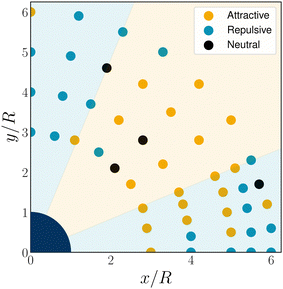 | ||
| Fig. 3 Attraction-repulsion zones between two-dimensional interacting quadrupolar colloids with radius R = 10. One colloid is fixed at the origin (navy blue quarter circle) and a second mobile colloid probes the interaction at surrounding points. The colour of each point represents attractive (orange), repulsive (blue) or neutral (black) interactions. Background shading shows the far-field expectation for interacting quadrupoles (eqn (18)). | ||
The expectation breaks down at small angles and distances (Fig. 3). The N-MPCD algorithm produces attraction at these sampled points, in contrast with the idealised prediction (eqn (18)). This is partly because the far-field assumptions are less valid but, more importantly, is related to the mechanics of self-assembly: the dimer pair quickly self-assembles into a linear chain,8,70 causing the colloids to become attractively bound (Fig. 11c). Unlike 3D,71 two-dimensional nematic colloids have a pair of −1/2 point defects (Fig. 10c), which can be freely shared between colloids (Fig. 11c). While this section has demonstrated the far-field elastic interactions and a self-assembled 2D chain within N-MPCD, the next section will explore disclination line entanglements between colloidal pairs in 3D.
3.3 Entangled defect lines around colloidal dimers
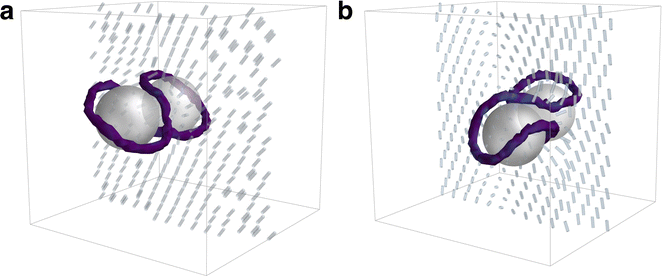
Extending into systems with two or more colloids in 3D brings a rich topological interplay between point defects and disclination loops,9,72 resulting in a range of defect structures including disclination lines that surround multiple colloids.73,74 Entangled states are metastable, and can be induced by a thermal quench,26 laser manipulation,75 chiral ordering,76 or high colloidal volume fractions.4 In this study, the entangled states are reached by randomly initialising the director field from a thermal quench. Two mobile colloids are initialised at q1 = [20, 20, 13] and q2 = [20, 20, 27], each with homeotropic anchoring in a Lx = Ly = Lz = 40 domain with periodic boundary conditions on all walls. A warmup phase is applied (TW = 200) where nematic order forms and no data is collected. Simulations are then run for the duration TS = 1000. Loops are identified via the disclination density tensor (Section 5.677). Eight disclination states are observed from the N-MPCD simulations with either one or two −1/2 disclination loops (Fig. 4). Of these, the two states that are not considered entangled are extensions of the single colloid case, with either two Saturn rings or two dipolar halos that assemble into a chain. The others are entangled with at least one loop (n ≥ 1) that wraps around the colloidal dimers. These states derive their names from the shape of their disclinations. In the case of the figure-of-theta (Fig. 4c), two loops exist (n = 2): one large ring that encircles both colloids, and another smaller ring positioned between them. The figure-of-omega (Fig. 4e) and figure-of-eight (Fig. 4g) are single loop entanglements (n = 1). Each of these states have been well-documented in experiments and simulations.26,75,78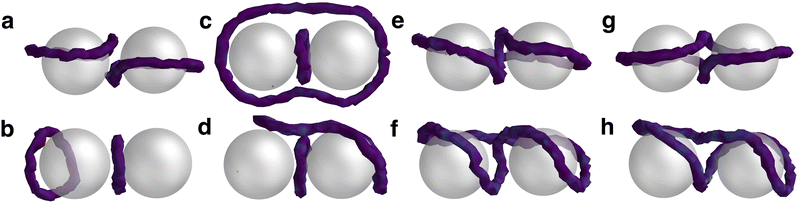 | ||
| Fig. 4 Defect states accompanying colloidal dimers. (a) Saturn rings. (b) Dipolar halos. (c) Figure-of-theta. (d) Tilted-figure-of-theta. (e) Figure-of-omega. (f) Tilted-figure-of-omega. (g) Figure-of-eight. (h) Tilted-figure-of-eight. Disclinations are visualised as in Fig. 1, confirming each configuration is associated with −1/2 disclination loops. | ||
Additionally, the N-MPCD algorithm reveals the existence of tilted analogues of the figure-of-theta (Fig. 4d), figure-of-omega (Fig. 4f) and figure-of-eight (Fig. 4h). These are tilted with respect to the axis the colloids reside in. While rare, these tilted entangled dimer states emerge when the director field does not form a uniform alignment axis away from the colloids (see Fig. 12). This generates modulated order that cannot relax to the ground state. In these simulations, the combination of colloids, periodic boundary conditions and quenched disorder are able to trap these tilted entangled states.
With the disclination states identified, we next characterise their topological and geometric properties. To obtain these, the framework by Čopar and Žumer is followed.6,7 Since colloidal anchoring enforces a geometric constraint for the local director to lie in a plane perpendicular to T (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = −1, in this case), the disclination loop can be assigned a framing vector w that is everywhere perpendicular to the tangent (Fig. 5a; see Section 5.7). A convenient choice of w is one of the three radially pointing director orientations of the −1/2 disclination (Fig. 5a). The framing vector allows the topological properties of the −1/2 disclination loop to be found via the self-linking number Sl, which counts the number of times the framing turns around the tangent on traversing the loop. The self-linking number can be calculated from geometric properties of the disclination through the Călugăreanu–White–Fuller theorem
β = −1, in this case), the disclination loop can be assigned a framing vector w that is everywhere perpendicular to the tangent (Fig. 5a; see Section 5.7). A convenient choice of w is one of the three radially pointing director orientations of the −1/2 disclination (Fig. 5a). The framing vector allows the topological properties of the −1/2 disclination loop to be found via the self-linking number Sl, which counts the number of times the framing turns around the tangent on traversing the loop. The self-linking number can be calculated from geometric properties of the disclination through the Călugăreanu–White–Fuller theorem
| Sl = Wr + Tw, | (19) |
| ν = 3Sl + 2 (mod 4), | (20) |
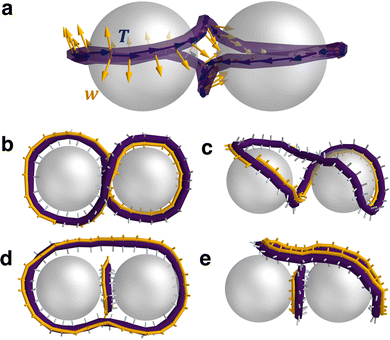 | ||
| Fig. 5 Minus-half disclination loops as ribbons with self-linking numbers Sl. (a) Figure-of-eight presented as ribbons constructed through identifying the disclination line tangent T (navy blue arrows) and local framing vector w (orange arrows). Disclination loops are as in Fig. 1. (b) Figure-of-eight from (a) as viewed from second perspective. (c) Tilted-figure-of-eight. (d) Figure-of-theta. (e) Tilted-figure-of-theta. In each of (b)–(e), the orange framing curve smoothly connects the −1/2 wedge orientations denoted by orange cylinders. Silver cylinders illustrate the other two radially outward pointing orientations. In (b) and (c), the end points do not meet the starting points of the orange framing curve, which indicates a net rotation and implies Sl ≠ 0. On the other hand, the orange framing curve is continuous and Sl = 0 in (d) and (e). | ||
First, the properties for the entangled single loop (n = 1) states are examined. For the figure-of-eight, figure-of-omega and their tilted analogues, the self-linking number is found to be Sl ≈ ±2/3 (Table 1). Additionally, the Sl ≈ ±2/3 can be visualised for the two figure-of-eight states by tracking the orientation of the −1/2 profile (Fig. 5b and c). In choosing a reference and tracking the profile rotations along the loop (orange ribbon curve), the orientation is rotated by ±2π/3 over the entire contour of the loop. For each n = 1 state, the Sl is composed entirely from writhe, while the twist remains essentially zero in each state (Table 1). Self-linkings composed entirely of writhe were previously observed for the figure-of-eight and figure-of-omega,6 since the strong radial constraint on the disclination profile penalises twisting of the orientation. We show the same writhe/twist balance also hold when the disclinations are in tilted conformations. The ± sign on the Sl relates only to the chirality of the conformation and does not influence the topological classification of the loop. Indeed, mapping to the disclination loop index reveals that all four states are topologically trivial ν = 0 (uncharged with p = even). The n = 1 disclination line balances the two point charges provided by the colloids by forming a state with net writhe Wr.
| n | Wr | Tw | Sl | p | |||||
|---|---|---|---|---|---|---|---|---|---|
| Saturn rings | 2 | 0.014 | 0.001 | 0.029 | 0.053 | 0.044 | 0.054 | Odd | Odd |
| Dipolar halos | 2 | 0.009 | 0.003 | 0.048 | 0.003 | 0.057 | 0.005 | Odd | Odd |
| Figure-of-theta | 2 | 0.035 | 0.002 | 0.025 | −0.011 | 0.060 | −0.008 | Odd | Odd |
| Figure-of-eight | 1 | 0.699 | −0.027 | 0.673 | Even | ||||
| Figure-of-omega | 1 | 0.652 | 0.009 | 0.661 | Even | ||||
| Tilted-figure-of-theta | 2 | 0.005 | 0.005 | −0.008 | 0.013 | −0.003 | 0.018 | Odd | Odd |
| Tilted-figure-of-eight | 1 | −0.705 | 0.051 | −0.654 | Even | ||||
| Tilted-figure-of-omega | 1 | 0.618 | 0.065 | 0.683 | Even | ||||
Next, the disclination states with n = 2 are examined. Each state has a self-linking of Sl ≈ 0 (Table 1). This is the case for the individual rings (Saturn rings and dipolar halos) and the entangled figure-of-theta structures, each presenting Wr ≈ 0 and Tw ≈ 0. We visualise the ribbon (orange curve) for the two figure-of-theta states in Fig. 5d and e, which confirm the calculated properties. The reference orientation smoothly connects to the final orientation, with no local (or global) twisting or coiling over the circuit. The Sl = 0 properties finds that each loop carries a hedgehog charge p = odd (ν = 2), balancing the global charge neutrality between the two loops (modulo 2). These results show that each n = 2 state is topologically equivalent with identical geometric decomposition into Wr = 0 and Tw = 0. Therefore, the tilted states are simply smooth transformations of their non-tilted counterparts.
3.4 Entanglement kinetics
With each of the disclination states identified and characterised, we study the relaxation pathways that lead to the formation of these states. As already demonstrated for a single colloid (Fig. 1d), disclinations contour lengths generally decrease as the system relaxes from the thermal quench. For dimers, the temporal evolution of the disclination contour lengths eventually leads to the long-time configurations from Fig. 4. Since N-MPCD simulates fluctuating nematohydrodynamics, the simulations stochastically sample states as they relax towards accessible lower free energy configurations.16,41Four instances of the stochastic relaxation of the entangled dimers are shown in Fig. 6. An example of the relaxation passing through a figure-of-theta is shown in Fig. 6a. At early times (Fig. 6a.1), a small loop exists sandwiched between the colloids with a contour length 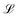 comparable-to-but-less-than the circumference of the colloids. Simultaneously, a large disclination loop rapidly collapses around the colloids, forming the figure-of-theta state (Fig. 6a.2). The number of loops is n = 2 throughout. In N-MPCD, the figure-of-theta is only sampled transiently, passing rapidly through loop-reconnections to form two Saturn ring colloids (Fig. 6a.3). Despite sharp transitions in the individual loop lengths (Fig. 6a), the total contour length has a negligible change between the two states—with two equal-sized Saturn rings that sum to the total disclination length of the two figure-of-theta loops.
comparable-to-but-less-than the circumference of the colloids. Simultaneously, a large disclination loop rapidly collapses around the colloids, forming the figure-of-theta state (Fig. 6a.2). The number of loops is n = 2 throughout. In N-MPCD, the figure-of-theta is only sampled transiently, passing rapidly through loop-reconnections to form two Saturn ring colloids (Fig. 6a.3). Despite sharp transitions in the individual loop lengths (Fig. 6a), the total contour length has a negligible change between the two states—with two equal-sized Saturn rings that sum to the total disclination length of the two figure-of-theta loops.
Another kinetic trajectory observed in N-MPCD is a single (n = 1) quenched disclination loop (Fig. 6b.1) that collapses to form a figure-of-omega state (Fig. 6b.2). The figure-of-omega entangled state is found to be metastable with a constant contour length for t ≈ 100, after which time the entangled loop transitions to two Saturn rings (Fig. 6b.3). Unlike the transition from the figure-of-theta state in Fig. 6a, the transition from the figure-of-omega state involves a topological conversion from Sl ≈ 2/3 to two rings with Sl ≈ 0 (Table 1). Equivalently, this corresponds to a transition from a single uncharged loop, to two charged loops.
The tilted entanglements can show somewhat different trajectories because of their non-uniform global director alignment (Fig. 6c). The tilted state arises because the disclination collapses at an off-set to the colloidal axis (Fig. 6c.1), passing into the tilted-figure-of-theta (Fig. 6c.2). The tilted figure-of-theta state endures for an extended time (100 ≤ t ≤ 200) with minimal changes to the conformation, until a segment of the disclination line reconnects into a fleetingly brief tilted-figure-of-omega state (Fig. 6c.3). Finally, the disclination divides into two dipolar halos with orientations tilted with respect to each other (Fig. 6c.4).
An n = 1 tilted relaxation trajectory can also occur, starting with a larger loop (Fig. 6d.1) that encloses the colloid pair to form the tilted-figure-of-omega state (Fig. 6d.2). As in Fig. 6c, this tilted-figure-of-omega state is short lived and, in this case, transitions to the tilted-figure-of-eight without transitioning through n = 2 (Fig. 6d.3). Interestingly, the tilted-figure-of-eight is observed to be the most stable of any of the entangled states observed in N-MPCD simulations, remaining in the same configuration for the entire simulation, with minimal variation in contour length. This parallels experimental observations,81 albeit for different states and surrounding order, where chirality or modulated order can offer protection from reaching the global free energy minimum.82 In addition, figure-of-eights have been associated with the greatest stability of all entangled structures.75 Despite the intrinsic stochasticity of the numerical approach, the tilted-figure-of-eight was not observed to relax into states with n = 2 rings.
Infrequently, less conventional entangled-dimer relaxation dynamics are revealed by N-MPCD, such as the situation shown in Fig. 7. Similar to the tilted structures, this trajectory eventually relaxes into a modulated global director field (Fig. 12). However, at early times, an unexpected entangled state emerges in which the disclination loop has a localised segment with a +1/2 wedge profile (Fig. 7a). The +1/2 profile is smoothly connected by fleeting twist to a majority −1/2 loop. This wedge-twist state necessarily contains p = even to balance the charge of the dimers. Generally, such +1/2 wedge profiles are discouraged since the global director alignment cannot coexist with the low-symmetry of the +1/2 wedge and out-of-plane twist is penalised by the radial colloidal anchoring. In this case, the penalty against twist is resolved by a rapid reorientation of the rotation vector Ω, which rotates by π relative to the global basis over a small disclination segment (Fig. 7a). The +1/2 segment of the disclination gradually approaches the colloids (Fig. 7b.2) until it combines with a −1/2 profile, facilitating a topological transition from a single loop (n = 1) to a state with a pair of −1/2 dipolar halos (Fig. 7b.3).
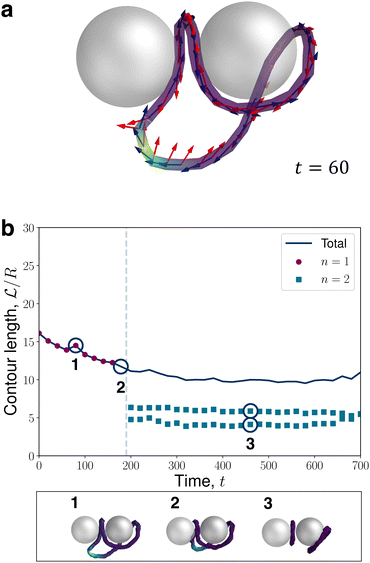 | ||
Fig. 7 Quenched disorder can sample out-of-equilibrium disclination configurations. (a) Early-time snapshot of a charge-neutral disclination with a localised +1/2 profile (yellow segment), visualised as in Fig. 1. (b) Relaxation trajectory of the normalised contour length 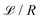 with time t. Markers, lines and colouring the same as Fig. 6. Example snapshots are shown directly below the panel. with time t. Markers, lines and colouring the same as Fig. 6. Example snapshots are shown directly below the panel. | ||
4 Conclusions
This work has utilised Nematic Multi-Particle Collision Dynamics (N-MPCD) to simulate nematic colloids as mobile surfaces that can resolve stresses at the interfaces. In three-dimensions, N-MPCD reproduces the experimentally observed and theoretically predicted colloid-disclination complexes for solitary colloids. These include (i) Boojums with handle-shaped semi-loops, (ii) Saturn rings and (iii) dipolar halos. Furthermore, N-MPCD mediates elastic interactions between colloidal inclusions. The elastic forces in N-MPCD are seen to decay with the expected power-laws in two- and three-dimensions. Likewise, the anisotropy of quadrupoles interacting in the far-field-limit has been demonstrated for colloids and their accompanying pairs of free point defects in 2D. If the colloids are too near to each other, the far-field approximation breaks down and N-MPCD predicts that dimer structures are formed through shared point defects. For nearby colloidal dimers subjected to a 3D thermal quench, N-MPCD reproduces expected defect structures, including disclination loops that entangle both colloids. In addition to the expected defect structures, previously unobserved analogous tilted entanglements are revealed by N-MPCD in systems with periodic boundary conditions. The periodic boundaries allow the director to rotate by π along one axis of the system and the tilted state then becomes topologically protected. Although nematic systems in which the far-field director is fixed would not allow tilted entangled structures, they could feasibly be created via micropatterning or by colloids in twisted nematic cells that could imposed a rotation by π. In these tilted states, the far-field directors are not uniform compared to the previously observed states.Despite being a noisily fluctuating algorithm, N-MPCD not only respects topological constraints but also resolves details of defect topology and disclination structure, such as self-linking numbers or localised wedge/twist profiles. Furthermore, as a linearised nematohydrodynamic approach, N-MPCD simulates the entanglement kinetics. This allows the algorithm to explore relaxation from a quench—revealing that topological point charge is not evenly distributed around the loop, but instead carried by segments of the disclination loop closest to the colloidal surface. This illustrates that N-MPCD is ideal for accessing and exploring metastable states, owing to the intrinsic thermal fluctuations and dynamics beyond overdamped free-energy steepest descent which allows the system to stochastically hop free-energy barriers. In particular, the simulations produced an early-time charge-neutral disclination state that does not conform to an entirely −1/2 disclination loop.
This study demonstrates that the N-MPCD algorithm is well-suited for studies on topological kinetics, field-driven assembly and colloidal self-assembly. The versatility of combining complex embedded21 or confining geometries,22 fluctuating nematohydrodynamic flows and out-of-equilibrium dynamics23 makes N-MPCD highly suitable coarse-grained approach for studying dynamics of topological phenomena. Further work could apply the N-MPCD algorithm to study the interactions and defect structures surrounding nematic colloids in active nematic systems, or topological features of the percolated −1/2 disclination loops in colloid nematic gels.4 The control over complex surfaces could be used to explore colloids in complex geometries, including the possibility of kinetics and fluctuations in non-trivial knotted fields.83 This work contributes to a numerical approach to study the relationship between topology and rheological properties.
Data availability
All data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendices
Kleman-de Gennes extrapolation length
The extrapolation length is a length scale that measures the competing influence of elasticity against anchoring strength ξK = K/W, where K is the elastic constant under the one constant approximation, and W is the anchoring strength.84 To compare the influence of anchoring applied only to proportion of particles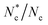 against the stronger anchoring method described in Section 2.2, applied to all Nc particles in cells that intersect the surface, the extrapolation length is measured in a two-dimensional hybrid-aligned-nematic cell with homeotropic anchoring on the top boundary y = L and planar anchoring on the bottom boundary y = 0 (Fig. 8a). In the ex direction, periodic boundary conditions are applied. The system size is Lx = Ly = L = 50, with 20 simulation runs of 104 timesteps, outputted every 100 timesteps to establish an average for the orientation angle ϕ(y) (defined from the positive ex axis) over all runs and timesteps.
against the stronger anchoring method described in Section 2.2, applied to all Nc particles in cells that intersect the surface, the extrapolation length is measured in a two-dimensional hybrid-aligned-nematic cell with homeotropic anchoring on the top boundary y = L and planar anchoring on the bottom boundary y = 0 (Fig. 8a). In the ex direction, periodic boundary conditions are applied. The system size is Lx = Ly = L = 50, with 20 simulation runs of 104 timesteps, outputted every 100 timesteps to establish an average for the orientation angle ϕ(y) (defined from the positive ex axis) over all runs and timesteps.
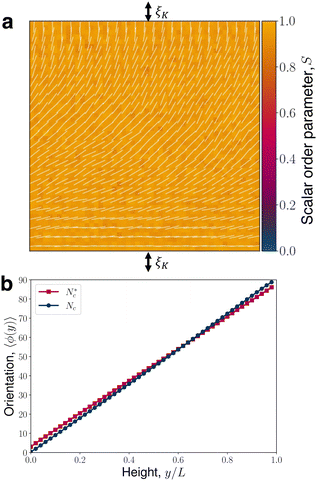 | ||
Fig. 8 Extrapolation length ξK. (a) A hybrid-aligned nematic cell of size L = 50 with planar anchoring on the bottom surface and homeotropic on the top, and periodic boundaries on the sides. The director field is shown as the white line field over the instantaneous scalar order parameter field S. For finite strength anchoring, the anchoring starts an effective distance ξK behind each surface. (b) Director orientation 〈ϕ(y)〉 with vertical height y, averaged over horizontal position x, time t, and N = 20 simulation runs. Red squares present orientation when only the 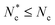 particles that directly violate eqn (6) have the anchoring conditions applied. Dark blue circles are for transformations applied to all particles within a cell Nc. particles that directly violate eqn (6) have the anchoring conditions applied. Dark blue circles are for transformations applied to all particles within a cell Nc. | ||
Assuming that the anchoring condition begins a small distance ξK beyond each boundary, so that the nematic orientation ϕ(−ξK) = 0° and ϕ(L + ξK) = 90°, the extrapolation length can be found from
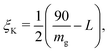 | (21) |
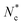 case (Fig. 8b). For a colloid with radius R, the strength of the anchoring is given by the dimensionless ratio of the surface free energy WR2 cost against elastic energy KR, which produces a reduced colloid size, RW/K = R/ξK. All simulations use the strong anchoring method (Nc case). Three-dimensional colloids in this paper have a radius of R = 6 in simulation units, giving R/ξK = 40.8. In two-dimensions, R = 10 gives R/ξK = 68.0.
case (Fig. 8b). For a colloid with radius R, the strength of the anchoring is given by the dimensionless ratio of the surface free energy WR2 cost against elastic energy KR, which produces a reduced colloid size, RW/K = R/ξK. All simulations use the strong anchoring method (Nc case). Three-dimensional colloids in this paper have a radius of R = 6 in simulation units, giving R/ξK = 40.8. In two-dimensions, R = 10 gives R/ξK = 68.0.
This has a substantial effect on the topological impact of the suspended colloid (Fig. 9). When only the 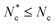 particles that directly violate eqn (6) have the anchoring conditions applied, the anchoring condition is weak and the colloid does not significantly perturb the surrounding director field (Fig. 9a). In this case, the colloid does not induce −1/2 companion defects in the surrounding nematic. However, when all Nc particles in cells overlapping with the surface have the anchoring applied, the anchoring is strong (Fig. 9b). Such strong anchoring does induce two −1/2 defects on opposite sides of the colloid to negate the +1 topological charge created by the strong anchoring conditions on the circular inclusion.
particles that directly violate eqn (6) have the anchoring conditions applied, the anchoring condition is weak and the colloid does not significantly perturb the surrounding director field (Fig. 9a). In this case, the colloid does not induce −1/2 companion defects in the surrounding nematic. However, when all Nc particles in cells overlapping with the surface have the anchoring applied, the anchoring is strong (Fig. 9b). Such strong anchoring does induce two −1/2 defects on opposite sides of the colloid to negate the +1 topological charge created by the strong anchoring conditions on the circular inclusion.
 | ||
Fig. 9 Snapshots of the director field around colloids of radius R = 10 with (a) weak anchoring and (b) strong anchoring. (a) Weak anchoring occurs when only the 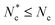 particles that directly violate eqn (6) have the anchoring conditions applied. This results in R/ξK = 5.9 and the director field is not sufficiently perturbed to exhibit −1/2 defects in the fluid. (b) Strong anchoring occurs when all Nc particles in cells overlapping with the surface have the anchoring applied. In this case, R/ξK = 68.0 and the colloid induces a pair of −1/2 defects in the fluid. particles that directly violate eqn (6) have the anchoring conditions applied. This results in R/ξK = 5.9 and the director field is not sufficiently perturbed to exhibit −1/2 defects in the fluid. (b) Strong anchoring occurs when all Nc particles in cells overlapping with the surface have the anchoring applied. In this case, R/ξK = 68.0 and the colloid induces a pair of −1/2 defects in the fluid. | ||
Anchoring torque
The particle orientation transformations described in Section 2.3 are implemented as hard anchoring conditions that align MPCD particle i. The initial orientation of the particle prior to colliding with the surface is ui. The change in nematogen orientation due to the collision is δui. This orientational change must be converted into a force on the colloid. We infer the torque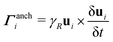 as the rotation through the fluid with rotational friction coefficient γR. The final particle orientation, post anchoring, can be written in terms of the scalar multipliers as
as the rotation through the fluid with rotational friction coefficient γR. The final particle orientation, post anchoring, can be written in terms of the scalar multipliers as 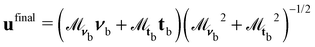 . Taking the cross product gives eqn (13). One caveat to inferring the torque in this manner, is that the periodicity of (ui·νb)(ui × νb) only infers the correct torque magnitude for angles −π/4 ≤ α ≤ π/4. In the N-MPCD simulations presented here, reorientations greater than π/4 are rare.
. Taking the cross product gives eqn (13). One caveat to inferring the torque in this manner, is that the periodicity of (ui·νb)(ui × νb) only infers the correct torque magnitude for angles −π/4 ≤ α ≤ π/4. In the N-MPCD simulations presented here, reorientations greater than π/4 are rare.
Torque to force
The elastic force exerted on a colloid (mobile boundary), due to the anchoring transformation of a single N-MPCD particle, is determined by the torque on a virtual N-MPCD particle (Section 2.3). This torque conserves angular impulse (eqn (12)). Since the torque is a pseudovector, converting a torque into a force is not generally possible—there can be colinear contributions between the force F and radial vector r that return the same value of torque Γ. The non-unique nature of the force is demonstrated by the identity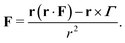 | (22) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) u/2)ub,i which corresponds to half of the nematogen rod length.
u/2)ub,i which corresponds to half of the nematogen rod length.
Methods for colloid–wall repulsion
Systems in two-dimensions have Lx = Ly = L with periodic boundary conditions in ex, and solid walls in ey, i.e. periodic boundary conditions to the sides and solid walls above and below. Both upper and lower solid walls have impermeable, no-slip boundary conditions, but only the lower boundary has anchoring conditions applied, with strong homeotropic alignment (Section 5.1). Since the distant top wall has no imposed anchoring, it does not produce any long-range elastic forces. Though the strong anchoring on the nearby bottom wall should screen the majority of nematoelastic self-interactions through the periodic boundaries, any remaining image effects will be in the ex direction and are not expected to influence the equilibrium distance heq. Four colloid radii are sampled R ∈ [6, 8, 10, 12] with system sizes L ∈ [50, 55, 60, 80] respectively, to adjust for system-size effects. The director field is initialised vertically as n(t = 0) = ey, which produces a pair of near-surface point defects with −1/2 charge in 2D. After being initialised along ey, the simulation is allowed to warmup for a time of TW = 1000, during which the colloid is held fixed and the director relaxes to the equilibrium configuration. Simulations are then performed for TS = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, with the colloid mobile and responsive to the nematic environment. A total of 40 independent simulation runs are performed for each R.
000, with the colloid mobile and responsive to the nematic environment. A total of 40 independent simulation runs are performed for each R.
In three-dimensions, two colloid radii are used. The first is R = 4 with Lx = Ly = Lz = 30, and the second is R = 6 with Lx = Ly = 30, Lz = 35. Simulations have periodic boundary conditions in ex and ey, and impermeable no-slip walls in ez. Similar to two-dimensions, only the lower plate has homeotropic anchoring conditions. The director field is intialised along n(t = 0) = ez, leading to a quadrupolar Saturn ring. The simulations run for TS = 4000 following a warmup period of TW = 1000, where the colloid is held static. Statistics are generated from 30 independent measurements for each R.
The decaying power-law nature of the elastic forces are determined by measuring the interaction forces of a nematic colloid with a centre of mass distance h away from a homeotropic anchored wall. In the proximity of the wall, the colloid experiences a strong elastic repulsive force, Fwall, that decays with distance. This can be represented as a quadrupole–quadrupole elastic interaction between the colloid and its mirror image on the other side of the wall (eqn (17)). In addition, the motion of the colloid through the fluid experiences a drag force due to viscosity Fdrag and a fluctuating force Ffluc that enters due to the stochasticity of the collision operators. To measure Fwall, we apply an external gravitational-like body force to the colloid
| FG = McG, | (23) |
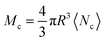 is the mass of the colloid in 3D or Mc = πR2〈Nc〉 in 2D. The constant acceleration G = −Gνwall is directed towards the homeotropic wall with surface normal νwall and magnitude G. The applied body force (eqn (23)) probes the elastic force by introducing an equilibrium distance heq at which Fwall + FG = 0 (Fig. 10a). When the elastic and applied forces balance, the colloid only fluctuates about heq (grey trajectories in Fig. 10b). Therefore, the fluctuating and drag forces can be neglected in the force measurements provided there is statistical certainty on heq. For this reason, the simulations are iteratively re-initialised from new start positions h ≈ heq (example director configuration in Fig. 10c), so that when data collection begins, the mean of all runs at time t > TW (blue solid line) has unbiased fluctuations about the time-averaged mean (red solid line). The equilibrium position heq is taken as the time-independent mean, with the standard error as the statistical uncertainty (red shading). Here, we have chosen an ensemble in which the force is fixed and the position fluctuates, though one could alternatively choose a fixed-position/fluctuating-force ensemble.
is the mass of the colloid in 3D or Mc = πR2〈Nc〉 in 2D. The constant acceleration G = −Gνwall is directed towards the homeotropic wall with surface normal νwall and magnitude G. The applied body force (eqn (23)) probes the elastic force by introducing an equilibrium distance heq at which Fwall + FG = 0 (Fig. 10a). When the elastic and applied forces balance, the colloid only fluctuates about heq (grey trajectories in Fig. 10b). Therefore, the fluctuating and drag forces can be neglected in the force measurements provided there is statistical certainty on heq. For this reason, the simulations are iteratively re-initialised from new start positions h ≈ heq (example director configuration in Fig. 10c), so that when data collection begins, the mean of all runs at time t > TW (blue solid line) has unbiased fluctuations about the time-averaged mean (red solid line). The equilibrium position heq is taken as the time-independent mean, with the standard error as the statistical uncertainty (red shading). Here, we have chosen an ensemble in which the force is fixed and the position fluctuates, though one could alternatively choose a fixed-position/fluctuating-force ensemble.
 | ||
| Fig. 10 Measurements for determining the force–distance relation (Fig. 2). (a) Schematic of colloid (navy circle) with radius R, initialised within the far-field director n, forming equatorial −1/2 defects (blue trefoil symbols). The colloid experiences an elastic repulsion force due to the wall Fwall, which is probed by a gravitational-like external force FG = −McGnwall. The distance h between the colloids centre of mass and the wall is heq when FG = 〈Fwall〉. (b) An example of 30 colloidal trajectories (grey) for a two-dimensional colloid with radius R = 10. The time-dependent ensemble mean is shown by the dark blue curve, which fluctuates about the time-averaged mean (red horizontal line). The red shading is the standard error about the time-averaged mean. (c) An example snapshot of a colloid interacting with the homeotropic anchored wall (black horizontal line). The white line field is the director and background colouring is the scalar order parameter S. | ||
Methods for attraction and repulsion zones
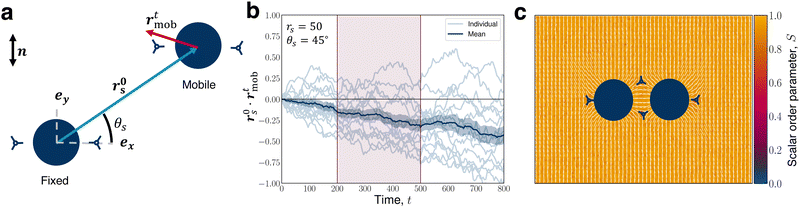
The force anisotropy measurements are obtained in two-dimensions for simplicity. The angular dependence of the interaction between two colloids is determined by fixing one colloid, placing a mobile probe colloid in its vicinity and measuring the response of the probe colloid (Fig. 11a). The director alignment is initialised along ey, which preferentially positions two −1/2 defects on either side of the colloids, establishing consistent initial quadrupole orientations. A short warmup period of TW = 5 allows the defects to form but not reorient away from alignment in ey. The two colloids are placed, one fixed at (40,40) and the other mobile initialised from (40 + Δx, 40 + Δy), where Δx = rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs and Δy = rs
θs and Δy = rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs with separation magnitude rs ∈ [40, 50, 55, 60] and orientation angle, relative to ex, of θs ∈ [0°, 6°, 11°, 17°, 22°, 33°, 45°, 56°, 68°, 79°, 90°]. Simulations have periodic boundary conditions on all walls, with system size Lx = 80 + 40
θs with separation magnitude rs ∈ [40, 50, 55, 60] and orientation angle, relative to ex, of θs ∈ [0°, 6°, 11°, 17°, 22°, 33°, 45°, 56°, 68°, 79°, 90°]. Simulations have periodic boundary conditions on all walls, with system size Lx = 80 + 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs and Ly = 80 + 40
θs and Ly = 80 + 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs. The simulation time is TS = 3000.
θs. The simulation time is TS = 3000.
Two vectors are measured to determine the attractive or repulsive behaviour of the mobile colloidal probe placed at varying separations rs and angular positions θs relative to a fixed colloid (Fig. 11a). The first is the initial separation vector between the colloids r0s = r02 − r01 (blue arrow). This establishes a constant reference to measure the response of the mobile colloid. The second rtmob = rt2 − r02 is a temporally varying separation vector, which records the displacement of the mobile colloid at time t from the start position (red arrow). Individual mobile colloids are regarded to have repulsive or attractive behaviour if the projection of rtmob on r0s is positive or negative respectively. The individual trajectories are noisy (grey trajectories in Fig. 11b) and, after some time, the −1/2 defects reorient to aid self-assembly into chains (Fig. 11c). This reorientation misaligns the relative quadrupole orientations. Therefore, N = 15 simulation runs are performed for each combination of rs and θs, and the response behaviours are measured from the early time dynamics chosen to be 200 ≤ t ≤ 500. The minimum time of t = 200 is chosen to establish sufficient statistical certainty on the attraction–repulsion trajectories. Ensemble averages of the projection magnitude r0s·rtmob are performed, extracting the mean μ and standard error  . The nature of each colloidal site (rs
. The nature of each colloidal site (rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs, rs
θs, rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs) is calculated as attractive if μ ≤ −σM, repulsive if μ ≥ σM and neutral otherwise.
θs) is calculated as attractive if μ ≤ −σM, repulsive if μ ≥ σM and neutral otherwise.
 | ||
| Fig. 12 Director field slices around standard and tilted figure-of-eight colloidal-dimer states. (a) Standard figure-of-eight structures are associated with a uniaxial far-field director field. (b) Tilted-figure-of-eight entanglements have a director field that modulates away from the dimer. The director is shown in grey. Disclinations are visualised as in Fig. 1. | ||
Defect analysis
Disclination loops are identified using the disclination density tensor, proposed by Schimmings and Vinals.77 Using Einstein-index summation convention for clarity, the tensor is conveniently constructed from derivatives of the nematic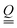 -tensor
-tensor| Dij = εiμνεjlk∂lQμα∂kQνα, | (24) |
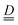 can be directly interpreted as the dyad
can be directly interpreted as the dyad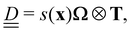 | (25) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = Ω·T illustrates if the local disclination has a wedge profile (with cos
β = Ω·T illustrates if the local disclination has a wedge profile (with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = +1 for +1/2 defect profiles and cos
β = +1 for +1/2 defect profiles and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = −1 for −1/2 defect profiles) or a twist profile (with cos
β = −1 for −1/2 defect profiles) or a twist profile (with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β ≈ 0).
β ≈ 0).
The scalar field s(x) is non-negative, and is maximum at the core of the disclination – therefore providing a useful quantity for identifying disclinations, with an appropriately defined lower bound. Throughout this study, disclinations are identified as s(x) ≥ 0.9, which was found to produce smoother disclinations than using isosurfaces of the nematic scalar order parameter S(x). Extracting s(x), Ω and T from eqn (25) utilises the methods outlined in ref. 77. The vectors Ω and T are ensured to be continuous and have the correct relative sign by: (1) applying a clustering algorithm that groups disclination cells into disclination lines, (2) ensuring the tangent vector smoothly varies along the line and (3) fixing the sign using 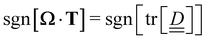 .
.
A second clustering algorithm groups disclination cells into an ordered sequence of larger points, that combines together a group of nearest neighbours, without reusing cells from other groups. The start and end point of the sequence connect together to form a loop. The T and Ω of composite cells are averaged over to return a single dyad per point. This construction into points enables geometric properties of the loop to be established, particularly those required to calculate the ribbon properties of the disclination line.
Through this approach to defect analysis, N-MPCD is able to resolve defect structures with the correct winding. This remains true even as the nematic background phase approaches the isotropic–nematic transition (Fig. 13). With consistent scalar isosurface s = 0.9, the Saturn ring is resolved for all U until just above the isotropic to nematic transition, including correctly identifying the −1/2 profiles (purple). The smoothness of the loop does reduce for lower U, although this can be remedied by choosing a smaller s value.
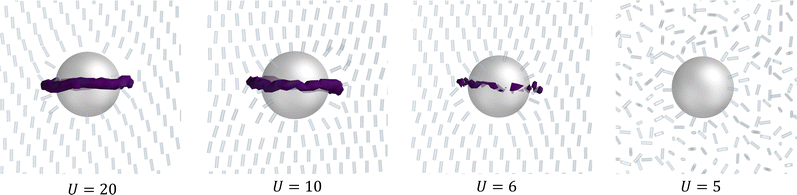 | ||
| Fig. 13 Saturn ring disclination loop for different mean field interaction strengths U. In each, the isosurfaces shown are s = 0.9 (eqn (25)). | ||
Ribbon framing
To construct the ribbon, a framing vector w perpendicular to T is required that varies continuously along the disclination loop. In the proximity of the disclination, n is oriented in a plane with normal vector Ω, which is anti-parallel to T as confirmed by the colouring Ω·T = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = −1. We therefore make an arbitrary choice to track one of the three radially pointing orientations of the −1/2 profile along the disclination. To extract the three radial orientations, w1, w2, w3, we construct a small cube of 5 × 5 × 5 lattice cells centred on each of the ordered points. For each of these cubes, a rotation matrix
β = −1. We therefore make an arbitrary choice to track one of the three radially pointing orientations of the −1/2 profile along the disclination. To extract the three radial orientations, w1, w2, w3, we construct a small cube of 5 × 5 × 5 lattice cells centred on each of the ordered points. For each of these cubes, a rotation matrix 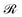 is constructed and applied to the director field within the cube, which aligns the local disclination tangent T with ez. This enables the director radial orientation to be identified on the transformed exey plane, on which we construct a test vector rtest = (cos
is constructed and applied to the director field within the cube, which aligns the local disclination tangent T with ez. This enables the director radial orientation to be identified on the transformed exey plane, on which we construct a test vector rtest = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θtest, sin
θtest, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θtest) oriented radially outwards from the core. On a circuit of points xl surrounding the core, rtest is compared with the local director n(xl). Determined over all points xl and test orientations θtest, w1 is chosen as the rtest that maximises the absolute value |rtest·n(xl)|. The inverse rotation transform
θtest) oriented radially outwards from the core. On a circuit of points xl surrounding the core, rtest is compared with the local director n(xl). Determined over all points xl and test orientations θtest, w1 is chosen as the rtest that maximises the absolute value |rtest·n(xl)|. The inverse rotation transform 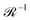 is applied to w1 to revert back to the original basis, and w2, w3 are determined as orientations 2π/3 rotated relative to each other about T. The framing vector is initialised as w = w1 for the first point along the loop, and subsequent points choose from one of the three w1, w2, w3 orientations that minimise the rotation angle compared with w from the previous point in the sequence.
is applied to w1 to revert back to the original basis, and w2, w3 are determined as orientations 2π/3 rotated relative to each other about T. The framing vector is initialised as w = w1 for the first point along the loop, and subsequent points choose from one of the three w1, w2, w3 orientations that minimise the rotation angle compared with w from the previous point in the sequence.
Calculating the self-linking number
The self-linking number is calculated through the geometric writhe Wr and twist Tw properties of the disclination viaeqn (19). Twisting is the local winding of the framing vector around the tangent curve, which gives Tw when integrated. Writhe is a non-local geometric property that describes the coiling of the curve, through tracking the relative rotation of locally parallel tangent bundles along the loop.7 Writhe and twist are calculated as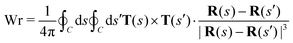 | (26) |
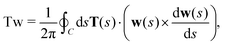 | (27) |
 is the local tangent vector,85 and C is a closed curve composing the disclination loop. The framing vector w(s) is everywhere perpendicular to T(s) and sets up the local framing direction (Section 5.7).
is the local tangent vector,85 and C is a closed curve composing the disclination loop. The framing vector w(s) is everywhere perpendicular to T(s) and sets up the local framing direction (Section 5.7).
Acknowledgements
This research has received funding from the European Research Council under the European Unions Horizon 2020 research and innovation programme (Grant Agreement No. 851196). For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.Notes and references
- H. Stark, Phys. Rep., 2001, 351, 387–474 CrossRef CAS.
- I. I. Smalyukh, Annu. Rev. Condens. Matter Phys., 2018, 9, 207–226 CrossRef.
- O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5143–5144 CrossRef CAS PubMed.
- T. A. Wood, J. S. Lintuvuori, A. B. Schofield, D. Marenduzzo and W. C. Poon, Science, 2011, 334, 79–83 CrossRef CAS PubMed.
- I. Muševič, M. Škarabot, U. Tkalec, M. Ravnik and S. Žumer, Science, 2006, 313, 954–958 CrossRef PubMed.
- S. Čopar and S. Z. Žumer, Phys. Rev. Lett., 2011, 106, 177801 CrossRef PubMed.
- S. Čopar, T. Porenta and S. Z. Žumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051702 CrossRef PubMed.
- M. Tasinkevych, N. Silvestre, P. Patricio and M. Telo da Gama, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 341–347 CrossRef CAS PubMed.
- G. P. Alexander, B. G.-G. Chen, E. A. Matsumoto and R. D. Kamien, Rev. Mod. Phys., 2012, 84, 497–514 CrossRef CAS.
- E. M. Terentjev, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1330–1337 CrossRef CAS PubMed.
- Y. Gu and N. L. Abbott, Phys. Rev. Lett., 2000, 85, 4719–4722 CrossRef CAS PubMed.
- N. D. Mermin, Rev. Mod. Phys., 1979, 51, 591 CrossRef CAS.
- S. Čopar, Phys. Rep., 2014, 538, 1–37 CrossRef.
- J. S. Lintuvuori, K. Stratford, M. Cates and D. Marenduzzo, Phys. Rev. Lett., 2011, 107, 267802 CrossRef CAS PubMed.
- T. N. Shendruk and J. M. Yeomans, Soft Matter, 2015, 11, 5101–5110 RSC.
- H. Híjar, Condens. Matter Phys., 2019, 22, 13601 CrossRef.
- K.-W. Lee and M. G. Mazza, J. Chem. Phys., 2015, 142, 164110 CrossRef PubMed.
- K.-W. Lee and T. Pöschel, Soft Matter, 2017, 13, 8816–8823 RSC.
- S. Mandal and M. G. Mazza, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2019, 99, 063319 CrossRef CAS PubMed.
- S. Mandal and M. G. Mazza, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 64 CrossRef CAS PubMed.
- H. Híjar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2020, 102, 062705 CrossRef PubMed.
- K. Wamsler, L. C. Head and T. N. Shendruk, Soft Matter, 2024, 20, 3954–3970 RSC.
- T. Kozhukhov and T. N. Shendruk, Sci. Adv., 2022, 8, eabo5788 CrossRef PubMed.
- J. Macas-Durán, V. Duarte-Alaniz and H. Hjar, Soft Matter, 2023, 19, 8052–8069 RSC.
- B. Senyuk, Q. Liu, S. He, R. D. Kamien, R. B. Kusner, T. C. Lubensky and I. I. Smalyukh, Nature, 2013, 493, 200–205 CrossRef CAS PubMed.
- M. Ravnik and S. Žumer, Soft Matter, 2009, 5, 269–274 RSC.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- R. Winkler, M. Ripoll, K. Mussawisade and G. Gompper, Comput. Phys. Commun., 2005, 169, 326–330 CrossRef CAS.
- A. Lamura, T. W. Burkhardt and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061801 CrossRef CAS PubMed.
- D. Reyes-Arango, J. Quintana-H., J. C. Armas-Pérez and H. Híjar, Phys. A, 2020, 547, 123862 CrossRef CAS.
- T. N. Shendruk, R. Tahvildari, N. M. Catafard, L. Andrzejewski, C. Gigault, A. Todd, L. Gagne-Dumais, G. W. Slater and M. Godin, Anal. Chem., 2013, 85, 5981–5988 CrossRef CAS PubMed.
- A. W. Zantop and H. Stark, J. Chem. Phys., 2021, 155, 134904 CrossRef CAS PubMed.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 61 CrossRef PubMed.
- A. Sengupta, Liq. Cryst. Today, 2015, 24, 70–80 CrossRef.
- S. Čopar, M. Ravnik and S. Žumer, Crystals, 2021, 11, 956 CrossRef.
- Y. Luo, D. A. Beller, G. Boniello, F. Serra and K. J. Stebe, Nat. Commun., 2018, 9, 3841 CrossRef PubMed.
- H. Noguchi, N. Kikuchi and G. Gompper, EPL, 2007, 78, 10005 CrossRef.
- I. O. Götze, H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 046705 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, in Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids, ed. C. Holm and K. Kremer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, pp. 1–87 Search PubMed.
- H. Híjar, R. Halver and G. Sutmann, Fluct. Noise Lett., 2019, 18, 1950011 CrossRef.
- H. Híjar and A. Majumdar, Soft Matter, 2024, 20, 3755–3770 RSC.
- J. Armendáriz and H. Híjar, Int. J. Mod. Phys. B, 2021, 35, 2150124 CrossRef.
- J. Armendáriz and H. Híjar, Materials, 2021, 14, 2886 CrossRef PubMed.
- V. Duarte Alaniz and H. Híjar, Phys. A, 2023, 609, 128298 CrossRef.
- A. Lamura and G. Gompper, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 477–485 CrossRef CAS PubMed.
- M. Cui and J. R. Kelly, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 331, 49–57 CrossRef.
- Ž. Kos, J. Aplinc, U. Mur and M. Ravnik, in Mesoscopic Approach to Nematic Fluids, ed. F. Toschi and M. Sega, Springer International Publishing, Cham, 2019, pp. 51–93 Search PubMed.
- N. D. Mermin, Boojums All the Way Through, Cambridge University Press, 1990 Search PubMed.
- Q. Liu, S. Bohdan, M. Tasinkevych and I. I. Smalyukh, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9231–9236 CrossRef CAS PubMed.
- M. Tasinkevych, N. Silvestre and M. T. Da Gama, New J. Phys., 2012, 14, 073030 CrossRef.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770–1773 CrossRef CAS PubMed.
- J.-I. Fukuda, M. Yoneya and H. Yokoyama, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 87–98 CrossRef CAS PubMed.
- Y. Wang, P. Zhang and J. Z. Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 96, 042702 CrossRef PubMed.
- D. Andrienko, G. Germano and M. P. Allen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041701 CrossRef CAS PubMed.
- R. W. Ruhwandl and E. M. Terentjev, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5561–5565 CrossRef CAS.
- J. Friedel and P. De Gennes, CR Acad. Sci. Paris B, 1969, 268, 257–259 CAS.
- J. X. Velez, Z. Zheng, D. A. Beller and F. Serra, Soft Matter, 2021, 17, 3848–3854 RSC.
- G. Duclos, R. Adkins, D. Banerjee, M. S. Peterson, M. Varghese, I. Kolvin, A. Baskaran, R. A. Pelcovits, T. R. Powers and A. Baskaran, et al. , Science, 2020, 367, 1120–1124 CrossRef CAS PubMed.
- T. N. Shendruk, K. Thijssen, J. M. Yeomans and A. Doostmohammadi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2018, 98, 010601 CrossRef CAS PubMed.
- G. Negro, L. C. Head, L. N. Carenza, T. N. Shendruk, D. Marenduzzo, G. Gonnella and A. Tiribocchi, Research Square, 2024 DOI:10.21203/rs.3.rs-3945915/v1.
- T. C. Lubensky, D. Pettey, N. Currier and H. Stark, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 610–625 CrossRef CAS.
- S. B. Chernyshuk and B. I. Lev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011707 CrossRef CAS PubMed.
- V. M. Pergamenshchik and V. A. Uzunova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021704 CrossRef CAS PubMed.
- P. V. Dolganov and V. K. Dolganov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041706 CrossRef CAS PubMed.
- D. Müller, T. A. Kampmann and J. Kierfeld, Sci. Rep., 2020, 10, 12718 CrossRef PubMed.
- C. M. Noël, G. Bossis, A.-M. Chaze, F. Giulieri and S. Lacis, Phys. Rev. Lett., 2006, 96, 217801 CrossRef PubMed.
- K. Takahashi, M. Ichikawa and Y. Kimura, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 020703 CrossRef PubMed.
- I. Muševič, Materials, 2018, 11, 24 CrossRef PubMed.
- N. M. Silvestre, P. Patrício, M. Tasinkevych, D. Andrienko and M. M. T. da Gama, J. Phys.: Condens. Matter, 2004, 16, S1921 CrossRef CAS.
- M. S. Škarabot, M. Ravnik, S. Z. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman and I. Muševič, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031705 CrossRef PubMed.
- G. P. Alexander and R. D. Kamien, Liq. Cryst. Rev., 2022, 10, 91–97 CrossRef CAS.
- O. Guzmán, E. B. Kim, S. Grollau, N. L. Abbott and J. J. de Pablo, Phys. Rev. Lett., 2003, 91, 235507 CrossRef PubMed.
- T. Araki and H. Tanaka, Phys. Rev. Lett., 2006, 97, 127801 CrossRef PubMed.
- M. Ravnik, M. S. Škarabot, S. Z. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman and I. Muševič, Phys. Rev. Lett., 2007, 99, 247801 CrossRef CAS PubMed.
- U. Tkalec, M. Ravnik, S. Z. Žumer and I. Muševič, Phys. Rev. Lett., 2009, 103, 127801 CrossRef CAS PubMed.
- C. D. Schimming and J. Viñals, Soft Matter, 2022, 18, 2234–2244 RSC.
- U. Tkalec and I. Muševič, Soft Matter, 2013, 9, 8140–8150 RSC.
- S. Čopar and S. Žumer, Proc. R. Soc. A, 2013, 469, 20130204 CrossRef.
- K. Jänich, Acta Appl. Math., 1987, 8, 65–74 CrossRef.
- V. S. R. Jampani, M. S. Škarabot, M. Ravnik, S. Čopar, S. Z. Žumer and I. Muševič, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031703 CrossRef CAS PubMed.
- U. Tkalec, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Science, 2011, 333, 62–65 CrossRef CAS PubMed.
- T. Machon, Liq. Cryst. Today, 2019, 28, 58–67 CrossRef.
- P.-G. De Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, 1993 Search PubMed.
- R. D. Kamien, Rev. Mod. Phys., 2002, 74, 953–971 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |

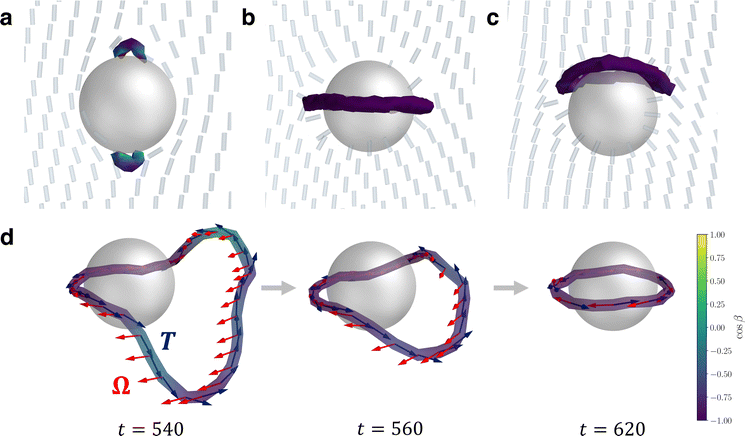
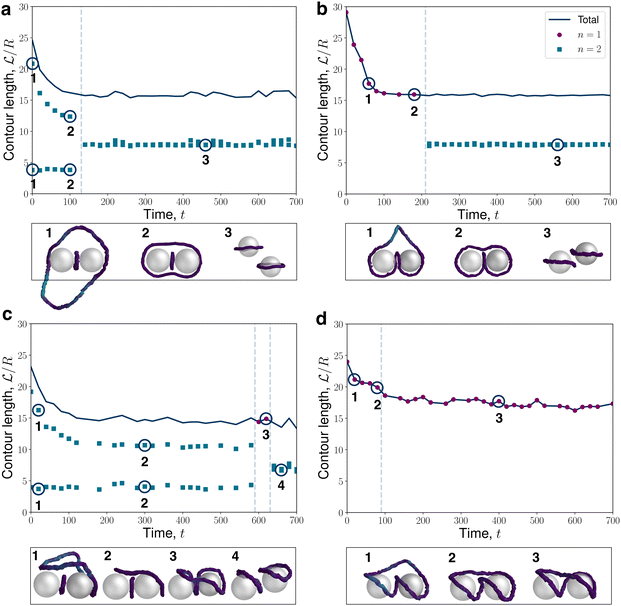
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) scaled by colloid radius
scaled by colloid radius