Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Soft matter physics of the ground beneath our feet
Anne
Voigtländer†
 *az,
Morgane
Houssais†
*az,
Morgane
Houssais†
 *b,
Karol A.
Bacik
*b,
Karol A.
Bacik
 c,
Ian C.
Bourg
c,
Ian C.
Bourg
 d,
Justin C.
Burton
d,
Justin C.
Burton
 e,
Karen E.
Daniels
e,
Karen E.
Daniels
 f,
Sujit S.
Datta
f,
Sujit S.
Datta
 g,
Emanuela
Del Gado
g,
Emanuela
Del Gado
 h,
Nakul S.
Deshpande
h,
Nakul S.
Deshpande
 f,
Olivier
Devauchelle
f,
Olivier
Devauchelle
 i,
Behrooz
Ferdowsi
i,
Behrooz
Ferdowsi
 j,
Rachel
Glade
j,
Rachel
Glade
 k,
Lucas
Goehring
k,
Lucas
Goehring
 l,
Ian J.
Hewitt
l,
Ian J.
Hewitt
 m,
Douglas
Jerolmack
m,
Douglas
Jerolmack
 n,
Ruben
Juanes
n,
Ruben
Juanes
 o,
Arshad
Kudrolli
o,
Arshad
Kudrolli
 b,
Ching-Yao
Lai
b,
Ching-Yao
Lai
 p,
Wei
Li
p,
Wei
Li
 oy,
Claire
Masteller
oy,
Claire
Masteller
 q,
Kavinda
Nissanka
q,
Kavinda
Nissanka
 e,
Allan M.
Rubin
e,
Allan M.
Rubin
 r,
Howard A.
Stone
r,
Howard A.
Stone
 *s,
Jenny
Suckale
*s,
Jenny
Suckale
 t,
Nathalie M.
Vriend
t,
Nathalie M.
Vriend
 u,
John S.
Wettlaufer
u,
John S.
Wettlaufer
 vw and
Judy Q.
Yang
vw and
Judy Q.
Yang
 x
x
aGerman Research Centre for Geosciences (GFZ), Geomorphology, Telegrafenberg, 14473 Potsdam, Germany. E-mail: avoigtlaender@lbl.gov
bDepartment of Physics, Clark University, 950 Main St, Worcester, MA 01610, USA
cDepartment of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
dCivil and Environmental Engineering (CEE) and High Meadows Environmental Institute (HMEI), Princeton University, E208 EQuad, Princeton, NJ 08540, USA
eDepartment of Physics, Emory University, 400 Dowman Dr, Atlanta, GA 30033, USA
fNorth Carolina State University, 2401 Stinson Dr, Raleigh, NC 27607, USA
gDepartment of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA
hDepartment of Physics, Institute for Soft Matter Synthesis and Metrology, Georgetown University, Washington, DC, USA
iInstitut de Physique du Globe de Paris, Université Paris Cité, 1 rue Jussieu, CNRS, F-75005 Paris, France
jDepartment of Civil and Environmental Engineering, jUniversity of Houston, Houston, TX 77204, USA
kEarth & Environmental Sciences Department and Mechanical Engineering Department, University of Rochester, 227 Hutchison Hall, P.O. Box 270221, Rochester, NY 14627, USA
lSchool of Science and Technology, Nottingham Trent University, Nottingham NG11 8NS, UK
mMathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, UK
nDepartment of Earth & Environmental Science, University of Pennsylvania, Philadelphia, PA 19104, USA
oDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
pDepartment of Geophysics, Stanford University, Stanford, CA 94305, USA
qDepartment of Earth and Planetary Sciences, Washington University in St. Louis, St. Louis, MO, USA
rDepartment of Geosciences, Princeton University, Princeton, NJ 08544, USA
sDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
tComputational and Mathematical Engineering, and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
uDepartment of Mechanical Engineering, University of Colorado at Boulder, Boulder, CO 80309, USA
vDepartments of Earth & Planetary Sciences, Mathematics and Physics, Yale University, New Haven, CT 06520, USA
wNordic Institute for Theoretical Physics, 106 91, Stockholm, Sweden
xSaint Anthony Falls Laboratory and Department of Civil, Environmental, and Geo-Engineering, University of Minnesota, Minneapolis, MN, USA
yStony Brook University, Department of Civil Engineering, Stony Brook, NY 11794, USA
zLawrence Berkeley National Laboratory (LBNL), Energy Geosciences Division, 1 Cyclotron Rd, Berkeley, CA 94720, USA
First published on 16th July 2024
Abstract
The soft part of the Earth's surface – the ground beneath our feet – constitutes the basis for life and natural resources, yet a general physical understanding of the ground is still lacking. In this critical time of climate change, cross-pollination of scientific approaches is urgently needed to better understand the behavior of our planet's surface. The major topics in current research in this area cross different disciplines, spanning geosciences, and various aspects of engineering, material sciences, physics, chemistry, and biology. Among these, soft matter physics has emerged as a fundamental nexus connecting and underpinning many research questions. This perspective article is a multi-voice effort to bring together different views and approaches, questions and insights, from researchers that work in this emerging area, the soft matter physics of the ground beneath our feet. In particular, we identify four major challenges concerned with the dynamics in and of the ground: (I) modeling from the grain scale, (II) near-criticality, (III) bridging scales, and (IV) life. For each challenge, we present a selection of topics by individual authors, providing specific context, recent advances, and open questions. Through this, we seek to provide an overview of the opportunities for the broad Soft Matter community to contribute to the fundamental understanding of the physics of the ground, strive towards a common language, and encourage new collaborations across the broad spectrum of scientists interested in the matter of the Earth's surface.
The ground beneath our feet, plain and static as it might seem, holds the key to many pressing global issues. More than ever, in a world that is experiencing global warming and changing precipitation patterns, we need to better understand, predict, and feasibly control processes within the ground that can cause natural hazards,1 shape future landscapes,2–5 impact the health of our agricultural lands,6 and sequester carbon.7
What we are calling the ground is all the complex material at the surface of the Earth that is not essentially a single-phase natural fluid, such as air and water. It is either a composite solid (e.g., crystalline or sedimentary rocks, or ice, of various compositions, age, and deformation history) or – and most commonly – an assembly of grains of different types (e.g., sand grains, clay platelets, shells, ice crystals, boulders, bacteria). The ground evolves because it is constantly being processed by reactive solutions, biological activity, capillary and thermal stresses, and sheared by gravitational forces and fluid flows. As a result, locally and at a given time t, the ground exhibits normal and shear strains γ(t), an effective solid – or packing – fraction ϕ(t), and associated porosity s(t) = 1 − ϕ(t) occupied by a volume fraction w(t) of an effective liquid, most often natural water. Over time, w can vary from 0% (dry) to 100% (fully saturated, and sometimes overflowing), through intermediate values (partially saturated). Studies of the physical and chemical dynamics of such a system – coarsely, a heterogeneous and fragile “sponge” or pile of sticky grains – give rise to a multitude of Soft Matter problems.
Echoing the richness of the ground, a multitude of disciplines investigate the thin layer making the Earth's surface, including the Earth, environmental, and material sciences, engineering, physics, chemistry, and biology. Different disciplines tend to have different cultures and approaches, as well as different motivations, constraints, and even notations. As a result, a wide and complementary range of foci regarding temporal and spatial scales, concepts, laboratory, and field study methods coexist. Nevertheless, opportunities for scientific exchanges between these different communities which study processes happening at Earth's surface remain rare. This article is a perspective on the key-concepts and main challenges one faces in and out of well-controlled experiments and models of the ground (Fig. 1). Through specific examples, it also attempts to present some of the fantastic messiness one is confronted with, and enriched by, while studying the natural environment. Once clarified what are the mechanics of various systems over different length and time scales, field site location and conditions, process interactions and feedbacks, the fundamental questions at the heart of the discussion are: how can the complexity of natures dynamics and mechanics be simplified, measured, down-scaled, and structured to fit into a model, or are such simplifications impossible? How can the development of complex material rheology frameworks be of future use? How do we treat intermittency in natural phenomena? What are the expressions of near-criticality in nature, and over what scales should we consider it?
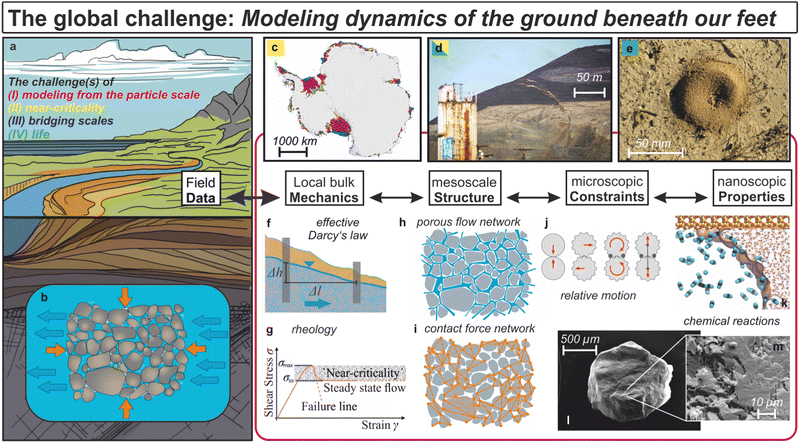 | ||
| Fig. 1 (a) Overview sketch of the four challenges of modeling the soft matter physics of the ground identified in this paper: (I) modeling processes from the grain scale; (II) measuring and capturing the ground dynamics near critical states; (III) connecting laboratory and theory results to field-scale observations; (IV) understanding and taking into account the many effects of life. (b) In a given element of the ground, subjected to normal stresses (orange arrows) and a mean groundwater flow (blue arrows), the soft matter physics of the ground encompasses simultaneously multiple phases, processes, dimensions, and scales, which can have various expressions at the Earth's surface, e.g., (c) an Antarctica map showing ice-shelf areas vulnerable to hydro-fracture (marked in red) in a warming world by Lai et al.;8 (d) a photograph of a crack that appeared on Jan 3 2018 in Rattlesnake Ridge, near Union Gap, WA, April 2018 (200 km from the 2014 Oso landslide with industrial infrastructure in the foreground, Photo credit: Shawn Gust, Yakima Herald-Republic via AP); and (e) a photograph of a mound of grains built by ants (imaggeo/EGU). To model the multi-dynamics of the ground, diverse methods, concepts, and approaches are used to link the ground's properties, constraints, structures, mechanics, and observational data. For example, models of (f) effective groundwater flow, or (g) rheological behavior in experiments and simulations, rely on assumptions relative to (h) porous flow and (i) contact force networks. (j) Individual motions in these networks are constrained by the properties and mechanisms of the phases involved.9 Often a phase can both be a constituent of the bulk system and define an interface where chemical reactions occur, e.g., (k) a CO2 bubble in contact with a water meniscus in a silica nanopore (courtesy of I.C. Bourg). As a result of these interactions, for example, a mineral particle such as a natural quartz sand grain (l) can display a chemo-mechanically altered surface topography (m), as seen in the scanning electron microscopy images (courtesy of A. Voigtländer). Such nanoscale phenomena can in turn affect the effective rheology of the ground and groundwater flow. | ||
Our intention here is to be both broad and specific. Broad in the sense of the conceptual framework outlined, and what we consider as soft matter (Fig. 1). Specific in highlighting some of the ongoing fronts of the scientific research and techniques on the ground beneath our feet, to inspire future, new and collaborative works. The effort was initiated by a workshop organized by the princeton center for theoretical science (PCTS) in January 2022, where the authors discussed recent results from their individual field of expertise. These contributions, enriched by the authors' collective conversation and efforts, turned into this article. Albeit their heterogeneity, they share similar broad challenges concerning concepts and scales, technical and methodological issues. The specific sub-sections represent only a small fraction of the many outstanding questions related to the field of “physics of the ground”, nevertheless they allow to present how this is an emerging research area where fundamental soft matter questions come together with interdisciplinary problems and impact. With this perspective paper we want to highlight this new research direction for soft matter by sharing examples of specific efforts and results recently obtained on such fronts.
The paper is organized into four sections, corresponding to four major scientific challenges we have identified as what is mainly ahead of us to model the ground (Fig. 1). These challenges are integral to the field of soft matter, yet they also have unique aspects when one studies the natural environment.
I – The challenge of modeling from the grain scale.
The ground is essentially a range of partially-wet particulate (hence porous) systems where chemical, physical, and biological processes occur (see magenta box in Fig. 1). Modeling each of these processes from the smaller scale is both fundamental and essential to building larger-scale and multi-parameter, multi-physics models.
II – The challenge of near-criticality.
The Earth surface constantly evolves and sets itself near its material yield criterion (typically, a critical shear stress σc). As a result, we mainly live in and observe a quasi-static environment – an apparently stable ground – but which is often about to fail (Fig. 1c and d). Surveying and predicting the ground's mechanical behavior, in particular the rare times it deforms plastically (e.g., during floods and landslides), requires good understanding and modeling of its near-critical behavior. This challenge demands advancements in both fundamental physics and development of new methods of quantitative observations.
III – The challenge of bridging scales.
All Earth (near-)surface processes occur at given length and time scales. Some mechanisms are universal across a wide range of spatial and temporal scales, some structures are hierarchical and emergent, some material properties are bounded with typical magnitudes, lengths, and characteristic times or rates. Knowledge of how and when to bridge scales, mathematically, numerically, and methodologically from the laboratory to the field sites (and vice versa) is a difficult key to forge (dark blue arrow on Fig. 1), but one unlocks advanced predictive capabilities.
IV – The challenge(s) of life.
Living matter has the unique property of reproducing itself, and growing or decaying over time. The self-propelled motion of many organisms is another specific impact of life on the environment. Many organisms contribute to the constant alteration of their surroundings, while also depending on it (Fig. 1d and e). The interconnections between all forms of life – including human life – and the dynamics of the ground, although obeying the laws of physics, bring additional complexity and carry a large number of original and pressing questions.
Within each one of these four main challenges (section), each contribution (sub-section) present a specific topic: its specific context, some recent advances, and open questions. These sub-sections are only a selection of topics, which illustrate through specific problems the four main challenges.
1 The challenge of modeling from the grain scale
Efforts to understand the dynamics of the ground from the scale of a single grain inform our definitions of transients, steady state dynamics (e.g., rheology), fundamental causes for instability growth, and the interactions between different physical processes. Fundamentally, these efforts aim to identify, visualize or parameterize, and quantify the relevant elementary phenomena happening at the grain scale. This section presents a few examples of ongoing efforts in this domain based on experimental, numerical, and analytical approaches (Fig. 1).In particular, Sections 1.1 and 1.2 illustrate advances by considering Earth materials, such as fault gouge or soils, as granular assemblages, eventually impacted by pore fluid pressure. Section 1.3 highlights how in situ observations are generating new insight on flow, transport, and mechanics in these heterogeneous porous materials. Section 1.4 discusses Eulerian computational approaches that can capture the complex deformation of ductile, cohesive Earth materials (such as erosion or desiccation cracking). Finally, Section 1.5 highlights how grain–fluid interactions can add significant complexity to grain scale processes, for example in situations where solid surfaces impact the stability of interfacial liquid water films.
1.1 The role of granular flow in fault friction – A. M. Rubin & B. Ferdowsi
Numerical models of fault slip require a constitutive law for fault friction. The current state-of-the-art, originally conceived for two rough surfaces in contact but observed to apply to sheared gouge layers as well, falls under the heading of “rate- and state-dependent” friction. In this formalism, friction depends upon the fault sliding rate (or strain rate), and a more nebulous property termed “state”.14 State is conventionally thought to reflect a combination of the true contact area and the intrinsic strength of those contacts.15 Also conventionally, the state dependence is thought to be due to time-dependent plastic flow or chemical bonding at those contacts, although the opaque nature of rock makes the origin of state evolution difficult to decipher.16 How state evolves for surfaces not at steady-state sliding is parameterized by “state evolution laws” that are largely empirical, yet still do not adequately describe all the relevant features of laboratory experiments.17
Numerical simulations of faults obeying rate-state friction show that the precise description of state evolution significantly influences processes of interest to Earth scientists (e.g., earthquake nucleation18). The lack of an accurate or physics-based description of state evolution thus severely hampers our ability to extrapolate the results of numerical models of fault slip to the Earth.
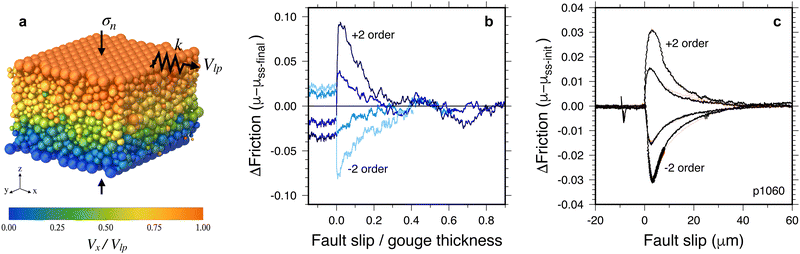 | ||
| Fig. 2 (a) Snapshot from a DEM simulation of a sheared granular layer.19 Grains are spherical, polydisperse, and have elastic properties appropriate for glass beads. Colors indicate grain velocity in the x direction, relative to the load-point velocity, averaged over an upper-plate sliding displacement of 1 mean grain diameter. (b) The friction signal, relative to the future steady-state value, following simulated velocity steps of ±1 or 2 orders of magnitude from an initial velocity of 0.01 m s−1.19 Slip distance is defined to be zero at the time of the step. (c) Solid black lines indicate the friction signals, relative to the prior steady-state value, following velocity steps of ±1 or 2 orders of magnitude at sliding speeds from 1 to 100 μs−1, from experiments conducted in the Penn State Rock and Sediment Mechanics Lab.17 The starting material is a 3-mm-thick layer of synthetic quartz gouge, with particles ranging from 50–150 μm in diameter (shear ultimately localizes to a narrower zone where particles have been comminuted, a process not modeled in the DEM). The synthetic quartz gouge is nearly steady-state velocity neutral, whereas the DEM is steady-state velocity strengthening. The red lines are a fit to the data using the empirical “Slip” version of the rate-state friction equations (“direct effect” coefficient a = 0.0073; “state evolution effect” coefficient b = 0.0075; e-folding slip distance Dc = 12.2 μm). | ||
These results are similar to those from laboratory friction experiments on rock and many other materials. The solid black lines in Fig. 2c indicate the friction signals, relative to the prior steady state value, following velocity steps of ±1 or 2 orders of magnitude from experiments on synthetic quartz gouge.17 The magnitude of the logarithmic rate- and state-dependence in the DEM and lab experiments are similar to within a factor of ∼2 (there is some rounding and diminishing of the peaks in panel (c) not present in panel (b) because the elastic stiffness of the lab system is smaller). The red lines in Fig. 2c are a fit to the data using the empirical “slip” version of the rate-state friction equations,11,14,17 using a single set of parameter values for all 4 steps.
1.2 Force chains underpin emergent poromechanical behavior in granular media – W. Li & R. Juanes
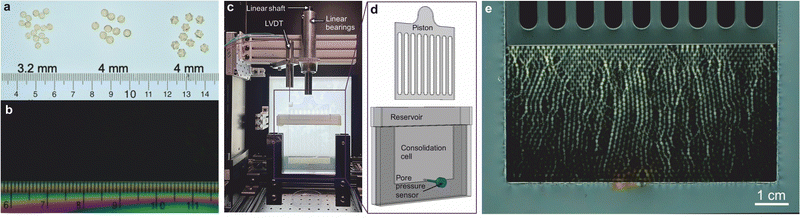 | ||
| Fig. 3 Consolidation test using photoporomechanics. (a) Millimeter-size photoelastic particles in two different shapes (spheres and icosahedra) under white light. (b) Photoelastic particles under a circular polariscope. The polystyrene ruler, having residual stress, shows color stripes. The particles, being residual-stress-free, are hardly visible.36 (c) Experimental setup for the 1D consolidation experiment. A granular pack of fluid-saturated photoelastic spheres is loaded suddenly with a constant weight, while the video, deformation, and excess pore pressure are recorded. (d) Detailed schematic of the consolidation cell. Two glass plates are glued with a 2 mm thick U-shaped spacer where the beads are inserted to form a monolayer pack. The excess pore pressure is measured at the bottom of the cell with a pressure sensor. The pore fluid fills the cell to provide a constant-pressure boundary condition. A piston made of a 1.8 mm acrylic plate (with slots cut out to reduce resistance to fluid flow) allows the fluid to seep out of the cell.36 (e) Snapshot of the photoelastic response of the granular pack during a consolidation test. The force chains – which quantify the Terzaghi stress in the granular pack – develop from the top boundary, then progress downwards through the pack as the pore–fluid pressure diffuses upwards. | ||
1.3 In situ visualization of soft matter dynamics in granular and porous media – S. S. Datta
For example, despite its importance in geophysics and in a wide variety of natural and engineered processes,42–77 prediction and control of complex fluid flow, particle transport, and solid mechanics in porous media is challenging and often operates by trial and error. Even basic prediction of where injected fluid distributes through a porous medium, and of the associated macroscopic resistance to flow, remains elusive due to the time-dependent and multi-scale nature of the associated phenomena. Disentangling these interactions through in situ visualization is an exciting research frontier. While even basic characterization has traditionally been difficult due to the opacity and complexity of most three-dimensional (3D) environments, confocal microscopy of refractive index-matched fluids and model solid media now enables researchers to directly visualize soft matter dynamics in 3D porous media with controlled pore structures and chemistries.78
A second example is the phenomenon whereby as colloidal particles navigate a porous medium, they can alter the medium by depositing onto (or eroding from) its solid matrix, making prediction of macroscopic particle distributions challenging.87–103 Advances in direct visualization have enabled identification of the fundamental mechanisms by which particles are distributed throughout a porous medium, demonstrating that the interplay between hydrodynamic and colloidal interaction forces controls this process.104 These advances also have enabled characterization of how interactions between particles and trapped non-aqueous fluids influence subsequent transport (Fig. 4a).105 These results help shed light on the multi-scale interactions between fluids, particles, and porous media that have traditionally been represented in black-box models using “lumped” empirical parameters – guiding the development of more accurate and generalizable models that could be applied in diverse geophysical settings and beyond, for example, in the complex flow behavior of polymer solutions.106–111
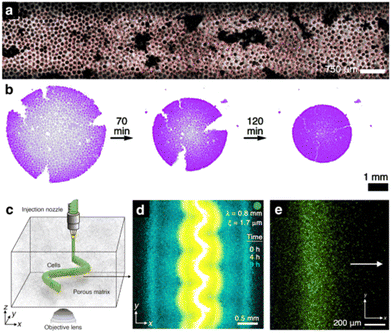 | ||
| Fig. 4 Illustrations of the capability for in situ visualization of soft matter dynamics in granular and porous media. (a) Large-scale confocal micrograph taken inside a 3D porous medium (section through solid matrix shown by black circles), showing trapped oil (additional black) and deposited colloidal particles (red) in the pore space.105 (b) Self-healing of a cracked packing of hydrogel beads; color shows fluorescence due to an excited dye that has diffused within the hydrogel beads, with an intensity that increases with bead shrinkage.112 (c) Schematic showing 3D printing of bacteria inside a porous granular hydrogel matrix. (d) Superimposed experimental confocal micrographs (different colors show different times) of bacteria spreading collectively from a 3D-printed population with an undulatory initial structure; the spreading cells smooth out these morphological perturbations. (λ) and (ξ) refer to the undulation wavelength and hydrogel matrix mean pore size, respectively.113 (e) Magnified view of a front of bacteria spreading by chemotaxis in a crowded, porous, granular hydrogel matrix.114 | ||
A third illustration is the use of in situ visualizations of hydrogels, i.e., elastic networks of hydrophilic polymers that can absorb large quantities of water, as models of shrinkable granular media, e.g., soft clay-rich soils whose deformations influence the integrity of built structures and barriers for waste isolation.115–117 Deforming such a soft porous material alters fluid transport through its pores, which in turn further deforms the material. Direct visualization of this coupling between fluid transport and solid deformations has shown how material physicochemical properties that regulate fluid permeability and mechanical deformations, as well as interactions with external boundaries, together control how these materials swell, shrink and deform,112 fracture,118 and potentially even self-heal112 (Fig. 4b) – providing new insights into the desiccation of soft earth materials.
Finally, the development of “transparent soils” using, e.g., granular hydrogels has helped shed light on the behavior of bacteria in 3D granular media over length scales ranging from the single-cell to the community scale119 (Fig. 4c–e). This capability has revealed that understanding of bacterial motility – which is based on studies performed in bulk liquid – was incomplete: for example, confinement in a crowded medium fundamentally alters how bacteria move, both at the single cell120 and population scales,114 in previously unknown ways. Ultimately, these results could guide the development of new theoretical models121 to more accurately predict the motion and growth of bacterial populations in complex environments akin to those in the ground beneath our feet, potentially helping to provide quantitative guidelines for the control of these dynamics in processes ranging from bioremediation to agriculture.
1.4 Coupled flow and mechanics of clays and muds – I. C. Bourg
An important aspect of the complex properties of clays and muds is that they can transition from cohesive to non-cohesive and from solid- to liquid-like mechanics depending on conditions, with important implications in efforts to predict phenomena such as fault slip, debris flow, and sediment transport (Sections 1.1, 2.2 and 2.4). A challenge in understanding these properties from the grain scale is that they are inherently multiphysics: whereas interparticle interactions in coarse grained materials predominantly consist of repulsive grain contact forces, potentially supplemented by attraction due to capillary fluid menisci,126 interparticle interactions in clayey materials involve a variety of attractive and repulsive interactions across thin water films, such as osmotic, electrostatic, van der Waals, hydration, and configurational entropy effects. All these interactions generally have different length scales and sensitivities to particle shape, surface charge, and solution chemistry to take into account.127,128
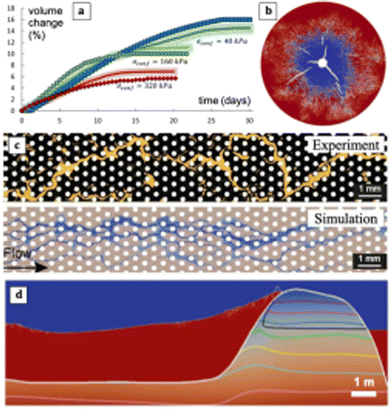 | ||
| Fig. 5 Darcy-Brinkman-Biot (DBB) simulation of clay: (a) expansion of a clay plug caused by a salinity decrease in a water reservoir in contact with the clay (symbols: measurements at different confining stresses;135 lines, model predictions124). (b) Cracking of a clayey medium in a Hele–Shaw cell upon injection of a non-wetting fluid from the center (red: water-saturated clay, blue: dry clay, white: cracks). Model predictions132 are qualitatively consistent with experimental observations.136,137 (c) Experiments and simulations showing flow channelization during biofilm growth in a microfluidic device (channels and biofilm matrix in yellow/black in the experiments, blue/tan in the simulations). The simulations correctly predict the emergence of flow intermittency and channelization associated with intermittent erosion.133 (d) Wave impact on a poroelastic barrier illustrating the coupling of multiphase flow and Earth surface mechanics on scales of tens of meters (colored lines show von Mises stresses within the barrier).134 | ||
Another important challenge is that the Eulerian treatment of clays illustrated in Fig. 5 requires constitutive relations reflecting the microscale material properties of clay (e.g., rheology, swelling pressure, permeability) as a function of saturation, salinity, compaction, and clay composition (i.e., the relative abundance of different clay minerals or biopolymers). These constitutive relations remain incompletely known, because of the complexity associated with the irregular shapes and the strong impact of interfacial fluids on interparticle interactions between nanometer scale clay colloids and/or biopolymers.128,138,142,143
1.5 Nonequilibrium statistical physics of inclusions in ice – J. S. Wettlaufer
In cold climates, roads are salted in winter harnessing the freezing point depression of impurities. Each salt crystal, however, abuts an ice surface where the phase change occurs. Less commonly thought of, but equally important, are other mechanisms that can extend the equilibrium domain of a liquid phase into the solid region of the normal phase diagram. The causes of this “premelting”, which, in addition to impurities,145 include surface melting, interface curvature and substrate disorder, allow for the persistence of water at interfaces well below the bulk melting point. The thickness of the liquid film depends on the temperature, soluble impurities, the material properties underlying intermolecular forces, and geometry. A temperature gradient is accompanied by a thermomolecular pressure gradient that drives the unfrozen interfacial liquid from high to low temperatures and hence particles in ice, as shown in Fig. 6, migrate from low to high temperatures. Such premelting dynamics are operative in a wide range of settings, from the heaving of frozen ground and planetary regolith, to the scavenging of atmospheric trace gases by snow and the redistribution of climate proxies in ice sheets, to the collisional processes in protoplanetary disks. Moreover, the unfrozen films act both as a refuge for biota and a transport mechanism for nutrients, waste and the biota themselves.
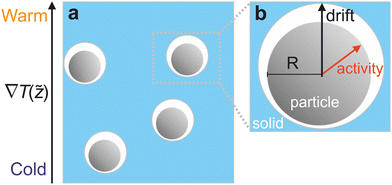 | ||
| Fig. 6 The interface between ice and inert or living particles is separated by what is called a premelted water film below the bulk melting point. (a) Perspective view of few active particles embedded inside ice against which they premelt and experience an external temperature gradient ∇T, which creates a thermomolecular pressure gradient driving the flow of liquid from high to low temperatures, so that particles translate from low to high temperatures. (b) An expanded view of one active particle inside the solid. The radius of the particle is R, the black arrow shows the drift velocity induced by the temperature gradient, and the red arrow denotes the activity given by an active force (from Vachier and Wettlaufer146). | ||
2 The challenge of near-criticality
Traditionally, the field of geophysics has been mainly subdivided between two areas: solid Earth geophysics—concerned with the application of solid mechanics to measuring and modeling rocks and ice over a variety of length and time scales149,150—and geophysical fluid dynamics – deeply rooted in applied mathematics and its application to atmospheric and ocean dynamics. Yet, many of the materials in the Earth's critical zone transit between many regimes: athermal to thermal (large to small particles), chemically inert to reactive (sand to clay), dense to dilute, jammed to creeping to catastrophic (submarine) avalanches and sand storms; and vice versa via deposition and lithification. There can be sharp spatial or temporal gradients between these regimes, and often these regimes are mixed with repeated transitions between them. The topics highlighted in this section consider near-critical behaviors in the “soft Earth” regime,151 which cannot be addressed by fluid or solid mechanics alone.The study of near-critical behavior in soft materials has a long history and encompasses problems such as the glass transition and deformation, shear-thickening behavior of suspensions, particulate material jamming, solid creep, and fracture dynamics. Most of these systems exhibit behaviors that are non-linear functions (e.g., Fig. 1) of the system's temperature, applied stresses, and density of grains or atoms. Material failure in the environment shares these common features and presents specific challenges. The Earth surface, just as any soft condensed matter near one of their failure criteria, is generally far from equilibrium and nonisotropic. Finding insightful measurements of such system responses, and how to use them practically to predict material failure, has been a crucial scientific endeavor. Section 2.1 presents recent experimental results on this front and their implications for further developing failure prediction in the environment. Different types of environments exhibit near-critical behavior, and they have been recorded and analyzed in different ways: for example, Section 2.2 covers the failure of hillslopes, Section 2.3 presents a recent highly-resolved spatial and temporal recording of iceberg collective dynamics along the coast of Greenland; Section 2.4 presents the challenge of observing and modeling river bed dynamics from flood to flood. In these natural granular systems, as in experiments presented in Section 2.1, the stress – or energy – landscape in the system appears significantly changed after a failure event, leading to hysteretic behavior. Finally, Section 2.5 presents some of the major challenges in modeling the intermittency and near-criticality of volcanic processes from the fundamental scale of mineral crystals and gas bubbles.
2.1 Rigidity, nonlocality, and acoustics in dense granular materials – K. Daniels
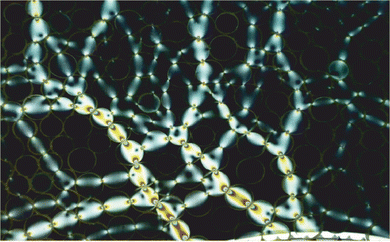 | ||
| Fig. 7 An image of photoelastic disks (of ≃1 cm diameter) resisting a shear force applied by the roughened boundary visible at the lower right, imaged with a darkfield polariscope.29,30 These methods allow for the quantitative determination of the vector contact forces between particles when performed in monochromatic light. In this image, the brighter particles are those carrying more force, while the darker particles carry little force. Under increased shear, the chains of forces buckle and rearrange (Source: E. Berthier, F. Fazelpour, C. Kirberger, NC State Physics). | ||
2.2 Soft matter of post-wildfire debris flows – D. Jerolmack and N. Deshpande
2.3 Floating granular materials – J. Burton and K. Nissanka
 | ||
| Fig. 8 Adapted from Cassotto et al.199 (a) View of ice mélange at Sermeq Kujalleq (Jakobshavn Isbræ) on the Western coast of Greenland. The ground-based radar visible in the center of the image is a few meters in size and is perched on the rocky cliffs above the fjord. (b) Top-left, divergence of velocity field under steady flow. Red areas represent extension of the flow, and blue areas represent compression. Overall, the field is smoothly varying. Top-right: Variation of velocity field in the black rectangle after subtracting the mean of the underlying steady flow. Bottom-left, divergence of velocity field less than 1 hour before a calving event (the fracture and discharge of a cubic-kilometer-sized iceberg from the glacier into the ice mélange). The divergence field is rapidly-varying and noisy. Bottom-right: variation of velocity field before calving, showing heterogeneous flow patterns. | ||
2.4 River sediment beds remember past flows – C. Masteller
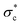 (or critical Shields stress), as the threshold parameter, it is now understood212 that such a universal threshold should be applied with caution. For example, field measurements show that longer inter-flood duration may lead to increases in
(or critical Shields stress), as the threshold parameter, it is now understood212 that such a universal threshold should be applied with caution. For example, field measurements show that longer inter-flood duration may lead to increases in 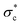 and reduced sediment transport rates.213
and reduced sediment transport rates.213
Laboratory experiments confirm that the magnitude and duration of inter-event flows affect 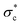 evolution and show that with little to no active sediment transport, grain-scale changes in interlocking, and subtle surface reorganization increase particle resistance to motion.214,215 These observations suggest that the increase in particle resistance under inter-event flows is akin to granular creep and compaction of granular materials under low to moderate shear rates. In response to higher magnitude flows (e.g., floods) surface reorganization of the bed leads to a decrease in particle entrainment thresholds via an increase in surface roughness, akin to dilation of granular materials under high shear rates.
evolution and show that with little to no active sediment transport, grain-scale changes in interlocking, and subtle surface reorganization increase particle resistance to motion.214,215 These observations suggest that the increase in particle resistance under inter-event flows is akin to granular creep and compaction of granular materials under low to moderate shear rates. In response to higher magnitude flows (e.g., floods) surface reorganization of the bed leads to a decrease in particle entrainment thresholds via an increase in surface roughness, akin to dilation of granular materials under high shear rates.
A high-resolution, multi-year time series of entrainment critical stress, 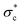 , from the Erlenbach torrent, a mountain stream in Switzerland,216 revealed that the magnitude of antecedent flows was the dominant control on the evolution of
, from the Erlenbach torrent, a mountain stream in Switzerland,216 revealed that the magnitude of antecedent flows was the dominant control on the evolution of 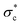 , with a secondary, short-lived duration effect.217 Consistent with laboratory experiments,218,219 these direct measurements showed increases in
, with a secondary, short-lived duration effect.217 Consistent with laboratory experiments,218,219 these direct measurements showed increases in 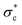 with increasing inter-event flow magnitude. In higher-magnitude, sediment-transporting flows, strengthening effects were also observed following low to intermediate-magnitude bedload-transporting floods; however, following high-magnitude flows,
with increasing inter-event flow magnitude. In higher-magnitude, sediment-transporting flows, strengthening effects were also observed following low to intermediate-magnitude bedload-transporting floods; however, following high-magnitude flows, 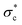 for motion decreased.217
for motion decreased.217
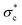 evolves through time as a function of bed shear stress can be used to capture these variations in particle erosion thresholds.220 A more fundamental, particle-scale-based approach could provide more insight. One possible explanation for the observed history-dependence217 is that the transition from bed strengthening to bed weakening is associated with a transition from sparse local rearrangement of particles to a more established sediment transport flow, capable of significantly disrupting bed structure via particle collisions or long-distance particle transport.221
evolves through time as a function of bed shear stress can be used to capture these variations in particle erosion thresholds.220 A more fundamental, particle-scale-based approach could provide more insight. One possible explanation for the observed history-dependence217 is that the transition from bed strengthening to bed weakening is associated with a transition from sparse local rearrangement of particles to a more established sediment transport flow, capable of significantly disrupting bed structure via particle collisions or long-distance particle transport.221
Another key challenge requiring a soft matter approach is to better understand how deformable boundaries (such as river bed channels) respond to variations in bed shear stress σ*, and by extension, to variations in 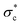 . Dilation occurs at shear stresses well above those commonly observed to result in channel widening,171 suggesting that bed disruption or weakening may be infrequent or buffered by channel width adjustments. Thus, further exploration of the feedbacks between adjustments in
. Dilation occurs at shear stresses well above those commonly observed to result in channel widening,171 suggesting that bed disruption or weakening may be infrequent or buffered by channel width adjustments. Thus, further exploration of the feedbacks between adjustments in 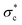 and channel widening onset should be explored.
and channel widening onset should be explored.
Further afield, definitive links between granular processes observed in laboratory experiments and field observations in gravel-bed rivers are precluded by various technical limits. The difficulty to acquire accurate in situ measurements of complex shapes of natural grains, fine-scale dynamical changes of grain-scale topography,222 grain motion beyond the bed surfaces, and small changes in 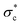 values are some of them. Indirect geophysical methods, including environmental seismology223–226 and distributed acoustic systems,227 which are currently explored in fluvial contexts, could allow bypassing some of these limits and connecting the dynamics over the different scales of the river-channel granular system.
values are some of them. Indirect geophysical methods, including environmental seismology223–226 and distributed acoustic systems,227 which are currently explored in fluvial contexts, could allow bypassing some of these limits and connecting the dynamics over the different scales of the river-channel granular system.
2.5 Why do persistently degassing volcanoes erupt? – J. Suckale
Fig. 9 shows an example of a lava fountain during the 1959 eruption at Klauea Iki, Hawaii, and a close-up photo of the crystal clusters later found in erupted samples.245 This crystal cluster formed by two particles drifting together during flow and intergrowing over time.245 The puzzling aspect of such crystal clusters is the abundance of relatively large misalignment angles separating the two crystals.246 A smaller angle would be hydrodynamically more favorable, but is only observed in a surprisingly small percentage of clusters. However, it is known that in linear shear flows, particles tumble along in Jeffery orbits,247 but wavy flows align crystals248,249 towards a preferential angle that depends on both the flow conditions and the particle geometry. As such, observations of crystal geometry suggest that the high percentage of large misalignment angles is indicative of a downward propagating wave in a volcanic conduit with low crystallinity.250 The inferred crystallinity is consistent with the lower range of observed crystallinities251 and with the possibility that a spatially heterogeneous arrangement of crystals inside the volcanic conduit could trigger a transition from flow to localized sliding over a thin interfacial layer within the magma mixture.242
 | ||
| Fig. 9 Photo of a lava fountain during the 1959 Kilauea Iki eruption (courtesy of USGS) in the background and a photo of a crystal cluster later identified in erupted samples by Schwindinger and Anderson.245 | ||
Many questions and challenges regarding the eruptive behavior of persistently active volcanoes remain, and require expertise outside of classical volcanology: multi-phase flow, non-linear dynamics, thermodynamics, and numerical analysis. These challenges touch on several themes discussed in this paper, particularly the challenge of modeling the grain scale (1) and the challenge of bridging scales (3). Like many other natural systems, volcanic systems span an enormous range of physical conditions and scales from microns to hundreds of kilometers.
3 The challenge of bridging scales
Earth surface processes occur over a vast range of scales, from the near instantaneous transport of millimeter-sized sand grains in a stream to the slow drift of entire continents over millions of years. Further, Earth materials that are seemingly solid on short timescales (e.g., soil, rock) can behave like soft materials over long timescales (e.g., soil creep, convection of Earth's mantle). This results in unique challenges in our ability to directly observe Earth surface dynamics in the field, highlighting the need for ways to use experiments and models at shorter length and time scales to better understand dynamics at larger, geologically relevant scales (Fig. 1). This section highlights some recent studies that use a combination of experiments, remote sensing, fieldwork, numerical modeling and theory to understand how small-scale dynamics lead to large-scale patterns and behavior, leveraging connections between Earth and soft matter systems.Section 3.1 highlights that mechanisms of viscous and elastic deformations might differ in the temporal and spatial domains, in the specific case of Antarctic ice dynamics. Section 3.2 tests if rainfall time signals, modulated in space via groundwater flow, can be approximated by averaging over time. Such results highlight the importance of fluctuations in Earth science, which do not simply add noise but act as a fundamental feature on Earth's surface and in other nonlinear systems. Section 3.3 considers the complex fluid dynamics at the bottom of glaciers as it relates to reactive porous media flow, exploring how to reproduce the evolution of subglacial channel systems, coupling models of sediment transport and ice melting. Section 3.4 focuses on understanding how porous media convection and physicochemical mechanisms in the ground result in the striking formation of surficial salt patterns. Section 3.5 presents a scaling analysis and remote sensing measurements of Arctic soil patterns and investigates their similarity to fluid–flow instabilities. Finally, the dynamics of dunes – fragile but perpetual forms in deserts – remains challenging to predict; Section 3.6 uses laboratory-scale experiments to show how dunes persist and set a length scale in landscapes by interacting, attracting, and repelling each other.
3.1 Ice cracks in a warming climate – Y. Lai
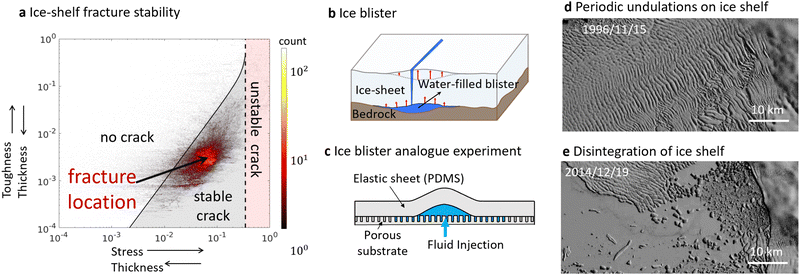 | ||
| Fig. 10 (a) Fracture stability diagram for Antarctic ice shelf fractures. Most ice shelf fractures identified by a neural network on Antarctic satellite imagery (red dots) lie in the stable-fracture regime. Adapted from Lai et al.8 (b) Formation of water-filled “blister” at the bottom of the ice sheet after a lake drains. Adapted from Lai et al.280 (c) Analogue laboratory experiment mimicking a water-filled blister beneath an ice sheet relaxing on a porous water network.281 (d) Satellite image showing undulation patterns on ice shelves due to fracture formations on the Thwaites Ice Shelf in 1996. (e) Same region as (d), in 2014 when the ice shelf was broken into icebergs ((d) and (e) are from Landsat image). | ||
Besides theory and field observations, analogue experiments can make a unique contribution to the understanding of ice sheet processes. The benefit of analogue experiments is that essential parameters can be well controlled. The findings in analogue experiments can be connected with the large-scale geophysical observations by matching the relevant nondimensional parameters. For example, laboratory analogue experiments have been developed280,281 to mimic the formation and relaxation of a water-filled “blister” (Fig. 10b) beneath an ice sheet due to the injection of meltwater.282 The analogue experiment280,281 (Fig. 10c) validated a mathematical model describing meltwater leaking from a pressurized “blister” into the surrounding water network (modeled as a porous substrate) beneath the ice sheet (modeled as an elastic sheet). The mathematical model has been used to constrain the hydrological property of the water network beneath the ice sheets, which is otherwise difficult to measure.280
3.2 Can the groundwater flow be time averaged? – O. Devauchelle
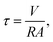 where V is the groundwater volume, A is the area of the catchment, and R is the rainfall rate287 (typically expressed in mm year−1). Residence time is thus tantamount to storage. It is also a prime control on the biological and chemical reactions that weather the porous matrix, and a good estimate of the time it takes for groundwater to recover from pollution.288,289 It is therefore crucial to the management of water resources, and to the understanding of the vadose zone and therefore of the global carbon cycle.290,291
where V is the groundwater volume, A is the area of the catchment, and R is the rainfall rate287 (typically expressed in mm year−1). Residence time is thus tantamount to storage. It is also a prime control on the biological and chemical reactions that weather the porous matrix, and a good estimate of the time it takes for groundwater to recover from pollution.288,289 It is therefore crucial to the management of water resources, and to the understanding of the vadose zone and therefore of the global carbon cycle.290,291
 | ||
| Fig. 11 Analytical solutions of flow in unconfined aquifers, of different volumes and water table heights (increasing from (a)–(c)) of hydraulic conductivity K recharged by a constant rainfall R.292 Rainwater infiltrates into the ground (blue arrows), and joins the water table (solid blue line). From there, it follows the groundwater flow lines (dashed blue lines) until it reaches the outlet (orange line), where it seeps into a river. The river flows towards the reader. The solid black lines are impervious (left: groundwater divide, right: axis of symmetry). All lengths are made dimensionless with the distance that separates the river from the divide. There remains only one dimensionless parameter in this problem: R/K. | ||
In reality, of course, precipitation is intermittent, and so is the rainfall it generates. Since the groundwater flow is non-linear, one cannot expect that a time average will gracefully propagate through the equations, as it would in a linear system.294 Therefore, there is no reason to believe that the steady flow of Fig. 11 is the average of the actual groundwater flow. To find the latter, one generally needs to solve the non-stationary problem, and average the result over time – a procedure far more costly than solving the steady-state problem. In short, finding the average groundwater flow is a difficult problem, because it is not just the solution of the average equations. There is a simple solution to this problem when the groundwater flow is very shallow: the steady-state solution gives the root mean square of the storage volume.294 This solution, unfortunately, breaks down when the groundwater flow extends deep into the ground.
3.3 Subglacial drainage as a reactive multiphase flow – I. Hewitt
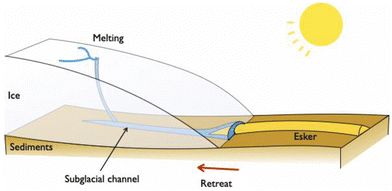
One aspect of these channels is that they are believed to be responsible for depositing eskers (Fig. 12). Eskers are long, sinuous ridges of sand and gravel, found particularly in areas of Canada and Scandinavia, which were deposited as the ice sheets retreated at the end of the last glacial period. Suggested formation mechanisms for an esker include continual deposition at the widening mouth of the channel as the ice sheet margin retreats.300 Sediments are deposited as the flow velocity in a water-filled subglacial channel decreases near the retreating ice margin. The spatial distribution of the sediment size dependence on the flow velocity might be used to test this hypothesis. A better understanding of the formation mechanism of eskers can inform more about the plumbing system under present-day ice sheets.
3.4 Patterns in dry salt lakes – L. Goehring
Briefly, the resulting model considers the Darcy flow of water in the porous sand or sediment of a dry lake, where the water table remains close to the surface of the ground.308,309 The water contains salt, which accumulates at the evaporating surface. The salt moves advectively with the water, and diffusively along any concentration gradients. It adds to the density of the water, providing buoyancy forces that can drive additional flows. As boundary conditions, there is a continuous loss of water at the surface, caused by evaporation, and the groundwater is recharged from below by some distant reservoir. This leads to the accumulation of salt-rich, denser water near the surface, which can be unstable to convection. The convective dynamics are captured by a single dimensionless group, the Rayleigh number, which describes the ratio of convective to diffusive effects. Essentially, this group describes the vigor of any convection,308 as it also characterizes the speed of the convective flows, relative to the background flows caused by the surface evaporation.
Building on a body of recent field observations,305,306,309 this model of a salt playa allows for the dynamic evolution of convection cells, which then modulate the salt flux into the surface crust.309 As confirmed by direct field data of crust growth rates305 and subsurface flow patterns,309 it predicts that surface salts will accumulate fastest above down-welling flows that spontaneously arrange into a polygonal network (Fig. 13b and c) when simulated in large, three-dimensional domains.309 When the model parameters are constrained by relevant field data, it also accurately accounts for the observed growth rates of the polygons, and their remarkably consistent size, which arises naturally from a balance between evaporation rates and salt diffusivity.
3.5 Fluid-like patterns in slow-moving soils – R. Glade
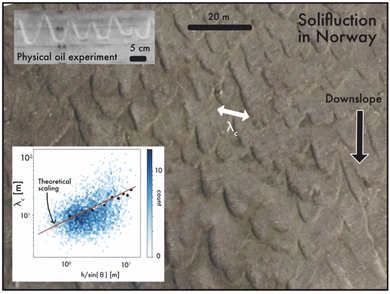 | ||
Fig. 14 Background: Aerial image of solifluction lobes with wavelength λc of tens of meters in Norway (image credit: The Norwegian Mapping Authority). Top left inset: Fluid contact line instability in a laboratory experiment with wavelength of centimeters.318 Bottom left inset: λc plotted against lobe thickness divided by topographic slope, h/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, measured from a remote-sensing derived digital elevation model. Blue color indicates the number of data points in each hexagonal bin. Black dots represent average wavelengths binned by h θ, measured from a remote-sensing derived digital elevation model. Blue color indicates the number of data points in each hexagonal bin. Black dots represent average wavelengths binned by h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Red line is theoretical prediction from fluid-inspired scaling analysis, θ. Red line is theoretical prediction from fluid-inspired scaling analysis, 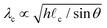 . Because there are no constraints on the cohesive length scale, . Because there are no constraints on the cohesive length scale, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c, here it is assumed to be constant. Figure modified from Glade et al.319 c, here it is assumed to be constant. Figure modified from Glade et al.319 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), and a length scale characterizing spatial variations in cohesion (
θ), and a length scale characterizing spatial variations in cohesion (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c):
c): 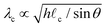 .
.
Applied to remote sensing data of thousands of solifluction lobes across Norway, the theoretical scaling relation is able to predict average wavelengths.319 Typical of field data, the solifluction wavelengths contain a large amount of scatter. Data show that average lobe heights and wavelengths also increase with elevation and decrease with mean annual temperature, pointing toward a broad climate control on solifluction patterns and illustrating the possible importance of external driving factors in addition to smaller-scale soil dynamics. This work demonstrates that even granular material in the non-inertial regime can exhibit instabilities fundamentally similar to those found in small scale systems, at time and length scales orders of magnitude larger than previously observed. The presence of these patterns only in cold landscapes suggests that the exceptionally large amount of heterogeneity found in icy landscapes may allow for the development of sub-critical instabilities in non-inertial flows.
3.6 Bedform dynamics: interaction, attraction and repulsion of dunes – N. M. Vriend and K. A. Bacik
 | ||
| Fig. 15 Two equal-size miniature dunes are initially placed 45° apart in a periodic annular channel. Due to drag imposed by the water current, they start migrating and drift apart, and converge over long times to a symmetric antipodal configuration 180° apart.333 | ||
First, pairwise interaction between two dunes is explored, leading to either coalescence (merging), ejection (sediment exchange),334 or wake-induced repulsion of bedforms333 which can be categorized in a phase-space diagram outlining the possible interaction outcomes derived from experiments and cellular automaton simulations.335 Second, as a first step towards understanding the system-level dynamics of a dune field, the long-term behavior of a periodic two-dune system336 is investigated: is this system always attracted to a symmetric state with two identical equi-spaced dunes, or are there conditions where the symmetry is spontaneously broken? The key to understanding the dynamics is turbulence: for flows with a relatively low turbulence intensity, the dunes will display fast-slow dynamics before settling at a stable equilibrium, but for high levels of turbulence an asymmetric attractor appears. This indicates that, at least in theory, the hydrodynamic coupling between neighboring dunes can either promote or inhibit regular organization of a dune field. Third, by placing idealized objects in the path of the model dunes, the engineering challenge of dune-obstacle interaction are addressed. Interestingly, both object size and shape of the obstacle determine whether the dune is blocked or able to overcome an obstacle and reform on the other side,337 and once again, the importance of turbulent flow structures is established. Indeed, the outcome of the dune-obstacle interaction can be predicted with a simple data-driven tool based on the modal decomposition of the flow field around the obstacle (without sediment or dunes present).
4 The challenge(s) of life
Life has an impact on the dynamics and is impacted by the physicochemical evolution of the ground. Over time, plants, fungi, and burrowing animals alter the ground composition, constitutive structure, and consequently, its mechanical properties (e.g., Fig. 1e). Sometimes the presence of life makes the ground more cohesive and enhances its resistance to erosion, sometimes its own dynamics pull apart or alter the ground such that it is destabilized. Such puzzling observations illustrate why it is crucial to isolate and study the biophysical processes happening in the ground. We present here two examples of such studies: in Section 4.1, recent results and outlooks on the dynamics and impact of invertebrates (such as worms) in the ground are presented, while Section 4.2 highlights a newly recognized effect bacteria can have on fluid dynamics in porous media. Finally, Section 4.3 presents recent results to support a fundamentally different usage of the ground as a resource; it reminds us that human beings, via the building of our infrastructure, are also a major part of the life disturbance of the Earth's ground and atmosphere.4.1 Intruder dynamics in granular sediments – A. Kudrolli
Context. The ground is constantly shaped by animal and human activities that can further impact the movement of fluids and erosion.338 Exopedonic and endopedonic activities leading to creation of mounds, voids, and burrows in loose sediments, besides anthropogenic activities leading to desertification, and trawling for resources on the ocean floor are problems of great importance in ecosystem management. To overcome the opacity of granular matter, where much of these activities occur, X-ray imaging and index-matching techniques have been employed to understand locomotion strategies from undulatory to peristaltic motions in situ.339,340 Besides water jets and fluidization, various strategies have been discovered for movements in subsurface materials, from plastic grain rearrangements to sand fluidization and burrow extension by fracture, which vary depending on depth, compaction, and grain size.341 Considerable work is underway to understand the observed locomotion speeds, and the link to the observed gaits employed, based on the rheology of the medium, as well as in developing models starting from resistive force theory and slender-body theory, which are known in the context of viscously dominated fluid dynamics.342,343 To understand intruded dynamics in granular media representative of the ground beneath our feet, further work is required to extend rheological models developed under uniform flow and shear conditions to time-dependent and unsteady flows encountered in such dynamics.While the above has focused on the limit where the intruder is strong enough to move the material, a complementary limit is where the intruder cannot move the material, but is restricted to moving within the pore spaces. Thigmotactic behavior, as in motion along the edges of surfaces due to sensory feedback and environmental cues, can play an important role in determining transport.350 One example is the dynamics of centimeter-scale oligochaeta Lumbriculus variegatus in model porous media, where its natural strokes are hindered by the tight passages between idealized grains. A persistent random walk model along boundaries was found to capture the observed time-distributions to escape the dynamical traps posed by the pore-throats.351 Active polymer models where simple steric interactions are emphasized have a significant role to play in determining general principles of transport in this limit.352–354 The importance of body shape, stroke, and topology is receiving attention in determining the dynamics of bacteria as also discussed in the following Section 4.2.
4.2 Bacteria-mediated processes in porous media – H. A. Stone and J. Q. Yang
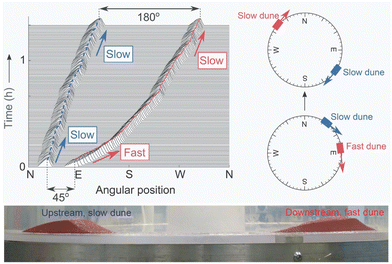
The first study revealed the protection of carbon by clay through microfluidic experiments, which incorporated important elements of the soil carbon problem, including clay aggregates, different molecular weight carbon molecules, bacteria, and enzymes embedded in flows of water.357 Confocal microscopy was used to document the space and time dependence of how molecules adsorb onto and diffuse into and out of transparent clay aggregates (Fig. 16a). Smaller molecular weight molecules displayed reversible transport while the larger molecular weight molecules were quasi-irreversibly adsorbed, i.e., diffusion into the aggregates occurred rapidly (within minutes), but most molecules remained adsorbed even after flushing for tens of hours with water (Fig. 16b). Bacteria were too large to fit into the nano-size pore space of the aggregates, so accumulated on the outside of clay aggregates, whereas enzymes were shown to effectively penetrate the small pores where they broke down and released the trapped large-molecular-weight sugars. The experimental results were used to suggest improvements to models of soil carbon storage.
 | ||
| Fig. 16 (a) Microfluidic experiments showing the sorption and desorption of a fluorescently-labeled organic matter in clay. The propagation of the green fluorescent dextran (sugar) into the clay (gray color) was visualized in 3-dimensional space over time.357 (b) The quasi-irreversible sorption of a large molecular weight (>3 kDa) dextran with a clay aggregate.357 (c) A surfactant-producing bacterium, Pseudomonas aeruginosa (labeled with green fluorescence), spreads into a synthetic soil placed on top of the bacterial solution, while a surfactant-deficient mutant does not.358 The scale bars in (a) and (c) are 100 μm and 2 mm, respectively. | ||
The second study documented a previously unreported mechanism of transport of bacterial cells in unsaturated porous media. In particular, experiments showed that surfactant-producing bacteria cause changes in the wettability (to a hydrophilic state) of an initial hydrophobic substrate, which, through a capillary pressure change, causes millimeter-per-hour fluid flow, comparable to other rapid bacterial swimming speeds, along corners of a model chamber.358 Similar experimental observations of bacterial transport were also demonstrated in a porous medium of packed angular grains (Fig. 16c), which served as a model soil. The dynamics were controlled by quorum sensing, which regulates biosurfactant production. This transport process can also lead to movement of non-motile bacteria in the solution. The results suggest that this kind of surfactant-driven transport through changes in wettability, instead of the better-known Marangoni motion, may be relevant to natural porous environments.
4.3 Nanoscale forces in hydrated clays and the physics of sustainable construction materials – E. Del Gado
 | ||
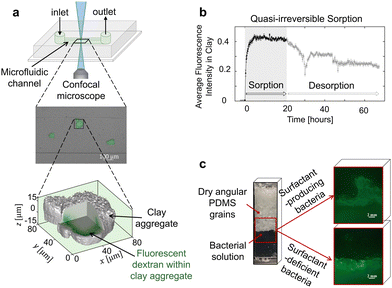
| Fig. 17 Earth construction materials, examples, and scientific questions: (a) rammed earth constructions, (b) rural brick kiln, (c) water-ion structures from semiatomistic simulations of Ca ions solutions confined between charged surfaces,364 and (d) mesoscale porous structures of cement hydrate gels from coarse-grained simulations, where particle sizes are on the order of 10–50 nm.365 | ||
Molecular simulations effectively fill the gap with the experimental characterization of cohesive forces in hydrated clays and cement, providing novel insight into the strong ionic correlations that govern them, to be used in continuum theories and larger scale studies.364,370,371 The nanoscale forces, in fact, together with the non-equilibrium environmental conditions, eventually determine the growth of microscale grain assemblies, layered meso-phases, and porous structures that can be obtained via coarse-grained simulations (Fig. 17d). These forces then also govern the rheology and mechanics of clay-based soil and construction materials, providing the missing link from the nanoscale physical chemistry to the meso-scale aggregation kinetics and morphological variability of soil and clay-based binders.365,372,373
Discussion
In each contribution associated with one of the four challenges identified in the introduction, a unique research topic, combining soft matter and geosciences, was addressed. The outstanding open questions raised by each author show commonalities that relate to the multi-dimensional, multi-scale, multi-phase, and multi-process character of the ground beneath our feet. Some of the most crucial shared questions are briefly summarized and discussed here.The opaque and time-dependent nature of the ground profoundly hinders our capacity to observe and understand it. In the laboratory, advancements in microscopic visualization and experimental techniques are, on the one hand, key to remediating this difficulty (see Sections 1.3 and 4.2); yet illuminating all spatial dimensions, while allowing temporal dependencies, is a technical frontier. On the other hand, at the cost of simplifications, properties, stresses, and flow fields in 2D–3D granular porous media can be visualized and quantified (see Sections 1.1, 1.2 and 2.1). In the field, the time-dependent and temporally variable nature of surface and subsurface processes requires additional efforts for monitoring (see Sections 2.4, 3.3 and 3.5). Extension and advancements in the use of geophysical techniques, such as seismology, hold promise in enabling tracking of the temporal evolution of e.g., transport processes.224,374 Simultaneously, temporally resolved remote sensing techniques are making details of large-scale phenomena, like ice shelf dynamics, observable (see Sections 2.3 and 3.1).
Though the ground is becoming more observable, seemingly basic questions of when grains start moving, where particles jam, or where and when landslides rupture, are still wide open. Especially in natural systems, identifying the essential conditions (see Sections 1.4 and 1.5), material properties (see Sections 2.1, 2.5 and 4.3), and processes (see Sections 1.1, 2.3 and 2.4) to understand and model the bulk dynamics remains a research frontier. Beyond the relevant components, modeling approaches still struggle to represent key relations (e.g., how microscale processes change the bulk observations, or how to integrate over local conditions or time to obtain bulk mechanical behavior), feedbacks (e.g., how macrostructures affect the microscale conditions, or co-dependent processes and scales321), and temporal evolution. While computational advancements enable the modeling of complex systems, coupled dynamics require further efforts in developing the proper way to implement relationships governing elementary phenomena (see Sections 1.5, 3.2, 3.4 and 4.3), including life-related ones (see Sections 1.3, 4.1 and 4.2).
Fundamental open questions, for many of the topics addressed here, emerge from the complex interplay of several phases. The dynamics of, for example, three-phase systems where interfaces of liquid-air-grains evolve over time, are key to a better understanding how natural rafts, such as ice mélanges, behave (see Section 2.3), how debris flows start and stop (see Section 2.2), and how groundwater evaporates into salt crusts (see Section 3.4). Conceptually taming the interactions and feedbacks to understand more than two-phase systems challenges concepts, experiments, and observation throughout the Earth sciences (e.g., ref. 321 and 375–378).
Understanding and modeling contact lines, capillary stresses, and resulting cohesion in particulate materials is a vast and ongoing effort for the case of a single-phase liquid in contact with another fluid and solid particles.126,379 While, more often than not, flows in the ground are themselves suspensions of minerals (see Sections 1.3 and 1.4), or biological (active) particles (see Sections 4.2 and 4.1), the solid part of the ground itself can be composed of vastly different materials in terms of wettability properties (see Sections 1.4 and 4.2), density (see Sections 1.5 and 2.5), and rigidity (see Section 2.1). Especially where life is involved and shapes its surroundings (see Sections 1.3, 4.1 and 4.2), or where landforms and patterns of different scales interact (see Sections 2.5, 3.4, 3.5 and 3.6), modeling the ground accurately requires solving among the most difficult questions of multi-phases systems.
Another recurrent question for many of the addressed topics is how to model transience in materials state and behavior. The ground is heterogeneous in composition and properties, therefore it presents diverse physicochemical behaviors and properties, such as rigidity (see Section 2.1), plasticity (see Section 1.4), or viscosity (see Section 2.5). As the ground evolves over time under external physicochemical forcings, it also undergoes change in the material bulk dynamics. Such transients may result in instability growth and produce characteristic patterns. In the field these transience dynamics are most often observed indirectly, deduced from the resulting expressions of these dynamics hidden in the ground, like ordered patterns in salt lakes (see Section 3.4), arctic soils (see Section 3.5), ice shelves (see Sections 3.1 and 2.3), or glacial deposits (see Section 3.3). Linking these dynamics to climatic changes, geology, as well as anthropogenic and biogenic activities, poses further outstanding open questions, including topics related to subsurface storage and transport of gases and fluids (see Sections 3.2 and 2.5), or the anticipation of ruptures that can turn into devastating natural hazards (see Sections 1.1 and 2.2).
Conclusion
Most Earth surface materials can be categorized as soft materials. Studying their dynamics necessitates a diversity of approaches, thus understanding the ground is intrinsically a highly interdisciplinary field (Fig. 1). We presented here a soft matter perspective of the “physics of the ground beneath our feet”, though diverse, the field contains many commonalities.As the field is still evolving, it is inhomogeneous and still lacks some common vocabulary; the variations across our sub-sections reflect that reality. While this perspective brought together many disciplines, we are aware of the inherent limited scope covered, and necessary further linkages to, e.g., the biosphere, atmospheric processes, or transitions from continuum and solid to soft matter. Especially in times of climate changes and resource limitations, gains of fundamental knowledge of the soft matter of the ground will be valuable in our understanding of anthropogenic, climatic, and geophysical hazards.
We are confident that the seeds of ideas presented here will mature as researchers engage with the subject, nucleate new investigations, and help building a percolating framework that supports the field as it grows. We hope for this collective effort to provide a new broad perspective on the field and invite more soft matter scientists to study the fascinating ground on which we live and build our future.
Author contributions
AV and MH contributed equally to this work in leading the manuscript development and writing of the general introduction and discussion sections, in particular. All following authors drafted their sub-section and contributed to the whole manuscript writing, in alphabetical order. Six of the authors contributed equally to this work, in writing their sub-section, and also in overviewing the homogeneity over one entire section; specifically, ICB overviewed Section 1, JCB and KED overviewed Section 2, RG overviewed Section 3, EDG and HAS overviewed Section 4. All authors were involved in the conceptualization and reviewing the entire article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AV and MH are indebted to Abhinindra Singh, for fruitful discussions on the early design of the manuscript. SSD, ICB, C-Y Lai, and HAS thank the Princeton Center for Theoretical Science at Princeton University for their support of the 2022 workshop that stimulated the writing of this paper. In particular, we are grateful for the help provided by Charlene Borsack, both leading up to and during the workshop. HAS and JQY thank the High Meadows Environmental Institute (Princeton University) and the NSF (grant MCB-1853602). These projects were led by Judy Yang (first a postdoc at Princeton and now a Professor at the University of Minnesota) and the wonderful collaborations included Niki Abbasi, Bonnie Bassler, Ian Bourg, Zemer Gitai, Joe Sanfilippo, and Xinning Zhang. SSD acknowledges funding from the High Meadows Environmental Institute and Andlinger Center for Energy and Environment (Princeton University), NSF Grant CBET-1941716, a Camille Dreyfus Teacher-Scholar Award of the Camille and Henry Dreyfus Foundation, and the Princeton Center for Complex Materials, a Materials Research Science and Engineering Center supported by NSF grants DMR-1420541 and DMR-2011750. OD is indebted to E. Lajeunesse, V. Jules, A. Guérin and F. Métivier for sustained and enjoyable collaboration on groundwater flows. ICB thanks NSF Grant EAR-2150797 for financial support. JCB thanks NSF Grant OPP-2025795 for financial support. Emanuela del Gado was funded by: grant DMREF CBET-2118962.Notes and references
- T. Dauxois, T. Peacock, P. Bauer, C. P. Caulfield, C. Cenedese, C. Gorlé, G. Haller, G. N. Ivey, P. F. Linden, E. Meiburg, N. Pinardi, N. M. Vriend and A. W. Woods, Phys. Rev. Fluids, 2021, 6, 020501 CrossRef.
- R. P. Sharp, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 4477–4486 CrossRef.
- W. E. Dietrich, D. G. Bellugi, L. S. Sklar, J. D. Stock, A. M. Heimsath and J. J. Roering, Prediction Geomorphology, 2003, 103–132 Search PubMed.
- M. Houssais and D. J. Jerolmack, Geomorphology, 2017, 277, 251–264 CrossRef.
- D. J. Jerolmack and K. E. Daniels, Nat. Rev. Phys., 2019, 1, 716–730 CrossRef.
- J. K. Jansson and K. S. Hofmockel, Nat. Rev. Microbiol., 2020, 18, 35–46 CrossRef CAS PubMed.
- S. Doetterl, A. A. Berhe, E. Nadeu, Z. Wang, M. Sommer and P. Fiener, Earth-Sci. Rev., 2016, 154, 102–122 CrossRef CAS.
- C.-Y. Lai, J. Kingslake, M. G. Wearing, P.-H. C. Chen, P. Gentine, H. Li, J. J. Spergel and J. M. van Wessem, Nature, 2020, 584, 574–578 CrossRef CAS PubMed.
- A. Singh, G. L. Jackson, M. van der Naald, J. J. de Pablo and H. M. Jaeger, Phys. Rev. Fluids, 2022, 7, 054302 CrossRef.
- C. G. Sammis and R. L. Biegel, Pure Appl. Geophys., 1989, 131, 255–271 CrossRef.
- C. Marone, Annu. Rev. Earth Planet. Sci., 1998, 26, 643–696 CrossRef CAS.
- J. R. Rice, J. Geophys. Res.: Solid Earth, 2006, 111, B05311 Search PubMed.
- A. W. Rempel, Earthquakes: Radiated Energy and the Physics of Faulting, American Geophysical Union, 2006, pp. 263–270 Search PubMed.
- A. Ruina, J. Geophys. Res.: Solid Earth, 1983, 88, 10359–10370 CrossRef.
- T. Baumberger and C. Caroli, Adv. Phys., 2006, 55, 279–348 CrossRef.
- Q. Li, T. E. Tullis, D. Goldsby and R. W. Carpick, Nature, 2011, 480, 233–236 CrossRef CAS.
- P. Bhattacharya, A. M. Rubin, E. Bayart, H. M. Savage and C. Marone, J. Geophys. Res.: Solid Earth, 2015, 120, 6365–6385 CrossRef.
- J.-P. Ampuero and A. M. Rubin, J. Geophys. Res.: Solid Earth, 2008, 113, B01302 Search PubMed.
- B. Ferdowsi and A. M. Rubin, J. Geophys. Res.: Solid Earth, 2020, 125, e2019JB019016 CrossRef.
- J. R. Rice, N. Lapusta and K. Ranjith, J. Mech. Phys. Solids, 2001, 49, 1865–1898 CrossRef.
- S. Kim and K. Kamrin, Phys. Rev. Lett., 2020, 125, 088002 CrossRef CAS.
- P. Jop, C. R. Phys., 2015, 16, 62–72 CrossRef CAS.
- D. L. Henann and K. Kamrin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6730–6735 CrossRef CAS.
- Y. Forterre and O. Pouliquen, Annu. Rev. Fluid Mech., 2008, 40, 1–24 CrossRef.
- G. Lois, A. Lematre and J. M. Carlson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051303 CrossRef PubMed.
- L. E. Silbert, D. Ertas, G. S. Grest, T. C. Halsey, D. Levine and S. J. Plimpton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051302 CrossRef CAS PubMed.
- P. A. Thompson and G. S. Grest, Phys. Rev. Lett., 1991, 67, 1751 CrossRef PubMed.
- W. Li, Y. Meng, B. K. Primkulov and R. Juanes, Phys. Rev. Appl., 2021, 16, 024043 CrossRef CAS.
- A. Abed Zadeh, J. Barés, T. A. Brzinski, K. E. Daniels, J. Dijksman, N. Docquier, H. O. Everitt, J. E. Kollmer, O. Lantsoght, D. Wang, M. Workamp, Y. Zhao and H. Zheng, Granular Matter, 2019, 21, 83 CrossRef.
- K. E. Daniels, J. E. Kollmer and J. G. Puckett, Rev. Sci. Instrum., 2017, 88, 051808 CrossRef PubMed.
- T. S. Majmudar and R. P. Behringer, Nature, 2005, 435, 1079–1082 CrossRef CAS PubMed.
- M. A. Biot, J. Appl. Phys., 1941, 12, 155–164 CrossRef.
- R. Juanes, Y. Meng and B. K. Primkulov, Phys. Rev. Fluids, 2020, 5, 110516 CrossRef.
- K. Terzaghi, Erdbaumechanik auf Bodenphysikalischer Grundlage, F. Deuticke, 1925 Search PubMed.
- K. Terzaghi, Theoretical Soil Mechanics, John Wiley & Sons, Ltd, 1943, pp. 265–296 Search PubMed.
- M. M. Frocht, Photoelasticity, John Wiley & Sons, 1941 Search PubMed.
- J. Palmer, Nature, 2017, 548, 384–386 CrossRef CAS.
- A. Skarke, C. Ruppel, M. Kodis, D. Brothers and E. Lobecker, Nat. Geosci., 2014, 7, 657 CrossRef CAS.
- Y. Guglielmi, F. Cappa, J.-P. Avouac, P. Henry and D. Elsworth, Science, 2015, 348, 1224–1226 CrossRef CAS PubMed.
- M. M. Frocht and R. Guernsey, A special investigation to develop a general method for three-dimensional photoelastic stress analysis, National Advisory Committee for Aeronautics technical report, 1952 Search PubMed.
- W. Li and R. Juanes, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2319160121 CrossRef CAS.
- N. R. Morrow and G. Mason, Curr. Opin. Colloid Interface Sci., 2001, 6, 321–337 CrossRef CAS.
- C. C. Mattax and J. Kyte, Soc. Pet. Eng. J., 1962, 2, 177–184 CrossRef.
- K. Li and R. N. Horne, SPE Journal, 2001, 6, 375–384 CrossRef.
- C. Nicolaides, B. Jha, L. Cueto-Felgueroso and R. Juanes, Water Resour. Res., 2015, 51, 2634–2647 CrossRef.
- D. B. Bennion and S. Bachu, SPE Reservoir Eval. Eng., 2008, 11, 487–496 CrossRef CAS.
- D. B. Bennion and S. Bachu, SPE Annual Technical Conference and Exhibition, 2010.
- C. U. Hatiboglu and T. Babadagli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 066311 CrossRef PubMed.
- M. A. Celia, S. Bachu, J. Nordbotten and K. Bandilla, Water Resour. Res., 2015, 51, 6846–6892 CrossRef CAS.
- C. Schaefer, D. DiCarlo and M. Blunt, Water Resour. Res., 2000, 36, 885–890 CrossRef.
- A. Esposito and S. M. Benson, Energy Procedia, 2011, 4, 3216–3223 CrossRef CAS.
- H. Penvern, M. Zhou, B. Maillet, D. Courtier-Murias, M. Scheel, J. Perrin, T. Weitkamp, S. Bardet, S. Caré and P. Coussot, Phys. Rev. Appl., 2020, 14, 054051 CrossRef CAS.
- M. Zhou, S. Caré, A. King, D. Courtier-Murias, S. Rodts, G. Gerber, P. Aimedieu, M. Bonnet, M. Bornert and P. Coussot, Phys. Rev. Res., 2019, 1, 033190 CrossRef CAS.
- N. Weisbrod, M. R. Niemet and J. S. Selker, Adv. Water Resour., 2002, 25, 841–855 CrossRef CAS.
- F. Tesoro, E. Choong and O. Kimbler, Wood Fiber Sci., 2007, 6, 226–236 Search PubMed.
- R. Hassanein, H. Meyer, A. Carminati, M. Estermann, E. Lehmann and P. Vontobel, J. Phys. D: Appl. Phys., 2006, 39, 4284 CrossRef CAS.
- T. Phenrat, H.-J. Kim, F. Fagerlund, T. Illangasekare, R. D. Tilton and G. V. Lowry, Environ. Sci. Technol., 2009, 43, 5079–5085 CrossRef CAS.
- X. Zhao, W. Liu, Z. Cai, B. Han, T. Qian and D. Zhao, Water Res., 2016, 100, 245–266 CrossRef CAS.
- S. R. Kanel, J.-M. Greneche and H. Choi, Environ. Sci. Technol., 2006, 40, 2045–2050 CrossRef CAS.
- J. Schijven, H. De Bruin, S. Hassanizadeh and A. de Roda Husman, Water Res., 2003, 37, 2186–2194 CrossRef CAS.
- H. Zhong, G. Liu, Y. Jiang, J. Yang, Y. Liu, X. Yang, Z. Liu and G. Zeng, Biotechnol. Adv., 2017, 35, 490–504 CrossRef CAS.
- R. W. Harvey and S. P. Garabedian, Environ. Sci. Technol., 1991, 25, 178–185 CrossRef CAS.
- O. Braun, C. Coquery, J. Kieffer, F. Blondel, C. Favero, C. Besset, J. Mesnager, F. Voelker, C. Delorme and D. Matioszek, Molecules, 2021, 27, 42 CrossRef PubMed.
- C. D. V. Nascimento, J. C. A. Mota, Í. V. Nascimento, G. H. da Silva Albuquerque, R. W. Simmons, C. T. dos Santos Dias and M. C. G. Costa, Geoderma Regional, 2021, 26, e00407 CrossRef.
- S. Bandak, S. A. R. M. Naeini, E. Zeinali and I. Bandak, Arab. J. Geosci., 2021, 14, 1–10 CrossRef.
- M. Garbowski, C. S. Brown and D. B. Johnston, Restor. Ecol., 2020, 28, A13–A23 Search PubMed.
- J. Misiewicz, S. S. Datta, K. Lejcus and D. Marczak, Materials, 2022, 15, 4465 CrossRef CAS.
- A. Dechesne, G. Wang, G. Gaolez, D. Or and B. F. Smets, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14369–14372 CrossRef CAS PubMed.
- R. D. Souza, A. Ambrosini and L. M. Passaglia, Genet. Mol. Biol., 2015, 38, 401–419 CrossRef.
- G. A. Turnbull, J. A. W. Morgan, J. M. Whipps and J. R. Saunders, FEMS Microbiol. Ecol., 2001, 36, 21–31 CrossRef CAS PubMed.
- M. Watt, J. Kirkegaard and J. Passioura, Soil Res., 2006, 44, 299–317 CrossRef.
- O. O. Babalola, Biotechnol. Lett., 2010, 32, 1559–1570 CrossRef CAS.
- J. S. Adadevoh, C. A. Ramsburg and R. M. Ford, Environ. Sci. Technol., 2018, 52, 7289–7295 CrossRef CAS PubMed.
- J. S. T. Adadevoh, S. Triolo, C. A. Ramsburg and R. M. Ford, Environ. Sci. Technol., 2016, 50, 181–187 CrossRef CAS.
- R. M. Ford and R. W. Harvey, Adv. Water Resour., 2007, 30, 1608–1617 CrossRef.
- M. Wang, R. M. Ford and R. W. Harvey, Environ. Sci. Technol., 2008, 42, 3556–3562 CrossRef CAS.
- J.-B. Raina, V. Fernandez, B. Lambert, R. Stocker and J. R. Seymour, Nat. Rev. Microbiol., 2019, 17, 284–294 CrossRef CAS PubMed.
- A. Anbari, H.-T. Chien, S. S. Datta, W. Deng, D. A. Weitz and J. Fan, Small, 2018, 14, 1703575 CrossRef.
- J. Bear, Dynamics of Fluids in Porous Media, Courier Corporation, 2013 Search PubMed.
- W. E. Galloway and D. K. Hobday, Terrigenous Clastic Depositional Systems: Applications to Fossil Fuel and Groundwater Resources, Springer Science & Business Media, 2012 Search PubMed.
- S. Gasda and M. A. Celia, Adv. Water Resour., 2005, 28, 493–506 CrossRef CAS.
- H. King, M. Sansone, P. Kortunov, Y. Xu, N. Callen, S. Chhatre, H. Sahoo and A. Buono, Petrophysics, 2018, 59, 35–43 Search PubMed.
- N. B. Lu, C. A. Browne, D. B. Amchin, J. K. Nunes and S. S. Datta, Phys. Rev. Fluids, 2019, 4, 084303 CrossRef.
- H. S. Rabbani, D. Or, Y. Liu, C.-Y. Lai, N. B. Lu, S. S. Datta, H. A. Stone and N. Shokri, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4833–4838 CrossRef CAS.
- N. B. Lu, A. A. Pahlavan, C. A. Browne, D. B. Amchin, H. A. Stone and S. S. Datta, Phys. Rev. Appl., 2020, 14, 054009 CrossRef CAS.
- N. B. Lu, D. B. Amchin and S. S. Datta, Phys. Rev. Fluids, 2021, 6, 114007 CrossRef.
- N. Bizmark, J. Schneider, E. de Jong and S. S. Datta, Polymer Colloids: Formation, Characterization and Applications, The Royal Society of Chemistry, 2019, pp. 289–321 Search PubMed.
- E. Dressaire and A. Sauret, Soft Matter, 2016, 13, 37–48 RSC.
- M. Sahimi and A. Imdakm, Phys. Rev. Lett., 1991, 66, 1169 CrossRef PubMed.
- L. J. Zeman and A. L. Zydney, Microfiltration and ultrafiltration: principles and applications, Routledge, 2017 Search PubMed.
- J. Linkhorst, T. Beckmann, D. Go, A. J. Kuehne and M. Wessling, Sci. Rep., 2016, 6, 22376 CrossRef CAS PubMed.
- I. L. Molnar, W. P. Johnson, J. I. Gerhard, C. S. Willson and D. M. O'Carroll, Water Resour. Res., 2015, 51, 6804–6845 CrossRef.
- G. Gerber, M. Bensouda, D. A. Weitz and P. Coussot, Phys. Rev. Lett., 2019, 123, 158005 CrossRef CAS PubMed.
- Y. Kusaka, J. F. Duval and Y. Adachi, Environ. Sci. Technol., 2010, 44, 9413–9418 CrossRef CAS.
- Y.-J. Lin, P. He, M. Tavakkoli, N. T. Mathew, Y. Y. Fatt, J. C. Chai, A. Goharzadeh, F. M. Vargas and S. L. Biswal, Langmuir, 2016, 32, 8729–8734 CrossRef CAS PubMed.
- M. Auset and A. A. Keller, Water Res. Res., 2006, 42, W12S02 CrossRef.
- H. M. Wyss, D. L. Blair, J. F. Morris, H. A. Stone and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061402 CrossRef.
- M. R. de Saint Vincent, M. Abkarian and H. Tabuteau, Soft Matter, 2016, 12, 1041–1050 RSC.
- Y.-J. Lin, P. He, M. Tavakkoli, N. T. Mathew, Y. Y. Fatt, J. C. Chai, A. Goharzadeh, F. M. Vargas and S. L. Biswal, Energy Fuels, 2017, 31, 11660–11668 CrossRef CAS.
- D. C. Mays, O. T. Cannon, A. W. Kanold, K. J. Harris, T. C. Lei and B. Gilbert, J. Colloid Interface Sci., 2011, 363, 418–424 CrossRef CAS PubMed.
- E. J. Roth, B. Gilbert and D. C. Mays, Environ. Sci. Technol., 2015, 49, 12263–12270 CrossRef CAS.
- X. Li, C.-L. Lin, J. D. Miller and W. P. Johnson, Environ. Sci. Technol., 2006, 40, 3769–3774 CrossRef CAS.
- G. Gerber, S. Rodts, P. Aimedieu, P. Faure and P. Coussot, Phys. Rev. Lett., 2018, 120, 148001 CrossRef CAS.
- N. Bizmark, J. Schneider, R. D. Priestley and S. S. Datta, Sci. Adv., 2020, 6, eabc2530 CrossRef CAS PubMed.
- J. Schneider, R. D. Priestley and S. S. Datta, Phys. Rev. Fluids, 2021, 6, 014001 CrossRef.
- C. A. Browne, A. Shih and S. S. Datta, Small, 2020, 16, 1903944 CrossRef CAS PubMed.
- C. A. Browne, A. Shih and S. S. Datta, J. Fluid Mech., 2020, 890, A2 CrossRef CAS.
- C. A. Browne and S. S. Datta, Sci. Adv., 2021, 7, eabj2619 CrossRef CAS PubMed.
- C. A. Browne, R. B. Huang, C. W. Zheng and S. S. Datta, J. Fluid Mech., 2023, 963, A30 CrossRef CAS.
- V. C. Ibezim, R. J. Poole and D. J. Dennis, J. Non-Newtonian Fluid Mech., 2021, 296, 104638 CrossRef CAS.
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding, A. Frishman, M. D. Graham, J. S. Guasto, S. J. Haward, A. Q. Shen, S. Hormozi, A. Morozov, R. J. Poole, V. Shankar, E. S. G. Shaqfeh, H. Stark, V. Steinberg, G. Subramanian and H. A. Stone, Phys. Rev. Fluids, 2022, 7, 080701 CrossRef.
- H. J. Cho, N. B. Lu, M. P. Howard, R. A. Adams and S. S. Datta, Soft Matter, 2019, 15, 4689–4702 RSC.
- T. Bhattacharjee, D. B. Amchin, R. Alert, J. A. Ott and S. S. Datta, eLife, 2022, 11, e71226 CrossRef CAS PubMed.
- T. Bhattacharjee, D. B. Amchin, J. A. Ott, F. Kratz and S. S. Datta, Biophys. J., 2021, 120, 3483–3497 CrossRef CAS PubMed.
- L. Goehring, A. Nakahara, T. Dutta, S. Kitsunezaki and S. Tarafdar, Desiccation cracks and their patterns: formation and modeling in science and nature, John Wiley and Sons, Inc, 2015 Search PubMed.
- W. P. Gates, A. Bouazza and G. J. Churchman, Elements, 2009, 5, 105 CrossRef CAS.
- D. N. Espinoza and J. C. Santamarina, Int. J. Greenhouse Gas Control, 2012, 10, 351–362 CrossRef CAS.
- H. J. Cho and S. S. Datta, Phys. Rev. Lett., 2019, 123, 158004 CrossRef CAS.
- T. Bhattacharjee and S. S. Datta, Soft Matter, 2019, 15, 9920–9930 RSC.
- T. Bhattacharjee and S. S. Datta, Nat. Commun., 2019, 10, 2075 CrossRef.
- D. B. Amchin, J. A. Ott, T. Bhattacharjee and S. S. Datta, PLoS Comput. Biol., 2022, 18, e1010063 CrossRef CAS.
- R. C. Grabowski, I. G. Droppo and G. Wharton, Earth-Sci. Rev., 2011, 105, 101–120 CrossRef.
- M. Kleber, I. C. Bourg, E. K. Coward, C. M. Hansel, S. C. B. Myneni and N. Nunan, Nat. Rev. Earth Environ., 2021, 2, 402–421 CrossRef.
- F. J. Carrillo and I. C. Bourg, Water Resour. Res., 2019, 55, 8096–8121 CrossRef.
- T. A. Ghezzehei and D. Or, Soil Sci. Soc. Am. J., 2001, 65, 624–637 CrossRef CAS.
- E. Koos and N. Willenbacher, Science, 2011, 331, 897–900 CrossRef CAS PubMed.
- T. R. Underwood and I. C. Bourg, J. Phys. Chem. C, 2020, 124, 3702–3714 CrossRef CAS.
- X. Shen and I. C. Bourg, J. Colloid Interface Sci., 2021, 584, 610–621 CrossRef CAS PubMed.
- C. Soulaine and H. A. Tchelepi, Trans. Porous Media, 2016, 113, 431–456 CrossRef CAS.
- M. A. Murad and C. Moyne, Comput. Geosci., 2008, 12, 47–82 CrossRef.
- P. Coussot, Phys. Rev. Lett., 1995, 74, 3971–3974 CrossRef CAS PubMed.
- F. J. Carrillo and I. C. Bourg, Phys. Rev. E, 2021, 103, 063106 CrossRef CAS PubMed.
- D. L. Kurz, E. Secchi, F. J. Carrillo, I. C. Bourg, R. Stocker and J. Jimenez-Martinez, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122202119 CrossRef CAS.
- F. J. Carrillo and I. C. Bourg, Water Res. Res., 2021, 57, e2020WR028734 CrossRef.
- C. Di Maio, Geotechnique, 1996, 46, 695–707 CrossRef.
- A. C. Wiseall, R. J. Cuss, C. C. Graham and J. F. Harrington, Mineral. Mag., 2015, 79, 1335–1342 CrossRef.
- S. Rocco, A. W. Woods, J. Harrington and S. Norris, Geophys. Res. Lett., 2017, 44, 751–759 CrossRef.
- I. C. Bourg and J. B. Ajo-Franklin, Acc. Chem. Res., 2017, 50, 2067–2074 CrossRef CAS.
- A. Seiphoori, X.-G. Ma, P. E. Arratia and D. J. Jerolmack, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2275–2281 CrossRef PubMed.
- R. Kaitna, M. C. Palucis, B. Yohannes, K. M. Hill and W. E. Dietrich, J. Geophys. Res.: Earth Surface, 2016, 121, 415–441 CrossRef.
- K. M. Hill, J. Gaffney, S. Baumgardner, P. Wilcock and C. Paola, Water Resour. Res., 2017, 53, 923–941 CrossRef.
- X. Zheng and I. C. Bourg, NANO, 2023, 17, 19211–19223 CAS.
- A. A. Agles and I. C. Bourg, J. Phys. Chem. B, 2023, 127, 1828–1841 CrossRef CAS.
- J. S. Wettlaufer, Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 2019, 377, pp. 1–17 Search PubMed.
- N. K. Marath and J. S. Wettlaufer, Soft Matter, 2020, 16, 5886–5891 RSC.
- J. Vachier and J. S. Wettlaufer, Phys. Rev. E, 2022, 105, 024601 CrossRef CAS.
- S. Tyagi, C. Monteux and S. Deville, Soft Matter, 2022, 18, 4178–4188 RSC.
- D. Gerber, L. A. Wilen, F. Poydenot, E. R. Dufresne and R. W. Style, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200748119 CrossRef CAS.
- H. Gupta, Encyclopedia of Solid Earth Geophysics, Springer Science & Business Media, 2011 Search PubMed.
- D. L. Turcotte and G. Schubert, Geodynamics, Cambridge University Press, 2002 Search PubMed.
- D. J. Jerolmack and K. E. Daniels, Nat. Rev. Phys., 2019, 1, 716–730 CrossRef.
- N. S. Deshpande, D. J. Furbish, P. E. Arratia and D. J. Jerolmack, Nat. Commun., 2021, 12, 3909 CrossRef CAS PubMed.
- R. Kostynick, H. Matinpour, S. Pradeep, S. Haber, A. Sauret, E. Meiburg, T. Dunne, P. Arratia and D. Jerolmack, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2209109119 CrossRef CAS.
- L. Cascini, M. R. Scoppettuolo and E. Babilio, Landslides, 2022, 2839–2851 CrossRef.
- M. Wyart, Annales De Physique, 2005, 30, 1 Search PubMed.
- X. Mao and T. C. Lubensky, Ann. Rev. Condens. Matter Phys., 2018, 9, 413–433 CrossRef.
- K. Liu, J. E. Kollmer, K. E. Daniels, J. M. Schwarz and S. Henkes, Phys. Rev. Lett., 2021, 126, 088002 CrossRef CAS PubMed.
- T. A. Brzinski and K. E. Daniels, Phys. Rev. Lett., 2018, 120, 218003 CrossRef PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef PubMed.
- E. Berthier, M. A. Porter and K. E. Daniels, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16742–16749 CrossRef CAS.
- E. T. Owens and K. E. Daniels, Soft Matter, 2013, 9, 1214–1219 RSC.
- A. Tordesillas, Z. Zhou and R. Batterham, Mech. Res. Commun., 2018, 92, 137–141 CrossRef.
- R. M. Iverson, Rev. Geophys., 1997, 35, 245–296 CrossRef.
- D. L. Roth, T. H. Doane, J. J. Roering, D. J. Furbish and A. Zettler-Mann, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 25335–25343 CrossRef CAS.
- R. J. Eyles and R. Ho, J. Tropical Geography, 1970, 31, 40–42 Search PubMed.
- R. W. Fleming and A. M. Johnson, Q. J. Eng. Geol., 1975, 8, 1–29 CrossRef.
- A.-V. Auzet and B. Ambroise, Earth Surf. Processes Landforms, 1996, 21, 531–542 CrossRef CAS.
- N. Matsuoka, Permafrost Periglacial Processes, 1998, 9, 121–133 CrossRef.
- N. S. Deshpande, P. E. Arratia and D. J. Jerolmack, Geophys. Res. Lett., 2023, 50, e2023GL102938 CrossRef.
- M. Houssais, C. Maldarelli and J. F. Morris, Phys. Rev. Fluids, 2021, 6, L012301 CrossRef.
- F. D. Cunez, E. M. Franklin, M. Houssais, P. Arratia and D. J. Jerolmack, Phys. Rev. Res., 2022, 4, L022055 CrossRef CAS.
- B. Ferdowsi, C. P. Ortiz and D. J. Jerolmack, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4827–4832 CrossRef CAS.
- D. J. Furbish, J. J. Roering, T. H. Doane, D. L. Roth, S. G. W. Williams and A. M. Abbott, Earth Surf. Dyn., 2021, 9, 539–576 CrossRef.
- D. J. Furbish, S. G. W. Williams, D. L. Roth, T. H. Doane and J. J. Roering, Earth Surf. Dyn., 2021, 9, 577–613 CrossRef.
- D. J. Furbish, S. G. W. Williams and T. H. Doane, Earth Surf. Dyn., 2021, 9, 615–628 CrossRef.
- D. J. Furbish and T. H. Doane, Earth Surf. Dyn., 2021, 9, 629–664 CrossRef.
- R. M. Iverson, 3rd International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, 2003.
- K. R. Hubbert, P. M. Wohlgemuth, J. L. Beyers, M. G. Narog and R. Gerrard, Fire Ecology, 2012, 8, 143–162 CrossRef.
- E. J. Gabet, Earth Surf. Processes Landforms, 2003, 28, 1341–1348 CrossRef.
- P. Alessio, T. Dunne and K. Morell, J. Geophys. Res.: Earth Surf., 2021, 126, e2021JF006108 CrossRef.
- P. Shen, L. Zhang, H. Chen and R. Fan, Geosci. Model Dev., 2018, 11, 2841–2856 CrossRef.
- S. H. Cannon, E. R. Bigio and E. Mine, Hydrolog. Processes, 2001, 15, 3011–3023 CrossRef.
- L. Schippa, Granularity in Materials Science, IntechOpen, 2018 Search PubMed.
- R. Sosio and G. B. Crosta, Water Resour. Res., 2009, 45, W03412 CrossRef.
- J. D. Parsons, K. X. Whipple and A. Simoni, J. Geology, 2001, 109, 427–447 CrossRef.
- J. Baker, N. Gray and P. Kokelaar, Int. J. Erosion Control Eng., 2016, 9, 174–178 CrossRef.
- J. Kean, D. Staley, J. Lancaster, F. Rengers, B. Swanson, J. Coe, J. Hernandez, A. Sigman, K. Allstadt and D. Lindsay, Geosphere, 2019, 15, 1140–1163 CrossRef.
- D. Larson, Am. Sci., 1993, 81, 166–177 Search PubMed.
- R. Ettema, J. Hydraulic Res., 1990, 28, 673–684 CrossRef.
- A. Herman, Ann. Glaciol., 2013, 54, 114–120 CrossRef.
- M. Jutzeler, R. Marsh, R. J. Carey, J. D. White, P. J. Talling and L. Karlstrom, Nat. Commun., 2014, 5, 1–10 Search PubMed.
- N. J. Mlot, C. A. Tovey and D. L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7669–7673 CAS.
- J. C. Burton, J. M. Amundson, R. Cassotto, C.-C. Kuo and M. Dennin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5105–5110 CrossRef CAS.
- A. A. Robel, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- J. M. Amundson and J. Burton, J. Geophys. Res.: Earth Surf., 2018, 123, 2243–2257 CrossRef.
- GDRMiDi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 341–365 CrossRef.
- T. Murray, M. Nettles, N. Selmes, L. Cathles, J. C. Burton, T. D. James, S. Edwards, I. Martin, T. O’Farrell and R. Aspey, et al. , Science, 2015, 349, 305–308 CrossRef CAS PubMed.
- J. M. Amundson, M. Fahnestock, M. Truffer, J. Brown, M. P. Lüthi and R. J. Motyka, J. Geophys. Res.: Earth Surf., 2010, 115, F1 Search PubMed.
- R. K. Cassotto, J. C. Burton, J. M. Amundson, M. A. Fahnestock and M. Truffer, Nat. Geosci., 2021, 14, 417–422 CrossRef CAS.
- F. Engelund and J. Fredsoe, Hydrology Res., 1976, 7, 293–306 Search PubMed.
- R. F. Luque and R. V. Beek, J. Hydraulic Res., 1976, 14, 127–144 CrossRef.
- E. Meyer-Peter and R. Müller, IAHSR 2nd meeting, Stockholm, appendix 2, 1948.
- M. Wong and G. Parker, J. Hydraulic Eng., 2006, 132, 1159–1168 CrossRef.
- A. Shields, Application of similarity principles and turbulence research to bed-load movement, California institute of technology technical report, 1936 Search PubMed.
- P. L. Wiberg and J. D. Smith, Water Resour. Res., 1987, 23, 1471–1480 CrossRef.
- G. Parker, J. Fluid Mech., 1978, 89, 127–146 CrossRef.
- P. R. Wilcock and J. C. Crowe, J. Hydraulic Eng., 2003, 129, 120–128 CrossRef.
- C. B. Phillips and D. J. Jerolmack, Science, 2016, 352, 694–697 CrossRef CAS.
- C. B. Phillips, C. C. Masteller, L. J. Slater, K. B. J. Dunne, S. Francalanci, S. Lanzoni, D. J. Merritts, E. Lajeunesse and D. J. Jerolmack, Nat. Rev. Earth Environ., 2022, 3, 406–419 CrossRef.
- F. Metivier, E. Lajeunesse and O. Devauchelle, Earth Surf. Dyn., 2017, 5, 187–198 CrossRef.
- E. R. Mueller, J. Pitlick and J. M. Nelson, Water Resour. Res., 2005, 41, W04006 CrossRef.
- J. M. Buffington and D. R. Montgomery, Water Resour. Res., 1997, 33, 1993–2029 CrossRef.
- I. Reid, L. E. Frostick and J. T. Layman, Earth Surf. Processes Landforms, 1985, 10, 33–44 CrossRef.
- C. C. Masteller and N. J. Finnegan, J. Geophys. Res.: Earth Surf., 2017, 122, 274–289 CrossRef.
- A.-M. Ockelford and H. Haynes, Earth Surf. Processes Landforms, 2013, 38, 717–727 CrossRef.
- D. Rickenmann and B. McArdell, Earth Surf. Processes Landforms, 2007, 32, 1362–1378 CrossRef.
- C. C. Masteller, N. J. Finnegan, J. M. Turowski, E. M. Yager and D. Rickenmann, Geophys. Res. Lett., 2019, 46, 2583–2591 CrossRef.
- H. Monteith and G. Pender, Water Resour. Res., 2005, 41, W12401 CrossRef.
- H. Haynes and G. Pender, J. Hydraulic Eng., 2007, 133, 343–349 CrossRef.
- C. C. Masteller and J. P. Johnson, AGU Fall Meeting Abstracts, 2020, pp. EP008-04.
- J. M. Turowski, E. M. Yager, A. Badoux, D. Rickenmann and P. Molnar, Earth Surf. Processes Landforms, 2009, 34, 1661–1673 CrossRef.
- E. Deal, J. G. Venditti, S. J. Benavides, R. Bradley, Q. Zhang, K. Kamrin and J. T. Perron, Nature, 2023, 613, 298–302 CrossRef CAS PubMed.
- A. Burtin, N. Hovius, D. T. Milodowski, Y.-G. Chen, Y.-M. Wu, C.-W. Lin, H. Chen, R. Emberson and P.-L. Leu, J. Geophys. Res.: Earth Surf., 2013, 118, 1956–1974 CrossRef.
- K. L. Cook and M. Dietze, Annu. Rev. Earth Planet. Sci., 2022, 50, 183–204 CrossRef CAS.
- E. Larose, S. Carrière, C. Voisin, P. Bottelin, L. Baillet, P. Guéguen, F. Walter, D. Jongmans, B. Guillier, S. Garambois, F. Gimbert and C. Massey, J. Appl. Geophys., 2015, 116, 62–74 CrossRef.
- B. Schmandt, D. Gaeuman, R. Stewart, S. M. Hansen, V. C. Tsai and J. Smith, Geology, 2017, 45, 299–302 CrossRef.
- D. L. Roth, G. Jin, M. Bezada, A. Titov, C. C. Masteller, B. Tate and M. Siegfried, AGU Fall Meeting Abstracts, 2022, pp. EP33A-01.
- H. Albert, F. Costa and J. Mart, Geology, 2016, 44, 211–214 CrossRef CAS.
- L. Passarelli and E. E. Brodsky, Geophys. J. Int., 2012, 188, 1025–1045 CrossRef CAS.
- M. Ripepe, M. Pistolesi, D. Coppola, D. Delle Donne, R. Genco, G. Lacanna, M. Laiolo, E. Marchetti, G. Ulivieri and S. Valade, Sci. Rep., 2017, 7, 1–9 CrossRef CAS.
- National Academies of Sciences, Engineering and Medicine, Volcanic Eruptions and Their Repose, Unrest, Precursors, and Timing, National Academies Press technical report, 2017.
- R. Stoiber and S. Williams, J. Geophys. Res., 1986, 91, 12215–12231 CrossRef.
- P. Allard, J. Carbonnelle, N. Métrich, H. Loyer and P. Zettwoog, Nature, 1994, 368, 326–330 CrossRef CAS.
- K. Kazahaya, H. Shinohara and G. Saito, Bull. Volcanol., 1994, 56, 207–216 CrossRef.
- J. L. Palma, E. S. Calder, D. Basualto, S. Blake and D. A. Rothery, J. Geophys. Res.: Solid Earth, 2008, 113, 201 Search PubMed.
- C. Oppenheimer, A. S. Lomakina, P. R. Kyle, N. G. Kingsbury and M. Boichu, Earth Planet. Sci. Lett., 2009, 284, 392–398 CrossRef CAS.
- J. Woitischek, A. W. Woods, M. Edmonds, C. Oppenheimer, A. Aiuppa, T. D. Pering, T. Ilanko, R. D'Aleo and E. Garaebiti, J. Volcanol. Geotherm. Res., 2020, 398, 106869 CrossRef CAS.
- N. Métrich, A. Bertagnini, P. Landi and M. Rosi, J. Petrology, 2001, 42, 1471–1490 CrossRef.
- L. Francalanci, S. Tommasini and S. Conticelli, J. Volcanol. Geotherm. Res., 2004, 131, 179–211 CrossRef CAS.
- L. Francalanci, G. R. Davies, W. Lustenhouwer, S. Tommasini, P. R. Mason and S. Conticelli, J. Petrology, 2005, 46, 1997–2021 CrossRef CAS.
- J. Suckale, T. Keller, K. V. Cashman and P.-O. Persson, Geophys. Res. Lett., 2016, 43, 12–071 CrossRef.
- Z. Qin and J. Suckale, J. Geophys. Res.: Solid Earth, 2020, 125, e2019JB018549 CrossRef.
- J. Suckale, J. A. Sethian, J.-D. Yu and L. T. Elkins-Tanton, J. Geophys. Res.: Planets, 2012, 117, E08004 Search PubMed.
- Z. Qin, K. Allison and J. Suckale, J. Comput. Phys., 2020, 401, 109021 CrossRef CAS.
- K. R. Schwindinger and A. T. Anderson, Contrib. Mineral. Petrol., 1989, 103, 187–198 CrossRef CAS.
- P. E. Wieser, Z. Vukmanovic, R. Kilian, E. Ringe, M. B. Holness, J. Maclennan and M. Edmonds, Geology, 2019, 47, 948–952 CrossRef CAS.
- G. B. Jeffery, Proc. R. Soc. B, 1922, 102, 161–179 Search PubMed.
- M. H. DiBenedetto and N. T. Ouellette, J. Fluid Mech., 2018, 856, 850–869 CrossRef.
- M. H. DiBenedetto, J. R. Koseff and N. T. Ouellette, Phys. Rev. Fluids, 2019, 4, 034301 CrossRef.
- M. DiBenedetto, Z. Qin and J. Suckale, Sci. Adv., 2020, 6, eabd4850 CrossRef PubMed.
- D. H. Richter and K. J. Murata, US Geological Survey Professional Paper, 1966, 537-D, D1–D12.
- A. Fowler, Proc. R. Soc. A, 1986, 407, 147–170 Search PubMed.
- C. Schoof, Nature, 2010, 468, 803–806 CrossRef CAS.
- C. Schoof and I. Hewitt, Annu. Rev. Fluid Mech., 2013, 45, 217–239 CrossRef.
- I. J. Hewitt, C. Schoof and M. A. Werder, J. Fluid Mech., 2012, 702, 157–187 CrossRef CAS.
- C. Schoof, J. Fluid Mech., 2007, 573, 27–55 CrossRef.
- S. S. Pegler, J. Fluid Mech., 2018, 857, 648–680 CrossRef CAS.
- R. Sayag and M. G. Worster, J. Fluid Mech., 2019, 881, 722–738 CrossRef CAS.
- B. Rallabandi, Z. Zheng, M. Winton and H. A. Stone, Phys. Rev. Lett., 2017, 118, 128701 CrossRef PubMed.
- J. Wettlaufer and M. G. Worster, Annu. Rev. Fluid Mech., 2006, 38, 427–452 CrossRef.
- D. Vella and J. Wettlaufer, Phys. Rev. Lett., 2007, 98, 088303 CrossRef PubMed.
- D. Vella and J. Wettlaufer, J. Geophys. Res.: Oceans, 2008, 113, C11011 CrossRef.
- R. Sayag and M. G. Worster, Geophys. Res. Lett., 2013, 40, 5877–5881 CrossRef.
- T. J. Wagner, T. D. James, T. Murray and D. Vella, Geophys. Res. Lett., 2016, 43, 232A–240A CrossRef.
- T. J. Wagner, P. Wadhams, R. Bates, P. Elosegui, A. Stern, D. Vella, E. P. Abrahamsen, A. Crawford and K. W. Nicholls, Geophys. Res. Lett., 2014, 41, 5522–5529 CrossRef.
- J. Fannon, A. Fowler and I. Moyles, Proc. R. Soc. A, 2017, 473, 20170220 CrossRef CAS.
- L. K. Zoet and N. R. Iverson, Science, 2020, 368, 76–78 CrossRef CAS.
- K. Warburton, D. Hewitt and J. Neufeld, Proc. R. Soc. A, 2023, 479, 20220536 CrossRef.
- A. W. Rempel, J. Wettlaufer and M. G. Worster, J. Fluid Mech., 2004, 498, 227–244 CrossRef CAS.
- C. R. Meyer and I. J. Hewitt, The Cryosphere, 2017, 11, 2799–2813 CrossRef.
- A. Moure, N. Jones, J. Pawlak, C. Meyer and X. Fu, Water Res. Res., 2023, e2022WR034035 CrossRef.
- D. I. Benn, C. R. Warren and R. H. Mottram, Earth-Sci. Rev., 2007, 82, 143–179 CrossRef.
- J. N. Bassis and S. Jacobs, Nat. Geosci., 2013, 6, 833–836 CrossRef CAS.
- T. A. Scambos, C. Hulbe, M. Fahnestock and J. Bohlander, J. Glaciology, 2000, 46, 516–530 CrossRef.
- J. Weertman, Symposium on the Hydrology of Glaciers, Cambridge, 1969, vol. 7–13, pp. 139–145 Search PubMed.
- C. Van der Veen, Cold Regions Sci. Technol., 1998, 27, 31–47 CrossRef.
- A. F. Banwell, D. R. MacAyeal and O. V. Sergienko, Geophys. Res. Lett., 2013, 40, 5872–5876 CrossRef.
- A. A. Robel and A. F. Banwell, Geophys. Res. Lett., 2019, 46, 12092–12100 CrossRef.
- R. M. DeConto and D. Pollard, Nature, 2016, 531, 591–597 CrossRef CAS PubMed.
- C.-Y. Lai, L. A. Stevens, D. L. Chase, T. T. Creyts, M. D. Behn, S. B. Das and H. A. Stone, Nat. Commun., 2021, 12, 1–10 CrossRef.
- D. L. Chase, C.-Y. Lai and H. A. Stone, Phys. Rev. Fluids, 2021, 6, 084101 CrossRef.
- V. C. Tsai and J. R. Rice, J. Geophys. Res.: Earth Surf., 2010, 115, F03007 Search PubMed.
- A. Luckman, D. Jansen, B. Kulessa, E. King, P. Sammonds and D. Benn, The Cryosphere, 2012, 6, 113–123 CrossRef.
- D. McGrath, K. Steffen, T. Scambos, H. Rajaram, G. Casassa and J. L. R. Lagos, Ann. Glaciol., 2012, 53, 10–18 CrossRef.
- W. R. Buck and C.-Y. Lai, Geophys. Res. Lett., 2021, 48, e2021GL093110 CrossRef.
- N. B. Coffey, D. R. MacAyeal, L. Copland, D. R. Mueller, O. V. Sergienko, A. F. Banwell and C.-Y. Lai, J. Glaciology, 2022, 68, 867–878 Search PubMed.
- V. Jules, E. Lajeunesse, O. Devauchelle, A. Guérin, C. Jaupart and P.-Y. Lagrée, J. Fluid Mech., 2021, 917, A13 CrossRef.
- K. Maher, Earth Planet. Sci. Lett., 2011, 312, 48–58 CrossRef CAS.
- C. J. Harman and M. Kim, Hydrological Processes, 2019, 33, 466–475 CrossRef.
- J. W. Kirchner, X. Feng and C. Neal, Nature, 2000, 403, 524–527 CrossRef CAS.
- C. Dessert, B. Dupré, J. Gaillardet, L. M. François and C. J. Allègre, Chem. Geol., 2003, 202, 257–273 CrossRef CAS.
- V. Jules, PhD thesis, Université de Paris, 2020.
- J. W. Kirchner, Water Resour. Res., 2009, 45, W02429 CrossRef.
- A. Guérin, O. Devauchelle, V. Robert, T. Kitou, C. Dessert, A. Quiquerez, P. Allemand and E. Lajeunesse, Geophys. Res. Lett., 2019, 46, 7447–7455 CrossRef.
- D. J. Furbish, P. K. Haff, J. C. Roseberry and M. W. Schmeeckle, J. Geophys. Res.: Earth Surf., 2012, 117, F03031 Search PubMed.
- D. Chandler, J. Wadham, G. Lis, T. Cowton, A. Sole, I. Bartholomew, J. Telling, P. Nienow, E. Bagshaw, D. Mair, S. Vinen and A. Hubbard, Nat. Geosci., 2013, 6, 195–198 CrossRef CAS.
- M. A. Werder, I. J. Hewitt, C. G. Schoof and G. E. Flowers, J. Geophys. Res.: Earth Surf., 2013, 118, 2140–2158 CrossRef.
- J. F. Nye, J. Glaciology, 1976, 17, 181–207 CrossRef.
- A. Damsgaard, J. Suckale, J. A. Piotrowski, M. Houssais, M. R. Siegfried and H. A. Fricker, J. Glaciology, 2017, 63, 1034–1048 CrossRef.
- I. J. Hewitt and T. T. Creyts, Geophys. Res. Lett., 2019, 46, 6673–6680 CrossRef.
- T. K. Lowenstein and L. A. Hardie, Sedimentology, 1985, 32, 627–644 CrossRef CAS.
- Y. Dang, L. Xiao, Y. Xu, F. Zhang, J. Huang, J. Wang, J. Zhao, G. Komatsu and Z. Yue, J. Geophys. Res.: Planets, 2018, 123, 1910–1933 CrossRef.
- F. W. Christiansen, Science, 1963, 139, 607–609 CrossRef CAS PubMed.
- J. C. Dixon, in Aridic Soils, Patterned Ground, and Desert Pavements, Springer, Dordrecht, The Netherlands, 2009 DOI:10.1007/978-1-4020-5719-9_5.
- J. M. Nield, R. G. Bryant, G. F. Wiggs, J. King, D. S. Thomas, F. D. Eckardt and R. Washington, Geology, 2015, 43, 31 CrossRef.
- J. Lasser, J. M. Nield and L. Goehring, Earth System Sci. Data, 2020, 12, 2881–2898 CrossRef.
- S. Lokier, J. Arid Environ., 2012, 79, 32–47 CrossRef.
- J. Lasser, M. Ernst and L. Goehring, J. Fluid Mech., 2021, 917, A14 CrossRef.
- J. Lasser, J. M. Nield, M. Ernst, V. Karius, G. F. S. Wiggs, M. R. Threadgold, C. Beaume and L. Goehring, Phys. Rev. X, 2023, 13, 011025 CAS.
- D. R. Hewitt, G. G. Peng and J. R. Lister, J. Fluid Mech., 2020, 883, A37 CrossRef.
- R. Wooding, J. Fluid Mech., 1960, 9, 183–192 CrossRef.
- R. A. Wooding, S. W. Tyler, I. White and P. A. Anderson, Water Resour. Res., 1997, 33, 1199–1217 CrossRef.
- J. D. Stevens, J. M. S. Jr., C. T. Simmons and T. Fenstemaker, J. Hydrology, 2009, 375, 394–409 CrossRef.
- D. Groeneveld, J. Huntington and D. Barz, J. Hydrology, 2010, 392, 211–218 CrossRef CAS.
- H. Eloukabi, N. Sghaier, S. B. Nasrallah and M. Prat, Int. J. Heat Mass Transfer, 2013, 56, 80–93 CrossRef CAS.
- P. K. Haff, The Scientific Nature of Geomorphology: Proceedings of the 27th Binghamton Symposium in Geomorphology, 1996, p. 337.
- N. Matsuoka, Earth-Sci. Rev., 2001, 55, 107–134 CrossRef.
- H. E. Huppert, Nature, 1982, 300, 427–429 CrossRef.
- R. C. Glade, M. M. Fratkin, M. Pouragha, A. Seiphoori and J. C. Rowland, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2101255118 CrossRef CAS.
- N. S. Deshpande, D. J. Furbish, P. E. Arratia and D. J. Jerolmack, Nat. Commun., 2021, 12, 3909 CrossRef CAS PubMed.
- M. Houssais, C. Maldarelli and J. F. Morris, Phys. Rev. Fluids, 2021, 6, L012301 CrossRef.
- F. Fazelpour, Z. Tang and K. E. Daniels, Soft Matter, 2022, 18, 1435–1442 RSC.
- S. Mandal, M. Nicolas and O. Pouliquen, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 8366–8373 CrossRef CAS.
- C. Harris, M. C. Davies and B. R. Rea, Earth Surf. Processes Landforms, 2003, 28, 1289–1301 CrossRef.
- M. Harkema, W. Nijland, S. de Jong, T. Kattenborn and J. Eichel, Geomorphology, 2023, 433, 108727 CrossRef.
- R. A. Bagnold, The Physics of Blown Sand and Desert Dunes, Dover Publications Inc, 1941 Search PubMed.
- R. D. Lorenz and J. R. Zimbelman, Dune Worlds. How Windblown Sand Shapes Planetary Landscapes, Springer Praxis Books, 2014 Search PubMed.
- I. Livingstone, G. S. S. Wiggs and C. S. Weaver, Earth-Sci. Rev., 2007, 80, 239–257 CrossRef.
- C. J. Berte, Fighting sand encroachment. Lessons from Mauritania, Food and Agriculture Organisation of the United Nations, Rome, 2010 Search PubMed.
- B. Andreotti, Y. Forterre and O. Pouliquen, Granular Media: Between Fluid and Solid, Cambridge University Press, 2013 Search PubMed.
- K. Kroy, G. Sauermann and H. J. Herrmann, Phys. Rev. Lett., 2002, 88, 054301 CrossRef PubMed.
- F. Charru, B. Andreotti and P. Claudin, Annu. Rev. Fluid Mech., 2013, 45, 469–493 CrossRef.
- K. A. Bacik, S. Lovett, C. P. Caulfield and N. M. Vriend, Phys. Rev. Lett., 2020, 124, 054501 CrossRef CAS PubMed.
- P. A. Jarvis, K. A. Bacik, C. Narteau and N. M. Vriend, J. Geophys. Res.: Earth Surf., 2022, 127, e2021JF006492 CrossRef.
- P. A. Jarvis, C. Narteau, O. Rozier and N. M. Vriend, Earth Surf. Dyn. Discussions, 2023, 11, 803–815 CrossRef.
- K. A. Bacik, C. P. Caulfield and N. M. Vriend, Phys. Rev. Lett., 2021, 127, 154501 CrossRef CAS PubMed.
- K. A. Bacik, P. Canizares, C. P. Caulfield, M. J. Williams and N. M. Vriend, Phys. Rev. Fluids, 2021, 6, 104308 CrossRef.
- F. D. Hole, Geoderma, 1981, 25, 75–112 CrossRef.
- A. Hosoi and D. I. Goldman, Annu. Rev. Fluid Mech., 2015, 47, 431–453 CrossRef.
- A. Kudrolli and B. Ramirez, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25569–25574 CrossRef CAS.
- K. M. Dorgan, C. J. Law and G. W. Rouse, Proc. R. Soc. B, 2013, 280, 20122948 CrossRef.
- R. Maladen, Y. Ding, C. Li and D. Goldman, Science, 2009, 325, 314–318 CrossRef CAS.
- D. Hewitt and N. Balmforth, J. Fluid Mech., 2022, 936, A17 CrossRef CAS.
- A. Panaitescu, X. Clotet and A. Kudrolli, Phys. Rev. E, 2017, 95, 032901 CrossRef.
- R. Jewel, A. Panaitescu and A. Kudrolli, Phys. Rev. Fluids, 2018, 3, 084303 CrossRef.
- B. Allen and A. Kudrolli, Phys. Rev. E, 2019, 100, 022901 CrossRef CAS.
- A. Pal and A. Kudrolli, Phys. Rev. Fluids, 2021, 6, 124302 CrossRef.
- B. Chang and A. Kudrolli, Phys. Rev. E, 2022, 105, 034901 CrossRef CAS PubMed.
- F. Boyer, É. Guazzelli and O. Pouliquen, Phys. Rev. Lett., 2011, 107, 188301 CrossRef PubMed.
- S. Park, P. M. Wolanin, E. A. Yuzbashyan, H. Lin, N. C. Darnton, J. B. Stock, P. Silberzan and R. Austin, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13910–13915 CrossRef CAS PubMed.
- A. Biswas and A. Kudrolli, Soft Matter, 2023, 19, 4376–4384 RSC.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- Z. Mokhtari and A. Zippelius, Phys. Rev. Lett., 2019, 123, 028001 CrossRef CAS PubMed.
- C. Kurzthaler, S. Mandal, T. Bhattacharjee, H. Lowen, S. Datta and H. Stone, Nat. Commun., 2021, 12, 7088 CrossRef CAS PubMed.
- J. M. Melillo, S. D. Frey, K. M. DeAngelis, W. J. Werner, M. J. Bernard, F. P. Bowles, G. Pold, M. A. Knorr and A. S. Grandy, Science, 2017, 358, 101–105 CrossRef CAS PubMed.
- S. Doetterl, A. Stevens, J. Six, R. Merckx, K. Van Oost, M. Casanova Pinto, A. Casanova-Katny, C. Munoz, M. Boudin, E. Zagal Venegas and P. Boeckx, Nat. Geosci., 2015, 8, 780–783 CrossRef CAS.
- J. Yang, X. Zhang, I. Bourg and H. Stone, Nat. Commun., 2021, 12, 622 CrossRef CAS PubMed.
- J. Yang, J. Sanfilippo, N. Abbasi, Z. Gitai, B. Bassler and H. Stone, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2111060118 CrossRef CAS PubMed.
- C. Stanley, G. Grossmann, X. C. I. Solvas and A. DeMello, Lab Chip, 2016, 16, 228–241 RSC.
- K. Aleklett, E. Kiers, P. Ohlsson, T. Shimizu, V. Caldas and E. Hammer, ISME J., 2018, 12, 312–319 CrossRef PubMed.
- L. Fontaine and R. Auger, Batir en terre, Bélin, 2009 Search PubMed.
- H. Guillaud, in Terra Literature Review. An Overview of Research in Earthen Architecture Conservation, ed. E. Avrami, H. Guillaud and M. Hardy, The Getty Conservation Institute, Los Angeles, 2009 Search PubMed.
- T. Abergel, B. D. Dean and J. Dulac, Global Alliance for Buildings and Construction, 2017 Search PubMed.
- F. Dragulet, A. Goyal, K. Ioannidou, R. J.-M. Pellenq and E. Del Gado, J. Phys. Chem. B, 2022, 126, 4977 CrossRef CAS.
- A. Goyal, K. Ioannidou, C. Tiede, P. Levitz, R. J.-M. Pellenq and E. Del Gado, J. Phys. Chem. C, 2020, 124, 15500–15510 CrossRef CAS.
- G. Habert, S. A. Miller, V. M. John, J. L. Provis, A. Favier, A. Horvath and K. L. Scrivener, Nat. Rev. Earth Environ., 2020, 1, 559–573 CrossRef.
- A. Gangotra, E. Del Gado and J. I. Lewis, Commun. Eng., 2023, 2, 6 CrossRef.
- D. Malakoff, Science, 2020, 369, 894–895 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2015 Search PubMed.
- A. Goyal, I. Palaia, K. Ioannidou, F.-J. Ulm, H. van Damme, R. J.-M. Pellenq, E. Trizac and E. Del Gado, Sci. Adv., 2021, 7, eabg5882 CrossRef CAS.
- I. Palaia, A. Goyal, E. Del Gado, L. Samaj and E. Trizac, J. Phys. Chem. B, 2022, 126, 3143 CrossRef CAS PubMed.
- K. Ioannidou, M. Kanduc, L. Li, D. Frenkel, J. Dobnikar and E. Del Gado, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- K. Ioannidou, K. J. Krakowiak, M. Bauchy, C. G. Hoover, E. Masoero, S. Yip, F.-J. Ulm, P. Levitz, R. J.-M. Pellenq and E. Del Gado, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2029–2034 CrossRef CAS.
- D. L. Roth, N. J. Finnegan, E. E. Brodsky, D. Rickenmann, J. M. Turowski, A. Badoux and F. Gimbert, J. Geophys. Res.: Earth Surf., 2017, 122, 1182–1200 CrossRef.
- S. Lovejoy, H. Gaonac'h and D. Schertzer, Mathematical Geosciences, 2008, 40, 533–573 CrossRef.
- P. M. Sadler and D. J. Jerolmack, Geological Society, London, Special Publications, 2015, 404, 69–88 Search PubMed.
- R. Hébert, U. Herzschuh and T. Laepple, Nat. Geosci., 2022, 15, 899–905 CrossRef.
- C. L. Franzke, S. Barbosa, R. Blender, H. B. Fredriksen, T. Laepple, F. Lambert, T. Nilsen, K. Rypdal, M. Rypdal, M. G. Scotto, S. Vannitsem, N. W. Watkins, L. Yang and N. Yuan, Rev. Geophys., 2020, 58, e2019RG000657 CrossRef.
- J. Ha and H.-Y. Kim, Annu. Rev. Fluid Mech., 2020, 52, 263–284 CrossRef.
Footnote |
| † These authors contributed equally to this work. The following authors are in alphabetical order. |
| This journal is © The Royal Society of Chemistry 2024 |