 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the stability of a model quasicrystal and its approximants with a periodic substrate
Nydia Roxana
Varela-Rosales
 and
Michael
Engel
and
Michael
Engel
 *
*
Institute for Multiscale Simulation, Friedrich-Alexander-Universität Erlangen-Nürnberg, 91058 Erlangen, Germany. E-mail: michael.engel@fau.de
First published on 29th February 2024
Abstract
Quasicrystals and their periodic approximants are complex crystalline phases. They have now been observed in many metallic alloys, soft matter systems, and particle simulations. In recent experiments of thin-film perovskites on solid substrates, the type of complex phase was found to change depending on thermodynamic conditions and the type of substrate used. Here, we investigate the effect of a substrate on the relative thermodynamic stability of a two-dimensional model quasicrystal and its approximants. Our simulation model is particles interacting via the Lennard-Jones–Gauss potential. Our numerical methods are molecular dynamics simulations and free energy calculations that take into account phason flips explicitly. For substrates interacting weakly with the particles, we observe an incommensurate–commensurate transition, in which a continuous series of quasicrystal approximants locks into a small number of approximants. Interestingly, we observe that the 3/2 approximant exhibits phason mode fluctuations in thermodynamic equilibrium. Such fluctuations are reminiscent of random tiling and a phenomenon usually associated only with quasiperiodic order. For stronger substrates, we find an enhancement of the stability of the dodecagonal quasicrystal and variants of square lattices. We explain all observed phenomena by the interplay of the model system with the substrate. Our results demonstrate that designing novel complex periodic and quasiperiodic structures by choice of suitable substrates is a promising strategy.
1 Introduction
The discovery of structures with point group symmetries forbidden in periodic crystals1 created a new field of crystallography, the field of quasicrystals2,3 (QCs). Bulk, three-dimensional QCs became popular as candidates for materials with functional properties such as thermal insulators,4 coating materials,5,6 photonic crystals7 and superconductors.8 The first atomic QC in two dimensions was found only recently in the thin-film perovskite BaTiO3 on a Pt substrate.9 This discovery inspired follow-up work on thin-film perovskite QCs as well as their approximants at different chemical compositions.10–15 Despite significant efforts, how these perovskite QCs form and why they are stable remain mostly open questions. Answering these questions is of interest to simulation studies but is difficult to address with quantum mechanical methods at the atomic scale because the lack of periodicity and slow phason relaxation in QCs require large systems over long simulation times.16,17 Coarse-grained model systems are advantageous because they capture the essential physics and offer a route towards elucidating the relative thermodynamic stability of the involved phases and their phase transformation pathways.Two-dimensional particle systems in the presence of a substrate exhibit intricate structure formation phenomena caused by the competition of two length scales. These length scales are the size of the unit cell of the unperturbed particle system and the periodicity of the substrate. The competition of the length scales can introduce novel commensurate and incommensurate phases.18,19 Incommensurability also plays a role in nanotribology by influencing Aubry transitions in systems of colloids sliding on a substrate.20–23 Three factors are relevant for controlling the phase behavior in such systems: substrate potential depth, substrate periodicity, and the crystallographic symmetries of the particle system and the substrate.24
The investigation of thin QC films on a substrate can be divided into two classes of systems. The first class comprises systems, which are templated to have QC order using a QC substrate. Such QC films have been realized at the nanoscale as atomic adlayers.25–28 And at the colloidal scale, QC laser fields can be finely tuned to induce a gradual transition from an unperturbed system to a frozen QC.29–33 The second class comprises systems with intrinsic QC order. That is, such systems are QCs even in the absence of the substrate. It is suspected that thin film perovskite QCs fall into the latter class.9 Both classes of systems can show interesting phase behavior as the substrate is tuned.
There exist many simulation models for two-dimensional QCs. Prominent examples are binary mixtures of particles that interact with the Lennard-Jones potential,34,35 one-component systems of particles with interaction potential minima on two length scales,36–38 and anisotropic particles with patchy interactions.39,40 Here, we study the Lennard-Jones–Gauss (LJG) potential, which stabilizes a number of one-component QCs and approximants already in the absence of a substrate.37,41 We use this coarse-grained model to investigate the possibility of targeting specific approximants by tuning substrate parameters. As we will see, the LJG system can behave like a thin film QC in both the first and the second classes, depending on the choice of thermodynamic conditions and the substrate.
2 Methods
2.1 Coarse-grained model
As in our previous work,41 we investigate a coarse-grained two-dimensional model system, which is known to form different types of periodic and quasiperiodic phases.37 In this model, identical particles interact isotropically with the LJG potential given by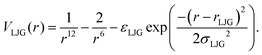 | (1) |
The potential parameters are fixed in this work at εLJG = 1.8, rLJG = 1.42, and σLJG2 = 0.042 to stabilize a dodecagonal QC at intermediate temperatures.41 The phase diagram of the LJG potential at these parameters contains a number of phases described by tilings made from squares, triangles, and pentagons. The sequence of phases can be described according to the underlying symmetry change41
 | (2) |
The phase behavior of the LJG system is only known in the absence of a substrate. Here, we add a substrate by including an external potential. We mimic the effect of the Pt (111) substrate for thin-film perovskite QCs by choosing an external potential in the form of a hexagonal lattice by superposition of three plane waves,
 | (3) |
To justify the choice of a model system for this work, we need to discuss phason modes. Phason modes are dynamic modes characteristic of QCs. They are realized as a collective rearrangement of finite clusters of tiles and can be decomposed into a series of elementary particle displacements called phason flips. In many common QCs, like for example, the Penrose tiling, phason mode excitation requires only a low activation energy and can occur locally with only a small number of phason flips. We call phason modes such as those found in the Penrose tiling continuously excitable. In other QCs, for example the square-triangle tiling, phason mode excitation requires creating a pair of defects and propagating each defect along a path rearranging the tiling in the process until the defects annihilate. In the square-triangle tiling, this process is called a zipper.42 Zippers are not efficient in relaxing the square triangle-tiling. We call phason modes such as those found in the square-triangle tiling therefore not continuously excitable. Continuously excitable phason modes are found in thin-film perovskite QCs where they involve rhomb tiles with small interior angle 30°. Because of the presence of continuously excitable phason modes, perovskite QCs can efficiently relax their tiling and transform to and from approximants.10,11 We chose to study the LJG model system because it stabilizes and includes continuously excitable phason modes in the p6m and p12m phases.41 This means that our model system is similar to perovskite QCs in the character of its phason flips and the phase transformations between approximants and the QC.
2.2 Tiling construction in hyperspace
The tilings of the dodecagonal QC and its approximants in the LJG model system can be described by the cut-and-project method43,44 in a four-dimensional hyperspace. We construct tiling models in two steps.In the first construction step, approximants of the quasicrystalline shield tiling45 are constructed. The projection matrices on the two-dimensional physical (or parallel) space are
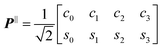 | (4) |
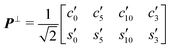 | (5) |
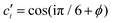 and
and  . The occupation domain for the shield tiling is a dodecagon with twelve vertices
. The occupation domain for the shield tiling is a dodecagon with twelve vertices  , i = 1,…,12. The parameter
, i = 1,…,12. The parameter | (6) |
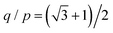 for the quasicrystal with wallpaper group p12m. This means that the simple periodic approximant is identified as a 2/1 approximant. All approximants with wallpaper group p6m can be constructed in the range
for the quasicrystal with wallpaper group p12m. This means that the simple periodic approximant is identified as a 2/1 approximant. All approximants with wallpaper group p6m can be constructed in the range  . The approximants have rectangular unit cells with lattice constants
. The approximants have rectangular unit cells with lattice constants  and
and  . The approximants of the shield tiling constructed so far are built from three basic tiles: square, triangle, and shield.45
. The approximants of the shield tiling constructed so far are built from three basic tiles: square, triangle, and shield.45
In a second construction step, the basic tiles square, triangle, and shield are decorated by placing one particle in the center of the square tiles, one particle in the center of the triangle tiles, and three particles as a regular triangle in the center of the shield tiles. The result is the tilings of interest, built from three larger tile types: square, triangle, and slightly deformed pentagon. Examples of these resultant tilings are found in Fig. 1 and Fig. 6. The combination of these tile decorations forms a substitution rule.
2.3 Simulations and free energy calculations
We perform simulations and free energy calculations using a combination of molecular dynamics (MD) and Monte Carlo (MC) to accelerate relaxation and exploration of phase space. MD is used to sample phonon modes and configurational entropy. MC is used to sample phason modes.46 From the van Hove autocorrelation function,38 we observe that all phason flips readily occur over a single flip distance near r = 1 and that most particles can perform phason flips. This demonstrates that phason modes are continuously excitable via local phason flips and do not require significant activation energy. We use the HOOMD-blue molecular dynamics simulation package47,48 as the basis for our simulations and further extend it to include MC moves. For MD, the integration timestep is 0.01. The NVT ensemble with Nosé–Hoover thermostat is used and open boundary conditions are applied. The Boltzmann constant is set to 1. For MC, we attempt a phason flip in MC by choosing a particle at random and a flip vector uniformly distributed in the ring 0.9 < r < 1.1. The MC move is accepted according to the Metropolis acceptance criterion. The measured acceptance rate of MC phason flips is about 10%. Periodic boundary conditions are employed to minimize finite size effects. We now discuss the two different simulation modes used in this work.In the first simulation mode, used for generating a diagram summarizing assembly behavior as a function of model parameters, called an assembly diagram, and for studying phase transitions, we perform MD simulations without MC moves. We simulate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles in a quadratic simulation box of a box edge length 300. The particles are initially placed in a central circle with a number density of 0.3. The particles crystallize over time into a roughly circular, compact cluster, which corresponds to a solid–gas coexistence. We chose this setup to effectively obtain open boundaries for the crystalline cluster. Such open boundaries are essential for efficient phason relaxation because phason relaxations are generally suppressed by the topological constraints of periodic boundary conditions.
000 particles in a quadratic simulation box of a box edge length 300. The particles are initially placed in a central circle with a number density of 0.3. The particles crystallize over time into a roughly circular, compact cluster, which corresponds to a solid–gas coexistence. We chose this setup to effectively obtain open boundaries for the crystalline cluster. Such open boundaries are essential for efficient phason relaxation because phason relaxations are generally suppressed by the topological constraints of periodic boundary conditions.
In the second simulation mode, used for the calculation of Helmholtz free energies, we combine MD and MC. 5000 MD sweeps, i.e., moving each particle 5000 times, are alternated with 5000 MC steps, i.e., attempting to perform a phason flip for 5000 randomly chosen particles. System size varies for different approximants and the QC between 4000 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles. In contrast to the first simulation mode, the simulation box for approximants is now completely filled to prevent solid–gas coexistence and to avoid phase transitions between approximants. For the QC, we simulate with open boundaries and only consider particles sufficiently fare from the surface. We first relax constructed approximants in an NPT simulation and then perform free energy integration in the NVT ensemble. In this way, the number density of simulations in the second simulation mode is guaranteed to agree with that of simulations in the first simulation mode.
000 particles. In contrast to the first simulation mode, the simulation box for approximants is now completely filled to prevent solid–gas coexistence and to avoid phase transitions between approximants. For the QC, we simulate with open boundaries and only consider particles sufficiently fare from the surface. We first relax constructed approximants in an NPT simulation and then perform free energy integration in the NVT ensemble. In this way, the number density of simulations in the second simulation mode is guaranteed to agree with that of simulations in the first simulation mode.
We use the Frenkel–Ladd (FL) method49 to compute free energies. FL performs a thermodynamic integration over a parameter λ. It interpolates between the system of interest at λ = 0 and an Einstein crystal at λ = 1. In an Einstein crystal, each particle is connected to a reference position by a harmonic spring. The integration is performed as
 | (7) |
It is important to check that the system remains in equilibrium throughout the FL integration. We perform such a check by calculating the free energy in the forward direction (increasing λ) and in the backward direction (decreasing λ) and by checking for hysteresis. The absence of hysteresis is an indication that the free energy calculation is accurate. A test FL integration for the 2/1 approximant is shown in Fig. 2. Forward and backward curves for ΔF agree, except for a small difference near λ = 0. At small λ, particles diffuse strongly through the system, which slows down equilibration. We use our test FL integration to adjust the numerical parameter to ensure that the hysteresis is sufficiently small. For numerical integration in production calculations, we use Legendre–Gauss quadrature with 20 λ points. Each λ point is simulated for 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD sweeps. The spring constant of the Einstein crystal is ΛE = 100. This value guarantees similar vibrational dynamics in the Einstein crystal and the system of interest as indicated by an approximately flat integrand.50
000 MD sweeps. The spring constant of the Einstein crystal is ΛE = 100. This value guarantees similar vibrational dynamics in the Einstein crystal and the system of interest as indicated by an approximately flat integrand.50
We validate the FL implementation by comparison to reported free energies41 for the continuous transition p3m1 → p12m in the absence of a substrate at ε = 0. We calculate free energies Fn(T) for six constructed approximants q/p = n/10 with n ∈ [15,…,20] and a well-equilibrated QC. We follow the continuous transition from the 2/1 approximant to the quasicrystal via the superstructure wave vector41
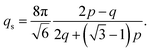 | (8) |
This wave vector is calculated from the distance between first-order satellite peaks and main diffraction peaks in reciprocal space.41 The appearance of satellite peaks is a consequence of the presence of structural modulations in the approximants. We define the stability temperature of the approximant n/10 as the intersection of Fn−1 and Fn+1. As an exception, instead of the 14/10 approximant, we use a well-equilibrated quasicrystal.
Our implementation of the FL plus phason mode relaxation algorithm shown in Fig. 3(a) accurately reproduces prior work.41 In particular, we reproduce the reported linear increase of the wave vector qs as a function of temperature (Fig. 3(b)). The agreement with prior work validates our free energy calculation with the FL plus phason model relaxation method.
 | ||
| Fig. 3 (a) Helmholtz free energies Fn(T) for a well-equilibrated quasicrystal and six approximants n/10, n = 15,…,20. Standard errors are estimated from eight independent FL calculations. Purple plus markers indicate the stability temperatures of approximants. Data shows the forward branch of the free energy calculation. (b) Validation of the free energy calculation with the FL plus phason model relaxation method. The superstructure vector grows linearly with temperature from the 2/1 approximant to the QC. Error bars on the temperature axis connect the FL calculation for the forward and the backward calculations. Stability temperatures for approximants agree with reference values41 within the error bars. | ||
3 Results
3.1 Molecular dynamics simulations
We analyze the crystallization behavior of our system by performing 77 MD simulations at seven temperatures 0.2 ≤ T ≤ 0.5 in steps of 0.05 and for eleven substrate potential depths 0.0 ≤ ε ≤ 0.1 in steps of 0.01. Substrate periodicity is fixed at λ = 0.5. This value is inspired by a direct comparison of relevant length scales in our simulations and the perovskite QCs on a Pt substrate.11 Each simulation is run for 108 integration steps and the final simulation snapshot at the end of the run is analyzed. In this subsection, we first perform a general analysis of the orientational order and then conduct a more in-depth analysis of the observed structures by visual inspection and with the help of diffraction patterns. | (9) |
The results of the local orientational order analysis are shown in Fig. 4. Indeed, there exists a competition between quadratic and hexagonal local orientational order. Hexagonal local order dominates at high T. Here the liquid phase is expected. In contrast, the quadratic local order dominates at intermediate T and high ε. Apparently, the substrate does not promote local hexagonal order but instead local quadratic order. This observation will be discussed further below. The gradual variation of local orientational order across the T–ε parameter plane indicates that the particles can react smoothly to changes in temperature and the substrate at a local level. We also observe that the presence of thermal fluctuations dominates over crystallographic symmetry in our two-dimensional system, smearing out the boundaries separating ordered phases. This precludes using the Mermin order parameters for automatic calculation of an assembly diagram without relaxation or temporal averaging.
We summarize the structure classification in the assembly diagram of Fig. 5. In the absence of a substrate, ε = 0, the known phase behavior of eqn (2) is reproduced. Notice that due to low resolution along the temperature axis, the continuous series of q/p approximants reported previously41 is not fully resolved. Phase boundaries shift with ε according to four trends. First, the dodecagonal QC and the 3/2 approximant become stable over broader temperature ranges and shift towards lower temperatures. This finding demonstrates that a hexagonal substrate can, in fact, stabilize a dodecagonal quasicrystal despite it having lower symmetry than the quasicrystal. Second, the stability region of the square lattice shifts towards high T with an increase of ε, and a new structure, called the modulated square lattice (msq), appears. Third, melting temperature increases with ε. Fourth, at low T and high ε we find a novel chiral quasicrystal (cqc). In cqc, the inversion symmetry of the dodecagonal quasicrystal is broken. Because this manuscript focuses on weak substrate potentials, cqc will be the subject of follow-up work. Three simulation snapshots at parameters marked by asterisks in Fig. 5, the 2/1 approximant at (T,ε) = (0.25,0.00), the 3/2 approximant at (0.25,0.02), and the quasicrystal at (0.25,0.04) are shown in Fig. 6. A fourth simulation snapshot at parameters marked by an asterisk at (0.3,0.09) corresponding to msq is shown in Fig. 8.
 | ||
| Fig. 5 Assembly diagram of the LJG potential in the T–ε parameter plane. Each data point corresponds to the dominant structure observed in the final simulation snapshot after long relaxation. The ordered structures are modulated square lattice (msq), square lattice (sq), 2/1 approximant (2/1), 3/2 approximant (3/2), dodecagonal QC (QC), and chiral structure (cqc). Snapshots at the parameter position indicated by four asterisks are shown in Fig. 6 and 8. | ||
We make two further observations: first, in the absence of a substrate, the phase transformation from the 2/1 approximant to the QC was continuous via a series of q/p approximants. This continuous behavior is not sustained towards finite ε. Instead, higher-order approximants are generally suppressed. Specifically, we identify the low-order approximants 2/1 and 3/2 repeatedly in our snapshots for ε > 0 but no other approximants. Second, there remain significant phason mode fluctuations in the 3/2 approximant at elevated temperatures. Such phason mode fluctuations are apparent when comparing Fig. 6(b)-left, which shows a simulation snapshot, to Fig. 6(b)-right, which shows the ideal tiling of the 3/2 approximant obtained after slow relaxation to T = 0 to remove phason fluctuations. Notice the similarity of the diffraction patterns calculated for both snapshots (two halves in Fig. 6(b)-middle). Apparently, the 3/2 approximant behaves like a random tiling in that it permits phason mode fluctuations in thermodynamic equilibrium. This means we must rely on characterization of average crystallographic order by identification of diffraction spots in the diffraction pattern to distinguish the approximants in the generation of the assembly diagram.
The presence of phason mode fluctuations in an approximant is unexpected and to the best of our knowledge has not been reported. It is unclear whether such behavior is related to the dimensionality of our system and can also occur in three dimensions. We observe random tiling behavior only in sufficiently complex approximants. For example, in the 2/1 approximant, there are no square tiles (green squares in Fig. 6) except if connected to structural defects. This means phason flips cannot occur inside a 2/1 approximant but must be initiated from the surface or from a grain boundary. In contrast, the 3/2 approximant has many square tiles and thus readily supports phason mode fluctuations.
3.2 Incommensurate–commensurate transition
While the unperturbed (i.e., in the absence of a substrate) 2/1 approximant transforms into the dodecagonal QC continuously via a series of hexagonal approximants, all approximants except 2/1 and 3/2 quickly disappear when the substrate is turned on (Fig. 5). Why is this the case? To understand the disappearance of higher-order approximants, we resort to free energy calculations. We calculate free energies for a well-relaxed QC and a number of low-order approximants. Recall that hexagonal approximants are labeled by two integers as q/p with . Without loss of generality, we can require q and p to be coprime. Finally, q and p should be small such that the approximants have small unit cells. The simplest such approximants are 2/1 = 2, 9/5 = 1.8, 5/3 ≈ 1.67, 3/2 = 1.5, and 7/5 = 1.4. We arrange the approximants in decreasing order of the q/p ratio from the 2/1 approximant, which is the energetic ground state, to the QC, which is the equilibrium state at intermediate temperature.
. Without loss of generality, we can require q and p to be coprime. Finally, q and p should be small such that the approximants have small unit cells. The simplest such approximants are 2/1 = 2, 9/5 = 1.8, 5/3 ≈ 1.67, 3/2 = 1.5, and 7/5 = 1.4. We arrange the approximants in decreasing order of the q/p ratio from the 2/1 approximant, which is the energetic ground state, to the QC, which is the equilibrium state at intermediate temperature.
Fig. 7 depicts the phase diagram predicted by free energy calculations. In the absence of a substrate, ε = 0, the phase diagram cycles through the approximants 2/1, 9/5, 5/3, 3/2, 7/5, and QC in correct (that is, in q/p decreasing) order with temperature. We also confirm the disappearance of all approximants except 2/1 and 3/2 with increasing ε. Note that we did not include in the free energy calculations the square lattice and its modulation and the liquid. Besides this omission, there is good agreement of the phase diagram in Fig. 7 with the assembly diagram obtained from MD in Fig. 5.
Situations where the competition of two length scales dominates phase behavior have long been studied in the field of modulated crystals.52 Because the two length scales are of different physical or chemical origins, their ratio is not expected to be any special number and typically will be irrational. The requirement of the system to satisfy both length scales simultaneously then causes the emergence of structural complexity in the form of modulated crystals. One distinguishes two cases: incommensurately modulated crystals are aperiodic crystals where both length scales are realized without compromise. The dodecagonal QC in our system can be interpreted as an incommensurately modulated crystal. A related example is Moiré patterns, where not a competition of length scales but the competition of crystallographic orientations and translation generates interference effects. Incommensurately modulated crystals are accompanied by phason modes in thermodynamic equilibrium. In contrast, commensurately modulated crystals are periodic crystals with large unit cells. The lattice constants of commensurately modulated crystals simultaneously approximate integer multiples of both length scales. Commensurately modulated crystals result from a lock-in transition where the irrational ratio of the two length scales locks into a rational approximation. q/p approximants are examples of commensurately modulated crystals.
Phase diagrams that include modulated crystals are usually studied as a function of length scale ratio and coupling strength. The first parameter, the length scale ratio, is often controlled indirectly by changing the composition or local structure. In our system, the length scale ratio is linked to the temperature T because temperature affects tile energy and thus the tile type that is dominant. The second parameter, the coupling strength, is measured relative to thermal energy. In our system, the coupling strength is given by substrate potential depth ε. With these identifications, we can compare our phase diagram to past phase diagrams of modulated crystals. The comparison shows that Fig. 7 closely resembles the mean field phase diagram for the 3D Ising model with competing interactions (Fig. 24 in ref. 53) and the FVdM model as suggested by Aubry (Fig. 25 in ref. 53). Such characteristic phase diagrams of incommensurate–commensurate transitions have been called the Devils flower phenomenon by Bak.54 Our results confirm that the increase of substrate strength locks modulated crystals into certain approximants and drives new complex phase behavior as expected from the Devil's flower phenomenon.
The appearance of the Devil's flower in our phase diagram helps us interpret the observed stabilization mechanism and particle dynamics. In the absence of a substrate in the temperature range 0.24 < T < 0.36, the system is incommensurately modulated. Phason modes are unlocked and critical for thermodynamic stabilization because they contribute to the free energy. As substrate potential depth increases, phason modes may still be present (see Fig. 6) but gradually disappear. Eventually, the system locks into the 2/1 and 3/2 approximants. To the best of our knowledge, Fig. 7 is the first report of an incommensurate–commensurate transition in any two-dimensional system of freely moving particles.
3.3 Square lattice and its variants
The presence of the substrate drives the incommensurate–commensurate transition at low substrate potential depth ε < 0.03. For ε > 0.03, the square lattice (sq) and its variants appear dominantly in the phase diagram (Fig. 5). For intermediate substrate potentials, a novel modulated square lattice (msq) is observed (Fig. 8(a) and (b)). For a high substrate potential, ε ≫ 1.0, above the range covered in Fig. 5, a coexistence of grains with rectangular lattice (rec) and hexagonal lattice is eventually observed (Fig. 8(c) and (d)). All of these phenomena are yet other examples of commensurate–incommensurate transitions induced by the competition of the length scales imparted by the LJG interaction potential with the unit cell of the substrate.Msq and rec are typically polycrystalline with individual grains locking into one of three distinct orientations. This locking is a consequence of the six-fold symmetry of the substrate. Diffraction patterns confirm the global six-fold symmetry. In the diffraction pattern of msq (inset in Fig. 8(a)), isolated peaks (circled) are present for each grain. Besides the locking of grain orientations, individual grains are only weakly affected by the substrate (see modulations discussed below). In the diffraction pattern of rec (inset in Fig. 8(c)), some peak triplets merge into single peaks (indicated by black hexagons in Fig. 8(a) and (c)). The merging is caused by a stretching of squares into rectangles to improve compatibility with the substrate. This means that the four-fold symmetry is already lost in individual grains of rec and the system is closer to six-fold symmetry than msq. While small patches of triangles are sometimes already present in rec (central part of Fig. 8(c) labelled ‘4’), only very high ε transforms the system completely into a hexagonal crystal (not shown).
A zoom-in on grain ‘2’ of rec is shown in Fig. 8(d). We plot the substrate potential in the background to visualize particle locations (red) relative to maxima (yellow) and minima (green) of the potential. Potential maxima form a hexagonal lattice separated by channels of low potential that trace the nearest–neighbor bond network of a honeycomb lattice. The stretching of squares into rectangles can now be understood. Recall that the nearest–neighbor distance is rNN ≈ 1.0, and the substrate periodicity is chosen as λ = 0.5. A lattice constant lx = 2λ allows particles to retain their preferred nearest–neighbor distance without penalty. And a slight adjustment of the lattice constant to  ensures commensurability with the substrate also in the y-direction.
ensures commensurability with the substrate also in the y-direction.
A zoom-in on grain ‘2’ of msq is shown in Fig. 8(b). Just like before, a lattice constant lx = 2λ allows particles to retain their preferred nearest–neighbor distance without penalty. The y-direction is again more complicated. A lattice constant ly = lx now guarantees four-fold symmetry in the diffraction pattern but can do so only on average and by allowing positional modulations along the y-axis. A close inspection reveals the presence of this modulation in the form of weak satellite peaks in the diffraction pattern (inset in Fig. 8(b)). The separation of satellite peaks from the central peaks corresponds to a superstructure periodicity of ls ≈ 0.20. Analysis of other snapshots suggests that ls is not unique but is a function of T and ε. We also observe that particles are unusually mobile in channels along the y-direction (purple in Fig. 8(b)). This high mobility can be directly associated with a phason mode. All evidence combined demonstrates that msq is an incommensurately modulated crystal.
4 Conclusions
Research in this paper was originally motivated by the discovery of approximants in the thin-film perovskites (Ba, Sc)TiO3 on solid metal substrates. Importantly, experiments demonstrated that the type of approximant changes as a function of substrate interaction and periodicity. Our findings reproduce and explain aspects of these experimental observations. Our findings also highlight a number of new phenomena, not yet seen in experiments or simulations.The new phenomena we observed and that we believe could be general consequences of the competition between a QC and a periodic substrate, are as follows:
1. Existence of incommensurate–commensurate phase transitions. In these phase transitions, the QC locks into one or several approximants. We observed the stabilization of the 3/2 approximant via a lock-in transition.
2. Approximants with phason fluctuations. We observed that the 3/2 approximant resembles a random tiling rather than an ideal crystal despite having a well-defined periodicity as indicated by the presence of a reciprocal lattice.
3. Enhanced stability of the QC. Counter-intuitively, the substrate enhanced the thermodynamic stability of the dodecagonal quasicrystal for some parameter values.
4. Incommensurately modulated crystals, where the modulation is a consequence of competition between two length scales. We observed the modulated square lattice.
5. Novel structures commensurate with the substrate that are not approximants. We observed the rectangular lattice.
While observation 1 is similar to that in thin-film perovskites and observation 3 could explain the existence of perovskite QCs, the other observations have not yet been reported in the experimental system. It will be interesting to search for them.
Generally, we see a trend that the competition between the inherent symmetry of the model system, i.e., the crystal structure that the system prefers to form in the absence of a substrate, and the imposed symmetry of the substrate can occur in multiple steps involving both commensurate and incommensurate phases. We find in our system, as we increase the strength of the substrate potential, at T = 0.25 (see Fig. 5), a complex sequence of phase transformation alternating between commensurate and incommensurate: from (i) 2/1 approximant (crystal) to (ii) 3/2 approximant (commensurate) to (iii) quasicrystal (incommensurate) to (iv) modulated square lattice (incommensurate) to (v) rectangle lattice (commensurate) to (vi) hexagonal lattice (substrate).
Future work should further expand this research by testing more parameters or conducting similar studies in more realistic systems. An important parameter that should be varied, but was not in this work, is the substrate periodicity. Varying this parameter, it should be possible to target desired crystal structures and approximants by inverse design. Given that many recent model systems of quasicrystals have been found in soft matter systems and the fact that such systems are highly tunable and thus ideally suited for parameter studies, we believe that soft matter quasicrystals are ideal candidates to test many of the discoveries reported in this work.
Author contributions
N. R. V.-R. implemented the model and performed all simulations and free energy calculations. Both authors conceived the idea, discussed the results, and wrote the manuscript. M. E. developed code to construct tilings and supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) through grant EN 905/4-1. The authors gratefully acknowledge the HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) under the NHR project CRC1411D04.Notes and references
- D. Shechtman, I. Blech, D. Gratias and J. W. Cahn, Phys. Rev. Lett., 1984, 53, 1951–1953 CrossRef CAS.
- D. Levine and P. J. Steinhardt, Phys. Rev. Lett., 1984, 53, 2477–2480 CrossRef CAS.
- W. Steurer, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 1–11 CrossRef CAS PubMed.
- C. Janot, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 181–191 CrossRef CAS PubMed.
- S. Takeuchi, H. Iwanaga and T. Shibuya, Jpn. J. Appl. Phys., 1991, 30, 561 CrossRef CAS.
- D. S. Shatura and A. A. Enaleeva, Crystallogr. Rep., 2007, 52, 945–952 CrossRef.
- Z. V. Vardeny, A. Nahata and A. Agrawal, Nat. Photonics, 2013, 7, 177–187 CrossRef CAS.
- K. Kamiya, T. Takeuchi, N. Kabeya, N. Wada, T. Ishimasa, A. Ochiai, K. Deguchi, K. Imura and N. K. Sato, Nat. Commun., 2018, 9, 154 CrossRef CAS PubMed.
- S. Förster, K. Meinel, R. Hammer, M. Trautmann and W. Widdra, Nature, 2013, 502, 215–218 CrossRef PubMed.
- S. Förster, M. Trautmann, S. Roy, W. A. Adeagbo, E. M. Zollner, R. Hammer, F. O. Schumann, K. Meinel, S. K. Nayak, K. Mohseni, W. Hergert, H. L. Meyerheim and W. Widdra, Phys. Rev. Lett., 2016, 117, 095501 CrossRef PubMed.
- S. Foerster, J. I. Flege, J. Falta, E. M. Zollner, F. O. Schumann, R. Hammer, A. Bayat, K.-M. Schindler and W. Widdra, Ann. Phys., 2017, 529, 1–7 Search PubMed.
- S. Förster, S. Schenk, E. Maria Zollner, O. Krahn, C.-T. Chiang, F. O. Schumann, A. Bayat, K.-M. Schindler, M. Trautmann, R. Hammer, K. Meinel, W. A. Adeagbo, W. Hergert, J. Ingo Flege, J. Falta, M. Ellguth, C. Tusche, M. DeBoissieu, M. Muntwiler, T. Greber and W. Widdra, Phys. Status Solidi B, 2020, 257, 1900624 CrossRef.
- M. Maniraj, L. V. Tran, O. Krahn, S. Schenk, W. Widdra and S. Förster, Phys. Rev. Mater., 2021, 5, 084006 CrossRef CAS.
- E. M. Zollner, S. Schenk, M. Setvin and S. Förster, Phys. Status Solidi B, 2020, 257, 1900620 CrossRef CAS.
- E. Maria Zollner, F. Schuster, K. Meinel, P. Stötzner, S. Schenk, B. Allner, S. Förster and W. Widdra, Phys. Status Solidi B, 2020, 257, 1900655 CrossRef CAS.
- E. Cockayne, M. Mihalkovič and C. L. Henley, Phys. Rev. B, 2016, 93, 020101 CrossRef PubMed.
- T. T. Dorini, F. Brix, C. Chatelier, A. Kokalj and E. Gaudry, Nanoscale, 2021, 13, 10771–10779 RSC.
- A. Patrykiejew, W. Rżysko and S. Sokołowski, Adsorption, 2009, 15, 254–263 CrossRef CAS.
- T. Neuhaus, M. Marechal, M. Schmiedeberg and H. Löwen, Phys. Rev. Lett., 2013, 110, 118301 CrossRef CAS PubMed.
- T. Brazda, A. Silva, N. Manini, A. Vanossi, R. Guerra, E. Tosatti and C. Bechinger, Phys. Rev. X, 2018, 8, 011050 CAS.
- M. Z. Baykara, M. R. Vazirisereshk and A. Martini, Appl. Phys. Rev., 2018, 5, 041102 Search PubMed.
- S. Amiri, C. A. Volkert and R. L. C. Vink, Phys. Rev. E, 2021, 104, 014802 CrossRef CAS.
- X. Cao, E. Panizon, A. Vanossi, N. Manini, E. Tosatti and C. Bechinger, Phys. Rev. E, 2021, 103, 012606 CrossRef CAS PubMed.
- C. Reichhardt and C. J. O. Reichhardt, Rep. Prog. Phys., 2016, 80, 026501 CrossRef.
- T. Flückiger, Y. Weisskopf, M. Erbudak, R. Lüscher and A. R. Kortan, Nano Lett., 2003, 3, 1717–1721 CrossRef.
- N. Ferralis, R. D. Diehl, K. Pussi, M. Lindroos, I. Fisher and C. J. Jenks, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075410 CrossRef.
- B. Bilki, M. Erbudak, M. Mungan and Y. Weisskopf, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045437 CrossRef.
- J. A. Smerdon, K. M. Young, M. Lowe, S. S. Hars, T. P. Yadav, D. Hesp, V. R. Dhanak, A. P. Tsai, H. R. Sharma and R. McGrath, Nano Lett., 2014, 14, 1184–1189 CrossRef CAS PubMed.
- J. Mikhael, J. Roth, L. Helden and C. Bechinger, Nature, 2008, 454, 501–504 CrossRef CAS PubMed.
- M. Schmiedeberg and H. Stark, Phys. Rev. Lett., 2008, 101, 218302 CrossRef PubMed.
- M. Schmiedeberg, J. Mikhael, S. Rausch, J. Roth, L. Helden, C. Bechinger and H. Stark, Eur. Phys. J. E, 2010, 32, 25–34 CrossRef CAS PubMed.
- J. Mikhael, G. Gera, T. Bohlein and C. Bechinger, Soft Matter, 2011, 7, 1352–1357 RSC.
- A. Jagannathan and M. Duneau, Eur. Phys. J. B, 2014, 87, 149 CrossRef.
- P. W. Leung, C. L. Henley and G. V. Chester, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 446–458 CrossRef PubMed.
- E. Fayen, M. Impéror-Clerc, L. Filion, G. Foffi and F. Smallenburg, Soft Matter, 2023, 19, 2654–2663 RSC.
- A. Quandt and M. P. Teter, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8586–8592 CrossRef CAS.
- M. Engel and H.-R. Trebin, Phys. Rev. Lett., 2007, 98, 225505 CrossRef PubMed.
- M. Engel, M. Umezaki, H.-R. Trebin and T. Odagaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134206 CrossRef.
- M. N. van der Linden, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2012, 136, 054904 CrossRef PubMed.
- A. Reinhardt, F. Romano and J. P. K. Doye, Phys. Rev. Lett., 2013, 110, 255503 CrossRef PubMed.
- M. Engel, Phys. Rev. Lett., 2011, 106, 095504 CrossRef.
- M. Oxborrow and C. L. Henley, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 6966–6998 CrossRef CAS PubMed.
- N. de Bruijn, Indag. Math., 1981, 84, 39–52 CrossRef.
- N. de Bruijn, Indag. Math., 1981, 84, 53–66 CrossRef.
- F. Gähler, Quasicryst. Mater., Proc., 1988, 272–284 Search PubMed.
- A. Kiselev, M. Engel and H.-R. Trebin, Phys. Rev. Lett., 2012, 109, 225502 CrossRef PubMed.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- D. Frenkel and A. J. C. Ladd, J. Chem. Phys., 1984, 81, 3188–3193 CrossRef CAS.
- R. K. R. Addula, S. K. Veesam and S. N. Punnathanam, Mol. Simul., 2021, 47, 824–830 CrossRef.
- N. D. Mermin, Phys. Rev., 1968, 176, 250–254 CrossRef.
- S. van Smaalen, Incommensurate Crystallography (International Union of Crystallography Monographs on Crystallography), Oxford University Press, Oxford, 2007 Search PubMed.
- P. Bak, Rep. Prog. Phys., 1982, 45, 587 CrossRef.
- P. Bak, Phys. Today, 1986, 39, 38–45 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |






