 Open Access Article
Open Access ArticleFrom a distance: Shuttleworth revisited†
Stefanie
Heyden‡
a and
Nicolas
Bain‡
 b
b
aETH Zürich, Institute for Building Materials, 8093 Zürich, Switzerland. E-mail: stefanie.heyden@mat.ethz.ch
bUniversite Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, UMR5306, F-69100, Villeurbanne, France. E-mail: nicolas.bain@cnrs.fr
First published on 1st July 2024
Abstract
The Shuttleworth equation: a linear stress–strain relation ubiquitously used in modeling the behavior of soft surfaces. Its validity in the realm of materials subject to large deformation is a topic of current debate. Here, we allow for large deformation by deriving the constitutive behavior of the surface from the general framework of finite kinematics. We distinguish cases of finite and infinitesimal surface relaxation preceding an infinitesimal applied deformation. The Shuttleworth equation identifies as the Cauchy stress measure in the fully linearized setting. We show that both in finite and linearized cases, measured elastic constants depend on the utilized stress measure. In addition, we discuss the physical implications of our results and analyze the impact of surface relaxation on the estimation of surface elastic moduli in the light of two different test cases.
1 Introduction
In most solids, small forces lead to small deformations. A soft solid, on the opposite, undergoes large deformations under minute forces: a phenomenon as minor as depositing a millimetric droplet leads to large surface deformations1–4 (Fig. 1). Such materials, which can take the form of gels, pastes, or elastomers, are ubiquitous in our lives: They amount to most of our body tissues, and serve as lubricants, glues, and water-repellent coatings. In the past years, it has been shown that surface stresses are essential in wetting, adhesion, and fracture, and can be exploited in composites.1–11 Yet, the physical origins of surface stresses are poorly understood. This is especially true in gels, in which the cohabitation of a crosslinked polymer network and a liquid solvent complexifies the link between molecular structure and mechanical properties. | ||
| Fig. 1 Experimental surface profiles of initially flat soft solids in contact with (a) a drop of glycerol, (b) a silica bead, and (c) a glass coverslip. Data were obtained from confocal imaging of fluorescent beads deposited on a silicone gel of shear modulus μ ∼ 2 kPa (same protocol as 3,12–14). Each blue circle represents a detected fluorescent bead, and the light blue areas represent the contacting objects. | ||
The dominant approach to tackle this fundamental question consists in investigating surface elastic properties.12,15–18 For instance, surface topography measurements of a stretched patterned silicone gel revealed an elastic surface, where surface stresses increase with surface deformations.15 This result hints towards a role of the crosslinked polymeric network in the surface constitutive behavior of silicone gels. Conversely, deformation measures of a spinning hydrogel bead evidenced constant surface stresses, independent of surface deformations, akin to the solvent surface tension.18
In its simplest form, the most common description for the surface mechanics of soft solids relates surface stresses σs (in N m−1) to surface strains εs and free energy Ws (in J m−2 or N m−1),
 | (1) |
and is called the Shuttleworth equation.19 This description is restricted to the linear regime, where small deformations prevail. It is, however, largely applied to estimate surface elastic constants (also in N m−1) of systems undergoing large deformations, where its validity and resulting physical interpretations have been rightfully questioned.20–23
The major drawback of the Shuttleworth equation is to ignore key features that can only be captured by accounting for finite deformations. Before applied deformations, for instance, soft solids are usually detached from a container, and their surfaces undergo an initial relaxation, inducing residual bulk stresses. Because soft solids are easy to deform, this surface relaxation can be large.13,24
Although extensive works in continuum mechanics laid out the framework of surface elasticity (see, e.g.,25–30), employing it in finite element simulations,31,32 sometimes accounting for the surface bending stiffness,27,32 the effect of initial surface relaxations on the estimation of surface elastic constants has so far not been assessed.
Here, we briefly expose the finite kinematics theory without initial surface relaxation. We leverage the framework of finite kinematics to rigorously derive surface stress–strain relations from a strain energy density while accounting for prior surface relaxations. We distinguish infinitesimal and finite surface relaxations and show that, in either case, different stress measures do not coincide, unlike the usual assumption in linear mechanics. While the classical description eqn (1) is valid for the Cauchy stress measure when the surface relaxations are infinitesimal, significant deviation terms appear when they are finite. We express these deviations in the general case and estimate their magnitude in two test cases. This framework should incite experimentalists to choose the suitable stress–strain relation and carefully interpret measured surface elastic parameters.
2 Without initial surface relaxations
A. Finite kinematics
We start with a brief outline of finite kinematics without initial surface relaxations. We can consider a solid in two states. A reference state, before deformation, and a deformed state (Fig. 2). In the reference state, the surface exhibits mechanical stresses, which, in the simplest case, have the form of a uniform and isotropic surface tension.1,2 We furthermore assume that the surface stresses can be thermodynamically defined by a surface strain energy density WR in the reference configuration.Following the Piola transform specialized to two dimensions, we define a free energy density expressed in the current configuration WC as
 | (2) |
 . Here, and from now on, all vector quantities, such as displacement fields, and all tensor quantities, such as stress- and strain fields, are projected onto the surface (see Section S1, ESI†).
. Here, and from now on, all vector quantities, such as displacement fields, and all tensor quantities, such as stress- and strain fields, are projected onto the surface (see Section S1, ESI†).
B. Different stress measures
Depending on the experimental conditions, different stress measures may be used for comparison to theory. The first Piola–Kirchhoff stress measure Ps, also known as the engineering stress, represents forces in the current configuration per unit referential area. Therefore, it is the quantity of interest in traction-controlled experiments.30 In contrast, the second Piola–Kirchhoff stress measure Ss constitutes forces mapped back to the reference configuration per unit referential area. Finally, the Cauchy stress measure σs, also denoted as true stress, refers to forces in the current configuration per unit current area. It is the stress measure used in an Eulerian setting or phenomena where the reference state is ill-defined, as in liquid flows. By definition, the second Piola–Kirchhoff stress derives from the free energy density in the reference configuration, | (3) |
 | (4) |
If one considers the free energy in the current configuration eqn (2), as is implicitly assumed in the Shuttleworth equation, the Cauchy stress takes a form similar to eqn (1)
 | (5) |
C. Surface stress–strain relations
It is now instructive to define a constitutive equation for the surface free energy. Assuming the surface energy is strain-independent WC = γ, as in liquids, the Cauchy stresses eqn (5) correspond to an isotropic surface tension σs = γI.For a strain-dependent surface energy, without loss of generality, we use the St. Venant-Kirchhoff model, which is the simplest extension of linear elasticity that captures geometric nonlinearities. To account for the surface stresses in the reference state, we enrich this model with a constant surface energy in the current configuration,
 | (6) |
| σs = γI + Fs(2μsEs + λstr(Es)I)FTs, | (7) |
and similarly to the first and second Piola–Kirchhoff stresses
| Ps = γJsFs(FTsFs)−1 + 2μsFsEs + λstr(Es)Fs, | (8) |
| Ss = γJs(FTsFs)−1 + 2μsEs + λstr(Es)I. | (9) |
D. Infinitesimal deformations
When surface deformations are finite, the stress measures eqn (7)–(9) represent different physical quantities and hence differ from one another. When surface deformations are infinitesimal, however, linearized mechanics do not distinguish between the reference and current states, and all stress measures coincide.33 This is the case in the absence of prior surface relaxation: all stress-strains relations give the same constitutive relation upon linearization![[P with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0050_0303.gif) s = s = ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) s = s = ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) s = γI + 2μsεs + λstr(εs)I, s = γI + 2μsεs + λstr(εs)I, | (10) |
![[P with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0050_0303.gif) s,
s, ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) s,
s, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) s) are the linearized stress measures. It is then straightforward to extract surface elastic coefficients when applying small surface deformations.32 In the latter, we will show that this property does not hold when we account for surface relaxations before applied deformations.
s) are the linearized stress measures. It is then straightforward to extract surface elastic coefficients when applying small surface deformations.32 In the latter, we will show that this property does not hold when we account for surface relaxations before applied deformations.
3 With initial surface relaxations
A. General setting
Soft solids are often cured within a mold, from which they are detached before being used. Upon detachment, they undergo a surface relaxation due to an interface change, enhanced wherever the local curvature is nonzero.7,13,24 We, therefore, distinguish three mechanical states (Fig. 3). The soft solid with the shape of the mold before it relaxes, Ω*, after it relaxes but before any external load or displacement, Ω0, and after being deformed by external loads Ω.In the first state, Ω*, the bulk of the soft solid is stress-free. For this reason, we denote this state as the reference configuration (Fig. 2). The surface, however, is not stress-free, as is accounted for in our definition of the surface energy eqn (6). While the second state, Ω0, is the one experimentalists work with, we consider it as an intermediate state because it can contain finite residual bulk stresses due to prior surface relaxation. We note, however, that these two states coincide when the surface does not undergo prior relaxation, which happens when the soft solid is tested in the state it was prepared.
In the framework of finite kinematics, the deformation gradient Fs maps material points from the stress-free configuration Ω* to the deformed configuration Ω. We also have  mapping from the stress-free configuration Ω* to the relaxed configuration Ω0, and F0s = I + ∇su0 mapping from the relaxed configuration Ω0 to the deformed configuration Ω. By composition of mappings, the total deformation follows as
mapping from the stress-free configuration Ω* to the relaxed configuration Ω0, and F0s = I + ∇su0 mapping from the relaxed configuration Ω0 to the deformed configuration Ω. By composition of mappings, the total deformation follows as  .
.
In practice, experiments impose deformations E0s from the relaxed state Ω0 to the deformed state Ω. Here, we focus on the case where imposed deformations are small, for which E0s ∼ ε0s. We then elucidate how the measured stresses vary with imposed surface strain ε0s = [∇su0 + (∇su0)T]/2, both when the relaxation deformation  is infinitesimal and finite.
is infinitesimal and finite.
B. Linearized kinematics
Let us assume the deformation due to the relaxation of the surface is small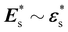 . Then, the resultant total strain is an additive decomposition
. Then, the resultant total strain is an additive decomposition 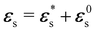 .
.
After linearization, stress measures are usually assumed to coincide. This assumption, however, fails whenever initial stresses are present,29 as in the case of solid surfaces. We thus need to carefully distinguish different stress measures in the realm of linearized kinematics.
At first order in strains εs, the linearized Cauchy stress ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) s simplifies to the Hookean form
s simplifies to the Hookean form
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) s = γI+ 2μsεs + λstr(εs)I. s = γI+ 2μsεs + λstr(εs)I. | (11) |
Based on the additive decomposition of strains, Cauchy stresses result in a contribution from the surface relaxation 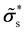 and a contribution from the imposed deformations
and a contribution from the imposed deformations ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0s
0s
 | (12) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10d.gif) αs= 2μsεαs + λstr(εαs)I, with α ∈ [*,0]. Unsurprisingly, the surface relaxation here comes as an additive stress, as in the classical principle of superposition in linear elasticity. In this context, the prior surface relaxation does not influence the estimation of the surface elastic moduli μs and λs from applied strains ε0s.
αs= 2μsεαs + λstr(εαs)I, with α ∈ [*,0]. Unsurprisingly, the surface relaxation here comes as an additive stress, as in the classical principle of superposition in linear elasticity. In this context, the prior surface relaxation does not influence the estimation of the surface elastic moduli μs and λs from applied strains ε0s.
Similarly, the second Piola–Kirchhoff stress takes the form
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) s = γI+ 2μIIsεs + λIIstr(εs)I, s = γI+ 2μIIsεs + λIIstr(εs)I, | (13) |
![[P with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0050_0303.gif) s = γI+ 2μIsεs + λIstr(εs)I + γωs, s = γI+ 2μIsεs + λIstr(εs)I + γωs, | (14) |
with μIs = μs − γ/2, λIs = λIIs, and ωs = (∇su − ∇suT)/2 the infinitesimal rotation tensor (see Section S3, ESI†). Both the first and second Piola–Kirchhoff stress measures can also be decomposed akin to the Cauchy stress eqn (12).
From eqn (11)–(14), we note that the three linearized stress measures are only equal in two scenarios. First, when the solid is unstretched εs = 0. All stress measures are then trivially equal to the prestress γI, which is the surface stress of the solid at rest. Second, when the prestress is much smaller than the surface elastic constants γ β (μs,λs). In this case, which primarily pertains to hard solids, all stress measures are equal to the Hookean form eqn (11).
Besides these cases, when the surface moduli is of the order of the surface tension at rest or smaller, we should distinguish the different linearized stress measures. Otherwise, the surface shear modulus μs can be misestimated by a value of the order of the surface tension γ, eqn (13) and (14). This applies to soft solids and complex fluid–fluid interfaces, for which surface tension and surface elasticity can be of the same magnitude.15,17,34
C. Finite kinematics
If the surface relaxation induces large deformations, we expand to linear order in ∇u0 the imposed deformations and keep the relaxation deformations F* finite. At first order, we write the dependence of Cauchy stress with imposed deformations | (15) |
 is the stress contribution due to surface relaxation (see Section S3, ESI†). Here, not only does the relaxation impose an additional stress term
is the stress contribution due to surface relaxation (see Section S3, ESI†). Here, not only does the relaxation impose an additional stress term  , but it also mixes non-trivially into the terms that include the surface elastic parameters (λs,μs). In practice, the exact contribution from the finite surface relaxation depends on the sample geometry and has to be estimated accordingly. For the sake of completeness, we estimate the strain dependence of the Second Piola–Kirchhoff stress as
, but it also mixes non-trivially into the terms that include the surface elastic parameters (λs,μs). In practice, the exact contribution from the finite surface relaxation depends on the sample geometry and has to be estimated accordingly. For the sake of completeness, we estimate the strain dependence of the Second Piola–Kirchhoff stress as | (16) |
Finally, the First Piola–Kirchhoff stress tensor follows as
 | (17) |
 is the Second Piola–Kirchhoff stress contributions to surface relaxation. Although the expressions (15)–(17) are cumbersome, they do not coincide even in the case of no imposed deformations ε0s = 0.
is the Second Piola–Kirchhoff stress contributions to surface relaxation. Although the expressions (15)–(17) are cumbersome, they do not coincide even in the case of no imposed deformations ε0s = 0.
Overall, whether the surface relaxation induces small or finite deformations, the different stress measures differ from each other. While we can extract effective surface elastic coefficients in the case of infinitesimal surface relaxation, eqn (11)–(14), accounting for finite relaxation prevents having a simple constitutive equation between stresses and imposed deformation ε0s, eqn (15)–(17). Still, we approximate from the full expression for the Cauchy stress eqn (15) that, at first order in relaxation strain  , the surface moduli (μs,λs) will be misestimated by a factor (1 + 4
, the surface moduli (μs,λs) will be misestimated by a factor (1 + 4 ). Although this suggests that one cannot neglect prior surface relaxations as soon as they reach a few percent, being more precise requires investigating specific test cases.
). Although this suggests that one cannot neglect prior surface relaxations as soon as they reach a few percent, being more precise requires investigating specific test cases.
4 Test cases
Let us examine how an incompressible soft solid of bulk shear modulus μ, surface tension γ, and surface elastic material moduli (μs,λs) responds in two canonical examples (Fig. 4a and b). For both examples, we compute scaling factors to highlight the magnitude by which surface moduli deviate from linear elastic predictions with increasing initial relaxation strain. | ||
| Fig. 4 (a) Surface profile of periodic grooves of wavelength w. Left: initial profile, with amplitude a0. Right: after relaxation, with amplitude a1, estimated for a material of shear modulus μ = 2 kPa, surface tension γ = 20 mN m−1, wavelength w = 50 μm and initial amplitude a0 = 2 μm. (b) Cylindrical rod before (left) and after relaxation (right). (c) Deviation factors P and L, quantifying the effect of surface relaxation on estimated surface modulus (eqn (18) and (21)). (d) Contour plot for the surface relaxation axial strain εs‖ as a function of shear modulus and cylinder radius, computed from eqn (20) with surface tension γ = 20 mN m−1. The black dashed line represents stands for R = Lec. | ||
First, we consider a soft solid cured into a mold with periodic rectangular grooves of wavelength w and initial amplitude a0. For simplicity, we assume that the solid is much thicker than the pattern wavelength, akin to the experimental system in ref. 15. After demolding, the surface topography relaxes to a nearly sinusoidal wave with final amplitude a1 ∼ a0/(1 + |q|Lec), where q = 2π/w is the pattern wavevector and Lec = γ/2μ is the elastocapillary length7,13,15 (Fig. 4a). During this process, one period of the surface goes from its initial length l0 = w + 2a0 to a final length l1 ∼ w + 2a1. We define the surface relaxation strain 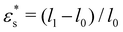 from the difference in surface length before and after demolding.
from the difference in surface length before and after demolding.
With no loss of generality, we assume that the surface relaxation strains are tangential to the surface profile  , without shear, and that we impose an external deformation that manifests as a longitudinal strain
, without shear, and that we impose an external deformation that manifests as a longitudinal strain  and no transverse applied strain
and no transverse applied strain  . The longitudinal Cauchy stress,
. The longitudinal Cauchy stress,
 | (18) |
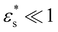 , we recover the surface modulus (2μs + λs) that can be calculated from the fully linear Cauchy stress eqn (11). Otherwise, the estimated surface modulus deviates from the true modulus by a factor
, we recover the surface modulus (2μs + λs) that can be calculated from the fully linear Cauchy stress eqn (11). Otherwise, the estimated surface modulus deviates from the true modulus by a factor 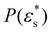 . This deviation factor increases when the relaxation places the surface in tension,
. This deviation factor increases when the relaxation places the surface in tension,  , and decreases when the surface is in compression
, and decreases when the surface is in compression  (Fig. 4c). In the experimental conditions of ref. 15 (recalled in the legend of Fig. 4a), we estimate the relaxation strain to be
(Fig. 4c). In the experimental conditions of ref. 15 (recalled in the legend of Fig. 4a), we estimate the relaxation strain to be  and the resulting correction factor P(−0.05) = 0.7. Therefore, accounting for the surface relaxation, as done in ref. 15 with nonlinear theories, avoided a 30% underestimation of the surface elastic moduli.
and the resulting correction factor P(−0.05) = 0.7. Therefore, accounting for the surface relaxation, as done in ref. 15 with nonlinear theories, avoided a 30% underestimation of the surface elastic moduli.
Second, we assume the soft solid is cured into a slender cylindrical mold of length L and radius R, with L ≫ R.35 Once removed from the mold, the length and radius change to l and r, respectively (Fig. 4b). At first order, this relaxation follows the uniform deformation field
 | (19) |
In this framework, the stretch created by the surface relaxation that minimizes the total elastic energy,
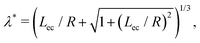 | (20) |
 and the circumferential strain
and the circumferential strain  . From eqn (20), surface strains are infinitesimal when the elastocapillary length is much smaller than the cylinder radius, Lec β R, where bulk elasticity dominates.
. From eqn (20), surface strains are infinitesimal when the elastocapillary length is much smaller than the cylinder radius, Lec β R, where bulk elasticity dominates.
Otherwise, the relaxation-induced deformations are finite (Fig. 4d). If we assume they have no shear component and impose a longitudinal deformation that results in small surface strains  , the longitudinal Cauchy stress
, the longitudinal Cauchy stress
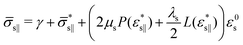 | (21) |
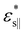 through
through  and the polynomial function L(ε) = (1 + ε)(1 + 8ε + 12ε2 + 4ε3) (see Section S4, ESI†). We recover the correct surface modulus (2μs + λs/2) calculated from eqn (11) in the case of infinitesimal surface relaxation and increasing deviation factors when surface relaxation is finite (Fig. 4c). While the bulk material properties may behave linearly up to large deformations,15 surface elastic constants scale by a factor of 2 in the case of prior surface relaxation on the order of ±10% (Fig. 4c).
and the polynomial function L(ε) = (1 + ε)(1 + 8ε + 12ε2 + 4ε3) (see Section S4, ESI†). We recover the correct surface modulus (2μs + λs/2) calculated from eqn (11) in the case of infinitesimal surface relaxation and increasing deviation factors when surface relaxation is finite (Fig. 4c). While the bulk material properties may behave linearly up to large deformations,15 surface elastic constants scale by a factor of 2 in the case of prior surface relaxation on the order of ±10% (Fig. 4c).
5 Conclusions
In this work, we derive the different surface stress–strain relations for a soft solid with and without prior surface relaxations in the regime of finite deformations. We show that the Shuttleworth equation is only valid for the Cauchy stress without prior relaxations. It does not apply to other stress measures, and prior relaxations result in deviation factors that lead to misestimating the surface elastic properties.This has direct implications for the determination of surface elastic constants. First, experimentalists need to assess if the way the solid reached its rest state results in surface relaxations, and if so estimate their amplitude. Second, they have to evaluate which stress measure is the most relevant depending on how measurements are done. This calls for a careful notion of which configuration forces and areas are measured. If forces are measured in the deformed state and areas in the rest state configuration, the first Piola stress measure should be considered, whereas the Cauchy stress should be used when the areas are also measured in the deformed state. Different constitutive relations need to be employed depending on the stress measure, and the measured elastic moduli will depend on the used stress measure even without prior surface relaxation.
As more experimental work is required to determine under which conditions a soft solid has an elastic surface, our results provide a robust framework to interpret measurements of surface elastic constants from different stress measures, whether the surface has or hasn't relaxed during the fabrication process.
Author contributions
N. B. and S. H. contributed equally to the development of the theory and the writing of the manuscript. N. B. performed the experimental measurements and data analysis of surface deformations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. H. gratefully acknowledges funding via the SNF Ambizione grant PZ00P2186041. The authors thank Eric R. Dufresne for useful discussions and suggestions.Notes and references
- R. Style, A. Jagota, C.-Y. Hui and E. Dufresne, Ann. Rev. Cond. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
- R. W. Style, R. Boltyanskiy, Y. Che, J. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 066103 CrossRef PubMed.
- C.-Y. Hui and A. Jagota, Proc. R. Soc. A, 2014, 470, 0085 CrossRef.
- K. Smith-Mannschott, Q. Xu, S. Heyden, N. Bain, J. H. Snoeijer, E. R. Dufresne and R. W. Style, Phys. Rev. Lett., 2021, 126, 158004 CrossRef CAS PubMed.
- R. D. Schulman, M. Trejo, T. Salez, E. Raphaël and K. Dalnoki-Veress, Nat. Commun., 2018, 9, 1–6 CrossRef CAS PubMed.
- C.-Y. Hui, Z. Liu, N. Bain, A. Jagota, E. R. Dufresne, R. W. Style, R. Kiyama and J. P. Gong, Proc. R. Soc. A, 2020, 476, 20200477 CrossRef PubMed.
- R. W. Style, C. Hyland, R. Boltyanskiy, J. S. Wettlaufer and E. R. Dufresne, Nat. Commun., 2013, 4, 1–6 Search PubMed.
- K. E. Jensen, R. Sarfati, R. W. Style, R. Boltyanskiy, A. Chakrabarti, M. K. Chaudhury and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14490–14494 CrossRef CAS PubMed.
- M. Grzelka, J. B. Bostwick and K. E. Daniels, Soft Matter, 2017, 13, 2962–2966 RSC.
- R. W. Style, R. Boltyanskiy, B. Allen, K. E. Jensen, H. P. Foote, J. S. Wettlaufer and E. R. Dufresne, Nat. Phys., 2015, 11, 82–87 Search PubMed.
- Q. Xu, R. W. Style and E. R. Dufresne, Soft Matter, 2018, 14, 916–920 RSC.
- A. Jagota, D. Paretkar and A. Ghatak, Phys. Rev. E, 2012, 85, 051602 CrossRef PubMed.
- Q. Xu, K. E. Jensen, R. Boltyanskiy, R. Sarfati, R. W. Style and E. R. Dufresne, Nat. Commun., 2017, 8, 1–6 CrossRef PubMed.
- N. Bain, A. Jagota, K. Smith-Mannschott, S. Heyden, R. W. Style and E. R. Dufresne, Phys. Rev. Lett., 2021, 127, 208001 CrossRef CAS PubMed.
- S. Heyden, N. Bain, Q. Xu, R. W. Style and E. R. Dufresne, Proc. R. Soc. A, 2021, 477, 20200673 CrossRef.
- S. Heyden, P. M. Vlahovska and E. R. Dufresne, J. Mech. Phys. Solids, 2022, 161, 104786 CrossRef.
- A. Carbonaro, K.-N. Chagua-Encarnacion, C.-A. Charles, T. Phou, C. Ligoure, S. Mora and D. Truzzolillo, Soft Matter, 2020, 16, 8412–8421 RSC.
- R. Shuttleworth, Proc. Phys. Soc., London, Sect. A, 1950, 63, 444 CrossRef.
- E. M. Gutman, Soft Matter, 2022, 18, 4638–4640 RSC.
- N. Bain, S. Heyden, Q. Xu, R. W. Style and E. R. Dufresne, Soft Matter, 2022, 18, 4641–4642 RSC.
- A. Pandey, B. Andreotti, S. Karpitschka, G. J. van Zwieten, E. H. van Brummelen and J. H. Snoeijer, Phys. Rev. X, 2020, 10, 031067 CAS.
- R. Masurel, M. Roché, L. Limat, I. Ionescu and J. Dervaux, Phys. Rev. Lett., 2019, 122, 248004 CrossRef CAS PubMed.
- S. Mora, C. Maurini, T. Phou, J.-M. Fromental, B. Audoly and Y. Pomeau, Phys. Rev. Lett., 2013, 111, 114301 CrossRef PubMed.
- M. Gurtin and A. Murdoch, Arch. Ration. Mech. Anal., 1975, 57, 291–323 CrossRef.
- M. Gurtin, J. Weissmueller and F. Larché, Philos. Mag. A, 1998, 78, 1093–1109 CAS.
- D. J. Steigmann and R. Ogden, Proc. R. Soc. London, Ser. A, 1999, 455, 437–474 CrossRef.
- Z. Huang and J. Wang, Micromechanics of Nanocomposites with Interface Energy Effect, 2007, pp. 51–59 Search PubMed.
- S. Krichen, L. Liu and P. Sharma, J. Mech. Phys. Solids, 2019, 127, 332–357 CrossRef.
- K. Mozaffari, S. Yang and P. Sharma, Surface Energy and Nanoscale Mechanics, Springer International Publishing, 2020, pp. 1949–1974 Search PubMed.
- H. Wu, Z. Liu, A. Jagota and C.-Y. Hui, Soft Matter, 2018, 14, 1847–1855 RSC.
- Z. Liu, A. Jagota and C.-Y. Hui, Soft Matter, 2020, 16, 6875–6889 RSC.
- L. Anand and S. Govindjee, Continuum mechanics of solids, Oxford University Press, 2020 Search PubMed.
- G. G. Fuller and J. Vermant, Ann. Rev. Chem. Biomol. Eng., 2012, 3, 519–543 CrossRef CAS PubMed.
- M. Zafar and S. Basu, Phys. Rev. E, 2021, 103, 063003 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00078a |
| ‡ Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |


