Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Collective behavior of squirmers in thin films†
Bohan
Wu-Zhang
 ,
Dmitry A.
Fedosov
,
Dmitry A.
Fedosov
 and
Gerhard
Gompper
and
Gerhard
Gompper

Theoretical Physics of Living Matter, Institute of Biological Information Processing and Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: b.zhang@fz-juelich.de; d.fedosov@fz-juelich.de; g.gompper@fz-juelich.de
First published on 12th April 2024
Abstract
Bacteria in biofilms form complex structures and can collectively migrate within mobile aggregates, which is referred to as swarming. This behavior is influenced by a combination of various factors, including morphological characteristics and propulsive forces of swimmers, their volume fraction within a confined environment, and hydrodynamic and steric interactions between them. In our study, we employ the squirmer model for microswimmers and the dissipative particle dynamics method for fluid modeling to investigate the collective motion of swimmers in thin films. The film thickness permits a free orientation of non-spherical squirmers, but constraints them to form a two-layered structure at maximum. Structural and dynamic properties of squirmer suspensions confined within the slit are analyzed for different volume fractions of swimmers, motility types (e.g., pusher, neutral squirmer, puller), and the presence of a rotlet dipolar flow field, which mimics the counter-rotating flow generated by flagellated bacteria. Different states are characterized, including a gas-like phase, swarming, and motility-induced phase separation, as a function of increasing volume fraction. Our study highlights the importance of an anisotropic swimmer shape, hydrodynamic interactions between squirmers, and their interaction with the walls for the emergence of different collective behaviors. Interestingly, the formation of collective structures may not be symmetric with respect to the two walls. Furthermore, the presence of a rotlet dipole significantly mitigates differences in the collective behavior between various swimmer types. These results contribute to a better understanding of the formation of bacterial biofilms and the emergence of collective states in confined active matter.
1 Introduction
Collective motion of microswimmers is a popular topic in the field of active matter due to its wide applicability in the context of both biological and artificial systems as well as the richness of observed behaviors and physical mechanisms.1–3 A prominent example of the collective behavior of biological microswimmers is biofilms, which represent complex dynamic communities of microorganisms at surfaces.4,5 Biofilms are often associated with various infectious diseases, such as dental plaque formation on teeth6 and chronic wounds that resist healing,7 driving the research to better understand surface colonization by bacteria and biofilm development.5,8 In the context of artificial microswimmers, there exist a variety of active systems, including collectives of diffusiophoretic and thermophoretic Janus particles,9–11 active droplets,12,13 and Quincke rollers.14 Studies with artificial microswimmers primarily focus on understanding the emergence of collective motion and the governing physical mechanisms.1–3One of the prominent examples of collective behavior is motility-induced phase separation (MIPS), which can occur without any attractive or alignment interactions between self-propelled particles.15–19 MIPS are characterized by the co-existence of low and high density phases of active particles, where the latter is generally represented by nearly immobile large clusters of particles.9,10,20 In the initial stage of biofilm formation, a collective motility of bacteria known as swarming is frequently observed.5,21 In contrast to MIPS clusters, bacterial swarms are stable and highly mobile aggregates, which generally migrate along surfaces. The formation of swarms often requires some type of alignment interactions between microswimmers.22,23 Another collective phenomenon observed for bacterial suspensions is called active turbulence,24–26 which is similar to the traditional Kolmogorov–Kraichnan-type hydrodynamic turbulence,27 but occurs at very low Reynolds numbers. The state of active turbulence is observed for a sufficiently large density of microswimmers, which each generates a force-dipolar flow field around it.28–31 Finally, the motion of microswimmers in confinement, such as in channels and pores, can result in a hydrodynamic instability and the formation of complex flow patterns.24,32,33
Different properties of microswimmers and their environment affect the emerging collective behavior. These include shape anisotropy,34–36 the generated flow field around a swimmer,31,37,38 hydrodynamic interactions,38–40 the presence of confinement,32,41 and dimensionality.12,42 Biological microswimmers (e.g., bacteria) have complex geometries and propulsion mechanisms, such that their detailed modeling is computationally challenging, especially in systems with a large number of swimmers. One of the popular models of simplified swimmers is the squirmer model,43,44 which represents a microswimmer by a spherically- or spheroidally-shaped active particle with a prescribed slip velocity at its surface.45 Despite its simplicity, the squirmer model is flexible enough to capture various swimming modes, including pushers (e.g., E. coli), neutral microswimmers (e.g., Paramecium), and pullers (e.g., Chlamydomonas). In particular, the squirmer model mimics well both the far- and near-field flow of a variety of realistic microswimmers.
The squirmer model has been used to study collective behavior of microswimmers in quasi two-dimensional (2D) systems (i.e., a monolayer of swimmers)31,38,39,41,46–49 and three-dimensional (3D) settings with periodic boundary conditions (BCs).37,50–53 In quasi-2D systems, the positions of spherical squirmers are restricted to a monolayer, while their orientation can still cover a large range of angles in 3D, depending on their aspect ratio.38,41,49 As a result, the in-plane velocity of squirmers is not constant, but has a wide distribution. Nevertheless, these systems show MIPS at large enough concentrations of squirmers, which is qualitatively consistent with quasi-2D simulations where the squirmer orientation is restricted to a plane.46–48 The presence of hydrodynamic interactions shifts the binodal curve for MIPS to larger Péclet numbers (characterizes the propulsion strength of swimmers) in comparison with active Brownian particles (ABPs).38,40 This means that for a fixed Péclet number, as the swimmer volume fraction ϕ is increased, the transition to MIPS for ABPs takes place at lower ϕ than that transition for swimmers with hydrodynamics. Pullers show the onset of MIPS at lower ϕ values in comparison to pushers. For spheroidal squirmers in quasi-2D systems,31,38 the collective behavior is qualitatively similar to spherical squirmers, but a larger aspect ratio of the spheroidal body favors cluster formation, leading to shape-induced jamming and alignment. The alignment interaction due to the anisotropy of spheroidal shape can lead to swarming behavior at moderate ϕ values. For the 3D systems with periodic BCs,37,50–53 the MIPS phase also develops at large volume fractions of squirmers.
In our study, we investigate the collective behavior of spheroidal squirmers in thin films that are thick enough to allow a full freedom of squirmer orientation. However, the squirmers are still restricted in their vertical position, so that they can form only a two-layered structure. Thus, we address some aspects of biofilm formation beyond the monolayer structure, when the development of further bacterial layers takes place. In particular, we address the following questions:
• Do swimmers within a thin film primarily assume orientations parallel or perpendicular to the wall?
• Under which conditions can swimmers spontaneously leave the wall to form multi-layered structures?
• Does the collective behavior of squirmers in thin films differ qualitatively from that of quasi-2D systems?
In our simulations, the volume fraction of squirmers, their swimming mode, and the strength λ of rotlet dipole, which mimics a counter-rotating flow field of swimmers whose body and flagella bundle rotate in opposite directions, are varied. In agreement with the quasi-2D systems, pullers display MIPS phase at lower ϕ values in comparison with pushers and neutral swimmers. At moderate volume fractions, all squirmers with rotlet dipole and pushers with λ = 0 show swarming behavior. Pullers prefer a nearly perpendicular orientation to the wall, which leads to the formation of flower-like structures at low ϕ and provides the nucleation for larger clusters as ϕ is increased. Pullers rarely switch between the two walls, while pushers do so frequently, indicating that a collection of pushers would quickly develop a multi-layered structure. In all investigated cases, a two-layered structure is dominant with the orientation of squirmers parallel to the walls. Interestingly, the presence of rotlet dipole significantly reduces differences in the collective behavior of squirmers with different swimming modes. These results provide the first steps in bridging very confined quasi-2D systems with much less confined situations of the collective behavior of swimmers in 3D.
The paper is organized as follows. Section 2 contains all necessary details about the employed methods and models, including parameters used in simulations. In Section 3.1, structural properties of squirmer suspensions are analyzed, including cluster size distribution, position and orientation of squirmers within the slit, and the radial distribution function. Dynamic properties are characterized in Section 3.2, where effective rotational diffusion, mean-squared displacement, and the average speed of squirmers are presented. The main results are discussed in Section 4, with short conclusions.
2 Methods and models
2.1 Squirmer model
We consider a spheroidal squirmer model, whose surface is described by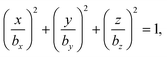 | (1) |
Locomotion of a spheroidal squirmer is imposed through the prescribed surface slip velocity given by38,57–59
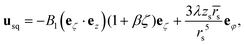 | (2) |
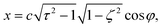 | (3) |
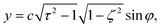 | (4) |
| z = cτζ. | (5) |
Here, 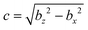 , and the spheroidal coordinates have the ranges −1 ≤ ζ ≤ 1, 1 ≤ τ < ∞ and 0 ≤ φ < 2π. The parameter B1 determines self-propulsion speed of the squirmer U0 = B1τ0(τ0 − (τ02 − 1)coth−1τ0) with τ0 = bz/c.45,60 The coefficient β defines different swimming modes of the squirmer, including a pusher (β < 0), a neutral swimmer (β = 0), and a puller (β > 0). The second term in eqn (2) defines a rotlet dipole with the strength λ, where rs = (xs,ys,zs), rs = |rs|,
, and the spheroidal coordinates have the ranges −1 ≤ ζ ≤ 1, 1 ≤ τ < ∞ and 0 ≤ φ < 2π. The parameter B1 determines self-propulsion speed of the squirmer U0 = B1τ0(τ0 − (τ02 − 1)coth−1τ0) with τ0 = bz/c.45,60 The coefficient β defines different swimming modes of the squirmer, including a pusher (β < 0), a neutral swimmer (β = 0), and a puller (β > 0). The second term in eqn (2) defines a rotlet dipole with the strength λ, where rs = (xs,ys,zs), rs = |rs|, 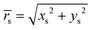 with the subscript s denoting points at the squirmer surface. The rotlet dipole mimics a counter-rotating flow field, e.g. of E. coli whose body and flagella bundle rotate in opposite directions.61 To verify the correctness of squirmer-model implementation, the flow field generated by a squirmer has been compared with the corresponding analytical solution,45 yielding good agreement.
with the subscript s denoting points at the squirmer surface. The rotlet dipole mimics a counter-rotating flow field, e.g. of E. coli whose body and flagella bundle rotate in opposite directions.61 To verify the correctness of squirmer-model implementation, the flow field generated by a squirmer has been compared with the corresponding analytical solution,45 yielding good agreement.
2.2 Boundary conditions
The suspension of squirmers is confined between two walls in the h direction, while periodic BCs are applied along the other two perpendicular-to-h directions. Fluid flow is modeled by the dissipative particle dynamics (DPD) method,62,63 which is a particle-based hydrodynamics simulation technique (see Appendix B for details). Solid walls are represented by frozen DPD particles within a layer of thickness rc (the cutoff radius for DPD interactions) with the same number density as that for the DPD fluid. To prevent wall penetration by fluid particles, a reflective surface is placed at the fluid–solid interface, where bounce-back reflection of fluid particles is enforced. No-slip BCs at the walls are imposed by the dissipative interaction between fluid and frozen-wall particles, and through the bounce-back reflection at the interface.To restrict the motion of squirmers between the two walls, particles within the squirmer discretization are subject to the repulsive Lennard-Jones (LJ) potential
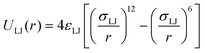 | (6) |
Squirmers are submerged within a DPD fluid, and also filled by DPD fluid particles due to their membrane-like representation. The membrane surfaces of all suspended squirmers serve as a boundary separating DPD particles inside and outside of the membranes. This is achieved through the reflection of fluid particles at the membrane surfaces from inside and outside. Note that the dissipative and random forces between the internal and external fluid particles are deactivated, and only the conservative force is employed to maintain uniform fluid pressure across the membranes. To enforce the slip velocity usq at the squirmer surface, the dissipative interaction (see Appendix B) between the squirmer particles and those of the surrounding fluid is altered as follows
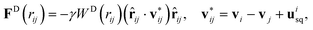 | (7) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij, rij = |ri − rj|, uisq is the slip velocity at the position of squirmer particle i, while j corresponds to an outer-fluid DPD particle. Furthermore, the friction coefficient γ between fluid and squirmer particles is properly adjusted55 to ensure the imposition of usq at the squirmer surface.
ij = (ri − rj)/rij, rij = |ri − rj|, uisq is the slip velocity at the position of squirmer particle i, while j corresponds to an outer-fluid DPD particle. Furthermore, the friction coefficient γ between fluid and squirmer particles is properly adjusted55 to ensure the imposition of usq at the squirmer surface.
2.3 Simulation setup and parameters
The simulation setup corresponds to a domain of dimensions L × H × L, where L = 28bz and H = 2.5bz (bz = 4 in simulations), see Fig. 1(b). The number density of fluid particles is nf = 320/b3z, with a particle mass m = 1. The energy unit is kBT = 1. Parameters selected for the DPD fluid (see Appendix B) yield a fluid dynamic viscosity of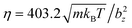 .
.
Each squirmer in simulations consists of Np = 1024 particles. Excluded-volume interactions between different squirmers and between squirmers and the walls are implemented through the LJ potential with parameters εLJ = kBT and σLJ = 0.125bz. The computed three-dimensional rotational diffusion coefficient around the major axis of a spheroid without confinement is 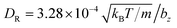 , which is close to the theoretical prediction of
, which is close to the theoretical prediction of 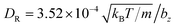 .45 To present simulation results, the half length bz of the semi-major axis is chosen as a length scale, and the characteristic rotational time τR = 1/DR as a time scale. In all simulations, the activity parameter B1 is fixed at 56.8bzDR. We have verified that the swimming velocity of a single squirmer is U0 = 45.5bzDR, in agreement with the theoretical prediction.45 Using these values, we can define a dimensionless Péclet number Pe = U0/(2bzDR) ≈ 28.4. Furthermore, the Reynolds number Re = 2bzU0mnf/η ≈ 0.03 is small enough to eliminate possible inertial effects.
.45 To present simulation results, the half length bz of the semi-major axis is chosen as a length scale, and the characteristic rotational time τR = 1/DR as a time scale. In all simulations, the activity parameter B1 is fixed at 56.8bzDR. We have verified that the swimming velocity of a single squirmer is U0 = 45.5bzDR, in agreement with the theoretical prediction.45 Using these values, we can define a dimensionless Péclet number Pe = U0/(2bzDR) ≈ 28.4. Furthermore, the Reynolds number Re = 2bzU0mnf/η ≈ 0.03 is small enough to eliminate possible inertial effects.
Different volume fractions ϕ = 4Nsqπbxbybz/(3L2H) ∈ {0.18,0.35,0.44,0.56} are considered, corresponding to different numbers of squirmers Nsq ∈ {228,456,576,720}. The three values of active stress β ∈ {−5,0,5} represent simulation systems with pusher, neutral, and puller swimmers, respectively. Finally, we also consider two values of the non-dimensional rotlet dipole strength ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = λ/(b4zDR) ∈ {0,133.5}. For
= λ/(b4zDR) ∈ {0,133.5}. For ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5, a single squirmer moves in a circular trajectory at a wall with a radius of approximately 2bz. For comparison, the rotlet dipole strength of
= 133.5, a single squirmer moves in a circular trajectory at a wall with a radius of approximately 2bz. For comparison, the rotlet dipole strength of ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ∈ {0,561.1} has been used in ref. 31 where squirmers were confined to a single layer. All simulations are first run for a time of at least 1.5τR to reach a steady state, and afterwards various structural and dynamical characteristics of the system are measured during the time 1.5τR.
∈ {0,561.1} has been used in ref. 31 where squirmers were confined to a single layer. All simulations are first run for a time of at least 1.5τR to reach a steady state, and afterwards various structural and dynamical characteristics of the system are measured during the time 1.5τR.
2.4 Mapping to experimental systems
Squirmer parameters used in simulations can also be mapped to the properties of real swimmers. In the far-field approximation, the hydrodynamic field of a microswimmer is dominated by its force-dipole strength χ = fdld/(8πη),64–66 where fd and ld are the characteristic force and length of the dipole. The active stress β of a spheroidal squirmer can be expressed as45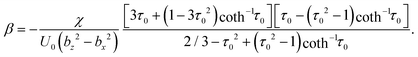 | (8) |
Average properties of E. coli bacteria swimming in water correspond to U0 = 29 μm s−1, fd = 0.42 pN, ld = 1.9 μm, bz = 1.5 μm, bx = 0.5 μm, and η = 10−3 Pa s,54,61,65 resulting in β ≈ −3. Note that a direct comparison is possible only in the far-field limit, while the near-field flow of each swimmer depends on its geometric and propulsion details.
3 Results
In our investigation, we analyze the collective structural and dynamical properties of swimmer ensembles in thin fluid films as a function of volume fraction ϕ and squirmer characteristics of active stress β and rotlet dipole strength![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) . Snapshots of the emergent structures are displayed in Fig. 2. We characterize these phases through the analysis of cluster sizes and radial distribution functions of the squirmers. Furthermore, the distribution of squirmers along the h-direction (perpendicular to the walls) and their orientation are considered to distinguish a two-layered arrangement with an average orientation within the x–z plane from the stacked packing with the orientation perpendicular to the walls. Finally, dynamical properties, such as velocity distribution, and effective rotational and translational diffusivities, are computed to characterize squirmer motility within collective states.
. Snapshots of the emergent structures are displayed in Fig. 2. We characterize these phases through the analysis of cluster sizes and radial distribution functions of the squirmers. Furthermore, the distribution of squirmers along the h-direction (perpendicular to the walls) and their orientation are considered to distinguish a two-layered arrangement with an average orientation within the x–z plane from the stacked packing with the orientation perpendicular to the walls. Finally, dynamical properties, such as velocity distribution, and effective rotational and translational diffusivities, are computed to characterize squirmer motility within collective states.
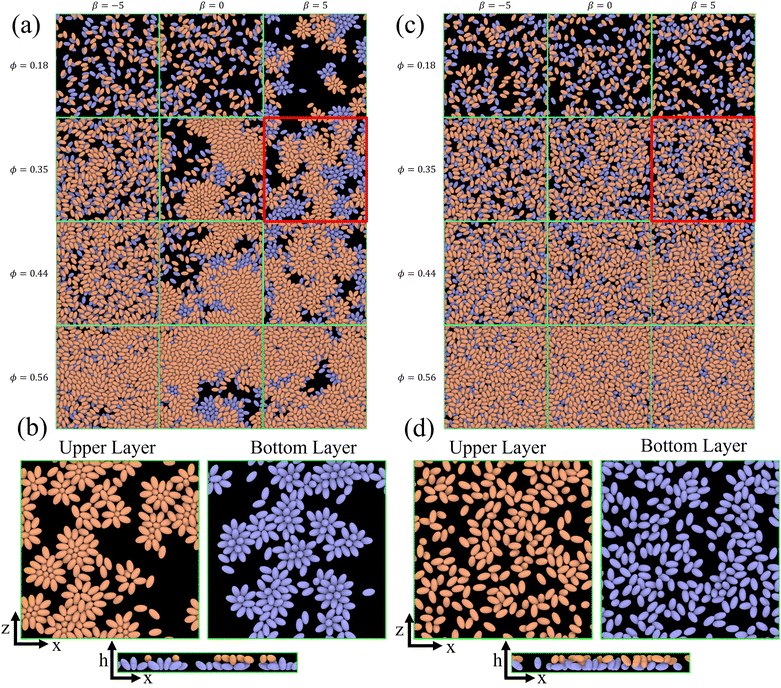 | ||
Fig. 2 Snapshots of the emergent structures for different active stresses β, volume fractions ϕ, and rotlet dipole strengths ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) . (a) Simulated structures for . (a) Simulated structures for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, ϕ = 0.18 and 0.35, and β ∈ {0, ±5}. Squirmers in the upper (bottom) half of the slit are colored in orange (blue). See also corresponding Movies S1–S6 (ESI†). (b) Squirmer structures within the upper and bottom layers of the simulated system for ϕ = 0.35, β = 5, and = 0, ϕ = 0.18 and 0.35, and β ∈ {0, ±5}. Squirmers in the upper (bottom) half of the slit are colored in orange (blue). See also corresponding Movies S1–S6 (ESI†). (b) Squirmer structures within the upper and bottom layers of the simulated system for ϕ = 0.35, β = 5, and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. See also Movie S6 (ESI†). (c) Snapshots of the simulated systems for = 0. See also Movie S6 (ESI†). (c) Snapshots of the simulated systems for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5, ϕ = 0.35 and β ∈ {0, ±5}. See also Movies S7–S9 (ESI†). (d) Squirmer structures within the upper and bottom layers of the slit for ϕ = 0.35, β = 5, and = 133.5, ϕ = 0.35 and β ∈ {0, ±5}. See also Movies S7–S9 (ESI†). (d) Squirmer structures within the upper and bottom layers of the slit for ϕ = 0.35, β = 5, and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5. Squirmers belong to the upper (orange) or bottom (blue) layers, when the h-coordinate of their center of mass is in the upper or lower half of the slit, respectively. See also Movie S9 (ESI†). = 133.5. Squirmers belong to the upper (orange) or bottom (blue) layers, when the h-coordinate of their center of mass is in the upper or lower half of the slit, respectively. See also Movie S9 (ESI†). | ||
An important question for any two-layered structure is to which extent the two layers interact with and affect each other. The snapshots in Fig. 2 nicely demonstrate that the correlation between the two layers strongly depends on volume fraction and strength of the rotlet dipole. Without rotlet dipole, i.e. for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, the layer correlation is very weak for small ϕ, but becomes very significant for large ϕ, where the clusters in the top and bottom layers are essentially in registry. With strong rotlet dipole, i.e. for
= 0, the layer correlation is very weak for small ϕ, but becomes very significant for large ϕ, where the clusters in the top and bottom layers are essentially in registry. With strong rotlet dipole, i.e. for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5, the situation is very different, as there is hardly any visible correlation between the two layers.
= 133.5, the situation is very different, as there is hardly any visible correlation between the two layers.
Previous studies of structure formation of artificial and biological microswimmers in two- and three-dimensional systems1,2,31,67,68 report the existence of various phases, including
• A gas of small clusters, where the distribution of swimmers is homogeneous and dynamic clusters are formed by a few swimmers;
• Large clusters or motility-induced phase separation (MIPS), where the cluster size is often comparable with the size of the entire system; such large clusters are nearly immobile;
• Swarming and flocking, which is characterized by the collective locomotion of dense swimmer clusters with swirling and streaming patterns.
A similar behavior is found in our system (see Fig. 2); however, the possibility of the formation of two distinct layers at the walls gives rise to novel structures and dynamics.
3.1 Structural properties
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) is calculated as
(n) is calculated as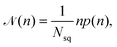 | (9) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) represents the fraction of squirmers belonging to clusters of size n, and p(n) denotes the number of clusters of size n. The distribution is normalized, such that
(n) represents the fraction of squirmers belonging to clusters of size n, and p(n) denotes the number of clusters of size n. The distribution is normalized, such that 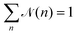 . Different squirmers belong to the same cluster when the nearest surface-to-surface distance ds between them satisfies ds/bz < 0.25. The average cluster size 〈n〉 is then:68
. Different squirmers belong to the same cluster when the nearest surface-to-surface distance ds between them satisfies ds/bz < 0.25. The average cluster size 〈n〉 is then:68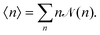 | (10) |
The cluster-size distribution is used to distinguish the different collective phases21,68 mentioned above. For the gas of small clusters, ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) exhibits an exponential decay, as shown in Fig. 3(a) for ϕ = 0.18. For MIPS or large clusters, a bimodal distribution of
(n) exhibits an exponential decay, as shown in Fig. 3(a) for ϕ = 0.18. For MIPS or large clusters, a bimodal distribution of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) is observed, with the second peak at large n signaling the presence of large clusters, see Fig. 3(b) and (c) for ϕ = 0.35 and ϕ = 0.56. Finally, swarming can be characterized by a power-law decay of
(n) is observed, with the second peak at large n signaling the presence of large clusters, see Fig. 3(b) and (c) for ϕ = 0.35 and ϕ = 0.56. Finally, swarming can be characterized by a power-law decay of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) with an exponential cutoff and without the presence of a distinct peak.31,47 This implies a slow decline of cluster sizes over a broad range, compared to the fast decay for a gas of small clusters.
(n) with an exponential cutoff and without the presence of a distinct peak.31,47 This implies a slow decline of cluster sizes over a broad range, compared to the fast decay for a gas of small clusters.
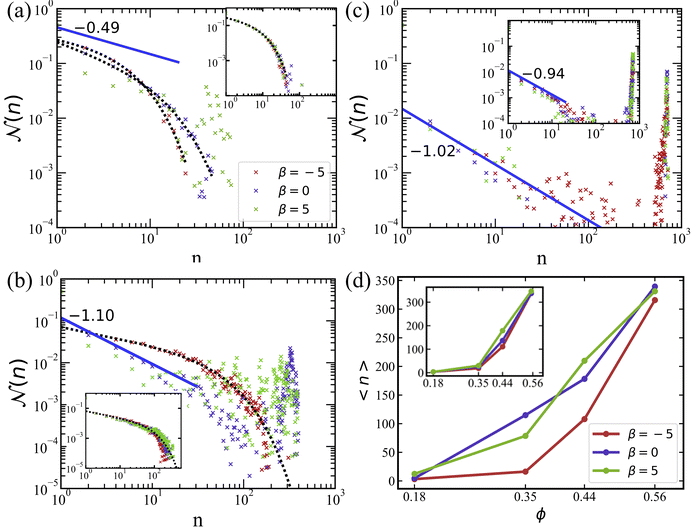 | ||
Fig. 3 Cluster size distributions for different volume fractions of squirmers. (a) ϕ = 0.18, (b) ϕ = 0.35, and (c) ϕ = 0.56. The curves with different colors represent various swimming modes: pusher with β = −5 (red), neutral with β = 0 (blue), and puller with β = 5 (green). The blue solid lines are the power-law fits, while the black-dotted lines are the fits using eqn (11) with the parameters shown in Table 1. (d) The average cluster size for various conditions as a function of volume fraction. The average cluster size is calculated using eqn (10). All plots are for the simulations without rotlet dipole (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0), while the insets show data from the corresponding simulations with = 0), while the insets show data from the corresponding simulations with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5. = 133.5. | ||
The described characteristics of different phases can be extracted by fitting ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) with the function47
(n) with the function47
f(x) = Ax−γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp−x/α, exp−x/α, | (11) |
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = λ/(bz4DR). A “—” sign in the α-column indicates that the exponential term in eqn (11) is omitted, so that the fitting function becomes f(x) = Ax−γ. The last column provides the classification of different simulation cases into the defined phases
= λ/(bz4DR). A “—” sign in the α-column indicates that the exponential term in eqn (11) is omitted, so that the fitting function becomes f(x) = Ax−γ. The last column provides the classification of different simulation cases into the defined phases
| ϕ | β |
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif)
|
A | α | γ | Phase |
|---|---|---|---|---|---|---|
| 0.18 | −5 | 0 | 0.33 | 5.07 | 0.19 | Gas |
| 0.18 | 0 | 0 | 0.26 | 13.1 | 0.57 | Gas |
| 0.18 | 5 | 0 | 0.09 | — | 0.49 | MIPS |
| 0.18 | −5 | 133.5 | 0.32 | 7.1 | 0.4 | Gas |
| 0.18 | 0 | 133.5 | 0.31 | 7.61 | 0.43 | Gas |
| 0.18 | 5 | 133.5 | 0.34 | 8.55 | 0.54 | Gas |
| 0.35 | −5 | 0 | 0.07 | 49.4 | 0.4 | Swarming |
| 0.35 | 0 | 0 | 0.1 | — | 1.1 | MIPS |
| 0.35 | 5 | 0 | 0.05 | — | 0.99 | MIPS |
| 0.35 | −5 | 133.5 | 0.07 | 45 | 0.45 | Swarming |
| 0.35 | 0 | 133.5 | 0.07 | 72.5 | 0.58 | Swarming |
| 0.35 | 5 | 133.5 | 0.07 | 90 | 0.62 | Swarming |
| 0.44 | −5 | 0 | 0.04 | — | 0.89 | MIPS |
| 0.44 | 0 | 0 | 0.02 | — | 0.93 | MIPS |
| 0.44 | 5 | 0 | 0.03 | — | 1.28 | MIPS |
| 0.44 | −5 | 133.5 | 0.03 | — | 0.62 | MIPS |
| 0.44 | 0 | 133.5 | 0.03 | — | 0.69 | MIPS |
| 0.44 | 5 | 133.5 | 0.03 | — | 0.83 | MIPS |
| 0.56 | −5 | 0 | 0.01 | — | 1.02 | MIPS |
| 0.56 | 0 | 0 | 0.03 | — | 1.64 | MIPS |
| 0.56 | 5 | 0 | 0.01 | — | 0.81 | MIPS |
| 0.56 | −5 | 133.5 | 0.01 | — | 0.9 | MIPS |
| 0.56 | 0 | 133.5 | 0.01 | — | 0.94 | MIPS |
| 0.56 | 5 | 133.5 | 0.01 | — | 1.04 | MIPS |
For ϕ = 0.18, the simulated systems exhibit a homogeneous gas-like phase, except for the case of pullers (β = 5) without rotlet dipole (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0), shown in Fig. 2(a). Here, the exponential term dominates, as can be seen well in Fig. 3(a). At low packing fractions of squirmers, there is a limited chance for squirmer collisions, leading to a gas-like phase, compare also Fig. 2. For β = 5 at ϕ = 0.18,
= 0), shown in Fig. 2(a). Here, the exponential term dominates, as can be seen well in Fig. 3(a). At low packing fractions of squirmers, there is a limited chance for squirmer collisions, leading to a gas-like phase, compare also Fig. 2. For β = 5 at ϕ = 0.18, ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) resembles a bimodal distribution, indicating the existence of large clusters (n ≈ 60), whose formation is primarily governed by the attractive hydrodynamic field around pullers.
(n) resembles a bimodal distribution, indicating the existence of large clusters (n ≈ 60), whose formation is primarily governed by the attractive hydrodynamic field around pullers.
Swarming-like behavior is observed in several cases at ϕ = 0.35, characterized by the relatively large values of α and moderate values of γ ∈ [0.4,0.7], indicating the dominance of the power-law term in eqn (11). Note that for the cases of neutral swimmers and pullers (without rotlet dipole), the value of γ is close to unity, and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) exhibits a bimodal distribution in Fig. 3(b), suggesting the presence of a MIPS phase. For even larger volume fraction ϕ = 0.56, Fig. 3(c) shows a prominent peak in
(n) exhibits a bimodal distribution in Fig. 3(b), suggesting the presence of a MIPS phase. For even larger volume fraction ϕ = 0.56, Fig. 3(c) shows a prominent peak in ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) at large n for all cases, which is the main characteristic for the MIPS phase. This is also confirmed in Table 1 through γ values close to unity. At large packing fractions, steric interactions between squirmers dominate due to crowding, so that the differences in
(n) at large n for all cases, which is the main characteristic for the MIPS phase. This is also confirmed in Table 1 through γ values close to unity. At large packing fractions, steric interactions between squirmers dominate due to crowding, so that the differences in ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) for different swimming modes nearly disappear.
(n) for different swimming modes nearly disappear.
For squirmers without rotlet dipole (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0), the swimming mode affects their collective behavior when the volume fraction is small enough, i.e.
= 0), the swimming mode affects their collective behavior when the volume fraction is small enough, i.e. 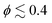 . In this case, the local hydrodynamic flow field generated by the squirmers is relevant for cluster formation and dynamics, in agreement with previous studies.31,38 However, when the rotlet dipole is activated (
. In this case, the local hydrodynamic flow field generated by the squirmers is relevant for cluster formation and dynamics, in agreement with previous studies.31,38 However, when the rotlet dipole is activated (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5), differences in
= 133.5), differences in ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) for various active stresses β nearly disappear, as displayed in the insets of Fig. 3. With rotlet dipole, we obtain the gas phase at ϕ = 0.18, swarming at ϕ = 0.35, and MIPS at ϕ = 0.56, independently of active stress – see also Fig. 2(c). Note that the systems with ϕ = 0.56 are very crowded, and MIPS is more difficult to recognize for
(n) for various active stresses β nearly disappear, as displayed in the insets of Fig. 3. With rotlet dipole, we obtain the gas phase at ϕ = 0.18, swarming at ϕ = 0.35, and MIPS at ϕ = 0.56, independently of active stress – see also Fig. 2(c). Note that the systems with ϕ = 0.56 are very crowded, and MIPS is more difficult to recognize for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 in Fig. 2(c) than for
= 133.5 in Fig. 2(c) than for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 in Fig. 2(a). Additional simulations (not shown) indicate that the suspension of squirmers with
= 0 in Fig. 2(a). Additional simulations (not shown) indicate that the suspension of squirmers with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 transits from swarming to the MIPS at ϕ ≈ 0.4.
= 133.5 transits from swarming to the MIPS at ϕ ≈ 0.4.
The average cluster size 〈n〉 as a function of ϕ is shown in Fig. 3(d). For ϕ ≳ 0.18, 〈n〉 increases rapidly with increasing volume fraction of squirmers for all β and λ values. The simulation systems with different active stresses result in a similar range of average cluster sizes for both rotlet dipole strengths.
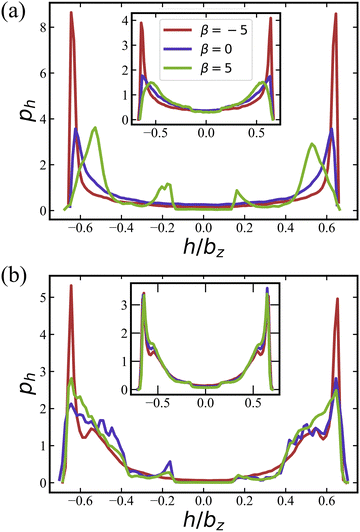
Pushers (β = −5) exhibit a distinctive two-layered structure with the orientation parallel to the walls, which is reminiscent of E. coli behavior in in vitro observations.73,74 For pushers, the far-field flow re-orients the squirmers parallel to the wall.65,66,72 Furthermore, the elongated spheroidal body of the squirmers favors their orientation parallel to the walls.75,76 For pullers (β = 5), Fig. 4(a) show two small peaks at h/bz ≈ ±0.2 at small volume fraction ϕ = 0.18, which indicates a nearly perpendicular orientation with respect to the walls [see also corresponding conformations in Fig. 2(b)]. Note that the far-field flow generated by pullers favors such a perpendicular-to-the-wall orientation,65,66,72 while the spheroidal shape promotes parallel-to-the-wall orientation. Thus, pullers in Fig. 4(a) show their major peaks in ph at h/bz ≈ ±0.5, such that their most probable orientation has about 40 degree angle with respect to the walls [see also Fig. 5(a)]. ph for neutral swimmers at ϕ = 0.18 is close to that for pushers.
At the higher volume fraction of ϕ = 0.56, differences in ph for the three swimming modes significantly diminish, and all cases essentially show a two-layered structure, see Fig. 4(b). Note that the two peaks in ph at h/bz ≈ ±0.6 become broader than those for ϕ = 0.18, which can be attributed to an increasing importance of steric interactions at large volume fractions, such that close packing introduces a larger deviation to the two-layered structure. Insets in Fig. 4 demonstrate that the activation of rotlet dipole mitigates the influence of active stress on ph, in agreement with the results for the cluster-size distribution in Section 3.1.1.
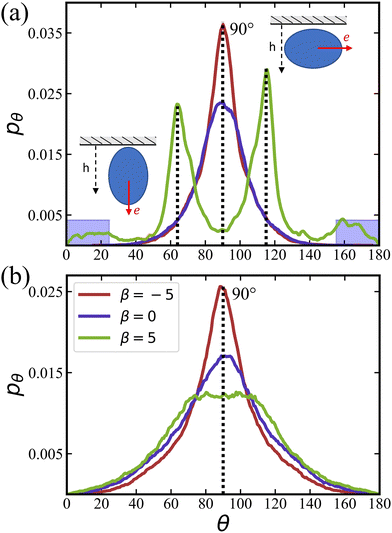
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 at ϕ = 0.18 are primarily oriented parallel to the wall, in agreement with the results in Fig. 4(a). In contrast, pullers show several peaks at θ ≈ 20° and 160° (small peaks) and θ ≈ 60° and 120° (large peaks), which correspond to a nearly perpendicular-to-the-wall orientation and a tilted orientation with about 40° angle to the walls, respectively [compare also snapshots in Fig. 2(b)]. These results are consistent with the position distributions ph discussed in Section 3.1.2.
= 0 at ϕ = 0.18 are primarily oriented parallel to the wall, in agreement with the results in Fig. 4(a). In contrast, pullers show several peaks at θ ≈ 20° and 160° (small peaks) and θ ≈ 60° and 120° (large peaks), which correspond to a nearly perpendicular-to-the-wall orientation and a tilted orientation with about 40° angle to the walls, respectively [compare also snapshots in Fig. 2(b)]. These results are consistent with the position distributions ph discussed in Section 3.1.2.
Fig. 5(b) shows pθ for a non-zero rotlet dipole (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5) at ϕ = 0.18, which again demsontrates a significant reducuction of differences between different swimming modes due to the rotlet dipole. In particular, for all β, a single peak in pθ centered around 90° is observed, confirming the preferred squirmer orientation parallel to the walls, as illustrated in Fig. 2(d). As the volume fraction of squirmers increases, the dominant role of steric interactions also leads to a diminished effect of different swimming modes (even for
= 133.5) at ϕ = 0.18, which again demsontrates a significant reducuction of differences between different swimming modes due to the rotlet dipole. In particular, for all β, a single peak in pθ centered around 90° is observed, confirming the preferred squirmer orientation parallel to the walls, as illustrated in Fig. 2(d). As the volume fraction of squirmers increases, the dominant role of steric interactions also leads to a diminished effect of different swimming modes (even for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0) with the formation of a two-layered structure.
= 0) with the formation of a two-layered structure.
The probability P⊥ of squirmers to be oriented nearly perpendicular to the walls is displayed in Fig. 6 for different values of β as a function of ϕ. The probability is computed by integrating the orientation distributions over the ranges [0,25°] and [155°,180°], as indicated by the blue shaded areas in Fig. 5(a). At low ϕ, the probability of perpendicular orientation to the walls is zero for pushers and neutral squirmers, while P⊥ ≈ 0.11 for pullers. This simply confirms the tendency of pushers and neutral swimmers to align with the walls, due to their hydrodynamic interactions with the walls. Interestingly, the majority of pullers does not have a perpendicular-to-the-wall orientation, despite of such predictions for a single puller.66,72 This is due to collective effects between pullers, which will be discussed in Section 3.1.4 below.
 | ||
Fig. 6 Probability P⊥ of squirmers to be aligned with the h axis (i.e., wall normal vector) for different volume fractions and swimming modes at ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. Data for pushers with β = −5 (red), neutral squirmers with β = 0 (blue), and pullers with β = 5 (green). The probability is calculated by integrating the orientation distributions in Fig. 5(a) over the ranges [0,25] and [155,180] degrees. = 0. Data for pushers with β = −5 (red), neutral squirmers with β = 0 (blue), and pullers with β = 5 (green). The probability is calculated by integrating the orientation distributions in Fig. 5(a) over the ranges [0,25] and [155,180] degrees. | ||
As the volume fraction of squirmers increases, P⊥ for pullers decreases because steric interactions between squirmers become dominant, forcing the formation of a two-layered structure, as discussed above. For neural squirmers, P⊥ first increases with increasing ϕ, but then closely follows P⊥ for pullers when ϕ ≳ 0.4. For pushers, there is only a slight increase in P⊥ with increasing ϕ. Nevertheless, we expect that for large volume fractions ϕ ≳ 0.6, orientational differences between squirmers with various swimming modes essentially disappear.
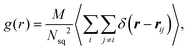 | (12) |
Fig. 7(a) presents g(r) for different swimming modes at low volume fraction ϕ = 0.18 and without rotlet dipole, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. Only the suspension of pullers with β = 5 exhibits pronounced peaks in g(r), which represent the most frequent structural elements illustrated in Fig. 7(b). The existence of structure for pullers, but not for pushers and neutral squirmers, is primarily related to the fact that pullers form large clusters already at ϕ = 0.18, while the other squirmer types yield a gas-like phase, see Table 1. Interestingly, the x–y perspective plot in Fig. 2(b) shows that pullers frequently form flower-like arrangements with one or two squirmers oriented perpendicular to the walls and surrounded by several “petal” squirmers [also illustrated in Fig. 7(b)]. These structures form due to the attractive flow field generated by pullers, which slide along the walls until they collide and form the flower-like structures through the attractive hydrodynamic interactions. When the rotlet dipole is turned on at ϕ = 0.18 [see the inset in Fig. 7(a)], the suspension of pullers becomes gas-like and thus looses its internal structure.
= 0. Only the suspension of pullers with β = 5 exhibits pronounced peaks in g(r), which represent the most frequent structural elements illustrated in Fig. 7(b). The existence of structure for pullers, but not for pushers and neutral squirmers, is primarily related to the fact that pullers form large clusters already at ϕ = 0.18, while the other squirmer types yield a gas-like phase, see Table 1. Interestingly, the x–y perspective plot in Fig. 2(b) shows that pullers frequently form flower-like arrangements with one or two squirmers oriented perpendicular to the walls and surrounded by several “petal” squirmers [also illustrated in Fig. 7(b)]. These structures form due to the attractive flow field generated by pullers, which slide along the walls until they collide and form the flower-like structures through the attractive hydrodynamic interactions. When the rotlet dipole is turned on at ϕ = 0.18 [see the inset in Fig. 7(a)], the suspension of pullers becomes gas-like and thus looses its internal structure.
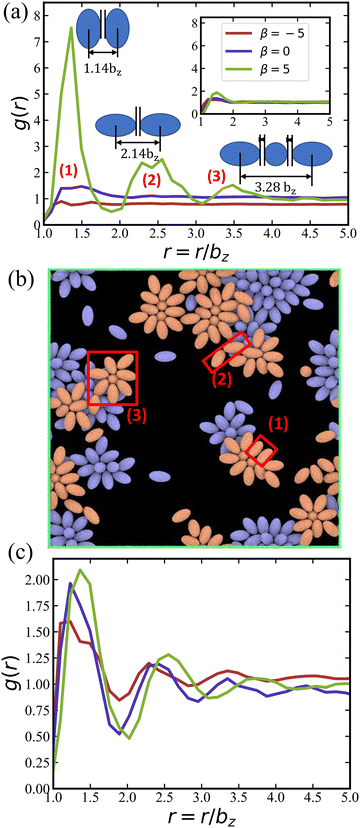 | ||
Fig. 7 (a) 2D radial distribution function g(r) of squirmers with ϕ = 0.18 and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, for pushers (red), neutral squirmers (blue), and pullers (green). The locations of peaks of g(r) for pullers correlate well with local structural arrangements illustrated next to the peaks. The inset presents the corresponding g(r) functions for = 0, for pushers (red), neutral squirmers (blue), and pullers (green). The locations of peaks of g(r) for pullers correlate well with local structural arrangements illustrated next to the peaks. The inset presents the corresponding g(r) functions for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 and the same ϕ. (b) Snapshot of the simulated system for ϕ = 0.18, = 133.5 and the same ϕ. (b) Snapshot of the simulated system for ϕ = 0.18, ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, and β = 5, which illustrates the most frequent squirmer structures, see also Movie S3 (ESI†). (c) g(r) of squirmers for ϕ = 0.56 and = 0, and β = 5, which illustrates the most frequent squirmer structures, see also Movie S3 (ESI†). (c) g(r) of squirmers for ϕ = 0.56 and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. The legend for the curves is the same as in (a). = 0. The legend for the curves is the same as in (a). | ||
Fig. 7(c) shows g(r) at the high volume fraction ϕ = 0.56, where several peaks are observed for all squirmer types. At this high volume fraction, all squirmer suspensions are in MIPS phase (see Table 1), so that large clusters are present with an internal fluid structure. Furthermore, due to the dominance of steric interactions, radial distribution functions are again very similar for different β, indicating that the internal structure is nearly independent of the swimming mode at large ϕ.
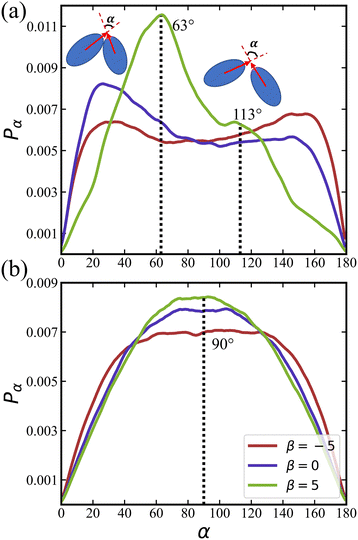
We calculate distributions pα of the relative angle α between orientation vectors of two neighboring squirmers within a defined cutoff radius as
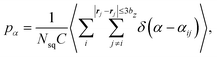 | (13) |
The distribution of pα for an active rotlet dipole with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 is shown in Fig. 8(b). For all β values, pα is centered at α ≈ 90°, indicating that hydrodynamic interactions favor the perpendicular orientation between squirmer pairs. Note that for pushers, the central region in pα is flatter than that for pullers and neutral squirmers.
= 133.5 is shown in Fig. 8(b). For all β values, pα is centered at α ≈ 90°, indicating that hydrodynamic interactions favor the perpendicular orientation between squirmer pairs. Note that for pushers, the central region in pα is flatter than that for pullers and neutral squirmers.
3.2 Dynamical properties
| 〈e(t)·e(t + Δt)〉 = e−DRΔt, | (14) |
 . Fig. 9 shows the dependence of DR on ϕ, β, and λ. In most cases, DR/D0R > 1, indicating that the rotational dynamics of squirmers within a suspension is enhanced in comparison with the rotational diffusion D0R of a spheroid in an unconfined system. This is due to hydrodynamic interactions between squirmers, and their collisions during motion. Only for the case of β = 0, ϕ = 0.56, and
. Fig. 9 shows the dependence of DR on ϕ, β, and λ. In most cases, DR/D0R > 1, indicating that the rotational dynamics of squirmers within a suspension is enhanced in comparison with the rotational diffusion D0R of a spheroid in an unconfined system. This is due to hydrodynamic interactions between squirmers, and their collisions during motion. Only for the case of β = 0, ϕ = 0.56, and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, rotational diffusion is reduced, DR < D0R, which is likely due to the crowding of squirmers at large volume fractions [compare Fig. 2(a)].
= 0, rotational diffusion is reduced, DR < D0R, which is likely due to the crowding of squirmers at large volume fractions [compare Fig. 2(a)].
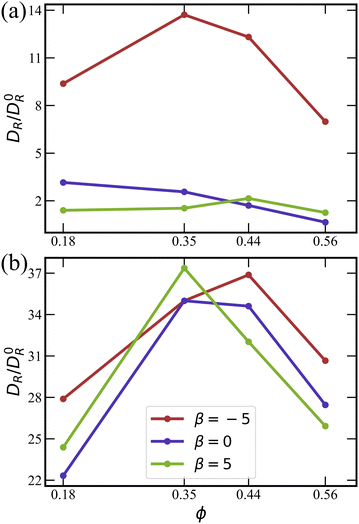 | ||
Fig. 9 Effective rotational diffusion DR as a function of ϕ for (a) ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 and (b) = 0 and (b) ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5. DR is obtained by fitting auto-correlation functions of squirmer orientation using eqn (14), and normalized by the rotational diffusion D0R of a spheroid. Data for pushers (red), for neutral squirmers (blue), and for pullers (green). = 133.5. DR is obtained by fitting auto-correlation functions of squirmer orientation using eqn (14), and normalized by the rotational diffusion D0R of a spheroid. Data for pushers (red), for neutral squirmers (blue), and for pullers (green). | ||
Fig. 9(a) (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0) shows that the enhancement of rotational diffusion coefficient for pushers is significantly larger than for pullers and neutral squirmers. This occurs due to repulsive hydrodynamic interactions between pushers,45,46 which leads to the enhanced scattering between squirmers. The dependence of DR on ϕ first exhibits an increase, followed by a maximum and subsequent decrease. With increasing ϕ, the collision rate between squirmers increases, resulting in the enhancement of DR. However, at large ϕ, squirmer clustering and the transition to the MIPS phase take place [compare Fig. 2(a)], so that the effective rotational diffusion is significantly slowed down.
= 0) shows that the enhancement of rotational diffusion coefficient for pushers is significantly larger than for pullers and neutral squirmers. This occurs due to repulsive hydrodynamic interactions between pushers,45,46 which leads to the enhanced scattering between squirmers. The dependence of DR on ϕ first exhibits an increase, followed by a maximum and subsequent decrease. With increasing ϕ, the collision rate between squirmers increases, resulting in the enhancement of DR. However, at large ϕ, squirmer clustering and the transition to the MIPS phase take place [compare Fig. 2(a)], so that the effective rotational diffusion is significantly slowed down.
Noteworthy is the difference in DR for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 and
= 0 and ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 in Fig. 9(a) and (b), respectively, where the enhancement for squirmers with rotlet dipole is at least a factor three larger than that without. Interestingly, squirmers with
= 133.5 in Fig. 9(a) and (b), respectively, where the enhancement for squirmers with rotlet dipole is at least a factor three larger than that without. Interestingly, squirmers with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 switch between the two layers (i.e. migrate from one wall to the other) much more frequently than squirmers with
= 133.5 switch between the two layers (i.e. migrate from one wall to the other) much more frequently than squirmers with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, which will be discussed in Section 3.2.4. The ability of interchange between the two layers increases significantly the effective rotational diffusion. The DR curves for
= 0, which will be discussed in Section 3.2.4. The ability of interchange between the two layers increases significantly the effective rotational diffusion. The DR curves for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) > 0 are similar for different swimming modes β, in agreement with the structural characteristics for suspensions of squirmers with the rotlet dipole, as discussed in Section 3.1 above.
> 0 are similar for different swimming modes β, in agreement with the structural characteristics for suspensions of squirmers with the rotlet dipole, as discussed in Section 3.1 above.
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0, pullers yield the lowest effective diffusivity, followed by neutral squirmers and pushers, because the suspension of pullers at these conditions is already in the MIPS phase (see Table 1). The effective diffusivity of squirmers at ϕ = 0.56 is lower than at ϕ = 0.18 due to crowding and the formation of large clusters.
= 0, pullers yield the lowest effective diffusivity, followed by neutral squirmers and pushers, because the suspension of pullers at these conditions is already in the MIPS phase (see Table 1). The effective diffusivity of squirmers at ϕ = 0.56 is lower than at ϕ = 0.18 due to crowding and the formation of large clusters.
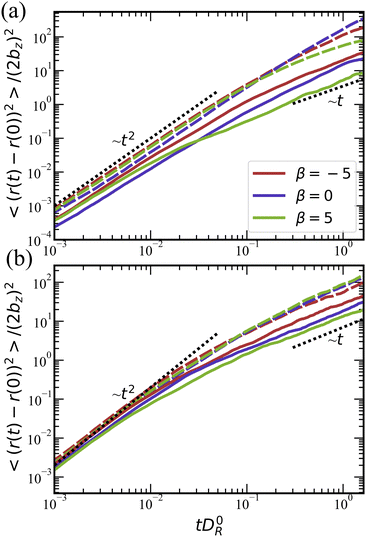
The transition from the ballistic to the diffusive regime for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 in Fig. 10(a) occurs around tD0R ≃ 0.2–0.5. Theoretically, this transition should take place around tDR ≃ 1,78 which is consistent with the values of DR/D0R ≃ 2 in Fig. 9(a). Note that the ballistic-to-diffusive transition for squirmers with rotlet dipole occurs at tD0R ≳ 0.1, which is also consistent with the values of DR/D0R ≃ 10 in Fig. 9(b). Furthermore, mean-square-displacement curves for
= 0 in Fig. 10(a) occurs around tD0R ≃ 0.2–0.5. Theoretically, this transition should take place around tDR ≃ 1,78 which is consistent with the values of DR/D0R ≃ 2 in Fig. 9(a). Note that the ballistic-to-diffusive transition for squirmers with rotlet dipole occurs at tD0R ≳ 0.1, which is also consistent with the values of DR/D0R ≃ 10 in Fig. 9(b). Furthermore, mean-square-displacement curves for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 in Fig. 10(b) are similar to each other for various β at a fixed volume fraction, confirming once more that the rotlet dipole nearly offsets the effects of different swimming modes.
= 133.5 in Fig. 10(b) are similar to each other for various β at a fixed volume fraction, confirming once more that the rotlet dipole nearly offsets the effects of different swimming modes.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) . For a single squirmer i, the instantaneous swim speed is calculated as
. For a single squirmer i, the instantaneous swim speed is calculated as| vi(t) = |ri(t + Δt) − ri(t)|/Δt, | (15) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is then obtained by an ensemble and time average as a function of the volume fraction ϕ.
is then obtained by an ensemble and time average as a function of the volume fraction ϕ.
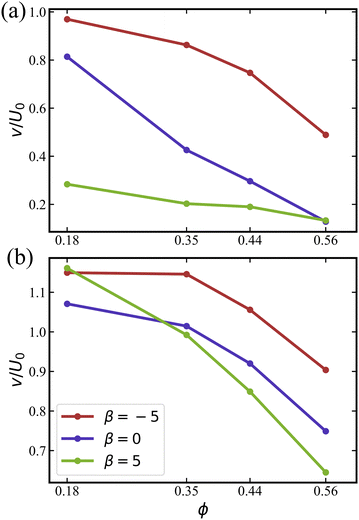
As shown in Fig. 11, pushers are the most mobile, displaying the largest average speed ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) among all squirmer types. For the case without rotlet dipole in Fig. 11(a),
among all squirmer types. For the case without rotlet dipole in Fig. 11(a), ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) decreases with increasing ϕ due to crowding at large volume fractions and the transition to MIPS or clustering regime. For all studied β values, the average speed of squirmers is below U0, which is the speed of a single squirmer in an unconfined system.
decreases with increasing ϕ due to crowding at large volume fractions and the transition to MIPS or clustering regime. For all studied β values, the average speed of squirmers is below U0, which is the speed of a single squirmer in an unconfined system.
The average speeds of squirmers with rotlet dipole in Fig. 11(b) are larger than those with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. Furthermore, the decay in
= 0. Furthermore, the decay in ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for
for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 with increasing ϕ is slower than for
= 133.5 with increasing ϕ is slower than for ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. Interestingly, for
= 0. Interestingly, for  , the average speed of squirmers with rotlet dipole is slightly larger than U0, indicating motility enhancement due to interactions with the walls. An increased mobility near walls was reported previously for pushers without rotlet dipole.46,76,79 The results in Fig. 11 confirm that the presence of rotlet dipole enhances the mobility of squirmers and delays the transition to MIPS as a function of ϕ.
, the average speed of squirmers with rotlet dipole is slightly larger than U0, indicating motility enhancement due to interactions with the walls. An increased mobility near walls was reported previously for pushers without rotlet dipole.46,76,79 The results in Fig. 11 confirm that the presence of rotlet dipole enhances the mobility of squirmers and delays the transition to MIPS as a function of ϕ.
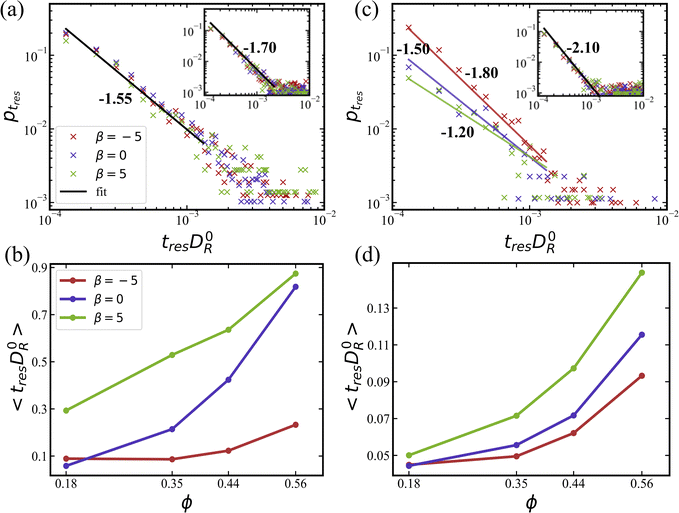
In fact, it is more informative to look at average residence times 〈tres〉, which are shown in Fig. 12(b) and (d) for simulations without and with rotlet dipole, respectively. Pushers display the lowest values of 〈tres〉 in comparison to the other two swimming modes, regardless of the rotlet dipole strength. This means that pushers have the highest switching frequency, which is consistent with previous studies45,57,79–81 showing that the residence of pushers near a wall is unstable due to local hydrodynamic interactions which orient them slightly away from the wall. The average residence time increases with increasing ϕ for all squirmer types due to significant crowding at large ϕ, which limits the migration between the two layers. Pullers possess the largest average residence times, which is consistent with their preferred orientation toward a wall (see Section 3.1.3) as well as with the formation of stable flower-like structures (see Section 3.1.4). It is likely that switching between the two layers for pullers is facilitated by squirmer collisions, rather than occurring spontaneously.
Finally, for squirmers with a rotlet dipole (![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5), average residence times are about one order of magnitude lower than for squirmers without rotlet dipole. Therefore, the presence of rotlet dipole significantly destabilizes the residence of squirmers near walls, and thereby enhances their switching frequency between the two layers. It is also consistent with an enhanced motility of squirmers with rotlet dipole, as shown in Fig. 9 and 11.
= 133.5), average residence times are about one order of magnitude lower than for squirmers without rotlet dipole. Therefore, the presence of rotlet dipole significantly destabilizes the residence of squirmers near walls, and thereby enhances their switching frequency between the two layers. It is also consistent with an enhanced motility of squirmers with rotlet dipole, as shown in Fig. 9 and 11.
4 Discussion and conclusions
In this study, we have performed mesoscale hydrodynamic simulations of a confined system of squirmers in a thin fluid film between two parallel walls, in order to better understand the intricate interplay between hydrodynamic and steric interactions and their impact on the collective behavior of squirmers. In contrast, previous studies that considered hydrodynamic interactions between swimmers have mainly focused on quasi-2D systems (i.e., a monolayer of squirmers)31,38,39,46–49 or 3D systems with periodic boundary conditions.37,50–53 The considered film thickness is large enough to allow the formation of two-layered structures. This situation is of interest when the formation of a biofilm, which starts from a monolayer of bacteria, proceeds toward the development of further layers. In particular, an interesting question is whether bacteria can spontaneously leave the surface layer.By systematically varying relevant parameters, such as the volume fraction of squirmers, their active stress, and their rotlet dipole strength, we show the emergence of different structures and phases (Fig. 2). As expected, at low volume fractions of squirmers, the system is in a gas-like phase. As ϕ is increased, a swarming state is observed, with the formation of mobile clusters with a wide range of sizes. The elongated shape of squirmers is essential for the emergence of these swarming clusters, as it provides an alignment interaction, which has been observed previously for self-propelled rods, spheroids, and semi-flexible filaments.22,38,82 Swarming clusters form at intermediate values of ϕ for pushers and squirmers with the rotlet dipole. The absence of the swarming state for pullers with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0 suggests that contractile hydrodynamic interactions between swimmers suppress the formation of swarming clusters.
= 0 suggests that contractile hydrodynamic interactions between swimmers suppress the formation of swarming clusters.
At large enough volume fractions, a single large cluster of squirmers emerges, surrounded by a few mobile swimmers (see Fig. 2(a) at ϕ = 0.44 or 0.56), indicating formation of MIPS. Pullers exhibit MIPS already at low volume fraction, ϕ ≈ 0.18, while neutral squirmers and pushers require larger volume fractions, in agreement with previous studies.38,46 Our simulations also suggest that hydrodynamic interactions suppress motility-induced clustering and phase separation, in agreement with previous reports38,40 for particles with aspect ratios not far from unity. Note that the suspension of pushers at ϕ = 0.56 does not show a transition to the state of active turbulence, because the strength of the induced force dipole is likely too weak.25,29
An interesting aspect of our investigation is the interplay of simultaneous hydrodynamic and steric interaction both between squirmers and of squirmers with the confining walls, and its effect on the collective behavior. In particular, pullers favor a nearly perpendicular orientation with the walls, resulting in the formation of flower-like clusters [Fig. 2(b)] at low volume frations, where pullers first slide along the surface, and upon collisions form a structure with a single puller oriented nearly perpendicular to the wall surrounded by a few petal pullers. This leads to the nucleation of clusters for pullers already at low ϕ, promoting MIPS at low ϕ. Pushers and neutral squirmers favor an orientation parallel to the walls, which does not significantly hinder their mobility. Therefore, pushers can frequently switch between the layers of a two-layer structure, substantially delaying the formation of large clusters with increasing ϕ. Thus, a colony of pusher-like swimmers (e.g., E. coli) should be able to spontaneously switch from an initial monolayer structure to a multi-layered configuration. Recent experiments74 suggest that E. coli bacteria also employ tumbling (i.e., active turning due to the rotation reversal of one of its flagella) to leave a surface, indicating that the aspect ratio of a swimmer is very important for its interaction with the wall. In our simulations, bz/bx = 2, which is somewhat smaller than that for E. coli.
For all studied cases, there is a clear preference for the two-layered structure. Only pullers at 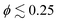 show partial preference for the perpendicular-to-the-wall orientation due to their hydrodynamic interactions with the walls. Pushers and neutral squirmers display mostly parallel-to-wall alignment.
show partial preference for the perpendicular-to-the-wall orientation due to their hydrodynamic interactions with the walls. Pushers and neutral squirmers display mostly parallel-to-wall alignment.
Our comprehensive simulations reveal that the the effect of a rotlet dipole is to offset the effect of active stress, characterized by β, to a large extent. Even at relatively low volume fractions, the presence of a rotlet dipole of dimensionless strength ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) ≠ 0 nearly eliminates differences in the behavior of pullers, neutral squirmers, and pushers. With the rotlet dipole, squirmers assume a parallel-to-the-wall orientation and therefore, remain mobile up to moderate volume fractions, frequently switching between the two layers. This enhancement of layer switching can be attributed to the rotational flow field of rotors, which implies an induced motion around their center of mass. Furthermore, the rotlet dipole leads to a circular trajectories of squirmers near the walls,83,84 which further contributes to the mobility of squirmers within the confinement. In our study, a single squirmer with
≠ 0 nearly eliminates differences in the behavior of pullers, neutral squirmers, and pushers. With the rotlet dipole, squirmers assume a parallel-to-the-wall orientation and therefore, remain mobile up to moderate volume fractions, frequently switching between the two layers. This enhancement of layer switching can be attributed to the rotational flow field of rotors, which implies an induced motion around their center of mass. Furthermore, the rotlet dipole leads to a circular trajectories of squirmers near the walls,83,84 which further contributes to the mobility of squirmers within the confinement. In our study, a single squirmer with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 133.5 circles at the wall with a radius of approximately 2bz. However, the circling motion near a wall is difficult to detect at higher volume fractions due to frequent squimer–squirmer scattering. As a result, the effective rotational diffusivity of squirmers with rotlet dipole is approximately one order of magnitude larger than that for squirmers with
= 133.5 circles at the wall with a radius of approximately 2bz. However, the circling motion near a wall is difficult to detect at higher volume fractions due to frequent squimer–squirmer scattering. As a result, the effective rotational diffusivity of squirmers with rotlet dipole is approximately one order of magnitude larger than that for squirmers with ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = 0. Thus, swimmers with rotlet dipole are expected to spontaneously initiate multi-layered structures within a biofilm.
= 0. Thus, swimmers with rotlet dipole are expected to spontaneously initiate multi-layered structures within a biofilm.
Finally, we would like to discuss some limitations of our study. Despite the fact that the squirmer model can produce various swimming modes, the near-field flow of real microswimmers, like bacteria, is unavoidably species-specific, arising from body shape, the geometry and dynamics of propelling flagella, and the ability to navigate (e.g., E. coli tumbling). Furthermore, steric interactions between microswimmers including their flagella are likely different from interactions between idealized spheroidal shapes. However, modeling of swimmers with explicit appendages84 is computationally expensive, significantly limiting the number of simulated swimmers in a study. Therefore, the direct comparison of our simulation results with experiments requires some calibration, including the aspect ratio of squirmers, and the strengths of active stress and rotlet dipole. Furthermore, biofilms in vivo are generally bound by a solid wall and an air–water interface, in contrast to the two solid walls in our study. The air–water interface is deformable and such simulations are beyond the scope of our work. However, our setup with the two non-slip walls may capture qualitatively the collective behavior of bacteria in porous media and microfluidic devices.85–87 Future work should also consider thicker films to bridge these results with those from three-dimensional periodic systems.37,50–53
Author contributions
G. G. and D. A. F. designed the research project. B. W.-Z. performed the simulations and analysed the obtained data. All authors participated in the discussions and writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: Vesicle-like squirmer model
Each squirmer surface is represented by Np = 1024 particles connected by springs into a triangulated network. Shear elasticity of the squirmer membrane is supplied by the spring potential55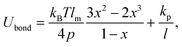 | (16) |
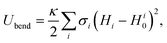 | (17) |
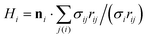 , where ni is the unit normal at the vertex i,
, where ni is the unit normal at the vertex i, 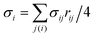 , j(i) spans all vertices linked to vertex i, and σij = rij(cot
, j(i) spans all vertices linked to vertex i, and σij = rij(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + cot
θ1 + cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2)/2 is the bond length in the dual lattice with θ1 and θ2 being the angles at the two vertices opposite to the edge ij in the dihedral. The spontaneous curvature Hi0 is set locally after the triangulation of the spheroidal surface of the squirmer.
θ2)/2 is the bond length in the dual lattice with θ1 and θ2 being the angles at the two vertices opposite to the edge ij in the dihedral. The spontaneous curvature Hi0 is set locally after the triangulation of the spheroidal surface of the squirmer.
The area and volume conservation constraints are represented by the potential55
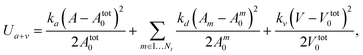 | (18) |
The membrane-like representation of squirmers has the shear modulus μ0 = 1.44 × 105kBT/b2z, the bending modulus κ = 250kBT, the area-constraint coefficients kd = 1.6 × 103kBT/b2z and ka = 8 × 103kBT/b2z, the volume-constraint coefficient kv = 3.2 × 104kBT/b3z, the total area Atot0 = 5.36bz2, and the total volume Vtot0 = 1.05bz3. In all simulations, kBT = 1 and bz = 4.
Appendix B: Modeling fluid flow
To model fluid flow, we employ the dissipative particle dynamics (DPD) method,62,63 which is a mesoscopic hydrodynamics simulation technique. DPD is a particle-based Lagrangian method, where each particle represents a small fluid volume. DPD particles i and j interact through three types (conservative, dissipative, and random) of pairwise forces given byFC(rij) = aWC(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (19) |
FD(rij) = −γWD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (20) |
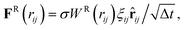 | (21) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij, and vij = vi − vj is the velocity difference. ξij = ξji is a symmetric Gaussian random variable with zero mean and unit variance, and Δt is the time step. All forces act within a cutoff radius rc and vanish beyond it. The conservative force controlls fluid compressibility, while the dissipative and random forces form a thermostat, so that the DPD fluid has an isotropic temperature T. Thus, FD and FR are related through the fluctuation–dissipation theorem63 as
ij = rij/rij, and vij = vi − vj is the velocity difference. ξij = ξji is a symmetric Gaussian random variable with zero mean and unit variance, and Δt is the time step. All forces act within a cutoff radius rc and vanish beyond it. The conservative force controlls fluid compressibility, while the dissipative and random forces form a thermostat, so that the DPD fluid has an isotropic temperature T. Thus, FD and FR are related through the fluctuation–dissipation theorem63 as| σ2 = 2γkBT, WD(rij) = [WR(rij)]2. | (22) |
The weight functions are defined as
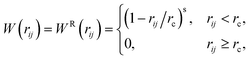 | (23) |
Time evolution of each DPD particle follows the Newton's second law
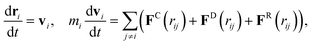 | (24) |
DPD parameters for the interactions between fluid particles and between fluid and wall particles are a = 200kBT/bz, 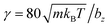 (m = 1 in all simulations), s = 0.15, and rc = bz/4. Furthermore, friction coupling of squirmers to fluid flow is performed using DPD parameters a = 0,
(m = 1 in all simulations), s = 0.15, and rc = bz/4. Furthermore, friction coupling of squirmers to fluid flow is performed using DPD parameters a = 0, 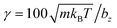 , s = 0.1, and rc = 0.175bz. The time step for integration is
, s = 0.1, and rc = 0.175bz. The time step for integration is 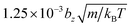 .
.
Acknowledgements
We thank Roland G. Winkler for numerous discussions related to the study. We acknowledge funding from the ETN-PHYMOT “Physics of microbial motility” within the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 955910. The authors also gratefully appreciate computing time on the supercomputer JURECA89 at Forschungszentrum Jülich under grant no. actsys.References
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp, L. Alvarez, T. Kiorboe, E. Lauga, W. C. K. Poon, A. DeSimone, S. Muiños-Landin, A. Fischer, N. A. Söker, F. Cichos, R. Kapral, P. Gaspard, M. Ripoll, F. Sagues, A. Doostmohammadi, J. M. Yeomans, I. S. Aranson, C. Bechinger, H. Stark, C. K. Hemelrijk, F. J. Nedelec, T. Sarkar, T. Aryaksama, M. Lacroix, G. Duclos, V. Yashunsky, P. Silberzan, M. Arroyo and S. Kale, J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- L. Hall-Stoodley, J. W. Costerton and P. Stoodley, Nat. Rev. Microbiol., 2004, 2, 95–108 CrossRef CAS PubMed.
- N. Verstraeten, K. Braeken, B. Debkumari, M. Fauvart, J. Fransaer, J. Vermant and J. Michiels, Trends Microbiol., 2008, 16, 496–506 CrossRef CAS PubMed.
- P. D. Marsh, BMC Oral Health, 2006, 6, S14 CrossRef PubMed.
- C. Attinger and R. Wolcott, Adv. Text. Wound Care, 2012, 1, 127–132 CrossRef PubMed.
- M. G. Mazza, J. Phys. D: Appl. Phys., 2016, 49, 203001 CrossRef.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- T. Bäuerle, R. C. Löffler and C. Bechinger, Nat. Commun., 2020, 11, 2547 CrossRef PubMed.
- C. Krüger, C. Bahr, S. Herminghaus and C. C. Maass, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 64 CrossRef PubMed.
- S. Thutupalli, D. Geyer, R. Singh, R. Adhikari and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5403–5408 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- J. Bialké, H. Löwen and T. Speck, Europhys. Lett., 2013, 103, 30008 CrossRef.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- G. Liu, A. Patch, F. Bahar, D. Yllanes, R. D. Welch, M. C. Marchetti, S. Thutupalli and J. W. Shaevitz, Phys. Rev. Lett., 2019, 122, 248102 CrossRef CAS PubMed.
- A. Be'er, B. Ilkanaiv, R. Gross, D. B. Kearns, S. Heidenreich, M. Bär and G. Ariel, Commun. Phys., 2020, 3, 66 CrossRef.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 030904 CrossRef PubMed.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 268102 CrossRef PubMed.
- V. A. Martinez, E. Clément, J. Arlt, C. Douarche, A. Dawson, J. Schwarz-Linek, A. K. Creppy, V. Skultéty, A. N. Morozov, H. Auradou and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2326–2331 CrossRef CAS PubMed.
- S. Guo, D. Samanta, Y. Peng, X. Xu and X. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7212–7217 CrossRef CAS PubMed.
- R. H. Kraichnan and D. Montgomery, Rep. Prog. Phys., 1980, 43, 547–619 CrossRef CAS.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- J. Stenhammar, C. Nardini, R. W. Nash, D. Marenduzzo and A. Morozov, Phys. Rev. Lett., 2017, 119, 028005 CrossRef PubMed.
- D. Bárdfalvy, H. Nordanger, C. Nardini, A. Morozov and J. Stenhammar, Soft Matter, 2019, 15, 7747–7756 RSC.
- K. Qi, E. Westphal, G. Gompper and R. G. Winkler, Commun. Phys., 2022, 5, 49 CrossRef.
- E. Lushi, H. Wioland and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9733–9738 CrossRef CAS PubMed.
- M. Theillard, R. Alonso-Matillaa and D. Saintillan, Soft Matter, 2017, 13, 363–375 RSC.
- A. Suma, G. Gonnella, D. Marenduzzo and E. Orlandini, Europhys. Lett., 2014, 108, 56004 CrossRef.
- M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Condens. Matter Phys., 2020, 11, 441–466 CrossRef.
- S. E. Moran, I. R. Bruss, P. W. A. Schönhöfer and S. C. Glotzer, Soft Matter, 2022, 18, 1044–1053 RSC.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- R. Matas-Navarro, R. Golestanian, T. B. Liverpool and S. M. Fielding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032304 CrossRef PubMed.
- J.-T. Kuhr, F. Rühle and H. Stark, Soft Matter, 2019, 15, 5685–5694 RSC.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- M. J. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- M. Theers, E. Westphal, G. Gompper and R. G. Winkler, Soft Matter, 2016, 12, 7372–7385 RSC.
- K. Kyoya, D. Matsunaga, Y. Imai, T. Omori and T. Ishikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 063027 CrossRef CAS PubMed.
- F. Alarcón, C. Valeriani and I. Pagonabarraga, Soft Matter, 2017, 13, 814–826 RSC.
- N. Yoshinaga and T. B. Liverpool, Phys. Rev. E, 2017, 96, 020603 CrossRef PubMed.
- J. Blaschke, M. Maurer, K. Menon, A. Zöttl and H. Stark, Soft Matter, 2016, 12, 9821–9831 RSC.
- T. Ishikawa and T. J. Pedley, J. Fluid Mech., 2007, 588, 437–462 CrossRef.
- B. Delmotte, E. E. Keaveny, F. Plouraboué and E. Climent, J. Comput. Phys., 2015, 302, 524–547 CrossRef.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, J. Fluid Mech., 2008, 615, 401–431 CrossRef.
- A. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702 CrossRef.
- N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, J. Bacteriol., 2007, 189, 1756–1764 CrossRef CAS PubMed.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2010, 98, 2215–2225 CrossRef CAS PubMed.
- D. A. Fedosov, H. Noguchi and G. Gompper, Biomech. Model. Mechanobiol., 2014, 13, 239–258 CrossRef PubMed.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 61 CrossRef PubMed.
- T. Ishikawa, M. P. Simmonds and T. J. Pedley, J. Fluid Mech., 2006, 568, 119–160 CrossRef.
- I. Pagonabarraga and I. Llopis, Soft Matter, 2013, 9, 7174–7184 RSC.
- K. Qi, H. Annepu, G. Gompper and R. G. Winkler, Phys. Rev. Res., 2020, 2, 033275 CrossRef CAS.
- J. Hu, M. Yang, G. Gompper and R. G. Winkler, Soft Matter, 2015, 11, 7867–7876 RSC.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates and J. Tailleur, Phys. Rev. Lett., 2015, 114, 198301 CrossRef PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Bialké, T. Speck and H. Löwen, Phys. Rev. Lett., 2012, 108, 168301 CrossRef PubMed.
- D. Levis and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062301 CrossRef PubMed.
- G. Li and J. X. Tang, Phys. Rev. Lett., 2009, 103, 078101 CrossRef PubMed.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810–8815 RSC.
- J. Elgeti and G. Gompper, Europhys. Lett., 2013, 101, 48003 CrossRef CAS.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- P. D. Frymier, R. M. Ford, H. C. Berg and P. T. Cummings, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 6195–6199 CrossRef CAS PubMed.
- G. Junot, T. Darnige, A. Lindner, V. A. Martinez, J. Arlt, A. Dawson, W. C. K. Poon, H. Auradou and E. Clément, Phys. Rev. Lett., 2022, 128, 248101 CrossRef CAS PubMed.
- M. A.-S. Vigeant, R. M. Ford, M. Wagner and L. K. Tamm, Appl. Environ. Microbiol., 2002, 68, 2794–2801 CrossRef CAS PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- I. O. Götze and G. Gompper, Europhys. Lett., 2011, 92, 64003 CrossRef.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J.: Spec. Top., 2012, 202, 1–162 CAS.
- J. S. Lintuvuori, A. T. Brown, K. Stratford and D. Marenduzzo, Soft Matter, 2016, 12, 7959–7968 RSC.
- K. Ishimoto and E. A. Gaffney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062702 CrossRef PubMed.
- K. Schaar, A. Zöttl and H. Stark, Phys. Rev. Lett., 2015, 115, 038101 CrossRef PubMed.
- Ö. Duman, R. E. Isele-Holder, J. Elgeti and G. Gompper, Soft Matter, 2018, 14, 4483–4494 RSC.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- J. Hu, A. Wysocki, R. G. Winkler and G. Gompper, Sci. Rep., 2015, 5, 9586 CrossRef PubMed.
- J. E. Keymer, P. Galajda, C. Muldoon, S. Park and R. H. Austin, Proc. Nat. Acad. Sci. USA, 2006, 103, 17290–17295 CrossRef CAS PubMed.
- T. Bhattacharjee and S. S. Datta, Nat. Commun., 2019, 10, 2075 CrossRef PubMed.
- G. Frangipane, G. Vizsnyiczai, C. Maggi, R. Savo, A. Sciortino, S. Gigan and R. Di Leonardo, Nat. Commun., 2019, 10, 2442 CrossRef.
- W. Helfrich, Z. Naturforsch., 1973, 28, 693–703 CrossRef CAS PubMed.
- Jülich Supercomputing Centre, J. Large-Scale Res. Facil., 2021, 7, A182.
Footnote |
| † Electronic supplementary information (ESI) available: Movies S1–S9 illustrating collective behavior of squirmers for different conditions and description of the movies are included. See DOI: https://doi.org/10.1039/d4sm00075g |
| This journal is © The Royal Society of Chemistry 2024 |