DOI:
10.1039/D4SM00061G
(Paper)
Soft Matter, 2024,
20, 5456-5463
Plateau–Rayleigh instability of a soft layer coated on a rigid cylinder
Received
16th January 2024
, Accepted 7th June 2024
First published on 13th June 2024
Abstract
We study the Plateau–Rayleigh instability of a soft viscoelastic solid layer coated on a rigid cylinder i.e., a soft fibre with a rigid core. The onset of instability is examined using a linear stability analysis. We find that increasing the rigid cylinder radius or the stiffness of the layer reduces the growth rate of the fastest growing mode. For each rigid cylinder radius, a critical elastocapillary number is found below which all wavelengths of disturbances are stable. The critical value for a soft fibre with a thick rigid cylindrical core can be several orders of magnitudes larger than that for a totally soft fibre (no rigid core). This highlights the strong stabilizing effect of the rigid core on the system. Increasing the relaxation timescale of the viscoelastic material also slows down the growth of disturbances, but has no effect on the critical elastocapillary number. Interestingly, the wavelength of the fastest growing mode is independent of the rigid cylinder radius for the purely elastic case.
1 Introduction
Significant stress is usually required for a solid to deform, and as such the effects due to surface tension have often been ignored. Soft solids such as elastomers and gels,1 and biological materials such as protein condensates,2 cells and tissues,3 on the other hand, have elastic moduli ranging between kPa and MPa, which means that they can deform much easier. In recent years, there has been significant attention to how capillary effects can lead to soft solid deformations, and fascinating elastocapillary phenomena have been discovered.4–8 The Plateau–Rayleigh instability (PRI),9,10 namely the instability driven by surface tension and often illustrated by the breakup of liquid jets into droplets,11 has currently been examined for fibres made of soft solids.12–21
Studies of the PRI of soft fibres have focused on soft materials that demonstrate elastic or viscoelastic responses.12–21 An experimental study using soft agar gel fibres by Mora et al.14 has shown that the instability occurs when the elastocapillary length γ/μ ≥ 6R, where R is the radius of the soft fibre, γ is the solid surface tension and μ is the shear modulus. Other studies of the PRI on a soft fibre include, for example, the formation of bead-on-string structures.12,16,18,22 Another interesting factor that might significantly modify the instability is having an inner rigid core, i.e. a fibre consists of a soft-layer-coated on a rigid cylinder. Such a kind of setup, but with a coated liquid film instead of a soft solid layer, has been studied extensively23–32 since the early works in the 1960s by Goren.33,34 Recent studies on this problem have addressed the effects of liquid slip on the solid surface28,32 and the dynamics of the droplets formed on the fibre.25 However, investigations on situations in which the coated layer is a soft solid are still missing. How viscoelastic properties and the rigid core influence the PRI of a soft-layer-coated fibre remain unclear, which is addressed in this article.
Soft solids have recently been used in many applications, for example in 3D bioprinting,35 mimicking muscle tissues in biomedicine36 and water harvesting.37 In living organisms, soft fibrous-shaped structures are often found in cellular tubes and compartments of cells. Instability of these biological ingredients have been rationalised through the PRI.38–42 One example is a recent study on the undulation and droplet formation of a layer of condensed protein TPX2 on a microtubule.42 Hence, investigating the PRI of fibrous soft solids is becoming more important for both understanding the fundamental physical problems and the development of new technologies. In this study, we examine the onset of PRI of a soft layer coated on a rigid cylinder through a linear stability analysis.
2 Formulation
We consider a rigid cylinder of radius r0 coated with a layer of incompressible viscoelastic material of density ρ and uniform thickness H at an undeformed state. The whole fibre consisting of the rigid cylinder and the coated soft layer has a total radius R = r0 + H as shown in Fig. 1. Consider that the fiber is thin enough such that the Bond number Bo ≡ ρgR2/γ ≪ 1, where g is the gravitational acceleration, which allows us to neglect the effect of gravity. By only consider viscoelastic stresses, the equation of motion of a soft material element is given by| |  | (1) |
where σij(x,t) and ui(x,t) are respectively the stress tensor and the displacement vector in index notation at a position vector x and time t. Assuming a linear viscoelastic response of the incompressible soft material, the relation between σij and the strain tensor εij is| |  | (2) |
where μ(t) is the shear relaxation function, p is the pressure, δij is the Kronecker delta, and the strain tensor εij is related to the displacement as| | 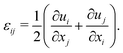 | (3) |
 |
| | Fig. 1 Schematic representation of an infinitely long, rigid cylinder of radius r0 coated with a layer of incompressible viscoelastic material of uniform thickness H at an undeformed state. A random disturbance of the interface of the viscoelastic layer is decomposed into sinusoidal deformations of wavenumber k. In cylindrical coordinate systems, r and z are respectively the radial coordinate and the longitudinal coordinate. | |
There are different models that have been used to describe viscoelastic materials. The simplest models are the Kelvin–Voigt model or the Maxwell model, which consists of a spring and a viscous damper connected in parallel or in series respectively. In this study, we consider the soft material to behave as a gel described by the Chasset–Thirion model assuming a power law response given by
| |  | (4) |
where
μ0 is the static shear modulus,
τ is the relaxation timescale of the viscoelastic response,
Γ is the gamma function and
n is a parameter typically smaller than or equal to unity.
To compute the growth rate of disturbance on the viscoelastic layer, we follow the approach delineated by previous studies.17,32 We decompose the time-dependent variables into normal modes est, where s is the growth rate. The amplitude of the normal mode of a function f(t) is obtained by the Laplace transform defined as
| |  | (5) |
We apply the Laplace transform to the constitutive relation (2) and obtain
| | 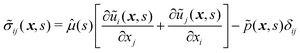 | (6) |
where
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ij
ij,
ũi and
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
are respectively the Laplace transform of
σij,
ui and
p, and
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif)
(
s) is the shear modulus in Laplace space defined as
| |  | (7) |
Thus the governing eqn (1) in Laplace space can be written as
| |  | (8) |
Next, we scale the lengths with the radius of the whole fibre R, the time with the inertial-capillary time  and the stresses by μo. We define the following dimensionless variables as
and the stresses by μo. We define the following dimensionless variables as
| |  | (9) |
| |  | (10) |
Note that variables in Laplace space have an additional dimension of time. The dimensionless form of the governing equation (eqn (8)) in Laplace space is
| |  | (11) |
where
| |  | (12) |
is the inverse of the dimensionless shear modulus in Laplace space which is a function of
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
and consists of 2 parameters:
Σ ≡
γ/(
μ0R) and
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)
≡
τ/
tc. In general, the expression of
β depends on the viscoelastic model. The parameter
Σ is called the elastocapillary number which compares the capillary pressure to the elastic stress. When
Σ → ∞, capillarity dominates over elasticity. The other parameter
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)
is the ratio of the viscoelastic relaxation timescale to the inertial-capillary time and can be interpreted as the Deborah number since the material responds purely elastically when
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)
= 0. When
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)
→ ∞, viscoelastic effects are expected to dominate over inertial effects. To sum up, the dimensionless control parameters of the system are:
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0,
Σ,
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif)
and
n.
We consider only the longitudinal disturbance and neglect the azimuthal disturbance as azimuthal normal modes always increase the surface energy.11 The deformation of the soft layer is axisymmetric. We hence use the cylindrical coordinate system (r,ϕ,z) and the corresponding unit vectors are denoted as (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ,
,![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ,ẑ). The displacement vector is denoted as u(r,z,t) = ur(r,z,t)
,ẑ). The displacement vector is denoted as u(r,z,t) = ur(r,z,t)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) + uz(r,z,t)ẑ. Note that uϕ = 0 due to axisymmetry.
+ uz(r,z,t)ẑ. Note that uϕ = 0 due to axisymmetry.
The governing eqn (11) can be solved by applying the Helmholtz decomposition of the displacement as described in ref. 17 and 32. The general solutions are given as
| | ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ( (![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) = − ) = −![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) 2[A1I0( 2[A1I0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) +A3K0( ) +A3K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei )]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) , , | (13) |
| | ūr = [A1![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1( I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A2(i ) − A2(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I1(α )I1(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A3 ) − A3![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1( K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A4(i ) − A4(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K1(α )K1(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei )]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) , , | (14) |
and
| | ūz = [A1(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I0( )I0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) + A2αI0(α ) + A2αI0(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) + A3(i ) + A3(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K0( )K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A4αK0(α ) − A4αK0(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei )]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) | (15) |
where
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
≡
kR is the dimensionless wavenumber,
I and
K are respectively the modified Bessel functions of the first and second kind,

is a function of
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
and
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
, and is introduced here to simplify the expressions of equations, and
Am(
m = 1,2,3,4) are the undermined coefficients.
Next we impose the boundary conditions. At ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =
= ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 ≡ r0/R, there is no penetration of material, thus
0 ≡ r0/R, there is no penetration of material, thus
| | ūr|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = =![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0. 0 = 0. | (16) |
For the z-direction, we impose a no-slip condition
| | ūz|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = =![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0. 0 = 0. | (17) |
At ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 1, we assume the slope of the deformed interface to be small. Balancing the Laplace pressure due to solid surface tension and the viscoelastic stresses gives
= 1, we assume the slope of the deformed interface to be small. Balancing the Laplace pressure due to solid surface tension and the viscoelastic stresses gives
| | 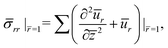 | (18) |
in the
r-direction, and gives the vanishing shear stress
| | ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) rz| rz|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =1 = 0 =1 = 0 | (19) |
in the
z-direction.
3 Dispersion relation
Using the expressions of the general solutions (eqn (13)–(15)) for the boundary conditions (eqn (16)–(19)) yields a set of linear equations for the unknowns Am which is given in Appendix 6.1. The solvability condition for non-trivial solutions of the linear equations with unknowns Am is that the determinant is vanishing, which gives the following dispersion relation| |  | (20) |
where
when ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 → 0, the modified Bessel functions I0(
0 → 0, the modified Bessel functions I0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) and I1(
0) and I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) are bounded, but K0(
0) are bounded, but K0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) and K1(
0) and K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) diverge. These unbounded terms are eliminated for the case of
0) diverge. These unbounded terms are eliminated for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.17 To examine the feature of the dispersion relation for small
0 = 0.17 To examine the feature of the dispersion relation for small ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, we expand the determinant of the dispersion relation (20) in series of
0, we expand the determinant of the dispersion relation (20) in series of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. The result for the leading order terms is given in Appendix 6.2 which consists of logarithmic terms of
0. The result for the leading order terms is given in Appendix 6.2 which consists of logarithmic terms of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
4 Results
The validation of the dispersion relation (eqn (20)) is presented in Appendix 6.3 in which we compare our results in the Newtonian fluid limit with previous studies in the literature. In this section, we first consider the purely elastic solid limit and then we focus on the effects of viscoelasticity.
4.1 Purely elastic solid limit
When the viscoelastic relaxation timescale τ is small compared to the inertial-capillary time  , i.e. taking the limit
, i.e. taking the limit ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → 0, our viscoelastic model reduces to the purely elastic model. In this limit,
→ 0, our viscoelastic model reduces to the purely elastic model. In this limit,  and β = Σ in the dispersion relation (eqn (20)). We examine how the instability depends on the dimensionless parameters Σ and
and β = Σ in the dispersion relation (eqn (20)). We examine how the instability depends on the dimensionless parameters Σ and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
4.1.1 Dependence on the rigid core radius and the elastocapilliary number.
We show the dispersion relation (eqn (20)) by plotting the dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as a function of the dimensionless wavenumber
as a function of the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of Σ and a fixed
for different values of Σ and a fixed ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 in Fig. 2(a). We see that for each curve, the unstable modes (i.e.
0 = 0.1 in Fig. 2(a). We see that for each curve, the unstable modes (i.e. ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) > 0) lie within a certain range of dimensionless wavenumbers, i.e.
> 0) lie within a certain range of dimensionless wavenumbers, i.e. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 <
1 < ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) <
< ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2, where
2, where ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and
1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 are defined as
2 are defined as ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1) = 0 and
1) = 0 and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2) = 0. Within each range of unstable modes, there is a dimensionless wavenumber
2) = 0. Within each range of unstable modes, there is a dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) =
= ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m that corresponds to the fastest growing mode with a maximum dimensionless growth rate
m that corresponds to the fastest growing mode with a maximum dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m ≡
m ≡ ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) =
= ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m). To study how the characteristic quantities depend on the control parameters, we plot
m). To study how the characteristic quantities depend on the control parameters, we plot ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m,
m, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m, and
m, and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 (and
1 (and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2) as a function of Σ respectively in Fig. 2(b)–(d) for three different dimensionless rigid core radii, i.e.
2) as a function of Σ respectively in Fig. 2(b)–(d) for three different dimensionless rigid core radii, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9,
0 = 10−9, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. We also add the result of Tamim et al.17 for the situation of a soft fibre without a rigid cylindrical core (i.e.
0 = 0.1 and 0.9. We also add the result of Tamim et al.17 for the situation of a soft fibre without a rigid cylindrical core (i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0). We see in Fig. 2(b) that for a fixed value of Σ,
0 = 0). We see in Fig. 2(b) that for a fixed value of Σ, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m is smaller for a larger
m is smaller for a larger ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. For all four different
0. For all four different ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, the dimensionless growth rate of the fastest growing mode
0, the dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing Σ. When Σ is reduced to a critical value Σc,
m decreases with decreasing Σ. When Σ is reduced to a critical value Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m drops to zero. There is no positive solution of
m drops to zero. There is no positive solution of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) for Σ < Σc. This means that the coated elastic layer is stable under disturbance of any wavelength when Σ < Σc. We would also point out that, firstly, the critical value Σc for
for Σ < Σc. This means that the coated elastic layer is stable under disturbance of any wavelength when Σ < Σc. We would also point out that, firstly, the critical value Σc for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 is orders of magnitude larger than that for
0 = 0.9 is orders of magnitude larger than that for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1. This can be understood as follows: when the coated layer becomes thinner, the strain is larger and hence a softer layer can still generate strong enough elastic stress to resist the growth of disturbance. Secondly, even for the rigid cylindrical core radius as small as
0 = 0.1. This can be understood as follows: when the coated layer becomes thinner, the strain is larger and hence a softer layer can still generate strong enough elastic stress to resist the growth of disturbance. Secondly, even for the rigid cylindrical core radius as small as ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9,
0 = 10−9, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m starts to deviate significantly from that for the case of
m starts to deviate significantly from that for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 when Σ is close to Σc. Moreover, the critical value Σc for
0 = 0 when Σ is close to Σc. Moreover, the critical value Σc for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9 (Σc = 8.7) is not the same as that for
0 = 10−9 (Σc = 8.7) is not the same as that for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (Σc = 6)14,17 but larger. These features will be discussed in details in Section 4.1.2 where a stability phase diagram of Σcvs.
0 = 0 (Σc = 6)14,17 but larger. These features will be discussed in details in Section 4.1.2 where a stability phase diagram of Σcvs. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 will be examined.
0 will be examined.
 |
| | Fig. 2 (a) The dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as a function of the dimensionless wavenumber as a function of the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of Σ and a fixed for different values of Σ and a fixed ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0 = 0.1 and ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0 (purely elastic). (b)–(d): The characteristic quantities = 0 (purely elastic). (b)–(d): The characteristic quantities ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m in (b), m in (b), ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m in (c), and m in (c), and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and 1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 in (d) as a function of Σ for four different dimensionless rigid core radius, i.e. 2 in (d) as a function of Σ for four different dimensionless rigid core radius, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (from Tamim et al.17), 0 = 0 (from Tamim et al.17), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9, 0 = 10−9, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. Other parameters: 0 = 0.1 and 0.9. Other parameters: ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0. = 0. | |
Interestingly, as shown in Fig. 2(c), we find that the dimensionless wavenumber of the fastest growing mode ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m is independent of the dimensionless radius of the rigid core
m is independent of the dimensionless radius of the rigid core ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, and decreases with reducing Σ. It is thus expected that elastic beads formed on a softer coated layer are closer together. When Σ → ∞, we find
0, and decreases with reducing Σ. It is thus expected that elastic beads formed on a softer coated layer are closer together. When Σ → ∞, we find ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m = 0.7, which agrees with the dimensionless wavenumber of the fastest growing mode for the classical PRI of inviscid fluid threads.10,11 Another remarkable point is that
m = 0.7, which agrees with the dimensionless wavenumber of the fastest growing mode for the classical PRI of inviscid fluid threads.10,11 Another remarkable point is that ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m starts to drop significantly with reducing Σ only when Σ ⪅ 102. For cases with Σc > 102, e.g. for
m starts to drop significantly with reducing Σ only when Σ ⪅ 102. For cases with Σc > 102, e.g. for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9, the dimensionless wavenumber of the fastest growing mode is always close to the asymptotic value, i.e.
0 = 0.9, the dimensionless wavenumber of the fastest growing mode is always close to the asymptotic value, i.e. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≈ 0.7. Regarding the range of unstable modes, as we can see in Fig. 2(a) and (d), it shrinks when Σ is reduced. In contrast to the
m ≈ 0.7. Regarding the range of unstable modes, as we can see in Fig. 2(a) and (d), it shrinks when Σ is reduced. In contrast to the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 case for which
0 = 0 case for which ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 remains zero, for non-zero
1 remains zero, for non-zero ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 cases,
0 cases, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 increases when Σ is reduced. This also means that the transition from unstable fibers to stable fibers (i.e. at Σ = Σc) occurs at
1 increases when Σ is reduced. This also means that the transition from unstable fibers to stable fibers (i.e. at Σ = Σc) occurs at ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≠ 0, which needs to be verified experimentally. It is expected that the bead separation formed on a soft fiber with a rigid core is finite (
m ≠ 0, which needs to be verified experimentally. It is expected that the bead separation formed on a soft fiber with a rigid core is finite (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≠ 0) at the transition, instead of diverging for the
m ≠ 0) at the transition, instead of diverging for the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 case.
0 = 0 case.
4.1.2. Stability phase diagram.
To show how the onset of instability depends on Σ and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, we plot Σc (in log scales) as a function of
0, we plot Σc (in log scales) as a function of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 in a phase diagram, see Fig. 3(a). We see that increasing the radius of the rigid cylindrical core or decreasing the elastocapillary number can make the coated film more stable. Hence both the stiffness and the rigid core have a stabilizing effect. In Fig. 3(b), we plot Σc as a function of the thickness of the coated layer, i.e.
0 in a phase diagram, see Fig. 3(a). We see that increasing the radius of the rigid cylindrical core or decreasing the elastocapillary number can make the coated film more stable. Hence both the stiffness and the rigid core have a stabilizing effect. In Fig. 3(b), we plot Σc as a function of the thickness of the coated layer, i.e. ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = 1 −
= 1 − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, in log–log scales. We find that when
0, in log–log scales. We find that when ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 ⪆ 0.2, the curve follows a power law Σc = 21.5
0 ⪆ 0.2, the curve follows a power law Σc = 21.5 ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) λ where λ ≈ −2.75. Hence the critical value Σc for a thin coated elastic film is orders of magnitudes larger than a thick film. In the opposite limit of
λ where λ ≈ −2.75. Hence the critical value Σc for a thin coated elastic film is orders of magnitudes larger than a thick film. In the opposite limit of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 → 0, we find that our results can be approximately described by a logarithmic relation given as
0 → 0, we find that our results can be approximately described by a logarithmic relation given as| |  | (21) |
where Σco = 6 is the critical value for a soft elastic fibre without a rigid cylindrical core obtained by Mora et al.14 or Tamim et al.,17 and a = 37 is a fitting parameter. The comparison is shown in Fig. 3(c) for small ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. This result is consistent with the series expansion of the dispersion relation (eqn (20)) for small
0. This result is consistent with the series expansion of the dispersion relation (eqn (20)) for small ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 given in Appendix 6.2.
0 given in Appendix 6.2.
 |
| | Fig. 3 (a) Stability phase diagram. Line: the critical elastocapillary number Σc (log scale) as a function of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. (b) The critical elastocapillary number Σc as a function of 1 − 0. (b) The critical elastocapillary number Σc as a function of 1 − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 in log–log scales. (c) A linear-log plot of the critical elastocapillary number Σc as a function of 0 in log–log scales. (c) A linear-log plot of the critical elastocapillary number Σc as a function of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. 0. | |
4.2. Viscoelastic effects
We study the instability when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0. We show results for two different rigid cylindrical core radii, namely
≠ 0. We show results for two different rigid cylindrical core radii, namely ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 (a thick coated layer) and
0 = 0.1 (a thick coated layer) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 (a thin coated layer). Since the critical elastocapillary numbers for
0 = 0.9 (a thin coated layer). Since the critical elastocapillary numbers for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and
0 = 0.1 and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 are different by orders of magnitude, we take a fixed value of Σ = 50 for the case of
0 = 0.9 are different by orders of magnitude, we take a fixed value of Σ = 50 for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and a fixed value of Σ = 15
0 = 0.1 and a fixed value of Σ = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the case of
000 for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9. In Fig. 4(a) and (b), we present the dispersion relation from eqn (20) for different
0 = 0.9. In Fig. 4(a) and (b), we present the dispersion relation from eqn (20) for different ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) , and in Fig. 4(c) and (d) for different n. We see that both
, and in Fig. 4(c) and (d) for different n. We see that both ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and
1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 are independent of
2 are independent of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and n. The dimensionless growth rate of the fastest growing mode
and n. The dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases when
m decreases when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) is enhanced. This means that the viscoelastic relaxation of the material slows down the growth of disturbance. We also see that when
is enhanced. This means that the viscoelastic relaxation of the material slows down the growth of disturbance. We also see that when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) is increased, the dimensionless wavenumber of the fastest growing mode becomes smaller for
is increased, the dimensionless wavenumber of the fastest growing mode becomes smaller for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 but remains constant for
0 = 0.1 but remains constant for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9. When varying the other viscoelastic parameter n, the dimensionless growth rate of the fastest growing mode
0 = 0.9. When varying the other viscoelastic parameter n, the dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing
m decreases with decreasing ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Hence smaller values of n have a larger damping effect. The change of
. Hence smaller values of n have a larger damping effect. The change of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m with varying
m with varying ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is more sensitive for
is more sensitive for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 than for
0 = 0.9 than for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 as we can see in Fig. 4(c) and (d). The dimensionless wavenumber of the fastest growing mode
0 = 0.1 as we can see in Fig. 4(c) and (d). The dimensionless wavenumber of the fastest growing mode ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m decreases slightly when n is increased from n = 0.2 to n = 1 for
m decreases slightly when n is increased from n = 0.2 to n = 1 for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 but remains constant for
0 = 0.1 but remains constant for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9.
0 = 0.9.
 |
| | Fig. 4 The dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as a function of the dimensionless wavenumber as a function of the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of for different values of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and a fixed value of exponent n = 1 with and a fixed value of exponent n = 1 with ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and Σ = 50 in (a), and 0 = 0.1 and Σ = 50 in (a), and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 and Σ = 15 0 = 0.9 and Σ = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in (b). The dimensionless growth rate 000 in (b). The dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) vs. the dimensionless wavenumber vs. the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of exponent n and a fixed value of for different values of exponent n and a fixed value of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 1 with = 1 with ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and Σ = 50 in (c), and 0 = 0.1 and Σ = 50 in (c), and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 and Σ = 15 0 = 0.9 and Σ = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in (d). 000 in (d). | |
Next, we take ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and n = 0.5, and show the results for
= 100 and n = 0.5, and show the results for ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m as a function of Σ for three different
m as a function of Σ for three different ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0, 0.1 and 0.9 in Fig. 5. We see that the behaviors of
0 = 0, 0.1 and 0.9 in Fig. 5. We see that the behaviors of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m for
m for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 are similar to those shown in Fig. 2(b) and (c) for the purely elastic case, i.e.
= 100 are similar to those shown in Fig. 2(b) and (c) for the purely elastic case, i.e. ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0, except that when Σ is close to the critical value Σc. When Σ is approaching Σc, the curves for both
= 0, except that when Σ is close to the critical value Σc. When Σ is approaching Σc, the curves for both ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m bend concavely, and the value of
m bend concavely, and the value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m becomes dependent on
m becomes dependent on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. However, varying the values of
0. However, varying the values of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or n does not change the critical values Σc, namely Σc remains the same as for the purely elastic case (
or n does not change the critical values Σc, namely Σc remains the same as for the purely elastic case (![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0). When Σ → ∞, viscoelastic effects disappear, and the results are the same as for the PRI of an inviscid fluid.11
= 0). When Σ → ∞, viscoelastic effects disappear, and the results are the same as for the PRI of an inviscid fluid.11
 |
| | Fig. 5 The characteristic quantities ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m in (a) and m in (a) and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m in (b) as a function of Σ for three different dimensionless rigid core radii, i.e. m in (b) as a function of Σ for three different dimensionless rigid core radii, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (from Tamim et al.17), 0 = 0 (from Tamim et al.17), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. Other parameters: 0 = 0.1 and 0.9. Other parameters: ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and n = 0.5. = 100 and n = 0.5. | |
It is also interesting to investigate the situation when keeping Σ finite, and taking the limit that the Deborah number ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. It is then expected that viscoelastic effects dominate over inertial effects. We then introduce a dimensionless growth rate using the viscoelastic timescale τ (instead of the inertial-capillary time tc) for the rescaling, i.e.
→ ∞. It is then expected that viscoelastic effects dominate over inertial effects. We then introduce a dimensionless growth rate using the viscoelastic timescale τ (instead of the inertial-capillary time tc) for the rescaling, i.e. ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ ≡ sτ =
τ ≡ sτ = ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) . The expression of β can be written as β = Σ/(1 +
. The expression of β can be written as β = Σ/(1 + ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) nτ). In the limit of
nτ). In the limit of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞,
→ ∞, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) =
= ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ/
τ/![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → 0, and thus α =
→ 0, and thus α = ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . Hence the dispersion relation (eqn (20)) consists of only the quantities
. Hence the dispersion relation (eqn (20)) consists of only the quantities ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, β and
0, β and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . Inertia plays no role in this limit. A plot of β vs.
. Inertia plays no role in this limit. A plot of β vs. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) from eqn (20) for
from eqn (20) for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 is shown in Fig. 6(a). The dimensionless maximum growth rate
0 = 0.1 is shown in Fig. 6(a). The dimensionless maximum growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m(
τ,m(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m) can be computed from the value of βm, defined as the minimum of β. Namely,
m) can be computed from the value of βm, defined as the minimum of β. Namely, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m = [Σ/βm − 1]1/n. We can then find the critical elastocapillary number by putting
τ,m = [Σ/βm − 1]1/n. We can then find the critical elastocapillary number by putting ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m = 0, and thus obtain Σc = βm. For
τ,m = 0, and thus obtain Σc = βm. For ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1, we find that Σc = 21.7 (see Fig. 6(a)), which is the same as for the purely elastic case.
0 = 0.1, we find that Σc = 21.7 (see Fig. 6(a)), which is the same as for the purely elastic case.
 |
| | Fig. 6 (a) The relation between β and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for the limiting case of for the limiting case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. (b) and (c) The characteristic quantities → ∞. (b) and (c) The characteristic quantities ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m in (b) and m in (b) and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m in (c) as a function of Σ for different values of m in (c) as a function of Σ for different values of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) . In (c) for . In (c) for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞, the dashed-dotted curve represents → ∞, the dashed-dotted curve represents ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m/100 vs. Σ. Other parameters: τ,m/100 vs. Σ. Other parameters: ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and n = 0.5. 0 = 0.1 and n = 0.5. | |
Lastly, we compare the results when varying ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) . In Fig. 6(b), we plot
. In Fig. 6(b), we plot ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) mvs. Σ for
mvs. Σ for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0, 100 and when
= 0, 100 and when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. We can see that the curve of
→ ∞. We can see that the curve of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m for
m for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 becomes flat when Σ is approaching Σc, which collapses with the constant value
= 100 becomes flat when Σ is approaching Σc, which collapses with the constant value ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m = 0.586 for the case of
m = 0.586 for the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. In Fig. 6(c), we plot
→ ∞. In Fig. 6(c), we plot ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) mvs. Σ for
mvs. Σ for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0 and 100. To compare the results of
= 0 and 100. To compare the results of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and the case of
= 100 and the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞, we divide
→ ∞, we divide ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m for the case of
τ,m for the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞ by the value
→ ∞ by the value ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 since
= 100 since ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) =
= ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ/
τ/![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) , and add a curve for
, and add a curve for ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m/100 vs. Σ in Fig. 6(c). We can see that for Σ close to Σc,
τ,m/100 vs. Σ in Fig. 6(c). We can see that for Σ close to Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m for τ = 100 and
m for τ = 100 and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m/100 collapse. Hence for
τ,m/100 collapse. Hence for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0, when Σ is approaching Σc,
≠ 0, when Σ is approaching Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m ≪ 1 and viscoelastic effects dominate over inertial effects.
m ≪ 1 and viscoelastic effects dominate over inertial effects.
5 Conclusions
We investigate the onset of the PRI of a soft layer coated on a rigid cylinder by analytically deriving the dispersion relation using the linear stability analysis. We implement the Chasset–Thirion model for the viscoelastic response of the soft layer. We find that the stiffness (characterized by 1/Σ) and the rigid cylindrical core (characterized by ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) have a stabilizing effect. The dimensionless growth rate of the fastest growing mode
0) have a stabilizing effect. The dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing Σ or increasing
m decreases with decreasing Σ or increasing ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. Importantly, there exists a critical elastocapillary number Σc for each
0. Importantly, there exists a critical elastocapillary number Σc for each ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 such that the coated layer is stable for any Σ < Σc. The critical value depends strongly on
0 such that the coated layer is stable for any Σ < Σc. The critical value depends strongly on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. For example, for
0. For example, for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9, the soft layer becomes unstable only when the fibre is very soft, namely when Σ ≥ 12
0 = 0.9, the soft layer becomes unstable only when the fibre is very soft, namely when Σ ≥ 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. While for a soft fibre without a rigid core (
100. While for a soft fibre without a rigid core (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0), the onset of instability occurs at Σ ≈ 6, which is three to four orders of magnitudes smaller. This remarkable result would be interesting to be verified by performing experiments for different soft coatings on a fibre. Regarding the dimensionless wavenumber of the fastest growing mode
0 = 0), the onset of instability occurs at Σ ≈ 6, which is three to four orders of magnitudes smaller. This remarkable result would be interesting to be verified by performing experiments for different soft coatings on a fibre. Regarding the dimensionless wavenumber of the fastest growing mode ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m, we find that
m, we find that ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m decreases with decreasing Σ. Interestingly,
m decreases with decreasing Σ. Interestingly, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m is independent of
m is independent of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 for the purely elastic case.
0 for the purely elastic case.
Regarding the roles of the viscoelastic parameters ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and n, we find that increasing the relaxation timescale of viscoelastic material
and n, we find that increasing the relaxation timescale of viscoelastic material ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or reducing the power n can slow down the growth of disturbance. Changing either
or reducing the power n can slow down the growth of disturbance. Changing either ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or n has no effect on the critical elastocapillary number. However, for
or n has no effect on the critical elastocapillary number. However, for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0, the curves for both
≠ 0, the curves for both ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) mvs. Σ and
mvs. Σ and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) mvs. Σ bend concavely when Σ is approaching Σc, and viscoelastic effects become dominant over inertial effects. The value of
mvs. Σ bend concavely when Σ is approaching Σc, and viscoelastic effects become dominant over inertial effects. The value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m becomes dependent on
m becomes dependent on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 when Σ is around Σc. On the other hand, viscoelastic effects disappear in the limit of Σ → ∞.
0 when Σ is around Σc. On the other hand, viscoelastic effects disappear in the limit of Σ → ∞.
Our linear stability analysis predicts the threshold of instability14 and the fastest growing modes. When the undulation of the interface grows, elastic stresses become larger and could stop the growth.14,18 To study the evolution of the undulation and the equilibrium shape of the deformed soft layer, nonlinear elastic or viscoelastic models are required as large deformation is expected.18
6 Appendices
6.1 Expressions of the boundary conditions
Using the expressions of the general solutions (eqn (13)–(15)) for the boundary conditions (eqn (16)–(19)) yields the following set of linear equations for the unknowns Am.| | A1![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1( I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A2i ) − A2i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1( I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) − A3 0α) − A3![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1( K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A4i ) − A4i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1( K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) = 0, 0α) = 0, | (22) |
| | A1(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I0( )I0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A2αI0( ) + A2αI0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) + A3(i 0α) + A3(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K0( )K0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A4αK0( ) − A4αK0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) = 0, 0α) = 0, | (23) |
| | 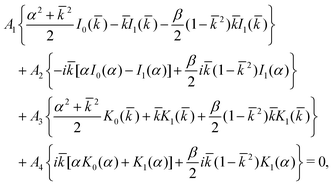 | (24) |
and| | A12i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2I1( 2I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A2( ) + A2(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)I1(α) − A32i 2 + α2)I1(α) − A32i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2K1( 2K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A4( ) + A4(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)K1(α) = 0 2 + α2)K1(α) = 0 | (25) |
6.2 Dispersion relation for small core radii
We expand the determinant D(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ,
,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,
,![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0,
0,![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ,n) of the dispersion relation (eqn (20)) in series of
,n) of the dispersion relation (eqn (20)) in series of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and the leading order terms are given as follows:
0 and the leading order terms are given as follows:| | D(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) , ,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ; ;![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, 0,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) , ,![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ,n) = F1 + F2ln( ,n) = F1 + F2ln(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) + …, 0) + …, | (26) |
where| | F1 = 2(C2D1 − C1D2)γE(α − ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )(α + )(α + ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − 2iα2(B2D1 − B1D2) ) − 2iα2(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K0(α) + i(B2D1−B1D2) K0(α) + i(B2D1−B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) (α2+ (α2+![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2)K0( 2)K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + α[2α2(B2C1 − B1C2) − i(2 + β)(B2D1 − B1D2) ) + α[2α2(B2C1 − B1C2) − i(2 + β)(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) + 2(B2C1 − B1C2) + 2(B2C1 − B1C2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + iβ(B2D1 − B1D2) 2 + iβ(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 3]K1(α) + i 3]K1(α) + i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2[(2 + β)(B2D1 − B1D2) + 4i(B2C1 − B1C2) 2[(2 + β)(B2D1 − B1D2) + 4i(B2C1 − B1C2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) + β(−B2D1 + B1D2) + β(−B2D1 + B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2]K1( 2]K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ), ), | (27) |
| | F2 = 2α2ln(α/2)(C2D1 − C1D2) + 2(−C2D1 + C1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2ln( 2ln(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) /2) /2) | (28) |
and
B2 = αI0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α), 0α), |
D1 = 2i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2I1( 2I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ), ), |
D2 = (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)I1(α), 2 + α2)I1(α), |
γ
E is Euler's constant ≈ 0.57721.
6.3 Validation of our model: the Newtonian fluid limit
Our viscoelastic model reduces to the Newtonian fluid when n = 1 and in the limits of μo → 0 and μoτ → η, where η is the dynamic viscosity of the fluid. In terms of the dimensionless parameters, it means Σ → ∞ and  , where Oh is called the Ohnesorge number. In this limiting situation, the dimensionless governing eqn (11) is reduced to
, where Oh is called the Ohnesorge number. In this limiting situation, the dimensionless governing eqn (11) is reduced to| |  | (29) |
where we have introduced a new rescaled growth rate ŝ ≡ ηRs/γ = Oh![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) . The dispersion relation is obtained by substituting
. The dispersion relation is obtained by substituting 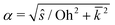 and β = 1/ŝ in eqn (20). The dimensionless control parameters are Oh and
and β = 1/ŝ in eqn (20). The dimensionless control parameters are Oh and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
6.3.1 Stokes flow case.
Taking further the limit that Oh → ∞, eqn (29) reduces to the Stokes equation in Laplace space. The remaining dimensionless control parameter is only ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. We validate the expression of our dispersion relation (eqn (20)) in this limiting case by comparing our results with that of Zhao et al.32 in which the dispersion relation is obtained using the normal mode method to solve the Stokes equations. Fig. 7 shows the comparison for the cases of very small fibre radius (
0. We validate the expression of our dispersion relation (eqn (20)) in this limiting case by comparing our results with that of Zhao et al.32 in which the dispersion relation is obtained using the normal mode method to solve the Stokes equations. Fig. 7 shows the comparison for the cases of very small fibre radius (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9), thick coated liquid film (
0 = 10−9), thick coated liquid film (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1) and thin coated liquid film (
0 = 0.1) and thin coated liquid film (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9).
0 = 0.9).
 |
| | Fig. 7 The dispersion relation between the growth rate ŝ and the wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) in the Stokes flow limit for in the Stokes flow limit for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9 in (a), 0 = 10−9 in (a), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 in (b) and 0 = 0.1 in (b) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 in (c). Solid lines: our results when substituting α = 0 = 0.9 in (c). Solid lines: our results when substituting α = ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) and β = 1/ŝ for eqn (20). Dashed lines: results of Zhao et al.32 and β = 1/ŝ for eqn (20). Dashed lines: results of Zhao et al.32 | |
Data availability
Data for this article, including the codes used to compute the data shown in the figures, are available at https://doi.org/10.11582/2024.00099.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge financial support from the Research Council of Norway (Project No. 315110).
References
- Y. Guo, J. Bae, Z. Fang, P. Li, F. Zhao and G. Yu, Chem. Rev., 2020, 120, 7642–7707 CrossRef CAS PubMed.
- Z. G. Qian, S. C. Huang and X. X. Xia, Nat. Chem. Biol., 2022, 18, 1330–1340 CrossRef CAS PubMed.
- I. Levental, P. C. Georges and P. A. Janmey, Soft Matter, 2007, 3, 299–306 RSC.
- B. Roman and J. Bico, J. Phys.: Condens. Matter, 2010, 22, 493101 CrossRef CAS PubMed.
- A. Jagota, D. Paretkar and A. Ghatak, Phys. Rev. E, 2012, 85, 051602 CrossRef PubMed.
- M. L. Wei, Europhys. Lett. (EPL), 2014, 106, 14002 CrossRef.
- R. W. Style, A. Jagota, C. Y. Hui and E. R. Dufresne, Annual Rev. Cond. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- J. Bico, É. Reyssat and B. Roman, Annu. Rev. Fluid Mech., 2018, 50, 629–659 CrossRef.
- J. A. F. Plateau, Acad. Sci. Bruxelles Mem., 1843, 16, 3 Search PubMed.
- L. Rayleigh, Proc. Roy. Soc. London, 1879, 10, 4 Search PubMed.
- J. Eggers and E. Villermaux, Rep. Progr. Phys., 2008, 71, 036601 CrossRef.
- M. Taffetani and P. Ciarletta, Phys. Rev. E, 2015, E91, 032413 CrossRef PubMed.
- C. Xuan and J. Biggins, Phys. Rev. E, 2017, 95, 1–8 CrossRef PubMed.
- S. Mora, T. Phou, J. M. Fromental, L. M. Pismen and Y. Pomeau, Phys. Rev. Lett., 2010, 105, 1–4 CrossRef PubMed.
- C. Lestringant and B. Audoly, Proc. R. Soc. A, 2020, 476, 20200337 CrossRef.
- Y. Fu, L. Jin and A. Goriely, J. Mech. Phys. Solids, 2021, 147, 104250 CrossRef.
- S. I. Tamim and J. B. Bostwick, Soft Matter, 2021, 17, 4170–4179 RSC.
- A. Pandey, M. Kansal, M. A. Herrada, J. Eggers and J. H. Snoeijer, Soft Matter, 2021, 17, 5148–5161 RSC.
- B. Dortdivanlioglu and A. Javili, Extreme Mech. Lett., 2022, 55, 101797 CrossRef.
- G. Yang, C. F. Gao and C. Q. Ru, Int. J. Solids Struct., 2022, 241, 111491 CrossRef.
- C. Q. Ru, Mech. Res. Communicat., 2022, 124, 103959 CrossRef.
- P. P. Bhat, S. Appathurai, M. T. Harris, M. Pasquali, G. H. McKinley and O. A. Basaran, Nat. Phys., 2010, 6, 625–631 Search PubMed.
- D. Quéré, Annu. Rev. Fluid Mech., 1999, 31, 347–384 CrossRef.
- H.-C. Chang and E. A. Demekhin, J. Fluid Mech., 1999, 380, 233–255 CrossRef CAS.
- I. L. Kliakhandler, S. H. Davis and S. G. Bankoff, J. Fluid Mech., 2001, 429, 381–390 CrossRef CAS.
- C. Ruyer-quil, P. Treveleyan, F. Giorgiutti-dauphiné, C. Duprat and S. Kalliadasis, J. Fluid Mech., 2008, 603, 431–462 CrossRef.
- Y. Zheng, H. Bai, Z. Huang, X. Tian, F.-Q. Nie, Y. Zhao, J. Zhai and L. Jiang, Nature, 2010, 463, 640–643 CrossRef CAS PubMed.
- S. Haefner, M. Benzaquen, O. Bäumchen, T. Salez, R. Peters, J. D. McGraw, K. Jacobs, E. Raphaël and K. Dalnoki-Veress, Nat. Commun., 2015, 6, 7409 CrossRef CAS PubMed.
- A. Sadeghpour, Z. Zeng and Y. S. Ju, Langmuir, 2017, 33, 6292–6299 CrossRef CAS PubMed.
- H. Chen, T. Ran, Y. Gan, J. Zhou, Y. Zhang, L. Zhang, D. Zhang and L. Jiang, Nat. Mater., 2018, 17, 935–942 CrossRef CAS PubMed.
- H. Ji, C. Falcon, A. Sadeghpour, Z. Zeng, Y. S. Ju and A. L. Bertozzi, J. Fluid Mech., 2019, 865, 303–327 CrossRef CAS.
- C. Zhao, Y. Zhang and T. Si, J. Fluid Mech., 2023, 954, 1–22 Search PubMed.
- S. L. Goren, J. Fluid Mech., 1962, 12, 309–319 CrossRef.
- S. L. Goren, J. Colloid Sci., 1964, 19, 81–86 CrossRef CAS.
- Y. Zhang, S. T. Ellison, S. Duraivel, C. D. Morley, C. R. Taylor and T. E. Angelini, Bioprinting, 2021, 21, e00121 CrossRef.
- M. M. Fitzgerald, K. Bootsma, J. A. Berberich and J. L. Sparks, Biomacromolecules, 2015, 16, 1497–1505 CrossRef CAS PubMed.
- D. K. Nandakumar, Y. Zhang, S. K. Ravi, N. Guo, C. Zhang and S. C. Tan, Adv. Mater., 2019, 31, 1806730 CrossRef PubMed.
- R. Bar-Ziv and E. Moses, Phys. Rev. Lett., 1994, 73, 1392–1395 CrossRef PubMed.
- E. Hannezo, J. Prost and J.-F. M. C. Joanny, Phys. Rev. Lett., 2012, 109, 018101 CrossRef PubMed.
- D. Gonzalez-Rodriguez, S. Sart, A. Babataheri, D. Tareste, A. I. Barakat, C. Clanet and J. Husson, Phys. Rev. Lett., 2015, 115, 088102 CrossRef PubMed.
- M. R. King and S. Petry, Nat. Commun., 2020, 11, 270 CrossRef CAS PubMed.
- S. U. Setru, B. Gouveia, R. Alfaro-Aco, J. W. Shaevitz, H. A. Stone and S. Petry, Nat. Phys., 2021, 17, 493–498 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Tak Shing
Chan
and
Tak Shing
Chan
 *
*


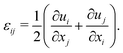


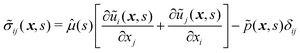
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ij, ũi and
ij, ũi and ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) are respectively the Laplace transform of σij, ui and p, and
are respectively the Laplace transform of σij, ui and p, and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (s) is the shear modulus in Laplace space defined as
(s) is the shear modulus in Laplace space defined as

 and the stresses by μo. We define the following dimensionless variables as
and the stresses by μo. We define the following dimensionless variables as



![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) and consists of 2 parameters: Σ ≡ γ/(μ0R) and
and consists of 2 parameters: Σ ≡ γ/(μ0R) and ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≡ τ/tc. In general, the expression of β depends on the viscoelastic model. The parameter Σ is called the elastocapillary number which compares the capillary pressure to the elastic stress. When Σ → ∞, capillarity dominates over elasticity. The other parameter
≡ τ/tc. In general, the expression of β depends on the viscoelastic model. The parameter Σ is called the elastocapillary number which compares the capillary pressure to the elastic stress. When Σ → ∞, capillarity dominates over elasticity. The other parameter ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) is the ratio of the viscoelastic relaxation timescale to the inertial-capillary time and can be interpreted as the Deborah number since the material responds purely elastically when
is the ratio of the viscoelastic relaxation timescale to the inertial-capillary time and can be interpreted as the Deborah number since the material responds purely elastically when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0. When
= 0. When ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞, viscoelastic effects are expected to dominate over inertial effects. To sum up, the dimensionless control parameters of the system are:
→ ∞, viscoelastic effects are expected to dominate over inertial effects. To sum up, the dimensionless control parameters of the system are: ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, Σ,
0, Σ, ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and n.
and n.
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ,
,![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) ,ẑ). The displacement vector is denoted as u(r,z,t) = ur(r,z,t)
,ẑ). The displacement vector is denoted as u(r,z,t) = ur(r,z,t)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) + uz(r,z,t)ẑ. Note that uϕ = 0 due to axisymmetry.
+ uz(r,z,t)ẑ. Note that uϕ = 0 due to axisymmetry.![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (
(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) = −
) = −![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) 2[A1I0(
2[A1I0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) +A3K0(
) +A3K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei
)]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ,
,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1(
I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A2(i
) − A2(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I1(α
)I1(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A3
) − A3![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1(
K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A4(i
) − A4(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K1(α
)K1(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei
)]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ,
,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I0(
)I0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) + A2αI0(α
) + A2αI0(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) + A3(i
) + A3(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K0(
)K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) − A4αK0(α
) − A4αK0(α![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )]ei
)]ei![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif)
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ≡ kR is the dimensionless wavenumber, I and K are respectively the modified Bessel functions of the first and second kind,
≡ kR is the dimensionless wavenumber, I and K are respectively the modified Bessel functions of the first and second kind,  is a function of
is a function of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) and
and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) , and is introduced here to simplify the expressions of equations, and Am(m = 1,2,3,4) are the undermined coefficients.
, and is introduced here to simplify the expressions of equations, and Am(m = 1,2,3,4) are the undermined coefficients.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =
= ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 ≡ r0/R, there is no penetration of material, thus
0 ≡ r0/R, there is no penetration of material, thus![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =
=![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.
0 = 0.![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =
=![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.
0 = 0.![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 1, we assume the slope of the deformed interface to be small. Balancing the Laplace pressure due to solid surface tension and the viscoelastic stresses gives
= 1, we assume the slope of the deformed interface to be small. Balancing the Laplace pressure due to solid surface tension and the viscoelastic stresses gives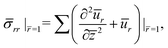
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) rz|
rz|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) =1 = 0
=1 = 0
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 → 0, the modified Bessel functions I0(
0 → 0, the modified Bessel functions I0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) and I1(
0) and I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) are bounded, but K0(
0) are bounded, but K0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) and K1(
0) and K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) diverge. These unbounded terms are eliminated for the case of
0) diverge. These unbounded terms are eliminated for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.17 To examine the feature of the dispersion relation for small
0 = 0.17 To examine the feature of the dispersion relation for small ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, we expand the determinant of the dispersion relation (20) in series of
0, we expand the determinant of the dispersion relation (20) in series of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. The result for the leading order terms is given in Appendix 6.2 which consists of logarithmic terms of
0. The result for the leading order terms is given in Appendix 6.2 which consists of logarithmic terms of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
 , i.e. taking the limit
, i.e. taking the limit ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → 0, our viscoelastic model reduces to the purely elastic model. In this limit,
→ 0, our viscoelastic model reduces to the purely elastic model. In this limit,  and β = Σ in the dispersion relation (eqn (20)). We examine how the instability depends on the dimensionless parameters Σ and
and β = Σ in the dispersion relation (eqn (20)). We examine how the instability depends on the dimensionless parameters Σ and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as a function of the dimensionless wavenumber
as a function of the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of Σ and a fixed
for different values of Σ and a fixed ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 in Fig. 2(a). We see that for each curve, the unstable modes (i.e.
0 = 0.1 in Fig. 2(a). We see that for each curve, the unstable modes (i.e. ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) > 0) lie within a certain range of dimensionless wavenumbers, i.e.
> 0) lie within a certain range of dimensionless wavenumbers, i.e. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 <
1 < ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) <
< ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2, where
2, where ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and
1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 are defined as
2 are defined as ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1) = 0 and
1) = 0 and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2) = 0. Within each range of unstable modes, there is a dimensionless wavenumber
2) = 0. Within each range of unstable modes, there is a dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) =
= ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m that corresponds to the fastest growing mode with a maximum dimensionless growth rate
m that corresponds to the fastest growing mode with a maximum dimensionless growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m ≡
m ≡ ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) (
(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) =
= ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m). To study how the characteristic quantities depend on the control parameters, we plot
m). To study how the characteristic quantities depend on the control parameters, we plot ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m,
m, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m, and
m, and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 (and
1 (and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2) as a function of Σ respectively in Fig. 2(b)–(d) for three different dimensionless rigid core radii, i.e.
2) as a function of Σ respectively in Fig. 2(b)–(d) for three different dimensionless rigid core radii, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9,
0 = 10−9, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. We also add the result of Tamim et al.17 for the situation of a soft fibre without a rigid cylindrical core (i.e.
0 = 0.1 and 0.9. We also add the result of Tamim et al.17 for the situation of a soft fibre without a rigid cylindrical core (i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0). We see in Fig. 2(b) that for a fixed value of Σ,
0 = 0). We see in Fig. 2(b) that for a fixed value of Σ, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m is smaller for a larger
m is smaller for a larger ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. For all four different
0. For all four different ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, the dimensionless growth rate of the fastest growing mode
0, the dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing Σ. When Σ is reduced to a critical value Σc,
m decreases with decreasing Σ. When Σ is reduced to a critical value Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m drops to zero. There is no positive solution of
m drops to zero. There is no positive solution of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) for Σ < Σc. This means that the coated elastic layer is stable under disturbance of any wavelength when Σ < Σc. We would also point out that, firstly, the critical value Σc for
for Σ < Σc. This means that the coated elastic layer is stable under disturbance of any wavelength when Σ < Σc. We would also point out that, firstly, the critical value Σc for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 is orders of magnitude larger than that for
0 = 0.9 is orders of magnitude larger than that for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1. This can be understood as follows: when the coated layer becomes thinner, the strain is larger and hence a softer layer can still generate strong enough elastic stress to resist the growth of disturbance. Secondly, even for the rigid cylindrical core radius as small as
0 = 0.1. This can be understood as follows: when the coated layer becomes thinner, the strain is larger and hence a softer layer can still generate strong enough elastic stress to resist the growth of disturbance. Secondly, even for the rigid cylindrical core radius as small as ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9,
0 = 10−9, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m starts to deviate significantly from that for the case of
m starts to deviate significantly from that for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 when Σ is close to Σc. Moreover, the critical value Σc for
0 = 0 when Σ is close to Σc. Moreover, the critical value Σc for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9 (Σc = 8.7) is not the same as that for
0 = 10−9 (Σc = 8.7) is not the same as that for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (Σc = 6)14,17 but larger. These features will be discussed in details in Section 4.1.2 where a stability phase diagram of Σcvs.
0 = 0 (Σc = 6)14,17 but larger. These features will be discussed in details in Section 4.1.2 where a stability phase diagram of Σcvs. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 will be examined.
0 will be examined.

![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) as a function of the dimensionless wavenumber
as a function of the dimensionless wavenumber ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) for different values of Σ and a fixed
for different values of Σ and a fixed ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and
0 = 0.1 and ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0 (purely elastic). (b)–(d): The characteristic quantities
= 0 (purely elastic). (b)–(d): The characteristic quantities ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m in (b),
m in (b), ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m in (c), and
m in (c), and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and
1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 in (d) as a function of Σ for four different dimensionless rigid core radius, i.e.
2 in (d) as a function of Σ for four different dimensionless rigid core radius, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (from Tamim et al.17),
0 = 0 (from Tamim et al.17), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9,
0 = 10−9, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. Other parameters:
0 = 0.1 and 0.9. Other parameters: ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0.
= 0.![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m is independent of the dimensionless radius of the rigid core
m is independent of the dimensionless radius of the rigid core ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, and decreases with reducing Σ. It is thus expected that elastic beads formed on a softer coated layer are closer together. When Σ → ∞, we find
0, and decreases with reducing Σ. It is thus expected that elastic beads formed on a softer coated layer are closer together. When Σ → ∞, we find ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m = 0.7, which agrees with the dimensionless wavenumber of the fastest growing mode for the classical PRI of inviscid fluid threads.10,11 Another remarkable point is that
m = 0.7, which agrees with the dimensionless wavenumber of the fastest growing mode for the classical PRI of inviscid fluid threads.10,11 Another remarkable point is that ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m starts to drop significantly with reducing Σ only when Σ ⪅ 102. For cases with Σc > 102, e.g. for
m starts to drop significantly with reducing Σ only when Σ ⪅ 102. For cases with Σc > 102, e.g. for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9, the dimensionless wavenumber of the fastest growing mode is always close to the asymptotic value, i.e.
0 = 0.9, the dimensionless wavenumber of the fastest growing mode is always close to the asymptotic value, i.e. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≈ 0.7. Regarding the range of unstable modes, as we can see in Fig. 2(a) and (d), it shrinks when Σ is reduced. In contrast to the
m ≈ 0.7. Regarding the range of unstable modes, as we can see in Fig. 2(a) and (d), it shrinks when Σ is reduced. In contrast to the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 case for which
0 = 0 case for which ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 remains zero, for non-zero
1 remains zero, for non-zero ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 cases,
0 cases, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 increases when Σ is reduced. This also means that the transition from unstable fibers to stable fibers (i.e. at Σ = Σc) occurs at
1 increases when Σ is reduced. This also means that the transition from unstable fibers to stable fibers (i.e. at Σ = Σc) occurs at ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≠ 0, which needs to be verified experimentally. It is expected that the bead separation formed on a soft fiber with a rigid core is finite (
m ≠ 0, which needs to be verified experimentally. It is expected that the bead separation formed on a soft fiber with a rigid core is finite (![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m ≠ 0) at the transition, instead of diverging for the
m ≠ 0) at the transition, instead of diverging for the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 case.
0 = 0 case.![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, we plot Σc (in log scales) as a function of
0, we plot Σc (in log scales) as a function of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 in a phase diagram, see Fig. 3(a). We see that increasing the radius of the rigid cylindrical core or decreasing the elastocapillary number can make the coated film more stable. Hence both the stiffness and the rigid core have a stabilizing effect. In Fig. 3(b), we plot Σc as a function of the thickness of the coated layer, i.e.
0 in a phase diagram, see Fig. 3(a). We see that increasing the radius of the rigid cylindrical core or decreasing the elastocapillary number can make the coated film more stable. Hence both the stiffness and the rigid core have a stabilizing effect. In Fig. 3(b), we plot Σc as a function of the thickness of the coated layer, i.e. ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = 1 −
= 1 − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, in log–log scales. We find that when
0, in log–log scales. We find that when ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 ⪆ 0.2, the curve follows a power law Σc = 21.5
0 ⪆ 0.2, the curve follows a power law Σc = 21.5 ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) λ where λ ≈ −2.75. Hence the critical value Σc for a thin coated elastic film is orders of magnitudes larger than a thick film. In the opposite limit of
λ where λ ≈ −2.75. Hence the critical value Σc for a thin coated elastic film is orders of magnitudes larger than a thick film. In the opposite limit of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 → 0, we find that our results can be approximately described by a logarithmic relation given as
0 → 0, we find that our results can be approximately described by a logarithmic relation given as
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. This result is consistent with the series expansion of the dispersion relation (eqn (20)) for small
0. This result is consistent with the series expansion of the dispersion relation (eqn (20)) for small ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 given in Appendix 6.2.
0 given in Appendix 6.2.
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0. We show results for two different rigid cylindrical core radii, namely
≠ 0. We show results for two different rigid cylindrical core radii, namely ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 (a thick coated layer) and
0 = 0.1 (a thick coated layer) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 (a thin coated layer). Since the critical elastocapillary numbers for
0 = 0.9 (a thin coated layer). Since the critical elastocapillary numbers for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and
0 = 0.1 and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 are different by orders of magnitude, we take a fixed value of Σ = 50 for the case of
0 = 0.9 are different by orders of magnitude, we take a fixed value of Σ = 50 for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and a fixed value of Σ = 15
0 = 0.1 and a fixed value of Σ = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the case of
000 for the case of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9. In Fig. 4(a) and (b), we present the dispersion relation from eqn (20) for different
0 = 0.9. In Fig. 4(a) and (b), we present the dispersion relation from eqn (20) for different ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) , and in Fig. 4(c) and (d) for different n. We see that both
, and in Fig. 4(c) and (d) for different n. We see that both ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 1 and
1 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 are independent of
2 are independent of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and n. The dimensionless growth rate of the fastest growing mode
and n. The dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases when
m decreases when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) is enhanced. This means that the viscoelastic relaxation of the material slows down the growth of disturbance. We also see that when
is enhanced. This means that the viscoelastic relaxation of the material slows down the growth of disturbance. We also see that when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) is increased, the dimensionless wavenumber of the fastest growing mode becomes smaller for
is increased, the dimensionless wavenumber of the fastest growing mode becomes smaller for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 but remains constant for
0 = 0.1 but remains constant for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9. When varying the other viscoelastic parameter n, the dimensionless growth rate of the fastest growing mode
0 = 0.9. When varying the other viscoelastic parameter n, the dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing
m decreases with decreasing ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Hence smaller values of n have a larger damping effect. The change of
. Hence smaller values of n have a larger damping effect. The change of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m with varying
m with varying ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is more sensitive for
is more sensitive for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9 than for
0 = 0.9 than for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 as we can see in Fig. 4(c) and (d). The dimensionless wavenumber of the fastest growing mode
0 = 0.1 as we can see in Fig. 4(c) and (d). The dimensionless wavenumber of the fastest growing mode ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m decreases slightly when n is increased from n = 0.2 to n = 1 for
m decreases slightly when n is increased from n = 0.2 to n = 1 for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 but remains constant for
0 = 0.1 but remains constant for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9.
0 = 0.9.
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and n = 0.5, and show the results for
= 100 and n = 0.5, and show the results for ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m as a function of Σ for three different
m as a function of Σ for three different ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0, 0.1 and 0.9 in Fig. 5. We see that the behaviors of
0 = 0, 0.1 and 0.9 in Fig. 5. We see that the behaviors of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m for
m for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 are similar to those shown in Fig. 2(b) and (c) for the purely elastic case, i.e.
= 100 are similar to those shown in Fig. 2(b) and (c) for the purely elastic case, i.e. ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0, except that when Σ is close to the critical value Σc. When Σ is approaching Σc, the curves for both
= 0, except that when Σ is close to the critical value Σc. When Σ is approaching Σc, the curves for both ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m and
m and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m bend concavely, and the value of
m bend concavely, and the value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m becomes dependent on
m becomes dependent on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. However, varying the values of
0. However, varying the values of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or n does not change the critical values Σc, namely Σc remains the same as for the purely elastic case (
or n does not change the critical values Σc, namely Σc remains the same as for the purely elastic case (![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0). When Σ → ∞, viscoelastic effects disappear, and the results are the same as for the PRI of an inviscid fluid.11
= 0). When Σ → ∞, viscoelastic effects disappear, and the results are the same as for the PRI of an inviscid fluid.11
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m in (a) and
m in (a) and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m in (b) as a function of Σ for three different dimensionless rigid core radii, i.e.
m in (b) as a function of Σ for three different dimensionless rigid core radii, i.e. ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0 (from Tamim et al.17),
0 = 0 (from Tamim et al.17), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 and 0.9. Other parameters:
0 = 0.1 and 0.9. Other parameters: ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and n = 0.5.
= 100 and n = 0.5.![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. It is then expected that viscoelastic effects dominate over inertial effects. We then introduce a dimensionless growth rate using the viscoelastic timescale τ (instead of the inertial-capillary time tc) for the rescaling, i.e.
→ ∞. It is then expected that viscoelastic effects dominate over inertial effects. We then introduce a dimensionless growth rate using the viscoelastic timescale τ (instead of the inertial-capillary time tc) for the rescaling, i.e. ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ ≡ sτ =
τ ≡ sτ = ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) . The expression of β can be written as β = Σ/(1 +
. The expression of β can be written as β = Σ/(1 + ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) nτ). In the limit of
nτ). In the limit of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞,
→ ∞, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) =
= ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ/
τ/![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → 0, and thus α =
→ 0, and thus α = ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . Hence the dispersion relation (eqn (20)) consists of only the quantities
. Hence the dispersion relation (eqn (20)) consists of only the quantities ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0, β and
0, β and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . Inertia plays no role in this limit. A plot of β vs.
. Inertia plays no role in this limit. A plot of β vs. ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) from eqn (20) for
from eqn (20) for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1 is shown in Fig. 6(a). The dimensionless maximum growth rate
0 = 0.1 is shown in Fig. 6(a). The dimensionless maximum growth rate ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m(
τ,m(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m) can be computed from the value of βm, defined as the minimum of β. Namely,
m) can be computed from the value of βm, defined as the minimum of β. Namely, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m = [Σ/βm − 1]1/n. We can then find the critical elastocapillary number by putting
τ,m = [Σ/βm − 1]1/n. We can then find the critical elastocapillary number by putting ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m = 0, and thus obtain Σc = βm. For
τ,m = 0, and thus obtain Σc = βm. For ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1, we find that Σc = 21.7 (see Fig. 6(a)), which is the same as for the purely elastic case.
0 = 0.1, we find that Σc = 21.7 (see Fig. 6(a)), which is the same as for the purely elastic case.![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) . In Fig. 6(b), we plot
. In Fig. 6(b), we plot ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) mvs. Σ for
mvs. Σ for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0, 100 and when
= 0, 100 and when ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. We can see that the curve of
→ ∞. We can see that the curve of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m for
m for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 becomes flat when Σ is approaching Σc, which collapses with the constant value
= 100 becomes flat when Σ is approaching Σc, which collapses with the constant value ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m = 0.586 for the case of
m = 0.586 for the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞. In Fig. 6(c), we plot
→ ∞. In Fig. 6(c), we plot ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) mvs. Σ for
mvs. Σ for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 0 and 100. To compare the results of
= 0 and 100. To compare the results of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 and the case of
= 100 and the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞, we divide
→ ∞, we divide ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m for the case of
τ,m for the case of ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) → ∞ by the value
→ ∞ by the value ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) = 100 since
= 100 since ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) =
= ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ/
τ/![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) , and add a curve for
, and add a curve for ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m/100 vs. Σ in Fig. 6(c). We can see that for Σ close to Σc,
τ,m/100 vs. Σ in Fig. 6(c). We can see that for Σ close to Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m for τ = 100 and
m for τ = 100 and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) τ,m/100 collapse. Hence for
τ,m/100 collapse. Hence for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0, when Σ is approaching Σc,
≠ 0, when Σ is approaching Σc, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m ≪ 1 and viscoelastic effects dominate over inertial effects.
m ≪ 1 and viscoelastic effects dominate over inertial effects.![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) have a stabilizing effect. The dimensionless growth rate of the fastest growing mode
0) have a stabilizing effect. The dimensionless growth rate of the fastest growing mode ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) m decreases with decreasing Σ or increasing
m decreases with decreasing Σ or increasing ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. Importantly, there exists a critical elastocapillary number Σc for each
0. Importantly, there exists a critical elastocapillary number Σc for each ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 such that the coated layer is stable for any Σ < Σc. The critical value depends strongly on
0 such that the coated layer is stable for any Σ < Σc. The critical value depends strongly on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. For example, for
0. For example, for ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9, the soft layer becomes unstable only when the fibre is very soft, namely when Σ ≥ 12
0 = 0.9, the soft layer becomes unstable only when the fibre is very soft, namely when Σ ≥ 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. While for a soft fibre without a rigid core (
100. While for a soft fibre without a rigid core (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0), the onset of instability occurs at Σ ≈ 6, which is three to four orders of magnitudes smaller. This remarkable result would be interesting to be verified by performing experiments for different soft coatings on a fibre. Regarding the dimensionless wavenumber of the fastest growing mode
0 = 0), the onset of instability occurs at Σ ≈ 6, which is three to four orders of magnitudes smaller. This remarkable result would be interesting to be verified by performing experiments for different soft coatings on a fibre. Regarding the dimensionless wavenumber of the fastest growing mode ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m, we find that
m, we find that ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m decreases with decreasing Σ. Interestingly,
m decreases with decreasing Σ. Interestingly, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m is independent of
m is independent of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 for the purely elastic case.
0 for the purely elastic case.
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and n, we find that increasing the relaxation timescale of viscoelastic material
and n, we find that increasing the relaxation timescale of viscoelastic material ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or reducing the power n can slow down the growth of disturbance. Changing either
or reducing the power n can slow down the growth of disturbance. Changing either ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) or n has no effect on the critical elastocapillary number. However, for
or n has no effect on the critical elastocapillary number. However, for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ≠ 0, the curves for both
≠ 0, the curves for both ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) mvs. Σ and
mvs. Σ and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) mvs. Σ bend concavely when Σ is approaching Σc, and viscoelastic effects become dominant over inertial effects. The value of
mvs. Σ bend concavely when Σ is approaching Σc, and viscoelastic effects become dominant over inertial effects. The value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) m becomes dependent on
m becomes dependent on ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 when Σ is around Σc. On the other hand, viscoelastic effects disappear in the limit of Σ → ∞.
0 when Σ is around Σc. On the other hand, viscoelastic effects disappear in the limit of Σ → ∞.![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1(
I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A2i
) − A2i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) I1(
I1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) − A3
0α) − A3![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1(
K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A4i
) − A4i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K1(
K1(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) = 0,
0α) = 0,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I0(
)I0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A2αI0(
) + A2αI0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) + A3(i
0α) + A3(i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )K0(
)K0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − A4αK0(
) − A4αK0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α) = 0,
0α) = 0,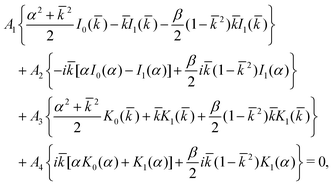
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2I1(
2I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A2(
) + A2(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)I1(α) − A32i
2 + α2)I1(α) − A32i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2K1(
2K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + A4(
) + A4(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)K1(α) = 0
2 + α2)K1(α) = 0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ,
,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,
,![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0,
0,![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ,n) of the dispersion relation (eqn (20)) in series of
,n) of the dispersion relation (eqn (20)) in series of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and the leading order terms are given as follows:
0 and the leading order terms are given as follows:![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ,
,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ;
;![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0,
0,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ,
,![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ,n) = F1 + F2ln(
,n) = F1 + F2ln(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0) + …,
0) + …,![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )(α +
)(α + ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) − 2iα2(B2D1 − B1D2)
) − 2iα2(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K0(α) + i(B2D1−B1D2)
K0(α) + i(B2D1−B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) (α2+
(α2+![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2)K0(
2)K0(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) + α[2α2(B2C1 − B1C2) − i(2 + β)(B2D1 − B1D2)
) + α[2α2(B2C1 − B1C2) − i(2 + β)(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) + 2(B2C1 − B1C2)
+ 2(B2C1 − B1C2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + iβ(B2D1 − B1D2)
2 + iβ(B2D1 − B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 3]K1(α) + i
3]K1(α) + i![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2[(2 + β)(B2D1 − B1D2) + 4i(B2C1 − B1C2)
2[(2 + β)(B2D1 − B1D2) + 4i(B2C1 − B1C2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) + β(−B2D1 + B1D2)
+ β(−B2D1 + B1D2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2]K1(
2]K1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ),
),![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2ln(
2ln(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) /2)
/2)![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )I0(
)I0(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0
0![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ),
),![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0α),
0α),![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2I1(
2I1(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ),
),![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) 2 + α2)I1(α),
2 + α2)I1(α), , where Oh is called the Ohnesorge number. In this limiting situation, the dimensionless governing eqn (11) is reduced to
, where Oh is called the Ohnesorge number. In this limiting situation, the dimensionless governing eqn (11) is reduced to
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) . The dispersion relation is obtained by substituting
. The dispersion relation is obtained by substituting 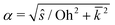 and β = 1/ŝ in eqn (20). The dimensionless control parameters are Oh and
and β = 1/ŝ in eqn (20). The dimensionless control parameters are Oh and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0.
0.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0. We validate the expression of our dispersion relation (eqn (20)) in this limiting case by comparing our results with that of Zhao et al.32 in which the dispersion relation is obtained using the normal mode method to solve the Stokes equations. Fig. 7 shows the comparison for the cases of very small fibre radius (
0. We validate the expression of our dispersion relation (eqn (20)) in this limiting case by comparing our results with that of Zhao et al.32 in which the dispersion relation is obtained using the normal mode method to solve the Stokes equations. Fig. 7 shows the comparison for the cases of very small fibre radius (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 10−9), thick coated liquid film (
0 = 10−9), thick coated liquid film (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.1) and thin coated liquid film (
0 = 0.1) and thin coated liquid film (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = 0.9).
0 = 0.9).








