 Open Access Article
Open Access ArticleSpontaneous crumpling of active spherical shells†
M. C.
Gandikota
 a,
Shibananda
Das
a,
Shibananda
Das
 ab and
A.
Cacciuto
*a
ab and
A.
Cacciuto
*a
aDepartment of Chemistry, Columbia University, 3000 Broadway, NY 10027, New York, USA. E-mail: ac2822@columbia.edu
bInstitute for Theoretical Physics, Georg-August University, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
First published on 15th April 2024
Abstract
The existence of a crumpled phase for self-avoiding elastic surfaces was postulated more than three decades ago using simple Flory-like scaling arguments. Despite much effort, its stability in a microscopic environment has been the subject of much debate. In this paper we show how a crumpled phase develops reliably and consistently upon subjecting a thin spherical shell to active fluctuations. We find a master curve describing how the relative volume of a shell changes with the strength of the active forces, that applies for every shell independent of size and elastic constants. Furthermore, we extract a general expression for the onset active force beyond which a shell begins to crumple. Finally, we calculate how the size exponent varies along the crumpling curve.
1 Introduction
It is well known that the energy cost required to deform an elastic surface is well accounted for by a bending and a stretching energy term.1–3 Despite its apparent simplicity, the coupling between bending and stretching modes of deformation is highly nonlinear for thin elastic materials such as sheets and shells giving rise to mechanical behavior that is hard to predict. What makes these materials particularly exciting is that the ratio between stretching, Es, and bending, Eb, energies for an arbitrary deformation of amplitude h on a surface of thickness t scales as Es/Eb ≃ (h/t)2.1 Therefore, for sufficiently thin surfaces, (t ≪ h), only stretch-free deformations are allowed. Skin wrinkling under applied stress,4,5 stress focusing via cone formation of crumpled paper,6 and buckling of thin shells,7 are just a few examples arising from this global constraint.The theory of elasticity developed for continuum mechanics has been successfully used to study a number of microscopic systems, including viral capsids,8 graphite-oxide9,10 and graphene sheets,11,12 cross polymerized membranes13 and gels,14 the spectrin-actin network forming the cytoskeleton of red blood cells15,16 and close-packed nanoparticle arrays.17 Significantly, at this length-scale, the nonlinear coupling between the different elastic modes can also be induced by thermal fluctuations with significant consequences for the structure of microscopic surfaces. Thermal fluctuations renormalize the bending rigidity of thin elastic sheets which become stiffer as their size increases18–20 leading to the stabilization of a flat phase for two-dimensional unsupported surfaces. In thin spherical shells, thermal fluctuations act as an effective negative internal pressure capable of buckling the shell.21
Simple Flory-like arguments22 that work so well in establishing the scaling laws of self-avoiding polymers,23 predict that self-avoiding elastic sheets should be found in a crumpled state for negligible bending rigidities. This state is characterized by the scaling of the radius of gyration of the sheet, Rg, with its side length, L, of the form Rg ∼ Lν with the Flory exponent ν = 4/5.24,25 Yet, numerical simulations of fully crystalline, self-avoiding elastic sheets indicate that these surfaces always acquire a rough, but overall extended (flat), state with a size exponent along their longitudinal directions ν ≃ 1, even in the absence of bending rigidity.26–29 As of today, it is fair to say that the existence of a crumpled phase for large tethered membranes in equilibrium remains uncertain.
Inspired by early experiments of graphite-oxide sheets in poor solvent30 which seemed to indicate the presence of a crumpled phase upon improving the quality of the solvent, simulations were performed to include the presence of attractive interactions, but the crumpled phase was not observed.29 Interestingly, thin elastic spherical shells in the presence of explicit attractive forces were initially reported to have a Flory exponent compatible with a crumpled phase in a temperature window that falls between the flat and the compact regimes,31 but simulations with larger shells did not find such intermediate regime.32 For a comprehensive review on the subject, we refer the reader to ref. 3, 21, 22, 28 and 33. What is certain at this point is that the one way to reliably obtain a crumpled phase out of elastic thin surfaces is by quickly compressing them using a large external force,34–37 or by rapidly dehydrating graphene-oxide nanopaper.38
In this paper, we reconsider this problem within the framework of active matter, and study the effect of active, non-equilibrium fluctuations on the structure of a thin spherical shell. Crucially, we show how a crumpled phase, develops systematically and reliably for sufficiently large active forces. While a significant amount of work has been done to understand the structural and dynamic properties of active linear and ring polymers,39–44 and more recent work considered the behavior of fluid vesicles in the presence of active fluctuations or active agents,45–49 apart from a few recent papers,50–52 very little is known about how elastic surfaces respond to non-equilibrium fluctuations, and this is an important problem given their relevance to biological and synthetic materials.53–55
2 Numerical model
We model the thin spherical shell using a triangulated network of harmonic bonds56 organized as an icosadeltahedron.57 All vertices in icosadeltahedra are six-coordinated apart from twelve five-coordinated vertices (disclinations) as required by topological constraints. This structures are characterized by two integers (a,b) which define the relative position on the spherical lattice of the disclinations, and set the total number of vertices to N = 10(a2 + ab + b2) + 2. Although most of our data are obtained with this crystalline structure, we also considered amorphous shells with a disordered distribution of nodes on the sphere. We construct amorphous shells by running Monte Carlo simulations of a fluid membrane (bond flip moves allows for neighbor exchange58) for sufficiently long time until the bonds are randomized. We then freeze the bonds and use this as the initial configuration for our simulations. The rest shape of the crystalline shell is an icosahedron8 while that for an amorphous shell is a sphere.59To enforce self-avoiding interactions, we place a spherical particle of diameter σ at each vertex. Each of these vertex particles are connected to their nearest neighbors with a harmonic potential. The interaction potential of the system can be written as
 | (1) |
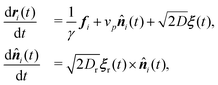 | (2) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) is the axis of propulsion. The conservative forces on each particle are denoted by fi = −∂U/∂ri. The translational diffusion coefficient D, temperature T0 and the translational friction γ are constrained to follow the Stokes–Einstein relation D = kBT0γ−1. Likewise, the rotational diffusion coefficient is constrained to be Dr = kBT0γr−1, with Dr = 3Dσ−2. The Gaussian white-noise terms induced by the solvent for the translational ξ and rotational ξr motions are characterized by the relations 〈ξ(t)〉 = 0 and 〈ξp(t)ξq(t′)〉 = δpqδ(t − t′) (here the indices p and q stand for the Cartesian components x, y, z).
is the axis of propulsion. The conservative forces on each particle are denoted by fi = −∂U/∂ri. The translational diffusion coefficient D, temperature T0 and the translational friction γ are constrained to follow the Stokes–Einstein relation D = kBT0γ−1. Likewise, the rotational diffusion coefficient is constrained to be Dr = kBT0γr−1, with Dr = 3Dσ−2. The Gaussian white-noise terms induced by the solvent for the translational ξ and rotational ξr motions are characterized by the relations 〈ξ(t)〉 = 0 and 〈ξp(t)ξq(t′)〉 = δpqδ(t − t′) (here the indices p and q stand for the Cartesian components x, y, z).
The simulations have been carried out using the numerical package LAMMPS63 and the units of length, time and energy respectively are set to be σ, τ = σ2D−1 and kBT0. Consequently, the spring constant K, bending constant κ and self-propulsion speed vp are measured in units of kBT0/σ2, kBT0 and σ/τ respectively. Physically, τ is the time taken for a passive particle to diffuse a length of σ. All simulations were run with a time step smaller than Δt = 2 × 10−6τ. We record the state of the system every 105 time steps. After the system reaches a steady state as indicated by the saturating values of the shell volume, we collect statistics for a time period ∼(103 − 104)τ, which amounts to a minimum of one billion time steps for the smaller systems and up to 10 billion time steps for the largest. For both crystalline and amorphous shells, most of the data we report are for elastic constants of K = 160 and κ = 10.
3 Crumpling of active shells
With our choice of elastic constants K and κ, crystalline shells acquire a well-defined icosahedral state when thermalized in the absence of active fluctuations. This is expected8 given that with our parameters, the Föppl–von Kármán number for every shell radius R considered in this study for N ∈ [1922, 12
for every shell radius R considered in this study for N ∈ [1922, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002]. We begin our analysis by monitoring the volume of the shell as a function of increasing values of the strength of the active forces. For small values of vp, the shells develop smooth surface undulations on the scale of the shell radius without altering its overall shape. Upon increasing the activity, these undulations deepen resulting in a monotonically decreasing shell volume and a disruption of its global symmetry. For even larger self-propulsion velocities, the shell crumples to a volume that saturates at roughly 20% of its original value V0 = (4/3)πR3. See the ESI† for the cross-sections of locally flat and crumpled spheres.
002]. We begin our analysis by monitoring the volume of the shell as a function of increasing values of the strength of the active forces. For small values of vp, the shells develop smooth surface undulations on the scale of the shell radius without altering its overall shape. Upon increasing the activity, these undulations deepen resulting in a monotonically decreasing shell volume and a disruption of its global symmetry. For even larger self-propulsion velocities, the shell crumples to a volume that saturates at roughly 20% of its original value V0 = (4/3)πR3. See the ESI† for the cross-sections of locally flat and crumpled spheres.
Interestingly, repeating the same calculations with different crystalline8 and amorphous shell59 sizes N ∈ [1922, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002] result in normalized volume V/V0 curves with only a weak size dependence at larger self-propulsion speeds (ESI†). Fig. 1 shows the results of this analysis. We find the flex of this curve, calculated by evaluating the maximum of |dV/dvp|, to be a reasonable estimator of the onset self-propulsion speed,
002] result in normalized volume V/V0 curves with only a weak size dependence at larger self-propulsion speeds (ESI†). Fig. 1 shows the results of this analysis. We find the flex of this curve, calculated by evaluating the maximum of |dV/dvp|, to be a reasonable estimator of the onset self-propulsion speed, 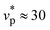 , beyond which the shells begin to crumple. Our results clearly show that the activity-induced crumpling of the shell is quite general and does not depend on the initial specific structure of the shell (crystalline or amorphous). We should also stress that the maximum of |dV/dvp| does not show a diverging peak with system size, suggesting that for this system, crumpling is a smooth process devoid of singularities rather than a real phase transition.
, beyond which the shells begin to crumple. Our results clearly show that the activity-induced crumpling of the shell is quite general and does not depend on the initial specific structure of the shell (crystalline or amorphous). We should also stress that the maximum of |dV/dvp| does not show a diverging peak with system size, suggesting that for this system, crumpling is a smooth process devoid of singularities rather than a real phase transition.
To understand how the onset value, 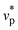 , depends on the elastic parameters of the membrane, we performed the same calculations with different sets of stretching and bending rigidities, in the range of K ∈ [160, 3000] and κ ∈ [10, 80]. Remarkably, as shown in Fig. 2, all data collapse into an empirical master curve of V/V0 against vp/(K0.125κ0.5). This suggests a universal crumpling onset for any shell size and any set of elastic constants beyond
, depends on the elastic parameters of the membrane, we performed the same calculations with different sets of stretching and bending rigidities, in the range of K ∈ [160, 3000] and κ ∈ [10, 80]. Remarkably, as shown in Fig. 2, all data collapse into an empirical master curve of V/V0 against vp/(K0.125κ0.5). This suggests a universal crumpling onset for any shell size and any set of elastic constants beyond  . To ensure that the collapse of data is not an artifact of the choice of bending energy chosen in eqn (1), we also considered a bending energy based on calculating squares of local averages of mean curvature.58,64 We find that the results stand independently of the specific discretization of the bending energy (ESI†). If the dependence on κ could be, in principle, rationalized by reinterpreting activity as an effective temperature generating fluctuations that carry an energy that scales as vp2, and one would expect vp2 > κ, i.e. vp > κ1/2, for the shell to begin to crumple, this simple argument does not, however, explain the weaker dependence on the stretching constant. Furthermore, despite our best attempts, we were unable to use temperature to crumple our shells in equilibrium. Although, partial buckling of the shell can be achieved by increasing the temperature of the bath at equilibrium,21,59 our simulations at high temperatures show no crumpling of the shell.
. To ensure that the collapse of data is not an artifact of the choice of bending energy chosen in eqn (1), we also considered a bending energy based on calculating squares of local averages of mean curvature.58,64 We find that the results stand independently of the specific discretization of the bending energy (ESI†). If the dependence on κ could be, in principle, rationalized by reinterpreting activity as an effective temperature generating fluctuations that carry an energy that scales as vp2, and one would expect vp2 > κ, i.e. vp > κ1/2, for the shell to begin to crumple, this simple argument does not, however, explain the weaker dependence on the stretching constant. Furthermore, despite our best attempts, we were unable to use temperature to crumple our shells in equilibrium. Although, partial buckling of the shell can be achieved by increasing the temperature of the bath at equilibrium,21,59 our simulations at high temperatures show no crumpling of the shell.
 | ||
| Fig. 2 The collapse of normalized volumes (V/V0) as a function of vp/(K0.125κ0.5) for various elastic spring constants K and bending constants κ. The size of the crystalline shell is N = 4322. | ||
As a possible estimate of the size of the active fluctuations to be mapped into an effective temperature in our system, we considered a recent work on ideal active membranes which used the same model for an open elastic sheet. In that case an effective temperature was obtained by matching temperature and activity at the crumpling transition point, yielding an effective temperature Teff = (1 + 1/42vp2)T0.50 For a bending of κ = 10, the crumpling of active shells at  would then correspond to Teff ≈ 22 T0. Alternatively, one could try to estimate the extent of the active fluctuations using the active energy scale ksTs = γvp2/(6Dr).65 In this case one would obtain an effective temperature Teff ≈ 55T0. We however find that even at temperatures of the thermal bath reaching values as large as 100–200T0, passive equilibrated shells do not show signs of crumpling. For instance, at T = 100T0, even when we provide a crumpled shell as the initial configuration, the volume of the shell re-swells over time to 60% of its original volume (ESI†). This suggests that the crumpled conformation of the shell is distinctly non-equilibrium in nature, and a simple temperature mapping of the activity is not sufficient to explain our data.
would then correspond to Teff ≈ 22 T0. Alternatively, one could try to estimate the extent of the active fluctuations using the active energy scale ksTs = γvp2/(6Dr).65 In this case one would obtain an effective temperature Teff ≈ 55T0. We however find that even at temperatures of the thermal bath reaching values as large as 100–200T0, passive equilibrated shells do not show signs of crumpling. For instance, at T = 100T0, even when we provide a crumpled shell as the initial configuration, the volume of the shell re-swells over time to 60% of its original volume (ESI†). This suggests that the crumpled conformation of the shell is distinctly non-equilibrium in nature, and a simple temperature mapping of the activity is not sufficient to explain our data.
4 The Flory phase
So far, we have used the term crumpled quite loosely and with the only intent of providing a visual description of the shape of the shell at large active forces. To accurately characterize the physical properties of this phase, we now calculate the size exponent, ν, for the shells deep into the crumpled phase. For a shell with elastic constants K = 160 and κ = 10 discussed in Fig. 1, we set vp = 100. We evaluate the size exponent by computing the shell structure factor S(q) for different values of the shell radii R ∝ N1/2. We then plot S(q) against qRν, and find the value ν for which all data points collapse onto the same curve within the range 2π/Rg and 2π/σ. The results of this analysis are shown in Fig. 3. The best collapse is obtained for ν = 0.76(6), a result within error bars of the Flory exponent ν = 4/5 predicted for the crumpled phase of self-avoiding membranes, and clearly different from ν = 1 and ν = 2/3 associated with the flat and the compact phase, respectively.We also evaluated how the size exponent of the shell depends on the strength of the active forces along the full spectrum of the shape transformation. What we find is that the size exponent crosses over continuously from ν = 1 in the icosahedral/spherical state, to ν = 0.76 in the collapsed state. We do observe somewhat faster change beyond vp = 30 which we had identified as the onset self-propulsion speed for crumpling. The results are shown in Fig. 4. Given the computational cost of these calculations, the values of ν in Fig. 4 for the largest values of vp are obtained by collapsing the power-law regime of the structure factor as discussed above using five curves (rather than seven) associated with shells of size N = 1922, 3002, 4322, 5882, 7682. We calculate the exponents and error bars using a measure that quantifies the quality of collapse.66 Given that for vp ≤ 30, the shell has a simpler icosahedral shape, the structure factor has multiple peaks and does not exhibit a power-law behaviour. In this low-activity regime, we instead find the size exponent by fitting the size scaling of the radius of gyration Rg(R) = aRν.
5 Conclusions
In this paper, we carried out extensive numerical simulations to understand the role of active fluctuations on the structural properties of thin elastic shells. Remarkably, we observe that thin shells easily and fully crumple under the presence of active fluctuations. Furthermore, we discovered that for different elastic constants, the curves describing the relative volume change of the shells as a function of the strength of the active forces, collapse into a single universal curve when appropriately normalized. Along this curve, the size exponent continuously decreases from ν = 1.00 to ν = 0.76 ± 0.06, and the latter is compatible with the elusive crumpled Flory phase postulated for thermalized self-avoiding elastic membranes. While thermalized membranes are found to depart their flat phase only with explicit attractive interactions,27 active shells which are distinctly out of equilibrium are seen to crumple even in the absence of explicit attractive interactions.The crumpled structures of quasi non-extensile surfaces such as paper or aluminium-foil unattainable by simple equilibration of their microscopic counterparts can also only be formed by non-equilibrium means and are found to be in the Flory phase.35–37 While these remain static in a quenched disordered state, the crumpled phase of active shells continuously fluctuates exploring the ensemble of crumpled configurations.
It is known that sufficiently large thin spherical shells buckle due to an effective negative pressure generated by thermal fluctuations.21,59 However, in the absence of an explicit internal pressure,67 we found no evidence of crumpling in such equilibrated shells even when the strength of the thermal fluctuations become comparable to that of the harmonic bonds that keep the shell together. This is not surprising as a crumpled phase at such large temperatures would be entropically unfavorable, suggesting that activity cannot be mapped into an effective temperature for thin spherical shells. For equilibrated shells with large negative internal pressure, the shells collapse into shapes with a size exponent of ν = 1.00 ± 0.03 (ESI†). Thus the crumpled phase of active shells cannot be qualitatively mapped to shells that are collapsed using explicit inward pressure. The crumpling of active shells is a particularly intriguing result because we have recently shown that active elastic sheets (rather than spherical shells) behave similarly to high temperature passive sheets.50 Specifically, a crumpled phase was not found in that instance as the sheet remained extended for all self-propulsion velocities considered in that study. Our results thus raise questions about the role of intrinsic curvature and topology in these systems. More work is currently underway to sort out their roles.
It is worth noting that studies of the one-dimensional analogs of our system, active rings in two dimensions, present a re-entrant behavior of the radius of gyration with activity. In that case, a narrow region for intermediate activities where the ring collapses has also been observed, but this is immediately followed by a re-swelling at larger activities.44 We verified that re-swelling does not occur in our system by running a few simulations at larger activities vp = 200, 400 (data not shown), making the two-dimensional shell qualitatively different from its lower dimensional counterpart.
More recently, the role of non-equilibrium fluctuations on the shape of an elastic shell has also been tested by performing Monte Carlo simulations with an explicit detail-balance breaking rule.52 In this case, buckling of the shell was observed as a function of the degree of detailed balance breaking, but a crumpled phase was not observed.
Potential realizations of active shells could be constructed with water permeable elastic capsules using polymers. In principle one could use porous cross-linked polymeric vesicles with tethers connecting active particles to their surface, or cross-polymerized colloidosomes built from active particles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. acknowledges financial support from the National Science Foundation under Grant No. DMR-2003444. We acknowledge useful discussions with Andrej Košmrlj.References
- L. D. Landau, L. P. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theoretical Physics, Theory of Elasticity, Butterworth-Heinemann, Oxford, England, UK, 1986, vol. 7 Search PubMed.
- A. E. H. Love, A Treatise on the Mathematical Theory of Elasticity (Dover Books on Engineering), Dover Publications, Mineola, NY, USA, 2011 Search PubMed.
- D. Nelson, S. Weinberg and T. Piran, Statistical Mechanics of Membranes and Surfaces, World Scientific Publishing Company, Singapore, 2nd edn, 2004 Search PubMed.
- E. Cerda, K. Ravi-Chandar and L. Mahadevan, Nature, 2002, 419, 579–580 CrossRef CAS PubMed.
- K. Efimenko, M. Rackaitis, E. Manias, A. Vaziri, L. Mahadevan and J. Genzer, Nat. Mater., 2005, 4, 293–297 CrossRef CAS PubMed.
- T. A. Witten, Rev. Mod. Phys., 2007, 79, 643 CrossRef.
- T. Von Karman and H.-S. Tsien, J. Aeronaut. Sci., 1939, 7, 43 CrossRef.
- J. Lidmar, L. Mirny and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051910 CrossRef PubMed.
- M. S. Spector, E. Naranjo, S. Chiruvolu and J. A. Zasadzinski, Phys. Rev. Lett., 1994, 73, 2867 CrossRef CAS PubMed.
- X. Wen, C. W. Garland, T. Hwa, M. Kardar, E. Kokufuta, Y. Li, M. Orkisz and T. Tanaka, Nature, 1992, 355, 426–428 CrossRef CAS.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60–63 CrossRef CAS PubMed.
- J. H. Fendler and P. Tundo, Acc. Chem. Res., 1984, 17, 3–8 CrossRef CAS.
- P. C. Georges and P. A. Janmey, J. Appl. Physiol., 2005, 98, 1547–1553 CrossRef PubMed.
- C. F. Schmidt, K. Svoboda, N. Lei, I. B. Petsche, L. E. Berman, C. R. Safinya and G. S. Grest, Science, 1993, 259, 952–955 CrossRef CAS PubMed.
- S. E. Lux, Blood, 2016, 127, 187–199 CrossRef CAS PubMed.
- K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Nat. Mater., 2007, 6, 656–660 CrossRef CAS PubMed.
- D. Nelson and L. Peliti, J. Phys., 1987, 48, 1085–1092 CrossRef CAS.
- J. A. Aronovitz and T. C. Lubensky, Phys. Rev. Lett., 1988, 60, 2634 CrossRef PubMed.
- P. M. Chaikin, T. C. Lubensky and T. A. Witten, Principles of condensed matter physics, Cambridge University Press, Cambridge, 1995, vol. 10 Search PubMed.
- A. Košmrlj and D. R. Nelson, Phys. Rev. X, 2017, 7, 011002 Search PubMed.
- K. J. Wiese, Phase Transitions and Critical Phenomena, Elsevier, 1st edn, 2000, vol. 19 Search PubMed.
- P.-G. Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- K. J. Wiese, Phase transitions and critical phenomena, Elsevier, 2001, vol. 19, pp. 253–480 Search PubMed.
- M. Paczuski, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1988, 60, 2638 CrossRef PubMed.
- M. Plischke and D. Boal, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4943 CrossRef PubMed.
- F. F. Abraham and M. Kardar, Science, 1991, 252, 419–422 CrossRef CAS PubMed.
- M. J. Bowick, A. Cacciuto, G. Thorleifsson and A. Travesset, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 149–160 CrossRef CAS.
- F. F. Abraham, W. Rudge and M. Plischke, Phys. Rev. Lett., 1989, 62, 1757 CrossRef CAS PubMed.
- X. Wen, C. W. Garland, T. Hwa, M. Kardar, E. Kokufuta, Y. Li, M. Orkisz and T. Tanaka, Nature, 1992, 355, 426–428 CrossRef CAS.
- D. Liu and M. Plischke, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7139 CrossRef CAS PubMed.
- G. S. Grest and I. B. Petsche, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, R1737 CrossRef CAS PubMed.
- D. Nelson, T. Piran and S. Weinberg, Statistical mechanics of membranes and surfaces, World Scientific, 2004 Search PubMed.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1988, 60, 238 CrossRef PubMed.
- M. Gomes, J. Phys. A, 1987, 20, L283–L284 CrossRef.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 3056 CrossRef CAS PubMed.
- M. Gomes, T. Jyh, T. Ren, I. Rodrigues and C. Furtado, J. Phys. D: Appl. Phys., 1989, 22, 1217 CrossRef.
- X. Ma, M. R. Zachariah and C. D. Zangmeister, Nano Lett., 2012, 12, 486–489 CrossRef CAS PubMed.
- R. G. Winkler and G. Gompper, J. Chem. Phys., 2020, 153, 040901 CrossRef CAS PubMed.
- S. Das and A. Cacciuto, Phys. Rev. Lett., 2019, 123, 087802 CAS.
- S. Das, N. Kennedy and A. Cacciuto, Soft Matter, 2021, 17, 160–164 RSC.
- M. C. Gandikota and A. Cacciuto, Phys. Rev. E, 2022, 105, 034503 CrossRef CAS PubMed.
- R. G. Winkler, J. Elgeti and G. Gompper, J. Phys. Soc. Jpn., 2017, 86, 101014 Search PubMed.
- S. M. Mousavi, G. Gompper and R. G. Winkler, J. Chem. Phys., 2019, 150, 064913 CrossRef PubMed.
- P. Iyer, G. Gompper and D. A. Fedosov, Soft Matter, 2022, 18, 6868–6881 RSC.
- F. Cagnetta, V. SŠkulteéty, M. R. Evans and D. Marenduzzo, Phys. Rev. E, 2022, 105, L012604 CrossRef CAS PubMed.
- H. Turlier and T. Betz, Physics of Biological Membranes, Springer, Cham, Switzerland, 2018, pp. 581–619 Search PubMed.
- Y. Kulkarni, J. Mech. Phys. Solids, 2023, 173, 105240 CrossRef.
- P. Iyer, G. Gompper and D. A. Fedosov, Soft Matter, 2023, 19, 3436–3449 RSC.
- M. Gandikota and A. Cacciuto, Soft Matter, 2023, 19, 5328–5335 RSC.
- S. A. Mallory, C. Valeriani and A. Cacciuto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012314 CrossRef CAS PubMed.
- V. Agrawal, V. Pandey and D. Mitra, Phys. Rev. E, 2023, 108, L032601 CrossRef CAS PubMed.
- H. Turlier, D. A. Fedosov, B. Audoly, T. Auth, N. S. Gov, C. Sykes, J.-F. Joanny, G. Gompper and T. Betz, Nat. Phys., 2016, 12, 513–519 Search PubMed.
- M. J. Bowick, N. Fakhri, M. C. Marchetti and S. Ramaswamy, Phys. Rev. X, 2022, 12, 010501 Search PubMed.
- R. Kusters, C. Simon, R. L. Dos Santos, V. Caorsi, S. Wu, J.-F. Joanny, P. Sens and C. Sykes, Soft Matter, 2019, 15, 9647–9653 RSC.
- Y. Kantor and D. R. Nelson, Phys. Rev. Lett., 1987, 58, 2774–2777 CrossRef CAS PubMed.
- A. SŠiber, Symmetry, 2020, 12, 556 CrossRef.
- G. Gompper and D. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- J. Paulose, G. A. Vliegenthart, G. Gompper and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19551–19556 CrossRef CAS PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Guckenberger and S. Gekle, J. Phys.: Condens. Matter, 2017, 29, 203001 CrossRef PubMed.
- S. Takatori, W. Yan and J. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS PubMed.
- S. M. Bhattacharjee and F. Seno, J. Phys. A: Math. Gen., 2001, 34, 6375 CrossRef CAS.
- G. Vliegenthart and G. Gompper, New J. Phys., 2011, 13, 045020 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00015c |
| This journal is © The Royal Society of Chemistry 2024 |





