Open Access Article
Open Access ArticleMethyl-β-cyclodextrin asymmetrically extracts phospholipid from bilayers, granting tunable control over differential stress in lipid vesicles†
Tyler
Reagle
,
Yuxin
Xie
,
Zheyuan
Li
,
Warner
Carnero
and
Tobias
Baumgart
 *
*
University of Pennsylvania, Chemistry Department, 231 South 34th Street, Philadelphia, PA 19104, USA. E-mail: baumgart@sas.upenn.edu
First published on 6th May 2024
Abstract
Lipid asymmetry – that is, a nonuniform lipid distribution between the leaflets of a bilayer – is a ubiquitous feature of biomembranes and is implicated in several cellular phenomena. Differential tension – that is, unequal lateral monolayer tensions comparing the leaflets of a bilayer- is closely associated with lipid asymmetry underlying these varied roles. Because differential tension is not directly measurable in combination with the fact that common methods to adjust this quantity grant only semi-quantitative control over it, a detailed understanding of lipid asymmetry and differential tension are impeded. To overcome these challenges, we leveraged reversible complexation of phospholipid by methyl-β-cyclodextrin (mbCD) to tune the direction and magnitude of lipid asymmetry in synthetic vesicles. Lipid asymmetry generated in our study induced (i) vesicle shape changes and (ii) gel–liquid phase coexistence in 1-component vesicles. By applying mass-action considerations to interpret our findings, we discuss how this approach provides access to phospholipid thermodynamic potentials in bilayers containing lipid asymmetry (which are coupled to the differential tension of a bilayer). Because lipid asymmetry yielded by our approach is (i) tunable and (ii) maintained over minute to hour timescales, we anticipate that this approach will be a valuable addition to the experimental toolbox for systematic investigation into the biophysical role(s) of lipid asymmetry (and differential tension).
Introduction
Interest in membrane lipid asymmetry dates back to the 1970s.1,2 In the time since, its relevance for lipid-mediated signaling,3 lipid phase separation,4,5 membrane shape change/bending,6,7 and coupling with transmembrane protein structure/activity8 has been considered. The lipid asymmetry of a membrane can be broken down into two contributions: (i) area asymmetry9/area difference6,7/packing asymmetry10 – that is, unequal monolayer surface areas that two apposed leaflets would tend to favor were they uncoupled and (ii) compositional asymmetry – that is, different lipid compositions between the leaflets.11 Mechanical consequences of lipid asymmetry include bending stress and differential tension.10,12,13 Differential tension accumulates within an asymmetric bilayer when the apposed leaflets comprising it contain unequal lateral tensions. Though differential tension may underlie a general importance of lipid asymmetry for membrane biology,14,15 this quantity cannot be directly measured by micromechanical techniques (such as micropipette aspiration). This impedes investigation into the biological role of lipid asymmetry.To this end, the molecule methyl-β-cyclodextrin (mbCD) has been an important experimental tool. mbCD reversibly forms inclusion complexes with phospholipids16 which has been leveraged for preparation of compositionally asymmetric vesicles17 and for studying activation of mechanosensitive ion channels.18,19 Several studies have also demonstrated the utility of mbCD for investigating the chemical activity of cholesterol.20–22 Motivated by these studies, we used mbCD to investigate the mechanics and thermodynamics of area asymmetry generation in 1-component bilayers.
First, we confirmed that mbCD asymmetrically extracts lipid from intact vesicles thereby generating area asymmetry. Next, we show that mbCD can be kinetically trapped with supersaturating amounts of lipid and thereby used to tune the area asymmetries of giant unilamellar vesicles (GUVs). Generation of area asymmetry in these GUVs resulted in (i) membrane bending and (ii) the generation of gel–liquid phase coexistence from a laterally homogeneous membrane. Finally, we provide estimates of the chemical activity of lipid in the outer leaflets of 1-component bilayers undergoing mbCD-mediated collapse/solubilization. We find two different values for this quantity depending on the osmotic conditions to which vesicles are subjected. We use both values to determine microscopic/mechanical quantities in these vesicles. We begin by reviewing some details of mbCD–lipid complexation.
Description of mbCD–lipid equilibrium
A model for complexation between mbCD and bilayer-forming phospholipids was first proposed by Anderson et al.23 These authors suggested that the complexes formed between monomeric phospholipid and mbCD have an average stoichiometry of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively (agreeing with structure–activity predictions drawn from complexes formed between cyclodextrins and various surfactants).16,24 The Anderson model maps this complexation in an mbCD–lipid phase diagram. Large enough concentrations of mbCD can solubilize all self-assembled lipid particles (vesicles) and the concentrations of mbCD and lipid at which this occurs constitute a solubilization boundary. This boundary divides phase space into two regions: (i) the coexistence region in which vesicles coexist with complexes and (ii) the solubilization region in which no vesicles persist. mbCD–lipid complexation is thought to proceed via:
4, respectively (agreeing with structure–activity predictions drawn from complexes formed between cyclodextrins and various surfactants).16,24 The Anderson model maps this complexation in an mbCD–lipid phase diagram. Large enough concentrations of mbCD can solubilize all self-assembled lipid particles (vesicles) and the concentrations of mbCD and lipid at which this occurs constitute a solubilization boundary. This boundary divides phase space into two regions: (i) the coexistence region in which vesicles coexist with complexes and (ii) the solubilization region in which no vesicles persist. mbCD–lipid complexation is thought to proceed via:| lipid(x) + 4 mbCD(aq) ⇌ complex(aq) | (1) |
Anderson et al. treated each bilayer according to the lipid partition model,25 assuming that lipid in 1-component bilayers remains in its reference state throughout the coexistence region. This is based on the rationale that the mole fraction of the lipid component in the bilayer is fixed (regardless of extraction). However, because (i) the free energy of a lipid molecule residing within a bilayer is intimately coupled to its local chemical/mechanical environment26–28 combined with (ii) evidence that mbCD-mediated extraction/insertion of lipids alters membrane mechanics,18,29 we propose that (iii) lipid in bilayers deviate from their reference state when exposed to mbCD. We now discuss how this feature could contribute to mbCD–lipid equilibria.
To do so, we first define the equilibrium constant for mbCD–lipid complexation, Ktotal. According to eqn (1), Ktotal is given by:
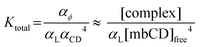 | (2) |
To highlight the supposed variation of αL and its contribution to an experimentally accessible parameter, we define an effective equilibrium constant, Keff (i.e. a ratio of concentrations raised to some powers, being more reminiscent of the standard form of equilibrium constants in biochemical/biophysical literature); this quantity is obtained by rearranging eqn (2):
 | (3) |
Experimentally, the solubilization boundary is located by identifying so-called breakpoints. These are defined as the endpoints of mbCD–lipid titrations (identified via isothermal titration calorimetry23,31,32 and light scattering23,31,33 measurements). mbCD–lipid mixtures falling along the solubilization boundary are identified by total lipid concentrations, denoted by [lipid]total, and [mbCD]total at which vesicles no longer coexist with complexes. These unique values of [mbCD]total are denoted as [mbCD]total, being the total mbCD concentrations at which such breakpoints (or endpoints) occur. The solubilization boundary is mapped by fitting multiple determinations of [mbCD]end for various [lipid]total.
To obtain the fitting equation for the solubilization boundary, Anderson et al. noted that essentially all lipid (except for a negligible portion <0.46 nM)30 is complexed by mbCD at a breakpoint. Therefore, at the solubilization boundary, [mbCD]free in eqn (2) and (3) is given by:
| [mbCD]free = [mbCD]total − 4[complex] ≅ [mbCD]total − 4[lipid]total | (4) |
 | (5) |
Materials and methods
Solvents and reagents
HPLC-grade methanol and chloroform were purchased from Fisher Scientific. Ultrapure water (Millipore Milli-Q) was used for all aqueous solutions. mbCD was purchased from Sigma-Aldrich. Chloroform solutions of 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC), 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(7-nitro-2-1,3-benzoxadiazol-4-yl) (NBD-PE; headgroup-labelled) were obtained from Avanti Polar Lipids. Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (Texas Red DHPE) was dissolved in methanol before use. All lipid stock solutions were stored in sealed vials at −20 °C. Vials containing POPC and NBD-PE stock solutions were flushed with research-grade Argon before sealing to prevent oxidation. 2-(N-(7-Nitrobenz-2-oxa-1,3-diazol-4-yl)amino)-2-deoxyglucose (NBD-Gluc), sucrose, glucose, HEPES, and sodium chloride were purchased from Fisher Scientific. β-casein from bovine milk was purchased from Sigma-Aldrich. All reagents were used without further purification.Solution preparation and characterization
Stock solutions of mbCD and sucrose were prepared in ultrapure water or in buffer (20 mM HEPES, 100 mM sodium chloride, pH 7.4). All solutions were filtered through 0.22 μm filters (bottle-top; polystyrene; corning or syringe-top; PVDF; Millipore). We determined osmolalities using an automated osmometer (Advanced Instruments; Model 3300).Preparation of large unilamellar vesicle (LUV) dispersions
LUV dispersions containing vesicles of defined average diameter were obtained by extrusion as described elsewhere.9 The only difference from this prior procedure was that the resuspended lipid film was vortexed to resuspend the lipid before 4 freeze–thaw cycles, performed by rapidly transferring the dispersion between liquid nitrogen and a hot water bath (50 °C). The size distributions of the LUVs were determined via dynamic light scattering (Zetasizer Nano ZS; Malvern; ZEN3500). The average hydrodynamic diameters of LUVs extruded through 100 nm pores were 137 nm.Preparation of giant unilamellar vesicle (GUV) dispersions
GUVs were prepared via electroformation using conductive Indium Tin Oxide (ITO) glass slides (Rs = 4–8 Ω; Delta Technologies; CG-40IN-S115) as described elsewhere.34 For all preparations, a lipid composition of 99.6% POPC and 0.4% Texas Red-DHPE (mole percentages) in 150 mM sucrose was exposed to a sinusoidal alternating current of 4 Hz and 4 Vpp for 2 hours at room temperature using a function generator (Rigol; DG1000Z). GUV dispersions were annealed at 50 °C overnight and then kept at room temperature with no agitation. GUVs were used within 72 hours after annealing. Lipid concentrations of the GUV dispersions were quantified via direct injection onto a single quadrupole mass detector (ACQUITY SQ Detector; Waters; SQD). A calibration curve was prepared from POPC standards of various concentrations (Fig. S2a in the ESI†). For each standard, intensities from peaks corresponding to 760 m/z and 761 m/z were summed, averaged among triplicates, and plotted versus POPC concentration. GUV samples for this purpose were prepared by diluting GUV dispersions 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (v
50 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) with methanol (POPC standards were measured in 1
v) with methanol (POPC standards were measured in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (v
50 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) diluted sucrose
v) diluted sucrose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol matching these samples); quadruplicate measurements were made for each GUV dispersion. Additional assessment of the lipid accessibility and morphologies of GUVs in these dispersions were also made (see Fig. S2b–d and associated discussion in the ESI†).
methanol matching these samples); quadruplicate measurements were made for each GUV dispersion. Additional assessment of the lipid accessibility and morphologies of GUVs in these dispersions were also made (see Fig. S2b–d and associated discussion in the ESI†).
LUV–mbCD titrations
Multiple titrations were performed in which mbCD was titrated into POPC and vice versa. Identical titration series were performed in unbuffered and buffered solutions under 400 rpm stirring. Pure POPC LUVs were used in these titration series. Breakpoints were identified in these mixtures by measuring the intensity of 285 nm light scattered at a 90° angle relative to the incident beam using a fluorometer (“Synchronous” scanning mode; JASCO; FP-8300).35 Each breakpoint came from a single titration (except for one which was performed in duplicate) performed in one of two ways: (1) in separate, equal volume mixtures or (2) in a single cuvette containing titrand into which titrant was incrementally added. When mbCD was titrated with POPC, breakpoints were identified as the intersection of two linear fits of scattering signal versus total POPC concentration for distinct regimes within a single titration. When POPC was titrated with mbCD, light scattering signal versus total mbCD concentration was fit to a Boltzmann sigmoidal function using Origin. From these fitted titration curves, breakpoints were identified as concentrations of mbCD where the scattering signal approached the baseline (i.e. the lower plateau for large concentrations of mbCD). For single-cuvette titrations, the effects of dilution from added titrant were accounted for during breakpoint determination.Fluorescence quenching measurements
NBD-based quenching experiments were carried out as described elsewhere.36 LUVs composed of 99.7% POPC and 0.3% NBD-PE (mole percentages) were prepared in buffered sucrose solution (150 mM). LUVs composed of pure POPC with encapsulated NBD-Gluc were prepared by suspending the lipid films in the same solution supplemented with NBD-Gluc (100 μM). Quencher solutions were prepared by dissolving sodium dithionite (AKA quencher; 10 mM) in the same buffered sucrose solutions. Due to rapid decomposition of quencher under our conditions,37 these solutions were used within 10 minutes of preparation. The fluorescence signal from NBD-PE and NBD-Gluc in these mixtures was monitored at 541 nm with excitation at 463 nm (“Emission” scanning mode; JASCO; FP-8300). After addition of quencher, LUVs remaining in these mixtures were solubilized by addition of 10% (v:v) Triton X-100 detergent solution (Sigma-Aldrich; X100) to observe complete loss of fluorescence after addition of quencher solution.Temperature-cycling measurements and evaluation of vesicle re-nucleation
Temperature-dependent 90° light scattering measurements were performed using a temperature-controller/stirrer attachment (JASCO; ETC-815). POPC–mbCD mixtures were continuously stirred at 400 rpm. Pure POPC LUVs and mbCD were first mixed at room temperature. Then, the mixture was heated until all POPC became complexed by mbCD. This mixture was cycled between 10 and 70 °C at least two times while light scattering measurements were made. The temperature was varied in 2 °C increments and held for a specified amount of time (75 seconds, 130 seconds, and 360 seconds in separate measurements). Hysteresis was quantified as the difference between the solubilization and re-nucleation temperatures in these cycles. Transition temperatures were identified where scattering was 50% of the maximal signal observed during each measurement.Kinetic trapping of mbCD–POPC complexes
Mixtures of POPC, mbCD, and sucrose were prepared in plastic tubes (0.2 mL; Brandtech; 781300). The concentration of sucrose was adjusted to ensure that the summed concentrations of mbCD/sucrose matched the concentration of sucrose encapsulated within GUVs (150 mM). These mixtures were heated to 85 °C for 20 minutes and then cooled to 25 °C for 10 minutes using a thermocycler (Bio-RAD; T100). Subsequently, mechanical agitation of these mixtures was avoided because this accelerated lipid re-nucleation. Care was taken to avoid transfer of condensation back into these solutions as, similarly, dilution accelerated lipid re-nucleation. These solutions were used for several hours after kinetic trapping.Bulk GUV–mbCD incubation and evaluation
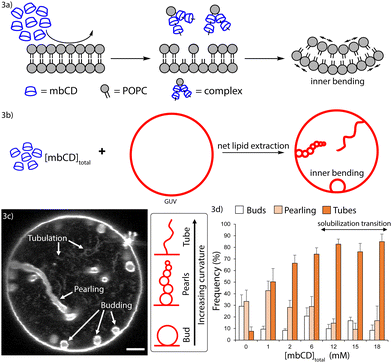
For incubating free-floating GUVs with mbCD, equal volumes of GUV dispersions and mbCD/sucrose solutions (in which the sum of the concentrations of these solutes were 150 mM, matching the encapsulated sucrose concentration inside the GUVs) were mixed in 0.2 mL plastic tubes. Upon addition, the GUV–mbCD mixtures were gently pipetted to ensure mixing; then, the mixtures were kept with no agitation. At the end of incubation, 10 μL of each mixture was added to 90 μL of osmotically balanced glucose solution. GUVs were concentrated in the bottom of the glucose medium whereas all solutes were diluted ten-fold throughout the whole volume. The bottommost 10 μL containing GUVs was added into a closed imaging chamber for observation. The GUVs rapidly settled onto the lower coverslip and were observed via confocal microscopy (Olympus; IX83) with a 60× objective (UPlanSApo; Olympus). During observation, a 561 nm laser was used for excitation and emission of 618 nm light was collected to generate images. Closed imaging chambers were made by sandwiching small-volume samples between two 25 × 25 mm glass coverslips (Fisherbrand; 12542C) separated by a thin layer of grease (Dow-Corning). These coverslips were passivated with 5 μL of 1 mg mL−1 β-casein dissolved in ultrapure water. Passivation was accomplished by spreading this solution on the coverslip surface with a plastic pipette, evaporating it to dryness, and rinsing the excess protein with ultrapure water. Passivated coverslips were air-dried before use.During observation, the frequencies of GUVs containing at least one instance of various bending protrusions (either buds, pearls, or tubes; see Results section) and their direction (inward or outward) of these structures were tabulated. Additionally, the frequencies of GUVs containing at least one instance of a high-curvature protrusion (of any type) directed towards its interior and/or exterior and those containing no protrusions were tabulated. At least one image showing a representative cross-section of each GUV contributing to these statistics were collected; in some cases, short videos were obtained to properly show the bending protrusions which fluctuated in-and-out of the focal plane. Some dispersions contained a high density of vine-like tendrils with lengths spanning several hundreds of micrometers, resembling intermediate structures of electroformation38 which form during electroosmotic deformation of lipid films.39 These structures were usually entangled in networks composed of several other tendrils/GUVs. Because these structures were independent of exposure to mbCD, the following criteria were implemented to minimize the contribution of these structures to morphological statistics: protrusions were only tabulated if they (1) could be associated with a single GUV and (2) had a length less than the diameter of the associated GUV.
Local delivery of mbCD to single GUVs
Single GUVs were exposed to mbCD by injecting mbCD solution from a micropipette held closely to the vesicles. Micropipettes were fabricated as described elsewhere34 using 1.0 mm OD, 0.78 mm ID, 100 mm L glass capillaries. Micropipettes were filled with mbCD solutions and then affixed into a stainless-steel dosing unit (Luigs and Neumann) held by a micromanipulator (Luigs and Neumann; SM 7). Local delivery of mbCD solutions to single GUVs was performed as described elsewhere;40 a water reservoir mounted onto a stepper motor (Thor Labs; LTS150) was used to regulate the direction and speed of solution-flow through the tip of the micropipette. Experiments were performed in open-air imaging chambers (described elsewhere)41 which were filled with unbuffered, osmotically balanced glucose solution (approximately 700 μL). Then, a small volume of GUV dispersion (between 0.2–0.6 μL, depending on GUV density) was pipetted into the chamber to distribute the vesicles throughout the chamber before they settled on the lower coverslip. Because the outward solution-flow from micropipettes pushed GUVs away, the stage was manually adjusted to keep the GUV in focus and near the micropipette tip. Videos were captured on an EM-CCD camera (Hamamatsu; C9000-13).Results
Characterizing osmotic effects on solubilization equilibria between mbCD and phospholipid
In vesicles, both membrane bending and lateral stresses are coupled to osmotic differentials across the bilayer.42 Previous experiments characterizing vesicle solubilization by mbCD were carried out under conditions of large, variable osmotic differentials (i.e. hypertonicity). This is because mbCD was present in the external solutions with no secondary osmolyte encapsulated inside vesicles to offset the osmotic pressure of mbCD. Because this balance was neglected, vesicles exposed to mbCD in earlier studies were subjected to extensive osmotic stress (from unbalanced mbCD in the external solution). This could have influenced the solubilization behavior of mbCD. To evaluate the consequences of this coupling, we introduced sucrose as a secondary, balancing osmolyte to perform measurements under conditions of minimal osmotic stress. By simultaneously adjusting mbCD/sucrose concentrations in the external solution to maintain a total concentration equivalent to the encapsulated sucrose inside the vesicles (150 mM sucrose), we minimized osmotic differentials in our experiments (by maintaining approximate isotonicity; see Fig. S1a–f in the ESI†).To evaluate solubilization behavior under minimal osmotic differentials, we carried out 90° light scattering titrations of lipid and mbCD at room-temperature (RT; i.e. 23 ± 2 °C). The goal of these titrations was the determination of breakpoints (see background section);23,31 each breakpoint was identified by bulk concentrations of mbCD and POPC denoted by [mbCD]end and [POPC]total, respectively. We determined breakpoints by titrating POPC with mbCD (see Fig. 1a) and vice versa (see Fig. 1b), constituting two trajectories by which the solubilization boundary could be approached at fixed RT. Sets of [mbCD]end and [POPC]total characterizing these breakpoints resulted in a two-dimensional phase diagram. The solubilization boundary and associated estimate of Keff at RT under isotonicity were obtained by fitting the experimental boundary to eqn (5) (see Fig. 1c).
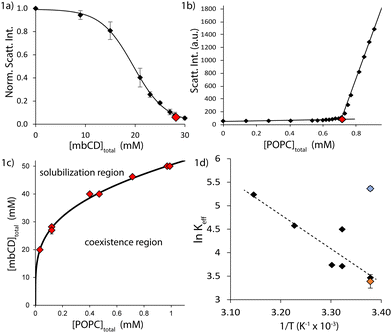 | ||
| Fig. 1 The mbCD–POPC solubilization boundary is affected by osmotic differentials. (a) Titrating a POPC dispersion with mbCD at a fixed concentration of [POPC]total = 0.12 mM. POPC LUVs were 90 nm in diameter. Vertical axis = intensity of 285 nm light scattered at an angle of 90° normalized by the signal of the 0 mM mbCD mixture. Red diamond = location of breakpoint. Error bars = SEMs from triplicate titrations. The line is a fitting of this data. (b) Titrating a mbCD solution in a single cuvette. 1.8 mL of mbCD solution initially containing [mbCD]total = 49 mM was titrated with a dispersion of 137 nm POPC LUVs of [POPC]total = 0.13 mM. Effect of dilution upon the initial [mbCD]total was accounted for to provide the plot. Vertical axis = absolute intensity of scattered 285 nm light. Red diamond = location of breakpoint. Dotted lines = linear fits before and after the breakpoint. (c) mbCD–POPC phase diagram for isotonic conditions at 23 °C. Red diamond = location of breakpoint. Error bar on one breakpoint = SEM from triplicate titrations performed by a single experimenter. Solid black line = fitting of the breakpoints to eqn (5) with v = 4; Keff = 214 M−3 was provided from this fit. (d) Keff at different temperatures and osmotic conditions. Black diamonds = literature estimates under hypertonic conditions (see text). Blue diamond = our estimate at 23 °C under isotonic conditions. Orange diamond = our estimate of Keff at 23 °C under hypertonic conditions. Dotted line = fitting of literature data. Error bars = uncertainty from fitting. 150 mM sucrose solutions were used for background correction in the above measurements. | ||
Six breakpoints were obtained by titrating mbCD with POPC and two were determined by titrating POPC with mbCD. The fact that breakpoints from both titration schemes fell along a single boundary implies that chemical equilibrium was suitably approached. We found that chemical equilibrium was approached within 20 minutes but we typically incubated these mixtures for 1 hour or more. Our fit of the solubilization boundary at RT under isotonic conditions provided an estimate of Keff = 214 ± 5 M−3 (fitted value ± uncertainty using eqn (5). The area below the solid curve in Fig. 1c is the coexistence regime, where vesicles and mbCD complexes coexist (see background section).
Table 1 summarizes all estimates of Keff currently available in the literature and the osmotic conditions (i.e. tonicity) under which they were determined;23,31–33Fig. 1d plots these estimates. Our estimate of Keff at RT under isotonic conditions is significantly larger than the value predicted from literature data (in which osmotic balance of mbCD was neglected). We hypothesized that differences between this estimate of Keff and earlier values could be due to osmotic effects.
| K eff (M−3) | ln[Keff] | T (°C) | 1/T (K−1) | Source | Tonicity |
|---|---|---|---|---|---|
| 90 | 4.50 | 28 | 0.00332 | Anderson et al. | Hypertonic |
| 42 | 3.74 | 30 | 0.00330 | Bozelli et al. | |
| 97 | 4.57 | 37 | 0.00323 | Bozelli et al. | |
| 188 | 5.24 | 45 | 0.00314 | Bozelli et al. | |
| 41 | 3.71 | 28 | 0.00332 | Markones et al. | |
| 32 | 3.47 | 23 | 0.00338 | Huang et al. | |
| 30 | 3.39 | 23 | 0.00338 | This study | |
| 214 | 5.37 | 23 | 0.00338 | This study | Isotonic |
To test the above hypothesis, we performed duplicate titrations without adjusting the external sucrose concentration to offset the osmotic pressure applied by mbCD. Restated, a fixed 150 mM sucrose concentration was maintained inside/outside the LUVs while the mbCD concentration was adjusted; thereby, a hypertonic differential was applied to the LUVs. This scheme matched the osmotic conditions used in earlier studies.23,31–33 From these titrations, we obtained Keff = 30 ± 1 M−3 (average value ± standard error of the mean [SEM]) at RT in good agreement with literature data33 at the same temperature, confirming our hypothesis. This finding also suggests that the interaction between sucrose and the headgroups of phospholipids43,44 (which is thought to alter mechanical properties of bilayers)45,46 does not seem to influence mbCD–lipid equilibrium.
Assessing lipid flipping and vesicle leakage in response to lipid extraction
Having identified the solubilization boundary, we next asked if transmembrane leaflet area asymmetry was maintained within the coexistence regime in vesicles exposed to mbCD on our experimental timescales (1–2 hours). While mbCD is thought to interact with lipids in the outer leaflets of vesicles only, we asked if loss of lipid from outer leaflets results in an extensive, spontaneous flow of lipid from the inner leaflets to compensate for depletion of the outer leaflet (through directional/biased lipid flipping, driven by mechanical stress).47,48 We asked if this process occurs detectably and on a similar timescale as lipid extraction.Whereas mbCD-mediated extraction plateaus within minutes,49,50 flip-flop is generally regarded as a much slower process.51,52 If that is the case here, mbCD and inclusion complexes would rapidly achieve a preequilibrium53/metastable state48,54 with lipid in the outer leaflets before appreciable lipid flip-flop occurred (thereby allowing accumulation of area asymmetry). However, recent observation of accelerated flip-flop in experimental55,56 and simulated54 bilayers containing area asymmetry suggest that biased flip-flop could occur on a similar timescale as lipid extraction. In these cases, it is likely that rapid flipping occurred via bilayer defects,57 including pre-pores58 or micelle-like defects.54 Therefore, we monitored lipid flipping as well as vesicle leakage (to monitor pre-pore formation) in mbCD–lipid mixtures.
To do so, we probed the accessibility of NBD-labelled compounds to the exterior solution via irreversible quenching of NBD fluorescence by the membrane-impermeant salt, sodium dithionite (quencher).36 NBD-labelled molecules on the interior of vesicles (i.e. inner leaflets or encapsulated solution) are inaccessible to the quencher whereas molecules on the exterior of vesicles (i.e. outer leaflets or exterior solution) are accessible. We added sodium dithionite to mbCD–vesicle mixtures, reaching a final concentration of 5 mM (matching optimal conditions recently reported for this experiment).59 We monitored changes in the accessibility of a lipid probe (i.e. NBD-PE) and an encapsulated, aqueous probe NBD-Gluc (i.e. an aqueous fluorescent probe) after exposing our LUVs to mbCD for 1–2 hours. After these incubations, we performed quenching measurements.
An example set of NBD-PE quenching measurements is shown in Fig. 2a. The fractional reduction in the dilution-corrected fluorescence (plateaus occurring after the time point marked by “+ quencher” in Fig. 2a) allowed us to monitor the accessibility of the labelled compounds to the exterior solution (i.e. NBD-PE in the outer leaflets and in-complex with mbCD; NBD-Gluc in the external solution). The appearance of stable plateaus in NBD-PE signal after addition of quencher implies that scrambling (i.e. flip-flop which is uncoupled to mechanical stress and, instead, equilibrates compositional gradients) did not occur detectably during quenching reactions.60 Only after addition of detergent (at the time-point marked by “+ Triton-X” in Fig. 2a) was fluorescence completely abrogated. We assessed the accessible fractions of both NBD-PE and NBD-Gluc in separate mbCD–LUV mixtures of fixed [POPC]total and increasing [mbCD]total (see Fig. 2b and c).
According to Fig. 2b, half of the total NBD-PE was accessible to quencher before exposure to mbCD. This showed that our vesicle preparations were unilamellar.61 As [mbCD]total was increased initially, Fig. 2b and c show only slight increases in the fraction of accessible NBD-PE and NBD-Gluc (we refer to this as the shallow regime). Then, as [mbCD]total was increased further, the accessible fractions of both probes increased steeply until nearly all the NBD-compounds became accessible (we refer to this as the steep regime). We identified transitions from shallow to steep regimes by determining the intersection of linear fits to the data in these regions (AKA discontinuities).
From multiple quenching series for NBD-PE and NBD-Gluc for various [POPC]total, we found that discontinuities between the shallow and steep regimes occurred at significantly lower mbCD concentrations than associated breakpoints (falling along the solubilization boundary). Specifically, we found that discontinuities in NBD-PE and NBD-Gluc accessibilities occurred at 41 ± 2% and 41 ± 1% of [mbCD]end (average ± SEM). Fig. 2d shows that the discontinuities identified in NBD-PE and NBD-Gluc quenching series fall along a common boundary within the coexistence region. This means that, for a given [POPC]total, steep increases in NBD-Gluc and NBD-PE accessibility coincide at a single threshold concentration of mbCD. Since these discontinuities occurred with rapid decreases in light scattering intensity (which, to a first approximation, is proportional to vesicle concentration),35 this suggested that vesicle solubilization accounted for the pronounced changes in lipid accessibility in the steep regime.
We denote the concentration of mbCD associated with a discontinuity in NBD-PE/NBD-Gluc quenching as [mbCD]onset; [mbCD]onset and [mbCD]end are related by [mbCD]onset = 0.4 × [mbCD]end. Each discontinuity is classified by paired [mbCD]onset and [POPC]total. Because these discontinuities identify the onset of vesicle collapse/solubilization as lipid is titrated with mbCD, we therefore refer to the line formed by the unity of all such discontinuities as the onset boundary (dotted line in Fig. 2d). This boundary divides the coexistence region. The onset and solubilization boundaries trace-out a third region of the mbCD–lipid phase diagram (labelled as region II in Fig. 2d; AKA the solubilization transition).
Generating area asymmetry in GUVs with increasing concentrations of mbCD
The shallow regime in Fig. 2b suggests a small but detectable increase in lipid accessibility and vesicle leakage (though not exceeding a 3% change in either case) as the onset boundary is approached. This suggests that defect-mediated, biased flip-flop within intact vesicles occurred on a similar timescale as lipid extraction. We hypothesized that this could relax the area asymmetries of LUVs in the previous measurements. To assess this hypothesis, we turned to GUVs whose large diameters (10–100 μm) allow them to be observed via optical microscopy in a native, fluid environment (in contrast to electron microscopy which involves staining, fixation, and/or freezing to observe the LUVs). If mbCD-mediated lipid extraction generates area asymmetry in vesicles, then this would induce bending (a schematic of this phenomenon at the molecular-scale is shown in Fig. 3a).6,7 Therefore, to address whether biased lipid flip-flop precludes accumulation of area asymmetry in vesicles, we monitored mbCD-mediated bending transitions in GUVs.Fig. 3b shows the GUV shape changes induced by asymmetric lipid extraction (emerging from the molecular-scale phenomenon shown in Fig. 3a). If area asymmetry was rapidly dissipated by biased flip-flop, then only spherical GUVs would persist (because the bilayer has no tendency to bend). If area asymmetry was maintained for longer timescales, then GUV shapes like that shown in Fig. 3b would persist. By this logic, we assessed generation of area asymmetry in GUVs by identifying high curvature bending protrusions directed towards their interiors after exposure to mbCD for 30 minutes. The kinds of high-curvature protrusions that we observed (such as those shown in Fig. 3c) have been ubiquitously associated with area asymmetry generation29,34,62 and reflect that negative curvature was generated in these GUVs. We increased [mbCD]total in this series while holding [POPC]total constant (contributed from the GUVs added to these mixtures) (at 22 ± 2 μM [mean ± SEM] from eleven separate GUV dispersions; see Table S1 in the ESI†).
Fig. 3d shows statistics generated from observation of multiple GUVs incubated with increasing [mbCD]total. GUVs exposed to increasing [mbCD]total up to 6 mM showed an increase in the frequency of high-curvature tubes (with diameters below the optical resolution); after this concentration, the frequency of these tubes plateaued. The frequencies of lower-curvature morphologies (buds and pearls) underwent a continual decrease for [mbCD]total greater than 1 mM. These observations imply an increase in the negative curvature and area asymmetry of GUVs from 0–6 mM mbCD followed by an apparent plateau. These trends confirm that area asymmetry was generated within the intact GUVs exposed to mbCD.
Earlier definitions of [mbCD]end and [mbCD]onset can be used to contextualize this behavior in the mbCD–POPC phase diagram of Fig. 2d. Since GUV–mbCD mixtures contain [POPC]total = 22 μM, we can use eqn (5) with Keff = 214 M−3 to obtain [mbCD]end = 18 mM and [mbCD]onset = 0.4 × [mbCD]end = 7 mM. The similarity between [mbCD]onset = 7 mM for the mbCD–GUV mixtures and the start of the plateau in Fig. 3d (occurring in the vicinity of 6 mM mbCD) implies that the plateau falls within the onset and solubilization boundaries (i.e. region II of Fig. 2d). Increasing [mbCD]total prior to the onset boundary (i.e. within region I of Fig. 2d) generates area asymmetry in a concentration-dependent manner. This confirms that biased lipid flip-flop (which would have abrogated area asymmetry generation and shape changes in this region) must be slower than lipid extraction by mbCD.
Supercooling of mbCD–lipid complexes to control lipid delivery to/from GUVs
In the experiments described above, we showed that increasing [mbCD]total generated a concentration-dependent increase in the negative area asymmetry and negative curvature of GUVs. We next asked if we could generate positive curvature by driving excess lipid into the outer leaflets of vesicles (i.e. positive area asymmetry) via mbCD-complexed lipids.To test if excess lipid could be delivered to the outer leaflets of vesicles, we adapted previously reported methods for delivery of cholesterol20 and fatty acids63 between membranes and external solutions using cyclodextrins. These methods utilized heating to facilitate complexation between the cyclodextrins and corresponding guest molecules followed by cooling to yield solutions containing the corresponding complexes. These solutions were then used to drive the guest molecules into membranes. Here, we asked if kinetic trapping of mbCD with supersaturated concentrations of lipid (“loaded” mbCD solutions) could provide a driving force through which vesicles would accept excess lipid into their outer leaflets.
It was previously shown that Keff increases when the temperature of a mbCD–POPC mixture is elevated.31 We exploited this behavior to solubilize vesicles in mbCD–POPC mixtures via heating to 70 °C. Then, we rapidly cooled these complex solutions back to 25 °C (i.e. with negligible times at each intermediate temperature) under continuous stirring. The process of re-nucleation was monitored via 90° light scattering, resulting in an increase in the amount of scattered light over time. We classified each mixture based on re-nucleation behaviors upon cooling (see Fig. 4a): (i) no re-nucleation (green datapoints), (ii) slow re-nucleation (i.e. detectable increase in light scattering was delayed and did not plateau within 5 minutes) (pink datapoints), or (iii) immediate re-nucleation (i.e. achieving a plateau within 5 minutes after cooling) (red datapoints). Fig. 4a shows the results of these tests mapped onto the mbCD–POPC phase diagram. We interpreted the re-nucleation behavior of these cooled solutions through the lens of mass-action.
 | ||
| Fig. 4 mbCD can be kinetically trapped with supersaturating concentrations of POPC by supercooling. (a) Re-nucleation behavior of mbCD–lipid solutions cooled to 25 °C mapped onto the phase diagram. Black line = isotonic solubilization boundary at RT from Fig. 1c. Each point summarizes results from a single mixture after cooling from 70 °C (see text about the three groups used to classify these solutions). Diamonds show states that were also surveyed in dilution experiments as shown in Fig. S3a in the ESI.† (b) Three thermal cycles measured for a mbCD–POPC mixture of Qϕ = 1990 M−3 with [mbCD]total = 38 mM. The amount of time the mixtures were held at each temperature is specified for each dataset. Vertical axis = normalized light scattering intensity (at 285 nm) relative to maximal scattering intensity at 10 °C from that measurement. | ||
A lipid–mbCD mixture in the coexistence region is a biphasic mixture consisting of a mesophase of all free-floating vesicles and a solution-phase (which we refer to as a “complex solution”). Contained in the complex solution are inclusion complexes, free mbCD, and a negligible concentration of lipid at its critical bilayer concentration (CBC; <0.46 nM).30 The complex solution is free to exchange lipid with the vesicles in which it is held in contact; the tendency for such a complex solution to donate lipid to such vesicles is defined as the following (denoted as Qϕ; AKA the mass-action quotient):
 | (6) |
For Qϕ < 214 M−3 we observed no vesicle re-nucleation after cooling (i.e. all mixtures in Fig. 4a falling above the solubilization boundary correspond to a green datapoint). For values of Qϕ < 214 M−3 at 25 °C, lipid re-nucleation occurred after cooling (i.e. all mixtures in Fig. 4a falling below the solubilization boundary).65 We found that delayed re-nucleation was observed increasingly in cooled mixtures falling closer to the solubilization boundary. A separate boundary, at approximately Qϕ ≅ 1000 M−3, divided slow/delayed and fast/immediate re-nucleation (i.e. regions formed by all pink and red datapoints, respectively, in Fig. 4a). Without stirring or any other agitation, loaded mbCD solutions with Qϕ values between 214 M−3 and roughly 1000 M−3 were metastable for >20 hours at RT with no detectable re-nucleation (i.e. pink datapoints in Fig. 4a). We hypothesized that complex solutions that mapped to this region of mbCD–lipid phase space were kinetically trapped as a result of supercooling.
The notion of supercooling implies hysteresis and we thus sought further evidence for this phenomenon. To do so, we cycled three, identical mixtures between two temperatures above and below RT; these mixtures were characterized by Qϕ = 1990 M−3 and [mbCD]total = 38 mM after lipid complexation (see eqn (6)). Each mixture was held at a temperature for a specified waiting time before proceeding to the next temperature. 90° light scattering readings were taken at each temperature after these waiting times. We varied the waiting times used for each mixture.
Fig. 4b shows three hysteresis loops resulting from the above measurements. In each hysteresis loop, we identified the occurrence of solubilization/re-nucleation as states that gave half maximal scattering signal (identified by linear interpolation); the temperatures associated with these locations were taken as transition temperatures. The extent of hysteresis was quantified as the difference between transition temperatures (ΔT = Tsolubilize − Tnucleate). There was minimal change with respect to the surveyed waiting times. The large degree of undercooling required for re-nucleation in these experiments confirms that loaded mbCD solutions with Qϕ values of 214 M−3 and roughly 1000 M−3 were kinetically trapped via supercooling.
We also characterized lipid release behavior of loaded mbCD solutions in response to dilution (see Fig. S3a and b and associated text in the ESI†). Observations from these experiments (1) suggest that re-nucleation of lipid from loaded mbCD is path-independent and (2) demonstrated that dilution of a complex solution causes an instantaneous increase in Qϕ (which is related to the dilution-factor). Both points are relevant for using loaded mbCD solutions to insert lipid into GUVs (and interpret other behaviors in these experiments).
Tuning the area asymmetries of GUVs from bulk mixing with loaded mbCD
We next evaluated whether loaded mbCD could control net lipid delivery between the external solution and intact vesicles. To do so, we once again utilized GUVs to monitor generation of membrane curvature. This was accomplished by mixing loaded mbCD solutions and GUV dispersions in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) ratio and incubating for 1.5 minutes. Fig. 5a is a schematic showing inward and outward bending transitions of GUVs (example images of GUVs with outer bending protrusions are shown in Fig. 5b and c). Identification of these structures provided information about the direction of net curvature-generation which we related to area asymmetry generation: negative curvature corresponded to lipid extraction from the GUVs (resulting in negative area asymmetry) whereas positive curvature corresponded to lipid insertion into the GUVs (resulting in positive area asymmetry).
v) ratio and incubating for 1.5 minutes. Fig. 5a is a schematic showing inward and outward bending transitions of GUVs (example images of GUVs with outer bending protrusions are shown in Fig. 5b and c). Identification of these structures provided information about the direction of net curvature-generation which we related to area asymmetry generation: negative curvature corresponded to lipid extraction from the GUVs (resulting in negative area asymmetry) whereas positive curvature corresponded to lipid insertion into the GUVs (resulting in positive area asymmetry).
We introduced the parameter Qdilϕ for these experiments; this quantity describes the instantaneous mass-action quotient of the external solution after mixing GUVs and loaded mbCD; these values were calculated using eqn (6) as described in the ESI† (see Fig. S3a and b and associated discussion). Briefly, values of Qdilϕ for these experiments were calculated by multiplying the initial values of Qϕ for the undiluted loaded mbCD solutions (i.e. prior to mixing) by a factor of 23 = 8, corresponding to the two-fold dilution during mixing of loaded mbCD solutions with GUV dispersions in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) ratio. We prepared a series of loaded mbCD solutions spanning a range of Qϕ: [0 M−3, 456 M−3] with [mbCD]total = 28 mM. Thus, after accounting for dilution, the range spanned in the mbCD–GUV mixtures was Qdilϕ: [0 M−3, 3644 M−3] with [mbCD]total = 14 mM.
v) ratio. We prepared a series of loaded mbCD solutions spanning a range of Qϕ: [0 M−3, 456 M−3] with [mbCD]total = 28 mM. Thus, after accounting for dilution, the range spanned in the mbCD–GUV mixtures was Qdilϕ: [0 M−3, 3644 M−3] with [mbCD]total = 14 mM.
Because the concentration of uncomplexed lipid was negligible (approximately 0.46 nM)30 compared to the millimolar concentrations of lipid complexed by mbCD, lipid exchange between GUVs and the complexes was likely to be the most relevant contribution to GUV shape changes. After incubating the GUVs with loaded mbCD, we generated the statistics contained in Fig. 5d–f by monitoring the frequencies of GUVs containing at least one instance of various high-curvature protrusions. GUVs containing no bending protrusions were also tabulated (these contributed to the “None” classification). From Fig. 5d, the frequency of GUVs displaying at least one inward protrusion (of any kind) in these mixtures decreased with increasing Qdilϕ. Simultaneously, the frequency of GUVs containing at least one outward protrusion (of any kind) increased with increasing Qdilϕ.
Among inner bending morphologies, Fig. 5e shows that GUVs containing high-curvature tubules were the dominant inner morphology for Qdilϕ: [0 M−3, 912 M−3], coinciding with a decrease in the frequencies of GUVs containing inner morphologies (of any kind) along Qdilϕ: [0 M−3, 1500 M−3]. This suggests a decrease in the magnitude of negative area asymmetry/curvature along these ranges. Analogously, for outer bending morphologies, Fig. 5f shows that GUVs containing low-curvature morphologies (buds and pearls) were the dominant outer structures for Qdilϕ: [912 M−3, 3644 M−3], coinciding with an increase in the frequencies of GUVs containing outer morphologies (of any kind) along Qdilϕ: [750 M−3, 3644 M−3]. This suggests an increase in the magnitude of positive area asymmetry/curvature along these ranges.
The findings above provide qualitative evidence that loaded mbCD of suitable Qϕ drives lipid insertion into intact GUVs. We asked whether these findings agreed with the formalism proposed by Anderson et al.23—i.e., αL = 1, implying that Keff at the RT, isotonic solubilization boundary should dictate the direction of net lipid exchange between mbCD and GUVs with respect to Qdilϕ. The above trends reveal that there is a value of Qdilϕ (which we refer to as Qcrossϕ) at which neither inner nor outer bending protrusions are favored. We identified Qcrossϕ as the location at which empirically chosen, quadratic fits to the inner/outer bending frequencies intersected (see Fig. 5g). From these fits, we found that Qcrossϕ = 1200 ± 109 M−3 (intersection ± propagated uncertainty). This value is significantly larger than Keff = 214 M−3, illustrating disagreement between our findings and implications of the Anderson formalism.
We speculated that the increased appearance of composite GUV structures (i.e. those composed of two or more adhered GUVs; see schematic in Fig. 5h) in the loaded mbCD–GUV mixtures might relate to this disagreement. These structures coexisted with isolated GUVs containing bending protrusions used to collect the bending statistics in Fig. 5d–f. Fig. 5i and j are examples of composite structures formed between two GUVs whereas Fig. 5k is an example of a so-called GUV aggregate, being composed of many adhered GUVs. Composite GUV structures appeared more frequently when Qdilϕ ≥ 912 M−3, falling near the boundary separating delayed/rapid lipid re-nucleation (i.e. Qϕ ≅ 1000 M−3; see Fig. 4a). This also fell near Qcrossϕ = 1200 ± 109 M−3, supporting the above premise.
It is conceivable that rapid re-nucleation of nascent lipid assemblies (from release of lipid from complexes) could drive GUV aggregation as a means of cloaking the hydrophobic areas of lipids with suboptimal packing in re-nucleated assemblies.66,67 Indeed, composite GUV structures similar to those in Fig. 5i and j have been considered previously,68 concluding that substantial adhesive energies are required for their formation. Highly strained lipids with tails embedded between GUVs and re-nucleated lipid particles (similar conformations observed in simulations)69 could provide such adhesive forces. Such bridging interactions could even underly heterogeneous nucleation on the surfaces of GUVs. If the above phenomena preferentially drew de-complexed lipid into nascent lipid assemblies as opposed to pre-formed GUVs, then the data in Fig. 5d–f might convey the delivery-tendency of the nucleates (and not loaded mbCD).53,70 Accordingly, we devised our next experiments to limit unconstrained lipid re-nucleation and assess whether this process explains Qcrossϕ ≠ 214 M−3.
Local delivery of loaded mbCD to monitor remodelling of single GUVs in real-time
We thought that local delivery of mbCD to single GUVs might minimize the occurrence of re-nucleation and subsequent adhesion/aggregation events (described above). We accomplished this by using micropipettes to locally administer mbCD solutions of different Qϕ to single GUVs (see schematic in Fig. 6a). This scheme contrasted with bulk mixing experiments where loaded mbCD was homogeneously distributed throughout the entire external solution (i.e. those experiments leading to data in the panels of Fig. 5). | ||
| Fig. 6 Local delivery of loaded mbCD achieves morphological remodeling and gel–liquid phase coexistence in 1-component POPC GUVs (a) A schematic of how single GUVs were treated with locally-delivered mbCD. A micropipette was filled with mbCD solution and inserted into an open imaging chamber containing GUVs settled onto the lower surface. A positive pressure was maintained in the micropipette to achieve an outward flow of mbCD solution from the micropipette tip. (b) Timelapse of a GUV treated with a loaded mbCD solution of Qϕ = 100 M−3 and [mbCD]total = 10 mM. White arrows in the first frame (prior to micropipette insertion) highlight outward buds on the GUV. Over the course of treatment, the outward buds are retracted, the GUV becomes more tense, and inner bending protrusions emerge. Frame 3 shows the time at which the first inward protrusion began to emerge. Scale bar = 10 μm. (c) Timelapse of a GUV treated with a loaded mbCD solution of Qϕ = 1100 M−3 and [mbCD]total = 10 mM. White arrows show domains within the GUV bilayer. Frame 2 shows the point at which the first domain could be identified. Scale bar = 10 μm. (d) An example epifluorescence image of a GUV that underwent gel–liquid (g and L, respectively) coexistence after local delivery to Qϕ = 1100 M−3 and [mbCD]total = 10 mM solution. This image was obtained after 6 minutes of exposure to loaded mbCD. Scale bar = 5 μm. (e) Tube-to-pearl transformation from the timelapse of Fig. 6c with a schematic of this process. Scale bars = 5 μm. | ||
We anticipated that these experiments would either (i) yield a more accurate estimate of Qcrossϕ (thereby addressing why Qcrossϕ ≠ 214 M−3 in bulk mixing experiments) or (ii) validate our estimate of Qcrossϕ from bulk mixing. We flushed single GUVs with mbCD solutions of Qϕ = 0, 100, 550, 1100 M−3 and [mbCD]total = 10 mM to observe generation of area asymmetry in real-time. These mbCD solutions spanned the entire range of Qϕ for which mbCD could be kinetically trapped at RT. For single GUVs treated with Qϕ = 0, 100, 550 M−3, we observed inner bending protrusions emerge from GUVs, agreeing with observations from bulk mixing. Fig. 6b shows a time-lapse of a GUV flushed with loaded mbCD of Qϕ = 100 M−3. These findings confirmed that Qcrossϕ ≠ 214 M−3 because Qϕ above and below 214 M−3 induced inner bending protrusions exclusively. If Qcrossϕ = 214 M−3, then lipid insertion would have occurred during Qϕ = 550 M−3 delivery. These observations are therefore consistent with the occurrence of negative area asymmetry when Qϕ < ∼1200 M−3 (as determined from bulk mixing experiments; see Fig. 5d and g).
Because observations for Qϕ = 0, 100, and 550 M−3 validated the bending statistics from bulk mixing experiments, we next asked if delivery of Qϕ = 1100 M−3 loaded mbCD would induce outer bending protrusions in single GUVs. Surprisingly, we did not observe outer bending. Instead, we observed phase separation at RT in 99.7% POPC//0.4% Texas Red-DHPE GUVs (mole percentages) (in three GUVs from a total of five). A timelapse showing emergence and ripening of these domains (dark spots indicated by white arrows) is contained in Fig. 6c. Texas Red-DHPE is known to partition strongly to more disordered phases,71 suggesting that these domains were more ordered compared to the enriched phase. The domains were initially circular but then ripened into more complex shapes (such as the example shown in Fig. 6d). This behavior suggests that these domains were initially fluid-like but became gel-like the longer GUVs were exposed to loaded mbCD of Qϕ = 1100 M−3. These observations agree with recent theoretical predictions that area asymmetry can induce gel–liquid phase coexistence at temperatures above typical transition temperatures determined in symmetric bilayers (i.e. −5 °C for POPC, well-below the temperature of these experiments).5,10,72
In all cases, the morphological transformation shown in Fig. 6e preceded emergence of these domains (they can also be seen by close-inspection of the time-lapse in Fig. 6c). These tube-to-pearl transformations are consistent with a reduction in the magnitude of negative spontaneous curvature (from lipid insertion) under the constraint of fixed volume.73,74 We are uncertain why these inward bending protrusions were not retracted into the flat portions of these GUVs (a phenomenon implied by the bending statistics in Fig. 5d–f); this finding might relate to the metastability of closed necks in these vesicles.75 Occurrence of lipid insertion for Qϕ = 1100 M−3 agrees with our estimate of Qcrossϕ = 1200 ± 109 M−3 (within associated uncertainty) (please see indicated note).76 The significance of this finding will be emphasized in the Discussion section.
Discussion
mbCD–lipid equilibrium shares some characteristics with that between “slow” solubilizing detergents and lipids
During our characterization of the chemical equilibrium between mbCD and lipid, we identified a new boundary in mbCD–lipid phase space: i.e., the onset boundary (refer to Fig. 2d). The onset and solubilization boundaries enclose an additional region in mbCD–lipid phase space. Interestingly, this region seems to be analogous to regions in detergent-lipid phase diagrams in which bilayers coexist with mixed detergent-lipid micelles.77Proceeding with this analogy, the scrambling/leakage behaviors leading to the onset boundary are reminiscent of so-called “slow” solubilizing detergents.78,79 These amphiphiles are thought to possess a limited capacity to rapidly flip-flop between the leaflets of intact vesicles (AKA “crack in”);80 this matches the long timescales (hours to days) associated with phospholipid flip-flop.51,52 Our finding that intact, POPC vesicles exposed to mbCD had (i) minimal changes in NBD-PE and NBD-Gluc accessibility (<3% in both cases; refer to Fig. 2b and c) and (ii) could support long-lived morphological/phase transformations (see GUV experiments) mimics the behaviors attributed to detergents in this category.
Our observations contrast with scrambling/leakage behaviors attributed to “fast” detergents.81,82 Such amphiphiles rapidly penetrate across bilayers, possibly via pre-pores.58,83 “Fast” detergents readily dissipate area asymmetry on minute timescales (as shown in this study),82 differing from long-lived (hour timescales) asymmetries generated by mbCD.32 The metastability of area asymmetry in our study is likely owed to the fact that the molecular shape of POPC27,84 is not expected to facilitate pre-pore formation (differing from conical amphiphiles which do serve this role).85–87
mbCD-mediated lipid extraction generates differential tension and net bilayer tension
Our observations of GUVs exposed to mbCD (in both the bulk mixing and local delivery schemes) provide evidence that lipid is asymmetrically extracted from the outer leaflets of intact vesicles in a concentration-dependent manner (throughout region I of Fig. 2d). This process appears to induce differential tension (denoted by ΔΣ). ΔΣ is defined as the difference between the mechanical tensions of the outer and inner leaflets (denoted by σout and σin, respectively) given by ΔΣ = σout − σin.5,54 Asymmetric lipid extraction accumulates ΔΣ by causing lipids in the depleted, outer leaflets to be relatively stretched compared to those contained in the inner leaflets (as in Fig. 3a).When ΔΣ accumulates within a bilayer, the bilayer possesses an increased tendency to undergo bending/shape transitions.5,7,88 Thus, our observation of an increase in the average negative curvature of GUVs with respect to [mbCD]total implies an increase in ΔΣ as the onset boundary is approached (see bending statistics in Fig. 3d). Likewise, our observation of a plateau in negative curvature during the solubilization transition (region II of Fig. 2d) indicates that ΔΣ seems to approach a fixed value between the onset and solubilization boundaries. By extension, this implies that lipids in the outer leaflets of intact vesicles during the solubilization transition experience similar degrees of stretching (and similar values of σout) in this region of phase space.
Along with ΔΣ, real-time observation of asymmetric lipid extraction from GUVs during local delivery experiments (refer to Fig. 6b) revealed a tensing effect. This observation implies that vesicles exposed to mbCD also accumulated net bilayer tension (denoted by σnet) distributed uniformly across the bilayer; this is consistent with reports of the mbCD-mediated activation of mechanosensitive ion channels.18 Nonzero σnet must result from (i) net loss of lipid from the GUVs and (ii) impedance to bending (from osmotic constraints) as ΔΣ is accumulated. The former contribution pertains to tension from osmotic/hydrostatic pressure whereas the latter pertains to the so-called spontaneous tension.42,74,89
We propose that the combination of nonzero ΔΣ and σnet distributed within these vesicles drove mbCD-mediated collapse/solubilization. Though the exact events involved in vesicle collapse are unclear at this time, one hypothesis is that the onset boundary corresponds to a location in mbCD–lipid phase space at which biased flipping (possibly via bilayer defects) was initiated on short timescales. If this process occurred in coordination with mbCD-mediated extraction, then vesicle collapse could result. Possible candidates for the bilayer-defects involved in this process include pre-pores58 or micelle-like defects.54 As [mbCD]total is continually increased beyond the onset boundary, we propose that different subpopulations of vesicles (harboring relatively similar ΔΣ and σnet) undergo collapse/solubilization until no vesicles persist in the mixture (occurring at the breakpoint of a titration, along the solubilization boundary). Further increase of [mbCD]total (into region III of Fig. 2d) drives additional, undetectable complexation of lipid monomers in the solution.
Hypertonic deflation enhances the survivability of vesicles exposed to mbCD
We found that hypertonic conditions lead to a smaller Keff during the solubilization transition under hypertonic conditions compared to osmotic balance. Phenomenologically, this means that larger [mbCD]total are required to achieve solubilization under hypertonic conditions for equivalent [POPC]total. We determined Keff = 214 ± 5 M−3 under isotonic conditions and Keff = 30 ± 1 M−3 under hypertonic conditions. Using eqn (3) and (5) with these values of Keff (and the relation [mbCD]onset = 0.4 × [mbCD]break), we can predict the percentage of extracted lipid in the vicinity of the onset boundary under both osmotic conditions. Performing this calculation over the complete range of [POPC]total used in both cases, we report that 3% and 5% lipid extraction (of the total lipid) led to collapse/solubilization in the isotonic and hypertonic cases, respectively. This reveals that hypertonicity allows vesicles to sustain a greater amount of asymmetric extraction prior to collapse.One hypothesis for this finding is that hypertonic stress partially alleviates osmotic constraints and thereby facilitates vesicle shape transitions (as in these studies).73,90 Hypertonic deflation would thereby allow a greater fraction of a bilayer to undergo bending transitions in response to asymmetric extraction (compared to vesicles in the isotonic case). This would minimize the fraction of the bilayer that is unable to match its preferred or spontaneous curvature (from area asymmetry generation).34,91,92 Failure to adapt in such a fashion results in accumulation of large, nonzero σnet (from spontaneous tension, referred to earlier)74,89 within these portions of the bilayer. Osmotic deflation (as in the hypertonic case could (i) reduce the fraction of the bilayer subjected to this large, nonzero σnet and (ii) thereby reduce the free energy density of the bilayer. Both effects could oppose defect-formation underlying vesicle collapse/solubilization. Ultimately, this could allow vesicles in the hypertonic case to survive to a greater degree of lipid extraction compared to vesicles under isotonic conditions.
Changes in lipid chemical activity due to area asymmetry can be detected through mbCD–lipid chemical equilibrium
Based on the Anderson formalism (i.e. that αL = 1 throughout the coexistence region),23 we hypothesized that Qcrossϕ from loaded mbCD experiments should match the value of Keff at the RT solubilization boundary under corresponding osmotic conditions. We found that the value of Keff = 214 ± 5 M−3 disagrees with our estimate of Qcrossϕ = 1200 ± 109 M−3 from GUV experiments. We propose that this disagreement can be explained by variation of αL in 1-component bilayers containing area asymmetry. This implies that the assumption proposed by Anderson et al. for mbCD–lipid complexation (i.e. that αL = 1 in intact, 1-component vesicles) is invalid. To demonstrate this, we will make use of the definitions for Ktotal and Keff (from eqn (2) and (3); see background section).We propose that identification of Qcrossϕ provides an estimate of the equilibrium constant for mbCD–POPC complexation (that is, Ktotal). By Le Chatelier's Principle, when Qϕ < Ktotal, asymmetric extraction will be driven spontaneously (yielding net negative curvature in the GUVs); when Qϕ > Ktotal asymmetric insertion will be driven spontaneously (yielding net positive curvature in the GUVs). When Qϕ = Ktotal, however, there is no net tendency for extraction or insertion. Since we have defined Qcrossϕ as the value of Qϕ at which neither inward nor outward bending is favored, it follows that Qcrossϕ = Ktotal. Therefore, we report an estimate of Ktotal = 1200 ± 109 M−3 for the complexation of POPC by mbCD. Importantly, this constant is different from the parameters obtained by fitting solubilization boundaries in mbCD–lipid phase space.
Through such fitting, Keff is obtained and not Ktotal (see background section). Whereas Ktotal is constant, Keff = Ktotal × αL. Therefore, Keff captures variation from αL. For example, if αL < 1, then Keff < Ktotal. By fitting the RT solubilization boundary under different osmotic conditions, we obtained estimates of Keff = 214 ± 5 M−3 (isotonicity) and Keff = 30 ± 1 M−3 (hypertonicity). Comparison of these values to Ktotal = 1200 ± 109 M−3 shows that αL < 1 at these boundaries. Using our estimates of Ktotal and Keff under both osmotic conditions yields αL = 0.18 ± 0.02 (isotonicity) and αL = 0.025 ± 0.002 (hypertonicity) (estimates ± propagated uncertainties) in the outer leaflets of vesicles on the verge of collapse. These estimates of αL can be related to microscopic and mechanical quantities in vesicles.
Lipid chemical activity allows estimation of area-per-lipid values and the differential tension in vesicles exposed to mbCD
Jähnig proposed an equation for the chemical potential of lipid in the outer leaflets of vesicles (eqn (9) in the reference).53 From this equation, αL is found to be:93 | (7) |
Using eqn (7), we can use our estimates of αL for vesicles on the verge of collapse (i.e. during the solubilization transition) to predict associated values of aout. Doing so, we obtain aout = 0.71 ± 0.01 nm2 (isotonicity) and aout = 0.80 ± 0.01 nm2 (hypertonicity) (estimate ± propagated uncertainty); these estimates correspond to 13% and 26% relative lipid expansion, respectively. Recalling our earlier calculation, the larger relative expansion in the hypertonic case is associated with a larger percentage of lipid extraction (5%) compared to the isotonic case (3%). These relative lipid expansions found above are comparable to the 18% relative expansion in the underfilled leaflet of planar bilayers containing the maximal amount of area asymmetry for which this assembly remained metastable/defect-free during microsecond simulations.54 The fact that our real-world bilayers seemed to contain σnet > 0 mN m−1 (see earlier discussion) whereas the simulated bilayers were tensionless (i.e. σnet = 0 mN m−1) could explain the differences between our estimates and this literature value.
Using the above estimates of aout, it is also possible to predict associated values of σout and ΔΣ in this location of phase space. By extending a model proposed by Israelachvilli,27 Levadnyy et al. described σout using the following equation:97
 | (8) |
| Isotonicity | Hypertonicity | |
|---|---|---|
| α L | 0.18 ± 0.02 | 0.025 ± 0.002 |
| Extracted lipid (%) | 3% | 5% |
| a out (nm2 per lipid) | 0.71 ± 0.01 | 0.80 ± 0.01 |
| σ out (mN m−1) | 8.5 ± 0.2 | 15.2 ± 0.2 |
| ΔΣ (mN m−1) | 17.0 ± 0.4 | 30.4 ± 0.4 |
We note the following caveat to the above estimates of ΔΣ. Even though asymmetric bilayers are typically simulated under the constraint of σnet = 0 mN m−1,54,99–101 we reiterate that real-world vesicles exposed to mbCD appear to contain σnet > 0 mN m−1 (from contributions explained above). Nonzero σnet results in additional stretching contributions distributed between both leaflets which contribute to αL, aout, and σout but which drop out of ΔΣ (because they are evenly distributed between the leaflets). Accordingly, the tensionless condition probably provides an upper limit to ΔΣ in vesicles on the verge of collapse: i.e. ΔΣ ≤ 2σout. In other words, estimates of ΔΣ reported above are probably overestimates.
Relating to the above, bilayer stiffening and gel–liquid phase coexistence from accumulation of ΔΣ has been studied for σnet = 0 mN m−1 only.5,102 We observed such transitions in the flat portions of GUVs which were studded with high-curvature, inward protrusions (see time-lapse of Fig. 6c), revealing that these GUVs possessed nonzero, negative spontaneous curvatures during exposure to loaded mbCD. Accordingly, the flat portions of these GUVs in which the gel domains formed must have harbored a nonzero spontaneous tension (which applies an additional stretching contribution to lipids within these regions).74,89 This contribution was presumably opposed by a compressive contribution due to net lipid insertion into the bilayer (under the constraint of fixed encapsulated volume). The direction and magnitude of σnet is unclear because the magnitudes of the above contributions are unknown.
Because application of mechanical tensions alters coexistence in bilayers,103,104 the above contributions are likely to be relevant for understanding phase behaviors4,105 associated with lipid asymmetry. Therefore, these contributions should be considered in future experiments and theory. The fact that σnet ≠ 0 mN m−1 before/during lipid insertion might relate to why we were unable to induce outward bending during local delivery (which was expected based on bulk mixing experiments) and, instead, induced gel domains.
Carbohydrate asymmetries did not bias our assessment of mbCD-mediated transformations in GUVs
Because we diluted GUVs with encapsulated sucrose solutions into osmotically-balanced glucose solutions at different stages of our experiments, we must consider the effects of carbohydrate asymmetry upon our study.45 Shape changes associated with this phenomenon could have confounded our determination of Qcrossϕ, for example, since this was based on assessment of GUV bending transitions. This does not seem to have occurred because we observed (i) similar frequencies of GUVs containing inner/outer bending protrusions in the absence of mbCD and (ii) almost half of the GUVs contained no bending protrusions in the absence of mbCD (see Fig. 5d). Therefore, the electroformed GUVs used in the bulk mixing experiments were flat, on average, across the eleven dispersions. If solution asymmetry had a more pronounced effect on our study, then outer bending protrusions would have dominated in the control (due to the larger size of sucrose compared to glucose) (as in this study).45Moreover, the striking outer pearling morphologies associated with carbohydrate asymmetry are associated with more extensive deflation (>10% deflation)45 compared to that experienced by GUVs in our study (no more than 2% deflation; see ESI†). Finally, we note that GUVs used in our study appeared to be mechanically relaxed – on average, across all vesicles within each dispersion – in the absence of mbCD (see Fig. 5d and Fig. S2/associated discussion in the ESI†).7,106 This implies that the GUVs occupied their reference states (characterized by αL = 1) prior to lipid exchange with mbCD. Since the GUVs appeared to occupy their reference state, this validates Qcrossϕ = Ktotal (which requires that the GUVs exposed to the corresponding mbCD solution are characterized by αL = 1).
Conclusions
We have leveraged mbCD–lipid complexation to generate area asymmetry in 1-component vesicles. This conclusion reiterates the bases of important preparatory schemes for in vitro membrane asymmetry research17,32 and highlights the synthetic utility gained by kinetic trapping of mbCD–lipid complexes. Specifically, kinetic trapping was required to achieve net lipid insertion into GUVs, yielding (i) tunable curvature-generation and (ii) gel–liquid coexistence at 23 °C. It is already established that compositional asymmetry influences phase coexistence in multicomponent bilayers,4,105 but here we have studied the effect of area asymmetry/differential tension in isolation (in confirmation of recent theoretical predictions).5,102We also showed that (1) neglecting variation in lipid chemical activity underestimates equilibrium constants for mbCD–lipid complexation and (2) this variation is related to mechanical stresses in vesicles. Practically, this indicates that a re-evaluation of reported equilibrium constants23,31,32 is warranted. Furthermore, our study highlights the usefulness of lipid chemical activity (accessible through systematic treatment of mbCD–lipid equilibrium) for quantitative study of lipid asymmetry. To this end, we applied a basic thermodynamic model to calculate microscopic/mechanical parameters using two estimates of lipid chemical activity yielded by our study.
In the future, mbCD–lipid equilibrium could be used to validate models for transmembrane protein allostery with respect to lipid asymmetry.8 These ideas are relevant, for example, in the mbCD-mediated opening of mechanosensitive ion channels which has received recent attention.18,19 Based on our findings, the allosteric bias applied by mbCD in these experiments seems to result from a combination of differential tension and net bilayer tension. Similarly, it is likely that allosteric bias and adjustment of lipid thermodynamic gradients due to differential tension is relevant for the activities of lipid flippases and scramblases.107
Author contributions
T. R. and T. B. designed research. T. R., Y. X., Z. A., and W. C. performed research. T. R. and T. B. wrote the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge funding through NIH grant NIGMS 097552.Notes and references
- M. S. Bretscher, J. Mol. Biol., 1972, 71, 523–528 CrossRef CAS PubMed.
- M. P. Sheetz, R. G. Painter and S. J. Singer, J. Cell Biol., 1976, 70, 193–203 CrossRef CAS PubMed.
- M. Doktorova, J. L. Symons and I. Levental, Nat. Chem. Biol., 2020, 16, 1321–1330 CrossRef CAS PubMed.
- M. D. Collins and S. L. Keller, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 124–128 CrossRef CAS PubMed.
- S. L. Foley, A. Hossein and M. Deserno, Biophys. J., 2022, 121, 2997–3009 CrossRef CAS PubMed.
- H. G. Dobereiner, E. Evans, M. Kraus, U. Seifert and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4458–4474 CrossRef.
- L. Miao, U. Seifert, M. Wortis and H. G. Dobereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389–5407 CrossRef CAS PubMed.
- P. Piller, E. A.-O. Semeraro, G. N. Rechberger, S. A.-O. Keller and G. A.-O. Pabst, PNAS Nexus, 2023, 2, pgad126 CrossRef PubMed.
- B. L. S. Mui, H. G. Dobereiner, T. D. Madden and P. R. Cullis, Biophys. J., 1995, 69, 930–941 CrossRef CAS PubMed.
- S. L. Foley, M. Varma, A. Hossein and M. Deserno, Emerging Top. Life Sci., 2023, 1, 95–110 CrossRef PubMed.
- E. London, Acc. Chem. Res., 2019, 52, 2382–2391 CrossRef CAS PubMed.
- E. Farge and P. F. Devaux, J. Phys. Chem., 1993, 97, 2958–2961 CrossRef CAS.
- M. Traikia, D. E. Warschawski, O. Lambert, J. L. Rigaud and P. F. Devaux, Biophys. J., 2002, 83, 1443–1454 CrossRef CAS PubMed.
- M. A.-O. Doktorova, I. A.-O. Levental and F. A. Heberle, Cold Spring Harbor Perspect. Biol., 2023, 15, 1–13 Search PubMed.
- G. K. Voeltz and W. A. Prinz, Nat. Rev. Mol. Cell Biol., 2007, 8, 258–264 CrossRef CAS PubMed.
- L. Szente and E. Fenyvesi, Struct. Chem., 2017, 28, 479–492 CrossRef CAS.
- M. Doktorova, F. A. Heberle, B. Eicher, R. F. Standaert, J. Katsaras, E. London, G. Pabst and D. Marquardt, Nat. Protoc., 2018, 13, 2086–2101 CrossRef CAS PubMed.
- C. D. Cox, Y. X. Zhang, Z. J. Zhou, T. Walz and B. Martinac, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104820118 CrossRef CAS PubMed.
- Y. X. Zhang, G. Angiulli, B. Martinac, C. D. Cox and T. Walz, J. Struct. Biol.: X, 2021, 5, 100053 CAS.
- A. G. Ayuyan and F. S. Cohen, Biophys. J., 2018, 114, 904–918 CrossRef CAS PubMed.
- A. Radhakrishnan and H. M. McConnell, Biochemistry, 2000, 39, 8119–8124 CrossRef CAS PubMed.
- T. R. Shaw, K. C. Wisser, T. A. Schaffner, A. D. Gaffney, B. B. Machta and S. L. Veatch, Biophys. J., 2023, 122, 1105–1117 CrossRef CAS PubMed.
- T. G. Anderson, A. Tan, P. Ganz and J. Seelig, Biochemistry, 2004, 43, 2251–2261 CrossRef CAS PubMed.
- L. D. S. Araujo, G. Lazzara and L. Chiappisi, Adv. Colloid Interface Sci., 2021, 289, 102375 CrossRef PubMed.
- D. Lichtenberg, Biochem. Biophys. Acta, 1985, 821, 470–478 CAS.
- I. R. Cooke and M. Deserno, Biophys. J., 2006, 91, 487–495 CrossRef CAS PubMed.
- J. Israelachvili, Intermolecular and Surface Forces, Academic Press, 3rd edn, 2010 Search PubMed.
- B. Sorre, A. Callan-Jones, J. B. Manneville, P. Nassoy, J. F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626 CrossRef CAS PubMed.
- M. Rahimi, D. Regan, M. Arroyo, A. B. Subramaniam, H. A. Stone and M. Staykova, Biophys. J., 2016, 111, 2651–2657 CrossRef CAS PubMed.
- R. Smith and C. Tanford, J. Mol. Biol., 1972, 67, 75–83 CrossRef CAS PubMed.
- J. C. Bozelli, Y. H. Hou and R. M. Epand, Langmuir, 2017, 33, 13882–13891 CrossRef CAS PubMed.
- M. Markones, C. Drechsler, M. Kaiser, L. Kalie, H. Heerklotz and S. Fiedler, Langmuir, 2018, 34, 1999–2005 CrossRef CAS PubMed.
- Z. Huang and E. London, Langmuir, 2013, 29, 14631–14638 CrossRef CAS PubMed.
- S. Shukla, R. Jin, J. Robustelli, Z. E. Zimmerman and T. Baumgart, Biophys. J., 2019, 117, 962–974 CrossRef CAS PubMed.
- J. Pencer and F. R. Hallett, Langmuir, 2003, 19, 7488–7497 CrossRef CAS.
- A. Ghanbarpour, D. P. Valverde, T. J. Melia and K. M. Reinisch, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2101562118 CrossRef CAS PubMed.
- K. Telfeyan, A. A. Migdisov, S. Pandey, V. V. Vesselinov and P. W. Reimus, Appl. Geochem., 2019, 101, 160–169 CrossRef CAS.
- J. Steinkuhler, P. De Tillieux, R. L. Knorr, R. Lipowsky and R. Dimova, Sci. Rep., 2018, 8, 11838 CrossRef PubMed.
- S. E. Ghellab and X. J. Han, Chem. Phys. Lett., 2018, 706, 515–519 CrossRef.
- N. Khalifat, N. Puff, S. Bonneau, J. B. Fournier and M. I. Angelova, Biophys. J., 2008, 95, 4924–4933 CrossRef CAS PubMed.
- A. Tian and T. Baumgart, Biophys. J., 2009, 96, 2676–2688 CrossRef CAS PubMed.
- R. Dimova and C. Marques, The Giant Vesicle Book, CRC Press LLC, Milton, 1st edn, 2019 Search PubMed.
- H. D. Andersen, C. H. Wang, L. Arleth, G. H. Peters and P. Westh, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1874–1878 CrossRef CAS PubMed.
- A. Roy, R. Dutta, N. Kundu, D. Banik and N. Sarkar, Langmuir, 2016, 32, 5124–5134 CrossRef CAS PubMed.
- T. Bhatia, S. Christ, J. Steinkuhler, R. Dimova and R. Lipowsky, Soft Matter, 2020, 16, 1246–1258 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- R. J. Bruckner, S. S. Mansy, A. Ricardo, L. Mahadevan and J. W. Szostak, Biophys. J., 2009, 97, 3113–3122 CrossRef CAS PubMed.
- M. S. Miettinen and R. Lipowsky, Nano Lett., 2019, 19, 5011–5016 CrossRef CAS PubMed.
- M. Denz, I. Haralampiev, S. Schiller, L. Szente, A. Herrmann, D. Huster and P. Muller, Chem. Phys. Lipids, 2016, 194, 37–48 CrossRef CAS PubMed.
- T. Sugiura, K. Ikeda and M. Nakano, Langmuir, 2016, 32, 13697–13705 CrossRef CAS PubMed.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef CAS PubMed.
- H. Watanabe, S. Hanashima, Y. Yano, T. Yasuda and M. Murata, Langmuir, 2023, 39, 15189–15199 CrossRef CAS PubMed.
- F. Jahnig, Biophys. J., 1984, 46, 687–694 CrossRef CAS PubMed.
- A. Sreekumari and R. Lipowsky, Soft Matter, 2022, 18, 6066–6078 RSC.
- M. Hasan, S. K. Saha and M. Yamazaki, J. Chem. Phys., 2018, 148, 245101 CrossRef PubMed.
- R. M. Raphael and R. E. Waugh, Biophys. J., 1996, 71, 1374–1388 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- K. C. Melikov, V. A. Frolov, A. Shcherbakov, A. V. Samsonov, Y. A. Chizmadzhev and L. V. Chernomordik, Biophys. J., 2001, 80, 1829–1836 CrossRef CAS PubMed.
- S. C. L. Fernanda, S. Mareike, A. R. Karin and D. Rumiana, bioRxiv, 2023, preprint DOI:10.1101/2023.02.03.526964.
- M. J. Moreno, L. Estronca and W. L. C. Vaz, Biophys. J., 2006, 91, 873–881 CrossRef CAS PubMed.
- H. L. Scott, A. Skinkle, E. G. Kelley, M. N. Waxham, I. Levental and F. A. Heberle, Biophys. J., 2019, 117, 1381–1386 CrossRef CAS PubMed.
- R. Jin and T. Baumgart, Soft Matter, 2021, 17, 7506–7515 RSC.
- K. Brunaldi, N. Huang and J. A. Hamilton, J. Lipid Res., 2010, 51, 120–131 Search PubMed.
- We define all complex solutions as though they are held in contact with a vesicle mesophase which fixes uncomplexed, monomeric lipid in the solution-phase at its CBC. This ensures all mass-action quotients that are applied to complex solutions describe the tendency for lipid delivery into intact vesicles in their reference state.
- Because the region of the phase diagram falling between the onset and solubilization boundaries is associated with vesicles on the verge of collapse (region II of Fig. 2d), we propose that lipid nucleates resulting from complex solutions that map to this region are likely to be stressed (relative to bilayers in their reference state).
- A. Gouda, O. S. Sakr, M. Nasr and O. Sammour, J. Drug Delivery Sci. Technol., 2021, 61, 102174 CrossRef CAS.
- C. Tanford, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 1811–1815 CrossRef CAS PubMed.
- P. Ziherl and S. Svetina, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 761–765 CrossRef CAS PubMed.
- Y. G. Smirnova, S. J. Marrink, R. Lipowsky and V. Knecht, J. Am. Chem. Soc., 2010, 132, 6710–6718 CrossRef CAS PubMed.
- M. Nakano, M. Fukuda, T. Kudo, M. Miyazaki, Y. Wada, N. Matsuzaki, H. Endo and T. Handa, J. Am. Chem. Soc., 2009, 131, 8308–8312 CrossRef CAS PubMed.
- T. Baumgart, G. Hunt, E. R. Farkas, W. W. Webb and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 2182–2194 CrossRef CAS PubMed.
- K. Tada, M. Goto, N. Tamai, H. Matsuki and S. Kaneshina, in High-pressure Bioscience and Biotechnology, ed. D. H. Bartlett, 2010, ch. 5th International High-Pressure Bioscience and Biotechnology Conference, vol. 1189, pp. 77–85 Search PubMed.
- T. Bhatia, T. Robinson and R. Dimova, Soft Matter, 2020, 16, 7359–7369 RSC.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- R. Lipowsky, Adv. Biol., 2022, 6, 2101020 CrossRef PubMed.
- As a practical aside, we found that the capacity of loaded mbCD solutions to drive lipids into single GUVs decreased as more time passed after kinetic-trapping and after repeated exposure to GUV dispersions. This suggests that lipid in the loaded mbCD solution underwent re-nucleation (AKA crashed-out), abrogating its delivery capacity. This conclusion reflects the fact that net lipid insertion can only be achieved in the vicinity of the upper-limit for kinetic-trapping (see Fig. 4a and associated discussion). To reproducibly drive lipids into GUVs in this experimental scheme, we found that repeated preparation/refilling of the loaded mbCD was required. Failure to implement these measures heralded a return to inward bending (indicating that lipid was no longer being inserted).
- D. Lichtenberg, E. Opatowski and M. M. Kozlov, Biochim. Biophys. Acta, Biomembr., 2000, 1508, 1–19 CrossRef CAS PubMed.
- L. Dietel, L. Kalie and H. Heerklotz, Biophys. J., 2020, 119, 767–779 CrossRef CAS PubMed.
- M. G. Lete, B. G. Monasterio, M. I. Collado, M. Medina, J. Sot, A. Alonso and F. M. Goñi, Colloids Surf., B, 2019, 183, 110430 CrossRef CAS PubMed.
- H. Y. Fan, D. Das and H. Heerklotz, Langmuir, 2016, 32, 11655–11663 CrossRef CAS PubMed.
- H. Ahyayauch, M. Bennouna, A. Alonso and F. M. Goñi, Langmuir, 2010, 26, 7307–7313 CrossRef CAS PubMed.
- T. P. Sudbrack, N. L. Archilha, R. Itri and K. A. Riske, J. Phys. Chem. B, 2011, 115, 269–277 CrossRef CAS PubMed.
- D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2006, 128, 12462–12467 CrossRef CAS PubMed.
- B. Kollmitzer, P. Heftberger, M. Rappolt and G. Pabst, Soft Matter, 2013, 9, 10877–10884 RSC.
- P. Boonnoy, V. Jarerattanachat, M. Karttunen and J. Wong-ekkabut, J. Phys. Chem. Lett., 2015, 6, 4884–4888 CrossRef CAS PubMed.
- K. Tazawa and M. Yamazaki, J. Chem. Phys., 2023, 158, 081101 CrossRef CAS PubMed.
- R. Volinsky, L. Cwiklik, P. Jurkiewicz, M. Hof, P. Jungwirth and P. K. J. Kinnunen, Biophys. J., 2011, 101, 1376–1384 CrossRef CAS PubMed.
- S. Svetina and B. Zeks, Adv. Colloid Interface Sci., 2014, 208, 189–196 CrossRef CAS PubMed.
- M. Deserno, Chem. Phys. Lipids, 2015, 185, 11–45 CrossRef CAS PubMed.
- G. Hollo, Y. Miele, F. Rossi and I. Lagzi, Phys. Chem. Chem. Phys., 2021, 23, 4262–4270 RSC.
- R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761 CrossRef CAS PubMed.
- B. Rozycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101 CrossRef PubMed.
- P. Atkins and J. de Paula, Physical Chemistry: Thermodynamics, Structure, and Change, Oxford University Press, 2016 Search PubMed.
- C. Kataoka-Hamai and K. Kawakami, J. Phys. Chem. B, 2020, 124, 8719–8727 CrossRef CAS PubMed.
- C. Kataoka-Hamai and K. Kawakami, Langmuir, 2021, 37, 7527–7535 CrossRef CAS PubMed.
- N. Kucerka, M. P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef CAS PubMed.
- V. Levadnyy, M. Hasan, S. K. Saha and M. Yamazaki, J. Phys. Chem. B, 2019, 123, 4645–4652 CrossRef CAS PubMed.
- E. Evans, V. Heinrich, F. Ludwig and W. Rawicz, Biophys. J., 2003, 85, 2342–2350 CrossRef CAS PubMed.
- S. Esteban-Martin, H. J. Risselada, J. Salgado and S. J. Marrink, J. Am. Chem. Soc., 2009, 131, 15194–15202 CrossRef CAS PubMed.
- S. Foley and M. Deserno, J. Chem. Theory Comput., 2020, 16, 7195–7206 CrossRef CAS PubMed.
- S. Park, A. H. Beayen, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2015, 11, 3466–3477 CrossRef CAS PubMed.
- A. Hossein and M. Deserno, J. Chem. Phys., 2021, 154, 014704 CrossRef CAS PubMed.
- D. Chen and M. M. Santore, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 179–184 CrossRef CAS PubMed.
- T. Portet, S. E. Gordon and S. L. Keller, Biophys. J., 2012, 103, L35–L37 CrossRef CAS PubMed.
- T. A. Enoki and F. A. Heberle, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2308723120 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CrossRef CAS PubMed.
- S. Shukla and T. Baumgart, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183534 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01772a |
| This journal is © The Royal Society of Chemistry 2024 |