Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Confinement controls the creep rate in soft granular packings
Joshua A.
Dijksman
 *a and
Tom
Mullin
*a and
Tom
Mullin
 b
b
aVan der Waals-Zeeman Institute, Institute of Physics, Science Park 904, 1094KS, Amsterdam, The Netherlands. E-mail: j.a.dijksman@uva.nl
bThe Mathematical Institute and Linacre College, University of Oxford, OX2 6GG, UK. E-mail: tom.mullin@maths.ox.ac.uk
First published on 1st May 2024
Abstract
Flow in soft materials encompasses a wide range of viscous, plastic and elastic phenomena which provide challenges to modelling at the microscopic level. To create a controlled flow, we perform falling ball viscometry tests on packings of soft, frictionless hydrogel spheres. Systematic creep flow is found when a controlled driving stress is applied to a sinking sphere embedded in a packing. Here, we take the novel approach of applying an additional global confinement stress to the packing using an external load. This has enabled us to identify two distinct creep regimes. When confinement stress is small, the creep rate is independent of the load imposed. For larger confinement stresses, we find that the creep rate is set by the mechanical load acting on the packing. In the latter regime, the creep rate depends exponentially on the imposed stress. We can combine the two regimes via a rescaling onto a master curve, capturing the creep rate over five orders of magnitude. Our results indicate that bulk creep phenomena in these soft materials can be subtly controlled using an external mechanical force.
Introduction
The physical properties of athermal particle packings have a variety of non-trivial features which are of interest at both the fundamental and applied levels. Collections of materials such as sand, foams, emulsions and other particulate media have a “rigid” phase that can bear a finite amount of stress.1–10 However, the definition of “rigid” is sometimes not clear cut since slow mechanical motion or creep can exist in thermally driven amorphous materials.11,12 Specifically, packings of inelastic particles might be considered rigid, yet they also display slow relaxation dynamics when deformation is imposed, even in the absence of thermal fluctuations; they are considered to self-fluidize.13,14 Alternatively, when stress is imposed, granular packings also display very small magnitude logarithmic aging.15,16 Hence, the origin of creep in athermal packings is unclear. Despite the introduction of concepts such as non-locality, there is no general framework to connect the microscopic details of (a)thermal particle packings and their fluctuations to their rheology at a coarse grained level. Furthermore, it is difficult to reproduce these observations numerically using techniques such as discrete element methods without introducing (ad hoc) noise.In this study we focus on elastic phenomena using packings of hydrated hydrogels. Previous work17 on this material has revealed systematic dependence of creep flow rates on driving stress. Here we show that the creep in athermal soft particle packings can also be controlled via an external mechanical stress applied to the particle phase. We again find that the local stress that the intruder applies to the packing exponentially enhances the creep rate. We can merge these two competing effects using a master curve, in which a stress-time superposition principle is captured. Our work highlights sensitivity to boundary stresses of bulk creep phenomena.
Experimental setup
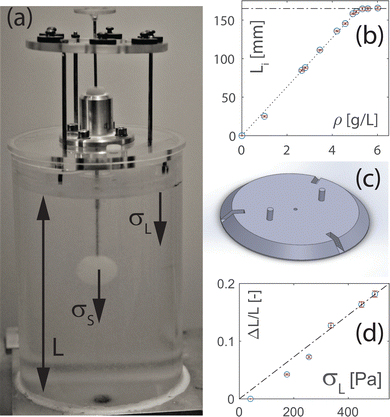
We prepare a packing of hydrogel spheres using a successfully established approach.17 Briefly, we swell hydrogel beads (JRM Chemicals, type “snow”) in a fixed volume of 2 litres of triply boiled Oxford tap water. The particles are swollen in a 124 mm diameter plexiglass container – see Fig. 1(a). The dry particles are sprinkled into the water in measured amounts of ≈2 g. They are heavier than the water and sink and swell to form a layer of swollen particles at the bottom of the container. A gentle stir of the layer is applied between additions of particles and the layer is left for 2 hours to settle between additions. Interestingly, it is found that the depth of the layer is linearly dependent on the weight of the dry beads as shown in Fig. 1(b). This observation provides evidence for the uniformity of the density of the layer. We find it convenient to define the volume fraction where m is the weight of the dry hydrogel powder and V is the volume of water. The fixed volume of 2 litres of water used in our experiments, corresponds to a water level at L = 165 mm. At the experimentally used concentration of hydrogel powder of 6.02 g L−1 (and no additional confinement of the packing), the packing reaches the surface of the water i.e. there is no clear water above the hydrogels – see Fig. 1(b). All experiments were performed at 6.02 g L−1, as this is well into the plateau regime where adding more hydrogel makes the swollen particles reach to and push against the liquid surface. We apply confinement stress by placing a rigid lid on the surface of the packing. The lid is always submersed so that there is no influence of surface tension on the particle packing. For the first set of experiments, a lid was designed and 3D printed in plastic (PLA), partially hollow and weighing ≈50.3 gram as shown in Fig. 1(c). The lid rests freely on the surface of the packing; when submersed, its contribution to the stress on the particles is negligible. We added weights to the upper surface of this free lid (FL) to increase the confinement stress σL. The lid remained level when small masses were added but it tended to tilt when adding more than ≈300 grams in calibrated weights to the lid. We therefore designed a second, guided lid (GL) for subsequent experiments as shown in Fig. 1(a). In this setup, the same container is used, but the lid is now guided by three rods which pass through closely fitting holes in the cover of the container. The three rods are connected by a 2 mm thick ring on which we can add weights to increase the confinement stress – see Fig. 1(d). We also observe that the amount of compression of the packing ΔL/L increases approximately linearly with the amount of applied confinement stress, indicating a packing stiffness of about 3.3 kPa as indicated in Fig. 1(d). The measured packing stiffness is lower than that of the particles themselves (about 10 kPa), which is reasonable as the packing is a loose, porous collection of soft, deformable and slippery particles. The rods ensure that the lid remains horizontal over the range of confinement stresses investigated. All experiments above 200 Pa confinement stress level are achieved with the GL, which allows us to apply a stress of up to ≈1000 Pa.
where m is the weight of the dry hydrogel powder and V is the volume of water. The fixed volume of 2 litres of water used in our experiments, corresponds to a water level at L = 165 mm. At the experimentally used concentration of hydrogel powder of 6.02 g L−1 (and no additional confinement of the packing), the packing reaches the surface of the water i.e. there is no clear water above the hydrogels – see Fig. 1(b). All experiments were performed at 6.02 g L−1, as this is well into the plateau regime where adding more hydrogel makes the swollen particles reach to and push against the liquid surface. We apply confinement stress by placing a rigid lid on the surface of the packing. The lid is always submersed so that there is no influence of surface tension on the particle packing. For the first set of experiments, a lid was designed and 3D printed in plastic (PLA), partially hollow and weighing ≈50.3 gram as shown in Fig. 1(c). The lid rests freely on the surface of the packing; when submersed, its contribution to the stress on the particles is negligible. We added weights to the upper surface of this free lid (FL) to increase the confinement stress σL. The lid remained level when small masses were added but it tended to tilt when adding more than ≈300 grams in calibrated weights to the lid. We therefore designed a second, guided lid (GL) for subsequent experiments as shown in Fig. 1(a). In this setup, the same container is used, but the lid is now guided by three rods which pass through closely fitting holes in the cover of the container. The three rods are connected by a 2 mm thick ring on which we can add weights to increase the confinement stress – see Fig. 1(d). We also observe that the amount of compression of the packing ΔL/L increases approximately linearly with the amount of applied confinement stress, indicating a packing stiffness of about 3.3 kPa as indicated in Fig. 1(d). The measured packing stiffness is lower than that of the particles themselves (about 10 kPa), which is reasonable as the packing is a loose, porous collection of soft, deformable and slippery particles. The rods ensure that the lid remains horizontal over the range of confinement stresses investigated. All experiments above 200 Pa confinement stress level are achieved with the GL, which allows us to apply a stress of up to ≈1000 Pa.
We probe the mechanical behavior of the prepared packing via what is essentially a falling ball viscometry test. Inside the packing of swollen hydrogel spheres, we embed an intruder. The intruder is a spherical plastic object, 2 cm in diameter and mounted on a rod. The rod is guided by a vertical bearing to maintain the alignment of the rod and allow for tracking of the intruder motion, while the intruder can sink into the packing of spheres as a result of the gravitationally induced stresses it exerts on the packing. The intruder stress σS that the intruder is exerting is varied by adding calibrated weights to the tray which is connected to the 23 mm diameter plastic sphere by a thin rod. The 3D printed tray alone weighs 2 grams which enables stresses down to ≈100 Pa to be applied. We compute the intruder stress from the buoyancy corrected total weight of the intruder, the volume of the sphere and the surface of the sphere. We also test sinking rates without the lid (NL) to verify reproducibility of previous results.17 We collect displacement data via photographs taken at set intervals and post-processing of the images to extract the penetration depth δ(t) as a function of time. We measure δ from the starting position of the sphere, which is always fully submersed in the packing.
We found it to be essential to stir the packing, and allow a settling period of three hours between rehearsals of the experiment as in previous work. Stirring the packing is carried out carefully to avoid introducing bubbles, as the presence of bubbles creates poorly reproducible sinking dynamics. We stir the packing by burying a long rod at the bottom of the container. The rod is nearly as wide as the container and has two neodymium magnets at its ends. The magnets are held with other magnets on the outside of the container. Slow movement of the external magnets allows us to change the position of the rod within the packing and thereby induce stirring while keeping the lid in place.
Experimental results
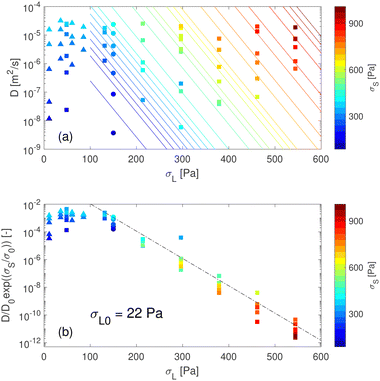
The main experimental results for the sinking characteristics of the sphere are presented in Fig. 2(a). Note that only one third of all the data collected over about one year of experimental efforts are shown here. The examples are randomly selected and displayed in this short form for reasons of clarity whereas the full dataset is used in the analysis. All data and analysis script can be found in an online repository.18 The color coding spans different experimental settings in σL and σS and its purpose is to highlight the time dependence δ(t). For all three cases NL, FL, GL, and a wide variety of σS,σL, we observe the characteristic non-linear displacement dynamics as reported in our previous experiments. The data is well represented by square root behavior, as observed previously and indicated in Fig. 2(a) and on log scale in Fig. 2(b). The error on the determination of the position is small, as indicated. Consistently, we find that δ2(t) ∝ t as evidenced by the collapse of data in Fig. 2(c). Here we divide out the fitted prefactor D from δ2 = Dt to find that all data follows a single master curve. We observe small deviations from linearity in the δ2vs. t plot, but see no systematic trend in the deviations with any experimental control parameter.Intruder stress dependence
We measure the sinking rate D for a range of intruder stresses σS and confinement stresses σL. Having access to all D(σS,σL), we can establish the stress dependence via two different representations of the data. We first discuss how D(σL) depends on σS. We show all measured D(σS,σL) in Fig. 3(a). Given the quality of the collapse of Fig. 2(c), we conclude that the error bars on the slope estimate D is less than 20% and hence becomes negligible on the log scale representation used henceforth. There are three main observations: (i) at low confinement stress σL, D appears to be approximately independent of the confinement stress: both FL and GL data here suggests there is a plateau in D(σL); the tentative plateau value depend on σS. Note that the subtle color gradient in blue covers six data sets. (ii) The data of the NL case are consistent with the FL and GL case. This consistency indicates that current experiments probe the same dynamics as previous work17 in which no lid was used, (iii) above approximately 100 Pa of confinement stress, the creep rate has a definite dependence on the confinement stress. We find that the previously observed exponential stress dependence (shown in solid lines) captures the overall trend well: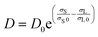 | (1) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = D/exp(σS/σS0). We see again that (i) the high stress data collapses onto a single master curve
= D/exp(σS/σS0). We see again that (i) the high stress data collapses onto a single master curve ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ∝ exp(−σL). Furthermore, data taken in the low stress regime provides a reasonable collapse onto a single line, suggesting that the low stress regime is governed by a single σS0, despite its independence of confinement stress. We find that for D0 = 2 × 10−6, σS0 = 35 Pa, σL0 = 22 Pa, all data collapses onto a single confinement stress dependent curve, suggesting that the bulk creep rate is indeed set by the mechanical boundary stress acting on the particles and competing with the local stress from the intruder. It should be emphasized that we show here all the data, from NL, FL and GL experiments, demonstrating consistency across different lid types and hence ways to exert boundary stress. Note that to estimate the amplitude of the surface stress in the NL case, we need to make assumptions concerning the typical radius of curvature of the water surface between the hydrogel beads. An estimate of about 100 Pa was previously considered reasonable, but this value has considerable uncertainty. As we can see, a value of 150 Pa produces a good match between the NL data and the trend line; however a surface tension stress of 100 Pa would also keep the NL data consistent with the FL and GL cases. We emphasize here that the visible change in the behavior of the hydrogels at D(σL) around 100 Pa is therefore unrelated to the surface tension pressure scale, as we shall see with more careful analysis in the following section.
∝ exp(−σL). Furthermore, data taken in the low stress regime provides a reasonable collapse onto a single line, suggesting that the low stress regime is governed by a single σS0, despite its independence of confinement stress. We find that for D0 = 2 × 10−6, σS0 = 35 Pa, σL0 = 22 Pa, all data collapses onto a single confinement stress dependent curve, suggesting that the bulk creep rate is indeed set by the mechanical boundary stress acting on the particles and competing with the local stress from the intruder. It should be emphasized that we show here all the data, from NL, FL and GL experiments, demonstrating consistency across different lid types and hence ways to exert boundary stress. Note that to estimate the amplitude of the surface stress in the NL case, we need to make assumptions concerning the typical radius of curvature of the water surface between the hydrogel beads. An estimate of about 100 Pa was previously considered reasonable, but this value has considerable uncertainty. As we can see, a value of 150 Pa produces a good match between the NL data and the trend line; however a surface tension stress of 100 Pa would also keep the NL data consistent with the FL and GL cases. We emphasize here that the visible change in the behavior of the hydrogels at D(σL) around 100 Pa is therefore unrelated to the surface tension pressure scale, as we shall see with more careful analysis in the following section.
 | ||
| Fig. 3 (a) All D obtained for all σL,S measured shown versus confinement stress. Symbols indicate experiments NL (○), FL (△) and GL (□). Solid lines indicate the trend as described in eqn (1) (b) rescaled data. The dashed line indicates the exponential decay with confinement stress; the stress scale σL0 is indicated in the panel. | ||
Confinement stress dependence
Even though the collapse displayed in Fig. 3(b) is satisfying, small but systematic deviations can be observed over the range of σS. Further, the low confinement stress regime appears to be different—careful inspection of the data reveals that the plateau shows significant scatter over about two orders of magnitude, even in the rescaled D. In fact, scatter of about one order of magnitude is present in the rescaled D values at higher values of σL. We can gain a better understanding of the physical mechanisms at play by plotting D as a function of the intruder stress. We show D(σS) and its dependence on σL in Fig. 4(a). We observe that the FL, NL and the GL observations with low σL have approximately the same, but not identical trend with σS. This trend with σS is the reason why the rescaling with eqn (1) as shown in Fig. 3 does not collapse onto a single master curve. At larger confinement stress, the intruder stress effect shows dependence on confinement. Moreover, the magnitude of the confinement stress dependence becomes larger with σL. To capture the effects of the change of slope in both low and high confinement stress regimes, we fit all constant confinement stress data with an additional compensatory linear function on a semilog scale. The fits are shown as solid lines. Specifically, we have fitted| log(D) = A(σL)σS + B(σL), | (2) |
 | ||
| Fig. 4 (a) All D obtained for all σL,S measured shown versus sphere stress. Symbols indicate experiments NL (○), FL (△) and GL (□). Solid lines indicate the trend of eqn (1). (b) Intruder stress scale factor A fitted with free B (black circles) or fixed B = −11.2 (blue squares). The red dash-dotted line represents 1/A ∝ σL with A0 = 18 Pa and k = 0.09 (c) B(σL) from the fits (black circles) or fixed at their average fitted value B = −11.2 (blue line). | ||
It is instructive to consider the behavior of the fitted prefactors A,B. We show their dependence on σL in Fig. 4(b) and (c). The prefactor 1/A sets the slope of the intruder stress dependence on the creep rate and hence is essentially a pressure scale. It is therefore natural to assume that 1/A ∝ σL, and the data confirm this. The results of two different fitting methods to extract 1/A are shown in Fig. 4(b) and (c). One can keep B free to have a B(σL), or fix it at some B. Both methods of extracting A yield the dependence to be well-fitted by 1/A = A0 + kσL, with A0 = 18 Pa and k = 0.09 (red dashed line).
Discussion
The different portrayals of D in eqn (1) and (2) can be seen as two different representations of the same behavior. Indeed, we can understand that the weak σL dependence makes eqn (2) the more broadly applicable description than eqn (1), as we found that| D = e(A(σL)σS+B), | (3) |
 | (4) |
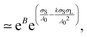 | (5) |
In the limit of σL < σS explored in ref. 17, the weak confinement stress dependence appears to be the balance of stresses used to construct eqn (1). There, σS0 ≈ σL0 and also in eqn (1) we see that A0 ≈ kσS/A02 for σS ≈ 100 Pa. To further highlight the compatibility of the two equations, we can scale out the dependence of both the stress variables. The creep rate D can be corrected for the confinement stress by plotting D/exp(B(σL)), while the driving stress σS can be normalized by A(σL). The collapse of the data over more than six orders of magnitude is visible in Fig. 5(a): clearly there is a universal rate-stress superposition principle at play here, in which simply the rescaling factors depend on the applies stresses. Also, in the limit of σS → 0, the intercept for D ≈ D0 ≈ eB as expected. The offset A0 of about 18 Pa is the most likely source of the qualitatively different creep behavior observed at low confinement stresses, and has a physical interpretation: besides the confinement from the lid, the hydrogel particles experience a weak hydrostatic pressure gradient because the hydrogels are not perfectly density matched. Our previous work estimated this pressure scale to be about 10 Pa for the geometry and materials used. We thus conjecture that the finite slope in log(D(σS)) to which the creep data converges at low σL as visible in Fig. 4(a) is due to hydrostatic pressure effects.
 | ||
Fig. 5 (a) Rescaled data, dividing out the σL dependence for the freely fitted eqn (2), providing σL-dependent A and B. (b) Rescaled data, now with the fixed B = −11.2 while fitting A(σL) as shown as blue squares in Fig. 4(b). The colorbar applies to both panels. The dashed line indicates the exponential intruder stress dependence D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σS) in both panels. exp(σS) in both panels. | ||
The meaning of dimensionless factor B is less obvious. The variation in B is significant, particularly as it appears in an exponential factor. Even so, any change in B, e.g. the apparent low value of B at low σL, is somewhat offset by a change in the value of 1/A, as visible when comparing Fig. 4(b) and (c). As the effect of a changing B can also be absorbed in an effective diffusion constant D0, there are good reasons to assume that B depends on the experimental settings. For example, fluctuations in temperature or perhaps small mis-alignments of the lid could potentially produce such deviations in the prefactor. Pragmatically, keeping B fixed to the average value of freely fitted B(σL) of course yields a lower, yet still satisfactory, quality fit and collapse of the data. We show this collapse in Fig. 5(b). We observe that fixing B does not essentially affect the quality of the rescaling. We can thus conclude that eqn (2) captures very well the creep response of the hydrogel packing.
Conclusions
We report a consistent set of results on creep behavior found using a spherical intruder in a packing of hydrogel particles under a variety of confinement conditions. By varying the confinement stress on the packing, we observe that the boundary induced stress influences the creep rate. The creep is also observed to be dependent on the intruder stress, in agreement with published results. The creep rate depends exponentially on both local and global stress scales. This rate-stress dependence can be rescaled and collapses onto a master curve. The rescaling factors reveal a residual role for a small hydrostatic pressure gradient. Our results highlight the relevance of boundary stresses on creep dynamics.Author contributions
Conceptualization, methodology, data curation, formal analysis and writing were all developed by TM and JAD. TM performed the experiments and initial data curation; JAD made visualizations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge stimulating discussions at the Salamina workshop in Bari, and the feedback from Jorge Peixinho, Edan Lerner and Tommaso Pettinari. We appreciate the help of Raoul Fix in designing and constructing part of the setup. We are grateful to Keith Long who built the majority of the apparatus in Oxford. This project was completed in part by funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska Curie grant agreement no. 812638.Notes and references
- I. D. Evans and A. Lips, J. Chem. Soc., Faraday Trans., 1990, 86, 3413 RSC.
- E. Bartsch, T. Eckert, C. Pies and H. Sillescu, J. Non-Cryst. Solids, 2002, 307–310, 802–811 CrossRef CAS.
- M. V. Hecke, J. Phys.: Condens. Matter, 2009, 22, 033101 CrossRef PubMed.
- Z. Shao, A. S. Negi and C. O. Osuji, Soft Matter, 2013, 9, 5492 RSC.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- P. Coussot, J. Non-Newtonian Fluid Mech., 2014, 211, 31–49 CrossRef CAS.
- A. Basu, Y. Xu, T. Still, P. Arratia, Z. Zhang, K. Nordstrom, J. M. Rieser, J. Gollub, D. Durian and A. Yodh, Soft Matter, 2014, 10, 3027–3035 RSC.
- M. M. Villone and P. L. Maffettone, Rheol. Acta, 2019, 58, 109–130 CrossRef CAS.
- C. S. O’Bryan, C. P. Kabb, B. S. Sumerlin and T. E. Angelini, ACS Appl. Bio Mater., 2019, 2, 1509–1517 CrossRef PubMed.
- H. M. Shewan, G. E. Yakubov, M. R. Bonilla and J. R. Stokes, Soft Matter, 2021, 17, 5073–5083 RSC.
- E. N. D. C. Andrade, Proc. R. Soc. London, Ser. A, 1910, 84, 1–12 CAS.
- F. Spaepen, Acta Metall., 1977, 25, 407–415 CrossRef CAS.
- P. Hébraud and F. Lequeux, Phys. Rev. Lett., 1998, 81, 2934–2937 CrossRef.
- L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001 CrossRef PubMed.
- V. B. Nguyen, T. Darnige, A. Bruand and E. Clement, Phys. Rev. Lett., 2011, 107, 138303 CrossRef PubMed.
- N. S. Deshpande, D. J. Furbish, P. E. Arratia and D. J. Jerolmack, Nat. Commun., 2021, 12, 1–7 CrossRef PubMed.
- J. A. Dijksman and T. Mullin, Phys. Rev. Lett., 2022, 128, 238002 CrossRef CAS PubMed.
- J. A. Dijksman and T. Mullin, Supplementary data repository, 2024 DOI:10.5281/zenodo.11004260.
| This journal is © The Royal Society of Chemistry 2024 |