DOI:
10.1039/D3SM01737K
(Paper)
Soft Matter, 2024,
20, 4707-4714
Analytical description of elastocapillary membranes held by needles†
Received
21st December 2023
, Accepted 29th April 2024
First published on 6th May 2024
Abstract
Fluid objects bounded by elastocapillary membranes display intriguing physical properties due to the interplay of capillary and elastic stresses arising upon deformation. Increasingly exploited in foam or emulsion science, the mechanical properties of elastocapillary membranes are commonly characterised by the shape analysis of inflating/deflating bubbles or drops held by circular needles. These impose complex constraints on the membrane deformation, requiring the shape analysis to be done using elaborate numerical fitting procedures of the shape equations. While this approach has proven quite reliable, it obscures insight into the underlying physics of the problem. We therefore propose here the first fully theoretical approach to this problem using the elastic theory for a membrane with additive contributions of capillary and Hookean-type elastic stresses. We exploit this theory to discuss some of the key features of the predicted pressure-deformation relations. Interestingly, we highlight a breakdown of the quadratic approximation at a well-defined value of the elastocapillary parameter depending on the shape of the reference state, which is regularized by the non-quadratic terms. Additionally, we provide an analytical relationship which allows experimentalists to obtain the elastocapillary properties of a membrane by simple measurement of the height and the width of a deformed bubble (or a drop).
1 Introduction
The adsorption and cross-linking of polymers, proteins or particles at liquid interfaces creates “membranes” whose deformation energy combines a capillary-type response from the interface with a solid-like elastic response from the adsorbed layer.1,2 The coupling of these two energies leads to intriguing properties of objects created from these “elastocapillary membranes”, whose reliable description is of interest from a scientific point of view and for applications. For example, such membranes can completely stop the ageing of foams or emulsions,3 and they can play an important role in controlling the response of micro-capsules.4 The properties of these membranes can also teach us about the interactions of their constituents.1,2,5
The theoretical description of elastocapillary membranes evokes many fundamental questions, the first being how exactly the capillary and elastic stresses are coupled within the membrane.5–8 Often, a simple additive relation is assumed, neglecting the likely coupling of both contributions in most experimental systems. However, this simplifying assumption has been proven to describe reasonably well a wide range of experiments5–9 and provides an important first step to grasping the properties of such membranes.
Due to their increasing importance, different experimental techniques have been developed to characterise the often non-linear visco-elastic properties of elastocapillary membranes. One of the most commonly used approaches relies on the analysis of the shape changes of a drop or bubble held by a circular needle upon inflation/deflation,6,10–12 as sketched in Fig. 1a and b. While this problem can be treated easily in the Young–Laplace framework for interfaces with liquid-like elasticity, the addition of a solid-like elasticity makes this problem intrinsically non-linear due to the constraints imposed on the deformation by the needle, acting like a non-deformable inclusion.5–8,13 Due to the complexity of the resulting stress-deformation relation, currently used approaches for the extraction of the visco-elastic properties of the interfacial membrane require delicate numerical fitting by shape equations.6,9,14 While this has proven fairly successful from an experimental point of view, it obscures the underlying physical picture and is also prone to numerous experimental artefacts.
 |
| | Fig. 1 Sketch of the investigated configuration and associated key quantities. (a) The spherical cap shape of radius R0 corresponds to the reference state of the elastocapillary membrane, when Pint,0 − Pext = ΔP0 = 2γ/R0. The needle radius Rn and the angle θn are related by sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn = Rn/R0 (for future reference, we indicate also ψn the surface rotation angle at the needle). (b) For ΔP ≠ ΔP0, the internal volume is different due to the motion of all surface elements from their position r to θn = Rn/R0 (for future reference, we indicate also ψn the surface rotation angle at the needle). (b) For ΔP ≠ ΔP0, the internal volume is different due to the motion of all surface elements from their position r to ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) = r + u(r). The axial symmetry of the deformation implies that |u| depends only on θ and the torsionless hypothesis implies that u ⊥ eφ (with eφ = er × eθ). (c) Predictions of typical bubbloon (droploon) shapes for different values of the elastocapillary number α and an area stretch λ = A/A0 = 1.2, noting the associated normalised pressure change ξ = (ΔP − ΔP0)/ΔP0. Dashed contour = (initial) reference shape; dotted contour = spherical shape passing through the apex and the needle of the deformed bubbloon. The actual shape of the bubbloon (droploon) is at the boundary between the light and dark grey regions. Ha and Re are the height and the equatorial radius of the bubbloon. = r + u(r). The axial symmetry of the deformation implies that |u| depends only on θ and the torsionless hypothesis implies that u ⊥ eφ (with eφ = er × eθ). (c) Predictions of typical bubbloon (droploon) shapes for different values of the elastocapillary number α and an area stretch λ = A/A0 = 1.2, noting the associated normalised pressure change ξ = (ΔP − ΔP0)/ΔP0. Dashed contour = (initial) reference shape; dotted contour = spherical shape passing through the apex and the needle of the deformed bubbloon. The actual shape of the bubbloon (droploon) is at the boundary between the light and dark grey regions. Ha and Re are the height and the equatorial radius of the bubbloon. | |
We therefore treat here for the first time in a fully theoretical approach the simplest possible configuration of this problem: as sketched in Fig. 1a and b, an initially spherical bubble (or drop) of radius R0 is inflated/deflated on a circular needle of radius Rn. The fact that we neglect gravity corresponds either to experiments with density-matched liquids or to sufficiently small systems in which the elasto-capillary stresses outweigh those created by gravity. We consider a homogeneous, isotropic and Hookean-type membrane of thickness t and bulk shear modulus G. This membrane is assumed to have a non-zero and constant interfacial tension γ with the bubble (drop) and negligible interfacial tension with the surrounding liquid. This allows us to define an elastocapillary number
| | 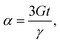 | (1) |
which compares the relative importance of elastic and capillary contributions upon deformation. While this seems a crude simplification, it allows to capture the most important features of this elastocapillary problem.
Using quadratic theory, we predict analytically the full shapes and the associated pressure-deformation relation of what we call “bubbloons” (elastocapillary bubbles) or “droploons” (elastocapillary drops).13 We restrict the description to small deformations which preserve the axial symmetry of the reference spherical cap, and exclude any wrinkling of the structure which arises experimentally when elastocapillary capsules are deflated.
Examples of shapes obtained by our theory for an overall interfacial area increase of λ = A/A0 = 1.2 for different elastocapillary numbers α are shown in Fig. 1c together with
| |  | (2) |
which is the the normalised change in the pressure difference from the reference state value Δ
P0 = 2
γ/
R0, where the elastic stresses are zero.
Two of the key properties of these systems are directly visible in these examples:
(1) For the same magnitude of inflation, for α < 0.5, the pressure jump Δ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) is negative, while for α ≥ 0.5 it is positive.
is negative, while for α ≥ 0.5 it is positive.
(2) While for a small elastocapillary number α the overall shape remains spherical, for larger capillary numbers, the bubbloon (droploon) expands increasingly in the vicinity of the needle.
In the remaining article, we introduce the main theoretical relations and results before discussing in detail some of the specific features created by the interplay of elasticity and capillarity.
The obtained theoretical relations do not only provide important insights into the underlying – sometimes counter-intuitive – physics of the problem but they also provide guidance for reliable experiments together with analytical expressions which can be fitted directly to experimental results to extract the main properties of the elastocapillary membrane. To this end, we provide a simple theoretical relation which allows extracting the elastocapillary number of an in/deflated balloon (droploon) simply by measuring its change in height and width.
For simplicity, we will only talk about elastocapillary bubbles (i.e. bubbloons). However, all derived theory is equally valid for elastocapillary drops, i.e. droploons.
2 Definitions
2.1 System definition
We consider the experimental setup sketched in Fig. 1: a membrane is attached to the extremity of a circular needle of radius Rn and acts as a boundary between an external chamber at pressure Pext and an internal chamber at pressure Pint. Both chambers may be filled with a liquid, or one of them may be a gas. The separating membrane is of “elastocapillary type”, meaning that it displays both elastic and capillary properties: as an elastic membrane, it has a reference state, for which its elastic stresses are zero. We assume that this reference state is a spherical cap of radius R0 as sketched in Fig. 1. Away from this reference state, the interface stores an elastic energy Eel. As a capillary interface, it has also a constant interfacial tension γ and an energy term Eγ = γA, proportional to the interfacial area A.
An important feature of our model is to assume that the interfacial and elastic energies sum up to define the membrane free energy
an approach which has been successfully exploited in the past.
5–9 Microscopically, this kind of model may correspond to an interface where a cross-linked and percolated network of a polymer (with interfacial affinity) covers the whole surface but with a small overall surface density, like a three-dimensional fisherman's net covering the interface. In this case, the membrane displays both elastic and capillary properties, and
γ will be approximately constant and close to that of the liquid.
2.1.2 Surface energy.
The capillary energy term of the elastocapillary membrane retains by assumption the usual expression γA, with A being the interfacial area. A priori, any parametrisation of the surface is possible, but the presence of the elastic component gives the natural parametrisation (θ,ϕ) ↦ r + u and hence the expression| |  | (9) |
2.1.3 Gibbs functional.
The total free energy of the membrane is Eel + γA, and its variation stems from the work of pressure forces applied on each side of the membrane: δEel + γδA = (ΔP)δVi. Here Vi is the interior volume of the bubbloon, virtually closed horizontally at the orifice of the needle (gray line in Fig. 1a).
As a result, the equilibrium shape of the bubbloon is given by the minimisation of the Gibbs energy Eel + γA − (ΔP)Vi with respect to the variations of the displacement field u(θ), with the constraint u(θn) = 0. The latter has a physical origin: the elastic membrane is clamped at the needle orifice, prohibiting local displacement. This problem has hence the structure of a Lagrange minimisation which can be tackled using the techniques of variational mechanics.‡ For this approach, it is convenient to use the strain tensor components (εθ(θ),εϕ(θ)) instead of the displacement field u(θ) as the varying field, since it happens to simplify greatly the equations. This is made possible by noting (see Section 3 in the ESI†) that the variations of Vi are also those of
| |  | (10) |
although
Vi ≠
Ṽi. We therefore define the Gibbs functional as
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif)
[
εθ,
εϕ] =
Eel +
γA − (Δ
P)
Ṽi. This is a functional of (
εθ(
θ),
εϕ(
θ)) only, because
ψ can be written as
| |  | (11) |
For a clearer physical picture, it is relevant to switch from (
εϕ,
εθ) to the (equivalent) fields (
εϕ,
Δε). Combining
eqn (4)–(10), we define the Lagrangian

(note the absence of

as a consequence of the
Oz-translational invariance of the energy) associated with
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif)
using the formula
| |  | (13) |
with
| |  | (14) |
where
α is the dimensionless elastocapillary number defined in
eqn (1) and
ξ is the normalised pressure change defined in
eqn (2).
3 Results
3.1 Quadratic approximation
A quadratic expansion of the Lagrangian given using eqn (14) with respect to the displacement field u and in the limit ξ ≪ 1 yields| | 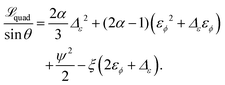 | (15) |
Notice that the last term assumes implicitly that |u| = O(ξ). Even though it is well-known16 that this quadratic approximation predicts wrong results for purely elastic, clamped membranes, due to a slightly singular behaviour of ψ in the vicinity of the needle (namely ψ′(θ) ∝ |θ − θn|−1/2), it will be shown that the capillary energy term removes this singularity, and allows a purely quadratic approach to the elastic limit.
To solve eqn (15), it is interesting to use the Routh method,17 which consists in performing only incompletely the Lagrangian to Hamiltonian transformation. More precisely, the (quadratic expansion of the) Routh Hamiltonian is defined by 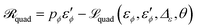 , where
, where  is the conjugate momentum. From eqn (15), one therefore obtains
is the conjugate momentum. From eqn (15), one therefore obtains
| |  | (16) |
| | W = ψ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + (1 − 2α)εϕ + ξ. θ + (1 − 2α)εϕ + ξ. | (17) |
The Routh equations of motion are the usual Hamiltonian equations, supplemented by a Lagrange equation for
Δε, which gives readily

.
Via a suitable canonical change of variables (details given in Section 5 in the ESI
†), we arrive at a linear equation for
ψ| |  | (18) |
Note that this equation is independent of
ξ, so
ψ is only globally proportional to
ξ (see
eqn (19) and (22)), as a consequence of the quadratic approximation. Its solution, regular (and vanishing) at
θ = 0, is given in terms of the associated Legendre function,
18 namely
| |  | (19) |
| |  | (20) |
where
ψn =
ψ(
θn) is the rotation angle of the membrane at the needle, as sketched in
Fig. 1b. Note that

if
α > 3/4, in which case the Legendre function (termed also Mehler or conical function) is still real-valued, and the evolution of
ψ(
θ) with
α is altogether smooth.
εϕ is obtained once
ψ is known (
cf. Section 5 in the ESI
†)
| |  | (21) |
where
Pν =
P0ν.
εθ is obtained
via the last Routh equation

and
eqn (17). It can be verified (
cf. Section 5 in the ESI
†) that
Δε(0) =
εθ(0) −
εϕ(0) = 0, as required by the rotation symmetry at the apex
θ = 0. The problem is solved (at the level of the strain tensor components) if one determines
ψn. This is achieved using
eqn (21) and the fact that
εϕ(
θn) = 0, imposed by the clamping of the elastic membrane. From
eqn (21) and the general properties of the Legendre functions, we obtain
| |  | (22) |
This normalised bending angle at the needle can be interpreted as a susceptibility coefficient, namely the ratio of the response over excitation intensity upon inflation/deflation. In Fig. 2a are plotted the values of the ratio |ψn/ξ| for various values of α and θn (we remind the reader that sin(θn) = Rn/R0). In this graph, the dashed lines correspond to negative values of |ψn/ξ|. First, it can be noted that all curves tend to zero for θn → 180° which is expected, because in this limit, the bubbloon becomes a sphere and the tilt angle at the needle is necessarily zero. Second, for very small values of α, the bubbloon behaves almost like a bubble with a non-elastic interface and its response to a pressure increase ξ depends on θn: for θn < 90° (lens-shaped membranes), the spherical cap experiences a lowering of its radius for ξ > 0 which corresponds to an outward rotation at the clamping, i.e. a negative ψn (dashed curves). Reciprocally, for θn > 90° (horseshoe-shaped membranes) and α ≪ 1, the bubble deflates for ξ > 0 in order to increase its curvature and accommodate the Young–Laplace law, yielding ψn > 0 (solid curves), as can be checked for instance in the curve for α = 0.01 in Fig. 2a. At the transition between the two behaviours – which arises at a critical angle  – the linear regime is no longer defined: the normalised bending angle |ψn/ξ| diverges as
– the linear regime is no longer defined: the normalised bending angle |ψn/ξ| diverges as  , since the bracketed term in eqn (22) vanishes linearly at the transition. For the sake of completeness, Fig. 2b shows the reciprocal behaviour of |ψn/ξ| when θn is fixed and α varied.
, since the bracketed term in eqn (22) vanishes linearly at the transition. For the sake of completeness, Fig. 2b shows the reciprocal behaviour of |ψn/ξ| when θn is fixed and α varied.
 |
| | Fig. 2 (a) Magnitude of the normalised bending angle at the needle |ψn/ξ| = |ψ(θn)/ξ|, as a function of θn (in degrees), for various values of the elastocapillary number α. The dashed branches correspond to negative values, while the solid branches are positive. For α < 0.5, there is a critical angle  where the limiting value of ψn/ξ is not defined, due to the vanishing of the bracket term in (22). The limiting case α = 0.5 (eqn (27)) is shown with black dots. Notice that for α ≥ 0.5, the positive domain of ψn/ξ no longer exists. (b) |ψn/ξ| as a function of α/α* for various values of θn. The dashed parts of the curves correspond again to negative branches. Inset: where the limiting value of ψn/ξ is not defined, due to the vanishing of the bracket term in (22). The limiting case α = 0.5 (eqn (27)) is shown with black dots. Notice that for α ≥ 0.5, the positive domain of ψn/ξ no longer exists. (b) |ψn/ξ| as a function of α/α* for various values of θn. The dashed parts of the curves correspond again to negative branches. Inset:  (in degrees). The reciprocal function defines α*(θn). (in degrees). The reciprocal function defines α*(θn). | |
At or near the critical angle  , the quadratic approximation is no longer valid, since the predicted value of ψn/ξ diverges. This region is theoretically investigated in Section 3.3. In the inset of Fig. 2b is plotted
, the quadratic approximation is no longer valid, since the predicted value of ψn/ξ diverges. This region is theoretically investigated in Section 3.3. In the inset of Fig. 2b is plotted  , which shows that on approaching α = 1/2, the critical angle converges toward 180°.
, which shows that on approaching α = 1/2, the critical angle converges toward 180°.
3.2 Stress tensor elements and displacement fields
All other physically relevant quantities can be computed from ψ(θ). Of interest are the membrane (2D) excess stress tensor elements σexθ,ϕ = σθ,ϕ − γ in the polar (θ) and the azimuthal (ϕ) direction. These are represented in Fig. 3 for the example of θn = 120° (horseshoe-shaped) and various values of α after normalisation by γξ. They are calculated from the expressions| | 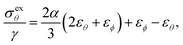 | (23) |
| |  | (24) |
 |
| | Fig. 3 Normalised excess 2D stress tensor elements [σj − γ]/γξ in the polar (j = θ, dot-dashed line) and azimuthal directions (j = ϕ, dotted line), for different values of α for a reference shape with θn = 120°. Left ordinate (blue curves): α ∈ {0,0.2,0.5}. Right ordinates (red curves): α ∈ {10,50}. | |
The limit of vanishing elasticity (α = 0) gives excess stresses σexθ,ϕ which are non constant but whose sum is zero, as the local mechanical equilibrium only requires σθ + σϕ = 2γ everywhere for α = 0. For α = 0.2, the main effect of the elastic component is to shift the typical value of the total excess stress to a negative value. This comes from the elastic response following the surface decrease due to the contraction of the membrane. In the example shown in Fig. 3, the critical value of α* defined by θ*(α*) = θn (see the inset of Fig. 2b) is α* ∼ 0.32 and crossed when passing from α = 0.2 to α = 0.5. This crossing explains the inversion of roles of σexθ and σexϕ in the blue curves of Fig. 3 at α = 0.5: at the needle, σexθ = (4α/3 − 1)εθ(θn) whereas σexϕ = (2α/3 + 1)εθ(θn). For α < 0.5, the prefactor of εθ(θn) in the former (resp. latter) expression is negative (resp. positive). As a result, the decreasing behaviour of σθ(θ) for α* < α < 0.5 is explained by the fact that εθ(θn) is here positive because the response of the bubbloon to a pressure is “balloon-like”, i.e. it inflates when ξ > 0. Notice that, for α > 3, it can be checked that σexθ(θn) > σexϕ(θn) > 0, a reinversion which corresponds to what is observed in the red curves in Fig. 3.
For α ≫ 1, the stress fields are mainly influenced by the elastic part of the energy. The present quadratic approximation is therefore unable to describe satisfactorily these regimes, because for the strict elastic case, the harmonic expansion fails at describing the singularity caused by a nonanalytical 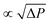 behaviour of ψn, described by the Föppl–von Karman theory (see Section 7 in the ESI†).
behaviour of ψn, described by the Föppl–von Karman theory (see Section 7 in the ESI†).
The displacement fields (ur(θ),uθ(θ)) can be computed from the knowledge of εθ,ϕ(θ) and eqn (ESI S7†), which can then be used to compute the bubbloon shapes. Some results are shown in Fig. 1c for θn = 120° and different values of the elastocapillary number α. The higher the elastic modulus of the membrane, the more strongly the shape deviates from a spherical cap for a given deformation. To quantify this asphericity in the case of a horseshoe-shaped bubbloon, we define a susceptibility
| |  | (25) |
| |  | (26) |
where ∂
Ha is the variation of the vertical distance of the apex from the base of the bubbloon, and ∂
Re is the variation of the equatorial radius of the bubbloon (half the width of the bubbloon), as sketched in
Fig. 1c.
χ is normalized by (∂
Re/∂
Ha)
b = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn
θn/(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn
θn − 1), the value of this ratio for pure bubbles (
α = 0). These quantities can be measured easily in experiments. If the bubbloon retains a spherical shape,
χ = 1, whilst 0 <
χ < 1 if the needle clamping imposes an oblate deformation away from a spherical sector. The predicted variation of
χ with
α is shown in
Fig. 4 for different
θn. This curve allows using
χ to measure the value of
α, provided
α is neither too large nor too small (notice in
eqn (26) that
α is present explicitly and implicitly,
via ν). This susceptibility has the experimental asset of being simple and not requiring the measurement of the pressure difference. For large
α,
χ tends to cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn
θn/(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn
θn − 1), accounting for an isotropic inflation of the sole upper part of the membrane, coherent with what a purely elastic Föppl–von Karmán approach would give (see Section 7 in the ESI
†). A precise quantitative study of the parameter range
α ≫ 1 building on a perturbation of the pure elastic theory is left for future work. Notice however that the combined limits
α → ∞,
θn → π do not commute: at fixed
α,
χ tends smoothly to 1 for
θn → π, namely when the system becomes a sphere attached to a single point. The not entirely elastic membrane is insensitive (in its response) to this singularity. If now one considers first the elastic limit
α → ∞, and only afterwards the limit
θn = π limit, one realises that
χ → 1/2, showing that the singular attachment, which imposes
εϕ(π) = 0 (in contrast to the homogenous, nonzero value of the strain tensor elements for a inflated “free” sphere), has a profound, non local impact on the elastic response of the sphere, a consequence of the long range of the elastic interactions. The value 1/2 corresponds roughly to an object inflating isotropically, but only in its upper half.
 |
| | Fig. 4 Susceptibility parameter χ (eqn (26)) as a function of α, for various (horseshoe) bubble shapes. The plotted equations are given in (26). | |
3.3 Nonanalytical response close to the critical angle 
The presence of a shifted critical angle  is of theoretical and experimental interest, since it realises indirectly a measure of the elastocapillary number α. It is therefore interesting to theoretically characterise the response of the bubbloon to a nonzero small excess pressure ξ near this critical angle. In the light of the arguments provided in the preceding paragraphs, one expects that the displacement field scales as
is of theoretical and experimental interest, since it realises indirectly a measure of the elastocapillary number α. It is therefore interesting to theoretically characterise the response of the bubbloon to a nonzero small excess pressure ξ near this critical angle. In the light of the arguments provided in the preceding paragraphs, one expects that the displacement field scales as  , and the actual response magnitude is fixed by the first non-quadratic order of the Hamiltonian. Using the so-called Hamiltonian perturbation method detailed in Section 8 in the ESI,† we extended the quadratic theory to calculate the correct finite value of the amplitude ψn in the vicinity of
, and the actual response magnitude is fixed by the first non-quadratic order of the Hamiltonian. Using the so-called Hamiltonian perturbation method detailed in Section 8 in the ESI,† we extended the quadratic theory to calculate the correct finite value of the amplitude ψn in the vicinity of  . Eqn (ESI S57) of the ESI† creates a continuous matching between the quadratic result ψn ∝ ξ, far from
. Eqn (ESI S57) of the ESI† creates a continuous matching between the quadratic result ψn ∝ ξ, far from  , and the
, and the  saturation in the vicinity of
saturation in the vicinity of  . To illustrate the difference between the purely quadratic result and the Hamiltonian perturbative result, we plot in Fig. 5a both results for |ψn/ξ|, for different values of ξ, and α = 0.4.
. To illustrate the difference between the purely quadratic result and the Hamiltonian perturbative result, we plot in Fig. 5a both results for |ψn/ξ|, for different values of ξ, and α = 0.4.
 |
| | Fig. 5 (a) |ψn|/ξ versus θn for α = 0.4. The weakly non-quadratic theory (WNQ) is plotted for several values of ξ. For comparison, the quadratic theory is plotted in black, and corresponds to the limit ξ → 0 of the WNQ theory. The divergence at the maximum for ξ → 0 arises because  . Inset: . Inset:  versus versus for α = 0.4 (same color code). (b) For α = 0.4, evolution of for α = 0.4 (same color code). (b) For α = 0.4, evolution of  with ξ. The negative ψn are dashed. Notice that the sign of ξ cannot be negative in this critical region. with ξ. The negative ψn are dashed. Notice that the sign of ξ cannot be negative in this critical region. | |
It can be seen that for ξ → 0 the theory accounting for both O(ξ) and  regimes merges to the quadratic diverging theory (in black). The proper scaling representing the vicinity of
regimes merges to the quadratic diverging theory (in black). The proper scaling representing the vicinity of  is shown in the inset of Fig. 5a, namely a neat collapse of the curves is observed for
is shown in the inset of Fig. 5a, namely a neat collapse of the curves is observed for  plotted against
plotted against  . This comes from the fact that the leading term of ψn in the vicinity of
. This comes from the fact that the leading term of ψn in the vicinity of  is proportional to
is proportional to  where σ is a scaling variable proportional to
where σ is a scaling variable proportional to  for
for  . This leading term predicts a strict sign reversal of
. This leading term predicts a strict sign reversal of  on passing
on passing  , which is not observed for ξ = 10−2 for instance. This is due to the fact that the next-to-leading order O(ξ) is also taken into account in eqn (ESI 57†), a term which is continuous at
, which is not observed for ξ = 10−2 for instance. This is due to the fact that the next-to-leading order O(ξ) is also taken into account in eqn (ESI 57†), a term which is continuous at  and not completely negligible at ξ = 10−2.
and not completely negligible at ξ = 10−2.
Another striking feature must be noted: while any sign of ξ is possible in the quadratic regime, i.e. the membrane can be probed in inflation and deflation, this is not the case in the vicinity of the avoided singularity: as explained in more detail in the ESI† (see eqn (ESI 54)–(ESI 57)), the proper 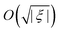 regime is possible only for ξ having the sign of a quantity constructed with the cubic terms of the Gibbs energy. Note that this restriction on the sign of ξ cannot be shown in Fig. 5a, because only ψn/ξ is plotted. For the parameters of Fig. 5a, only positive values of ξ are allowed on this
regime is possible only for ξ having the sign of a quantity constructed with the cubic terms of the Gibbs energy. Note that this restriction on the sign of ξ cannot be shown in Fig. 5a, because only ψn/ξ is plotted. For the parameters of Fig. 5a, only positive values of ξ are allowed on this  branch, but this sign cannot be predicted a priori for other parameters, since it depends on the integral of eqn (ESI 54†) whose sign cannot be ascertained on general grounds. We checked that for
branch, but this sign cannot be predicted a priori for other parameters, since it depends on the integral of eqn (ESI 54†) whose sign cannot be ascertained on general grounds. We checked that for  negative ξ values are associated with this
negative ξ values are associated with this  regime, and positive for higher α. This is coherent with the α → 0 limit, where
regime, and positive for higher α. This is coherent with the α → 0 limit, where  , and for which only negative pressure differences are allowed, since the bubble is at its maximum curvature. Note that for α ≠ 0 a tiny regime of the opposite sign for ξ does exist for θn distinct but close to
, and for which only negative pressure differences are allowed, since the bubble is at its maximum curvature. Note that for α ≠ 0 a tiny regime of the opposite sign for ξ does exist for θn distinct but close to  , with a maximal accessible value for
, with a maximal accessible value for  , probably too narrow to be observable. In contrast, the nature of the transition near α ∼ 0.27 is interesting and left for a future work.
, probably too narrow to be observable. In contrast, the nature of the transition near α ∼ 0.27 is interesting and left for a future work.
Fig. 5b shows how, at constant θn, the leading order  and the next order O(ξ) are mixed when θn is close to
and the next order O(ξ) are mixed when θn is close to 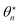 and ξ is varied. First, it must be stressed that at precisely
and ξ is varied. First, it must be stressed that at precisely  , the curve is not constant, because a O(ξ) term is provided to the expression (ESI 57†) by the next-to-leading order in the correspondence between ψ and the canonical coordinates (see eqn (ESI 19) in the ESI†). As a result, the common behaviour of all curves at large ξ is affine (what the semilog representation hides somewhat), decreasing for the dashed curves, and increasing for the solid ones. This splitting according to the sign of
, the curve is not constant, because a O(ξ) term is provided to the expression (ESI 57†) by the next-to-leading order in the correspondence between ψ and the canonical coordinates (see eqn (ESI 19) in the ESI†). As a result, the common behaviour of all curves at large ξ is affine (what the semilog representation hides somewhat), decreasing for the dashed curves, and increasing for the solid ones. This splitting according to the sign of  comes from the fact that far from the immediate vicinity of
comes from the fact that far from the immediate vicinity of  , ψn is ∝ ξsgn(ξ
, ψn is ∝ ξsgn(ξ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) n). By the way, another experimental signature of whether an experiment takes place at
n). By the way, another experimental signature of whether an experiment takes place at  or the opposite, beyond the sign of ψn/ξ, is given by the monotony of the curves shown in Fig. 5b: a non monotonous evolution of
or the opposite, beyond the sign of ψn/ξ, is given by the monotony of the curves shown in Fig. 5b: a non monotonous evolution of  with
with  would be unambiguously associated with
would be unambiguously associated with  . Finally, one notices that when ξ → 0,
. Finally, one notices that when ξ → 0,  is returning to zero for all cases but
is returning to zero for all cases but  . These curves are the most relevant from the experimental point of view, since in rising bubble (or pendant drop) experiments, θn and α are both fixed by the initial makeup of the bubbloon, and the control parameter of the essays being indirectly ξ via the volume control.
. These curves are the most relevant from the experimental point of view, since in rising bubble (or pendant drop) experiments, θn and α are both fixed by the initial makeup of the bubbloon, and the control parameter of the essays being indirectly ξ via the volume control.
3.4 The exceptional case α = 1/2
For α = 1/2, the quadratic theory simplifies somewhat, due to a cancellation of the quadratic terms with respect to εϕ. As a result, one obtains from eqn (16) and the boundary conditions| |  | (27) |
| | 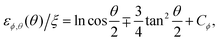 | (28) |
(the minus (resp. plus) for εϕ (resp. εθ)), where Cϕ is such that εϕ(θn) = 0. The limit θn → 180° is clearly singular, as a result of contradictory constraints imposed on the bubbloon: on the one hand, this limit re-establishes the spherical symmetry, where εθ = εϕ = constant. On the other hand, the clamping boundary conditions impose εϕ = 0 at θ → π. Since they are fundamentally incompatible, this entails a divergence of  for θn → 180°. As a result, according to eqn (11), two cases are possible: either
for θn → 180°. As a result, according to eqn (11), two cases are possible: either  diverges as well, or
diverges as well, or  compensates the divergence of
compensates the divergence of  and ψ(θn). The latter case always occurs except for α = 1/2. For α ≲ 1/2, the behaviour of ψn is bubble-like (ψn/ξ → 0+) whereas for α ≳ 1/2 it is balloon-like (ψn/ξ → 0−). This rather complicated and convoluted behaviour near (α = 1/2,θn = 180°) may complicate the analysis of experiments carried out in this parameter range. Interestingly, α = 0.5 is particularly relevant for foam and emulsions science. Often called the “Gibbs criterion”, it assigns the critical value of the elastocapillary number beyond which the interfacial elasticity is strong enough to counterbalance interfacial tension and prohibit Ostwald ripening.19,20
and ψ(θn). The latter case always occurs except for α = 1/2. For α ≲ 1/2, the behaviour of ψn is bubble-like (ψn/ξ → 0+) whereas for α ≳ 1/2 it is balloon-like (ψn/ξ → 0−). This rather complicated and convoluted behaviour near (α = 1/2,θn = 180°) may complicate the analysis of experiments carried out in this parameter range. Interestingly, α = 0.5 is particularly relevant for foam and emulsions science. Often called the “Gibbs criterion”, it assigns the critical value of the elastocapillary number beyond which the interfacial elasticity is strong enough to counterbalance interfacial tension and prohibit Ostwald ripening.19,20
4 Conclusion
We analysed the mechanical response of thin elastocapillary membranes framing initially spherical caps clamped on circular needles with no internal elastic stresses in their reference state. The energy of the membranes was assumed to be the sum of a capillary term proportional to the deformed interfacial area and an elastic term at its Hookean limit. It is important to mention that this additivity together with a constant interfacial tension is a simplified physical assumption which in actual cases could have to be refined.
We considered the linear regime where only quadratic terms can be kept in the effective Hamiltonian of the problem and showed that this elastocapillary quadratic theory yields bona fide solutions, in contrast with the purely elastic capsules where the inclusion of non-quadratic terms is necessary (Föppl–von Karman theory). However, we noticed for elastocapillary numbers α = 3Gt/γ < 1/2 the systematic presence of “exceptional” horseshoe-shaped reference states around which the quadratic theory fails. Despite a completely different origin, the response of ψn (rotation angle at the needle) is also proportional to the square root of the excess pressure, very much like the purely elastic capsules (of all shapes). We showed how to compute the actual response of ψn in these cases. It is interesting to note that the actual value of  at the singularity involves explicitly an integral over the lowest-order non-quadratic term, which could provide an experimental probe of the beyond-hookean properties of elastocapillary membranes.
at the singularity involves explicitly an integral over the lowest-order non-quadratic term, which could provide an experimental probe of the beyond-hookean properties of elastocapillary membranes.
Where the quadratic theory is valid, we propose a very simple susceptibility parameter χ ∝ δHa/δRe, defined as the ratio of the response of the base-to-apex distance Ha to that of the equatorial radius Re, normalised by the value of the pure bubble. For all shapes of the initial bubbloons (i.e. all values of θn), it offers a one-to-one correspondence with the elastocapillary number and gives an efficient estimation of α without the need of complex shape or pressure measurements (provided the underlying physical assumptions are correct). Considering the precision of modern experiments, this verification should be reasonably straightforward. A similarly simple approach was suggested by Hutlzer at al.21 to measure the surface tension of purely liquid interfaces on a bubble or drop deformed by gravity. It should be noted that for these measurements the near-hemispherical horseshoe geometries are the most sensitive (see Fig. 4) and that particular care needs to be taken to start with a stress-free reference state.
Finally, the elastocapillary membranes for which α → ∞ should have a specific analytical treatment to match correctly the Föppl–von Karman solution of the pure elastic membrane. We showed that the susceptibility parameter χ tends to the correct elastic limit for α → ∞, but a detailed study of the mechanical equilibrium of the near elastic elastocapillary capsules still needs to be carried out.
Author contributions
WD and JF defined the research problem. JF developed the theory in collaboration with WD. JF and WD wrote the article.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge fruitful discussions with Friedrich Walzel, Fabrice Thalmann, Leandro Jacomine, Gael Ginot, Jan Kierfeld and Felix Kratz. This work has been financed by an ERC Consolidator Grant (agreement 819511 METAFOAM). It was conducted in the framework of the Interdisciplinary Institute HiFunMat, as part of the ITI 2021–2028 program of the University of Strasbourg, CNRS and Inserm, was supported by IdEx Unistra (ANR-10-IDEX-0002) and SFRI (STRATUS project, ANR-20-SFRI-0012) under the framework of the French Investments for the Future Program.
Notes and references
- L. M. C. Sagis and P. Fischer, Curr. Opin. Colloid Interface Sci., 2014, 19, 520–529 CrossRef CAS
 .
.
- G. G. Fuller and J. Vermant, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 519–543 CrossRef CAS PubMed
 .
.
- E. Rio, W. Drenckhan, A. Salonen and D. Langevin, Adv. Colloid Interface Sci., 2014, 205, 74–86 CrossRef CAS PubMed
 .
.
- M. P. Neubauer, M. Poehlmann and A. Fery, Adv. Colloid Interface Sci., 2014, 207, 65–80 CrossRef CAS PubMed
 .
.
- N. Jaensson and J. Vermant, Curr. Opin. Colloid Interface Sci., 2018, 37, 136–150 CrossRef CAS
 .
.
- M. Nagel, T. A. Tervoort and J. Vermant, Adv. Colloid Interface Sci., 2017, 247, 33–51 CrossRef CAS PubMed
 .
.
- M. Pepicelli, N. Jaensson, C. Tregouët, B. Schroyen, A. Alicke, T. Tervoort, C. Monteux and J. Vermant, J. Rheol., 2019, 63, 815–828 CrossRef CAS
 .
.
- L. M. C. Sagis and P. Fischer, Curr. Opin. Colloid Interface Sci., 2014, 19, 520–529 CrossRef CAS
 .
.
- J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage and J. Kierfeld, J. Colloid Interface Sci., 2018, 513, 549–565 CrossRef CAS PubMed
 .
.
- F. Ravera, G. Loglio and V. I. Kovalchuk, Curr. Opin. Colloid Interface Sci., 2010, 15, 217–228 CrossRef CAS
 .
.
- V. C. Suja, M. Rodríguez-Hakim, J. Tajuelo and G. G. Fuller, Adv. Colloid Interface Sci., 2020, 286, 102295 CrossRef PubMed
 .
.
- E. Guzmán, A. Maestro, C. Carbone, F. Ortega and R. G. Rubio, Fluids, 2022, 7(10), 335 CrossRef
 .
.
- G. Ginot, F. S. Kratz, F. Walzel, J. Farago, J. Kierfeld, R. Höhler and W. Drenckhan, Soft Matter, 2021, 17, 9131–9153 RSC
 .
.
- S. Knoche, D. Vella, E. Aumaitre, P. Degen, H. Rehage, P. Cicuta and J. Kierfeld, Langmuir, 2013, 29, 12463–12471 CrossRef CAS PubMed
 .
.
-
B. Audoly and Y. Pomeau, Elasticity and Geometry: From hair curls to the non-linear response of shells, Oxford Science Publications, 2010 Search PubMed
 .
.
-
L. D. Landau, L. P. Pitaevskii, A. M. Kosevich and E. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, 1986 Search PubMed
 .
.
-
H. Goldstein, Classical Mechanics, Addison-Wesley, 1980 Search PubMed
 .
.
- NIST Digital Library of Mathematical Functions, https://dlmf.nist.gov/, Release 1.2.0 of 2024-03-15, 2024, https://dlmf.nist.gov/, ed. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain.
- A. Stocco, W. Drenckhan, E. Rio, D. Langevin and B. P. Binks, Soft Matter, 2009, 5, 2215–2222 RSC
 .
.
- A. Salonen, C. Gay, A. Maestro, W. Drenckhan and E. Rio, EPL, 2016, 116, 46005 CrossRef
 .
.
- S. Hutzler, J. C. F. Ryan-Purcell, F. F. Dunne and D. Weaire, Philos. Mag. Lett., 2018, 98, 9–16 CrossRef CAS
 .
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01737k |
‡ With the minor difference that the variation of the profile occurs with nonzero variation of the displacement field at θ = 0, contrary to the usual scheme. But the Lagrangian has a factor sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ which makes the discrepancy inconsequential. θ which makes the discrepancy inconsequential. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Wiebke
Drenckhan-Andreatta
* and
Wiebke
Drenckhan-Andreatta

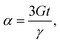

![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) is negative, while for α ≥ 0.5 it is positive.
is negative, while for α ≥ 0.5 it is positive.
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) − r = ur(θ)er + uθ(θ)eθ where
− r = ur(θ)er + uθ(θ)eθ where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) is the current position of a physical element of the membrane having been displaced from the original position r = R0er(θ,ϕ) (see Fig. 1b and Fig. S1 in the ESI†). The strain tensor elements (εθθ,εϕϕ) are expressed in terms of the components of u: we define first their linear components by
is the current position of a physical element of the membrane having been displaced from the original position r = R0er(θ,ϕ) (see Fig. 1b and Fig. S1 in the ESI†). The strain tensor elements (εθθ,εϕϕ) are expressed in terms of the components of u: we define first their linear components by![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ]/R0,
θ]/R0,
 which – in the limit |u|/R0 ≪ 1 – is also the rotation angle of the material element normal. The three quantities (εϕ,εθ,ψ) enter the definitions of
which – in the limit |u|/R0 ≪ 1 – is also the rotation angle of the material element normal. The three quantities (εϕ,εθ,ψ) enter the definitions of



![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) [εθ,εϕ] = Eel + γA − (ΔP)Ṽi. This is a functional of (εθ(θ),εϕ(θ)) only, because ψ can be written as
[εθ,εϕ] = Eel + γA − (ΔP)Ṽi. This is a functional of (εθ(θ),εϕ(θ)) only, because ψ can be written as
 (note the absence of
(note the absence of  as a consequence of the Oz-translational invariance of the energy) associated with
as a consequence of the Oz-translational invariance of the energy) associated with ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) using the formula
using the formula

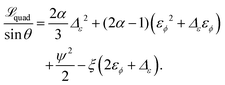
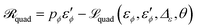 , where
, where  is the conjugate momentum. From eqn (15), one therefore obtains
is the conjugate momentum. From eqn (15), one therefore obtains
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + (1 − 2α)εϕ + ξ.
θ + (1 − 2α)εϕ + ξ. . Via a suitable canonical change of variables (details given in Section 5 in the ESI†), we arrive at a linear equation for ψ
. Via a suitable canonical change of variables (details given in Section 5 in the ESI†), we arrive at a linear equation for ψ


 if α > 3/4, in which case the Legendre function (termed also Mehler or conical function) is still real-valued, and the evolution of ψ(θ) with α is altogether smooth. εϕ is obtained once ψ is known (cf. Section 5 in the ESI†)
if α > 3/4, in which case the Legendre function (termed also Mehler or conical function) is still real-valued, and the evolution of ψ(θ) with α is altogether smooth. εϕ is obtained once ψ is known (cf. Section 5 in the ESI†)
 and eqn (17). It can be verified (cf. Section 5 in the ESI†) that Δε(0) = εθ(0) − εϕ(0) = 0, as required by the rotation symmetry at the apex θ = 0. The problem is solved (at the level of the strain tensor components) if one determines ψn. This is achieved using eqn (21) and the fact that εϕ(θn) = 0, imposed by the clamping of the elastic membrane. From eqn (21) and the general properties of the Legendre functions, we obtain
and eqn (17). It can be verified (cf. Section 5 in the ESI†) that Δε(0) = εθ(0) − εϕ(0) = 0, as required by the rotation symmetry at the apex θ = 0. The problem is solved (at the level of the strain tensor components) if one determines ψn. This is achieved using eqn (21) and the fact that εϕ(θn) = 0, imposed by the clamping of the elastic membrane. From eqn (21) and the general properties of the Legendre functions, we obtain
 – the linear regime is no longer defined: the normalised bending angle |ψn/ξ| diverges as
– the linear regime is no longer defined: the normalised bending angle |ψn/ξ| diverges as  , since the bracketed term in eqn (22) vanishes linearly at the transition. For the sake of completeness, Fig. 2b shows the reciprocal behaviour of |ψn/ξ| when θn is fixed and α varied.
, since the bracketed term in eqn (22) vanishes linearly at the transition. For the sake of completeness, Fig. 2b shows the reciprocal behaviour of |ψn/ξ| when θn is fixed and α varied.
 where the limiting value of ψn/ξ is not defined, due to the vanishing of the bracket term in (22). The limiting case α = 0.5 (eqn (27)) is shown with black dots. Notice that for α ≥ 0.5, the positive domain of ψn/ξ no longer exists. (b) |ψn/ξ| as a function of α/α* for various values of θn. The dashed parts of the curves correspond again to negative branches. Inset:
where the limiting value of ψn/ξ is not defined, due to the vanishing of the bracket term in (22). The limiting case α = 0.5 (eqn (27)) is shown with black dots. Notice that for α ≥ 0.5, the positive domain of ψn/ξ no longer exists. (b) |ψn/ξ| as a function of α/α* for various values of θn. The dashed parts of the curves correspond again to negative branches. Inset:  (in degrees). The reciprocal function defines α*(θn).
(in degrees). The reciprocal function defines α*(θn). , the quadratic approximation is no longer valid, since the predicted value of ψn/ξ diverges. This region is theoretically investigated in Section 3.3. In the inset of Fig. 2b is plotted
, the quadratic approximation is no longer valid, since the predicted value of ψn/ξ diverges. This region is theoretically investigated in Section 3.3. In the inset of Fig. 2b is plotted  , which shows that on approaching α = 1/2, the critical angle converges toward 180°.
, which shows that on approaching α = 1/2, the critical angle converges toward 180°.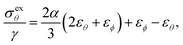

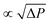 behaviour of ψn, described by the Föppl–von Karman theory (see Section 7 in the ESI†).
behaviour of ψn, described by the Föppl–von Karman theory (see Section 7 in the ESI†).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn/(cos
θn/(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn − 1), the value of this ratio for pure bubbles (α = 0). These quantities can be measured easily in experiments. If the bubbloon retains a spherical shape, χ = 1, whilst 0 < χ < 1 if the needle clamping imposes an oblate deformation away from a spherical sector. The predicted variation of χ with α is shown in Fig. 4 for different θn. This curve allows using χ to measure the value of α, provided α is neither too large nor too small (notice in eqn (26) that α is present explicitly and implicitly, via ν). This susceptibility has the experimental asset of being simple and not requiring the measurement of the pressure difference. For large α, χ tends to cos
θn − 1), the value of this ratio for pure bubbles (α = 0). These quantities can be measured easily in experiments. If the bubbloon retains a spherical shape, χ = 1, whilst 0 < χ < 1 if the needle clamping imposes an oblate deformation away from a spherical sector. The predicted variation of χ with α is shown in Fig. 4 for different θn. This curve allows using χ to measure the value of α, provided α is neither too large nor too small (notice in eqn (26) that α is present explicitly and implicitly, via ν). This susceptibility has the experimental asset of being simple and not requiring the measurement of the pressure difference. For large α, χ tends to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn/(cos
θn/(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn − 1), accounting for an isotropic inflation of the sole upper part of the membrane, coherent with what a purely elastic Föppl–von Karmán approach would give (see Section 7 in the ESI†). A precise quantitative study of the parameter range α ≫ 1 building on a perturbation of the pure elastic theory is left for future work. Notice however that the combined limits α → ∞,θn → π do not commute: at fixed α, χ tends smoothly to 1 for θn → π, namely when the system becomes a sphere attached to a single point. The not entirely elastic membrane is insensitive (in its response) to this singularity. If now one considers first the elastic limit α → ∞, and only afterwards the limit θn = π limit, one realises that χ → 1/2, showing that the singular attachment, which imposes εϕ(π) = 0 (in contrast to the homogenous, nonzero value of the strain tensor elements for a inflated “free” sphere), has a profound, non local impact on the elastic response of the sphere, a consequence of the long range of the elastic interactions. The value 1/2 corresponds roughly to an object inflating isotropically, but only in its upper half.
θn − 1), accounting for an isotropic inflation of the sole upper part of the membrane, coherent with what a purely elastic Föppl–von Karmán approach would give (see Section 7 in the ESI†). A precise quantitative study of the parameter range α ≫ 1 building on a perturbation of the pure elastic theory is left for future work. Notice however that the combined limits α → ∞,θn → π do not commute: at fixed α, χ tends smoothly to 1 for θn → π, namely when the system becomes a sphere attached to a single point. The not entirely elastic membrane is insensitive (in its response) to this singularity. If now one considers first the elastic limit α → ∞, and only afterwards the limit θn = π limit, one realises that χ → 1/2, showing that the singular attachment, which imposes εϕ(π) = 0 (in contrast to the homogenous, nonzero value of the strain tensor elements for a inflated “free” sphere), has a profound, non local impact on the elastic response of the sphere, a consequence of the long range of the elastic interactions. The value 1/2 corresponds roughly to an object inflating isotropically, but only in its upper half.


 is of theoretical and experimental interest, since it realises indirectly a measure of the elastocapillary number α. It is therefore interesting to theoretically characterise the response of the bubbloon to a nonzero small excess pressure ξ near this critical angle. In the light of the arguments provided in the preceding paragraphs, one expects that the displacement field scales as
is of theoretical and experimental interest, since it realises indirectly a measure of the elastocapillary number α. It is therefore interesting to theoretically characterise the response of the bubbloon to a nonzero small excess pressure ξ near this critical angle. In the light of the arguments provided in the preceding paragraphs, one expects that the displacement field scales as  , and the actual response magnitude is fixed by the first non-quadratic order of the Hamiltonian. Using the so-called Hamiltonian perturbation method detailed in Section 8 in the ESI,† we extended the quadratic theory to calculate the correct finite value of the amplitude ψn in the vicinity of
, and the actual response magnitude is fixed by the first non-quadratic order of the Hamiltonian. Using the so-called Hamiltonian perturbation method detailed in Section 8 in the ESI,† we extended the quadratic theory to calculate the correct finite value of the amplitude ψn in the vicinity of  . Eqn (ESI S57) of the ESI† creates a continuous matching between the quadratic result ψn ∝ ξ, far from
. Eqn (ESI S57) of the ESI† creates a continuous matching between the quadratic result ψn ∝ ξ, far from  , and the
, and the  saturation in the vicinity of
saturation in the vicinity of  . To illustrate the difference between the purely quadratic result and the Hamiltonian perturbative result, we plot in Fig. 5a both results for |ψn/ξ|, for different values of ξ, and α = 0.4.
. To illustrate the difference between the purely quadratic result and the Hamiltonian perturbative result, we plot in Fig. 5a both results for |ψn/ξ|, for different values of ξ, and α = 0.4.
 regimes merges to the quadratic diverging theory (in black). The proper scaling representing the vicinity of
regimes merges to the quadratic diverging theory (in black). The proper scaling representing the vicinity of  is shown in the inset of Fig. 5a, namely a neat collapse of the curves is observed for
is shown in the inset of Fig. 5a, namely a neat collapse of the curves is observed for  plotted against
plotted against  . This comes from the fact that the leading term of ψn in the vicinity of
. This comes from the fact that the leading term of ψn in the vicinity of  is proportional to
is proportional to  where σ is a scaling variable proportional to
where σ is a scaling variable proportional to  for
for  . This leading term predicts a strict sign reversal of
. This leading term predicts a strict sign reversal of  on passing
on passing  , which is not observed for ξ = 10−2 for instance. This is due to the fact that the next-to-leading order O(ξ) is also taken into account in eqn (ESI 57†), a term which is continuous at
, which is not observed for ξ = 10−2 for instance. This is due to the fact that the next-to-leading order O(ξ) is also taken into account in eqn (ESI 57†), a term which is continuous at  and not completely negligible at ξ = 10−2.
and not completely negligible at ξ = 10−2.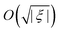 regime is possible only for ξ having the sign of a quantity constructed with the cubic terms of the Gibbs energy. Note that this restriction on the sign of ξ cannot be shown in Fig. 5a, because only ψn/ξ is plotted. For the parameters of Fig. 5a, only positive values of ξ are allowed on this
regime is possible only for ξ having the sign of a quantity constructed with the cubic terms of the Gibbs energy. Note that this restriction on the sign of ξ cannot be shown in Fig. 5a, because only ψn/ξ is plotted. For the parameters of Fig. 5a, only positive values of ξ are allowed on this  branch, but this sign cannot be predicted a priori for other parameters, since it depends on the integral of eqn (ESI 54†) whose sign cannot be ascertained on general grounds. We checked that for
branch, but this sign cannot be predicted a priori for other parameters, since it depends on the integral of eqn (ESI 54†) whose sign cannot be ascertained on general grounds. We checked that for  negative ξ values are associated with this
negative ξ values are associated with this  regime, and positive for higher α. This is coherent with the α → 0 limit, where
regime, and positive for higher α. This is coherent with the α → 0 limit, where  , and for which only negative pressure differences are allowed, since the bubble is at its maximum curvature. Note that for α ≠ 0 a tiny regime of the opposite sign for ξ does exist for θn distinct but close to
, and for which only negative pressure differences are allowed, since the bubble is at its maximum curvature. Note that for α ≠ 0 a tiny regime of the opposite sign for ξ does exist for θn distinct but close to  , with a maximal accessible value for
, with a maximal accessible value for  , probably too narrow to be observable. In contrast, the nature of the transition near α ∼ 0.27 is interesting and left for a future work.
, probably too narrow to be observable. In contrast, the nature of the transition near α ∼ 0.27 is interesting and left for a future work. and the next order O(ξ) are mixed when θn is close to
and the next order O(ξ) are mixed when θn is close to 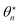 and ξ is varied. First, it must be stressed that at precisely
and ξ is varied. First, it must be stressed that at precisely  , the curve is not constant, because a O(ξ) term is provided to the expression (ESI 57†) by the next-to-leading order in the correspondence between ψ and the canonical coordinates (see eqn (ESI 19) in the ESI†). As a result, the common behaviour of all curves at large ξ is affine (what the semilog representation hides somewhat), decreasing for the dashed curves, and increasing for the solid ones. This splitting according to the sign of
, the curve is not constant, because a O(ξ) term is provided to the expression (ESI 57†) by the next-to-leading order in the correspondence between ψ and the canonical coordinates (see eqn (ESI 19) in the ESI†). As a result, the common behaviour of all curves at large ξ is affine (what the semilog representation hides somewhat), decreasing for the dashed curves, and increasing for the solid ones. This splitting according to the sign of  comes from the fact that far from the immediate vicinity of
comes from the fact that far from the immediate vicinity of  , ψn is ∝ ξsgn(ξ
, ψn is ∝ ξsgn(ξ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) n). By the way, another experimental signature of whether an experiment takes place at
n). By the way, another experimental signature of whether an experiment takes place at  or the opposite, beyond the sign of ψn/ξ, is given by the monotony of the curves shown in Fig. 5b: a non monotonous evolution of
or the opposite, beyond the sign of ψn/ξ, is given by the monotony of the curves shown in Fig. 5b: a non monotonous evolution of  with
with  would be unambiguously associated with
would be unambiguously associated with  . Finally, one notices that when ξ → 0,
. Finally, one notices that when ξ → 0,  is returning to zero for all cases but
is returning to zero for all cases but  . These curves are the most relevant from the experimental point of view, since in rising bubble (or pendant drop) experiments, θn and α are both fixed by the initial makeup of the bubbloon, and the control parameter of the essays being indirectly ξ via the volume control.
. These curves are the most relevant from the experimental point of view, since in rising bubble (or pendant drop) experiments, θn and α are both fixed by the initial makeup of the bubbloon, and the control parameter of the essays being indirectly ξ via the volume control.
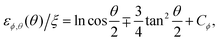
 for θn → 180°. As a result, according to eqn (11), two cases are possible: either
for θn → 180°. As a result, according to eqn (11), two cases are possible: either  diverges as well, or
diverges as well, or  compensates the divergence of
compensates the divergence of  and ψ(θn). The latter case always occurs except for α = 1/2. For α ≲ 1/2, the behaviour of ψn is bubble-like (ψn/ξ → 0+) whereas for α ≳ 1/2 it is balloon-like (ψn/ξ → 0−). This rather complicated and convoluted behaviour near (α = 1/2,θn = 180°) may complicate the analysis of experiments carried out in this parameter range. Interestingly, α = 0.5 is particularly relevant for foam and emulsions science. Often called the “Gibbs criterion”, it assigns the critical value of the elastocapillary number beyond which the interfacial elasticity is strong enough to counterbalance interfacial tension and prohibit Ostwald ripening.19,20
and ψ(θn). The latter case always occurs except for α = 1/2. For α ≲ 1/2, the behaviour of ψn is bubble-like (ψn/ξ → 0+) whereas for α ≳ 1/2 it is balloon-like (ψn/ξ → 0−). This rather complicated and convoluted behaviour near (α = 1/2,θn = 180°) may complicate the analysis of experiments carried out in this parameter range. Interestingly, α = 0.5 is particularly relevant for foam and emulsions science. Often called the “Gibbs criterion”, it assigns the critical value of the elastocapillary number beyond which the interfacial elasticity is strong enough to counterbalance interfacial tension and prohibit Ostwald ripening.19,20
 at the singularity involves explicitly an integral over the lowest-order non-quadratic term, which could provide an experimental probe of the beyond-hookean properties of elastocapillary membranes.
at the singularity involves explicitly an integral over the lowest-order non-quadratic term, which could provide an experimental probe of the beyond-hookean properties of elastocapillary membranes..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ which makes the discrepancy inconsequential.
θ which makes the discrepancy inconsequential.






