 Open Access Article
Open Access ArticleComment on “Effects of topological constraints on linked ring polymers in solvents of varying quality” by Z. A. Dehaghani, I. Chubak, C. N. Likos and M. R. Ejtehadi, Soft Matter, 2020, 16, 3029
Hao
Guo
 and
Mesfin
Tsige
and
Mesfin
Tsige
 *
*
School of Polymer Science & Polymer Engineering, The University of Akron, Akron, Ohio 44325, USA. E-mail: mtsige@uakron.edu
First published on 22nd May 2024
Abstract
This comment critically evaluates the work of Dehaghani et al., who investigated the conformational behavior of catenated polymers under diverse solvent conditions using coarse-grained molecular dynamics simulations. While their study provides valuable insights into the scaling behavior of poly[n]catenane's radius of gyration in a good solvent, significant discrepancies arise, particularly concerning the reported θ-temperature trends. The validity of their methodology in determining θ-temperatures for linear and ring polymers is questioned, given observed disparities in chosen number of bead ranges that imply varying molecular weights. This comment underscores the need for a meticulous reassessment of the methodologies and interpretations presented in Dehaghani et al.'s study, emphasizing the importance of rigorous considerations in the investigation of the physical properties of catenated polymers.
Dehaghani et al. recently investigated the influence of topological constraints on the conformational behavior of catenated polymers under different solvent conditions using coarse-grained molecular dynamics simulations.1 The study yielded insightful results and discussions, notably shedding light on the scaling behavior of poly[n]catenane's radius of gyration in a good solvent. But there is a notable disagreement with their main result about the θ-temperature of catenated polymers. Especially when compared to linear and ring polymers, it contradicts what we recently concluded through a similar simulation approach.2 They arrived at the conclusion that the presence of links in poly[n]catenanes increases the θ-temperature of both the poly[n]catenane and a single linked ring, in contrast to unlinked rings and linear polymers. Interestingly, our simulations showed an inverse outcome, indicating a discrepancy in the observed behavior between their findings and our results.
The common approach to determine a polymer chain's θ-temperature in a dilute solution involves monitoring its topological size, represented by the mean-squared radius of gyration, Rg2, as a function of degree of polymerization, N, across different solvent qualities. The graphical representation of Rg2/N versus solvent quality across different N values is expected to reveal a consistent intersection point, serving as a reliable indicator of the θ-temperature.3–6 However, caution is warranted, as polymer chains may exhibit ideal chain behavior at temperatures marginally distinct from the θ-temperature depending on solvent quality. For a given solvent quality, the deviations from ideal statistical behavior in the conformations of a polymer chain become noticeable only on length scales larger than the thermal blob size,  where v is the excluded volume and b is the Kuhn monomer size.7,8 This results in the following temperature window at which chains behave like ideal chain:
where v is the excluded volume and b is the Kuhn monomer size.7,8 This results in the following temperature window at which chains behave like ideal chain:
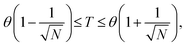 | (1) |
Implicit solvent models play a prominent role in studying polymer chain conformation across varied solvent and concentration conditions due to their substantial enhancement of computational speed.9 In implicit solvent simulations, the solvent's impact on the conformation of the polymer chain is effectively averaged out, resulting in either attractive or repulsive effective interactions between the monomers or segments of the polymer chain under consideration.3 This is commonly done by manipulating the attractive and repulsive components of the Lennard-Jones (LJ) pair interaction potential between two polymer beads in coarse-grained simulations. Various methods can be employed for this purpose, and in our specific approach, we varied the solvent quality by adjusting the LJ cutoff distance, rc, as detailed in our recent work2 and Dehaghani et al. varied the solvent quality by using a dimensionless coupling parameter λ to control the depth of the LJ potential well.1 In our case, the magnitude of the effective interaction potential between the polymer beads was varied by systematically changing rc from rc = 21/6σ (athermal solvent) to 1.7σ (poor solvent) to change the quality of solvent.2 Reducing the cutoff distance rc corresponds to a temperature increase in experimental settings. This approach mimics a more favorable solvent condition, particularly in systems exhibiting only an upper critical solution temperature (UCST).
The methodology employed by Dehaghani et al. in determining the θ-temperature of linear and ring polymers raises questions about its validity. In the determination of the θ-temperature for linear and ring polymers (Fig. 3b and c in their paper), the authors utilized a range of 32 to 128 beads per chain, indicative of low molecular weights. In contrast, when determining the θ-temperature for poly[n]catenane (Fig. 3a in their paper), a substantially higher range of 1024 to 4096 beads per chain was employed, representing high molecular weights. As elucidated in eqn (1) above, the θ-temperature is contingent upon the molecular weight, and the θ-temperature for a specific polymer corresponds to the value determined for long chains. Therefore, Dehaghani et al. θ-temperature results for linear and ring polymers are deemed incorrect, as substantiated below.
Initially, akin to Dehaghani et al., we determined the θ-temperature for linear and ring polymers within the chain length range of 32 to 128, and within a chain length range of 1024 to 4096 for poly[n]catenane. Within these molecular weight ranges, it is evident from Fig. 1 (left column), below, that poly[n]catenane exhibits a higher θ-temperature (lowest rc value) than linear and ring polymers, as reported by Dehaghani et al. However, a different conclusion emerges when determining the θ-temperature for linear and ring polymers within the same long chain length range as that of poly[n]catenane, as illustrated in Fig. 1 (right column). It is evident that the θ-temperature of poly[n]catenane is lower (highest rc value) compared to its linear and ring counterparts, following the relationship Tθcatenane < Tθring < Tθlinear, consistent with our recent findings.2Table 1 below presents the rc values associated with the predicted θ-temperatures.
 | ||
| Fig. 1 The graph depicts 〈Rg2〉/N (for linear and ring) and 〈Rg2〉/n (for poly[n]catenane) against rc as a method for determining the θ-temperature. In the left column (a, c, e), the comparison is made between linear and ring polymers in the low molecular weight range, as well as poly[n]catenane in the long molecular weight range. The right column (b, d, f) extends this analysis to include linear and ring polymers in the long molecular weight range as that of the poly[n]catenane. Each vertical dashed line represents the respective the system's θ-temperature and the values are recorded in the TOC and Table 1 below. The rc value corresponding to the θ-temperature of poly[n]catenane is the lowest (implying highest θ-temperature) in the left column and is the largest (implying lowest θ-temperature) in the left column. | ||
| Low Mw | High Mw | |
|---|---|---|
| Linear | 1.528 | 1.491 |
| Ring | 1.535 | 1.495 |
| Poly[n]catenane | 1.504 |
In summary, the observed discrepancies warrant a careful reevaluation of the methodology employed and conclusions drawn by Dehaghani et al., urging a nuanced consideration of molecular weights in determining the θ-temperature of polymers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors acknowledge financial support from the National Science Foundation DMR-2114640.References
- Z. Ahmadian Dehaghani, I. Chubak, C. N. Likos and M. R. Ejtehadi, Effects of Topological Constraints on Linked Ring Polymers in Solvents of Varying Quality, Soft Matter, 2020, 16(12), 3029–3038, 10.1039/c9sm02374g.
- H. Guo, K. Qian and M. Tsige, Theta Temperature Depression of Mechanically Interlocked Polymers: [2]Catenane as a Model Polymer, Macromolecules, 2023, 56(22), 9164–9174, DOI:10.1021/acs.macromol.3c01509.
- Z. G. Wang, 50th Anniversary Perspective: Polymer Conformation - A Pedagogical Review, Macromolecules, 2017, 50(23), 9073–9114, DOI:10.1021/acs.macromol.7b01518.
- P. Zhang, N. M. Alsaifi and Z. G. Wang, Revisiting the Θ Point, Macromolecules, 2020, 53(23), 10409–10420, DOI:10.1021/acs.macromol.0c01317.
- I. M. Lifshitz, A. Yu Grosberg and A. R. Khokhlov, Some Problems of the Statistical Physics of Polymer Chains with Volume Interaction, Rev. Mod. Phys., 1978, 50(3), 683–713, DOI:10.1103/RevModPhys.50.683.
- A. R. Khokhlov, On the θ-Behaviour of a Polymer Chain, J. Phys., 1977, 38(7), 845–849, DOI:10.1051/jphys:01977003807084500.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- B. Roux and T. Simonson, Implicit Solvent Models, Biophysical Chemistry, Elsevier, 1999, vol. 78, pp. 1–20 DOI:10.1016/S0301-4622(98)00226-9.
| This journal is © The Royal Society of Chemistry 2024 |
