Magnetophoresis of paramagnetic metal ions in porous media

Abstract

We report a numerical investigation of the magnetophoresis of solutions containing paramagnetic metal ions. Using a simulated magnetic field of a superconducting magnet and the convection-diffusion model, we study the transport of transition metal salts through a porous medium domain. In particular, through a detailed comparison of the numerical results of magnetophoretic velocity and ion concentration profiles with prior published experiments, we validate the model. Subsequent to model validation, we perform a systematic analysis of the model parameters on the magnetophoresis of metal ions. Magnetophoresis is quantified with a magnetic Péclet number Pe_m. Under a non-uniform magnetic field, Pe_m initially rises, exhibiting a local maximum, and subsequently declines towards a quasi-steady value. Our results show that both the initial and maximum Pe_m values increase with increasing magnetic susceptibility, initial concentration of metal solutes, and ion cluster size. Conversely, Pe_m decreases as the porosity of the medium increases. Finally, the adsorption of metal salts onto the porous media surface is modeled through a dimensionless Damkohler number Da_ad. Our results suggest that the adsorption significantly slows the magnetophoresis and self-diffusion of the paramagnetic metal salts, with a net magnetophoresis velocity dependent on the kinetics and equilibrium adsorption properties of the metal salts. The latter result underscores the crucial role of adsorption in future magnetophoresis research.

---

I. Introduction

Magnetically assisted separation provides an environmentally benign and cost-effective strategy for a broad range of applications including transport and separation of nanoparticles for drug delivery,^1,2 in chemical kinetics,³ as magnetic contrast agents in magnetic resonance imaging,⁴ for microfluidic applications,⁵ and for water purification.^6–9 In particular, this method is superior to chemical and size-based separation methods in cases where the solutes to be separated are chemically and physically similar but differ in magnetic properties. When subjected to a nonuniform external magnetic field, a magnetic material dissolved in a solution experiences a net magnetic force expressed as follows:^10–12where Δχ_m, μ₀, R_c, c, and B are the difference between the molar magnetic susceptibility of a metal solute and the surrounding medium, the permeability of the vacuum, the effective radius of the magnetic material, the concentration of solute in the fluid, and the magnetic flux density, respectively. The motion of solutes through a solution due to this force is known as magnetophoresis. In addition to the influence of the magnetic force, magnetic particles suspended in a fluidic environment can experience random molecular diffusion caused by thermal motions.¹³ The presence of thermal motions acting on a particle in the solvent counteracts the formation of concentration gradients by nonuniform magnetic fields. Consequently, for a net magnetophoresis motion to occur, the magnetic force must surpass the random thermal diffusion, gravitational, and inertial forces acting on the particle. For a magnetic particle and in the absence of inertial and gravitational forces, the magnetophoresis velocity of the particle (v_mig) can be estimated by balancing the magnetic force with the Stokes' drag (F_d = 6πηv_migR_c) as:Here, η is the viscosity of the surrounding medium. Therefore, the magnetophoresis of particles depends strongly on the creation of a large magnetic field gradient, the particle size, and the difference in magnetic susceptibility between the particle and the surrounding medium.

Magnetic materials that are not ferromagnetic can be divided into two general categories, paramagnetic and diamagnetic. A paramagnetic ion exhibits a positive magnetic susceptibility (χ_m > 0) and, under magnetic field gradients, undergoes a magnetic force towards stronger magnetic fields. Conversely, a diamagnetic material possesses a negative magnetic susceptibility (χ_m < 0) and is pushed away from regions of stronger magnetic fields.¹⁴ Previous studies have demonstrated that, in the absence of inertial and gravitational forces, the magnetic force can surpass the forces due to thermal motions for superparamagnetic nanoparticles composed of iron oxide (with a size larger than 50 nm) that are subjected to high magnetic field gradients (>10³ T m⁻¹).^15,16 Yavuz and co-workers showed that the superparamagnetic nanoparticles based on iron oxide (with a size of 20 nm) could be separated from the solution at low magnetic field gradients of <10² T m⁻¹.⁷ This initially surprising outcome was later rationalized by direct observations that suggest that magnetic nanoparticles do not behave independently under the influence of a magnetic field; instead, they form aggregates that tend to move much faster than individual units.^7,17–20

In the case of transition metal ions from compounds like copper(II) chloride or manganese(II) chloride, which possess a hydration radius of approximately 10⁻¹⁰ m²¹ and significantly lower magnetic susceptibilities than the superparamagnetic iron oxide (by several orders of magnitude), it is logical to anticipate that the magnetic force would be considerably weaker than the thermal diffusion under conditions of low to medium magnetic field gradients. Quite surprisingly, Fujiwara and co-workers demonstrated successful magnetophoresis for a range of weakly magnetic transition metal ions (e.g., Cr³⁺, Mn²⁺, Ni²⁺, and Cu²⁺) within a porous silica gel medium under a magnetic field gradient of (B·∇)B|_max ≈ 400 T² m⁻¹.^22–24 A force balance on these single metal ions predicts no detectable magnetophoresis for the experimental conditions reported by Fujiwara and co-workers. Nonetheless, these authors measured a magnetophoresis velocity much faster (by five orders of magnitude) than the calculated velocities based on a force balance on individual metal ions. Fujiwara and co-workers invoked a similar hypothesis to those suggested by Yavuz and co-workers,⁷ wherein under a non-uniform magnetic field, the metal ions form clusters with an effective size that is much larger than individual ions.^22–24 According to Fujiwara and co-workers, transition metal ions may form clusters with an approximate size in the range of micrometers under such external magnetic fields.²³ The cluster of transition metal ions is expected to move much faster in a magnetic field compared to a single ion. In addition, these researchers showed that the magnetophoresis velocity is faster for greater magnetic susceptibility and for greater initial concentration of the metal solute.²³

While Fujiwara et al. have provided some experimental data on the magnetophoresis of weakly magnetic salts, a comprehensive theoretical framework that captures the magnetophoresis of transition metal ions under non-uniform magnetic fields is still lacking. A comprehensive magnetophoresis model necessitates the coupling of the complete set of magnetic field equations with the equations of motion and the transport of magnetic species in a fluidic environment. The resulting multi-physics model not only allows for the prediction and elucidation of magnetophoresis behavior of magnetic metal ions under non-uniform magnetic fields, but also may inform and expedite the development of practical laboratory, pilot, and industrial-scale processes for the transport of magnetic materials using high gradient magnetic fields. In this paper, we aim to construct a model for the transport of weakly magnetic species (or solutes) in a fluidic environment. The inherent non-linearity of the static magnetic field and the coupled momentum and mass differential equations necessitates their numerical solution, which will be achieved through the utilization of the finite element method using COMSOL Multiphysics software.

This paper is organized as follows: first, the simulations of the transport of weakly magnetic solutes in a porous medium will be compared and validated with those reported in experiments by Fujiwara et al.^24,25 Next, an exploration of the impact of varying pertinent physical parameters on magnetophoresis will be undertaken. This investigation will include parameters such as ion concentration, magnetic susceptibility, effective cluster radius, and porous medium properties. Finally, we will consider the impact of ion adsorption to the porous medium on the magnetophoresis of magnetic ions.

II. Problem formulation and governing equations

The problem that we consider in this study involves a closed two-dimensional simulation domain that is placed inside a superconducting magnet. We present one case of a three-dimensional simulation and show the findings are similar to those produced by 2D simulations (details are given in the ESI†). However, the high computational cost of the 3D simulation prevents a full systematic study in a realistic time, and therefore, we mainly use a 2D domain for simulating the magnetophoresis. The dimensions and the location of the simulation domain and magnet match those reported in experiments of Fujiwara and co-workers.^22–24Fig. 1 shows the dimensions and arrangement of the simulation channel and the magnet coil cross-section. The width of the simulated flow channel matches that reported in experiments at 40 mm, while the length of the computational domain ranges from 20 mm beyond the initial spot location to 20 mm past the center of the field in the direction of migration. The simulation channel contains a porous medium with a porosity that matches those reported by Fujiwara and co-workers. We will come back to this point in a later section. The magnet coil is a hollow cylinder with the cylinder axis oriented along the simulation channel; in the cross-section, it is simulated as two rectangular regions with equal and opposite currents normal to the simulation plane. The dimensions of the magnet are chosen to produce a magnetic field best matching that reported in prior experiments.²²

Fig. 1 Domains used for simulations showing dimensions of the coil and the computational domain that contains the porous medium. The dimensions of the magnet are as follows: inner radius of the magnet coil 35 mm, outer radius 65 mm, length 160 mm, number of turns × current 1.6 MA.

To study the magnetophoresis of magnetic metal ions in a fluidic environment, simultaneous solutions for the static magnetic field, convective-diffusion, and momentum equations are necessary. In the following, we discuss these equations in detail.

A. Static magnetic field

Prior to modeling the transport of ions, the details of the magnetic field surrounding the magnetophoresis cell must be known. In the static magnetic field, the total magnetization is given by Maxwell-Ampere's law as:

∇ × H = A, (3)

where H and A are the strength of the magnetic field and the current density. Another important equation is Gauss's law that is expressed as follows:

∇·B = 0, B = μ₀μ_rH. (4)

Here, μ_r is the relative permeability. The magnetic field is simulated inside a circular region of radius R_f = 5 m to approximate an infinite domain for the magnetic field. The condition at the field boundary is zero magnetic flux through the boundary (i.e., n·B = 0). For the materials studied by Fujiwara et al., μ_r ≈ 1, B_r = 0, and the moving solutes are assumed to have negligible effect on μ_r and therefore on the magnetic field. The steady-state magnetic field in the coil is simulated by solving eqn (3) and (4) at the start of each simulation.

B. Mass and momentum transport

In principle, there are two basic possible physical models for the transport of species in solutions: (a) the system is considered as two phases (the particles being the solid phase) dispersed throughout another phase (the fluid medium), or (b) it can be considered as a single phase containing two or more components. The latter is applicable to systems where the length scales that are measured or modeled are all much larger than the length scales of the units that undergo magnetophoresis (i.e., the continuum approach). For our study, the smallest length scale resolved in our model is the initial size of the ion-rich liquid drop (about 4 mm), while the ion clusters are smaller by three orders of magnitude. Therefore, we consider the domain as effectively a single phase containing the metal ions (associated with clusters), the surrounding water, and the porous medium. In order to analyze the transport of a single phase solution of metal ions under a non-uniform magnetic field, we must solve the convective-diffusion equation as presented below:where c_i and N_i are the concentration, and the total molar flux of species i in the solution, respectively. The total molar flux is given by the following expression:

N_i = J_i + c_iv_i (6)

Here J_i denotes the diffusion flux and v_i is the velocity of the solute due to body forces. For dilute solutions such as those studied in this paper, the diffusion flux is given by Fick's law as: J_i = −D_i∇c_i, where D_i is the self-diffusion coefficient of species i in the solution. For paramagnetic metal salts, body forces can arise through any of three phenomena: buoyancy due to gravity, electrophoresis due to an electric field, and magnetophoresis due to a magnetic field. Net gravitational forces are negligible in the porous medium domain and zero in the direction of magnetophoresis; therefore, buoyancy can be omitted from the model. Although net movement of the metal ions in response to an electric field is possible, all resolved length scales are much longer than the Debye length (0.12–16 nm) and there are no reactions or boundary fluxes (see ESI† for more information). Therefore, the metal salt can be modeled as a single, electro-neutral species. This leaves magnetophoresis, with a velocity characterized by eqn (2). By incorporating eqn (2) into eqn (6), we can arrive at the total molar flux for a non-reacting solute in a non-uniform magnetic field:Once the details of the magnetic field are known from simulations of the static magnetic field, eqn (5) and (7) are solved numerically to obtain the evolution of the solute concentration throughout the channel domain over time. For the boundary conditions, we use zero flux through the channel boundaries (ends and edges): n·J_i = 0. The initial solute concentration throughout the domain is a radially symmetric Gaussian distribution centered on (x₀, 0) and with standard deviation r₀. It is given by the expression: c_i|_t=0 = c₀ exp[−(x − x₀)²/r₀² − y²/r₀²].

C. Porous medium modeling

Fujiwara and co-workers used a silica gel that consisted of particles of size 0.075–0.15 mm and saturated with de-ionized water. The pores in the silica gel particles and the voids between them were much smaller than the channel dimensions and the initial size of the ion spot. Therefore, the porous medium in this study is simulated as a homogeneous domain with one phase representing an aqueous solution in a porous solid with an effective porosity ε. The effective diffusivity is calculated based on Millington and Quirk model ε^4/3 = D/D₀,²⁶ where D and D₀ denote the diffusion coefficients of the ion in the porous and free medium, respectively. Using the experimental parameters used by Fujiwara and co-workers, we calculate a porosity of ε ≈ 0.61, which will be used in simulations that are compared with experimental data.

D. Dimensionless numbers

In principle, several forces could affect the magnetophoresis of metal ions in a porous medium: inertia, diffusion, buoyancy due to gravity, and magnetic force. To assess the importance of these forces, we use a range of dimensionless numbers.

The role of inertia can be evaluated through the Reynolds number, which can be expressed as: . For the simulations presented in this paper, Re ≪ 1, therefore, the effect of inertia is negligible. In addition, net gravitational forces are negligible in the domain and zero in the direction of magnetophoresis. This leaves us with the two remaining forces: the magnetic force and the forces associated with thermal motions. As noted before, if the magnetic force exceeds the forces due to thermal motions, the metal ions (solutes) can successfully undergo net magnetophoresis. To probe the relative importance of these two forces, a dimensionless magnetic Péclet number can be formulated. The Péclet number for mass transport conventionally compares convection with diffusion using a characteristic length scale. This definition can be adapted to compare magnetic force induced motion with diffusion as:

where r_1/2 is the radius of the spot of solute (half-width at half-maximum concentration). In eqn (8), Pe_m depends on r_1/2, c, and (B·∇)B, which can vary with space and/or time. Therefore, the Péclet number will vary in a spatio-temporal manner Pe_m = f(x, y, t). To simplify our analysis, we opt to assess the temporal evolution of the Péclet number for c_max|_y=0 and a magnetic field gradient oriented along the x-axis. Here c_max refers to the maximum local concentration of the solute within the whole domain and y = 0 denotes the center-line of the porous medium domain. Therefore, the time dependent magnetic Péclet number is defined as:Note that with no magnetic field, diffusion of the spot of ions acts in a radially symmetric manner, and an analytical solution is possible.²⁴ The time evolution of r_1/2 is related to c_max by the expression:However, applying the magnetic field breaks this radial symmetry, and r_1/2 no longer has a well-defined, spatially-independent value. Nonetheless, mass is conserved, and a characteristic r_1/2 for an asymmetric peak can be defined by considering a symmetric peak with the same overall amount of solute and c_max as the asymmetric peak. For such a peak, r_1/2 can be obtained using eqn (10). Therefore, for the remainder of this analysis, eqn (10) is used to estimate r_1/2 for use in eqn (9) to obtain the value for Pe_m|_max.

III. Numerical details

Finite-element numerical simulations were performed using COMSOL Multiphysics 6.1. The computational porous medium domain was modeled as a 40 mm × 140 mm domain filled with 124 620 triangular mesh elements, each 0.33 mm in size. Simulation results do not noticeably change when a finer mesh is used, which shows that these results closely approximate an exact solution to the governing equations. Outside the magnetophoresis channel, the mesh elements gradually increased in size with distance from the channel boundaries, up to a maximum size of 6 mm in and around the magnet coils. The overall magnetic field domain was a circle of radius 5 m filled with 142 210 triangular mesh elements.

The solution procedure consists of two steps. First, at the start of each simulation, the magnetic field is solved in the steady state by applying eqn (3) and (4) throughout the full domain. Then, the solved magnetic field is applied to eqn (5)–(7) in the time-dependent solver simulating only the channel. The solver used adaptive time stepping with the maximum time step no longer than 0.05 h; the end time in all simulations is 14 h. With these parameters, a minimum of 280 independent intermediate time solutions are obtained.

IV. Results and discussion

A. Diffusion in the absence of a magnetic field

We begin our discussion by validating the model discussed above. The first step in the validation process is to model the broadening of the spot due to diffusion reported in experiments inside the porous medium in the absence of a magnetic field. Therefore, we initially validate the outcomes of our simulations under the condition of zero magnetic field. Fig. 2(a)–(c) depicts a time sequence of snapshots obtained from simulations, illustrating the diffusion behavior of a copper(II) chloride solution spot in the absence of an applied external magnetic field. The initial spot is modeled with the maximum concentration 1 M and a radius of 4.5 mm in order to be consistent with the diffusion experiments reported by Fujiwara et al.²⁴

Fig. 2 Simulated copper(II) chloride spot (a) initially applied, (b) after 4 h and (c) 14 h of diffusion with no magnetic field. Contour lines are shown to emphasize the temporal evolution of the spot shape. (d) Normalized center-line concentration profiles at these times. (e) Evolution of the maximum spot concentration and spot radius at half-maximum over time. Circular markers show the times plotted in subfigures (a)–(c), and diamond-shaped markers are experimental results reported in ref. 24. Reprinted (adapted) with permission from Fujiwara et al.²⁴ Copyright 2001 American Chemical Society.

In Fig. 2(d), the normalized solute concentration along the central axis of the droplet is presented. Evidently, as the diffusion proceeds, the intensity of normalized solute dispersion progressively increases towards a more uniform concentration profile. In Fig. 2(e), the evolution of the maximum concentration of ions (c_max; left axis) and spot radius (r_1/2; right axis) are displayed, encompassing both simulation results and the data reported by Fujiwara et al. for copper(II) chloride solution. Overall, there exists a good agreement between the simulation results and the experimental data, further corroborating the validity of our model.

B. Details of the magnetic field

With simulations of diffusion under no field validated, we now begin our discussion on magnetophoresis by simulating the domain under a magnetic field that was matched to experiments. The most relevant experiments reported by Fujiwara and co-workers on the magnetophoresis of transition metal ions were performed in a superconducting magnet that produced a uniform magnetic field of 8 T in the middle of the magnet bore. Fig. 3(a) shows the map of the magnetic flux density (B) for a simulated electromagnet producing a matching field. Additionally, Fig. 3(b) shows the calculated (B·∇)B inside the computational domain, where transition metal ions undergo transport. Fujiwara and co-workers did not provide a full 2D map of the magnetic field produced by their superconducting magnet, however, they reported the magnetic field and the (B·∇)B along the center line (y = 0) as a function of axis location (x). Fig. 3(c) compares the measured magnetic field reported by Fujiwara and co-workers with those simulated in this paper. The simulated magnetic field exhibits a good agreement with the magnetic field data reported by Fujiwara and colleagues. This alignment serves as a validation of the static magnetic field simulations to be used for investigating the magnetophoresis of the transition metal ions.

Fig. 3 Simulated magnetic field used for magnetomigration studies. (a) 2D map of the magnetic flux density throughout the domain. (b) 2D map of the magnetic field gradients ((B·∇)B) in the porous medium domain. (c) Magnetic flux density and the gradients along the magnet center line are shown for both experiments and simulations. Reprinted (adapted) with permission from Fujiwara et al.²² Copyright 2001 American Chemical Society.

C. Magnetophoresis under a non-uniform magnetic field

Fujiwara and co-workers reported magnetophoresis of a range of transition metal ions. In particular, the 2006 report on copper(II) chloride features studies of magnetomigration and diffusion over time with sufficient reported data for a thorough validation of the computational model presented here. Therefore, below we provide a detailed comparison between our simulations and the results of Fujiwara and co-workers on this metal ion. Fig. 4 shows the simulated magnetophoresis of a spot of copper(II) chloride solution under the magnetic field reported in Fig. 3. The magnetic susceptibility of the copper(II) ion used in the simulation is 1.89 × 10⁻⁸ m³ mol⁻¹, consistent with what Fujiwara et al. reported for copper(II) chloride. Note Fujiwara et al. report magnetic susceptibility in cgs units. To convert to ESI,† it is necessary to multiply by a factor of 4π. In addition, the cluster size R_c is 2.3 μm to be consistent with what Fujiwara et al. report in their study.²⁴ To compare the experiments of Fujiwara et al.²⁴ and simulations, we first start by comparing the 2D map of ion concentration profiles. Fujiwara et al.²⁴ only reported the 2D image of concentration profiles after 4 hours. At first sight it seems that the tail of ion concentration profile of simulations is a bit more dispersed in the y-direction compared to experimental images reported by Fujiwara et al.²³ Note that Fujiwara et al. do not report any calibration of the imaging procedure in their study using known solute concentrations, and there is no guarantee of any particular quantitative relation of the plotted image intensity to the solute concentration. Therefore, a quantitative comparison of the reported image intensity from experiments of Fujiwara et al. with the predicted solute concentration maps from simulations is not feasible.

Fig. 4 Simulated copper(II) chloride spot (a) initially applied, (b) after 4 h and (c) 14 h of the magnetic field exposure. Contour lines are shown to emphasize the temporal evolution of the shape of the spot. (d) Normalized center line concentration profiles at those times shown in part (a)–(c). (e) Temporal evolution of the spot location and maximum spot concentration over time. Circular markers show the times plotted in subfigures (a)–(c), and diamond-shaped markers are experimental results reported in Fujiwara et al.²⁴ Reprinted (adapted) with permission from Fujiwara et al.²⁴ Copyright 2006 American Chemical Society.

A more meaningful quantitative comparison between the simulations and experiments involves comparing the axial location (x_max) of the point of maximum metal ion concentration (c_max). In Fig. 4(d), the time-dependent variation of normalized solute concentration along the axial direction is presented. Consistent with reported experiments, the spot moves approximately 40 mm towards the field center under 4 h of field exposure, and the concentration profile at the center line is skewed in the direction of movement. Fig. 4(e) shows that the temporal evolution of the maximum concentration of solute c_max and the displacement of the point of maximum concentration from the initial location (i.e., x_max − x₀) throughout the duration of exposure to the external magnetic field. Included in this figure are also the data reported by Fujiwara and co-workers that show excellent agreement with the results of our simulations. To further assess the validity of 2D simulations, we performed a 3D simulation that replicates the data of Fig. 4. As shown in the ESI† (Fig. S1 and S2), the 3D simulation results are similar to 2D results and not much difference is observed. However, the computational cost of the 3D simulation is significantly greater, and this would limit the number of simulations that can be feasibly conducted in a study. Therefore, for the rest of the manuscript, we report the results of 2D simulations.

Subsequent to a detailed and successful comparison with the available experimental data, we perform a detailed analysis of the important parameters (e.g., magnetic field strength, magnetic susceptibility, cluster size, initial ion concentration and porosity of the medium) that may affect the magnetophoresis. Fig. 5(a) shows the spatio-temporal evolution of copper(II) chloride ions at different magnetic field and gradient strengths. For a field strength of 0.8 T, the thermal diffusion is dominant and the magnetophoresis is negligible. As the field gradient increases towards 4 T, the magnetophoresis is strengthened. However, the total travel distance is much smaller than when the magnetic field strength is increased to 140% of the magnetic gradients shown in Fig. 3.

Fig. 5 Effects of varied magnetic field strength on transport of metal ions. (a) Simulated copper(II) chloride spot when initially applied, after 4 h, and after 14 h for magnetic field strengths of 0.1, 0.5, and 1.4 times that used in Fig. 3. (b) Evolution of the magnetic Pe_m|_max number over time for different field strengths.

Fig. 5(b) shows the variation of the Pe_m|_max as a function of time for those conditions noted in Fig. 5(a). At a low magnetic gradient strength of 0.8 T, Pe_m|_max is always below unity highlighting the dominant role of thermal diffusion. As magnetic field strength increases, Pe_m|_max increases beyond unity. At some point, Pe_m|_max exhibits a local maximum before it decays toward a steady limit at longer times. This initial rise in Pe_m|_max is due to the movement of the spot towards higher (B·∇)B. It is most prominent at the strongest field strength, where increasing (B·∇)B with movement acts faster than decreasing c_max with time. As time progresses, the Pe_m|_max decreases indicating the importance of thermal diffusion at longer times. Furthermore, as the field strength increases, the local maximum in Pe_m|_max increases and occurs at shorter time scales.

Next we report a systematic analysis of the impact of other important parameters on magnetophoresis of metal ions. As shown in Fig. 5(b), Pe_m|_max varies both in space and time. Therefore, for the sake of clarity, we assess the impact of each of those aforementioned parameters through a characteristic Pe_m|_max at time t = 0 and at the time when a local maximum (if any) is observed for the magnetic Péclet number. From now onward, we will denote these Péclet numbers as .

Fig. (6) illustrates the impact of magnetic susceptibility, ion cluster size, initial concentration and the porous medium characteristics on the magnetophoresis of ions under a magnetic field of 8 T. In these graphs, filled symbols correspond to the maximum local Péclet number and hollow symbols are the initial Péclet number. In particular, Fig. 6(a) shows the variation of as a function of magnetic susceptibility for a range of metal solutes. For those metal ions that produce , thermal diffusion is the dominant force, and the magnetic field is too weak to cause any magnetophoresis. As the magnetic susceptibility increases, increases linearly and goes beyond unity. At much higher magnetic susceptibilities, the local maximum in appears (filled data) and deviates from the initial as metal ion becomes strongly paramagnetic. Fig. 6(b) shows as a function of ion cluster size for copper(II) chloride (χ_m = 1.88 × 10⁻⁸ m³ mol⁻¹) and manganese(II) chloride (χ_m = 1.78 × 10⁻⁷ m³ mol⁻¹). As expected, increases monotonically with the cluster size. Interestingly, there is a critical cluster size below which magnetophoreis does not occur . This critical cluster size decreases as the magnetic susceptibility of the metal ion increases. The initial concentration of the ion has a similar effect to those of the magnetic susceptibility and the cluster size. Finally, the effect of porosity of the porous medium on is reported in Fig. 6(d). Generally, as the medium becomes sparsely porous, the magnetophoresis is weakening. This is mainly because the thermal diffusion in a fluidic environment is much faster than that in a porous medium. In a porous medium, the diffusion of ions is restricted, and therefore, magnetophoresis proceeds with a larger .

Fig. 6 Effects of simulation parameters on the initial (large empty symbol) and maximum (small filled symbol) numbers: (a) molar magnetic susceptibility of solute; (b) effective ion cluster radius for χ_m = 1.88 × 10⁻⁸ m³ mol⁻¹ (blue circles) and χ_m = 1.78 × 10⁻⁷ m³ mol⁻¹ (orange squares); (c) initial maximum concentration of the spot; (d) medium porosity for c₀ = 1 M (blue circles) and 100 mM (orange squares). Except otherwise specified, parameters are as shown in Fig. 4. Lines are a visual aid only.

It should be noted that in these simulations, the cluster size is assumed to remain independent of both the initial concentration, the magnetic susceptibility of the ion, the time, and the location. In principle, the formation of magnetic clusters in a uniform magnetic field can be attributed to a balance between dipole–dipole interactions, electrostatic repulsion, and van der Waals forces.^27–30 In the presence of a non-uniform magnetic field, the magnetophoresis force introduces an additional driving mechanism, potentially accelerating the process of cluster formation.²⁹ As a result, in a non-uniform magnetic field the ion cluster size should be R_c ∼ f(c, χ, t, x, y). While existing research has predominantly investigated the formation of clusters for super paramagnetic nanoparticles in both uniform^27,28,30,31 and non-uniform magnetic fields,^6,29 there appears to be a notable gap in the literature regarding studies on the formation of clusters of metal ions in non-uniform magnetic fields. Fujiwara and colleagues inferred the formation of clusters of transition metal ions through magnetomigration experiments.²³ To the best of our knowledge, there is a lack of direct (experimental) evidence supporting the formation of metal ion clusters. Consequently, the relationship between ion cluster size and factors such as time, space, initial concentration, and magnetic susceptibility remains unknown. In this study, we have assumed that cluster size is independent of these variables as an initial approximation. However, to offer a more precise assessment of cluster size and to elucidate the influence of ion concentration, magnetic susceptibility, time, and space on magnetic metal ion cluster formation in a non-uniform magnetic field, a more systematic series of experiments and/or atomistic simulations are needed.

D. Adsorption of metal ions onto a substrate

The silica gel porous medium used by Fujiwara and co-workers presents an active solid substrate with a large surface area (450 m² g⁻¹) where the metal ions can be adsorbed.^32,33 The adsorption of metal ions to the surface of the silica beads provides a new mechanism that may compete against the magnetophoresis of metal ions under an external magnetic field. Therefore, to provide a more realistic description of magnetophoresis of metal ions in porous media, the continuum model should consider the effect of adsorption on the transport of species. Indeed, Chie et al.²⁵ reported cases where the magnetomigration distances of some metal ions on silica gel do not consistently correlate with their magnetic susceptibility, likely due to the adsorption of metal ions to the silica gel. In particular, they showed that despite having a smaller magnetic susceptibility, cobalt(II) ions travel a longer distance than iron(II) ions under otherwise identical ion concentration and magnetic field gradients. Note that the molar magnetic susceptibility of iron(II) solutes is 54% greater molar magnetic susceptibility of cobalt(II) ions. Although Chie et al.²⁵ linked the discrepancy to different adsorption activities onto silica gel, the effect of adsorption on magnetophoresis was not quantified or discussed in detail. Therefore, we added the adsorption physics to our continuum model and assessed how adsorption affects magnetomigration using the cobalt/iron case reported by Chie et al.²⁵

Adsorption is incorporated into the mass transport equations as a reversible reaction that is expressed as: c_i ⇌ c_i,ad. Here c_i is the concentration of free solute in the porous medium and c_i,ad is the concentration of adsorbed solute. The reaction rate is added to the right-hand side of eqn (5), and a new species mass transfer equation for c_i,ad is added to obtain:

There is no flux term in eqn (11b) because the solute is assumed to be effectively immobile in its adsorbed state. For the initial condition, c_i,ad = 0, indicating that all ions are initially free in solution. Although the experimental data on adsorption of transition metal ions on silica gel surface are scarce, the limited experiments suggest that equilibrium adsorption of cobalt(II) and iron(II) salts on silica gel is best described by a Langmuir isotherm and that adsorption and desorption kinetics are on the order of hours.^34–36 The available Langmuir isotherm parameters and rate constants are given in Table 1.

Table 1 Adsorption coefficients and rate constant obtained from available literature data

Metal ion	K L [M^−1]	C L [M]	k ad [h^−1 M^−1]
Co^2+	4.24 × 10^3 ^34	9.81 × 10^−2 ^34	3.42^34
Fe^2+	30.6^35	8.05 × 10^−2 ^35	0.299^36

---

The reaction term R_i for a Langmuir isotherm can be expressed as:

Here, k_ad, C_L, and K_L are the adsorption rate constant, maximum possible concentration of adsorbed species, and equilibrium constant, respectively. The introduction of the reaction term associated with adsorption to eqn (11) gives rise to a new relevant time scale (adsorption time), and its magnitude relative to diffusion and/or magnetomigration may affect the magnetophoresis behavior of the metal ions. The relative importance of adsorption compared to diffusion is quantified by the adsorption Damkohler number, which is defined as:

Fig. 7(a) and (b) show the temporal evolution of dimensionless Pe_m|_max and Damkohler numbers as a function of time for cobalt ions at different relative equilibrium constants (the denominator is the value for K_L obtained from the literature as presented in Table 1). At early stages of magnetophoresis (t < 0.5 h), the Pe_m|_max and Damkohler numbers are insensitive to variations in the adsorption equilibrium constant. However, over time, the Pe_m|_max decreases to lower values for lower values of . Conversely, the Damkohler number (Da_ad) increases with time, with the resulting number rising at a faster rate for lower values of 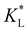. The corresponding time-resolved 2D concentration plots for two values of are illustrated in Fig. 7(c). Interestingly, as 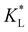increases, the impact of thermal diffusion decreases and the metal ions are less likely to disperse in the y direction and that gives rise to the increase in Pe_m|_max and the decline in Da_ad numbers. A similar trend can be observed for iron(III) chloride (see Fig. S1 in the ESI†). Varying has a similar effect to the and sample plots are shown in Fig. S2 and S3 of the ESI,† for cobalt(II) chloride and iron(III) chloride.

Fig. 7 Effect of the non-dimensional Langmuir adsorption coefficient on magnetophoresis behavior of cobalt(II) ions. Temporal evolution of the magnetic Péclet (a) and the adsorption Damkohler (b) numbers. (c) Concentration distribution at selected times for (base case) and 2.5 × 10⁻³ (matched case).

In Fig. 8(a), the temporal evolution of the cobalt(II) ion movement is shown for various values. Initially, the ions move rapidly and as time goes by, the magnetophoresis slows down until it levels off at longer times. As increases, the overall distance by which ions travel decreases, with the difference being most significant at longer times. This is consistent with the evolution of Da_ad as seen in Fig. 7, where greater values of Da_ad indicate a stronger effect of adsorption compared to diffusion and magnetomigration. The simulation prediction for 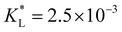shows the same movement after 4 hours as reported in experiments of Chie et al.²⁵ Additionally, Fig. 8(b) shows the effects of on the predicted movement of the concentration maximum over time while is held fixed. As increases, the movement distance decreases, and for 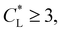nearly all movement of the concentration maximum is within the first few minutes. A similar trend is reported for iron(III) chloride (see Fig. S4 in the ESI†).

Fig. 8 Predicted movement of the spot of cobalt(II) chloride for varied adsorption parameters. Effect of the Langmuir adsorption coefficient (a) and (b) on the temporal movement of the concentration maximum. For this study, the product k_adC_L was held fixed. (c) Movement of the point of maximum concentration for various pairs resulting in movement after 4 h matched to the results of Chie et al.²⁵ shown as a black dot.

Clearly, the experimental and 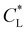values reported in Table 1 do not yield a similar magnetophoresis behavior to those reported by Chie et al.²⁵ Using values reported in Table 1, the simulations underpredict the total ion movement reported by Chie et al. (see black dots in Fig. 8(a) and (b)). This discrepancy could be due to several factors, which include the following: first, there may be other sets of parameter values yielding the same predictions for magnetophoresis in the presence of adsorption. For example, Fig. 8(c) compares the movement over time of the cobalt(II) ion, where both parameters ( and ) are varied such that [x_max − x₀]_t=4h is consistent with the results reported in ref. 25. As decreases, the value of producing the experimental match increases, and the movement of the spot changes from a fast initial movement that slows significantly over time to an initially slower but more steady movement. Secondly, there are several varieties of silica gel with different adsorption activities for the transition metal ions. The values given in Table 1 were obtained from the available literature and likely differ from those that would best represent the silica gel used in experiments of Chie et al.²⁵ For example, Chie et al. reported a stronger adsorption for iron(II) than cobalt(II) ions, whereas the existing data reported in Table 1 suggest that cobalt(II) ions are more prone to adsorption than iron(II) ions. Third, the adsorption of ions onto the substrate may separate the metal ions from the chloride counter-ions, and electric field effects may need to be included. Consequently, to perform a more comprehensive and quantitative comparison with experiments on the magnetomigration of ions in the presence of adsorption, it is imperative to conduct a systematic study of the adsorption kinetics and isotherm of the metal ions for the same types of silica gel utilized in either the previously reported experiments or new studies of magnetophoresis.

V. Conclusions

In summary, a numerical model for diffusion and magnetomigration of paramagnetic metal solutes in porous media has been developed. By employing the hypothesis of cluster formation under non-uniform magnetic fields as documented by Fujiwara et al.,²⁴ our simulation results closely correspond to the experimental findings as reported. Moreover, we demonstrated that magnetophoresis can be characterized by the magnetic Péclet number, which exhibits a transition from a monotonic decrease for weak magnetophoresis to an initial increase leading to a local maximum, followed by a subsequent decline as magnetophoresis becomes more pronounced. The magnetic Péclet number demonstrates a consistent increase with changes in magnetic susceptibility, initial ion concentration, and ion cluster size. Conversely, the magnetophoresis, represented by the magnetic Péclet number, diminishes as the medium shifts into a sparsely porous state. Finally, our findings indicate that the adsorption of ions onto the surfaces of the porous media impedes both the magnetophoresis and self-diffusion of ions, with its effects being most pronounced over longer time scales.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work is partially sponsored by the Defense Advanced Projects Research Agency (DARPA) grant HR001122C0155 and the Army Research Office grant W911NF-22-1-0265. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the state of Florida. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government.

References

1. I. Venugopal, S. Pernal, T. Fusinatto, D. Ashkenaz and A. Linninger, Quantum Dot Conjugated Magnetic Nanoparticles for Targeted Drug Delivery and Imaging, Nano Biomed. Eng., 2016, 8(1), 24–38.
2. P. Dames, B. Gleich, A. Flemmer, K. Hajek, N. Seidl and F. Wiekhorst, et al., Targeted delivery of magnetic aerosol droplets to the lung, Nat. Nanotechnol., 2007, 2(8), 495–499.
3. U. E. Steiner and T. Ulrich, Magnetic field effects in chemical kinetics and related phenomena, Chem. Rev., 1989, 89(1), 51–147.
4. J. H. Lee, Y. M. Huh, Y. W. Jun, J. W. Seo, J. T. Jang and H. T. Song, et al., Artificially engineered magnetic nanoparticles for ultra-sensitive molecular imaging, Nat. Med., 2007, 13(1), 95–99.
5. A. Munaz, M. J. Shiddiky and N. T. Nguyen, Recent advances and current challenges in magnetophoresis based micro magnetofluidics, Biomicrofluidics, 2018, 12(3), 031501.
6. S. S. Leong, Z. Ahmad and J. Lim, Magnetophoresis of superparamagnetic nanoparticles at low field gradient: hydrodynamic effect, Soft Matter, 2015, 11(35), 6968–6980.
7. C. T. Yavuz, J. Mayo, W. W. Yu, A. Prakash, J. C. Falkner and S. Yean, et al., Low-field magnetic separation of monodisperse Fe₃O₄ nanocrystals, Science, 2006, 314(5801), 964–967.
8. S. S. Leong, Z. Ahmad, S. C. Low, J. Camacho, J. Faraudo and J. Lim, Unified view of magnetic nanoparticle separation under magnetophoresis, Langmuir, 2020, 36(28), 8033–8055.
9. J. Lim, S. P. Yeap and S. C. Low, Challenges associated to magnetic separation of nanomaterials at low field gradient, Sep. Purif. Technol., 2014, 123, 171–174.
10. M. Simon and A. Geim, Diamagnetic levitation: Flying frogs and floating magnets, J. Appl. Phys., 2000, 87(9), 6200–6204.
11. M. Zborowski, L. Sun, L. R. Moore, P. S. Williams and J. J. Chalmers, Continuous cell separation using novel magnetic quadrupole flow sorter, J. Magn. Magn. Mater., 1999, 194(1–3), 224–230.
12. R. J. Parker, Advances in permanent magnetism, Wiley-Interscience, USA, 1990, p. 337.
13. S. Wiegand, Thermal diffusion in liquid mixtures and polymer solutions, J. Phys.: Condens. Matter, 2004, 16(10), R357.
14. J. Svoboda, Magnetic techniques for the treatment of materials, Springer Science & Business Media, 2004.
15. G. D. Moeser, K. A. Roach, W. H. Green, T. Alan Hatton and P. E. Laibinis, High-gradient magnetic separation of coated magnetic nanoparticles, AIChE J., 2004, 50(11), 2835–2848.
16. A. Ditsch, S. Lindenmann, P. E. Laibinis, D. I. Wang and T. A. Hatton, High-gradient magnetic separation of magnetic nanoclusters, Ind. Eng. Chem. Res., 2005, 44(17), 6824–6836.
17. G. De Las Cuevas, J. Faraudo and J. Camacho, Low-gradient magnetophoresis through fieldinduced reversible aggregation, J. Phys. Chem. C, 2008, 112(4), 945–950.
18. D. Heinrich, A. Goni and C. Thomsen, Dynamics of magnetic-field-induced clustering in ionic ferrofluids from Raman scattering, J. Chem. Phys., 2007, 126(12), 124701.
19. J. Faraudo and J. Camacho, Cooperative magnetophoresis of superparamagnetic colloids: theoretical aspects, Colloid Polym. Sci., 2010, 288, 207–215.
20. A. Spatafora-Salazar, D. M. Lobmeyer, L. H. Cunha, K. Joshi and S. L. Biswal, Hierarchical assemblies of superparamagnetic colloids in time-varying magnetic fields, Soft Matter, 2021, 17(5), 1120–1155.
21. R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767.
22. M. Fujiwara, D. Kodoi, W. Duan and Y. Tanimoto, Separation of transition metal ions in an inhomogeneous magnetic field, J. Phys. Chem. B, 2001, 105(17), 3343–3345.
23. M. Fujiwara, K. Chie, J. Sawai, D. Shimizu and Y. Tanimoto, On the movement of paramagnetic ions in an inhomogeneous magnetic field, J. Phys. Chem. B, 2004, 108(11), 3531–3534.
24. M. Fujiwara, K. Mitsuda and Y. Tanimoto, Movement and diffusion of paramagnetic ions in a magnetic field, J. Phys. Chem. B, 2006, 110(28), 13965–13969.
25. K. Chie, M. Fujiwara, Y. Fujiwara and Y. Tanimoto, Magnetic separation of metal ions, J. Phys. Chem. B, 2003, 107(51), 14374–14377.
26. R. Millington and J. Quirk, Permeability of porous solids, Trans. Faraday Soc., 1961, 57, 1200–1207.
27. J. Faraudo, J. S. Andreu, C. Calero and J. Camacho, Predicting the self-assembly of superparamagnetic colloids under magnetic fields, Adv. Funct. Mater., 2016, 26(22), 3837–3858.
28. J. S. Andreu, J. Camacho and J. Faraudo, Aggregation of superparamagnetic colloids in magnetic fields: the quest for the equilibrium state, Soft Matter, 2011, 7(6), 2336–2339.
29. D. Heinrich, A. R. Goñi, T. M. Osán, L. M. C. Cerioni, A. Smessaert and S. H. Klapp, et al., Effects of magnetic field gradients on the aggregation dynamics of colloidal magnetic nanoparticles, Soft Matter, 2015, 11(38), 7606–7616.
30. J. Faraudo, J. S. Andreu and J. Camacho, Understanding diluted dispersions of superparamagnetic particles under strong magnetic fields: a review of concepts, theory and simulations, Soft Matter, 2013, 9(29), 6654–6664.
31. A. Darras, J. Fiscina, M. Pakpour, N. Vandewalle and G. Lumay, Ribbons of superparamagnetic colloids in magnetic field, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 1–6.
32. H. Tran, F. Roddick and J. O’Donnell, Comparison of chromatography and desiccant silica gels for the adsorption of metal ions—I. adsorption and kinetics, Water Res., 1999, 33(13), 2992–3000.
33. M. S. Iamamoto and Y. Gushikem, Adsorption of metal ions from aqueous and ethanol solutions by silica gel functionalized with pyridinium ions, J. Colloid Interface Sci., 1989, 129(1), 162–165.
34. H. Yang, L. Yuan, M. Yuan and P. Ning, Insight into the Mechanism of Cobalt–Nickel Separation Using DFT Calculations on Ethylenediamine-Modified Silica Gel, Materials, 2023, 16(9), 3445.
35. L. Gromadskaya, I. Romanova, O. Vyshnevskyi and S. Kirillov, Near-stoichiometric adsorption of phosphate by silica gel supported nanosized hematite, Int. Scholarly Res. Not., 2013, 2013, 969746.
36. D. Gómez-Carnota, J. L. Barriada and R. Herrero, Green development of iron doped silica gel materials for chromium decontamination, J. Environ. Chem. Eng., 2022, 10(5), 108258.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01607b

---