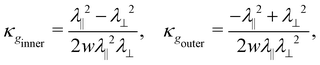Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Geometry, mechanics and actuation of intrinsically curved folds†
Fan
Feng‡
 ,
Klaudia
Dradrach‡
,
Klaudia
Dradrach‡
 ,
Michał
Zmyślony
,
Michał
Zmyślony
 ,
Morgan
Barnes
and
John S.
Biggins
,
Morgan
Barnes
and
John S.
Biggins
 *
*
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK. E-mail: jsb56@cam.ac.uk
First published on 5th February 2024
Abstract
We combine theory and experiments to explore the kinematics and actuation of intrinsically curved folds (ICFs) in otherwise developable shells. Unlike origami folds, ICFs are not bending isometries of flat sheets, but arise via non-isometric processes (growth/moulding) or by joining sheets along curved boundaries. Experimentally, we implement both, first making joined ICFs from paper, then fabricating flat liquid crystal elastomer (LCE) sheets that morph into ICFs upon heating/swelling via programmed metric changes. Theoretically, an ICF's intrinsic geometry is defined by the geodesic curvatures on either side, κgi. Given these, and a target 3D fold-line, one can construct the entire surface isometrically, and compute the bending energy. This construction shows ICFs are bending mechanisms, with a continuous family of isometries trading fold angle against fold-line curvature. In ICFs with symmetric κgi, straightening the fold-line culminates in a fully-folded flat state that is deployable but weak, while asymmetric ICFs ultimately lock with a mechanically strong finite-angle. When unloaded, freely-hinged ICFs simply adopt the (thickness t independent) isometry that minimizes the bend energy. In contrast, in LCE ICFs a competition between flank and ridge selects a ridge curvature that, unusually, scales as t−1/7. Finally, we demonstrate how multiple ICFs can be combined in one LCE sheet, to create a versatile intrinsically curved gripper that lifts a heavy weight.
Curved folds lend strength, form and function to surfaces throughout biology and engineering (Fig. 1), and have been extensively studied in the beautiful and useful art of origami.6,11–14 However, not all curved folds are equal. The defining mechanics of thin sheets is that they are essentially inextensible, as isometric bend has a much lower elastic cost than in-plane stretch. Origami artists bend flat paper, making their folds extrinsic (isometric to the plane) but there is no such restriction on folds formed by stitching flat sheets,15,16 or by non-isometric processes such as differential growth17–19 or moulding. Such processes can thus create intrinsically curved folds (ICFs), which can only be flattened by stretch, giving richer geometry and stronger mechanics. Here, we present the basic kinematic rules for describing and classifying ICFs, which provide insight into their (lack of) rigidity, and also into their utility as mechanisms and deployable structures.
 | ||
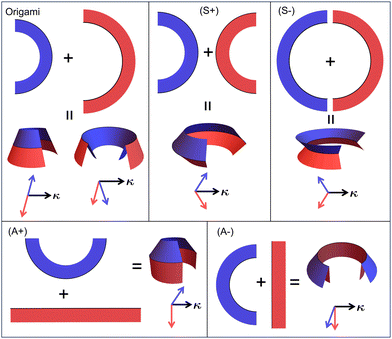
| Fig. 1 Curved folds in biology, architecture, and engineering. Top: Leaf of Salix babylonica ‘Annularis’ (S−),1 giant water lilly (A+),2 carambola fruit (S+, S−).3 Middle: LCE ribbon (S−), Cupola, Sedgwick Museum (S+),4 origami tower (D. Huffman,5–7 extrinsic). Bottom: Top hat (A−),8 tent (A+),9 umbrella (S+).10 Labels (SA/±) show sign/symmetry of the geodesic curvatures. | ||
An additional motivation for ICFs stems from the topical field of “metric mechanics”,20 which studies flat actuating sheets that morph into intrinsically curved surfaces. Such morphing requires a programmed spatial pattern of actuation, reminiscent of differential growth during morphogenesis, and has been implemented with swelling-gels,21 phase-changing liquid crystal elastomers (LCEs),22–24 dielectric elastomers25 and pneumatic baromorphs.26 The generation of intrinsic (Gauss) curvature gives dramatically strong actuation: for example, LCE disks that morph into conical shells can lift 1000× their weight.27 Thus inspired, we also demonstrate how to program an LCE sheet to morph into an ICF,28,29 leading to flat ribbons that macroscopically “bend” into arcs but via strong Gaussian actuation.
1 Geometry of intrinsically curved folds
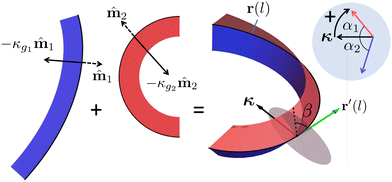
The elementary way to fabricate an ICF is to stitch together two flat sheets of material along curved boundaries. The seam then forms an ICF through an otherwise developable surface (Fig. 2). This approach is routinely used by engineers, architects and tailors to create intrinsically curved surfaces from flat material. Before stitching, the boundary of each flat piece (i = 1, 2) may be assigned a local outward normal![[m with combining circumflex]](https://www.rsc.org/images/entities/b_char_006d_0302.gif) i and curvature vector −κgi
i and curvature vector −κgi![[m with combining circumflex]](https://www.rsc.org/images/entities/b_char_006d_0302.gif) i, so that κgi > 0 is an inward curvature vector and vice versa. After stitching, both boundaries must follow the same (arc-length parameterized) 3D space curve r(l) which defines the fold line. The resultant ICF geometry is characterized by the fold's curvature vector κ = r′′(l), and, in a cross-section perpendicular to the fold-line tangent, r′(l), the fold angles αi between κ and each flank. As marked in Fig. 2, α > 0 indicates a clockwise rotation from κ to flank (around the tangent), so the total fold angle is α1 − α2.
i, so that κgi > 0 is an inward curvature vector and vice versa. After stitching, both boundaries must follow the same (arc-length parameterized) 3D space curve r(l) which defines the fold line. The resultant ICF geometry is characterized by the fold's curvature vector κ = r′′(l), and, in a cross-section perpendicular to the fold-line tangent, r′(l), the fold angles αi between κ and each flank. As marked in Fig. 2, α > 0 indicates a clockwise rotation from κ to flank (around the tangent), so the total fold angle is α1 − α2.
The geodesic curvature κg of a curve on a surface is computed as the projection of its 3D curvature vector into the tangent plane. However, a foundational result in differential geometry dictates that κg is an intrinsic quantity that is invariant under isometric deformations.30 Accordingly, in the ICF, the geodesic curvatures of the original flat boundaries, κgi, must match the projection of κ into the respective flank:
κg1 = |κ|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1, κg2 = |κ|cos α1, κg2 = |κ|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2. α2. | (1) |
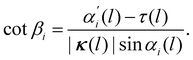 | (2) |
Another celebrated intrinsic property of surfaces is Gaussian curvature, K, computed as the product of the two principal curvatures. An ICF's Gaussian curvature defies direct computation due to the sharp apex. However, the Gauss–Bonnet theorem allows us to compute the total curvature 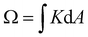 in any patch of surface from the geodesic curvature of its boundary. A simple application to ICFs gives the distribution of total curvature along the fold as29
in any patch of surface from the geodesic curvature of its boundary. A simple application to ICFs gives the distribution of total curvature along the fold as29
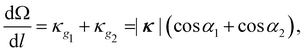 | (3) |
2 Kinematics and classification of curved folds
eqn (1) reveals that the kinematics of an ICF are governed by its two geodesic curvatures. To explore what deformation are permitted, we focus on homogeneous ICFs, made by joining pieces with constant κgi (annular sectors) along the arc of a circle, leading to uniform fold angles. Such ICFs can also be fabricated straightforwardly by joining annular arcs of craft paper (ESI,† Section S6), enabling observations of kinematics and mechanics. Five ICF categories emerge, based on combinations of κgi, as illustrated in Fig. 3 and Movies M1–M5 (ESI†).Regular surfaces are often classified by the sign of their Gaussian curvature, with K = 0 (flat), K > 0 (cap-like) and K < 0 (saddle-like) giving different geometry and mechanics. Accordingly, we first consider a K = 0 fold (origami case in Fig. 3) which requires κg1 = −κg2 ≡ κg. The two initial pieces are thus complimentary, and can fit together whilst flat, confirming the fold is extrinsic. The kinematic constraints (eqn (1)) give the fundamental rules of origami folds,11,12α1 = cos−1(κg/|κ|), and α2 = π − α1. The least curved state, |κ| = κg, is the completely flat state (α1 = 0 and α2 = π), while, during folding, increasing curvature creates an increasingly sharp fold, with the fold-line bi-normal bisecting the flanks (Movie M1, ESI†).
Alternatively, an elementary K > 0 fold can be made by taking κg1 = κg2 = κg > 0, a symmetric positive ICF (S+). eqn (1) now requires α1 = −α2 = cos−1(κg/|κ|), so κ itself bisects the flanks, ensuring an equal projection into each (Fig. 3 (S+), Movie M2, ESI† and Fig. 1 cupola/umbrella). The least curved state, |κ| = κg, is a flat-folded closed-book configuration, and increasing |κ| requires the book to open, tending towards an unfolded state, α1 = −α2 = π/2, as |κ| diverges. The fold line and apex curvature have the same sense, as expected for K > 0 surfaces, and these isometries can be interpreted as trading fold-line curvature and folding angle at constant K. A corresponding symmetric negative fold (S−) is made as κg1 = κg2 ≡ −κg < 0, giving a fold with almost identical behavior (Fig. 3 (S−), Movie M3, ESI† and leaf in Fig. 1) except the book-like state is inverted α1 = −α2 = π and, as the curvature increases the flanks approach the unfolded α1 = −α2 = π/2 from above.
However, ICFs are not fully characterized by their Gaussian curvature, as eqn (1) applies to each flank individually. Thus folds with asymmetric curvatures (A±) behave differently. We focus on two prototypical examples made by joining a straight strip, κg1 = 0 with an anulus of each sign κg2 = ±κg (Fig. 3 A+ and A−, Movies M4, M5, ESI†). Either way, the folding condition on the straight strip requires α1 = π/2 so κ has zero projection. The least curved states still have |κ| = κg, giving α2 = 0, −π respectively, so the A+ fold resembles a capped cylinder (Fig. 1 lilly pad), and A− a flanged pipe (Fig. 1 top hat). Thus, asymmetric ICFs have finite fold angles even in their least curved state. As previously, increasing |κ| causes unfolding, with the highly curved but completely unfolded state α1 = π/2, α2 = −π/2 reached as |κ| diverges.
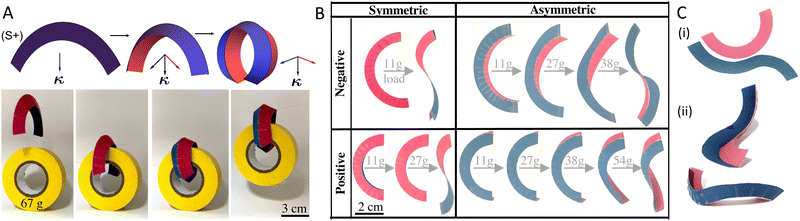
The essential kinematic feature of ICFs is that fold angle dictates curvature and vice-versa, giving a continuous family of isometries in which the two change in tandem (Movies M1–M5, ESI†). ICF's are thus simple mechanisms, and a small actuator controlling fold angle can be used to manipulate the fold's curvature. Furthermore, if the fold-angle is fixed then any deviation of the curvature from its isometric value is strongly resisted. A simple illustration of this mechanism principle is that a symmetric positive fold fashioned from paper can be used as a simple but effective grabber (Fig. 4A and Movie M6, ESI†).
For symmetric folds, unbending of the fold-line (reducing |κ|) culminates in a flat-folded state. Symmetric folds are thus attractive deployable structures, which can be constructed whilst flat, then unfurled into a 3D Gauss-curved surface.
The different ICF catagories also have different mechanical responses. If a load seeks to unbend an asymmetric ICF, it will deform isometrically until it locks rigidly in its least curved state—a 3D shape with finite fold angle—with further unbending requiring stretch. In contrast, unbending a symmetric fold culminates in the flat-folded state that, mechanically, is a single floppy sheet that can easily buckle to accommodate further unbending. This pattern is confirmed by simple tensile tests (Fig. 4B). Interestingly, both A+ and A− folds do eventually buckle out of plane into inhomogeneous ICF geometries, but A+ are considerably stronger than A−. The key difference is that further unbending requires tensile stretches in the annular flank of A+, but compression in A−, which promote buckling. A+ folds are thus particularly suitable for applications requiring rigidity or strong actuation.
3 Flank bending energy
An ICF formed by joining inextensible flat sheets is limited to the isometric conformations discussed above. However, these configurations are not elastically equivalent, as they have different bends in the flanks. Quantifying this bend energy allows one to assess which isometry will be observed whilst unloaded, and the ICF's stiffness as it deforms. When a flank is bent from the initial flat state to form an ICF, it stores elastic energy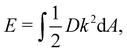 D being flexural rigidity, k the single finite curvature of a developable surface, and the integral is over flank area. In the special case of a homogeneous ICF, the whole ICF is a surface of revolution with conical flanks connected by a circular fold. In this case, the bending energy of an individual flank (per-unit length of fold) may be precisely evaluated as
D being flexural rigidity, k the single finite curvature of a developable surface, and the integral is over flank area. In the special case of a homogeneous ICF, the whole ICF is a surface of revolution with conical flanks connected by a circular fold. In this case, the bending energy of an individual flank (per-unit length of fold) may be precisely evaluated as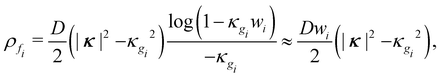 | (4) |
In general, eqn (2) allows one to reconstruct the flanks of any ICF, and then, following Wunderlich,31–34 compute the associated bend energy as a 1D fold-line integral containing |κ| and τ (ESI,† Section S2). In the narrow limit, this procedure gives
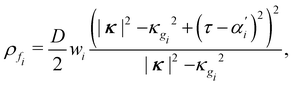 | (5) |
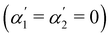 and symmetric ICFs
and symmetric ICFs 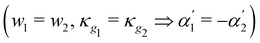 will form torsion-free plane curves. However inhomogeneous asymmetric ICFs generically do have torsion in their minimizing configuration, generating non-planar fold lines (Fig. 4C).
will form torsion-free plane curves. However inhomogeneous asymmetric ICFs generically do have torsion in their minimizing configuration, generating non-planar fold lines (Fig. 4C).
4 Intrinsically curved folds via metric mechanics
ICFs in biological tissues are not formed by stitching of flat sheets, but by patterns of differential growth that directly alter a single sheet's metric.17 The emerging field of metric mechanics21,35 provides an enticing engineering analogue, by programming patterns of shape-change into flat sheets of soft actuating material. ICFs formed via growth or metric-mechanics follow the same kinematics as their joined counterparts, but with the added feature of actuating from flat, and different mechanics stemming from their non-hinged fold. To investigate these differences, we fabricate flat LCE ribbons that morph into ICFs upon stimulation, due to a spatially programmed molecular alignment direction n(x,y) ≡ (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ(x,y), sin
ψ(x,y), sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ(x,y)). The actuation mechanism is that heating or swelling the LCE disrupts this alignment (mirroring the conventional nematic–isotropic phase transition) and causes a large uniaxial shape change, with markedly different stretching factors λ‖ along n, and λ⊥ in the orthogonal direction, n⊥ (Fig. 5A and B).
ψ(x,y)). The actuation mechanism is that heating or swelling the LCE disrupts this alignment (mirroring the conventional nematic–isotropic phase transition) and causes a large uniaxial shape change, with markedly different stretching factors λ‖ along n, and λ⊥ in the orthogonal direction, n⊥ (Fig. 5A and B).
In metric terms, this means an infinitesimal vector dl = (dx, dy) in the flat sheet changes length from dl2 = dl·I·dl to dlA2 = dl·ā(x,y)·dl, where the new metric has the form
| ā(x,y) = λ‖2n(x,y) ⊗ n(x,y) + λ⊥2n⊥(x,y) ⊗ n⊥(x,y). | (6) |
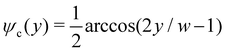 ,37 where w is the width of the ribbon, and the profile varies from along
,37 where w is the width of the ribbon, and the profile varies from along ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) to ŷ over the ribbon's width. A direct computation (ref. 38, ESI,† Section S4) gives the geodesic curvatures of the strip's boundaries as
to ŷ over the ribbon's width. A direct computation (ref. 38, ESI,† Section S4) gives the geodesic curvatures of the strip's boundaries asconfirming they follow circular arcs, and hence that the strip becomes annular. Here κgouter > 0 and κginnter < 0 follow the sign convention in Fig. 2. As sketched in Fig. 5C, we may then form positive and negative symmetric ICFs by combining pairs of patterns in a single sheet, with the join becoming the ICF. Similarly, asymmetric ICFs can be created by combining a single pattern with a ribbon of uniform director.
To verify these designs, we fabricated LCE ribbons via extrusion-based 3D printing39 (materials and methods), using the extrusion direction to encode the spatial alignment pattern, and each printed layer adding ≈100 μm of thickness. After printing, actuation was tested on mono-domain ribbons. Swelling in toluene produced actuation factors of λ‖ ≈ 0.9 and λ⊥ ≈ 2.4 (Fig. S10, ESI†), while thermal actuation yields λ‖ ≈ 0.5 and λ⊥ ≈ 1.3 by 130 °C (Fig. S9, ESI†). Swelling of a ribbon printed with a single copy of the pattern ψc(y) indeed produces an annular arc, and ribbons with the four pair-wise combinations of patterns indeed produce the four categories of ICF (Fig. 5B and C). The actuated shapes of the ICFs were also computed numerically using the bespoke active-shell C++ code Morphoshell,38 producing excellent agreement with the experiments.
5 Relaxed shape of metric-mechanic ICFs
Interestingly, the LCE ICFs do not adopt the simple bend-minimizing forms discussed above: for example the symmetric ICFs are far from fully closed. The key difference is that now the fold is not a freely jointed hinge, so the elastic sheet resists the singular bending deformations required to create a sharp apex. Indeed, one may readily observe in experiments and numerics that the central fold is not sharp, but rather blunted over some lengthscale f, that is short compared to flank-width and radius, but not compared to thickness. Such blunting requires a competition between stretch and bend, with small strains (deviations from isometry) occurring to relieve the singular curvature of a sharp ridge. To capture this competition, we consider a homogeneous ICF with fixed curvature |κ|, as created in our experiments. A perfect isometry of the ICF would form a surface of revolution consisting of two conical flanks connected by a sharp ridge at radius R0 = 1/|κ|, which we may describe in cylindrical coordinates as![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (s) = R0 − |s|cos
(s) = R0 − |s|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi, with s being the arc-length transverse to the fold, s = 0 being the apex, and αi switching value between the flanks in accord with eqn (1). Similarly, we describe the blunted form of the ICF by the smooth curve R(s) =
αi, with s being the arc-length transverse to the fold, s = 0 being the apex, and αi switching value between the flanks in accord with eqn (1). Similarly, we describe the blunted form of the ICF by the smooth curve R(s) = ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (s) + ΔR(s), and also define the θ(s) as the angle between the local tangent and the radial direction (see Fig. 6(A)). During blunting, the dominant bend-stretch competition is between s curvature θ′(s) (which would diverge at a sharp fold) and hoop strain, ε = ΔR/
(s) + ΔR(s), and also define the θ(s) as the angle between the local tangent and the radial direction (see Fig. 6(A)). During blunting, the dominant bend-stretch competition is between s curvature θ′(s) (which would diverge at a sharp fold) and hoop strain, ε = ΔR/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) , leading to the simplified shell energy density
, leading to the simplified shell energy density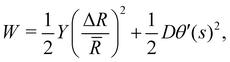 | (7) |
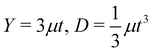 are stretching and bending moduli respectively, μ being the (incompressible) LCE's shear modulus, and t the actuated thickness. Assuming that the length-scale of blunting is short compared to R0, and also that the isometery is nearly cylindrical so that θ′(s) = ΔR′′(s), we may write the energy of the ridge as
are stretching and bending moduli respectively, μ being the (incompressible) LCE's shear modulus, and t the actuated thickness. Assuming that the length-scale of blunting is short compared to R0, and also that the isometery is nearly cylindrical so that θ′(s) = ΔR′′(s), we may write the energy of the ridge as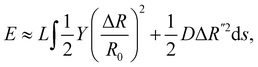 | (8) |
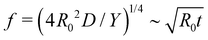 as the emergent blunting length-scale, which matches the blunting lengthscale of (extrinsic) Pogorelov ridges created by mirror inverting a portion of a shell,40–43 and ensures our approximations are self consistent (ESI,† Section S5). The full form of ΔR is constructed by taking the decaying solutions on either side of s = 0, and joining them to produce a smooth and energy minimizing solution, giving
as the emergent blunting length-scale, which matches the blunting lengthscale of (extrinsic) Pogorelov ridges created by mirror inverting a portion of a shell,40–43 and ensures our approximations are self consistent (ESI,† Section S5). The full form of ΔR is constructed by taking the decaying solutions on either side of s = 0, and joining them to produce a smooth and energy minimizing solution, giving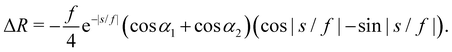 | (9) |
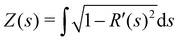 . To validate this form, we use Mathematica to numerically minimize a full geometrically-nonlinear energy for an axisymmetric shell (ESI,† Section S5) for multiple symmetric ICFs, revealing strong agreement over a large range of α (Fig. 6 and Fig. S6, ESI†).
. To validate this form, we use Mathematica to numerically minimize a full geometrically-nonlinear energy for an axisymmetric shell (ESI,† Section S5) for multiple symmetric ICFs, revealing strong agreement over a large range of α (Fig. 6 and Fig. S6, ESI†).
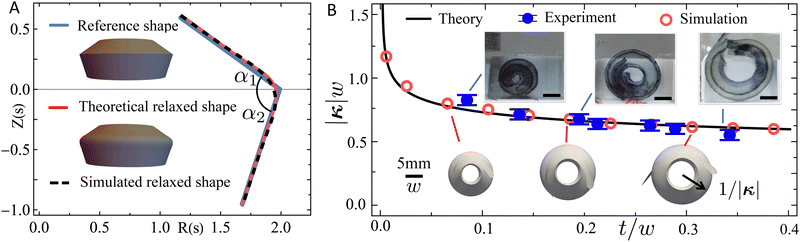 | ||
| Fig. 6 (A) Reference (isometric) shape of an ICF with α1 = 0.2π and α2 = 0.4π, and its theoretical (eqn (9)) and simulated relaxation. (B) Equilibrium ICF curvature against thickness for an (S+) fold: theory (eqn (11)), experiments, and simulations. All simulation and experiment have equal planar dimensions (reference half-width w = 50 mm and length 3 cm) and span a range of actuated thicknesses t. | ||
Substituting the shape expression into eqn (8), we obtain the effective ridge energy density ρr = E/L as
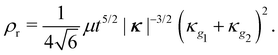 | (10) |
To predict the relaxed shape of an ICF, we take the total energy as the ridge energy plus the previously computed bending energy of the two flanks. Minimizing this total energy ρr + ρf1 + ρf2 of the fold over curvature yields
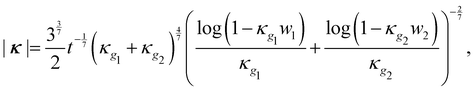 | (11) |
| |κ| = (33/25)1/7κg4/7t−1/7w−2/7. | (12) |
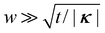 . Secondly, we require that the proposed flank isometry actually exists and is physically reasonable, a condition that can fail, for example, if the width is too large (κgiwi > 1), so the conical flank to extend right out to a tip, or if the achieved curvature rolls the strip so tight that itself intersects. However, we are able to validate the effect by numerically (Morphoshell) and experimentally actuating S+ LCE ICFs spanning a magnitude of thickness. Experimentally, thickness was varied via changing the number of printed layers, and actuation was again by swelling in toluene. As seen in Fig. 6, both experiment and numerics clearly exhibit higher curvature at lower thickness, in very satisfactory agreement with eqn (11).
. Secondly, we require that the proposed flank isometry actually exists and is physically reasonable, a condition that can fail, for example, if the width is too large (κgiwi > 1), so the conical flank to extend right out to a tip, or if the achieved curvature rolls the strip so tight that itself intersects. However, we are able to validate the effect by numerically (Morphoshell) and experimentally actuating S+ LCE ICFs spanning a magnitude of thickness. Experimentally, thickness was varied via changing the number of printed layers, and actuation was again by swelling in toluene. As seen in Fig. 6, both experiment and numerics clearly exhibit higher curvature at lower thickness, in very satisfactory agreement with eqn (11).
Such stretch-bend competitions are ubiquitous in the mechanics of realistic non-Euclidean shells, leading, for example, to buckling transitions from flat to curved,44,45 mechanically rich boundary layers,45,46 and the blunting of conical tips.22,26,27 However, the competition in ICFs produces the unusual feature that the selected shape also diverges in the thin limit. Generally, when an initially flat sheet is programmed with an intrinsically curved metric, the different thickness scaling of stretch and bend means that the stretch energy turns into a constraint in the thin limit, allowing only isometric deformations, with bend only entering as a tie breaker between these zero-stretch states. Furthermore, since the bending energy only depends on thickness via a t3 prefactor, the resultant bend-minimising isometry is thickness independent:45 for example, a given (anti-)conical metric always generates the same (anti-)cone, independent of thickness,27 as would a pattern generating a saddle or spherical cap. Freely hinged ICFs follow this usual rule, as do LCE sheets encoded with either finite Gaussian curvature, or point-wise concentrations at (anti-)conical tips. However, beyond metric mechanics, similar thickness effects are seen in curved-fold origami, if the hinge is formed from an angular spring, setting up a contest between spring energy (thickness independent) and flank bend (t3) to determine which isometry is observed.13,47 Similarly, the thickness dependent behavior of ICFs (line-like curvature concentrations) emerges from the contest between the stretch/bend energy of the blunted fold (t5/2) and the bend energy of the flanks (t3). However, the effects in curved-fold origami and LCE folds are fundamentally different: origami creases only fold because of the hinge-spring motivates finite fold angles, leading thinner sheets fold more as the spring becomes more significant. In contrast, ICFs fold because of their intrinsic geometry, with the ridge inhibiting folding so that thinner sheets fold less.
6 Discussion
Our principle results on the rich kinematics of ICFs highlight how, provided they are constructed from bendable sheets, they form useful mechanisms, with potential applications across soft robotics and morphing/deployable structures. Particular highlights include symmetric ICFs which, pseudo-paradoxically, allow a truly Gauss curved surface to be deployed from a planar flat-packed state, and also asymmetric positive ICFs which can show great strength and rigidity. Our results also highlight the similarities and differences between hinged ICFs and those formed by morphing active sheets, with both obeying the same basic kinematics but having quite different mechanics and shape selection.Our treatment has focused on shells containing single ICFs, but a natural extension is to combine multiple ICFs for more complex morphing. As a simple demonstration, we design and fabricate an LCE Gaussian-gripper, by combining multiple strong asymmetric positive folds in a cross-like configuration, (Fig. 7A and B). Upon convenient thermal actuation by a heat lamp, the cross morphs into a claw shape that is capable of gripping and lifting a simple load (Fig. 7C) up to 40× the gripper's own weight (Movie M7, ESI†). Although this weight multiple is naturally scale dependent, it considerably exceeds the performance of previous bend-driven soft grabbers of comparable dimensions.39,48 The gripper is also versatile, lifting a wide range of objects with different shapes, weights, textures and levels of compliance (Fig. 7D and Movie M8, ESI†).
Looking ahead, our results also motivate many directions for further exploration. Can one design an ICF that traces an arbitrary 3D space curve in its equilibrium state, or even an elephant's-trunk ICF that can morphs between many space-curves via angular actuators along its length? What is the effective rod-theory47,49 for ICF ribbons? How do ICF kinematics change when they pass through intrinsically curved ribbons?50 What are the kinematics of surfaces containing multiple ICFs, such as our gripper? Overall, the rich geometry and mechanics of ICFs coupled with their straightforward manufacture, suggests these questions, any many others, will be a very fruitful area for further exploration.
7 Materials and methods
7.1 Materials
LC ink was synthesised by creating oligomers via aza-Michael addition from a reactive mesogen (RM82; CAS: 125248-71-7), amine linker (n-butylamine, nBA; CAS: 109-73-9) and photoinitiator (Ir2959; CAS: 106797-53-9). RM82 was purchased from Daken Chemical, China, and both nBA and Ir2959 from Merck Life Science, UK. All compounds were put to a glass vial (with molar ratio of RM82 to nBA: 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 and with 1 wt% of initiator), melted with a heat gun and vigorously mixed, first by vortex mixer and then on a hot plate with magnetic stirrer bar for ca. 30 min. A (pre-heated) metal syringe for printing was then filled with the ink and left in the oven for around 18 h for full oligomerisation (75–80 °C).
1.0 and with 1 wt% of initiator), melted with a heat gun and vigorously mixed, first by vortex mixer and then on a hot plate with magnetic stirrer bar for ca. 30 min. A (pre-heated) metal syringe for printing was then filled with the ink and left in the oven for around 18 h for full oligomerisation (75–80 °C).
7.2 3D-printing of ICFs
The syringe with the ink was mounted in Hyrel's KR2-15 used with System 30 M 3D printer with a 2D array of UV LED (365 nm). All the patterns were printed on glass slides coated with 5% solution of poly(vinyl alcohol) in water, after careful calibration of the printing parameters for 0.30 mm MK8 nozzle (printed line width: 0.20 mm, first layer height: 0.125 mm, layer height: 0.1 mm, printing speed: 260 mm min−1, extrusion rate: 5.2 μL min−1, priming: 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pulses with rate 10
000 pulses with rate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pulses per s, where 1297 pulses correspond to 1 μL; temperature of printing: 80 °C), with UV LEDs working on 30–50% of max power. After printing all samples were additionally cured for 1 h in a UV curing station with two UV LEDs (LuxiGen LZ1-10UV0R, 365 nm) irradiating a sample placed on a distance of 65 mm from both top and bottom diode. Printed LCE sheets were then detached from their glass substrates with a blade.
000 pulses per s, where 1297 pulses correspond to 1 μL; temperature of printing: 80 °C), with UV LEDs working on 30–50% of max power. After printing all samples were additionally cured for 1 h in a UV curing station with two UV LEDs (LuxiGen LZ1-10UV0R, 365 nm) irradiating a sample placed on a distance of 65 mm from both top and bottom diode. Printed LCE sheets were then detached from their glass substrates with a blade.
7.3 Actuation
Initial thermal strain data was collected on monodomain (linear) samples, using a hot plate (Fig. S9, ESI†). Swelling strain data was obtained by placing monodomain samples in a glass container filled with toluene for around 3 h (Fig. S10, ESI†). ICF samples were actuated by swelling in the same way, and then imaged using a Canon EOS 1200D camera, with either EFS 18–55 mm lens or with macro 100 mm lens. ICFs in Fig. 5C were imaged shortly after removal from toluene. The precisely characterized ICFs in Fig. 6B were imaged whilst still in toluene, with the camera directly facing the axis of the fold's surface of revolution for accurate extraction of the ICF radius. Thickness, before and after actuation, was measured using digital calipers (Hilka 0–150 mm). The LCE grippers were actuated thermally with a heat lamp (Panasonic, 300 W) in a custom box coated internally with 0.4 mm thick black paper. The LCE sample was prepared by 3D printing, then painted with a black marker to aid absorption, and the lamp was directed at an angle of 30° from the vertical. The same camera was used to record experiments of grasping and lifting different objects with a weight range 0.24–19.24 g. Temperatures up to 150 °C were recorded during heat lamp irradiation, using a digital thermometer (CELTEK T2001) with the probe placed between a gripper and a weight.Author contributions
Conceptualization: F. F., K. D., J. S. B. Methodology: F. F., K. D., J. S. B. Investigation: F. F., K. D., M. Z., M. B., J. S. B. Supervision: J. S. B. Writing—original draft: F. F., K. D., M. B., J. S. B.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a UKRI ‘future leaders fellowship’ grant (grant no. MR/S017186/1). Additionally, M. Z. received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 956150.Notes and references
- P. Shaw, 2014, https://treesofsantacruzcounty.blogspot.com/2014/06/salix-babylonica-annularis-curly-leaved.html.
- Haraldius, 2005, https://commons.wikimedia.org/wiki/File:551_Nymphaeaceae.JPG (Creative Commons Attribution-Share Alike 2.5 Generic license).
- K. Denby and A. C. Takiwasi, 2016, https://commons.wikimedia.org/wiki/File:Fruto_de_Carambola_(Averrhoa_carambola).jpg (Creative Commons Attribution-Share Alike 4.0 International license).
- Millcam, Cupola Roof, University of Cambridge, 2023, https://millcam.co.uk/case-studies/cupola-roof-university-of-cambridge/.
- E. D. Demaine, M. L. Demaine and D. Koschitz, Origami, 2011, 5, 39–52 Search PubMed.
- J. Mitani, Curved-folding origami design, CRC Press, 2019 Search PubMed.
- J. Mitani, An imitation of D. Huffman's Tower, 2010, https://flickr.com/photos/jun_mitani/4250985156 Search PubMed.
- Costume Institute, 1984, https://commons.wikimedia.org/wiki/File:Top_hat_MET_DT7973.jpg (Creative Commons CC0 1.0 Universal Public Domain Dedication).
- Amuzujoe, 2022, https://commons.wikimedia.org/wiki/File:Wikilovesafrica9699.jpg (Creative Commons Attribution-Share Alike 4.0 International license).
- DLG Images, 2014, https://commons.wikimedia.org/wiki/File:Red_Umbrella_1.jpg (Creative Commons Attribution 2.0 Generic license).
- J. P. Duncan and J. Duncan, Proc. R. Soc. London, Ser. A, 1982, 383, 191–205 Search PubMed.
- D. Fuchs and S. Tabachnikov, Am. Math. Monthly, 1999, 106, 27–35 CrossRef.
- M. A. Dias, L. H. Dudte, L. Mahadevan and C. D. Santangelo, Phys. Rev. Lett., 2012, 109, 114301 CrossRef PubMed.
- H. Liu and R. D. James, J. Mech. Phys. Solids, 2024, 105559 CrossRef.
- M. Liu, L. Domino and D. Vella, Soft Matter, 2020, 16, 7739–7750 RSC.
- Z. Zhai, Y. Wang, K. Lin, L. Wu and H. Jiang, Sci. Adv., 2020, 6, eabe2000 CrossRef PubMed.
- J. A. Thomson, On growth and form, 1917 Search PubMed.
- A. Goriely, The mathematics and mechanics of biological growth, Springer, 2017, vol. 45 Search PubMed.
- P. Plucinsky, B. A. Kowalski, T. J. White and K. Bhattacharya, Soft Matter, 2018, 14, 3127–3134 RSC.
- M. Warner, Ann. Rev. Condens. Matter Phys., 2020, 11, 125–145 CrossRef CAS.
- Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120 CrossRef CAS PubMed.
- C. Modes, K. Bhattacharya and M. Warner, Proc. R. Soc. A, 2011, 467, 1121–1140 CrossRef.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- H. Aharoni, Y. Xia, X. Zhang, R. D. Kamien and S. Yang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7206–7211 CrossRef CAS PubMed.
- E. Hajiesmaili, N. M. Larson, J. A. Lewis and D. R. Clarke, Sci. Adv., 2022, 8, eabn9198 CrossRef PubMed.
- E. Siéfert, E. Reyssat, J. Bico and B. Roman, Nat. Mater., 2019, 18, 24–28 CrossRef PubMed.
- T. Guin, M. J. Settle, B. A. Kowalski, A. D. Auguste, R. V. Beblo, G. W. Reich and T. J. White, Nat. Commun., 2018, 9, 2531 CrossRef PubMed.
- D. Duffy, L. Cmok, J. S. Biggins, A. Krishna, C. D. Modes, M. K. Abdelrahman, M. Javed, T. H. Ware, F. Feng and M. Warner, J. Appl. Phys., 2021, 129, 224701 CrossRef CAS.
- F. Feng, D. Duffy, M. Warner and J. S. Biggins, Proc. R. Soc. A, 2022, 478, 20220230 CrossRef PubMed.
- B. O'neill, Elementary differential geometry, Elsevier, 2006 Search PubMed.
- W. Wunderlich, Monatsh. Math., 1962, 66, 276–289 CrossRef.
- R. E. Todres, J. Elasticity, 2015, 119, 23–34 CrossRef.
- T. Yu, I. Andrade-Silva, M. A. Dias and J. Hanna, Mech. Res. Commun., 2021, 103700 Search PubMed.
- E. Starostin and G. Van Der Heijden, Nat. Mater., 2007, 6, 563–567 CrossRef CAS PubMed.
- M. Warner, Ann. Rev. Condens. Matter Phys., 2020, 11, 125–145 CrossRef CAS.
- F. Feng, J. S. Biggins and M. Warner, Phys. Rev. E, 2020, 102, 013003 CrossRef CAS PubMed.
- C. Mostajeran, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062405 CrossRef PubMed.
- D. Duffy and J. S. Biggins, Soft Matter, 2020, 16, 10935–10945 RSC.
- M. O. Saed, C. P. Ambulo, H. Kim, R. De, V. Raval, K. Searles, D. A. Siddiqui, J. M. O. Cue, M. C. Stefan and M. R. Shankar, et al. , Adv. Funct. Mater., 2019, 29, 1806412 CrossRef.
- A. V. Pogorelov, Bendings of surfaces and stability of shells, American Mathematical Soc., 1988, vol. 72 Search PubMed.
- M. Gomez, D. E. Moulton and D. Vella, Proc. R. Soc. A, 2016, 472, 20150732 CrossRef PubMed.
- K. A. Seffen, Phys. Rev. E, 2016, 94, 063002 CrossRef PubMed.
- D. Duffy, J. M. McCracken, T. S. Hebner, T. J. White and J. S. Biggins, Phys. Rev. Lett., 2023, 131, 148202 CrossRef CAS PubMed.
- E. H. Mansfield, Proc. R. Soc. London, Ser. A, 1962, 268, 316–327 Search PubMed.
- E. Efrati, E. Sharon and R. Kupferman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016602 CrossRef PubMed.
- I. Levin and E. Sharon, Phys. Rev. Lett., 2016, 116, 035502 CrossRef PubMed.
- M. A. Dias and B. Audoly, J. Mech. Phys. Solids, 2014, 62, 57–80 CrossRef.
- S. Y. Zheng, Y. Shen, F. Zhu, J. Yin, J. Qian, J. Fu, Z. L. Wu and Q. Zheng, Adv. Funct. Mater., 2018, 28, 1803366 CrossRef.
- M. A. Dias and B. Audoly, The Mechanics of Ribbons and Möbius Bands, Springer, 2016, pp. 49–66 Search PubMed.
- E. Efrati, J. Elasticity, 2015, 119, 251–261 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01584j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |