Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolution dynamics of thin liquid structures investigated using a phase-field model†
Yanchen
Wu
 *ab,
Fei
Wang
*ab,
Sai
Zheng
a and
Britta
Nestler
abc
*ab,
Fei
Wang
*ab,
Sai
Zheng
a and
Britta
Nestler
abc
aInstitute for Applied Materials – Microstructure Modelling and Simulation (IAM-MMS), Karlsruhe Institute of Technology (KIT), Straße am Forum 7, Karlsruhe 76131, Germany. E-mail: yanchen.wu@kit.edu; fei.wang@kit.edu
bInstitute of Nanotechnology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz Pl. 1, 76344, Eggenstein-Leopoldshafen, Germany
cInstitute of Digital Materials Science (IDM), Karlsruhe University of Applied Sciences, Moltkestraße 30, Karlsruhe, 76133, Germany
First published on 15th January 2024
Abstract
Liquid structures of thin-films and torus droplets are omnipresent in daily lives. The morphological evolution of liquid structures suspending in another immiscible fluid and sitting on a solid substrate is investigated by using three-dimensional (3D) phase-field (PF) simulations. Here, we address the evolution dynamics by scrutinizing the interplay of surface energy, kinetic energy, and viscous dissipation, which is characterized by Reynolds number Re and Weber number We. We observe special droplet breakup phenomena by varying Re and We. In addition, we gain the essential physical insights into controlling the droplet formation resulting from the morphological evolution of the liquid structures by characterizing the top and side profiles under different circumstances. We find that the shape evolution of the liquid structures is intimately related to the initial shape, Re, We as well as the intrinsic wettability of the substrate. Furthermore, it is revealed that the evolution dynamics are determined by the competition between the coalescence phenomenology and the hydrodynamic instability of the liquid structures. For the coalescence phenomenology, the liquid structure merges onto itself, while the hydrodynamic instability leads to the breakup of the liquid structure. Last but not least, we investigate the influence of wall relaxation on the breakup outcome of torus droplets on substrates with different contact angles. We shed light on how the key parameters including the initial shape, Re, We, wettability, and wall relaxation influence the droplet dynamics and droplet formation. These findings are anticipated to contribute insights into droplet-based systems, potentially impacting areas like ink-jet printing, drug delivery systems, and microfluidic devices, where the interplay of surface energy, kinetic energy, and viscous dissipation plays a crucial role.
1 Introduction
Droplets of various shapes either floating in a surrounding fluid or sitting on a solid substrate are ubiquitous in life science from the subcellular to the tissue scale, where cell organelle, cells, tissues, and membranes are shaped to execute specific functions.1 A comprehensive understanding of the dynamic interactions of liquid–fluid and liquid–solid is of fundamental importance for exploring the rich phenomena appearing in the life science and colloidal systems. The precise control of droplet production, droplet shaping, droplet dynamics, and bubble dynamics is critical in applications such as inkjet printing, drug delivery, drag reduction, microfluidics, and lab-on-a-chip systems, among others.2–7 For instance, in medical applications, the spray formation assists the drug delivery3 and the cavitation caused by bubble bursting is used to remove kidney stones.8Manipulation of droplet behaviors including droplet movement, morphological transition, coalescence, and breakup etc. can be either active or passive. Various methods have been applied to actively manipulate droplet behaviors by making use of additional energy input. In contrast, the passive manipulation of droplet behaviors is without external actuation, and the droplet characteristics are determined by the competition of interfacial tension forces, viscous forces, and inertial forces. The interfacial tension force tends to minimize the interfacial area, while the viscous and inertial forces balance the interfacial tension force and seek to deform the liquid interface.9 In passive microfluidic devices, one immiscible dispersed fluid flows into another continuous fluid, which leads to typical modes of droplet formation: squeezing, dripping, jetting, tip-streaming, and tip-multi-breaking.9 For open droplet microfluidic platforms, the devices and substrates are designed with gradients in topography10,11 and wettability12 so that the movements of droplets can be directly driven by the Laplace pressure.
Although droplet breakup and drop formation in two-phase flow have been extensively researched, complete control of the droplet breakup process necessitates a thorough understanding of the mechanism for the involved energy interplay and the morphological transition. Plateau and Lord Rayleigh13,14 pioneered the study for the breakup of fluid cylinders and other interface-driven problems. The formation of drops results from the motion of free surfaces, but it is indeed difficult to predict the size distributions and to detect the complex dynamics. In previous studies, the evolution of a floating droplet has been extensively investigated.15–17 For instance, Fragkopoulos et al.15 theoretically and experimentally analyzed the flow field inside the shrinking toroidal droplets and revealed the morphology property. Lavrenteva et al.16 theoretically investigated the deformation of viscous drops subject to a linear flow in an immiscible viscous fluid. But the breakup phenomenon was not addressed in both works.15,16 Novkoski et al.18 optically observed gravity-capillary waves on a torus of fluid depositing on a superhydrophobic groove substrate. Pairam et al.19 and Fragkopoulos et al.20 investigated the instability and breakup of neutral and charged toroidal droplets on a substrate, respectively, but none of them took the wettability of the substrate into consideration. Edwards et al.21 experimentally and theoretically studied slender liquid filament breakup due to surface tension with wetting conditions. The authors demonstrated how controlling static and dynamic wetting can result in switching between a toroidal film and well-defined droplet patterns through dielectrophoresis forces. However, a systematic numerical modeling of free-surface motion caused by diffusion and convection coupling with the wettability of the solid substrate is still lacking.
Usually, the experimental techniques are limited to capture the interface in the two-phase flow systems, making it difficult to study real-world applications of two-phase flow systems through experiments.22 This motivates the development of numerical approaches for capturing the interface evolution, which is coupled with the diffusion and the momentum conservation equations. A variety of numerical models have been established to depict the interface evolution. A straightforward way of modeling the moving interfaces is to apply a moving mesh on the interfaces that deforms according to the flow conditions. For instance, Ambravaneswaran et al.23 implemented this method in a finite-element method. But this method requires a track of moving mesh and it suffers from mesh entanglement for large deformation and singular topological changes of droplets such as breakup and coalescence. The fixed-grid methods including the volume-of-fluid (VOF), the level-set (LS), and the front-tracking (FT) methods, are all common interface-capturing approaches with a sharp interface. We refer to a recent review paper24 for more details of the sharp interface methods for studying free surface flows. In the sharp interface model, the physical properties such as density and viscosity values jump across the interface22 and the contact line movement is either allowed by a Navier-slip condition or by a numerical slip at the contact line.25 In addition, a lot of efforts have been made to increase the accuracy of curvature estimation and the numerical implementation of well-balanced surface tension force is required for reducing spurious flows. For diffuse interface models, the density and viscosity are functions of the local order parameter and the contact line movement on the substrate is achieved through diffusion. A typical diffuse interface model is the phase-field (PF) model, which is a promising method for overcoming the shortcomings in tracking the interface position. In the framework of the PF model, the interface thickness is thin but with finite value. Since the diffuse interface is introduced through an energetic variational procedure, the PF model describes a thermodynamic consistent coupling system.26 The diffuse interface allows for numerical consideration of the topological changes and the modeling of near-singular interfacial events including droplet breakup and coalescence, as well as moving contact line.27,28 The Shan-Chen model-based lattice Boltzmann method (LBM)29,30 and LBM with thermodynamically consistent potentials31 allow the contact line movement by evaporation and condensation near the contact line, whereas the PF type LBM32 achieves the contact line motion via diffusion. There are commonly used open-source codes in this area. For instance, the open source CFD software OpenFOAM has been developed primarily by OpenCFD Ltd since 2004, and it provides solvers and libraries for simulating multi-phase flows. Marschall and Wörner et al.33,34 implemented a phase-field multiphase flow solver in OpenFOAM (FOAMextend), which was named phaseFieldFoam, to study the dynamics of droplets and bubbles. Popinet et al. developed freely available codes such as Gerris35 and Basilisk,36 which are based on a VOF model with adaptive mesh refinement.37 Krause et al. released OpenLB based on a lattice Boltzmann method (LBM).38
In this work, we use the PF model of Cahn–Hilliard (CH) type. For the CH model, Jacqmin28 formulated the surface tension force such that the total energy is only dissipated and the spurious currents can be avoided.22 Unlike the continuum surface force (CSF) model widely used in the VOF method, the free energy formulation in the CH model does not require curvature computation.34 The CH model in two-phase flow with wetting boundary conditions has been investigated extensively.28,39–41 Yue et al.40,42 provided guidelines to choose the model parameters such as interface thickness, mobility or the CH diffusivity, and wall relaxation through calibration with experiment and sharp-interface limit analysis. Carlson et al.43 systematically studied spontaneously wetting liquid droplets on the substrates with a wall relaxation effect through introducing a phenomenological parameter in the PF model, which quantitatively matches with experimental data. They demonstrated that the wetting dynamics can be largely altered by the physico-chemistry property of the substrate even when the equilibrium contact angle is the same.44,45
Most of the previous CH models for two-phase flow are based on the Ginzburg–Landau double-well potential with a constant mobility.43,46,47 The Ginzburg–Landau double-well potential is formulated in the form of a fourth-order polynomial and it was originally used for the mathematical theory of superconductivity. Normally, the Ginzburg–Landau double-well potential requires a strict restriction of the order parameter in the bulk phases as ±1. However, the curvature effect and bulk diffusion lead to the deviation of the order parameter in the bulk phases from ±1, which affects the computational accuracy and cost.48 This can be handled in PF formulations involving fourth order polynomials in the free energy by using stabilizing functions and additional degeneracies.49 In this work, we adopt a thermodynamically consistent logarithmic Flory–Huggins potential based on the entropy and enthalpy of mixing. Contrary to previous constant mobilities, we employ an order parameter dependent mobility assigned with the Onsagers relationship. The logarithmic Flory–Huggins energy potential is often recognized to be more physically realistic than the polynomial free energy because the former one is derived from regular or ideal solution theories.50,51 Therefore, our model is constructed in a natural way with the possibility to be extended for modeling rich phenomena of fluid dynamics, in combination with nucleation, spinodal decomposition as well as evaporation and condensation. Moreover, by adjusting the Flory parameter in the logarithmic Flory–Huggins potential, the order parameter is restricted within the interval (0,1). In this way, the present model avoids the singularity problem as mentioned in ref. 51. In addition, we adopt the dynamic wetting boundary condition containing the wall relaxation parameter τw. The thermodynamic consistency and the energy dissipation law of the coupled model are rigorously deduced in the present work, which shows the importance of τw in the energy dissipation process on the substrate. To the best of our knowledge, the logarithmic Flory–Huggins potential and the order parameter dependent mobility used in the current CH model are verified for the first time to adequately reproduce experimental results of droplet dynamics.
In this work, we investigate thin liquid films and torus droplets by using CH model coupling with the Navier–Stokes (NS) equations. Specifically, we consider several key factors influencing droplet breakup and drop formation, including the droplet sizes, velocities, viscosities and densities, surface tension, the wettability, wall relaxation, and geometry. These factors are systemically studied by introducing the following dimensionless parameters: droplet aspect ratio ξ (width/height for the thin films and major radius/minor radius for the torus droplets), Reynolds number Re, Weber number We, the Young's contact angle of the substrate θeq, and the wall relaxation parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w. This work provides accurate predictions concerning the evolution of droplet shape under various conditions, particularly when influenced by wettability and wall relaxation effects, which have been seldom systematically investigated in existing literature. Our study has fundamental significance for the application of multiphase systems with interfaces exhibiting non-constant mean curvature and casts light on controlling droplet formation by manipulating wettability and the wall relaxation effect.
w. This work provides accurate predictions concerning the evolution of droplet shape under various conditions, particularly when influenced by wettability and wall relaxation effects, which have been seldom systematically investigated in existing literature. Our study has fundamental significance for the application of multiphase systems with interfaces exhibiting non-constant mean curvature and casts light on controlling droplet formation by manipulating wettability and the wall relaxation effect.
This work is organized as follows. In Section 2, we present the CH model coupled with Navier–Stokes (NS) equations. In Section 3, we validate the model and present simulation results for the fast spreading and impacting process of water droplets. The results are compared with the literature. In Section 4, we show simulations for the evolution of thin-film and torus droplets under various conditions. The conclusions and outlook for future directions are provided in Section 5.
2 Governing equations
2.1 CH model coupled with NS equations (CHNS model)
We consider an isotherm incompressible flow with two immiscible fluids. The free energy functional for the bulk of the system![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is described with the order parameter c:52–54
is described with the order parameter c:52–54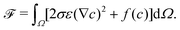 | (1) |
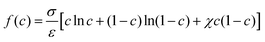 | (2) |
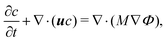 | (3) |
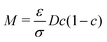 is the phase-field dependent mobility with D indicating the chemical diffusion coefficient. In our simulations, the Peclet number Pe is set as 100, so the type of mobility in the diffusion equation may have a minor influence on the results. The formulation of M in this work is derived by comparing the diffusion flux expressed in terms of the chemical potential to the Ficks flux in terms of concentration; it is based on the ideal solution free energy model. In the literature, various types of mobility have been employed; for a more in-depth discussion of different mobility formulations, we refer to ref. 58. For example, Wörner et al.47 investigated droplet impact behaviors using constant mobility, which is determined through fitting to experimental data. In the context of the Flory–Huggins free energy model, a more generalized mobility formulation is applied to simulate phase separation in polymer solutions.59 To account for the surface diffusion effect, it has been shown that the mobility should take the form of a fourth-order polynomial to prevent spurious bulk diffusion.49,60,61 The variable
is the phase-field dependent mobility with D indicating the chemical diffusion coefficient. In our simulations, the Peclet number Pe is set as 100, so the type of mobility in the diffusion equation may have a minor influence on the results. The formulation of M in this work is derived by comparing the diffusion flux expressed in terms of the chemical potential to the Ficks flux in terms of concentration; it is based on the ideal solution free energy model. In the literature, various types of mobility have been employed; for a more in-depth discussion of different mobility formulations, we refer to ref. 58. For example, Wörner et al.47 investigated droplet impact behaviors using constant mobility, which is determined through fitting to experimental data. In the context of the Flory–Huggins free energy model, a more generalized mobility formulation is applied to simulate phase separation in polymer solutions.59 To account for the surface diffusion effect, it has been shown that the mobility should take the form of a fourth-order polynomial to prevent spurious bulk diffusion.49,60,61 The variable 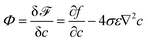 is the chemical potential and at the equilibrium state, Φ = const. The Cahn–Hilliard equation is derived based on the assumption that the diffusion flux is proportional to the gradient of the chemical potential.53,62
is the chemical potential and at the equilibrium state, Φ = const. The Cahn–Hilliard equation is derived based on the assumption that the diffusion flux is proportional to the gradient of the chemical potential.53,62
Substituting eqn (1) into eqn (3), the following equation is obtained
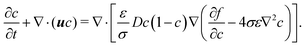 | (4) |
The Navier–Stokes equation reads
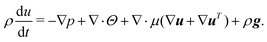 | (5) |
The density and viscosity ρ and μ are linearly interpolated with the order parameter c:
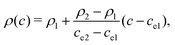 | (6) |
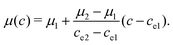 | (7) |
For an incompressible system, the densities for the two immiscible fluids do not change. For a small density ratio, usually the Boussinesq approximation is used to handle the densities.66 The Boussinesq approximation ignores density differences except where buoyancy force is important. Under the Boussinesq approximation, we obtain
| ∇·u = 0. | (8) |
In summary, the NS equations are coupled with the CH equation through order parameter dependent surface tension force, density and viscosity, and the advection term. The governing equations are discretized by using the finite difference method for space derivative and explicit Euler schemes for the time derivative. Our model is implemented within the multi-physics framework of “Parallel Algorithms for Crystal Evolution in 3D” (PACE3D), which is an efficient phase-field solver based on C language and parallelized with message passing interface (MPI). The PACE3D solver contains diverse implemented models allowing a wide range of multi-physics applications.
2.2 Non-dimensional calculation
By choosing the surface tension σ*, viscosity μ*, and length x* as characteristic parameters, the related physical variables are non-dimensionalized. We chose the length of one mesh element as the characteristic length to study the phenomena occurring at the interfacial region. However, the choice of x* is not unique and other scales such as interface thickness and the initial droplet diameter can also be used as the characteristic length scale for the non-dimensionalization.67 The selection of characteristic variables and the model parameters in the diffuse interface model is related to the investigated problem. On the one hand, the chosen characteristic length x* is in the scale of interface length because our focus in this work is mainly on the breakup process occurring within the interfacial region. On the other hand, Langer68 suggested the calculation of the capillary length as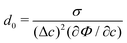 with
with 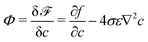 denoting the chemical potential. Through dimensional analysis, we estimate the capillary length as d0 ∝ σ/(σ/ε) = ε. Moreover, in this work, the mesh size has a fixed value of 2 × 10−5 [m] (e.g., see Table 1), thus it has a physical meaning of a micro-meter scale length. This characteristic length x* = 2 × 10−5 [m] together with two other characteristic parameters, the surface tension σ* = 7.28 × 10−2 [kg s−2], and viscosity μ* = 1.0 × 10−3 [kg (ms)−1], are used to conduct non-dimensional calculations. In the current work, the scaling factors are as follows: velocity u* = σ*/μ*, time t* = μ*x*/σ*, and pressure p* = ρ*(u*)2. The dimensionless variables are calculated by these scaling factors such that we obtain ũ = u/u*,
denoting the chemical potential. Through dimensional analysis, we estimate the capillary length as d0 ∝ σ/(σ/ε) = ε. Moreover, in this work, the mesh size has a fixed value of 2 × 10−5 [m] (e.g., see Table 1), thus it has a physical meaning of a micro-meter scale length. This characteristic length x* = 2 × 10−5 [m] together with two other characteristic parameters, the surface tension σ* = 7.28 × 10−2 [kg s−2], and viscosity μ* = 1.0 × 10−3 [kg (ms)−1], are used to conduct non-dimensional calculations. In the current work, the scaling factors are as follows: velocity u* = σ*/μ*, time t* = μ*x*/σ*, and pressure p* = ρ*(u*)2. The dimensionless variables are calculated by these scaling factors such that we obtain ũ = u/u*, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t/t*,
= t/t*, ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = p/p*,
= p/p*, ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x/x*, and so on. The variables labeled with tilde are dimensionless values. The dimensionless CH equation is expressed as
= x/x*, and so on. The variables labeled with tilde are dimensionless values. The dimensionless CH equation is expressed as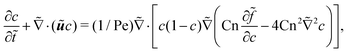 | (9) |
| Parameters | Value | Unit |
|---|---|---|
| Characteristic length x* (mesh size) | 2 × 10−5 | [m] |
| Characteristic viscosity μ* | 1.0 × 10−3 | [kg (ms)−1] |
| Characteristic surface tension σ* | 7.28 × 10−2 | [kg s−2] |
| Dynamic viscosity of gas μ1 | 1.8 × 10−5 | [kg (ms)−1] |
| Dynamic viscosity of water μ2 | 1.0 × 10−3 | [kg (ms)−1] |
| Density of gas ρ1 | 1.2 | [kg (m−3)] |
| Density of water ρ2 | 998 | [kg (m−3)] |
| Peclet number Pe = u*x*/D | 100 | [—] |
| Cahn number Cn = ε/x* | 4 | [—] |
| Reynolds number Re = ρ2x*u*/μ2 | 1447 | [—] |
| Weber number We = ρ2(u*)2x*/σ* | 1447 | [—] |
| Bond number Bo = (ρ2 − ρ1)g(x*)2/σ* | 5.4 × 10−5 | [—] |
The dimensionless NS equation is
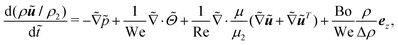 | (10) |
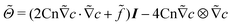 is the nondimensionalized stress tensor and ez is the unit vector in the z-direction (the direction of gravity). The incompressible constraint for the case of a small density ratio reads
is the nondimensionalized stress tensor and ez is the unit vector in the z-direction (the direction of gravity). The incompressible constraint for the case of a small density ratio reads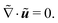 | (11) |
2.3 Calculation of surface tension
The surface tension between two immiscible fluids can be considered as the total grand chemical potential excess across the interface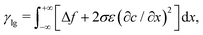 | (12) |
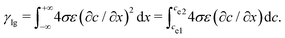 | (13) |
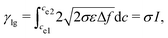 | (14) |
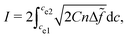 | (15) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) = εΔf/σ. By choosing appropriate parameters in the above equation, the integration is unity, i.e., I = 1. In this case, we have γlg = σ. The nondimensionalized double-well function is given as:
= εΔf/σ. By choosing appropriate parameters in the above equation, the integration is unity, i.e., I = 1. In this case, we have γlg = σ. The nondimensionalized double-well function is given as:Cn![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (c) = c (c) = c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c + (1 − c)ln(1 − c) + χc(1 − c), c + (1 − c)ln(1 − c) + χc(1 − c), | (16) |
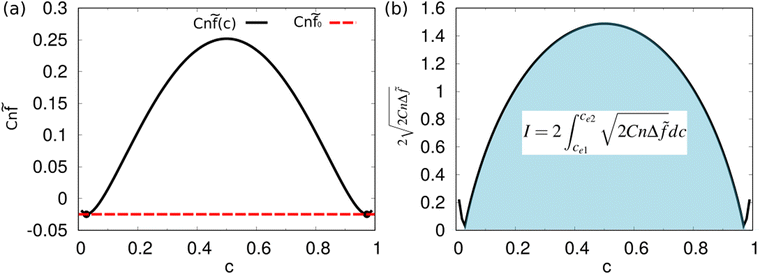 | ||
Fig. 1 (a) The free energy Cn![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) as a function of c: Cn as a function of c: Cn![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (c) = c (c) = c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c + (1 − c)ln(1 − c) + χc(1 − c) with χ = 3.78. The two highlighted points (ce1,Cn c + (1 − c)ln(1 − c) + χc(1 − c) with χ = 3.78. The two highlighted points (ce1,Cn![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (ce1)) and (ce2,Cn (ce1)) and (ce2,Cn![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (ce2)) are the free energy minimum states, corresponding to the two immiscible fluids bulk phases, respectively. (b) A schematic for the integration I (see eqn (15)), which is used to calculate the surface tension. (ce2)) are the free energy minimum states, corresponding to the two immiscible fluids bulk phases, respectively. (b) A schematic for the integration I (see eqn (15)), which is used to calculate the surface tension. | ||
2.4 The natural boundary condition
At the substrate, the free energy functional reads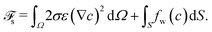 | (17) |
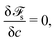 | (18) |
| 4σε∇c·n − (γgs − γls)l′(c) = 0. | (19) |
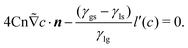 | (20) |
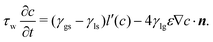 | (21) |
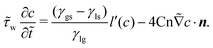 | (22) |
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w = τw/μ*x*. When
w = τw/μ*x*. When ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w is sufficiently small, the term on the left hand side can be neglected, which corresponds to a quasi-equilibrium effect, as described by eqn (21). However, a large
w is sufficiently small, the term on the left hand side can be neglected, which corresponds to a quasi-equilibrium effect, as described by eqn (21). However, a large ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w leads to a nonequilibrium effect of the contact line. The value of
w leads to a nonequilibrium effect of the contact line. The value of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w can be determined through experiments since it is dependent on the real physics of the molecular interaction at the contact line.43 This dynamic boundary condition has already been validated in our previous work and applied to analyze the nonequilibrium contact line movements of droplets under condensation and evaporation.75 To accurately model extremely low and high contact angles, we have addressed this issue in a separate paper by considering the presence of surface composition76,77 based on Cahn's theory. The present work directly employs the contact angle correction method.
w can be determined through experiments since it is dependent on the real physics of the molecular interaction at the contact line.43 This dynamic boundary condition has already been validated in our previous work and applied to analyze the nonequilibrium contact line movements of droplets under condensation and evaporation.75 To accurately model extremely low and high contact angles, we have addressed this issue in a separate paper by considering the presence of surface composition76,77 based on Cahn's theory. The present work directly employs the contact angle correction method.
The derivation of energy dissipation is provided in the ESI,† which proves the thermodynamic consistency of the present CHNS model combined with an Allen–Cahn type dynamic wetting boundary condition. The parameter τw controls the energy dissipation rate on the substrate, which will be discussed in the following.
3 Validation of the CHNS model
3.1 Validation of the CHNS model for the Young–Laplace equation and sensitivity study for mesh resolution
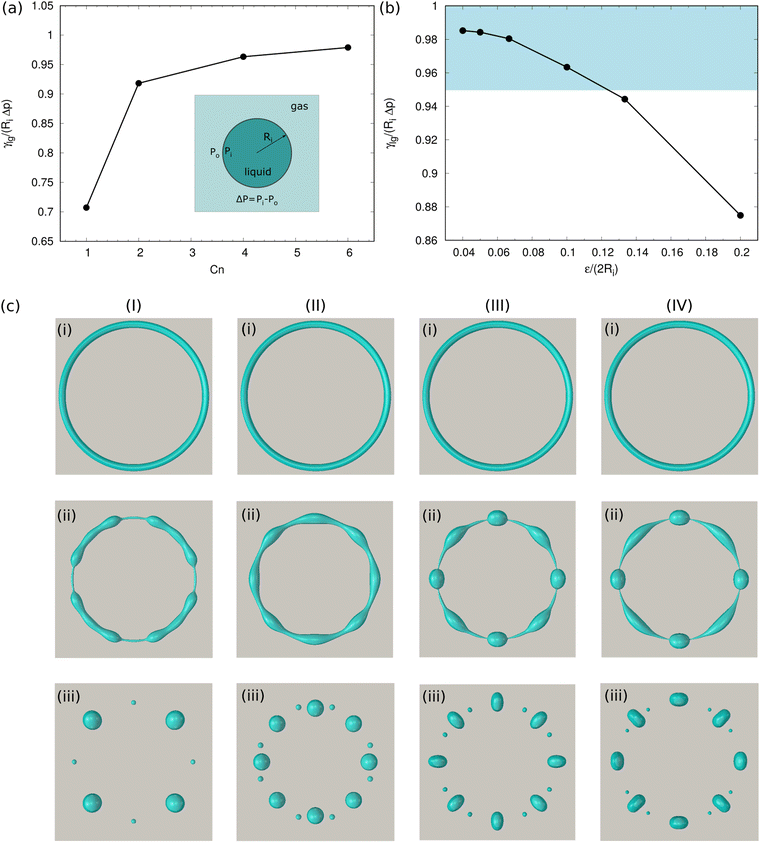
Firstly, we validate the CHNS model by comparing PF simulations with the Young–Laplace equation. We fill a two-dimensional (2D) liquid droplet with a radius Ri in the domain center, which is in equilibrium with the surrounding gas (see the schematic inset in Fig. 2(a)). At the equilibrium state, the relationship between the pressure difference Δp and the droplet radius Ri meets with the Young–Laplace equation: Δp = γlg/Ri. Here, we have Δp = pi − po with pi and po indicating the pressure in the droplet and in the surrounding gas, respectively. Fig. 2(a) displays the influence of Cahn number Cn to the simulation results, where we found Cn ≥ 4 is sufficient to guaranty the mesh resolution of the interface. In this work, Cn = 4 does not mean that there are 4 discretization points in the interface. Instead, it corresponds to 8 discretization points, which is larger enough than the conventional number of the used discretization points (around 6).47 Table S1 in the ESI,† lists the measured number of discretization points N from simulations as a function of Cn. Fig. 2(b) illustrates the simulated values of γlg/(RiΔp) for different values of ε/(2Ri). Here, we keep Cn = 4 constant and vary Ri/x* from 10 to 50 such that ε/(2Ri) changes from 0.04 to 0.2. It is observed that as ε/(2Ri) decreases, the value of γlg/(RiΔp) gradually approaches 1. When ε/(2Ri) < 0.125, the value of γlg/(RiΔp) lies in the highlighted area in Fig. 2 with a relative error smaller than 5%. To show the sensitivity of the resolution to the formation of the satellite droplets, which are the features of interest in the present work, we conduct four simulations for torus droplets dewetting on a substrate at different resolutions, as shown in Fig. 2(c); similar structures to Fig. 2(c) are applied and considered in the following with regard to the sensitivity of the resolution. By fixing the number of discretization points N = 8 (i.e., Cn = 4), we increase the resolution by decreasing the length of one mesh element. From (I) to (IV), ε/2ri (ri is the initial minor radius of the torus droplet) changes from 0.2 to 0.05, and the images (i)–(iii) illustrate the snapshots of the top view of the evolving droplets. We find that as ε/2Ri ≤ 0.067, the breakup dynamics of the torus droplet become convergent. The simulations for the torus droplets are constrained under the condition of ε/2ri < 0.067, so that the results for the formation of small liquid structures are within the numerical convergence region. Previous simulations used the corresponding values ranging from 0.005 to 0.3.39,42,78,79 Ref.42,80,81 provide guidelines to satisfy the so-called sharp interface limit when the CHNS model is applied to address interfacial problems and moving contact line problems.3.2 Validation of the CHNS model for fast spreading on homogeneous surfaces
In this section, the capability of the CHNS model is validated for simulating the fast spreading of the droplet on homogeneous surfaces. The simulation setups are according to the experimental work of ref. 82 and in Table 1, we list the related values for the simulations. In experiments, water droplets with an initial radius Ri = 0.82 mm are released on four different substrates (θeq = 3°, 43°, 117°, 180°) to observe how the surface chemistry affects the shape of the droplet as it spreads. The early stages of the droplet spreading are investigated. As illustrated in Fig. 3(a) (left part), the evolution of droplet shapes on the four different substrates is distinguished. Accordingly, we run the corresponding simulations under the same conditions to reproduce the experimental results (Fig. 3(a) (right part)). The dynamic contact angle θD < 90° is immediately formed for the superhydrophilic surface with θeq = 3°, while it maintains greater than 90° (θD > 90°) for the case θeq = 117°. For the case of θeq = 43°, θD undergoes a transition to 90°. As a reference case with θeq = 180°, the droplet keeps the nonwetting spherical shape all the time. The generation of capillary waves is perfectly reproduced for the cases of the partial wetting in the simulations. Moreover, in Fig. 3(b), we compare the time evolution of the droplet base radii for the three partial wetting cases, where the base radius Rb and time t are rescaled by the initial radius Ri and a characteristic inertial time (ρRi3/σ*)1/2, respectively. The simulation results (hollow circles) agree very well with the experiments (filled circles). Note that as a fitting parameter,![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w is accordingly adjusted for different substrates to obtain the agreements with experiments. In addition, we run two other groups of simulations with different initial radii (Ri = 0.64 mm and 0.54 mm), indicated by hollowed squares and triangles, respectively. It is found that the data in Fig. 3(b) collapses onto three master curves, each of which corresponds to a different equilibrium contact angle. This reveals that the initial stages of wetting are inertially dominated and the substrate also has an important role. Bird et al.82 explained that the contact-angle-dependent spreading possibly results from a rearrangement of liquid near the droplet surface. It should be noted that when the initial stage spreading occurs, in this very rapid wetting situation, the contact angle deviates significantly from the static equilibrium value due to the strong wall-liquid bonds in the hydrophilic surfaces.78 This can be clearly observed in the cases of θe = 3° and 43°. To address this effect, we introduce a time relaxation parameter
w is accordingly adjusted for different substrates to obtain the agreements with experiments. In addition, we run two other groups of simulations with different initial radii (Ri = 0.64 mm and 0.54 mm), indicated by hollowed squares and triangles, respectively. It is found that the data in Fig. 3(b) collapses onto three master curves, each of which corresponds to a different equilibrium contact angle. This reveals that the initial stages of wetting are inertially dominated and the substrate also has an important role. Bird et al.82 explained that the contact-angle-dependent spreading possibly results from a rearrangement of liquid near the droplet surface. It should be noted that when the initial stage spreading occurs, in this very rapid wetting situation, the contact angle deviates significantly from the static equilibrium value due to the strong wall-liquid bonds in the hydrophilic surfaces.78 This can be clearly observed in the cases of θe = 3° and 43°. To address this effect, we introduce a time relaxation parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w in the boundary condition. As a phenomenological parameter,
w in the boundary condition. As a phenomenological parameter, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w accounts for the relaxation toward the equilibrium state and it is an intrinsic material property of the substrate interacting with the wetting liquid. Yue et al.83 emphasized that in the phase-field model for simulating contact line movement, it is imperative to appropriately adjust both the mobility value M and the parameter τw in order to achieve a sharp interface limit and accurately reproduce macroscopic dynamics. Additionally, Carlson et al.43,44 successfully captured the dynamics of rapid wetting observed in the experimental work by Bird et al.82 by accounting for nonequilibrium conditions at the contact line. They identified the necessity of a phenomenological parameter, referred to as the “contact-line friction parameter,” in the wetting boundary condition, which is equivalent to the parameter τw used in our study. Through comparing simulations with experiments, we have determined the non-dimensional values of
w accounts for the relaxation toward the equilibrium state and it is an intrinsic material property of the substrate interacting with the wetting liquid. Yue et al.83 emphasized that in the phase-field model for simulating contact line movement, it is imperative to appropriately adjust both the mobility value M and the parameter τw in order to achieve a sharp interface limit and accurately reproduce macroscopic dynamics. Additionally, Carlson et al.43,44 successfully captured the dynamics of rapid wetting observed in the experimental work by Bird et al.82 by accounting for nonequilibrium conditions at the contact line. They identified the necessity of a phenomenological parameter, referred to as the “contact-line friction parameter,” in the wetting boundary condition, which is equivalent to the parameter τw used in our study. Through comparing simulations with experiments, we have determined the non-dimensional values of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w = 1500, 2600, 1, and 1 for the cases (i)–(iv). The dependence of
w = 1500, 2600, 1, and 1 for the cases (i)–(iv). The dependence of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w on the equilibrium contact angle is still an open question; apart from the surface chemistry, the surface topology also plays an important role. Physically, the parameter
w on the equilibrium contact angle is still an open question; apart from the surface chemistry, the surface topology also plays an important role. Physically, the parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w is essentially related to the slip length. The difficulty is that the slip length is generally unknown; it may depend on the surface topology, the equilibrium contact angle, the viscosity and density of the fluid, the free energy of the liquid involving the short-range van der Waals interaction between liquid and solid, electrostatic potential, etc. Samuel et al.84 reported that when the water drop initially contacts the surface, the attractive force during the wetting process on the hydrophilic surface is higher than on the hydrophobic surface. For the superhydrophobic surface, this attractive force even becomes negligible, especially for textured silicon surfaces (see Table 1 in ref. 84 for more details). This conclusion qualitatively confirms our choice of large
w is essentially related to the slip length. The difficulty is that the slip length is generally unknown; it may depend on the surface topology, the equilibrium contact angle, the viscosity and density of the fluid, the free energy of the liquid involving the short-range van der Waals interaction between liquid and solid, electrostatic potential, etc. Samuel et al.84 reported that when the water drop initially contacts the surface, the attractive force during the wetting process on the hydrophilic surface is higher than on the hydrophobic surface. For the superhydrophobic surface, this attractive force even becomes negligible, especially for textured silicon surfaces (see Table 1 in ref. 84 for more details). This conclusion qualitatively confirms our choice of large ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w for the cases (i) & (ii) and small
w for the cases (i) & (ii) and small ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w for the cases (iii) & (iv). Furthermore, the validity of the dynamical contact angle boundary condition has been proved in our previous work by comparing with an exponential power law for partial droplet spreading.75 By comparing with the experimental work of Bird et al., we demonstrated the essential nature of including the wall relaxation parameter τw in our model and to elucidate its physical significance in the context of dynamic wetting processes.
w for the cases (iii) & (iv). Furthermore, the validity of the dynamical contact angle boundary condition has been proved in our previous work by comparing with an exponential power law for partial droplet spreading.75 By comparing with the experimental work of Bird et al., we demonstrated the essential nature of including the wall relaxation parameter τw in our model and to elucidate its physical significance in the context of dynamic wetting processes.
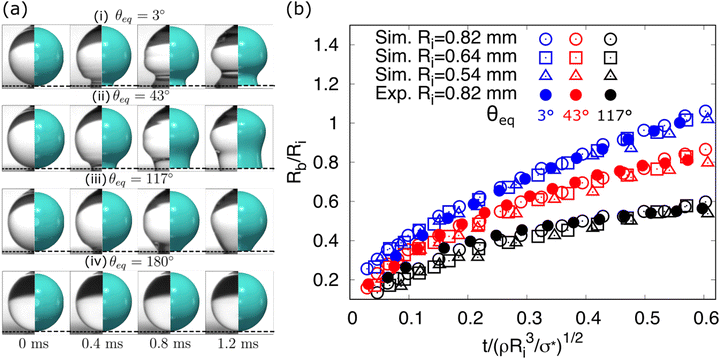 | ||
| Fig. 3 Comparison of droplet shape evolution on different substrates. (a) Snapshots of droplet side views. Left: Experimental results reproduced with permission from ref. 82. Copyright 2008 American Institute of Physics (AIP); right: present simulations. From (i) to (iv) the equilibrium contact angles are θeq = 3°, 43°, 117°, and 180°, respectively. (b) Base radius with time. Here, the base radius Rb and time t are rescaled by the initial radius Ri and a characteristic inertial time (ρRi3/σ*)1/2, respectively. The filled circles and hollow symbols denote experimental results from ref. 82 and the present simulation results, respectively. The symbols highlighted with the same color correspond to the same contact angle (blue-3°; red-43°; black-117°). | ||
In addition, we compare the simulation results with Cox's theoretical outcomes.86,87 The comparison is achieved via illustrating the functional relationship between the dynamic contact angle and capillary number. Building on this comparison with Cox's theory, we perform a sharp interface limit analysis, as elucidated in the ESI.† However, one must note that Cox's theory assumes a steady-state spreading. In the present case, the spreading of the droplet deviates from this assumption; we have discussed the details in the ESI.†
3.3 Validation of the CHNS model for droplet dynamics on mechanically heterogeneous surfaces
In this section, by using the same setups shown in Table 1, the CHNS model is further validated to simulate the droplet impacting process on a flat superhydrophobic substrate with a point-like superhydrophobic macrotexture (spherical shape with radius r = 0.2 mm). The Young's contact angles for the flat substrate and the point-like macrotextures are both set as θeq = 160°. The point-like macrotexture makes the impacting droplets rebound as rings, reducing the contact time with the substrate. Fig. 4 shows the comparison of the experimental result (top panel) from ref. 85 with the present simulation result (bottom panel). The droplet spreads quickly to form a pancake shape and then the droplet center is punctured by the point-like defect. The thin film in the center spreads outwards and comes across the retreating rim, leading to the rebounding of the droplet in a ring shape. The simulation perfectly reproduces the impacting process and shows great consistency both in the shape evolution and timescale. The irregular surface in the experiment is possibly attributed to the perturbation from the roughness of the real hydrophobic surface. This perturbation may strengthen the tendency of Rayleigh instability. In simulations, however, the substrate is ideally smooth so that only a smooth surface can be observed. Therefore, the perturbation from the substrate is less profound in simulations. | ||
| Fig. 4 Snapshots of a water droplet with initial radius Ri = 1.6 mm impacting the point-like defect on a superhydrophobic substrate at the velocity U = 1.2 m s−1 (centered impact). Top: Experimental results reproduced with permission from ref. 85. Copyright 2018 Royal Society of Chemistry; bottom: present PF simulation. The contact angle in the simulation is set as θeq = 160°. | ||
In Fig. 5, the high-angle views and cross-sections of the droplet impacting process are displayed to show the ring formation (at t = 3.7 ms), the collision between opposite rims (at t = 6.1 ms), and the rebound (at t = 6.7 ms). In this simulation, a droplet with an initial radius Ri = 1.3 mm and impact velocity U = 1.28 m s−1 is considered. The top and bottom panels are the Lattice–Boltzmann simulation from ref. 85 and the present PF simulation, respectively, where satisfactory agreement is observed.
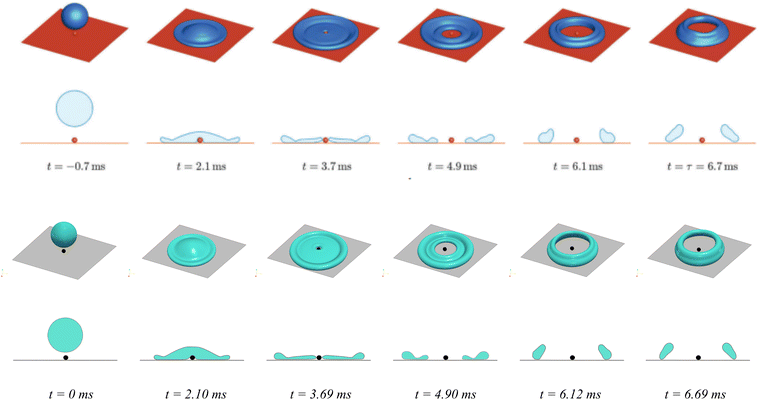 | ||
| Fig. 5 Simulation of a droplet (Ri = 1.3 mm) impacting on a substrate textured by a sphere with radius rs = 0.2 mm. The impact velocity is U = 1.28 m s−1. Top panel: Lattice–Boltzmann simulation results reproduced with permission from the work.85 Copyright 2018 Royal Society of Chemistry; bottom panel: present phase-field simulation. For each panel, high-angle views and cross-sections are shown in the first and second rows, respectively. The Young's contact angle is set as θeq = 160°. | ||
The consistency between the present PF simulation and literature85 demonstrates the robustness and justifiability of the CHNS model for simulating the dynamic evolution process of droplets on solid substrates.
4 Analysis of evolution dynamics of thin liquid films and torus droplets
After the validation of the CHNS model, the model is applied to simulate the evolution dynamics of thin liquid films and torus droplets. In order to stress the surface-tension effects, the following calculations are restricted to a Boussinesq fluid with the two phases having the same density and viscosity, i.e., ρ1 = ρ2 and μ1 = μ2. The Peclec number and Cahn number are set as Pe = 100 and Cn = 4. We set![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w = 1, unless specified otherwise. The gravity effect is neglected in the following. We systematically change Re and We, the aspect ratios of the droplets ξ, the wettability of the substrate, as well as
w = 1, unless specified otherwise. The gravity effect is neglected in the following. We systematically change Re and We, the aspect ratios of the droplets ξ, the wettability of the substrate, as well as ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w in the simulations. To obtain a quantitative description, we scrutinize the droplet evolution processes through a combination of morphological and free energy analysis.
w in the simulations. To obtain a quantitative description, we scrutinize the droplet evolution processes through a combination of morphological and free energy analysis.
4.1 Thin liquid films
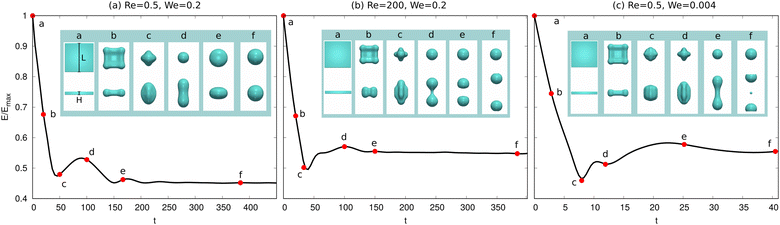
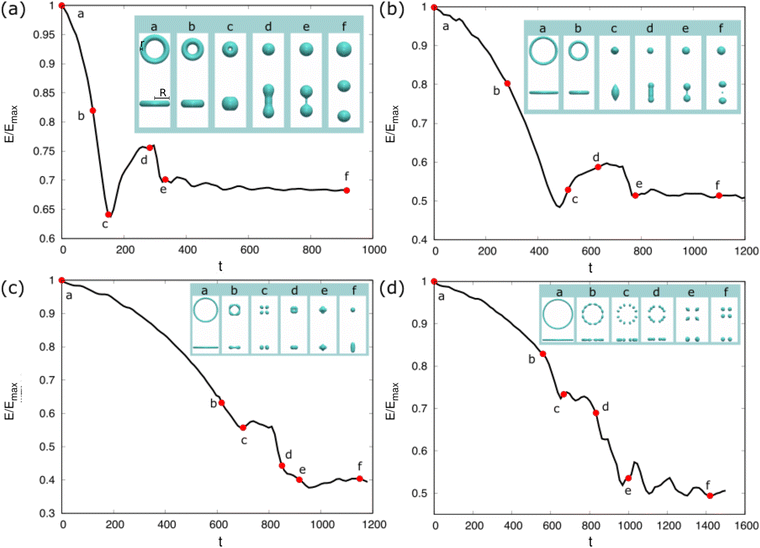
We now consider the shape evolution of a square floating thin-film with an aspect ratio ξ = 10 (width/height) under different conditions. Fig. 6 shows three typical outcomes for the floating thin-film evolution with different values of Re and We. The floating thin-film finally becomes (a) one single sphere; (b) two droplets with the same size; (c) two equally-sized droplets with a tiny satellite droplet in between. In Fig. 6(a)–(c), the solid lines illustrate the time evolution of the surface energy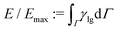 which is integrated over the droplet surface Γ and scaled by the maximum surface energy Emax. The insets indicate the morphology snapshots at different times a–f, as highlighted by the red circles on the solid lines. In all three cases, (a), (b), and (c), the surface energies of the droplets reduce rapidly and transfer into kinetic energies in the time interval a–c; the thin-films evolve into quasi-spherical shapes. In the time interval c and d, the kinetic energies are in turn transferred into surface energies, leading to a vertical elongation of the droplets and an increase in the surface area. At the late stage from d to f, the three cases are quite different from each other. In case (a), the surface energy of the droplet reduces gradually and the kinetic energy is dissipated until a spherical droplet is formed at the end. Whereas in case (b), the droplet elongation in the vertical dimension cannot be dissipated since the viscous effect becomes less pronounced for a larger Re compared with the case (a). As displayed in the inset of Fig. 6(b), a dumbbell-shaped droplet is formed at the time point d and breaks up into two smaller droplets, driven by the surface energy minimization. This breakup exhibits similarities to the Rayleigh–Plateau instability, particularly in the way that the droplet undergoes necking and subsequent separation. This similarity is evident in the characteristic formation of a thin liquid bridge and its eventual rupture, which resembles the behavior seen in the Rayleigh–Plateau instability. In case (c), Re is the same as case (a), but We is reduced from 0.2 to 0.004, which gives rise to a more profound surface tension effect. In this case, the evolution process is accelerated and the time interval from the initial state to the state with a maximum elongation in the vertical direction before breakup (i.e. a–e) is enormously shortened. The stronger inertial effect due to a smaller Weber number results in a larger elongation of the droplet than that in (a) and (b) (see the insets in Fig. 6(a)d, (b)d and (c)e). The long wavelength deformation gives rise to a nonlinear breakup of the liquid structures into two equally-sized droplets with a tiny satellite droplet in between. This phenomenon is also observed in ref. 88, in which the floating droplet is deformed into a thin-film through steady flow and thereafter the thin-film evolution is dominated by the capillary force.
which is integrated over the droplet surface Γ and scaled by the maximum surface energy Emax. The insets indicate the morphology snapshots at different times a–f, as highlighted by the red circles on the solid lines. In all three cases, (a), (b), and (c), the surface energies of the droplets reduce rapidly and transfer into kinetic energies in the time interval a–c; the thin-films evolve into quasi-spherical shapes. In the time interval c and d, the kinetic energies are in turn transferred into surface energies, leading to a vertical elongation of the droplets and an increase in the surface area. At the late stage from d to f, the three cases are quite different from each other. In case (a), the surface energy of the droplet reduces gradually and the kinetic energy is dissipated until a spherical droplet is formed at the end. Whereas in case (b), the droplet elongation in the vertical dimension cannot be dissipated since the viscous effect becomes less pronounced for a larger Re compared with the case (a). As displayed in the inset of Fig. 6(b), a dumbbell-shaped droplet is formed at the time point d and breaks up into two smaller droplets, driven by the surface energy minimization. This breakup exhibits similarities to the Rayleigh–Plateau instability, particularly in the way that the droplet undergoes necking and subsequent separation. This similarity is evident in the characteristic formation of a thin liquid bridge and its eventual rupture, which resembles the behavior seen in the Rayleigh–Plateau instability. In case (c), Re is the same as case (a), but We is reduced from 0.2 to 0.004, which gives rise to a more profound surface tension effect. In this case, the evolution process is accelerated and the time interval from the initial state to the state with a maximum elongation in the vertical direction before breakup (i.e. a–e) is enormously shortened. The stronger inertial effect due to a smaller Weber number results in a larger elongation of the droplet than that in (a) and (b) (see the insets in Fig. 6(a)d, (b)d and (c)e). The long wavelength deformation gives rise to a nonlinear breakup of the liquid structures into two equally-sized droplets with a tiny satellite droplet in between. This phenomenon is also observed in ref. 88, in which the floating droplet is deformed into a thin-film through steady flow and thereafter the thin-film evolution is dominated by the capillary force.
In summary, the evolution process for a floating thin-film is controlled by the interplay of the capillary force, the viscous force, and the inertial force. The outcome is closely related to the dissipation rate of the free energy. The Weber number We controls the time scale of the inertial and capillary dynamics while the Reynolds number Re is related to the viscous dissipation. Thus the evolution dynamics of the thin-film can be manipulated through varying We and Re. Note that in the current work, we focus on the thin-films with a relatively small aspect ratio ξ. For the thin-films with very large ξ, the rupture process is caused by capillary enhancement of fluctuations so that the rupture behavior tends to be stochastic.89
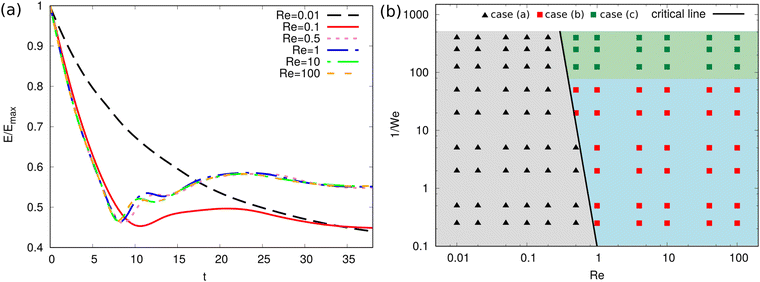
To quantify the influence of Re to the evolution dynamics of the floating thin-film, we fix We = 0.004 and aspect ratio ξ = 10 and change Re from 0.01 to 100. The surface energy evolution for different Re is displayed in Fig. 7(a). It is observed that small values of Re (Re = 0.01, 0.1) give rise to slow kinetics because of pronounced dissipation. Specifically, when Re = 0.01, the surface energy monotonously decreases and converges to a certain value. When Re = 0.1, the surface energy decreases to a local minimum value and then after a weak oscillation, it evolves to a constant value. For small Re, the final surface energy is also relatively low, which corresponds to the state of a single spherical droplet (case (a) in Fig. 6). As Re increases above 0.5, the surface energy quickly decreases and then increases with oscillations. A higher surface energy is achieved at the end, which corresponds to the case (c) in Fig. 6. Note that the curves for Re = 0.5, 1, 10, 100 almost overlap with each other, showing that when Re ≥ 0.5, the influence of the viscous effect becomes limited compared with the capillary effect for a Weber number of 0.004.
To analyze the effect of Re and We on the morphological evolution, we conduct comprehensive simulations for the evolution of the floating thin-film by varying Re and We. The results are summarized in the morphological diagram for Re vs. 1/We, where the whole region is divided into three sub-regions: (a) gray region filled with black triangles; (b) green region filled with green squares; (c) blue region filled with red squares. Here, the cases (a), (b), and (c) correspond to the outcomes of (a), (b), and (c) in Fig. 6, respectively. The black guide line divides the diagram into the non-breakup (triangle symbols) and breakup (square symbols) regions. When Re is sufficiently small (Re ∈ [0.01, 0.2]), the floating thin-film eventually evolves into a single droplet due to the large dissipation. For intermediate values of Re (Re ∈ (0.2, 1)), the end-state is dependent on We. For instance, at Re = 0.5, when 1/We ≤ 5, case (a) appears; whereas when 1/We ∈ (10, 100) and 1/We ≥ 125, cases (b) and (c) occur, respectively, due to the stronger capillary effect. When Re is sufficiently large (Re ≥ 1), the capillary effect dominants over the viscous effect in a wide range of We (1/We ∈ [0.25, 400]), only cases (b) and (c) are observed, namely, the blue region (high We) and green region zone (low We). In short, the competition of viscous effect and capillary effect determines the evolution of the floating thin-film. In the whole process, as the droplet evolves, the surface energy and kinetic energy transfer into each other, and meanwhile the viscous dissipation plays a non-negligible role until the final state is achieved.
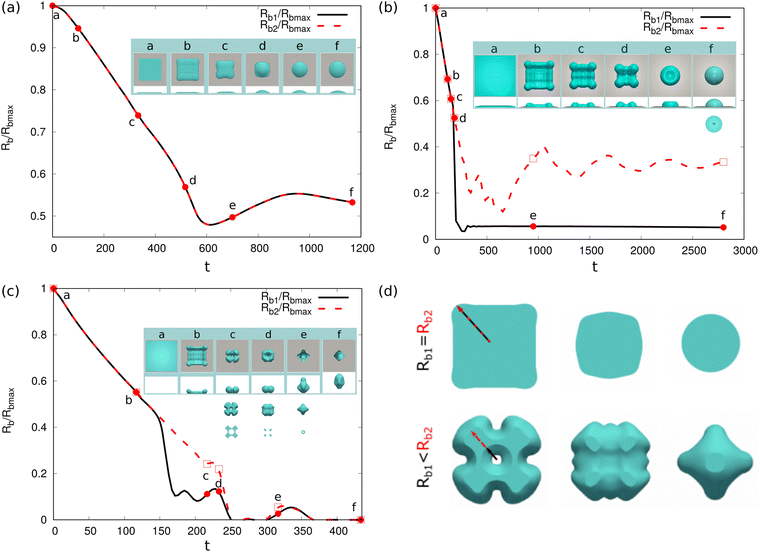
Next, we consider the thin-film dewetting process on a solid substrate. In the following, we keep (Re,We) = (10,0.2) unchanged. To quantify the effect of the wettability of the substrate on the dewetting process, we investigate the morphological transition of the thin-film with an aspect ratio ξ = 40 on the substrates with different contact angles. Fig. 8(a)–(c) display the scaled base radius Rb/Rbmax as a function of time during the dewetting on substrates with θeq = 30°, 90°, and 150°, respectively. Here, Rb and Rbmax denote the transient and maximum base radii in the diagonal direction, respectively. The solid and dashed lines indicate the time evolution for Rb1/Rbmax and Rb2/Rbmax, respectively. The notations Rb1 and Rb2 are schematically illustrated on the bottom views of the droplets in Fig. 8(d). In the top row of Fig. 8(d), there is no droplet encapsulation, thus Rb1 = Rb2. Whereas in the bottom row, the droplet encapsulation leads to two different base radii Rb1 and Rb2, as highlighted by the black and red arrows, respectively. The insets in Fig. 8(a)–(c) describe the snapshots for the dewetting process at the time points a–f, which are highlighted by the red circles and hollow squares on the solid and dashed lines. The first and second rows show the top and side views of the thin-film at different time points. It is observed that for the case of θeq = 30°, the solid and dashed lines coincide with each other, showing that there is no droplet encapsulation beneath the droplet. The base radius decreases quickly and then oscillates until the droplet reaches the equilibrium state. For the cases of θeq = 90° and 150°, the solid and dashed lines deviate from each other (the time interval d–f in (b) and the time interval b–d in (c)), which is caused by the droplet encapsulation. The droplet encapsulation can also be confirmed by the snapshots of the bottom views in the insets of Fig. 8(b) (f, the third row) and Fig. 8(c) (c, d, e, the third row). The fourth row in the inset of Fig. 8(c) illustrates the bottom cut of the droplet at the corresponding time points, which describes the profile of the base contact line. It is found that as θeq increases, the dewetting process is accelerated. This is because of the relatively low adhesion dissipation for the hydrophobic substrate and when θeq = 150°, the droplet rebounds from the substrate due to the excess kinetic energy. The acceleration of the dewetting process for the thin-film on the substrate with relatively large contact angles gives rise to the droplet encapsulation.
4.2 Torus droplets
We now turn to investigate another typical liquid structure – the torus droplets. The creation of torus droplets and the observation for its breakup were previously reported in ref. 19 and 90 in macroscopic and nano-meter scales, respectively. We set the parameters Re and We as (Re,We) = (10,0.2), and focus on the floating torus droplets as well as its interaction with a solid substrate.The aspect ratio of the floating torus droplets is defined as ξ = R/r, where R and r are the major and minor radii, respectively. When ξ ≫ 1, the breakup process can be addressed by the straight filament theory.91 When ξ is relatively small, the evolution dynamics of the fat torus droplets becomes much complex due to the existence of azimuthal curvature.92,93 Here, we consider the latter situation for torus droplets with ξ ranging from 4 to 20. The minor radius r is set as 30 for the simulations in the following. Fig. 9(a)–(d) show the time evolution of E/Emax for the torus droplets floating in a surrounding fluid with aspect ratios ξ = 4, 10, 15, 20, respectively. The insets display the top (first row) and side views (second row) for the droplet at the time points a–f. For a relatively smaller aspect ratio (ξ = 4 and 10, see Fig. 9(a) and (b)), the evolution dynamics is similar to the floating thin-film, as shown in Fig. 6(b) and (c). The surface energy decreases promptly in the initial time interval (a–c) and the ring-shaped droplet shrinks and coalesces onto a quasi-spherical shape. Thereafter, from c to d, the kinetic energy transfers into surface energy, leading to an increase in the surface energy, and the droplet is elongated in the vertical direction. In the last stage (d–f), the surface energy declines and the dumbbell-shaped droplet breaks up into two droplets (Fig. 9(a)) or into two equally-sized droplets with a tiny satellite droplet between them (Fig. 9(b)). The generation of the tiny satellite droplet is due to the fact that more surface energy is initially stored for the torus droplet with ξ = 10, and the vertical elongation is also larger.
For a relatively larger aspect ratio (ξ = 15 and 20, see Fig. 9(c) and (d)), the evolution dynamics is quite distinct. The surface energy decreases with time with small oscillations caused by the exchange of surface energy and kinetic energy. In the initial stage (a–c), the droplets shrink and undergo a breakup process in the circumferential direction due to the classical hydrodynamic instabilities. At the time point c, the torus droplets break up into a certain number (N) of separated droplets (N = 4 and 12 for ξ = 15 and 20, respectively). This number N depends on the initial aspect ratio ξ of the torus droplets and the viscosity ratio of the two liquids μ1/μ2, as discussed in the experimental work of Pairam and Fernández-Nieves.19 At a later stage (c–d), the neighboring droplets coalesce with each other due to the shrinking tendency of the droplets and the geometrical restriction.94 For the case of ξ = 15, the four small droplets coalesce into one larger droplet which then oscillates until a single spherical droplet is formed. For the case of ξ = 20, the 12 separated droplets merge into four larger droplets which further coalesce into one single droplet undergoing a similar process as in the case of ξ = 15. It is observed that the breakup (b–c) and merging (c–e) processes of the separated droplets remarkably dissipate the surface energy and finally the droplets are not able to break up in the vertical direction.
The above analysis suggests that the outcome for the evolving torus droplet is highly dependent on the competition of the shrinkage behavior and the hydrodynamic instability in the initial stage, which can be controlled through the aspect ratio ξ. For a small aspect ratio ξ, the shrinkage is relatively fast and the droplet quickly coalesces onto itself and then the vertical elongation results in the breakup. Whereas for large ξ, the hydrodynamic instability inevitably leads to the breakup of the torus droplet in the circumferential direction. The breakup and the subsequent merging process lead to a great energy lost and eventually a single droplet is formed without further breakup in the vertical direction.
We then address the morphological transition for the torus droplets on a solid substrate. To understand the evolving features of the torus droplets associated with the aspect ratio ξ and the wettability of the substrate, we systematically change ξ and the contact angles θeq in the simulations. There are typically four outcomes for the evolution process, as demonstrated in Fig. 10(a)–(d). In each panel, the top and bottom rows describe the top and side views, respectively, for the droplet shapes at different times. In Fig. 10(a), the initial aspect ratio is ξ = 4 and the contact angle is θeq = 150°. The droplet shrinks to coalesce onto itself and then rebounds from the hydrophobic substrate. In the shrinkage process, the minor radius or the tube radius r remains almost uniform along the circumferential direction. In Fig. 11(a), we plot the time evolution of the base radius Rb, normalized through the maximum base radius Rbmax. The evolution of inner and outer base radii Rb1 and Rb2 (see the inset figure) is displayed by the solid and dashed lines, respectively. From a to b and c, both Rb1 and Rb2 reduce quickly to zero, indicating that the torus droplet retreats the contact line and rebounds from the substrate. Afterwards (c–e), the droplet is vertically elongated and shortly touches the substrate before it bounces off the substrate. The insets a−f show the transparent snapshots for the side view of the droplet, which illustrates the droplet entrapment within the rebounding droplet formed by the initial torus droplet. A dedicated control of the droplet encapsulation behavior shows an essential guidance for the drug delivery technique.95
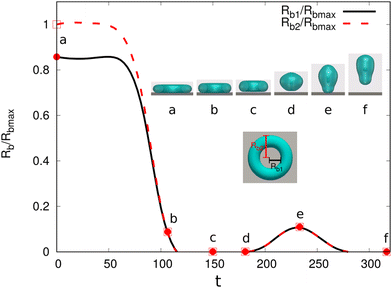 | ||
| Fig. 11 Base radii Rb1 and Rb2 (scaled by the maximum base radius Rbmax) evolution of a dewetting liquid torus with an aspect ratio ξ = 4 and θeq = 150° (case (a) in Fig. 10(a)). The insets show the simulation snapshots for different time points a–f and the schematic for Rb1 and Rb2. The transparent snapshots vividly illustrate the dynamics of droplet entrapment within the rebounding droplet formed by the initial torus droplet. | ||
In Fig. 10(b)–(d), we set the contact angle θeq as 90°, 120°, and 150°, respectively. The initial aspect ratio ξ = 20 is constant. Because of the hydrodynamic instability for the liquid structure with a large aspect ratio (ξ = 20), the torus droplet shrinks; the tube radius becomes non-uniform with time and the so-called swell and neck appear. When θeq = 90°, the necks do not break and the droplet coalesces onto itself and stays on the substrate. This is due to the relatively large adhesion dissipation appearing on the hydrophilic substrate. While for θeq = 120° and θeq = 150°, the adhesion dissipation on the substrate becomes less pronounced and the necks are morphologically unstable, leading to the formation of a number of small droplets. For θeq = 120° as shown in Fig. 10(c), tiny satellite droplets are observed after the breakup of the torus droplet (see (v) and (vi)). For θeq = 150°, the generated small droplets rebound from the substrate due to the excess kinetic energy right after the breakup. According to ref. 96, the tiny satellite droplets are caused by the sudden separation of the previous formed macro-thread and micro-thread during the evolution and the maximum length of the thread is strongly dependent on liquid viscosity. This thread structure is also observed in Fig. 10(c)(iv). From Fig. 10(b)–(d), it reveals that the wettability takes a significant role in the dewetting of the torus droplet with the same aspect ratio. The breakup process as well as the number of generated small droplets can be controlled through the wettability of the substrate.
Fig. 12 summarizes the outcomes of the torus droplet dewetting process for different ξ and θeq. In the studied ranges for ξ ∈ [4, 25] vs. θeq ∈ [60°, 165°], there are four outcomes, namely, the cases (a), (b), (c), and (d), as illustrated in Fig. 10. We find that for the torus droplets with a small aspect ratio (ξ ≤ 15), a hydrophobic substrate with θeq > 90° leads to the rebounding of droplets from the substrate without breakup (case (a)), while a hydrophilic substrate with θeq ≤ 90° results in the outcome where the torus droplet coalesces onto itself and stays on the substrate (case (b)). However, the droplets with a large aspect ratio (ξ ≥ 20) tend to break up (case (c) or (d)) due to the Rayleigh–Plateau instability. It is worth noting that a relatively hydrophilic substrate with contact angle θeq = 60°) can even give rise to the breakup of the torus droplet (case (c)) and a superhydrophobic substrate (θeq ≥ 135°) facilitates the rebounding of the small droplets generated by the breakup of the torus structures (case (d)).
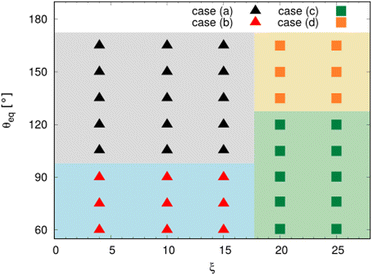 | ||
| Fig. 12 Regime diagram for the dewetting of liquid torus as a function of ξ and θeq. The cases (a)–(d) correspond to the four typical outcomes in Fig. 10. | ||
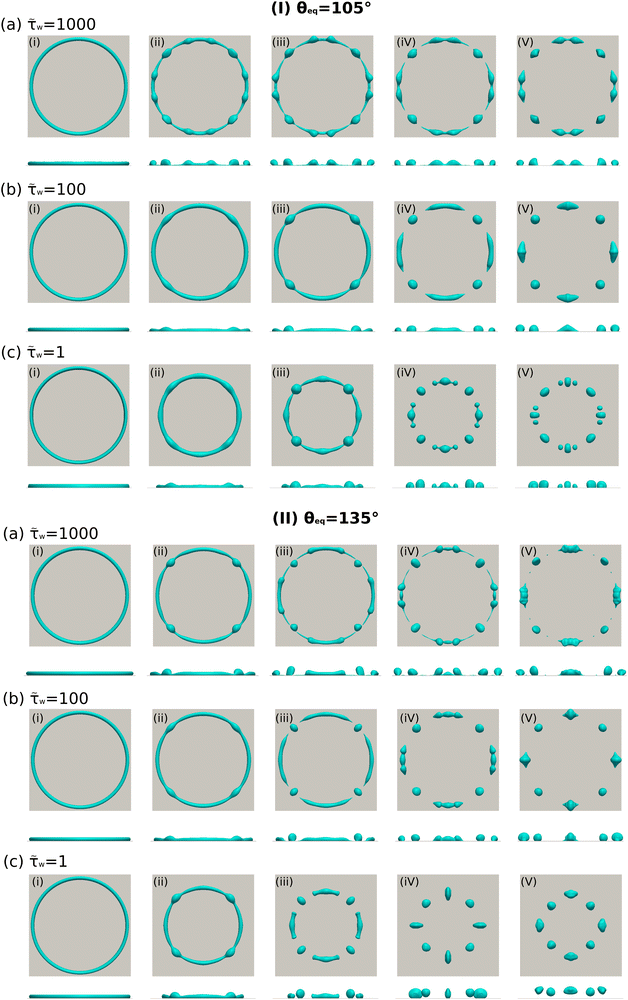
The breakup of a torus droplet on a substrate is a dynamic process, where the liquid–solid interaction force takes an important role. In the following, we will discuss the influence of the phenomenological parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w to the breakup dynamics of torus droplets on different substrates. We investigate torus droplets with a relatively large aspect ratio (ξ = 25) on substrates with two different Young's contact angles, namely, θeq = 105° and θeq = 135°. By changing
w to the breakup dynamics of torus droplets on different substrates. We investigate torus droplets with a relatively large aspect ratio (ξ = 25) on substrates with two different Young's contact angles, namely, θeq = 105° and θeq = 135°. By changing ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w from 1 to 100 and 1000, we observe the breakup processes, as illustrated in Fig. 13. For each panel of Fig. 13, the first and second rows present the top and side views of the morphological evolution, respectively. When
w from 1 to 100 and 1000, we observe the breakup processes, as illustrated in Fig. 13. For each panel of Fig. 13, the first and second rows present the top and side views of the morphological evolution, respectively. When ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w equals 1, the torus droplets show an obvious shrinking tendency and subsequently break up due to the Rayleigh–Plateau instability, as shown in Fig. 13(I)(c) and (II)(c). This result is quite similar to the cases (c) and (d) in Fig. 10. However, because of the larger aspect ratio (ξ = 25) compared to Fig. 10, the formation of satellite droplets is more profound in Fig. 13(I)(c), where the droplet pinch-off behavior is clearly recognized in the images (iv) and (v). The formation of satellite droplets can be manipulated by changing
w equals 1, the torus droplets show an obvious shrinking tendency and subsequently break up due to the Rayleigh–Plateau instability, as shown in Fig. 13(I)(c) and (II)(c). This result is quite similar to the cases (c) and (d) in Fig. 10. However, because of the larger aspect ratio (ξ = 25) compared to Fig. 10, the formation of satellite droplets is more profound in Fig. 13(I)(c), where the droplet pinch-off behavior is clearly recognized in the images (iv) and (v). The formation of satellite droplets can be manipulated by changing ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w. As presented in Fig. 13(I)(a)(b) (or (II)(a)(b)), the increase of
w. As presented in Fig. 13(I)(a)(b) (or (II)(a)(b)), the increase of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w prohibits the shrinking tendency of the torus droplets and slows down the contact line movements along the circumferential direction. In this quasi-no-slip condition, the droplet pinch-off is absent during the circumferential retraction of the droplet contact line. This result is consistent with the findings revealed by Peschka et al.97 who have investigated the droplet pinch-off behavior during the thin-film dewetting process which is influenced by the no-slip and intermediate-slip conditions. The immobility of the contact line caused by a large value of
w prohibits the shrinking tendency of the torus droplets and slows down the contact line movements along the circumferential direction. In this quasi-no-slip condition, the droplet pinch-off is absent during the circumferential retraction of the droplet contact line. This result is consistent with the findings revealed by Peschka et al.97 who have investigated the droplet pinch-off behavior during the thin-film dewetting process which is influenced by the no-slip and intermediate-slip conditions. The immobility of the contact line caused by a large value of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w leads to the thin liquid ridges, as can be observed in the images (iii) and (iv) both in Fig. 13(I)(a) and (II)(a). The breakup of these thin liquid ridges is crucial to forming satellite droplets and sub-satellite droplets. As strong evidence, we find the formation of satellite droplets in the image (v) of Fig. 13(II)(a) for a very large
w leads to the thin liquid ridges, as can be observed in the images (iii) and (iv) both in Fig. 13(I)(a) and (II)(a). The breakup of these thin liquid ridges is crucial to forming satellite droplets and sub-satellite droplets. As strong evidence, we find the formation of satellite droplets in the image (v) of Fig. 13(II)(a) for a very large ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w (
w (![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w = 1000), whereas no satellite droplet is observed in Fig. 13(II)(c) for a small
w = 1000), whereas no satellite droplet is observed in Fig. 13(II)(c) for a small ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w (
w (![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w = 1). Our simulation results are qualitatively similar to the experimental observations for the morphological evolution of the liquid ridges under the no-slip and intermediate-slip conditions. It should be noted that the formation of satellite droplets in Fig. 13(I)(c) and (II)(c) is due to different mechanisms. The former is caused by the breakup of the thin liquid ridges, thus very tiny droplets are formed. While the latter is caused by the perturbation of the capillary wave to the primary torus droplets, and the generated satellite droplets are relatively large in size.
w = 1). Our simulation results are qualitatively similar to the experimental observations for the morphological evolution of the liquid ridges under the no-slip and intermediate-slip conditions. It should be noted that the formation of satellite droplets in Fig. 13(I)(c) and (II)(c) is due to different mechanisms. The former is caused by the breakup of the thin liquid ridges, thus very tiny droplets are formed. While the latter is caused by the perturbation of the capillary wave to the primary torus droplets, and the generated satellite droplets are relatively large in size.
Our investigation shows that the parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w significantly changes the contact line dynamics during the torus droplet breakup process by controlling the interface dissipation with different slip conditions of the contact line. The value of
w significantly changes the contact line dynamics during the torus droplet breakup process by controlling the interface dissipation with different slip conditions of the contact line. The value of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w determines the slip behavior of the contact line; a very large value of
w determines the slip behavior of the contact line; a very large value of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w corresponds to the no-slip condition. By choosing appropriate values of
w corresponds to the no-slip condition. By choosing appropriate values of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w, together with the control of Young's contact angle and aspect ratio, the breakup outcome of torus droplets can be elaborately maneuvered. As already mentioned in Fig. 3, in a real liquid–solid system, the value of
w, together with the control of Young's contact angle and aspect ratio, the breakup outcome of torus droplets can be elaborately maneuvered. As already mentioned in Fig. 3, in a real liquid–solid system, the value of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w is dependent on various factors including surface chemistry, surface topology, and liquid viscosity. For instance, Carlson et al. controlled this parameter in experiments by changing liquid viscosities and surface coatings.44 Huang et al.98 used molecular dynamics simulations to study the slippage of water on various types of smooth hydrophobic surfaces. They found that the contact angle is the crucial parameter controlling water slippage and they observed that water slippage at hydrophobic surfaces shows an enormous range of values. This conclusion also motivates us to choose a wide range of
w is dependent on various factors including surface chemistry, surface topology, and liquid viscosity. For instance, Carlson et al. controlled this parameter in experiments by changing liquid viscosities and surface coatings.44 Huang et al.98 used molecular dynamics simulations to study the slippage of water on various types of smooth hydrophobic surfaces. They found that the contact angle is the crucial parameter controlling water slippage and they observed that water slippage at hydrophobic surfaces shows an enormous range of values. This conclusion also motivates us to choose a wide range of ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w for hydrophobic surfaces.
w for hydrophobic surfaces.
5 Conclusion
In this work, we adopted a CH model by using thermodynamically consistent logarithmic Flory–Huggins energy potential and order parameter dependent mobility. We coupled the Cahn–Hilliard model with Navier–Stokes equations (i.e., CHNS model) combined with dynamic wetting boundary conditions, which is rigorously proved to be consistent with the principle of energy dissipation and this model is successfully validated for simulating the spreading process of droplets on different substrates for the first time. By using the CHNS model, we present the 3D simulations of morphological evolution of two distinct liquid structures, namely, the thin-film and torus droplet floating in another liquid and sitting on a solid substrate. The influences of the key parameters including the droplet aspect ratio ξ, Re, We, the wettability of the substrate as well as the wall relaxation on the evolution dynamics are elaborated in detail.For the floating thin-film with a certain aspect ratio ξ, we find three typical outcomes for the shape evolution (Fig. 6(a)–(c)), which was rarely discussed in the literature. We explain the dynamics by analyzing the interplay of surface energy, kinetic energy, and viscous dissipation. The dimensionless numbers Re and We precisely control the viscous effect and the capillary effect, and thus the dynamic process and the outcome for the evolution of the floating thin-film can be elaborately manipulated. We obtain a regime map for the outcome as a function of Re and 1/We, which provides guidance for better control of floating thin films. For the thin-film on the substrate with certain values of aspect ratio ξ, Re, and We, the dewetting process is intimately determined by the contact angle θeq. Large θeq accelerates the dewetting process because of the low adhesion dissipation, which gives rise to the droplet encapsulation. In particular, when θeq = 150°, the thin-film retracts quickly and rebounds from the substrate, similar to the retraction and bouncing stage of an impacting droplet on a superhydrophobic substrate.99 Our investigation of thin film dewetting on substrate under different conditions shows great potential for the application of the production of monocrystalline nanostructures.100
Furthermore, we have investigated the effect of the initial aspect ratio on the shape evolution of the floating torus droplet through surface energy and morphological analysis. It reveals that the evolution dynamics is highly dependent on the competition of the shrinkage behavior and the hydrodynamic instability in the initial stage. For a small aspect ratio (ξ < 15), the shrinkage behavior is dominant and the droplet quickly merges onto itself and then becomes elongated and breaks up in the vertical direction. Whereas for a large aspect ratio (ξ ≥ 15), the hydrodynamic instability or Rayleigh–Plateau instability is important which leads to the breakup in the circumferential direction. Moreover, we consider the morphological transition for the torus droplets on the substrate associated with wettability and the initial aspect ratio ξ. We vary these two parameters and present four typical outcomes (Fig. 10(a)–(d)) in terms of ξ and θeq. The combined influence of wettability and aspect ratio for the torus droplets is summarized in a regime map, which provides a supplement to previous literature. We highlight the droplet encapsulation phenomenology in the case (a) in Fig. 10, which shall be further quantitatively explored. Nevertheless, we have identified the connection of droplet encapsulation to the surface wettability, which helps us to design functional surfaces facilitating or avoiding droplet encapsulation. We have also shown that the breakup process and the number of resulting small droplets are closely related to the wettability as well as the wall relaxation effect. By changing the wall relaxation parameter ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) w, the associated physics of slip and no-slip on the wall is scrutinized; the breakup outcome of torus droplets and the formation of satellite droplets can be elaborately maneuvered. We speculate that different numbers of droplets and satellite droplets can be generated through the Rayleigh–Plateau instability with a larger viscosity, compared with the low-viscosity used herein. However, open questions still remain. The exact number of the small droplets and satellite droplets generated on a substrate via the breakup is also determined by the influence of the viscosity ratio of the two fluids if we consider a large viscosity scenario, which deserves a dedicated study in the future. Moreover, another new direction is about the surface diffusion effect, which drives the acceleration of the dewetting process and the formation of more droplets for a large contact angle.101,102 This opens up new possibilities within the morphology transition regime diagram. The current study towards the typical liquid structures provides insight into the issues that involve dedicated control of droplet shapes and droplet dynamics, which shows broad applications in droplet-based systems, such as ink-jet printing, drug delivery systems, and microfluidic devices.
w, the associated physics of slip and no-slip on the wall is scrutinized; the breakup outcome of torus droplets and the formation of satellite droplets can be elaborately maneuvered. We speculate that different numbers of droplets and satellite droplets can be generated through the Rayleigh–Plateau instability with a larger viscosity, compared with the low-viscosity used herein. However, open questions still remain. The exact number of the small droplets and satellite droplets generated on a substrate via the breakup is also determined by the influence of the viscosity ratio of the two fluids if we consider a large viscosity scenario, which deserves a dedicated study in the future. Moreover, another new direction is about the surface diffusion effect, which drives the acceleration of the dewetting process and the formation of more droplets for a large contact angle.101,102 This opens up new possibilities within the morphology transition regime diagram. The current study towards the typical liquid structures provides insight into the issues that involve dedicated control of droplet shapes and droplet dynamics, which shows broad applications in droplet-based systems, such as ink-jet printing, drug delivery systems, and microfluidic devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Yanchen Wu is thankful for the funding of the research through the Gottfried-Wilhelm Leibniz prize NE 822/31-1 of the German research foundation (DFG). Fei Wang is grateful to the VirtMat project P09 “Wetting Phenomena” of the Helmholtz association. Impulses for the geometrical arrangements were contributed by funding in the MSE program of the Helmholtz Association (no. 43.31.01). The authors acknowledge support by the state of Baden-Württemberg through bwHPC.References
- A. Voigt, J. Fluid Mech., 2019, 878, 1–4 CrossRef CAS.
- D. Lohse, Annu. Rev. Fluid Mech., 2022, 54, 349–382 CrossRef.
- D. Vishali, J. Monisha, S. Sivakamasundari, J. Moses and C. Anandharamakrishnan, J. Controlled Release, 2019, 300, 93–101 CrossRef CAS PubMed.
- H. Li, S. Ji, X. Tan, Z. Li, Y. Xiang, P. Lv and H. Duan, Phys. Fluids, 2020, 32, 122111 CrossRef CAS.
- Y. Xiang, S. Huang, T.-Y. Huang, A. Dong, D. Cao, H. Li, Y. Xue, P. Lv and H. Duan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2282–2287 CrossRef CAS PubMed.
- J. Hartmann, M. T. Schür and S. Hardt, Nat. Commun., 2022, 13, 1–10 Search PubMed.
- H. Geng, J. Feng, L. M. Stabryla and S. K. Cho, Lab Chip, 2017, 17, 1060–1068 RSC.
- Y. A. Pishchalnikov, O. A. Sapozhnikov, M. R. Bailey, J. C. Williams Jr, R. O. Cleveland, T. Colonius, L. A. Crum, A. P. Evan and J. A. McAteer, J. Endourol., 2003, 17, 435–446 CrossRef PubMed.
- P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75 RSC.
- É. Ruiz-Gutiérrez, C. Semprebon, G. McHale and R. Ledesma-Aguilar, J. Fluid Mech., 2018, 842, 26–57 CrossRef.
- Y. Wu, F. Wang, W. Huang, M. Selzer and B. Nestler, Phys. Rev. Fluid, 2022, 7, 054004 CrossRef.
- I. U. Chowdhury, P. Sinha Mahapatra and A. K. Sen, Phys. Fluids, 2019, 31, 042111 CrossRef.
- J. A. F. Plateau, Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires, Gauthier-Villars, Paris, 1873, vol. 2 Search PubMed.
- L. Rayleigh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1892, 34, 145–154 CrossRef.
- A. A. Fragkopoulos, E. Pairam, E. Berger, P. N. Segre and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2871–2875 CrossRef CAS PubMed.
- O. Lavrenteva, B. Ee, I. Smagin and A. Nir, J. Fluid Mech., 2021, 921, A5 CrossRef CAS.
- S. Malik, O. Lavrenteva and A. Nir, J. Fluid Mech., 2021, 923, A3 CrossRef CAS.
- F. Novkoski, E. Falcon and C.-T. Pham, Phys. Rev. Lett., 2021, 127, 144504 CrossRef CAS PubMed.
- E. Pairam and A. Fernández-Nieves, Phys. Rev. Lett., 2009, 102, 234501 CrossRef CAS PubMed.
- A. A. Fragkopoulos and A. Fernández-Nieves, Phys. Rev. E, 2017, 95, 033122 CrossRef PubMed.
- A. M. Edwards, É. Ruiz-Gutiérrez, M. I. Newton, G. McHale, G. G. Wells, R. Ledesma-Aguilar and C. V. Brown, Sci. Rep., 2021, 11, 8120 CrossRef CAS PubMed.
- S. Mirjalili, S. S. Jain and M. Dodd, Center Turbul. Res. Annual Res. Briefs, 2017, 2017, 13 Search PubMed.
- B. Ambravaneswaran, E. D. Wilkes and O. A. Basaran, Phys. Fluids, 2002, 14, 2606–2621 CrossRef CAS.
- C. R. Anthony, H. Wee, V. Garg, S. S. Thete, P. M. Kamat, B. W. Wagoner, E. D. Wilkes, P. K. Notz, A. U. Chen and R. Suryo, et al. , Annu. Rev. Fluid Mech., 2023, 55, 707–747 CrossRef.
- S. Afkhami, S. Zaleski and M. Bussmann, J. Comput. Phys., 2009, 228, 5370–5389 CrossRef CAS.
- J. J. Feng, C. Liu, J. Shen and P. Yue, Model. Soft Matter, 2005, 1–26 Search PubMed.
- D. M. Anderson, G. B. McFadden and A. A. Wheeler, Annu. Rev. Fluid Mech., 1998, 30, 139–165 CrossRef.
- D. Jacqmin, J. Comput. Phys., 1999, 155, 96–127 CrossRef.
- X. Shan and H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1815 CrossRef PubMed.
- M. Kamali, J. Gillissen, S. Sundaresan and H. Van den Akker, Chem. Eng. Sci., 2011, 66, 3452–3458 CrossRef CAS.
- A. Briant, A. Wagner and J. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031602 CrossRef CAS PubMed.
- A. Briant and J. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031603 CrossRef CAS PubMed.
- X. Cai, H. Marschall, M. Wörner and O. Deutschmann, Chem. Eng. Technol., 2015, 38, 1985–1992 CrossRef CAS.
- F. Jamshidi, H. Heimel, M. Hasert, X. Cai, O. Deutschmann, H. Marschall and M. Wörner, Comput. Phys. Commun., 2019, 236, 72–85 CrossRef CAS.
- S. Popinet, https://gfs.sf.net.
- S. Popinet, https://basilisk.fr.
- S. Popinet, J. Comput. Phys., 2009, 228, 5838–5866 CrossRef CAS.
- M. J. Krause, A. Kummerländer, S. J. Avis, H. Kusumaatmaja, D. Dapelo, F. Klemens, M. Gaedtke, N. Hafen, A. Mink and R. Trunk, et al. , Comput. Math. Appl., 2021, 81, 258–288 CrossRef.
- H. Ding and P. D. Spelt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 046708 CrossRef PubMed.
- P. Yue and J. J. Feng, Phys. Fluids, 2011, 23, 012106 CrossRef.
- H. Wu, arXiv, 2021, preprint, arXiv:2112.13812, DOI:10.48550/arXiv.2112.13812.
- P. Yue, C. Zhou and J. J. Feng, J. Fluid Mech., 2010, 645, 279–294 CrossRef.
- A. Carlson, M. Do-Quang and G. Amberg, Phys. Fluids, 2009, 21, 121701 CrossRef.
- A. Carlson, G. Bellani and G. Amberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 045302 CrossRef PubMed.
- P. Johansson, A. Carlson and B. Hess, J. Fluid Mech., 2015, 781, 695–711 CrossRef CAS.
- F. Bai, X. He, X. Yang, R. Zhou and C. Wang, Int. J. Multiphase Flow, 2017, 93, 130–141 CrossRef CAS.
- M. Wörner, N. Samkhaniani, X. Cai, Y. Wu, A. Majumdar, H. Marschall, B. Frohnapfel and O. Deutschmann, Appl. Math. Modell., 2021, 95, 53–73 CrossRef.
- Y. Li, J.-I. Choi and J. Kim, Commun. Nonlinear Sci. Numer. Simul., 2016, 30, 84–100 CrossRef.
- C. Gugenberger, R. Spatschek and K. Kassner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016703 CrossRef PubMed.
- M. Doi, Soft matter physics, Oxford University Press, USA, 2013 Search PubMed.
- W. Chen, C. Wang, X. Wang and S. M. Wise, J. Comput. Phys.: X, 2019, 3, 100031 Search PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. W. Cahn, J. Chem. Phys., 1965, 42, 93–99 CrossRef CAS.
- J. D. van der Waals, J. Stat. Phys., 1979, 20, 200–244 CrossRef.
- F. Wang, A. Choudhury, M. Selzer, R. Mukherjee and B. Nestler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 066318 CrossRef CAS PubMed.
- Y. Wu, PhD thesis, Karlsruhe Institute of Technology, 2021.
- F. Wang and B. Nestler, J. Chem. Phys., 2021, 154, 094704 CrossRef CAS PubMed.
- F. Wang, P. Altschuh, L. Ratke, H. Zhang, M. Selzer and B. Nestler, Adv. Mater., 2019, 31, 1806733 CrossRef PubMed.
- Y. Mino, T. Ishigami, Y. Kagawa and H. Matsuyama, J. Membr. Sci., 2015, 483, 104–111 CrossRef CAS.
- A. Münch and E. Süli, et al. , Appl. Phys. Lett., 2015, 107, 081603 CrossRef.
- A. Voigt, Appl. Phys. Lett., 2016, 108, 036101 CrossRef.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- C. Liu and J. Shen, Phys. D, 2003, 179, 211–228 CrossRef.
- V. Khatavkar, P. Anderson, P. Duineveld and H. Meijer, J. Fluid Mech., 2007, 581, 97–127 CrossRef CAS.
- H. Bonart, C. Kahle and J.-U. Repke, J. Comput. Phys., 2019, 399, 108959 CrossRef CAS.
- J. Shen and X. Yang, SIAM J. Sci. Comput., 2010, 32, 1159–1179 CrossRef.
- V. Khatavkar, P. Anderson and H. Meijer, J. Fluid Mech., 2007, 572, 367–387 CrossRef CAS.
- J. S. Langer, Rev. Mod. Phys., 1980, 52, 1 CrossRef CAS.
- H. Zhang, F. Wang and B. Nestler, Phys. Rev. E, 2023, 108, 054121 CrossRef CAS PubMed.
- M. Ben Said, M. Selzer, B. Nestler, D. Braun, C. Greiner and H. Garcke, Langmuir, 2014, 30, 4033–4039 CrossRef CAS PubMed.
- Y. Wu, F. Wang, M. Selzer and B. Nestler, Phys. Rev. E, 2019, 100, 041102 CrossRef CAS PubMed.
- Y. Wu, F. Wang, S. Ma, M. Selzer and B. Nestler, Soft Matter, 2020, 16, 6115–6127 RSC.
- Y. Wu, M. Kuzina, F. Wang, M. Reischl, M. Selzer, B. Nestler and P. A. Levkin, J. Colloid Interface Sci., 2022, 606, 1077–1086 CrossRef CAS PubMed.
- F. Wang, Y. Wu and B. Nestler, Adv. Mater., 2023, 2210745 CrossRef CAS PubMed.
- Y. Wu, F. Wang, M. Selzer and B. Nestler, Langmuir, 2019, 35, 8500–8516 CAS.
- H. Zhang, Y. Wu, F. Wang and B. Nestler, J. Chem. Phys., 2023, 159, 164701 CrossRef CAS PubMed.
- F. Wang, H. Zhang, Y. Wu and B. Nestler, J. Fluid Mech., 2023, 970, A17 CrossRef CAS.
- D. Jacqmin, J. Fluid Mech., 2000, 402, 57–88 CrossRef CAS.
- D. Jacqmin, J. Fluid Mech., 2004, 517, 209–228 CrossRef.
- F. Magaletti, F. Picano, M. Chinappi, L. Marino and C. M. Casciola, J. Fluid Mech., 2013, 714, 95–126 CrossRef CAS.
- X. Xu, Y. Di and H. Yu, J. Fluid Mech., 2018, 849, 805–833 CrossRef CAS.
- J. C. Bird, S. Mandre and H. A. Stone, Phys. Rev. Lett., 2008, 100, 234501 CrossRef PubMed.
- P. Yue and J. Feng, Eur. Phys. J.: Spec. Top., 2011, 197, 37–46 CAS.
- B. Samuel, H. Zhao and K.-Y. Law, J. Phys. Chem. C, 2011, 115, 14852–14861 CrossRef CAS.
- P. Chantelot, A. M. Moqaddam, A. Gauthier, S. S. Chikatamarla, C. Clanet, I. V. Karlin and D. Quéré, Soft Matter, 2018, 14, 2227–2233 RSC.
- R. Cox, J. Fluid Mech., 1986, 168, 169–194 CrossRef CAS.
- H. Kusumaatmaja, E. J. Hemingway and S. M. Fielding, J. Fluid Mech., 2016, 788, 209–227 CrossRef CAS.
- L. Leal, Phys. Fluids, 2004, 16, 1833–1851 CrossRef CAS.
- E. Chatzigiannakis, N. Jaensson and J. Vermant, Curr. Opin. Colloid Interface Sci., 2021, 53, 101441 CrossRef CAS.
- J. D. McGraw, J. Li, D. L. Tran, A.-C. Shi and K. Dalnoki-Veress, Soft Matter, 2010, 6, 1258–1262 RSC.
- H. Mehrabian and J. J. Feng, J. Fluid Mech., 2013, 717, 281–292 CrossRef.
- Y. Wu, J. D. Fowlkes, P. D. Rack, J. A. Diez and L. Kondic, Langmuir, 2010, 26, 11972–11979 CrossRef CAS PubMed.
- A. G. González, J. A. Diez and L. Kondic, J. Fluid Mech., 2013, 718, 246–279 CrossRef.
- F. Wang, O. Tschukin, T. Leisner, H. Zhang, B. Nestler, M. Selzer, G. C. Marques and J. Aghassi-Hagmann, Acta Mater., 2020, 192, 20–29 CrossRef CAS.
- G. Pontrelli, E. Carr, A. Tiribocchi and S. Succi, Phys. Rev. E, 2020, 102, 023114 CrossRef CAS PubMed.
- T. A. Kowalewski, Fluid Dyn. Res., 1996, 17, 121 CrossRef.
- D. Peschka, S. Haefner, L. Marquant, K. Jacobs, A. Münch and B. Wagner, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9275–9284 CrossRef CAS PubMed.
- D. M. Huang, C. Sendner, D. Horinek, R. R. Netz and L. Bocquet, Phys. Rev. Lett., 2008, 101, 226101 CrossRef PubMed.
- D. Khojasteh, M. Kazerooni, S. Salarian and R. Kamali, J. Ind. Eng. Chem., 2016, 42, 1–14 CrossRef CAS.
- M. Naffouti, R. Backofen, M. Salvalaglio, T. Bottein, M. Lodari, A. Voigt, T. David, A. Benkouider, I. Fraj and L. Favre, et al. , Sci. Adv., 2017, 3, eaao1472 CrossRef PubMed.
- W. Jiang, W. Bao, C. V. Thompson and D. J. Srolovitz, Acta Mater., 2012, 60, 5578–5592 CrossRef CAS.
- R. Backofen, S. M. Wise, M. Salvalaglio and A. Voigt, Int. J. Numer. Anal. Model., 2019, 16, 192–209 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01553j |
| This journal is © The Royal Society of Chemistry 2024 |