Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coalescence of biphasic droplets embedded in free standing smectic A films
Christoph
Klopp
 *ab,
Torsten
Trittel
*ab,
Torsten
Trittel
 bc,
Kirsten
Harth
bc,
Kirsten
Harth
 bc and
Ralf
Stannarius
bc and
Ralf
Stannarius
 *abc
*abc
aInstitute of Physics, Otto von Guericke University Magdeburg, Universitätsplatz 2, D-39106 Magdeburg, Germany. E-mail: christoph.klopp@ovgu.de; ralf.stannarius@ovgu.de
bMARS, Otto von Guericke University Magdeburg, Universitätsplatz 2, D-39106 Magdeburg, Germany
cDepartment of Engineering, Brandenburg University of Applied Sciences, Magdeburger Straße 50, D-14770 Brandenburg an der Havel, Germany
First published on 27th December 2023
Abstract
We investigate micrometer-sized flat droplets consisting of an isotropic core surrounded by a nematic rim in freely suspended smectic A liquid-crystal films. In contrast to purely isotropic droplets which are characterized by a sharp edge and no long-range interactions, the nematic fringe introduces a continuous film thickness change resulting in long-range mutual attraction of droplets. The coalescence scenario is divided in two phases. The first one consists in the fusion of the nematic regions. The second phase involves the dissolution of a thin nematic film between the two isotropic cores. The latter has many similarities with the rupture of thin liquid films between droplets coalescing in an immiscible viscous liquid.
1 Introduction
1.1 Droplet coalescence
The coalescence of fluid droplets and bubbles has been a picturesque field of fluid mechanics over more than 100 years. Merging of droplets within a fluid environment is a ubiquitous phenomenon that has been studied for more than a century, starting with pioneering experiments by Rayleigh,1–3 Boys4 and Kaiser.5 The process occurs in manifold natural phenomena, like rain or dew drop growth, and it has considerable technological relevance6,7e.g. for ink-jet printing, self-cleaning surfaces or condensation as well as foam and emulsion technologies. Particularly, understanding the merging process of meniscus-bearing droplets on fluid interfaces or films has significant implications across various fields, from materials science to biology and engineering. It can impact processes such as emulsification, fluid mixing, in particular near fluid interfaces, and even the behavior of open-surface micro-fluidic systems.Several coalescence scenarios have been analyzed experimentally, theoretically, and by numerical simulations in 3-dimensional (3D)8–23 and two-dimensional (2D)24–34 geometries. A special problem is the coalescence of sessile droplets on surfaces.35–45 This literature list is by far not exhaustive.
The dynamic viscosities and densities of the involved fluids, the interface tension and the size of the objects decide whether an oscillatory relaxation or an overdamped or creeping relaxation towards the final shape governs the late coalescence stages. The effect is mainly characterized by the Ohnesorge number Oh.46 In the expansion of the bridge formed between the droplets at contact, inertial and viscous scaling regimes have been identified.20,47,48 Normally, the droplet fluid dominates over the contribution of the outer fluid in the bridge growth between the drops,17,32 but exceptions will be discussed later.
Besides the above-mentioned clean 3D and 2D cases and droplets on substrates, there are additional interesting geometries, most importantly the coalescence of flat liquid lenses suspended in a thin film49,50 or at fluid–fluid interfaces.51,52
The liquid lenses studied so far49–53 had no meniscus near their contact lines. However, this meniscus-free approximation is not always valid, e.g. for droplets on a liquid layer of limited depth, so that the film or pool surrounding the droplet is not plane even on large scales. Then, one expects a distance-dependent capillary attraction or repulsion, known e.g. from the (inverse) Cheerios effect.54 It may be exploited for the capillary assembly of small objects floating on a liquid surface. These complex long-range interactions between meniscus-bearing droplets introduce a complex interplay of forces. Menisci can also drastically affect the coalescence process itself, by contributing a non-negligible added volume of viscous liquid to the actual droplet. So far, the coalescence process of meniscus-bearing droplets has not been investigated.
For droplets embedded in a thin freely-suspended fluid film as considered here, the coalescence situation is simplified by the top-bottom symmetry of the system as long as gravity is not relevant. In addition, one can rely on the well-justified assumption that the surrounding air is negligible except on very small scales. Widely known examples of such films are soap films, where droplets of other liquids can be deposited and observed. These films are rather easy to prepare, but their handling requires thorough measures to prevent them from evaporation and drainage, and usually their thickness is inhomogeneous and hard to control. A presence of surfactants complicates the situation.
1.2 Droplets and islands in freely suspended smectic films
Here, we employ freely suspended liquid crystalline films in the layered smectic A phase. Their advantage is a well-controllable uniform thickness from few nanometers to micrometers in equilibrium, without drainage or evaporation. Layers are oriented parallel to the film plane, and the surface tension of smectic materials to air is only little lower than that of typical soap films. Within the film plane, there is no long-range positional molecular order, and the material practically represents a viscous fluid in 2D. By increasing the temperature, one can achieve a phase transition to less ordered phases, e.g. the nematic phase with orientational order only, or the isotropic liquid phase, depending on the specific material. The intrinsic preference of molecular layer formation in smectic phases together with the preferential molecular orientation at the smectic-air interface introduces a disjoining pressure that stabilizes the freely suspended films even in a certain range above the bulk transition temperature into a phase without long-range positional order (nematic or isotropic).55By carefully overheating the smectic films above this temperature, one can obtain droplets of the lower-ordered phase embedded in the surrounding thin and uniformly flat smectic film:56 because of the stabilizing surface-induced order, interior layers of the smectic film melt first,55 while the surfaces remain in the layered phase. The thin molten layer breaks up into droplets surrounded by a thin smectic skin. The phase transition to a nematic or isotropic phase is of first order and there is a small interface tension of the order of 0.1 mN m−1 between the material in the isotropic and the smectic phase.57 The interface tension is expexted to be even smaller between the same material in the nematic and the smectic phases. Consequently, the droplets form stable liquid lenses of typical diameters between several micrometers to tens of micrometers with small opening angles of only few degrees towards the film plane. The droplets in their quasi-equilibrium shapes do not experience attractive or repulsive interactions across the surrounding thin film unless they touch each other. The surrounding film remains flat in excellent approximation, even in presence of gravity. The enclosed liquid lenses can consist of isotropic or nematic material. These objects form an ideal system to study the coalescence of liquid lenses. In contrast to such lenses on a fluid bath,51 the droplets in smectic films are top-down mirror symmetric,58 as sketched in Fig. 1, left.
 | ||
| Fig. 1 Comparison of the shapes of isotropic, nematic and biphasic droplets in SmA films (left to right). Note that all droplets are covered by at least one smectic layer. | ||
Previous studies of such droplets in smectic films focused on their elastic interactions and their spontaneous pattern formation (e.g.31,59–64). This occurs primarily in the tilted smectic C phase, where elastic interactions in the film plane are mediated by the vector field of the c-director. But even in the smectic A (SmA) phase, which has no preferred direction in the film plane and resembles a quasi-2D isotropic liquid, interactions occur.64 The motion of micro-objects in free-standing smectic films has been exploited as well to study problems of 2D hydrodynamics.65
In free-standing smectic films, diverse coalescence scenarios of liquid inclusions can be observed. Several experimental studies dealt with the coalescence of disk-like thicker domains in the films, so-called islands,30–32 and thinner regions, so-called holes.66 It was shown that the classical model for 2D droplet coalescence,24 developed for infinitely long parallel cylinders and disregarding the surrounding fluid, only qualitatively describes the merging process. The dynamics is found to be much slower than theoretically predicted on the basis of Hopper's model.24,26,67,68 The surrounding air apparently slows down the coalescence dynamics. The flow in the film also needs to be taken into account.32 The process is still not fully understood so far.
Coalescence of droplets in these films, even though these lentil-shaped inclusions are also very flat, is qualitatively different and even more complex. The merging of droplets consisting of molten material in the isotropic phase has been studied experimentally49 and theoretically49,50,53 in previous work. Similar to the above-mentioned islands or holes, these objects lack long-range attractive interactions. Coalescence takes place only if they coincidentally touch each other during their diffusive motion in the film, or if they are deliberately brought in contact by external forces.
The coalescence of isotropic droplets in a smectic film was compared to the thin film model of liquid lens coalescence51 by Klopp et al.49 As in the island coalescence, a significant unexplained retardation of the merging dynamics was observed. Note that droplet coalescence is qualitatively different from island coalescence: The former is driven by the reduction of the surface energy of the complete liquid lenses, the latter only by a line tension around the islands.
Many smectogens do not possess a direct transition into the isotropic phase at higher temperatures but melt into the nematic phase. For nematic droplets in the films, one may expect a slower relaxation, because of additional dissipation in the droplet and possible stabilizing elastic forces of the nematic director field, but this process has not been investigated yet. Nematic droplets possess significantly different thickness profiles,63 sketched in Fig. 1: The left image shows a droplet in the isotropic phase of a material with direct SmA to isotropic transition. It consists of two sphere caps symmetric to the film plane and possesses a well-defined circular contact line, similar to immiscible liquid lenses on a bath. For a nematic droplet, a contact line towards the smectic film is usually not visible, and their cross-section perpendicular to the film plane is not a spherical cap, but the profile has an inflection point.63 Since those droplets create a slight film thickness gradient in the neighborhood, they are exposed to attractive interactions among each other.
In the present study, we employed a material (8CB) with only a narrow nematic phase range above the SmA phase. The original idea was to create nematic droplets in the film to observe their coalescence. However, the overheating technique employed to create the droplets produced biphasic droplets. These structures combine the merging of isotropic bulk droplets with the attractive interactions mediated by the nematic rim. We identified sphere cap profiles in the central part of the drops, separated from an extended meniscus towards the surrounding film area by a focusable line, and a slight kink in the height profile that is discussed in Section 3. This geometry is caused by an isotropic droplet surrounded by a nematic meniscus continuously extending to the smectic film, sketched in Fig. 1 right. The intricate coalescence dynamics of these meniscus-bearing droplets in a thin film is studied in Section 4. We conclude this paper with a comparison to literature and an outlook.
2 Materials and experimental setup
2.1 Liquid-crystalline material and film preparation
Experiments are performed with free-standing liquid-crystalline films in the smectic A (SmA) phase. These structures can be prepared with areas up to several square centimeters and thicknesses in the range between few nanometers up to micrometers. Their layered molecular structure makes them very robust against thickness fluctuations and rupture. The films can be prepared with uniform thickness on a molecular level. Thus, one can describe them as quasi-two-dimensional (2D) fluids.We prepare the freely suspended films across a circular hole (diameter of 10 mm) of our film holder (used also as pressure chamber), which is placed in a self-made heating stage with an electric power of 48 W, equipped with 3 PT1000 temperature sensors (at different positions). The liquid inclusions, here the biphasic droplets, are created by heating the complete setup above the bulk phase transition temperature from the smectic to the isotropic phase (see also phase sequence). As described below, due to the nematic rim of the droplets, they interact and attract each other until they finally merge. To enforce this process, we are also able to partially evacuate the pressure chamber (film holder) below the film to bend the film slightly downwards. Then, the droplets in the film experience an effective gravitational force and move towards the lowest region at the center of the film. Here, they interact with each other.
The heating stage with the film holder is placed under a polarizing microscope (ZEISS Axioscope 40) where we use a high-intensity mercury lamp and a green filter (λ = 546 nm) to illuminate the film with monochromatic light. We observe the coalescence processes with a Phantom VEO 710L high-speed camera with a frame rate of 1000 fps and a typical frame size of 1024 × 768 pixels (image exposure time: 70 μs). The liquid crystal material is the commercial 8CB (4-cyano-4′-octylbiphenyl) with the bulk phase sequence:
| Cr 21.5 °C SmA 33.5 °C N 40.5 °C Iso. |
The surface tension is 25.5 mN m−1 in the nematic phase (at normal anchoring of the director) and 26.2 mN m−1 in the isotropic phase, respectively. For the droplet profile determination from the reflected light intensity (see Section 2.2), we used the refractive indices for the nematic phase of no = 1.524 and ne = 1.65769 at the clearing point. The isotropic refractive index is niso = 1.568.
The emerging biphasic droplets have initial diameters between 10 μm and 280 μm. The initial heights (elevation of the apex over the film surface) range between 0.05 μm and 1.9 μm.
2.2 Observation technique
Under monochromatic illumination, we observe interference between light reflected at the top and bottom surfaces of the films or the droplets. The intensity profiles provide the local droplet heights during the coalescence process with a high accuracy (the height difference between adjacent constructive and destructive interference fringes is 45 nm).49,50 An example is shown in Fig. 2. The top image shows a profile of a coalescing droplet pair of two droplets with nearly equal sizes (the left one is only slightly larger). The clip shows a section of the film around the two droplet apexes. In this particular case, there is another droplet at the right-hand side of the coalescing droplet pair, outside the selected field of view. The nematic rims overlap slightly, thus the intensity does not drop to the film level at the right-hand side. Positions of maxima are marked by red dots, minima by green ones. The graph of this intensity profile is shown below, where the same extrema are labeled.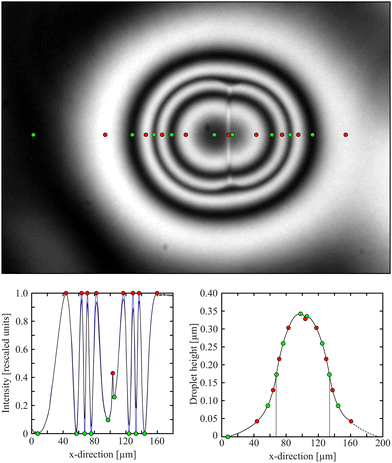 | ||
| Fig. 2 Experimental image of coalescing biphasic droplets with a bright vertical stripe indicating a nematic membrane between the isotropic cores. Colored dots mark minima (green) and maxima (red) of the intensity profile (bottom left). The intensities (blue curve) were rescaled to 0 and 1 in the minima/maxima values (black curve), and the complete droplet profile (bottom right) was retrieved using eqn (1). The small peak near the center, indicating the position of the bright line, is discussed in the text. The same coalescing pair is shown in Fig. 5, 6, 7, 8 and 9. | ||
For a complete height profile determination, we did not only use the extrema, but the complete light intensity profile between the interference fringes to calculate the full profile. As a first evaluation step, we extracted the intensity profile across a line connecting the droplet centers and normalized it, as shown in the bottom left graph. The surrounding plane film level is always lower than that of the first interference maximum. The transition of the droplet profile into the flat film is smooth (cf.Fig. 2, top), a finite contact angle is not recognizeable within our experimental resolution.
Using an equation for the reflectivity R of unpolarized light of a planar film at normal incidence,70 we determine the height profile of the isotropic core with an accuracy better than few nm.
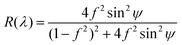 | (1) |
3 Results
3.1 Droplet height profiles
The height profile of the coalescing droplet pair in Fig. 2 along the line connecting the droplet centers (mirror symmetry axis) is shown in the bottom right graph of that figure. Most characteristic of this profile are the inflection points on both sides (highlighted by vertical lines) which characterize the boundary between convex and concave regions of the droplet surface. Near the center, there is a clear dip of roughly 10 nm that marks the border between both isotropic droplet cores. The nature of this border will be described in the next section. Droplet cross-section profiles and the positions of the inflection points for inclusions of different sizes are shown in Fig. 3.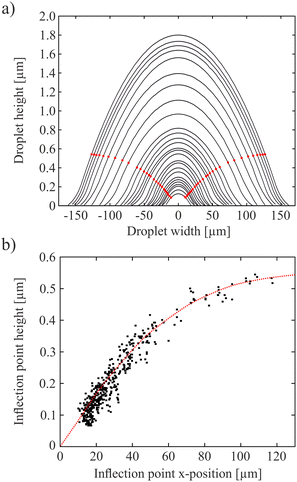 | ||
| Fig. 3 Inflection point determination: (a) selected cross-section profiles of droplets of different sizes, (b) height of the inflection point in dependence on the droplet size. | ||
In equilibrium, the surface above the isotropic droplet must be a sphere cap on each side of the film. This represents a minimum surface area at a given droplet volume. In absence of the smectic film, the isotropic droplet would have sphere shape, yet the film tension pulls this sphere to a lens consisting of two sphere caps and the side interface. The inflection indicates the position of that side boundary of the isotropic core. Beneath the surface, the nematic–isotropic border with a smaller, but non-negligible surface tension pulls the upper and lower air interfaces towards the film plane. Because of that, the upper and lower surfaces should even have a slight kink to compensate for the forces generated at the nematic–isotropic interface, but the related interface tension is obviously too small to be detectable in our droplet shapes. The isotropic-nematic interface will be regarded in approximation to be straight vertical. Strictly, it may be bent slightly outward (towards the nematic phase) since the pressure in the isotropic droplet (positive Laplace pressure because of the convex interface to air) will be larger than in the nematic region, but we cannot resolve this detail with our experimental techniques.
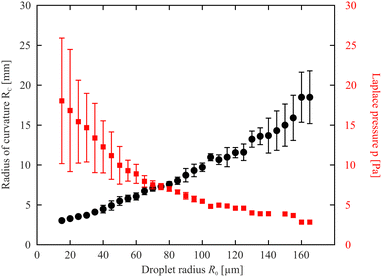
Fig. 4 shows the radius of curvature Rc of the isotropic droplet surface for droplets of different radii R0, determined from cross-section profiles such as in Fig. 3a. Here, a remark is needed concerning the parameter R0 used to compare droplet sizes: For isotropic droplets in material with a direct SmA – isotropic transition, this radius is clearly defined, there is a sharp bend and finite contact angle with the film. The situation is very different for the biphasic droplets. There is no clear feature defining the outer limits. We use the term droplet radius R0 here to characterize the distance between the outermost interference rings, thus the droplets actually extend further than R0. The exact value of R0 has therefore no physical meaning and it is not used for any evaluation purposes. It serves as a measure to compare different biphasic droplets in size. One could use other features for that, like the radius of the isotropic core, but that one is also difficult to determine exactly. An alternative would be the characterization of the droplet sizes by their heights. The radius of curvature grows almost linearly with the droplet radius, but not proportional to it because of the offset. For purely isotropic droplets in smectic films, without nematic seam, these two quantities are proportional to each other because the contact angle given by the surface tension ratios is constant.57 This is not the case here.
Underneath the concave regions of the surface, the nematic part of the inclusion is found. Here, the surface profile is more complicated. In principle, it should be possible to determine the shape of that profile by energy minimization, under the condition of a given volume of the nematic fringe, but the anchoring of the nematic director and the deflection of the director field possibly play a role as well. We have not attempted to calculate the analytical surface shape in the present study. It suffices to understand that qualitatively, the radial cross-section must be concave to minimize the surface energy.
3.2 Coalescence dynamics
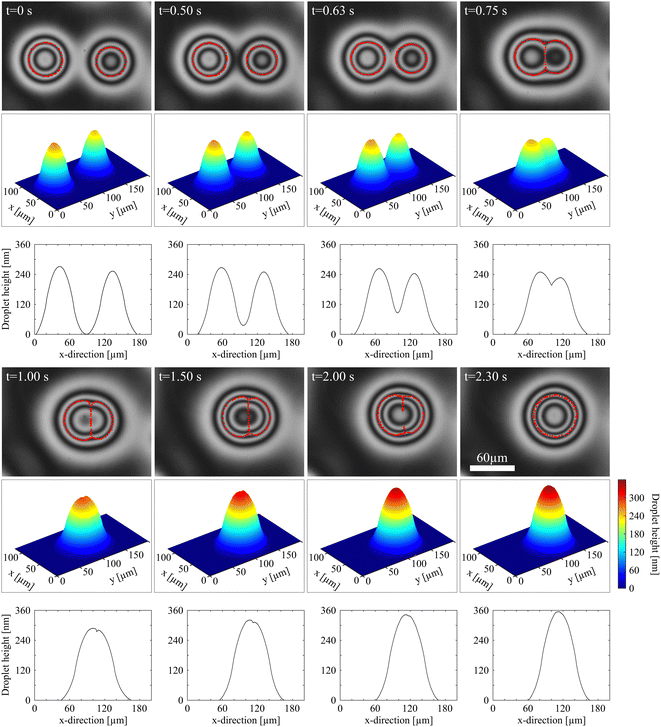
In contrast to isotropic droplets described earlier, the coalescence of the biphasic droplets starts with mutual attraction of the two partners over long distances. As soon as the neighbors experience the fringe of the other droplet, an attractive capillary force comes into effect. Fig. 5 shows a sequence of snapshots of two coalescing droplets. It is difficult to define a start of coalescence because of the smooth droplet profile without noticeable contact angle between the nematic fringe and the adjacent plane smectic film. For simplicity, we count the time t with respect to an arbitrarily chosen instant where the first bright rings of both droplets were connected (which is not very well-defined). Thus, t = 0 has no distinguished physical meaning.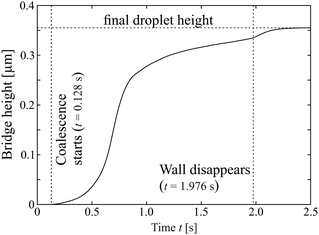 | ||
| Fig. 6 Measured time dependence of the bridge height. The step in the curve near t = 2 s indicates the vanishing film between the droplets. | ||
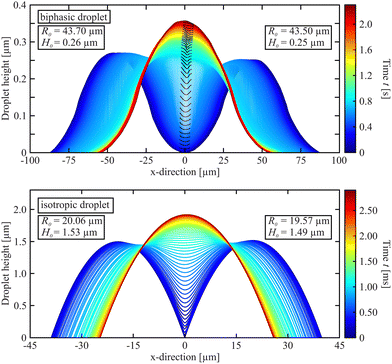 | ||
| Fig. 9 Cross-section of coalescing biphasic droplets (top) and of isotropic droplets (bottom) in comparison. The material in the top graph is 8CB (clearing point 40.5 °C), in the bottom graph it is a mixture of two phenyl–pyrimidines49 (clearing point 54 °C). The region near the nematic membrane is highlighted by black line segments in the biphasic droplet profiles. Note that biphasic droplets are much flatter than isotropic droplets. The timescales for the coalescence processes differ by three orders of magnitude. R0 and H0 are the initial radii and heights of the merging pair. | ||
The smooth character of the initial phase of coalescence is evident also in Fig. 6. There, we plotted the height of the saddle point at the line connecting the two droplet centers, which corresponds to a local minimum of that curve. One can see that its growth starts quite gradually without any noticeable signature that can be defined as the begin of coalescence.
In the image sequence of Fig. 5, one can see that the nematic regions of the droplet gradually merge. The boundary of the isotropic droplet core is not directly distinguishable during the initial phase of coalescence, until t ≈ 0.65 s when these cores reach each other. Then, the nematic region between the two isotropic cores transforms into a narrow film that does not dissolve immediately. The feature is seen in the images of Fig. 5 between t = 0.75 s and 2 s. An enlarged view of the t = 1.5 s image shows the distortion of the interference rings by the membrane.
In order to visualize the different droplet parts, we have marked the inflection points in the droplet profiles as well as the nematic membrane in the height profiles in Fig. 7 in red. The red lines encircle the isotropic cores of each droplet and they show the straight nematic film that separates both cores until it dissolves. The figure also shows the complete droplet height profiles (with the vertical coordinate strongly enlarged) and the cross-sections along the line connecting the two droplet cores.
The structure of the nematic membrane between the isotropic cores is not accessible with our optical observation technique. This refers both to the thickness and the nematic director orientation. Two effects could in principle cause the apparently shorter optical path of the reflected light in the film region. The first one is the difference of refractive indices of the isotropic and nematic phases. This difference would depend upon the alignment of the director within the nematic membrane, which is mainly determined by the anchoring of the director at the nematic–isotropic interface. With our measurement technique, this anchoring condition cannot be resolved. When one considers the observations reported in literature, there is no clear picture of which anchoring could be expected. Several publications presume a planar degenerate anchoring at the interface for some nematics (e.g. ref. 71–74), while there are also several reports of oblique anchoring (e.g. ref. 72, 75 and 76). The only report of a homologue (7CB) of the material studied here claims a tilted alignment with about 52° tilt angle. If such an oblique orientation is assumed in our nematic membranes, then the refractive index difference between the nematic and isotropic phases cannot explain the observed optical features. Only if we assume that the director is planar at the nematic–isotropic interface, oriented along the film normal, the optical appearance of the membrane could be explained by the effective lower refractive index no. The second explanation is that the nematic film might lead to a local contraction of the droplet cross-section, thus the shorter optical path in fact represents a lower droplet height. This explanation is highly unprobable, given the very low interface tension between the nematic and isotropic regions.
During a second phase of the coalescence, the nematic film gradually disappears. This process is apparently quite similar to scenarios where liquid droplets merge within another, immiscible liquid. It is analyzed in more detail in the following section.
3.3 Rupture of the nematic membrane
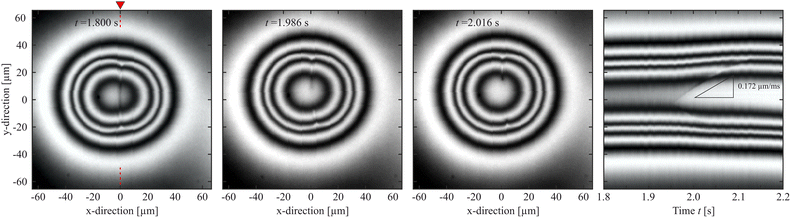
It is interesting to have a closer look at the dynamics of the dissolution of this nematic membrane separating the isotropic cores. There are two signatures of this process. The first one is the rapidly increasing height of the bridge, as seen in Fig. 6. It provides a good impression of the timescale of that process, which takes place during approximately 200 ms. The second one is the gradual disappearance of the separating line in the images. The line begins to vanish near its center first, and then the two segments retract sideward, like in a rupture. Fig. 8 shows a space-time plot of this process. While the left hand three pictures show the top view of the droplet at different instants, the right image is a space-time plot taken at the original position of the nematic membrane. It is seen that the front opens to both sides, the upper front is very clear in the plot, but the lower one is also present, less clearly seen. Each front propagates with a velocity of about 150 μm s−1, and this retraction speed appears to be rather constant in time. After 200 ms, the membrane with an original width of about 60 μm is completely dissolved.This scenario reminds very much of the rupture of other fluid membranes. Thin fluid films separating other fluids are known in very different manifestations. Often, such thin films are metastable and they are destroyed by rupture. The driving force is the reduction of the surface energy. A bursting soap film in air as a classical example was already demonstrated in 19th century by J. W. Strutt (Lord Rayleigh).77 After a hole has opened locally, the edges of the film retract, collecting the excess film material. The rupture velocity is related to the surface tension, film thickness and mass density.78–80 The released surface energy is partially converted into kinetic energy of the retracting film material, the rest is dissipated. A low viscosity of the film material does not influence the retraction speed but only the shape of the retracting edge.81 Rupturing smectic films have been studied, too.82,83
The situation is different if a thin liquid film is embedded in another, immiscible viscous fluid, like oil films in water. When two oil droplets coalesce in water84 or vice versa,85 a thin film separates the droplets immediately after contact. Similar films also form when droplets of one liquid (e.g. water/glycerol) penetrate a layer of another, immiscible liquid (e.g. silicone oil) and subsequently coalesce with a layer of the first liquid.34,86,87 The dissolution of such films determines the droplet coalescence. Aryafar and Kavehpour88 investigated the influence of the two involved viscosities on the coalescence of a droplet with a plane surface of the same liquid in that geometry. They found the retraction velocity of the thin film edges to depend on the larger of the two viscosities. A problem of these systems is that they normally involve surfactants as a third constituent, and the surfactant has a significant influence on the stability of the thin liquid film as well as on the rupture dynamics. An overview of several related scenarios can be found in a review by Kamp et al.6
In the present system, the coalescence has some similarities with that of 3D droplets in a viscous medium, yet without surfactants. Since the droplets observed here are extremely flat compared to the true 3D systems (the in-plane width of the nematic membrane is approximately 100 times larger than its height), they may be considered a 2D analogon of the former.
The present system is distinctly different from the earlier described purely isotropic droplets in smectic films49 or from flat oil droplets studied by Hack et al.51 In the latter geometries, the droplets merge without forming a thin membrane.
For the interpretation of the retraction speed of the membrane edges, we refer to the study of rupturing silicone films between mineral oil droplets by Aryafar and Kavehpour.88 They compared the measured retraction speed with a viscocapillary velocity scale Vvc = σ/μ, where σ is the interface tension of the two involved liquids and μ is a viscosity. The released surface energy is dissipated in the involved shear flow. If both the viscosities of the droplets and the film material are nearly equal, the membrane edges were found to retract with v ≈ 0.6 Vvc. Otherwise, the larger of the two viscosities dominates the retraction process. The membrane width enters this model in the prefactor, but only logarithmically.87
We can apply this estimate to our system in order to get a crude estimate of the expected membrane rupture dynamics. The viscosity of 8CB has been determined by Patrício et al.89 In the isotropic phase, μ is approximately 0.03 Pa s. In the nematic phase, the viscosity depends upon the director orientation respective to flow direction and gradient. Since it is reasonable to assume flow alignment, the value should not differ much from the isotropic viscosity (Fig. 5d in ref. 89). The interface tension was determined from the relaxation of droplet shapes by Oswald and Poy90 for the homologous cyanobiphenyl 7CB. We use their value of σ ≈ (1.1 ± 0.2) × 10−5 N m−1. Faetti et al.91,92 reported a slightly smaller value of 0.95 × 10−5 N m−1 for 8CB. Combining these data yields Vvc = (0.37 ± 0.10) mm s−1. This is a very reasonable result, in the right order of magnitude. The retraction velocity measured in our nematic membranes amounts to ≈0.47 Vvc (cf.Fig. 8). The prefactor is lower than the value 0.6 reported for the silicon oil films.88 This is reasonable, since we have to keep in mind that our geometry is nearly 2D. A shear gradient does presumably not only exist at both sides of the nematic membrane, but there is also a gradient in vertical direction. The height of the film is only few hundred nanometers (see Fig. 2). This implies more dissipation and thus a slower retraction.
4 Discussion and summary
Our experiments demonstrate that the existence of a nematic fringe around isotropic droplets in a smectic film has dramatic consequences for the coalescence process. The most striking difference between the coalescence of isotropic droplets and the biphasic droplets with isotropic core and nematic seam can be seen in Fig. 9 that visualizes the comparison of the height profiles during the merging process. The top diagram shows the central cross-sections of merging biphasic droplets, the bottom diagram is the same presentation for purely isotropic droplets. Even though the droplet pairs shown are of the same order of magnitude in size, the dynamics of the coalescence processes is completely different. With nematic seam, the process is three orders of magnitude slower, irrespective of the retardations by the formation of the nematic membrane at some point. The different materials, viscosities and temperatures may account for part of that difference, but certainly not more than one order of magnitude. The viscosity of the mixture is only 0.014 Pa s, the surface tensions are comparable.The discrepancy found here is even more surprising because it was already noted in the coalescence experiments with purely isotropic droplets that their velocity is one order of magnitude smaller than predicted.49,50 When one has a closer look at the bridge height dynamics in Fig. 6, one can at least find qualitative reasons for the slower dynamics of the biphasic droplets in comparison to the purely isotropic ones. During the first phase, when only the nematic ranges are in contact, their slopes are much smoother than those of the isotropic droplets. Note that the bridge height growth in the lubrication model49,51 is quadratic in the contact angle. Thus, the process starts much slower for the biphasic droplets. The attraction speeds up when the drops come closer and there is a short phase where the bridge grows rather fast, just before the nematic membrane is formed. Thereafter, the dynamics is determined mainly by the dissolution of that membrane, which sets the slow time scale for the complete merging.
What is understood fairly well, even quantitatively, is the dynamics of this coalescence of the isotropic cores by the retraction of the separating nematic membrane. This process appears to be very similar to the 3D coalescence of viscous droplets in a viscous medium.88 Some small quantitative corrections are required because of the nearly 2D geometry of the membrane.
It is interesting to compare our experiment with the coalescence of isotropic droplets separated by a nematic bridge of the same material in flat cells. This scenario was studied by Dolganov et al.93,94 The situation is different there because the experiments were performed in Hele-Shaw cells. The presence of the upper and lower glass plates changes the situation completely. In particular, wetting of the glass plates by either the nematic or isotropic material determines the three-dimensional structure of the nematic bridges. Furthermore, it seems that the droplets in these systems grow continuously, within the process of melting or freezing. The individual droplets cannot be considered metastable static structures but grow in size, and this is the primary reason for their contact and coalescence. Even though this is not explicitly stated there, the dynamics of droplets merging in the overheated nematic confined to a Hele-Shaw cell may be primarily governed by the droplet growth. In the present droplets on smectic films, isolated droplets that are not in contact with others can be observed quasi-statically for minutes, probably even longer, i.e. on time scales much longer than the coalescence. The volume of molten material remains practically constant during the coalescence.
Summarizing, we have shown that droplet coalescence by material with a nematic phase between the smectic A and isotropic phases is qualitatively different from that in material that has a direct smectic-isotropic transition. The nematic acts, during a decisive phase of the merging process, like a thin film separating 3D droplets merging in a viscous environment. The latter process can be monitored and its dynamics can be explained semiqualitatively, considering the viscosity and interface tension of the nematic and isotropic droplet material. The width of the nematic membrane plays no role in this merging process. It is expected to be in the submicrometer range.
A remaining open question is the overall extraordinarily slow dynamics of the coalescence scenario, compared to measurements on isotropic droplets of a phenyl–pyrimidine mixture.49 In order to confirm our interpretation, one has to exclude that the differences are indeed due to the different droplet structures and not to strongly different material parameters of the mesogenic materials. For this purpose, we would like to acknowledge one of the anonymous reviewers for the suggestion to perform experiments with the homologue 10CB (4-cyano-4′-decyl-biphenyl), which is chemically very similar to 8CB but has a direct transition into the isotropic phase without intermediate nematic phase.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the German Science Foundation (DFG) for support with project STA 425/40-3 and the German Aerospace Center (DLR) for support with project OASIS-CO (50WM2054). We thank P. V. Dolganov for stimulating discussions.References
- Rayleigh, Proc. R. Soc. London, 1879, 28, 406 Search PubMed.
- Rayleigh, Proc. R. Soc. London, 1879, 29, 71 CrossRef.
- Rayleigh, Proc. R. Soc. London, 1883, 34, 130 CrossRef.
- C. V. Boys, Philos. Mag., 1888, 25, 409 Search PubMed.
- E. Kaiser, Ann. Phys., 1894, 289, 667–683 CrossRef.
- J. Kamp, J. Villwock and M. Kraume, Rev. Chem. Eng., 2017, 33, 1–47 CrossRef.
- D. Lohse, Annu. Rev. Fluid Mech., 1999, 54, 349 CrossRef.
- S. G. Bradley and C. D. Stow, Philos. Trans. R. Soc., A, 1978, 287, 635 CrossRef.
- D. G. A. L. Aarts, H. N. W. Lekkerkerker, H. Guo, G. H. Wegdam and D. Bonn, Phys. Rev. Lett., 2005, 95, 164503 CrossRef PubMed.
- J. C. Burton and P. Taborek, Phys. Rev. Lett., 2007, 98, 224502 CrossRef CAS.
- M. Wu, T. Cubaud and C.-M. Ho, Phys. Fluids, 2004, 16, L51 CrossRef CAS.
- W. Yao, H. J. Maris, P. Pennington and G. M. Seidel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 016309 CrossRef CAS PubMed.
- U. Kornek, F. Müller, K. Harth, A. Hahn, S. Ganesan, L. Tobiska and R. Stannarius, New J. Phys., 2010, 12, 073031 CrossRef.
- J. E. Sprittles and Y. D. Shikhmurzaev, Phys. Fluids, 2012, 24, 122105 CrossRef.
- J. E. Sprittles and Y. D. Shikhmurzaev, J. Fluid Mech., 2014, 751, 480–499 CrossRef CAS.
- F. H. Zhang, M.-J. Thoraval, S. T. Thoroddsen and P. Taborek, J. Fluid Mech., 2015, 782, 209–239 CrossRef CAS.
- J. D. Paulsen, R. Carmigniani, A. Kannan, J. C. Burton and S. R. Nagel, Nat. Commun., 2014, 5, 3182 CrossRef PubMed.
- J. D. Paulsen, J. C. Burton, S. R. Nagel, S. Appathurai, M. T. Harris and O. A. Basaran, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6857 CrossRef CAS.
- J. D. Paulsen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 063010 CrossRef.
- Y. Xia and J.-L. Reboud, Chem. Eng. Res. Des., 2019, 144, 472–482 CrossRef CAS.
- X. Xia, C. He and P. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23467–23472 CrossRef CAS.
- C. R. Anthony, M. T. Harris and O. A. Basaran, Phys. Rev. Fluids, 2020, 5, 033608 CrossRef.
- P. M. Kamat, C. R. Anthony and O. A. Basaran, J. Fluid Mech., 2020, 902, A8 CrossRef CAS.
- R. W. Hopper, J. Am. Ceram. Soc., 1984, 67, C-262–264 CrossRef.
- R. W. Hopper, J. Am. Ceram. Soc., 1993, 76, 2947–2952 CrossRef CAS.
- R. W. Hopper, J. Am. Ceram. Soc., 1993, 76, 2953–2960 CrossRef CAS.
- E. K. Mann, S. Hénon, D. Langevin, J. Meunier and L. Leger, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 5708 CrossRef CAS.
- U. Delabre, C. Richard, J. Meunier and A.-M. Cazabat, EPL, 2008, 83, 66004 CrossRef.
- U. Delabre and A.-M. Cazabat, Phys. Rev. Lett., 2010, 104, 227801 CrossRef CAS.
- N. S. Shuravin, P. V. Dolganov and V. K. Dolganov, Phys. Rev. E, 2019, 100, 019901 CrossRef CAS PubMed.
- P. V. Dolganov, P. Cluzeau and V. K. Dolganov, Liq. Cryst. Rev., 2019, 7, 1 CrossRef CAS.
- Z. H. Nguyen, K. Harth, A. M. Goldfain, C. S. Park, J. E. Maclennan, M. A. Glaser and N. A. Clark, Phys. Rev. Res., 2021, 3, 033143 CrossRef CAS.
- M. Yokota and K. Okumura, J. Phys. Soc. Jpn., 2012, 81, SA015 CrossRef.
- K. Okumura, Adv. Colloid Interface Sci., 2018, 255, 64–75 CrossRef CAS.
- N. Kapur and P. H. Gaskell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 056315 CrossRef PubMed.
- A. Eddi, K. G. Winkels and J. H. Snoeijer, Phys. Rev. Lett., 2013, 111, 144502 CrossRef CAS.
- M. Irshad Khodabocus, M. Sellier and V. Nock, Adv. Math. Phys., 2018, 2018, 4906016 Search PubMed.
- M. W. Lee, D. K. Kang, S. S. Yoon and A. L. Yarin, Langmuir, 2012, 28, 3791–3798 CrossRef CAS PubMed.
- Y. Sui, M. Maglio, P. D. M. Spelt, D. Legendre and H. Ding, Phys. Fluids, 2013, 25, 101701 CrossRef.
- Y. Zhang, S. D. Oberdick, E. R. Swanson, S. L. Anna and S. Garoff, Phys. Fluids, 2015, 27, 022101 CrossRef.
- S. Moghtadernejad, M. Tembely, M. Jadidi, N. Esmail and A. Dolatabadi, Phys. Fluids, 2015, 27, 032106 CrossRef.
- S. Moghtadernejad, M. Jadidi, N. Esmail and A. Dolatabadi, Proc. Inst. Mech. Eng., Part C, 2016, 230, 793–803 CrossRef.
- P. M. Somwanshi, K. Muralidhar and S. Khandekar, Phys. Fluids, 2018, 30, 092103 CrossRef.
- M. A. Bruning, M. Costalonga, S. Karpitschka and J. H. Snoeijer, Phys. Rev. Fluids, 2018, 3, 073605 CrossRef.
- N. D. Pawar, S. S. Bahga, S. R. Kale and S. Kondaraju, Phys. Fluids, 2019, 31, 092106 CrossRef.
- M. A. Fardin, M. Hautefeuille and V. Sharma, Soft Matter, 2022, 18, 3291 RSC.
- J. Eggers, J. Lister and H. Stone, J. Fluid Mech., 1999, 401, 293 CrossRef CAS.
- J. D. Paulsen, J. C. Burton and S. R. Nagel, Phys. Rev. Lett., 2011, 106, 114501 CrossRef PubMed.
- C. Klopp, T. Trittel and R. Stannarius, Soft Matter, 2020, 16, 4607 RSC.
- C. Klopp and A. Eremin, Langmuir, 2020, 36, 10615–10621 CrossRef CAS PubMed.
- M. A. Hack, W. Tewes, Q. Xie, C. Datt, K. Harth, J. Harting and J. H. Snoeijer, Phys. Rev. Lett., 2020, 124, 194502 CrossRef CAS.
- T. Scheel, Q. G. Xie, M. Sega and J. Harting, Phys. Rev. Fluids, 2023, 8, 074201 CrossRef.
- E. S. Pikina, B. I. Ostrovskii and S. A. Pikin, Soft Matter, 2020, 16, 4591 RSC.
- D. Vella and L. Mahadevan, Am. J. Phys., 2005, 73, 817 CrossRef.
- F. Picano, P. Oswald and E. Kats, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 021705 CrossRef CAS PubMed.
- P. Cluzeau, P. Poulin, G. Joly and H. T. Nguyen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031702 CrossRef CAS.
- H. Schüring and R. Stannarius, Langmuir, 2002, 18, 9735 CrossRef.
- C. Klopp, R. Stannarius and A. Eremin, Phys. Rev. Fluids, 2017, 2, 124202 CrossRef.
- P. Cluzeau, V. Bonnand, G. Joly, V. Dolganov and H. T. Nguyen, Eur. Phys. J., 2003, 10, 231 CAS.
- C. Völtz and R. Stannarius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061702 CrossRef PubMed.
- P. Cluzeau, F. Bougrioua, G. Joly, L. Lejček and H. T. Nguyen, Liq. Cryst., 2004, 31, 365 Search PubMed.
- P. Cluzeau, F. Bougrioua, G. Joly, L. Lejček and H. T. Nguyen, Czech. J. Phys., 2005, 55, 719 CrossRef CAS.
- C. Bohley and R. Stannarius, Soft Matter, 2008, 4, 683 RSC.
- C. Klopp, T. Trittel, A. Eremin, K. Harth and R. Stannarius, Soft Matter, 2019, 15, 8156 RSC.
- A. Eremin, S. Baumgarten, K. Harth, R. Stannarius, Z. H. Nguyen, A. Goldfain, C. S. Park, J. E. Maclennan, M. A. Glaser and N. A. Clark, Phys. Rev. Lett., 2011, 107, 268301 CrossRef CAS PubMed.
- P. V. Dolganov, N. S. Shuravin and V. K. Dolganov, Phys. Rev. E, 2020, 101, 052701 CrossRef CAS PubMed.
- R. Hopper, J. Fluid Mech., 1990, 213, 349–375 CrossRef CAS.
- R. Hopper, J. Fluid Mech., 1992, 243, 171–181 CrossRef CAS.
- W. Martienssen and H. Warlimont, Springer Handbook of Condensed Matter and Materials Data, Springer-Verlag GmbH Berlin Heidelberg New York, 2005 Search PubMed.
- R. Stannarius and K. Harth, in Liquid Crystals with Nano and Microparticles, ed. J. P. F. Lagerwall and G. Scalia, World Scientific Publishing Co. Pte. Ltd., Singapore, 2015, ch. Inclusions in freely suspended smectic films Search PubMed.
- D. Langevin and M. A. Bouchiat, Mol. Cryst. Liq. Cryst., 1973, 22, 317 CrossRef.
- S. Faetti, Mol. Cryst. Liq. Cryst., 1990, 179, 217 CrossRef CAS.
- S.-D. Kim, B. Lee, S.-W. Kang and J.-K. Song, Nat. Commun., 2015, 6, 7936 CrossRef PubMed.
- K. Perera, R. Saha, P. Nepal, R. Dharmarathna, M. S. Hossain, M. Mostafa, A. Adaka, R. Waroquet, R. J. Twiegd and A. Jákli, Soft Matter, 2023, 19, 347 RSC.
- S. Faetti and V. Palleschi, J. Phys., Lett., 1984, 45, 313 CrossRef CAS.
- P. V. Dolganov and N. A. Spiridenko, Liq. Cryst., 2022, 49, 1933 CrossRef CAS.
- Rayleigh, Nature, 1891, 44, 249 CrossRef.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1959, 253, 313 Search PubMed.
- F. E. C. Culick, J. Appl. Phys., 1960, 31, 1128 CrossRef.
- A. B. Pandit and J. F. Davidson, J. Fluid Mech., 1990, 212, 11 CrossRef CAS.
- G. Sünderhauf, H. Raszillier and F. Durst, Phys. Fluids, 2002, 14, 198 CrossRef.
- F. Müller, U. Kornek and R. Stannarius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 065302 CrossRef PubMed.
- T. Trittel, T. John, K. Tsuji and R. Stannarius, Phys. Fluids, 2013, 25, 052106 CrossRef.
- M. Dudek, J. Chicault and G. Øye, Energy Fuels, 2020, 34, 110 CrossRef.
- S. Narayan, I. Makhnenko, D. B. Moravec, B. G. Hauser, A. J. Dallas and C. S. Dutcher, Langmuir, 2020, 36, 9827–9842 CrossRef CAS PubMed.
- Z. Mohamed-Kassim and E. K. Longmire, Phys. Fluids, 2004, 16, 2170 CrossRef CAS.
- A. Eri and K. Okumura, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 030601 CrossRef PubMed.
- H. Aryafar and H. P. Kavehpour, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 037302 CrossRef CAS PubMed.
- P. Patrício, C. R. Leal, L. F. V. Pinto, A. Boto and M. T. Cidade, Liq. Cryst., 2012, 39, 25 CrossRef.
- P. Oswald and G. Poy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062512 CrossRef PubMed.
- S. Faetti and V. Palleschi, J. Chem. Phys., 1984, 81, 6254 CrossRef.
- S. Faetti and V. Palleschi, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 3241 CrossRef CAS.
- P. V. Dolganov, A. S. Zverev, K. D. Baklanova and V. K. Dolganov, Phys. Rev. E, 2021, 104, 014702 CrossRef CAS PubMed.
- P. V. Dolganov, A. S. Zverev, K. D. Baklanova and V. K. Dolganov, Soft Matter, 2022, 18, 126 RSC.
| This journal is © The Royal Society of Chemistry 2024 |