Droplet jump from a particle bed

Abstract

Drop tower experiments have been performed to study droplet jump from a particle bed across a wide range of fluid viscosities. Here the droplet jumps from the particle bed in response to the apparent step reduction from terrestrial gravity to microgravity when the experiment is dropped and enters free fall. The presence of a particle layer has been found to affect contact line dissipation and the overall jumping behavior of droplets. Additionally, the study has identified the impact of the Ohnesorge number (Oh) on droplet morphology. The investigation has yielded results that not only validate a modified version of the spring-mass-damper model for droplet rebound [Jha et al., Soft Matter, 2020, 16, 7270] but also extend its applicability to previously unexplored initial conditions. In particular, the model predicts droplet jump time and velocity. Moreover, the presence of particle layers has been found to effectively eliminate contact line dissipation without introducing substantial additional forms of dissipation. Experiments have been conducted at the Dryden Drop Tower facility at Portland State University. Particle beds have been constructed using polyethylene and polystyrene poly-dispersed spheres with diameters ranging from 125–150 μm and 600–1000 μm, respectively. The beds have been created by depositing a thin layer of particles on a glass substrate. The experimental conditions have allowed the exploration of a large parameter space of Bo₀ 1.8–8.6, We 0.05–1.40, and Oh 0.001–1.900.

---

Droplet-substrate interactions may seem like a mundane occurrence in our everyday lives: from raindrops hitting the ground to water splashing in a sink. However, the study of droplet impact holds immense importance and has far-reaching implications that are yet to be fully understood. The core of works in the topic focus on drop rebound; specifically, the most fundamental scenario of droplet impact on a flat, rigid substrate.^1–3 In recent years, the body of work has been extended to include compliant substrates.⁴ Nevertheless, natural and industrial substrates are often covered with a granular substrate such as dust, sand, spores, etc. It is unclear how the presence of the latter might affect the droplet impact process. This is an exciting scientific endeavor as droplet interactions with dirty surfaces are central to understand processes including erosion,⁵ disease spread within crops,⁶ solar panel cleaning,⁷ among many others.

The impact of a droplet on a sufficiently hydrophobic substrate may be followed by the droplet rebounding from the substrate. Such a rebound can be considered in two stages. In the first stage, the droplet spreads, flattens, and reaches maximal radial extension. In the second stage, the flattened droplet retracts and rebounds from the substrate. Numerous studies have looked at water droplet rebound from superhydrophobic substrates.^8–10 Specially, Jha et al.¹ studied the rebound of viscous droplets from a super hydrophobic surface and developed a model for droplet rebound time and coefficient of restitution.

Droplet jump is physically similar in its phenomenology to the second stage of droplet rebound. The experimental procedure for droplet jump is as follows: a substrate which exhibits high liquid mobility for the test fluid is placed in the drop rig. A liquid volume is deposited on the substrate and allowed to settle to its equilibrium shape in the presence of gravity. The drop rig is released and the free fall starts, subjecting the liquid to an apparent step reduction in gravity. The liquid reorients towards its new equilibrium shape in the absence of gravity and jumps from the substrate.

Note that before the jump occurs, the droplet is in equilibrium with no internal flow which is in contrast to the case of drop rebound where a recirculating flow is present near the rim of the spreading droplet.¹¹ Attari et al.¹² studied water droplet jump from superhydrophobic substrates. Notably, they studied volumes in the range 0.04–400 ml, and showed that, by considering the change in droplet surface energy, the jump velocities could be reasonably predicted for volumes 0.5 ⪅ V_d ⪅ 2 ml. More recently, Juboori¹³ extended the data of Attari et al.¹² by considering the jump of viscous glycerol solutions. Droplet jump has been used as a mechanism to generate droplets for the study impact phenomena in drop towers.^12,14,15

When particles are added to the substrate from which the droplet jumps, the problem becomes more complex albeit closer to reality. For instance, drop impact on granular substrates has received significant attention with particular interest in crater morphology.^16–22 Marston et al.²³ Investigated the initial dynamics of liquid drop impact onto particle beds and obeserved regimes of spreading, rebound, splashing and powder ejectas. Supakar et al.²⁴ focused on the spreading of water droplets onto particle beds and subsequent formation of liquid marbles (i.e. volumes of water completely encapsulated by particles) during impact onto hydrophobic powder surfaces. They identified a variety of resulting configurations including partial coverage, full encapsulation with spherical liquid marbles, and frozen deformed liquid marbles across a broad range of parameters.

Here, droplet jump from a particle bed is investigated. Drop tower experiments are performed for two different particle sizes. The drop rebound model of Jha et al.¹ is extended to droplet jump from a particle bed and shown to be in agreement with experiments. The effects of the particle bed are discussed, including contact line dissipation during the retraction phase of droplet jump as well as particle size effects.

This investigation provides a unique platform to explore a large range of dimensionless parameters relevant to the problem via a drop tower. The presented experiment provides an ideal scenario to study fundamental drop jump behavior. Consider a droplet of fluid with density ρ, surface tension γ, and dynamic viscosity μ deposited on substrate which provides high droplet mobility. The droplet reaches a somewhat flattened equilibrium shape under the influence of terrestrial gravitational acceleration g₀. If the system is exposed to a step reduction in gravity, the flattened droplet will reorient producing a force normal to the substrate surface. In this scenario, droplet jump from the substrate may occur as a droplet of radius R traveling with velocity v. This droplet jump process can be characterized by three dimensionless groups: Bond number Bo₀ = ρg₀R²/γ, Weber number We = ρRv²/γ, and Ohnesorge number .

Jha et al.¹ developed a model for the rebound of viscous droplets from a superhydrophobic surface which showed good agreement with experiments. Here, this model is revisited to account for new initial conditions to predict the velocity of a droplet jump. The model considers the droplet as a spring-mass-damper system, with each component associated with surface tension, droplet mass, and viscosity, respectively.

The particle beds are constructed with either polyethylene or polystyrene poly-dispersed spheres with diameters in the ranges 125–150 μm and 600–1000 μm, respectively. The particle bed is created by depositing a thin layer of particles on a slightly concave 50 mm diameter glass substrate. For the larger particles, the bed consists of a single layer of particles. For the smaller particles, a mound of particles is deposited in the middle of the concave lens and spread by compressing the mound with a convex lens of the same curvature until the particles have spread to a layer 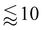particles thick. The glass substrate is cleaned with ethanol before every test. Compared to previous studies with deep particle beds,^{16–20,22–25} the thin layer of particles on top of the rigid glass substrate provides minimal compliance during the droplet jump. The liquids used to form droplets consist of water-glycerol mixtures with viscosity 1–1410 mPa s and surface tension 63–72 mN m⁻¹. Drop volumes are 0.2–2.0 ml. The fluid is delicately deposited on the particle bed before each test using a syringe. Note that if done carelessly, the liquid would push the particles aside, touch the hydrophilic base substrate, and spread on the base substrate displacing the particles and creating a puddle.

These experimental conditions allow the exploration of the problem in the following parameter ranges: Bo₀ 1.8–8.6, We 0.05–1.40, and Oh 0.001–1.900. Note that, these experiments include jumps up to Oh = 1.9, over twice the parameter range of previous studies.^1,8–10

All experiments are performed at the Dryden Drop Tower (DDT) facility at Portland State University. The DDT is a safe, low-cost, high-rate facility located in the atrium of an engineering building on campus. The experimental apparatus is mounted to an aluminum chassis, or ‘drop rig’, which hangs inside the DDT drag shield before each drop. During a drop, the rig and drag shield are released simultaneously and do not make contact throughout the microgravity period of the drop; note that because the rig is enclosed in the drag shield, it is largely protected from aerodynamic drag during free fall. The drag shield and experiment rig fall 22 m providing 2.1 s of high quality low-gravity g < 10⁻⁴g₀. Additional information can be found in Wollman.²⁶

Experiments are imaged at 60 fps using a consumer-grade camera (Panasonic, HC-WX970) or, when faster acquisition was needed, 300 fps using a high speed camera (Kron Technologies, Chronos 2.1-HD). A diffuse LED array is adopted to backlight the phenomena, as it has been done extensively by our group.^14,27,28 Images from a typical drop tower test are shown in Fig. 1. Finally, droplet positions are determined by fitting an ellipse to the droplet and recording the centroid position using image analysis software Fiji.²⁹ Maximum uncertainty for the velocity is 0.03 cm s⁻¹.

Fig. 1 Montage from a drop tower test showing a 1.0 ml droplet jumping from a bed of 125–150 μm polyethylene particles. A circular region of clean glass where the particles have been carried away by the droplet is clearly visible. Particles which have detached from the droplet are visible after the third frame.

The droplet jump is modeled as a mass-spring-damper system. A diagram of the system considered is provided in Fig. 2. The mass is taken as the droplet mass, neglecting any attached particle mass. and the spring constant is assumed as the surface tension of the fluid, γ. A scaling argument for the viscous dissipation denoted as 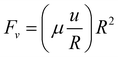.¹ Therefore, the damping coefficient is μR. The free length of the ‘spring’ is 2R. The equation of motion can then be written as:

mr̈ +μRṙ + γr = 0, (1)

where r designates drop deformation and dot(s) derivative(s) with respect to time.

Fig. 2 Diagram depicting how the droplet is modeled as a spring-mass-damper system with stiffness γ, damping μR, mass m, and free length 2R. Left: the initial condition of the droplet under terrestrial gravitational acceleration g₀ with height 2l_c. Right: droplet in a spherical geometry so the spring is uncompressed (r = x= 0).

For the relatively large fluid volumes studied here, the initial gravitational acceleration, g₀ = 9.81 m s⁻², induces a body force that is significant compared to surface tensions as revealed by the Bond number Bo₀ = (R/l_c)² > 1, where l_c is the capillary length and Δρ is the density difference between the liquid and gas phase. As a result of the balance between gravity and surface tension, the droplets adopt a puddle or disk shape with a height of 2l_c when deposited onto the particle bed. Therefore, the initial condition for drop deformation is r = −2(R − l_c). The second initial condition is ṙ = 0 as the drop initially being completely static without any internal flow, which may not be the case for a rebounding droplet.¹¹

Eqn (1) is non-dimensionalized by scaling the length by the drop radius R, and the time by the inertio-capillary time scale t₀ ≡ (m/γ)^1/2 yielding:

ẍ + Ohẋ + x = 0, (2)

where x ≡ r/R is the dimensionless deformation. The initial conditions become x = (4/Bo₀)^1/2 − 2 and ẋ = 0. It is noted that with this non-dimensionalization ẋ ≡ We. The solutions to eqn (2) for x(Oh, Bo₀) and ẋ(Oh, Bo₀) are the product of exponentially decaying sine and cosine functions.

One interpretation of the solution to eqn (2) is that the droplet detaches from the surface when the spring reaches its free length. Such an interpretation would lead to a jump time of a quarter cycle or:

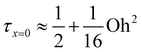Performing a series expansion of Eqn 3 yields . Taking the pre-factor of Oh² as a free parameter, the experimental data can be fitted to the equation resulting in a jump time:This equation is plotted in Fig. 3 along with the experimental data. This equation is exactly one half the rebound time found by Jha et al.¹ Such a result is expected since the experiments presented here do not include the spreading phase of droplet rebound. Notably, no additional dissipation is being introduced by the presence of the particle raft.

Fig. 3 Experimental data for non-dimensional jump time compared against τ_x=0 from eqn (4).

The droplet morphology at the jump time provides insight to the error in the the prediction of eqn (4). The error in the model can be explained by considering the droplet morphology and the moment of jumping compared to the model assumption of a spherical droplet. With reference to Fig. 4, it is shown that for droplets with small Oh the droplet leaves the substrate as a prolate droplet. This larger droplet extension before leaving the substrate explains the larger jump time compared to the model. Furthermore, as Oh is increased there is a transition in morphology from a prolate droplet to an oblate droplet. In particular, at Oh ∼ 1.0, Fig. 4 shows a oblate drop jump, such a jump is accompanied by an over-prediction of the jump time. At these large viscosities, droplet mobility can be reduced even on superhydrophobic substrates due to sticking/pinning of the liquid on the substrate.¹³ The details of the droplet morphology are not captured by the presented model, but these observations suggest valuable future work.

Fig. 4 Images from drop tower tests showing the moment the droplet detaches from the substrate for Oh ∼ 0.001, 0.1, 1.0 increasing from left to right.

A prediction for the Weber number is evaluated as ẋ(τ_x=0). A comparison between the predicted Weber number and the measured Weber number is presented in Fig. 5 Overall, droplet jumps from particle beds tend to exhibit Weber numbers closer to the predicted Weber number. A comparison between the predicted Weber number and the measured Weber number, including data for Oh and Bo, is presented in Fig. 6. Agreement is shown across the full parameter range. It is shown that experimental Weber numbers approach zero near the critical value of Oh = 2 where the system becomes overdamped and viscosity is expected to suppress jumping. The model shows a shift from slight We over-prediction for Bo₀ < 5 to a slight under-prediction for Bo₀ > 5. Additionally, droplet jump Weber numbers are slightly smaller for jumps from the larger particles.

Fig. 5 Drop tower data for jump Weber number compared against the predictive model. Circles correspond to droplet jump from a particle bed and square markers correspond to droplet jump from a superhydrophobic surface.^12,13

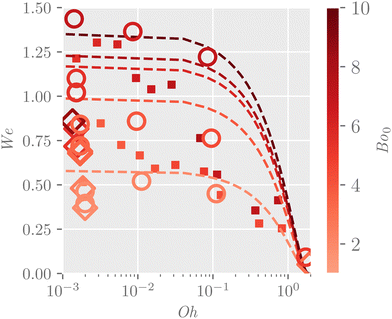Fig. 6 Drop tower data for jump Weber number compared against the predictive model. Hollow markers are experimental data for droplet jump from a particle bed. Circles and diamond markers correspond to d_p = 125–150 μm and 600–1000 μm, respectively. Square markers are experimental data from Attari et al.,¹² Juboori¹³ for droplet jump from a superhydrophobic surface. Lines are solutions to We(τ_x=0) for Bo₀ = 2,4,6,8,10 to assist visual inspection.

The data from Attari et al.¹² and Juboori¹³ is included for reference in Fig. 6. For water droplets, Oh ≈ 10⁻³, jump from a particle bed shows similar behavior to water jump from a superhydrophobic surface with resulting jump Weber number range of 0.4–1.4. When considering more viscous fluids, the data of Juboori¹³ shows that drop jump velocities decrease above Oh ≈ 10⁻². The data for droplet jump from a particle bed shows consistently higher jump velocities that jump from a superhydrophobic surface. Additionally, a less steep decrease in jump velocities in response to increasing fluid viscosity is observed. Contact line dissipation and stick-slip behaviors of viscous aqueous glycerol solutions significantly decrease the dewetting velocity of a droplet, even in superhydrophobic surfaces. This investigation undoubtedly shows that when a droplet jumps from a particle bed, dewetting is no longer required and these sources of dissipation are avoided. It is also interesting to note that the presence of the particle raft does not impede this energy transfer.

The droplet surface area initially resting on the particles increases with droplet volume because the puddles have an approximately constant height, H = 2l_c. For a given area in contact with the particle bed, the mass carried away by the droplet when the jump occurs is greater for larger diameter particles. As expected, the partially wetting particles remain largely in a particle raft as the droplet travels away from the substrate, see Fig. 1. The raft does not significantly alter the geometry of the oscillating droplet as it travels away from the substrate. Further study into a greater range of particle wettability would be interesting but is beyond the scope of this work.

The first investigation of droplet jump from a particle bed has been presented. This study sheds light on the accuracy of the spring-mass-damper model of droplet jump for a wide range of fluid viscosities. The presence of the particle layer is shown to effectively remove contact line dissipation while not introducing any significant additional forms of dissipation. The effect of the Ohnesorge number on the morphology of the jumping droplet is identified. In addition to the larger viscosity range, the results match the model of Jha et al.¹ even for the unique initial conditions for the droplets in this study.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. Cardin is supported by NASA Space Technology Research Fellowship (NSTRF) – Grant No. 80NSSC19K1191. F. Cabrera and R. B. Cal are supported by the National Science Foundation – Grant No. NSF-CBET-2223235 and NSF-CBET-2224469.

References

1. A. Jha, P. Chantelot, C. Clanet and D. Quéré, Soft Matter, 2020, 16, 7270–7273.
2. B. Zhang, V. Sanjay, S. Shi, Y. Zhao, C. Lv, X.-Q. Feng and D. Lohse, Phys. Rev. Lett., 2022, 129, 104501.
3. Y. Wang, Y. Zhao, L. Sun, A. A. Mehrizi, S. Lin, J. Guo and L. Chen, Langmuir, 2022, 38, 3860–3867.
4. R. E. Pepper, L. Courbin and H. A. Stone, Phys. Fluids, 2008, 20, 082103.
5. P. Sharma, S. Gupta and W. Rawls, Soil Sci. Soc. Am. J., 1991, 55, 301.
6. T. Gilet and L. Bourouiba, J. R.Soc., Interface, 2015, 12, 20141092.
7. G. Hassan, B. S. Yilbas, S. Bahatab, A. Al-Sharafi and H. Al-Qahtani, Sci. Rep., 2020, 10, 14746.
8. D. Richard, C. Clanet and D. Quéré, Nature, 2002, 417, 811.
9. D. Bartolo, C. Josserand and D. Bonn, J. Fluid Mech., 2005, 545, 329.
10. A.-L. Biance, F. Chevy, C. Clanet, G. Lagubeau and D. Quéré, J. Fluid Mech., 2006, 554, 47.
11. C. Clanet, C. Béguin, D. Richard and D. Quéré, J. Fluid Mech., 2004, 517, 199–208.
12. B. Attari, M. Weislogel, A. Wollman, Y. Chen and T. Snyder, Phys. Fluids, 2016, 28, 102104.
13. T. A. Juboori, PhD thesis, 2021.
14. K. Cardin, C. Josserand and R. B. Cal, Phys. Rev. Fluids, 2023, 8, 043601.
15. M. M. Weislogel, J. C. Graf, A. P. Wollman, C. C. Turner, K. J. T. Cardin, L. J. Torres, J. E. Goodman and J. C. Buchli, npj Microgravity, 2022, 8, 16.
16. H. Katsuragi, Phys. Rev. Lett., 2010, 104, 218001.
17. G. Delon, D. Terwagne, S. Dorbolo, N. Vandewalle and H. Caps, Phys. Rev. E, 2011, 84, 046320.
18. H. Katsuragi, J. Fluid Mech., 2011, 675, 552–573.
19. H. N. Emady, D. Kayrak-Talay and J. D. Litster, AIChE J., 2012, 59, 96–107.
20. E. Nefzaoui and O. Skurtys, Exp. Therm. Fluid Sci., 2012, 41, 43–50.
21. R. Zhao, Q. Zhang, H. Tjugito and X. Cheng, Proc. Natl. Acad. Sci., 2014, 112, 342–347.
22. S.-C. Zhao, R. de Jong and D. van der Meer, Soft Matter, 2015, 11, 6562–6568.
23. J. Marston, S. Thoroddsen, W. Ng and R. Tan, Powder Technol., 2010, 203, 223–236.
24. T. Supakar, M. Moradiafrapoli, G. Christopher and J. Marston, J. Colloid Interface Sci., 2016, 468, 10–20.
25. E. J. Long, G. K. Hargrave, J. R. Cooper, B. G. B. Kitchener, A. J. Parsons, C. J. M. Hewett and J. Wainwright, Phys. Rev. E, 2014, 89, 032201.
26. A. Wollman, Capillarity-Driven Droplet Ejection, Portland State University Library, 2000.
27. F. Cabrera, M. Z. Sheikh, B. Mehlig, N. Plihon, M. Bourgoin, A. Pumir and A. Naso, Phys. Rev. Fluids, 2022, 7, 024301.
28. K. Cardin, S. Wang, O. Desjardins and M. Weislogel, Phys. Rev. Fluids, 2021, 6, 014003.
29. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.

---