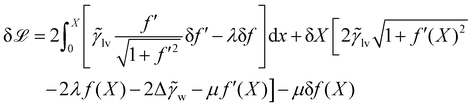Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Partial and complete wetting of droplets of active Brownian particles
Francesco
Turci
 *a,
Robert L.
Jack
bc and
Nigel B.
Wilding
*a,
Robert L.
Jack
bc and
Nigel B.
Wilding
 a
a
aH. H. Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK. E-mail: f.turci@bristol.ac.uk
bDepartment of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
cYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
First published on 7th February 2024
Abstract
We study wetting droplets formed of active Brownian particles in contact with a repulsive potential barrier, in a wedge geometry. Our numerical results demonstrate a transition between partially wet and completely wet states, as a function of the barrier height, analogous to the corresponding surface phase transition in passive fluids. We analyse partially wet configurations characterised by a nonzero contact angle θ between the droplet surface and the barrier including the average density profile and its fluctuations. These findings are compared with two equilibrium systems: a Lennard-Jones fluid and a simple contour model for a liquid–vapour interface. We locate the wetting transition where cos(θ) = 1, and the neutral state where cos(θ) = 0. We discuss the implications of these results for possible definitions of surface tensions in active fluids.
1 Introduction
Active matter systems display a wide range of surprising phenomena in their non-equilibrium steady states. Among the simplest active systems are fluids comprised of self-propelled particles without aligning interactions, which are known as scalar active matter.1–3 Many such systems exhibit motility-induced phase separation (MIPS),4 which resembles equilibrium coexistence of dense and dilute fluid phases. However, the interfacial properties of these active fluids phases differ significantly from their equilibrium counterparts which can lead – for example – to microphase separation and bubbly phases.5Given such observations, it is natural to ask about other interfacial properties of active fluids, and their similarities and differences with equilibrium systems. An interesting example occurs when a system undergoing MIPS is placed in contact with a solid or penetrable substrate (or “wall”). In this case, one may expect analogues of the rich phenomenology of wetting, as occurs in equilibrium fluids at liquid–vapor coexistence.6 Processes reminiscent of equilibrium wetting appear to play a crucial role in active systems composed of living cells, soft responsive materials, and embedded energy sources. For example, wetting and dewetting on soft substrates enables tunable adhesion, motility, and shape change of cells7–10 and control the motility of bacteria at interfaces.11
In equilibrium, wetting behaviour can be analysed in several different settings. A famous example is the formation of a liquid droplet on a (weakly attractive) solid substrate. The contact angle θ of this droplet obeys Young's equation:
γlvcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = γwv − γwl, θ = γwv − γwl, | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as the transition is approached. Measurements of contact angle thus permit the characterisation of wetting transitions on planar surfaces16 as well as related situations such as the filling transitions that occur in capillaries.17,18
θ as the transition is approached. Measurements of contact angle thus permit the characterisation of wetting transitions on planar surfaces16 as well as related situations such as the filling transitions that occur in capillaries.17,18
For computational model fluids like Lennard-Jonesium, measurement of contact angles tends to be challenging. However, there are convenient alternative approaches which either exploit the grand canonical ensemble, or a slit geometry with a fluid confined between two walls (and periodic boundaries in the other direction). Droplets do not form in these cases, and one instead focusses on the average density profile ρ(z), as a function of the distance z from the wall. For a grand canonical system with a single wall, one defines the adsorption  where ρb is the bulk density at z → ∞. This quantity is accessible experimentally19,20 as well as in density functional theories15,21 and in simulations21,22 (with the aid of finite-size scaling). Increasing the attraction between the fluid and the wall, a wetting transition occurs when Γ becomes infinite, which may occur either by a smooth divergence (critical wetting) or by a discontinuous jump (first-order wetting), depending on the range of fluid–fluid and wall–fluid interactions. A similar analysis can be performed for the slit geometry in the canonical ensemble, in which case the wetting transition is signalled by a symmetry breaking of the density profile ρ(z) with respect to the two walls.22,23
where ρb is the bulk density at z → ∞. This quantity is accessible experimentally19,20 as well as in density functional theories15,21 and in simulations21,22 (with the aid of finite-size scaling). Increasing the attraction between the fluid and the wall, a wetting transition occurs when Γ becomes infinite, which may occur either by a smooth divergence (critical wetting) or by a discontinuous jump (first-order wetting), depending on the range of fluid–fluid and wall–fluid interactions. A similar analysis can be performed for the slit geometry in the canonical ensemble, in which case the wetting transition is signalled by a symmetry breaking of the density profile ρ(z) with respect to the two walls.22,23
In all these equilibrium cases, statistical mechanical theories place strong constraints on the phenomenology. For example, the surface tensions in (1) can be defined unambiguously through derivatives of an appropriate free energy, as can the adsorption Γ.15,21 This provides consistency requirements between different ensembles and geometrical settings: studies based on the adsorption and the contact angle both deliver the same results for the locations and properties of surface phase transitions, as long as finite-size effects are controlled.
By contrast, active fluids are not ruled by a free energy, and the status of their wetting transitions is much less well-understood. Indeed, there are several different proposals for active generalisations of the liquid–vapour surface tension.24–34 It is not clear a priori whether any suitably generalised version of Young's equation should apply for these systems; if some such generalisation does exist then one may ask which (if any) of the liquid–vapour surface tensions might appear, and what should be used in place of γwv−γwl.
In recent work by some of us,23 an approach based on the adsorption Γ was used to analyse the wetting properties of an archetypical active fluid, comprised of active Brownian particles (ABPs) in d = 2 and d = 3 dimensions. An important difference from equilibrium fluids is that active particles tend to accumulate at walls, even in the absence of attractive interactions.35,36 As a result, an infinitely repulsive ‘hard’ wall is always completely wet for these active fluids, in contrast to equilibrium fluids for which a hard wall remains completely dry.37 However, on replacing a solid wall with a penetrable barrier, behaviour similar to first-order wetting was found in d = 3, for the slit geometry.23
In this work, we take a complementary approach to ref. 23, which is to examine the wetting behaviour of droplets in the same 3d system of ABPs. Such studies are numerically challenging due to finite-size effects which appear in the form of large fluctuations of the droplet shape and position. We sh ow that this can be mitigated by confining droplets in a wedge geometry. We identify a first-order-like wetting transition for droplets (where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ → 1). The nature and location of this transition are consistent with the slit geometry. We also characterise the situation of neutral wetting (cos
θ → 1). The nature and location of this transition are consistent with the slit geometry. We also characterise the situation of neutral wetting (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0). We give a critical analysis of Young's equation in this setting. We argue that by defining surface tensions in terms of the probabilities of droplet shape fluctuations, Young's equation holds by definition for the most likely shape, as long as shape fluctuations are controlled by local properties of the interface. In this case, the liquid–vapour surface tension also determines the probability of large-wavelength capillary waves.
θ = 0). We give a critical analysis of Young's equation in this setting. We argue that by defining surface tensions in terms of the probabilities of droplet shape fluctuations, Young's equation holds by definition for the most likely shape, as long as shape fluctuations are controlled by local properties of the interface. In this case, the liquid–vapour surface tension also determines the probability of large-wavelength capillary waves.
Our paper is organised as follows: the ABP model is defined in Section 2 and its wetting behaviour is discussed extensively in Section 3. Then Section 4 discusses analogous behaviour in a passive LJ fluid. Section 5 introduces the simple contour model for equilibrium interfacial fluctuations and compares it with the particle-based models. These results are discussed in Section 6, which also summarises our main conclusions.
2 Model and geometrical setup
We analyse ABPs as a prototypical model of scalar active matter that displays MIPS in the bulk.38,39 We follow a previous parameterization40 described in Appendix A, with ABPs interacting via the Weeks–Chandler–Anderson potential of lengthscale σ, and energy scale ε, with coupled translation and rotational diffusion constants DR = 3Dt/σ2 and self-propulsion velocity v0 defining a Péclet number Pe = v0/σDR. Timescales are expressed in units of the rotational diffusion time τR = 1/DR.We simulate this model in a fully periodic orthorhombic box of dimensions Lx × Ly × Lz. We consider various box sizes, but we typically elect to work with Lz = 20σ, smaller than both Lx and Ly. In order for a surface phase transition to occur, the system must be at a state point for which bulk liquid–vapor coexistence occurs. Accordingly, we choose model parameters well inside the MIPS region, specifically number density ρ = 0.60 and constant Péclet number Pe = 60 (see41 for the bulk phase diagram). The behaviour of active fluids depends quantitatively on Pe but the general phenomenology of the motility-induced phase separation is robust for sufficiently large Pe. We also expect the wetting behaviour to be robust throughout this range as long as the system is far enough from any critical points that dense and dilute fluid phases are clearly defined.
Applying the lever rule,42 this corresponds to an approximate liquid fraction of the system f = (ρ − ρLD)/(ρHD − ρLD) ≈ (0.6 − 0.45)/(1.25 − 0.45) = 0.1875, which results in a cylindrical liquid domain with its axis parallel to the z axis. Such a geometry allows us to monitor the changes in the liquid–vapour interfaces (and, in particular, the contact angle) via its two-dimensional projections in the x–y plane. We note that while MIPS is metastable with respect to vapor-crystal phase separation in this model,41,43 crystallisation is not observed on our simulation timescales.
To induce wetting, we introduce a penetrable wall, which we model as a static short-ranged repulsive barrier.23 We focus on short-range barrier–fluid interactions for reasons of simplicity and computational convenience and to minimise the barrier's influence on the overall fluid structure. We identify a piecewise surface S and employ an external repulsive potential perpendicular to the surface, which takes the form of a cosine hump:
 | (2) |
Simulations of liquid droplets of ABPs are challenging because of large fluctuations of the droplet shape. This can be mitigated by increasing the system size, but the dilute (vapor) phase of MIPS has a relatively high concentration ρLD ≈ 0.45, which means that such simulations quickly become expensive, involving very large numbers (hundreds of thousands) of particles. While planar walls are natural for wetting, we have found it helpful to choose S to take a wedge shape; this localises the droplet (reducing fluctuations) and accelerates its nucleation. To achieve this, we choose S to comprise two finite planes that are joined together at an aperture angle α by a cylindrical section, which gives the wedge a rounded corner. Fig. 1(a)–(c) illustrate the resulting setup, showing the planar density ρ(x,y) (details of its numerical estimation are given below). The x–y force field generated by the barrier is illustrated in Fig. 1(d). Typical simulations have Lx = Ly= 100σ and Lz = 20σ with the wedge occupying one quadrant of the box. At the density considered, this results in simulations of N = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles. Working in three dimensions ensures that the density fluctuations are more controlled than the two-dimensional case and connects to previous evidence for a wetting transition that becomes sharper in the large N limit.23
000 particles. Working in three dimensions ensures that the density fluctuations are more controlled than the two-dimensional case and connects to previous evidence for a wetting transition that becomes sharper in the large N limit.23
Our choice to work in the wedge geometry links our previous work on the planar case23 to the literature on equilibrium filling transitions, which are the manifestations of wetting phenomena on wedges and corners.17,18,44–46 The presence of a wedge facilitates the emergence of a phase transition in regimes for which wetting could be hindered (for example, by lowering the wetting temperature or by allowing wetting to occur in the gas phase), especially for small apertures. Here, however, we use the wedge as a means to facilitate the analysis of droplets and leave the study of the effects of the aperture to future work.
3 Wetting phenomenology for active Brownian particles
3.1 Average local density profiles: contact angles and wetting transition
Our analysis of wetting is based on the local density profile, which is obtained by discretizing space in subvolumes of side![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2σ. We define the instantaneous number of particles in bin j of center bj
= 2σ. We define the instantaneous number of particles in bin j of center bj | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (x) is 1 if x is within the cube of side
(x) is 1 if x is within the cube of side ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) centered at the origin and zero otherwise. The instantaneous number density at site j is defined as
centered at the origin and zero otherwise. The instantaneous number density at site j is defined asρj = Nj/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 3, 3, | (4) |
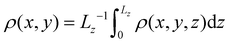 . Following a relaxation time of 100τR, the average local density
. Following a relaxation time of 100τR, the average local density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (x,y) is formed by sampling at intervals of τR, and averaging over a period of 1500τR.
(x,y) is formed by sampling at intervals of τR, and averaging over a period of 1500τR.
Fig. 1 shows two-dimensional projections of the density map for three different wedge aperture angles α. The density profiles are smooth and – for the value of εw = 12 studied – exhibit a liquid drop confined within the wedge. From such profiles one can, in principle, extract the vapor–liquid interface and estimate the contact angle θ between the active droplet and the repulsive barrier. For our system, the macroscopic notion of sharp contact between a circular vapor–liquid interface and the barrier is somewhat blurred by the ubiquitous presence of a thin layer of particles all around the wedge. To deal with this, we work with estimates of an apparent contact angle, defined by fitting a circular arc to circular regions of the density profile as described further in Appendix C. If a non-equilibrium analogue of Young's equation applies to these systems (valid in the large-system limit), then θ should be determined only by local properties of the three-phase contact line, so that θ is independent of α. For the three value of α shown in Fig. 1, we find θ ≈ 75°–85°: this relatively small range seems consistent with the applicability of Young's equation. Note that for small equilibrium droplets, Young's equation includes line tension terms and Tolman corrections to the Laplace pressure,47–49 while in the active case curvature effects on swim pressure of confined ABPs have also been reported;50 we explicitly neglect these effects in this work.
Henceforth we elect to work at fixed aperture α = π/2. Fig. 2 illustrates how the stationary average density field ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (x,y) for this value of α varies with the barrier strength εw. At the largest values of εw studied, thick liquid layers are present on both the interior and exterior of the wedge and the density profile flattens close to the corner of the wedge and terminates with a rounded shape at the tips. On lowering the barrier height from εw = 18 to εw = 15, liquid progressively accumulates in the wedge interior. At εw ≈ 18 the curvature of the interface between the interior liquid and the vapor changes sign from positive to negative and a recognisable droplet forms within the wedge having an apparent contact angle θ < π/2. The fitting procedure to obtain θ is appropriate only when the density profile exhibits such a region of negative curvature, i.e. for εw ≲ 18. We assert (and confirm via a comparison with equilibrium wetting in a comparable geometry- see Sections 4 and 5.2) that the change in sign of the interfacial curvature corresponds to the transition from partial to complete wetting. In other words that the barrier is partially wet, (with θ > 0) for εw ≲ 18, and is completely wet (i.e. θ = 0) for εw ≳ 18. Within the partially wet regime, most liquid resides in the drop in the wedge interior. However some liquid resides on the exterior wall of the wedge forming a pair of symmetrical “lobes” of liquid-like density. A εw decreases, progressively more liquid accumulates in the drop whose contact angle θ increases, while the extent of the lobes decreases. In Section 3.4 we discuss the finite-size scaling behaviour of the lobes and the liquid drop.
(x,y) for this value of α varies with the barrier strength εw. At the largest values of εw studied, thick liquid layers are present on both the interior and exterior of the wedge and the density profile flattens close to the corner of the wedge and terminates with a rounded shape at the tips. On lowering the barrier height from εw = 18 to εw = 15, liquid progressively accumulates in the wedge interior. At εw ≈ 18 the curvature of the interface between the interior liquid and the vapor changes sign from positive to negative and a recognisable droplet forms within the wedge having an apparent contact angle θ < π/2. The fitting procedure to obtain θ is appropriate only when the density profile exhibits such a region of negative curvature, i.e. for εw ≲ 18. We assert (and confirm via a comparison with equilibrium wetting in a comparable geometry- see Sections 4 and 5.2) that the change in sign of the interfacial curvature corresponds to the transition from partial to complete wetting. In other words that the barrier is partially wet, (with θ > 0) for εw ≲ 18, and is completely wet (i.e. θ = 0) for εw ≳ 18. Within the partially wet regime, most liquid resides in the drop in the wedge interior. However some liquid resides on the exterior wall of the wedge forming a pair of symmetrical “lobes” of liquid-like density. A εw decreases, progressively more liquid accumulates in the drop whose contact angle θ increases, while the extent of the lobes decreases. In Section 3.4 we discuss the finite-size scaling behaviour of the lobes and the liquid drop.
At εw = 10 we find θ ≈ π/2, which – in the context of Young's equation – is interpreted as a neutral point, where the tensions between the barrier and liquid and the barrier and the vapor balance each other. This point separates the partial wetting and partial drying regimes. On decreasing the barrier strength still further, we find that within the timescale of our simulations, the stationary state becomes harder to define: if we initiate the system in a homogeneous density state, the nucleation of the droplet becomes very slow; if we start instead from a pre-formed droplet and instantaneously decrease the barrier strength, the droplet progressively detaches from the barrier. The detachment indicates that the vapor phase is favoured near the barrier in the stationary state. Henceforth, we restrict our analysis to the range of barrier strength for which the liquid is attached to the barrier. Our results for the dependence of the measured contact angle on the barrier strength are displayed in Fig. 3. For the weakest accessible barrier strengths at which the droplet is attached to the wedge, we find cos(θ) ≈ 0, i.e. the droplet is close to the neutral point. As εw increases, cos(θ) increases approximately linearly and appears to attain the wetting point cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 1 with a nonzero slope, suggesting a first-order wetting transition around εw = 18 ± 1, which is the value that was independently obtained via a very different method previously from our previous analysis of this system in the slit geometry.23 The match between the two estimates of the complete wetting transition points towards an equivalence between the adsorption and the contact angle routes, as expected in the equilibrium case.
θ = 1 with a nonzero slope, suggesting a first-order wetting transition around εw = 18 ± 1, which is the value that was independently obtained via a very different method previously from our previous analysis of this system in the slit geometry.23 The match between the two estimates of the complete wetting transition points towards an equivalence between the adsorption and the contact angle routes, as expected in the equilibrium case.
 | ||
| Fig. 3 Cosine of the apparent contact angle θ for ABPs in a 90° wedge for a range of repulsive strengths εw, as calculated from a circular arc fit to the portion of the liquid–vapor interface having negative curvature. The vertical dashed line indicates the transition from partial to complete wetting determined previously via a different approach.21 The hatched area indicates the regime in which the droplet detaches from the barrier. Error bars are bootstrap estimates for three standard deviations. | ||
3.2 Local density fluctuations
Density fluctuations play a central role in characterising phase transitions, both in passive and active systems. In the case of surface phase transitions studied within a grand canonical framework, the behaviour of the local compressibility (which quantifies the magnitude of the density fluctuations relative to the average density) allows the order of a surface phase transition15 to be ascertained and provides information on the character of interfaces.To quantify the density fluctuations in our system, we accumulate the local variance of the density field Var[ρ(x,y)] = 〈ρ2(x,y) 〉 − 〈ρ(x,y) 〉2 on the same scale ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2σ over which the field is defined. This provides a fine-grained description of the spatial dependence of the density fluctuations. Fig. 2 shows that the fluctuations are greatest at the liquid–vapor interface: both for the droplet in the wedge interior and for the exterior lobes. In particular, the complete wetting regime at large εw corresponds to small overall fluctuations, with higher values occurring around points of higher curvature. As the repulsive barrier gets weaker (moving from right to left in Fig. 2), the fluctuations at the liquid–vapor interface in the interior increase in magnitude, and become progressively more localised in the vicinity of the contact region between the interface and the barrier.
= 2σ over which the field is defined. This provides a fine-grained description of the spatial dependence of the density fluctuations. Fig. 2 shows that the fluctuations are greatest at the liquid–vapor interface: both for the droplet in the wedge interior and for the exterior lobes. In particular, the complete wetting regime at large εw corresponds to small overall fluctuations, with higher values occurring around points of higher curvature. As the repulsive barrier gets weaker (moving from right to left in Fig. 2), the fluctuations at the liquid–vapor interface in the interior increase in magnitude, and become progressively more localised in the vicinity of the contact region between the interface and the barrier.
3.3 Polarisation field
The orientation of the self-propulsion force of ABPs rotates via a diffusive process. For a bulk system, every particle orientation is equally likely, and thus, the average orientation vector of each particle is zero. When interfaces are formed (as in MIPS), the local stationary orientation can take nonzero values, indicating a local polarisation of the system.We define the instantaneous polarisation ϕ from the particle orientation ni on a grid of spacing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . For bin j
. For bin j
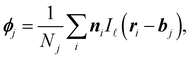 | (5) |
In Fig. 4(a)–(d), we track the changes to the stationary polarisation that occur as we vary the barrier strength εw. As expected, the polarisation fields are non-zero only at interfaces and closely follow the density gradient, directed from the dilute towards the denser phase. The principal effect of varying εw is manifest in the barrier region: for large εw, the particles at liquid-like densities on both the interior and exterior of the wedge are oriented against the barrier. For weaker barriers (e.g. εw = 12), the particles inside the droplet change orientation and point towards the droplet interior. This contrasts with the behaviour of exterior particles in the vicinity of the barrier, which are always polarised towards the barrier, independent of εw.
3.4 Finite size effects
The density profiles display the formation of both an interior liquid layer and some accumulation on the exterior of the wedge. These exterior density “lobes” are a consequence of the non-equilibrium accumulation mechanism and its coupling with the barrier strength. In the limit of very repulsive barriers, the liquid covers both the interior and exterior approximately symmetrically, whereas, in the partial wetting regime that occurs for εw < 18, the liquid is primarily localised as a droplet in the interior.If we now consider increasing the overall system size at partial wetting, whilst maintaining the overall number density constant, then one expects the volume of liquid in the wedge interior to increase in size accordingly. However, the thickness of the exterior lobes should remain approximately unchanged because they arise from the usual accumulation of ABPs at a barrier, combined with a local balance of particles crossing the barrier: these aspects only depend on the liquid density.
Fig. 5 confirms this: the top panel shows that on increasing the repulsion strength, the thickness of the lobes grows, and eventually saturates as the complete wetting regime is approached. (This thickness is measured as the stationary average of the largest distance between the outer liquid–vapor interface and the exterior of the wedge). The lower panel of Fig. 5 shows that in the partially wet regime ε < 18, the lobe thickness is independent of system volume. Thus, the exterior lobes in the partial wetting regime can be regarded as a finite-size effect such that for a sufficiently large system, the liquid phase is essentially confined in the wedge interior.
3.5 Flow fields
The internal self-propulsion force renders the system dissipative, promoting flows coupled to the geometric features of the barriers. For example, in the case of ellipsoidal impenetrable barriers, distinctive quadrupolar flow patterns have been reported previously.51In order to quantify the flow field, we track the particle displacements Δri = ri(t + Δt) − ri(t) with Δt = 0.005τR, a time interval that is sufficiently small to allow us to follows the local patterns of motion. We estimate the flow patterns from the η = x, y, z components of the field
 | (6) |
Fig. 4(e)–(h) illustrates the flow patterns occurring at weak (εw = 12) intermediate (εw = 18), strong (εw = 30) and very strong repulsive (εw = 40) barriers. In all cases, the wedge geometry shapes the structure of the flow field. Consider first the results for the strongest repulsive barrier (εw = 40). Here the end-points of the wedge correspond to regions of opposing counterflows, reminiscent of the quadrupolar structure of hard objects mentioned above; the flow in the interior of the wedge is from the vapor into the liquid, consistent with the orientation field; particle flow through the wedge occurs only at the wedge corner, where two other counter-flows are formed, and where the flow field rotates in order to be orthogonal to the exterior of the wedge.
These overall features persist on decreasing εw, but the flow patterns become more complex. In particular, the flow field reorients itself around the contact points between the droplet and the barrier, forming two additional local regions of nonzero circulation. Lower energy barriers also engender interesting changes in the flow patterns inside the liquid droplet. One is a marked increase in the flow through the wedge corner. Another is that while for the largest εw particles are trapped in the liquid region, with any flow occurring parallel to the barriers (for example, Fig. 4(h)) in the positive x and y directions, for weaker εw the particles can traverse the barrier, creating perpendicular flow patterns as seen in Fig. 4(e). These changes are accompanied by a reversal in the net flux direction, with x and y flux components being net negative for small εw and net positive for large εw. Forces on asymmetric objects have been previously linked52 to the flow patterns of active particles, and the changes observed here indicate a change in the direction of the net force on the wedge as we vary the repulsion strength, a prediction that can potentially be tested in experiments.
These results emphasise that the dissipative non-equilibrium flow patterns generated by the soft wedge can be highly non-trivial, with exquisite features that start to develop even well inside the dilute phase. Notwithstanding these fine-grained phenomena, as we show in the next section, coarse-graining over sufficiently large scales reproduces closely the principal features of the density profiles and their fluctuations that occur in comparable equilibrium systems.
We conclude this section by summarising the key findings from our simulations of the active system: (i) imposing a wedge-shaped, penetrable, repulsive barrier on a metastable fluid of active Brownian particles promotes the formation of a droplet of the dense phase whose shape depends on the strength of the repulsive potential; (ii) the barrier strength at which the transition from complete to partial wetting occurs can be extracted from the apparent contact angle and matches that previously measured in a different (slab) geometry;23 (iii) the apparent contact angle is almost independent of the geometry of the wedge, indicating that a non-equilibrium version of Young's equation is applicable; (iv) local fluctuations maps can be extracted from density profiles and reveal the presence of enhanced fluctuations at the contact points between the droplet and the barrier; (v) the polarisation of the particles’ orientations and the particle flows are sensitive to the barrier strength, with more complex patterns for weak barrier strength corresponding to the partially wet regime; (vi) particle accumulation occurs both inside and outside the wedge, but the thickness of the exterior layer is sub-extensive with respect to the system size in the partially wet regime.
With these observations in mind, we now compare the behaviour of active Brownian particles with that of a particle-based equilibrium model known to undergo a first-order wetting transition.
4 Comparison with equilibrium wetting in a passive fluid
The phenomenology of the active system displays specific spatial density profiles, local density fluctuations and flow patterns. While the non-equilibrium flows have no counterpart in equilibrium, we can compare the stationary density distributions and their fluctuations to a conventional passive system undergoing a wetting transition in an analogous geometry. To do so, we consider the prototypical model for equilibrium wetting in which a liquid droplet of Lennard-Jones particles interacting via a truncated and shifted potential, in coexistence with the vapor, interacts with an impenetrable wall supplemented by a long-ranged attraction, as described by a Lennard-Jones 9-3 interaction potential. Such long-ranged wall–fluid attractions are sufficient for a planar substrate to engender a first-order wetting transition.21 We note that for our active system, the competition between attraction and repulsion that engenders a wetting transition arises from a single repulsive potential barrier alone. This contrasts with passive systems, where the necessary ingredients are separate attractive and repulsive parts of the wall–fluid potential and wetting is driven by increasing the strength of attraction.To make contact with the behaviour of droplets in our active system, we arrange the wall to form a wedge with aperture angle α = 90° (see details of the equilibrium model in Appendix B). We control the affinity of particles for the wall by varying the strength of the interaction εLJw between the wedge and the fluid. Note, however, that in contrast to the active case where increasing εw increases the degree of repulsion between the barrier and the fluid particles, here increasing εLJw strengthens the wall–fluid attraction.
Fig. 6 shows the evolution of the density profile with increasing attractive strength εLJw. The boundary conditions of the simulation box are such that the LJ walls are located on the left and bottom edges while the top and right edges present reflective boundary conditions; the z dimension, orthogonal to the projection plane, is periodic. The qualitative dependence on wall–fluid interaction strength is very similar to that seen for the active case in Fig. 2: a droplet is formed in the corner of the wedge, and gradually spreads out as the attractive strength is increased. Complete wetting occurs at the largest wall strengths where the particles coat the wall (note that the rounding of the density profile at the end of the simulation box is a consequence of the reflective boundary conditions required in this ensemble and is not a genuine point of contact). As in the active case, the changes in the density profiles are accompanied by changes in the local density fluctuations, as shown in Fig. 6. The regions of highest variance (greatest fluctuation) are located at the vapor–liquid interface, and on approaching the neutral point, θ = π/2, the variance exhibits maxima near the point of contact with the wall.
When the attractive wall strength is reduced further, a situation similar to that observed in the active case arises: the liquid drop pinches off and detaches from the wall. Fig. 7 plots cos(θ) as a function of εLJw as extracted from circular fits to the interface. The main difference from the active case is that the passive system can access a larger range of cos(θ) before detachment occurs: specifically for the passive system we can stabilize droplets with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ −0.5 (θ ≈ 2π/3), whereas the active system becomes unstable around the neutral point θ = π/2.
θ ≈ −0.5 (θ ≈ 2π/3), whereas the active system becomes unstable around the neutral point θ = π/2.
 | ||
Fig. 7 Cosine of the apparent contact angle θ between the droplet of Lennard-Jones liquid and the 9-3 Lennard-Jones walls of strength εLJw, as estimated by circular arc fits to the liquid–vapor interface. The hatched area indicates where the droplet detaches from the walls. Note that, differently from Fig. 3, the range of cosines extends to the partially dry regime (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0) before detaching is observed. Error bars are bootstrap estimates for three standard deviations. θ < 0) before detaching is observed. Error bars are bootstrap estimates for three standard deviations. | ||
5 Theoretical model for droplet shape fluctuations
On sufficiently large (hydrodynamic) length scales, it is natural to describe wetting droplets in a continuum formalism, with a sharp interface separating liquid and vapour domains. We discuss here a simple model for the fluctuations of such an interface, which is useful for rationalising the density fluctuations observed in active and passive systems. We describe the interface as a line in two dimensions, in order to model the planar profiles in Fig. 2.5.1 Contour model
For a wedge with opening angle α, we describe the interface in polar co-ordinates, with the origin at the corner of the wedge. The distance from the origin to the interface R(ϕ) is parameterised as | (7) |
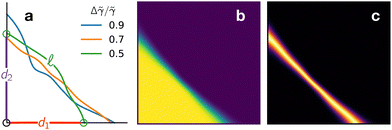 | ||
Fig. 8 (a) Example paths generated by Monte–Carlo according to the free energy in eqn (9). The quantities ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,d1,d2 are illustrated for a specific contour. (b) Average and (c) variance of the density determined by the statistics of the contours generated at fixed Δ ,d1,d2 are illustrated for a specific contour. (b) Average and (c) variance of the density determined by the statistics of the contours generated at fixed Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) / /![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.7. For these profiles, no Gaussian convolution is performed. Every sampled contour has fixed area A and the maps have dimensions 2√A × 2√A. = 0.7. For these profiles, no Gaussian convolution is performed. Every sampled contour has fixed area A and the maps have dimensions 2√A × 2√A. | ||
We formulate our model in terms of the probability distribution for the droplet shape, encoded by the function R(ϕ). Since we describe the interface as a line – or contour – we refer to this as the contour model. For simplicity, we suppose that the area of the liquid region is fixed at some reference value A0, so the probability (or probability density) of a given contour is
 | (8) |
 is the area enclosed by the liquid–vapour interface,
is the area enclosed by the liquid–vapour interface, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [R] is a free-energy-like quantity that controls the shape fluctuations, and Z is a suitable normalisation constant.
[R] is a free-energy-like quantity that controls the shape fluctuations, and Z is a suitable normalisation constant.
By analogy with equilibrium systems we propose that the dominant terms in ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) on hydrodynamic scales are
on hydrodynamic scales are
 | (9) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) lv is the length of the liquid–vapour interface, dwl is the (total) length of the liquid–wall interface, and
lv is the length of the liquid–vapour interface, dwl is the (total) length of the liquid–wall interface, and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv,Δ
lv,Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w play the role of surface tensions (see below for a more detailed discussion). One sees immediately that dwl = R(0) +R(α) and the interfacial length is
w play the role of surface tensions (see below for a more detailed discussion). One sees immediately that dwl = R(0) +R(α) and the interfacial length is  .
.
In equilibrium, (9) is valid on hydrodynamic scales12 and its parameters are related to the surface tensions between the phases as ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv = γlv/(kBT) and Δ
lv = γlv/(kBT) and Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w = (γwv − γwl)/(kBT): here T is the temperature and kB is Boltzmann's constant.† In principle other terms might also appear in F but these are constrained by locality – the probability of an interfacial perturbation should not depend on the shape of the interface far away – and by the symmetries of the problem, and the restriction to large length scales.
w = (γwv − γwl)/(kBT): here T is the temperature and kB is Boltzmann's constant.† In principle other terms might also appear in F but these are constrained by locality – the probability of an interfacial perturbation should not depend on the shape of the interface far away – and by the symmetries of the problem, and the restriction to large length scales.
For active systems, non-local contributions to ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) cannot be ruled out, but the symmetries of the system (isotropy and translation invariance) suggest that (9) is a natural starting point for a hydrodynamic theory. Moreover, for large droplets one sees that
cannot be ruled out, but the symmetries of the system (isotropy and translation invariance) suggest that (9) is a natural starting point for a hydrodynamic theory. Moreover, for large droplets one sees that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) lv and dwl are O(L) and
lv and dwl are O(L) and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv,Δ
lv,Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = O(1) which means that shape fluctuations are small, as happens for thermal fluctuations in the thermodynamic limit. As in that case, the result is that the distribution of shapes is dominated by the most likely contour. Applying calculus of variations to minimise
= O(1) which means that shape fluctuations are small, as happens for thermal fluctuations in the thermodynamic limit. As in that case, the result is that the distribution of shapes is dominated by the most likely contour. Applying calculus of variations to minimise ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) at fixed droplet area A0 one arrives at Young's equation in the form
at fixed droplet area A0 one arrives at Young's equation in the form
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = Δ θ = Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) | (10) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) =
= ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv and
lv and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = Δ
= Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w.
w.
For completeness, a derivation of this result is given in Appendix D, which also shows that the curvature of the liquid–vapour interface must be constant everywhere, so that the droplet boundary is an arc of a circle. Analysing small fluctuations about this most-likely shape also recovers the standard theory of capillary fluctuations. This suggests that the appropriate γlv that should appear in a Young's equation for active fluids is a capillary surface tension,32 see Section 6 below for further discussion of this point.
5.2 Comparison with wetting simulations
To investigate the predictions of this model, we sample contour fluctuations numerically by a straightforward Monte Carlo algorithm as detailed in Appendix E. Assuming sharp interfaces, this yields a density field ρ(x,y|t) at every iteration t, by taking a value of unity for the liquid and zero for the vapor. These sharp profiles are then averaged to return the equilibrium density profile, and its variance, which are both computed by partitioning the 2d domain into bins of size δx.
Fig. 8 illustrates the procedure for a particular choice of Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) , connecting collections of paths (Fig. 8(a)) to a density profile and its variance (panels (b) and (c)). For a specific choice of Δ
, connecting collections of paths (Fig. 8(a)) to a density profile and its variance (panels (b) and (c)). For a specific choice of Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) the average density profile converges to form a specific contact angle, such that cos
the average density profile converges to form a specific contact angle, such that cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = Δ
θ = Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) : in the specific example of panel (b) and (c) we have Δ
: in the specific example of panel (b) and (c) we have Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.7 → θ ≈ 45°. While the density profile closely resembles that produced by the passive system (and the interior of the wedge in the active system), the variance profiles are typically sharper and do not display a marked relative increase of the variance in the regions where the contour contacts the wall.
= 0.7 → θ ≈ 45°. While the density profile closely resembles that produced by the passive system (and the interior of the wedge in the active system), the variance profiles are typically sharper and do not display a marked relative increase of the variance in the regions where the contour contacts the wall.
This deficiency of the model arises from our assumption of perfectly sharp instantaneous interfaces. In reality, the density across the instantaneous interfaces (e.g. in the Lennard-Jones system) evolves smoothly, interpolating between the liquid and the vapor density with a characteristic interface width. (The observed width is also affected by the projection of the three-dimensional system onto a planar density, because of capillary waves along the z-direction.) To account for this width, we perform a convolution of the instantaneous density profiles with a Gaussian kernel of size σblur. As illustrated in Fig. 9, the convolution promotes the emergence of peaks in local density fluctuations in the vicinity of the contacts with the wedge, similarly to what is observed in both the active and passive particle systems.
 | ||
Fig. 9 Effect of the Gaussian convolution of scale σblur = 0.1, 1, 2, 3δx where δx = 0.022√A on the two-dimensional variance profile, at Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) / /![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.7. The maps have dimensions 2√A × 2√A. = 0.7. The maps have dimensions 2√A × 2√A. | ||
It is interesting to quantify the similarities of the fluctuation profiles for the active fluid (Fig. 2) and the contour model as a function of the contact angle (or equivalently in the contour model, Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ). To achieve this, we use Monte Carlo to sample contours with a fixed area A. First, we calibrate the spatial discretisation of the contour model on the active model in the partially wet regime εw = 10, by tuning the binsize δx of the contour model to match the bin location of the contact point in the active system. This gives δx = 0.066√A. We fix the discretisation, and by using a blurring scale σblur = 2δx, we compute the average particle density in each bin. Then, we optimise the parameters of the contour model so that this density profile matches the ABP system at a given state point, by adjusting Δ
). To achieve this, we use Monte Carlo to sample contours with a fixed area A. First, we calibrate the spatial discretisation of the contour model on the active model in the partially wet regime εw = 10, by tuning the binsize δx of the contour model to match the bin location of the contact point in the active system. This gives δx = 0.066√A. We fix the discretisation, and by using a blurring scale σblur = 2δx, we compute the average particle density in each bin. Then, we optimise the parameters of the contour model so that this density profile matches the ABP system at a given state point, by adjusting Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) to minimise
to minimise
 | (11) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/char_e0d1.gif) ABPj is the average of the local density ρj defined as in (4), but now scaled to lie between 0 and 1; also ρcontourj is the corresponding (blurred) density for the contour model (which lies between 0 and 1 by definition).
ABPj is the average of the local density ρj defined as in (4), but now scaled to lie between 0 and 1; also ρcontourj is the corresponding (blurred) density for the contour model (which lies between 0 and 1 by definition).
Results are shown in Fig. 10. The contour model generates density profiles which closely match those of the ABPs not only for near-neutral conditions (e.g. εw = 10) but also close to the wetting transition εw = 18. The best fit profiles are associated with a contact angle cos(θ) = Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) which confirms the wetting transition to occur around εw = 18 (Δ
which confirms the wetting transition to occur around εw = 18 (Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.95) and accords with direct measurements of θ via circular fits to the interfaces of Fig. 3. In generating each density profile, we take advantage of the low computational cost of the contour model by performing averages over 104 independent contours.
= 0.95) and accords with direct measurements of θ via circular fits to the interfaces of Fig. 3. In generating each density profile, we take advantage of the low computational cost of the contour model by performing averages over 104 independent contours.
We also show the local variance of the density. This is not part of the fitting procedure so it can be interpreted as a prediction of the contour model. As expected, the variance is large at the liquid–vapour interface. In the contour model, it also tends to be large where this interface meets the barrier. For the ABPs under partial wetting conditions, the same behaviour is observed, with large fluctuations near points of contact with the barrier. However, close to the transition point εw = 18, the strongest density fluctuations in the ABPs occur away from these contact points. In fact, the contour model behaves analogously to the passive Lennard-Jones fluid (recall Fig. 6), with large fluctuations restricted to the contact points. This suggests that the geometrical setup of the active system may be influencing these density fluctuations, via the tips of the wedge, which are not explicitly accounted for either in the LJ system (which has walls terminating at reflective boundary conditions) or the contour model (which assumes infinite walls). Future work should clarify these potential finite-size effects and their coupling with the nonequilibrium fluxes of Fig. 4.
To analyse the density fluctuations in more detail, we characterise the behaviour of the local variance w(x,y) = Var[ρ], along the interface. To identify the interfacial region we take two density thresholds ρlo,ρhi and define a top-hat function Πρlo,ρhi(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ) that is equal to unity for ρlo <
) that is equal to unity for ρlo < ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) < ρhi (which is the interfacial region) and zero otherwise. Then we integrate this local variance over the interfacial region to obtain
< ρhi (which is the interfacial region) and zero otherwise. Then we integrate this local variance over the interfacial region to obtain
 | (12) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is the local density).
is the local density).
To determine how much w varies as we move along the interface, we compute a corresponding spatial variance:
 | (13) |
We vary the barrier and the wall strength in the ABP model and the (passive) LJ system respectively, to obtain systems with various contact angles. As different models have different scales for the variance w = Var[ρ(x,y)], we rescale Var[w]interface of the active and passive model by their maximal values. Results are shown in Fig. 11, which also shows corresponding quantities for the contour model, computed as a function of Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . To reduce the noise of our estimates, we repeat the measurements over a number of independent runs, which depend on the complexity of the models (5 for the active system, 20 for the passive system and 100 for the contour model), limited by the computational costs of the different models.
. To reduce the noise of our estimates, we repeat the measurements over a number of independent runs, which depend on the complexity of the models (5 for the active system, 20 for the passive system and 100 for the contour model), limited by the computational costs of the different models.
The contour model results can be accurately fitted with a polynomial expression (dashed line), and indicate an increasing spatial variance of the fluctuations, as the system moves from complete wetting [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ 1] towards the neutral point [cos
θ ≈ 1] towards the neutral point [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ 0]. The particle-based simulations exhibit more pronounced statistical errors, but follow a comparable trend. In particular, the ABP simulations have significant statistical uncertainties, both in determination of contact angle and the spatial variance. This is due to relatively large density fluctuations in the active fluids as well as limitations on available statistics due to the large system sizes and computational costs. It would be interesting to explore in more detail the agreement of the particle systems with the contour model but we postpone such a study to future work.
θ ≈ 0]. The particle-based simulations exhibit more pronounced statistical errors, but follow a comparable trend. In particular, the ABP simulations have significant statistical uncertainties, both in determination of contact angle and the spatial variance. This is due to relatively large density fluctuations in the active fluids as well as limitations on available statistics due to the large system sizes and computational costs. It would be interesting to explore in more detail the agreement of the particle systems with the contour model but we postpone such a study to future work.
Overall, Fig. 11 illustrates that – for a given choice of the contact angle – and notwithstanding the very different specific interaction mechanisms with the wall/barrier, the three model systems display similar characteristic fluctuations of their interfaces, which match quantitatively (up to an overall scale factor). More generally, Fig. 2, 6 and 10 demonstrate similar phenomenology for ABPs, passive LJ particles and the contour model, indicating that the principal features of the steady state density distribution in the wedge interior are well described by the minimal contour model, within which the most likely droplet shape is determined by a ratio of surface-tension-like quantities. This idea is developed further in the next Section.
6 Discussion and conclusions
We have considered active Brownian particles subject to a finite repulsive external potential as a simple model for surface phase transitions in active fluids. Our findings connect the behaviour of stable droplets to previously identified sharp spontaneous symmetry-breaking transitions from completely to partially wet states in three-dimensional systems.23 In order to stabilise active droplets with nonzero contact angles, we utilise a wedge-shaped external potential. The droplets thus formed display distinctive density distributions as well as non-trivial steady currents.A comparison with the wetting behaviour of a (Lennard-Jones) passive fluid confined by impenetrable, long-range attractive walls shows quantitative correspondences between the characteristic features of the density field and its fluctuations. Increasing the strength of the attractive wall–fluid interaction in the passive system plays an analogous role to increasing the potential barrier height in the active system, promoting a continuous change in curvature in the liquid–vapor interfaces and the promotion of density fluctuations in the vicinity of the contact line that increases as one moves from complete wetting (cos(θ) = 1) through the partial wetting regime to the neutral point (cos(θ) = 0).
Our results for the partial to complete wetting transition in ABPs provide new insights into phase separation phenomena in dry active matter. They suggest that, despite the inherent non-equilibrium mechanisms that engender phase separation and non-trivial flow patterns, the large-scale properties of the active model can be mapped onto an equilibrium one, an assertion that is supported by the finite-size scaling analysis of the density profiles in the partially wet regime. Such a scenario is similar to the hydrodynamic models proposed to rationalise motility-induced phase separation in the bulk53 and connects to recent attempts to recover capillary-wave-like fluctuations in the nonequilibrium case.28,33,54 It will be interesting to study whether these findings generalize to more complex active matter systems with anisotropic interactions or long-ranged hydrodynamic effects: in such systems, MIPS may be modified55 or suppressed,56 hence affecting dramatically one of the key ingredients for surface phase transitions.
The agreement of the contour model with the ABP system supports the correspondence between the interfacial behaviour of MIPS systems and equilibrium fluids. The parameters ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv,Δ
lv,Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w appearing in F are similar to (rescaled) surface tensions in equilibrium systems in that they set the probabilities of interfacial fluctuations. Indeed, one may use (8), (9) to write the suggestive expression,
w appearing in F are similar to (rescaled) surface tensions in equilibrium systems in that they set the probabilities of interfacial fluctuations. Indeed, one may use (8), (9) to write the suggestive expression,
 | (14) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w = (∂/∂dwl)lnP. However, it should not be assumed that
w = (∂/∂dwl)lnP. However, it should not be assumed that ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv,Δ
lv,Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w are related to mechanical aspects of interfaces, in contrast to equilibrium systems where the surface tension controls anisotropic contributions to the stress tensor,57 as well as the magnitude of capillary fluctuations, and the Laplace pressure. It is a familiar feature of active matter that there is no a priori connection between fluctuations and mechanical forces, because standard fluctuation–dissipation theorems do not hold in these non-equilibrium steady states. In deriving Young's equation, the central (albeit trivial) assumption is that the observed large-scale droplet configuration is the one that maximises the probability, so its shape is naturally determined by probabilistic quantities.
w are related to mechanical aspects of interfaces, in contrast to equilibrium systems where the surface tension controls anisotropic contributions to the stress tensor,57 as well as the magnitude of capillary fluctuations, and the Laplace pressure. It is a familiar feature of active matter that there is no a priori connection between fluctuations and mechanical forces, because standard fluctuation–dissipation theorems do not hold in these non-equilibrium steady states. In deriving Young's equation, the central (albeit trivial) assumption is that the observed large-scale droplet configuration is the one that maximises the probability, so its shape is naturally determined by probabilistic quantities.
To the extent that the contour model is an accurate description of interfacial fluctuations, the quantity ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv can be deduced from fluctuations of a planar MIPS interface: it is closely related to the capillary surface tensions discussed in.32,33 In equilibrium, Δ
lv can be deduced from fluctuations of a planar MIPS interface: it is closely related to the capillary surface tensions discussed in.32,33 In equilibrium, Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w is the difference between liquid–wall and vapour–wall surface tensions: these can be computed separately from simulations of the fluid in contact with the wall, under appropriate conditions. In this case, all the quantities that appear in Young's equation are known, and the contact angle θ can be predicted. In the active case, it is not clear how Δ
w is the difference between liquid–wall and vapour–wall surface tensions: these can be computed separately from simulations of the fluid in contact with the wall, under appropriate conditions. In this case, all the quantities that appear in Young's equation are known, and the contact angle θ can be predicted. In the active case, it is not clear how Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w can be estimated without direct simulation of a wetting droplet, so the modified Young's eqn (10) cannot predict the value of θ. Instead, one might infer Δ
w can be estimated without direct simulation of a wetting droplet, so the modified Young's eqn (10) cannot predict the value of θ. Instead, one might infer Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w by measuring the contact angle, under the assumption that (8), (9) are suitable as a model for droplet-shape fluctuations. Under this assumption, the theory does make non-trivial predictions, for example, that the contact angle of a fluid in a wedge should be independent of the aperture angle α, as found (at least approximately) in Fig. 1. Predictions of the most likely shape and its fluctuations would then also be available for other wall geometries. However, the existence of steady-state currents in active fluids should be borne in mind since this could mediate non-local interaction terms in
w by measuring the contact angle, under the assumption that (8), (9) are suitable as a model for droplet-shape fluctuations. Under this assumption, the theory does make non-trivial predictions, for example, that the contact angle of a fluid in a wedge should be independent of the aperture angle α, as found (at least approximately) in Fig. 1. Predictions of the most likely shape and its fluctuations would then also be available for other wall geometries. However, the existence of steady-state currents in active fluids should be borne in mind since this could mediate non-local interaction terms in  , in which case (8), (9) would not hold. More detailed tests of this theory would be desirable.
, in which case (8), (9) would not hold. More detailed tests of this theory would be desirable.
Conflicts of interest
There are no conflicts to declare.Appendix
A Active Brownian particles model
We follow previous literature and simulate repulsive active Brownian particles of equal mass m interacting via the Weeks–Chandler–Anderson potential | (15) |
The equations of motion for the particle positions and orientations are:
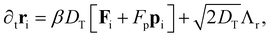 | (16) |
 | (17) |
The translational and rotational diffusion constants DT and DR coupling is DT = DRσ2/3, with inverse thermal energy scale β and friction ξ such that βξ = 1/Dt. Following Stenhammar et al.,40 we keep the self-propulsion force constant Fp = 24ε/σ as well as the friction 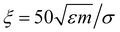 . The noise terms Λr,Λq,Λp are unit-variance stochastic vectors in three dimensions whose Cartesian components satisfy 〈Λi(r,t)Λj(r′,t′)〉 = δijδ(r − r′)δ(t − t′). The rotational diffusion constant defines a natural timescale for the system, the rotational diffusion time τR = 1/DR. We work at constant Péclet number Pe = Fp/ξDrσ = 60. We choose this value as a compromise between the need to work away from criticality (Pe ≈ 3641) and the requirement of system sizes that are comparable or larger than the persistence length
. The noise terms Λr,Λq,Λp are unit-variance stochastic vectors in three dimensions whose Cartesian components satisfy 〈Λi(r,t)Λj(r′,t′)〉 = δijδ(r − r′)δ(t − t′). The rotational diffusion constant defines a natural timescale for the system, the rotational diffusion time τR = 1/DR. We work at constant Péclet number Pe = Fp/ξDrσ = 60. We choose this value as a compromise between the need to work away from criticality (Pe ≈ 3641) and the requirement of system sizes that are comparable or larger than the persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p = σPe.
p = σPe.
To integrate the equations of motion, we implement an Euler–Maruyama scheme with constant timestep dt = 4 × 10−5τR, following the Ermak–McCammon method described in detail in ref. 58, with an in-house implementation for the molecular dynamics package LAMMPS.59
B Lennard-Jones droplet
We performed molecular dynamics simulations of a system of point-like particles interacting via the short-range Lennard-Jones potential | (18) |
The potential was truncated and shifted at cutoff rc = 2.5σ.
To mimic the setup of the active case, we considered a three-dimensional system with Lz ≪ Lx = Ly, with Lz = 20σ and Lx = Ly = 100σ. While the z dimension is periodic, particles interact with a Lennard-Jones 9-3 wall interaction on two of the remaining faces (forming a corner), while the opposite walls have reflective boundary conditions. The wall–fluid interactions took the form
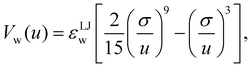 | (19) |
The simulations were performed in the NVT ensemble at temperature T = 0.91954εLJ for a system of N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles of mass m and number density ρ = 0.1σ−3 using a timestep
000 particles of mass m and number density ρ = 0.1σ−3 using a timestep  .
.
C Fitting contact angles
Measuring contact angles relies on fitting procedures. To validate our results, we follow two alternative procedures to fit the contact angles from stationary density profiles of the active and passive models: (1) a three-parameter fit with a circular profile; (2) a seven-parameter fit with a Fourier series representing the liquid–vapor interface.For method (1), we identify the interface between vapor and liquid by thresholding the absolute value of the gradient of the density profile to extract the (x,y) coordinates of points exclusively at the vapor–liquid. We ignore interfacial points close to the walls as they worsen the quality of the result. We then perform a least-square circular fit with parameters R,xc,yx where R is the radius of the circle xc and yc are the coordinates of the centre of the circle. The centre of the circle corresponds to the tip of the wedge only when the contact angle is 90°. In general, the wedge identifies the sector of a circle with the centre inside or outside of the wedge. When the centre is outside, the contact angle is measured as θ = π/2 − arcsin(|yc|/R), when it is inside, the angle is θ = π/2 + arcsin(|yc|/R).
For method (2), we use the parametrisation of eqn (7) with M = 5 to fit the interface between the vapor and the liquid. In this case, we include all the points of the interface that are inside the wedge and evaluate the local slope of the interface at a fixed distance dθ = 3σ from the wall in order to approximate the contact angle. We take advantage of the closed form parameterisation (eqn (7)) by taking its derivative analytically, which improves the numerical stability of the estimate of the contact angle.
The two methods yield comparable results in the partially wet regime. Method 2 breaks down on the approach to the wetting transition, although it continues to provide a lower bound for the contact angle at high εw. This is illustrated in Fig. 12.
 | ||
| Fig. 12 Comparison of the two independent measures of contact angles in the case of the active droplets. The hatched area indicates the detached regime. | ||
D Variational derivation of Young's equation
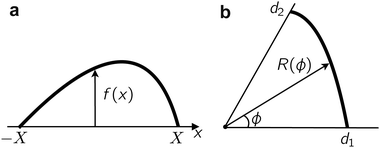
We show that Young's equation can be obtained by minimising the free-energy-like quantity (9), subject to a constraint of fixed enclosed area. We emphasize however than in the active case F is not a thermodynamic free energy, instead it describes the log-probability of shape fluctuations, such that its minimum is the most likely shape. For convenience we consider a planar wall instead of a wedge geometry and define f(x) as the normal distance from the wall to the interface, see Fig. 13. We explain below how results for other geometries can be deduced from this computation. (In order for f to be single-valued our derivation also requires that θ ≤ π/2, this assumption can be also be relaxed.) We assume that the interface meets the wall at x = ±X so f(X) = 0 = f(−X): here X is a variational parameter. The length of the liquid–vapour interface is and the length of the liquid–wall interface is 2X. The enclosed area is
and the length of the liquid–wall interface is 2X. The enclosed area is 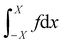 .
.
 | ||
| Fig. 13 (a) Sketch of geometry for derivation of Young's equation in Appendix D. (b) Corresponding geometry for the contour model, see Appendix E. | ||
The problem can be simplified by a symmetry argument: the optimal droplet shape is symmetric about x = 0 so f′(0). We enforce the constraints of enclosed area A0 and f(X) = 0 by Lagrange multipliers λ,μ. Hence it remains to extremise
 | (20) |
Within the calculus of variations we write f = f + δf and X = X + δX. Substituting this into ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , the optimal droplet shape is identified by setting the first variation
, the optimal droplet shape is identified by setting the first variation  . We find
. We find
Integration by parts and using f(X) = 0 and f′(0) = 0 yields
 | (21) |
The optimal droplet has  for any δf,δX, so all the terms in square brackets need to vanish. The second of these terms yields an Euler–Lagrange equation for f whose solutions are circular arcs with radius 1/|
for any δf,δX, so all the terms in square brackets need to vanish. The second of these terms yields an Euler–Lagrange equation for f whose solutions are circular arcs with radius 1/|![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lvλ|.‡ To obtain the contact angle one must deal with the end points of these arcs, for which the first term in (21) implies that
lvλ|.‡ To obtain the contact angle one must deal with the end points of these arcs, for which the first term in (21) implies that
 | (22) |
Putting this into the third term, we get (after simplification)
 | (23) |
Finally note that f′(X) is the gradient with which the liquid–vapour meets the wall, which is tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where θ is the contact angle. We assumed 0 < θ ≤ π/2 so
θ, where θ is the contact angle. We assumed 0 < θ ≤ π/2 so  and we recover Young's equation in the form (10).
and we recover Young's equation in the form (10).
Note that we performed this computation for a particular parameterisation of a droplet on a planar substrate, but the condition that the terms in square brackets vanish in (21) gives local geometrical constraints on the shape of the optimal droplet, which can be formulated in terms of the local curvature and the contact angle, independent of the parameterisations. As a result, the geometrical properties of the minimiser can be transferred to other geometrical settings even if the natural parameterisations are different in that case [recall (7)]. Specifically, the optimal shape has sections of liquid–vapour interfaces that form arcs of circles, and Young's equation is obeyed at points of contact with (locally) planar substrates.
E Contour sampling
We describe a numerical procedure for sampling droplet shapes according to (8), subject to a constraint of fixed area . To achieve this note that
. To achieve this note that | (24) |
Given parameters (B,a1,…,aM) and a target area A0 this is a quadratic equation that can be solved for R0. We fix R0 in this way and perform Metropolis MC on u = (B,a1,…,aM).§ As MC updates we propose
 | (25) |
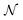 is a vector of Gaussian random numbers where each component has mean zero and variance s2. We take s = 0.01. The proposed update is accepted with probability
is a vector of Gaussian random numbers where each component has mean zero and variance s2. We take s = 0.01. The proposed update is accepted with probability  , evaluation of
, evaluation of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) requires the integral
requires the integral 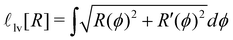 , which is performed numerically.
, which is performed numerically.
Note that scaling the droplet as R(ϕ) → λR(ϕ) for any scale factor λ, we find that A → λ2A and  . This scale invariance means that there are only two non-trivial parameters in this sampling problem, which are Δ
. This scale invariance means that there are only two non-trivial parameters in this sampling problem, which are Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) w/
w/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv and
lv and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) lv2A0. For numerical purposes we therefore fix A0 = 1 without loss of generality.
lv2A0. For numerical purposes we therefore fix A0 = 1 without loss of generality.
For the range of Δ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /
/![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) here considered we observe (after an initial transient) decorrelation of
here considered we observe (after an initial transient) decorrelation of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) over approximately MC 50 steps, which allows us to accumulate large statistics. For example, we produce 200
over approximately MC 50 steps, which allows us to accumulate large statistics. For example, we produce 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent profiles to evaluate the density and variance of the density field in blocks of 2000 contours, to produce 100 samples of the variance in the interface region, from which we estimate the scale of variance fluctuations within the interface (Fig. 11).
000 independent profiles to evaluate the density and variance of the density field in blocks of 2000 contours, to produce 100 samples of the variance in the interface region, from which we estimate the scale of variance fluctuations within the interface (Fig. 11).
Author contributions
All authors were involved in conceiving and directing the research. FT performed the numerical calculations. All authors wrote the paper.Acknowledgements
We thank R. Evans for a helpful conversation on the role of fluctuations in surface phase transitions and M. Cates for discussions of interfacial properties of active fluids. The computer simulations were carried out using the computational facilities of the Advanced Computing Research Centre, University of Bristol, as well as the Isambard 2 UK National Tier-2 HPC Service (https://gw4.ac.uk/isambard/) operated by GW4 and the UK Met Office, and funded by EPSRC (EP/T022078/1).Notes and references
- R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 4351 CrossRef CAS PubMed.
- A. Solon, J. Stenhammar, M. Cates, Y. Kafri and J. Tailleur, Phys. Rev. E, 2018, 97, 020602 CrossRef CAS PubMed.
- T. Speck, Phys. Rev. E, 2022, 105, 064601 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- E. Tjhung, C. Nardini and M. E. Cates, Phys. Rev. X, 2018, 8, 031080 CAS.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- A. Brugués, E. Anon, V. Conte, J. Veldhuis, M. Gupta, J. Colombelli, J. Muñoz, G. Brodland, B. Ladoux and X. Trepat, Nat. Phys., 2014, 10, 683–690 Search PubMed.
- R. Alert and X. Trepat, Annu. Rev. Condens. Matter Phys., 2020, 11, 77–101 Search PubMed.
- T. Bhattacharjee, D. Amchin, R. Alert, J. Ott and S. Datta, eLife, 2022, 11, e71226 Search PubMed.
- M. E. Pallarès, I. Pi-Jaumà, I. C. Fortunato, V. Grazu, M. Gómez-González, P. Roca-Cusachs, J. M. de la Fuente, R. Alert, R. Sunyer and J. Casademunt, Nat. Phys., 2023, 19, 279–289 Search PubMed.
- R. Harshey, Annu. Rev. Microbiol., 2003, 57, 249–273 CrossRef CAS PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- D. Bonn, Curr. Opin. Colloid Interface Sci., 2001, 6, 22–27 CrossRef CAS.
- R. Evans and N. B. Wilding, Phys. Rev. Lett., 2015, 115, 016103 CrossRef PubMed.
- R. Evans, M. C. Stewart and N. B. Wilding, J. Chem. Phys., 2017, 147, 044701 CrossRef PubMed.
- T. Ingebrigtsen and S. Toxvaerd, J. Phys. Chem. C, 2007, 111, 8518–8523 CrossRef CAS.
- E. H. Hauge, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 4994 CrossRef CAS PubMed.
- K. Rejmer, S. Dietrich and M. Napiórkowski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4027 CrossRef CAS PubMed.
- B. M. Law, Prog. Surf. Sci., 2001, 66, 159–216 CrossRef CAS.
- S. M. Gatica and M. W. Cole, J. Low Temp. Phys., 2009, 157, 111–136 CrossRef CAS.
- R. Evans, M. C. Stewart and N. B. Wilding, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23901–23908 CrossRef CAS PubMed.
- M. J. P. Nijmeijer, C. Bruin, A. F. Bakker and J. M. J. van Leeuwen, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 6052 CrossRef CAS PubMed.
- F. Turci and N. Wilding, Phys. Rev. Lett., 2021, 127, 238002 CrossRef CAS PubMed.
- T. Speck, Soft Matter, 2020, 16, 2652–2663 RSC.
- A. K. Omar, Z.-G. Wang and J. F. Brady, Phys. Rev. E, 2020, 101, 012604 CrossRef CAS PubMed.
- N. Lauersdorf, T. Kolb, M. Moradi, E. Nazockdast and D. Klotsa, Soft Matter, 2021, 17, 6337–6351 RSC.
- S. Hermann, D. de las Heras and M. Schmidt, Mol. Phys., 2021, 119, e1902585 CrossRef.
- E. Chacón, F. Alarcón, J. Ramrez, P. Tarazona and C. Valeriani, Soft Matter, 2022, 18, 2646–2653 RSC.
- L. Li, Z. Sun and M. Yang, arXiv, 2308.04917v1, 2023.
- J. Bialké, J. T. Siebert, H. Löwen and T. Speck, Phys. Rev. Lett., 2015, 115, 098301 CrossRef PubMed.
- R. Zakine, Y. Zhao, M. Knežević, A. Daerr, Y. Kafri, J. Tailleur and F. van Wijland, Phys. Rev. Lett., 2020, 124, 248003 CrossRef CAS PubMed.
- G. Fausti, E. Tjhung, M. Cates and C. Nardini, Phys. Rev. Lett., 2021, 127, 068001 CrossRef CAS PubMed.
- L. Langford and A. K. Omar, arXiv, 2308.08531v2, 2023.
- A. Omar, H. Row, S. Mallory and J. Brady, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219900120 CrossRef CAS PubMed.
- T. Speck and R. L. Jack, Phys. Rev. E, 2016, 93, 062605 CrossRef PubMed.
- J. Elgeti and G. Gompper, EPL, 2013, 101, 48003 CrossRef CAS.
- J. Henderson and F. van Swol, Mol. Phys., 1985, 56, 1313–1356 CrossRef CAS.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef PubMed.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- F. Turci and N. B. Wilding, Phys. Rev. Lett., 2021, 126, 038002 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, Elsevier, 2013, vol. 5 Search PubMed.
- A. Omar, K. Klymko, T. GrandPre and P. Geissler, Phys. Rev. Lett., 2021, 126, 188002 CrossRef CAS PubMed.
- D. Abraham and A. Maciołek, Phys. Rev. Lett., 2002, 89, 286101 CrossRef CAS PubMed.
- A. Malijevský and A. O. Parry, Phys. Rev. Lett., 2013, 110, 166101 CrossRef PubMed.
- A. Malijevský and A. Parry, Phys. Rev. Lett., 2021, 127, 115703 CrossRef PubMed.
- B. Toshev, D. Platikanov and A. Scheludko, Langmuir, 1988, 4, 489–499 CrossRef CAS.
- B. Widom, J. Phys. Chem., 1995, 99, 2803–2806 CrossRef CAS.
- H. Dobbs, Int. J. Mod. Phys. B, 1999, 13, 3255–3259 CrossRef CAS.
- F. Smallenburg and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032304 CrossRef PubMed.
- C. G. Wagner, M. F. Hagan and A. Baskaran, J. Stat. Mech.: Theory Exp., 2022, 2022, 013208 CrossRef.
- N. Nikola, A. Solon, Y. Kafri, M. Kardar, J. Tailleur and R. Voituriez, Phys. Rev. Lett., 2016, 117, 098001 CrossRef PubMed.
- M. Kourbane-Houssene, C. Erignoux, T. Bodineau and J. Tailleur, Phys. Rev. Lett., 2018, 120, 268003 CrossRef CAS PubMed.
- M. Besse, G. Fausti, M. Cates, B. Delamotte and C. Nardini, Phys. Rev. Lett., 2023, 130, 187102 CrossRef CAS PubMed.
- A. Jayaram, A. Fischer and T. Speck, Phys. Rev. E, 2020, 101, 022602 CrossRef CAS PubMed.
- M. Theers, E. Westphal, K. Qi, R. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1949, 17, 338–343 CrossRef CAS.
- S. Das, G. Gompper and R. G. Winkler, New J. Phys., 2018, 20, 015001 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
Footnotes |
| † The notation with tildes is a reminder that the parameters in F have the units of inverse length, while surface tensions γ (without tilde) have units of energy per length in this 2d setup. |
| ‡ In equilibrium, λ is related to the Laplace pressure. |
| § Note that the interpretation of (8) as a probability density for functions R has some ambiguity, but the most likely droplet shape is unambigous and obeys Young's equation. Our choice of MC sampling method corresponds to a specific interpretation of the probability density P[R]. |
| This journal is © The Royal Society of Chemistry 2024 |