Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Obstructed swelling and fracture of hydrogels†
Abigail
Plummer‡
 a,
Caroline
Adkins‡
a,
Caroline
Adkins‡
 b,
Jean-François
Louf
b,
Jean-François
Louf
 cd,
Andrej
Košmrlj
cd,
Andrej
Košmrlj
 *ef and
Sujit S.
Datta
*ef and
Sujit S.
Datta
 *c
*c
aPrinceton Center for Complex Materials, Princeton University, Princeton, NJ 08540, USA
bDepartment of Civil and Environmental Engineering, Princeton University, Princeton, NJ 08544, USA
cDepartment of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: ssdatta@princeton.edu
dDepartment of Chemical Engineering, Auburn University, Auburn, AL 36849, USA
eDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: andrej@princeton.edu
fPrinceton Materials Institute, Princeton University, Princeton, NJ 08544, USA
First published on 22nd January 2024
Abstract
Obstructions influence the growth and expansion of bodies in a wide range of settings—but isolating and understanding their impact can be difficult in complex environments. Here, we study obstructed growth/expansion in a model system accessible to experiments, simulations, and theory: hydrogels swelling around fixed cylindrical obstacles with varying geometries. When the obstacles are large and widely-spaced, hydrogels swell around them and remain intact. In contrast, our experiments reveal that when the obstacles are narrow and closely-spaced, hydrogels fracture as they swell. We use finite element simulations to map the magnitude and spatial distribution of stresses that build up during swelling at equilibrium in a 2D model, providing a route toward predicting when this phenomenon of self-fracturing is likely to arise. Applying lessons from indentation theory, poroelasticity, and nonlinear continuum mechanics, we also develop a theoretical framework for understanding how the maximum principal tensile and compressive stresses that develop during swelling are controlled by obstacle geometry and material parameters. These results thus help to shed light on the mechanical principles underlying growth/expansion in environments with obstructions.
I. Introduction
Many growth and expansion processes are sculpted through confinement by rigid obstructions. Familiar examples include muffins rising into their characteristic shape during baking,1 trees growing around boulders,2 and even cities expanding around inhospitable geographic features.3 Obstructed growth and expansion also play pivotal roles—both harmful and beneficial—in many practical applications. For example, excessive tissue growth around metal mesh tubes inserted into blood vessels is a common, but life-threatening, complication of stenting;4–6 conversely, the expansion of spray foam into cracks and in between walls underlies the thermal insulation of many energy-efficient buildings.7 More broadly, obstructed growth and expansion critically influence the emergence of form and function across diverse non-living and living systems, ranging from hydrogels added to soil for water retention to biofilms and biological tissues in complex environments.8–14 Therefore, we ask: are there general principles that dictate how obstructions influence growth and expansion? And if so, how do we discover them?When the growth/expansion of a body is resisted by surrounding obstructions, large and spatially-nonuniform stresses can develop, influencing subsequent growth/expansion in turn.15,16 Being able to understand the distribution and magnitude of these stresses is thus a necessary step in the development of widely-applicable, predictive models of growth and expansion. However, model systems in which the coupling between growth and stress can be systematically studied in structured environments are scarce. Here, we address this issue using studies of spherical hydrogel beads swelling in 3D-printed obstacle arrays with defined geometries. Hydrogels are cross-linked networks of hydrophilic polymers that can absorb large amounts of water and swell while still retaining integrity. As a result, they are extensively used in biomedical, environmental, and manufacturing applications, and have well-characterized and highly-tunable properties such as their degree of swelling and elasticity.17–20 Indeed, the comprehensive theoretical literature on hydrogel swelling makes computations of shape and internal stresses accessible for a variety of boundary conditions. While much work has focused on the case of a hydrogel swelling while adhered to another material,21–30 non-adhered swelling around obstructions has received more limited attention,22,31–35 often in the context of indentation testing.
Our study extends this body of work. First, we use experiments to directly visualize how hydrogel swelling is altered by obstacles of systematically-varying geometries. When obstacles are positioned further apart, the hydrogel swells through the spaces between them and maintains its integrity. By contrast, when the obstacles are closer together, we observe a dramatic phenomenon: the hydrogel fractures, repeatedly tearing itself apart as it swells! We then use theory and simulations to rationalize these observations, and importantly, quantify and understand the distribution of stresses. Taken together, our work provides a prototypical example of obstructed growth/expansion and uncovers complex swelling behaviors and mechanical instabilities that can result during this process—highlighting the rich physics waiting to be explored in this area of soft mechanics.
II. Experiments
Our experimental platform is schematized in Fig. 1(A) and detailed in Materials and methods (Section VI). To define the obstacles, we 3D-print four rigid cylindrical columns of radius robs to be placed an equal distance rctr from a central point; in the experiments, we vary robs and rctr between 2.5–15 mm and 7.5–25 mm, respectively. The cylinders are securely attached to horizontal, parallel laser-engraved acrylic plates spaced vertically by a fixed amount, Δz = 40 mm (see ESI,† Section B for a discussion on the selection of this value). Importantly, these plates are transparent, permitting direct visualization of a hydrogel as it swells between the cylindrical obstacles and parallel plates. Hence, at the beginning of each experiment, we place a spherical polyacrylamide hydrogel bead of initial radius ∼6 mm (initial state characterized in ESI,† Section A) in the center and submerge the entire apparatus in a bath of ultrapure Milli-Q water—thereby initiating swelling, which we track using a camera focused on the top plate.We first examine the case of obstacles that are spaced further apart. As the hydrogel swells, it contacts the top and bottom plates, as well as the cylinders, and continues to swell through the space between them (Fig. 1(B) and Movie S1, ESI†). It eventually reaches an unchanging four-lobed equilibrium shape. As the hydrogel swells, the yellow dye fixed in its polymer network becomes more dilute; thus, the color intensity serves as a proxy for the local polymer concentration. However, the deformed 3D shape of the hydrogel makes it challenging to extract quantitative information about relative expansion from a purely top-down view. We leave this effort for future work.
The case of closer-spaced obstacles of the same size is dramatically different. We observe similar behavior to the previous case of less confinement at early times: the hydrogel contacts the surrounding surfaces and swells through the space between them. As these lobes continue to swell, however, cracks abruptly form at the hydrogel surface (48 h in Fig. 1(C)), reflecting the development of large stresses during obstructed swelling. Remarkably, this sequence then continues, resulting in elaborate, multi-step fracturing of the hydrogel as it swells, repeatedly ejecting fragments of the hydrogel outward (Fig. 1(C) and Movie S2, ESI†). The fracturing process is dynamic: As cracks propagate through compressed areas, releasing stresses, those regions are then able to increase their solvent content and swell. The process eventually stops as the central hydrogel body reaches its final equilibrium degree of swelling. Another representative example of a fracturing hydrogel with a different obstacle geometry is shown in Movie S3 (ESI†). The fracturing process varies significantly between samples, reflecting the acute sensitivity of crack formation and propagation on the random imperfections in the hydrogel and the complex topography arising from previous fracturing.36–38
These observations suggest that, when appropriately obstructed, a growing/expanding body can tear itself apart. To characterize the dependence of this phenomenon on confinement, we repeat these experiments with obstacles of varying sizes robs and spacings rctr. We observe a similar phenomenon in all cases, as summarized in the state diagram in Fig. 2. When the obstacles are far apart, the hydrogel swells and retains its integrity (□), while when the obstacles are closer i.e., rctr is below a threshold value, the hydrogel repeatedly self-fractures as it swells (×). The fracturing threshold also depends on the size of the obstacles: For a given rctr, fracturing occurs below a threshold value of robs. The finding that smaller obstacles promote fracture is reminiscent of wire cutting tests in fracture mechanics, in which thin wires pushed into soft materials induce cutting.39,40 The two geometric parameters rctr and robs thus delineate a boundary between swelling without fracture and obstructed swelling causing fracture, as shown by the light and dark green regions, respectively, in Fig. 2. Intuitively, this non-trivial dependence of the onset of fracturing on both obstacle spacing and size reflects the balance between the osmotic pressure driving swelling—which is set by the difference between the solvent chemical potential in the unswollen hydrogel compared to at its boundary—and the tensile stresses that develop in the hydrogel as it swells against narrow obstacles.8,41 We theoretically model and computationally quantify this balance in the following sections.
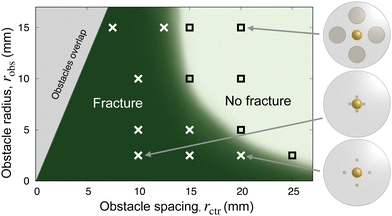 | ||
| Fig. 2 Experiments reveal a hydrogel fracture threshold that depends on obstacle radius and spacing. Each □ indicates an experiment in which the hydrogel reached an intact equilibrium shape as in Fig. 1(B), while each × indicates an experiment that resulted in fracture as in Fig. 1(C). Schematics show a top view of the obstacle geometries for the indicated points. The grey excluded region in the top left shows parameters for which the obstacles would overlap. The green background shading provides a guide to the eye. | ||
To demonstrate the generality of this phenomenon, we repeat our experiments in fully 3D granular packings, which more closely mimic the obstructions experienced by hydrogels in many applications.42–51 Our previous experiments8 using this platform used a solvent that promoted only slight hydrogel swelling, and therefore accessed the case of weak confinement; however, repeating these experiments with a solvent that promotes more hydrogel swelling indeed gives rise to self-fracturing, as shown in Fig. S4 (ESI,† Section C). Thus, this phenomenon of obstructed growth/expansion causing fracture arises not just in idealized geometries, but also in more realistic complex spaces.
III. Theory and simulations
What are the essential physical principles that govern this phenomenon? To address this question, we develop finite element simulations that incorporate the energetic penalty of contacting obstructions into a model of hydrogel swelling based on classic Flory–Rehner theory. Our goal is to better understand the complex distribution of stresses that arises during obstructed swelling, not to quantitatively capture all the features of the experiments; as such, we use a simplified two-dimensional (2D) model that permits straightforward visualization of stresses and thereby enables us to develop an intuitive and analytic description of the underlying physics. The dimensional reduction is discussed at length in ESI,† Section D.We describe stretching of the hydrogel polymer network and solvent-polymer interactions with the commonly-used free energy density:22–24,33,52,53
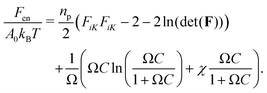 | (1) |
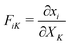 is the deformation gradient tensor, with
is the deformation gradient tensor, with 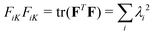 in terms of principal stretches λi. Following standard conventions, deformed/current configurations are denoted by lowercase letters and dry reference configurations are denoted by capital letters unless otherwise noted.16 The second term describes the mixing free energy: Ω is the area of a solvent molecule, C is the nominal concentration of solvent (number of solvent molecules per unit dry reference area), and χ is the Flory–Huggins interaction parameter. Both terms are scaled by the product of the Boltzmann constant and temperature, kBT.
in terms of principal stretches λi. Following standard conventions, deformed/current configurations are denoted by lowercase letters and dry reference configurations are denoted by capital letters unless otherwise noted.16 The second term describes the mixing free energy: Ω is the area of a solvent molecule, C is the nominal concentration of solvent (number of solvent molecules per unit dry reference area), and χ is the Flory–Huggins interaction parameter. Both terms are scaled by the product of the Boltzmann constant and temperature, kBT.
Given that the hydrogel network is held together by permanent cross-links between its polymer chains, we additionally assume that it only changes volume by uptake of solvent, which allows us to express concentrations in terms of the deformation: det(F) = 1 + ΩC. We require the chemical potential μ to be zero on the boundary of the hydrogel to mimic submerging it in pure water, as in the experiments. To impose this boundary condition, we perform the standard Legendre transform of eqn (1) and derive a new free energy ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) en in terms of μ as
en in terms of μ as ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) en(xi,μ) = Fen(xi,C) − μC.23 Finally, we model contact by imposing an energy penalty for overlap between the hydrogel and obstacles; as detailed in Materials and methods, our results are insensitive to the choice of this parameter. Note that the chemical potential boundary condition μ = 0 is enforced in the regions of contact between the hydrogel and the obstacles. It would be interesting to also consider the impact of dynamic boundary conditions in this problem: for example, a boundary condition requiring no normal solvent flux in the regions where the hydrogel contacts obstacles could be imposed.33 Since we focus on equilibrium quantities in this work, we use a constant chemical potential boundary for simplicity.
en(xi,μ) = Fen(xi,C) − μC.23 Finally, we model contact by imposing an energy penalty for overlap between the hydrogel and obstacles; as detailed in Materials and methods, our results are insensitive to the choice of this parameter. Note that the chemical potential boundary condition μ = 0 is enforced in the regions of contact between the hydrogel and the obstacles. It would be interesting to also consider the impact of dynamic boundary conditions in this problem: for example, a boundary condition requiring no normal solvent flux in the regions where the hydrogel contacts obstacles could be imposed.33 Since we focus on equilibrium quantities in this work, we use a constant chemical potential boundary for simplicity.
To visualize and track hydrogel deformation during obstructed swelling, along with the concomitant development of internal stresses, we implement this model in FEniCS,54 an open-source finite element platform. Our simulations consider a circular hydrogel swelling around four fixed obstacles. Although our primary focus is the stress distribution in the hydrogel at equilibrium, we simulate the full dynamics of obstructed swelling to provide numerical stability and ensure that there is a realistic path from the initial to the final equilibrium swollen state (ESI,† Section E).
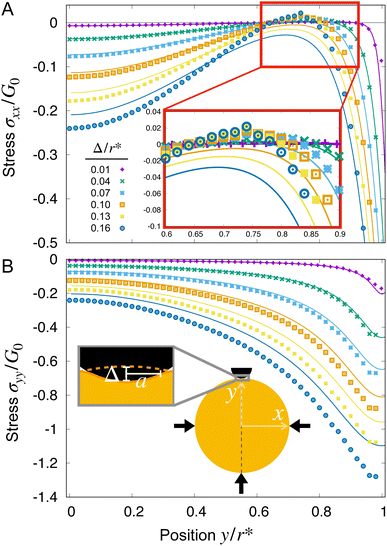
We begin by examining hydrogel swelling around obstacles that have the same size, but varying spacing—just as in the experiments shown in Fig. 1(B) and (C). Four representative examples, varying from the case of weak to strong confinement, are shown in Fig. 3(A)–(D). The corresponding maximum tensile and compressive principal stresses on the line connecting the hydrogel center to an obstacle center are plotted in panels (E) and (F). We quantify these variations using Δ/r* ≡ (r* − rctr)/r*, where r* is the equilibrium, fully-swollen, unconfined radius of the hydrogel and Δ is the difference between r* and the distance from the center to the closest obstacle rctr. The case of weak confinement in (A) has Δ/r* = 0.02, increasing to Δ/r* = 0.6 for the case of strong confinement in (D). As seen by the color maps of solvent concentration and principal stresses in panel (A), in this limit of weak confinement, the hydrogel is barely deformed and the resultant stresses are not visible when plotted on the same scale as (B–D). Thus, as we describe in Section IIIA, the hydrogel stresses can be captured analytically using linear theories in this regime. Increasing hydrogel confinement to the point shown in panel (B) causes the magnitudes of the stresses to increase (panels E and F), but they still remain primarily localized near the obstacles; as discussed in Sections IIIB and C, the largest compressive stresses can still be described by linear theory, but the largest tensile stresses require consideration of a geometric nonlinearity due to their connection to the rotation of material as it conforms to the obstacle boundary. As the separation between obstacles decreases further, large compressive stresses span the entirety of the hydrogel (panel C), eventually triggering a symmetry-breaking instability (panel D) as discussed in Section IIID. Finally, while our model is not suitable to treat fracture directly, we discuss the connection between our calculations of stresses and the experimental observations of swelling-induced self-fracture in Section IV.
 | ||
| Fig. 3 Finite element simulations quantify how the equilibrium strains and stresses that develop in the hydrogel depend on obstacle geometry. (A)–(D) Maps of the solvent concentration per unit dry reference area with the finite element grid superimposed (left column) and the principal stresses (right column) in the hydrogel at equilibrium, normalized by the area of the solvent molecule Ω and the fully-swollen hydrogel shear modulus G0, respectively. Confinement increases from top to bottom, in this case by changing the obstacle spacing with fixed robs/r* = 0.3; thus, Δ/r* = 1 − rctr/r* = 0.02, 0.1, 0.5, 0.6 from top to bottom, where Δ is the difference between the unconfined swollen hydrogel radius r* and the distance to an obstacle from the center rctr. Each mesh point in the right column bears two perpendicular lines, oriented and scaled according to the direction and magnitude of the principal stresses σ1, σ2 at that point, and colored such that compressive stresses are blue and tensile stresses are red. The stresses exceed the range of the color bar for (C) and (D). (E) and (F) Points show the maximum principal tensile and compressive stresses obtained from the simulations, taken along the line connecting the hydrogel center to an obstacle center, at this same fixed robs/r* = 0.3 as a function of Δ/r*. Stresses are again normalized by G0. The values of Δ/r* corresponding to (A)–(D) are marked by the grey diamonds. The predictions of linear indentation theory (solid lines) agree well with the simulation data for small Δ/r* (purple shaded region). With increasing Δ/r*, the maximum tension exceeds linear predictions, but can be reproduced by a geometrically nonlinear elastic theory with a linear constitutive law (blue shaded region, ESI,† Section H). For compression, the linear theory is accurate over a larger range of Δ/r*, but the geometrically nonlinear theory cannot explain the deviations; instead, an elastic model incorporating material nonlinearities better captures the data (eqn (10) and Fig. S9, ESI†). As Δ/r* increases even further, the hydrogel exhibits a symmetry-breaking instability (D, red shaded region). | ||
A. Weak confinement
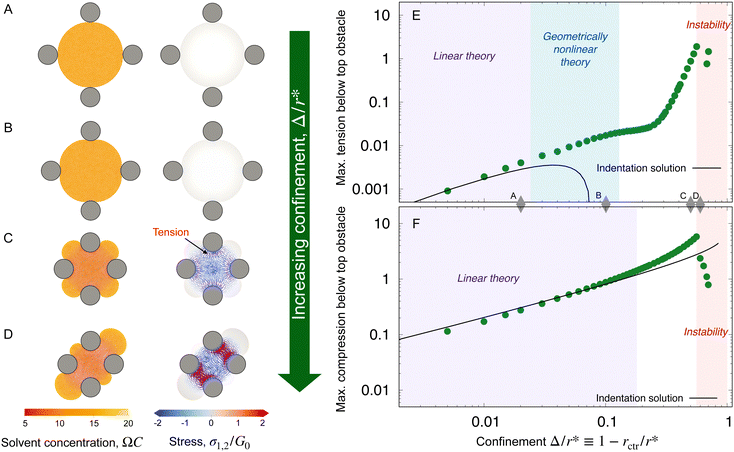
Consider a hydrogel disk that has swollen around obstacles to reach equilibrium. The chemical potential is spatially uniform and therefore all solvent transport has stopped. Nonetheless, due to contact with the obstacles, the distribution of solvent is inhomogeneous through the hydrogel: solvent preferentially enters the uncompressed lobes of the hydrogel between the obstacles, as shown by the yellow color in Fig. 1(B).41 Now, consider another hydrogel that was first swollen, unobstructed, to its equilibrium size, and then slowly and incrementally squeezed by an identical set of obstacles moving towards its center, acting as four indenters. Solvent must exit the hydrogel where it is indented by the obstacles; recall our condition 1 + ΩC = det(F). For the same final obstacle geometry, these two scenarios must have identical solvent distributions and stress profiles at equilibrium. Thus, the long time limit of obstructed swelling can be treated as an indentation problem, which is well-studied in the limit of small deformations. Making this analogy between obstructed swelling and indentation allows us to apply lessons from a large body of literature on linear contact mechanics and poroelasticity to derive expressions for the stress tensor in the hydrogel.31,32,55,56Assuming that deformations relative to the fully swollen state are small, we linearize eqn (1) to find effective linear elastic parameters in equilibrium (ESI,† Section F,57,58). In particular, for a 2D hydrogel, the effective equilibrium Poisson's ratio ν and Young's modulus E are given by
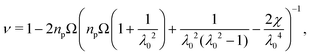 | (2) |
| E = 2(1 + ν)npkBT, | (3) |
Given these effective equilibrium elastic parameters, we solve for the stresses in the hydrogel as a 2D linear contact mechanics problem (ESI,† Section G,59,60). This approach provides expressions for the stress tensor σij along the line directly beneath the top obstacle as a function of y as shown in Fig. 4(B):
 | (4) |
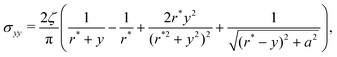 | (5) |
| σxy = 0, | (6) |
 | (7) |
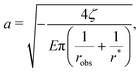
Given these analytical expressions, we next ask: under what confinement regimes (as parameterized by Δ/r*) does this linearized theory work, and when does it break down? And since we would like to gain an intuitive understanding of obstructed swelling-induced fracture, how does the maximal principal tensile stress—which can be used to approximate material strength36—vary with confinement? To address these questions, we first re-cast eqn (4) and (5) in terms of Δ/r* to facilitate direct comparison with the results of the nonlinear simulations. To do so, we integrate the strain 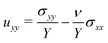 using eqn (4) and (5) to find the displacement at the surface of the indenter relative to the center of the hydrogel, and expand the result to linear order in a/r*. This procedure gives
using eqn (4) and (5) to find the displacement at the surface of the indenter relative to the center of the hydrogel, and expand the result to linear order in a/r*. This procedure gives
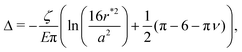 | (8) |
As expected, when Δ/r* ≪ 1, the linearized indentation solution agrees well with the nonlinear simulation results, while as Δ/r* increases, the discrepancy between the two becomes more apparent. In particular, as exemplified by the data for Δ/r* = 0.16 (dark blue circles) and Δ/r* = 0.13 (yellow squares) in Fig. 4, the linear solution underestimates the compression at both the center y = 0 and boundary y = r* of the hydrogel, as well as the tension that builds up at y/r* ≈ 0.75 (Fig. 4(A), inset). Indeed, though tension (σxx > 0) does appear in the linear solutions for small Δ/r*, it disappears with increasing Δ/r*, in contrast to the simulation results (see arrow in Fig. 3(C), for example).
Since we are interested in fracture behavior, we thus focus our attention on the maximal value of this tensile stress for the same illustrative case of robs/r* = 0.3. By symmetry, we expect the largest stresses to lie beneath each obstacle, since stresses must go to zero at the hydrogel boundary away from obstacles in the weak confinement regime. Moreover, because the straight edges of the finite element mesh can introduce spurious tensile forces at the edge of the hydrogel-obstacle contact (described further in ESI,† Section I), we plot the maximum and minimum values of the principal stresses along the x = 0 line shown in the schematic inset of Fig. 4(B). The results are displayed in Fig. 3(E) and (F). As noted in Fig. 4(A), the linear theory only predicts the presence of tension for small confinement before deviating from the nonlinear simulation results at Δ/r* ≳ 0.02, as shown by the solid line and points in Fig. 3(E), respectively. Interestingly, however, linear theory captures the maximum compressive stress over a broader range of confinement, shown by the solid line in Fig. 3(F), which agrees well with the simulation data up to Δ/r* ≈ 0.2.
Thus, while linear indentation theory can predict both tensile and compressive stresses during obstructed swelling in weak confinement, it underpredicts both for larger deformations—suggesting that the assumptions made in the linear theory are no longer valid. We revisit these assumptions for both tension and compression in the next two sections, respectively.
B. Tension beyond the linear regime
The linear theory in the previous section relies on a number of assumptions that can fail as deformations increase:(1) The effective equilibrium elastic parameters [eqn (2) and (3)] are independent of strain,
(2) The stress is linearly related to the strain,
(3) The strain tensor is linear in the displacements.
To assess the validity of these assumptions, we compare the results of our full nonlinear simulations to those of more complex elastic models that incorporate material/geometric nonlinearities.
First, we explore the limits of assumption 1 by relaxing assumptions 2 & 3. Specifically, we compare the hydrogel simulation results to those of a compressible neo-Hookean elastic material with elastic parameters given by eqn (2) and (3). As detailed in ESI,† Section F, the neo-Hookean model closely reproduces the stress profiles of the hydrogel simulations over a broad range of Δ/r* up to ≈0.4, well beyond the limits of the linear theory at ∼0.02. Therefore, nonlinearities due to the effective elastic parameter mapping can be neglected up to this point.
Next, we explore the limits of assumption 2 by relaxing assumption 3. Specifically, we use a St. Venant–Kirchhoff elastic model with strain tensor 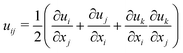 ; thus, the strain tensor is nonlinear in displacements, but we still require that the hydrogel material follows a linear constitutive law. Note that derivatives are taken with respect to coordinates in the unobstructed, fully-swollen state, denoted here with lowercase letters for simplicity of presentation. Intriguingly, as detailed in ESI,† Section H, the St. Venant–Kirchhoff model quantitatively reproduces the maximum principal tensile stress in the hydrogel simulations up to Δ/r* ≈ 0.1, well beyond the limit of the linear theory at ≈0.02. Hence, the excess tension σxx that develops beneath the obstacles just beyond the linear regime is driven by geometric nonlinearity, related to the rotations of the hydrogel material as it accommodates the obstacles during swelling, and does not require a nonlinear constitutive relationship. At even larger displacements Δ/r* > 0.1, the St. Venant–Kirchhoff simulations are unstable and we expect that both geometric and material nonlinearities contribute to the tensile stress.
; thus, the strain tensor is nonlinear in displacements, but we still require that the hydrogel material follows a linear constitutive law. Note that derivatives are taken with respect to coordinates in the unobstructed, fully-swollen state, denoted here with lowercase letters for simplicity of presentation. Intriguingly, as detailed in ESI,† Section H, the St. Venant–Kirchhoff model quantitatively reproduces the maximum principal tensile stress in the hydrogel simulations up to Δ/r* ≈ 0.1, well beyond the limit of the linear theory at ≈0.02. Hence, the excess tension σxx that develops beneath the obstacles just beyond the linear regime is driven by geometric nonlinearity, related to the rotations of the hydrogel material as it accommodates the obstacles during swelling, and does not require a nonlinear constitutive relationship. At even larger displacements Δ/r* > 0.1, the St. Venant–Kirchhoff simulations are unstable and we expect that both geometric and material nonlinearities contribute to the tensile stress.
How exactly does geometric nonlinearity generate tension during obstructed swelling? We answer this question using an illustrative argument reminiscent of the derivation of the Föppl–von Kármán equation.61 As detailed in Materials and methods, we first find the variation of the integrated St. Venant–Kirchhoff strain energy function with respect to displacements, which can be written in terms of the second Piola–Kirchhoff stress tensor, σPKij. In 2D, this quantity gives the stress component in a material direction i perpendicular to a line that has unit length and normal j in the reference configuration.62 We then make approximations specific to our obstacle geometry. Ultimately, we find
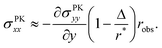 | (9) |
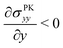 (Fig. 4(B)), and therefore σPKxx > 0 indicating tension. Thus, geometric nonlinearity generates tension beneath an indenter perpendicular to the indentation direction, qualitatively matching our simulations.
(Fig. 4(B)), and therefore σPKxx > 0 indicating tension. Thus, geometric nonlinearity generates tension beneath an indenter perpendicular to the indentation direction, qualitatively matching our simulations.
C. Compression beyond the linear regime
A notable result shown in Fig. 3 is that while linear indentation theory predicts tensile stresses for Δ/r* < 0.02, it captures the compressive stresses over a broader range, up to Δ/r* ≈ 0.2. Intuitively, this robustness is due to the fact that the large compressive stresses appear perpendicular to the obstacles and are relatively unaffected by rotations of the hydrogel material around the obstacles. Which nonlinearities drive the deviations that arise at even larger displacements? We answer this question by following the same procedure as in the previous section, detailed further in ESI,† Sections F and H. In contrast to the case of tension, we do not find any parameters for which the St. Venant–Kirchhoff model is more accurate than the linear model. Furthermore, as shown in Fig. S9 (ESI†), past the linear regime, the compressive (Cauchy) stress underneath the top obstacle scales like that of a compressible neo-Hookean elastic material experiencing uniaxial compression, with the principal stretch parallel to indentation set to λ1 = 1 − Δ/r* and the principal stretch perpendicular to the indentation set to 1: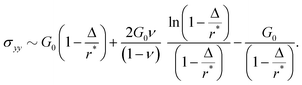 | (10) |
D. Symmetry-breaking instability
A striking phenomenon arises in our simulations as the separation between obstacles decreases further: as shown in Fig. 3(D), the hydrogel displays a symmetry-breaking instability and swells preferentially along a diagonal. Why does this instability arise? Inspecting the spatial distribution of compressive stresses provides a clue. As the hydrogel swells in increasing amounts of confinement, its central core becomes increasingly compressed (see, e.g., Fig. 3(C) and (D)). Compressing this circular core along a single axis, forming an ellipse, requires less energy than does compressing this core isotropically. Thus, as confinement increases, one expects the case of asymmetric swelling to be energetically preferred, leading to this instability—as described further in ESI,† Section J.IV. Comparison between simulations and experiments
Our theoretical analyses and simulations capture the essential features of the hydrogel deformation observed in experiments (e.g., Fig. 1(B) and 3(C)). They also enabled us to explore how stresses develop during obstructed swelling more generally (Fig. 3 and 4). While our model is not suitable to directly treat the swelling-induced self-fracture observed experimentally, the simulated stresses help rationalize this phenomenon. To this end, we compare the simulations to the experimental state diagram shown in Fig. 2 by plotting the maximum principal tensile and compressive stresses as a function of robs and rctr. The results, shown in Fig. 5, bear a compelling resemblance to the experimental results. In particular, the convexity and shape of the experimental fracture boundary are similar to the simulated contours of maximum principal stress. Indeed, appealing to a commonly-used fracture criterion for brittle materials,36 we expect that hydrogel fracture occurs when the maximum tensile stress exceeds a threshold—whose exact value would establish the position of the experimental fracture boundary in Fig. 5(A). We conjecture that this threshold is reached prior to the symmetry-breaking instability revealed by the simulations, as we do not observe it in our experiments; experiments using tougher hydrogels than those studied here may be a useful way to probe this deformation mode in future work.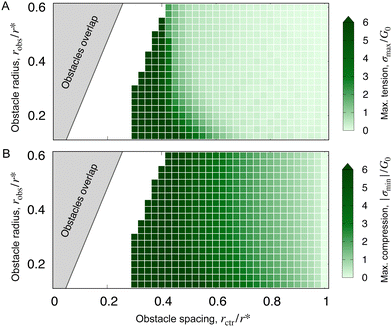 | ||
| Fig. 5 Simulations predict that hydrogel stresses grow as obstacles are made smaller and brought closer together in a manner similar to the experimental findings. (A) and (B) Most positive (tensile) principal stress σmax and magnitude of the most negative (compressive) principal stress |σmin|, respectively, again normalized by the fully-swollen shear modulus G0. Each (light or dark) green square corresponds to a simulation. As in Fig. 2, the grey region corresponds to overlapping obstacles. Note that we take the maxima/minima over the entire mesh, rather than just beneath an obstacle, to avoid non-monotonic behavior in the instability regime. | ||
V. Discussion
Despite the ubiquity of obstructed growth and expansion in our everyday lives, how exactly this process generates large, spatially non-uniform stresses in a body—and how these stresses influence its subsequent growth/expansion in turn—has remained challenging to systematically study. One reason is the lack of model systems in which this intricate coupling between growth and stress can be probed both experimentally and theoretically. We addressed this need by studying the swelling of spherical hydrogel beads in obstacle arrays of tunable geometries. Our experiments revealed a striking phenomenon: under weak confinement, a hydrogel retains its integrity and assumes a symmetric, four-lobed clover-like shape, while in stronger confinement, it repeatedly tears itself apart as it swells. We elucidated the underlying physics by adopting established models of hydrogel swelling to map the tensile and compressive stresses arising during swelling. In particular, we found that when a hydrogel is weakly deformed, stresses are well-described by linear indentation theory, while as a hydrogel is increasingly deformed, geometric and material nonlinearities engender large tensile and compressive stresses tangential and normal to the obstacles, respectively, driving the hydrogel towards fracture.Because our study represents a first step toward fully unravelling the mechanics of obstructed growth and expansion, it necessarily has limitations. For example, while the experimental results shown in Fig. 2 revealed a fracture threshold that varies with obstacle geometry, quantitative comparison to theory and simulation will require more precise control over the system geometry and dimensionality,63,64 both in experiments and in the model, along with a more detailed treatment of the microscopic processes underlying fracturing.65–70 Moreover, many more experimental trials near this threshold and with hydrogels of varying mechanical properties, along with high-resolution imaging of crack propagation,71 will be useful in characterizing the details of the fracturing process, which likely depend on the presence of microscopic imperfections in the hydrogel. Finally, although here we restricted our attention to the case of rigid obstacles, many scenarios involve growth/expansion around compliant constraints—e.g., the development of biofilms, tissues, and organs in the body,72–75 with potential implications for biological function.76,77 Extending our study to the case of deformable obstacles would therefore be a useful direction for future work.
Our results may be especially relevant to diverse applications of hydrogels, and other swellable materials, that frequently involve their confinement in tight and tortuous spaces. For example, driven by growing demands for food and water, hydrogels are increasingly being explored as additives to soils to absorb and release water to plants and therefore reduce the burden for irrigation.42,47–50 They are also widely adopted in other applications, such as oil recovery, construction, mechanobiology, and filtration, all of which involve hydrogel swelling in confinement.43–46 A common assumption made in all these cases is that the hydrogel retains integrity as it swells; however, our study indicates that these applications should be evaluated for the possibility of swelling-induced self-fracture. Indeed, fracture could lead to the production and dispersal of many small hydrogel fragments, potentially reducing their utility and leading to environmental contamination. This process should therefore be carefully considered in a wide range of real-world contexts.
VI. Materials and methods
A. Experimental design
To create the obstacle array, we 3D print cylindrical columns in Clear v4 resin using a Form3+ industrial 3D printer (Formlabs), and cut the acrylic plates using an Epilog Laser Mini 24 laser cutter and engraving system. We secure the columns to the acrylic plates using a twist-and-lock mechanism. The hydrogels are polyacrylamide beads (“water gel beads” obtained from Jangostor) and are stored in a screw cap container prior to experiments; as such, they experience some slight swelling due to ambient humidity. The hydrogel beads have varying sizes and colors, but all appear to have the same swelling behavior and beads of similar sizes are used for experiments (ESI,† Section A). These hydrogel beads were extensively characterized in our previous experiments,8,41 which provide additional detail.Early in the swelling process (e.g. 2 h in Fig. 1(B) and (C)), each hydrogel appears out of focus since it has not yet made contact with the top plate (focal plane for imaging), and cusps are visible on its surface due to differential swelling as water enters the hydrogel from its outer surface.21,78–80 We verify that the hydrogel beads swell to an equilibrium shape without rupturing when no obstacles are present (either with or without the 40 mm z-confinement), indicating the transient stresses are insufficient to drive fracture as in other less tough gels.71,81 Because the plates and obstacles are made of acrylic or a polymeric resin, respectively, we do not expect or see evidence of adhesion between the polyacrylamide hydrogel surface and the confining surfaces. For experiments in which we image the entire process of obstructed swelling, we verify that the hydrogel reaches an equilibrium shape (in the cases of no fracturing) when its size/shape does not noticeably change for at least three hours. In the trial shown in Fig. 1, for example, equilibration took 88 h. In other trials where we do not image the entire process of obstructed swelling, we let the hydrogel swell either until fracture has occurred or for at least 40 h past the time to fracture for a trial with the same robs and a smaller rctr. If we already recorded an outcome of 'no fracture' for a trial with the same robs and a smaller rctr, we waited a minimum of 8 h beyond the equilibration time for an imaged reference trial with similar geometry. Each symbol in Fig. 2 represents a single experiment.
B. Simulation design
We create meshes using FEniCS's built-in mesh generation function with cell size set such that there are 30 vertices along the radius. We confirmed that this mesh resolution was sufficient for numerical convergence. We set npΩ = 0.001 and χ = 0.3. The penalty function is integrated over the hydrogel boundary, and is given by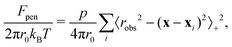 | (11) |
 . Thus, when evaluated at positions away from any obstacles, the penalty function is zero, but takes a large positive value inside the obstacles. We set p = 6.25π/r04 to generate the data shown in this text, and have verified that using p = 62.5π/r04 produces the same results.
. Thus, when evaluated at positions away from any obstacles, the penalty function is zero, but takes a large positive value inside the obstacles. We set p = 6.25π/r04 to generate the data shown in this text, and have verified that using p = 62.5π/r04 produces the same results.
Following the suggestions of ref. 33, 82 and 83, we use the backwards Euler scheme for time integration (see ESI,† Section E for further discussion of dynamics), Taylor–Hood mixed elements (quadratic elements for the displacement field and linear elements for the chemical potential field), and early time ramping of the chemical potential boundary condition to ensure numerical stability. The Newton–Raphson method is used at each time step, and equilibrium is defined by when zero iterations are required for a step to complete.
To find the maximum/minimum principal Cauchy stresses, we first calculate the eigenvalues of the stress tensor for a given displacement field. We project these eigenvalue fields onto a function space of discontinuous Lagrange elements of order 1. We then compare the eigenvalues defined on this mesh. The largest positive eigenvalue is the maximum principal (tensile) stress σmax, and the most negative eigenvalue is the minimum principal (compressive) stress, σmin. To find the minimum and maximum stresses beneath an obstacle (data in Fig. 3(E) and (F)), we instead project the stress tensor onto the vertical line directly beneath the top obstacle. The minimum value of σyy and the maximum value of σxx along this line are plotted as the below top obstacle minimum and maximum stresses respectively.
C. Tension generated by geometric nonlinearity
We describe the argument leading up to eqn (9) in more detail, which demonstrates how tension can appear beneath an obstacle when a nonlinear strain tensor is used. The variation of the integrated St. Venant–Kirchhoff strain-energy function with respect to displacements in terms of the second Piola–Kirchhoff stress tensor is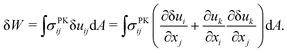 | (12) |
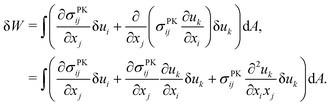 | (13) |
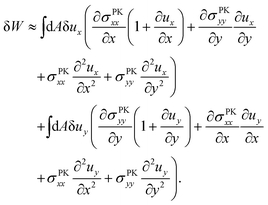 | (14) |
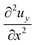 , is determined by the curvature of the obstacle, 1/robs. With these substitutions, the equilibrium condition becomes
, is determined by the curvature of the obstacle, 1/robs. With these substitutions, the equilibrium condition becomes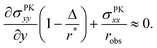 | (15) |
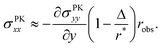 | (16) |
Author contributions
Conceptualization: AP, AK, SSD. Investigation: AP, CA, JFL. Writing – original draft: AP, AK, SSD. Writing – review & editing: AP, CA, JFL, AK, SSD.Conflicts of interest
There are no conflicts to declare.Acknowledgements
It is a pleasure to acknowledge John Kolinski, Amaresh Sahu, and Carolyn Bull for helpful discussions, as well as funding from the NSF through the Princeton MRSEC DMR-2011750, the Project X Innovation Fund, a Princeton Materials Science Postdoctoral Fellowship (AP), and the Camille Dreyfus Teacher-Scholar Program of the Camille and Henry Dreyfus Foundation (SSD). This material is also based upon work by SSD supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Geothermal Technologies Office (GTO) Innovative Methods to Control Hydraulic Properties of Enhanced Geothermal Systems Award Number DE-EE0009790.References
- M. Ding, X. Han, S. Wang, T. F. Gast and J. M. Teran, A thermomechanical material point method for baking and cooking, ACM Trans. Graph., 2019, 38, 1, DOI:10.1145/3355089.3356537.
- I. Taylor, K. Lehner, E. McCaskey, N. Nirmal, Y. Ozkan-Aydin, M. Murray-Cooper, R. Jain, E. W. Hawkes, P. C. Ronald, D. I. Goldman and P. N. Benfey, Mechanism and function of root circumnutation, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018940118, DOI:10.1073/pnas.2018940118.
- A. Borsdorf and A. Haller, Urban montology: Mountain cities as transdisciplinary research focus, The Elgar Companion to Geography, Transdisciplinarity and Sustainability, 2020, 140–154, DOI:10.4337/9781786430106.
- R. A. Byrne, M. Joner and A. Kastrati, Stent thrombosis and restenosis: what have we learned and where are we going? The Andreas Grüntzig Lecture ESC 2014, Eur. Heart J., 2015, 36, 3320, DOI:10.1093/eurheartj/ehv511.
- E. Kuhl, R. Maas, G. Himpel and A. Menzel, Computational modeling of arterial wall growth, Biomech. Model. Mechanobiol., 2007, 6, 321, DOI:10.1007/s10237-006-0062-x.
- J. Cheng and L. T. Zhang, Finite Element Simulation of In-Stent Restenosis with Tissue Growth Model, J. Biomed. Sci. Eng., 2021, 14, 33, DOI:10.4236/jbise.2021.142005.
- L. F. Cabeza, A. Castell, M. Medrano, I. Martorell, G. Pérez and I. Fernández, Experimental study on the performance of insulation materials in Mediterranean construction, Energy Build., 2010, 42, 630, DOI:10.1016/j.enbuild.2009.10.033.
- J.-F. Louf, N. B. Lu, M. G. O’Connell, H. J. Cho and S. S. Datta, Under pressure: Hydrogel swelling in a granular medium, Sci, Adv., 2021, 7, eabd2711, DOI:10.1126/sciadv.abd2711.
- D. J. Beebe, J. S. Moore, J. M. Bauer, Q. Yu, R. H. Liu, C. Devadoss and B.-H. Jo, Functional hydrogel structures for autonomous flow control inside microfluidic channels, Nature, 2000, 404, 588, DOI:10.1038/35007047.
- S. Alben, Packing of elastic rings with friction, Proc. R. Soc. A, 2022, 478, 20210742, DOI:10.1098/rspa.2021.0742.
- E. K. Chu, O. Kilic, H. Cho, A. Groisman and A. Levchenko, Self-induced mechanical stress can trigger biofilm formation in uropathogenic Escherichia coli, Nat. Commun., 2018, 9, 1, DOI:10.1038/s41467-018-06552-z.
- S. J. Streichan, C. R. Hoerner, T. Schneidt, D. Holzer and L. Hufnagel, Spatial constraints control cell proliferation in tissues, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5586, DOI:10.1073/pnas.1323016111.
- A. Bengough, C. Croser and J. Pritchard, A biophysical analysis of root growth under mechanical stress, Plant Roots-From Cells to Systems, Springer, 1997, pp. 107–116 DOI:10.1007/978-94-011-5696-7_11.
- B. Alric, C. Formosa-Dague, E. Dague, L. J. Holt and M. Delarue, Macromolecular crowding limits growth under pressure, Nat. Phys., 2022, 18, 411, DOI:10.1038/s41567-022-01506-1.
- D. Ambrosi, M. Ben Amar, C. J. Cyron, A. DeSimone, A. Goriely, J. D. Humphrey and E. Kuhl, Growth and remodelling of living tissues: perspectives, challenges and opportunities, J. R. Soc., Interface, 2019, 16, 20190233, DOI:10.1098/rsif.2019.0233.
- A. Goriely, The mathematics and mechanics of biological growth, Springer, 2017, vol. 45 DOI:10.1007/978-0-387-87710-5.
- Y. S. Zhang and A. Khademhosseini, Advances in engineering hydrogels, Science, 2017, 356, eaaf3627, DOI:10.1126/science.aaf3627.
- M. Oyen, Mechanical characterisation of hydrogel materials, Int. Mater. Rev., 2014, 59, 44, DOI:10.1179/1743280413Y.0000000022.
- K. Deligkaris, T. S. Tadele, W. Olthuis and A. van den Berg, Hydrogel-based devices for biomedical applications, Sens. Actuators, B, 2010, 147, 765, DOI:10.1016/j.snb.2010.03.083.
- Y. Guo, J. Bae, Z. Fang, P. Li, F. Zhao and G. Yu, Hydrogels and Hydrogel-Derived Materials for Energy and Water Sustainability, Chem. Rev., 2020, 120, 7642, DOI:10.1021/acs.chemrev.0c00345.
- T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Mechanical instability of gels at the phase transition, Nature, 1987, 325, 796, DOI:10.1038/325796a0.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, A theory of coupled diffusion and large deformation in polymeric gels, J. Mech. Phys. Solids, 2008, 56, 1779, DOI:10.1016/j.jmps.2007.11.010.
- W. Hong, Z. Liu and Z. Suo, Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load, Int. J. Solids Struct., 2009, 46, 3282, DOI:10.1016/j.ijsolstr.2009.04.022.
- M. K. Kang and R. Huang, A Variational Approach and Finite Element Implementation for Swelling of Polymeric Hydrogels Under Geometric Constraints, J. Appl. Mech., 2010, 77(6), 061004, DOI:10.1115/1.4001715.
- R. Marcombe, S. Cai, W. Hong, X. Zhao, Y. Lapusta and Z. Suo, A theory of constrained swelling of a pH-sensitive hydrogel, Soft Matter, 2010, 6, 784, 10.1039/B917211D.
- M. B. Amar and P. Ciarletta, Swelling instability of surface-attached gels as a model of soft tissue growth under geometric constraints, J. Mech. Phys. Solids, 2010, 58, 935, DOI:10.1016/j.jmps.2010.05.002.
- J. Dervaux and M. Ben Amar, Mechanical Instabilities of Gels, Annu. Rev. Condens. Matter Phys., 2012, 3, 311, DOI:10.1146/annurev-conmatphys-062910-140436.
- J. Kim, J. Yoon and R. C. Hayward, Dynamic display of biomolecular patterns through an elastic creasing instability of stimuli-responsive hydrogels, Nat. Mater., 2010, 9, 159, DOI:10.1038/nmat2606.
- H. J. Cho, N. B. Lu, M. P. Howard, R. A. Adams and S. S. Datta, Crack formation and self-closing in shrinkable, granular packings, Soft Matter, 2019, 15, 4689, 10.1039/C9SM00731H.
- B. Dortdivanlioglu, N. E. D. Yilmaz, K. Goh, X. Zheng and C. Linder, Swelling-induced interface crease instabilities at hydrogel bilayers, J. Elasticity, 2021, 1, 31–47, DOI:10.1007/s10659-020-09810-8.
- C.-Y. Hui, Y. Y. Lin, F.-C. Chuang, K. R. Shull and W.-C. Lin, A contact mechanics method for characterizing the elastic properties and permeability of gels, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 359, DOI:10.1002/polb.20613.
- Y. Hu, X. Zhao, J. J. Vlassak and Z. Suo, Using indentation to characterize the poroelasticity of gels, Appl. Phys. Lett., 2010, 96, 121904, DOI:10.1063/1.3370354.
- N. Bouklas, C. M. Landis and R. Huang, A nonlinear, transient finite element method for coupled solvent diffusion and large deformation of hydrogels, J. Mech. Phys. Solids, 2015, 79, 21, DOI:10.1016/j.jmps.2015.03.004.
- M. Levin and N. Cohen, Swelling under Constraints: Exploiting 3D-Printing to Optimize the Performance of Gel-Based Devices, Adv. Mater. Technol., 2023, 2202136, DOI:10.1002/admt.202202136.
- T. He, M. Li and J. Zhou, Modeling deformation and contacts of pH sensitive hydrogels for microfluidic flow control, Soft Matter, 2012, 8, 3083, 10.1039/C2SM06749H.
- E. E. Gdoutos, Fracture Mechanics: an Introduction, Springer Nature, 2020, vol. 263 DOI:10.1007/1-4020-3153-X.
- M. Wang, M. Adda-Bedia, J. M. Kolinski and J. Fineberg, How hidden 3D structure within crack fronts reveals energy balance, J. Mech. Phys. Solids, 2022, 161, 104795, DOI:10.1016/j.jmps.2022.104795.
- C. Li, X. Wei, M. Wang, M. Adda-Bedia and J. M. Kolinski, Crack tip kinematics reveal the process zone structure in brittle hydrogel fracture, J. Mech. Phys. Solids, 2023, 105330, DOI:10.1016/j.jmps.2023.105330.
- F. Baldi, F. Bignotti, I. Peroni, S. Agnelli and T. Riccò, On the measurement of the fracture resistance of polyacrylamide hydrogels by wire cutting tests, Polym. Test., 2012, 31, 455, DOI:10.1016/j.polymertesting.2012.01.009.
- I. Kamyab, S. Chakrabarti and J. Williams, Cutting cheese with wire, J. Mater. Sci., 1998, 33, 2763, DOI:10.1023/A:1017517332112.
- J.-F. Louf and S. S. Datta, Poroelastic shape relaxation of hydrogel particles, Soft Matter, 2021, 17, 3840, 10.1039/D0SM02243H.
- J. Misiewicz, S. S. Datta, K. Lejcuś and D. Marczak, The Characteristics of Time-Dependent Changes of Coefficient of Permeability for Superabsorbent Polymer-Soil Mixtures, Materials, 2022, 15, 4465, DOI:10.3390/ma15134465.
- M. J. Krafcik, N. D. Macke and K. A. Erk, Improved Concrete Materials with Hydrogel-Based Internal Curing Agents, Gels, 2017, 3, 46, DOI:10.3390/gels3040046.
- V. Kapur, J. C. Charkoudian, S. B. Kessler and J. L. Anderson, Hydrodynamic Permeability of Hydrogels Stabilized within Porous Membranes, Ind. Eng. Chem. Res., 1996, 35, 3179, DOI:10.1021/ie960015z.
- M. E. Dolega, M. Delarue, F. Ingremeau, J. Prost, A. Delon and G. Cappello, Cell-like pressure sensors reveal increase of mechanical stress towards the core of multicellular spheroids under compression, Nat. Commun., 2017, 8, 14056, DOI:10.1038/ncomms14056.
- W. Lee, N. Kalashnikov, S. Mok, R. Halaoui, E. Kuzmin, A. J. Putnam, S. Takayama, M. Park, L. McCaffrey, R. Zhao, R. L. Leask and C. Moraes, Dispersible hydrogel force sensors reveal patterns of solid mechanical stress in multicellular spheroid cultures, Nat. Commun., 2019, 10, 144, DOI:10.1038/s41467-018-07967-4.
- J. Woodhouse and M. Johnson, Effect of superabsorbent polymers on survival and growth of crop seedlings, Agric. Water Manage., 1991, 20, 63, DOI:10.1016/0378-3774(91)90035-H.
- C. Demitri, F. Scalera, M. Madaghiele, A. Sannino and A. Maffezzoli, Potential of Cellulose-Based Superabsorbent Hydrogels as Water Reservoir in Agriculture, Int. J. Polym. Sci., 2013, 2013, 435073, DOI:10.1155/2013/435073.
- M. R. Guilherme, F. A. Aouada, A. R. Fajardo, A. F. Martins, A. T. Paulino, M. F. Davi, A. F. Rubira and E. C. Muniz, Superabsorbent hydrogels based on polysaccharides for application in agriculture as soil conditioner and nutrient carrier: A review, Eur. Polym. J., 2015, 72, 365, DOI:10.1016/j.eurpolymj.2015.04.017.
- K. Lejcuś, M. Śpitalniak and J. Dąbrowska, Swelling Behaviour of Superabsorbent Polymers for Soil Amendment under Different Loads, Polymers, 2018, 10, 271, DOI:10.3390/polym10030271.
- Y. Wei and D. J. Durian, Effect of hydrogel particle additives on water-accessible pore structure of sandy soils: A custom pressure plate apparatus and capillary bundle model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 053013, DOI:10.1103/PhysRevE.87.053013.
- P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling, J. Chem. Phys., 1943, 11, 521, DOI:10.1063/1.1723792.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- M. Alnæs, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes and G. N. Wells, The FEniCS Project Version 1.5, Arch. Numer. Software, 2015, 3(100), 9–23 Search PubMed.
- A. Goriely, J. Weickenmeier and E. Kuhl, Stress Singularities in Swelling Soft Solids, Phys. Rev. Lett., 2016, 117, 138001, DOI:10.1103/PhysRevLett.117.138001.
- J. Weickenmeier, E. Kuhl and A. Goriely, The mechanics of decompressive craniectomy: Bulging in idealized geometries, J. Mech. Phys. Solids, 2016, 96, 572, DOI:10.1016/j.jmps.2016.08.009.
- Y. Hu, X. Chen, G. M. Whitesides, J. J. Vlassak and Z. Suo, Indentation of polydimethylsiloxane submerged in organic solvents, J. Mater. Res., 2011, 26, 785, DOI:10.1557/jmr.2010.35.
- N. Bouklas and R. Huang, Swelling kinetics of polymer gels: comparison of linear and nonlinear theories, Soft Matter, 2012, 8, 8194, 10.1039/C2SM25467K.
- J. R. Barber, Contact mechanics, Springer, 2018 DOI:10.1007/978-3-319-70939-0.
- K. L. Johnson, Contact mechanics, Cambridge University Press, 1987 DOI:10.1017/CBO9781139171731.
- L. D. Landau, L. P. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, Oxford, 1986 Search PubMed.
- B. Audoly and Y. Pomeau, Elasticity and geometry: from hair curls to the non-linear response of shells, Oxford University Press, 2010 Search PubMed.
- C. Joshi, D. Goldstein, C. Wennerholm, E. Downey, E. Hamilton, S. Hocking, A. Andrei, J. H. Adler and T. J. Atherton, Morpho – A programmable environment for shape optimization and shapeshifting problems, arXiv, 2022, preprint, arXiv:2208.07859 DOI:10.48550/arXiv.2208.07859.
- C. Joshi, M. Q. Giso, J.-F. Louf, S. S. Datta and T. J. Atherton, An energy-optimization method to study gel-swelling in confinement, Soft Matter, 2023, 19, 7184, 10.1039/D3SM00465A.
- Y. Lai and Y. Hu, Probing the swelling-dependent mechanical and transport properties of polyacrylamide hydrogels through AFM-based dynamic nanoindentation, Soft Matter, 2018, 14, 2619, 10.1039/C7SM02351K.
- M. Kuna, Finite elements in fracture mechanics, Solid Mechanics and Its Applications, 2013, 201, 153, DOI:10.1007/978-94-007-6680-8.
- Y. Mao and L. Anand, A theory for fracture of polymeric gels, J. Mech. Phys. Solids, 2018, 115, 30, DOI:10.1016/j.jmps.2018.02.008.
- X. Wang and W. Hong, Delayed fracture in gels, Soft Matter, 2012, 8, 8171, 10.1039/C2SM25553G.
- T. Baumberger and O. Ronsin, Environmental control of crack propagation in polymer hydrogels, Mech. Soft Mater., 2020, 2, 1, DOI:10.1007/s42558-020-00027-2.
- Y. Yang, H. Guo, Z. Du, W. Hong, T. Lu and T. Wang, Rate-dependent fracture of hydrogels due to water migration, J. Mech. Phys. Solids, 2022, 105007, DOI:10.1016/j.jmps.2022.105007.
- K.-A. Leslie, R. Doane-Solomon, S. Arora, S. J. Curley, C. Szczepanski and M. M. Driscoll, Gel rupture during dynamic swelling, Soft Matter, 2021, 17, 1513, 10.1039/D0SM01718C.
- G. Helmlinger, P. A. Netti, H. C. Lichtenbeld, R. J. Melder and R. K. Jain, Solid stress inhibits the growth of multicellular tumor spheroids, Nat. Biotechnol., 1997, 15, 778, DOI:10.1038/nbt0897-778.
- Q. Zhang, J. Li, J. Nijjer, H. Lu, M. Kothari, R. Alert, T. Cohen and J. Yan, Morphogenesis and cell ordering in confined bacterial biofilms, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2107107118, DOI:10.1073/pnas.2107107118.
- G. T. Fortune, N. M. Oliveira and R. E. Goldstein, Biofilm Growth under Elastic Confinement, Phys. Rev. Lett., 2022, 128, 178102, DOI:10.1103/PhysRevLett.128.178102.
- K. Goodwin, S. Mao, T. Guyomar, E. Miller, D. C. Radisky, A. Košmrlj and C. M. Nelson, Smooth muscle differentiation shapes domain branches during mouse lung development, Development, 2019, 146, dev181172, DOI:10.1242/dev.181172.
- W. Möbius, A. W. Murray and D. R. Nelson, How Obstacles Perturb Population Fronts and Alter Their Genetic Structure, PLoS Comput. Biol., 2015, 11, e1004615, DOI:10.1371/journal.pcbi.1004615.
- S. Atis, B. T. Weinstein, A. W. Murray and D. R. Nelson, Microbial Range Expansions on Liquid Substrates, Phys. Rev. X, 2019, 9, 021058, DOI:10.1103/PhysRevX.9.021058.
- T. Tanaka, Kinetics of phase transition in polymer gels, Phys. A, 1986, 140, 261, DOI:10.1016/0378-4371(86)90230-X.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Dynamics of Swelling and Drying in a Spherical Gel, Phys. Rev. Appl., 2016, 6, 064010, DOI:10.1103/PhysRevApplied.6.064010.
- M. Curatolo, P. Nardinocchi, E. Puntel and L. Teresi, Transient instabilities in the swelling dynamics of a hydrogel sphere, J. Appl. Phys., 2017, 122, 145109, DOI:10.1063/1.5007229.
- U. K. de Silva and Y. Lapitsky, Preparation and Timed Release Properties of Self-Rupturing Gels, ACS Appl. Mater. Interfaces, 2016, 8, 29015, DOI:10.1021/acsami.6b09370.
- J. Zhang, X. Zhao, Z. Suo and H. Jiang, A finite element method for transient analysis of concurrent large deformation and mass transport in gels, J. Appl. Phys., 2009, 105, 093522, DOI:10.1063/1.3106628.
- I. Ang, Z. Liu, J. Kim, C.-Y. Hui and N. Bouklas, Effect of elastocapillarity on the swelling kinetics of hydrogels, J. Mech. Phys. Solids, 2020, 145, 104132, DOI:10.1016/j.jmps.2020.104132.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01470c |
| ‡ A. P. and C. A. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |