Control of liquid crystals combining surface acoustic waves, nematic flows, and microfluidic confinement

Abstract

The optical properties of liquid crystals serve as the basis for display, diagnostic, and sensing technologies. Such properties are generally controlled by relying on electric fields. In this work, we investigate the effects of microfluidic flows and acoustic fields on the molecular orientation and the corresponding optical response of nematic liquid crystals. Several previously unknown structures are identified, which are rationalized in terms of a state diagram as a function of the strengths of the flow and the acoustic field. The new structures are interpreted by relying on calculations with a free energy functional expressed in terms of the tensorial order parameter, using continuum theory simulations in the Landau-de Gennes framework. Taken together, the findings presented here offer promise for the development of new systems based on combinations of sound, flow, and confinement.

---

1 Introduction

Optofluidic devices, which combine the transport features of liquids with the remote addressability offered by optical properties, offer considerable potential applications in sensing and display technologies.^1–4 In particular, liquid crystals (LCs), which exhibit versatile and anisotropic optical properties associated with their alignment, provide attractive platforms for optofluidic applications.^5–8 LCs are highly sensitive to external stimuli, including electric and optical fields, and have been widely used in displays and photonic systems.^9–11 Recently, advances in nanofabrication techniques have created new opportunities for the combined application of multiple fields, such as ultrasound and flow.

Acoustic fields are typically used in miniaturized devices in the form of bulk acoustic waves or surface acoustic waves (SAWs). Here we focus on SAWs, which exhibit enhanced sensitivity compared to bulk wave devices.¹² The frequency of SAWs ranges from several hundred MHz to a few GHz; they have been considered in applications that include radio-electronic components and sensors.^13,14 Recently, techniques that rely on standing SAWs (SSAWs), formed by two opposite and coaxial waves, have also been used for manipulation of biological cells and microparticles, serving to highlight their potential for manipulation of soft materials.^15–20 Past studies of the effects of SAWs on nematic LCs (NLCs) have considered periodic pressure fields, acoustic streaming flows, and other applied fields, mostly in LC cells.^21–32 It has been shown that, for perpendicular (homeotropically) anchored nematics, SAWs lead to the formation of stripe patterns that gradually transition into a dynamic scattering regime characterized by turbulent-like flow behavior, where the nematic director orientation is randomized. While a variety of demonstrations have focused on tuning transparency and light scattering in cholesteric LCs, polymer-dispersed LC screens, acoustic images visualized on LCs, medical imaging, and LC tunable lenses,^33–39 a fundamental understanding of the interaction between non-equilibrium structures and SAWs in LCs is still missing. In this work, we present a systematic theoretical and experimental study of the structures of NLC induced by acoustic fields in a microfluidic environment under both steady-state and pressure-driven flow conditions.

Applied flows are known to have a strong effect on the orientation and order of NLCs.⁴⁰ Recent studies have revealed the existence of different topological states in channel-confined nematic flows, such as bowser, chiral, and dowser states.⁴¹ Our understanding of their response to external fields remains limited. For example, experiments with laser tweezers have demonstrated local creation and control of these topological states.⁴² However, the effect of an acoustic field on these states in channel-confined nematic flows remains unexplored.

The optofluidic system considered in this work consists of a NLC confined by a PDMS microfluidic channel that is coupled to a SSAW generator. We show that different structures arise in the LC depending on the acoustic and flow field intensities. First, we characterize optical patterns driven only by the SSAWs. We rely on polarized optical microscopy (POM) and fluorescence confocal polarizing microscopy (FCPM) to visualize the reorientation of the LC mesogens. We also characterize the temperature changes in the system in terms of acoustic strength and determine the level of influence on the observed optical transitions. After identifying the characteristics of the LC under acoustic fields, we add microfluidic flows and examine the response of the LC, thereby producing a state diagram of optical texture in terms of relevant non-dimensional parameters such as the streaming Reynolds number and the Ericksen number. The experimental results are interpreted using continuum simulations with a Landau-de Gennes (LdG) free energy functional for the tensor order parameter. By combining simulations and experiments, this work provides a detailed picture of the transition between different structures and helps provide a foundation for design of LC-based optofluidic devices controlled by acoustic waves.

2 Experimental

2.1 Materials and experimental procedures

We use NLC 5CB (4-Cyano-4′-pentylbiphenyl) (Sigma-Aldrich), which exhibits a nematic phase between 22 and 35 °C. Experiments were performed within microfluidic channels having a rectangular cross section, with height h = 40 μm, width w = 400 μm, and length L = 12 mm. The channels were fabricated out of polydimethylsiloxane (PDMS) (1 : 10 curing agent to PDMS base; SYLGARD 184, Dow Corning) and bonded to the piezoelectric substrate after components were exposed to air plasma (Harrick Plasma, Plasma Cleaner Model PDC-001). The channel walls were chemically treated with a 0.4 wt% aqueous solution of N-dimethyl-n-octadecyl-3-aminopropyl-trimethoxysilyl chloride (DMOAP, Sigma-Aldrich) to induce strong homeotropic surface anchoring of 5CB molecules. Interdigitated transducers (IDTs) were patterned into a 128° Y-cut of LiNbO₃ piezoelectric substrate (Roditi) by using standard lithography techniques and vapor deposition of 10 nm Pt adhesion layer followed by 80 nm Au layer. The single electrode transducer pitch was set to 50 μm to achieve a wavelength of 200 μm. The high voltage RF signal was generated using a GHz generator (Hewlett Packard, Model E4431B), and subsequently amplified using a power amplifier (Minicircuits, Model ZHL-1-2W-N+). Before any measurement, channels were filled with 5CB in the isotropic phase and then slowly cooled down to room temperature. The temperature was controlled using a Linkam PE120 temperature controller on a hot stage under the microscope. The local temperature of various states was measured using a tiny thermocouple inserted into the microfluidic channel from the top, passing through the PDMS. This allowed the thermocouple to directly measure the temperature of the liquid crystal.

2.2 Polarized optical microscopy, fluorescence confocal polarizing microscopy, and pressure-driven flow

Acousto-optical characterization was performed with a polarized optical microscope (POM) Olympus BX60 with 4×/10× air objectives, in transmission mode, and a fluorescence confocal polarizing microscope (FCPM) with Leica SP5 STED under 5×/10× air objectives. For FCPM imaging, 5CB was doped with 0.01 wt% of the fluorescent dye Nile Red (Sigma Aldrich) and excited by a 561 nm laser beam. Transmitted light intensity was measured by ImageJ. We precisely controlled and manipulated the flow by using a pressure controller-driven system (OB1, Elveflow). The flow rate was varied in the range from 0.01 to 10.80μL h⁻¹, corresponding to flow velocities ranging from 0.05 to 85 μm s⁻¹. The characteristic Reynolds number Re = ρvl/v ranged between 10⁻⁷ and 10⁻⁴, considering an effective dynamic viscosity of v = 50 mPa s. The material density for 5CB is ρ = 1.024 kg m⁻³, and the hydraulic diameter of the rectangular microfluidic channel is estimated to be l = 4wd/2(w + h) = 72.7 μm. The corresponding Ericksen number Er = hvl/K, with a single elastic constant approximation K = 5.5 pN, was varied between 0.03 and 55.

2.3 Numerical simulations

Continuum simulations are based on the LdG theory.⁴³ The details are described in ESI.†

3 Results and discussion

3.1 Identification of acoustically induced structures in steady state of NLC

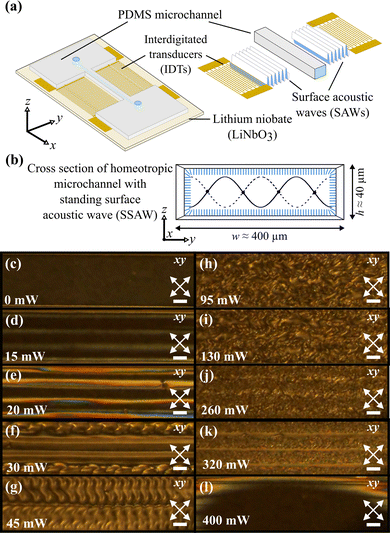
The first set of experiments presented here shows the emergence of two previously unidentified states in NLCs under the influence of acoustic fields: (I) nematic counterflows with periodic ripples and (II) dynamic scattering with birefringent bands. Previously described patterns also emerge in the LC when subject to acoustic waves and confined within a microchannel.

All experiments are performed on 5CB confined in a linear microfluidic channel. The channel has a rectangular cross section, with height h = 40 μm and width w = 400 μm, and is fabricated out of a PDMS (polydimethylsiloxane) relief bounded to a piezoelectric lithium niobate (LiNbO₃) substrate [Fig. 1(a)]. The NLC is loaded into the channel after treating it with DMOAP to achieve homeotropic surface alignment [Fig. 1(b)]. As shown in Fig. 1(a), the channel is centrally positioned between two parallel interdigitated transducers (IDTs) patterned on the piezoelectric substrate. A radio frequency (RF) signal from a signal generator is applied to the IDTs to convert the electric signal into SAWs that propagate on the substrate surface in the y-direction. The superposition of two counter-propagating SAWs results in a SSAW with wavelength around 200 μm [Fig. 1(b)], determined by the IDT pitch. The SSAW transmitted through the channel filled with the NLC is a standing pressure wave with 4 nodes, as illustrated in Fig. 1(b).

Fig. 1 NLC in homeotropic microfluidic channel under SSAWs. (a) Schematic representation of PDMS channel on a lithium niobate substrate (LiNbO₃) with two pairs of parallel IDTs that generate SSAWs. (b) Cross section of the channel with dimensions 400 μm × 40 μm, showing the nodes and anti-nodes of the standing pressure wave with a wavelength of 200 μm. (c)–(l) Experimental POM images showing a top view of the NLC in a channel under SSAWs. Different values of the input power applied to the IDTs result in different structures: (c) no patterns, (d) white stripe patterns, (e) color stripe patterns, (f) brown stripe patterns, (g) dynamical behavior of spatially periodic patterns, (h) and (i) dynamic scattering characterized by turbulent-like flow behavior, (j) and (k) dynamic scattering with stripes, and (l) isotropic phase transition. White crossed double arrows indicate the orientation of the polarizers. Scale bars are 100 μm.

The acoustically induced structures of NLC in the microfluidic channel are observed under POM [Fig. 1(c)–(l)]. Without an acoustic field, the channel appears dark, corresponding to a uniformly aligned director field along the z-axis [Fig. 1(c)]. Application of the acoustic field leads to the formation of structures in the NLC. With an applied input power of the RF signal of 15 mW, the SSAW induces the formation of stripe patterns perpendicular to the sound propagation direction, located at the SSAW pressure nodes [white stripes, Fig. 1(d) and Movie S1, ESI†]. The pattern undergoes a transition when the input power increases to 20 mW, characterized by the appearance of colors in the stripes due to birefringence [color stripes, Fig. 1(e) and Movie S2, ESI†]. Further increasing the power induces a discontinuous transition of the patterns, where the birefringent colors are replaced by broader stripes with lower intensity of transmitted light [brown stripes, Fig. 1(f) and Movie S3, ESI†]. This transition is similar to the homeotropic-to-dowser transition typically observed in homeotropic nematic samples.⁴⁴ Additionally, a disruption of the texture is observed near the channel walls, consistent with streaming-induced rolls. Around an input power of 45 mW, the stripes transition into previously unidentified dynamical behavior consisting of nematic crossflows with spatially periodic patterns, as seen in Fig. 1(g) (Movie S4, ESI†). The velocity of the crossflow and the periodicity of the patterns vary as the acoustic intensity increases. Higher acoustic intensity leads to a transition into a dynamic scattering state characterized by a disorganized, turbulent-like flow of the nematic [Fig. 1(h), (I) and Movie S5, S6, ESI†]. This state is analogous to the dynamic scattering observed with an electric field.⁴⁵ As the acoustic intensity increases, a novel state emerges characterized by the formation of birefringent stripes amidst the dynamic scattering, located at the acoustic wave pressure anti-nodes [Fig. 1(j), (k) and Movie S7, S8, ESI†]. Lastly, applying an input power above 400 mW induces a transition into an isotropic phase [Fig. 1(l) and Movie S9, ESI†]. Previous experimental results conducted in LC cells reported the formation of stripe patterns and dynamic scattering.^{21–23,27,29,30} In the experimental conditions presented here, we report the influence of microfluidic confinement on the dynamics of nematogens under acoustic fields. Previously unobserved structures highlight the unique pattern formation of NLCs when including first and second order hydrodynamic effects from the oscillatory walls.

As can be seen in Fig. S1(a) (ESI†), the temperature within the channel does not increase significantly at low acoustic intensities when the stripe patterns appear. An increase in the input power generating the SSAW results in a linear increase in temperature, leading to the nematic–isotropic phase transition. Experiments also indicate that the transmitted light intensity through acoustically induced structures increases once the system reaches the white stripe patterns, achieving maximum intensity with the colored stripe pattern, followed by a decrease in intensity in the brown stripes region [Fig. S1(b), ESI†].

To characterize the time scales associated with acoustically induced structures of NLCs, we first measure the time to reach a stable optical appearance after turning on the acoustic; we refer to this time as the response time. We also measure the relaxation time, which is the time needed for the structures to relax back to the initial homeotropic dark state after switching off the acoustic field. Both the response and relaxation times corresponding to all structures are of the order of seconds (Fig. S2, ESI†). Furthermore, the response time gradually increases when increasing the input power until it reaches a maximum for the color stripes [Fig. S2(a), ESI†]; the peak corresponds to the highest transmitted light intensity. After that, the response time decreases, reaching a plateau after brown stripes. In contrast, the relaxation time increases when increasing the input power throughout the striped patterns, reaching a plateau during the dynamic scattering regime [Fig. S2(b), ESI†]. Once the system reaches dynamic scattering with lines [Fig. 1(j) and (k)], the relaxation time increases again until the isotropic phase is formed.

The spatial orientation of the NLC molecules in the acoustically induced structures can be resolved by performing FCPM. The observations are made along the top view (xy plane) and cross section (yz plane) of the channel, as shown in Fig. 2(a)–(d). We focus on the region of stripe patterns that appear at low acoustic field intensities. High fluorescence intensity indicates that the director field is oriented parallel to the polarization of the laser beam, while a low fluorescence signal indicates an orthogonal orientation. Applying SSAWs to the NLCs induces an intense fluorescent signal in the vicinity of the acoustic pressure nodes, indicating a tilting of the director field. Increasing the input power increases the FCPM signal, corresponding to an even stronger tilting of the director towards the polarized laser beam. As a reference, Fig. 2(a) and sketch Fig. 2(e), show the behavior of the NLC in a relaxed homeotropic state. The reorientation gradually evolves from a relatively small tilting, which corresponds to the formation of the white stripes [Fig. 2(b) and sketch Fig. 2(f)], to a more pronounced tilted director, corresponding to the colored stripes [Fig. 2(c) and sketch Fig. 2(g)]. At higher input power the color stripes undergo a discontinuous transition into brown stripes, whose formation results from a larger inclination of the molecules [Fig. 2(d) and sketch Fig. 2(h)]. Stripe patterns collapse once the system switches into the dynamic scattering regime. The measured fluorescent signal intensities for all stripe patterns as a function of the channel width are summarized in Fig. 2(i). All the results of FCPM experiments indicate that reorientation of molecules in the pressure nodes is responsible for the observed structures.

Fig. 2 Formation of stripe patterns. (a)–(d) FCPM top view (xy plane) and cross section (yz plane) of a microfluidic channel, corresponding to NLC in (a) the absence of patterns, and in (b) the presence of white, (c) color, and (d) brown stripe patterns, as described in Fig. 1. Scale bars are 100 μm (xy plane) and 20 μm (yz plane). (e)–(h) Corresponding schematic representation of the director orientation across the channel cross section for stripe patterns in (e) the absence of patterns, and in (f) the presence of white, (g) color, and (h) brown stripe patterns. The grey area in (f) indicates the pressure node regions tilting the NLC molecules. Side walls are not included. (i) Fluorescent signal intensity as a function of channel width for all stripe patterns. (j) Cross polarized image of stripe patterns with the corresponding director field orientation [due to a small angle difference see also Fig. S3, ESI†] and scalar order parameter (see color bar) predicted by numerical simulations. Tilted molecules at the pressure nodes result in a periodic distribution of the order parameter across the channel. (k) Numerically predicted angle θ of the director field across the channel at 1/6 of the maximum channel height under the acoustic field. Black arrows indicate regions of pressure nodes.

To better understand the influence of the acoustic field on the confined nematic, we turn to continuum simulations based on the LdG theory.⁴³ The total free energy of the system is expressed as a function of a tensorial order parameter Q = S(nn − I/3), where n is a unit vector representing the nematic field, S is the scalar order parameter of the nematic, and I is the identity tensor. Under this framework, the energy of the acoustic field is modeled as f_A = I cos²(2πx/λ_x)k·Q·k, where k is the propagation vector, I is the acoustic intensity, and λ_x is a wavelength of applied acoustic field.⁴⁶ Combining the acoustic field with the hydrodynamic evolution of the confined NLC, the numerical simulations use a hybrid lattice Boltzmann method to simultaneously solve the Beris–Edwards and the momentum equations. The details of the model are summarized in the ESI.† As shown in the predicted cross polarized image for low acoustic intensity in Fig. 2(j), we find that the stripe patterns arise because of the periodic distribution of the order parameter across the channel imposed by the periodicity of the acoustic wave. The acoustic wave tilts the molecules in the vicinity of the pressure nodes [see also Fig. 2(k)] corresponding to the balance between the elastic forces of NLC and acoustic forces. The simulations also indicate the onset of acoustic streaming flows (Fig. S3, ESI†), which have been theorized as an important phenomenon driving the alignment of molecules under SSAWs.⁴⁷ Based on these results, we hypothesize that the stripe patterns become unstable and collapse into a turbulent-like flow behavior once the acoustic forces and acoustic streaming dominate over the elastic forces. While numerical predictions support experimental observations in the case of low acoustic intensity, high acoustic intensity dynamics are beyond the limitations and assumptions of our model.

3.2 Acoustically induced structures in nematic flow

In this section we present results that combine the acoustic field with pressure-driven flow in the microfluidic channel. We use the Ericksen number, a relative measure of the viscous and elastic forces, as a dimensionless quantity for the flow velocity of the NLC. The Ericksen number is defined as Er = (γul)/K, with γ being the rotational viscosity, u being the average measured flow velocity, l being the channel hydraulic diameter, and K being the single elastic constant of the nematic 5CB. Similarly, we use the streaming Reynolds number as a dimensionless quantity for the acoustic wave intensity. The streaming Reynolds number relates the oscillatory forces and the viscous dissipation forces, being defined as R_s = U₀²/vζ. Here, U₀ is the characteristic velocity of the wave, v is the kinematic viscosity, and ζ is the frequency associated with the oscillatory flow. As shown in the ESI,†R_s ∼ V², where V is the input voltage from the RF signal generator.

We first perform experiments under pressure-driven flow for 5CB in a microfluidic channel without an acoustic field (R_s = 0) [Fig. 3(a)]. Without flow (Er = 0), the channel is dark under POM due to the homeotropic alignment of the NLC. Upon starting the flow, birefringent colors start to appear, indicating a slightly bowed uniform director field towards the flow direction—known as the bowser state.⁴¹ The bowser state is stable only in the weak flow regime (0 < Er < 21), where the orientational order and flow are only weakly coupled and the structure is largely dictated by the surface anchoring. An increase in the pressure to reach the medium flow regime (21 ≤ Er < 50) induces a continuous transformation of the bowser state into a chiral nematic state, with left- and right-handed domains separated by a flexible soliton-like structure in the center of the channel.⁴¹ In the chiral state, the coupling of orientational order and flow leads to backflow effects. With higher flow rates (Er ≥ 50), the nematic undergoes a discontinuous transition into a flow-aligned state known as a dowser state.⁴¹ A flow-aligned dowser state is observed only in the strong flow regime, in which LC molecules are primarily oriented along the main axis of the channel. All these nematic flow states have been observed and reported in previous publications and are in agreement with our observations.^40,41

Fig. 3 Acoustically induced structures in nematic flow. (a) Optical responses are obtained by applying an acoustic field to the topological states of the nematic flow. Without acoustic field (R_s = 0), characteristic bowser, chiral and dowser states arise for Er < 21, 21 ≤ Er < 50, and Er ≥ 50, respectively. In the bowser state, low acoustic intensities (R_s < 1.8 × 10⁻¹²) lead to stripe patterns. As the acoustic intensity is increased, the NLC transitions into a dynamic scattering regime. Chiral and dowser states dominate orientation of the director field until the acoustic intensity is not high enough (R_s < 5.5 × 10⁻¹²). In the range 5.5 × 10⁻¹² < R_s < 1.7 × 10⁻¹¹ the system exhibits a dynamic scattering regime due to the domination of acoustic forces. At R_s > 1.7 × 10⁻¹¹ the NLC transitions into an isotropic phase, regardless of flow strength. White empty arrows indicate the direction of pressure-driven flow. Scale bars are 100 μm. (b) State diagram of NLC 5CB under SSAWs and pressure-driven flow obtained from the experimental observations marked by symbols.

Applying SSAWs to different topological states under flow in an orthogonal direction generates a reorientation of the director field [Fig. 3(a)]. Low SSAW input power within the range 1.8 × 10⁻¹³ < R_s < 1.8 × 10⁻¹² leads to the formation of stripe patterns in the bowser state (0 < Er < 21) (Movies S10–S15, ESI†). As the input power increases up to R_s ∼ 4.4 × 10⁻¹², the stripe patterns undergo a discontinuous transition to brown stripes. Higher input powers (R_s > 5.5 × 10⁻¹²) induce a transition into a dynamic scattering phase (Movie S16, ESI†). In contrast to the bowser state, chiral and dowser states (Er ≥ 21) dominate the alignment of nematic molecules when R_s < 1.8 × 10⁻¹². At higher acoustic intensities, acoustically induced reorientation competes with the flow realignment until the system reaches the dynamic scattering phase. Regardless of the flow velocity, the system evolves into the isotropic phase when a sufficient input power of SSAW is applied. The small values of the streaming Reynolds number arise as a consequence of a Reynolds number ∼O(10⁻⁸) and a Strouhal number ∼O(10⁵). The small Reynolds number is typical for microfluidic systems because of their low characteristic length values. Additionally, the magnitude of the Strouhal number is dominated by the high values of the wave frequency. The ∼O(10⁻¹²) of the streaming Reynolds number validates its use to study the contributions of the vorticity using singular perturbation theory.^48,49

The acoustically induced structures observed under flow are summarized in a state diagram in Fig. 3(b). The diagram shows three distinct regions of interest. The first region (B, C, and D) corresponds to the regimes where the molecular orientation of the NLC is dominated by the nematic flow, representing the bowser, chiral, and dowser states, respectively. The second region (T and TT) corresponds to the dynamic scattering regime, with turbulent-like flow behavior dominated by acoustic forces. The third region (BAS, DAS, and CFS) includes the stripe regimes, where the molecular orientation consists of superimposed stripe patterns induced by acoustic forces, in addition to the nematic flow-mediated molecular alignment of the bowser or chiral states. The isotropic state (I) is located at the top of the diagram.

Numerical simulations support the experimental observations in the bowser state in the presence of the acoustic field and a Poiseuille flow applied orthogonal to each other (Fig. 4). In the case of the bowser state with Er = 0.05, and in the absence of an acoustic field, the uniform homeotropic director is bowed slightly in the flow direction [Fig. 4(a)]. Applying a low acoustic intensity on the same bowser state promotes the tilting of the molecules across the width of the channel (y-direction) in the vicinity of the acoustic pressure nodes [Fig. 4(b)]. Changes in the scalar order parameter can also be detected and visualized as stripe patterns in the simulated cross polarizer images. Without an acoustic field, an increment of the nematic flow to Er = 0.65 increases the bowing of the director in the direction of the flow, as shown in Fig. 4(c) by the change in the scalar order parameter. If the same acoustic field in the low intensity regime is now applied simultaneously (with Er = 0.65), the tilting of the molecules across the width of the channel in the vicinity of the acoustic pressure nodes becomes more visible than before. This corresponds to the formation of sharper stripe patterns in the cross polarizer images [Fig. 4(d)]. In Fig. 4(e) and (f) we quantify the changes of the director orientation on the bowser state across the width (angle θ) and along the length (angle φ) of the channel (Fig. S4, ESI†) induced by the acoustic field. The analysis corresponds to the pressure nodes at 1/6 of the total height of the channel, where the bowing is most pronounced according to numerical calculations spanning the entire height of the channel (Fig. S5, ESI†). As seen in Fig. 4(e), increments in the acoustic intensity increase the tilting of the molecules across the width of the channel as the acoustic forces overcome the elastic forces, reaching a plateau around the Rayleigh angle θ_r = sin⁻¹(v_LC/v_s)∼23°.⁴⁶ Here, v_LC ≈ 1500 m s⁻¹ and v_s ≈ 3900 m s⁻¹ are the speed of sound in 5CB and lithium niobate, respectively.^50,51 Slight variations are noticeable when changing the Ericksen number in the range 0.00 < Er < 0.65. Our simulations suggest a decrease in the tilting of the molecules along the length of the channel in the vicinity of the pressure nodes when the intensity of the acoustic field is increased (Fig. 4). As observed in Fig. 4(f), an increase in the flow velocity bows the director along the channel increasing the value of φ. In addition, increments in the acoustic intensity reduce the values of φ, and compete with the reorientation of the director field in the direction of the flow. Similar behaviors regarding angles θ and φ are observed on the pressure nodes placed at 1/2 of the maximum channel height (Fig. S6, ESI†). However, the values of φ remain small, with no significant variations even at different velocities.

Fig. 4 Simulations showing the predicted molecular orientation under weak nematic flows and acoustic fields. (a)–(d) Predicted cross polarizer images, three-dimensional scalar order parameter, and orientation of director field in yz and xz planes of microchannel. White empty arrows indicate the direction of flow. (a) Bowser state with Er = 0.05 and no acoustic field. (b) Low-intensity acoustic field in a bowser state with Er = 0.05. (c) Bowser state with Er = 0.65 and no acoustic field. (d) Low acoustic field in a bowser state with Er = 0.65. (e) Angle θ of tilted nematic molecules across the width of the channel, measured at the acoustic pressure nodes located at 1/6 of the maximum height. Variations in θ are observed for different flow velocities. Dotted line indicates the Rayleigh angle of incidence. (f) Angle φ of tilted nematic molecules along the channel, measured at the acoustic pressure nodes at 1/6 of the maximum height. Variations in φ are observed for different flow velocities. Numerical analysis with Er between 0 and 0.65. Note that the length scales in simulations are smaller than those in experiments.

3.3 Optical manipulation of the acoustic optofluidic device

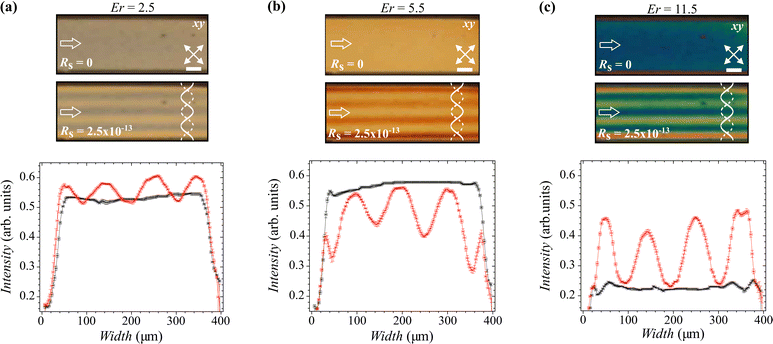
We next examine how changes to the SSAWs at a constant flow rate modify the optical intensity. Fig. 5(a) shows only a nematic flow with Er = 2.5 without SSAWs, resulting in a uniform increase in optical intensity within the channel. For the same flow, the application of an acoustic intensity with R_s = 2.5 × 10⁻¹³ generates peaks of transmitted light intensity located at the pressure nodes [Fig. 5(a)]. In contrast, increasing the flow to Er = 5.5 while maintaining the same acoustic intensity induces a shift in the spatial location of the peaks of transmitted light intensity. The peaks now appear at the pressure anti-nodes, along with a reduction in the maximum intensity compared to the base intensity when only flow is applied [Fig. 5(b)]. Further increasing the flow velocity to Er = 11.5 at the same acoustic intensity, shifts the location of the transmitted light intensity peaks back to the pressure nodes [Fig. 5(c)]. In this case, the intensity is significantly higher than the base value observed with flow alone. Applying an alternative flow to acoustically induced stripe patterns results in sub-millisecond response times [Fig. S7, ESI†], indicating that the NLC responds much faster to changes induced by flow than changes induced by SSAWs (Fig. S2, ESI†).

Fig. 5 POM images of stripe patterns in bowser state and analysis of the transmitted light intensity. (a) Applying an acoustic field with R_s = 2.5 × 10⁻¹³ in the bowser state with Er = 2.5 leads to peaks of transmitted light intensity in the vicinity of the pressure nodes of SSAWs. (b) The same acoustic field in a stronger nematic flow with Er = 5.5 shows peaks of transmitted light intensity at the SSAWs anti-nodes. (c) Further increasing the flow velocity to Er = 11.5 switches the peaks of intensity back to the acoustic pressure nodes. In graphs, black lines represent the optical response without acoustic field (R_s = 0), and red lines with acoustic field applied (R_s = 2.5 × 10⁻¹³). White empty arrows indicate the direction of the flow. Scale bars are 100 μm.

4 Conclusions

The results of experiments and simulations presented in this work indicate that combinations of SAWs and fluid flow enable formation of previously unknown stable nematic morphologies/states that do not exist at equilibrium. These structures, which are the combined result of hydrodynamic forces, acoustic forces, and elastic forces, exhibit sub-millisecond on/off states of brightness that can cover the entire dimensions of a microfluidic channel, or that can be localized to narrow stripes located in the corresponding pressure nodes (or anti-nodes) of the acoustic waves. Their formation can be controlled by the applied fields, and could be used to affect the spatial distribution and rate of reaction between molecules in specific regions of the material (e.g. pressure nodes) by imposing density and elasticity constrains in the NLC solvent using acoustic waves. In addition, this system can be used to spatially patterns, aggregate or actuate particles according to a range of characteristics, including density, compressibility, and size.

By increasing the complexity of the IDTs, the strategy introduced here offers the potential to control the shape, location, and frequency of the SAWs and the corresponding location of pressure nodes, paving the way for creation of optical devices with fast response times. Such devices could be further enhanced by the application of electric fields, which would offer yet another level for control of these materials.

We conclude with a word of caution regarding temperature effects in acoustically driven LCs. Specifically, care must be exercised to avoid overheating the system upon application of SAWs, thereby limiting the geometries and strength of the fields that can be used. Such temperature effects are discussed in the ESI† [Fig. S1(a)].

Author contributions

G. A. V. M. and T. E. contributed equally to this work. G. A. V. M., T. E., and A. T. V. conducted the experiments and analyzed the results. N. A. and J. J. d. P. performed the numerical simulations and analyzed the data. A. M., R. Z., and O. G. contributed to the discussion about numerical simulations. G. A. V. M., T. E., A. T. V., and J. J. d. P. wrote the manuscript. J. J. d. P. supervised the research. All authors discussed the progress of the research and contributed to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank X. Li and J. A. Martínez-González for their contributions to the pilot experiments that led to this work. This work was supported by the Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering. The authors gratefully acknowledge the MRSEC Shared User Facilities at the University of Chicago (NSF DMR-1420709). This work made use of the Pritzker Nanofabrication Facility of the Institute for Molecular Engineering at the University of Chicago, which receives support from Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205), a node of the National Science Foundation's National Nanotechnology Coordinated Infrastructure. The fluorescence confocal polarizing microscopy technique was performed in the Integrated Light Microscopy Core at the University of Chicago, which receives financial support from the Cancer Center Support Grant (P30CA014599), RRID: SCR_019197.

References

1. D. Psaltis, S. R. Quake and C. Yang, Nature, 2006, 442, 381.
2. C. Monat, P. Domachuk and B. J. Eggleton, Nat. Photonics, 2007, 1, 106.
3. A. H. J. Yang, S. D. Moore, B. S. Schmidt, M. Klug, M. Lipson and D. Erickson, Nature, 2009, 457, 71.
4. D. Erickson, D. Sinton and D. Psaltis, Nat. Photonics, 2011, 5, 583.
5. J. G. Cuennet, A. E. Vasdekis, L. D. Sio and D. Psaltis, Nat. Photonics, 2011, 5, 234.
6. H. Huang and Y. Zhao, J. Micromech. Microeng., 2019, 29, 73001.
7. W. M. Gibbons, P. J. Shannon, S.-T. Sun and B. J. Swetlin, Nature, 1991, 351, 49.
8. M. Schadt, H. Seiberle and A. Schuster, Nature, 1996, 381, 212.
9. F. Reinitzer, Monatsh. Chem., 1888, 9, 421.
10. I. C. Khoo, Liquid Crystals: Physical Properties and Nonlinear Optical Phenomena, Wiley, 1995.
11. M. F. Schiekel and K. Fahrenschon, Appl. Phys. Lett., 1971, 19, 391.
12. X. Ding, P. Li, S.-C. S. Lin, Z. S. Stratton, N. Nama, F. Guo, D. Slotcavage, X. Mao, J. Shi, F. Costanzo and T. J. Huang, Lab Chip, 2013, 13, 3626.
13. K. Hashimoto, Liquid Crystals: Physical Properties and Nonlinear Optical Phenomena, Springer-Verlag, Berlin, 2000.
14. B. Liu, X. Chen, H. Cai, M. M. Ali, X. Tian, L. Tao, Y. Yang and T. Ren, J. Semicond., 2016, 37, 21001.
15. F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522.
16. X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105.
17. K. Länge, F. Gruhl and M. Rapp, Methods Mol. Biol., 2013, 949, 491.
18. A. Zhang, Y. Zha and J. Zhang, AIP Adv., 2014, 4, 127144.
19. Y. Chen, A. A. Nawaz, Y. Zhao, P.-H. Huang, J. P. McCoy, S. J. Levine, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 916.
20. X. Ding, Z. Peng, S.-C. S. Lin, M. Geri, S. Li, P. Li, Y. Chen, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12992.
21. M. Witkowska-Borysewicz and A. Sliwinski, J. Phys. France, 1983, 44, 411.
22. C. Sripaipan, C. F. Hayes and G. T. Fang, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 1297.
23. S. Sato and H. Ueda, Jpn. J. Appl. Phys., 1981, 20, L511.
24. M. Inoue, K. Yoshino, H. Moritake and K. Toda, J. Appl. Phys., 2002, 91, 2798.
25. W. Lee and S.-H. Chen, Appl. Opt., 2001, 40, 1682.
26. L. K. Migara and J.-K. Song, NPG Asia Mater., 2018, 10, e459.
27. M. Mailer, K. L. Likins, T. R. Taylor and J. L. Fergason, Appl. Phys. Lett., 1971, 18, 105–107.
28. M. Bertolotti, S. Martellucci, F. Scudieri and D. Sette, Appl. Phys. Lett., 1972, 21, 74–75.
29. F. Scudieri, M. Bertolotti, S. Melone and G. Albertini, J. Appl. Phys., 1976, 47, 3781–3783.
30. K. Miyano and Y. R. Shen, Appl. Phys. Lett., 1976, 28, 473–475.
31. S. Nagai and K. Iizuka, Jpn. J. Appl. Phys., 1974, 13, 189.
32. S. Nagai, A. Peters and S. Candau, Rev. Phys. Appl., 1977, 12, 21–30.
33. H. Moritake, J. Kim, K. Yoshino and K. Toda, Jpn. J. Appl. Phys., 2004, 43, 6780.
34. R. Ozaki, T. Shinpo, M. Ozaki and H. Moritake, Jpn. J. Appl. Phys., 2008, 47, 1363.
35. Y. J. Liu, X. Ding, S.-C. S. Lin, J. Shi, I.-K. Chiang and T. J. Huang, Adv. Mater., 2011, 23, 1656.
36. Ultrasonic liquid crystal-based underwater acoustic imaging. Liquid Crystal Materials, Devices, and Applications VII, 1999, p. 58.
37. Acoustography: it could be a practical ultrasonic NDE tool for composites. Nondestructive Evaluation of Materials and Composites V, 2001, 129.
38. J. S. Sandhu, R. A. Schmidt and P. J. L. Rivière, Med. Phys., 2009, 36, 2324.
39. Y. Shimizu, D. Koyama, M. Fukui, A. Emoto, K. Nakamura and M. Matsukawa, Appl. Phys. Lett., 2018, 112, 161104.
40. A. Sengupta, U. Tkalec, M. Ravnik, J. M. Yeomans, C. Bahr and S. Herminghaus, Phys. Rev. Lett., 2013, 110, 48303.
41. S. Čopar, Ž. Kos, T. Emeršič and U. Tkalec, Nat. Commun., 2020, 11, 59.
42. T. Emeršič, R. Zhang, Ž. Kos, S. Čopar, N. Osterman, J. J. De Pablo and U. Tkalec, Sci. Adv., 2019, 5, 4283.
43. P. G. de Gennes, The physics of liquid crystals, Clarendon Press, 1995.
44. P. Pieranski, S. Čopar and M. D. M. H. Godinho, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 121.
45. E. A. Konshina and D. P. Shcherbinin, Liq. Cryst., 2018, 45, 292.
46. J. V. Selinger, M. S. Spector, V. A. Greanya, B. T. Weslowski, D. K. Shenoy and R. Shashidhar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 51708.
47. O. A. Kapustina, Acoust. Phys., 2008, 54, 180.
48. P. G. Chun and T. G. Wang, J. Acoust. Soc. Am., 1990, 5, 2367.
49. N. Riley, Theor. Comput. Fluid Dyn., 1998, 10, 349.
50. C. Grammes, J. K. Kruger, K.-P. Bohn, J. Baller, C. Fischer, C. Schorr, D. Rogez and P. Alnot, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 430.
51. T. Li, Q. Huang, S. Li, Y. Xie, J. Han, Y. Han, Y. Lei, H. Hu and D. Zhu, AIP Adv., 2020, 10, 125116.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01443f

‡ These authors contributed equally to this work.

---