Measuring mechanical cues for modeling the stromal matrix in 3D cell cultures

Abstract

A breast-cancer tumor develops within a stroma, a tissue where a complex extracellular matrix surrounds cells, mediating the cancer progression through biomechanical and -chemical cues. Current materials partially mimic the stromal matrix in 3D cell cultures but methods for measuring the mechanical properties of the matrix at cell-relevant-length scales and stromal-stiffness levels are lacking. Here, to address this gap, we developed a characterization approach that employs probe-based microrheometry and Bayesian modeling to quantify length-scale-dependent mechanics and mechanical heterogeneity as in the stromal matrix. We examined the interpenetrating network (IPN) composed of alginate scaffolds (for adjusting mechanics) and type-1 collagen (a stromal-matrix constituent). We analyzed viscoelasticity: absolute-shear moduli (stiffness/elasticity) and phase angles (viscous and elastic characteristics). We determined the relationship between microrheometry and rheometry information. Microrheometry reveals lower stiffness at cell-relevant scales, compared to macroscale rheometry, with dependency on the length scale (10 to 100 μm). These data show increasing IPN stiffness with crosslinking until saturation (≃15 mM of Ca²⁺). Furthermore, we report that IPN stiffness can be adjusted by modulating collagen concentration and interconnectivity (by polymerization temperature). The IPNs are heterogeneous structurally (in SEM) and mechanically. Interestingly, increased alginate crosslinking changes IPN heterogeneity in stiffness but not in phase angle, until the saturation. In contrast, such changes are undetectable in alginate scaffolds. Our nonlinear viscoelasticity analysis at tumor-cell-exerted strains shows that only the softer IPNs stiffen with strain, like the stromal-collagen constituent. In summary, our approach can quantify the stromal-matrix-related viscoelasticity and is likely applicable to other materials in 3D culture.

---

1. Introduction

In invasive breast cancer, a tumor is typically surrounded by a tissue called stroma, an extracellular matrix which houses several cell types (Fig. 1A). This stromal matrix not only has distinct biochemical properties, but also presents 3D biomechanical cues to cells that relate to the cancer initiation and progression.^1–4 Therefore, cell cultures with matrix (3D cell cultures) are required to mimic the stromal confinement, instead of conventional, flat cultures without matrix (2D cell cultures) (Fig. 1B). Multiple physiological mechanical properties need to be considered for accurate modeling of the heterogeneous and complex stromal matrix in 3D culture. The stiffness within the stromal matrix varies spatially from ≃100 Pa up to ≃10 kPa in Young's modulus^3,5–8 based on ex vivo biopsies. The stiffness cues of the matrix mediate initiation of and invasion in breast cancer^2,3 (Fig. 1A and B). A continuous spatial change in stiffness, called a stiffness gradient, inside the stromal matrix may direct migration of cancer cells^9,10 (Fig. 1B). Besides, the stromal matrix stiffens with an increased strain.^11,12 The stromal matrix components—including collagen,¹³ hyaluronan,¹⁴ and fibronectin¹⁵—have not only specific stiffness (elasticity) but also exhibit time-dependent mechanics, arising from each component's solid-like elastic and liquid-like viscous nature (viscoelasticity), relevant to breast-cancer malignancy.^16–18 So far, matrix materials used in 3D cultures to mimic breast-cancer stroma typically failed to fully recapitulate the biomechanical complexity of the stromal matrix—that remains inadequately characterized.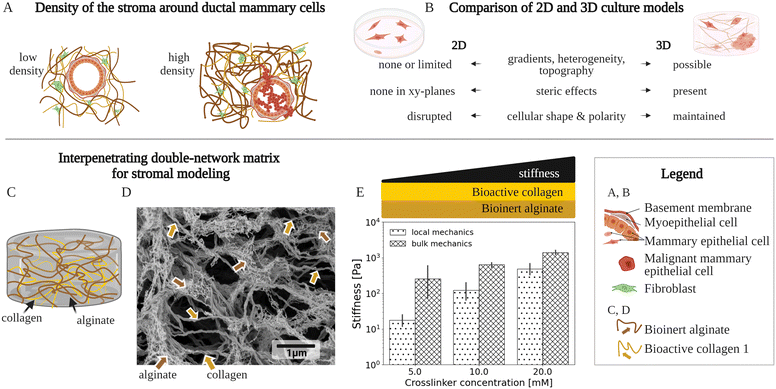

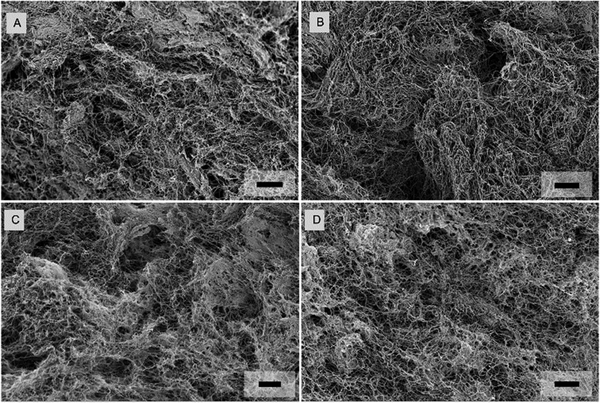
Fig. 1 A variety of matrix model types have been used to mimic the microscale environment of the breast-cancer stroma using 3D culture. (A) Density of two stromal environments, each with a fibrillar matrix, a mammary duct and cells. An increased density of the matrix components, especially collagen type 1, is typically associated with breast cancer.^2,3,19 The illustration shows these stromal components, at a low density with a normal mammary duct, as well at a high density with cancer cells invading the stromal matrix. (B) Key differences between conventional 2-dimensional (2D) and 3-dimensional (3D) cell culture models of the stromal environments. The 2D and 3D culture models are compared in respect to: biomechanical/structural, spatially varying properties (gradients, heterogeneity, and topography), biochemical steric effects, and cell-growth patterns (shape and polarity). (C) Schematic of an existing fibrillar matrix model, composed of a bioinert alginate scaffold and bioactive collagen type 1 filaments, called the interpenetrating network (IPN). (D) High-resolution scanning electron microscopy (SEM) micrograph showing a typical fibrillar structure of an IPN network composed of crosslinked alginate and collagen type 1. The alginate and the collagen concentrations are 5 mg ml⁻¹ and 2 mg ml⁻¹, respectively, while the Ca²⁺ crosslinker molarity is 20 mM. (E) Graph of the IPN's local and bulk mechanics that show an increased stiffness with elevated crosslinking. For local mechanics, the localized IPN stiffness data at the cell-relevant scales is presented, which is provided by this work for the first time, and compared to data on macroscale bulk mechanics, already previously^20–22 studied. The stiffness denotes the absolute complex shear modulus values. The bars and error bars show mean values and standard deviations, respectively. A Ca²⁺ crosslinker, for constant concentrations of alginate (5 mg ml⁻¹) and the collagen (2 mg ml⁻¹), has been used.

Mechanical contributions of the stroma have been characterized using several 3D culture matrix-material types, such as one-component bioactive collagen or hyaluronan matrices,^23,24 and artificial matrices (i.e., polyacrylamide^25,26). There is a challenge that increasing the concentration of such a one-component biopolymer-based matrix not only stiffens the matrix but also increases the bioactive ligand density, altering biochemical interactions that regulate cell behaviors.^2,27,28 To overcome the issue, Baker et al.²⁹ have developed a method to separately control the hyaluronan-matrix ligand density and the matrix stiffness. As another distinct solution, the interpenetrating network (IPN) based on alginate has been designed to enable investigations of mechanical parameters in the stromal matrix, independent of the density of the ligands, including collagen,^30,31 or collagen and hyaluronan together³² (Fig. 1C). The collagen type 1 used within the IPNs is the breast-cancer stroma's most abundant component.³ The alginate-based IPNs provide a compact, rigid, and porous hydrogel that has been recently gaining popularity^20,30,33,34 in the design of 3D culture matrices³⁵ due to their controllable mechanical and chemical properties, as well as their biocompatibility.³⁶ So far, these IPNs have been used to investigate how the averaged properties of matrix stiffness and other viscoelastic properties regulate cell behaviors.^30,32 The investigations of the IPNs^20–22 as well as other stromal-matrix models²³ have utilized macroscale, bulk rheometry information for the averaged data about the heterogeneous materials. Furthermore, stromal-matrix materials^25,37 have been studied for their localized viscoelasticity at the microscale, using atomic-force microscopy and optical tweezers for data at a material's surface proximity, as well as using magnetic microrheometry for data from inside of a material.^38–41 However, the IPNs and other stromal-matrix materials for 3D culture are mechanically unquantified at varied cell-relevant length scales from 10 to 100 μm with physiological stiffness (order of magnitude of 1 kPa in Young's modulus),³ with respect to viscoelastic cues, as well as their heterogeneity.

Here, we have developed a characterization approach, which combines magnetic micro-rheometry and Bayesian hierarchical modeling, to quantify length scale (10 to 100 μm) dependent viscoelasticity and its variations, within the stromal-matrix model IPN, at physiologically relevant stiffness up to 2 kPa in Young's modulus (Section 2.1, Fig. 1C and D). Initially, we investigated how the microscale viscoelasticity of the IPN's bioinert component, alginate, changes as a function of the alginate crosslinker (Section 2.2 and Fig. 1E). Next, we used this approach to analyze the IPNs with their two components, the bioinert alginate and the bioactive collagen type 1, to extract the separate contributions of the components to the viscoelasticity. Furthermore, we investigated the effects—of varying the bioactive collagen concentrations and crosslinking-related polymerization temperature—on microscale viscoelasticity (Section 2.3). These microscale results were compared to macroscale, bulk viscoelasticity values, and we also characterized the related microstructures using scanning electron microscopy (SEM) (Section 2.4 and Fig. 1D). In all of the microscale viscoelasticity data, we accounted for the probe-size (10 to 100 μm) related biases using Bayesian hierarchical modeling (Section 2.5), and we used this modeling to quantify the heterogeneity in viscoelasticity (Section 2.6). Furthermore, we characterized the IPN's strain-dependent stiffness via rheometry to investigate its mechanical integrity⁴² at different strains which tumor cells exert on a stromal matrix (Section 2.7). To summarize, we have presented an approach to quantify the matrix-model IPN that has the potential to provide more accurate analyses of stromal mechanical parameters in 3D culture matrix models for biomedical applications.^42–44

2. Results

2.1. Approach to measuring viscoelasticity on the microscales at stroma-relevant stiffness

Our approach was used to quantify stiffness and other viscoelastic properties of the stroma-modeling hydrogel, the IPN, at the cell-size-relevant length scales (Fig. 1C–E). This was realized by combining magnetic microrheometry and Bayesian hierarchical modeling.

We have utilized a probe-based magnetic microrheometer, by Pokki et al.⁴⁵ for breast-cancer 3D culture research,^39,40 to obtain data on the localized mechanics at the microscale and the related mechanical heterogeneity within the hydrogel samples. Specifically, we performed shear tests that involved the exertion of oscillatory forces on magnetic probes in the hydrogels at a low frequency, relevant to cancer-cell invasion dynamics (i.e., 0.05 Hz).³⁹ Simultaneously, we detected the probes’ displacements to measure the mechanical properties within each hydrogel sample. In this method, the magnetic forces, which move magnetic probes within the sample, scale with the probe volume. Consequently, larger probes are required to detect probe displacements in hydrogels with increased stiffness. For each hydrogel stiffness, we chose appropriately sized probes (scheme in Fig. S1 in the ESI†) to achieve measurable but small strains for operation in the linear viscoelasticity regime (LVR) (strain and frequency sweeps shown in Fig. S2 in the ESI).†

We supplemented this microscale mechanical information with macroscale bulk mechanical data. We used parallel-plate rheometry to provide averaged data about each hydrogel sample and to reveal sample-to-sample repeatability at the LVR. These mechanical measurements at the micro- and macroscale consist of viscoelasticity data. To describe viscoelasticity, we used absolute (complex) shear modulus (|G*|) that is a measure of hydrogel stiffness and phase angle (Φ) that is a metric describing the viscous and elastic (0 rad) nature of the hydrogels. Additionally, SEM images were captured to elucidate the structural basis behind the detected mechanical properties.

We used a Bayesian hierarchical model to analyze the mechanical data from microrheometry and rheometry, because the experimental data have systematic errors and uncertainties, complicating direct comparisons of investigated conditions.⁴⁰ Therefore, the reported results hereafter are based on the model output, unless stated otherwise. The hydrogel material's viscoelastic properties (|G*| or ϕ) of interest may be hidden due to biased parameters, such as changing magnetic probe size, which necessitates a more principled approach to the analysis. Therefore, we developed a multilevel Bayesian model to capture the relationships and facilitate the comparison of different conditions. In simplified terms, the model is as follows:

where y represents the measured viscoelastic property (|G*| or ϕ) at the log scale. Logarithmic transformation was used to facilitate the modeling,⁴⁶ while the positive data values allow this.⁴⁷ The function f is a linear function with a saturation point, allowing for a change in the slope for stiffness (|G*|) (e.g., Fig. 2A). Conversely, the f function is a linear regression slope for the phase angle (ϕ) due to unobserved saturation in the raw data. The parameter effects are allowed to vary among different groups. We account for the effects of different probe sizes (μ_{probe size}), related to probing of the material at different length scales (Fig. S5, ESI†). The probe coatings (μ_{probe coating}) and the effects (μ_experimental) due to experimental data collection⁴⁰ are also unique parameters shifting the measured values independently of the calcium crosslinker concentration. Collagen concentration (C_{collagen concentration}) and polymerization temperature (T) are assumed to have a linear correlation (k_{collagen concentration} and k_{polymerization temperature}) with the measured mechanical properties.

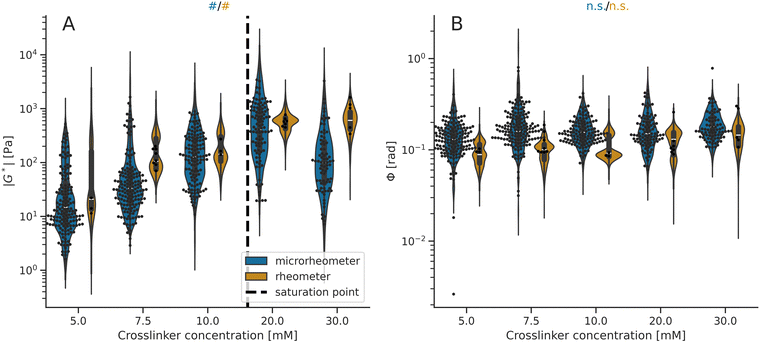Fig. 2 Viscoelasticity data of the alginate hydrogels at the microscale (microrheometry) and macroscale (rheometry). The violin plots illustrate the model distribution. (A) Stiffness values (|G*|) measured by microrheometry are smaller than the values detected using rheometry (Table S2 and Fig. S3, ESI†). Both techniques report increasing mean |G*| values with higher crosslinker concentrations (#Pr > 0.950 from Table S4, ESI†) up to the estimated saturation point, depicted by a dashed line. (B) Phase angle values (Φ) measured using microrheometry are larger than the values obtained using rheometry (Table S2 and Fig. S3, ESI†). Both techniques report that the mean Φ values neither decrease nor increase as a function of alginate crosslinking (n.s. Pr < 0.950 from Table S4, ESI†). For the microrheometer and rheometer measurements, the points indicate microscale values (within hydrogel samples) and macroscale values (from different hydrogel samples), respectively.

Furthermore, a key aspect explored by the magnetic microrheometer is the IPN material heterogeneity. We build on our previously reported model⁴⁰ to decouple the material's intrinsic variation in viscoelasticity from systematic biases. The heterogeneity in viscoelasticity is modeled as follows:

y_std = GP(C_Ca²⁺) + σ_{probe size} + σ_{collagen concentration} + σ_{polymerization temperature} (2)

The heterogeneity was quantified as the standard deviation (y_std) of the modeled data at the sample holder level, as outlined in our previous article.⁴⁷ The trend is modelled with a non-linear function, specifically with a Gaussian process (GP),⁴⁸ which is assumed to be a function of the calcium crosslinker concentration (C_Ca²⁺). Furthermore, the probe size (σ_{probe size}), collagen concentration (σ_{collagen concentration}) and polymerization temperature (σ_{polymerization temperature}) may affect the heterogeneity independently of calcium concentration. For both the analyses of viscoelasticity and heterogeneity in viscoelasticity, we have assumed a significant trend when the probability is at least 0.95, and the slope is positive (i.e., above 0.1 of the standard deviation of the data⁴⁹). Further details on the modeling can be found in Section S1 in the ESI.†

2.2. Viscoelasticity of alginate hydrogels and IPNs

Initially, we have validated the methods by investigating the alginate-hydrogel mechanics at the micro- and macroscales at varied stroma-related stiffness levels. The viscoelastic properties of the alginate hydrogels, the shear modulus (Fig. 2A) and phase angle (Fig. 2B) measured by microrheometry and parallel-plate rheometry were compared at different calcium (Ca²⁺) crosslinker concentrations (details on compositions listed in Table S1, ESI†). The microrheometer for microscale data reports lower mean stiffness values than the rheometer for macroscale data (Fig. 2A; details in Fig. S3 and Table S2, ESI†). In contrast, larger mean values of phase angles are provided by microrheometry than by rheometry (Fig. 2B; details in Fig. S3 and Table S2, ESI†).

Having analyzed the relationship of viscoelasticity between microrheometry and rheometry measurements motivated us to further investigate the microscale viscoelasticity at different stiffness levels. Both microrheometry and rheometry show that the alginate stiffness is elevated by an increasing Ca²⁺ concentration, from 5 mM to approximately 20 mM, whereas the stiffness value deviates from the increasing trend at the highest crosslinker concentration of 30 mM (Fig. 2A). For these data, we calculated separately the trends below and above a model-estimated saturation point at 16 mM of the Ca²⁺ crosslinker (Table S4, ESI†). On the other hand, we have not detected systematic changes in phase angles as a function of the crosslinker (Fig. 2B; details in Tables S2 and S4, ESI†). Since the micro- and macroscale mechanical analyses have reported distinct stiffness levels at the Ca²⁺ crosslinker concentrations of 5 mM, 10 mM, and 20 mM, we have selected these concentrations for further investigation.

Next, we measured the viscoelastic properties of the IPN hydrogels with the selected crosslinker concentrations (Fig. 3). We used the microrheometry to quantify the IPN microscale properties and compared these results with the corresponding macroscale values measured using the rheometry (details on IPN compositions in Table S5, ESI†). The mean stiffness values are lower at the microscale than at the macroscale (Fig. 3A; details in Fig. S3 and Table S6, ESI†), similarly as for the alginate hydrogels. On the other hand, the comparison of phase angles does not indicate any systematic difference between the micro- and macroscale data (Fig. S3 and Table S3, ESI†). Then, we analyzed the correlation between viscoelastic properties of the IPN hydrogels and the crosslinker concentration, which is in line with the results from the alginate hydrogels (Fig. 2). The stiffness of the IPN hydrogels increased as a function of the crosslinker concentration until the saturation point, both at the micro- and macroscales (Fig. 3A; details in Tables S4 and S6, ESI†). We assume that the Ca²⁺ crosslinker saturation points are practically identical for both alginate and IPN hydrogels because the number of crosslinking sites is the same, with some variations due to preparation errors. The model evaluated the saturation point of IPN around 15 mM of the Ca²⁺ crosslinker. Furthermore, the micro/macroscale measurements indicate no systematic alterations in phase angles with the crosslinking (Fig. 3B; details in Tables S4 and S6, ESI†).

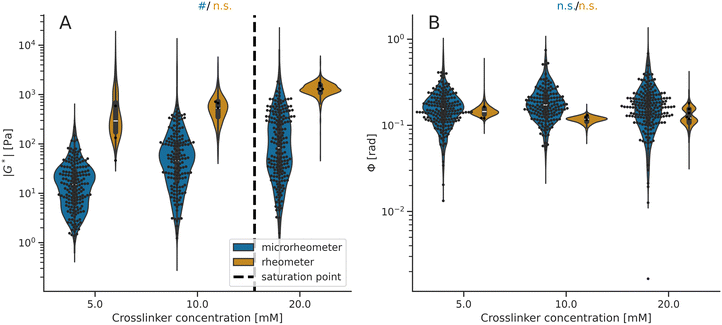Fig. 3 Viscoelasticity data of the IPN hydrogels at the microscale (microrheometry) and macroscale (rheometry). The violin plots illustrate the model distribution. (A) Stiffness values (|G*|) measured using microrheometry are systematically lower than rheometer measurements (Table S6 and Fig. S3, ESI†). Both techniques report on increasing mean |G*| values with higher crosslinker concentrations (#Pr > 0.950 from Table S4, ESI†) up to the estimated saturation point, depicted by a dashed line. (B) Phase angle (Φ) values are comparable between the two techniques (Table S6 and Fig. S3, ESI†) and they neither decrease nor increase with elevated crosslinker concentration (n.s. Pr < 0.950). For the microrheometer and rheometer measurements, the points indicate microscale values (within hydrogel samples) and macroscale values (from different hydrogel samples), respectively. The mean values and standard deviations are shown in Table S2 (ESI†).

So far, we have investigated how the viscoelastic properties of IPNs change with modifications, applied strictly to the bioinert alginate component, but it remains unclear what is the effect of the IPN's bioactive collagen component on viscoelasticity. In fact, a native breast cancer stroma has variation in its collagen content.⁵⁰ Therefore, we extended our study for modulating the properties of the collagen component within the IPN.

2.3. Viscoelasticity of IPNs as a function of collagen properties

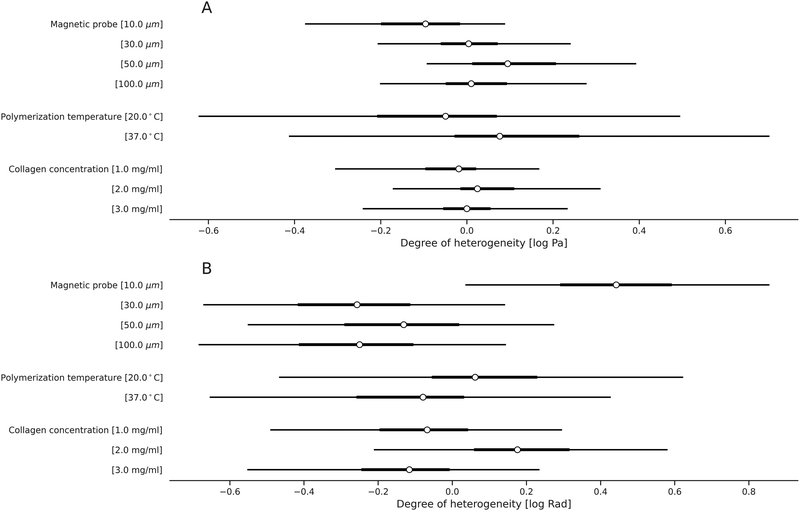
Next, we extended the use of our approach for quantification of the IPN hydrogels with respect to the effects of collagen concentration and crosslinking-related polymerization temperature, both of which regulate the microstructure of the collagen component within the IPN hydrogels. Specifically, we supplemented the microscale viscoelasticity data at a collagen concentration of 2 mg ml⁻¹ (Section 2.2) with lower (1 mg ml⁻¹) and higher (3 mg ml⁻¹) values (Fig. 4). We report that there is a positive correlation between the collagen content in the IPN and its stiffness (Fig. 4A). The quantification shows that when the collagen content is increased by 1 mg ml⁻¹, the mean local stiffness grows by 10% (Fig. 5). On the other hand—the phase angle does not systematically change (Fig. 4B and 5).

Fig. 4 Microscale viscoelasticity data of IPN hydrogels at different collagen concentrations. (A) Stiffness values (|G*|) and (B) phase angle (Φ) values of IPN hydrogels with 1 mg ml⁻¹ (blue), 2 mg ml⁻¹ (orange), and 3 mg ml⁻¹ (green) of collagen type 1, as a function of calcium crosslinker. The points indicate the measured microscale values, and the violin plots illustrate the model distribution. All hydrogels show increasing mean stiffness with increasing collagen and calcium crosslinker concentrations. Phase angle (Φ) values are comparable between all the hydrogels and they neither decrease nor increase with elevated crosslinker concentration.

Fig. 5 Effects of collagen concentration and polymerization temperature at the microscale stiffness and phase angle. Quantification of the relative effect of collagen concentration (grey box) and polymerization temperature of the IPN on the mean stiffness (|G*|) (black) and phase angle (Φ) (orange). The X-axis indicates the percentual increase or decrease of the material property as a function of collagen concentration or polymerization temperature. For instance, the stiffness value of IPN increases by ≃10% between collagen concentrations of 1.0 and 2.0 mg ml⁻¹. The lines represent 89% of the highest density interval.

Furthermore, we quantified how the viscoelasticity of the IPN hydrogels changes by adjusting the polymerization temperature to alter the collagen's degree of interconnectivity related to crosslinking (i.e., the collagen concentration of 2 mg ml⁻¹ was used). Specifically, we reduced the temperature from 37 °C, which was used in all the previous experiments, to a lower value of 20 °C (Fig. 5). In terms of local viscoelastic properties, the hydrogels which were polymerized at 20 °C show higher mean stiffness than hydrogels polymerized at 37 °C (Fig. 5). The polymerization temperature was found to reduce the microscale mean stiffness by 8% when increased from 20 °C to 37 °C (Fig. 5 and 6). In contrast, we did not observe effects on the bulk stiffness due to changing the polymerization temperature. As in the previous measurements, the bulk stiffness is higher than the mean local stiffness, for both temperatures at all crosslinker conditions. The phase angles of the IPNs polymerized at these different temperatures do not change (Fig. 5 and 6B).

Fig. 6 Viscoelasticity data of the IPN hydrogels polymerized at different temperatures (A) stiffness (|G*|) and (B) phase angle (Φ) of IPN hydrogels with 2 mg ml⁻¹ of collagen polymerized at 20 °C and at 37 °C. The points and triangles indicate microscale and macroscale values, respectively. The violin plots illustrate the model distribution. The macroscale |G*| values are higher than the corresponding microscale mean |G*|, and the IPNs polymerized at 20 °C are systematically softer than IPNs polymerized at 37 °C. Phase angle (Φ) values are comparable between all the hydrogels, for both microscale and macroscale, and they neither decrease nor increase with elevated crosslinker concentration.

Interestingly, we have found a larger scatter in the microscale data (microrheometry) than in the macroscale data (rheometry), in all studied hydrogels. This observation suggests that the hydrogels exhibit heterogeneity.

2.4. Microstructural characterization by scanning electron microscopy (SEM)

We used SEM to analyze the microstructure of the IPNs and their constituents, with the goal of elucidating the underlining structural basis that can plausibly be behind the mechanical properties. The SEM micrographs show the typical heterogeneous porous networks for all hydrogels: the reconstituted collagen type 1 (Fig. 7A) alginate hydrogels (Fig. 7B), as well as for the IPN hydrogels at a collagen concentration of 2 mg ml⁻¹ (Fig. 7C). Pure collagen consists of a disordered fibrillar mesh with fiber diameters in the range of nanometers. In contrast, the highly crosslinked alginates have a more compact and denser microstructure with randomly distributed pores, similar to the structure of highly crosslinked IPNs which contain porous spaces separated by distinct microphases (Fig. 7B and C).

Fig. 7 SEM micrographs of collagen, alginate and IPN hydrogels. (A) Fibrillar collagen type 1 at a concentration of 2 mg ml⁻¹. (B) Alginate hydrogel with 20 mM of the Ca²⁺ crosslinker. (C) IPN hydrogel with 20 mM of the Ca²⁺ crosslinker. The scale bars denote 20 μm.

The micrographs suggest increasingly dense structural regions with higher crosslinker concentrations (Fig. 8 and 9). In all the hydrogels, the mesh size is smaller than the nominal diameters of the probes (10 μm to 100 μm). This structural characterization qualitatively shows that the IPNs and their constituents (alginate and collagen) are heterogeneous. However, this characterization is unable to provide information on mechanical heterogeneity. To measure the variation in viscoelasticity, it is needed to identify how viscoelasticity depends on the measurement of probe-related properties.

Fig. 8 SEM micrographs about the topology of softer and stiffer IPN hydrogels. (A) and (B) Softer IPN hydrogels with 7.5 mM of the Ca²⁺ crosslinker. (C) and (D) Stiffer IPN hydrogels with 20 mM of the Ca²⁺ crosslinker. The scale bars denote 10 μm.

Fig. 9 High-resolution SEM micrographs of homogeneously distributed collagen type 1 mesh within the porous network of softer and stiffer IPN hydrogels. (A) Softer IPN hydrogels with 7.5 mM of the Ca²⁺ crosslinker. (B) Stiffer IPN hydrogels with 20 mM of the Ca²⁺ crosslinker. The scale bars denote 2 μm.

2.5. Effects of probes on microscale viscoelasticity measurements

In magnetic microrheometry, increasing the probe diameter is necessary to measure stiffer hydrogels.⁴⁷ We observed that the stiffness values measured by different sizes of probes vary systemically (Fig. S5, ESI†). For instance, larger probes report higher stiffness than the smaller probes, with the exception of the nominal probe diameter of 50 μm (i.e., giving lower stiffness values than the probes with the 30 μm nominal diameter). This revelation suggests variations in local stiffness values at different length scales from 10 to 100 μm. Besides the observed effect of probe size, we recognize that probe coating could also cause bias in the reported viscoelastic properties.⁵¹ Therefore, during the analysis, these probe effects—size and coating—were decoupled from the measured values to reveal the heterogeneity in viscoelasticity. This approach removed the impact of probe-size effects, but no systematic effects of probe-coating were detected (Fig. S6, ESI†). As expected, the model-corrected viscoelasticity values follow the same trends that were unveiled from the measured data (Fig. 2 and 3). These investigations of systematic errors enable us to evaluate the heterogeneity differences in viscoelastic properties.

2.6. Heterogeneity in viscoelasticity

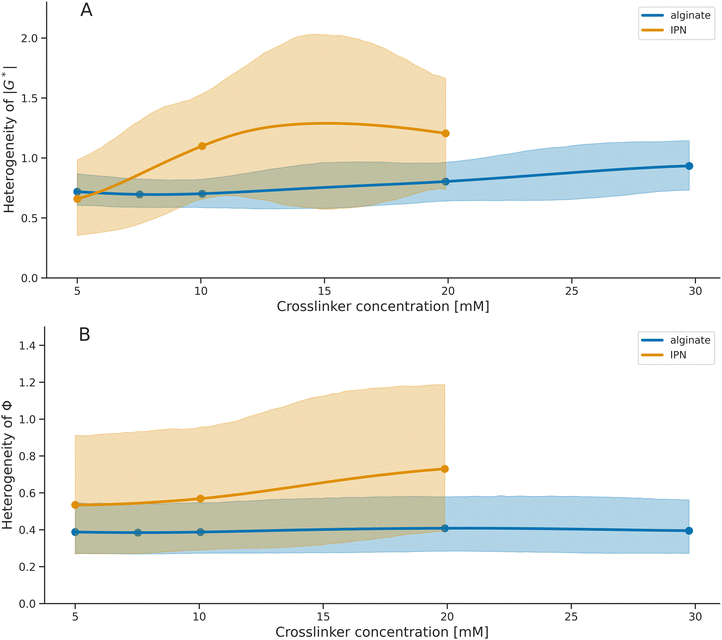
We analyzed the microrheometry-based viscoelasticity differences in the alginate and IPN hydrogels to quantify the corresponding heterogeneity in viscoelasticity (Fig. 10). We have estimated the heterogeneity of all studied hydrogels while accounting for the known confounding factors as in the work⁴³ and as we described in Section 2.5. We have compared the heterogeneity differences in stiffness (Fig. 10A) and phase angle (Fig. 10B) between alginate hydrogels and the IPNs. For the crosslinker concentrations over 7.5 mM, the alginate hydrogels exhibit lower heterogeneity than the IPN hydrogels, both in stiffness and in phase angles.

Fig. 10 Relative differences of heterogeneity in viscoelastic properties for the alginate and IPN hydrogels. (A) Heterogeneity in stiffness (|G*|) and (B) heterogeneity in phase angle (Φ) with respect to crosslinker concentration. The shaded area is the 95% credible interval, and the darker lines are the calculated means. Scatter points depict the crosslinker concentrations at which the hydrogels were measured, while the regions in between are the modelled estimates.

The quantification demonstrates how the increase in crosslinker is related to the changes in hydrogel heterogeneity in viscoelasticity. For alginate hydrogels, the results suggest that the heterogeneity in stiffness increases with crosslinker concentrations (Fig. 10A), while for IPNs, the increase is evident. In contrast, the heterogeneity in phase angle indicates no differences across crosslinker concentrations for both IPN and alginate hydrogels (Fig. 10B). Similarly, modifying the IPN collagen content or the polymerization temperature did not change the IPN heterogeneity (Fig. 11).

Fig. 11 Effects of specific probe sizes, polymerization temperatures, and collagen concentrations on the heterogeneity in viscoelastic properties. Quantification of various effects on the heterogeneity in stiffness (A) and heterogeneity in phase angle (B). The lines represent 89% of the highest density interval.

So far, we have quantified the viscoelasticity at the LVR and the heterogeneity in viscoelasticity for the alginate hydrogels and the IPNs. Yet, stroma-related matrices^52–59 experience varying strains, exerted by tumor cells. Therefore, this quantification benefits from complementary data on non-linear, strain-dependent viscoelasticity.

2.7. Strain-dependent viscoelastic properties

We have quantified the non-linear strain-dependent responses of alginate and IPN hydrogels with 2 mg ml⁻¹ of collagen. We compared the responses of these hydrogels to the values for ubiquitous pure collagen type 1 (Fig. 12). Specifically, the alginate and IPN hydrogels were measured at 7.5 mM and 20 mM of the crosslinker concentrations. For the relevant strains as exerted by the cells,^52–59 oscillatory strain sweeps from 0.01% to 40% were conducted on parallel-plate rheometry. Multiple regimes between 0.01% and 30% of strain were found. All the studied hydrogels consistently show a plateau in stiffness until a 1% strain at the LVR. This strain-independent range, as well as the critical strain for the onset of non-linear viscoelasticity, is comparable for both the alginate hydrogel and the IPN samples at equivalent crosslinker concentrations (i.e., 20 mM and 7.5 mM). The stiffer hydrogel samples with a crosslinker concentration of 20 mM exhibited a drop in stiffness, immediately after LVR, indicating a sudden structural failure. On the other hand, the softer hydrogels with a lower network density (7.5 mM of the crosslinker) displayed an onset of sharp increase in the moduli between the strains of 5 and 10%, reaching the maximum stiffness of 1.50–1.75-fold value of the steady-state LVR modulus, at a 27% strain. Above this strain, the shear moduli drop, which indicates a structural collapse of the hydrogels. Furthermore, the reconstituted collagen type 1 displayed strain-independent behavior up to the largest strains among the tested hydrogels (i.e., the maximum increase in stiffness reached approximately 1.25-fold the value of the steady-state modulus value). Further, as previously observed results for collagen,⁶⁰ we detected a minor softening before the onset of the strain-stiffening behavior. The presented results show the applicability of our methods for mechanical analyses of the stromal-matrix properties in breast cancer, in a cell-scale-relevant quantification within the IPN matrix model of the stroma, its heterogeneity, and its strain-stiffening characteristics.

Fig. 12 Non-linear stiffness responses of the alginate and IPN hydrogels obtained from oscillatory strain sweeps at 0.05 Hz on plate–plate rheometry after 50 minutes of gelation. Data are absolute shear moduli (|G*|) normalized by the modulus at a strain of 0.035% as a function of the oscillatory shear strain. The mean values for two repetitions at each strain are shown (standard deviations for the graph are shown in Fig. S2, ESI†).

3. Discussion and conclusions

Our results are discussed with respect to (Section 3.1) viscoelasticity from cell to macroscales, (Section 3.2) increasing hydrogel stiffness with Ca²⁺ crosslinking, (Section 3.3) modulating the collagen component, (Section 3.4) decoupling systematic biases from the data, (Section 3.5) mechanical and structural heterogeneity, and (Section 3.6) strain stiffening, with the final (Section 3.7) concluding remarks.

3.1. Viscoelasticity from cell to macroscales

Discrepancies in mechanical responses of biomaterials at different length scales are widely observed.^61–65 We acknowledge that microrheometry and rheometry investigate nonidentical length scales, and therefore, they measure different mechanical properties.⁶⁶ This likely originates from the intrinsic material hierarchy, typical for biopolymer networks.^67,68 While bulk rheometry reports the macroscopical response of the complex material, the network heterogeneities, which are experienced by cells, remain undetected. In contrast, when biomaterials are probed locally, within a small distinct volume as in magnetic microrheology, the response of the surrounding network correlates with the response of the stromal tissue when cells exert forces on its microenvironment. We accordingly suggest that local viscoelastic properties measured using a microrheometer are relevant for elucidating how cells sense mechanics at their location. Yet, to date, there are no clear explanations nor hypotheses on why fibrillar networks show lower mechanics^64,65 on meso- and microscales and we suggest this topic for future investigation.

Furthermore, our SEM characterization demonstrates that the organization of the material components is heterogeneous with interstitial spacings of smaller size than magnetic probes (10 μm to 100 μm of nominal diameter). Considering the choice of probing length scales, invasive cancer cells' size^21,69 is often over 10 μm, while the size of cellular spheroids can be in the order of 100 μm.⁷⁰ Therefore, we have chosen probe sizes from 10 μm to 100 μm, which corresponds to these length scales. Furthermore, we acknowledge that the use of the probes within the hydrogels could have an effect on the gelation by shifting the stiffness values (data with and without the probes in Fig. S4, ESI†); however, such an effect is likely small compared to the considerable dependency on the probing length scale.

3.2. Increasing hydrogel stiffness with Ca²⁺ crosslinking

Both our cell-scale-relevant and macroscale results are consistent with the literature reporting that alginate-based hydrogels’ stiffness is positively associated with alginate crosslinker concentration. We have detected a saturation for a maximum alginate crosslinking density corresponding to the maximum material stiffness. Based on the model estimation, the upper limit of stiffness is around 15–16 mM of Ca²⁺ crosslinker, for both alginate and IPN hydrogels (i.e., at an alginate concentration of 5 mg ml⁻¹). This finding on saturation is related to the principle of network formation at the molecular level. Anionic alginate chains are formed out of guluronic and mannuronic acid monomers, and it is widely accepted that the mesh formation proceeds via specific bridging of two guluronic residues by one divalent cation.^71–73 Therefore, at a constant alginate concentration, we expect that the network interconnectivity increases with Ca²⁺ crosslinker concentration until a saturation point, where all the available bridging sites become fully occupied.⁷⁴

Furthermore, our microrheometer data indicate a drop in the microscale stiffness for hydrogels at a 30 mM concentration of the Ca²⁺ crosslinker. We hypothesize the stiffness reduction at the measured locations to be related to the crosslinker oversaturation,⁶⁷ plausibly resulting in Ca²⁺ precipitates⁷⁵ which disturb the fibrillar distribution within the network, specifically, alignment and connectivity.

3.3. Modulating the collagen component

Our characterization shows that the microscale stiffness of the hydrogels increases with collagen concentration, and this observation is consistent with previous studies.^76,77 The higher stiffness is caused by a higher volume fraction of collagen fibres creating a denser network. Furthermore, we chose to study how microscale mechanical properties change with collagen crosslinking by modifying the preparation conditions, which are known to alter the polymerization kinetics of reconstituted collagen-containing hydrogels. These parameters, therefore, affect the hydrogel microstructure,^78,79 and consequently its mechanics. In line with previous research,⁷⁷ we found that lowering the polymerization temperature from 37 °C to 20 °C results in an increase in microscale stiffness, for IPN hydrogels with otherwise identical composition. Based on the published literature,^79,80 the polymerization rate governs the assembly of individual collagen molecules. Therefore, we explain that the higher stiffness of the hydrogels prepared at 20 °C is due to an increased collagen crosslinking forming thicker fibers. Conversely, a higher polymerization rate for hydrogels fabricated at 37 °C produced mechanically weaker materials, which we explain by decreased collagen crosslinking yielding thinner fibers. The difference in polymerization rate between these materials is evident from the rheology experiments. The gelation curves of IPNs polymerized at 20 °C reached a plateau after 80 minutes, in comparison to 40 minutes for the IPNs polymerized at physiological temperature. Overall, the collagen concentrations in this study are relevant for modeling breast cancer stroma⁸¹ and the employed polymerization temperatures are used to control the collagen crosslinking, and thus network interconnectivity.⁷⁷

3.4. Decoupling systematic biases from the data

The magnetic-probe coating shows no observable differences in the measured local viscoelasticity. On the other hand, the size of the magnetic probes affects the recorded viscoelasticity, and the effect was quantified for each probe size. This finding could be related to the fact that the probes’ contact area increases roughly up to 100-fold from the smallest to the largest probe (i.e., from 10 μm to 100 μm in nominal diameter), and consequently, this changes the alignment/distribution of fibers in contact with the probes. Also, varying probing volumes may lead to a mismatch in the measured network geometries.⁶¹ Further discussion on the length scales, which are probed, can be seen in Section 3.1.

3.5. Mechanical and structural heterogeneity

We report notable heterogeneity in viscoelasticity for all the studied alginate-based hydrogels. In line with that, the SEM micrographs of the hydrogels reveal a non-uniform hierarchical mesh with distinct local geometries in the fibrillar network, which is consistent with earlier findings on the heterogeneity of comparable biomaterials.^80,82 The length scales, at which we observed these structural differences on SEM, overlap with the selected sizes of the magnetic probes employed in microheometer measurements.^80,82 We showed that the individual alginate filaments, as well as the irregularly crosslinked alginate domains are randomly intertwined with a fibrillar collagen network. In detail, the hydrogels are composed of random collagen bundles and intermittent semi-flexible segments of alginate fibers with fluctuating lengths, which are located between adjacent stiff, crosslinked meshed regions of alginate.^71–73,83 The complex network architecture gives rise to the mechanical heterogeneity of the hydrogels.⁸⁴ In terms of crosslinker thermodynamics, its concentration fluctuations also complement the spatial inhomogeneities.⁸⁴

Here, microrheology revealed that the double-network IPN hydrogels have a consistently greater degree of spatial inhomogeneities than alginate hydrogels. This implies that the structural complexity, induced by adding components to the original network, affects mechanical properties. Furthermore, IPN hydrogels show increasing heterogeneity with higher crosslinking degrees until the saturation point. Such a dependency, yet with a weaker trend, is also present, for the alginate hydrogels. In line with the detected rise in the IPN's spatial heterogeneity at the higher crosslinker concentrations, the SEM micrographs depict increased local assembles of filaments, mainly in the meshed regions. We suggest that this finding is material-specific, originating from the insolubility of the crosslinker salt in water. The fast sedimentation of CaSO₄, despite thorough mixing of the crosslinking solution, generates non-uniformly suspended particles. During the preparation of hydrogels with higher Ca²⁺ crosslinker concentrations, the inconsistencies in the mixing solutions are greater, and consequently, the spatial variations could become more pronounced.

3.6. Strain stiffening

Non-linear stress–strain behavior⁷⁴ at increased strains is a universal property of biomaterials with semi-flexible filaments,⁸⁵ such as our stroma-model hydrogels. We rationalize that the structural disparities, which were induced by Ca²⁺ crosslinking, created differences in the onset and in the rate of strain-stiffening.^85,86 Specifically, the hydrogels with lower crosslinking density (7 mM Ca²⁺) contained a compliant network, and thus, the structural rearrangements induced by the shear strains promoted stiffening. Conversely, the hydrogels with higher crosslinking (20 mM Ca²⁺) may have reduced the freedom of the alginate filaments, rendered them inextensible, and consequently these stiff hydrogels ruptured immediately at the strains above LVR. For complementary data, we characterized strain-stiffening of pure collagen type 1 hydrogel to correlate the behavior of IPN/alginate hydrogels with an established single-network stroma-model material. In comparison to these collagen data, the bundles of crosslinked alginate could have led to superior robustness and allowed for a superior stiffening response of softer hydrogels over pure collagen. On the other hand, the flexible segments stored in filament undulations could be potentially reduced by random ionic crosslinks. As a result, the collagen hydrogel with only entangled helices sustained larger deformations before a structural failure, in comparison to softer alginate-containing gels.⁷⁵

3.7. Concluding remarks

To mimic the stromal matrix in 3D culture, there is a lack of approaches to characterize the matrix material's mechanical properties at cell-relevant length scales and at stromal-stiffness levels (Fig. 1A–D). Here, to address this gap, we have developed an approach—based on probe-based microrheometry, rheometry, and Bayesian modeling—to quantify microscale viscoelasticity and heterogeneity in viscoelasticity as in the stromal matrix.

As a matrix model, we have examined the IPNs with bioinert alginate scaffolds and bioactive collagen type 1 as in the stromal matrix (Fig. 1C–E). Initially, we determined the relationship between the microrheometry and rheometry information, and we found that microrheometry reveals lower stiffness, compared to macroscale rheometry (Fig. 2 and 3). These data show increasing IPN stiffness values with crosslinking until a saturation point (≃15 mM of Ca²⁺), with no systematic changes in phase angles. Furthermore, we complemented the study with viscoelasticity measurements of IPN with additional collagen concentrations, as well as with lower polymerization temperature. As expected, we observe that collagen concentration is positively correlated with IPN stiffness (Fig. 4), unlike polymerization temperature, which decreases the IPN microscale stiffness (Fig. 6). In this work, we outline that the IPNs are heterogeneous not only structurally but also mechanically. We have found that an increased crosslinking changes the IPN heterogeneity in stiffness but not in phase angle, until the saturation point (Fig. 10). In contrast, such changes are undetectable in alginate scaffolds of IPNs. Our analysis of nonlinear viscoelasticity at tumor-cell-exerted strains shows that only the softer IPNs stiffen with strain, like the stromal-collagen constituent (Fig. 12). The approach presented here can quantify the stromal-matrix mechanics and is likely applicable to other materials in 3D culture for biomedical applications.

4. Materials and methods

4.1. Hydrogel preparation

4.1.1. Alginate hydrogels. Initially, we studied the single-network alginate hydrogel at a concentration of 5 mg ml⁻¹ and used the Ca²⁺ crosslinker concentrations of 5 mM, 7.5 mM, 10 mM, 20 mM, and 30 mM to define a stiffness range of the structural backbone in the IPN hydrogels. To prepare the alginate hydrogels, we have used the recipe as given in Table S1 (ESI†). Specifically, we used a PRONOVA UltraPure VLVG alginate powder (<75 000 g mol⁻¹; NovaMatrix Sandvika, Norway) dissolved in DMEM/F12 to a concentration of 7 mg ml⁻¹ and aliquoted into a 1 mL syringe. The DMEM/F12 and the 0.75 M CaSO₄·2H₂O slurry were transferred into a second syringe, together with magnetic and reference probes needed for microrheometry.⁴⁰ Then, a female-to-female Luer lock connector was used to connect the two syringes. The solutions in the two syringes were mixed by alternately pushing the syringe plungers to homogenize the crosslinker in the alginate solution. For the rheometry, the pre-gelled solutions were promptly placed onto the bottom parallel plate of a rheometer. For the microrheometry, a pre-gelled solution was aliquoted into three sample holders. The samples were allowed to polymerize for 40 minutes at 20 °C.

4.1.2. IPN hydrogels. The IPN hydrogel preparation was identical to the alginate hydrogel preparation with the following alterations (Table S5, ESI†): the concentration of the alginate stock solution was increased to 13.125 mg ml⁻¹ and the rat tail collagen type 1 (Fischer Scientific cat. num. CB354249) was added to the second mixing syringe prior to mixing. Specifically, the IPN hydrogels were prepared based on the mechanical properties of the 5 mg ml⁻¹ alginate gels (i.e., we used the Ca²⁺ crosslinker concentrations of 5, 10, and 20 mM as selected in Section 2.1). We added the corresponding amounts of collagen type 1 to achieve the desired concentrations. The IPNs with 1 and 3 mg ml⁻¹ of collagen polymerized only at 37 °C, and the IPNs with 2 mg ml⁻¹ of collagen were polymerized at both 20 °C and 37 °C.

4.1.3. Collagen type 1 gels. Samples with pure collagen were prepared from the rat tail collagen type 1 stock solution (Fischer Scientific cat. num. CB354249) at a final concentration of 2 mg ml⁻¹ (Table S8, ESI†). The DMEM/F12 acted as a buffer maintaining the collagen solution at pH 7, which was confirmed by a pH indicator. The samples were allowed to polymerize for 40 minutes at 37 °C.

4.2. Mechanical characterization

We characterized the mechanics of samples using rheometry (Section 4.2.1) and microrheometry (Section 4.2.2). We quantified the linear viscoelastic properties of the hydrogels by both techniques. The non-linear response of the hydrogels was investigated using rheometry. Furthermore, we converted the absolute shear moduli results to Young's moduli. For this purpose, we assumed that the shear modulus (G) equals absolute shear modulus (G = |G*|), as well as that the hydrogels are isotropic and incompressible. Thus, the Young's modulus is E = G·2(1 + ν), where ν = 0.5 is an incompressible hydrogel's Poisson ratio.

4.2.1. Rheometry. All rheometry experiments were conducted by in situ preparation on an Anton Par MCR302 rheometer using a smooth parallel-plate geometry. Initially, the LVR of the hydrogels was determined via: oscillatory frequency sweeps from 0.01 to 10 Hz at a low strain of 1% at 20 °C (Fig. S2A, ESI†), as well as oscillatory strain sweeps from 0.05% to 40% shear strain at low frequency of 0.05 Hz at 20 °C (Fig. S2B, ESI†). The tests were measured at a 0.05 Hz frequency, 1% strain, after 40 minutes (alginate and IPN polymerized at 37 °C) or 80 minutes (IPN polymerized at 20 °C) of polymerization at the specific temperature conditions. The gelation kinetics was followed at a frequency of 0.05 Hz and a strain of 1% (the values within LVR) for 40 and 80 minutes (Fig. S9, ESI†). The temperature used was specific to the hydrogel as described in Sections 4.1.1–4.1.3. For all the rheometry experiments, pre-gelled mixed solutions were promptly placed onto the bottom parallel plate of a rheometer, which had been heated to the polymerization temperature of the specific sample. Rheometry oil was used to minimize the drying at the air–hydrogel interface.

4.2.2. Magnetic microrheometry. Magnetic microrheometry experiments were conducted using the microscope-integrated microrheometer described in the article.⁴⁰ The samples were measured in customized PMMA holders with a circular cavity with a diameter of 2.5 mm and a depth of 3 mm. Magnetic probe sizes were chosen for each crosslinker condition. The alginate hydrogels were measured with all three types of surface coatings (NH₂, COOH, plain) for each magnetic probe size. The IPN with 2 mg ml⁻¹ of collagen polymerized at 37 °C were measured only with COOH-coated and plain magnetic probes for each size. The IPN with 2 mg ml⁻¹ polymerized at 20 °C and IPNs with 1 and 3 mg ml⁻¹ polymerized at 37 °C were measured only with plain 30 μm magnetic probes.

For each crosslinker condition, duplicate samples with each magnetic probe size and coating were prepared. One pre-gelled hydrogel sample yielded three holders and three distinct locations were recorded within each holder, after the sample gelation was completed. As for the rheometry, the microrheometer measurement tests were performed at the LVR (i.e., at a frequency of 0.05 Hz and submicroscale and microscale probe displacements).

4.3. Scanning electron microscopy (SEM)

The SEM micrographs of dried hydrogels were obtained using a Zeiss Sigma VP system. Initially, the samples were prepared by critical-point drying with liquid CO₂ followed by snap-cracking in liquid nitrogen. Finally, the samples were mounted on aluminum stubs using a carbon tape and they were sputter-coated with a 4 nm of Pt/Pd using the Leica EM ACE600 high vacuum sputter.

Data and code availability

All the measured data is available at OSF (DOI: https://doi.org/10.17605/OSF.IO/7S4ZN) and the analysis codes are stored in https://github.com/arasalo1/switchpoint.

Author contributions

L. S., O. A., and A. L. performed the experiments/analyses. J. P. has initiated and led the research and obtained the related funding. All authors participated in writing.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

J. P. acknowledges the Instrumentarium Science Foundation grant of an Instrufoundation fellow (2020–2024), the Business Finland project 42468/31/2020 (2021–2022), the Seed Funding from Aalto University (2022–2023), and the project grant from the Jane and Aatos Erkko foundation (2024). All authors acknowledge the Aalto Nanomicroscopy Center for the use of the SEM. We also thank O. Ikkala and A. Kuzyk for kindly providing us for the access to their laboratory facilities. We are also thankful for M. Kielosto and V. Mäntylä for useful discussions on properties of collagen and its preparation.

References

1. A. Saraswathibhatla, D. Indana and O. Chaudhuri, Cell–extracellular matrix mechanotransduction in 3D, Nat. Rev. Mol. Cell Biol., 2023, 1–22.
2. J. J. Northey, A. S. Barrett, I. Acerbi, M. K. Hayward, S. Talamantes and I. S. Dean, et al., Stiff stroma increases breast cancer risk by inducing the oncogene ZNF217, J. Clin. Invest., 2020, 130(11), 5721–5737.
3. I. Acerbi, L. Cassereau, I. Dean, Q. Shi, A. Au and C. Park, et al., Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration, Integrative Biol., 2015, 7(10), 1120–1134.
4. R. J. Seager, C. Hajal, F. Spill, R. D. Kamm and M. H. Zaman, Dynamic interplay between tumour, stroma and immune system can drive or prevent tumour progression, Converg. Sci. Phys. Oncol., 2017, 3(3), 34002.
5. J. Alcaraz, J. Otero, I. Jorba and D. Navajas, Bidirectional mechanobiology between cells and their local extracellular matrix probed by atomic force microscopy, Semin. Cell Dev. Biol., 2018, 71–81.
6. A. Ansardamavandi, M. Tafazzoli-Shadpour, R. Omidvar and I. Jahanzad, Quantification of effects of cancer on elastic properties of breast tissue by atomic force microscopy, J. Mech. Behav. Biomed. Mater., 2016, 60, 234–242.
7. A. L. McKnight, J. L. Kugel, P. J. Rossman, A. Manduca, L. C. Hartmann and R. L. Ehman, MR elastography of breast cancer: preliminary results, Am. J. Roentgenol., 2002, 178(6), 1411–1417.
8. M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach and P. Oertle, et al., The nanomechanical signature of breast cancer, Biophys. J., 2013, 104(2), 321a.
9. P. Sáez and C. Venturini, Positive, negative and controlled durotaxis, Soft Matter, 2023, 19(16), 2993–3001.
10. B. J. DuChez, A. D. Doyle, E. K. Dimitriadis and K. M. Yamada, Durotaxis by human cancer cells, Biophys. J., 2019, 116(4), 670–683.
11. S. Nam, K. Hu, M. Butte and O. Chaudhuri, Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(20), 5492–5497.
12. Q. Wen and P. A. Janmey, Effects of non-linearity on cell–ECM interactions, Exp. Cell Res., 2013, 319(16), 2481–2489.
13. S. Nam, K. H. Hu, M. J. Butte and O. Chaudhuri, Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(20), 5492–5497.
14. M. K. Cowman, T. A. Schmidt, P. Raghavan and A. Stecco, Viscoelastic properties of hyaluronan in physiological conditions, F1000Res., 2015, 4 DOI:10.12688/f1000research.6885.1.
15. M. J. Bradshaw, G. A. Hoffmann, J. Y. Wong and M. L. Smith, Fibronectin fiber creep under constant force loading, Acta Biomater., 2019, 88, 78–85.
16. C. Balleyguier, A. Ben Lakhdar, A. Dunant, M. C. Mathieu, S. Delaloge and R. Sinkus, Value of whole breast magnetic resonance elastography added to MRI for lesion characterization, NMR Biomed., 2018, 31(1), e3795.
17. R. Sinkus, K. Siegmann, T. Xydeas, M. Tanter, C. Claussen and M. Fink, MR elastography of breast lesions: understanding the solid/liquid duality can improve the specificity of contrast-enhanced MR mammography, Magn. Reson. Med., 2007, 58(6), 1135–1144.
18. O. Chaudhuri, J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Effects of extracellular matrix viscoelasticity on cellular behaviour, Nature, 2020, 584(7822), 535–546.
19. M. Egeblad, M. G. Rasch and V. M. Weaver, Dynamic interplay between the collagen scaffold and tumor evolution, Curr. Opin. Cell Biol., 2010, 22(5), 697–706.
20. F. S. Majedi, M. M. Hasani-Sadrabadi, T. J. Thauland, S. Li, L. S. Bouchard and M. J. Butte, T-cell activation is modulated by the 3D mechanical microenvironment, Biomaterials., 2020, 252, 120058.
21. K. M. Wisdom, K. Adebowale, J. Chang, J. Y. Lee, S. Nam and R. Desai, et al., Matrix mechanical plasticity regulates cancer cell migration through confining microenvironments, Nat. Commun., 2018, 9(4144), 1.
22. O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif and J. C. Weaver, et al., Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2016, 15(3), 326–334.
23. A. P. Cameron, S. Gao, Y. Liu and C. X. Zhao, Impact of hydrogel biophysical properties on tumor spheroid growth and drug response, Biomater. Adv., 2023, 213421.
24. M. A. Serban and A. Skardal, Hyaluronan chemistries for three-dimensional matrix applications, Matrix Biol., 2019, 78, 337–345.
25. N. Barber-Pérez, M. Georgiadou, C. Guzmán, A. Isomursu, H. Hamidi and J. Ivaska, Mechano-responsiveness of fibrillar adhesions on stiffness-gradient gels, J. Cell Sci., 2020, 133(12), jcs242909.
26. J. L. Leight, A. P. Drain and V. M. Weaver, Extracellular matrix remodeling and stiffening modulate tumor phenotype and treatment response, Annu. Rev. Cancer Biol., 2017, 1, 313–334.
27. A. Kargerová and M. Pekař, Densitometry and ultrasound velocimetry of hyaluronan solutions in water and in sodium chloride solution, Carbohydr. Polym., 2014, 106, 453–459.
28. R. Malik, P. I. Lelkes and E. Cukierman, Biomechanical and biochemical remodeling of stromal extracellular matrix in cancer, Trends Biotechnol., 2015, 33(4), 230–236.
29. A. E. G. Baker, R. Y. Tam and M. S. Shoichet, Independently tuning the biochemical and mechanical properties of 3D hyaluronan-based hydrogels with oxime and Diels–Alder chemistry to culture breast cancer spheroids, Biomacromolecules, 2017, 18(12), 4373–4384.
30. C. B. da Cunha, D. D. Klumpers, W. A. Li, S. T. Koshy, J. C. Weaver and O. Chaudhuri, et al., Influence of the stiffness of three-dimensional alginate/collagen-I interpenetrating networks on fibroblast biology, Biomaterials, 2014, 35(32), 8927–8936.
31. J. Chang, A. Saraswathibhatla, Z. Song, S. Varma, C. Sanchez and S. Srivastava, Collective invasion of the basement membrane in breast cancer driven by forces from cell volume expansion and local contractility, bioRxiv, 2022, preprint DOI:10.1101/2022.07.28.501930.
32. J. Lou, R. Stowers, S. Nam, Y. Xia and O. Chaudhuri, Stress relaxing hyaluronic acid-collagen hydrogels promote cell spreading, fiber remodeling, and focal adhesion formation in 3D cell culture, Biomaterials, 2018, 154, 213–222.
33. Y. Li, N. Khuu, E. Prince, H. Tao, N. Zhang and Z. Chen, et al., Matrix stiffness-regulated growth of breast tumor spheroids and their response to chemotherapy, Biomacromolecules, 2020, 22(2), 419–429.
34. J. Chang, E. M. Pang, K. Adebowale, K. M. Wisdom and O. Chaudhuri, Increased Stiffness Inhibits Invadopodia Formation and Cell Migration in 3D, Biophys. J., 2020, 119(4), 726–736.
35. D. R. Sahoo and T. Biswal, Alginate and its application to tissue engineering, SN Applied Sciences, Springer Nature, 2021, vol. 3.
36. F. Abasalizadeh, S. V. Moghaddam, E. Alizadeh, E. Akbari, E. Kashani and S. M. B. Fazljou, et al., Alginate-based hydrogels as drug delivery vehicles in cancer treatment and their applications in wound dressing and 3D bioprinting, J. Biol. Eng., 2020, 14, 1–22.
37. J. R. Staunton, W. Vieira, K. L. Fung, R. Lake, A. Devine and K. Tanner, Mechanical properties of the tumor stromal microenvironment probed in vitro and ex vivo by in situ-calibrated optical trap-based active microrheology, Cell. Mol. Bioeng., 2016, 9(3), 398–417.
38. J. Pokki, I. Zisi, E. Schulman, D. Indana and O. Chaudhuri, Magnetic probe-based microrheology reveals local softening and stiffening of 3D collagen matrices by fibroblasts, Biomed. Microdevices, 2021, 23(2), 27.
39. L. Sikic, E. Schulman, A. Kosklin, A. Saraswathibhatla, O. Chaudhuri and J. Pokki, Nanoscale Tracking Combined with Cell-Scale Microrheology Reveals Stepwise Increases in Force Generated by Cancer Cell Protrusions, Nano Lett., 2022, 22(18), 7742–7750.
40. A. J. Lehtonen, O. Arasalo, L. Srbova, M. Heilala and J. Pokki, Magnetic microrheometry of tumor-relevant stiffness levels and probabilistic quantification of viscoelasticity differences inside 3D cell culture matrices, PLoS One, 2023, 18(3), e0282511.
41. M. Heilala, A. J. Lehtonen, O. Arasalo, A. Peura, J. Pokki and O. Ikkala, et al., Fibrin stiffness regulates phenotypic plasticity of metastatic breast cancer cells, Adv. Healthcare Mater., 2023, 12(31), 2370198.
42. V. Brancato, J. M. Oliveira, V. M. Correlo, R. L. Reis and S. C. Kundu, Could 3D models of cancer enhance drug screening?, Biomaterials, 2020, 232, 119744.
43. J. Y. Lee and O. Chaudhuri, Modeling the tumor immune microenvironment for drug discovery using 3D culture, APL Bioeng., 2021, 5(1), 10903.
44. V. Das, F. Bruzzese, P. Konečny, F. Iannelli, A. Budillon and M. Hajduch, Pathophysiologically relevant in vitro tumor models for drug screening, Drug Discovery Today, 2015, 20(7), 848–855.
45. J. Pokki, I. Zisi, E. Schulman, I. Dhiraj and O. Chaudhuri, Magnetic probe-based microrheology reveals local softening and stiffening of 3D collagen matrices by fibroblasts, Biomed. Microdev., 2021, 23(2), 27.
46. A. Gelman, J. Hill and A. Vehtari, Regression and other stories, Cambridge University Press, 2020.
47. A. J. Lehtonen, O. Arasalo, L. Srbova, M. Heilala and J. Pokki, Magnetic microrheometry of tumor-relevant stiffness levels and probabilistic quantification of viscoelasticity differences inside 3D cell culture matrices, PLoS One, 2023, 18(3), e0282511.
48. C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, 2006 [cited 2024 Jan 25], Available from: https://www.GaussianProcess.org/gpml.
49. J. K. Kruschke and T. M. Liddell, The Bayesian New Statistics: Hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective, Psychon. Bull. Rev., 2018, 25(1), 178–206.
50. J. J. Northey, A. S. Barrett, I. Acerbi, M. K. Hayward, S. Talamantes and I. S. Dean, et al., Stiff stroma increases breast cancer risk by inducing the oncogene ZNF217, J. Clin. Invest., 2020, 130(11), 5721–5737.
51. J. Pokki, J. Parmar, O. Ergeneman, H. Torun, M. Guerrero and E. Pellicer, et al., Mobility-enhancing coatings for vitreoretinal surgical devices: hydrophilic and enzymatic coatings investigated by microrheology, ACS Appl. Mater. Interfaces, 2015, 7(39), 22018–22028.
52. O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. Bencherif and J. Weaver, et al., Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2015, 15(3), 326–334.
53. D. E. Discher, P. Janmey and Y. L. Wang, Tissue cells feel and respond to the stiffness of their substrate, Science, 2005, 310(5751), 1139–1143.
54. W. R. Legant, J. S. Miller, B. L. Blakely, D. M. Cohen, G. M. Genin and C. S. Chen, Measurement of mechanical tractions exerted by cells in three-dimensional matrices, Nat. Methods, 2010, 7(12), 969–971.
55. W. R. Legant, A. Pathak, M. T. Yang, V. S. Deshpande, R. M. McMeeking and C. S. Chen, Microfabricated tissue gauges to measure and manipulate forces from 3D microtissues, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(25), 10097–10102.
56. D. Huh, B. D. Matthews, A. Mammoto, M. Montoya-Zavala, H. Y. Hsin and D. E. Ingber, Reconstituting organ-level lung functions on a chip, Science, 2010, 328(5986), 1662–1668.
57. A. M. Gordon, A. F. Huxley and F. J. Julian, The variation in isometric tension with sarcomere length in vertebrate muscle fibres, J. Physiol., 1966, 184(1), 170–192.
58. A. M. Wessendorf and D. J. Newman, Dynamic understanding of human-skin movement and strain-field analysis, IEEE Trans. Biomed. Eng., 2012, 59(12), 3432–3438.
59. C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Cell movement is guided by the rigidity of the substrate, Biophys. J., 2000, 79(1), 144–152.
60. C. Valero, H. Amaveda, M. Mora and J. Manuel García-Aznar, Combined experimental and computational characterization of crosslinked collagen-based hydrogels, PLoS One, 2018, 13(4), e0195820.
61. A. Stracuzzi, B. R. Britt, E. Mazza and A. E. Ehret, Risky interpretations across the length scales: continuum vs. discrete models for soft tissue mechanobiology, Biomech. Model. Mechanobiol., 2022, 21(2), 433–454.
62. J. Roether Id, S. Bertels, C. Oelschlaeger, M. Bastmeyer and N. Willenbacher, Microstructure, local viscoelasticity and cell culture suitability of 3D hybrid HA/collagen scaffolds, PLoS One, 2018, 13(12), e0207397.
63. M. Galluzzi, G. Tang, C. S. Biswas, J. Zhao, S. Chen and F. J. Stadler, Atomic force microscopy methodology and AFMech Suite software for nanomechanics on heterogeneous soft materials, Nat. Commun., 2018, 9(1), 1–10.
64. M. A. Kotlarchyk, S. G. Shreim, M. B. Alvarez-Elizondo, L. C. Estrada, R. Singh and L. Valdevit, et al., Concentration independent modulation of local micromechanics in a fibrin gel, PLoS One, 2011, 6(5), e20201.
65. G. Tronci, C. A. Grant, N. H. Thomson, S. J. Russell and D. J. Wood, Multi-scale mechanical characterization of highly swollen photo-activated collagen hydrogels, J. R. Soc., Interface, 2015, 12(102), 20141079.
66. C. A. R. Jones, M. Cibula, J. Feng, E. A. Krnacik, D. H. McIntyre and H. Levine, et al., Micromechanics of cellularized biopolymer networks, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(37), E5117–E5122.
67. J. L. Fredricks, A. M. Jimenez, P. Grandgeorge, R. Meidl, E. Law and J. Fan, et al., Hierarchical biopolymer-based materials and composites, J. Polym. Sci., 2023, 61(21), 2585–2632.
68. D. E. Ingber and I. Tensegrity, Cell structure and hierarchical systems biology, J. Cell Sci., 2003, 116(7), 1157–1173,  DOI:10.1242/jcs.00359.
69. B. Shashni, S. Ariyasu, R. Takeda, T. Suzuki, S. Shiina and K. Akimoto, et al., Size-based differentiation of cancer and normal cells by a particle size analyzer assisted by a cell-recognition PC software, Biol. Pharm. Bull., 2018, 41(4), 487–503.
70. C. Mark, T. J. Grundy, P. L. Strissel, D. Böhringer, N. Grummel, R. Gerum, J. Steinwachs, C. C. Hack, M. W. Beckmann, M. Eckstein, R. Strick, G. M. O’Neill and B. Fabry, Collective forces of tumor spheroids in three-dimensional biopolymer networks, eLife, 2020, 9, e51912.
71. K. Y. Lee and D. J. Mooney, Alginate: Properties and biomedical applications, Prog. Polym. Sci., 2012, 37(1), 106–126.
72. G. T. Grant, E. R. Morris, D. A. Rees, P. J. C. Smith and D. Thom, Biological interactions between polysaccharides and divalent cations: the egg-box model, FEBS Lett., 1973, 32(1), 195–198.
73. H. Hecht and S. Srebnik, Structural Characterization of Sodium Alginate and Calcium Alginate, Biomacromolecules, 2016, 17(6), 2160–2167.
74. S. M. Hashemnejad and S. Kundu, Strain stiffening and negative normal stress in alginate hydrogels, J. Polym. Sci., Part B: Polym. Phys., 2016, 54(17), 1767–1775.
75. C. K. Kuo and P. X. Ma, Ionically crosslinked alginate hydrogels as scaffolds for tissue engineering: Part 1. Structure, gelation rate and mechanical properties, Biomaterials, 2001, 22(6), 511–521.
76. J. Sapudom, S. Rubner, S. Martin, T. Kurth, S. Riedel and C. T. Mierke, et al., The phenotype of cancer cell invasion controlled by fibril diameter and pore size of 3D collagen networks, Biomaterials, 2015, 52, 367–375.
77. D. O. Velez, B. Tsui, T. Goshia, C. L. Chute, A. Han and H. Carter, et al., 3D collagen architecture induces a conserved migratory and transcriptional response linked to vasculogenic mimicry, Nat. Commun., 2017, 8(1), 1651.
78. K. A. Jansen, A. J. Licup, A. Sharma, R. Rens, F. C. MacKintosh and G. H. Koenderink, The Role of Network Architecture in Collagen Mechanics, Biophys. J., 2018, 114(11), 2665–2678.
79. Y. L. Yang, S. Motte and L. J. Kaufman, Pore size variable type I collagen gels and their interaction with glioma cells, Biomaterials, 2010, 31(21), 5678–5688.
80. B. Sun, The mechanics of fibrillar collagen extracellular matrix, Cell Reports Physical Science, 2021, 2(8), 19630–19637.
81. K. S. Hsu, J. M. Dunleavey, C. Szot, L. Yang, M. Beth Hilton and K. Morris, et al., Cancer cell survival depends on collagen uptake into tumor-associated stroma, Nat. Commun., 2022, 13(1), 7078.
82. M. C. Lampi, M. Guvendiren, J. A. Burdick, C. A. Reinhart-King and O. H. York, Photopatterned Hydrogels to Investigate the Endothelial Cell Response to Matrix Stiffness Heterogeneity, ACS Biomater. Sci. Eng., 2017, 3(11), 3007–3016.
83. C. K. Kuo and P. X. Ma, Ionically crosslinked alginate hydrogels as scaffolds for tissue engineering: Part 1. Structure, gelation rate and mechanical properties, Biomaterials, 2001, 22(6), 511–521.
84. S. Seiffert, Origin of nanostructural inhomogeneity in polymer-network gels, Polym. Chem., 2017, 8, 4472.
85. C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nonlinear elasticity in biological gels, Nature, 2005, 435(7039), 191–194.
86. E. M. Grad, I. Tunn, D. Voerman, A. S. de Léon, R. Hammink and K. G. Blank, Influence of Network Topology on the Viscoelastic Properties of Dynamically Crosslinked Hydrogels, Front. Chem., 2020, 8, 536.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01425h

---