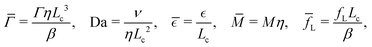Open Access Article
Open Access ArticleGeometric control by active mechanics of epithelial gap closure†
G.
Pozzi‡
 and
P.
Ciarletta
and
P.
Ciarletta
 *
*
MOX, Dipartimento di Matematica, Politecnico di Milano, piazza Leonardo da Vinci 32, 20133 Milano, Italy. E-mail: pasquale.ciarletta@polimi.it
First published on 14th December 2023
Abstract
Epithelial wound healing is one of the most important biological processes occurring during the lifetime of an organism. It is a self-repair mechanism closing wounds or gaps within tissues to restore their functional integrity. In this work we derive a new diffuse interface approach for modelling the gap closure by means of a variational principle in the framework of non-equilibrium thermodynamics. We investigate the interplay between the crawling with lamellipodia protrusions and the supracellular tension exerted by the actomyosin cable on the closure dynamics. These active features are modeled as Korteweg forces into a generalised chemical potential. From an asymptotic analysis, we derive a pressure jump across the gap edge in the sharp interface limit. Moreover, the chemical potential diffuses as a Mullins–Sekerka system, and its interfacial value is given by a Gibbs–Thompson relation for its local potential driven by the curvature-dependent purse-string tension. The finite element simulations show an excellent quantitative agreement between the closure dynamics and the morphology of the edge with respect to existing biological experiments. The resulting force patterns are also in good qualitative agreement with existing traction force microscopy measurements. Our results shed light on the geometrical control of the gap closure dynamics resulting from the active forces that are chemically activated around the gap edge.
Introduction
Living tissues have the ability to self-repair in response to injury by closing wounds and gaps through a series of coordinated cellular and supracellular processes. Wounds may not only result from surgery or accidental trauma, but also from pathological conditions, such as cancer, diabetes or inflammatory processes. Moreover, it is known that dysregulation of the physiological features of wound healing can result in severe infection and it can promote the onset of cancer.1Wound healing keeps attracting a lot of interest in soft matter physics.2
Early surgical data reported a linear decay of the radius of a circular wound over time in mammalians.3 Sherratt and Murray4–6 fitted this experimental trend using a model that only accounts for either an activator or an inhibitor of mitosis produced by epidermal cells in the healing process. Thus, they somewhat supported the view that the biochemical control of mitosis plays a major role in re-epithelialization.7
However, many in-vivo and in-vitro experiments performed during the last few decades pointed out the key role of a coordinated movement of epithelial cells in closing the wound and re-establishing tissue integrity for both embryonic and adult skin layers. Thus, several modelling approaches have been recently developed to elucidate the key mechano-biological features at play.
If epidermal cells are not motile under physiological conditions, it has been found that they undergo a marked phenotype alteration in the neighborhood of the wound, acquiring the ability to crawl via lamellipodia protrusions.8 Conversely, embryonic epidermal movement was found to be triggered by a circumferential tension at the free edge, acting like a purse string pulling.9
Wounds induced in Madin–Darby canine kidney epithelial cell monolayers were found to close by a crawling behavior involving Rac, phosphoinositides and active movement of multiple rows of cells, while active actin bundles were not found to be necessary for closure, yet playing a role in determining the regularity of closure.10 Moreover, specific signaling pathways were identified to control both such mechanical features for the dorsal wound closure in the Drosophila embryos.11
Later studies revealed that the wound closure is simultaneously driven by the cells actively crawling on the substrate through lamellipodia and the constriction produced by a supracellular actomyosin cable, referred to as the purse-string mechanism.12,13 However, even if these processes are not mutually exclusive, their coexistence is strongly influenced by the surrounding environment and by chemical factors.14 Cells indeed develop cytoskeletal protrusions (i.e. lamellipodia) in epithelia with abundant extracellular matrix (ECM) to spread over a substrate.15 The formation of an actomyosin supracellular structure, able to actively generate contractile mechanical forces, was instead the dominant mechanism found in other system models, either in the presence of apoptotic cells9 or in epithelia lacking the ECM.16 Moreover, traction force patterns at later stages of wound healing pointed out the existence of tensions transmitted by the actomyosin ring to the underlying substrate through focal adhesions.17,18
The mechano-biological coupling between the crawling and the purse-string mechanisms has been proven to be regulated by the curvature of the wound edge19,20 and by the substrate stiffness.21
Several mathematical approaches have been proposed to characterize such a complex interplay of geometrical and mechanical features in wound healing. A level-set model has been proposed to describe the edge motion regulated by cell mitosis and lamellipodia-induced migration, also accounting for the reaction diffusion dynamics of the epidermal growth factor.22 A continuous approach described the effect of the purse-string mechanisms as contraction of the healthy tissue surrounding the wound governed by the momentum balance equation and the mutual signaling among cells.23 The spontaneous formation of finger-like protrusions at the gap border and the consequent strong alignment of the velocity field within the fingers were captured by a continous model of unconstrained epithelial spreading considering long-range coupling between polarization and deformation.24 Other continuous approaches, exploiting the same idea of orientational order, considered the balance of forces acting on a single cell embedded in an epithelial monolayer, showing that single cell crawling is sufficient to drive the collective motion of a cell layer by means of cell–cell adhesion.25 The closure dynamics of small circular wounds in epithelial layers has been successfully reproduced by an inviscid fluid model driven by cell protrusions at the wound edge,26 possibly including an ad-hoc dependence of the bulk modulus on the cell density.27,28 Later, the combined effects of crawling and purse string were investigated using a free boundary model of a cell flowing as a viscous fluid subjected to localized forces at the moving edge.19 Crawling and purse-string are therefore considered as source terms in the momentum balance at the edge boundary, posing important challenges for the numerical discretization and the mathematical well-posedness at later stages of gap closure.
Alternatively, discrete modelling approaches were proposed to investigate the traction force patterns exerted by the cells during the wound closure, by means of both vertex and Voronoi models.17,29–32
In this work, we propose a diffuse interface approach with the aim to provide a suitable thermodynamic framework to characterize the evolution of the state variables driving the mechano-biological coupling and to implement a robust and computationally affordable numerical framework to simulate gap closure for any initial geometry. In contrast to existing sharp interface models that require additional regularity requirements and compatibility equations for the motion of the free-boundary, here the motion of the diffuse interface is intrinsically driven by the evolution of a chemo-mechanical potential, driving a phase transition similarly to a Gibbs potential in supercooling. Phase-field approaches have been successfully proposed for describing both individual and collective cell migration in tissue monolayers.33–35 Here, beyond the state-of-the-art, we consider epithelial wound healing as a non-equilibrium system whose evolution is governed by irreversible mass and energy flows. By introducing appropriate non-equilibrium state variables, we derive from mixture theory a diffuse interface model for the healing process that incorporates the crawling and the purse-string mechanisms in the free energy. Our modelling choice notably allows us to overcome the numerical difficulties in modelling the motion of the sharp-interface through forces dependent on the geometric properties of the free-boundary, such as the local curvature. Thus, the proposed model aims to bridge the gap between the tissue and the cellular scales by accounting for the mechanisms of the lower scales in the form of a chemical potential at the mesoscale.
In what follows, we exploit formal asymptotic analysis to highlight how the crawling and purse-string mechanisms at the wound edge and the friction with the substrate cooperate in regulating the wound closure process. Finally, we present finite element simulations to validate the model results against the existing experimental data, discussing the predictions against the evolution over time of the wounded area, the morphological transitions at the edge and the generated traction patterns with the substrate.
Results
The diffuse interface model
We consider a simple model system made of a confluent monolayer of epithelial cells immersed in a large bath, where a gap is created by positioning a stencil of well-defined geometry in its center, as in ref. 19. Under the hypothesis of neglecting the fast-scale dynamics of calcium and myosin traveling from the periphery to the wound,36 we model the monolayer as a biphasic mixture with a diffuse interface that separates the wound from the surrounding healthy epithelial tissue, whose near-equilibrium evolution is governed by slow, coarse-grained state variables. The variable ϕ(x,t) describes the relative volume fraction of the wound with respect to the healthy phase in the mixture, and it is defined in such a way that ϕ = 1 in the wound area and ϕ = −1 in the healthy tissue. The evolution of ϕ is partly driven by a gradient flow dependence with respect to a chemical potential μ, accounting for both the local interaction among cells by means of a free energy double-well potential, Ψ(ϕ), and a short-range nonlocal interaction at the interface expressed by a gradient dependence.37,38 By following the thermodynamic arguments in ref. 39–41 for extending the maximum dissipation principle accouting for active cellular phenomena and dissipation mechanisms (see ESI† Section 1 for model derivation), the evolution of the wounded monolayer is described by | (1) |
 | (2) |
 is a measure of the interface thickness and u is the volume-averaged velocity of the mixture. Under the assumption that the presence of homophilic interactions among cells within the tissue generates a non-negligible drag,19,25 the momentum balance equation,
is a measure of the interface thickness and u is the volume-averaged velocity of the mixture. Under the assumption that the presence of homophilic interactions among cells within the tissue generates a non-negligible drag,19,25 the momentum balance equation,| −∇·σ + ηu = (μ + fL)∇ϕ, | (3) |
 , with ν being the viscosity of the mixture,
, with ν being the viscosity of the mixture,  the symmetric part of the velocity gradient, p the hydrostatic pressure and
the symmetric part of the velocity gradient, p the hydrostatic pressure and  the identity matrix. In eqn (3), the cell–cell forces are balanced by cell–substrate friction, given by a friction coefficient η, by the Korteweg forces exerted by the chemical potential μ, and by the active crawling potential fL of the cellular lamellipodia. Overall, the mechanical forces exerted by the actomyosin cables are described as a surface tension at the wound edge in the chemical potential term μ through the parameter β. The cell crawling mechanism is also accounted for by introducing an extra chemical potential fL, which results in a Korteweg force in the momentum balance equation, and a source term Γ representing the local crawling rate of the cellular phase over the wound. In the present set-up, the velocity is assumed to be solenoidal, and thus
the identity matrix. In eqn (3), the cell–cell forces are balanced by cell–substrate friction, given by a friction coefficient η, by the Korteweg forces exerted by the chemical potential μ, and by the active crawling potential fL of the cellular lamellipodia. Overall, the mechanical forces exerted by the actomyosin cables are described as a surface tension at the wound edge in the chemical potential term μ through the parameter β. The cell crawling mechanism is also accounted for by introducing an extra chemical potential fL, which results in a Korteweg force in the momentum balance equation, and a source term Γ representing the local crawling rate of the cellular phase over the wound. In the present set-up, the velocity is assumed to be solenoidal, and thus| ∇·u = 0, | (4) |
| ∇ϕ·n = 0, ∇μ·n = 0, σn = 0, |
Asymptotic limit
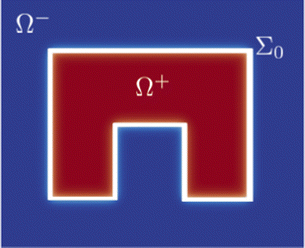
To clarify better how crawling and purse-string mechanisms and friction with the substrate are embedded in the proposed model, we exploit a formal asymptotic analysis42–47 on the model in the limit of zero thickness interface, i.e. taking . We proceed by subdividing the wounded monolayer into two distinct parts: a slender area including the diffuse interface, which is called the inner region, and the union of the two non-connected remaining portions of the monolayer, named the outer region, as sketched in Fig. 1. Hence, we identify
. We proceed by subdividing the wounded monolayer into two distinct parts: a slender area including the diffuse interface, which is called the inner region, and the union of the two non-connected remaining portions of the monolayer, named the outer region, as sketched in Fig. 1. Hence, we identify| Ω+ = {x ∈ Ω: ϕ0(x) = +1}, Ω− = {x ∈ Ω: ϕ0(x) = −1}, |
 for each variable in both the outer and the inner regions, we match the inner and the outer solutions by imposing the compatibility conditions at the interface.
for each variable in both the outer and the inner regions, we match the inner and the outer solutions by imposing the compatibility conditions at the interface.
Following this procedure (for more details see ESI† Section 2) we derive the corresponding sharp interface limit model
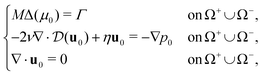 | (5) |
| [u0]+−n = 0, [p0]+− = 2(μ0 + fL) on Σ0, | (6) |
 | (7) |
 | (8) |
 are the local curvature and the normal velocity of the interface, respectively. Here with the subscript 0 we denote the principal component of the asymptotic outer expansion and with symbol [ · ]+− we denote the jump of the model variables at the interface.
are the local curvature and the normal velocity of the interface, respectively. Here with the subscript 0 we denote the principal component of the asymptotic outer expansion and with symbol [ · ]+− we denote the jump of the model variables at the interface.
In the sharp interface limit, we find that the mixture behaves as an incompressible Darcy–Brinkman fluid with two interfacial forces, corresponding to a normal crawling pressure with magnitude fL and an active purse-string tension with characteristic force per unit length β. The movement of the interface is driven by a Mullins–Sekerka problem, where Γ defines the crawling energy source for the chemical potential. In physical terms, the purse-string mechanism lets the interface carry a chemical potential, which results in an active surface tension β as given by the Gibbs–Thompson condition in eqn (7), and a friction with the substrate inversely proportional to the mobility parameter M as given by the Stefan condition in eqn (8).
Finite element simulations
Before implementing the numerical approximation of the model, we derive its dimensionless version to identify the reduced set of dimensionless parameters governing the evolution of the biological system. To this purpose, we set a characteristic length-scale as the domain size Lc, a characteristic time-scale Tc and a characteristic velocity Uc. We thus introduce the dimensionless variables![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = x/Lc,
= x/Lc, ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = t/Tc and û = u/Uc for space, time and velocity, respectively. We adopt the symbol
= t/Tc and û = u/Uc for space, time and velocity, respectively. We adopt the symbol  to denote the dimensionless differential operators. Standard manipulations of the diffuse interface model lead to
to denote the dimensionless differential operators. Standard manipulations of the diffuse interface model lead to | (9) |
having imposed the fundamental scaling β/(Lc2Ucη) = 1, so that the characteristic stress is Pc = ηLcUC = β/LC. Thus,
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = p/Pc and
= p/Pc and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = μ/Pc, and the characteristic time is Tc = LC/UC = ηLc3/β, i.e. the time at which frictional forces with the substrate are of the same order as the surface tension. The dimensionless parameter Da is the classical Darcy parameter for the Brinkman equation, i.e. the ratio between viscous and friction forces,
= μ/Pc, and the characteristic time is Tc = LC/UC = ηLc3/β, i.e. the time at which frictional forces with the substrate are of the same order as the surface tension. The dimensionless parameter Da is the classical Darcy parameter for the Brinkman equation, i.e. the ratio between viscous and friction forces, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) is the product between the crawling rate and the characteristic time,
is the product between the crawling rate and the characteristic time,  is the ratio between the interface and domain sizes,
is the ratio between the interface and domain sizes, ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) is the ratio between the viscous and the friction forces, and
is the ratio between the viscous and the friction forces, and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) L is the ratio between crawling and purse string forces.
L is the ratio between crawling and purse string forces.
We performed numerical simulations on a square domain with unit dimensionless side, subdivided into 3.2 × 105 uniformly distributed triangles and we fix the characteristic length Lc = 2.24 × 10−4 to reproduce in silico the experimental system adopted by Ravasio et al. in ref. 19. We explore three different scenarios by varying the initial shape of the wound: in particular we chose the three initial gap configurations shown in Fig. 2 (left), referred to as square inset, half moon and half circle. In every test case the initial area is about 4000–5000 μm2. The numerical simulations are obtained using the library FEniCS for solving partial differential equations using finite element methods.48,49
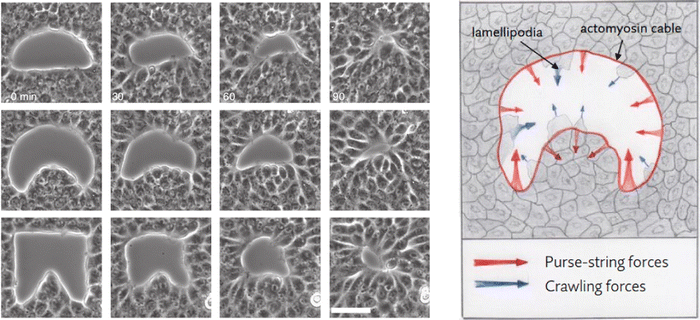 | ||
| Fig. 2 (left) Example time lapses of gap closure. Scale bar 50 mm. (right) Mechanical coupling between purse-string and crawling. Red and blue arrows indicate the direction of the local forces induced by purse-string and crawling, respectively. Image adapted from ref. 19. | ||
In order to reproduce the experimental trends presented in ref. 19, for all the three scenarios described above we found the values of the physical parameters from the literature, where present, by varying them in their physiological range and by defining as optimal set of parameters that better fit the area decay in time. Thus, we set fL = 100 Pa,17,25 M = 3.27 × 10−15 m2 Pa−1 s−1,38 and ν = 6.0 × 107 Pa s,50 while  m is prescribed by the spatial scale of the problem. Finally, we calibrate β = 4 × 10−3 Pa m, η = 3.09 × 105 Pa s m−2 and Γ = 5.62 × 10−5 s−1 to reproduce the experimental trends. Consequently, the dimensionless groups take the following values: Da = 3.87 × 109,
m is prescribed by the spatial scale of the problem. Finally, we calibrate β = 4 × 10−3 Pa m, η = 3.09 × 105 Pa s m−2 and Γ = 5.62 × 10−5 s−1 to reproduce the experimental trends. Consequently, the dimensionless groups take the following values: Da = 3.87 × 109,  ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) = 4.88 × 10−5,
= 4.88 × 10−5, ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) = 1.01 × 109 and
= 1.01 × 109 and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) L = 5.6. The finite element discretization of system (9) is discussed in the ESI† Section 3.
L = 5.6. The finite element discretization of system (9) is discussed in the ESI† Section 3.
As shown in Fig. 3, the evolution is characterized by a common trend in the local regulation of the closure mechanism. In accordance with the experimental observations in ref. 19, flat and negative curved edges, i.e. the ones protruding into the wound, advance at a considerably slower pace compared with boundary regions characterized by the presence of positive curvatures, see Fig. 4. Indeed, the early stage of the simulations consists of a regularization of the wound shape due to purse-string tension as observed in ref. 18. When the wound reaches a rounded shape and hence the whole border of the gap has positive curvature, each portion of the boundary moves with the same speed towards the center of the gap, up to the closure of the wound. This behavior, overlooking the initial shape of the wound, highlights the importance of the sign and the magnitude of the local curvature in governing the closure dynamics.
The in silico healing times are approximately 40–60 min, depending on the initial extension of the wound, as shown in Fig. 5. The wound area decreases in a near-linear manner over time up to the complete closure regardless of the initial shape of the gap. A comparison between the numerical results and the experimental data extracted from ref. 19 for each of the considered gap geometries is also shown in Fig. 5. In order to achieve a deeper understanding of the system behavior, we investigate the influence of the dimensionless parameters on the model response for square inset geometry. In Fig. S1 (ESI†), we notice that lower crawling, i.e. decreasing the value for the dimensionless term ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) , is correlated with longer healing times. The same behavior is also observed for the dimensionless motility
, is correlated with longer healing times. The same behavior is also observed for the dimensionless motility ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) , and so reducing the friction with the substrate increases the velocity of gap closure. We also observe that decreasing Da not only speeds up the closure process, but also creates swirling patterns in the normal velocity field surrounding the wound, as shown in Fig. S2 (ESI†), similar to the ones observed in other system models.31
, and so reducing the friction with the substrate increases the velocity of gap closure. We also observe that decreasing Da not only speeds up the closure process, but also creates swirling patterns in the normal velocity field surrounding the wound, as shown in Fig. S2 (ESI†), similar to the ones observed in other system models.31
 | ||
| Fig. 5 In silico simulated decrease of the area over time for three differently shaped wounds: square inset (blue line), half circle (green line) and half moon (orange line) with an initial area of 3500–5000 μm2. The horizontal bars coincide with the error bars of the experimental data extracted from ref. 19 for each geometry. The image shows also the overlay of outlines at different time points for each of the three wound shapes. | ||
Finally, we explore the effect of crawling on the closure dynamics given by the dimensionless parameters ![[f with combining overline]](https://www.rsc.org/images/entities/i_char_0066_0305.gif) L and
L and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) in determining the dynamics of gap closure. We find that
in determining the dynamics of gap closure. We find that ![[f with combining overline]](https://www.rsc.org/images/entities/i_char_0066_0305.gif) L acts as an extra pressure term in
L acts as an extra pressure term in ![[p with combining overline]](https://www.rsc.org/images/entities/i_char_0070_0305.gif) , not affecting directly the healing time and the shape evolution, which are indeed controlled by
, not affecting directly the healing time and the shape evolution, which are indeed controlled by ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) , as discussed earlier.
, as discussed earlier.
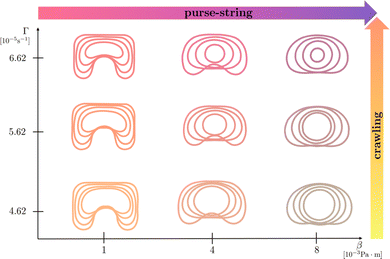
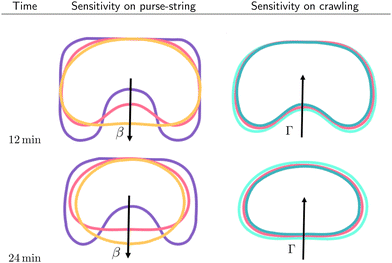
In Fig. 6, we report the resulting morphological diagrams of the closure dynamics by exploring different combinations between the crawling and the purse string dimensional parameters. We notice that an increase of the purse-string force results in regularization of the wound shapes at the same time instants, i.e. the wound protrusions in the healthy tissue tend to disappear early during the healing process. On the other hand, an increase of the crawling rate accelerates closure by preserving the initial morphology of the wound against the regularizing effect of the purse-string mechanism. In Fig. 7, we depict the morphological changes at given time instants by varying one parameter at a time, thus highlighting the different geometrical effects.
Finally, we plot the principal stress pattern σmax for the square inset geometry. We observe that in the early stages of the healing process, regions in the proximity of convex borders are characterized by a compressive stress pattern, indicating that the cell crawling contribution is suppressed by the actomyosin cable action. In contrast, areas in the vicinity of concave borders present a traction stress pattern. In later stages, when the wound evolves towards more regular shapes, with concave borders almost everywhere, the traction pattern becomes the dominant one (Fig. 8). These results are in good qualitative agreement with the traction force microscopy measurements presented in ref. 17, showing force components that are both radial and tangential to the wound for the effect of the substrate friction.
Discussion
In this work we present a novel diffuse interface model to characterize mechano-biological features during epithelial closure. The model is derived from thermodynamical principles within the mixture theory framework using the maximum dissipation principle to account for both active phenomena and dissipation mechanisms. We considered a viscous mixture behaving as a Darcy–Brinkman–Korteweg fluid with volumetric mass sources and a diffusive mass flux. The diffusive mass flux follows the gradient flow of a chemical potential μ, containing a local interaction term that acts as an active surface tension, mimicking the active purse-string mechanisms, and a regularising short-range nonlocal interaction that controls the width of the interface. The crawling of the lamellipodia appears as the combined effect of an extra-pressure in the chemical potential and a crawling rate Γ in the Cahn–Hilliard equation.We performed an asymptotic analysis obtaining the sharp interface limit of our model, in order to investigate the role of interfacial forces and of the frictional forces with the substrate in governing the wound edge movements. We found that the Korteweg forces driven by the diffusive chemical potential and the crawling impose a pressure jump across the interface. Moreover, the diffusion of the chemical potential is governed by a Mullins–Sekerka system, and its interfacial value is given by a Gibbs–Thompson relation driven by the purse-string tension and a Stefan law driven by the frictional forces.
The model has been finally numerically approximated using finite element discretization. We found that our in-silico numerical results are in good quantitative agreement with the in-vitro experiments reported in ref. 19. The quasi-linear trend in the decrease of the area over time is confirmed and the numerical closure time is aligned with the experimental one for all the considered gap geometries. We also found a similar morphological evolution of the wound edge during the closure dynamics. In particular, we observed a local regulation of the closure mechanism governed by the curvature of the gap edge: curved regions move at a significantly higher velocity than flat edges, thus resulting in a change in the gap geometry during the tissue repair process. Indeed, during the first stages of the process, the wound evolves towards a more regular shape to form an elliptical or a circular hole. Afterwards, the gap closes symmetrically with homogeneous velocity till the end of the closure process.
Our sharp interface limit is supporting evidence that the curvature of the edge has a major role in regulating the closure mechanism. Indeed, we showed that the local curvature affects the pressure jump at the border and tunes the direction of the purse-string force. In regions where the edge is positively curved the force is directed towards the inner of the wound; on the contrary, the purse-string action is oriented towards the healthy tissue when the curvature is negative. Therefore, our diffuse interface model is able to capture the observed gap closure dynamics dictated by the presence of the actomyosin cable. Its numerical implementation is finally robust and computationally much more affordable compared to its sharp interface counterpart.
In conclusion, this work sheds light on the geometric control by active mechanics during the epithelial closure dynamics. Compared to existing sharp interface approaches, the use of a diffuse interface significantly reduces the numerical complexities related to the need to track the border movements and to impose jump conditions on the forces across the free boundary. In our model, the use of the maximum dissipation principles allows us to account for the active mechanical forces around the edge, modeled as Korteweg forces in the bulk, and dissipation mechanism within the phases and with the substrate. The numerical results not only quantitatively predict the universal quasi-linear decrease of area over time and the observed morphological transitions of the wound edge, but also qualitatively agree with the traction force patterns reported in existing experiments, highlighting the interplay between edge and frictional forces.
However, we remark that our diffuse interface approach suffers from some limitations that require future developments. In particular, we plan to improve the current model by developing a chemo-mechanical coupling between the fast dynamics of calcium waves and myosin activation that trigger the purse-string and crawling forces during the closure dynamics. Although the near-equilibrium assumption imposed here by the maximum dissipation principle allows us to predict accurately the closure dynamics and the collective behaviors, the introduction of fast variables would require to extend the theoretical framework in the context of non-equilibrium reversible-irreversible thermodynamic coupling.51 Moreover, it would be physically relevant to investigate the effects of the orientational order on the cellular spreading, which are deemed to be particularly relevant in regimes of high-activity on non-adherent substrates.52 Finally, as a further next step of our work, we aim at exploring different model systems to perform a quantitative comparison of the numerical predictions against traction force microscopy measurements with varying adhesive properties with the substrate.
Author contributions
G. Pozzi: formal analysis, funding acquisition, software, writing – reviewing and editing and P. Ciarletta: conceptualization, supervision, methodology, formal analysis, funding acquisition, writing – reviewing and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project was supported by GNFM – INdAM through the program Progetto Giovani 2023 CUP_E53C22001930001 and by MUR through both the PRIN Research Project 2020F3NCPX and the grant Dipartimento di Eccellenza 2023-2027.References
- K. J. Sonnemann and W. M. Bement, Wound repair: toward understanding and integration of single-cell and multicellular wound responses, Annu. Rev. Cell Dev. Biol., 2011, 27, 237–263 CrossRef CAS PubMed.
- J. D. Murray, Mathematical biology II: spatial models and biomedical applications, Springer, New York, 2001, vol. 3 Search PubMed.
- H. A. S. van den Brenk, Studies in restorative growth processes in mammalian wound healing, Br. J. Surg., 2005, 43.181, 525–550 CrossRef PubMed.
- J. A. Sherratt and J. D. Murray, Models of epidermal wound healing, Proc. R. Soc. London, Ser. B, 1990, 241(1300), 290, DOI:10.1098/rspb.1990.0061.
- J. A. Sherratt, Mathematical models of wound healing, PhD thesis, University of Oxford, 1991 Search PubMed.
- J. A. Sherratt and J. D. Murray, Article Commentary: Epidermal Wound Healing: The Clinical Implications of a Simple Mathematical Model, Cell Transplant., 1992, 1.5, 365–371 CrossRef PubMed.
- T. T. Irvin, The healing wound, Wound healing for surgeons, 1984, pp. 3–28 Search PubMed.
- R. A. F. Clark, Wound repair, The molecular and cellular biology of wound repair, 1988, pp. 3–50 Search PubMed.
- P. Martin and J. Lewis, Actin cables and epidermal movement in embryonic wound healing, Nature, 1992, 360(6400), 179–183 CrossRef CAS PubMed.
- G. Fenteany, P. A. Janmey and T. P. Stossel, Signaling pathways and cell mechanics involved in wound closure by epithelial cell sheets, Curr. Biol., 2000, 10(14), 831–838 CrossRef CAS PubMed.
- B. G. Fernandez, A. M. Arias and A. Jacinto, Dpp signalling orchestrates dorsal closure by regulating cell shape changes both in the amnioserosa and in the epidermis, Mech. Dev., 2007, 124(11–12), 884–897 CrossRef CAS PubMed.
- M. T. Abreu-Blanco, et al., Drosophila embryos close epithelial wounds using a combination of cellular protrusions and an actomyosin purse string, J. Cell Sci., 2012, 125(24), 5984–5997 CrossRef CAS PubMed.
- S. Begnaud, et al., Mechanics of epithelial tissues during gap closure, Curr. Opin. Cell Biol., 2016, 42, 52–62 CrossRef CAS PubMed.
- K. E. Rothenberg and R. Fernandez-Gonzalez, Forceful closure: cytoskeletal networks in embryonic wound repair, Mol. Biol. Cell, 2019, 30(12), 1353–1358 CrossRef CAS PubMed.
- E. Anon, et al., Cell crawling mediates collective cell migration to close undamaged epithelial gaps, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(27), 10891–10896 CrossRef CAS PubMed.
- V. Nier, et al., Tissue fusion over nonadhering surfaces, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(31), 9546–9551 CrossRef CAS PubMed.
- A. Brugues, et al., Forces driving epithelial wound healing, Nat. Phys., 2014, 10(9), 683–690 Search PubMed.
- S. Vedula, et al., Mechanics of epithelial closure over non-adherent environments, Nat. Commun., 2015, 6(1), 6111 Search PubMed.
- A. Ravasio, et al., Gap geometry dictates epithelial closure eciency, Nat. commun., 2015, 6(1), 1–13 Search PubMed.
- T. Chen, et al., Large-scale curvature sensing by directional actin ow drives cellular migration mode switching, Nat. Phys., 2019, 15(4), 393–402 Search PubMed.
- V. Ajeti, et al., Wound healing coordinates actin architectures to regulate mechanical work, Nat. Phys., 2019, 15(7), 696–705 Search PubMed.
- E. Javierre, et al., A mathematical analysis of physiological and morphological aspects of wound closure, J. Math. Biol., 2009, 59(5), 605–630 CrossRef CAS PubMed.
- A. Sadovsky and F. Y. M. Wan, The elastodynamics of embryonic epidermal wound closure, Stud. Appl. Math., 2007, 118(4), 365–395 CrossRef.
- M. H. Kopf and L. M. Pismen, A continuum model of epithelial spreading, Soft Matter, 2013, 9(14), 3727–3734 RSC.
- P. Lee and C. W. Wolgemuth, Crawling cells can close wounds without purse strings or signaling, PLoS Comput. Biol. 7, 3, ( 2011) Search PubMed.
- O. Cochet-Escartin, et al., Border forces and friction control epithelial closure dynamics, Biophys. J., 2014, 106(1), 65–73 CrossRef CAS PubMed.
- J. C. Arciero, et al., Continuum model of collective cell migration in wound healing and colony expansion, Biophys. J., 2011, 100(3), 535–543 CrossRef CAS PubMed.
- J. C. Arciero, et al., Using a continuum model to predict closure time of gaps in intestinal epithelial cell layers, Wound Repair Regener., 2013, 21(2), 256–265 CrossRef PubMed.
- B. Li, et al., EML webinar overview: Dynamics of collective cells, Extreme Mech. Lett., 2021, 44, 101255 CrossRef.
- S.-Z. Lin, et al., Universal statistical laws for the velocities of collective migrating cells, Adv. Biosyst., 2020, 4(8), 2000065 CrossRef PubMed.
- S.-Z. Lin, et al., Collective dynamics of coherent motile cells on curved surfaces, Soft Matter, 2020, 16(12), 2941–2952 RSC.
- F. Ioannou, et al., Development of a new 3D hybrid model for epithelia morphogenesis, Front. Bioeng. Biotechnol., 2020, 8, 405 CrossRef PubMed.
- S. Najem and M. Grant, Phase-eld model for collective cell migration, Phys. Rev. E, 2016, 93(5), 052405 CrossRef PubMed.
- B. Palmieri, et al., Multiple scale model for cell migration in monolayers: Elastic mismatch between cells enhances motility, Sci. Rep., 2015, 5(1), 11745 CrossRef PubMed.
- A. Moure and H. Gomez, Phase-eld modeling of individual and collective cell migration, Archives Comput. Methods Eng., 2021, 28, 311–344 CrossRef.
- M. Antunes, et al., Coordinated waves of actomyosin ow and apical cell constriction immediately after wounding, J. Cell Biol., 2013, 202(2), 365–379 CrossRef CAS PubMed.
- D. Lee, et al., Physical, mathematical, and numerical derivations of the Cahn-Hilliard equation, Comput. Mater. Sci., 2014, 81, 216–225 CrossRef.
- A. Agosti, et al., A computational framework for the personalized clinical treatment of glioblastoma multiforme, Z. Angew. Math. Mech., 2018, 98(12), 2307–2327 CrossRef.
- M. Doi, Soft matter physics, Oxford University Press, 2013 Search PubMed.
- H. Wang, T. Qian and X. Xu, Onsager's variational principle in active soft matter, SoftMatter, 2021, 17(13), 3634–3653 RSC.
- M. Doi, et al., Application of the Onsager-Machlup integral in solving dynamic equations in nonequilibrium systems, Phys. Rev. E, 2019, 99(6), 063303 CrossRef CAS PubMed.
- M. Ebenbeck, H. Garcke and R. Nurnberg, Cahn–Hilliard–Brinkman systems for tumour growth, Discrete and Continuous Dynamical Systems-S, 2021, 14(11), 3989–4033 CrossRef.
- J. Lowengrub and L. Truskinovsky, Quasi-incompressible Cahn–Hilliarduids and topological transitions, Proc. R. Soc. London, Ser. A, 1998, 454(1978), 2617–2654 CrossRef CAS.
- A. A. Lee, A. Munch and E. Suli, Sharp-Interface limits of the Cahn–Hilliard equation with degenerate mobility, SIAM J. Appl. Math., 2016, 76(2), 433–456 CrossRef.
- H. Garcke, et al., A Cahn–Hilliard–Darcy model for tumour growth with chemotaxis and active transport, Math. Models Methods Appl. Sci., 2016, 26(06), 1095–1148 CrossRef CAS.
- W. Dreyer and B. A. Wagner, Sharp-interface model for eutectic alloys. Part I: Concentration dependent surface tension, Interfaces and Free Boundaries, 7, 2, ( 2005), 199–227.
- P. C. Fife and O. Penrose, Interfacial dynamics for thermodynamically consistent phase-eld models with nonconserved order parameter, ( 1995).
- M. S. Alns, et al., The FEniCS project version 1.5., Arch. Numer. Softw, 2015, 3 Search PubMed.
- A. Logg, G. N. Wells and J. Hake, DOLFIN: A C++/Python nite element library, Automated solution of di erential equations by the nite element method, Springer, 2012, pp. 173–225 Search PubMed.
- C. Blanch-Mercader, et al., Effective viscosity and dynamics of spreading epithelia: a solvable model, Soft Matter, 2017, 13(6), 1235–1243 RSC.
- H. C. Ottinger, Beyond equilibrium thermodynamics, John Wiley & Sons, 2005 Search PubMed.
- W. Mirza, et al., Variational formulation of active nematics: theory and simulation, arXiv, 2023, preprint, arXiv:2306.01515 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01419c |
| ‡ Current address: DISMA, Politecnico di Torino, corso Duca degli Abruzzi 24, 10129 Torino, Italy. |
| This journal is © The Royal Society of Chemistry 2024 |