 Open Access Article
Open Access ArticleAvalanche properties at the yielding transition: from externally deformed glasses to active systems
Carlos
Villarroel
 * and
Gustavo
Düring
* and
Gustavo
Düring
Instituto de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago, Chile. E-mail: cjvillarroel@uc.cl
First published on 2nd April 2024
Abstract
We investigated the yielding phenomenon in the quasistatic limit using numerical simulations of soft particles. Two different deformation scenarios, simple shear (passive) and self-random force (active), and two interaction potentials were used. Our approach reveals that the exponents describing the avalanche distribution are universal within the margin of error, showing consistency between the passive and active systems. This indicates that any differences observed in the flow curves may have resulted from a dynamic effect on the avalanche propagation mechanism. The evolution time required to reach a steady state differs significantly between active and passive scenarios under similar conditions. However, we demonstrated that plastic avalanches under athermal quasistatic simulation dynamics display a similar scaling relationship between avalanche size and relaxation time, which cannot explain the different flow curves.
I. Introduction
In recent decades, considerable theoretical, experimental, and computational efforts have been made to understand the complex rheology of amorphous materials, such as colloids, grains, foams, and emulsions, which are essential parts of various industrial processes.1 Today, high-density amorphous materials are known to be mechanically stable;2–5 however, they can exhibit an athermal transition between the solid and fluid states when subjected to a sufficiently large shear stress.6–9 These materials exhibit critical stress σc (sometimes called yield stress). When the applied stress σ < σc, the system moves due to an internal reorganisation, which ends when a configuration capable of bearing the applied stress is found. In this regime, the system behaves as an elastic solid.10 However, when σ > σc, the system cannot find a stable configuration leading to a flowing state, which is characterised by a singular flow curve relating the strain rate and the shear stress. The flow curve,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ (σ − σc)β, is defined by exponent β, which is the Herschel–bulkley (HB) exponent.11 This dynamic regime is controlled by avalanches composed of several chained irreversible plastic transformations, known as shear transformation zones (STZ), which reorganise a group of particles.12,13 As the flow vanishes, this dynamic becomes increasingly complex, and larger avalanches form, which is reflected in the existence of critical behaviour with a correlation length ξ ∼
∼ (σ − σc)β, is defined by exponent β, which is the Herschel–bulkley (HB) exponent.11 This dynamic regime is controlled by avalanches composed of several chained irreversible plastic transformations, known as shear transformation zones (STZ), which reorganise a group of particles.12,13 As the flow vanishes, this dynamic becomes increasingly complex, and larger avalanches form, which is reflected in the existence of critical behaviour with a correlation length ξ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −ν/β∼ (σ − σc)−ν that diverges in
−ν/β∼ (σ − σc)−ν that diverges in ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) →0.13,14
→0.13,14
Yielding-like behaviour is also observed in models of dense active systems subjected to a self-propelled force.15–19 In contrast to systems that exhibit a flow when subjected to sufficient shear stress, the size of the self-propelled force, f, must exceed fc. In our previous study,20 the exponents β and ν/β were calculated with good precision for the active and passive scenarios, and they exhibited a difference that did not fall within our range of error. The origin of this difference remains unclear and requires a detailed study of the avalanche statistics and relaxation, which are believed to control the yielding transition. However, obtaining a detailed description of avalanches in a flowing state (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≠ 0) is a complex task because of the difficulty in detecting and measuring avalanches when the system is not in mechanical equilibrium.
≠ 0) is a complex task because of the difficulty in detecting and measuring avalanches when the system is not in mechanical equilibrium.
A common approach to studying the yielding phenomenon and statistics of avalanches in passive systems is to use athermal quasistatic simulations (AQS).21–27 This very slow deformation limit is observed when the characteristic time at which the deformation is carried out is sufficient to permit the propagation of avalanches that reorganize the system. This allowed the system to reach a mechanical equilibrium after each deformation step, thereby facilitating the detection of plastic events. In practice, the system is placed under a small and homogeneous strain and then relaxed until mechanical equilibrium is reached. This process is repeated several times until the desired shear strain is achieved.21 Although the AQS does not allow a direct study of the fluid regime, this method allows the exploration of the properties and statistics of the avalanche size distribution at the critical point, which controls the dynamics near the critical point.21,28 In this regard, using mesoscopic elastoplastic models, both Lin et al.29 and Ferrero et al.30 made important advances in matching the exponents that describe the HB rheology with the exponents observed in AQS for simple shear deformation. Nonetheless, AQS for a self-random force is a field that has only recently been studied.31–33 Morse et al.32 have demonstrated similarities in stress drop values between active and passive systems. Here, we further investigate the similarities in the critical exponents that govern avalanche distributions.
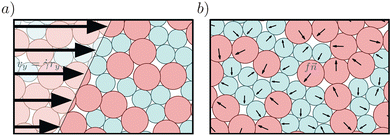
In this study, we performed a large number of simulations involving 2D soft particles in the AQS limit using two distinct models of driven deformation scenarios, simple shear (SS) and self-random force (SRF), for active particles with infinite persistence in the orientation of self-propulsion, as shown in Fig. 1. We primarily concentrate on the 2D case; nevertheless, there is evidence suggesting that the phenomenology resulting from avalanche reorganization in AQS remains comparable in 3D.25,28 The remainder of this paper is structured as follows: in Section 2, detailed information about the simulation protocols utilised throughout this study is provided. In Section 3, the results of the avalanche size distributions for both deformation scenarios in the AQS limit are presented. In Section 4, the propagation times with which the system undergoes reorganisation are examined. Finally, in Section 5, the most significant results are summarised.
II. Simulation methods and protocols
Previous molecular studies can be categorised based on the employed interparticle potential. One group of studies used potentials that diverged when two particles coincided at the centre (e.g., the LJ potential,12,28 LP potential, and σ/r12 potential23). Another group employed potentials in which a finite value is assigned to the same situation (e.g., the Hertzian potential34 and the harmonic potential22,34). To verify that this selection of potentials does not affect the critical exponents, we employed two potentials: the Hertzian potential and the potential used by Lerner and Procaccia (the LP potential).23 These potentials were chosen based on the fact that they are differentiable at least twice, thus preventing discontinuity problems in the elastic modulus.23We used athermal systems of frictionless soft discs for all the simulations in a 2D box of length L. To avoid crystallisation, we used a bidisperse mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4.35 In our simulations, the atomistic length scale was set according to the radius of the small particles (r0 = 1), and the mass of all the particles is equal to unity (m0 = 1). For each potential, the interaction between the particles is described by eqn (1) for the Hertzian potential and eqn (2) for the LP potential.
1.4.35 In our simulations, the atomistic length scale was set according to the radius of the small particles (r0 = 1), and the mass of all the particles is equal to unity (m0 = 1). For each potential, the interaction between the particles is described by eqn (1) for the Hertzian potential and eqn (2) for the LP potential.
 | (1) |
 | (2) |
In both cases, rij is the distance between the centres of particles i and j, dij is the mean of their radii, and ε is the energy scale. In our simulation, we considered a0 = 10 and b0 = 0.2. The temperature has units of ε/kB, where kB is Boltzmann's constant, and time is measured in units of  . To create systems with a Hertzian potential, we used infinite quenching,36 and for systems with an LP potential, we started equilibrating at T = 1.0 and cooled to T = 0.05 at a 10−6ε/(kBt0) rate; finally, the residual heat was removed using the FIRE algorithm.37 Throughout this study, the densities of both potentials were set using the packing fraction ϕ = 0.975, from the jamming point.38
. To create systems with a Hertzian potential, we used infinite quenching,36 and for systems with an LP potential, we started equilibrating at T = 1.0 and cooled to T = 0.05 at a 10−6ε/(kBt0) rate; finally, the residual heat was removed using the FIRE algorithm.37 Throughout this study, the densities of both potentials were set using the packing fraction ϕ = 0.975, from the jamming point.38
Quasistatic SS model
The AQS for a system under a simple shear deformation can be described using the following procedure:21,22,32 using the Less–Edwards boundary conditions,39 we imposed an affine shear strain Δγ = 10−4. In each step, we modified the position of each particle ri according to the following rule:![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i → i → ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i + Δγ( i + Δγ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i·ŷ) i·ŷ)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . . | (3) |
After applying the affine deformation, the total potential energy of the system was minimised. To determine the mechanical equilibrium parameters, we defined the residual force factor as λF = 〈|![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) |〉/
|〉/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , where 〈|
, where 〈|![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) |〉 is the mean of total force over all particles,
|〉 is the mean of total force over all particles, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is the mean interparticle force, and the mechanical balance is set to λF < 10−11. We primarily used the conjugate gradient (CG) algorithm40 to perform energy minimisation. However, in Appendix 6, we tried three energy minimisation methods: FIRE, CG, and Steepest Descent (SD),41 and we found that this did not affect our results for the occurrence and size of plastic events. The pressure p and shear stress σ were quantified following the Irving–Kirkwood calculations.42
is the mean interparticle force, and the mechanical balance is set to λF < 10−11. We primarily used the conjugate gradient (CG) algorithm40 to perform energy minimisation. However, in Appendix 6, we tried three energy minimisation methods: FIRE, CG, and Steepest Descent (SD),41 and we found that this did not affect our results for the occurrence and size of plastic events. The pressure p and shear stress σ were quantified following the Irving–Kirkwood calculations.42
Quasistatic SRF model
A key point in studying the SRF model is identifying quantities and algorithms equivalent to the SS model to be able to make an accurate comparison. Following an overdamped dynamic, the velocity of active particles that are subjected to a persistent self-force with size f can be determined by , where
, where ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) Ri is the direction in which the self-force is applied and D is the overdamp constant.43,44 Despite the simplicity of this approach for conducting simulations, our previous work showed that, to mitigate stagnation issues arising from finite size problems,20 it is more convenient to reformulate this equation, making the parallel velocity
Ri is the direction in which the self-force is applied and D is the overdamp constant.43,44 Despite the simplicity of this approach for conducting simulations, our previous work showed that, to mitigate stagnation issues arising from finite size problems,20 it is more convenient to reformulate this equation, making the parallel velocity  a control parameter as follows:
a control parameter as follows: | (4) |
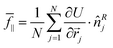 represents the mean of the contact force projection along the direction of deformation. In addition, we adopted the definition
represents the mean of the contact force projection along the direction of deformation. In addition, we adopted the definition  , which enabled us to obtain a control parameter with dimensions equivalent to the shear strain rate
, which enabled us to obtain a control parameter with dimensions equivalent to the shear strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in the SS model. Consequently, the self-force f is computed as
in the SS model. Consequently, the self-force f is computed as | (5) |
Notice that for both models, the SS and the SRF model, their names refer not to the control parameter but to the resulting stresses or forces, respectively. The final essential ingredient to establish an equivalence between SS and SRF is to define a ‘random’ stress  .32 By combining this with the overdamped equation, we obtain the following relationship:
.32 By combining this with the overdamped equation, we obtain the following relationship:
 | (6) |
In practice, a quasistatic regime is observed when, for dγ deformation, the system has enough time to reach a new equilibrium state. Using the above and dynamic eqn (4), we constructed a time-independent equation of motion, as described by eqn (7) that defines how the AQS–SRF should be
 | (7) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Rdt.
Rdt.
Consequently, the AQS algorithm for an SRF deformation can be described as follows: first, at each step of the simulation, an affine deformation displaces the particles in
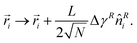 | (8) |
Second, the system is given the time required to reach mechanical equilibrium, which presents a constriction owing to the presence of a self-force f. In this sense, minimization is done in search of balance  .32
.32
III. Quasistatic yielding statistics
As shown in Fig. 2(a) and (b), we calculate the stress for the SS model over a range of 0 < γ < 6 and an SRF over 0 < γ < 60; using these ranges, we ensured that a stationary state was achieved in the last third of the data, where the data did not depend on the initial configuration. The significant differences in the ranges necessary to obtain these results are consistent with the results obtained in our previous study.20To improve the resolution of the plastic events for both models, we used the detection method described by Lerner and Procaccia.23 For each step of size Δγ, this method calculates the difference between the potential energy of the system immediately after making the affine deformation Uaff and its energy once it reaches its minimum U0. In Fig. 2(c) and (d), we show how the total reorganisation factor, 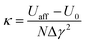 , fluctuates over the same range as γ. In intervals in which plastic events are not detected, κ assumes values within a well-determined range. However, when an event occurs, this value increases significantly, demonstrating its effectiveness for characterising events with high reorganisation. This allows us to reduce Δγ = 10−4 until Δγ = 10−6 and provides a better resolution in sections close to a plastic event.
, fluctuates over the same range as γ. In intervals in which plastic events are not detected, κ assumes values within a well-determined range. However, when an event occurs, this value increases significantly, demonstrating its effectiveness for characterising events with high reorganisation. This allows us to reduce Δγ = 10−4 until Δγ = 10−6 and provides a better resolution in sections close to a plastic event.
A more detailed analysis of the evolution of σ over γ reveals that the system exhibits sections with elastic behaviour, where it loads a shear stress δσ′ during a strain section of size δγ (see Fig. 3(a)). This behaviour was also observed when analysing the equivalent quantities for the SRF model. By examining these quantities, in elastic deformation sections we can calculate the shear modulus  at which the system loads the stress. In Fig. 3(b), the distribution of G for different system sizes is shown; notably, it follows a distribution centred on G0.
at which the system loads the stress. In Fig. 3(b), the distribution of G for different system sizes is shown; notably, it follows a distribution centred on G0.
This elastic section, where the system loads stress, is abruptly terminated by the origin of an avalanche (composed of several plastic events), where the reorganisation of particles occurs. This event is reflected in the gap in the shear stress of size δσ.
Despite the tremendous numerical effort, the δσ distribution shown in Fig. 4 demonstrates that our data have a minimum resolution δσmin, beyond which we cannot capture smaller avalanches. This minimum resolution is the product of Δγ, which is nonzero. In each step, the system loads, on average, a shear stress equivalent to G0Δγ, for which our algorithm that detects the drop in shear stress has problems detecting drops smaller than G0Δγ because the drop in stress can be hidden by the loading process of shear stress. Due to this, and to avoid the diffusion effect of distribution P(G) for small system sizes, we considered only δσ > 2G0Δγ to be sufficiently large to avoid minimal resolution problems.
The next important result corresponds to the size distribution of an avalanche S = δσLd, which is defined as the total stress released by an avalanche in a system of large size L. It has been observed that this distribution follows the power law described by P(S) ∼S−τ and exhibits a cutoff value of Sc, which is due to the finite size of the system.24–26,29,45 The cutoff corresponds to the size of the system Sc ∼ Ldf, where df is an exponent known as the fractal dimension.24,46 Together, these two exponents determine the size of the avalanche distribution in the systems.
Fig. 5 shows our results for P(S) in both the models and potentials used. We observed that all the distributions have the form P(S) ∼ S−τf(S/Sc), where f(x) is a rapidly decaying function. A good collapse of the distributions for different system sizes was observed when plotting P(S)Lτdfvs. S/Ldf.30 As can be seen in all configurations used, τ = 1.14 was consistently maintained. However, df presents a slight difference between the SS (df = 1.1) and SRF (df = 1) models. These values are consistent with those obtained for SS deformation in previous studies.24–27 Using both exponents, we can calculate the scale relation between 〈δσ〉 and the system size L as 〈δσ〉 ∼L−δ, where δ = d − df(2 − τ) with d dimension number. The latter result is obtained by integrating P(S) between 0 and Sc. The final scale relation was tested, as shown in Fig. 6 (blue line). Here, δ = 1.04 for the SS model using both potentials, thus reflecting the consistency of the data. Although the δ exponent that we computed is similar to one recently reported,33 it differs from that reported for systems with very similar simulation protocols.23,47 This difference is attributable to the fact that our data are truncated for avalanches smaller than 2G0Δγ because, by not differentiating, we recovered exponents similar to those mentioned (red line in Fig. 6).
IV. Avalanche relaxation time in AQS
The equivalence of results when analysing the avalanche distribution between both deformation scenarios suggests that the discrepancy observed in the exponents describing the fluid region is due to a dynamic component. This dynamic aspect is commonly examined through the exponent z, which corresponds to the time required for an avalanche to propagate and its extension length T∼lz. Additionally, this exponent plays a crucial role in bridging the quasistatic regime with the dynamic regime;29 however, measuring this exponent has proven to be a challenging task.30,45Table 1 presents a summary of the exponents calculated for both deformation scenarios. By utilizing these exponents and the relation of the scales studied by Lin et al.29 on mesoscopic systems (β = ν(d − df + z)), we can indirectly calculate the exponent z, resulting in z = 2.9 for the SS model and z = 8.1 for the SRF model. Similar to the findings of our previous work,20 applying this scaling relation indicates that the value of z should be significantly larger than that observed in mesoscopic models.29,30
| Exponent | SS model | SRF model |
|---|---|---|
| τ | 1.14 | 1.14 |
| d f | 1.1 | 1 |
| β | 2.3 | 1.7 |
| ν/β | 0.26 | 0.11 |
The natural next step is to calculate the exponent z directly. Time does not play an intrinsic role in AQS, as evident in eqn (7), here relaxation is allowed without imposing a time limit. Nevertheless, the finite size of the system constrains the maximum extent of an avalanche, thus limiting the duration of this process. In this context, we propose an algorithm that enables us to make a measurement from AQS. During each simulation step, the system was permitted to relax until it reached a state in which the residual force factor satisfied the equilibrium condition. As mentioned earlier, we measured the total shear stress release S and total reorganisation factor κ that occur when a plastic event is generated. Consequently, the time t* at which this reorganisation process occurs depends on S. Fig. 7(a) and (b) illustrate the evolution of S(t) and κ(t) over time for two specific events. In the first section (before the yellow dots), the system experiences minimal reorganisation, leading to almost negligible changes in S(t) and κ(t). This behaviour is interpreted as a region in which the system is still trying to relax energy following an elastic regime. Similarly, in the last section (after the green dot), the reorganisation is almost negligible, and the system solely aims to adapt to our mechanical stability criteria. In contrast, the central section between the yellow and green dots exhibits a concentration of stress drops and reorganisation.
This analysis allowed us to define t* as the elapsed time in the middle section, which we defined starting at κ(t)/κ > ζ and ending at κ(t)/κ <1 − ζ, where ζ = 0.015, and verify that variations in this choice do not affect our scale results. In Fig. 7(c), one million events were observed for a system of N = 8192 and LP potential. Here the average of these events indicates that the time needed to reach equilibrium increases in avalanches of larger sizes.
By using this algorithm, Fig. 8(a) and (b) show the distribution P(t*) for different system sizes with the LP potential method, GC relaxation method, and both deformation scenarios, respectively. The cutoff point of P(t*) corresponds to the propagation time of an avalanche with a length of the system L.29 Thus, a collapse can be observed with L0.9 for the SS model and L0.8 for the SRF model. These results provide the exponent z, which relates the linear extension of an avalanche vs. the time at which this process occurs using the relation T ∼ Lz. Here, we obtained z = 0.9 for passive systems and z = 0.8 for active systems. This final result represents an important change from the first estimate of the exponent z.
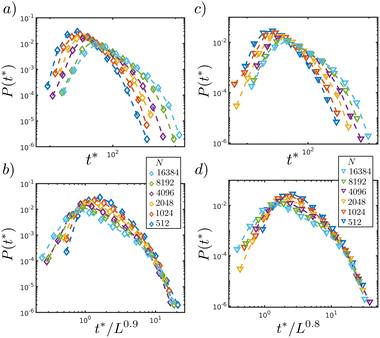 | ||
| Fig. 8 (a) and (b) Distribution P(t*) for different sizes in the SS and SRF models, respectively. (c) and (d) The same data collapsed by L0.9 and L0.8. | ||
A possible explanation for this radical difference could be the choice of relaxation method used in the simulations. Previous studies on mesoscopic systems found that the value of this exponent is sensitive to the methodology used to propagate the effects of an avalanche.30 Similarly, in our soft-particle systems, a point of contention arises regarding the energy minimisation method used in our simulations. The CG algorithms employed in our latest results, or the FIRE algorithms, require significantly less simulation effort than the SD algorithms. Consequently, it is reasonable to expect that this difference will translate into shorter avalanche propagation times for certain relaxation algorithms. Specifically, considering that FIRE incorporates inertia, CG considers the history of descent for faster convergence. A change in the exponent z due to the relaxation method can play an essential role in reconciling the dynamical regime with AQS, especially when considering that almost all studies involving dynamical regimes with particles (including our latest work20) use simulation algorithms from Durian's studies,48 where inertia or any temporary memory effect of the evolution algorithm does not play a role. To address this question, one possible solution would be to perform the same calculation as above for z using the steepest descent (SD) as the relaxation method. However, this requires significant computational effort, as our experience indicates that the simulation times increase between two to three orders of magnitude with SD, making it unfeasible with the current numerical capacity.
V. Conclusions
In this study, we observed that the differences in flow curves due to the modification of the deformation scenario type did not appear to be reflected in the avalanche probability distribution when the deformation was executed in a quasistatic regime. This is consistent with previous research that provided similar results.32,44,49Because no difference is observed in the avalanche statistics between the active and passive systems in the quasistatic regime, attention needs to shift towards studying the dynamic properties, specifically the relaxation process of avalanches. For passive systems, a single scaling relation connecting the duration of avalanches with their size has been suggested to link the flow state with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≠ 0 and avalanche statistics in the AQS regime.21,28,29 This property is characterised by the z-exponent introduced in Section 4. However, despite its significance, measurements of this exponent in molecular dynamics systems are scarce.50,51
≠ 0 and avalanche statistics in the AQS regime.21,28,29 This property is characterised by the z-exponent introduced in Section 4. However, despite its significance, measurements of this exponent in molecular dynamics systems are scarce.50,51
A preliminary measurement of the z-exponent under CG dynamics revealed a value much lower than expected, as predicted by the scale relation derived from mesoscopic elastoplastic models.29,30 However, this difference is largely explained by the relaxation method used in the simulations, or it could be because of the calculation methodology employing a pseudo-time definition derived from the relaxation method.
Conflicts of interest
There are no conflicts to declare.Appendix
A. P(S) consistency for different relaxation methods
This Appendix verifies that the probability distribution curve P(S) does not vary with the relaxation method used. Fig. 9 shows the results for P(S) for N = 1024 and the Hertzian potential. The coincidence of the curves can be interpreted as a difference in the relaxation method that did not affect the final equilibrium states.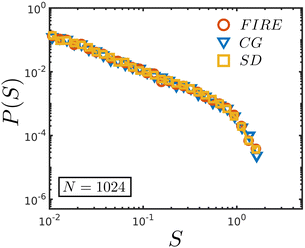 | ||
| Fig. 9 P(S) for a N = 1024 and the Hertzian potential using three relaxation methods. In red: FIRE, in blue: conjugate gradient (GC), and in yellow: steepest descent (SD). | ||
Acknowledgements
We thank Edan Lerner for the fruitful discussions and comments on the manuscript. G. D. acknowledges funding from ANID FONDECYT No 1210656. C. V. acknowledges the support from ANID for Scholarship no. 21181971.GS.References
- P. Coussot, Material Mechanics, John Wiley and Sons, Ltd, 2005, pp. 4–40. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/0471720577.ch1 Search PubMed.
- C. S. O’Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Jamming at zero temperature and zero applied stress: The epitome of disorder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.68.011306.
- M. van Hecke, Jamming of soft particles: geometry, mechanics, scaling and isostaticity, J. Phys.: Condens. Matter, 2009, 22(3), 033101, DOI:10.1088/0953-8984/22/3/033101 . https://iopscience.iop.org/article/10.1088/0953-8984/22/3/033101.
- P. Olsson and S. Teitel, Critical Scaling of Shear Viscosity at the Jamming Transition, Phys. Rev. Lett., 2007, 99, 178001 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.99.178001.
- D. Vågberg, P. Olsson and S. Teitel, Glassiness, rigidity, and jamming of frictionless soft core disks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031307 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.83.031307.
- P. Coussot, J. S. Raynaud, F. Bertrand, P. Moucheront, J. P. Guilbaud and H. T. Huynh, et al., Coexistence of Liquid and Solid Phases in Flowing Soft-Glassy Materials, Phys. Rev. Lett., 2002, 88, 218301 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.88.218301.
- J. Lauridsen, M. Twardos and M. Dennin, Shear-Induced Stress Relaxation in a Two-DimensionalWet Foam, Phys. Rev. Lett., 2002, 89, 098303 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.89.098303.
- B. S. Gardiner, B. Z. Dlugogorski, G. J. Jameson and R. P. Chhabra, Yield stress measurements of aqueous foams in the dry limit, J. Rheol., 1998, 42(6), 1437–1450, DOI:10.1122/1.550896.
- N. Xu and C. S. O’Hern, Measurements of the yield stress in frictionless granular systems, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061303 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.73.061303.
- A. H. Clark, J. D. Thompson, M. D. Shattuck, N. T. Ouellette and C. S. O’Hern, Critical scaling near the yielding transition in granular media, Phys. Rev. E, 2018, 97, 062901 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.97.062901.
- W. H. Herschel and R. Bulkley, Konsistenzmessungen von Gummi-Benzollösungen, Kolloid-Z., 1926, 39(4), 291–300, DOI:10.1007/BF01432034.
- A. Lemâitre and C. Caroli, Rate-Dependent Avalanche Size in Athermally Sheared Amorphous Solids, Phys. Rev. Lett., 2009, 103, 065501 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.103.065501.
- C. Maloney and A. Lemâitre, Subextensive Scaling in the Athermal, Quasistatic Limit of Amorphous Matter in Plastic Shear Flow, Phys. Rev. Lett., 2004, 93, 016001 CrossRef . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.93.016001.
- M. Bouzid, M. Trulsson, P. Claudin, E. Clément and B. Andreotti, Nonlocal Rheology of Granular Flows across Yield Conditions, Phys. Rev. Lett., 2013, 111, 238301 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.111.238301.
- R. Mandal, P. J. Bhuyan, P. Chaudhuri, C. Dasgupta and M. Rao, Extreme active matter at high densities, Nat. Commun., 2020, 11(1), 2581, DOI:10.1038/s41467-020-16130-x.
- S. Henkes, Y. Fily and M. C. Marchetti, Active jamming: Selfpropelled soft particles at high density, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 040301 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.84.040301.
- C. Reichhardt and C. J. Olson Reichhardt, Active matter transport and jamming on disordered landscapes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012701 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.90.012701.
- B. Loewe, M. Chiang, D. Marenduzzo and M. C. Marchetti, Solid–Liquid Transition of Deformable and Overlapping Active Particles, Phys. Rev. Lett., 2020, 125, 038003 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.125.038003.
- Y. E. Keta, J. Klamser, R. Jack and L. Berthier, Emerging mesoscale flows and chaotic advection in dense active matter, arXiv, 2023, preprint, arXiv:2306.07172 DOI:10.48550/arXiv.2306.07172.
- C. Villarroel and G. Düuring, Critical yielding rheology: from externally deformed glasses to active systems, Soft Matter, 2021, 17, 9944–9949, 10.1039/D1SM00948F.
- C. E. Maloney and A. Lemâitre, Amorphous systems in athermal, quasistatic shear, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 016118 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.74.016118.
- J. D. Thompson and A. H. Clark, Critical scaling for yield is independent of distance to isostaticity, Phys. Rev. Res., 2019, 1, 012002 CrossRef CAS . Available from: https://link.aps.org/doi/10.1103/PhysRevResearch.1.012002.
- E. Lerner and I. Procaccia, Locality and nonlocality in elastoplastic responses of amorphous solids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 066109 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.79.066109.
- D. Zhang, K. A. Dahmen and M. Ostoja-Starzewski, Scaling of slip avalanches in sheared amorphous materials based on large-scale atomistic simulations, Phys. Rev. E., 2017, 95, 032902 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.95.032902.
- B. Shang, P. Guan and J. L. Barrat, Elastic avalanches reveal marginal behavior in amorphous solids, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(1), 86–92 CrossRef CAS PubMed . Available from: https://www.pnas.org/doi/abs/10.1073/pnas.1915070117.
- N. Oyama, H. Mizuno and A. Ikeda, Unified view of avalanche criticality in sheared glasses, Phys. Rev. E, 2021, 104, 015002 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.104.015002.
- C. Ruscher and J. Rottler, Avalanches in the Athermal Quasistatic Limit of Sheared Amorphous Solids: An Atomistic Perspective, Tribol. Lett., 2021, 69(2), 64, DOI:10.1007/s11249-021-01439-5.
- K. M. Salerno and M. O. Robbins, Effect of inertia on sheared disordered solids: Critical scaling of avalanches in two and three dimensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062206 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.88.062206.
- J. Lin, E. Lerner, A. Rosso and M. Wyart, Scaling description of the yielding transition in soft amorphous solids at zero temperature, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(40), 14382–14387 CrossRef CAS PubMed . Available from: https://www.pnas.org/content/111/40/14382.
- E. E. Ferrero and E. A. Jagla, Criticality in elastoplastic models of amorphous solids with stress-dependent yielding rates, Soft Matter, 2019, 15, 9041–9055, 10.1039/C9SM01073D.
- A. Amiri, C. Duclut, F. Jülicher and M. Popović, Random traction yielding transition in epithelial tissues, Phys. Rev. Lett., 2023, 131, 188401 CrossRef CAS PubMed Available from: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.188401.
- P. K. Morse, S. Roy, E. Agoritsas, E. Stanifer, E. I. Corwin and M. L. Manning, A direct link between active matter and sheared granular systems, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(18), e2019909118 CrossRef CAS PubMed . Available from: https://www.pnas.org/doi/abs/10.1073/pnas.2019909118.
- Y. E. Keta, R. Mandal, P. Sollich, R. L. Jack and L. Berthier, Intermittent relaxation and avalanches in extremely persistent active matter, Soft Matter, 2023, 19, 3871–3883, 10.1039/D3SM00034F.
- P. Olsson and S. Teitel, Herschel-Bulkley Shearing Rheology Near the Athermal Jamming Transition, Phys. Rev. Lett., 2012, 109, 108001 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.109.108001.
- R. J. Speedy, Glass transition in hard disc mixtures, J. Chem. Phys., 1999, 110(9), 4559–4565, DOI:10.1063/1.478337.
- C. S. O’Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Random Packings of Frictionless Particles, Phys. Rev. Lett., 2002, 88, 075507 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.88.075507.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural Relaxation Made Simple, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.97.170201.
- S. Teitel, D. Vågberg and P. Olsson Glassiness, Rigidity and Jamming of Frictionless Soft Core Disks. In: APS March Meeting Abstracts. vol. 2011 of APS Meeting Abstracts; 2011. p. H13.005.
- D. J. Evans and G. P. Morriss, 6 – Computer Simulation Algorithms, in Statistical Mechanics of Nonequilibrium Liquids, ed. D. J. Evans and G. P. Morriss, Academic Press, 1990. pp. 121–168. Available from: https://www.sciencedirect.com/science/article/pii/B9780122440908500114 Search PubMed.
- J. R. Shewchuk, An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, Carnegie Mellon University, USA, 1994 Search PubMed.
- J. S. Arora, 8 – Numerical Methods for Unconstrained Optimum Design, in Introduction to Optimum Design, ed. J. S. Arora, Academic Press, San Diego, 2nd edn, 2004, pp. 277–304. Available from: https://www.sciencedirect.com/science/article/pii/B9780120641550500082 Search PubMed.
- J. H. Irving and J. G. Kirkwood, The Statistical Mechanical Theory of Transport Processes. IV. The Equations of Hydrodynamics, J. Chem. Phys., 1950, 18(6), 817–829, DOI:10.1063/1.1747782.
- R. Mo, Q. Liao and N. Xu, Rheological similarities between dense self-propelled and sheared particulate systems, Soft Matter, 2020, 16, 3642–3648, 10.1039/D0SM00101E.
- Q. Liao and N. Xu, Criticality of the zero-temperature jamming transition probed by self-propelled particles, Soft Matter, 2018, 14, 853–860, 10.1039/C7SM01909B.
- J. Lin and M. Wyart, Microscopic processes controlling the Herschel-Bulkley exponent, Phys. Rev. E, 2018, 97, 012603 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.97.012603.
- A. B. Kolton, A. Rosso, T. Giamarchi and W. Krauth, Creep dynamics of elastic manifolds via exact transition pathways, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 184207 CrossRef . Available from: https://link.aps.org/doi/10.1103/PhysRevB.79.184207.
- S. Karmakar, E. Lerner and I. Procaccia, Statistical physics of the yielding transition in amorphous solids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 055103 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.82.055103.
- D. J. Durian, Foam Mechanics at the Bubble Scale, Phys. Rev. Lett., 1995, 75, 4780–4783 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.75.4780.
- E. Agoritsas, Mean-field dynamics of infinite-dimensional particle systems: global shear versus random local forcing, J. Stat. Mech.: Theory Exp., 2021, 2021(3), 033501, DOI:10.1088/1742-5468/abdd18.
- J. T. Clemmer, K. M. Salerno and M. O. Robbins, Criticality in sheared, disordered solids. I. Rate effects in stress and diffusion, Phys. Rev. E, 2021, 103, 042605 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.103.042605.
- J. T. Clemmer, K. M. Salerno and M. O. Robbins, Criticality in sheared, disordered solids. II. Correlations in avalanche dynamics, Phys. Rev. E, 2021, 103, 042606 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.103.042606.
| This journal is © The Royal Society of Chemistry 2024 |

![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif)





