Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Confinement twists achiral liquid crystals and causes chiral liquid crystals to twist in the opposite handedness: cases in and around sessile droplets†
Jungmyung
Kim
 and
Joonwoo
Jeong
and
Joonwoo
Jeong
 *
*
Department of Physics, Ulsan National Institute of Science and Technology, Ulsan, Republic of Korea. E-mail: jjeong@unist.ac.kr
First published on 11th January 2024
Abstract
We study the chiral symmetry breaking and metastability of confined nematic lyotropic chromonic liquid crystals (LCLCs) with and without chiral dopants. The isotropic–nematic coexistence phase of the LCLC renders two confining geometries: sessile isotropic (I) droplets surrounded by the nematic (N) phase and sessile nematic droplets immersed in the isotropic background. In the achiral system with no dopants, LCLC's elastic anisotropy and topological defects induce a spontaneous twist deformation to lower the energetic penalty of splay deformation, resulting in spiral optical textures under crossed polarizers both in the I-in-N and N-in-I systems. While the achiral system exhibits both handednesses with an equal probability, a small amount of the chiral dopant breaks the balance. Notably, in contrast to the homochiral configuration of a chirally doped LCLC in the bulk, the spiral texture of the disfavored handedness appears with a finite probability both in the I-in-N and N-in-I systems. We propose director field models explaining how chiral symmetry breaking arises by the energetics and the opposite-twist configurations exist as meta-stable structures in the energy landscape. These findings help us create and control chiral structures using confined LCs with large elastic anisotropy.
Chiral structures are ubiquitous, ranging from molecules to astrophysical phenomena. Understanding the mechanism underlying this mirror symmetry breaking is an active field of investigation. Simultaneously, the control and separation of chiral structures are crucial in diverse applications.1–5 For instance, chiral molecules can be toxic in unwanted enantiomeric forms,6 and these chiral objects as building blocks or dopants can determine their assembled structures’ chirality. Additionally, external fields, including shear and confinement, are often employed to control chiral structures.7–10
Liquid crystals (LCs) are the quintessential model system for studying chiral structures.11–17 In particular, chiral nematic LCs, also known as the cholesteric phase, have been studied extensively. They are omnipresent in nature and deployed in various applications.18–24 In the cholesteric phase, LC mesogens twist along the helical axis, defining its handedness – right- or left-handed – and helical pitch, which are often determined by the intrinsic chirality of the mesogen or dopants. Thus, one may design chiral structures by choosing mesogens or the dopant's type and concentration at a given temperature.
The boundary conditions and elasticity of confined LCs also play a vital role in determining their chiral structures.8–10,25–41 The confining geometry and LC surface anchoring at the interface between LC and the surrounding phase can result in unexpected structures that differ from the ones in the bulk. For example, confinement may lead to an apparent helical pitch different from the bulk pitch.42,43 Furthermore, achiral LCs under confinement, e.g., droplets and cylinders, can form chiral structures8–10,29–32,44–48 and vice versa.34
Confinements may afford multiple meta-stable structures,43,49–51 often resulting in chiral structures having the opposite handedness to their bulk ones, of which the handednesses and helical pitch are determined by the chirality of the mesogens and dopants. For example, the twist handedness can be reversed locally,51–53 or domains of different handedness coexist,54–56 resulting in heterochiral structures despite their energetic penalty. These confinement effects involving surface anchoring, elastic anisotropy, saddle-splay elasticity, topological defects, and metastability, have advanced our understanding of the partially ordered matter and its applications.
Here, we report cases in and around sessile droplets where chiral nematic LC can exhibit a meta-stable structure of the disfavored handedness, i.e., opposite to the handedness in bulk, because of boundary conditions. We use achiral and chiral nematic lyotropic chromonic LCs to study their director configuration in and around sessile droplets on an anchoring-controlled substrate. Our experiments and numerical calculations demonstrate the roles of confinement and elastic anisotropy in the chiral symmetry breaking of achiral LC. Moreover, we elucidate how chiral LC can afford chiral structures of the opposite handedness as meta-stable states, thanks to confinements.
Materials and methods
Materials
Sunset Yellow FCF (SSY, a purity of 90%) was purchased from Sigma-Aldrich, and purified using the conventional method57 because impurities matter for the phase behavior58 and, presumably, elastic properties. Brucine sulfate heptahydrate (BSH) as a chiral dopant for SSY was purchased from Sigma-Aldrich and used without purification. Mixing deionized water, SSY, and BSH, we prepared an aqueous solution of 30.0% (wt/wt) SSY with 0 to 0.4% (wt/wt) of BSH as an achiral (without BSH) or chiral nematic LC solution at room temperature.Sample preparation
We coated glass slides and coverslips with parylene59 and used them as substrates for the homeotropically aligned cell. The substrates were placed in a parylene coating machine (LAVIDA 110; Femto Science) with 500 mg of parylene-N (diX N, Daisan Kasei), and the temperatures for the vaporizer, pyrolyzer, and deposition of parylene were 150 °C, 690 °C, and room temperature, respectively. The estimated thickness of the parylene film is approximately 400 nm.60 Utilizing Kapton films of 25 μm thickness on the surface-treated slide as spacers, we dropped 10 μL of LC solution on the parylene-coated slide and quickly covered the specimen with the coated coverslip. The edges of the sandwich cell were sealed with epoxy glue to minimize the drying of the aqueous LC solution. The sandwiched nematic SSY initially shows a transient stripe texture, but after several tens of minutes, the stripe texture is replaced by a full homeotropically aligned domain.59 However, when the dopant concentration surpasses 0.4% (wt/wt), the sandwiched nematic SSY no longer exhibits the homeotropic alignment but the fingerprint texture, not providing the proper initial condition for our droplet experiments, as shown in Fig. S1 (ESI†).Optical observation
We observed the sandwich cell with a polarized optical microscope (Olympus BX53-P) equipped with linear polarizers, a full waveplate (optical path difference = 550 nm; Olympus), a temperature-controlled stage (T95-PE120; Linkam Scientific Instruments), a CCD camera (INFINITY3-6URC; Lumenera), and a LED lamp (LED4D067; Thorlabs) providing quasi-monochromatic illumination at 660 nm wavelength (FWHM = 25 nm). We increased the temperature, 1 °C min−1, of the aligned LC cell to make the LC enter the isotropic–nematic coexistence phase at 45 °C. Repeating the heating–cooling sequence, we collected multiple polarized optical microscopy (POM) images from the same location of the same sample. Note that we employ the slow heating rate to control the droplet locations, i.e., only at the bottom, and propose experiments varying the rate as future work.Numerical calculations
The total elastic free energy F is the volume integral of the energy density f given by | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2
K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K3 = 1
K3 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the 30.0% (wt/wt) SSY61 and p0 = 1/(C × HTP) where C is BSH concentration in % (wt/wt) and HTP is helical twisting power, 0.123 ± 0.007 μm−1 (see Fig. S2 for details, ESI†). Note that we employ a constant p0 with no spatial dependency, assuming a uniform distribution of the chiral dopant. We believe that this assumption deserves further investigation, considering the fine structure of the topological defect cores of LCLCs.62 For a given director field n, we perform a numerical integration
1 for the 30.0% (wt/wt) SSY61 and p0 = 1/(C × HTP) where C is BSH concentration in % (wt/wt) and HTP is helical twisting power, 0.123 ± 0.007 μm−1 (see Fig. S2 for details, ESI†). Note that we employ a constant p0 with no spatial dependency, assuming a uniform distribution of the chiral dopant. We believe that this assumption deserves further investigation, considering the fine structure of the topological defect cores of LCLCs.62 For a given director field n, we perform a numerical integration 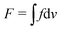 over domain
over domain ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) to draw the energy landscape such as in Fig. 3(a). For the I-in-N case, i.e., the sessile isotropic droplet surrounded by the nematic phase, we adopted
to draw the energy landscape such as in Fig. 3(a). For the I-in-N case, i.e., the sessile isotropic droplet surrounded by the nematic phase, we adopted ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) = {(x, y, z)|x2 + y2 ≤ (5R)2, 0 ≤ z ≤ 5R, x2 + y2 + z2 ≥ R2, x2 + y2 + (z − R)2 ≥ Rd2} where R is the radius of the hemispherical droplet. To facilitate the convergence of the numerical integration, we set a cutoff radius Rd = 10−3R around the point defect at the top of the droplet; Rd = 10−3R corresponds to 10 nm, which is of the same order of the persistence length of the SSY aggregates61 in a droplet of 10 μm radius. For the N-in-I case, we used
= {(x, y, z)|x2 + y2 ≤ (5R)2, 0 ≤ z ≤ 5R, x2 + y2 + z2 ≥ R2, x2 + y2 + (z − R)2 ≥ Rd2} where R is the radius of the hemispherical droplet. To facilitate the convergence of the numerical integration, we set a cutoff radius Rd = 10−3R around the point defect at the top of the droplet; Rd = 10−3R corresponds to 10 nm, which is of the same order of the persistence length of the SSY aggregates61 in a droplet of 10 μm radius. For the N-in-I case, we used ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) = {(x, y, z)|0 ≤ z, x2 + y2 + z2 ≤ R2, x2 + y2 + (z − R)2 ≥ Rd2} and Rd = 10−3R. After identifying the director configurations corresponding to local minima in the energy landscape of each director fields model, we simulated their POM textures using Jones calculus10 and compared the results with experimental observations.
= {(x, y, z)|0 ≤ z, x2 + y2 + z2 ≤ R2, x2 + y2 + (z − R)2 ≥ Rd2} and Rd = 10−3R. After identifying the director configurations corresponding to local minima in the energy landscape of each director fields model, we simulated their POM textures using Jones calculus10 and compared the results with experimental observations.
Results and discussion
Sessile isotropic droplets surrounded by nematic phase
We observe chiral symmetry breaking of achiral nematic LC around sessile isotropic liquid droplets. Fig. 1 shows our lyotropic chromonic LC, SSY, at its isotropic–nematic coexistence phase confined between two parallel substrates imposing homeotropic anchoring. When a homeotropically aligned nematic SSY enters the coexistence phase upon a temperature increase, as shown in Fig. 1(a), sessile droplets of the isotropic phase appear at the bottom substrate. Because the temperature-controlling Peltier plate contacts the bottom substrate, the isotropic droplets nucleate from the bottom substrate. We make and observe the droplets only at the bottom substrate and find that the contact angle at the three-phase boundary is close to 90 degrees, as shown in ESI.† We also confirm no memory effect by comparing the location, size, and handedness of droplets in different images. The sessile isotropic droplets deform the homeotropically aligned nematic director field, and the deformed regions exhibit spiral textures under POM, as shown in Fig. 1(b)–(f). The appearance of the chiral spiral texture, despite the absence of chirality in SSY, is notable. Non-deformed nematic regions remain dark under crossed polarizers because of the homeotropic alignment.We classify the spiral textures’ handedness, investigate their appearance probability, and find that each handedness is equally probable. In the right-handed spiral texture (RS), the dark line turns right while going from the center to the boundary. In three independent experiments, each collecting approximately 270 droplets, the average probability of observing the RS texture is 0.509 ± 0.021, where the error indicates the standard deviation of the three measurements. This half-and-half probability is consistent with the achiral nature of SSY, i.e., no preference for a specific handedness.
With a chiral dopant is added, the spiral texture prefers a specific handedness. As we increase the concentration of a dopant, BSH, the appearance probability of RS increases and excels left-handed spiral texture (LS)'s, as shown in Fig. 1(g). For example, with 0.4% (wt/wt) BSH added to 30% (wt/wt) SSY, almost 90% of the spiral texture becomes RS. It is unexpected that 10% remains as the energetically unfavorable LS at our maximum dopant concentration because a chirally doped LC in bulk would exhibit a homochiral director configuration with a well-defined helical pitch.33,63–67 On the other hand, we propose as future work the investigation of the appearance probability at very low concentration, i.e., between 0 and 0.1% (wt/wt), to find the critical concentration for the chiral symmetry breaking.55
To elucidate the observed chiral symmetry breaking in achiral SSY and metastability in chiral SSY, we propose a director field model of nematic LC around the isotropic droplet. We employ this ansatz approach instead of the numerical simulation adopted in a similar geometry29 for the following reason. The numerical simulation using the Q-tensor can find the energy-minimizing director configurations that better match experimental observations, although parameter choices for LCLCs require further studies. The director configurations found by the model with a finite number of parameters are undoubtedly approximated ones. However, the model approach often can be useful, enabling us to map the energy landscape of the problem systematically. Then, we can not only identify local minima leading to meta-stable configurations but also rationalize why and how the minima exist, which will be the main focus of this paper.
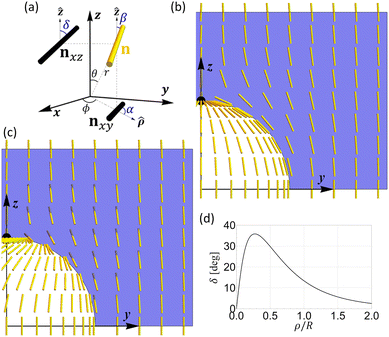
The first assumption of our model is that the isotropic sessile droplet in the model has a hemispherical shape, as shown in Fig. 1(a). This assumption is supported by the near 90-degree contact angle we estimate at the three-phase boundary. It is surrounded by the nematic phase satisfying the boundary conditions: an infinitely strong homeotropic anchoring both on the top and bottom substrates and a degenerate planar anchoring on the hemispherical droplet's surface. The hemispherical geometry and anchoring conditions differentiate our work from the chiral bipolar configuration reported in Nych et al. and Uzunova and Pergamenshchik.29,68 Additionally, the previous works study only the nematic phase, but our system investigates both achiral and chiral nematic phases. We parameterize the director field n with two spatially varying angles, α and β.
(nx, ny, nz) = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(ϕ + α), sin cos(ϕ + α), sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(ϕ + α), cos sin(ϕ + α), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β). β). | (2) |
The equation describes the Cartesian components (nx, ny, nz) of a director n at a position (r, θ, ϕ) in the spherical coordinate. For the angle β between a director and z-axis shown in Fig. 2(a), we adopt the bipolar planar quadrupole configuration.68
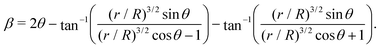 | (3) |
This ansatz adopted eqn (6) from Uzunova and Pergamenshchik68 satisfies our boundary conditions, i.e., the homeotropic alignment at the far field and the degenerate planar alignment on the hemispherical droplet's surface, resulting in a point defect at the droplet's pole, also known as a boojum. Note that our sessile-droplet geometry has one pole at the top of the droplet.
We hypothesize that the experimentally observed spiral POM textures result from a twisted director configuration. We add twist deformation to the planar quadrupole configuration by introducing the angle α in eqn (2). As shown in Fig. 2(a), α is the angle between the radial direction ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) in the cylindrical coordinate and the director's projection onto the x–y plane. If α = 0, the director field becomes the planar quadrupole configuration with no
in the cylindrical coordinate and the director's projection onto the x–y plane. If α = 0, the director field becomes the planar quadrupole configuration with no  -component.
-component.
Our ansatz adopts α as a power-law decaying function of ρ, satisfying the cylindrical symmetry and the far-field boundary condition. We choose this decaying profile because the splay cancellation by the twist deformation near a topological defect is a well-known mechanism for the chiral symmetry breaking in LCLCs;10 see ESI† for the detailed rationalization of the ansatz. Namely, α decreases along the radial direction from the z axis, i.e., from the boojum, and satisfies α(ρ → ∞) → 0, i.e., the deformation-free homeotropic alignment at infinity.
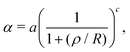 | (4) |
Two constants a and c determine the decaying α(ρ)'s profile and how the twist angle δ defined in Fig. 2(a) varies spatially. Fig. 2(d) is a representative δ–ρ profile for given a and c. A large a results in the large peak value of δ, and a large c leads to a fast decay as ρ increases.
The degenerate planar anchoring of the planar quadrupole configuration at the droplet surface can be violated when we adopt α ≠ 0 for the twist deformation. Varying the parameters a and c, we investigate the maximum polar deviation angle of the surface directors from the tangential plane at the droplet surface. Then, we exclude the parameter regimes having the maximum deviation angle greater than 20 deg from the region of interest, only allowing a slight violation of the planar anchoring condition at the isotropic–nematic interface.
By numerically calculating the total elastic free energy F of the above-mentioned director field model according to a and c, we find the director configurations at local energy minima, which agree well with experimental observations. See the Methods section for the details of the elastic free energy calculation. Fig. 3(a) shows the energy landscape of the achiral system, highlighting the local minima. In this achiral system, the energy landscape is symmetric about the axis of a = 0, i.e., F(a) = F(−a); the sign change of the angle α means the flipping of the spiral handedness. We locate (a, c) giving the two degenerate global minima of the energy landscape, simulate the corresponding POM textures using Jones calculus, and compare them with the experimental results, as shown in Fig. 3(b). The simulated textures well reproduce the spiral textures of different handednesses. Additionally, two degenerate global minima are consistent with the observation that the spiral textures of different handedness appear with equal probabilities in the achiral system.
The elastic anisotropy of the nematic SSY is responsible for two global minima at non-zero a and c, resulting in the two degenerate twisted ground states. Fig. S3 (ESI†) shows the energy difference between our twisted ground-state configuration and the twist-free planar quadrupole configuration. It indicates that the relatively cheap twist deformation cancels out the splay deformation near the topological defect, resulting in a net decrease in the total elastic free energy. This scenario is similar to the cases in the literature, where the achiral SSY under confinement breaks its chiral symmetry because of the very small K2 compared to other elastic moduli.10,31,32,55 Comparison of the energy landscapes at different K2 values corroborates the role of elastic anisotropy in the chiral symmetry breaking. Our close investigation of the energy landscape reveals that two degenerate global minima exist when k2 = K2/K3 ≤ 0.68; see ESI† for the determination of the critical k2 for the chiral symmetry breaking.
With chiral dopants added, as shown in Fig. 3(c), the energy landscape becomes asymmetric but still retains two minima. This is consistent with our experimental observation that the spiral textures of both handednesses appear. Because p0 in eqn (1) is no longer zero, the director configuration energetically favors a twist deformation of a given helical pitch and handedness imposed by the chiral dopant, making the energy landscape asymmetric. Notably, two global minima in the achiral system shown in Fig. 3(a) become one global minimum and one local minimum in the chiral system shown in Fig. 3(c). The director configuration of the preferred handedness has lower energy and corresponds to the global minimum, which is a more frequently observed spiral texture in our experiments. For instance, 0.4% (wt/wt) of chiral dopant gives right-handed spiral texture handedness with the probability 0.894 ± 0.032 out of 794 droplets. Intriguingly, the director configuration of the disfavored handedness exists with a finite probability, even though we add the chiral dopant to make the configuration favor a particular handedness. In fact, in the calculated energy landscape, there exists a local minimum with higher energy than the global minimum; see the top-right region of Fig. 3(c).
We find that a constraint from the symmetry and the far-field boundary condition results in the appearance of both handednesses. As shown in Fig. 2(c), the directors along the rotational axis, i.e., z-axis, are aligned vertically because of the symmetry. Starting from this symmetric axis, the directors twist along the radial direction ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) to lower the total elastic free energy in both achiral and chiral cases. However, to satisfy the far-field boundary condition, i.e., the uniform homeotropic alignment, the director should untwist to be vertical again unless the centrosymmetric directors twist by 180 degrees. In other words, as shown in Fig. 2(d), the system should have both twist-handedness, i.e., the positive and negative slopes in δ, regardless of the favored handedness of the system. This constraint justifies that, even in highly doped specimens preferring one-handedness and paying high energy penalty for the other-handedness, the disfavored spiral texture can be observed experimentally as a local minimum in the energy landscape. With different symmetry and boundary conditions allowing the homochiral twist deformation, one may expect chiral LCLCs to exhibit the homochiral spiral texture. We test this idea in the following section with the inverted system.
to lower the total elastic free energy in both achiral and chiral cases. However, to satisfy the far-field boundary condition, i.e., the uniform homeotropic alignment, the director should untwist to be vertical again unless the centrosymmetric directors twist by 180 degrees. In other words, as shown in Fig. 2(d), the system should have both twist-handedness, i.e., the positive and negative slopes in δ, regardless of the favored handedness of the system. This constraint justifies that, even in highly doped specimens preferring one-handedness and paying high energy penalty for the other-handedness, the disfavored spiral texture can be observed experimentally as a local minimum in the energy landscape. With different symmetry and boundary conditions allowing the homochiral twist deformation, one may expect chiral LCLCs to exhibit the homochiral spiral texture. We test this idea in the following section with the inverted system.
Sessile nematic droplets surrounded by isotropic phase
We observe the spiral textures again from sessile nematic LCLC droplets surrounded by the isotropic phase, i.e., N-in-I, of which the boundary conditions allow homochiral configurations. Fig. 4(b) shows the POM textures. In contrast to the I-in-N case at the temperature just above the nematic-to-coexistence phase transition temperature, the temperature of the N-in-I sample is at the one just below the coexistence-to-isotropic phase transition temperature. The isotropic regions grow and merge during the heating, and the nematic regions eventually become sessile droplets surrounded by the isotropic phase. We find that sessile droplets surrounded by air can implement the same boundary conditions: the near hemispherical shape and degenerate planar anchoring at the air–nematic interface. The spiral textures result from the twist deformation of the nematic phase confined within the sessile droplets. The absence of the far-field boundary condition, such as the homeotropic alignment in the I-in-N case, allows homochiral configurations. This chiral symmetry breaking and the energetics are similar to those in the suspended spherical droplets.10 The LCLC's cheapest twist deformation cancels out the high elastic energy penalty around the surface point defect, i.e., the black dot in Fig. 4(a). As expected, in the achiral system with no chiral dopant, we observe both handednesses in the spiral texture with equal probabilities: the ratio of RS to LS is 9 to 8.To our surprise, the sessile nematic droplets of chirally doped LCLC do not exhibit homochirality, even though the geometry and boundary conditions allow homochiral configurations. When 0.1% (wt/wt) of BSH is added, 41 out of 43 are left-handed. Namely, we observe the disfavored handedness experimentally, even though they are rarely observed. When we increase the dopant concentration to 0.2% (wt/wt), all droplets exhibit the homochiral configuration. Please note that we observe the same metastability in the N-in-air system; the data is not shown here because the sessile-droplet shapes surrounded by the air are not regular enough to be a well-defined confinement.
To investigate further the energetics of the meta-stable configuration having the disfavored handedness, we construct a parameterized director field model for the hemispherical sessile droplet, which is inspired by the twisted bipolar director configuration of the spherical droplet.10 As in the I-in-N case, we assume the hemispherical shape because of the near 90-deg contact angle, as shown in ESI.† The director n with a parameter γ is
n = nbipolar![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ + nconcentric γ + nconcentric![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, γ, | (5) |
We find that both achiral and chiral models can have two minima in the energy landscape of the parameter space (a, b, c). It is no surprise that the energy landscape of the achiral degenerate system with p0 = 0 renders the two energy minima with the same energy, and these two configurations correspond to each spiral texture of different handedness shown in the experiment. As shown in Fig. 4(b), the Jones calculus-simulated POM textures approximately match our experimental observation. However, the existence of the local minimum configuration having the disfavored handedness, which is experimentally observed, is unexpected. It is not straightforward to imagine why the directors twist in an energetically unfavorable handedness and remain stable enough to be observed experimentally, although the boundary conditions afford homochiral configurations.
Our investigation of the energetics reveals that the elastic anisotropy is responsible for the metastability in the chiral system, as in the chiral symmetry breaking of the achiral system. First, the energy landscape assuming the one-constant approximation, i.e., K1 = K2 = K3, shows only one minimum exhibiting the twisted director configuration of the favorable handedness. However, with K1 = K3 = 10 K2, in addition to the global minimum, there exists a local minimum having the opposite handedness. To rationalize the existence of the local minimum, we investigate the energy landscape in detail. As shown in Fig. S4 (ESI†), in the vicinity of the local minimum, the increase in b of γ = a(z/R)b(ρ/R)c results in the increase of the total splay energy within the droplet. But, both total twist and bend energy decrease, leading to a local minimum at a finite b. This trade-off results from the fact that the director configurations should satisfy the boundary conditions imposed by the confinement. Namely, because of the constraints by the boundary conditions, each deformation cannot change independently, but changes in a certain deformation affect the other deformation modes. It is the elastic anisotropy that leads to a local minimum in the trade-off situation. Notably, with K1 = K2 = K3 instead of K1 = K3 = 10K2, i.e., the decrease of total twist and bend energy upon the increase in b dominates over the increase of total splay, giving no local minimum but a monotonic decrease. In summary, a confinement-induced energy trade-off with small K2, or large enough elastic anisotropy in general, makes this local minimum reside even in the energy-landscape region of disfavored handedness.
Conclusions
We study the roles of confinement and elastic anisotropy in the chiral symmetry breaking of achiral LCLCs and the metastability of chiral LCLCs. The broad isotropic–nematic coexistence phase of LCLC enables us to study sessile isotropic droplets immersed in an aligned nematic phase and vice versa. Our director field models reproduce the spiral textures observed by POM and elucidate how their handedness population depends on the chiral dopant concentrations. In particular, energy landscape calculations reveal that the spirals of the disfavored handedness can exist as a local minimum. Regardless of the boundary conditions, i.e., both in I-in-N and N-in-I cases, the large elastic anisotropy K2 ≪ K1 = K3 is responsible for the local minimum.Looking forward, we should be able to utilize our findings and models for further studies of confined chiral chromonic LCs and their applications. We learn that energy-landscape study can be useful when one wants to create and control chiral structures, e.g., homochiral bipolar droplets33 or homochiral defect-free double-twist configurations,55 because meta-stable configurations may lead to the appearance of unwanted handedness and resultant defects between heterochiral domains. Self-assembly is a scalable technique to create chiral meta-materials,69–71 and LCs are popular building blocks for them.72,73 Achieving homochirality optimally – from the choice of materials, dopants, and concentrations to the design of confining geometries and anchoring conditions – may benefit from the energy-landscape approach.
Author contributions
J. M. K. conducted the experiments. J. M. K. and J. J. analyzed the results, performed the numerical calculations, and wrote the manuscript. J. J. supervised the research. All authors discussed the progress of the research and contributed to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Research Foundation of Korea through NRF-2021R1A2C101116312 and 2023 Research Fund (1.230077.01) of Ulsan National Institute of Science and Technology (UNIST).Notes and references
- M. Green and M. Reidy, J. Am. Chem. Soc., 1989, 6452–6454 CrossRef.
- L. Brunsveld, J. A. Vekemans, J. H. Hirschberg, R. P. Sijbesma and E. W. Meijer, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4977–4982 CrossRef CAS PubMed.
- S. Pakhomov, R. P. Hammer, B. K. Mishra and B. N. Thomas, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3040–3042 CrossRef PubMed.
- L. E. Hough, H. T. Jung, D. Krüerke, M. S. Heberling, M. Nakata, C. D. Jones, D. Chen, D. R. Link, J. Zasadzinski, G. Heppke, J. P. Rabe, W. Stocker, E. Körblova, D. M. Walba, M. A. Glaser and N. A. Clark, Science, 2009, 325, 456–460 CrossRef CAS PubMed.
- S. H. Kang, S. Shan, W. L. Noorduin, M. Khan, J. Aizenberg and K. Bertoldi, Adv. Mater., 2013, 25, 3380–3385 CrossRef CAS PubMed.
- S. W. Smith, Toxicol. Sci., 2009, 110, 4–30 CrossRef CAS PubMed.
- N. Petit-Garrido, J. Ignés-Mullol, J. Claret and F. Sagués, Phys. Rev. Lett., 2009, 103, 237802 CrossRef PubMed.
- L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163–5168 CrossRef CAS PubMed.
- E. Pairam, J. Vallamkondu, V. Koning, B. C. Van Zuiden, P. W. Ellis, M. A. Bates, V. Vitelli and A. Fernandez-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9295–9300 CrossRef CAS PubMed.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742–1747 CrossRef CAS PubMed.
- Chirality in Liquid Crystals, ed. H.-S. Kitzerow and C. Bahr, Springer-Verlag, New York, 2001 Search PubMed.
- I. Dierking, Symmetry, 2014, 6, 444–472 CrossRef.
- M. Salamonczyk, N. Vaupotič, D. Pociecha, R. Walker, J. M. D. Storey, C. T. Imrie, C. Wang, C. Zhu and E. Gorecka, Nat. Commun., 2019, 10, 1922 CrossRef PubMed.
- J. P. Abberley, R. Killah, R. Walker, J. M. D. Storey, C. T. Imrie, M. Salamonczyk, C. Zhu, E. Gorecka and D. Pociecha, Nat. Commun., 2018, 9, 228 CrossRef PubMed.
- W. Lewandowski, N. Vaupotič, D. Pociecha, E. Górecka and L. M. Liz-Marzán, Adv. Mater., 2020, 32, 1905591 CrossRef CAS PubMed.
- L. Wang, A. M. Urbas and Q. Li, Adv. Mater., 2020, 32, 1801335 CrossRef CAS PubMed.
- M. M. Majewska, E. Forsyth, D. Pociecha, C. Wang, J. M. D. Storey, C. T. Imrie and E. Gorecka, Chem. Commun., 2022, 58, 5285–5288 RSC.
- Y. Huang, Y. Zhou, C. Doyle and S.-T. Wu, Opt. Express, 2006, 14, 1236 CrossRef CAS PubMed.
- V. Sharma, M. Crne, J. O. Park and M. Srinivasarao, Science, 2009, 325, 449–451 CrossRef CAS PubMed.
- Y. Han, K. Pacheco, C. W. Bastiaansen, D. J. Broer and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 2961–2967 CrossRef CAS PubMed.
- H. Coles and S. Morris, Nat. Photonics, 2010, 4, 676–685 CrossRef CAS.
- J. Beeckman, Opt. Eng., 2011, 50, 081202 CrossRef.
- M. Mitov, Soft Matter, 2017, 13, 4176–4209 RSC.
- S. M. Hare, B. Lunsford-Poe, M. Kim and F. Serra, Materials, 2020, 13, 3761 CrossRef CAS PubMed.
- M. J. Press and A. S. Arrott, Phys. Rev. Lett., 1974, 33, 403–406 CrossRef CAS.
- H.-S. Kitzerow, B. Liu, F. Xu and P. P. Crooker, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 568–575 CrossRef CAS PubMed.
- M. Ambrožič and S. Žumer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5187–5197 CrossRef PubMed.
- M. Ambrožič and S. Žumer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 4153–4160 CrossRef.
- A. Nych, U. Ognysta, I. Muševič, D. Seč, M. Ravnik and S. Žumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062502 CrossRef CAS PubMed.
- Z. S. Davidson, L. Kang, J. Jeong, T. Still, P. J. Collings, T. C. Lubensky and A. G. Yodh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 1–5 CrossRef PubMed.
- K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- J. Jeong, L. Kang, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E1837–E1884 CAS.
- C. Peng and O. D. Lavrentovich, Soft Matter, 2015, 11, 7257–7263 RSC.
- Y. Guo, S. Afghah, J. Xiang, O. D. Lavrentovich, R. L. Selinger and Q. H. Wei, Soft Matter, 2016, 12, 6312–6320 RSC.
- S. H. Ryu and D. K. Yoon, Liq. Cryst., 2016, 43, 1951–1972 CrossRef CAS.
- Y. Zhou, E. Bukusoglu, J. A. Martínez-González, M. Rahimi, T. F. Roberts, R. Zhang, X. Wang, N. L. Abbott and J. J. De Pablo, ACS Nano, 2016, 10, 6484–6490 CrossRef CAS PubMed.
- F. Serra, Liq. Cryst., 2016, 43, 1920–1936 CrossRef CAS.
- A. Javadi, J. Eun and J. Jeong, Soft Matter, 2018, 14, 9005–9011 RSC.
- P. W. Ellis, K. Nayani, J. P. McInerney, D. Z. Rocklin, J. O. Park, M. Srinivasarao, E. A. Matsumoto and A. Fernandez-Nieves, Phys. Rev. Lett., 2018, 121, 247803 CrossRef CAS PubMed.
- H. Lee, V. Sunkara, Y. K. Cho and J. Jeong, Soft Matter, 2019, 15, 6127–6133 RSC.
- V. Palacio-Betancur, J. C. Armas-Pérez, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2023, 19, 6066–6073 RSC.
- I. I. Smalyukh and O. D. Lavrentovich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051703 CrossRef CAS PubMed.
- J. Eun, J. Pollard, S.-J. Kim, T. Machon and J. Jeong, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102926118 CrossRef CAS PubMed.
- G. E. Volovik and O. D. Lavrentovich, Sov. Phys. JETP, 1983, 58, 1159–1166 Search PubMed.
- R. D. Williams, J. Phys. A: Math. Gen., 1986, 19, 3211–3222 CrossRef.
- P. S. DRZAIC, Liq. Cryst., 1999, 26, 623–627 CrossRef CAS.
- J. Ignés-Mullol, G. Poy and P. Ostwald, Phys. Rev. Lett., 2016, 117, 1–5 CrossRef PubMed.
- C. F. Dietrich, P. Rudquist, K. Lorenz and F. Giesselmann, Langmuir, 2017, 33, 5852–5862 CrossRef CAS PubMed.
- D. Seč, T. Porenta, M. Ravnik and S. Žumer, Soft Matter, 2012, 8, 11982–11988 RSC.
- J. Yoshioka, F. Ito and Y. Tabe, Soft Matter, 2016, 12, 2400–2407 RSC.
- S. Li, X. Zhou, J. Zhu, K. Du, Y. Du and H. Gao, Phys. Rev. E, 2023, 107, 1–7 Search PubMed.
- P. J. Ackerman and I. I. Smalyukh, Phys. Rev. E, 2016, 93, 052702 CrossRef PubMed.
- J. Pollard, G. Posnjak, S. Čopar, I. Muševič and G. P. Alexander, Phys. Rev. X, 2019, 9, 021004 CAS.
- E. P. Raynes, Liq. Cryst., 2006, 33, 1215–1218 CrossRef CAS.
- J. Eun, S. J. Kim and J. Jeong, Phys. Rev. E, 2019, 100, 12702 CrossRef CAS PubMed.
- C. F. Dietrich, P. Rudquist, P. J. Collings and F. Giesselmann, Langmuir, 2021, 37, 2749–2758 CrossRef CAS PubMed.
- V. R. Horowitz, L. A. Janowitz, A. L. Modic, P. A. Heiney and P. J. Collings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 1–10 CrossRef PubMed.
- J. Eun, J. Cheon, S.-J. Kim, T. J. Shin and J. Jeong, J. Phys. Chem. B, 2020, 124, 9246–9254 CrossRef CAS PubMed.
- J. Jeong, G. Han, A. T. Johnson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Langmuir, 2014, 30, 2914–2920 CrossRef CAS PubMed.
- G. Y. Lee, H. Ko, H. W. Jung, S. J. Ye, M. H. Kim and J. C. Pyun, Procedia Eng., 2011, 25, 321–324 CrossRef CAS.
- S. Zhou, Y. A. Nastishin, M. M. Omelchenko, L. Tortora, V. G. Nazarenko, O. P. Boiko, T. Ostapenko, T. Hu, C. C. Almasan, S. N. Sprunt, J. T. Gleeson and O. D. Lavrentovich, Phys. Rev. Lett., 2012, 109, 1–5 Search PubMed.
- S. Zhou, S. V. Shiyanovskii, H.-S. Park and O. D. Lavrentovich, Nat. Commun., 2017, 8, 14974 CrossRef PubMed.
- H. Lee and M. M. Labes, Mol. Cryst. Liq. Cryst., 1982, 84, 137–157 CrossRef CAS.
- C. K. McGinn, L. I. Laderman, N. Zimmermann, H. S. Kitzerow and P. J. Collings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 1–9 CrossRef PubMed.
- T. Ogolla, S. B. Nashed and P. J. Collings, Liq. Cryst., 2017, 44, 1968–1978 CAS.
- T. Shirai, M. Shuai, K. Nakamura, A. Yamaguchi, Y. Naka, T. Sasaki, N. A. Clark and K. V. Le, Soft Matter, 2018, 14, 1511–1516 RSC.
- T. Ogolla, R. S. Paley and P. J. Collings, Soft Matter, 2019, 15, 109–115 RSC.
- V. A. Uzunova and V. M. Pergamenshchik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031702 CrossRef CAS PubMed.
- J. B. Pendry, Science, 2004, 306, 1353–1355 CrossRef CAS PubMed.
- C. M. Soukoulis and M. Wegener, Nat. Photonics, 2011, 5, 523–530 CrossRef CAS.
- P. F. Damasceno, A. S. Karas, B. A. Schultz, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2015, 115, 158303 CrossRef PubMed.
- G. Park, S. čopar, A. Suh, M. Yang, U. Tkalec and D. K. Yoon, ACS Cent. Sci., 2020, 6, 1964–1970 CrossRef CAS PubMed.
- H. K. Bisoyi and Q. Li, Chem. Rev., 2021, 122, 4887–4926 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01283b |
| This journal is © The Royal Society of Chemistry 2024 |