Interfacial rheology of linearly growing polyelectrolyte multilayers at the water–air interface: from liquid to solid viscoelasticity

Abstract

Despite the long history of investigations of polyelectrolyte multilayer formation on solid or liquid surfaces, important questions remain open concerning the construction of the first set of layers. These are generally deposited on a first anchoring layer of different chemistry, influencing their construction and properties. We propose here an in-depth investigation of the formation of NaPSS/PAH multilayers at the air/water interface in the absence of a chemically different anchoring layer, profiting from the surface activity of NaPSS. To analyse the mechanical properties of the different layers, we combine recently established analysis techniques of an inflating/deflating bubble exploiting simultaneous shape and pressure measurement: bubble shape elastometry, general stress decomposition and capillary meniscus dynanometry. We complement these measurements by interfacial shear rheology. The obtained results allow us to confirm, first of all, the strength of the aforementioned techniques to characterize complex interfaces with non-linear viscoelastic properties. Furthermore, their sensitivity allows us to show that the multilayer properties are highly sensitive to the temporal and mechanical conditions under which they are constructed and manipulated. We nevertheless identify a robust trend showing a clear transition from a liquid-like viscoelastic membrane to a solid-like viscoelastic membrane after the deposition of 5 layers. We interpret this as the number of layers required to create a fully connected multilayer, which is consistent with previous results obtained on solid or liquid interfaces.

---

1 Introduction

Polyelectrolyte multilayers are created by the successive deposition of oppositely charged polyelectrolytes on a surface.¹ The properties of multilayers deposited on solid surfaces have been explored in depth and they are starting to find their way into numerous applications.^2–7 Multilayer investigations at liquid–liquid interfaces are also on the rise, due to their interest for encapsulation applications^3,8,9 and the possibility to access more directly their mechanical properties than on solid substrates. The building and the properties of polyelectrolyte multilayers at the air/water interface has also stimulated a wide fundamental interest.^10–20

Studies on solid^21–23 or liquid^14,18 interfaces have shown a significant difference in structural (and hence mechanical) properties of the first 4–6 layers and the remaining ones, raising many questions concerning the detailed mechanisms of the build-up of these first layers. However, most available experimental investigations have been conducted with a first anchoring layer, which allows the multilayers to adhere to the surface. On solid surfaces, this first layer is typically poly(ethyleneimine) (PEI) while, on liquid surfaces, it is commonly an adsorption layer of ionic surfactants. The presence of this layer does not only influence the buildup of the following layers,^24–26 but also the mechanical properties of the multilayer membrane. This is particularly true for liquid interfaces,^14,16 where the mechanical stresses arising from the interfacial tension (and the adsorbed surfactants) are of the same order of magnitude as those arising from the elastic response of the multilayers for a small number of layers. We therefore investigate here the viscoelastic properties of multilayers constructed at the air/water interface without the presence of an attachment layer.

We use alternating layers of anionic sodium polystyrene sulfonate (NaPSS) and cationic poly(allylamine) hydrochloride (PAH), profiting from the fact that the NaPSS is surface active and therefore spontaneously adsorbs to the gas/liquid interface. We investigate the properties of this first layer and how it influences the adsorption and resulting mechanical properties of the following layers. The different layers are deposited on the interface by replacing in an alternating manner the liquid phase containing NaPSS or PAH, each alternation being separated by a washing step with brine. We combine dilational and shear deformations of the interface, in order to obtain a complete characterization of its tensiometric and viscoelastic properties.

The dilational investigations are performed combining shape analysis and pressure measurements²⁷ of a bubble held by a needle in solution during sinusoidal or linear volume changes. The dilational response of the interface being rapidly non-linear, we apply for the first time the method of general stress decomposition (GSD)^28–30 to polyelectrolyte multilayers. We show that this provides a clean separation of the linear and non-linear visco-elastic response, identifying GSD as a very promising analysis tool for multilayer investigation at liquid interfaces. We complement these results with an analysis of the shapes of deflated bubbles by capillary meniscus dynanometry (CMD)^31,32 and by a fit with a neo-Hookean constitutive shape equation.³³ Both approaches take into account the fact that the bubble is not perfectly spherical and the deformation of its interface constrained locally by the capillary. This creates non-isotropic stresses and shape changes, which provide additional information on the response of the surface to local shear and bending.

We complement these measurements with pure shear deformations of multilayers deposited at the air/water interface in a dedicated trough of an interfacial shear rheometer using the same overall deposition protocol as for the bubbles. To the best of our knowledge, this is the first time that the evolution of the pure shear response of polyelectrolyte multilayers (with time and number of layers) is investigated up to 6 layers.

This article is organised as follows. In Section 2 we introduce the materials and methods used. Since the methods are complex, we summarise here only the main concepts and refer the reader to the relevant (and recent) literature. In Section 3.1 we present the key results obtained for the dilational experiments on bubbles, starting with a detailed analysis of the first NaPSS adsorption layer. In Section 3.2 we discuss the shear response of the different layers paying particular attention to the influence of the deposition and manipulation protocols on the mechanical properties of the multilayers. In Section 4 we combine the different results to draw what we consider to become a coherent picture of the multilayer properties.

2 Materials and methods

2.1 Samples

Poly(sodium styrene sulfonate) (NaPSS, M_w = 77.8 kg mol⁻¹, polydispersity index = 1.9) was obtained from Acros Organic, poly(allylamine chloride) (PAH, M_w = 12.5 kg mol⁻¹) from Sigma Aldrich, NaCl from Roth. The sulfonation degree of NaPSS was ca. 75% as measured by elemental analysis and by NMR. NaCl was purified by oven pyrolysis at 600 °C for 4 h.³⁴ All provided information has been obtained by in-house characterisation. Details are provided in the ESI† Sections S1 and S2. Milli-Q water from an EMD Milli-Q Direct 8 (Merck Millipore) device was used to prepare the solutions. Each polymer in solid form was poured together with the salt ([NaCl] = 0.15 M) and the appropriate quantity of water into a volumetric flask. After placing an Argon cap on the flask, the solution was stirred at 360 rpm for 12 hours at room temperature. After solubilising the salt and polymers, the volume was corrected to the gauge by adding water, the pH lowered to pH = 4.00 ± 0.01 by adding HCl, and the solutions used for up to 15 days. For most experiments, we worked at pH = 4 since this increases the reproducibility of the experiments because no ageing effect induced by water carbonation is observed at this pH value.

2.2 Cleaning protocols

All the glassware used to prepare solutions as well as the glass cuvette of the tensiometer are cleaned thoroughly before use by immersing them successively in: Hellmanex^TM (5% v/v), HCl 0.1 M, NaOH 0.1 M, acetone, ethanol, during 15 min with sonication (30 kHz). Between each of these steps, glassware is thoroughly rinsed during 3 min with deionized water (except when passing from acetone to ethanol). Final drying is performed with N₂. This protocol allows us to measure a constant value for the surface tension of MilliQ water for several days, proving the absence of a measurable amount of impurities.

2.3 Tensiometry and dilatometry on rising bubbles

We use a commercial tensiometer (Tracker^TM, Teclis, France) to perform tensiometry and dilational interfacial rheology on a rising bubble.^32,35 The device is equipped with two additional features (Scheme S3 in ESI†). The first one is a gas pressure sensor that allows us to measure the inner bubble pressure relatively to the atmospheric pressure. Using the calibration procedure described in ESI† (Sections S3 and S4), we can thus track ΔP, the pressure difference across the interface at the apex of the rising bubble. The second feature is a two-channel peristaltic pump that allows us to exchange the surrounding liquid phase while maintaining the air bubble at the top of the needle and a constant liquid level in the cuvette. Tests performed by colorimetry showed that the initial volume of liquid (25 cm³) is fully replaced by circulating 200 cm³ of new solution and this is achieved within ca. 17 min with our pump. Except for the initial NaPSS layer adsorption, this is the time allocated for the adsorption of a layer, i.e., as soon as the 200 cm³ of new polymer solution have been circulated, we started the replacement by saline solution. Also, except for the initial NaPSS layer adsorption, all the other measurements are performed in brine solution (0.15 M NaCl) after the replacement of polymer solution. Thus the deposition of polymer layers and the measurement followed the same process: (1) replacement of the polymer solution by injection of 200 cm³ of saline solution, (2) measurement, (3) replacement of the saline solution by 200 cm³ of the next polymer solution, and again in step (1). The peristaltic pump is switched off during the two types of bubble deformation measurements.

Owing to our specific measurement of the effective surface tension through pressure values (see below) and not through Axisymmetric Drop Shape Analysis (ADSA), we kept a small volume for our bubbles (≈7.5 mm³), which were not much deformed by gravity (Bond number ≈ 0.2). An additional gain of this approach is to increase the stability of bubbles submitted to successive exchanges of the surrounding liquid.

Continuous deflation/inflation tests were conducted by imposing a final volume at a fixed deflating/inflating rate (0.05 mm³ s⁻¹). The corresponding area variation can be roughly described by a part of a sine wave with frequency equal to 0.004 Hz. The maximum deflation value in this type of experiments was λ_A = A/A₀ = 0.85, with A and A₀ the surface area value in the deformed and the reference state, respectively. No inflation was performed starting from the undeformed reference state of the bubble to avoid tearing the polymer skin at the bubble surface.

Sinusoidal deformation experiments were done by imposing an area variation A(t) = A₀(1 + λ₀sin(2πft)) with amplitude λ₀ = 0.05 = 5% at a frequency f = 0.02 Hz. We performed also tests at other amplitude or frequency values but they were often polluted by unsatisfying sinus wave quality of the area deformation. In fact, the PID parameters of the instrument had to be adjusted systematically to take into account the increasing elasticity of the bubble skin. For this reason, we report only results obtained with fixed amplitude and frequency values. Usually ten oscillations were applied to the bubble after each polyelectrolyte layer deposition.

All experiments were performed within one working day. Our procedure to take into account possible small and random pressure shifts during experiments is described in Section S5 of the ESI.† To avoid the formation of capillary bridges inside the needle, we found it useful to apply a hydrophobic treatment to this part.³⁶ This was done by an electrolytic treatment of the needle extremity, connected to a sacrificial Cu anode in a 1 M NaOH solution during 5 min under a 300 rpm stirring. Then the protocol developed by Larmour et al.³⁷ was used. The needle was held with a syringe to allow the aspiration of the different solutions inside the needle. The needle extremity was then polished with sand paper (Al₂O₃ – 2400 RS France) to limit the effect of the hydrophobic treatment on the profile of the bubble.³⁸

2.4 Oscillatory shear rheology of planar interfaces

For the interfacial shear rheology, we used a TA DHR3 rheometer (TA Instruments) equipped with a double-wall ring (DWR) geometry³⁹ and a subphase exchange cell.⁴⁰ In this setup a circular ring with diamond-shape cross-section is located at the liquid–air interface and moved relatively to the vertical inner and outer walls of the cell. The shear strain amplitude is then defined through the ratio of the circular displacement of the ring to the distance between the ring and the two walls. We refer the interested reader to the original paper³⁹ for the precise calculations of the equivalent shear geometry, which are similar to those performed for the double-wall concentric cylinders geometry used for shear rheology in the bulk. The oscillatory shear strain is then defined as λ(t) = λ₀sin(2πft).

We improved the efficiency of the subphase exchange by adding at the exit of each side inlet of the cell a sintered-glass filter, which improved the mixing of the liquids in the cell and reduced the hydrodynamic stresses on the interface. Tests with colored solutions showed that the subphase could be exchanged by circulating 240 cm³ of the new solution through the volume (≈17.8 cm³) of the cell. This was achieved with the help of a syringe driver with two channels (Pump 33 DDS – Harvard Apparatus). The exchange was performed with a flow rate of 6 cm³ min⁻¹ following the conclusions reached by the designers of the exchange cell.⁴⁰ Special care was taken to not curb the interface during this operation. At the start up of the exchange, a Labview script imposed a progressive increase of the flow rate to its nominal value over 60 seconds. By looking at the reflected image of a LED lamp, the planarity of the interface could be checked. Slight deformations were immediately corrected by injecting/removing some liquid with the help of a small syringe connected to one of the outlets of the cell. A small cup filled with water placed on top of the exchange cell and a lid covering the whole geometry preserved the humidity of the environment above the interface.

2.5 Data analysis of dilatometry

For data analysis, we took advantage of much recent progress in the field. The main difficulties come from the difference between liquid and solid surface elasticities, particularly because there is a constraint of zero deformation of the bubble at the needle boundary. The transition to solid elasticity then gives rise to deviatoric anisotropic stresses, which can no longer be taken into account as an effective isotropic and homogeneous surface tension γ_eff obtained by solving the usual Young–Laplace equation.^{17,27,29–33,41–44}

2.5.1 Pressure-deformation relationship in small bubbles. Ginot et al.²⁷ have shown recently that the transition between the two regimes of elasticity can be taken smoothly into account when spherical bubbles are weakly deformed and the value of the interfacial pressure drop ΔP is known. In particular, they showed that an effective interfacial tension can always be defined bywhere R is the radius of a perfectly spherical bubble. For a bubble held by a capillary, they computed the errors committed with this approximation as a function of the ratio of the needle diameter to the bubble radius R, of the deformation, and of the ratio of the elastic modulus to surface tension. In our experimental conditions, the errors remain below a few per cent when using this approximation. For our small and weakly deformed bubbles, we approximate the value of R in eqn (1) by the radius of curvature at the apex.

In the limit of small deformations, the constitutive equation reduces, whatever the liquid or solid state of the interface,²⁷ to

γ_eff(λ_A) − γ₀ = K(λ_A − 1), (2)

where γ₀ is the value of the effective surface tension in the absence of deformation and λ_A = A/A₀ is the area variation.²⁷eqn (2) defines K, which is the so-called dilational Gibbs modulus in the case of a liquid interface or the elastic dilatational interfacial modulus in the case of a solid elastic skin. We emphasize that γ_eff is obtained through eqn (2) and not by fitting the Young–Laplace equation to the bubble profile.

Therefore, in principle, we can obtain the values of K as a function of the number of polyelectrolyte layers from this simple result. However, until now, no viscous dissipative effects, which are present in the deformation of any complex viscoelastic interface, whether it is liquid or solid, have been considered. Eqn (2) predicts that the Lissajous representation of γ_eff − γ₀ as a function of λ_A(t) is a straight line, while dilatational rheology experiments yield notoriously deformed cycles that depart strongly from the ellipses expected for viscoelastic systems deformed in the linear regime.⁴⁵

2.5.2 General stress decomposition (GSD). Recently, Noskov et al.²⁹ and de Groot et al.³⁰ proposed to apply the method of General Stress Decomposition (GSD), developed by Yu et al.²⁸ in the field of bulk rheology, to the interpretation of dilatational rheology experiments. The principle is to decompose a general complex stress response σ(t) to a sinusoïdal strain input λ(t) = λ₀sin(ωt) as a sum of four components

σ(t) = σ(x,y) = τ₁(x) + τ₂(y) + τ₃(x,y) + τ₄(y), (3)

withwhere x(t) = sin(ωt) and y(t) = cos(ωt). This decomposition can be readily done by exploiting the symmetries of the τ_i's upon changes of x and y into −x and −y.²⁸ Then the Fourier coefficients of σ(t) can be obtained directly by exploiting the orthogonal properties of trigonometric functions. In particular, τ₁ and τ₂ describe respectively the purely elastic and dissipative response to the interface deformation and the linear elastic and viscous dilatational modulus, K′ and K′′, are given by^28–30

We have applied this approach to σ(t) = γ_eff(t) − γ₀. In our case of small deformations, all the non-linear behaviour of the Lissajous curves is due to the terms τ₃ and τ₄, which reflect the non-linearity of the equation of state of the interface, as analysed by de Groot et al.³⁰ On the contrary, τ₁ and τ₂ remain in the linear regime, i.e., the coefficients b_2k+1 and a_2k+1 are negligible compared to, resp., b₁ and a₁. Thus, we can apply eqn (2) to the purely elastic part of the stress, τ₁, and identify K and K′.

2.5.3 Capillary meniscus dynamometry (CMD). An other item in our toolbox is the capillary meniscus dynamometry (CMD) introduced by Danov et al.³¹ By writing the detailed local balance of stresses along the tangential and normal directions to the interface and using the measured pressure value, it is possible to reconstruct the profiles of the meridional and parallel components of the stress, resp., σ_s and σ_ϕ, from the digitized profile of the interface. Here we adopt the notations and parametrization proposed by Danov et al.:³¹ the interface is described by cylindrical coordinates (r, z, ϕ) where z is the altitude from the bubble apex located at z = 0 and r(z) the corresponding radius of the bubble at this altitude (Fig. 1). When the bubble shape is axisymmetric it does not depend on angle ϕ. Calculating the local curvatures along the interface is more convenient by using the curvilinear coordinate s(z). Solving the generalised Young–Laplace equation requires numerical derivation and Danov et al. proposed to parametrise the left or right profile of the bubble with a set of local parabolic interpolations to decrease the noise introduced by this step.³¹ However Nagel et al.³² argued that a smoother parametrization would be obtained by a global interpolation of the whole profile through a truncated series of Chebyshev polynomials of the first kind but setting z = 0 at the capillary boundary. Here we mixed the two approaches, setting z = 0 at the bubble apex and using a parabolic interpolation in this region, while using a series of Chebyshev polynomials away from the apex. With this choice we combine the advantages of each method and avoid the hypothesis of conserved axisymmetry made by Nagel et al. Indeed, for some of our experimental conditions, we found that axisymmetry was not conserved during the deflation of bubbles. The truncation of the series of Chebychev polynomials was fixed by their coefficients reaching values close to the experimental resolution (≈1 μm). This occurred typically after order N = 12. The subpixel resolution was achieved by scaling the dimensions of the images by a factor 5 while using the bilinear interpolation available in Fiji (ImageJ) software.^46,47 The CMD approach was used to check the liquid or solid nature of our multilayer skin. Indeed, the results by Ginot et al.²⁷ showed that the value of the elastic modulus is not a criterion to ascertain the transition from one state to the other. The hallmark of this transition is instead the appearance of inhomogenous and anisotropic stresses, σ_s(z) ≠ σ_ϕ(z) ≠ cst, which can be unveiled by the CMD analysis.³¹

Fig. 1 Definition of the cylindrical coordinates used to parametrize the bubble shape. The stresses σ_s and σ_ϕ along the two principal directions are also shown.

2.5.4 Fitting a constitutive equation to the shape of deflated bubbles. Finally, by using the shape equations of pendant elastic membranes, as discussed in ref. 33 and 42 it is possible to fit an elastic constitutive law to the shape of a deflated bubble. For this, we use a surface energy density accurate to second order in the stretch ratios λ_s and λ_ϕ. This produces a constitutive law in terms of the surface stress components σ_s, σ_ϕ⁴²where the two dimensional Young modulus Y_2D and two dimensional Poisson ratio ν_2D appear as material parameters. A similar equation holds for σ_ϕ by interverting indices s and ϕ in eqn (6). Here λ_s = ds/ds₀ and λ_ϕ = r/r₀ are the strains in the principal directions, with the index 0 referring to the values in the undeformed state. The shapes are optimized with a custom software derived from OpenCapsule.³³

This approach is interesting since it provides values for both the dilatational elastic modulus K′ = Y_2D/2/(1 − ν_2D) and the shear elastic modulus G′ = Y_2D/2/(1 + ν_2D). It allows for a smooth description of the transition from the liquid to the solid state. However it does not include dissipation (viscous) terms and can only provide estimations for K′ and G′ if the bubble shapes are not at equilibrium.

3 Results

3.1 Dilatational rheology on rising bubbles

3.1.1 Adsorption of the first NaPSS layer. Dynamic surface tension measurements (Fig. 2) show that our highly charged NaPSS display an affinity for the water/air interface but the formation of an interfacial layer detected by the surface tension value takes very long times, about 1000 s for an NaPSS concentration of 4.8 mM. Decreasing this concentration by a factor 10 increases this time by about the same factor. This confirms the results of previous pioneering studies:^34,48 although the diffusion time of the chains to the interface is much shorter, the progressive accumulation of charged species at the interface creates an electrostatic kinetic barrier that slows down further adsorption of chains. Increasing the ionic strength of the solution weakens this barrier and favours faster surface tension decay. Higher polymer concentration facilitates the formation of the interfacial layer, mainly by increasing the rate of trials towards the interface. For this particular investigation used to settle our experimental conditions before the pressure measurement was operational, the pH value was not set at 4 to better compare with previous work, and the surface tension γ was directly measured by classical axisymmetric drop shape analysis (ADSA) with the software provided with the tensiometer. For practical reasons, we will keep the higher polymer concentration to form the first layer. The next layers will be formed with a polyelectrolyte concentration of 0.48 mM to spare the amount of polymer lost during phase exchange.

Fig. 2 Effect of NaPSS monomer concentration on the dynamic surface tension during the adsorption of the first NaPSS layer: the ionic strength is fixed by the added salt concentration, [NaCl] = 0.15 M.

Other noticeable features mentioned by Théodoly et al.³⁴ include the lack of reproducibility and the sensitivity to deformation history when adsorption of NaPSS is studied at low ionic strength, low polymer concentration or high charge density. This has consequences also for dilatational rheology measured during the adsorption of this first layer (Fig. 3).

Fig. 3 Dilatometry experiments during the adsorption of the first NaPSS layer, the surface area value being periodically modulated by a sine wave with amplitude λ₀ = 0.05 = 5% and frequency f = 0.02 Hz: (a) zoom on the first 1500 s of the experiment in (b), where we plot the time dependence of effective surface tension (red) and bubble surface area (black). (c) Time dependence of the elastic and viscous dilatational moduli K′ (closed symbols) and K′′ (open symbols) for three experiments. Intervals between groups of points correspond to temporal sequences with no strain oscillations applied to the bubble, the red points correspond to the experiment in (a) and (b) ([NaPSS] = 4.8 mM).

Fig. 3a and b shows a typical elastometry experiment measuring the increase of the elastic and viscous dilatational moduli during the relaxation of the effective surface tension. Sinusoidal surface area deformations are applied to the bubble at regular intervals with rest times in between. The progressive increase of γ_eff modulations in response to the surface area deformation is clearly visible, superposed on the regular decay of the average γ_eff. We use eqn (1) and (2) together with the GSD approach (eqn (4) and (5)) to calculate the values of the elastic and viscous moduli in Fig. 3c, which shows their increase in time for three repetitions of this experiment. It illustrates the great variability in the interfacial elastic properties of the first NaPSS layer, even when the preparation and the rheological history are identical.

At this point, it is interesting to discuss the error bars in our results. The main source of experimental error is here the absolute value of ΔP. We can estimate the consequences on the values of the moduli by recalculating them with an arbitrary ±10 Pa shift of the measured ΔP value. For our small bubbles, this yields errors about ±5 mN m⁻¹ on γ_eff values, ±2 mN m⁻¹ (resp. ±4 mN m⁻¹) on K′ values between 10 and 100 mN m⁻¹ (resp. larger than 100 mN m⁻¹). On the other hand, K′′ values are totally insensitive to errors on ΔP and are good markers of the actual difference between samples. Therefore we can infer from the data in Fig. 3c that the large variability in the kinetics comes from the samples and not from the measurements.

In the following, we will always deposit the following polyelectrolyte layers with a shorter relaxation time of the first NaPSS layer, without waiting for equilibrium values of γ_eff, K′ and K′′.

3.1.2 Building the multilayers skin. Fig. 4a gives a typical example of the progressive deformation of the Lissajous curves γ_eff(λ_A) as oppositely charged polyelectrolytes layers are added. Strong non-linear effects are present since the Lissajous curves are never ellipses, except, in the example shown, for the first layer, which has relaxed during 120 min before the replacement of NaPSS solution by the brine and the measurement.

Fig. 4 Typical evolution of Lissajous curves (obtained after sinusoidal variation of the surface area with amplitude λ₀ = 0.05 = 5% and frequency f = 0.02 Hz) as layers of oppositely charged polyelectrolytes are added: (a) total effective surface tension γ_eff, (b)–(e) components τ_i. The meaning of the symbols remains the same for all plots.

Fig. 4(b–e) shows the corresponding curves for the components τ_i determined by the GSD method for the same data. The complex deformation of the Lissajous curves in the latter figure results from a regular growth of the τ_i components. In particular, τ₁, which reflects the elastic behaviour of the skin is a straight line, within experimental accuracy, with the slope increasing regularly as layers are added. The dissipative component τ₂ is an ellipse with increasing small axis. It would be a straight line with increasing slope if plotted as a function of deformation rate [small lambda, Greek, dot above]_A (not shown). Therefore the components τ₁ and τ₂ are here characteristic of a linear response. The non-linear effects visible in Fig. 4a are entirely due to the effects of growing τ₃ and τ₄ and not due to a too large strain amplitude.

Fig. 5 shows the increase of elastic and viscous interfacial moduli, obtained from τ₁ and τ₂, respectively, viaeqn (5) as the number of layers increases for four different experiments, with some differences in the experimental protocol regarding the duration of the first layer adsorption step and the number and frequency of oscillations applied to the bubble during the measurements.

Fig. 5 Increase of the elastic and viscous dilatational moduli K′ (closed symbols) and K′′ (open symbols) with the number of polyelectrolyte layers for four experiments using sinusoidal deformation of the surface area with amplitude λ₀ = 0.05 = 5% and frequency f = 0.02 Hz. Numbers in the legend correspond to the duration of the first NaPSS layer adsorption step and to the number of oscillations applied to the bubble for the measurement. Lines are guides for the eye.

Two experiments followed the same protocol (red and blue points): the first NaPSS layer was allowed to relax during 120 min in contact with the polyelectrolyte solution before the latter was replaced by saline solution and the measurement began with 10 oscillations with frequency f = 0.02 Hz and strain amplitude λ₀ = 0.05. These parameters remained the same for all the measurements.

The two other samples had a different duration for the adsorption of the first NaPSS layer, 5 min (black points) and 20 min (green points). One of them (black points) had the same rheological history than the first two (red and blue points). On the other hand, the last sample (green point) had many more deformations than the other three: a deflation to λ_A = 0.85 followed by an inflation back to the original size to perform the CMD analysis plus 15 oscillations of three different frequencies (f = 0.02, 0.067 and 0.2 Hz, λ₀ = 0.05).

For the four first layers, the trend is the same for these four examples, with a regular increase in the moduli, within possible experimental errors. It seems that the duration of the adsorption of the first layer remains correlated with an increase of its moduli, which would be consistent with the kinetics shown in Fig. 3, but this observation has to be pondered by the differences between the two samples with identical preparation and test protocols (blue and red points in Fig. 5), which reminds us of the variability observed in the kinetics of Fig. 3. The sample that was much more mechanically stressed (green points) differs markedly from the other ones, with no jump of its moduli when the fifth layer is added.

Therefore, in view of the possible perturbations of the interface by the larger area variation used in the CMD analysis, the bubbles were not systematically submitted to the continuous deflation/inflation step.

In Fig. 6 we plot the results of the two principal stresses σ_s and σ_ϕ along the symmetry z-axis of the bubbble for four (Fig. 6a–c) and five (Fig. 6d–f) layers, each time for the different area deformations λ_A. For the first four layers, the two principal stresses are identical and constant, within experimental errors, all over the interface with the exception of the close vicinity to the capillary tip for z > 2 mm. As shown in the Section S6 of the ESI,† this deviation is mainly due to the hydrophobic treatment used to prevent the formation of capillary bridges inside the needle. Thus, the interface is still in an isotropic liquid state up to the fourth layer.

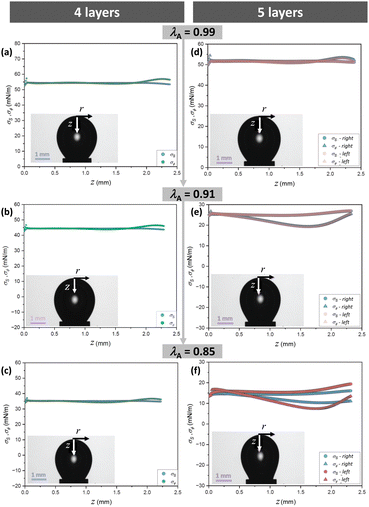Fig. 6 Profiles of the principal stresses σ_s et σ_ϕ for different values of the area deformation λ_A obtained after continuous deflation at a rate of 0.05 mm³ s⁻¹ after the adsorption of four layers (left) and after the adsorption of the fifth polyelectrolyte layer (right). Only the left profiles are plotted in the left column since the axial symmetry is preserved for this number of layers. For this sample, the adsorption time of the first NaPSS layer was 20 min (green points in Fig. 5) and the deflation/inflation experiment was done before the sinusoidal deformations.

There is a qualitative change after the adsorption of the fifth layer (Fig. 6d and e). In the undeformed reference state, the stress appears still uniform and isotropic (σ_s(z) = σ_ϕ(z), Fig. 6d). However, as the deflation proceeds, the stresses along the two principal directions become progressively different, σ_s(z) ≠ σ_ϕ(z) ≠ cst (Fig. 6e). Finally, for a large enough deformation, the axial symmetry is lost (Fig. 6f). To show this, we plot the principal stresses of the left and right side of the bubble separately. In this state, the CMD analysis fails and the values of the stresses should not be considered as quantitative. All these features indicate that the adsorbed layers behave as a viscoelastic solid once the fifth layer has been added.

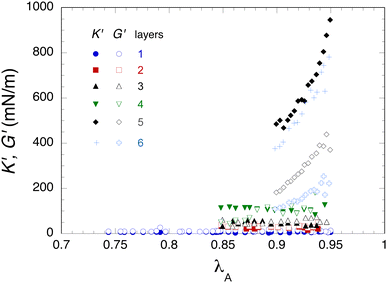
Finally we use the approach described in Section 2.5.4 to obtain a simultaneous estimation of the dilatational and shear moduli on the same bubble. Fig. 7 shows the obtained values of K′ and G′ as a function of the surface deformation. For the first four layers, they do not depend on the deformation within experimental accuracy and increase regularly with the number of layers. On the other hand, for the 5th and 6th layers, they depend on the deformation. The most likely explanation for this behaviour is the absence of any viscoelasticity effects in our constitutive eqn (6), which is a rough approximation for our soft polymer skins, especially for the 5th and 6th layer with larger values of K′′ (Fig. 5) and G′′ (see below). For a bilayer system, Pepicelli et al.⁴⁴ adopted a similar approach with a Neo-Hookean constitutive equation and avoided this issue by using small deflation steps and letting the bubble shape relax between steps. This was not possible in our case due to our much larger number of layers and the very long duration of our experiments. Therefore, we consider K′ and G′ values for the 5th and 6 layers as mere indicators of a rather large jump in the moduli values and of a qualitative change in the capacity of eqn (6) to describe the bubble shapes, when the number of layers becomes larger than four. Fig. 8 shows the average values of K′ and G′ calculated from the data in Fig. 7. For comparison, it shows also the K′ values measured in the oscillatory dilatational experiment on the same bubble (green points in Fig. 5). These K′ values compare fairly well up to the 4th layer, while clearly the K′ values measured in the deflation experiment are much larger than those measured under oscillatory sollicitation for the 5th and 6th layers. Lastly, considering only the moduli values for the deflation experiment, we notice also that G′ values are slightly higher than K′ ones up to the 4th layer, while it is the reverse for the 5th and 6th layers.

Fig. 7 Values of the dilatational (K′) and shear (G′) elastic moduli, obtained by using eqn (6) as described in Section 2.5.4 with a bubble progressively deflated at a rate of 0.05 mm³ s⁻¹, as a function of deflation ratio λ_A, for increasing number of deposited layers. Values for 0.95 <λ_A < 1 are strongly fluctuating because of a lack of numerical resolution for these small deformations of the bubble and are not shown.

Fig. 8 Average values of the dilatational (K′) and shear (G′) elastic moduli as a function of number of deposited layers. Averages are calculated from all the data shown in Fig. 7 and errors bars correspond to standard deviation. The green squares correspond to K′ values measured on the same bubble by oscillatory dilatation (Fig. 5).

3.2 Shear rheology of planar interfaces

Shear rheology on the first NaPSS layer after 120 min of relaxation yielded noisy signals with shear storage and loss moduli, resp. noted G′ and G′′, in the range of a few tens of nN m⁻¹ (ESI,† S8). Moreover the raw phase of the response was close to 180°, meaning that this signal is dominated by the inertia of the apparatus. In these conditions, the measurement is not reliable. In the following, we will characterise the first bilayer formation and then investigate how the adsorption of additional layers modifies the mechanical properties of the interface. In this last investigation, measurements are performed only for even numbers of adsorbed layers to shorten the duration of the total experiment.

3.2.1 First bilayer. Due to the lengthy preparation of each system, typical experiments combine several measurements in a complex shear history to gather a large amount of information on the same system. As depicted in Fig. 9, we begin with a time sweep (I, f = 0.01 Hz, amplitude 0.08%, 40 000 s) to observe how the system is equilibrating after the replacement of the PAH solution by the saline solution. Then we set a rest of 10 000 s (1) before doing a second shorter time sweep (II, 10 000 s) keeping the other experimental parameters as in the first one. Then follow a new rest time (2), an amplitude sweep from 0.01 to 5% (III), a rest time (3), an amplitude sweep from 5 to 0.01% (IV), a rest time (4) and a final time sweep (V).

Fig. 9 Temporal evolution of G′ (closed symbols) and G′′ (open symbols) measured on a NaPSS/PAH bilayer during a complex shear history including three time sweeps (I, II, V: f = 0.01 Hz, λ₀ = 0.08%, dots) and two amplitude sweeps (III, IV: f = 0.01 Hz, 0.01% < λ₀ < 5%, diamonds) separated by rest intervals (shaded time intervals 1, 2, 3 and 4). The experiment started 120 min after the exchange of PAH by saline solution.

During the first time sweep (I), both G′ and G′′ first increase, then show a strong maximum after about 5000 s before decreasing exponentially. This shows that the measurement is affecting strongly the bilayer. The existence of a maximum indicates that two competing processes are at work, both likely sensitive to the periodic deformation of the interface. Allowing the system to rest (1) restores higher values to the moduli, which are promptly reduced in the second time sweep (II). The second rest time (2) has the same effect as the first one and the moduli recover higher values before the first amplitude sweep with increasing amplitudes, where strong non-linear effects are observed (III). A possible recovery of the mechanical properties in the next rest (3) cannot be observed since the following amplitude sweep (IV) starts with a large amplitude in the non-linear regime. The final rest (4) does not promote any recovery measurable at low amplitude and the final time sweep (V) shows that the system is still sensitive to small oscillations at low frequency: even after 30 hours no steady values are measured for G′ and G′′.

In this experiment we set the maximal amplitude of the oscillations at 5% because it corresponds to the amplitude used for the dilatometry experiments. In the latter, the response of the system is still in the limits of the linear regime, while in the shear experiments, this value is far beyond these limits. Fig. 10 displays, as a function of the strain amplitude λ₀, the values of G′ and G′′ measured during the amplitude sweeps (III, IV) of the experiment shown in Fig. 9. For the sheared NaPSS/PAH bilayer, even an oscillation amplitude as small as 0.08% appears to be slightly out of the linear response regime since there is a slight decrease of G′ values in the whole 0.01–0.1% range of the strain amplitude. On the other hand, G′′ values are scattered, showing that we are working at the limit of experimental sensitivity for this variable. Moreover there is a clear thixotropy of the bilayer, which is strongly perturbed by the larger amplitude oscillations, despite the rest time (2) between the increasing and decreasing amplitude sweeps: G′ and G′′ values in the decreasing amplitude sweep are well below those measured in the increasing amplitude sweep. This can explain the continuous decrease of the interfacial mechanical properties tested with an oscillation amplitude of 0.08% (Fig. 9). The smaller extent of the linear regime in interfacial shear rheometry compared to dilatometry is well known, although not well understood.⁴⁵ The results in Fig. 9 show that the mechanical properties of the bilayer depend on the duration of the oscillations, on their amplitude and on the rest time between each set of measurements.

Fig. 10 Values of G′ (closed symbols) and G′′ (open symbols) measured in strain amplitude sweeps. Data from the experiment in Fig. 9 (f = 0.01 Hz). The increasing amplitude sweep (III, blue points) and the decreasing amplitude sweep (IV, red points) are separated by a rest time of 10 000 s.

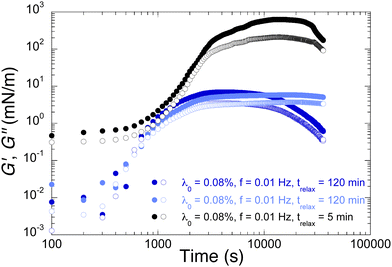
We focus now on the effects of these parameters on the temporal evolution of the moduli, after the PAH solution has been replaced by the saline solution. Fig. 11 displays the effect of shear history of the bilayer on the growth of its mechanical properties. The logarithmic scale of the time axis emphasizes the early times. It is clear that the addition of the PAH layer increases the moduli by several orders of magnitude but this occurs only after a latency time about a few hundreds of seconds (blue points). The position of the maximum in the moduli appears to be a weakly defined feature: for two identical experimental parameters (blue points), it is either visible after about a few thousands seconds or hardly guessed after 30 000 s. Probing the system with a higher frequency (1 Hz) seems to delay the increase of the moduli (red points). Starting 3600 s later an oscillation at 0.01 Hz results in an increase about 2 orders of magnitude of the maximum of the moduli, which happens at much later times (black points). This shows that even without periodic deformation of the interface, there is a slow rearrangement of the adsorbed polyelectrolyte chains yielding a strong enhancement of its mechanical properties. However the latter are soon degraded when the interface is sollicitated. The thorough investigation of these aspects is beyond the scope of this paper and is left for future investigations.

Fig. 11 Effect of the shear history on the growth of G′ (closed symbols) and G′′ (open symbols) after the replacement of PAH solution by the saline solution: no waiting time, at f = 0.01 Hz (blue points) or f = 1 Hz (red points); waiting 3600 s before starting the measurement at f = 0.01 Hz (black points). For all the experiments, the relaxation of the first NaPSS layer has proceeded for 120 min and the strain amplitude is λ₀ = 0.08%.

Finally we turn to the effect of the relaxation time of the first NaPSS layer on the properties of the bilayer. Previous results in Section 3.2.1 involved a bilayer built from a first NaPSS layer that was allowed to relax for 120 min before the replacement of NaPSS solution by saline solution and then by PAH solution. Fig. 12 compares those results (blue points) with the ones obtained when the first NaPSS layer was allowed to relax for only 5 min (black points). Surprisingly the less relaxed NaPSS layer yields a bilayer with much higher moduli, by nearly two orders of magnitude. On the other hand, it seems that these high values are obtained after a slightly longer latency time.

Fig. 12 Effect of relaxation time of the first NaPSS layer on the growth of G′ (closed symbols) and G′′ (open symbols): 120 min (blue points) and 5 min (black points) (f = 0.01 Hz, strain amplitude λ₀ = 0.08%).

3.2.2 From one to three bilayers. Building on the preceding results, we investigated the mechanical properties of the multilayers with the minimal amount of perturbations that allowed reliable measurements. First the initial time sweep was reduced to 10 000 s (Fig. 13a), a duration short enough to not damage the bilayers, then the frequency dependence was measured first increasing the frequencies from 0.01 Hz to 10 Hz and then decreasing them back (Fig. 13b), and, finally, two hysteresis loops were performed with strain amplitudes varying between 0.01% and 0.1%. Also, the measurements were restricted to even numbers of added layers. The results in Fig. 13 show that this protocol provided good quality data and did not damage even the first bilayer. In particular, no hysteresis is observed for the frequency loops with a very good superposition of the data. The same is true for the amplitude loops, with the exception of the two increasing amplitude sweeps for the third bilayer, which show some reproducible deviation for the data at the lowest strain amplitudes. After careful check of the data, it appears that these deviating data should not be taken into account: to shorten the duration of the experiment and also to decrease the risk of damaging the bilayers, we skipped the blank oscillation cycle that helps the rheometer to optimize its feed-back loop before the measurement starts and, for these specific points at the start of the frequency sweep, this procedure yielded erroneous values, which are excluded from further consideration.

Fig. 13 Evolution of the moduli G′ (closed symbols) and G′′ (open symbols) of the interface as bilayers are progressively added. The first NaPSS layer has relaxed for 120 min before the addition of the first PAH layer. (a) Initial growth f = 001 Hz, strain amplitude = 0.08%. (b) Frequency sweeps, strain amplitude = 0.08%. Points: increasing frequency sweep; lines: decreasing frequency sweep. (c) Strain amplitude sweep, f = 0.01 Hz. Points: increasing amplitude sweeps; lines: decreasing amplitude sweeps.

In the Section S7 of the ESI,† we provide similar data from an other experiment where the duration of the initial time sweep was 20 000 s with a strain amplitude of 0.3%, all other parameters of the measurements being identical to those of Fig. 13. Oscillatory shear at a larger amplitude (0.3%) during the first time sweep decreases clearly the values of G′ and G′′ measured afterwards with a smaller amplitude (0.08%).

4 Discussion

The first NaPSS layer formation is very slow for our experimental conditions: high sulfonation degree of the chains (≈75%), relatively low concentration (4.8 mM) and moderate ionic strength (0.15 M) explain the long latency time before any effect on the surface tension can be measured (Fig. 2), which is consistent with previous results.^34,48 Noskov et al.⁴⁸ have long ago emphasized that the elasticity growth is much faster than the surface tension decay for highly charged NaPSS. Perturbating the interface with an oscillation appears to fasten the kinetics of the surface tension decay (Fig. 3). Noskov et al.,⁴⁹ noticing that the approach to equilibrium elasticity values is faster for rising bubbles than for pendant drops, suggested that hydrodynamic fields close to the bubble surface could facilitate the dynamics of the rearrangement of the chains towards an equilibrium configuration. Although this suggestion was made for other polyelectrolytes with a general behaviour differing from the one of NaPSS, the same explanation could hold in our case.⁴⁹ Very recently, Dolmat et al.⁵⁰ demonstrated the same effect of hydrodynamic fields on the structure of polyelectrolyte multilayers at the solid/liquid interface. Yim et al.⁵¹ have shown the existence of two distinct zones in the adsorbed NaPSS layer: a thin (≈1–2 nm) proximal zone close to the interface with air, where the polymer concentration is high, and a thicker (≈10–30 nm) distal zone in contact with the bulk solution, where the polymer concentration profile decreases progressively to the bulk value. While surface tension depends mainly on polymer concentration in the proximal zone, surface elasticity depends on polymer interactions in both zones, and thus on the possible exchange of chains loops and trails between the two zones upon deformation. Noskov et al.^29,48 have argued that the experimental results with NaPSS are consistent with the existence of heterogeneities in surface concentration due to the formation of aggregates that restrict the chain motion between the two zones. Thus, it is no surprise that the growth kinetics of elastic and viscous moduli can depend a lot on the rheological history of the interface and even on its preparation (Fig. 3).

Since PAH chains have no amphiphilic character at low pH,⁵² they do not adsorb at the interface and can only make electrostatic complexes with previously adsorbed NaPSS. Therefore, we can understand that the shear moduli of the first NaPSS/PAH bilayer display a strong sensitivity to the history of formation and deformation of the first NaPSS layer (Fig. 12). In particular the density profile of NaPSS concentration in the proximal and distal zones depends on how long the layer has relaxed before PAH chains come into contact, and the accessibility to NaPSS segments will also depend on this density profile. Furthermore, periodic deformation of the bilayer can also modify this accessibility to charged sites. The results in Fig. 11 suggest that, for the same preparation of the NaPSS layer, building the bilayer in the absence of any deformation or in the presence of a more energetic shear at 1 Hz instead of 0.01 Hz, has about the same qualitative effects: increasing the latency time and yielding higher moduli. However, we think that the similar values of shear moduli do not necessary imply the same structure of the bilayer. Disentangling the effects of these different parameters would be a very demanding task requiring also reflectometry to make the link between the structure of the first bilayer and its mechanical properties.

As the number of adsorbed layers increases, both dilatational and shear moduli increase continuously (Table 1). Both types of moduli also show a larger increase when the fifth or the sixth layer is added. Despite the shortcomings of an analysis with a purely elastic constitutive equation, this trend is confirmed for a simultaneous determination of K′ and G′ by using eqn (6) (Fig. 8). Since CMD results from the dilatometry experiments demonstrated that the adsorption of the fifth layer marks the transition from liquid to solid viscoelasticity and is associated with a jump in K′ and K′′ values, it is reasonable to assume that the jump in G′ and G′′ values measured in the shear experiments is likely to reflect the same transition. Also, for shear rheology, it is remarkable that kinetic effects are considerably attenuated (Fig. 13a) and this is also a qualitative change of shear rheology behaviour upon addition of the third bilayer. Nevertheless, going further and assuming that the structure of the interfacial skin is the same in dilatometry and shear experiments is certainly bolder, since the preparation of the samples is not exactly the same, in particular regarding the exchange time of the polyelectrolyte solutions. Moreover in dilatational and shear experiments, the type of the mechanical stress of the interface differs deeply and it is clear from our results that the rheological history plays an important role in the measured properties.

Table 1 Average values for the rheological properties of the multilayers

	1 Bilayer	2 Bilayers	3 Bilayers
K′ (mN m^−1)	70 ± 21	181 ± 13	410 ± 21
K′′ (mN m^−1)	2.9 ± 0.5	24 ± 4	99 ± 12
G′ (mN m^−1)	7.2 ± 0.6	25.4 ± 0.9	190 ± 6
G′′ (mN m^−1)	3.2 ± 0.2	8.7 ± 0.2	53 ± 3
Exponent G′	0.21 ± 0.05	0.18 ± 0.05	0.13 ± 0.01
Exponent G′′	0.16 ± 0.05	0.13 ± 0.02	0.07 ± 0.01
K′ (eqn (6))	26 ± 5	106 ± 11	560 ± 130
G′ (eqn (6))	34 ± 6	93 ± 36	169 ± 43

---

Liquid cell atomic force microscopy (LC-AFM) on NaPSS/PAH multilayers at the solid/liquid interface^22,53 has revealed a granular structure of the adsorbed layers. The characteristics of this granular structure depend strongly on the conditions of adsorption, in particular on the pH and on the duration of the adsorption steps,⁵³ and seem to adopt steady values already after the adsorption of the first two layers, up to the eighth layer deposition.²² Depending on the technique used to measure the film thickness, the latter is found to increase steadily since the first layer deposition (LC-AFM) or only after the fourth layer deposition (scanning angle reflectometry).²¹ In both studies, the first NaPSS layer was deposited on an anchoring layer of PEI. At the air–water interface, previous studies with the same pair of electrolytes have shown linear or quasi-linear growth of the first three bilayers up to a few nanometers thickness^10,14,18 and revealed a strong increase of the dilatational elastic modulus measured by capillary wave experiments after the fifth layer adsorption.¹⁴ On the other hand, Cramer et al.¹⁸ observe a strong increase of the surface shear modulus up to the second bilayer followed by a quasi-stagnation for the third and fourth bilayer. In this case, the shear modulus is measured with an approach similar to the one described in Section 2.5.4 but on inflated bubbles and, based on our findings, we suspect this could damage the polymer skin and explain possibly the stagnation.

Thus there is a consistent set of results suggesting that the early multilayer structure consists in grains formed by polyelectrolyte complexes more or less connected by dangling chains, depending on the experimental conditions. The friction of these grains against each other yields a liquid-type viscoelastic behavior for the liquid interface, even when the number of adsorbed layers is low. Our CMD results are the first direct experimental evidence that this structure becomes gel-like after about 5–6 layers have been adsorbed. However this gel should be considered as rather loose, close to the sol–gel transition. Indeed, the achievement of selective gas permeance through dried films requires a much larger number of deposited NaPSS/PAH bilayers, indicating the presence of many remaining defects,⁵⁴ which can explain the sensitivity of rheological properties to the measurement conditions. Remarkably, hints to a liquid- to solid-like elasticity transition for about the same number of layers have also been provided for PAH/NaPSS multilayers built on an anchoring anionic lipid monolayer in the pendant drop configuration.¹⁸ Thus, despite the effect of the anchoring layer on the elastic moduli values, it seems that the occurrence of this transition above four adsorbed layers is a rather robust feature at moderate ionic strength value. At high ionic strength, however, saloplasticity⁵⁵ occurs and the transition seems to disappear.¹⁸

Table 1 gathers all the quantities that were measured for the multilayers interface. Average values for K′ and K′′ were calculated from the data in Fig. 5, excluding the experiment with a large number of deformations. For G′ and G′′, we averaged the final values of the time sweeps (Fig. 13a), the values measured at f = 0.01 Hz in Fig. 13b and all the values measured during the strain amplitude sweeps, excepting the first four points of the increasing amplitude sweeps on the third bilayer for the reason given above (Fig. 13c). The power law exponents for the frequency dependence of G′ and G′′ are determined from the slope in their log–log plots (Fig. 13b), their values in the increasing and decreasing frequency sweeps being averaged. The last two rows of the table report the values of K′ and G′ obtained by fitting the constitutive equation (eqn (6)) to the shape of one bubble during its deflation (Fig. 8).

The values obtained with the different approaches are only roughly consistent but we consider that the agreement is not so bad, taking into account the differences in the preparation of the samples, in their geometry and type of mechanical stress, and in their rheological history. Directly fitting an appropriate constitutive equation to the shape of a deflated bubble appears as a very promising tool, which needs to be improved by the inclusion of viscoelastic effects. This would however increase the number of fitting parameters and probably imply the design of more sophisticated experimental protocols.

With these important caveats in mind, we dare to provide an estimation of the 2-dimensional Poisson ratio of the interfacial layer after the deposition of the third bilayer, calculated as ν_2D = (K′ − G′)/(K′ + G′) ≈ 0.37 ± 0.06. This value is consistent with the one calculated from the fit of the constitutive equation (ν_2D = 0.54 ± 0.36) and is larger than the one estimated by Pepicelli et al.⁴⁴ for one bilayer formed by two polymers linked by hydrogen bonds. This difference results from both the larger values of our moduli K′ and G′ measured for our three bilayers and also from the larger difference between them. Owing to the caveats above, this difference cannot be further discussed. We can however notice that these two positive values for ν_2D appear more physical than the value −1, which has been assumed in some other works.^12,17 Indeed experimental evidence converge to positive values of ν_2D, i.e., K′ > G′, for polymer multilayers at the air/water interface.

5 Conclusions

We investigated the dilatational and shear rheological properties of polymer skins built at the air/water interface by successive adsorption of oppositely charged polyelectrolytes, focusing on the behaviour of the first six layers.

Dilatational rheology experiments performed on rising bubbles used for the first time a complementary set of recently developed theoretical tools: bubble shape elastometry, general stress decomposition and capillary meniscus dynamometry, which enables an unambiguous analysis of the experimental data. For the first time we thus demonstrate what seems a rather well-defined transition from liquid to solid viscoelasticity when the number of deposited layers increases from 4 to 5. Remarkably, this set of tools remains usable across the transition and could become a standard for the study of similar interfacial layers, either made from polymerisable surfactants or associating polymers.

Shear rheology of the same polymer skin at planar interfaces has confirmed the sensitivity of the system to the details of its building and probing history. Slow kinetics are involved in the equilibration of the system for all layers, either in the presence of polymer in the case of the first layer, or in the presence of brine for the subsequent layers. Moreover these kinetics are sensitive to the characteristics of the deformation of the system. Therefore the polymeric skin is likely out of equilibrium when it is progressively frozen at the transition to a solid-like viscoelasticity. It would be interesting to increase the salt concentration to check if it controls the characteristic relaxation time of the layers in the same way as for polyelectrolyte coacervates.⁵⁵ Moreover, in future work it will be important to complement the mechanical characterisation of the multi-layers with a detailed structural analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge fruitful discussions with Jean Farago, Reinhard Höhler, Cécile Monteux, Aurélie Hourlier-Fargette, Leonard Sagis, Friedrich Walzel and Gaël Ginot. Corentin Tregouët is thanked in particular for sharing his experience of building polymer multilayers at liquid interfaces. We thank the CARMAC plateform for experimental characterisation and Teclis for numerous interactions. This work has been financed by an ERC Consolidator Grant (agreement 819511 METAFOAM) and profited also from an IdEx Unistra “Attractivity grant” (Chaire W. Drenckhan). It was conducted in the framework of the Interdisciplinary Institute HiFunMat, as part of the ITI 2021–2028 program of the University of Strasbourg, CNRS and Inserm, was supported by IdEx Unistra (ANR-10-IDEX-0002) and SFRI (STRATUS project, ANR-20-SFRI-0012) under the framework of the French Investments for the Future Program.

Notes and references

1. G. Decher, J. D. Hong and J. Schmitt, Thin Solid Films, 1992, 210–211, 831–835.
2. J. A. Jaber and J. B. Schlenoff, Curr. Opin. Colloid Interface Sci., 2006, 11, 324–329.
3. E. M. Shchukina and D. G. Shchukin, Curr. Opin. Colloid Interface Sci., 2012, 17, 281–289.
4. M. A. Priolo, K. M. Holder, T. Guin and J. C. Grunlan, Macromol. Rapid Commun., 2015, 36, 866–879.
5. B. P. Das and M. Tsianou, Adv. Colloid Interface Sci., 2017, 244, 71–89.
6. L.-M. Petrila, F. Bucatariu, M. Mihai and C. Teodosiu, Materials, 2021, 14, 4152.
7. A. M. Yola, J. Campbell and D. Volodkin, Appl. Surf. Sci. Adv., 2021, 5, 100091.
8. D. Guzey and D. J. McClements, Adv. Colloid Interface Sci., 2006, 128–130, 227–248.
9. G. Bortnowska, Pol. J. Food Nutr. Sci., 2015, 65, 157–166.
10. J. Ruths, F. Essler, G. Decher and H. Riegler, Langmuir, 2000, 16, 8871–8878.
11. H. Ahrens, K. Büscher, D. Eck, S. Förster, C. Luap, G. Papastavrou, J. Schmitt, R. Steitz and C. A. Helm, Macromol. Symp., 2004, 211, 93–106.
12. E. Guzmán, H. Ritacco, F. Ortega, T. Svitova, C. J. Radke and R. G. Rubio, J. Phys. Chem. B, 2009, 113, 7128–7137.
13. D. G. Shchukin, K. Köhler, H. Möhwald and G. B. Sukhorukov, Angew. Chem., Int. Ed., 2005, 44, 3310–3314.
14. M. Safouane, R. Miller and H. Möhwald, J. Colloid Interface Sci., 2005, 292, 86–92.
15. J. K. Ferri, W.-F. Dong and R. Miller, J. Phys. Chem. B, 2005, 109, 14764–14768.
16. J. K. Ferri, W. F. Dong, R. Miller and H. Möhwald, Macromolecules, 2006, 39, 1532–1537.
17. J. K. Ferri, P. A. L. Fernandes, J. T. McRuiz and F. Gambinossi, Soft Matter, 2012, 8, 10352–10359.
18. A. D. Cramer, W.-F. Dong, N. L. Benbow, J. L. Webber, M. Krasowska, D. A. Beattie and J. K. Ferri, Phys. Chem. Chem. Phys., 2017, 19, 23781–23789.
19. M. Winterhalter and A. F. Sonnen, Angew. Chem., Int. Ed., 2006, 45, 2500–2502.
20. M. Ruano, A. Mateos-Maroto, F. Ortega, H. Ritacco, J. E. Rubio, E. Guzmán and R. G. Rubio, Langmuir, 2021, 37, 6189–6200.
21. G. Ladam, P. Schaad, J. C. Voegel, P. Schaaf, G. Decher and F. Cuisinier, Langmuir, 2000, 16, 1249–1255.
22. F. Tristan, J.-L. Menchaca, F. Cuisinier and E. Pérez, J. Phys. Chem. B, 2008, 112, 6322–6330.
23. J. Amim, F. C. B. Maia, P. B. Miranda, M. D. Urzúa and D. F. S. Petri, Soft Matter, 2012, 8, 6462–6470.
24. G. M. Lowman and S. K. Buratto, Thin Solid Films, 2002, 405, 135–140.
25. M. Kolasinska, R. Krastev and P. Warszynski, J. Colloid Interface Sci., 2007, 305, 46–56.
26. M. Kolasinska, R. Krastev, T. Gutberlet and P. Warszynski, Progr. Colloid Polym. Sci., 2008, 134, 30–38.
27. G. Ginot, F. S. Kratz, F. Walzel, J. Farago, J. Kierfeld, R. Höhler and W. Drenckhan, Soft Matter, 2021, 17, 9131–9153.
28. W. Yu, P. Wang and C. Zhou, J. Rheol., 2009, 53, 215–238.
29. B. A. Noskov and A. G. Bykov, Russ. Chem. Rev., 2015, 84, 634–652.
30. A. de Groot, J. Yang and L. M. Sagis, J. Colloid Interface Sci., 2023, 638, 569–581.
31. K. D. Danov, R. D. Stanimirova, P. A. Kralchevsky, K. G. Marinova, N. A. Alexandrov, S. D. Stoyanov, T. B. Blijdenstein and E. G. Pelan, J. Colloid Interface Sci., 2015, 440, 168–178.
32. M. Nagel, T. A. Tervoort and J. Vermant, Adv. Colloid Interface Sci., 2017, 247, 33–51.
33. J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage and J. Kierfeld, J. Colloid Interface Sci., 2018, 513, 549–565.
34. O. Théodoly, R. Ober and C. E. Williams, Eur. Phys. J. E, 2001, 5, 51–58.
35. R. Miller and D. Moebius, Drops and Bubbles in Interfacial Research, Elsivier Science B.V., 1998.
36. C. Trégouët, PhD thesis, Université Pierre et Marie Curie, 2016.
37. I. A. Larmour, S. E. Bell and G. C. Saunders, Angew. Chem., Int. Ed., 2007, 46, 1710–1712.
38. M. Hoorfar and A. W. Neumann, Adv. Colloid Interface Sci., 2006, 121, 25–49.
39. S. Vandebril, A. Franck, G. G. Fuller, P. Moldenaers and J. Vermant, Rheol. Acta, 2010, 49, 131–144.
40. B. Schroyen, D. Z. Gunes and J. Vermant, Rheol. Acta, 2017, 56, 1–10.
41. D. Carvajal, E. J. Laprade, K. J. Henderson and K. R. Shull, Soft Matter, 2011, 7, 10508–10519.
42. S. Knoche, D. Vella, E. Aumaitre, P. Degen, H. Rehage, P. Cicuta and J. Kierfeld, Langmuir, 2013, 29, 12463–12471.
43. C. Gu and L. Botto, Soft Matter, 2016, 12, 705–716.
44. M. Pepicelli, N. Jaensson, C. Tregouët, B. Schroyen, A. Alicke, T. Tervoort, C. Monteux and J. Vermant, J. Rheol., 2019, 63, 815–828.
45. L. M. Sagis and P. Fischer, Curr. Opin. Colloid Interface Sci., 2014, 19, 520–529.
46. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
47. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
48. B. A. Noskov, S. N. Nuzhnov, G. Loglio and R. Miller, Macromolecules, 2004, 37, 2519–2526.
49. B. A. Noskov, A. Bilibin, A. V. Lezov, G. Loglio, S. K. Filippov, I. M. Zorin and R. Miller, Colloids Surf., A, 2007, 298, 115–122.
50. M. Dolmat, V. Kozlovskaya, D. Inman, C. Thomas and E. Kharlampieva, J. Polym. Sci., 2023, 61, 1052–1064.
51. H. Yim, M. Kent, A. Matheson, R. Ivkov, S. Satija, J. Majewski and G. S. Smith, Macromolecules, 2000, 33, 6126–6133.
52. B. N. Dickhaus and R. Priefer, Colloids Surf., A, 2016, 488, 15–19.
53. J.-L. Menchaca, B. Jachimska, F. Cuisinier and E. Pérez, Colloids Surf., A, 2003, 222, 185–194.
54. Y. Wang, E. Stedronsky and S. L. Regen, J. Am. Chem. Soc., 2008, 130, 16510–16511.
55. E. Spruijt, J. Sprakel, M. Lemmers, M. A. Cohen Stuart and J. van der Gucht, Phys. Rev. Lett., 2010, 105, 208301.

---

Footnote

† Electronic supplementary information (ESI) available: NaPSS characterisation, thermogravimetric analysis of NaCl, scheme of the tensiometry set-up, determination of ΔP, correction of ΔP shifts, effect of hydrophobic treatment on the bubble profile, additional data for the increase of shear moduli with the number of bilayers, shear rheology of first NaPSS layer. See DOI: https://doi.org/10.1039/d3sm01161e

---