 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Room-temperature ferroelectric nematic liquid crystal showing a large and diverging density†
Charles
Parton-Barr
a,
Helen F.
Gleeson
 a and
Richard J.
Mandle
a and
Richard J.
Mandle
 *ab
*ab
aSchool of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK
bSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK. E-mail: r.mandle@leeds.ac.uk
First published on 19th December 2023
Abstract
The ferroelectric nematic phase (NF) is a recently discovered phase of matter in which the orientational order of the conventional nematic liquid crystal state is augmented with polar order. Atomistic simulations suggest that the polar NF phase would be denser than conventional nematics owing to contributions from polar order. Using an oscillating U-tube densitometer, we obtain detailed temperature-dependent density values for a selection of conventional liquid crystals with excellent agreement with earlier reports. Having demonstrated the validity of our method, we then record density as a function of temperature for M5, a novel room-temperature ferroelectric nematic material. We present the first experimental density data for a NF material as well as density data for a nematic that has not previously been reported. We find that the room-temperature NF material shows a large (>1.3 g cm−3) density at all temperatures studied, notably including phases without polar order. An increase in density at phase transitions is observed. The magnitude of the increase for the intermediate-to-ferroelectric nematic (NX–NF) transition is an order of magnitude smaller than the isotropic–nematic (I–N) transition. We then probe potential consequences that may result from an elevated density through measurement of the refractive indices (no and ne). The navg of M5 is compared with 5CB and polar smectic liquid crystals. We observe how the highly polar nature of the system counteracts the effects of an increase in density. With knowledge of experimental density, we are able to derive an approximation that yields the polar order parameter, 〈P1〉, from polarisation measurements. Present results may be typical of ferroelectric nematic materials, potentially guiding material development, and is especially relevant for informing ongoing studies into this emerging class of materials.
Introduction
The nematic (N) phase is the simplest liquid crystalline state, consisting of molecules or particles that have long-range orientational order but lack translational order. Despite this orientational order, the bulk nematic phase is apolar as there are an equal number of molecules oriented parallel and antiparallel.In the recently discovered ferroelectric nematic (NF) phase,1–6 the orientational order of the conventional nematic state is augmented by so-called polar order which arises due to parallel alignment of molecular electric dipole moments. This parallel alignment distinguishes it from the nematic phase, and virtually all other fluid states of matter. Depictions of nematic and polar nematic phases are given in Fig. 1.
 | ||
| Fig. 1 Depictions of the orientations of the molecular electric dipole moments in the (a) nematic and (b) ferroelectric nematic phases; the arrows are color-coded to represent the contribution to the bulk value of the polar order parameter, 〈P1〉 which is 0.08 for (a) and 0.86 for (b), respectively, while 〈P2〉 is 0.66 and 0.66 for (a) and (b), respectively. In both cases the director is oriented perfectly with the box height (z-axis). The molecular structures of the first reported NF materials; (c) RM734,1,2 and (d) DIO3 along with their transition temperatures (T, °C) on heating (↑) and cooling (↓). | ||
Having been the subject of some speculation,7–9 the NF phase has been now experimentally realised in several classes of materials, having originally been observed in RM734 and DIO, (Fig. 1(c) and (d)), both reported in 2017. In recent years the number of NF materials has been increased significantly as derivatives of RM734 and DIO10–14 have been developed, including those exhibiting a direct I–NF transition.15
In RM7341,2 the N–NF transition is accompanied by a softening of the K1 splay constant, and a growth of ferroelectric ordering.4,6 DIO3 behaves slightly differently, with an intermediate phase between the N and NF; crucially however, DIO was also shown to possess these same characteristic macroscopic domains of ferroelectric ordering in the low temperature nematic phase.5 When studied by DSC, there is a small enthalpy associated with the transition from nematic to polar nematic phase(s). Dielectric measurements have reported large dielectric permittivity values on the order of 104 for RM73416 and for DIO,3,17 although the validity of these has been questioned.18,19 Polarisation investigations have found values of spontaneous polarisation for RM734 (6 μC cm−2)5,20 and DIO (2.5–6 μC cm−2)3,17 which are comparable with polar columnar (5.8 μC cm−2)21 and bent core liquid crystals (LCs) (0.5–0.8 μC cm−2).22 The measured NF spontaneous polarisation values is far larger than typical chiral smectic C materials (e.g. DOBAMBAC, 42.0 nC cm−2)23 and somewhat smaller than that achieved by inorganic materials – e.g. the inorganic material PbSc0.5Ta0.5O3 (30.0 μC cm−2).24
Our investigations were driven by the predictions of atomistic molecular dynamics (MD) simulations. MD simulations can reproduce the polar nematic ordering and calculate mean densities from atomic scale interactions.25 Simulations predicted a high mass density, ρ of 1.3 g cm−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 in RM734. Considering the oft-used assumption that ρ in liquid crystals ≈1 cm−3, known to be an approximation for some LCs and is unjustified for many others, this raises a potential defining property of NF materials.
25 in RM734. Considering the oft-used assumption that ρ in liquid crystals ≈1 cm−3, known to be an approximation for some LCs and is unjustified for many others, this raises a potential defining property of NF materials.
As LCs undergo a first-order phase transition, they exhibit a density change that can be discontinuous.26 The temperature dependence of density, ρ(T) in a discrete liquid crystal phase can be described by a linear thermal expansion of its specific volume, vsp as described in eqn (1) and (2)
| vsp(T) = 1/ρ(T) | (1) |
 | (2) |
 is the specific volume at 0 °C, α is an empirical expansion coefficient describing how the material behaves with temperature changes, and T is the temperature.
is the specific volume at 0 °C, α is an empirical expansion coefficient describing how the material behaves with temperature changes, and T is the temperature.
The density of LCs has previously been measured by several methods including the capillary tube technique,25 the weight change of a submerged glass cylinder27 and a dilatometer measuring the height of a mercury interface.28 These methods all suffer from a difficulty in obtaining the precise temperature control that detailed study over phase transitions demands. Moreover, the lack of experimental density data for all but a handful of common LCs has led to the incorrect (vide infra) assumption about ρ being propagated.
Density data were available for 5CB,29–33 8CB,34–36 and (NCS)PCH6.37 A comprehensive list of the data and their properties are given in section 4 of the supplementary information. The 5CB dataset30 was chosen for comparison with high resolution data (between 5 °C and 0.2 °C) over a large temperature range. The available data for 8CB consisted of either sparse measurements35 or data taken over a temperature range near a single transition.34 The (NCS)PCH6 literature data37 were used out of necessity as no other data were available. We analyse the agreement of the experimental and literature data through Bland–Altman38 type plots (ESI,† Section S4). We find limits of agreement, l through eqn (3) where ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) is the mean difference between our experimental data and its corresponding literature data. σd is the standard deviation
is the mean difference between our experimental data and its corresponding literature data. σd is the standard deviation ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Its agreement can then be judged through the data's vicinity to
. Its agreement can then be judged through the data's vicinity to ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) .
.
l = ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ± 1.96σd ± 1.96σd | (3) |
The largest difference between the agreement comes from a systematic differences between the methods in the capillary tube investigation of 5CB32 and 8CB36 where a dilatometer is used. These methods have a systematic difference of approximately 1% and 3% respectively compared to 0.02%30 and 0.04%35 of the density meters. This is calculated from the average of the differences used in the Bland–Altman plots (Fig. S9–S17 in ESI†).
In this article we report an unusually large density (>1.3 g cm3) for a ferroelectric nematic liquid crystal, M5 (Merck Electronics KGaA). A density increase resulting from polar ordering on transition to an NF state is also shown. We benchmark our results against a set of standard liquid crystals, which we find to be in excellent agreement with the available literature data. Finally, we evaluate potential implications of a large density for liquid crystals by comparing its average refractive index with polar smectic liquid crystals and 5CB. Spontaneous polarisation measurements and an approximation of the polar order of DIO are examined with consideration of the experimentally confirmed NF density.
Methods and experimental
Density measurements were performed using an Anton-Paar DMA 4100M densitometer which operates on the oscillating U-tube principle (Fig. 2). A U-shaped borosilicate glass tube is filled with ≈1 mL material. Samples were loaded using a SGE precision syringe. A syringe heater was used for samples with above-ambient melting points; the syringe outlet was interfaced with the DMA 4100M inlet port using a short section of PTFE tubing with appropriate PEEK/ETFE microfluidic connectors (purchased from Darwin Microfluidics). The presence of bubbles within the tube was assessed through visual inspection. This experimental method requires a large amount of material; however, it can be largely recovered on the completion of the measurements. Recovered material was subjected to purification with a Teledyne Combiflash NextGen 300+ Flash chromatography system and filtration over a 0.2 micron PTFE filter. | ||
| Fig. 2 Schematic diagram of the oscillating U-tube setup used to measure density. The optical pickups determine the LC sample's characteristic frequency which corresponds to a density value. | ||
Once filled, the tube is excited to oscillate at its characteristic frequency in the direction of the normal to the tube. The density is calculated from eqn (4)
| ρ = A·Q2·f1 − B·f2 | (4) |
Refractive indices measurements were performed on a Bellingham + Stanley Abbe 60/DR refractometer. The refractometer finds the critical angle of total reflection of an LC sample at a wavelength of 589 nm. A polariser is used to differentiate between the ordinary and extraordinary refractive indices. Temperature control is achieved by circulating water with a temperature range from room temperature to ∼70 °C and an accuracy of ∼0.2 °C.
The temperature dependence of polarisation is measured through its switching current response.39 A triangular wave voltage with VRMS = 5 V and frequency = 63 Hz was produced by an Agilent 33220A waveform generator and applied to DIO in a 4 μm INSTEC cell with no alignment layer. Temperature control was achieved with a LINKAM THM600 hot stage. The output signal was recorded on RIGOL DHO 4204 oscilloscope. Integration of the current response peaks calculates the Ps through eqn (5)
 | (5) |
Materials
The materials selected were M5 (Merck Electronics KGaA), 4-cyano-4-pentylbiphenyl (5CB, Fluorochem), 4-cyano-4-octylbiphenyl (8CB, Fluorochem), 1-(trans-4-hexylcyclohexyl)-4-isothiocyanatobenzene ((NCS)PCH6), (Sigma-Aldrich) and trans-4-(trans-4′-n-propylcyclohexyl)-cyclohexyl-3,4,5-trifluorobenzene (CCU-3-F, prepared according to ref. 40). Both M5 and commercial materials were used as received. Fig. 3 presents the transition temperatures for the materials investigated in this work, and chemical structures in the case of single-component materials (Fig. 3(a)–(d)). The limits of the density meter's operating temperature range did not allow for measurements of RM734 and DIO. | ||
| Fig. 3 Chemical structures of the materials for which density measurements were undertaken. Transition temperatures (T, °C) on cooling (↓) were determined from density measurements and are in good agreement with DSC data (ESI,† Section S1). For single component materials (a)–(d) molecular structures are given. | ||
Results
Apolar liquid crystals
Our initial investigations focused on a set of relatively well-known materials, for some of which density data was available. We selected 5CB as it is an ambient temperature nematic; 8CB as it exhibits a transition between two LC phases (smectic A (SmA), a layered structure and N) and has a high viscosity at ambient temperature; (NCS)PCH6 as a non-nitrile room-temperature nematic LC; CCU-3-F as a fluorinated LC with an above-ambient melting point which enabled us to refine our technique for handling materials with elevated melting points. The temperature-dependent densities for the selected materials are given in Fig. 4. | ||
| Fig. 4 Densities of the liquid crystal materials at 1 °C intervals. Dashed lines denote transition temperatures as defined by the temperature of the largest density gradient. The density increases at the phase transition are readily observable for the I–N transitions, but more subtle for the N–SmA transition. Comparison is made with literature data where possible (orange plus points) for (a) 5CB,30 (b) 8CB35 and (c) (NCS)PCH6.37 (d) The CCU-3-F figure is representative of the scarcity of LC density data. | ||
The measurement runs for all materials began in the isotropic phase and were cooled through the phase range into their lowest temperature phase above crystallisation. The present results compare very favourably with available literature data for 5CB, 8CB and (NCS)PCH6. In all cases, the density of the LC materials is around 1 g cm−3. The I–N transitions for each material can be clearly observed as discontinuous increase in ρ. At the N–SmA transition (Fig. 4(b)) we do not find a discernible increase in density.
Ferroelectric nematic liquid crystal M5
Having shown our ability to reproduce and expand upon literature densities of common liquid crystals, we next performed density measurements on the room-temperature NF material M5, a multi-component mixture produced by Merck Electronics KGaA. A cursory inspection of the data in Fig. 5 reveals that, even in the isotropic liquid, the density of M5 is remarkably high, being ∼30% larger than 5CB and of the same magnitude as dichloromethane (1.33 g cm3 at 25 °C).In M5 there is a constant decrease in the expansion coefficients as it is cooled through its phase range (Table 1). This can also be observed in the rate of density change within the linear regimes of Fig. 5. As with the other materials investigated, an increase in the density can be seen at TIN and this feature is also clear at TNXNF though the TNNX density change appears to be continuous. Fig. 5 presents data obtained at an increased temperature resolution (0.15 °C compared to the 1 °C given in Fig. 4). The inset facilitates a more detailed look at the behaviour over the NX–NF transition where the density increase can be seen.
| Material | α 104 (cm3 g−1 K−1) | ||||
|---|---|---|---|---|---|
| NF | NX | SmA | N | I | |
| M5 | 5.30 | 6.08 | — | 6.57 | 7.09 |
| 5CB | — | — | — | 9.18 | 7.96 |
| 8CB | — | — | 8.16 | 11.5 | 8.76 |
| CCU-3-F | — | — | — | 7.81 | 9.00 |
| (NCS)PCH6 | — | — | — | 8.08 | 8.80 |
The linear relationship between density and temperature in a discrete phase can be explored through eqn (2). From this, vsp(T) is separated into discrete phases using the transition temperatures in Fig. 4 as their temperature ranges. The gradient of a linear fit of vsp(T) for each phase (see also Fig. S18 in ESI†) is taken to be the expansion coefficient. Expansion coefficients for the selected materials can be found in Table 1. The expansion coefficients are similar, although we do not find an explicit relationship between coefficient and LC phase type as the coefficient can be seen to either increase (5CB, 8CB) or decrease (CCU-3-F, (NCS)PCH6) through the I–N transition.
Table 2 gives the density increases for the selected materials. A linear fit of the higher temperature phase ρhighT was extrapolated into the lower temperature phase and used to calculate the density deviation of the lower temperature phase as it cools. The magnitude of change in density that occurs in the non-linear period between two linear regimes is then taken to be the density deviation of that transition. A representative example of this process is given in Fig. S6 (ESI†). The density deviation at (NCS)PCH6's I–N transition can be seen in Fig. 6(a). We find Δρ of the I–N transitions for all materials studied to be of the same order of magnitude, presumably a consequence the fact the same type of molecular reorganisation takes place for each material at TIN. For 8CB we find the N–SmA transition is ten times smaller than its I–N transition indicating that the change in molecular packing at the smectic transition is not as a drastic as a nematic one.
| Material | Δρ103 (g cm−3) | |||
|---|---|---|---|---|
| I–N | N–NX | NX–NF | N–SmA | |
| M5 | 3.1 | 0.05 | 0.75 | — |
| 5CB | 2.2 | — | — | — |
| 8CB | 2.5 | — | — | 0.20 |
| CCU-3-F | 2.0 | — | — | — |
| (NCS)PCH6 | 2.8 | — | — | — |
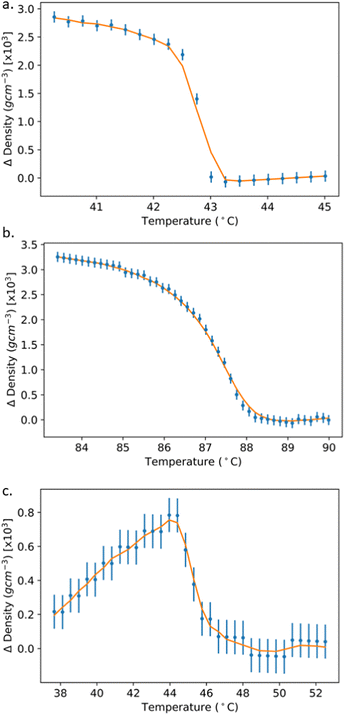 | ||
| Fig. 6 The density deviation (Δρ = ρ(T) − ρhighT(T)) through the I–N transition (a), (b) of (NCS)PCH6 and M5 respectively. The behaviour in (a) and (b) is the result of a conventional nematic ordering taking place. (C) Shows how the density changes in M5 as a result of polar ordering. Data are presented as scatter points whereas the solid line is a Savitzky–Golay filter41 smoothing intended to show the trend of Δρ. | ||
M5's increase in density from its I–N and NX–NF phase transitions can be seen in Fig. 6(b) and (c). The NX–NF transition is accompanied by a much smaller density change than that associated with the I–N transition, approximately 0.00075 g cm−3vs. 0.0031 g cm−3 (Table 2). The size of this I–N density change is the largest of the investigated materials. The density deviation of the NX–NF transition has been calculated at more than three times larger than that of the N–SmA transition. This suggests a significant structural reorganisation taking place through polar ordering when compared to that of the positional ordering of the N–SmA transition. It is interesting to note that M5 does not follow the loose positive correlation between density increase and transitional enthalpy (ESI,† Table S2), perhaps due to its composition as a mixture.
Implications of a large liquid crystal density
As the refractive index (or indices) of a material with induced dipoles depends significantly upon the density according to the Lorentz–Lorenz equation,46 it is interesting to explore whether the anomalously high density and the highly polar nature of M5 (and potentially other NF materials) impacts their optical properties. We measured the refractive indices and birefringence of M5, finding the latter to be comparable to DIO47 (but smaller than RM7345,25); see Fig. 7. Due to the temperature limits of the experimental method employed in this work, measurements were performed a significant distance from the I–N transition. Therefore, a pre-transitional monotonic reduction is not observed in the extraordinary, ne, and ordinary, n0, refractive indices as the system is heated towards the isotropic phase. Here, we focus on navg as no, ne and Δn are more strongly linked to the order parameter. Fig. 7(c) shows the navg as calculated by eqn (6) for M5. | (6) |
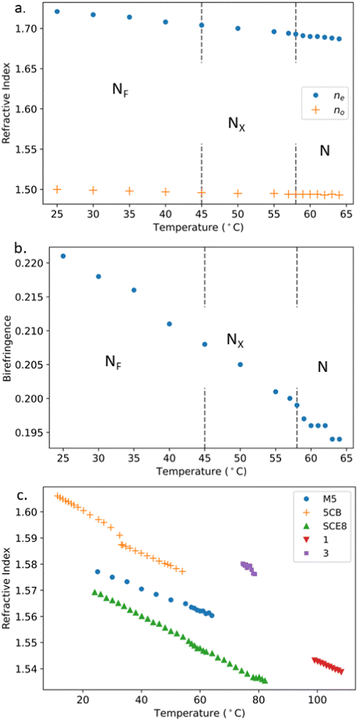 | ||
| Fig. 7 (a) The n0 and ne measurements of M5 at 589 nm as the sample is cooled through its N–NX–NF phase sequence. (b) The resulting birefringence (Δn = ne − no) values of M5. (c) A comparison is made of navg for M5 and 5CB42 as well as the polar smectics, SCE843 and compounds 1 and 3 from ref. 44 and 45. | ||
We find that navg is smaller than the equivalent values for the standard nematogen 5CB, a material ≈30% less dense than M5.42 Here we see direct evidence of contributions from the permanent dipole moments of a highly polar system influencing the refractive indices of a material. The observations of M5 and 5CB where an increased density does not result in a larger navg confirms that Lorentz–Lorenz equation does not adequately explain/should not be used in the explaining the behaviour of polar liquid crystal materials. To identify any relationship between navg and spontaneous polarisation M5 is compared with literature navg data for the polar smectics SCE8 (Ps ≈ 50 nC cm−2)43 and compounds 1 and 3 (Ps ≈ 150 nC cm−2) from ref. 44 and 45 (structures and phase sequences are given in ESI,† Section S6). There is a scattering of values with M5 and its polarisation magnitude of ≈5.5 μC cm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 resulting in a lower navg than the less polar compound 3 indicating there is no such relationship.
48 resulting in a lower navg than the less polar compound 3 indicating there is no such relationship.
It is possible to use measurements of the density and spontaneous polarisation in a ferroelectric material, together with knowledge of the molecular dipole moment to deduce a value for the polar order parameter 〈P1〉. In this case, as M5 is a multicomponent material of unknown composition it was impossible to measure the polar order. However, as there is a clear indication from simulations that DIO also has a density of 1.3 g cm−3, and our measurements of M5, show that such a high value is indeed realistic, the approach was used for that pure material in approximating the polar order parameter. If we consider polarisation as the number density of electric dipoles per unit volume, then we can infer that a larger density will increase the measured polarisation. Following this, we have approximated the polar order parameter of DIO, 〈P1〉 through temperature-dependent spontaneous polarisation measurements (Fig. 8). We define 〈P1〉 in eqn (7).
 | (7) |
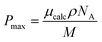 | (8) |
 | ||
| Fig. 8 (a) Spontaneous polarisation measurements of DIO (see Fig. 1 for DIO's structure and phase sequence) on cooling through its NF–NX–N phase sequence until crystallisation. Switching current response peaks are integrated to gives the magnitude of polarisation. (b) An approximation of 〈P1〉 for DIO from the contribution of average molecular dipole alignment to the polarisation. | ||
As can be seen in Fig. 8, DIO's N phase produces zero measured polarisation values and thus possesses no polar order. On cooling through the NX phase, some average polar order begins to grow at and below 73 °C, resulting in net polarisation. Within the NF phase the polarisation can be seen to increase until it saturates at a 4.5 μC cm−2 ± 10%. This produces a 〈P1〉 of 0.91 ± 15% with the increased error accounting for any density changes due to a temperature change. As this material is being supercooled, the polarisation decreases past the saturation point until crystallisation and it no longer provides any measured response.
Recalculating with a conventional density assumption of 1 g cm−3 results in an unphysical 〈P1〉 of 1.19. It may be of note that reliable density and polarisation measurements as well a realistic assumption for a maximum 〈P1〉 order parameter would provide a method for the experimental approximation of dipole moments. From a material design perspective, eqn (8) provides a means to estimate Ps directly from electronic structure calculations, although this does not mean that a given material will generate and sustain polar ordering. Additionally, knowledge of the density of a typical NF material enables the use of eqn (8) to check the physical validity of measured Ps values which, for a given material, are limited by the dipole moment and density.
Conclusions
We have shown that the density of the NF material M5 is significantly larger than conventional liquid crystals, a finding that is in keeping with that determined in the atomistic MD simulations.25 Here, we find that the NF material M5 possesses a much higher density (∼1.3 g cm−3) than that of conventional nematic systems where the density is assumed (and found) to be ∼1 g cm−3. We also observe experimentally an increase in density on entering the NF phase which is comparable to that seen in silico.25Refractive indices measurements of M5 were used to examine the relationship between density, polarisation magnitude and navg. M5, while being ≈30% denser than 5CB, possesses a lower navg. We believe this to be a result of M5's highly polar nature. M5 was compared to polar smectic liquid crystals with the polarisation magnitude possessing no direction correlation with navg. The 〈P1〉 of DIO is approximated from temperature-dependent spontaneous polarisation measurements. The calculation of 〈P1〉 includes the simulation supported and now experimentally verified density value for an NF material.
For classical apolar liquid crystals it is customary to assume a density of 1 g cm−3 if required for measurement or analysis. In the case of NF materials, we suggest that, in the absence of data for a specific material, a value of 1.3 g cm−3 be used.
Data availability
The data collected in this work has been made publicly available at the University of Leeds Research Data Archive https://doi.org/10.5518/1343.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Merck Electronics KGaA for gifting the sample of M5 used in this work, and for their continued partnership and support. HFG thanks EPSRC for funding via grant number EP/V054724/1. RJM thanks UKRI for funding via a Future Leaders Fellowship, grant number MR/W006391/1, and University of Leeds for funding a PhD studentship for CPB. The authors all thank Diana Nikolova of the University of Leeds for providing DSC data for M5.References
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Rational Design of Rod-Like Liquid Crystals Exhibiting Two Nematic Phases, Chem. – Eur. J., 2017, 23(58), 14554–14562, DOI:10.1002/chem.201702742.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, A nematic to nematic transformation exhibited by a rod-like liquid crystal, Phys. Chem. Chem. Phys., 2017, 19(18), 11429–11435, 10.1039/C7CP00456G.
- H. Nishikawa, et al., A Fluid Liquid-Crystal Material with Highly Polar Order, Adv. Mater., 2017, 29(43), 1702354, DOI:10.1002/adma.201702354.
- A. Mertelj, et al., Splay Nematic Phase, Phys. Rev. X, 2018, 8(4), 041025, DOI:10.1103/PhysRevX.8.041025.
- X. Chen, et al., First -principles experimental demonstration of ferroelectricity in a thermotropic nematic liquid crystal: Polar domains and striking electro-optics, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(25), 14021–14031, DOI:10.1073/pnas.2002290117.
- N. Sebastián, et al., Ferroelectric-Ferroelastic Phase Transition in a Nematic Liquid Crystal, Phys. Rev. Lett., 2020, 124(3), 037801, DOI:10.1103/PhysRevLett.124.037801.
- F. C. Frank, I. Liquid crystals. On the theory of liquid crystals, Discuss. Faraday Soc., 1958, 25, 19–28 RSC.
- H. Pleiner and H. Brand, Spontaneous splay phases in polar nematic liquid crystals, Europhys. Lett., 1989, 9(3), 243 CrossRef CAS.
- M. Born, Sitzungsber. Preuss. Akad Wiss, 1916 Search PubMed.
- J. Li, et al., General phase-structure relationship in polar rod-shaped liquid crystals: Importance of shape anisotropy and dipolar strength, Giant, 2022, 11, 100109, DOI:10.1016/j.giant.2022.100109.
- E. Cruickshank, R. Walker, J. M. D. Storey and C. T. Imrie, The effect of a lateral alkyloxy chain on the ferroelectric nematic phase, RSC Adv., 2022, 12(45), 29482–29490, 10.1039/D2RA05628C.
- Y. Song, et al., Development of emergent ferroelectric nematic liquid crystals with highly fluorinated and rigid mesogens, Phys. Chem. Chem. Phys., 2022, 24(19), 11536–11543, 10.1039/D2CP01110G.
- R. Saha, et al., Multiple ferroelectric nematic phases of a highly polar liquid crystal compound, Liq. Cryst., 2022, 1–13, DOI:10.1080/02678292.2022.2069297.
- S. Dai, J. Li, J. Kougo, H. Lei, S. Aya and M. Huang, Polar Liquid Crystalline Polymers Bearing Mesogenic Side Chains with Large Dipole Moment, Macromolecules, 2021, 54(13), 6045–6051, DOI:10.1021/acs.macromol.1c00864.
- A. Manabe, M. Bremer and M. Kraska, Ferroelectric nematic phase at and below room temperature, Liq. Cryst., 2021, 48(8), 1079–1086, DOI:10.1080/02678292.2021.1921867.
- J. Li, et al., Development of ferroelectric nematic fluids with giant-ε dielectricity and nonlinear optical properties, Sci. Adv., 2021, 7(17), eabf5047, DOI:10.1126/sciadv.abf5047.
- S. Brown, et al., Multiple Polar and Non-polar Nematic Phases, ChemPhysChem, 2021, 22(24), 2506–2510, DOI:10.1002/cphc.202100644.
- N. A. Clark, X. Chen, J. E. Maclennan and M. A. Glaser, Dielectric spectroscopy of ferroelectric nematic liquid crystals: Measuring the capacitance of insulating interfacial layers, arXiv, arXiv:2208.09784, 2022, preprint.
- A. Erkoreka, J. Martinez-Perdiguero, R. J. Mandle, A. Mertelj and N. Sebastián, Dielectric spectroscopy of a ferroelectric nematic liquid crystal and the effect of the sample thickness, J. Mol. Liq., 2023, 387, 122566, DOI:10.1016/j.molliq.2023.122566.
- X. Chen, et al., Ideal mixing of paraelectric and ferroelectric nematic phases in liquid crystals of distinct molecular species, Liq. Cryst., 2022, 49(11), 1531–1544, DOI:10.1080/02678292.2022.2058101.
- H. Takezoe and F. Araoka, Polar columnar liquid crystals, Liq. Cryst., 2014, 41(3), 393–401, DOI:10.1080/02678292.2013.834079.
- R. A. Reddy and C. Tschierske, Bent-core liquid crystals: polar order, superstructural chirality and spontaneous desymmetrisation in soft matter systems, J. Mater. Chem., 2006, 16(10), 907–961, 10.1039/B504400F.
- K. Yoshino, M. Ozaki, T. Sakurai, K. Sakamoto and M. Honma, Ferroelectric Liquid Crystal with Extremely Large Spontaneous Polarization, Jpn. J. Appl. Phys., 1984, 23(3A), L175, DOI:10.1143/JJAP.23.L175.
- B. Nair, et al., Large electrocaloric effects in oxide multilayer capacitors over a wide temperature range, Nature, 2019, 575(7783), 468–472, DOI:10.1038/s41586-019-1634-0.
- R. J. Mandle, N. Sebastián, J. Martinez-Perdiguero and A. Mertelj, On the molecular origins of the ferroelectric splay nematic phase, Nat. Commun., 2021, 12(1), 4962, DOI:10.1038/s41467-021-25231-0.
- P.-G. d Gennes, The physics of liquid crystals (The international series of monographs on physics), Clarendon Press, Oxford, 1974 Search PubMed.
- M. J. Press and A. S. Arrott, Expansion Coefficient of Methoxybenzylidene Butylaniline through the Liquid-Crystal Phase Transition, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8(3), 1459–1465, DOI:10.1103/PhysRevA.8.1459.
- S. Torza and P. E. Cladis, Volumetric Study of the Nematic-Smectic-A-Transition of N--Cyanobenzylidene-p-Octyloxyaniline, Phys. Rev. Lett., 1974, 32(25), 1406–1409, DOI:10.1103/PhysRevLett.32.1406.
- G. A. Oweimreen, A. K. Shihab, K. Halhouli and S. F. Sikander, Density Measurements in the Nematic and Isotropic Phases of 5CB and Dilute Solutions of Tetraethylmethane in 5CB, Mol. Cryst. Liq. Cryst., 1986, 138(1), 327–338, DOI:10.1080/00268948608071767.
- R. Shimada and H. Watanabe, Thermodynamic Effect on Viscosity and Density of a Mixture of 4-Cyano-4′-pentylbiphenyl (5CB) with Dilute Dimethyl Phthalate (DMP), Nihon Reoroji Gakkaishi, 2020, 48(4), 199–206, DOI:10.1678/rheology.48.199.
- H. R. Zeller, Dielectric relaxation in nematics and Doolittle's law, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26(3), 1785–1787, DOI:10.1103/PhysRevA.26.1785.
- M. Tintaru, R. Moldovan, T. Beica and S. Frunza, Surface tension of some liquid crystals in the cyanobiphenyl series, Liq. Cryst., 2001, 28(5), 793–797, DOI:10.1080/02678290010025459.
- J. Deschamps, J. P. M. Trusler and G. Jackson, Vapor Pressure and Density of Thermotropic Liquid Crystals:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MBBA, 5CB, and Novel Fluorinated Mesogens, J. Phys. Chem. B, 2008, 112(13), 3918–3926, DOI:10.1021/jp711211w.
MBBA, 5CB, and Novel Fluorinated Mesogens, J. Phys. Chem. B, 2008, 112(13), 3918–3926, DOI:10.1021/jp711211w. - G. A. Oweimreen, On the Nature of the Smectic A-to-Nematic Phase Transition of 8CB, J. Phys. Chem. B, 2001, 105(35), 8417–8419, DOI:10.1021/jp011749e.
- D. A. Dunmur, M. R. Manterfield, W. H. Miller and J. K. Dunleavy, The Dielectric and Optical Properties of the Homologous Series of Cyano-Alkyl-Biphenyl Liquid Crystals, Mol. Cryst. Liq. Cryst., 1978, 45(1–2), 127–144, DOI:10.1080/00268947808084998.
- A. J. Leadbetter, J. L. A. Durrant and M. Rugman, The Density Of 4 n-Octyl-4-Cyano-Biphenyl (8CB), Mol. Cryst. Liq. Cryst., 1976, 34(10), 231–235, DOI:10.1080/15421407708083712.
- W. Baran, Z. Raszewski, R. Dabrowski, J. Kedzierski and J. Rutkowska, Some Physical Properties of Mesogenic 4-(trans-4′-n-Alkylcyclohexyl) Isothiocyanatobenzenes, Mol. Cryst. Liq. Cryst., 1985, 123(1), 237–245, DOI:10.1080/00268948508074781.
- D. G. Altman and J. M. Bland, Measurement in Medicine: The Analysis of Method Comparison Studies, J. R. Stat. Soc. Ser. A Stat. Soc., 1983, 32(3), 307–317, DOI:10.2307/2987937.
- P. Martinot-Lagarde, Direct electrical measurement of the permanent polarization of a ferroelectric chiral smectic C liquid crystal (in English), J. Phys., Lett., 1977, 38(1), 17–19, DOI:10.1051/jphyslet:0197700380101700.
- D. Demus, Y. Goto, S. Sawada, E. Nakagawa, H. Saito and R. Tarao, Trifluorinated Liquid Crystals for TFT Displays, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1995, 260(1), 1–21, DOI:10.1080/10587259508038680.
- A. Savitzky and M. J. E. Golay, Smoothing and Differentiation of Data by Simplified Least Squares Procedures, Anal. Chem., 1964, 36(8), 1627–1639, DOI:10.1021/ac60214a047.
- J. Li, S. Gauza and S.-T. Wu, Temperature effect on liquid crystal refractive indices, J. Appl. Phys., 2004, 96(1), 19–24, DOI:10.1063/1.1757034.
- J. C. Jones, On the biaxiality of smectic C and ferroelectric liquid crystals, Liq. Cryst., 2015, 42(5–6), 732–759, DOI:10.1080/02678292.2015.1028492.
- N. W. Roberts, et al., An experimental and theoretical investigation into the reflection spectra of SmC* and SmC A* phases, J. Mater. Chem., 2003, 13(2), 353–359 RSC.
- J. Mills, R. Miller, H. Gleeson, A. Seed, M. Hird and P. Styring, The physical properties of a series of antiferroelectric hetrocyclic esters, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 303(1), 145–152 CrossRef CAS.
- E. Talebian and M. Talebian, A general review on the derivation of Clausius-Mossotti relation, Optik, 2013, 124(16), 2324–2326, DOI:10.1016/j.ijleo.2012.06.090.
- N. Yadav, Y. P. Panarin, W. H. Jiang, G. H. Mehl and J. K. Vij, Spontaneous mirror symmetry breaking and chiral segregation in the achiral ferronematic compound DIO, Phys. Chem. Chem. Phys., 2023, 25(13), 9083–9091, 10.1039/d3cp00357d.
- P. J. Tipping, Liquid Crystals for Energy Applications, 2022 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652, DOI:10.1063/1.464913.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, 6-31G* basis set for third-row atoms, J. Comput. Chem., 2001, 22(9), 976–984, DOI:10.1002/jcc.1058.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01282d |
| This journal is © The Royal Society of Chemistry 2024 |

