Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dual-view transport of intensity phase imaging devices for quantitative phase microscopy applications
Shouyu
Wang
 *abc,
Huachuan
Huang
d,
Aihui
Sun
e,
Lin
Zhu
be,
Wei
Guo
ab,
Keding
Yan
f and
Liang
Xue
g
*abc,
Huachuan
Huang
d,
Aihui
Sun
e,
Lin
Zhu
be,
Wei
Guo
ab,
Keding
Yan
f and
Liang
Xue
g
aJiangsu Province Engineering Research Center of Integrated Circuit Reliability Technology and Testing System, Wuxi University, Wuxi, Jiangsu 214105, China. E-mail: shouyu29@cwxu.edu.cn
bOptiX+ Laboratory, School of Electronics and Information Engineering, Wuxi University, Wuxi, Jiangsu 214105, China
cSingle Molecule Nanometry Laboratory (Sinmolab), Nanjing, Jiangsu, China
dSchool of Manufacture Science and Engineering, Key Laboratory of Testing Technology for Manufacturing Process, Ministry of Education, Southwest University of Science and Technology, Mianyang, Sichuan 621010, China
eComputational Optics Laboratory, Jiangnan University, Wuxi, Jiangsu 214122, China
fAdvanced Institute of Micro-Nano Intelligent Sensing (AIMNIS), School of Electronic Information Engineering, Xi'an Technological University, Xi'an, Shaanxi 710032, China
gCollege of Electronics and Information Engineering, Shanghai University of Electric Power, Shanghai, 200090, China
First published on 14th February 2024
Abstract
Because phase has significantly higher contrast than amplitude, particularly for label-free specimens, and provides a new perspective for morphology and shape testing, quantitative phase microscopy has become an effective means in optical imaging and testing. We designed dual-view transport of intensity phase imaging, which comprehensively considers real-time imaging, simple configuration, and fast phase retrieval. This technique employs two imaging recorders to simultaneously capture under- and over-focus images and recovers the quantitative phase distributions from these defocused images by solving the Poisson equation. Based on such an idea, we designed PhaseRMiC as a phase real-time microscopy camera and PhaseStation as a compact phase imaging work station, and they have been successfully used in live cell observation, whole-slide imaging, and flow cytometry for various purposes, such as specimen detection, counting, recognition, and differentiation. In this work, we first briefly introduce the principle of the dual-view transport of intensity phase imaging, next provide the details of our designed PhaseRMiC and PhaseStation, and finally demonstrate their applications in real-time, field of view scanning, and microfluidic imaging, respectively. Besides, we also compare PhaseRMiC and PhaseStation with other quantitative phase microscopy equipment and lay out their prospects for future applications. We believe our designed dual-view transport of intensity phase imaging as well as its derivatives, PhaseRMiC and PhaseStation, can be a promising choice for quantitative phase microscopy.
1 Introduction
Microscopy can magnify the sample under detection and thus provide details that are beyond the resolution range of the normal eye; therefore, it is an important tool widely used in various fields.1 For example, bright/dark-field microscopy is a widely used tool that provides global images of specimens; fluorescence microscopy provides another perspective for local imaging to support specific testing and observation;2,3 and their joint use proposes a global background and indicates local specifics cooperatively. However, bright/dark-field microscopy suffers from low imaging contrast, especially when the specimen is transparent (such as cells), and staining is suggested to significantly improve the imaging contrast. Besides, fluorescence labeling is essential for fluorescence microscopy. Though staining and labeling can improve the imaging contrast, they not only complicate the sample preparation but also inevitably cause irreversible damage to the samples. To avoid staining and labeling, many label-free microscopy techniques have been updated.4–11 Two- and multi-photon microscopy for detecting autofluorescent cellular species,4,5 second- and third-harmonic-generation microscopy for distinguishing fibrillar structures and lipid bodies,6 and Raman microscopy for determining chemical bonds are all used in local imaging mode.7,8 Phase contrast and differential interference contrast microscopy can offer higher imaging contrast compared to bright/dark-field microscopy. Furthermore, since quantitative phase microscopy can obtain morphology and shape measurements,9–11 which can hardly be obtained by phase contrast and differential interference contrast microscopy, it is a more promising tactic in global imaging mode.Various quantitative phase microscopy techniques have been designed. The most traditional quantitative phase microscopy technique relies on interference, like interferometry or holography.12,13 The phase information is coded in the fringes generated via sample and reference wave interference. Therefore, the sample phase can be demodulated from fringe patterns. Various phase retrieval algorithms have been designed, mainly according to spatial and spectral demodulations. Spatial demodulation, or phase-shifting demodulation, can extract phase from a series of phase-shifting fringe patterns with extremely high accuracy.14,15 While spectral demodulation can reconstruct phase from a single-shot fringe pattern with the carrier to pursue real-time imaging.16–18 The most successful application of interference-based quantitative phase imaging is optical shop testing.19 Combined with microscopy, it is not only used in micro-structure detection (such as MEMS) but is also employed in biomedical applications such as label-free tissue and cell imaging.9,11,20 Unfortunately, due to the requirement for dual-wave interference, interference-based quantitative phase imaging often relies on complicated and bulky systems. Developed from coherent diffraction imaging, ptychography can provide phase imaging with high accuracy and a large field of view (FoV) through scanning in hardware and iterative phase retrieval in software.21–26 Ptychography in the spatial domain, ptychographic iterative engine, reconstructs phase from a series of diffraction patterns obtained by scanning sample or probe light in space with overlapping in neighboring scanning.21–23 Besides, ptychography in the spectral domain, Fourier ptychography, retrieves phase from a series of images taken at different angles of illumination, which carry the information in different spectra with overlapping in the neighboring illumination.24–26 Ptychography can achieve quantitative phase imaging with high accuracy and a large FoV as an advantage, but it has the disadvantage of long-time data collection and phase reconstruction. Different from interferometry/holography and ptychography, which mostly require coherent light, differential phase contrast imaging, relying on spatially partially coherent light, can retrieve specimen phase from a series of images with asymmetric patterns in different illuminations or pupils.27–29 Therefore, it has better immunity to speckle noise, a simpler system, and a faster processing speed compared to interferometry/holography and ptychography. But it still needs multiple shots for phase retrieval. Also relying on partially coherent light, transport of intensity phase imaging can retrieve specimen phase from a series of multi-focus images by solving the Poisson equation.30–32 It shares the same advantages of differential phase contrast imaging as speckle immunity, a simple system, and faster processing speed, and suffers from multiple shots for phase retrieval. Besides these quantitative phase imaging techniques, there are still other methods, such as Shack–Hartmann sensing33 and coded aperture phase imaging.34–37 However, Shack–Hartmann sensing suffers from low spatial resolution, so it is widely used for wavefront sensing. Coded aperture phase imaging has a simple system but requires multiple shots and long-time phase retrieval. Therefore, interferometry/holography, ptychography, differential phase contrast imaging, and transport of intensity phase imaging are the mainstream techniques in quantitative phase microscopy.
To suit various kinds of applications, quantitative phase imaging techniques with simple systems, dynamic imaging capability, and fast processing speeds are preferred. Interferometry/holography supports dynamic imaging, but many of them rely on complicated and bulky systems. Many updated strategies have been reported to address the issue. For example, diffraction phase imaging integrates a grating and a pinhole to construct the single-path sample and reference beam configurations and reduce the system size.38 Quadriwave lateral shearing interferometry employs a chessboard grating instead of independent sample and reference systems to obtain shearing fringes and reduce the system size.39,40 Lensless digital holography, often based on in-line holography, can even miniaturize the system into a handheld size.41,42 But interferometry/holography still suffers from long-time phase unwrapping. Though coherent modulated imaging provides a way for single-shot quantitative phase imaging,43 ptychography is not a preferred solution for dynamic imaging due to its time-consuming iteration for phase retrieval. Differential phase contrast imaging has a relatively simple system and a fast-processing speed, and asymmetric patterns in different illuminations or pupils can be obtained simultaneously by relying on multi-wavelength illumination.44–47 But it cannot deal with dispersed specimens. Similarly, though relying on chromatic dispersion to simultaneously obtain multi-focus images is also a solution for real-time transport of intensity phase imaging,48 it cannot deal with dispersed specimens. Besides, using prism,49–53 grating,54–56 diffractive optical element,57 optical sieve,58,59 metasurface,60 and spatial light modulator,61 multi-focus images can also be simultaneously obtained; however, these methods suffer from limited FoVs and require complicated setups. To solve the problem, inspired by our previous works,62–64 we designed dual-view transport of intensity phase imaging,65–69 which comprehensively considers real-time imaging, simple configuration, and fast phase retrieval, as shown in Fig. 1(A). This technique employs two imaging recorders to simultaneously capture under- and over-focus images and recover the quantitative phase distributions. Additionally, based on the idea, we designed PhaseRMiC as a phase real-time microscopy camera and PhaseStation as a compact phase imaging work station, as revealed in Fig. 1(B) and (C), and they have been successfully used in live cell observation, whole-slide imaging, and flow cytometry for various purposes, such as specimen detection, counting, recognition, and differentiation.
 | ||
| Fig. 1 Dual-view transport of intensity phase imaging and devices. (A) Dual-view transport of intensity phase imaging. Reproduced from ref. 64 with permission from The Optical Society, copyright 2019; (B) PhaseRMiC. Reproduced from ref. 65 with permission from The Optical Society, copyright 2021; (C) PhaseStation. Reproduced from ref. 68 with permission from The Optical Society, copyright 2023. | ||
In this work, we introduce the dual-view transport of intensity phase imaging and demonstrate its derivatives, PhaseRMiC and PhaseStation, in applications. In detail, we introduce the principle of the dual-view transport of intensity phase imaging and provide its algorithms, including FoV correction and phase retrieval, in section 2. Then, we propose the scheme for the dual-view transport of intensity phase imaging and the configurations of the PhaseRMiC and PhaseStation in section 3. Subsequently, we demonstrate their various applications in dynamic imaging for live cell observation, whole slide imaging for target recognition and detection, and microfluidic imaging for flow cytometry in section 4. Finally, we compare PhaseRMiC and PhaseStation with other quantitative phase imaging equipment and point out the pros and cons of the dual-view transport of intensity phase imaging in section 5. Additionally, we also mention the future development directions of the PhaseRMiC and PhaseStation in the same section. We hope that this work will serve as a helpful resource for quantitative phase imaging.
2 Dual-view transport of intensity phase imaging
According to the principle of the dual-view transport of intensity phase imaging, the specimen phase can be retrieved from two defocus images captured simultaneously as under- and over-focus images. Different from classical techniques that directly capture the in-focus image, dual-view transport of intensity phase imaging computes the in-focus image as the average of the recorded under- and over-focus images; therefore, this way decreases the capture number of the multi-focus images, simplifies the optical system, and supports real-time imaging. Furthermore, because two image recorders capture under- and over-focus images, the large FoV is maintained. In this section, the phase retrieval principle is first illustrated, and then a numerical simulation is provided to prove the effectiveness of the dual-view transport of intensity phase imaging.2.1 Overview of the transport of intensity phase imaging
Different from interferometry and coherent diffraction imaging relying on coherent light sources, transport of intensity phase imaging, which is a non-interferometric approach, is a preferred solution in short-wavelength imaging such as X-ray imaging,70 transmission electron microscopy,71 and neutron radiography.72 Moreover, due to its simple optical system and unwrapping-free advantage, transport of intensity phase imaging extends its applications in visible light bands, such as adaptive optics in astronomy73,74 and optical imaging.75–83Like interferometry and coherent diffraction imaging, which code phase into fringe and diffraction pattern, respectively, transport of intensity phase imaging code phase into imaging intensity. In other words, a phase change distorts the wavefront and thus generates an inhomogeneity in the intensity distribution. From the phase-distorted inhomogeneous intensity, the phase can be reconstructed by solving the transport of intensity equation, as demonstrated in eqn (1). The theoretical background of the transport of intensity equation was first discussed84,85 from the classical Helmholtz equation. The derivative can be found in ref. 86 and 87 in detail. In eqn (1), φ is the phase distribution, λ is the wavelength, k as 2π/λ is the wave number, Δ is the defocus distance, and ∇⊥ is the lateral gradient operator.
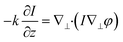 | (1) |
Various methods have been reported to solve the transport of intensity equation,88–93 and the most classical one is based on the auxiliary function proposed by Teague84 and the derivative feature of the Fourier transform. In brief, the auxiliary function ϕ is defined as eqn (2), and the transport of intensity equation can be derived into eqn (3) and (4).
| ∇⊥ϕ = I∇⊥φ | (2) |
| ∇⊥2ϕ = −k∂zI | (3) |
| ∇⊥2φ = ∇⊥·(I−1∇⊥ϕ) | (4) |
According to the two-dimensional derivative feature of the Fourier transform (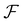 ), the auxiliary function can be extracted according to eqn (5), and the phase under detection can finally be retrieved according to eqn (6).
), the auxiliary function can be extracted according to eqn (5), and the phase under detection can finally be retrieved according to eqn (6).
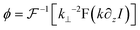 | (5) |
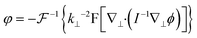 | (6) |
∂zI can be usually computed using center finite difference approach from under-, in- and over-focus images. But multi-distance approaches can obtain higher phase reconstruction accuracy but require more image captures.94–99 The tradeoff between phase retrieval accuracy and multi-focus images should be comprehensively considered in different applications.86,100,101 For example, multi-distance approaches are preferred to pursue high accuracy in phase reconstruction, and fewer multi-focus image captures can accelerate image recording efficiency and provide a solution for real-time quantitative phase imaging. Specifically, our proposed dual-view transport of intensity phase imaging techniques and devices can simultaneously capture under- and over-focus images, thus supporting real-time quantitative phase imaging.
2.2 Phase retrieval principle
Different from classical transport of intensity phase imaging, only the under- (I−Δ) and over-focus (IΔ) images are recorded. The in-focus image can then be calculated as the average of two defocus images using eqn (7). Therefore, three multi-focus images, under-, in-, and over-focus ones, can be obtained for further phase retrieval.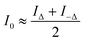 | (7) |
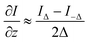 | (8) |
In the following, numerical simulation is employed to prove the effectiveness of the dual-view transport of intensity phase imaging.
2.3 Phase retrieval numerical simulation
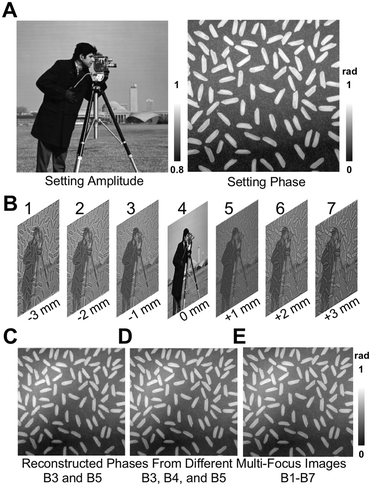
To test the accuracy of the dual-view transport of intensity phase imaging, numerical simulation was employed. Fig. 2(A) reveals the setting amplitude and phase distributions with pixel numbers of 256 × 256 and a pixel size of 10 μm. Fig. 2(B) lists the computed multi-focus images with the defocus distances of −3 mm, −2 mm, −1 mm, 0 mm, 1 mm, 2 mm, and 3 mm, respectively. In the multi-focus image computations, the angular spectrum method was adopted, and the used wavelength λ was 532 mm. Fig. 2(C) lists the retrieved phase using dual-view transport of intensity phase imaging from Fig. 2(B3) and (B5). Fig. 2(D) lists the retrieved phase using classical transport of intensity phase imaging from Fig. 2(B3)–(B5). Fig. 2(E) lists the retrieved phase using higher-order transport of intensity phase imaging from multi-focus images from Fig. 2(B1)–(B7). All these retrieved phases are close to the setting phase in Fig. 2(A), and the correlation coefficients are 0.9205, 0.9490, and 0.9513, and the peak signal-to-noise ratios (PSNRs) are 20.56 dB, 21.02 dB and 21.26 dB, respectively. The quantitative comparisons prove that the dual-view transport of intensity phase imaging can support high-quality quantitative phase imaging.According to the above numerical simulation, it is proven that the dual-view transport of intensity phase imaging can support quantitative phase imaging, and additionally, it only requires two image recordings, simplifying the optical system and supporting real-time imaging. Therefore, it is a promising way to develop devices for quantitative phase imaging. The following two devices, PhaseRMiC and PhaseStation, which have been developed and employed in many applications, are introduced in the next section.
3 PhaseRMiC and PhaseStation
Based on our designed dual-view transport of intensity phase imaging in Fig. 1(A), we proposed PhaseRMiC and PhaseStation: the former works with a commercial microscope as a camera in Fig. 1(B), and the latter equips microscopy and dual-view transport of intensity phase imaging as a miniaturized quantitative phase imaging device in Fig. 1(C). In this section, both the hardware and software of PhaseRMiC and PhaseStation are briefly introduced.3.1 Hardware
Dual-view intensity phase imaging was first used by mounting two image recorders on the binoculars of a commercial microscope.62–64 To make their imaging planes different for simultaneously capturing under- and over-focus images, C-mount brass spacer rings were adopted. It should be noted that this is PhaseRMiC's prototype. Verified using standard samples in statics and tested using practical samples in dynamics, the device can support dual-view transport of intensity phase imaging and provide specimen phase with high accuracy and fast speed. However, this device suffers from many problems, such as a non-stable system and complicated adjustments.To solve these problems, we proposed an updated PhaseRMiC device, as shown in Fig. 3(A),65 which is an image recorder that is linked to a commercial microscope. Its configuration is very simple, consisting only of a prism (Daheng Optics, China) and a board-level camera (Daheng Image, China) with two CMOS imaging sensors integrated using 3-D printed structures, as shown in Fig. 3(B)–(D). In detail, the wave carrying the specimen phase from the C-mount of the commercial microscope is first split by a prism and then reaches two CMOS imaging sensors. Additionally, because the interval between these two CMOS imaging sensors and the prism was different, these two images were captured in different focal planes. By adjusting the sample position, these imaging sensors can capture the under- and over-focus images for further phase retrieval.
 | ||
| Fig. 3 PhaseRMiC hardware. (A) Prototype. Reproduced from ref. 65 with permission from The Optical Society, copyright 2021; (B) configuration; (C) inner structure; (D) optical system. | ||
Different from PhaseRMiC, which only works as a phase imaging camera, PhaseStation combines microscopy and quantitative phase imaging, so it works as a quantitative phase microscope. Fig. 4(A) depicts the PhaseStation's prototype, and Fig. 4(B) reveals its scheme. The illumination was from an LED source filtered using an interference-based filter and collimated using two lenses. The almost parallel wavefront was incident on the sample, which was fixed on the sample stage, and the transmitted wavefront was collected and magnified using a micro-objective, then split by the prism, and finally imaged by two image sensors located in different imaging planes, as revealed in Fig. 4(C). By adjusting the sample position, these imaging sensors can capture the under- and over-focus images for further phase retrieval.
 | ||
| Fig. 4 PhaseStation hardware. (A) PhaseStation prototype; (B) PhaseStation scheme; (C) dual-view imaging part. Reproduced from ref. 68 with permission from The Optical Society, copyright 2023. | ||
3.2 System adjustment
To ensure the accuracy of phase retrieval, the systems of both PhaseRMiC and PhaseStation should be calibrated and adjusted before applications. Specifically, the defocus distance and FoV mismatch between the two image sensors should be calibrated, and the in-focus specimen position should be determined. These system adjustments are briefly mentioned in the following.The defocus distance between two imaging sensors was precisely measured by laser ranging. After fixing the laser ranger and prism-imaging sensor module, these two imaging sensors were measured in sequence; that is, one was detected while the other was blocked. The interval between these two imaging sensors was the difference between the two measured distances.
A standard target (grid plate) was used for FoV calibration, and the in-focus plane in the specimen space could be determined using the classic Brenner gradient in-focus criterion by laterally shifting the precision translation specimen stage. Afterward, the standard sample was shifted to the central positions of the in-focus planes, which corresponded to two image recorders, and two under- and over-focus images could be captured. Relying on the phase correlation-based FoV correction method, all the scale, rotation, and translation differences between the captured under- and over-focus images could be determined and compensated. For example, two images, i1 and i2, with a translation of Δx and Δy are illustrated in eqn (9).
| i2(x, y) = i1(x − Δx, y − Δy) | (9) |
| I2(u, v) = I1(u, v)e−j2π(uΔx+vΔy) | (10) |
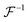 is the inverse Fourier transform and * indicates the conjugation.
is the inverse Fourier transform and * indicates the conjugation.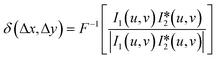 | (11) |
Besides translation, scale and rotation also exist in the under- and over-focus images. In the phase correlation-based FoV correction, scale and rotation are first determined and compensated, and translation is next determined and compensated. In detail, two images i and i′ with scale (s), rotation (θ), and translation (x0, y0) are listed in eqn (9), in which x′ = s·x·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + s·y·sin
θ + s·y·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − x0 and y′ = −s·x·sin
θ − x0 and y′ = −s·x·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + s·y·cos
θ + s·y·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − y0 describe the relation between (x, y) and (x′, y′).
θ − y0 describe the relation between (x, y) and (x′, y′).
| i(x, y) = i′(x′, y′) | (12) |
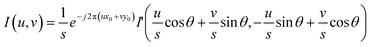 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ and v = r·sin
φ and v = r·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, and (r,φ) represents the polar coordinate.
φ, and (r,φ) represents the polar coordinate.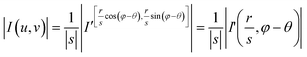 | (14) |
Taking the logarithm of r/s to convert the division into subtraction, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s and θ in eqn (15), which are equivalent to Δx and Δy in eqn (9), can be determined.
s and θ in eqn (15), which are equivalent to Δx and Δy in eqn (9), can be determined.
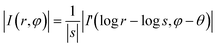 | (15) |
Before using PhaseRMiC and PhaseStation for quantitative phase imaging, the specimen under detection should first be set at the in-focus plane. In other words, it should be guaranteed that two image recorders can capture under- and over-focus images, respectively. With the prior FoV calibration, the mismatch between the two image sensors can be precisely determined. As a result, by first compensating the FoV and then computing the average, the average intensity of those captured by two image recorders can be quickly obtained while laterally shifting the sample. This computed average intensity is evaluated by an in-focus criterion (such as the classic Brenner gradient (B) in eqn (16), where s(i,j) represents pixel intensity at the pixel position (i,j) and m was chosen as 2), and the specimen position can be determined. In other words, it is the autofocus process of PhaseRMiC and PhaseStation.
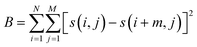 | (16) |
To summary the phase retrieval process, Fig. 5 demonstrate the flowchart of the dual-view transport of intensity phase imaging.
3.3 Software
To simplify the use of PhaseRMiC and PhaseStation, we designed software for them, as shown in Fig. 6. The main software functions are image recording and display, FoV correction, and phase retrieval. Note that the defocus distance and FoV mismatch of two fixed image sensors have been previously calibrated and introduced into the software. In the control module region, the “Camera Scan” and “Motor Scan” buttons are used for the image recorder and precision translation stage, respectively. The “Camera On” button is to record and display the multi-focal images. The “Serial Port On” button and serial port selection are for 3-D precision translation stage control. The “Phase Image” button is for phase retrieval, phase image display, and storage. After clicking the “Camera On” button, the image display region reveals the dual-view images recorded by two image recorders as well as their computed average after FoV correction. Via axial shifting of the specimen under detection, the in-focus specimen plane can be determined according to the average intensity using the in-focus criterion. After clicking the “Phase Imaging” button, the image display region also reveals the reconstructed phase. After the determination of the specimen position and the setting of the sampling rate, the software automatically records the under- and over-focus image, corrects the FoV, reconstructs the phase, and displays and saves the data. The software makes it convenient for PhaseRMiC and PhaseStation applications, thus paving the way for their practical applications in various fields. According to the above-mentioned hardware and software designs, PhaseRMiC and PhaseStation have been constructed for many applications. In the following section, these applications of PhaseRMiC and PhaseStation are demonstrated.4 Applications
The proposed PhaseRMiC and PhaseStation have been successfully employed in many applications, especially in dynamic imaging, whole-slide imaging, and microfluidic imaging. In this section, these applications have been briefly introduced to verify the performances of PhaseRMiC and PhaseStation.4.1 Dynamic imaging
Based on the single-shot quantitative phase imaging capability, dual-view transport of intensity phase imaging-based PhaseRMiC and PhaseStation are the preferred solutions for dynamic imaging. PhaseRMiC has been used successfully for dynamic cellular quantitative phase imaging when combined with a commercial microscope. The dual-view transport of intensity phase microscopy prototype was adopted to measure adenosine triphosphate (ATP)-induced cellular fluctuations.64 It is found that the cellular fluctuation amplitude and speed increased with ATP compared to those with ATP depletion, and the cellular fluctuation amplitude and speed decreased when adenylyl-imidodiphosphate (AMP-PNP) was introduced since AMP-PNP competes with ATP to bind to the ATP binding site. It is the first dynamic imaging trial for the dual-view transport of intensity phase imaging technique, though its system was still bulky and complicated. With the improved PhaseRMiC, dynamic imaging can be implemented using a simpler and more compact system as well as more convenient operations. For example, PhaseRMiC was used to observe live cell dynamics during trypsinization.65 Vero cells were cultured in 10 mL of Dulbecco's modified Eagle medium with 0.05% fetal bovine serum for 12–14 h until they were completely adherent and extended. Afterward, the culture medium was moved, and another 2 mL of phosphate buffer saline was introduced for cell cleaning three times before being finally sucked out. Following the addition of trypsin solution, under- and over-focus images were captured using PhaseRMiC at a frame rate of 20 fps. Fig. 7 depicts time-series images of under- and over-focus as well as the reconstructed phase distributions during 180 s. The dynamic quantitative phase imaging demonstrates that the Vero cell changed from rhombic to round with the trypsin solution introduction. | ||
| Fig. 7 Dynamic imaging applications. Time-series images of under- and over-focus as well as the reconstructed phase distributions of Vero cells during trypsinization in 180 s. Reproduced from ref. 65 with permission from The Optical Society, copyright 2021. | ||
Due to their excellent single-shot quantitative phase imaging capability and their convenience in applications, these dual-view transport of intensity phase imaging-based devices can be used in the future in many label-free dynamic observation applications.
4.2 Whole-slide imaging
Due to the microscopy system's small FoV, only a small portion of the specimens can be observed. To expand the observation throughput, FoV scanning is employed. Using PhaseRMiC, we proposed a label-free whole-blood detection tactic to detect the blood smear in Fig. 8.67 In detail, a freshly prepared blood smear with no labeling was scanned using the precision translation stage, and massive under- and over-focus images corresponding to different FoVs were recorded during blood smear scanning in Fig. 8(A). Using FoV stitching, two under- and over-focus images with extremely large FoVs were reconstructed in Fig. 8(B), and their FoVs were compensated for phase reconstruction in Fig. 8(C). In the applications, the central parts (central 50% in the area) were used for further FoV stitch, and the overlapping between two neighboring FoVs was set at 30% (in the area). In addition, Fig. 8(D) lists zoomed-in fields of interest (FoIs), showing the special biconcave structures of erythrocytes. Except for erythrocytes, leukocytes and platelets also exist in the blood smear. Using our designed BSRNet in Fig. 8(E), erythrocytes, leukocytes, and platelets can be automatically recognized and counted according to the retrieved phase distributions in extended FoVs, as shown in Fig. 8(F). According to the quantitative phase distributions, the deep learning-assisted blood cell recognition method works well not only in discrete cell-distributed cases but also in cell-overlapping conditions in Fig. 8(F). Therefore, this proposed method has great potential for application in blood testing aimed at disease diagnostics.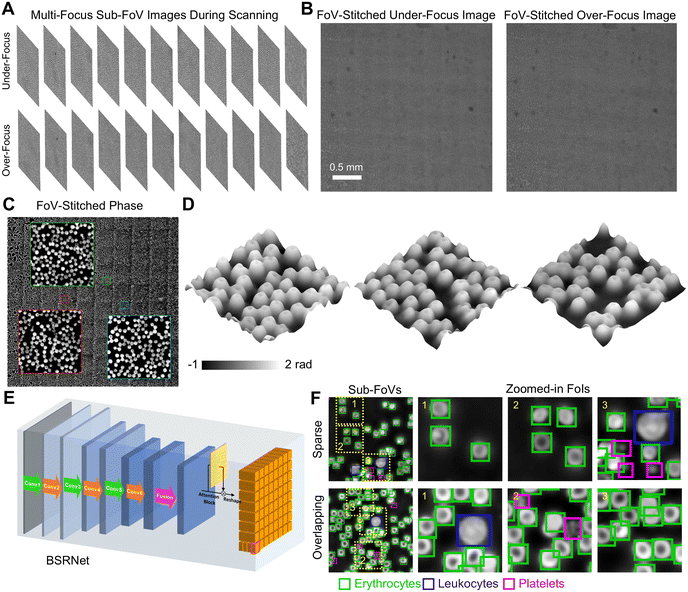 | ||
| Fig. 8 Whole-slide imaging applications. (A) Under- and over-focus images in different sub-FoVs during scanning; (B) FoV-stitched under- and over-focus images; (C) quantitative phase distribution reconstructed from (B); (D) FoIs; (E) BSRNet; (F) blood cell recognition. Reproduced from ref. 67 with permission from Elsevier Sciences, copyright 2022. | ||
Similarly, we also employed the same system to detect the bubbles in the transformer oil to evaluate its quality since bubbles are generated during transformer running.66 The transformer oil sample was first introduced into the specimen chamber; next, the specimen chamber was scanned to record under- and over-focus images in the extended FoVs; and finally, bubble volume can be quantified according to the bubble phase distributions. The quality of the transformer oil (new, available, and unavailable) can be determined according to the oil-to-gas volume ratio.
These dual-view transport of intensity phase imaging-based devices could be prototypes of the whole-slide quantitative phase imaging device, which may provide a new perspective for digital pathology.
4.3 Microfluidic imaging
Also based on the single-shot quantitative phase imaging capability, dual-view transport of intensity phase imaging is a suitable tool for imaging flow cytometry, which can be used for cell observation and analysis with high throughput and efficiency. To construct a phase imaging flow cytometry system, we first used polydimethylsiloxane (PDMS) to fabricate a microfluidic channel with a width and height of 200 μm, as shown in Fig. 9(A).69 Moreover, we connected the PhaseRMiC to a commercial microscope (TiE-2, Nikon, Japan) to construct the optical system. In addition, a micromolecular injection pump (LSP, Rongbai, China) was also used to drive the sample solution flowing in the microfluidic channel. Since the image processing time was around 25 ms, the frame rate of the CMOS camera was 33 fps, and the exposure time was 10 μs, the phase imaging flow cytometry system could support real-time imaging.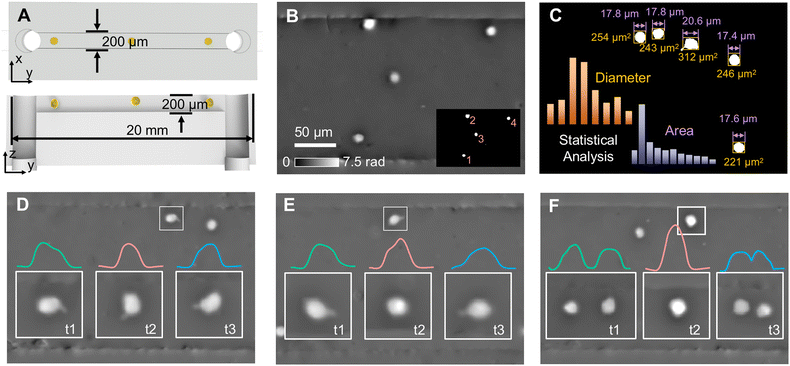 | ||
| Fig. 9 Microfluidic imaging applications. (A) Microfluidic chip; (B) phase image of a frame and cell recognition; (C) statistical analysis; (D) single-cell rotation in the x–y plane; (E) single-cell rotation in the y–z plane; (F) dual-cell binary rotation in the y–z plane. Reproduced from ref. 69 with permission from The Optical Society, copyright 2023. | ||
We used the phase imaging flow cytometry system for cell imaging and analysis. The C6 cell solution at a concentration of 2 × 105 cells per mL was injected into a microfluidic channel with a flow rate of 36 μL min−1, and phase images of a fixed FoV but with flowing C6 cells were reconstructed, such as one shown in Fig. 9(B). According to threshold segmentation, C6 cells could be recognized in Fig. 9(C). Besides, its morphological parameters, such as cellular diameter and area, can be quantified. With multiple frames, statistical cellular parameters can be obtained and analyzed. Besides high-throughput cellular imaging, this phase imaging flow cytometry system can also be applied for monitoring cell dynamics in the flow. For example, according to the serial phase images of cells flowing across the FoV, single-cell rotation in the x–y plane, in the y–z plane, and dual-cell binary rotation in the y–z plane can be distinguished, as revealed in Fig. 9(D), (E) and (F), respectively.
Relying on the PhaseRMiC, the phase imaging flow cytometry system has the advantages of simple configuration, accurate phase retrieval, and real-time imaging; therefore, dual-view transport of intensity phase imaging is a promising tool for developing phase imaging flow cytometry.
5 Comparisons and prospects
Besides the transport of intensity phase imaging, other quantitative phase imaging techniques have been employed to develop different kinds of devices. Table 1 compares the PhaseRMiC/PhaseStation with other quantitative phase imaging devices. It should be noted that ptychography-based techniques and devices have the highest accuracy in phase retrieval and support imaging in extremely large FoVs. However, they rely on multiple shots and time-consuming iterative phase retrieval; therefore, they cannot support real-time or dynamic imaging applications. Interferometry/holography balances the phase retrieval accuracy and captured image numbers, but it still requires time-consuming phase unwrapping and often relies on complex optical systems because of the reference arm. Differential phase contrast imaging simplifies the optical system and accelerates the phase retrieval speed, but the classical one does not support single-shot phase imaging, and the color coding-based one cannot suffer from sample dispersion-induced phase retrieval accuracy reduction. Transport of intensity phase imaging is a preferred solution with simple systems, dynamic imaging capability, and fast processing speeds. It is because it reduces the image captures, simplifies the optical system, and accelerates the phase retrieval speed. Our proposed dual-view transport of intensity phase imaging as well as PhaseRMiC and PhaseStation overcome the drawbacks such as focal scanning of the classical one, sample dispersion-induced phase retrieval accuracy reduction of the achromatic one, and FoV limitation of the FoV splitting one. Therefore, the proposed PhaseRMiC and PhaseStation are the preferred solutions for dynamic phase imaging applications.| Phase retrieval methods | Phase retrieval performance | ||||||
|---|---|---|---|---|---|---|---|
| Categories | Accuracy | Dynamic | Speed | Complexity | Field of view | Resolution | |
| Interferometry/holography | Spatial demodulation/on-axis | Very high | Multi-shots | Slow | Complex | Normal | High |
| Gold standard | Phase shifting | Unwrapping | Phase shifting | Depend on imaging system | Depend on imaging system | ||
| Spectral demodulation/off-axis | High | Single-shot | Slow | Complex | Normal | High | |
| Carrier frequency | Unwrapping | Often non-common path | Depend on imaging system | Depend on imaging system | |||
| Quadriwave lateral shearing interferometry/shearing | High | Single-shot | Normal | Simple | Normal | High | |
| Carrier frequency | Bidirectional processing | Common path | Depend on imaging system | Depend on imaging system | |||
| Ptychography | Ptychographic iterative engine | Very high | Multi-shots | Very slow | Normal | Very large | Very high |
| FoV scanning | Iteration | Lensfree but scanning required | FoV scanning | Diffraction limit | |||
| Fourier Ptychography | Very high | Multi-shots | Very slow | Complex | Large | Very high | |
| Spectral scanning | Iteration | Scanning required | Break through space bandwidth product | Break through space bandwidth product | |||
| Coherent modulated imaging | High | Single-shot | Very slow | Simple | Very small | High | |
| Single modulator | Iteration | Lens and scanning free | Limited by CMI principle | Depend on imaging system | |||
| Differential phase contrast imaging | Classical | High | Multi-shots | Fast | Complex | Normal | High |
| Illumination/pupil scanning | Unwrapping free | Illumination/pupil scanning | Depend on imaging system | Depend on imaging system | |||
| Color coding | Normal | Single-shot | Fast | Normal | Normal | High | |
| Dispersion | Simultaneous imaging with different illuminations/pupils | Unwrapping free | Color coding | Depend on imaging system | Depend on imaging system | ||
| Transport of intensity phase imaging | Classical | High | Multi-shots | Fast | Complex | Normal | High |
| Focal scanning | Unwrapping free | Focal scanning | Depend on imaging system | Depend on imaging system | |||
| Achromatic | Normal | Single-shot | Fast | Simple | Normal | High | |
| Dispersion | Simultaneous multi-focal imaging | Unwrapping free | Multi-wavelength sources | Depend on imaging system | Depend on imaging system | ||
| FoV splitting | High | Single-shot | Fast | Normal | Small | High | |
| Simultaneous multi-focal imaging | Unwrapping free | Extra elements | FoV splitting | Depend on imaging system | |||
| Dual-view | High | Single-shot | Fast | Simple | Normal | High | |
| Proposed | Simultaneous multi-focal imaging | Unwrapping free | Dual cameras and prism | Depend on imaging system | Depend on imaging system | ||
However, besides the advantages of the transport of intensity phase imaging and its dual-view versions, they still suffer from a series of problems. Firstly, its accuracy is limited, especially compared to ptychography and interferometry/holography. The main reason is low-frequency spatial noise due to the noise-resolution tradeoff in the transport of intensity phase imaging.86,100,101 Various approaches have been designed to alleviate the problem and thus improve phase retrieval accuracy, such as multi-distance approaches,91,94–99 computational illumination approaches,100–102 and iterative approaches.103,104 Unfortunately, multi-distance approaches can hardly support single-shot quantitative phase imaging because they need many defocus image captures, and iterative approaches consume a long time in phase retrieval. Besides, computational illumination approaches require heavy modifications to the commercial microscope. Though our designed dual-view transport of intensity phase imaging techniques and devices sacrifice the phase retrieval accuracy, they have the advantages of simple optical systems, fast phase retrieval, and real-time phase imaging capability. Therefore, they are preferred tools in dynamic imaging, whole-slide imaging, and microfluidic imaging. Secondly, the dual-view transport of intensity phase imaging techniques and devices depend on two cameras. Though they maintain relatively large FoVs and simple optical systems, they rely on the good consistency of two cameras. Therefore, intensity calibration and FoV compensation are required to improve phase retrieval accuracy. Besides the mentioned dual-camera tactic, a series of single-camera-based systems49–61 have also been reported to simultaneously capture multi-focus images for real-time quantitative phase imaging. These single-camera-based systems avoid the non-consistency problem, but they suffer from limited FoVs and require complicated and expensive setups.
Finally, it should be noted that quantitative phase imaging provides the global background of the specimen under detection. It is an updated version of bright/dark-field and phase contrast imaging since it provides not only high imaging contrast but also quantitative specimen information. Unfortunately, quantitative phase imaging loses the specificity that can provide more biological and chemical information on the specimen under detection. Therefore, to reflect more information, a combination of quantitative phase imaging and specific imaging (such as fluorescence imaging) as multi-modal imaging is a promising direction for various fields.
6 Conclusion
In this work, we provide the details of the dual-view transport of intensity phase imaging, including its principles, algorithms, devices, applications, and prospects. Compared to other quantitative phase imaging techniques, the dual-view transport of intensity phase imaging comprehensively considers real-time imaging, simple configuration, and fast phase retrieval, and it is thus suitable for dynamic and (mechanical or microfluidic) scanning imaging. Therefore, it is believed that our dual-view transport of intensity phase imaging design and its devices, PhaseRMiC and PhaseStation, can be a potential option for quantitative phase imaging and testing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work is supported by the National Natural Science Foundation of China (62105196), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (23KJB510034), the Qing Lan Project, and the Wuxi University Research Start-up Fund for Introduced Talents (2023r062). Additionally, authors thank Xiaolin Tian, Qingtao Gong, Chao Chen, Jian Wang, Yu-Nan Lu, Prof. Yanke Shan, Prof. Cheng Liu, and Prof. Fei Liu for their contributions to dual-view transport of intensity phase imaging, PhaseRMiC, and PhaseStation.References
- D. J. Stephens and V. J. Allan, Science, 2003, 300, 82–86 CrossRef CAS PubMed.
- M. Renz, Cytometry, Part A, 2013, 83, 767–779 CrossRef PubMed.
- R. Yuste, Nat. Methods, 2005, 2, 902–904 CrossRef CAS PubMed.
- F. Helmchen and W. Denk, Nat. Methods, 2005, 2, 932–940 CrossRef CAS PubMed.
- E. E. Hoover and J. A. Squier, Nat. Photonics, 2013, 7, 93–101 CrossRef CAS PubMed.
- C. Xu and F. Wise, Nat. Photonics, 2013, 7, 875–882 CrossRef CAS PubMed.
- J. P. Pezacki, J. A. Blake, D. C. Danielson, D. C. Kennedy, R. K. Lyn and R. Singaravelu, Nat. Chem. Biol., 2011, 7, 137–145 CrossRef CAS PubMed.
- W. Tipping, M. Lee, A. Serrels, V. Brunton and A. Hulme, Chem. Soc. Rev., 2016, 45, 2075–2089 RSC.
- Y. Park, C. Depeursinge and G. Popescu, Nat. Photonics, 2018, 12, 578–589 CrossRef CAS.
- Y. Jo, H. Cho, S. Y. Lee, G. Choi, G. Kim, H.-s. Min and Y. Park, IEEE J. Sel. Top. Quantum Electron., 2018, 25, 1–14 Search PubMed.
- T. Cacace, V. Bianco and P. Ferraro, Opt. Lasers Eng., 2020, 135, 106188 CrossRef.
- D. Gabor, Nature, 1948, 161, 777–778 CrossRef CAS PubMed.
- M. K. Kim, SPIE Rev., 2010, 1, 018005 Search PubMed.
- I. Yamaguchi and T. Zhang, Opt. Lett., 1997, 22, 1268–1270 CrossRef CAS PubMed.
- Z. Wang, L. Millet, M. Mir, H. Ding, S. Unarunotai, J. Rogers, M. U. Gillette and G. Popescu, Opt. Express, 2011, 19, 1016–1026 CrossRef CAS PubMed.
- M. Takeda, H. Ina and S. Kobayashi, J. Opt. Soc. Am., 1982, 72, 156–160 CrossRef.
- T. Ikeda, G. Popescu, R. R. Dasari and M. S. Feld, Opt. Lett., 2005, 30, 1165–1167 CrossRef PubMed.
- N. T. Shaked, V. Micó, M. Trusiak, A. Kuś and S. K. Mirsky, Adv. Opt. Photonics, 2020, 12, 556–611 CrossRef.
- D. Malacara, Optical Shop Testing, Wiley, New Jersey, 2006 Search PubMed.
- G. Dardikman and N. T. Shaked, Opt. Commun., 2018, 422, 8–16 CrossRef CAS.
- J. M. Rodenburg and H. M. L. Faulkner, Appl. Phys. Lett., 2004, 85, 4795–4797 CrossRef CAS.
- H. M. L. Faulkner and J. M. Rodenburg, Phys. Rev. Lett., 2004, 93, 023903 CrossRef CAS PubMed.
- A. Maiden, D. Johnson and P. Li, Optica, 2017, 4, 736–745 CrossRef.
- G. Zheng, R. Horstmeyer and C. Yang, Nat. Photonics, 2013, 7, 739–745 CrossRef CAS PubMed.
- G. Zheng, C. Shen, S. Jiang, P. Song and C. Yang, Nat. Rev. Phys., 2021, 3, 207–223 CrossRef.
- K. Guo, S. Dong and G. Zheng, IEEE J. Sel. Top. Quantum Electron., 2016, 22, 77–88 Search PubMed.
- S. B. Mehta and C. J. R. Sheppard, Opt. Lett., 2009, 34, 1924–1926 CrossRef PubMed.
- L. Tian and L. Waller, Opt. Express, 2015, 23, 11394–11403 CrossRef CAS PubMed.
- R. Cao, M. Kellman, D. Ren, R. Eckert and L. Waller, Biomed. Opt. Express, 2022, 13, 1671–1684 CrossRef PubMed.
- M. R. Teague, J. Opt. Soc. Am., 1983, 73, 1434–1441 CrossRef.
- F. Roddier, Appl. Opt., 1990, 29, 1402–1403 CrossRef CAS PubMed.
- C. Zuo, J. Li, J. Sun, Y. Fan, J. Zhang, L. Lu, R. Zhang, B. Wang, L. Huang and Q. Chen, Opt. Lasers Eng., 2020, 135, 106187 CrossRef.
- J. Liang, B. Grimm, S. Goelz and J. F. Bille, J. Opt. Soc. Am. A, 1994, 11, 1949–1957 CrossRef CAS PubMed.
- R. Horisaki, Y. Ogura, M. Aino and J. Tanida, Opt. Lett., 2014, 39, 6466–6469 CrossRef PubMed.
- Y. Wu, M. K. Sharma and A. Veeraraghavan, Light: Sci. Appl., 2019, 8, 44 CrossRef PubMed.
- C. Wang, X. Dun, Q. Fu and W. Heidrich, Opt. Express, 2017, 25, 13736–13746 CrossRef PubMed.
- C. Wang, Q. Fu, X. Dun and W. Heidrich, Opt. Express, 2020, 28, 5273–5287 CrossRef PubMed.
- B. Bhaduri, C. Edwards, H. Pham, R. Zhou, T. H. Nguyen, L. L. Goddard and G. Popescu, Adv. Opt. Photonics, 2014, 6, 57–119 CrossRef.
- G. Baffou, J. Phys. D: Appl. Phys., 2021, 54, 294002 CrossRef CAS.
- G. Baffou, ACS Photonics, 2023, 10, 322–339 CrossRef CAS.
- A. Greenbaum, W. Luo, T.-W. Su, Z. Göröcs, L. Xue, S. O. Isikman, A. F. Coskun, O. Mudanyali and A. Ozcan, Nat. Methods, 2012, 9, 889–895 CrossRef CAS PubMed.
- A. Ozcan and E. McLeod, Annu. Rev. Biomed. Eng., 2016, 18, 77–102 CrossRef CAS PubMed.
- F. Zhang, B. Chen, G. R. Morrison, J. Vila-Comamala, M. Guizar-Sicairos and I. K. Robinson, Nat. Commun., 2016, 7, 13367 CrossRef CAS PubMed.
- Z. F. Phillips, M. Chen and L. Waller, PLoS One, 2017, 12, e0171228 CrossRef PubMed.
- D. Lee, S. Ryu, U. Kim, D. Jung and C. Joo, Biomed. Opt. Express, 2015, 6, 4912–4922 CrossRef PubMed.
- W. Lee, D. Jung, S. Ryu and C. Joo, Opt. Express, 2017, 25, 8398–8411 CrossRef CAS PubMed.
- W. Lee, J.-H. Choi, S. Ryu, D. Jung, J. Song, J.-S. Lee and C. Joo, Methods, 2018, 136, 66–74 CrossRef CAS PubMed.
- L. Waller, S. S. Kou, C. J. R. Sheppard and G. Barbastathis, Opt. Express, 2010, 18, 22817–22825 CrossRef PubMed.
- C. Zuo, Q. Chen, W. Qu and A. Asundi, Opt. Lett., 2013, 38, 3538–3541 CrossRef PubMed.
- Y. Li, J. Di, C. Ma, J. Zhang, J. Zhong, K. Wang, T. Xi and J. Zhao, Opt. Express, 2018, 26, 586–593 CrossRef PubMed.
- Y. Li, J. Di, W. Wu, P. Shang and J. Zhao, Appl. Opt., 2019, 58, G162–G168 CrossRef PubMed.
- J. A. Picazo-Bueno and V. Micó, Opt. Express, 2021, 29, 39904–39919 CrossRef PubMed.
- A. K. Gupta, R. Mahendra and N. K. Nishchal, Opt. Commun., 2020, 477, 126347 CrossRef CAS.
- P. M. Blanchard, D. J. Fisher, S. C. Woods and A. H. Greenaway, Appl. Opt., 2000, 39, 6649–6655 CrossRef CAS PubMed.
- L. Waller, Y. Luo, S. Y. Yang and G. Barbastathis, Opt. Lett., 2010, 35, 2961–2963 CrossRef PubMed.
- Z. Yang and Q. Zhan, PLoS One, 2016, 11, e0159596 CrossRef PubMed.
- N. Hai, R. Kumar and J. Rosen, Opt. Lasers Eng., 2022, 151, 106912 CrossRef.
- X. Zhang, Y. Zhang, J. Zhang, P. Yang and J. Zhu, Appl. Phys. Lett., 2019, 115, 234101 CrossRef.
- X. Zhang, S. Yang, Y. Li, J. Zhang, G. Zheng, Y. Zhang, S. Zhou and J. Zhu, Opt. Lasers Eng., 2020, 126, 105898 CrossRef.
- H. Zhou, X. Li, N. Ullah, G. Geng, J. Li, X. Li, Y. Wang and L. Huang, Appl. Phys. Lett., 2022, 120, 161702 CrossRef CAS.
- W. Yu, X. Tian, X. He, X. Song, L. Xue, C. Liu and S. Wang, Appl. Phys. Lett., 2016, 109, 071112 CrossRef.
- X. Tian, W. Yu, X. Meng, A. Sun, L. Xue, C. Liu and S. Wang, Opt. Lett., 2016, 41, 1427–1430 CrossRef PubMed.
- Q. Gong, Q. Wei, J. Xu, Y. Kong, Z. Jiang, W. Qian, Y. Zhu, L. Xue, F. Liu, C. Liu and S. Wang, Opt. Eng., 2018, 57, 063102 Search PubMed.
- Y. Shan, Q. Gong, J. Wang, J. Xu, Q. Wei, C. Liu, L. Xue, S. Wang and F. Liu, Biomed. Opt. Express, 2019, 10, 2337–2354 CrossRef CAS PubMed.
- C. Chen, Y.-N. Lu, H. Huang, K. Yan, Z. Jiang, X. He, Y. Kong, C. Liu, F. Liu, L. Xue and S. Wang, Biomed. Opt. Express, 2021, 12, 5261–5271 CrossRef PubMed.
- X. Xing, L. Zhu, C. Chen, N. Sun, C. Yang, K. Yan, L. Xue and S. Wang, Appl. Opt., 2022, 61, 422–428 CrossRef PubMed.
- C. Chen, Y. Gu, Z. Xiao, H. Wang, X. He, Z. Jiang, Y. Kong, C. Liu, L. Xue, J. Vargas and S. Wang, Anal. Chim. Acta, 2022, 1229, 340401 CrossRef CAS PubMed.
- L. Zhu, Z. Xiao, C. Chen, A. Sun, X. He, Z. Jiang, Y. Kong, L. Xue, C. Liu and S. Wang, Appl. Opt., 2023, 62, 1886–1894 CrossRef PubMed.
- A. Sun, Y. Li, P. Zhu, X. He, Z. Jiang, Y. Kong, C. Liu and S. Wang, Biomed. Opt. Express, 2023, 14, 5199–5207 CrossRef PubMed.
- L. Tian, J. C. Petruccelli, Q. Miao, H. Kudrolli, V. Nagarkar and G. Barbastathis, Opt. Lett., 2013, 17, 3418–3421 CrossRef PubMed.
- S. Bajt, A. Barty, K. A. Nugent, M. McCartney, M. Wall and D. Paganin, Ultramicroscopy, 2000, 83, 67–73 CrossRef CAS PubMed.
- B. E. Allman, P. J. McMahon, K. A. Nugent, D. Paganin, D. L. Jacobson, M. Arif and S. A. Werner, Nature, 2000, 408, 158–159 CrossRef CAS PubMed.
- F. Roddier, Appl. Opt., 1988, 27, 1223–1225 CrossRef CAS PubMed.
- F. Roddier, Appl. Opt., 1990, 29, 1402–1403 CrossRef CAS PubMed.
- C. Zuo, Q. Chen, W. Qu and A. Asundi, Opt. Express, 2013, 21, 24060–24075 CrossRef PubMed.
- C. Zuo, Q. Chen and A. Asundi, Opt. Express, 2014, 22, 9220–9244 CrossRef PubMed.
- J. C. Petruccelli, L. Tian and G. Barbastathis, Opt. Express, 2013, 21, 14430–14441 CrossRef PubMed.
- L. Tian, J. C. Petruccelli and G. Barbastathis, Opt. Lett., 2012, 37, 4131–4133 CrossRef PubMed.
- C. Sheppard, Appl. Opt., 2002, 41, 5951–5955 CrossRef PubMed.
- J. Tang, J. Zhang, J. Dou, J. Zhang, J. Di and J. Zhao, Opt. Lasers Eng., 2022, 157, 107126 CrossRef.
- K. Wang, J. Di, Y. Li, Z. Ren, Q. Kemao and J. Zhao, Opt. Lasers Eng., 2020, 134, 106233 CrossRef.
- S. Kou, L. Waller, G. Barbastathis and C. Sheppard, Opt. Lett., 2010, 35, 447–449 CrossRef PubMed.
- K. Ichikawa, A. W. Lohmann and M. Takeda, Appl. Opt., 1988, 27, 3433–3436 CrossRef CAS PubMed.
- M. R. Teague, J. Opt. Soc. Am. A, 1983, 73, 1434–1441 CrossRef.
- L. J. Allen and M. P. Oxley, Opt. Commun., 2001, 199, 65–75 CrossRef CAS.
- C. Zuo, J. Li, J. Sun, Y. Fan, J. Zhang, L. Lu, R. Zhang, B. Wang, L. Huang and Q. Chen, Opt. Lasers Eng., 2020, 135, 106187 CrossRef.
- C. Liu, S. Wang and S. Veetil, Computational optical phase imaging, Springer, 2022 Search PubMed.
- T. E. Gureyev, D. M. Paganin, A. W. Stevenson, S. C. Mayo and S. W. Wilkins, Phys. Rev. Lett., 2004, 93, 068103 CrossRef CAS PubMed.
- T. E. Gureyev, A. Pogany, D. M. Paganin and S. W. Wilkins, Opt. Commun., 2004, 231, 53–70 CrossRef CAS.
- T. E. Gureyev, Y. I. Nesterets, D. M. Paganin, A. Pogany and S. W. Wilkins, Opt. Commun., 2004, 259, 569–580 CrossRef.
- C. Zuo, Q. Chen, Y. Yu and A. Asundi, Opt. Express, 2013, 21, 5346–5362 CrossRef PubMed.
- C. Zuo, Q. Chen, H. Li, W. Qu and A. Asundi, Opt. Express, 2014, 22, 18310–18324 CrossRef PubMed.
- M. Soto and E. Acosta, Appl. Opt., 2007, 46, 7978–7981 CrossRef PubMed.
- M. Soto and E. Acosta, Appl. Opt., 2007, 46, 7978–7981 CrossRef PubMed.
- L. Waller, L. Tian and G. Barbastathis, Opt. Express, 2010, 18, 12552–12561 CrossRef PubMed.
- R. Bie, X. Yuan, M. Zhao and L. Zhang, Opt. Express, 2012, 20, 8186–8191 CrossRef PubMed.
- B. Xue, S. Zheng, L. Cui, X. Bai and F. Zhou, Opt. Express, 2011, 19, 20244–20250 CrossRef PubMed.
- S. Zheng, B. Xue, W. Xue, X. Bai and F. Zhou, Opt. Express, 2012, 20, 972–985 CrossRef PubMed.
- J. Zhong, R. A. Claus, J. Dauwels, L. Tian and L. Waller, Opt. Express, 2014, 22, 10661–10674 CrossRef PubMed.
- L. Lu, Y. Fan, J. Sun, J. Zhang, X. Wu, Q. Chen and C. Zuo, Opt. Lett., 2021, 46, 1740–1743 CrossRef PubMed.
- C. Zuo, J. Sun, J. Li, J. Zhang, A. Asundi and Q. Chen, Sci. Rep., 2017, 7, 7654 CrossRef PubMed.
- J. Li, Q. Chen, J. Sun, J. Zhang, X. Pan and C. Zuo, Opt. Express, 2018, 26, 27599–27614 CrossRef PubMed.
- J. Sun, C. Zuo and Q. Chen, Opt. Express, 2015, 23, 28031–28049 CrossRef CAS PubMed.
- J. Li, J. Xu, L. Zhong, Q. Zhang, H. Wang and J. Tian, Opt. Lasers Eng., 2019, 120, 6–12 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |