Open Access Article
Open Access ArticleRecent developments in ionophore-based potentiometric electrochemical sensors for oceanic carbonate detection
Stefanny N.
Toala
 a,
Zhentao
Sun
a,
Zhentao
Sun
 bc,
Yanfeng
Yue
bc,
Yanfeng
Yue
 *a,
Stephen F.
Gonski
b and
Wei-Jun
Cai
*b
*a,
Stephen F.
Gonski
b and
Wei-Jun
Cai
*b
aDepartment of Chemistry, Delaware State University, Dover, DE 19901, USA. E-mail: yyue@desu.edu
bSchool of Marine Science and Policy, University of Delaware, Newark, DE 19716, USA. E-mail: wcai@udel.edu
cOcean College, Zhejiang University, Zhoushan 316021, China
First published on 15th February 2024
Abstract
The increasing level of atmospheric carbon dioxide (CO2) driven by human activities contributes to the global concern of climate change. A consequence of these circumstances is ocean acidification, which reduces seawater pH. The increasing absorption of atmospheric CO2 into the ocean decreases the concentration of carbonate ions and causes the sea to become more acidic, severely harming marine species. This harm to marine life has created the need for in situ carbonate sensing and monitoring to understand how marine ecosystems respond to pH reduction. Over the past few decades, many sensors with different compositions and structures have been developed to detect carbonate in seawater and other aquatic environments to simulate oceanic conditions. This review summarizes the recent developments in carbonate ionophores, a key component in carbonate electrochemical sensors, and compares the reported performance of these sensors through various parameters (e.g., sensitivity, response time, lifetime, testing media, and measuring range). Current challenges within the development of carbonate ionophores and sensors and possibilities for future research are also discussed.
1. Introduction
The atmospheric level of carbon dioxide (CO2) has been rising profusely since the Industrial Revolution with continual deforestation, cement production, and burning of fossil fuels.1–3 As of February 2023, the global monthly average of atmospheric CO2 peaked above 419 ppm, a 50% increase from preindustrial levels in 1750.4,5 Approximately 25% of atmospheric anthropogenic CO2 dissolves into the ocean each year.6,7 While this oceanic absorption of CO2 has mitigated climate change, the increase of aqueous CO2 within seawater creates another environmental concern called ocean acidification.8 When CO2 dissolves in seawater, it causes an equilibrium shift between the inorganic carbon species by shifting the net reaction, H2O + CO2 + CO32− → 2HCO3−, to form more bicarbonate (HCO3−).9–11 As a result, carbonate ion concentration [CO32−] decreases while the proton ion concentration [H+] and bicarbonate ion concentration [HCO3−] increase, which lowers the pH of the water.12 A decreasing seawater pH can alter the rates of redox reactions and the availability of metals and nutrients essential to biological processes.13–17 For example, a lowering pH leads to a reduction of the carbonate mineral saturation state (Ω), which is mainly controlled by the [CO32−].9,18,19 Thus, the decline of CO32− directly decreases the potential for calcite and aragonite mineral formation (CO32− + Ca2+ ⇌ CaCO3).12 Decreased production of these minerals negatively impacts the ability of marine calcifying organisms (e.g., coral, crustaceans, and shellfish) to form their shells or skeletons.20–24 As a result, reduced calcification and growth rates for calcifying organisms have been observed, which alters their function in marine ecosystems.25,26This harm to marine life has motivated new research efforts in ocean chemistry, including developing reliable and low-cost methods to monitor CO32− levels for ocean acidification research. Substantial advancements have been accomplished in the in situ sensing of CO2 and pH; however, reliable in situ CO32− sensing is still lacking.27,28 It is crucial to develop highly selective, sensitive, and stable sensing devices capable of monitoring [CO32−] to study ocean acidification and understand how marine organisms respond. Carbonate sensors may also lead to advancements in biological applications (e.g., disease screening and personalized medicine) since carbonate is also present in clinical samples.29 A few demonstrations of in situ carbonate sensing have been reported and reviewed; however, this review addresses the potential that carbonate electrochemical sensors based on novel carbonate ionophores have to be highly selective, sensitive, and stable in the marine environment.30–32 This review comprehensively summarizes and compares recent advancements within carbonate electrochemical sensors based on novel carbonate ionophores, including a discussion on ionophore characterization, membrane fabrication, and sensor evaluation. The current challenges within the development of carbonate ionophores and sensors and possibilities for future research are also discussed. Research on ocean acidification will continue to be relevant for protecting the environment, ensuring a promising and healthier aquaculture industry, and supporting the development and large-scale implementation of ocean-based carbon dioxide removal (CDR) technologies.33
2. Seawater carbonate chemistry and method of indirect [CO32−] determination
The carbonate system in seawater serves as the ocean's primary pH buffer through carbon dioxide gas-water equilibrium reactions.34,35 When atmospheric CO2 dissolves into seawater, aqueous CO2 is formed. Aqueous CO2 reacts with water molecules in the ocean to form carbonic acid (H2CO3), which gradually dissociates into HCO3− and H+ (H2O + CO2 ⇌ H2CO3 ⇌ HCO3− + H+).34 The newly formed HCO3− can also dissociate, forming CO32− and more H+ (H2O + CO2 ⇌ HCO3− + H+ ⇌ CO3− + 2H+).36 The spike in H+ concentration lowers ocean pH; however, the ocean attempts to mitigate the rise in acidity by limiting the dissociation of HCO3− (H2O + CO2 + CO32− → 2HCO3−) and shifting the equilibrium between HCO3− and CO32− (HCO3− ⇌ CO32− + H+). Through the equilibrium shift, some of the excess H+ are consumed to form more HCO3−, causing the drop in pH to be smaller than it would be in an unbuffered system.9 While this protects the ocean from greater declines in pH, this process consumes CO32− and decreases its availability to form calcite and aragonite minerals through the carbonate mineral saturation state (CO32− + Ca2+ ⇌ CaCO3). Reduced production of these minerals harms marine life, especially marine calcifying organisms.12 Overall, the increase of aqueous CO2 in seawater due to increasing atmospheric CO2 is causing the ocean to continually buffer increasingly higher H+ concentrations, which steadily lowers ocean pH. Research models predict ocean pH will drop to 7.8 or 7.7 by the end of this century if seawater continues to absorb CO2 at the current rate.37 To understand how marine ecosystems are responding to reduced pH, it has become increasingly important to monitor the [CO32−] in the ocean.At equilibrium, the concentrations of aqueous CO2, HCO3−, and CO32− are written in terms of two equilibrium constants:
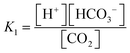 | (1) |
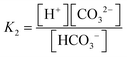 | (2) |
Consequently, the study of marine carbonate species has been accomplished through seawater sample collection during hydrography cruises and the mathematical relationships between four analytical parameters, including pH, total dissolved inorganic carbon (DIC), total alkalinity (TA), and CO2 fugacity or partial pressure (ƒCO2 or pCO2).26,40–44 Using the thermodynamic equilibrium relations of these parameters and the measured values of any two parameters, [CO32−] can be calculated along with the remaining unknown parameters.45 However, in situ temperature, salinity, and the concentrations of minor acids and bases are also needed for the calculation.46 These variables are not always measured or known, which severely lessens the reliability of the calculation since the K1 and K2 constants depend on in situ salinity and temperature.39,42 To obtain a highly accurate [CO32−] and examine internal consistency, all four parameters are required for the calculation; however, time, staff, and instrumentation typically allow for only two of them to be measured.47 Comparison of [CO32−] determined from various pairs of parameters (e.g., pH and TA versus DIC and pCO2) are subject to inaccuracies, increasing the challenges of using this indirect method of [CO32−] determination.48 Overall, three issues seriously impede our ability to obtain an accurate [CO32−] via the calculations from these parameters: 1) propagation of errors in isolated analytical methods, 2) the lack of knowledge of the organic acid contributions to alkalinity as part of the inorganic carbon model, and 3) a notable uncertainty in the first and second dissociation constants (K1 and K2) of carbonic acid in seawater and brackish waters.42,49–52 As a result, ocean acidification research has moved toward the development of in situ carbonate sensors to capture more accurate [CO32−].
3. In situ measurements for [CO32−] determination
3.1 The need for in situ measurements
The indirect method to determine [CO32−] briefly discussed in section 2 requires water sample collections at defined locations and depths before samples are transported, stored, and then later analyzed in a laboratory after a costly pretesting procedure performed by well-trained personnel.53,54 Based on the need for pretesting procedures and experienced personnel, this aggregate procedure is costly and disadvantageous. Furthermore, analytical methods that depend on collecting and analyzing discrete samples seldom produce representative datasets with enough data points for high spatial and temporal resolution to fully capture substantial simultaneous changes in temperature, salinity, and biogeochemistry that characterize marine ecosystems.55Conversely, in situ analysis is an approach that can create high spatial and temporal resolution data sets and satisfy the need for real-time measurements. In situ measurements are those taken instantaneously at the given location, alleviating most of the logistical and economic challenges of sampling, pretesting procedures, and analysis.53 Additionally, this process reduces limitations imposed by humans who may be unable to reach specific locations (i.e., various depths within the ocean or in ice-covered water).56 For these reasons, building in situ sensors for carbonate detection is vital to advancing ocean acidification and marine carbonate chemistry research.
3.2 Evaluating sensor types and their potential for oceanic in situ carbonate detection
Over the years, sensors based on the Severinghaus electrode, and others based on optical, voltametric, and potentiometric principles have been explored for ocean studies. The Severinghaus electrode consists of a pH electrode in contact with a thin layer of bicarbonate solution that is separated from the sample by a gas permeable membrane to measure dissolved CO2. With this setup, dissolved CO2 in the sample can diffuse through the membrane into the inner NaHCO3 solution, where pH changes occur until an equilibrium is established. The resulting pH of the bicarbonate solution in contact with the electrode correlates to dissolved CO2 levels in the sample.57 While these electrodes are relatively inexpensive and easy to handle, this sensor design has drawbacks that deem it unsuitable for oceanic in situ detection. Since this design requires equilibrium establishment before measurement, the response time cannot be suitably shortened to capture minute changes in analyte concentration.57 In addition, these sensors require a careful calibration process, and still exhibit sensitivity that is not ideal for seawater analysis.57,58 Considering ocean acidification research, Severinghaus based sensors cannot currently detect carbonate and are unlikely to collect the data necessary for high resolution data sets.Similarly, current optical sensors (e.g., optodes) are incompatible with the goals of ocean acidification research. Recently, many optodes have been tested in seawater and other natural waters.59–64 The working principle of this sensor type relies on the mass transfer between the sensing material and sample. Mass transfer can occur through ion-exchange between the target analyte and a reference ion (e.g., a proton) or the co-extraction of the target analyte and a counter ion in the sensing phase.59 In either case, the protonation of the indicator dye correlates to analyte concentration.60 Even though these sensors contain favorable characteristics (e.g., small size, versatility, ease of use, low drift, fast response time, and long lifetime), these sensors have only detected pH and dissolved O2 and CO2.61–64 Furthermore, the issue of Cl− interference has been reported.59
Electrochemical sensors, including voltametric and potentiometric sensors, have also been tested for ocean-based research. Potentiometric electrochemical sensors are the focus of this review, and their working principle is deeply covered in section 4. Unlike potentiometric sensors, voltametric sensors require a counter electrode along with a working and reference electrode in their structure. From voltametric sensors, qualitative and quantitative information of an active redox analyte can be obtained by measuring the current as the potential in the 3-electrode cell is varied.65 The type of voltammetry used (e.g., cyclic voltammetry, differential pulse voltammetry, square wave voltammetry, and chronoamperometry) depends on how the potential is varied. Current voltametric sensors for ocean-based research can measure pH and various trace metals (e.g., Zn2+, Cd2+, and Pb2+) and ions (e.g., NO3−, NO2−, HPO42−, PO43−, and H2PO4−).37,66–76 While these sensors have great analyte versatility, no voltametric sensors currently detect carbonate and sensor lifetime is limited.37,65 The lifetime of these sensors depends on the number of measurements recorded by the electrode, and frequent measurements age the electrode until peak potential cannot be reached.37 Thus, voltametric sensors may require maintenance too frequently for long-term oceanic in situ carbonate detection.
Currently, a few true demonstrations of in situ electrochemical sensors have been reported, even in seawater applications.65 To the best of our knowledge, the most recent sensor capable of oceanic in situ measurement is a submersible potentiometric probe composed of a flow cell based on miniaturized solid-state sensors that can measure pH and the concentrations of carbonate and calcium ions in seawater.31 Based on previous success, potentiometric electrochemical sensors currently demonstrate the most promise for ocean acidification research. Not only can these sensors detect carbonate, but also pH, dissolved CO2, and bicarbonate, which can all be used to study marine carbonate chemistry and ocean acidification.30,77 A recently developed novel potentiometric sensor for dissolved CO2 detection resolves issues frequently encountered using classical Severinghaus CO2 probes.30 The sensor created by Athavale and co-workers is based on EMF measurement between two solid-contact ISEs, a hydrogen selective sensor, and a carbonate selective senor and collects high resolution in situ data with insensitivity to changes in pressure and a response time of less than 10 seconds in freshwater lakes. Another recent advancement in the potentiometric sensing of dissolved CO2 and bicarbonate came from Li and co-workers.77 Their sensor is capable of sensing bicarbonate and dissolved CO2 in mineral water and beverage samples using neutral and charged calix[4]pyrroles with meso-substituted groups as ionophores. Based on these examples, potentiometric electrochemical sensors can be modified for various applications and have immense potential for the in situ detection of carbonate and other analytes crucial for monitoring ocean acidification. However, various challenges still complicate the wide-spread implementation of these devices for ocean acidification research (discussed later in section 4.3). As of June 2021, the European Marine Board stated that substantial progress is needed before in situ ocean observations can be incorporated into the global ocean observation system.78 Despite several unknowns in manufacturing and evaluating these robust devices, current research has compiled expected attributes for in situ electrochemical sensors that monitor natural waters such as seawater.79,80 The ideal sensor should simultaneously identify and quantify the concentration of a selected species (e.g., carbonate) while being small, simple, and relatively inexpensive. Additionally, the sensor should remain stable and not alter the sample composition during the test period.81 These sensors may require new technology and analytical or biophysical concepts to meet these standards, so the challenge of creating robust in situ electrochemical sensors will remain for several years.81
4. Electrochemical sensors for carbonate detection
4.1 The basis of electrochemical sensors
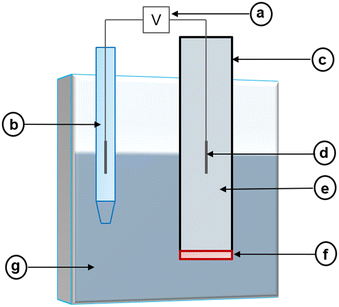
Electrochemical sensors can convert reactions between an electrode and a specific analyte into readable signals.82 Typically, these signals originate following changes in chemical and electrical interactions.82 However, a change in physical properties may also result in a signal.83 In its most basic form, the electrochemical sensor consists of a receptor unit, a sample containing an analyte, and a transducer (e.g., an electrode), which work together to produce a signal corresponding to the measurement of interest.83,84 Frequently, the signal corresponds to the activity of a target ion, and its strength will adjust based on the measured activity.84 Commonly, the receptor unit manifests as a membrane that should only interact with the target ion. When the membrane interacts with the target ion, it should alert the electrode to produce an assessable signal (Fig. 1).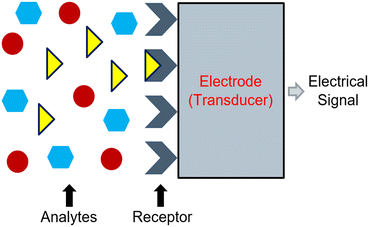 | ||
| Fig. 1 Representation of the working principle of an electrochemical sensor which operates based on a chemical reaction between a receptor unit and a specified analyte. | ||
4.2 Electrochemical sensors based on potentiometry
Potentiometric electrochemical sensors create a potentiometric cell where the potential difference at equilibrium (i.e., at zero current) between two electrodes relates to an analyte's activity.85 Because of this, these sensors may also be called potentiometric ion sensors.86 In the composition of a potentiometric electrochemical sensor, an external reference electrode (ERE) and an ion-selective electrode (ISE) are connected to a voltmeter (Fig. 2).| Ecell = EISE − EERE + EJ | (3) |
Assuming the liquid junction potential is correctly limited and stable, the potential of the ISE can be measured against the ERE. The potential of the ISE is controlled by the potential of the internal reference electrode (EIRE) and the ion-selective membrane (Emembrane).85 Thus, eqn (3) can be rewritten as:
| Ecell = EIRE + Emembrane − EERE + EJ | (4) |
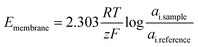 | (5) |
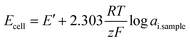 | (6) |
| ai = γiCi | (7) |
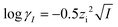 | (8) |
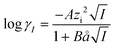 | (9) |
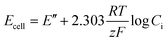 | (10) |
4.3 The current challenges surrounding in situ carbonate electrochemical sensors and measurements
Potentiometric response from potentiometric electrochemical sensors is complex. This type of response is a time-dependent process mainly controlled by the ion-selective membrane and the sample. The interface at which the membrane and sample meet consists of various properties that depend on the composition of the two. However, other factors also affect potentiometric response and create challenges in developing in situ carbonate electrochemical sensors and documenting [CO32−] long-term.86The composition of the internal reference solution is another structural component that can affect sensor functionality due to its potential to cause transmembrane ion fluxes.101,102 Theoretically, the composition of the internal reference solution should maintain the internal reference electrode's constant potential and generate no concentration gradient by allowing the same amount of target analyte and interfering ion to replace each other on both sides of the membrane.103 However, concentration gradients can arise if interfering ions replace the target analyte within the membrane, allowing target analytes from the membrane to leach into the sample. Once the target analytes flux into the sample, a significant difference between the concentration of the target analyte near the membrane and in the entire sample emerges and skews measurement readings. This negatively impacts the sensor's lower detection limit and selectivity (discussed in depth in section 7).
The possibility of transmembrane ion fluxes also depends on the sample composition. Any changes in the sample can also cause concentration gradients that lead to ion fluxes.104 Changes in samples frequently occur in environmental samples (e.g., ocean water samples at various locations and depths), so the design and optimization of the internal reference solution is critical to limit ion fluxes. Some strategies for optimizing internal reference solutions include lowering the concentration of ionic sites and adjusting the composition to induce ion exchange like a typical sample would.104,105 Adjustments to the ion-selective membrane can also reduce the prevalence of ion fluxes. These adjustments include increasing the thickness or polymer content of the membrane and designing it to be as resilient to concentration gradients as possible.103–105 Other potential avenues for avoiding ion fluxes include using a flow-through cell or rotating electrodes, using internal solution-free sensors (e.g., solid state ISEs), and covalently bonding the ionophore to the polymer backbone of the membrane.102,104,106–108 The ionophore and its role in ion-selective electrodes are discussed in depth in section 5. Additional drawbacks with using an internal reference solution include its sensitivity to changes in temperature and pressure, which may cause the solution to evaporate and lead to the delamination of the ion-selective membrane.109
5. Ionophores for carbonate detection
5.1 The definition of an ionophore and the framework of carbonate ionophores
An ionophore must be within the composition of the ion-selective membrane for the membrane to be selectively permeable to a target analyte. An ionophore is a substance capable of binding and transporting a particular ion through a membrane. Since the ionophore facilitates the identification and transport of the target ion, it must be highly selective and sensitive to the target. A carbonate ionophore capable of transporting only carbonate ions through the ion-selective membrane is needed to advance in situ carbonate electrochemical sensors for ocean acidification research.119Research completed by Wise, Herman, and Rechnitz notably provides the framework of the carbonate ionophore. In 1973, Wise reported trifluoroacetylbutylbenzene (TFABB) as an ionophore for bicarbonate detection using bicarbonate ISEs.120 Later, Herman and Rechnitz detailed that TFABB was most likely sensing carbonate instead of bicarbonate. With this ionophore, Nernstian behavior was present in the concentration range of 10−2 to 10−7 M of carbonate ions, and the sensor had a quick response time and an overall low noise level.121 Since these initial findings, various types of carbonate ionophores have been investigated, including small organic molecules, molecular tweezers, and metal-based complexes.
For some time, trifluoroacetophenones (TFAs), which include TFABB, were the only group of molecules identified as carbonate ionophores.124 Besides carbonate, TFAs can also sense propionate, lactate, benzoate, salicylate, phenylpyruvate, amino acids, sulfate, and phosphate.125–132 The ability of TFAs to act as ionophores for various target ions attests to the usefulness of these compounds; however, it also explains the challenges researchers have reported with their sensors experiencing interference from other ions.
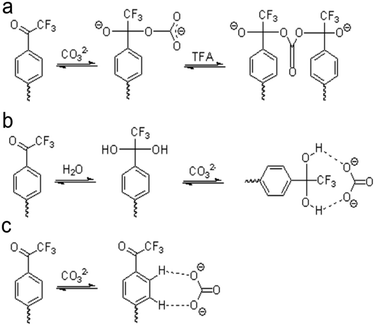
For TFAs, three possible mechanisms exist to explain how these molecules sense carbonate. Scott and co-workers suggest two mechanisms through studies of TFA-based polymeric membranes.133 Tetrahedral nucleophilic adducts can form after carbonate binds the carbonyl carbon on TFA (Fig. 3a), or hydrogen bonding between a hydrated TFA and carbonate can create carbonate-ionophore complexes (Fig. 3b). The third mechanism also involves the formation of hydrogen bonding but considers the effective charge on the carbonyl carbon in TFA (Fig. 3c). Considering the effective charge on the carbonyl carbon, hydrogen bonding would form between the phenyl hydrogens of TFA and carbonate.134 Through energy analysis and stoichiometric studies of all three mechanisms, Makarychev-Mikhailov and co-workers suggest that the hydrogen bond complex formation is the most realistic mechanism; however, Meyerhoff and co-workers report the occurrence of carbonate sensing through the nucleophilic adduction mechanism.124,135
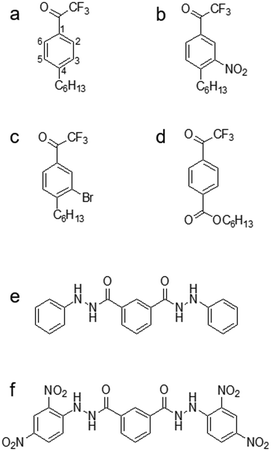
Even though TFA-based membranes can sense carbonate, the sensors exhibited a low selectivity and lipophilicity, a short lifetime (e.g., a couple of days), and a high detection limit.120,136 These disadvantages motivated researchers to modify the structure of TFA to determine whether any alteration could potentially alleviate the drawbacks. Research has explored placing substituents (e.g., hexyl, nitro, bromo, and carboxyl substituents) in the para-position, which corresponds to position 4 on the phenyl ring of TFA (Fig. 4a).137–139 Modifying the para-position of the ring affects the acidity of the group responsible for detecting carbonate and modifies the compound's ability to bind carbonate. Based on comparisons of lipophilicity, the carboxyl substituent may be the most promising due to a high Hammett constant value, which reflects its ability to potentially increase lipophilicity.136 Lipophilicity can impact selectivity depending on the presence of a lipophilic cation or anion. For example, cationic selectivity would be hindered if a lipophilic cation is present within a membrane.138
Substituents in the meta-position, which correspond to positions 3 or 5 on the phenyl ring (Fig. 4a), have also been evaluated. Makarychev-Mikhailov and co-workers built carbonate sensors using 4-hexyltrifluoroacetophenone (Hex-TFA) and its 3-nitro- (NO2-TFA) and 3-bromo- (Br-TFA) derivatives as ionophores. Hexyl trifluoroacetylbenzoate (HE) was used as a control to determine the effect of meta-position substituents on carbonate selectivity.136 The structures of Hex-TFA, NO2-TFA, Br-TFA, and HE are in Fig. 4. Results displayed that the –NO2 and –Br substituents increased the Lewis acidity of the fluoroketone group and the carbonate selectivity. The meta substitution of –NO2 resulted in increased carbonate selectivity, especially with NPOE-plasticized membranes; however, a higher detection limit and pH sensitivity greatly limit the practical use of this ionophore.136 The pH sensitivity eliminates this molecule as an effective carbonate ionophore for ocean acidification research. However, the meta substitution of –Br was similar in response to the control, which makes it appealing for future research.136 From these results, Makarychev-Mikhailov and co-workers moved to test TFA as a carbonate ionophore while containing bromo- and nitro-substituents simultaneously.124
Compared to the mono-substituted TFA, the double meta-substituted TFA had a higher carbonate selectivity than Br-TFA and higher lipophilicity than NO2-TFA. The lipophilicity increased by 0.5, positively impacting the detection limit and electrode lifetime.124 In addition, an increasing trend of carbonate selectivity against interferents (e.g., salicylate (Sal−), thiocyanate, and nitrate) occurred as ionophore concentration increased (Fig. 5).124
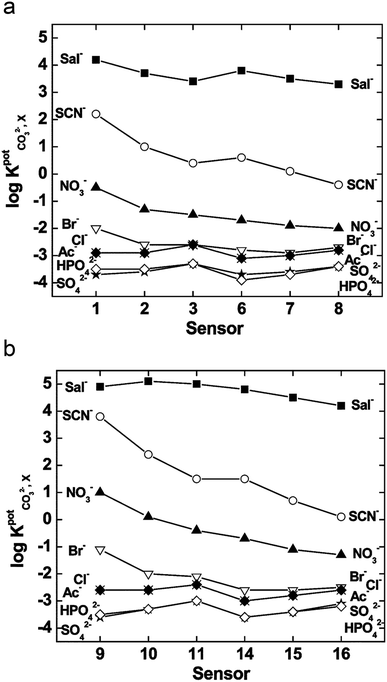 | ||
| Fig. 5 Selectivity of the sensors for various ions tested with membranes plasticized with bis(2-ethylhexyl)sebacate (a) and 2-nitrophenyloctyl ether (b), where the x-axis represents a sensor labeled by number designated by the authors in the original work. Used with permission from Royal Society of Chemistry 2004; permission conveyed through Copyright Clearance Center, Inc.124 | ||
Along with TFAs, hydrazides and their various forms have been assessed. N,NI-Bis(phenyl)isophthalohydrazide and N,N'-bis(2,4-dinitrophenyl)isophthalohydrazide (Fig. 4e and f), were mainly tested against the interferent Sal−. The potential of the sensor was measured as a function of carbonate activity while set concentrations of Sal− ions were added into the sample (1.0 × 10−4, 1.0 × 10−3, and 5.0 × 10−3 M).140 The potentials obtained from samples containing CO32− and Sal−versus those containing only CO32− remain identical until a distinct divergence point (Fig. 6), which indicates the presence of Sal− interference and marks the measuring range of the sensor for carbonate sensing.140
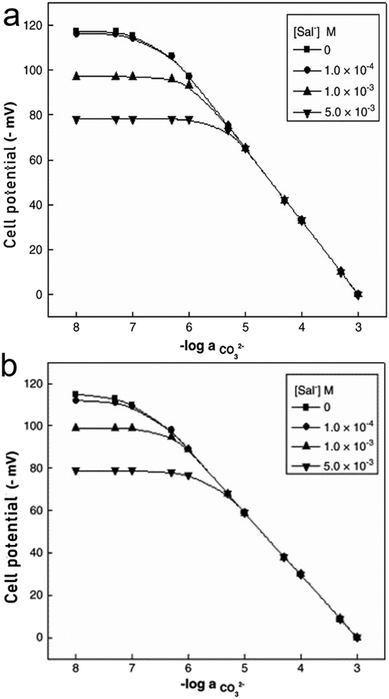 | ||
| Fig. 6 Variation of cell potential of sensor based on ionophore e (a) and ionophore f (b) with activity of CO32− at different concentration levels of Sal− ions. Reprinted from Electrochimica Acta, Copyright (2006), with permission from Elsevier.140 | ||
Comparing both ionophores (Fig. 4e and f), ionophore f allows for a broader measuring range, a shorter response time, a higher selectivity, and Nernstian behavior.140 Ionophore f contains multiple –NO2 groups, which increase the compound's hydrogen bond donor capacity and its bonding affinity with CO32− through the mechanism displayed in Fig. 3c. Similar trends in more successful carbonate ionophores based on hydrazides containing –NO2 groups have been reported. (E)-2-(2-(4-Nitrobenzylidene)hydrazinyl)pyridine, also referred to as PDZ-1, yielded optimal results for Thimaradka and co-workers where its detection limit and limit of quantification for carbonate were 0.11 mM and 0.36 mM, respectively.141 The structural design of PDZ-1 causes its –NH functionality to be more acidic due to an adjacent pyridine moiety and –NO2 functionality in the para-position. These structural characteristics contribute to a more effective binding site for CO32−. The mechanism by which PDZ-1 can bond with carbonate in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric manner is depicted in Fig. 7a. Similar to PDZ-1, ionophores labeled as R1 and R2 by Singh and co-workers also bind carbonate through a 2
1 stoichiometric manner is depicted in Fig. 7a. Similar to PDZ-1, ionophores labeled as R1 and R2 by Singh and co-workers also bind carbonate through a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio while exhibiting a high selectivity for carbonate over competing salts with a detection limit of 0.51 ppm and 0.47 ppm, respectively.142 Structurally, R1 and R2 are similar to PDZ-1. However, they feature different heterocyclic rings containing oxygen or sulfur along with a –NO2 group attached.142 These ionophores also rely on the nitro group leading to an increased acidity of the hydrogen atom on the –NH group to elevate the compound's hydrogen bond donor capacity and selectivity for carbonate. The mechanism of carbonate binding to R1 and R2 is shown in Fig. 7b and c, respectively.
1 stoichiometric ratio while exhibiting a high selectivity for carbonate over competing salts with a detection limit of 0.51 ppm and 0.47 ppm, respectively.142 Structurally, R1 and R2 are similar to PDZ-1. However, they feature different heterocyclic rings containing oxygen or sulfur along with a –NO2 group attached.142 These ionophores also rely on the nitro group leading to an increased acidity of the hydrogen atom on the –NH group to elevate the compound's hydrogen bond donor capacity and selectivity for carbonate. The mechanism of carbonate binding to R1 and R2 is shown in Fig. 7b and c, respectively.
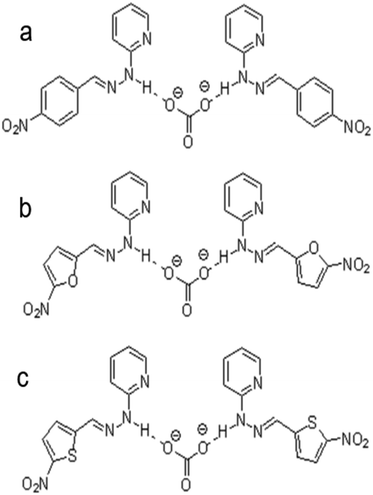 | ||
| Fig. 7 Interaction mechanism between ionophore and carbonate ion: (a) (E)-2-(2-(4-nitrobenzylidene)hydrazinyl)pyridine (labeled as PDZ-1 by Thimaradka et al.), (b) (E)-2-(2-(5-nitrofuranylidene)hydrazinyl)pyridine (labeled as R1 by Singh et al.), and (c) (E)-2-(2-(5-nitrothiophenylidene)hydrazinyl)pyridine (labeled as R2 by Singh et al.).142 | ||
Multiple papers reported that the best carbonate selectivity occurred when the TFAB groups had a greater distance between them than the predicted optimal distance. From the covalent bond mechanism suggested by Meyerhoff and co-workers (Fig. 3a), the optimal distance is deemed to be 4.8 Å.135,144 However, research has detailed that longer than 7.3 Å or exactly 6 Å led to effective ionophore performance and resulted in modifications to the proposed mechanisms of carbonate binding.145,146 Shim and co-workers have specifically detailed that ionophores with TFAB groups placed in the C3 and C12 positions displayed the best carbonate selectivity and suggest that a water molecule is also involved in the mechanism, meaning that a covalent bond with a carbonyl carbon on TFAB and a hydrogen bond with a water molecule provide the tweezer binding sites for incoming carbonates.146 These conclusions differ significantly from that of Lee and co-workers, who propose carbonate was binding covalently to a TFAB carbonyl carbon while also binding to the hydroxyl group of cholic acid through hydrogen bonding.145 However, in either mechanism, the greater distance between the two TFAB moieties could allow for a better conformational match.145 With the hydroxyl groups of cholic acid in fixed spatial positions, the TFAB groups can maintain a favorable conformational structure and provide binding sites for carbonate via covalent and hydrogen bonds.
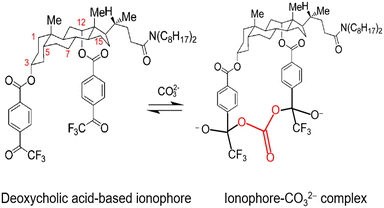
Further investigation of cholic and deoxycholic acid-based ionophores by Choi and co-workers using trifluoroacetyl-p-decylbenzene (TFADB), N,N-dioctyl-7α-acetoxy-3α,12α-bis(4-trifluoroacetylbenzoxy)-5β-cholan-24-amide (3,12-bis(TFAB)CA), and N,N-dioctyl-3α,12α-bis(4-trifluoroacetylbenzoxy)-5β-cholan-24-amide (deoxy-3,12-bis(TFAB)CA) displayed that deoxy-3,12-bis(TFAB)CA had the strongest carbonate selectivity with a greater distinction in selectivity to other anions as compared to the other two ionophores tested (Fig. 8).58 Testing in artificial seawater samples along with a wide range of carbonate selectivity has led researchers to conclude that deoxy-3,12-bis(TFAB)CA would be sufficient for seawater carbonate sensing applications.58,147 Due to the success of this specific ionophore over time, it is now coined as the commercial carbonate ionophore VII (Fig. 8) and has been tested in a variety of conditions, including within microsensors and with ion-to-electron redox probes through anion transfer voltammetry.119,148–150 After adjustments to ionophore quantity (16.6 mg to 16.0 mg), de Beer and co-workers found their microsensor exhibited similar interference levels to macrosensors that utilized the given ionophore and that it was sensitive to sulfide since the addition of 0.1 mol m−3 sulfide to a calibration solution caused carbonate selectivity to be lost.148 This sulfide sensitivity limits its usefulness near sediment covered with seawater; however, Xie and Bakker noted that hydrogen sulfide (HS−), a common form of sulfide, was not an interferent for their sensor composed of a carbonate selective ISE using carbonate ionophore VII and a pH electrode.57 It is important to note that sulfide does not exist in most oxygenated oceanic environments, which suggests that a sensor using carbonate ionophore VII is applicable for marine testing. The mechanism by which carbonate ionophore VII and carbonate bind is shown in Fig. 9.
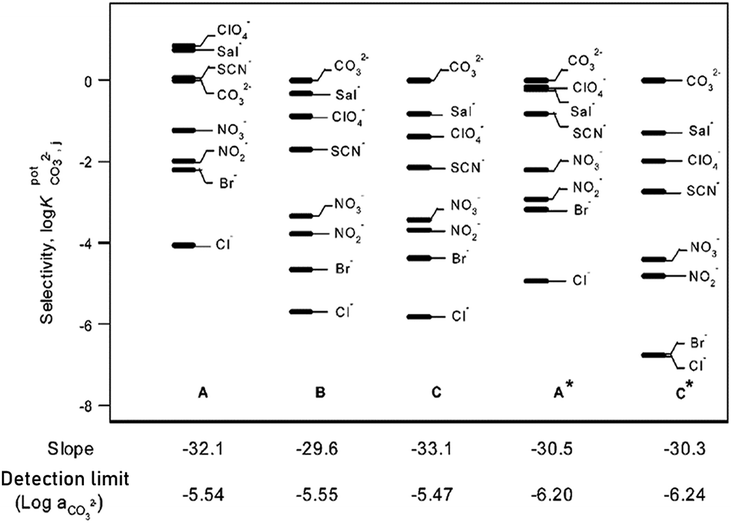 | ||
| Fig. 8 The carbonate selectivity coefficients, response slopes, and detection limits of the three electrodes prepared. Electrode A using TFADB, electrode B using 3,12-bis(TFAB)CA, and electrode C using deoxy-3,12-bis(TFAB)CA. A* and C* indicate the result was obtained at a pH of 8.0. Reprinted (adapted) with permission from ref. 58. Copyright 2002 American Chemical Society. | ||
As previously indicated, carbonate ionophore VII with anion transfer voltammetry for carbonate detection has been examined. Using river samples and various cationic [6]helicenes as ion-to-electron transducers in redox probes, it was determined that cationic [6]helicene diaza embedded with two bromine groups (Fig. 10d) was the best candidate for anion transfer through the thin sensing films compared to the other helicenes tested (Fig. 10).150 Upon progressive addition of carbonate to the sample, Nernstian peak shift behavior occurred (Fig. 11), displaying adequate performance for carbonate detection while being comparable to standard carbonate-selective electrodes that do not use redox probes at environmental pH.150 Even though it was only tested in river water samples, it did not display any interference in the environmental pH range, which means this assembly using ion-to-electron redox probes has potential for oceanic samples in similar pH ranges.
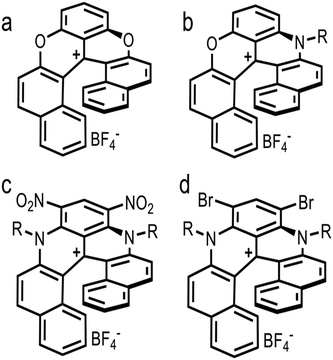 | ||
| Fig. 10 Structure of cationic [6]helicene. Dioxa+ (a), Azaoxz+C12: R = –C12H25 (b), Diaza+(C8)2(NO2)2: R = –C8H17 (c), and Diaza+(C8)2Br2: R = –C8H17 (d). | ||
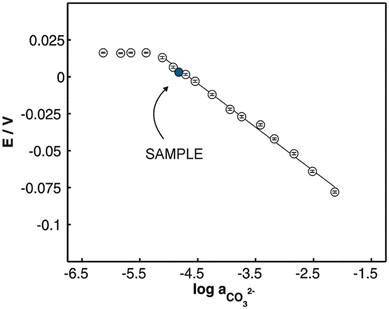 | ||
| Fig. 11 Observed Nernstian shift for progressive carbonate additions (MA14) in a sample containing a pH of 8.20 through the addition of 0.2 mM NaCl. Reprinted with permission from ref. 150. Copyright 2018 John Wiley and Sons. | ||
In summary, tweezer-type ionophores have displayed highly improved carbonate selectivity due to their ability to capture carbonate between two ion binding groups, commonly TFAB groups. A deoxycholic acid molecular base has been a fundamental component of previous ionophore design due to the steroidal backbone of cholic acid. Its base contains an adequate amount of rigidness to hold the binding groups and carbonate, while not restricting the interactions. Furthermore, the locations of the potential binding sites lie on the same side of the molecule, which prevents complications regarding conformation. Thus, ionophores with a deoxycholic base bearing two TFAB groups will remain a contender in future research of carbonate detection.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. However, Mn-2 exhibited a higher CO32− selectivity in these conditions. The slight difference in performance seems to occur because the structure of Mn-2 causes less steric hindrance, allowing the formation of 2
4. However, Mn-2 exhibited a higher CO32− selectivity in these conditions. The slight difference in performance seems to occur because the structure of Mn-2 causes less steric hindrance, allowing the formation of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. The steric hindrance present in the structure of Mn-1 favors 1
1 complexes. The steric hindrance present in the structure of Mn-1 favors 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes and allows the ionophore to perform more optimally with a 2
1 complexes and allows the ionophore to perform more optimally with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 cationic site-to-ionophore ratio.151 As demonstrated with tweezer-type ionophores, the formation of 2
3 cationic site-to-ionophore ratio.151 As demonstrated with tweezer-type ionophores, the formation of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between a given ionophore and carbonate is advantageous compared to others. Therefore, metal-based complex ionophores like Mn-2 should be further explored with seawater samples to determine their efficacy for ocean acidification research.
1 complexes between a given ionophore and carbonate is advantageous compared to others. Therefore, metal-based complex ionophores like Mn-2 should be further explored with seawater samples to determine their efficacy for ocean acidification research.
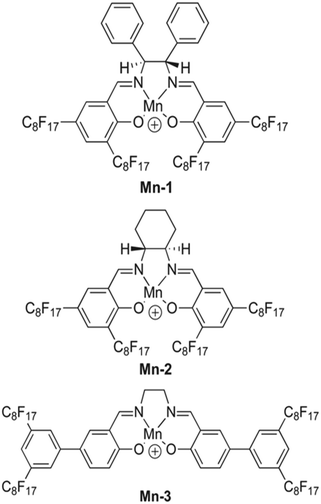 | ||
| Fig. 12 Structure of fluorophilic manganese(III) complexes, labeled as Mn-1, Mn-2, and Mn-3.151 | ||
6. Ion-selective membrane fabrication
While the ionophore is crucial to the analyte binding capability of a sensor, other components within the ion-selective membrane also affect the performance and properties of the device (e.g., measuring range, selectivity, sensitivity, response time, stability, and reproducibility). Thus, these membrane components must be chosen carefully to ensure the functionality of the sensor in its target environment. Various types of membranes, including glass, crystalline/solid-state, liquid, and polymeric membranes, have been studied for ISE preparations. Conventionally, liquid membranes have been a part of ISEs; however, more recent developments commented on the difficulties of this membrane type.152–154 Hence, polymeric membranes have become common for carbonate electrochemical sensors. They typically consist of a polymer or copolymer as a substrate, an ionophore, and ionic additives. However, with a polymer as a substrate, a plasticizer may also be added to the composition to adjust the mechanical property of the resultant membranes.155 Historically, the general breakdown of membranes that include plasticizer has been 1% ionophore, 33% poly(vinyl chloride) (PVC), and 66% plasticizer by mass.156 Over time, various combinations of these components with ionic additives have been tested and optimized to understand how each constituent affects the function of the membrane. Currently, the optimized composition of a membrane with PVC as the polymer substrate contains 33% PVC, 65% plasticizer, 2% ionophore, and 60 mol% additive relative to the ionophore.157The early addition of polymer, whether it was silicone rubber or PVC, led researchers to believe that polymers could provide elasticity and mechanical stability to the membrane.158–160 However, more recent research by Zhao and Cai has demonstrated that a polymer affects the adhesive properties (i.e., how well it attaches to the electrode body) and the mechanical strength of the membrane (i.e., how long the membrane can remain intact while undergoing biofouling), which both impact the lifetime of the sensor.161 Besides PVC, some other materials used for ion-selective membranes include silicone, polyurethane, and carboxylated PVC.159,162,163 Independent of the polymer, a solvent is required to stimulate the dissolution of the polymer substrate. Frequently, tetrahydrofuran (THF, bp 66 °C) is used as a solvent to dissolve the polymer; however, other commonly used solvents include dimethylformamide (DMF, bp 153 °C), N-methyl-2-pyrrolidone (NMP, bp 202.0 °C), dimethylacetamide (DMAc, bp 165 °C), and dimethyl sulfoxide (DMSO, bp 189 °C).57,58,86,111,119,123,136,138,140,145,148,161,164–168 These solvents are later evaporated out of the solution within the membrane preparation process.
Sensor lifetime is also dependent on the rates of diffusion of the ionophore and plasticizer in the membrane.169,170 Plasticizers have two main purposes within a polymeric membrane, which are to provide elasticity or fluidity and to act as a co-solvent for the ionophore.152 The chosen plasticizer must be compatible with the polymer substrate so it may encourage the high mobility of the other components in the membrane (i.e., the ionophore).160 The mobility of the ionophore, along with the identity and characteristics of the ionophore, influences sensor selectivity. Some examples of plasticizers in ion-selective membranes are dioctyl adipate (DOA), 2-nitrophenyl octyl ether (o-NOPE), dioctyl sebacate (DOS), dioctyl phthalate (DOP), bis(2-ethylhexyl)adipate (DEHA), tris(2-ethylhexyl)phosphate (TEHP), 1-chloronapthalene (CN), and diethyl phthalate (DEP).57,58,86,119,124,133,136,140,145–147,161,166,167 Generally, more plasticizer corresponds to greatly improved physical properties, higher flexibility, and higher ionic mobility.145 As a result, most membranes contain a higher amount of plasticizer than polymer substrate. Overall, the percentage of polymer should be limited to avoid complications with solubility; however, enough polymer should be present to support the adhesive and mechanical properties of the membrane.
In addition to the ionophore and its mobility, the concentration of other active sensing components, such as ion exchangers or ionic additives, in the membrane affects sensor selectivity.171 Previously, research showed that low amounts of ion exchangers or ionic additives would create the most effective membranes; however, newly developed neutral ionophores require ionic additives to preserve the membrane's composition.152,165 Furthermore, these additives can improve the permselectivity of neutral ionophores. Improvements in sensor selectivity have also been documented in sensors with charged ionophores and ionic additives in the membrane.172–178 Hence, ionic additives or ion exchangers can improve selectivity regardless of the selected ionophore. Research has shown that additives improve selectivity by reducing interference from the other ions a sensor may encounter.179 However, an optimal additive to ionophore molar ratio must be used to obtain these improvements.94 The current optimal additive to ionophore ratio is reported to be 60 mol% additive to ionophore.157 Improved selectivity positively impacts the reproducibility and lifetime of the sensor.180 Therefore, a key component for designing ISEs with a high selectivity is limiting or eliminating ionic impurities in the membrane so the ionic additives can function optimally within the membrane.165 Some examples of ionic additives used within polymeric membranes are methyltridodecylammonium chloride (MTDDACl), tridodecylmethylammonium chloride (TDMACl or TDDMACl), and potassium tetrakis(p-chlorophenyl)borate (KTpClPB).57,58,119,124,136,138,140,145–148
Various techniques exist for preparing polymeric membranes based on desired morphology, geometry, mechanical strength, and function. These membranes can be isotropic (e.g., nonporous dense membranes, microporous membranes, and electrically charged membranes) or anisotropic (e.g., integrated asymmetric membranes, composite membranes, and supported liquid membranes), which require different fabrication processes.181 A detailed discussion of various fabrication processes (e.g., extrusion, phase inversion, diffusion induced phase separation, and others) does not lie within the scope of this review, but has been reported in detail.182,183 The casting method is often used for membrane preparation for carbonate detection. This method normally involves the formation of a cocktail solution, or mixture of membrane constituents; however, the components included in this initial mixture vary.160 In most cases, the polymer, ionophore, plasticizer, and ionic additive are mixed and dissolved in solvent, resulting in an uniform solution before casting.57,58,124,136,138,140,145,146 However, in some cases, the ionophore, plasticizer, and ionic additive are dissolved in the solvent before the polymer substrate is mixed in.134 In either procedure, the resultant homogeneous mixture is poured onto a glass ring on a glass surface where it can be left for some time to evaporate the solvent slowly. Previously reported evaporation time lengths for THF include 24 hours, 48 hours, and overnight.57,58,124,133,136,138,140,145,146 After the solvent has evaporated, the desired membrane disks are punched out from the cast membrane and mounted onto the electrode body. This process contains modifications for microsensors or solid-state sensors.119,147,148
7. Evaluating a potentiometric electrochemical sensor
Evaluating a potentiometric electrochemical sensor requires the determination of various properties, including sensitivity, measuring range, selectivity, response time, and lifetime. As discussed in section 6, all components of the ion-selective membrane impact these properties, which control the functionality of the sensor. Ideally, measuring all properties results in the most precise evaluation of a sensor; however, publications usually only measure and report a few of these properties. The reported performance of carbonate electrochemical sensors using carbonate ionophores is listed in Table 1.| Carbonate ionophore | Testing media | Measuring range | Sensitivity | Response time | Lifetime | Ref. |
|---|---|---|---|---|---|---|
| Trifluoroacetyl-p-butylbenzene | Water & 0.1 M NaCl solution | 10−7–10−2 M | Near Nernstian | 30 s–2 min | — | 121 |
| p-Butyl-α,α,α-trifluoroacetophenone, p-decyl-α,α,α-trifluoroacetophenone | Hospital patient samples | — | 20–25 mV per decade | — | 1 week | 111 |
| BTFAB, HDTFAB, & DDTFAB | Bovine serum | Reached linearity | −29.9–−14.1 mV per decade | — | — | 138 |
| 3,7-Bis(TFAB)CA, 3,12-bis(TFAB)CA, & 7,12-bis(TFAB)CA | Diluted serum | — | −29.6–−18.5 mV per decade | — | — | 145 |
| 3,12-Bis(TFAB)CA, deoxy-3,12-bis(TFAB)CA, & TFADB | Artificial seawater | — | −33.1–−29.6 mV per decade | — | — | 58 |
| TFAP-CA | Artificial gradients | — | 27–30 mV per 10-fold concentration change | 60 s | 3–5 days | 148 |
| Mn-1, Mn-2, & Mn-3 | Treated water & NaHCO3 | — | Close to −29.6 mV | Few s | — | 151 |
| Carbonate ionophore VII | Freshwater aquarium | — | — | 5 s | — | 57 |
| Deoxy-3,12-bis(TFAB)CA | Seawater & marine sediment | 2–300 μmol kg−1 | 28–31 mV | — | 5–7 days | 119 |
| 3,12-BisTFAB with N,N-dioctyl-3α,12α-bis(4-trifluoroacetylbenzyloxy)-5-cholan-24-amide | Standard solutions with 0.05 M Tris-H2SO4 (pH 8) | Limit of 2 × 10−4 M | −29.5–−29.2 mV per decade | — | 2 weeks | 147 |
| Hex-TFA, NO2-TFA, & Br-TFA | 0.1 M of sodium salts & Tris 0.01 M + H2SO4 (pH 8.5) | Limit of 7 × 10−7 M | 29 ± 1.5 mV per decade | — | — | 136 |
| 3-Bromo-4-hexyl-5-nitrofluoroacetophenone | 0.1 M of interfering anions & sodium salts with Tris 0.01 M + H2SO4 (pH 8.5) | — | 92–121 mV dec−1 | — | — | 124 |
| −48.1–−30.1 mV pH−1 | ||||||
| Substituted cholic and deoxycholic acid derivatives | Artificial & real seawater | — | −63.3–52.9 mV per decade | — | — | 146 |
| N,NI-Bis(phenyl)isophthalohydrazide & N,NI-bis(2,4-dinitrophenyl)isophthalohydrazide | Tris 0.01 M + H2SO4 & varying NaHCO3 concentrations (pH 8.6) | 1.3 × 10−7–1 × 10−3 M | 28–32 mV per decade | 7–50 s | 2½ months | 140 |
| Carbonate ionophore VII | Arve river, Geneva | 2.3 μM–1 mM | 27.2 ± 0.8 mV per decade | 1 s | — | 197 |
| N,NI-Bis(2,4-dinitrophenyl)isophthalohydrazide | Artificial seawater | Limit of 5 ppt | Near Nernstian | — | — | 29 |
| Carbonate ionophore VII | Outdoor mesocosm & Genoa harbor | 10−5–10−1 M | −27.8 mV per decade | <10 s | 3 weeks | 31 |
| Carbonate ionophore VII | Seawater | 10−5–10−1 M | −30.4 mV per decade | <1 s | >60 days | 98 |
7.1 Sensitivity, detection limit, and measuring range
As described in section 4.2.2, the potentiometric response of a sensor should follow the Nernst equation (eqn (5)) and have an experimental response slope close or equal to −29.6 mV per decade or 59.2 mV/z. A calibration curve can be plotted with the line of best fit to determine the experimental response slope of the linear section of the curve. The slope of the linear section of the curve represents the sensitivity of the sensor by describing how its measurements fluctuate per change of analyte concentration in the sample. Ideally, it should be close or equal to Nernst slope to indicate optimal sensitivity.98 Evaluating the experimental response slope can also verify whether the intended target analyte is being measured. Research reports that response slopes around −30 mV per decade indicate response to carbonate, whereas slopes around −60 mV per decade indicate response to bicarbonate.35 In the past, unusually high Nernst slopes (i.e., super-Nernstian slopes) were attributed to transmembrane ion fluxes or the presence of primary and interfering ions in the ion-selective membrane.103,184–191 However, more recently, research suggests that super-Nernstian slopes may occur when the ionophore and target ion simultaneously form different stoichiometric complexes (e.g., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes) or when there is an excessive inward concentration gradient.99,192 Based on these new findings, researchers should carefully evaluate their device if super-Nernstian slopes are observed. If the sensor's sensitivity needs improvement, an effective process for improving sensor sensitivity is the activation of the membrane before sensor use, which is known as aging the membrane.193 Recently, improved sensitivity from aged membranes was demonstrated in carbonate microsensors by Han and co-workers. In their experiments, the carbonate electrodes were aged through submersion in an electrolyte before calibration and testing. The carbonate electrode aged in the electrolyte for 24 hours exhibited a sensitivity closer to the Nernst slope than the electrode submerged for only 8 hours.119 This improvement in sensitivity may be attributed to the change in potential that resulted from an equilibrium established between the inner and outer sides of the membrane when aged.
1 complexes) or when there is an excessive inward concentration gradient.99,192 Based on these new findings, researchers should carefully evaluate their device if super-Nernstian slopes are observed. If the sensor's sensitivity needs improvement, an effective process for improving sensor sensitivity is the activation of the membrane before sensor use, which is known as aging the membrane.193 Recently, improved sensitivity from aged membranes was demonstrated in carbonate microsensors by Han and co-workers. In their experiments, the carbonate electrodes were aged through submersion in an electrolyte before calibration and testing. The carbonate electrode aged in the electrolyte for 24 hours exhibited a sensitivity closer to the Nernst slope than the electrode submerged for only 8 hours.119 This improvement in sensitivity may be attributed to the change in potential that resulted from an equilibrium established between the inner and outer sides of the membrane when aged.
Along with the sensitivity, the detection limit and measuring range of a sensor can be determined using the calibration curve. The detection limit is the lowest concentration that can be measured while differing from a measurement obtained from a blank sample.194 Using a calibration curve, measurements from a blank sample, and extrapolation, the equation of best fit can reveal the detection limit.195 For ocean acidification research, carbonate ion concentrations in some oceanic and estuarine waters may vary between 30 to 300 μmol kg−1, so a detection limit as low as a few μmol L−1 (10−6 M) will be ideal. Sokalski and co-workers reported that the improvement in the lower detection limit of a sensor could be achieved with an internal solution containing a high concentration of an interfering ion with a low concentration of the target ion.196
Similar to sensor sensitivity, the measuring range is determined from the domain of linearity. Within this domain, the analyte concentrations encountered by the sensor represent the analyte concentration range that can be reliably measured since the sensor is operating with Nernstian behavior. Jain and co-workers plotted Fig. 13 to determine the sensitivity, detection limit, and measuring range for six of their sensors, which they labeled as sensors 7–12. Each of their sensors contained a PVC membrane with varying plasticizers. The membrane of sensor 7 contained no plasticizer, while the membranes of sensors 8–12 contained TEHP, DOS, DOP, CN, and DEP, respectively. Sensor 11 produced the greatest range of linearity, resulting in a detection limit of 1.3 × 10−7 M and a measuring range of 1.3 × 10−7 to 1.0 × 10−2 M while maintaining Nernstian behavior (29.0 mV per decade).140 Song and co-workers produced a similar figure (Fig. 14) to display sensitivity and detection limit. From Fig. 14, the slope and detection limit for electrodes a, b, and c were −29.3, −29.2, and −29.5 mV per decade and 2.0 × 10−4, 2.6 × 10−4, and 2.7 × 10−4 mol L−1, respectively.14 To date, multiple carbonate sensors have demonstrated near Nernstian and Nernstian behavior (Table 1). Almost all publications listed in Table 1 reported the sensitivity of their device. The detection limit, however, has not been consistently reported. The lowest detection limit of the sensors in Table 1 was reported by Makarychev and co-workers (2003) as 7.0 × 10−7 M.136 Like the detection limit, the measuring range of sensors is not as frequently reported as the sensitivity, but it is reported more often than the detection limit. For sensors tested with appropriate ion solutions, Herman and Rechnitz reported the widest measuring range of 10−7 to 10−2 M.121 Jain and co-workers reported a similar range of 1.3 × 10−7 to 1.0 × 10−3 M.140 For sensors tested in seawater or river water samples, reported measuring ranges include 2 to 300 μmol kg−1, 2.3 μM to 1 mM, and 10−5 to 10−1 M.65,99,119,197
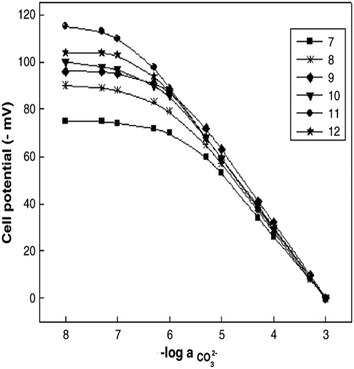 | ||
| Fig. 13 Calibration curves produced by sensors 7−12 from Jain et al. The membranes were PVC based without plasticizer (7) and with the plasticizers of TEHP (8), DOS (9), DOP (10), CN (11), and DEP (12). Reprinted from Electrochimica Acta, Copyright (2006), with permission from Elsevier.140 | ||
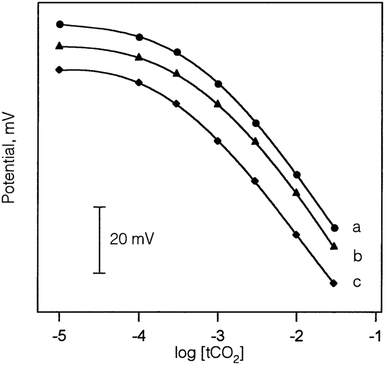 | ||
| Fig. 14 Calibration curves of sensors with an Ag/AgCl (a), a PHDP-modified Ag/AgCl (b), and a POT-modified Ag/AgCl electrode (c) produced by Song et al. All three sensors exhibited Nernst behavior and a similar detection limit of 2.0 × 10−4 M. Reprinted from Talanta, Copyright (2002), with permission from Elsevier.147 | ||
7.2 Selectivity
Selectivity is the property of ISEs that allows them to be useful for detecting target ions from a complicated matrix or environment of multiple ions. Many definitions exist, but the accepted IUPAC definition explains selectivity as a measure of how well a method can distinguish and quantify a particular analyte in the presence of interferents.198In seawater, the common interferents for carbonate include Cl−, Sal−, SCN−, NO3−, NO2−, Br−, SO42−, and HPO42−.58,126 As a result, the selectivity of a sensor for these ions and carbonate are compared to evaluate the sensor's ability to target carbonate. Usually, ISEs respond to anions according to the Hofmeister series.199 Because carbonate and bicarbonate are highly hydrophilic and fall on one end of the series (CO32− > SO42− > S2O32− > H2PO4− > F− > Cl− > Br− > NO3− > I− > ClO4− > SCN−), developing electrodes with high selectivity for them is challenging. Furthermore, the challenge becomes more profound if the electrode is intended for use in an environment with a high chloride concentration, such as seawater. The chloride level in seawater is about 0.5 M, while the level of bicarbonate/carbonate is only around 0.002 M. Therefore, the required selectivity to measure bicarbonate/carbonate in a 250-fold chloride environment should be 4 × 10−5 based on calculation.
Various techniques exist for measuring selectivity coefficients. Methods are typically categorized as either a mixed solution method or separate solution method.200 An in-depth discussion of each method does not fall within the scope of this review, but extensive detail has been reported elsewhere.200–203 Some examples of methods used in ocean acidification research include the separate solution method (Fig. 5) and the matched potential method (Fig. 8).58,126
As discussed in section 6, the selectivity of a sensor is greatly influenced by the membrane composition. The addition of plasticizer, which is critical for the mechanical properties of the membrane and the mobility of the ionophore, can improve selectivity. If the ionophore is electrically charged, an optimized ratio of ionophore and ionic sites in the sensing membrane is predicted to provide the highest selectivity. Furthermore, adding ionic sites with the same charge as interfering ions can also improve selectivity.195 To ensure the measured selectivity is accurate, the sensor should be evaluated for the presence of a gas leak, especially for CO2 diffusion in or out of the test setup. If a gas leak occurs, the error will be magnified on calibration curves once the carbonate concentration approaches 1 × 10−6 M.
7.3 Response time
The response time of a sensor is how quickly a sensor can produce a readable signal after exposure to an analyte.204 In their guidelines, IUPAC describes the dipping and injection methods as techniques for determining the response time of a sensor.205 For microsensors, Merikhi and co-workers describe the jet-nozzle method.204 Regardless of the method, it is ideal to test the sensor in field conditions (e.g., seawater) or similar conditions (e.g., artificial seawater or various solutions containing the target analyte and interferents) for an accurate response time.204 For example, Jain and co-workers measured the response time of their carbonate sensor using solutions containing CO32−.140 Initially, they exposed their sensor to a solution containing 1.0 × 10−5 M of CO32−. After the sensor stabilized in this solution, Jain and co-workers increased the [CO32−] to 1.0 × 10−4 M and measured the time it took the sensor to stabilize in the new solution as the response time. In their experiments, they tested 12 carbonate sensors with varying membrane compositions, analyzing two carbonate ionophores displayed in Fig. 4e and f and four plasticizers (TEHP, DOS, DOP, CN, and DEP). The sensor containing the ionophore f and the plasticizer CN demonstrated the lowest response time of 7 seconds. In their sensors containing ionophore e, the sensor membrane also containing CN performed the best with a response time of 10 seconds.For ocean acidification research, a short response time is vital to ensure that small, frequent changes in carbonate concentration are captured. As an example, Yuan and co-workers determined the response time of their sensor to be 1 second by adding successive additions of bicarbonate to 0.1 M Tris-H2SO4 buffer solution and monitoring the time until the sensor produced a stable potential after each addition (Fig. 15).197 Because this sensor was tested in field conditions (Arve river), it displays great promise for ocean acidification research. Another carbonate sensor built by Zhang and co-workers displayed an excellent response time of less than 1 second through the immersion method.98 At the time of this publication, this response time is the best reported for carbonate sensors to the best of our knowledge. The reported response times for multiple carbonate sensors can be found in Table 1. Some other notable response times include less than 10 seconds while operating in an outdoor mesocosm and in the Genoa Harbor and 60 seconds while operating in artificial gradients in agar, freshwater tufas, foraminifera, and microbial mats.32,148
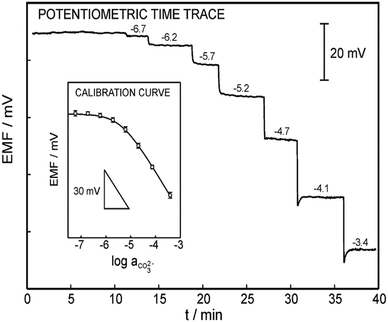 | ||
| Fig. 15 Analytical performance of the carbonate electrode made by Yuan et al. The response time was obtained by adding successive additions of bicarbonate to 0.1 M Tris-H2SO4 buffer (pH = 8.6). Inset: A triplicate of the calibration curve (RSD = 1.5%) as a function of the carbonate activity (slope = −27.2 ± 0.8 mV per decade, LOD = 2.3 μM). Reprinted (adapted) with permission from ref. 197. Copyright 2015 American Chemical Society. | ||
The response time of a sensor is related to the size and thickness of its sensing membrane. Generally, increasing the contact area between the test solution and the film and reducing the thickness of the membrane can improve the response speed of the electrode. A membrane that is too thick leads to larger resistance and will not properly facilitate electron transfer, resulting in a longer response time. The sensor lifetime is another important parameter which could be influenced by the thickness of the film (discussed in the next section). According to the environment where the sensor will be used, a balance should be made between the lifetime and response time when designing the membrane.
7.4 Lifetime
The lifetime, or how long a sensor can operate at a functional capacity, is affected by many factors. As previously mentioned, biofouling, the composition of the membrane, and size and thickness of the membrane affect the lifetime of sensors. Moreover, based on previous investigations by Sun and co-workers, proper activation of the membrane (i.e., aging) in a buffer solution is necessary for a newly prepared electrode to reach a relatively slow potential drift rate and respond effectively to target ions over time.206 Storing the device in a dry environment and avoiding strong redox active species could also be a good way to slow down the potential decrease and prolong the working life.206 Throughout the literature, lifetimes have been reported from three days to two and a half months for carbonate sensors (Table 1).140,148 On average, the lifetime of ISEs, including those not involved in ocean acidification research, is from 4 to 10 weeks.160 Commonly, the sensitivity of a sensor is measured at least once every week to confirm if the sensor is continuing to operate effectively.161 Zhao and Cai reported that once the sensitivity fell below 52 mV pH−1, the lifetime could be determined.161 However, Jain and co-workers used reproducible potential and a low standard deviation of 0.3 mV to determine a lifetime of two and a half months.140Lifetime is an important parameter, especially for liquid microelectrodes. Fabricating thin and large-diameter liquid-membraned microelectrodes facilitates fast response. However, such thin membranes are more susceptible to change because of gradual leakage, which may result in a reduced lifetime. Conversely, a thick membrane with a small tip diameter could provide a longer lifetime, but may lead to high impedance, high noise, slow response time, and a slow aging process. Han and co-workers sought to determine an optimal combination of membrane thickness and diameter to balance the response time and lifetime of liquid microelectrodes. They concluded that a carbonate microelectrode membrane with a thickness and tip diameter of 100 μm and 20 μm, respectively, provided a balance with adequate tip strength and quicker membrane aging. The CO32− microsensor fabricated to this specification can be used for 5–7 days and the drift rate can be decreased to nearly 1–2 mV h−1 after a stabilization period of 1 day.119
Overall, all properties used for evaluating an electrochemical sensor contribute to the lifetime of the device. Thus, a sensor's lifetime is the clearest indicator of a sensor's ability to function in the desired capacity.
7.5 Evaluating the connection between carbonate ionophore structure and sensor performance
In this review, three types of carbonate ionophores are discussed, including small molecules, molecular tweezers, and metal-based complexes. Each ionophore type is distinct and presents structural advantages and complications that impact sensor performance. It is necessary to note that other components of reported sensors may also boost or worsen performance. In other words, positive or poor performance cannot be solely attributed to the ionophore; however, specific structural characteristics within carbonate ionophore types may assist in enhancing carbonate detection and sensor performance.Small organic molecules are advantageous because they can be easily modified compared to molecular tweezers and metal-based complexes. Various substituents can be attached to the phenyl ring to adjust its properties and ability to bind carbonate. For example, increased acidity and hydrogen donor capacity have increased bonding with carbonate, leading to a lower detection limit and better carbonate selectivity, lipophilicity, and sensor lifetime. Incorporating –NO2 groups has been frequently credited for these enhancements.126,134,140–142 In addition, the simultaneous presence of a –Br substituent and a –NO2 group may lead to these improvements.124 Unlike small organic molecules, molecular tweezers and metal-based complexes are challenging to develop and adjust because of conformation complications like steric hindrance. However, highly improved carbonate selectivity has been reported with molecular tweezers and metal-based complexes, especially those forming 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with carbonate.141,142,145,146,151 The ability of molecular tweezers and metal-based complexes to bind with carbonate in two places seems to increase the reliability of carbonate detection, which small organic molecules do not currently offer. Even though all three carbonate ionophores experience some level of interference, small organic molecules tend to be more vulnerable to interferents. As a result, designing a molecular tweezer or metal-based complex ionophore with a strong base, two binding sites for carbonate, and functional groups that increase acidity and hydrogen donor capacity seems to be the most favorable ionophore structure.
1 complexes with carbonate.141,142,145,146,151 The ability of molecular tweezers and metal-based complexes to bind with carbonate in two places seems to increase the reliability of carbonate detection, which small organic molecules do not currently offer. Even though all three carbonate ionophores experience some level of interference, small organic molecules tend to be more vulnerable to interferents. As a result, designing a molecular tweezer or metal-based complex ionophore with a strong base, two binding sites for carbonate, and functional groups that increase acidity and hydrogen donor capacity seems to be the most favorable ionophore structure.
8. Summary and future research
Carbonate ions are present in various clinical and environmental processes. As a result, monitoring the carbonate concentration in clinical and environmental samples is essential for advancing disease screening and environmental monitoring. In the past few decades, tracking the carbonate concentration within ocean waters has become increasingly important due to ocean acidification. Research has shown that potentiometric electrochemical sensors based on novel carbonate ionophores have the potential to be highly selective and sensitive to carbonate while remaining stable in marine environments. Carbonate ionophores have proved to be a vital component of these devices by detecting carbonate through various mechanisms (e.g., hydrogen bonding, covalent bonding, the electron-withdrawing effect, and the entrapment of the analyte). However, many challenges currently complicate the ability of these sensors to capture accurate in situ carbonate measurements during long-term deployment. As a result, there are several possibilities for future research in this field.Further development of novel carbonate ionophores is anticipated. Based on the rich diversity of organic synthesis methods, ionophores with novel functionalities and structures to enhance carbonate selectivity over interfering ions are expected. At the time of this publication, a molecular tweezer or metal-based complex with a strong base and two binding sites for carbonate seems to be the most favorable carbonate ionophore structure. Multiple publications have also reported the positive effect of increased acidity and hydrogen donor capacity on carbonate selectivity. Because of this, functional groups that increase these properties must be considered and potentially added to molecular tweezers or metal-based complexes.
The issues caused by the internal reference solution must be addressed to extend the lifetime of sensors. Solid-state ISEs may overcome these issues since these devices replace the internal solution with a solid-contact transducer.109 A conductive polymer is typically used as a solid-contact transducer to increase the sensor's stability and reduce dissolved oxygen interference.29,109,147 Carbon nanotubes and carbon film can also be a solid-contact transducer to provide a large contact area with the ion-selective membrane, an adjustable surface, and resistance to CO2 and O2.98,109 Future research must continue to evaluate these materials and others (e.g., metal non-porous films) to determine which is best for sensor stability.109
Ocean acidification research efforts may move towards solid-state ISEs since they eliminate the internal reference solution and seem more suitable for long-term deployment. Two recent approaches using solid-state ISEs for in situ water monitoring include allowing direct contact between the electrodes and the water and containing the electrodes inside a fluidic-based submersible device.207,208 The first approach, which allows direct contact between the electrode and water, is advantageous because it can provide continuous measurements and capture minute changes in analyte concentration. However, this device has only been tested in freshwater environments for a short time, so more testing is needed to determine if the device is suitable for long-term deployment in seawater. Biofouling will likely be an issue with this sensor design because of the direct contact between the electrode and water. Overall, possibilities for preventing biofouling are desperately needed in this research field. The second approach of placing solid-state ISEs within a submersible fluidic device is incredibly appealing since it has been deployed in seawater for carbonate measurement. For three weeks, the device operated optimally; however, its design did not allow for continuous measurement due to its hour-long in situ calibration process. The in situ calibration process is beneficial for reducing interference, but it prevents the sensor from capturing minute changes in carbonate concentration. Future research should investigate how to simplify the in situ calibration process to increase the capture of carbonate concentration.
Future research may also move towards the creation of carbonate microsensors. Microsensors are likely to have a simple design and low production costs, which makes them appealing for large-scale implementation. A reported classical potentiometric carbonate microsensor was highly selective to carbonate with a response time of 60 seconds and a lifetime of 3–5 days following a simple calibration procedure.148 Based on these results, microsensors may require a relatively simple calibration process compared to macrosensors and be more suitable for continuous measurement. Further investigation of a reliable method for forming durable membranes of such a small radius (several micrometers) is needed. These membranes must be able to induce the diffusion process and lead to a rapid signal while remaining resistant to biofouling and pressure. Recently, a miniaturized carbonate solid-state ISE was tested in seawater, even in deep-sea conditions.98 The sensor's design had a 0.5 mm diameter and a 6 to 12 mm length with carbonate ionophore VII and carbon film in its structure. The device was resistant to seawater interference and displayed Nernstian behavior with a response time and lifetime of less than 1 second and over 60 days, respectively. Therefore, integrating solid-state ISEs into microsensors may be even more favorable for ocean acidification research. In this design, issues from the internal reference solution would be eliminated while lowering production costs. Furthermore, carbonate microsensors could be integrated into sensor devices with other electrodes to create a device capable of simultaneously monitoring multiple oceanic parameters (e.g., pH and pCO2).
In recent studies, optodes have been tested in seawater and other natural waters.61–64 They are reported as small and easy-to-use versatile sensors with low drift, fast response time, and long lifetime. In one study, an optode was designed with a battery that may enable deployment for over a year without required service.63 In addition, a simple copper guard can protect these sensors against biofouling.61 These characteristics demonstrate potential for ocean acidification research; however, these sensors have only detected dissolved oxygen, carbon dioxide, and pH. Future research could involve designing an optode for carbonate detection and testing the device in varying salinities, pressures, and temperatures.
As anthropogenic atmospheric CO2 continues to dissolve into the ocean at increased rates, the urgency to accurately monitor ocean acidification and limit anthropogenic CO2 emission amplifies. In the Paris Agreement, many countries committed to gradually reducing greenhouse gas emissions by 2030.209 Recently, a new clean strategy to reduce greenhouse gas emissions by transforming atmospheric CO2 into useable chemicals and fuels may become the driving force towards carbon neutrality.209–212 The large-scale implementation of ocean-based carbon dioxide removal (CDR) technologies coupled with this new promising strategy to reduce CO2 emission has enormous potential to mitigate climate change and prevent further ocean acidification.
Author contributions
Stefanny N. Toala: investigation, conceptualization, writing – original draft, and writing – review and editing. Zhentao Sun: writing – review and editing. Yanfeng Yue: funding acquisition, project administration, supervision, conceptualization, and writing – review and editing. Stephen F. Gonski: writing – review and editing. Wei-Jun Cai: conceptualization, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This publication was made possible by the National Science Foundation EPSCoR Grant No. 1757353 and the State of Delaware.References
- C. L. Sabine, R. A. Feely, N. Gruber, R. M. Key, K. Lee, J. L. Bullister, R. Wanninkhof, C. S. Wong, D. W. R. Wallace, B. Tilbrook, F. J. Millero, T.-H. Peng, A. Kozyr, T. Ono and A. F. Rios, Science, 2004, 305, 367–371 CrossRef CAS PubMed.
- P. Friedlingstein, M. W. Jones, M. O'Sullivan, R. M. Andrew, D. C. E. Bakker, J. Hauck, C. Le Quéré, G. P. Peters, W. Peters, J. Pongratz, S. Sitch, J. G. Canadell, P. Ciais, R. B. Jackson, S. R. Alin, P. Anthoni, N. R. Bates, M. Becker, N. Bellouin, L. Bopp, T. T. T. Chau, F. Chevallier, L. P. Chini, M. Cronin, K. I. Currie, B. Decharme, L. M. Djeutchouang, X. Dou, W. Evans, R. A. Feely, L. Feng, T. Gasser, D. Gilfillan, T. Gkritzalis, G. Grassi, L. Gregor, N. Gruber, Ö. Gürses, I. Harris, R. A. Houghton, G. C. Hurtt, Y. Lida, T. Ilyina, I. T. Luijkx, A. Jain, S. D. Jones, E. Kato, D. Kennedy, K. K. Goldewijk, J. Knauer, J. I. Korsbakken, A. Körtzinger, P. Landschützer, S. K. Lauvset, N. Lefèvre, S. Lienert, J. Liu, G. Marland, P. C. McGuire, J. R. Melton, D. R. Munro, J. E. M. S. Nabel, S.-I. Nakaoka, Y. Niwa, T. Ono, D. Pierrot, B. Poulter, G. Rehder, L. Resplandy, E. Robertson, C. Rödenbeck, T. M. Rosan, J. Schwinger, C. Schwingshackl, R. Séférian, A. J. Sutton, C. Sweeney, T. Tanhua, P. P. Tans, H. Tian, B. Tilbrook, F. Tubiello, G. R. van der Werf, N. Vuichard, C. Wada, R. Wanninkhof, A. J. Watson, D. Willis, A. J. Wiltshire, W. Yuan, C. Yue, X. Yue, S. Zaehle and J. Zeng, Earth Syst. Sci. Data, 2022, 14, 1917–2005 CrossRef.
- J. Blunden and D. S. Arndt, Bull. Am. Meteorol. Soc., 2020, 101, Si-S429 Search PubMed.
- X. Lan, P. Tans and K. W. Toning, https://gml.noaa.gov/ccgg/trends/global.html, (accessed 1 March 2023).
- F. Joos and R. Spahni, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1425–1430 CrossRef CAS PubMed.
- C. Le Quéré, R. M. Andrew, P. Friedlingstein, S. Sitch, J. Hauck, J. Pongratz, P. A. Pickers, J. I. Korsbakken, G. P. Peters, J. G. Canadell, A. Arneth, V. K. Arora, L. Barbaro, A. Nastos, L. Bopp, F. Chevallier, L. P. Chini, P. Cias, S. C. Doney, T. Gkritzalis, D. S. Goll, I. Harris, V. Haverd, F. M. Hoffman, M. Hoppema, R. A. Houghton, G. Hurtt, T. Ilyina, A. K. Jain, T. Johannessen, C. D. Jones, E. Kato, R. F. Keeling, K. K. Goldewijk, P. Landschützer, N. Lefèvre, S. Lienert, Z. Liu, D. Lombardozzi, N. Metzl, D. R. Munro, J. E. M. S. Nabel, S. Nakaoka, C. Neill, A. Olsen, T. Ono, P. Patra, A. Peregon, W. Peters, P. Peylin, B. Pfeil, D. Pierrot, B. Poulter, G. Rehder, L. Resplandy, E. Robertson, M. Rocher, C. Rödenbeck, U. Schuster, J. Schwinger, R. Séférian, I. Skjelvan, T. Steinhoff, A. Sutton, P. P. Tans, H. Tian, B. Tilbrook, F. N. Tubiello, I. T. van der Laan-Luijkx, G. R. van der Werf, N. Viovy, A. P. Walker, A. J. Wiltshire, R. Wright, S. Zaehle and B. Zheng, Earth Syst. Sci. Data, 2018, 10, 2141–2194 CrossRef.
- A. J. Watson, U. Schuster, J. D. Shutler, T. Holding, I. G. C. Ashton, P. Landschützer, D. K. Woolf and L. Goddijn-Murphy, Nat. Commun., 2020, 11, 4422 CrossRef CAS PubMed.
- Intergovernmental Panel on Climate Change, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, United Kingdom and New York, NY, USA, 2021 Search PubMed.
- S. Barker and A. Ridgewell, Nature Education Knowledge, 2012, 3, 21 Search PubMed.
- W.-J. Cai, Y.-Y. Xu, R. A. Feely, R. Wanninkhof, B. Jönsson, S. R. Alin, L. Barbero, J. N. Cross, K. Azetsu-Scott, A. J. Fassbender, B. R. Carter, L.-Q. Jiang, P. Pepin, B. Chen, N. Hussain, J. J. Reimer, L. Xue, J. E. Salisbury, J. M. Hernández-Ayón, C. Langdon, Q. Li, A. J. Sutton, C.-T. A. Chen and D. K. Gledhill, Nat. Commun., 2020, 11, 2691 CrossRef CAS PubMed.
- W.-J. Cai, R. A. Feely, J. M. Testa, M. Li, W. Evans, S. R. Alin, Y.-Y. Xu, G. Pelletier, A. Ahmed, D. J. Greeley, J. A. Newton and N. Bednaršek, Annu. Rev. Mar. Sci., 2021, 13, 23–55 CrossRef PubMed.
- R. Zeebe, Annu. Rev. Earth Planet. Sci., 2012, 40, 141–165 CrossRef CAS.
- A. G. González, N. Pérez-Almeida, J. M. Sanatana-Casiano, F. J. Millero and M. González-Dávila, Mar. Chem., 2016, 179, 12–22 CrossRef.
- R. H. Byrne, Geochem. Trans., 2002, 3, 11–16 CrossRef PubMed.
- F. J. Millero, R. Woosley, B. DiTrolio and J. Water, Oceanography, 2009, 22, 72–85 CrossRef.
- F. M. M. Morel, A. J. Milligan and M. A. Saito, Treatise Geochem., 2003, 6, 113–143 CrossRef.
- E. Brietbarth, R. J. Bellerby, C. C. Neill, M. V. Ardelan, M. Meyerhöfer, E. Zöllner, P. L. Croot and U. Riebesell, Biogeosciences, 2010, 7, 1065–1073 CrossRef.
- R. A. Feely, C. L. Sabine, K. Lee, W. Berelson, J. Kleypas, V. L. Fabry and F. J. Millero, Science, 2004, 305, 362–366 CrossRef CAS PubMed.
- L. Cao, K. Caldeira and A. K. Jain, Geophys. Res. Lett., 2007, 34, L05607 Search PubMed.
- U. Riebesell, I. Zondervan, B. Rost, P. D. Tortell, R. E. Zeebe and F. M. M. Morel, Nature, 2000, 407, 364–367 CrossRef CAS PubMed.
- I. Zondervan, R. E. Zeebe, B. Rost and U. Riebesell, Global Biogeochem. Cycles, 2001, 15, 507–516 CrossRef CAS.
- N. R. Mollica, W. Guo, A. L. Cohen and A. R. Solow, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1754–1759 CrossRef CAS PubMed.
- M.-D. Zheng and L. Cao, Adv. Clim. Chang. Res., 2014, 5, 189–196 CrossRef.
- R. Albright, Y. Takeshita, D. A. Koweek, A. Ninokawa, K. Wolfe, T. Rivlin, Y. Nebuchina, J. Young and K. Caldeira, Nature, 2018, 555, 516–519 CrossRef CAS PubMed.
- S. C. Doney, V. J. Fabry, R. A. Feely and J. A. Kleypas, Annu. Rev. Mar. Sci., 2009, 1, 169–192 CrossRef PubMed.
- S. M. Bushinsky, Y. Takeshita and N. L. Williams, Curr. Clim. Change Rep., 2019, 5, 207–220 CrossRef PubMed.
- Z. A. Wang, H. Moustahfid, A. V. Mueller, A. P. M. Michel, M. Mowlem, B. T. Glazer, T. A. Mooney, W. Michaels, J. S. McQuillan, J. C. Robidart, J. Churchill, M. Sourisseau, A. Daniel, A. Schaap, S. Monk, K. Friedman and P. Brehmer, Front. Mar. Sci., 2019, 6, 519 CrossRef.
- Q. Shangguan, A. Prody, T. S. Wirth, E. M. Briggs, T. R. Martz and M. D. DeGrandpre, Mar. Chem., 2022, 240, 104085 CrossRef CAS.
- L. Mendecki, T. Fayose, K. A. Stockmal, J. Wei, S. Granados-Focil, C. M. McGraw and A. Radu, Anal. Chem., 2015, 87, 7515–7518 CrossRef CAS PubMed.
- R. Athavale, N. Pankratova, C. Dinkel, E. Bakker, B. Wehrli and A. Brand, Environ. Sci. Technol., 2018, 52, 11259–11266 CrossRef CAS PubMed.
- M. Cuartero, N. Pankratova, T. Cherubini, G. A. Crespo, F. Massa, F. Confalonieri and E. Bakker, Environ. Sci. Technol. Lett., 2017, 4, 410–415 CrossRef CAS.
- G. Mills and G. Fones, Sens. Rev., 2012, 32, 17–28 CrossRef.
- National Academies of Sciences, Engineering, and Medicine, A Research Strategy for Ocean-based Carbon Dioxide Removal and Sequestration, The National Academies Press, Washington, DC, 2022 Search PubMed.
- D. Pines, J. Ditkovich, T. Mukra, Y. Miller, P. M. Kiefer, S. Daschakraborty, J. T. Hynes and E. Pines, J. Phys. Chem. B, 2016, 120, 2440–2451 CrossRef CAS PubMed.
- W. Stumm and J. J. Morgan, in Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, Wiley, 1995, pp. 157–163 Search PubMed.
- R. E. Zeebe and D. Wolf-Gladrow, in CO2 in Seawater: Equilibrium, Kinetics, Isotopes, Elsevier, 2001, pp. 1–26 Search PubMed.
- M. M. Mugica, C. Day, B. McHale, K. L. McGuinness, G. Lee, D. Pickup and N. S. Lawrence, Ocean Sci. Discuss., 2022, preprint, DOI:10.5194/os-2021-126.
- T. Loerting and J. Bernard, ChemPhysChem, 2010, 11, 2305–2309 CrossRef CAS PubMed.
- A. G. Dickson, in Guide to best practics for ocean acidification research and data reporting, ed. U. Riebesell, V. J. Fabry, L. Hansson and J.-P. Gattuso, Publications Office of the European Union, 2010, pp. 17–40 Search PubMed.
- L. D. Talley, R. A. Feely, B. M. Sloyan, R. Wanninkhof, M. O. Baringer, J. L. Bullister, C. A. Carlson, S. C. Doney, R. A. Fine, E. Firing, N. Gruber, D. A. Hansell, M. Ishii, G. C. Johnson, K. Katsumata, R. M. Key, M. Kramp, C. Langdon, A. M. Macdonald, J. T. Mathis, E. L. McDonagh, S. Mecking, F. J. Millero, C. W. Mordy, T. Nakano, C. L. Sabine, W. M. Smethie, J. H. Swift, T. Tanhua, A. M. Thurnherr, M. J. Warner and J.-Z. Zhang, Annu. Rev. Mar. Sci., 2015, 8, 185–215 CrossRef PubMed.
- N. Gruber, D. Clement, B. R. Carter, R. A. Feely, S. Van Heuven, M. Hoppema, M. Ishii, R. M. Key, S. K. Lauvset, C. Lo Monaco, J. T. Mathis, A. Murata, A. Olsen, F. F. Perez, C. L. Sabine, T. Tanhua and R. Wanninkhof, Science, 2019, 363, 1193–1199 CrossRef CAS PubMed.
- F. J. Millero, T. B. Graham, F. Hunag, H. Bustos-Serrano and D. Pierrot, Mar. Chem., 2006, 100, 80–94 CrossRef CAS.
- E. R. Lewis and D. W. R. Wallace, Program Developed for CO2 System Calculations, https://data.ess-dive.lbl.gov/view/doi:10.15485/1464255, (accessed 10 January 2023).
- F. J. Millero, Geochim. Cosmochim. Acta, 1995, 59, 661–677 CrossRef CAS.
- D. E. Pierrot, E. Lewis and D. W. R. Wallace, MS Excel Program Developed for CO2 System Calculations, https://cdiac.ess-dive.lbl.gov/ftp/co2sys/CO2SYS_calc_XLS_v2.1/, (accessed 10 January 2023) Search PubMed.
- F. J. Millero, Chem. Rev., 2007, 107, 308–341 CrossRef CAS PubMed.
- J. Ma, H. Shu, B. Yang, R. Byrne and D. Yuan, Anal. Chim. Acta, 2019, 1081, 18–31 CrossRef CAS PubMed.
- J. C. Orr, J.-M. Epitalon, A. G. Dickson and J.-P. Gattuso, Mar. Chem., 2018, 207, 84–107 CrossRef CAS.
- W.-J. Cai, Y. Wang and R. E. Hodson, Geochim. Cosmochim. Acta, 1998, 62, 473–483 CrossRef CAS.
- S. Song, Z. A. Wang, M. E. Gonneea, K. D. Kroeger, S. N. Chu, D. Li and H. Liang, Geochim. Cosmochim. Acta, 2020, 275, 123–139 CrossRef CAS.
- K. Kuliński, B. Schneider, B. Szymczycha and M. Stokowski, Earth Syst. Dyn, 2017, 8, 1107–1120 CrossRef.
- O. Sulpis, S. K. Lauvset and M. Hagens, Ocean Sci., 2020, 16, 847–862 CrossRef CAS.
- M. Ramsey, Accredit. Qual. Assur., 2021, 26, 183–192 CrossRef CAS.
- E. Bakker, G. Crespo, E. Grygolowicz-Pawlak, G. Mistlberger, M. Pawlak and X. Xie, Chimia, 2011, 65, 141–149 CrossRef CAS PubMed.
- S. F. Gonski, M. J. Horwith, S. Albertson, J. Bos, A. S. Brownlee, N. Coleman, C. F. Maloy, M. Keyzers, C. Krembs, G. Pelletier, E. Rauschl, H. R. Young and W.-J. Cai, Coast. Manage., 2021, 49, 487–509 CrossRef.
- J. Buffle and G. Horvai, in In Situ Monitoring of Aquatic Systems: Chemical Analysis and Speciation, ed. J. Buffle and G. Horvai, Wiley, 2000, pp. 1–17 Search PubMed.
- X. Xie and E. Bakker, Anal. Chem., 2013, 85, 1332–1336 CrossRef CAS PubMed.
- Y. S. Choi, L. Lvova, J. H. Shin, S. H. Oh, C. S. Lee, B. H. Kim, G. S. Cha and H. Nam, Anal. Chem., 2002, 74, 2435–2440 CrossRef CAS PubMed.
- X. Xie, M. Pawlak, M.-L. Tercier-Waeber and E. Bakker, Anal. Chem., 2012, 84, 3163–3169 CrossRef CAS PubMed.
- M. Moßhammer, M. Strobl, M. Kühl, S. M. Borisov and K. Koren, ACS Sens., 2016, 1, 681–687 CrossRef.
- E. Fritzsche, C. Staudinger, J. P. Fischer, R. Thar, H. W. Jannasch, J. N. Plant, M. Blum, G. Massion, H. Thomas, J. Hoech, K. S. Johnson, S. M. Borisov and I. Klimant, Mar. Chem., 2018, 207, 63–76 CrossRef CAS.
- D. Atamanchuk, A. Tengberg, P. J. Thomas, J. Hovdenes, A. Apostolidis, C. Huber and P. O. J. Hall, Limnol. Oceanogr.: Methods, 2014, 12, 63–73 CrossRef.
- C. Staudinger, M. Strobl, J. P. Fischer, R. Thar, T. Mayr, D. Aigner, B. J. Müller, B. Müller, P. Lehner, G. Mistlberger, E. Fritzsche, J. Ehgartner, P. W. Zach, J. S. Clarke, F. Geißler, A. Mutzberg, J. D. Müller, E. P. Achterberg, S. M. Borisov and I. Kilmant, Limnol. Oceanogr.: Methods, 2018, 16, 459–473 CrossRef CAS.
- M. Rosenberg, B. W. Laursen, C. G. Frankær and T. J. Sørensen, Adv. Mater. Technol., 2018, 3, 1800205 CrossRef.
- M. Cuartero, Sens. Actuators, B, 2021, 334, 129635 CrossRef CAS.
- M. L. Tercier, J. Buffle, A. Zirino and R. Rd. Vitre, Anal. Chim. Acta, 1990, 237, 429–437 CrossRef CAS.
- S. Chaiyo, E. Mehmeti, K. Zagar, W. Siangproh, O. Chailapakul and K. Kalcher, Anal. Chim. Acta, 2016, 918, 26–34 CrossRef CAS PubMed.
- X. Zhang, Y. Zhang, D. Ding, J. Zhao, J. Liu, W. Yang and K. Qu, Microchem. J., 2016, 126, 280–286 CrossRef CAS.
- S. Ma, H. Wei, D. W. Pan, F. Pan, C. C. Wang and Q. Kang, J. Electrochem. Soc., 2020, 167, 046519 CrossRef CAS.
- C. B. Jiang, Y. H. He and Y. Liu, Analyst, 2020, 145, 5400–5413 RSC.
- Y. Zhang, J. T. Nie, H. Y. Wei, H. T. Xu, Q. Wang, Y. Q. Cong, J. Q. Tao, Y. Zhang, L. L. Chu, Y. Zhou and X. Y. Wu, Sens. Actuators, B, 2018, 258, 1107–1116 CrossRef CAS.
- S. Sateanchok, N. Pankratova, M. Cuartero, T. Cherubini, K. Grudpan and E. Bakker, ACS Sens., 2018, 3, 2455–2462 CrossRef CAS PubMed.
- A. V. Kolliopoulos, D. K. Kampouris and C. E. Banks, Anal. Chem., 2015, 87, 4269–4274 CrossRef CAS PubMed.
- D. Talarico, F. Arduini, A. Amine, D. Moscone and G. Palleschi, Talanta, 2015, 141, 267–272 CrossRef CAS PubMed.
- S. Cinti, D. Talarico, G. Palleschi, D. Moscone and F. Arduini, Anal. Chim. Acta, 2016, 919, 78–84 CrossRef CAS PubMed.
- M. M. Grand, G. S. Clinton-Bailey, A. D. Beaton, A. M. Schaap, T. H. Johengen, M. N. Tamburri, D. P. Connelly, M. C. Mowlem and E. P. Achterberg, Front. Mar. Sci., 2017, 4, 255 CrossRef.
- L. Li, J. Tang, H. Liu, P. Du, Y. Zhang and Y. Qian, SSRN, 2022, 1–19 Search PubMed.
- European Marine Board, Sustaining in situ Ocean Observations in the Age of the Digital Ocean, Zenodo, 2021 Search PubMed.
- A. R. Sastri, J. R. Christian, E. P. Achterberg, D. Atamanchuk, J. J. H. Buck, P. Bresnahan, P. J. Duke, W. Evans, S. F. Gonski, B. Johnson, S. K. Juniper, S. Mihaly, L. A. Miller, M. Morley, D. Murphy, S.-i. Nakaoka, T. Ono, G. Parker, K. Simpson and T. Tsunoda, Front. Mar. Sci., 2019, 6, 653 CrossRef.
- T. R. Martz, K. L. Daly, R. H. Byrne, J. H. Stillman and D. Turk, Oceanography, 2015, 28, 40–47 CrossRef.
- J. Buffle, K. J. Wilkinson, M.-L. Tercier and N. Parthasarathy, Ann. Chim., 1997, 87, 67–83 CAS.
- N. P. Shetti, D. S. Nayak, K. R. Reddy and T. M. Aminabhvi, in Micro and Nano Technologies: Graphene-Clay-Based Hybrid Nanostructures for Electrochemical Sensors and Biosensors, ed. A. Pandikumar and P. Rameshkumar, Elsevier, 2019, pp. 235–274 Search PubMed.
- A. Hulanicki, S. Glab and F. Ingman, Pure Appl. Chem., 1991, 63, 1247–1250 CrossRef.
- P. K. Sekhar, E. L. Brosha, R. Mukundan and F. Garzon, Electrochem. Soc. Interface, 2010, 19, 35–40 CrossRef CAS.
- F. Rouessac and A. Rouessac, Chemical Analysis: Modern Instrumentation Methods and Techniques, John Wiley & Sons, Chichester, 2007, pp. 453–463 Search PubMed.
- J. Bobacka, A. Ivaska and A. Lewenstam, Chem. Rev., 2008, 108, 329–351 CrossRef CAS PubMed.
- J. Koryta, in Ion-Selective Microelectrodes and Their Use in Excitable Tissues, ed. E. Syková, P. Hník and L. Vyklický, Springer, Boston, MA, 1981, pp. 3–11 Search PubMed.
- J. J. Pedrotti, L. Angnes and I. G. R. Gutz, Electroanalysis, 1996, 8, 673–675 CrossRef.
- A. Yamada and M. Suzuki, 2017 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 2017, pp. 1–3 Search PubMed.
- M. P. S. Mousavi and P. Bühlmann, Anal. Chem., 2013, 85, 8895–8901 CrossRef CAS PubMed.
- J. A. Caram, J. Appl. Electrochem., 2005, 35, 1039–1039 CrossRef CAS.
- D. C. Harris, Quantitative Chemical Analysis, W. H. Freeman and Company, New York, 2007, pp. 270–288 Search PubMed.
- D. A. Skoog, D. M. West, F. J. Holler and S. R. Crouch, in Fundamentals of Analytical Chemistry, Cengage, Boston, 2022, pp. 505–534 Search PubMed.
- P. Bühlmann and L. D. Chen, in Supramolecular Chemistry: From Molecules to Nanomaterials, ed. P. A. Gale and J. W. Steed, John Wiley & Sons, 2012, pp. 1–41 Search PubMed.
- J. R. Black, in Encyclopedia of Geochemistry, ed. W. White, Cham Springer, 2016, pp. 1–3 Search PubMed.
- Y. Soda and E. Bakker, Sens. Actuators, B, 2021, 346, 130527 CrossRef CAS.
- B. N. Ciribelli, F. Colmati and E. C. de Souza, Int. J. Innov. Educ. Res., 2020, 8, 670–683 CrossRef.
- C. Zhang, Y. He, J. Wu, M. Ai, W. Cai, Y. Ye, C. Tao, P. Zhang and Q. Jin, Chemosensors, 2021, 9, 236 CrossRef CAS.
- E. Zdrachek and E. Bakker, Anal. Chem., 2020, 92, 2926–2930 CrossRef CAS PubMed.
- W. Gao, X. Xie and E. Bakker, ACS Sens., 2020, 5, 313–318 CrossRef CAS PubMed.
- W. Qin, T. Zwickl and E. Pretsch, Anal. Chem., 2000, 72, 3236–3240 CrossRef CAS PubMed.
- N. M. Ivanova, M. B. Levin and K. N. Mikhelson, Russ. Chem. Bull., 2012, 61, 926–936 CrossRef CAS.
- E. Bakker and E. Pretsch, Anal. Chem., 2002, 74, 420A–426A CrossRef CAS PubMed.
- M. Püntener, T. Vigassy, E. Baier, A. Ceresa and E. Pretsch, Anal. Chim. Acta, 2004, 503, 187–194 CrossRef.
- A. Ceresa, T. Sokalski and E. Pretsch, J. Electroanal. Chem., 2001, 501, 70–76 CrossRef CAS.
- Q. Ye and M. E. Meyerhoff, Anal. Chem., 2001, 73, 332–336 CrossRef CAS PubMed.
- A. Zirino, R. De Marco, I. Rivera and B. Pejcic, Electroanalysis, 2002, 14, 493–498 CrossRef CAS.
- T. Vigassy, R. E. Gyurcsányi and E. Pretsch, Electroanalysis, 2003, 15, 1270–1275 CrossRef CAS.
- M. Cuartero and G. A. Crespo, Curr. Opin. Electrochem., 2018, 10, 98–106 CrossRef CAS.
- J. Bobacka, M. Maj-Zurawska and A. Lewenstam, Biosens. Bioelectron., 2003, 18, 245–253 CrossRef CAS PubMed.
- W. J. Scott, E. Chapoteau and A. Kumar, Clin. Chem., 1986, 32, 137–141 CrossRef CAS.
- M. Pleniceany, M. Isvoranu and C. Spinu, J. Serb. Chem. Soc., 2005, 70, 269–276 CrossRef CAS.
- D. Vlascici, S. Pruneanu, L. Olenic, F. Pogacean, V. Ostafe, V. Chiriac, E. M. Pica, L. C. Bolundut, L. Nica and E. Fagadar-Cosma, Sensors, 2010, 10, 8850–8864 CrossRef CAS PubMed.
- A. W. Weber, G. D. O'Neil and S. P. Kounaves, Anal. Chem., 2017, 89, 4803–4807 CrossRef CAS PubMed.
- U.S. Integrated Ocean Observing System, Manual for Real-Time Quality Control of pH Data Observations Version 1.0: A Guide to Quality Control and Quality of pH Data Observations, 2019 Search PubMed.
- U.S. Integrated Ocean Observing System, Manual for Real-Time Quality Control of In-situ Temperature and Salinity Data Version 2.1: A Guide to Quality Control and Quality Assurance of In-situ Temperature and Salinity Observations, 2020 Search PubMed.
- L. Coppola, M. Ntoumas, R. Bozzano, M. Bensi, S. E. Hartman, M. Charcos Llorens, J. Craig, J.-F. Rolin, G. Giovanetti, D. Cano, J. Karstensen, A. Cianca, D. Toma, C. Stasch, S. Pensieri, V. Cardin, A. Tengberg, G. Petihakis and L. Cristini, Handbook of best practices for open ocean fixed observatories, European Commission, 2016 Search PubMed.
- S. Lauvset, K. Currie, N. Metzl, S.-i. Nakaoka, D. Bakker, K. Sullivan, A. Sutton, K. O'Brien and A. Olsen, SOCAT Quality Control Cookbook for SOCAT version 7, https://repository.oceanbestpractices.org/bitstream/handle/11329/1755/2018_SOCAT_QC_Cookbook_final_with-v2021-contact-details.pdf?sequence=1&isAllowed=y, (accessed 13 January 2023).
- C. Han, W.-J. Cai, Y. Wang and Y. Ye, J. Oceanogr., 2014, 70, 425–433 CrossRef CAS.
- W. M. Wise, U.S. Pat., 3723281, 1973 Search PubMed.
- H. B. Herman and G. A. Rechnitz, Anal. Chim. Acta, 1975, 76, 155–164 CrossRef CAS.
- W. Simon, E. Pretsch, W. E. Morf, D. Ammann, U. Oesch and O. Dinten, Analyst, 1984, 109, 207–209 RSC.
- J. J. Jasielec, T. Sokalski, R. Filipek and A. Lewenstam, Anal. Chem., 2015, 87, 8665–8672 CrossRef CAS PubMed.
- S. Makarychev-Mikhailov, A. Legin, J. Mortensen, S. Levitchev and Y. Vlasov, Analyst, 2004, 129, 213–218 RSC.
- E. A. Materova, T. Y. Bart, E. V. Soboleva, V. S. Karavan and L. O. Ishutkina, Electrokhimiya, 1981, 17, 499 CAS.
- T. Katsu and N. Hanada, Anal. Chim. Acta, 1996, 321, 21–25 CrossRef CAS.
- T. Katsu and Y. Mori, Talanta, 1996, 43, 755–759 CrossRef CAS PubMed.
- K. Watanabe, O. Noguchi, K. Okada and T. Katsu, Anal. Sci., 1997, 13, 209–212 CrossRef CAS.
- S. Sasaki, A. Hashizume, D. Citterio, E. Fujii and K. Suzuki, Angew. Chem., Int. Ed., 2002, 41, 3005–3007 CrossRef CAS PubMed.
- A. L. Smirnova, V. N. Tarasevitch and E. M. Rakhman'ko, Sens. Actuators, B, 1994, 19, 392–395 CrossRef CAS.
- V. L. Khitrova, N. B. Ivanenko, V. S. Karavan, E. M. Rakhman'ko and A. L. Smirnova, Russ. J. Appl. Chem., 1997, 70, 962 Search PubMed.
- K. N. Mikhelson, A. L. Smirnova and N. A. Malysh, Electrokhimiya, 1994, 30, 1109 CAS.
- W. J. Scott, E. Chapoteau and A. Kumar, Clin. Chem., 1986, 32, 137–141 CrossRef CAS.
- E. M. Rakhman'ko, A. L. Gulevich, A. P. Podterob and P. V. Senin, Zh. Anal. Khim., 1998, 53, 1–4 Search PubMed.
- M. E. Meyerhoff, E. Pretsch, D. H. Welti and W. Simon, Anal. Chem., 1987, 59, 144–150 CrossRef CAS.
- S. Makarychev-Mikhailov, O. Goryacheva, J. Mortensen, A. Legin, S. Levitchev and Y. Vlasov, Electroanalysis, 2003, 15, 1291–1296 CrossRef CAS.
- C. Behringer, B. Lehmann, J.-P. Haug, K. Seiler, W. E. Morf, K. Hartman and W. Simon, Anal. Chim. Acta, 1990, 233, 41–47 CrossRef CAS.
- T. Sokalski, D. Paradowski, J. Ostaszewska, M. Maj-Zurawska, J. Mieczkowski, A. Lewenstam and A. Hulanicki, Analyst, 1996, 121, 133–138 RSC.
- M. Maj-Zurawska, T. Sokalski, J. Ostaszewska, D. Paradowski, J. Mieczkowski, Z. Charnocki, A. Lewenstam and A. Hulanicki, Talanta, 1997, 44, 1641–1647 CrossRef CAS PubMed.
- A. K. Jain, V. K. Gupta and J. R. Raisoni, Electrochim. Acta, 2006, 52, 951–957 CrossRef CAS.
- V. Thimaradka, S. Pangannaya, M. Mohan and D. R. Trivedi, Spectrochim. Acta A Mol. Biomol. Spectrosc., 2017, 193, 330–337 CrossRef PubMed.
- A. Singh, M. Mohan and D. R. Trivedi, ChemistrySelect, 2019, 4, 14120–14131 CrossRef CAS.
- H. J. Pyun, J. Chu, Y. M. Jun and D. J. Kim, Bull. Korean Chem. Soc., 1999, 20, 112–116 CAS.
- H. J. Pyun, J. Chu, W. J. Yoon, Y. M. Jun and D. J. Kim, Bull. Korean Chem. Soc., 1999, 20, 179–186 CAS.
- H. J. Lee, I. J. Yoon, C. L. Yoo, H. J. Pyun, G. S. Cha and H. Nam, Anal. Chem., 2000, 72, 4694–4699 CrossRef CAS PubMed.
- J. H. Shim, I. S. Jeong, M. H. Lee, H. P. Hong, J. H. On, K. S. Kim, H. S. Kim, B. H. Kim, G. S. Cha and H. Nam, Talanta, 2004, 63, 61–71 CrossRef CAS PubMed.
- F. Song, J. Ha, B. Park, T. H. Kwak, I. T. Kim, H. Nam and G. S. Cha, Talanta, 2002, 57, 263–270 CrossRef CAS PubMed.
- D. de Beer, A. Bissett, R. de Wit, H. Jonkers, S. Köhler-Rink, H. Nam, B. H. Kim, G. Eickert and M. Grinstain, Limnol. Oceanogr.: Methods, 2008, 6, 532–541 CrossRef CAS.
- W. J. Cai, Y. Ma, B. M. Hopkinson, A. G. Grottoli, M. E. Warner, Q. Ding, X. Hu, X. Yuan, V. Schoepf, H. Xu, C. Han, T. F. Melman, K. D. Hoadley, D. T. Pettay, Y. Matsui, J. H. Baumann, S. Levas, Y. Ying and Y. Wang, Nat. Commun., 2016, 7, 11144 CrossRef CAS PubMed.
- Z. Jarolímová, J. Bosson, G. M. Labrador, J. Lacour and E. Bakker, Electroanalysis, 2018, 30, 1378–1385 CrossRef.
- L. D. Chen, D. Mandal, G. Pozzi, J. A. Gladysz and P. Bühlmann, J. Am. Chem. Soc., 2011, 133, 20869–20877 CrossRef CAS PubMed.
- K. N. Mikhelson and M. A. Peshkova, Russ. Chem. Rev., 2015, 84, 555–578 CrossRef.
- R. A. Durst, in Ion-Selective Electrodes in Analytical Chemistry, ed. H. Freiser, SpringerNew York, NY, 1978, pp. 311–338 Search PubMed.
- B. P. Nikol'skii and E. A. Materova, Ionoselektivnye Elektrody, Khimiya, Leningrad, 1980 Search PubMed.
- A. Kisiel, E. Woźnica, M. Wojciechowski, E. Bulska, K. Maksymiuk and A. Michalska, Sens. Actuators, B, 2015, 207, 995–1003 CrossRef CAS.
- G. J. Moody, R. B. Oke and J. D. R. Thomas, Analyst, 1970, 95, 910–918 RSC.
- N. Vladimirova, V. Polukeev, J. Ashina, V. Babain, A. Legin and D. Kirsanov, Chemosensors, 2022, 10, 43 CrossRef CAS.
- J. Pick, K. Tóth, M. Vasàk, E. Pungor and W. Simon, Anal. Chim. Acta, 1973, 64, 477–480 CrossRef CAS.
- U. Fiedler and J. Růžička, Anal. Chim. Acta, 1973, 67, 179–193 CrossRef CAS.
- F. Faridbod, M. R. Ganjali, R. Dinarvand and P. Norouzi, Afr. J. Biotechnol., 2007, 6, 2960–2987 CrossRef CAS.
- P. Zhao and W.-J. Cai, Anal. Chim. Acta, 1999, 395, 285–291 CrossRef CAS.
- J. H. Shin, D. S. Sakong, H. Y. Nam and G. S. Cha, Anal. Chem., 1996, 68, 221–225 CrossRef CAS PubMed.
- S. C. Ma, N. A. Chaniotakis and M. E. Meyerhoff, Anal. Chem., 1988, 60, 2293–2299 CrossRef CAS PubMed.
- Z. Pingsan and W.-J. Cai, Anal. Chem., 1997, 69, 5052–5058 CrossRef.
- Y. Qin and E. Bakker, Anal. Chem., 2001, 73, 4262–4267 CrossRef CAS PubMed.
- S. Dabrowska, J. Migdalski and A. Lewenstam, Electroanalysis, 2017, 29, 140–145 CrossRef CAS.
- B. H. Kim, C. S. Lee, J. H. Shim, H. P. Hong, G. S. Cha, Y. M. Jun and H. Nam, Talanta, 2003, 61, 393–401 CrossRef CAS PubMed.
- X. Dong, D. Lu, T. A. L. Harris and I. C. Escobar, Membranes, 2021, 11, 309 CrossRef CAS PubMed.
- U. Oesch and W. Simon, Anal. Chem., 1980, 52, 692–700 CrossRef CAS.
- O. H. LeBlanc Jr. and W. T. Grubb, Anal. Chem., 1976, 48, 1658–1660 CrossRef.
- R. Eugster, P. M. Gehrig, W. E. Morf, U. E. Spichiger and W. Simon, Anal. Chem., 1991, 63, 2285–2289 CrossRef CAS.
- E. Bakker, P. Bühlmann and E. Pretsch, Chem. Rev., 1997, 97, 3083–3132 CrossRef CAS PubMed.
- K. N. Mikhelson, Ion-Selective Electrodes (Lecture Notes in Chemistry), Springer, Heidelberg, New York, Dordrecht, London, 2013 Search PubMed.
- U. Shaller, E. Bakker, U. E. Spichiger and E. Pretsch, Anal. Chem., 1994, 66, 391–398 CrossRef.
- P. Bühlmann, S. Amemiya, S. Yajima and Y. Umezawa, Anal. Chem., 1998, 70, 4291–4303 CrossRef.
- K. N. Mikhelson and A. Lewenstam, Sens. Actuators, B, 1998, 48, 344–350 CrossRef CAS.
- K. N. Mikhelson and A. Lewenstam, Anal. Chem., 2000, 72, 4965–4972 CrossRef CAS PubMed.
- S. E. Didina, O. P. Chogin, K. N. Mikhelson and A. Levenstam, Vestn. S.-Peterb. Univ., 1999, 4, 39 Search PubMed.
- D. Ammann, Ion-Selective Microelectrodes: Principles, Design and Application, Springer, Berlin, Heidelberg, New York and Tokyo, 1986 Search PubMed.
- E. Linder and R. E. Gyurcsányi, J. Solid State Electrochem., 2009, 13, 51–68 CrossRef.
- R. W. Baker, Membrane Technology and Applications, John Wiley & Sons, Inc., New York, 2012 Search PubMed.
- J. Ren and R. Wang, in Membrane and Desalination Technologies: Handbook of Environmental Engineering, ed. L. K. Wang, J. P. Chen, Y. T. Hung and N. K. Shammas, Humana Press, Totowa, NJ, 2011, pp. 47–100 Search PubMed.
- C. Das and K. A. Gebru, Polymeric Membrane Synthesis, Modification, and Applications: Electro-Spun and Phase Inverted Membranes, CRC Press, Boca Raton, 2018 Search PubMed.
- T. Sokalski, M. Maj-Zurawska and A. Hulanicki, Microchim. Acta, 1991, 1, 285–291 CrossRef CAS.
- T. Sokalski, A. Ceresa, T. Zwickl and E. Pretsch, J. Am. Chem. Soc., 1997, 119, 11347–11348 CrossRef CAS.
- R. E. Gyurcsanyi, E. Pergel, R. Nagy, I. Kapui, B. T. T. Lan, K. Toth, I. Bitter and E. Lindner, Anal. Chem., 2001, 73, 2104–2111 CrossRef CAS PubMed.
- S. Amemiya, P. Bühlmann and Y. Umezawa, Anal. Chem., 1998, 70, 445–454 CrossRef CAS PubMed.
- P. Bühlmann and Y. Umezawa, Electroanalysis, 1999, 11, 687–693 CrossRef.
- E. Steinle, S. Amemiya, P. Bühlmann and M. Meyerhoff, Anal. Chem., 2000, 72, 5766–5773 CrossRef CAS PubMed.
- S. Amemiya, P. Bühlmann and K. Odashima, Anal. Chem., 2003, 75, 3329–3339 CrossRef CAS PubMed.
- S. S. Koseoglu, C.-Z. Lai, C. Ferguson and P. Bühlmann, Electroanalysis, 2008, 20, 331–339 CrossRef CAS.
- M. Miyake, L. D. Chen, G. Pozzi and P. Bühlmann, Anal. Chem., 2012, 84, 1104–1111 CrossRef CAS PubMed.
- T. Blaz, J. Migdalski and A. Lewenstam, Analyst, 2005, 130, 637–643 RSC.
- International Organization for Standardization, Capability of Detection, Genève, Switzerland, 2000 Search PubMed.
- D. MacDougall and W. B. Crummett, Anal. Chem., 1980, 52, 2242–2249 CrossRef CAS.
- T. Sokalski, A. Ceresa, M. Fibbioli, T. Zwickl, E. Bakker and E. Pretsch, Anal. Chem., 1999, 71, 1210–1214 CrossRef CAS.
- D. Yuan, A. H. C. Anthis, M. G. Afshar, N. Pankratova, M. Cuartero, G. A. Crespo and E. Bakker, Anal. Chem., 2015, 87, 8640–8645 CrossRef CAS PubMed.
- J. Vessman, R. I. Stefan, J. F. van Staden, K. Danzer, W. Linder, D. T. Burns, A. Fajgeji and H. Müller, Pure Appl. Chem., 2001, 73, 1381–1386 CrossRef CAS.
- B. Zang, H. Tang, Z. Zhao and S. Song, ACS Omega, 2020, 5, 6229–6239 CrossRef PubMed.
- Y. Umezawa, P. Bühlmann, K. Umezawa, K. Tohda and S. Amemiya, Pure Appl. Chem., 2000, 72, 1851–2082 CrossRef CAS.
- R. P. Buck and E. Lindner, Pure Appl. Chem., 1994, 66, 2527–2536 CAS.
- V. V. Egorov, E. A. Zdrachek and V. A. Nazarov, Anal. Chem., 2014, 86, 3693–3696 CrossRef CAS PubMed.
- K. Hiiro, S.-I. Wakida and M. Yamane, Anal. Sci., 1988, 4, 149–151 CrossRef CAS.
- A. Merikhi, P. Berg, V. Meyer and M. Huettel, Limnol. Oceanogr.: Methods, 2018, 16, 475–483 CrossRef.
- C. Macca, Anal. Chim. Acta, 2004, 512, 183–190 CrossRef CAS.
- Z. Sun, Q. Ma, Y. Wang and Y. Pan, J. Electrochem. Soc., 2020, 167, 047501 CrossRef CAS.
- R. Athavale, I. Kokorite, C. Dinkel, E. Bakker, B. Wehrli, G. A. Crespo and A. Brand, Anal. Chem., 2015, 87, 11990–11997 CrossRef CAS PubMed.
- R. Athavale, C. Dinkel, B. Wehrli, E. Bakker, G. A. Crespo and A. Brand, Environ. Sci. Technol. Lett., 2017, 4, 286–291 CrossRef CAS.
- J. Su, Y. Liu, Y. Song, L. Huang, W. Guo, X. Cao, Y. Dou, L. Chang, G. Li, Q. Hu and R. Ye, SmartMat, 2022, 3, 35–53 CrossRef CAS.
- Z. Sun, H. Yin, K. Liu, S. Cheng, G. K. Li, S. Kawi, H. Zhao, G. Jia and Z. Yin, SmartMat, 2022, 3, 68–83 CrossRef CAS.
- Z. Gao, M. Hou, Y. Shi, L. Li, Q. Sun, S. Yang, Z. Jiang, W. Yeng, Z. Zheng and W. Hu, Chem. Sci., 2023, 14, 6860–6866 RSC.
- M. Hou, Y. x. Shi, J. j. Li and Z. Gao, Chem. – Asian J., 2022, 17, e202200624 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |